1 Introduction

In the ecological sciences, the dynamical behavior of predator and its prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance [1]. Since Lotka Volterra’s pioneering work on population dynamics, various predator–prey models have been presented and studied widely by both applied mathematicians and ecologists [2–9]. There are a number of different functional responses used to model predator–prey interaction, such as Beddington–DeAngelis type, Hassell–Varley type, Holling–Tanner type and Holling II, III, IV types. The general predator–prey model with Holling type II response has the following form [7, 8]:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t)=rx\left( 1-\frac{x}{K}\right) -\frac{axy}{b+x},\\ \dot{y}(t)=-h(y)+\frac{mxy}{b+x}, \end{array} \right. \end{aligned}$$
(1)

where x and y are the population densities of prey and predator, respectively; r is the birth rate, K is the carrying capacity, and a is the maximum uptake rate of the prey; b is the prey density at which predator has the maximum kill rate; m is the birth rate and function h(y) reflects the mortality rate of the predator. Mortality rate of the predator is also essential in population dynamics. Note that when h(y) is linear, model (1) is the classic Holling type II predator–prey model. According to [7], taking

$$\begin{aligned} u= & {} \frac{x}{K},\quad v=ym,\quad \tilde{t}=rt,\quad s=\frac{a}{rmK}, \\ \alpha= & {} \frac{m}{r},\quad \beta =\frac{b}{K}, \end{aligned}$$

model (1) (after dropping the tildes) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{u}(t)=u\left( 1-u-\frac{sv}{\beta +u}\right) ,\\ \dot{v}(t)=\alpha \left( -h(v)+\frac{uv}{\beta +u}\right) , \end{array} \right. \end{aligned}$$
(2)

where \(h(v)=\frac{\gamma v^2}{1+\gamma v}\) for hyperbolic mortality, which dominates the mortality when population density is large [10]. Model (2) has always three equilibria, which consist of two boundary equilibria (0, 0) and (1, 0), and a nontrivial stationary state \((u^*, v^*)\) where \(u^*=\frac{(\beta \gamma -s-\beta ^2\gamma )+\sqrt{4\beta ^3\gamma ^2+(\beta \gamma -s-\beta ^2\gamma )^2}}{2\beta \gamma }\), \(v^*=\frac{u^*}{\beta \gamma }\). In this case of hyperbolic mortality, \((u^*, v^*)\) always exists, and it is locally asymptotically stable if \(0<sv^*-(\beta +u^*)^2<\alpha \beta \).

However, in the real life situations, population systems are always affected by environmental noise. May [11] pointed out that due to continuous fluctuation in the environment, the birth rates, death rates, carrying capacity, competition coefficients and all other parameters involved with the model exhibit random fluctuation to a great lesser extent. Up to now, stochastic population systems have been studied by many authors [12–20]. In this paper, we assume that environmental white noises are directly proportional to u(t) and v(t). This approach has been used by many literature, see, e.g., [12, 21]. In this way, predator–prey model with hyperbolic mortality in random environments will be deduced to the form:

$$\begin{aligned} \left\{ \begin{array}{l} \hbox {d} u(t)=u\left( 1-u-\frac{sv}{\beta +u}\right) \mathrm{d} t+\sigma _1 u \mathrm{d} B_1(t),\\ \hbox {d} v(t)=\alpha v\left( \frac{u}{\beta +u}-\frac{\gamma v}{1+\gamma v}\right) \mathrm{d} t+\sigma _2v \mathrm{d}B_2(t), \end{array} \right. \end{aligned}$$
(3)

where \(B_1(t)\), \(B_2(t)\) are mutually independent Brownian motions defined on a complete probability space \(({\varOmega }, \mathcal {F}, \{\mathcal {F}_{t}\}_{t\ge 0}, \mathcal {P})\) with a \(\sigma -\)field filtration \(\{\mathcal {F}_{t}\}_{t\ge 0}\) satisfying the usual conditions, and positive constants \(\sigma _1^2\), \(\sigma _2^2\) are intensities of the white noises.

The aim of this paper is to study the dynamical behavior of model (3). In the study of a population dynamics, global asymptotic stability of the positive equilibrium is an important topic. However, stochastic model (3) has no positive equilibrium. Therefore, it is impossible for the solution of model (3) tending to a fixed point. In this paper, we will show that model (3) has an ergodic stationary distribution mainly according to the theory of Has’minskii [22], if the white noises are small. The stationary distribution can be considered as a weak stability. The method adopted here is constructing new Lyapunov functions and rectangular set, which do not depend on the equilibrium \((u^*,v^*)\) of the deterministic model (2). Furthermore, we try to find the critical value between the extinction and persistence of predator population and analyze how the environmental noises affect the population dynamics.

2 Preliminaries

For simplicity, we introduce the following notations.

\(\mathbb {R}_+^2:=\{x=(x_1,x_2)\in \mathbb {R}^2:x_i>0, i=1,2\}\).

\(\langle f\rangle _t=\frac{1}{t}\int _{0}^{t}f(s)d s. \)

If g(t) is a bounded function on \([0,\infty )\), define \(\check{g}=\sup _{t\in [0,\infty )}g(t)\).

Lemma 1

[15] Suppose that \(Z(t)\in C({\varOmega }\times [0,\infty ),\mathbb {R}_+)\).

  1. (I)

    If there are two positive constants T and \(\delta _0\) such that

    $$\begin{aligned} \ln Z(t)\le \delta t-\delta _0\int _{0}^{t}Z(s)d s+\sum _{i=1}^{n}\alpha _i B(t)\ a.s. \end{aligned}$$

    for all \(t>T\), where \(\alpha _i\), \(\delta \) are constants, then

    $$\begin{aligned} \left\{ \begin{array}{ll} \limsup _{t\rightarrow \infty }\langle Z\rangle _t\le \frac{\delta }{\delta _0}\ a.s.,&{}\quad \mathrm {if}\ \delta \ge 0;\\ \lim _{t\rightarrow \infty }Z(t)=0\ a.s.,&{}\quad \mathrm {if}\ \delta < 0.\\ \end{array} \right. \end{aligned}$$
  2. (II)

    If there exist three positive constants T, \(\delta \), \(\delta _0\) such that

    $$\begin{aligned} \ln Z(t)\ge \delta t-\delta _0\int _{0}^{t}Z(s)d s+\sum _{i=1}^{n}\alpha _i B(t)\ a.s. \end{aligned}$$

    for all \(t>T\), then \(\liminf _{t\rightarrow \infty }\langle Z\rangle _t\ge \frac{\delta }{\delta _0}\ a.s..\)

Lemma 2

For any initial value \((u(0),v(0))\in \mathbb {R}_+^2\), there is a unique positive solution (u(t), v(t)) of model (3) on \(t\ge 0\), and the solution will remain in \(\mathbb {R}_+^2\) with probability 1. Moreover, there is a constant K such that

$$\begin{aligned} \mathbb {E}[u(t)]\le K,\ \ \ \mathbb {E}[v(t)]\le K,\ \ t\ge 0. \end{aligned}$$
(4)

Proof

Define a \(C^2\)-function \(V:\mathbb {R}_+^2\rightarrow \mathbb {R}_+\) as follows:

$$\begin{aligned} V(u,v)= & {} \frac{1}{\beta }\left( u-\beta -\beta \ln \frac{u}{\beta }\right) \\&+\,\frac{s}{\alpha \beta }\left( v-\frac{\alpha \beta }{s}-\frac{\alpha \beta }{s}\ln \frac{sv}{\alpha \beta }\right) . \end{aligned}$$

Applying Itô’s formula, we have

$$\begin{aligned} \begin{aligned}&\mathcal {L}V(u(t),v(t))\\&\quad =\frac{1}{\beta }\left( u-u^2-\frac{suv}{\beta +u}\right) -\left( 1-u-\frac{sv}{\beta +u}-\frac{\sigma _1^2}{2}\right) \\&\qquad +\,\frac{s}{\alpha \beta }\left( \frac{\alpha uv}{\beta +u}-\frac{\alpha \gamma v^2}{1+\gamma v}\right) \\&\qquad -\,\left( \frac{\alpha u}{\beta +u} -\frac{\alpha \gamma v}{1+\gamma v}-\frac{\sigma _2^2}{2}\right) \\&\quad \le -\frac{1}{\beta }u^2+\frac{\beta +1}{\beta }u +\,\frac{s}{\beta }v-\frac{s}{\beta }\frac{\gamma v^2}{1+\gamma v}+\alpha -1 \\&\qquad +\,\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}\\&\qquad = -\frac{1}{\beta }u^2+\frac{\beta +1}{\beta }u+\frac{s}{\beta }\frac{v}{1+\gamma v} \\&\qquad +\,\alpha -1+\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}\\&\quad \le -\frac{1}{\beta }u^2+\frac{\beta +1}{\beta }u +\,\frac{s}{\beta \gamma }+\alpha -1+\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}\\&\quad \le K_0, \end{aligned} \end{aligned}$$

where \(K_0\) is a positive constant. Following the proof of the remainder of Theorem 2.1 in [23], we obtain that model (3) admits a unique global positive solution \((u(t),v(t))\in \mathbb {R}_+^2\) for any initial value \((u(0),v(0))\in \mathbb {R}_+^2\).

Now we are in the position to prove (4). Define a Lyapunov function

$$\begin{aligned} V(u,v)=u+\frac{s}{\alpha }v. \end{aligned}$$

Applying Itô’s formula, we obtain

$$\begin{aligned}&\mathbb {E}\left( e^{\frac{\alpha }{2}t}V(u,v)\right) \\&\quad =V(u(0),v(0)) \\&\qquad +\,\mathbb {E}\int _{0}^{t}e^{\frac{\alpha }{2}s}\left[ \frac{\alpha }{2}V(u(s),v(s))+\mathcal {L}V(u(s),v(s))\right] d s, \end{aligned}$$

where for \((u,v)\in \mathbb {R}_+^2\) and \(t\ge 0\),

$$\begin{aligned} \mathcal {L}V(u,v):=u-u^2-\frac{\gamma sv^2}{1+\gamma v}. \end{aligned}$$

Then we can deduce that there exists a constant \(K_1>0\) such that

$$\begin{aligned} \begin{aligned}&\frac{\alpha }{2}V(u,v)+\mathcal {L}V(u,v)\\&\quad =\frac{\alpha }{2}\left( u+\frac{s}{\alpha }v\right) +u-u^2 -\frac{\gamma sv^2}{1+\gamma v}\\&\quad \le -u^2+\frac{\alpha +2}{2}u+\frac{sv}{2(1+\gamma v)}\\&\quad \le K_1. \end{aligned} \end{aligned}$$

Hence

$$\begin{aligned}&\mathbb {E}\left( e^{\frac{\alpha }{2}t}V(u,v)\right) \le V(u(0),v(0))\\&\quad +\int _{0}^{t}K_1e^{\frac{\alpha }{2}s}d s=V(u(0),v(0))+\frac{2K_1}{\alpha }\left( e^{\frac{\alpha }{2}t}-1\right) , \end{aligned}$$

which yields the desired assertion (4). \(\square \)

3 Discussion on the persistence and extinction

In this section, we will try to give the critical value which determines the extinction and persistence of stochastic predator–prey model (3) with hyperbolic mortality. To this end, we quote some concepts and lemmas.

Definition 1

[15]

  1. (1)

    If \(\lim _{t\rightarrow \infty }v(t)=0\) a.s., then species v(t) is said to be extinctive almost surely.

  2. (2)

    If \(\liminf _{t\rightarrow \infty }\langle v\rangle _t>0\) a.s., then model (3) is said to be persistent in the mean.

Lemma 3

[16] Consider the following one-dimensional stochastic system

$$\begin{aligned} d X(t)=X(t)(1-X(t))d t+\sigma _1X(t)d B_1(t), \end{aligned}$$
(5)

with \(X(0)=u(0)\).

  • If \(1-\frac{\sigma _1^2}{2}<0\), then \(\lim _{t\rightarrow \infty }X(t)=0\), a.s.

  • If \(1-\frac{\sigma _1^2}{2}>0\), then

    $$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}X(s)d s=1-\frac{\sigma _1^2}{2},\ \ a.s. \end{aligned}$$
    (6)

    Furthermore, if \(1-\frac{\sigma _1^2}{2}>0\), system (5) has a unique ergodic stationary distribution \(\nu (\cdot )\) with stationary density \(\mu (x)=Cx^{\frac{2-\sigma _1^2}{\sigma _1^2}-1}e^{-\frac{2}{\sigma _1^2}x}\), where \(C=(2/\sigma _1^2)^{(2-\sigma _1^2)/\sigma _1^2}/{\varGamma }((2-\sigma _1^2)/\sigma _1^2)\), and

    $$\begin{aligned}&\mathbb {P}\left\{ \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}f(X(s))\mathrm{d} s=\int _{\mathbb {R_+}}f(x)\mu (x)\mathrm{d}x\right\} \\&\quad =1, \end{aligned}$$

    where f is a function integrable with respect to the measure \(\nu \).

Remark 1

From stochastic comparison theory it follows that \(u(t)\le X(t), a.s.\).

Theorem 1

Assume that \(1-\frac{\sigma _1^2}{2}>0\). Let \(\lambda _1:=-\frac{\sigma _2^2}{2}+\alpha \int _{0}^{\infty }\frac{x}{\beta +x}\mu (x)d x\) and u(t), v(t) be a positive solution of model (3) with initial value \((u(0),v(0))\in \mathbb {R}_+^2\).

  1. (i)

    If \(\lambda _1<0\), then the predator populations go to extinction a.s..

  2. (ii)

    If \(\lambda _1>0\), then model (3) will be persistent in the mean.

Proof

(i). An application of Itô’s formula to the second equation of (3) shows that

$$\begin{aligned} \begin{aligned} d \ln v(t)&=\left( \frac{\alpha u(t)}{\beta +u(t)}-\frac{\sigma _2^2}{2}-\frac{\alpha \gamma v(t)}{1+\gamma v(t)}\right) d t\\&\quad +\sigma _2d B_2(t)\\&\le \left( \frac{\alpha X(t)}{\beta +X(t)}-\frac{\sigma _2^2}{2}\right) d t+\sigma _2d B_2(t). \end{aligned} \end{aligned}$$

Integrating above inequality from 0 to t and dividing t on both sides, we get

$$\begin{aligned}&\frac{\ln v(t)-\ln v(0)}{t}\le -\frac{\sigma _2^2}{2}+\alpha \frac{1}{t}\int _{0}^{t}\frac{X(r)}{\beta +X(r)}\mathrm{d} r\nonumber \\&\quad +\,\frac{M_2(t)}{t}, \end{aligned}$$
(7)

where \(M_2(t)=\int _{0}^{t}\sigma _2\mathrm{d}B_2(t)\) is a real-valued continuous local martingale. By strong law of large numbers [24], we have \(\lim _{t\rightarrow \infty }\frac{M_2(t)}{t}=0 \ a.s.\). Taking the superior limit on both sides of inequality (7) and then using Lemma 3 we obtain

$$\begin{aligned} \begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln v(t)}{t}&\le -\frac{\sigma _2^2}{2}+\limsup _{t\rightarrow \infty }\alpha \frac{1}{t}\int _{0}^{t}\frac{X(r)}{\beta +X(r)}\mathrm{d} r\\&\le -\frac{\sigma _2^2}{2}+\alpha \int _{0}^{\infty }\frac{x}{\beta +x}\mu (x)\mathrm{d} x \\&=:\lambda _1. \end{aligned} \end{aligned}$$

Obviously, the predator v(t) goes to extinction when \(\lambda _1<0\).

(ii). Applying Itô’s formula to the first equation of (3) and (5), respectively, we have

$$\begin{aligned} \begin{aligned}&\frac{\ln u(t)-\ln u(0)}{t}=\frac{1}{t}\int _{0}^{t}\left( 1-\frac{\sigma _1^2}{2}-u(r)\right) \mathrm{d} r \\&\quad -\frac{1}{t}\int _{0}^{t}\frac{sv(r)}{\beta +u(r)}\mathrm{d} B(r)+\frac{M_1(t)}{t}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned}&\frac{\ln X(t)-\ln X(0)}{t}=\frac{1}{t}\int _{0}^{t}\\&\quad \left( 1-\frac{\sigma _1^2}{2}-X(r)\right) \mathrm{d} r+\frac{M_1(t)}{t}, \end{aligned}$$

where \(M_1(t)=\int _{0}^{t}\sigma _1\mathrm{d} B_1(r)\) also has the property \(\lim _{t\rightarrow \infty }\frac{M_1(t)}{t}=0\) a.s. From the above two equations it follows that

$$\begin{aligned} \begin{aligned}&0\ge \frac{\ln u(t)-\ln X(t)}{t}\\&\quad =-\frac{1}{t}\int _{0}^{t}(u(r)-X(r))\mathrm{d} r -\,\frac{1}{t}\int _{0}^{t}\frac{sv(r)}{\beta +u(r)}\mathrm{d} r\\&\quad \ge -\frac{1}{t}\int _{0}^{t}(u(r)-X(r))\mathrm{d} r -\,\frac{s}{\beta t}\int _{0}^{t}v(r)\mathrm{d} r, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \frac{1}{t}\int _{0}^{t}(X(r)-u(r))\mathrm{d} r\le \frac{s}{\beta t}\int _{0}^{t}v(r)\mathrm{d} r. \end{aligned}$$
(8)

Applying Itô’s formula to the second equation of (3) again we have

$$\begin{aligned} \begin{aligned}&d \ln v(t) \\&\quad =\left( \frac{\alpha u(t)}{\beta +u(t)}-\frac{\sigma _2^2}{2}-\frac{\alpha \gamma v(t)}{1+\gamma v(t)}\right) \mathrm{d} t+\sigma _2\mathrm{d} B_2(t) \\&\quad =\left( -\frac{\sigma _2^2}{2}+\frac{\alpha X(t)}{\beta +X(t)}-\left( \frac{\alpha X(t)}{\beta +X(t)}-\frac{\alpha u(t)}{\beta +u(t)}\right) \right. \\&\qquad \left. -\,\frac{\alpha \gamma v(t)}{1+\gamma v(t)}\right) \mathrm{d} t+\sigma _2\mathrm{d} B_2(t) \\&\quad \ge \left( -\frac{\sigma _2^2}{2}+\frac{\alpha X(t)}{\beta +X(t)}-\frac{\alpha \beta (X(t)-u(t))}{(\beta +X(t))(\beta +u(t))} \right. \\&\qquad \left. -\,\alpha \gamma v(t)\right) \mathrm{d} t+\sigma _2\mathrm{d} B_2(t) \\&\quad \ge \left( -\frac{\sigma _2^2}{2}+\frac{\alpha X(t)}{\beta +X(t)}-\frac{\alpha }{\beta }(X(t)-u(t))-\alpha \gamma v(t)\right) \\&\quad \mathrm{d} t+\sigma _2\mathrm{d} B_2(t). \end{aligned} \end{aligned}$$
(9)

Substituting (8) into (9) and combining Lemma 3, we obtain that

$$\begin{aligned} \begin{aligned}&\frac{\ln v(t)-\ln v(0)}{t}\\&\quad \ge -\frac{\sigma _2^2}{2}+\frac{\alpha }{t}\int _{0}^{t}\frac{X(r)}{\beta +X(r)}\mathrm{d} r-\alpha \left( \frac{s}{\beta ^2}+\gamma \right) \\&\frac{1}{t}\int _{0}^{t}v(r)\mathrm{d} r+\frac{M_2(t)}{t}\\&\quad \ge -\frac{\sigma _2^2}{2}-\varepsilon +\alpha \int _{0}^{\infty }\frac{x}{\beta +x}\mu (x)\mathrm{d} x-\alpha \left( \frac{s}{\beta ^2}+\gamma \right) \\&\frac{1}{t}\int _{0}^{t}v(r)\mathrm{d} r+\frac{M_2(t)}{t}\\&\quad =\lambda _1-\varepsilon -\alpha \left( \frac{s}{\beta ^2}+\gamma \right) \langle v\rangle _t+\frac{M_2(t)}{t} \end{aligned} \end{aligned}$$

for sufficiently large t. Applying (II) in Lemma 1 and the arbitrariness of \(\varepsilon \), one can derive that

$$\begin{aligned} \liminf _{t\rightarrow \infty }\langle v\rangle _t\ge \frac{\lambda _1}{\alpha \left( \frac{s}{\beta ^2}+\gamma \right) },\ \ a.s. \end{aligned}$$

That is to say model (3) will be persistent in the mean when \(\lambda _1>0\). The proof is complete. \(\square \)

Remark 2

From Theorem 1, we can see that \(\lambda _1\) is the critical value between persistence in the mean and extinction for predator v(t). Furthermore, combining Lemma 3, we obtain that \(\lim _{t\rightarrow \infty }\langle u\rangle _t=1-\frac{\sigma _1^2}{2}\), \(\lim _{t\rightarrow \infty }v(t)=0\) a.s. when \(\lambda _1<0\).

Remark 3

Lemma 3 and Theorem 1 show that the two species will die out if \(1-\frac{\sigma _1^2}{2}<0\). That is to say, large white noise intensity \(\sigma _1^2\) can cause the species extinction. On the other hand, model (3) will be persistent in the mean if the white noise disturbances are small enough such that \(1-\frac{\sigma _1^2}{2}>0\) and \(\lambda _1>0\).

4 Existence of ergodic stationary distribution

Using the theory of Has’minskii [22] (see “Appendix”) and the Lyapunov function method, in this section, we prove that when the noises are small enough, model (3) has a stationary distribution which is ergodic.

Theorem 2

Assume that

$$\begin{aligned} \lambda :=1-\frac{\sigma _1^2}{2}-\frac{\beta +1}{2\alpha }\sigma _2^2>0, \end{aligned}$$

then there exists a stationary distribution \(m(\cdot )\) for model (3) and it has the ergodic property:

$$\begin{aligned} \begin{aligned}&\mathcal {P}\left\{ \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}u(r)\mathrm{d} r=\int _{\mathbb {R}_+^2}x m(\mathrm{d} x,\mathrm{d} y)\right\} =1,\\&\mathcal {P}\left\{ \lim _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}v(r)\mathrm{d} r=\int _{\mathbb {R}_+^2}y m(\mathrm{d} x,\mathrm{d} y)\right\} =1. \end{aligned} \end{aligned}$$
(10)

Proof

In order to prove Theorem 2, it suffices to verify Assumptions (B1) and (B2) in “Appendix.” To verify (B2), it suffices to prove that there exist a neighborhood \(U\subset \mathbb {R}_+^2\) and a nonnegative \(C^2\)-function V such that for any \((u,v) \in \mathbb {R}_+^2\setminus U\), \(\mathcal {L}V\) is negative (see [25]).

Define a \(C^2\)-function

$$\begin{aligned} h(u,v)= & {} M\left( -\ln u-\frac{\beta +1}{\alpha }\ln v+\ln (\beta +u)+\frac{K}{\alpha }v\right) \\&+\, \frac{(u+\frac{s}{\alpha }v)^{\theta +1}}{\theta +1}, \end{aligned}$$

here \(\theta \in (0,1)\), K and M are constants satisfying the following condition, respectively,

$$\begin{aligned}&K>\frac{s}{\beta }+\frac{\left( \gamma (\beta +1)+\frac{s}{\beta }-\lambda \gamma \right) ^2}{4\lambda \gamma }, \end{aligned}$$
(11)
$$\begin{aligned}&\qquad -\,CM+\check{f}+\check{g}\le -2, \end{aligned}$$
(12)

and positive constant C, functions f(x), g(x) will be determined later. It is not difficult to see that there exists a unique point \((u_0,v_0)\) which is the minimum point of h(u, v). Define a nonnegative \(C^2\)-Lyapunov function

$$\begin{aligned} V(u,v)= & {} M\left( -\ln u-\frac{\beta +1}{\alpha }\ln v+\ln (\beta +u)+\frac{K}{\alpha }v\right) \\&+\,\frac{(u+\frac{s}{\alpha }v)^{\theta +1}}{\theta +1}-h(u_0, v_0). \end{aligned}$$

Denote

$$\begin{aligned} V_1= & {} -\ln u-\frac{\beta +1}{\alpha }\ln v+\ln (\beta +u)+\frac{K}{\alpha }v, \\ V_2= & {} \frac{(u+\frac{s}{\alpha }v)^{\theta +1}}{\theta +1}. \end{aligned}$$

Direct calculations imply that

$$\begin{aligned} \begin{aligned} \mathcal {L}V_1=&-\left( 1-\frac{\sigma _1^2}{2}\right) +u+\frac{sv}{\beta +u}+(\beta +1) \\&\left( -\frac{u}{\beta +u}+\frac{\gamma v}{1+\gamma v}+\frac{\sigma _2^2}{2\alpha }\right) \\&+\,\frac{u}{\beta +u}-\frac{u^2}{\beta +u}-\frac{suv}{(\beta +u)^2} \\&-\,\frac{1}{2}\sigma _1^2\left( \frac{u}{\beta +u}\right) ^2-\frac{K\gamma v^2}{1+\gamma v}+\frac{Kuv}{\beta +u}\\ \le&-\left( 1-\frac{\sigma _1^2}{2}\right) +u+\frac{s}{\beta }v-(\beta +1)\frac{u}{\beta +u} \\&+\,\frac{\gamma (\beta +1)v}{1+\gamma v}+\frac{(\beta +1)\sigma _2^2}{2\alpha }\\&+\,(\beta +1)\frac{u}{\beta +u}-u-\frac{K\gamma v^2}{1+\gamma v}+\frac{Kuv}{\beta +u}\\ =&-\left( 1-\frac{\sigma _1^2}{2}-\frac{\beta +1}{2\alpha }\sigma _2^2\right) +\frac{s}{\beta }v+\frac{\gamma (\beta +1)v}{1+\gamma v} \\&-\,\frac{K\gamma v^2}{1+\gamma v}+\frac{Kuv}{\beta +u}\\ =&-\lambda +\frac{s}{\beta }v+\frac{\gamma (\beta +1)v}{1+\gamma v}-\frac{K\gamma v^2}{1+\gamma v}+\frac{Kuv}{\beta +u}\\ =&\frac{-\gamma \left( K-\frac{s}{\beta }\right) v^2+\left( \gamma (\beta +1)+\frac{s}{\beta }-\lambda \gamma \right) v-\lambda }{1+\gamma v} \\&+\,\frac{Kuv}{\beta +u}\\ =&-\frac{F(v)}{1+\gamma v}+\frac{Kuv}{\beta +u}, \end{aligned} \end{aligned}$$

where \(F(v)=\gamma \left( K-\frac{s}{\beta }\right) v^2-\left( \gamma (\beta \!+\!1)\!+\!\frac{s}{\beta }-\lambda \gamma \right) v+\lambda \). Note that \(\left( \gamma (\beta +1)+\frac{s}{\beta }-\lambda \gamma \right) ^2-4\lambda \gamma \left( K-\frac{s}{\beta }\right) <0\) when condition (11) holds. This implies that \(F(v)>0\) for all \(v\in (0,\infty )\). Therefore, define a positive constant \(C=\inf _{v\in (0,\infty )}\frac{F(v)}{1+\gamma v}\), then one derives

$$\begin{aligned} \mathcal {L}V_1\le -C+\frac{Kuv}{\beta +u}. \end{aligned}$$
(13)

Also

$$\begin{aligned} \mathcal {L}V_2&=\left( u+\frac{s}{\alpha }v\right) ^{\theta }\left( u-u^2-\frac{\gamma sv^2}{1+\gamma v}\right) \nonumber \\&\quad +\,\frac{\theta }{2}\left( u+\frac{s}{\alpha }v\right) ^{\theta -1} \nonumber \\&\quad \left( \sigma _1^2u^2+\left( \frac{s}{\alpha }\sigma _2\right) ^2v^2\right) \nonumber \\&\le 2^{\theta }u\left( u^{\theta }+\left( \frac{s}{\alpha }v\right) ^{\theta }\right) -u^{2+\theta }-\gamma s\left( \frac{s}{\alpha }\right) ^{\theta } \nonumber \\&\quad \frac{v^{2+\theta }}{1+\gamma v} +\,\frac{\theta }{2}\left( \sigma _1^2u^{1+\theta }+\sigma _2^2\left( \frac{s}{\alpha }v\right) ^{1+\theta }\right) \nonumber \\&\le 2^{\theta }u^{\theta +1}+2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }u^2+\frac{\theta }{2}\sigma _1^2u^{\theta +1}-u^{2+\theta } \nonumber \\&\quad +\,2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }v^{2\theta }+\frac{\theta }{2}\sigma _2^2\left( \frac{s}{\alpha }\right) ^{\theta +1}v^{\theta +1} \nonumber \\&\quad -\,\gamma s\left( \frac{s}{\alpha }\right) ^{\theta }\frac{v^{\theta +2}}{1+\gamma v} \nonumber \\&=:f(u)+g(v), \end{aligned}$$
(14)

where

$$\begin{aligned} f(u)= & {} 2^{\theta }u^{\theta +1}+2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }u^2+\frac{\theta }{2}\sigma _1^2u^{\theta +1}-u^{2+\theta }, \\ g(v)= & {} 2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }v^{2\theta }+\frac{\theta }{2}\sigma _2^2\left( \frac{s}{\alpha }\right) ^{\theta +1}v^{\theta +1} \\&- \,s\left( \frac{s}{\alpha }\right) ^{\theta }\frac{\gamma v^{\theta +2}}{1+\gamma v} \end{aligned}$$

It is not difficult to obtain

$$\begin{aligned} f(u)\rightarrow -\infty ,\ \ as\ u\rightarrow +\infty . \end{aligned}$$

Applying inequalities \(0<\theta <1\) and \(\frac{\sigma _2^2}{2\alpha }<1\) we obtain

$$\begin{aligned} \frac{\theta }{2}\sigma _2^2\left( \frac{s}{\alpha }\right) ^{\theta +1}<s\left( \frac{s}{\alpha }\right) ^{\theta },\ \ 2\theta <\theta +1, \end{aligned}$$
(15)

which implies

$$\begin{aligned} g(v)\rightarrow -\infty ,\ \ as\ v\rightarrow +\infty . \end{aligned}$$

Therefore

$$\begin{aligned} \mathcal {L}V\le M\left( -C+\frac{Kuv}{\beta +u}\right) +f(u)+g(v), \end{aligned}$$

where M satisfies

$$\begin{aligned} -MC+\check{f}+\check{g}\le -2. \end{aligned}$$
(16)

Now we are in the position to construct a bounded set \(U\subset \mathbb {R}_+^2\) such that \(\mathcal {L}V\le -1\), \((u,v)\in \mathbb {R}_+^2-U\). Consider the following bounded subset

$$\begin{aligned} U=\left\{ \varepsilon _1\le u\le \frac{1}{\varepsilon _1},\ \ \varepsilon _2\le v\le \frac{1}{\varepsilon _2}\right\} , \end{aligned}$$

where \(\varepsilon _1\), \(\varepsilon _2\in (0,1)\) are sufficiently small positive constants satisfying the following inequalities

$$\begin{aligned}&-MC+MK\varepsilon _2+\check{f}+\check{g}\le -1, \end{aligned}$$
(17)
$$\begin{aligned}&-MC+\frac{MK}{\beta }\varepsilon _2+\check{f}+\check{g}\le -1, \end{aligned}$$
(18)
$$\begin{aligned}&-MC+\check{f}+C_1-\frac{\rho \gamma }{\gamma +1}\frac{1}{\varepsilon _2^{\theta +1}}\le -1, \end{aligned}$$
(19)
$$\begin{aligned}&-MC+\check{g}_1+C_2-\frac{1}{2}\frac{1}{\varepsilon _1^{2+\theta }}\le -1, \end{aligned}$$
(20)
$$\begin{aligned} \varepsilon _1=\varepsilon _2^2, \end{aligned}$$

where inequalities (17) and (18) can be derived from (16), and the constants \(\rho \), \(C_1\), \(C_2\) and \(\check{g}_1\) will be determined later. Then

$$\begin{aligned} \mathbb {R}_+^2\setminus U=U_1^c\cup U_2^c\cup U_3^c\cup U_4^c, \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} U_1^c&=\left\{ (u,v)\in \mathbb {R}_+^2| \ 0<v<\varepsilon _2\right\} , \\ U_2^c&=\left\{ (u,v)\in \mathbb {R}_+^2| \ 0<u<\varepsilon _1,\ \ \varepsilon _2<v< \frac{1}{\varepsilon _2}\right\} ,\\ U_3^c&=\left\{ (u,v)\in \mathbb {R}_+^2|\ v>\frac{1}{\varepsilon _2}\right\} , \\ U_4^c&=\left\{ (u,v)\in \mathbb {R}_+^2| \ u>\frac{1}{\varepsilon _1}\right\} . \end{aligned} \end{aligned}$$

Case 1 If \((u,v)\in U_1^c\), (17) implies that

$$\begin{aligned} \mathcal {L}V\le & {} -MC+MKv+f(u)+g(v)\le \\&-MC+MK\varepsilon _2+\check{f}+\check{g}\le -1. \end{aligned}$$

Case 2 If \((u,v)\in U_2^c\), we obtain that

$$\begin{aligned} \mathcal {L}V\le -MC+\frac{MK}{\beta }\frac{\varepsilon _1}{\varepsilon _2}+\check{f}+\check{g}, \end{aligned}$$

Choosing \(\varepsilon _1=\varepsilon _2^2\) and combining (18), we have

$$\begin{aligned} \mathcal {L}V\le -MC+\frac{MK}{\beta }\varepsilon _2+\check{f}+\check{g} \le -1. \end{aligned}$$

Case 3 If \((u,v)\in U_3^c\), we have

$$\begin{aligned} \mathcal {L}V\le & {} -MC+\check{f}+C_1-\rho \frac{\gamma v^{\theta +2}}{1+\gamma v} \\\le & {} -MC+\check{f}+C_1-\frac{\rho \gamma }{\gamma +1}\frac{1}{\varepsilon _2^{\theta +1}}\le -1, \end{aligned}$$

which follows from (19), where

$$\begin{aligned} C_1= & {} \sup _{v\in (0,\infty )}\left\{ MKv+2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }v^{2\theta } \right. \\&\quad +\,\frac{\theta }{2}\sigma _2^2\left( \frac{s}{\alpha }\right) ^{\theta +1}v^{\theta +1} \\&\quad \left. -\, \left( s\left( \frac{s}{\alpha }\right) ^{\theta }-\rho \right) \frac{\gamma v^{\theta +2}}{1+\gamma v}\right\} <\infty , \end{aligned}$$

in which \(\rho \) is sufficiently small positive constant such that \(\frac{\theta }{2}\sigma _2^2\left( \frac{s}{\alpha }\right) ^{\theta +1}<s\left( \frac{s}{\alpha }\right) ^{\theta }-\rho \).

Case 4 If \((u,v)\in U_4^c\), it follows that

$$\begin{aligned} \mathcal {L}V\le & {} -MC+MKv+g(v)+C_2-\frac{u^{2+\theta }}{2} \\\le & {} -MC+\check{g}_1+C_2-\frac{1}{2}\frac{1}{\varepsilon _1^{2+\theta }}, \end{aligned}$$

where

$$\begin{aligned} C_2= & {} \sup _{u\in (0,\infty )}\left\{ 2^{\theta }u^{\theta +1}+2^{\theta -1}\left( \frac{s}{\alpha }\right) ^{\theta }u^2 \right. \\&\left. +\,\frac{\theta }{2}\sigma _1^2u^{\theta +1}-\frac{u^{2+\theta }}{2}\right\} <\infty , \end{aligned}$$

and

$$\begin{aligned} \check{g}_1=\sup _{v\in (0,\infty )}\{MKv+g(v)\}, \end{aligned}$$

which together with (20) imply that

$$\begin{aligned} \mathcal {L}V\le -1. \end{aligned}$$

From the above discussion it follows that

$$\begin{aligned} \mathcal {L}V\le -1, \ \ (u,v)\in \mathbb {R}_+^2\setminus U. \end{aligned}$$

On the other hand, in order to verify Assumption (B1), we only need to show that (21) holds. The diffusion matrix of model (3) is

$$\begin{aligned} \bar{A}(X)=\left( \begin{array}{cc} \sigma _1^2u^2 &{} 0 \\ 0 &{} \sigma _2^2v^2 \\ \end{array} \right) . \end{aligned}$$

It is not difficult to see that there exists a \(c >0\) such that

$$\begin{aligned} \sum _{i,j=1}^{2}\bar{a}_{ij}(X)\xi _i\xi _j=\sigma _1^2u^2\xi _1^2+\sigma _2^2v^2\xi _2^2>c|\xi |^2 \end{aligned}$$

for \((u,v)\in \bar{U}\) and \(\xi \in \mathbb {R}_+^2\). That is to say, Assumption (B1) holds. Consequently, model (3) has a stationary distribution \(m(\cdot )\) and it is ergodic.

Following the proof of the remainder of Theorem 2.1 in [15] and (4), we can get the ergodic property (10). The proof is complete. \(\square \)

Remark 4

There is no positive equilibrium for stochastic model (3). Hence we cannot show the permanence of the stochastic model by proving the stability of the positive equilibrium as the deterministic model. Theorem 2 shows that model (3) has an ergodic stationary distribution if the white noise is small. The stationary distribution can be considered as a stability of the model in weaksense, which appears as the solution is fluctuating in a neighborhood of the equilibrium point of the corresponding deterministic model. Theorem 2 also shows that small white noise can make model permanent.

Remark 5

According to the theory of Has’minskii, to prove the existence of the stationary distribution, it is critical to construct a bounded domain U and a nonnegative \(C^2\)-function V such that \(\mathcal {L}V\) is negative outside U. Here we construct a new Lyapunov function and a rectangular set which do not depend on the equilibrium \((u^*,v^*)\) of the deterministic model (2). From the ergodic property (10) it follows that the solution of model (3) tends to a fixed positive point in the sense of time average with probability one.

5 Numerical example

In this section, in order to illustrate the results developed, we introduce a numerical example. Using Milstein’s higher-order method [26], we get the discretization equation:

$$\begin{aligned} \left\{ \begin{array}{l} u^{k+1}=u^k+u^k\left( 1-u^k-\frac{sv^k}{\beta +u^k}\right) {\varDelta } t\\ \quad +\,\sigma _1 u^k\sqrt{{\varDelta } t}\xi _k+\frac{\sigma _1^2}{2}u^k({\varDelta } t\xi _k^2-{\varDelta } t),\\ v{k+1}=v^k+\alpha v^k\left( \frac{u^k}{\beta +u^k}-\frac{\gamma v^k}{1+\gamma v^k}\right) {\varDelta } t\\ \quad +\,\sigma _2 v^k\sqrt{{\varDelta } t}\eta _k+\frac{\sigma _2^2}{2}v^k({\varDelta } t\eta _k^2-{\varDelta } t), \end{array} \right. \end{aligned}$$

where time increment \({\varDelta } t>0\), and \(\xi _k\), \(\eta _k\) are N(0, 1)-distributed independent random variables.

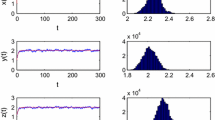
In model (3), let \(s=0.5\), \(\alpha =1.48\), \(\beta =0.4\), \(\gamma =2\), \(\sigma _1=0.1\), \(\sigma _2=0.2\), \(u(0)=0.6\), \(v(0)=0.8\). Then the nontrivial stationary state of the corresponding deterministic model (2) is \((u^*, v^*)=(0.6306,0.7907)\). Notice that

$$\begin{aligned} \lambda =1-\frac{\sigma _1^2}{2}-\frac{\beta +1}{2\alpha }\sigma _2^2=0.976>0. \end{aligned}$$

Theorem 2 shows that model (3) has a stationary distribution. (see Figs. 1, 2).

Fig. 1
figure 1

Simulations of prey population u(t) and its histogram to the stochastic model (3)

Full size image
Fig. 2
figure 2

Simulations of predator population v(t) and its histogram to the stochastic model (3)

Full size image

6 Conclusions

This paper presents a stochastic Holling type II response predator–prey model with hyperbolic mortality. The dynamical behavior of this model has been studied. According to the ergodic property of stochastic logistic model (5), we obtain the critical value \(\lambda _1\) for the persistence in the mean and extinction of this model. If \(\lambda _1<0\), predator population tends to zero. If \(\lambda _1>0\), predator population is persistent in the mean which means model (3) is persistent. Furthermore, by using the theory of Has’minskii and constructing Lyapunov function, we establish sufficient conditions for the existence of ergodic stationary distribution, which implies that the system is permanent. The theories and numerical examples we have presented show that small environmental noise can make the system persistent, while large noise may make the species extinct.