Nonholonomic dynamics of the Twistcar vehicle: asymptotic analysis and hybrid dynamics of frictional skidding

Abstract

The Twistcar vehicle is a classic example of a nonholonomic dynamical system. The vehicle model consists of two rigid links connected by an actuated rotary joint and supported by wheeled axles, where nonholonomic constraints are assumed to impose no skidding of the wheels. Recent experimental measurements conducted with a robotic Twistcar prototype have shown disagreements with previous theoretical analyses. In particular, significant skidding has been observed, in addition to discrepancies with respect to theoretical predictions of divergence in oscillations of the vehicle’s speed and orientation, as well as direction reversal depending on the vehicle’s structure. The goal of our research is to resolve this disagreement by generalizing the theoretical analysis. First, we extend previous asymptotic analysis by incorporating the effects of links’ inertia and oscillation amplitude of the input angle on the direction of net motion. Next, we formulate the vehicle’s hybrid dynamics under frictional bounds and skid-state transitions. Using numerical analysis, we obtain optimal values for the vehicle’s mean speed and energetic cost-of-transport as a function of the input frequency. Our results improve the agreement between theory and experiments and suggest directions for further experimental investigation.

1 Introduction

1.1 Scientific background

Underactuated locomotion systems are mobile robots whose number of degrees-of-freedom is larger than the number of controlled inputs. Thus, they typically contain passive degrees-of-freedom. The dynamics of such systems is often governed by nonholonomic constraints, which are non-integrable and locally restrict the system’s feasible directions of generalized velocities [1, 2]. A classical example is Chaplygin’s sleigh [3, 4] which is a planar rigid body with a blade which is restricted to slide along a body-fixed direction. The same principle holds for vehicles with unactuated wheeled axles which are restricted not to skid (i.e., slip in lateral direction).

In many of these nonholonomic systems, one assumes “kinematic inputs” directly prescribing m actuated joint angles or velocities, which indirectly affect the motion of all N degrees-of-freedom through interaction with the constraints. If the number of constraints n equals $N-m$, then the system is termed “purely kinematic.” Examples of such systems are the Dubins’ car [5], three-wheel kinematic snake [6] and truck-trailer(s) chains [7, 8]. On the other hand, if $n<N-m$, then the system’s motion involves dynamics, and is governed by interaction between the nonholonomic constraints and balance of generalized momentum variables. Examples of such systems are the snakeboard [9, 10], roller racer [11, 12], bicycle-like car models [13, 14], and several actuated variants of Chaplygin’s sleigh [15,16,17]. There have been many works on dynamics and control of nonholonomic locomotion systems, exploiting their geometric structure for analyzing periodic control inputs [18, 19].

Another closely related type of robotic locomotion systems are articulated swimmers, where velocity relations that are analogous to nonholonomic constraints are induced by the fluid-swimmer interaction. For micro-swimmers, where inertial effects are negligible, these relations originate from imposing quasistatic equilibrium [20, 21], whereas they come from added-mass effect and momentum conservation for inertia-dominated swimming in ideal fluid [22, 23]. Several works have analyzed such systems utilizing methods of differential geometry [24], optimal control [25,26,27] and perturbation expansion [28,29,30].

For wheeled vehicles moving on low-friction terrain, the no-skid nonholonomic constraints are not always realistic. For example, the kinematic three-wheel snake skids upon reaching singularities at symmetric configurations, as observed both experimentally [6] and theoretically [31]. Several relaxations of the no-skid constraints have been proposed and analyzed. The “skid-angle” model [32,33,34,35] introduces skid velocities with non-dissipative constraint forces. In contrast, assuming skidding under viscous frictional forces [36, 37] also involves energy dissipation. While those two models involve continuously varying friction forces and skid velocities, Coulomb’s dry friction model may induce non-smooth behavior of dynamic skid-state transitions [31, 38, 39] that also dissipate energy.

1.2 Twistcar—Review of recent relevant works

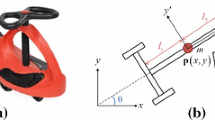
We now introduce the Twistcar toy and its simple theoretical model, and then review three recent works with high relevance. A picture of the Twistcar toy vehicle appears in Fig. 1a. A child can sit on the vehicle and generate propulsion on level ground by simply applying periodic oscillations of the steering handlebar. A simple planar model of the Twistcar is shown in Fig. 1b, including all notations. The model consists of two rigid links supported by wheeled axles, and connected by a rotary joint. Each link has mass $m_i$ and length $l_i$, for $i=1,2$. Each link has moment of inertia $J_i$ about its center-of-mass ${{\mathbf {c}}}_i$ (COM), which is located at a distance $b_i$ from the wheels’ axle. We attach a body-fixed reference frame to each link, such that ${{\mathbf {e}}}_i$ is aligned with the link’s longitudinal axis while ${{\mathbf {e}}}_i^\perp$ is perpendicular to it and parallel to link’s wheeled axle. Midpoints on the two wheeled axles are denoted by ${{\mathbf {p}}}_i$. The relative angle between the links is denoted by $\phi$ and the absolute orientation angle of link 1 is denoted by ${\theta }$. While a mechanical torque $\tau$ is applied at the joint through the steering handlebar, it is more convenient to assume that the joint angle $\phi$ is directly prescribed and oscillates in time t as

$$\begin{aligned} \phi (t)=\phi _0+{\varepsilon }\sin (\omega t). \end{aligned}$$

(1)

Fig. 1

a The Twistcar vehicle. b Its two-link model with notation

Fig. 2

Simulation results from the point-mass model [29]: a Forward speed $v_1(t)$ for two values of $b_1/l_2$, showing reversal in direction of net motion, along with mean acceleration and oscillations. b Orientation angle ${\theta }(t)$, showing diverging oscillations. c Illustration of direction reversal conditions from [29]

1.2.1 Asymptotic analysis of point-mass model [29]:

The first recent relevant work is that of Chakon and Or [29]. They studied a point-mass model of the Twistcar where $m_2=0$ and $J_1=J_2=0$, and also assumed zero skidding (lateral slippage) of the wheels, which implies

$$\begin{aligned} {\sigma }_i={{\dot{\mathbf{p}}}}_i \cdot {{\mathbf {e}}}_i^\perp =0 \text{ for } i=1,2 \end{aligned}$$

(2)

where upper dot represents time-derivative d/dt. We now review main observations from [29]. Figure 2 shows typical simulation results from [29] under parameter values of $l_1=0.5m$, $l_2=0.1m$, $b_1=0.3m$, $\phi _0=\pi$, ${\varepsilon }=0.6 rad$, and $\omega =1 rad/s$. Time plot of the speed of rear axle midpoint $v_1(t)={{\dot{\mathbf{p}}}}_1 \cdot {{\mathbf {e}}}_1$ appears as solid line in Fig. 2a. It can be seen that the mean speed has negative mean acceleration (i.e., moving backward), with superposed oscillations of slowly diverging amplitude. Time plot of the vehicle’s orientation angle ${\theta }(t)$ appears in Fig. 2b, showing that ${\theta }(t)$ also undergoes oscillations of diverging amplitude. This implies that for long-time simulations, the vehicle’s trajectories in (x, y) plane begin to curve into flower-like loops, as also observed in [40]. Another important effect that has been observed and analyzed in [29] is reversal in direction of the vehicle’s net motion depending on the vehicle’s structural parameters. Specifically, under oscillations about the straightened configuration $\phi _0=\pi$, the direction of net motion depends on the ratio of the steering link’s length $l_2$ to the distance $b_1$ of the body’s COM from the rear axle (see Fig. 1b). For $b_1<l_2$, the vehicle moves in backward direction, whereas for $b_1>l_2$ it moves in forward direction, see illustration in Fig. 2c. As an example, the dashed curve overlaid in Fig. 2a shows time plot of $v_1(t)$ for the same parameter values except for $b_1=0.05m<l_2$, which gives motion in reverse direction (positive). This non-intuitive phenomenon has been analyzed in [29] using leading-order asymptotic expansion of the point-mass model.

Fig. 3

Experimental results: a The robotic prototype. b Time plot of measured of forward speed $v_1(t)$. c Time plot of measured orientation angle ${\theta }(t)$. d Time plots of measured skid velocities ${\sigma }_i(t)$

1.2.2 Motion measurement experiments

The second recent work (unpublished) is a series of motion experiments we have conducted with a robotic prototype of the Twistcar vehicle, see Fig. 3a . We used modular parts of Actobotics series from ServoCity in order to construct the robot’s structure. The joint was actuated by servo motor powered by on-board lithium-ion battery, and controlled by Arduino Mega controller. We prescribed periodic input command of steering angle $\phi (t)$ as in (1), with $\phi _0=0$, ${\varepsilon }= \pi /6$ and $\omega = \pi \; rad/s$. Reflective markers have been attached to the vehicle’s links, and the motion has been tracked by an array of infrared cameras using VICON system. Figure 3b shows measurements of the vehicle’s forward speed $v_1(t)$ as a function of time, showing that it first accelerates from rest, and then seems to converge to a periodic solution with bounded oscillations about a mean value. In addition, Fig. 3c shows measurements of the vehicle’s orientation angle ${\theta }(t)$, showing oscillations of constant amplitude about a slowly drifting mean value. This drift in orientation can be attributed to some small calibration error in the steering angle’s servo motor and encoder, as well as asymmetry in the wheels’ rotational friction. Nevertheless, the results stand in clear disagreement with the theoretical prediction in [29] of indefinitely increasing mean value of $v_1(t)$, in addition to diverging oscillations of both $v_1(t)$ and ${\theta }(t)$, see Fig. 2a and b.

Next, Fig. 3d shows time plots of the measured skid velocities of the rear and front wheel’s axles, ${\sigma }_1(t)$ and ${\sigma }_2(t)$. Remarkably, one can see non-negligible skidding, with velocity magnitudes ranging up to $20\%$ of forward mean speed. This clearly indicates that the assumption of ideal no-skid constraints (2) is completely unrealistic and should be relaxed. Moreover, while ${\sigma }_2(t)$ shows alternating reversals in skidding direction, ${\sigma }_1(t)$ seems to display a more complex behavior of transitions between skid and no-skid states. This suggests that a Coulomb-like model of dry friction should be considered. Finally, in experiments where $\phi (t)$ oscillated about straightened configuration $\phi _0=\pi$, we were unable to reproduce the phenomenon of direction reversal which was predicted in [29] by changing the vehicle’s structure and mass distribution. This suggests that the point-mass model is too simplistic, and one should account for the mass and moment-of-inertia of both links.

1.2.3 Analysis of the Landshark model

The third recent relevant work is of Bazzi et al [33]. They considered a similar two-link model dubbed as “Landshark,” where the two links have non-negligible masses and moments of inertia, such that $J_i=m_il_i^2$ and $b_i=0$. Varying the mass ratio $m_2/m_1$ and length ratio $l_2/l_1$, they have identified conditions guaranteeing that the vehicle’s momentum grows in a sign-definite direction for any input of steering angle $\phi (t)$. In cases where these conditions are not satisfied, they have demonstrated a numerical simulation example where the direction of motion can be reversed for a vehicle with specific values of $m_i,l_i$ by only modulating the input’s amplitude and frequency of the steering angle $\phi (t)$ oscillating about $\phi _0=\pi$ as in (1). This interesting effect has not been captured by the leading-order asymptotic analysis in [29]. Finally, the work [33] also considered a relaxation of the no-skid assumption by using the “skid-angle” model [32, 34, 35] , which accounts for non-dissipative smooth changes in the skidding velocities. However, this model still predicts unbounded divergence of the forward speed and orientation angle, which again disagrees with our experimental observations in Fig. 3b.

1.3 Research goal and statement of contributions

The goal of this work is to extend the theoretical model of the Twistcar vehicle and its analysis in order to explain the discrepancies and disagreement between previous theoretical works and the experimental measurements. More specifically, we make four main contributions which are listed as follows. First, we extend the leading-order asymptotic analysis of [29] in order to incorporate the effect of links’ inertias on direction of net motion and its reversal. Second, we derive the next-order expansion term of the vehicles’ speed in order to find necessary and sufficient conditions for achieving direction reversal by changing only the oscillation amplitude ${\varepsilon }$ of the steering angle. Third, we generalize the theoretical model in order to incorporate Coulomb friction bounds and hybrid dynamics of skid-state transitions, and show numerical simulation results that qualitatively agree with our experimental measurements. Finally, we numerically analyze the influence of input frequency on characteristics of periodic motion with skid-state transitions, and obtain optimal frequencies that maximize mean speed as well as energetic efficiency.

The rest of the work is organized as follows. The next section formulates of the Twistcar’s dynamic equations as a nonholonomic system under ideal no-skid constraints, and presents some numerical simulation results. Section 3 conducts asymptotic analysis including links’ inertias and next-order expansion, and highlights the effect of links’ inertias and input’s amplitude on direction reversal. Section 4 provides expressions for normal reaction forces assuming “flat plane” model of the vehicle, and introduces Coulomb’s friction constraints and the hybrid dynamics of skid-state transitions. Section 5 presents numerical analysis of periodic motion and the influence of input’s frequency. Finally, Section 6 concludes the work.

2 Problem formulation with ideal constraints

We now present formulation of the system’s nonholonomic dynamics under ideal no-skid constraints. We choose generalized coordinates ${{\mathbf {q}}}=(x,y,{\theta },\phi )^T$, where x, y denote the position ${{\mathbf {c}}}_1$ of the COM of link 1, ${\theta }$ is the link’s orientation angle, and $\phi$ is the steering joint angle, see Fig. 1b. The skidding velocities ${\sigma }_1,{\sigma }_2$ defined in (2) can be expressed as

$$\begin{aligned} \begin{array}{l} \sigma _i={{\dot{\mathbf{p}}}}_i \cdot {{\mathbf {e}}}_i^\perp ={{\mathbf {w}}}_i({{\mathbf {q}}}) \cdot {{\dot{\mathbf{q}}}}=0 \text{, } \text{ for } i=1,2 \\ \text{ where } {{\mathbf {w}}}_1=(-\sin {\theta }\;\; \cos {\theta }\;\; -b_1 \;\; 0)^T , \\ {{\mathbf {w}}}_2=(-\sin ({\theta }\!+\! \phi ) \;\; \cos ({\theta }\!+\! \phi ) \;\; h_1 \cos \phi -l_2 \;\; -l_2)^T, \\ \text{ and } h_i=l_i-b_i. \end{array}\nonumber \\ \end{aligned}$$

(3)

Defining the matrix ${{\mathbf {W}}}({{\mathbf {q}}})=[{{\mathbf {w}}}_1({{\mathbf {q}}}) \; {{\mathbf {w}}}_2({{\mathbf {q}}})]^T$, the nonholonomic no-skid constraints can be written as

$$\begin{aligned} {{\mathbf {W}}}({{\mathbf {q}}}) {{\dot{\mathbf{q}}}}=0. \end{aligned}$$

(4)

The system’s constrained dynamic equations of motion can be obtained using Euler–Lagrange derivation as (cf. [41]):

$$\begin{aligned} \frac{d}{dt} \left( \frac{{\partial }L}{{\partial }{{\dot{\mathbf{q}}}}} \right) - \frac{{\partial }L}{{\partial }{{\mathbf {q}}}}= {{\mathbf {F}}}_q + {{\mathbf {W}}}({{\mathbf {q}}})^T {{\varvec{\Lambda }}}, \end{aligned}$$

(5)

where $L=T-U$ is the system’s Lagrangian, T is the total kinetic energy, U is the potential energy, ${{\mathbf {F}}}_q$ is the vector of generalized forces and ${{\varvec{\Lambda }}}=({\lambda }_1,{\lambda }_2)^T$ is the vector of constraint forces (Lagrange multipliers). Since the vehicle here moves in horizontal plane, the system is not governed by any changes in potential energy and U can thus be ignored. The kinetic energy for planar motion of the 2-link system can be obtained as

$$\begin{aligned} T=\frac{1}{2} \sum _{i=1}^{2} \left( m_i({{\dot{\mathbf{c}}}}_i \cdot {{\dot{\mathbf{c}}}}_i)+ J_i \omega _i^2 \right) =\frac{1}{2}{{\dot{\mathbf{q}}}}^t{{\mathbf {M}}}({{\mathbf {q}}}){{\dot{\mathbf{q}}}}, \end{aligned}$$

(6)

where full expressions for elements of the matrix of inertia ${{\mathbf {M}}}({{\mathbf {q}}})$ are given below in (8). Using (5) and (6), the equations of motion can be written in a standard matrix form as

$$\begin{aligned} \begin{array}{l} {{\mathbf {M}}}({{\mathbf {q}}}){{\ddot{\mathbf{q}}}}+{{\mathbf {B}}}({{\mathbf {q}}},{{\dot{\mathbf{q}}}})= {{\mathbf {E}}}\tau + {{\mathbf {W}}}({{\mathbf {q}}})^T {{\varvec{\Lambda }}}\\[6pt] \text{ where } {{\mathbf {E}}}= \left( 0 \; 0 \; 0\; 1 \right) ^T \end{array} \end{aligned}$$

(7)

and $\tau (t)$ is the actuation torque at the steering joint. Explicit expressions for the elements of ${{\mathbf {M}}}({{\mathbf {q}}})$ and the vector of velocity-dependent terms ${{\mathbf {B}}}({{\mathbf {q}}},{{\dot{\mathbf{q}}}})$ from (7) are given as:

$$\begin{aligned} \begin{array}{l} M_{11}=M_{22}=m_1+m_2, \; M_{12}=0 \\ M_{13}=m_2(h_2\sin (\phi + {\theta }) - h_1\sin {\theta })\\ M_{14}=m_2 h_2 \sin (\phi + {\theta }),\; M_{24}= -m_2 h_2 \cos (\phi + {\theta })\\ M_{23}=m_2(h_1 \cos {\theta }- h_2\cos (\phi + {\theta }) \\ M_{33}=J_1+J_2+m_2(h_1^2+h_2^2 - 2 h_1 h_2 \cos \phi )\\ M_{34}=J_2 + m_2(h_2^2 - h_1 h_2 \cos \phi ), \;M_{44}=J_2+ m_2 h_2^2 \\ B_1=m_2 \left( h_2({{\dot{\phi }}}+{{\dot{\theta }}})^2 \cos (\phi + {\theta }) - h_1 {{\dot{\theta }}}^2 \cos {\theta }\right) \\ B_2 = m_2 \left( h_2({{\dot{\phi }}}+{{\dot{\theta }}})^2 \sin (\phi + {\theta }) - h_1 {{\dot{\theta }}}^2 \sin {\theta }\right) \\ B_3=m_2 h_1 h_2 {{\dot{\phi }}}({{\dot{\phi }}}+ 2{{\dot{\theta }}}) \sin \phi , \; B_4=- m_2 h_1 h_2 {{\dot{\theta }}}^2 \sin \phi \end{array}\nonumber \\ \end{aligned}$$

(8)

Differentiating the velocity constraints in (4) with respect to time gives:

$$\begin{aligned} {{\mathbf {W}}}({{\mathbf {q}}}){{\ddot{\mathbf{q}}}}+{{{\dot{\mathbf{W}}}}}({{\mathbf {q}}},{{\dot{\mathbf{q}}}}){{\dot{\mathbf{q}}}}=0. \end{aligned}$$

(9)

Combining equations (7) and (9) gives a differential algebraic system where the vector of constraint forces ${{\varvec{\Lambda }}}$ can be eliminated, and thus the accelerations ${{\ddot{\mathbf{q}}}}$ can be integrated numerically under given input torque $\tau (t)$. Next, we consider the case where the steering angle is assumed to be a directly controlled input, so that $\phi (t)$ and all its time-derivatives are prescribed functions. We note that the torque $\tau$ appears only in the fourth row of (7). Thus, this row can be ignored, so that (7) and (9) now give a $5 \times 5$ linear system in the unknowns $\{\ddot{x},\ddot{y}, \ddot{\theta },{\lambda }_1,{\lambda }_2\}$, which can be numerically integrated to solve for $x(t),\; y(t)$ and $\theta (t)$. Note that one may choose to formulate the system dynamics using Appell–Gibbs approach [42, 43], which gives a more elegant elimination of the constraints [13, 14]. Nevertheless, we choose here to use Lagrangian formulation, following [29], since it enables explicit formulation of constraint forces which are crucial for checking friction inequalities, as detailed later

We now present numerical simulation results of the Twistcar. Physical parameter values which correspond to the robotic vehicle in Fig. 3a are chosen as $l_1=0.36m$, $l_2=0.19m$, $b_1=0.206m$, $b_2=0.5l_2$, $m_1=2.3Kg$, $m_2=0.23Kg$, $J_i=m_i l_i^2 / 12$. The simulations are conducted under periodic input of $\phi (t)$ as in (1) with $\phi _0=\pi$, ${\varepsilon }=0.6 rad$ and $\omega = 1 rad/s$. Initial conditions are $x(0)=y(0)={\theta }(0)=0$, ${{\dot{x}}}(0)=0$, while the rest of ${{\dot{\mathbf{q}}}}(0)$ is determined from (4). Figure 4a shows a time plot of the forward speed $v_1(t)$ in solid curve, while Fig. 4b plots the two constraint forces $\lambda _i(t)$ and the steering torque $\tau (t)$ (dotted curve, right axis scale). The dashed curve in Fig. 4a corresponds to $v_1(t)$ under the same parameter values except for $b_1=0.1m$. It can be seen that the condition $b_1<l_2$ derived in [29] is no longer sufficient for reversing the direction of net motion. However, changing the mass and inertia of link 1 to $m_1=4.3$, $J_1=0.025Kg\cdot m^2$ (equivalent to adding a uniform disk of mass 2Kg and radius 0.03m placed at the link’s COM), leads to direction reversal as shown in the dash-dotted curve of $v_1(t)$ in Fig. 4a. Analytical derivation of exact conditions for direction reversal with masses and inertias is presented in the next section. From Fig. 4b, it can be seen that the constraint forces ${\lambda }_i(t)$ are diverging in time. Moreover, since ${\lambda }_i(t)$ scale as $\omega ^2$ with actuation frequency, fast oscillations of the input $\phi (t)$ require large constraint forces which may exceed friction limitations, practically resulting in wheels skidding. This issue is addressed in Sect. 4. Finally, oscillations of the steering torque $\tau (t)$ are also diverging in time, which in unrealistic in any actuated robot due to saturation bounds on the motor’s torque.

Fig. 4

Numerical simulation results: a plots of forward speed $v_1(t)$ for three examples of parameter values. b plots of constraint forces ${\lambda }_i(t)$ and steering torque $\tau (t)$

3 Reduction and asymptotic analysis

In this section, we conduct reduction of the Twistcar’s dynamic equations of motion (7) and then present asymptotic analysis under small oscillation amplitude ${\varepsilon }$ of the steering angle input $\phi (t)$. This is a generalization of the analysis presented in [29] for the point-mass model.

3.1 Reduction in the dynamic equations

First, we define nondimensional parameters:

$$\begin{aligned} {\kappa }=\frac{m_2}{m_1},\; {\alpha }=\frac{l_2}{l_1},\; \beta _i=\frac{b_i}{l_i},\; \eta _i=\frac{J_i}{m_i l_i^2} \; \text{ for } i=1,2.\nonumber \\ \end{aligned}$$

(10)

The system’s velocities, accelerations, forces and torques are then normalized by characteristic scales of $\{l_1 \omega , l_1 \omega ^2, m_1 l_1 \omega ^2, m_1 l_1^2 \omega ^2 \}$, respectively. Time is normalized by characeristic scale of $1/\omega$.

Next, we define body-frame velocities $v_x={{\dot{\mathbf{c}}}}_1 \cdot {{\mathbf {e}}}_1$, $v_y={{\dot{\mathbf{c}}}}_1 \cdot {{\mathbf {e}}}_1^\perp$. The vector of generalized body velocities is then defined as

$$\begin{aligned} \begin{array}{l} {{\mathbf {v}}}_b={{\mathbf {R}}}({\theta })^T {{\dot{\mathbf{q}}}}, \text{ where } \\ {{\mathbf {v}}}_b= \left( \begin{array}{l} v_x \\ v_y \\ {{\dot{\theta }}}\\ {{\dot{\phi }}}\end{array} \right) \text{ and } {{\mathbf {R}}}({\theta })=\left( \begin{array}{c c c c} \cos {\theta }&{} -\sin {\theta }&{} \;0\; &{}0\\ \sin {\theta }&{} \cos {\theta }&{} 0 &{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\end{array} \right) \end{array}.\nonumber \\ \end{aligned}$$

(11)

Substituting ${{\dot{\mathbf{q}}}}={{\mathbf {R}}}{{\mathbf {v}}}_b$ into (7),(9) and pre-multiplying (7) by ${{\mathbf {R}}}^T$, one obtains the body-frame equations of motion as:

$$\begin{aligned} \begin{array}{l} {{\mathbf {M}}}_b(\phi ) {{\dot{\mathbf{v}}}}_b + {{\mathbf {B}}}_b(\phi ,{{\mathbf {v}}}_b)= {{\mathbf {E}}}\tau + {{\mathbf {W}}}_b^T {{\varvec{\Lambda }}}\\ {{\mathbf {W}}}_b {{\dot{\mathbf{v}}}}_b + {{{\dot{\mathbf{W}}}}}_b {{\mathbf {v}}}_b =0 \\ \text{ where } {{\mathbf {M}}}_b={{\mathbf {R}}}^T {{\mathbf {M}}}{{\mathbf {R}}},\\ {{\mathbf {B}}}_b={{\mathbf {R}}}^T({{\mathbf {M}}}{{\dot{\mathbf{R}}}}{{\mathbf {v}}}_b \!+\! {{\mathbf {B}}}),\, {{\mathbf {W}}}_b= {{\mathbf {W}}}{{\mathbf {R}}}\end{array} \end{aligned}$$

(12)

and we used ${{\mathbf {R}}}^T {{\mathbf {E}}}={{\mathbf {E}}}$. Note that this process eliminates the dependence of (12) on the orientation angle ${\theta }$ due to invariance of the system with respect to rigid-body transformation. The expressions for matrices from (12) are given as:

$$\begin{aligned} \begin{array}{l} {{\mathbf {M}}}_b={{\mathbf {M}}}({\theta }=0),\; {{\mathbf {W}}}_b={{\mathbf {W}}}({\theta }=0), \text{ and } \\ {{\mathbf {B}}}_b={{\mathbf {B}}}({\theta }=0)+\left( \begin{array}{l} -(1+{\kappa }){{\dot{\theta }}}v_y \\ (1+{\kappa }){{\dot{\theta }}}v_x \\ {\kappa }{{\dot{\theta }}}\left( v_x({\delta }_1-{\delta }_2 cos \phi ) -v_y {\delta }_2 \sin \phi \right) \\ -{\kappa }{{\dot{\theta }}}{\delta }_2 (v_x \cos \phi + v_y \sin \phi ) \end{array} \right) \end{array} \end{aligned}$$

where $\delta _i=1-\beta _i$.

The last reduction step is elimination of the constraints and constraint forces. This is done by defining a vector of constraint-free velocities ${{\mathbf {v}}}_f=(u \; v)^T$ as:

$$\begin{aligned} \begin{array}{l} {{\dot{\mathbf{q}}}}={{\mathbf {S}}}(\phi ) {{\mathbf {v}}}_f = {{\mathbf {w}}}_u(\phi ) u + {{\mathbf {w}}}_v(\phi ) v \text{, } \text{ where } \\ {{\mathbf {w}}}_v \! =\! \left( \begin{array}{l} \cos \phi \! -\! {\alpha }\\ {\beta }_1 \sin \phi \\ \sin \phi \\ 0 \end{array} \right) \!, {{\mathbf {w}}}_u \! =\! \left( \begin{array}{c} -{\alpha }\sin \phi (1+{\beta }_1^2) \\ -{\alpha }{\beta }_1 ({\alpha }- \cos \phi ) \\ -{\alpha }({\alpha }- \cos \phi ) \\ ({\alpha }\!-\! \cos \phi )^2 \! +\! (1\!+\! {\beta }_1^2) \sin ^2 \! \phi \end{array} \right) \end{array}\nonumber \\ \end{aligned}$$

(13)

Note that the vectors ${{\mathbf {w}}}_u(\phi ),{{\mathbf {w}}}_v(\phi )$ are mutually orthogonal and satisfy the constraints, that is, ${{\mathbf {W}}}_b {{\mathbf {w}}}_u = {{\mathbf {W}}}_b {{\mathbf {w}}}_v=0,\; {{\mathbf {w}}}_u \cdot {{\mathbf {w}}}_v =0$. Moreover, the choice of ${{\mathbf {w}}}_u,{{\mathbf {w}}}_v$ implies the relation:

$$\begin{aligned} {{\dot{\phi }}}= \left( ({\alpha }\!-\! \cos \phi )^2+ \sin ^2 \phi (1\!+\! {\beta }_1^2)\right) u \equiv g(\phi ) u . \end{aligned}$$

(14)

The constraint-free velocities in (13) have the same role as pseudo-velocities in Appell-Gibbs formulation, cf. [14]. The physical meaning of the constraint-free vector field ${{\mathbf {w}}}_v(\phi )$ is motion along an arc while the steering angle remains constant (${{\dot{\phi }}}=0$). The second vector field ${{\mathbf {w}}}_u(\phi )$ is orthogonal to ${{\mathbf {w}}}_v$ and also satisfies the constraints. That is, it involves varying steering angle such that u is proportional to ${{\dot{\phi }}}$ up to the scaling factor $g(\phi )$ given in (14).

Substituting (13) into (12) and pre-multiplying by ${{\mathbf {S}}}^T$ gives the reduced equations:

$$\begin{aligned} {{\mathbf {S}}}^T {{\mathbf {M}}}_b {{\mathbf {S}}}{{\dot{\mathbf{v}}}}_f + {{\mathbf {S}}}^T {{\mathbf {M}}}_b {{\dot{\mathbf{S}}}}{{\mathbf {v}}}_f + {{\mathbf {S}}}^T {{\mathbf {B}}}_b = {{\mathbf {S}}}^T {{\mathbf {E}}}\tau . \end{aligned}$$

(15)

Note that the constraint forces ${{\varvec{\Lambda }}}$ have been eliminated from (15). Assuming that the steering angle $\phi (t)$ is a prescribed function of time, u(t) can be extracted from the relation (14). Moreover, the structure of ${{\mathbf {S}}}$ and ${{\mathbf {E}}}$ implies that the steering torque $\tau$ does not appear at the second row in equation (15). This gives a scalar first-order differential equations that governs the dynamic evolution of the generalized unconstrained velocity v, taking the form:

$$\begin{aligned} \dot{v} = F(v,\phi , {{\dot{\phi }}}, {\ddot{\phi }}). \end{aligned}$$

(16)

The function F in (16) is highly complicated and its explicit expression is not shown here. It depends quadratically on ${{\dot{\phi }}}$, linearly on ${\ddot{\phi }},v$, and trigonometrically on $\phi$. Moreover, F is even in $\phi (t)$, which implies that:

$$\begin{aligned} F(v,\phi , {{\dot{\phi }}}, {\ddot{\phi }})=F(v,-\phi , -{{\dot{\phi }}}, -{\ddot{\phi }}) . \end{aligned}$$

(17)

Similar symmetry relation also holds about $\phi =\pi$.

3.2 Asymptotic analysis—perturbation expansion

We now derive approximate solution of (16) via perturbation expansion, assuming small amplitude ${\varepsilon }$ of input oscillations. We expand v(t) as a power series:

$$\begin{aligned} v(t)=v_0(t)+{\varepsilon }v_1(t)+{\varepsilon }^2 v_2(t)+ \cdots \end{aligned}$$

(18)

. Next, we expand $F(\cdot )$ in (16) as

Table 1 Expressions of coefficients from (20), (21)

$$\begin{aligned} \begin{array}{l} F(v,\phi , {{\dot{\phi }}}, {\ddot{\phi }})=F(v,\phi _0,0,0)+\displaystyle {\sum _{k=1}^{N}}\left. \dfrac{1}{k!} D^k F \right| _{(v,\phi _0,0,0)} \\ \text{ where } D=\left( (\phi -\phi _0) \dfrac{\partial }{\partial \phi }+ {{\dot{\phi }}}\dfrac{\partial }{\partial {{\dot{\phi }}}} + {\ddot{\phi }}\dfrac{\partial }{\partial {\ddot{\phi }}}\right) \end{array}\nonumber \\ \end{aligned}$$

(19)

The dependence on the angle $\phi$ is expanded about $\phi _0 \in \{0,\pi \}$. The expansions of $\dot{v}$ and F from (18) and (19) are substituted into (16), while $\phi (t)$ and its derivatives are taken from (1) under time-scaling $\omega =1$. We have used symbolic computations in MATLAB for this process. The resulting equation is then rearranged by different powers ${\varepsilon }^k$ in order to obtain a sequence of differential equations for $v_k(t)$ which can be solved iteratively, as follows. The zero-order term gives $\dot{v}_0 = 0$; hence, we obtain $v_0(t)=v_0 = const$. Due to the even-function symmetry of $F(\cdot )$ in (17), all odd powers also give $\dot{v}_k=0$ for odd k; hence, these terms are neglected. The ${\varepsilon }^2$-terms give the leading-order dynamics of the form $\dot{v}_2(t)=F_2(v_0,t)$. Integrating in time (assuming zero initial conditions) gives:

$$\begin{aligned} v_2(t)=a_2 t + b_2 \sin (2t), \end{aligned}$$

(20)

where $a_2,b_2$ are constant coefficients that depend on the system’s parameters, the value of $\phi _0=\{0,\pi \}$ and $v_0$. Explicit expressions for the coefficients are given in Table 1, where we assume starting from rest, $v_0=0$, for simplicity. Note that $a_2$ reduces to the simple expression in [29] for the point-mass case, by substituting ${\kappa }=\eta _1=\eta _2=0$. Expansion to the next order of ${\varepsilon }^4$-terms, which has not been considered previously in [29], gives equation of the form $\dot{v}_4(t)=F_4(v_0,v_2,t)$. Assuming $v_0=0$, integrating in time and substituting the expression for $v_2$ from (20), one obtains:

$$\begin{aligned} v_4(t)=a_4 t + b_4 \sin (2t) + d_4 t \cos (2t). \end{aligned}$$

(21)

The expression for $a_4$ appears in Table 1, whereas the lengthy expressions for $b_4,d_4$ (associated with higher-order oscillating terms) are not shown. Using (20) and (21), the expression for v(t) has oscillating parts superimposed on a constant-rate accelerating mean part ${{\bar{v}}}(t)$, which is expanded up to order 4 as

$$\begin{aligned} {{\bar{v}}}(t) = v_0 + ({\varepsilon }^2 a_2 + {\varepsilon }^4 a_4)t + O({\varepsilon }^6) . \end{aligned}$$

(22)

The mean acceleration ${{\bar{a}}}=d {{\bar{v}}} / dt$ of the vehicle is thus given as:

$$\begin{aligned} {{\bar{a}}} = a_2 {\varepsilon }^2 + a_4 {\varepsilon }^4 +O({\varepsilon }^6). \end{aligned}$$

(23)

The influence of system’s parameters and input amplitude ${\varepsilon }$ on ${{\bar{a}}}$, and particularly on its sign reversal, is analyzed next.

Fig. 5

a Solid curves: leading-order acceleration $a_2$ as a function of $\beta _1$ for three cases of different parameter values. Dashed curves: numerically computed mean acceleration ${{\bar{a}}} / {\varepsilon }^2$ for ${\varepsilon }=0.6 rad$. b Shaded region of $a_2 a_4<0$ in the plane of ${\kappa },{\alpha }$, which corresponds to amplitude-dependent direction reversal of the Landshark model. Hatched regions satisfy necessary-only conditions for reversal as obtained in [33]. Zoom-in inset: three points with ${\kappa }=1.8$ and ${\alpha }= \{0.5,0.57,0.75\}$. c Solid curves: asymptotic mean acceleration $a_2{\varepsilon }^2+a_4 {\varepsilon }^4$ as a function of input amplitude ${\varepsilon }$ for the Landshark model with ${\kappa }=1.8$ and ${\alpha }= \{0.5,0.57,0.75\}$. Dashed curves: numerically computed mean acceleration ${{\bar{a}}}$. The case of ${\alpha }= 0.57$ satisfies $a_2 a_4<0$ and thus enables direction reversal depending on amplitude ${\varepsilon }$

3.3 Small-amplitude parameter-dependent direction reversal

Assuming small amplitude ${\varepsilon }\ll 1$ of the oscillating steering angle $\phi (t)$, the leading-order term of mean acceleration in (23) is $a_2$. For oscillating about $\phi _0=0$, substituting $\zeta =1$ into the expression for $a_2$ in Table 1, it is easy to see that it is always positive. However, oscillating about $\phi _0=\pi$ (i.e., $\zeta =-1$) gives possible conditions for sign reversal of $a_2$ depending on the vehicle’s parameters. For simplicity, we assume that the COM of link 2 is located at its midpoint, $\beta _2=0.5$. Substituting this and $\zeta =-1$, we obtain:

$$\begin{aligned} a_2={\alpha }\frac{4 \beta _1({\alpha }-{\beta }_1)-4 \eta _1-{\kappa }(2-{\alpha })+4 {\alpha }\eta _2 {\kappa }}{8({\alpha }+1)^2({\kappa }+1)} .\nonumber \\ \end{aligned}$$

(24)

As an example, Fig. 5a plots the leading-order acceleration $a_2$ as a function of $\beta$ for $\alpha =0.5$ and ${\kappa }=0$ in three solid-colored curves corresponding to three different choices of other parameter values. Case (i) is “point-mass” model $\eta _1=\kappa =0$ as studied previously in [29]. It can be seen that the direction of net motion reverses to $a_2 >0$ for $\beta _1<{\alpha }$. Case (ii) adds mass and uniform inertia of the links $\eta _1=\eta _2=1/12$, $\kappa =0.22$ as in the experimental robot (Fig. 3a). It can be seen that the effect of added inertias precludes the possibility of direction reversal ($a_2<0$ for all $\beta _1$). This explain the difficulty to achieve direction reversal in our experiments. Case (iii) corresponds to adding a uniform disk to link 1 as described previously in the numerical simulations (Fig. 4a) which corresponds to $\eta _1=1/22$, $\kappa =0.1$. In this case, there is a narrow range of $\beta _1$ for which the sign of $a_2$ is reversed. All this can be explained by the leading-order expression in (24), which highlights the separate contribution of each parameter of links’ inertia. Finally, the dashed colored curves denote mean acceleration ${{\bar{a}}} / {\varepsilon }^2$ which is computed via numerical simulations for input amplitude of ${\varepsilon }=0.6 rad$, showing good agreement with the leading-order expression in (24). (Mean acceleration was numerically computed by taking the integrated v(t) and smoothing it using a moving-average filter, and then applying linear regression to the resulting smoothed signal in order to calculate mean slope).

3.4 Amplitude-dependent direction reversal

In case where the input’s amplitude ${\varepsilon }$ is not very small, the vehicle’s mean acceleration ${{\bar{a}}}$ depends on both $a_2$ and $a_4$, as given by (23). When they differ in signs, i.e., satisfy $a_2 a_4<0$, for small amplitudes ${\varepsilon }$, the sign of ${{\bar{a}}}$ is determined by that of $a_2$, whereas for increased amplitudes, the influence of $a_4$ causes sign reversal. The critical amplitude ${\varepsilon }_0$ for sign reversal can be obtained from (23) as

$$\begin{aligned} {\varepsilon }_0=\sqrt{\left| \frac{a_2}{a_4}\right| }. \end{aligned}$$

(25)

Moreover, for small amplitudes ${\varepsilon }<{\varepsilon }_0$, it is easy to show that there exists an optimal amplitude ${\varepsilon }^*={\varepsilon }_0 / \sqrt{2}$ for which $|{{\bar{a}}}|$ attains maximal value.

We now revisit the “Landshark” model and analyze the amplitude-dependent direction reversal observed in [33]. Using the definitions in (10), the Landshark’s nondimensional parameters are $\eta _1=\eta _2=1$, ${\beta }_1={\beta }_2=0$, leaving only the links’ length and mass ratio ${\alpha },{\kappa }$ as variables. Substituting this and $\zeta =-1$ (i.e., oscillations about $\phi _0=\pi$) into the expressions for $a_2$ and $a_4$ in Table 1 gives:

$$\begin{aligned} a_2=\frac{{\alpha }(1-{\alpha }{\kappa })}{2(1+{\alpha })^3(1+{\kappa })},\; a_4={\alpha }^2 \frac{{\kappa }(1-4 {\alpha })+4+{\alpha }}{16(1+{\alpha })^5(1+{\kappa })}\nonumber \\ \end{aligned}$$

(26)

Figure 5b plots regions of $\pm a_2 , \pm a_4 >0$ in the plane of ${\kappa },{\alpha }$. The shaded area denotes region of $a_2 a_4<0$, where amplitude-dependent direction reversal can occur. The result extends the analysis in [33], which only provided necessary conditions for possible direction reversal. For comparison, the hatched regions in Fig. 5b were labelled as ‘’ in [33], and satisfy necessary conditions for sign reversal under some input of $\phi (t)$. Figure 5b shows that these regions include the shaded regions satisfying our necessary and sufficient condition $a_2 a_4<0$. As specific examples, we fix ${\kappa }=1.8$ and choose three values ${\alpha }= \{0.5,0.57,0.75\}$, which are marked by ‘$\times ,+,*$’ in Fig. 5b, respectively. For each value of ${\alpha }$, we conduct numerical simulations with varying amplitudes ${\varepsilon }$ and compare the numerically computed mean acceleration ${{\bar{a}}}$ (dashed curves) to its four-order approximation in (23) (solid curves), all plotted as a function of ${\varepsilon }$ in Fig. 5c. It can be seen that only the value corresponding to marker “$+$” which lies within the shaded region in Fig. 5b exhibits direction reversal as a function of amplitude ${\varepsilon }$ in Fig. 5c. In contrast, the values corresponding to markers “$\times ,*$” which lie {inside, outside} the hatched region of [33] in Fig. 5b do not result in direction reversal. Finally, Fig. 5c shows that the deviations between numerical and $4^{th}$-order asymptotic approximation (dashed and solid curves) are vanishing for small ${\varepsilon }$ and begin to increase for ${\varepsilon }>1$, as expected. This concludes the first part of this work, which assumes ideal no-slip constraints. In the next section, we relax this assumption using Coulomb’s friction.

4 Friction-bounded hybrid dynamics of skid-state transitions

We now present bounds on the constraint forces of the wheel-ground contact according to Coulomb’s friction model, and then formulate of the vehicle’s hybrid dynamics under friction-induced skid state transitions.

4.1 Coulomb’s friction constraints and normal forces

For each wheel’s axle, the constraint force $\lambda _i$ has to satisfy Coulomb’s friction bound given by

$$\begin{aligned} |\lambda _i| \le \mu N_i \end{aligned}$$

(27)

where $N_i$ is the normal reaction force acting at the axle’s wheel(s) in ${{{{{\hat{\mathbf{z}}}}}}}$ direction, and $\mu$ is Coulomb’s coefficient of dry friction. Positions of the left and right wheels on the rear axle are denoted by ${{\mathbf {p}}}_{1a},{{\mathbf {p}}}_{1b}$, see Fig. 1b. The two normal forces acting on those wheels are denoted as $N_{1a},N_{1b}$, such that the total normal force on the back axle is $N_1=N_{1a}+N_{1b}$. For the front axle, the normal force $N_2$ acts on the single wheel positioned at ${{\mathbf {p}}}_2$. We now make a simplifying assumption that the vehicle is flat and the links lie within the horizontal xy plane with $z=0$. This assumption holds when the actual height of the links’ centers-of-mass is much smaller than the lengths $l_i$. Under this assumption, accelerations of the links in horizontal plane generate negligible moments about the wheels-ground contact points. This implies that the three normal forces $\{N_{1a},N_{1b},N_2\}$ are decoupled from the vehicle’s dynamics in xy plane and can be obtained from statically determinate equilibrium equations of total {force, torque} balance {along z, about xy } directions, which are written as:

$$\begin{aligned} \left\{ \begin{array}{l} N_{1a}+N_{1b}+N_2 = (m_1+m_2)g \\ \left( {{\mathbf {p}}}_{1a} N_{1a} \! + \! {{\mathbf {p}}}_{1b} N_{1b} \! + \! {{\mathbf {p}}}_{2} N_{2} \! - \! {{\mathbf {p}}}_{1} m_1 g \! - \! {{\mathbf {p}}}_{2} m_2 g \right) \! \times \! {{{{{\hat{\mathbf{z}}}}}}}\! = \! 0 \end{array} \right. \nonumber \\ \end{aligned}$$

(28)

This is a linear $3 \times 3$ system in the unknowns $\{N_{1a},N_{1b},N_2\}$, which is expressed in body-fixed frame as:

$$\begin{aligned}&\left( \!\begin{array}{crr} 1 &{} 1 &{} 1 \\ d &{} -d &{} -l_2 \sin \phi \\ 0 &{} 0\; &{} l_1 \!-\! l_2 \cos \phi \end{array} \! \right) \! \left( \begin{array}{c }{N_{1a}}\\ {N_{1b}}\\ {N_2}\end{array} \right) \nonumber \\&\quad \!=\! \left( \begin{array}{c }{m_1+m_2}\\ {m_2 h_2 \sin \phi }\\ {m_1 b_1 \! +\! m_2(l_1 \!-\! l_2 \cos \phi )} \end{array} \right) \! g \end{aligned}$$

(29)

The solution of (29) for normal forces depends only on the steering angle $\phi$. A singular case of unbounded forces occurs when $l_1=l_2 \cos \phi$, but this case is ruled out assuming $l_1>l_2$. In addition, tipover of the vehicle due to vanishing of one normal force may also occur, characterized by the two links’ common COM lying on the line connecting two wheels. This case is also rare for reasonable values of the vehicle’s geometric structure (more details appear in the thesis [44]).

4.2 Hybrid dynamics with skid-state transitions

We now formulate the system’s hybrid dynamics which accounts for friction bounds and transitions between skid state. First, consider the case where the no-skid constraint (3) at the $i^{th}$ wheel axle is satisfied. The constraint force ${\lambda }_i$ must satisfy Coulomb’s dry friction inequality (27), where the normal reaction force $N_i(\phi )$ is obtained from solving (29). When the friction bound in (27) is reached for the $i^{th}$ axle, it begins to skid, so that $\sigma _i(t)={{\mathbf {w}}}_i({{\mathbf {q}}}) \cdot {{\dot{\mathbf{q}}}}\ne 0$, and the constraint force reaches its maximal value, ${\lambda }_i=-\mu \text{ sgn }(\sigma _i)N_i$.

The skid states described above lead to $2^2=4$ possible “modes” of the system—combinations of the axles’ skid states. The dynamics of each mode is governed by a different set of equations, described as follows. First, Lagrange’s equations (7) still hold, giving three scalar equations (assuming $\phi (t)$ is prescribed and eliminating the third row in (7) which also contains the torque $\tau (t)$). However, the equation (9) of the time-derivative of the no-skid constraints does not always hold, and should be replaced by two equations which depend on the skid state of each axle, given as:

$$\begin{aligned} \left\{ \begin{array}{ll} {{\mathbf {w}}}_i({{\mathbf {q}}}) \cdot {{\ddot{\mathbf{q}}}}+ {{{\dot{\mathbf{w}}}}}_i({{\mathbf {q}}},{{\dot{\mathbf{q}}}}) \cdot {{\dot{\mathbf{q}}}}=0 \;\;\; &{} \text{ axle } i \hbox { is not skidding} \\ {\lambda }_i=- \mu N_i \mathrm {sgn}({{\mathbf {w}}}_i({{\mathbf {q}}}) \cdot {{\dot{\mathbf{q}}}}) \;\;\; &{} \text{ axle } i \hbox { is skidding} \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(30)

for $i=1,2$. Combining equations (30) with (7) gives a system of differential-algebraic equations which yields a $5 \times 5$ linear system in the unknowns, $\{{\ddot{x}},{\ddot{y}},{\ddot{\theta }}, {\lambda }_1, {\lambda }_2\}$ for a prescribed angle input $\phi (t)$.

Transitions between different modes of the hybrid dynamics are described as follows. A non-skidding axle begins to skid whenever its constraint forces reaches its frictional bound, $|{\lambda }_i|=\mu N_i$. When the slip velocity of a skidding axle vanishes ${{\mathbf {w}}}_i({{\mathbf {q}}}) \cdot {{\dot{\mathbf{q}}}}=0$, the wheel may switch back to no-skid state, provided that the constraint force at the initial instant right after switching satisfies its bound $|{\lambda }_i|\le \mu N_i$. Otherwise, the wheel’s slip velocity reverses its sign. All this gives rise to a hybrid dynamical system, containing transitions between different skid states.

Singularity of the hybrid dynamic equations should also be examined, by constructing the matrix of the linear system which governs the dynamics under each mode of skid states, and checking whether its determinant can cross zero. The details of this singularity analysis appear in Appendix, for both cases of controlled actuation torque $\tau (t)$ or controlled steering angle $\phi (t)$. Summarizing this analysis, it is concluded that for each state that involves skidding, the simplifying assumptions of point-mass model, ${\kappa }=\eta _1=0$ from [29], may lead to singularity. This justifies considering the two links’ masses and inertia in our work.

Fig. 6

Time plots of simulation results of the system’s hybrid dynamics under actuation frequency $\omega =2.5 \; rad/s$. Solid lines—no-skid motion. Dashed lines—skidding. a Forward speed $v_1(t)$. b Vehicle’s orientation angle $\theta (t)$. c Forces’ ratio ${\lambda }_i / (\mu N_i)$ vs. time for $i=1,2$, overlaid with skid velocities ${\sigma }_i(t)$

Fig. 7

Time plots of periodic solution of the system’s hybrid dynamics under actuation frequency $\omega =6 \; rad/s$ after convergence to steady-state. Solid lines—no-skid motion. Dashed lines—skidding of front axle only, ${\sigma }_1=0, {\sigma }_2 \ne 0$. Dotted lines—both axles are skidding, ${\sigma }_1, {\sigma }_2 \ne 0$. a Forward speed $v_1(t)$. b Vehicle’s orientation angle $\theta (t)$. c Forces’ ratio ${\lambda }_i / (\mu N_i)$ vs. time for $i=1,2$, overlaid with skid velocities ${\sigma }_i(t)$

5 Numerical simulation results of the hybrid dynamics

We now present numerical simulation results of the hybrid system. The simulations are conducted using ode45 procedure of MATLAB for adaptive-step integration, with event functions for detecting zero-crossing conditions for each mode’s termination. Parameter values are chosen based on the robot prototype in Fig. 3a, as $m_1\!=\!2.29 Kg$, $m_2\!=\!0.229 Kg$, $l_1\!=\!0.362m$, $l_2\!=\!0.19m$, $b_1\!=\!0.1249$, $b_2=0.5l_2$, $I_i=m_i l_i^2/12$ for $i=1,2$, $d=0.1 m$ and friction coefficient of $\mu =0.3$.

5.1 Periodic solutions with skid-state transitions

First, we show how the system’s motion converges to periodic solutions with skid-state transitions. The input steering angle is $\phi (t)={\varepsilon }\cos ({\omega }t)$ with ${\varepsilon }=0.6 rad$ and $\omega =2.5 rad/s$, under initial conditions of zero velocity ${{\dot{\mathbf{q}}}}(0)=0$. Figure 6a,b shows time plots of the forward speed $v_1(t)$ and orientation angle ${\theta }(t)$. Pieces of dashed curves represent motion, while the front axle is skidding, ${\sigma }_2(t) \ne 0$ whereas solid curves correspond to no-skid motion. It can be seen that the system begins with no-skid motion and accelerates until onset of skidding. Then, the solution converges to periodic motion with skid-state transitions, which contains bounded oscillations of $v_1(t)$ and ${\theta }(t)$ about mean speed and orientation, respectively. This result is remarkably different from the unrealistic solution divergence of the no-skid model [29], see Fig. 2a,b.

Figure 6c shows time plots of the forces’ ratio ${\lambda }_i / (\mu N_i)$ vs. time for $i=1,2$, overlaid with the skid velocities ${\sigma }_i(t)$. It can be seen that the constraint forces converge to periodic solution while staying bounded by the friction inequalities (27), in contrast to their divergence in the no-skid simulation (Fig. 4b). The slip velocity of the front wheel ${\sigma }_2(t)$ is initially zero, and then becomes nonzero whenever the constraint forces reaches its bound $|{\lambda }_2(t)|=\mu N_2(t)$. The motion converges to periodic solution, while the rear axle never skids, ${\sigma }_1(t) = 0$, since the associated constraint force is always below its friction bound, $|{\lambda }_1(t)|< \mu N_1(t)$. One can see that in steady state, the angle ${\theta }(t)$, contact forces ${\lambda }_i(t)$ and slip velocity ${\sigma }_2(t)$ are periodic in $t_p=2\pi /\omega$. Moreover, they satisfy half-period anti-symmetry $f(t+t_p/2)=-f(t)$ where $f \in \{\phi , {{\dot{\theta }}}, {\lambda }_i, {\sigma }_i \}$. Symmetry of the vehicle about $\phi =0$ implies that the forward speed is doubly periodic $v_1(t+t_p/2)=v_1(t)$. This also agrees with the asymptotic analysis of the no-slip system in [29]. (See also (20) where the frequency of forward speed is doubled).

Next, we consider simulation results with higher actuation frequency of $\omega =6 rad/s$. The system’s motion converges to a steady-state periodic solution with significantly different characteristics, as shown in the time plots of Fig. 7. One can see that the rear axle now undergoes alternating sequence of stick-slip transitions where ${\sigma }_1(t)$ switches between zero and nonzero values . On the contrary, the front axle always slips, ${\sigma }_2(t) \ne 0$, while its direction reverses alternately, every half period. This type of motion is remarkably similar (qualitatively) to the experimental measurements obtained with the robotic vehicle, see Fig. 3. Upon changing the actuation frequency, the mean value of $v_1(t)$ displays a small change (Figs. 6a, 7a). On the other hand the oscillation amplitude of the vehicle’s orientation angle ${\theta }(t)$ changes drastically ($\Delta {\theta }=\{124^\circ ,38^\circ \}$ for $\omega =\{2.5,6\}$ in Figs.  6b, 7b, respectively, where $\Delta {\theta }={\theta }_{max}-{\theta }_{min}$). In both cases, the angle ${\theta }(t)$ oscillates about a constant mean value, which implies net translation along a straight line with zero net rotation .

Fig. 8

Properties of simulated steady-state periodic solutions as a function of actuation frequency ${\omega }$: a Percentage of each skid state out of the period time. b Oscillation amplitude of body orientation angle $\Delta {\theta }= {\theta }_{max}-{\theta }_{min}$

Fig. 9

Peformance of simulated steady-state periodic solutions as a function of actuation frequency ${\omega }$: a Forward distance per cycle S (solid curve) and mean speed v (dashed). b Energetic cost of transport W/S

5.2 Influence of input frequency on performance

We now analyze the influence of input frequency ${\omega }$ on properties of the hybrid periodic solution. We conduct numerical simulations under input (1) with $\phi _0=0$, ${\varepsilon }=0.6 rad$ and frequency ${\omega }$ that varies in small increments within the range [0.3, 8.5]rad/s. For each frequency, we simulate the hybrid dynamics and detect the steady-state periodic solution to which the system converges. Several performance measures of the periodic solutions as a function of frequency ${\omega }$ are plotted in Figs. 8, 9. Figure 8a plots the percentage that each skid state occupies out of the period time $t_p=2\pi /\omega$. It can be seen that for low frequencies, the only existing states are no-skid (${\sigma }_1={\sigma }_2=0$, solid curve) and stick-skid (${\sigma }_1=0, {\sigma }_2 \ne 0$, dashed curve). As the frequency ${\omega }$ increases, the no-skid state become shorter. At ${\omega }\approx 3.25 rad/s$, the state skid-skid emerges (${\sigma }_1, {\sigma }_2 \ne 0$, dotted curve), and its relative time duration grows with ${\omega }$. At ${\omega }\approx 3.5 rad/s$ the no-skid state disappears. The “noisy” values around ${\omega }=3.5$ are a result of numerical sensitivity of the event-based integration when two different events are almost coinciding. The vertical dash-dotted lines in Figs. 8, 9 represent the frequencies $\omega =\{2.5,6\}$ from the simulations in Figs. 6, 7, respectively.

In the steady-state periodic solution, the body orientation angle ${\theta }(t)$ oscillates about a mean value ${{\bar{{\theta }}}}$ (see Figs. 6b, 7b), so that the net motion is pure translation with zero net rotation. Figure 8b plots the oscillation amplitude of ${\theta }(t)$ as a function of frequency ${\omega }$, showing that it decays with ${\omega }$. Next, we define the forward displacement per cycle as $S=\left( {{\mathbf {c}}}_1(t+t_p)-{{\mathbf {c}}}_1(t)\right) \cdot {{{{{\bar{\mathbf{e}}}}}}}_1$, where ${{{{{\bar{\mathbf{e}}}}}}}_1=(\cos {{\bar{{\theta }}}}, \sin {{\bar{{\theta }}}})^T$ is unit vector along the mean body orientation. The mean translation speed is defined as $v=S / t_p$. Plots of the displacement S (solid) and speed v (dashed) as a function of frequency ${\omega }$ are overlaid in Fig. 9a. One can see direction reversals for low frequencies, caused by large oscillation amplitudes of ${\theta }(t)$ which result in large rotations $\Delta {\theta }$ of more than a full revolution of the body orientation during cycle for ${\omega }<0.9 rad/s$. These large rotations are not physically realistic and did not occur in the experiments (Fig. 2), as they require very small amount of energy dissipation due to skid during the cycle. In addition, one can see in Fig. 9a extremum points of optimal frequencies for which |S| and |v| are maximized. Finally, we compute the mechanical energy expenditure per cycle $W=\int \tau (t) {{\dot{\phi }}}(t) dt$. A plot the energetic cost of transport W/|S| as a function of frequency appears in Fig. 9b. One can see three minimum points of optimal energy efficiency, corresponding to the three regions of reversed directions. If one considers only the more practical range of sufficiently large frequency with reasonable rotations, there are unique optimal frequencies for maximizing distance, speed and energy efficiency. (More precisely, the frequency ${\omega }$ should be replaced by the nondimensonal quantity $\psi =\dfrac{l{\omega }^2}{\mu g}$ which represents ratio of characteristic constraint forces to normal reaction forces. The ratio $\psi$ actually governs the system’s dynamic behavior. That is, increasing ${\omega }^2$ is equivalent to decreasing the friction coefficient $\mu$).

An open question which requires further exploration is whether this system has co-existing hybrid periodic solutions, stability transitions, bifurcations and chaos, cf. [45]. In our analysis, we focused only on periodic solutions that also possess half-period symmetry and involve zero net rotations. In such solutions, we did not find any co-existing solutions or stability loss of our solutions, which was assesed by numerical evaluation of Poincaré map linearization eigenvlaues. It could be possible that periodic solutions with nonzero net rotations exist, and the search for them and their stability analysis and bifurcations are left for future investigation.

6 Conclusion

We have presented significant extensions of the theoretical model of the Twistcar’s nonholonomic dynamics under oscillating steering angle. The point-mass model from our previous work [29] has been extended to include mass and inertia of both links, and the asymptotic expansion enabled studying the effect of the vehicle’s geometry and inertia parameters on reversal in direction of net motion. In addition, carrying the asymptotic expansion to next-order correction terms enabled discovering cases of direction reversal depending on the input amplitude ${\varepsilon }$, which provides explanation to results from [33] for the Landshark model. Next, we have relaxed the no-skid assumption of ideal nonholonomic constraints by considering Coulomb friction bounds on constraint forces, and introducing hybrid dynamics of skid-state transitions. Numerical simulations of the complex hybrid dynamics show convergence to periodic solution with skid-state transitions and bounded oscillations of both forward speed and body orientation angle, in agreement with previous experimental observations. Finally, the influence of actuation frequency ${\omega }$ on the vehicle’s performance in steady-state periodic solution was studied. We have found very close optimal values of frequencies that maximize the mean speed, travel distance per cycle, and energetic cost of transport (energy per distance).

We now briefly discuss limitations of the current results and sketch possible directions for future extension of the research. First, while the theoretical predictions agree qualitatively with observations from our preliminary experiments, a more thorough quantitative analysis of controlled motion experiments is crucially needed in order to study effects of actuation frequency and amplitude as well as vehicle’s structural parameters on its motion. Second, general models of frictional contact forces and other possible mechanisms of energy dissipation such as rolling resistance should be studied both experimentally and in mathematical analysis. From our preliminary experiments, the value of Coulomb’s dry friction coefficient is crudely estimated within the range $0.1 \le \mu \le 0.7$. However, it depends crucially on material properties of the terrain and the wheels’ structure, and may contain directional anisotropy. Thus, a more thorough analysis of the contact mechanics and dissipation is needed. In addition, the simplifying assumption of “flat vehicle” with negligible height of its COM should be relaxed in order to investigate the influence of COM accelerations on ground contact forces in dynamic maneuvers. Third, extending the small-amplitude asymptotic analysis from Section 3 and from [29] to the case of hybrid skid-states motion is a highly challenging analytical problem. Fourth, the current analysis is limited to the case of harmonic input of steering angle. Finding optimal gaits of arbitrary time-periodic inputs is still an open problem for this type of system. One may consider a purely computational approach as in [46], where the input is taken as a truncated Fourier series whose finite set of coefficients is optimized for maximal displacement. Alternatively, one can apply optimal control formulation as in [25] or its direct numerical solution as in [47]. Finally, the research should be extended to account for multi-link wheeled vehicles, possibly with passive elastic joints, as in [48,49,50].

Appendix—singularity analysis of the hybrid dynamics

Table 2 Determinants $\Delta _{ijk}$ of the system’s dynamics for all cases

Table 3 Singularity conditions

The dynamics of the constrained system in (7) and (9) can be rearranged into differential algebraic system as:

(31)

The inertia matrix ${{\mathbf {M}}}$ is positive definite, except for degenerate cases where $m_2$ and/or $I_1$ vanish ($\kappa ,\eta _1=0$), which result in ${{\mathbf {M}}}$ being only positive semi-definite (i.e., singular). Singularity of the constrained dynamics (31) depends on rank of the $6 \times 6$ matrix ${{\mathbf {A}}}$, whose determinant is denoted $\Delta$. It has been shown in [29] that this matrix has full rank ($\Delta \ne 0$) even for the degenerate point-mass model where $\kappa =\eta _1=0$ and $\mathrm {rank}({{\mathbf {M}}})=2$, as long as ${\beta }_1 \ne 0$.

We now investigate conditions for singularity of the dynamics under all possible skid states, considering both cases of controlled actuation torque $\tau (t)$ or controlled steering angle $\phi (t)$. In the latter case of controlled angle, since $\tau$ appears only in the fourth row of (31), and $\phi (t)$ is no longer unknown, both $\tau$ and ${\ddot{\phi }}$ can be eliminated by removing both fourth row and fourth column of ${{\mathbf {A}}}$ and reducing (31) to a $5 \times 5$ system. If the first axle skids, ${\sigma }_1(t)={{\mathbf {w}}}_1(q) \cdot {{\dot{\mathbf{q}}}}\ne 0$, the constraint in the fifth row of (31) no longer holds, and ${\lambda }_1$ can be eliminated from (31). Therefore, both the fifth row and fifth column of ${{\mathbf {A}}}$ should be removed. Similarly, if the second axle skids, the sixth row and sixth column of ${{\mathbf {A}}}$ should be removed. If additionally, the input is the steering angle, the fourth row and column of ${{\mathbf {A}}}$ should be removed as well. That is, each case is associated with removing the fourth and/or fifth and/or sixth row and column from ${{\mathbf {A}}}$. This results in $n \times n$ matrix for $n \in \{3,4,5,6\}$, which is still positive semi-definite. Singularity of each case can be assessed by analyzing the determinant $\Delta _{ijk}$ of the matrix obtained by removing the $\{i,j,k\}^{th}$ rows and columns of ${{\mathbf {A}}}$. (For example, we denote $\Delta _4$, $\Delta _{56}$, $\Delta _{456}$ etc.). For convenience, the matrix ${{\mathbf {A}}}$ is calculated using the nondimensional quantities defined in (10). Due to rotational invariance of (31), evaluation is made for ${\theta }=0$ without loss of generality. Expressions for the $n \times n$ determinants for all cases are given in Table 2. Conditions for singularity in all possible skid states and choice of controlled input are summarized in Table 3. We assume that ${\alpha }\in (0,1)$ and ${\beta }_1,{\beta }_2 \in [0,1]$, but alternative limits can be considered as well. The results in Table 3 show that in most of the skid states, the overly simplifying assumptions of massless link (${\kappa }=0$) and/or point masses ($\eta _i=0$) lead to singularity of the dynamics, where wither accelerations or constraint forces may grow unbounded.