Abstract
We consider the wrinkling of highly stretched, thin rectangular sheets—a problem that has attracted the attention of several investigators in recent years, nearly all of which employ the classical Föppl–von Kármán (F–K) theory of plates. We first propose a rational model that correctly accounts for large mid-plane strain. We then carefully perform a numerical bifurcation/continuation analysis, identifying stable solutions (local energy minimizers). Our results in comparison to those from the F–K theory (also obtained herewith) show: (i) For a given fine thickness, only a certain range of aspect ratios admit stable wrinkling; for a fixed length (in the highly stretched direction), wrinkling does not occur if the width is too large or too small. In contrast, the F–K model erroneously predicts wrinkling in those very same regimes for sufficiently large applied macroscopic strain. (ii) When stable wrinkling emerges as the applied macroscopic strain is steadily increased, the amplitude first increases, reaches a maximum, decreases, and then returns to zero again. In contrast, the F–K model predicts an ever-increasing wrinkling amplitude as the macroscopic strain is increased. We identify (i) and (ii) as global isola-center bifurcations—in terms of both the macroscopic-strain parameter and an aspect-ratio parameter. (iii) When stable wrinkling occurs, for fixed parameters, the transverse pattern admits an entire orbit of neutrally stable (equally likely) possibilities: These include reflection symmetric solutions about the mid-plane, anti-symmetric solutions about the mid-line (a rotation by π radians about the mid-line leaves the wrinkled shape unchanged) and a continuously evolving family of shapes “in-between”, say, parametrized by an arbitrary phase angle, each profile of which is neither reflection symmetric nor anti-symmetric.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Transverse wrinkles often form in extremely thin, rectangular elastic sheets when two opposing clamped ends are pulled apart. Apparently Friedl et al. (2000) was the first work to identify and analyze a model for the problem. Shortly thereafter it was taken up by Cerda et al. (2002) and Cerda and Mahadevan (2003), which drew a great deal of attention to the problem leading to many subsequent investigations; see, e.g., Jacques and Potier-Ferry (2005), Puntel et al. (2011), Nayyar et al. (2011) (the present work being no exception). Each of these papers gives a nice overview of wrinkling with applications and extensive bibliographies, which we do not attempt to reproduce here. From the point of view of analysis, a basic idea put forth in those works is that wrinkling, in the presence of small bending stiffness, can be treated as a bifurcation from the primary planar stretched state, with macroscopic (end) strain as the control parameter. For realistic aspect ratios and truly clamped boundary conditions, the pre-wrinkled planar state is non-homogenous; the clamped boundary conditions prevent uniform Poisson contraction in the transverse direction, potentially leading to transverse compression that is relieved by wrinkling. Apparently an accurate pre-wrinkled solution must be determined numerically. Most of the above-cited works incorporate various clever but nonetheless approximating assumptions concerning the pre-wrinkled state in order to carry out a linear instability analysis “by hand”, while relying on the classical Föppl–von Kármán theory, e.g., Dym and Shames (1973). The latter incorporates linear infinitesimal elasticity as a model for the planar unwrinkled behavior. An exception to this approach is the work of Nayyar et al. (2011); the commercial finite-element code Abaqus is employed using finite-deformation hyper-elastic shell elements. They investigate post-critical wrinkling via ad-hoc mode-imperfection “trials” near the critical state, the latter of which is highly singular due to the fine thickness of the film. While some of the correct post-critical phenomena is apparently captured in that work, the results are incomplete. A true bifurcation analysis is not carried out; more importantly no stability information is obtained. Also, the underlying two-dimensional continuum model is neither identified nor discussed in Nayyar et al. (2011).
Our contributions to this problem are the following. We first modify the Föppl–von Kármán model, in the simplest manner possible, accounting for the finite mid-plane deformation of the highly stretched state. We study the resulting continuum model, in particular noting the singularly perturbed structure of the bifurcation problem, and we discuss the existence of planar solutions via minimum-energy arguments. We then use a so-called conformal finite-element discretization (e.g., Reddy 2004) and employ Euler–Newton arc-length continuation (Keller 1987) or path-following to compute equilibria. The latter is greatly facilitated by the use of continuation parameters other than the applied macroscopic strain. In particular, for primary continuation we employ the naturally occurring reciprocal of the squared thickness of the film. Thus we avoid the potential numerical pitfalls of a singularly perturbed eigenvalue problem to determine the onset of wrinkling. We also introduce a rescaling parameter enabling continuation in the aspect ratio. We carefully perform an accurate bifurcation analysis and identify stable equilibria (local energy minimizers). We efficiently obtain numerous stable wrinkled states via continuation, often of striking consequence—especially in comparison with the numerical results for the Föppl–von Kármán model, which we also provide:
-
(1)
For a given fine thickness, only a certain range of aspect ratios admit stable wrinkling; for a fixed length (in the highly stretched direction), wrinkling does not occur if the width is too large or too small. In contrast, the Föppl–von Kármán model erroneously predicts wrinkling in those very same regimes for sufficiently large applied macroscopic strain.
-
(2)
When stable wrinkling emerges as the applied macroscopic strain is steadily increased, the amplitude first increases, reaches a maximum, decreases, and then returns to zero again. In contrast, the Föppl–von Kármán model predicts an ever-increasing wrinkling amplitude as the macroscopic strain is increased.
-
(3)
When stable wrinkling occurs, for fixed parameters, the transverse pattern admits an entire orbit of neutrally stable (equally likely) possibilities: These include reflection symmetric solutions about the mid-plane, anti-symmetric solutions about the mid-line (a rotation by π radians about the midline leaves the wrinkled shape unchanged) and a continuously evolving family of shapes “in-between”, say, parametrized by an arbitrary phase angle, each profile of which is neither reflection symmetric nor anti-symmetric.
We remark that the qualitative behavior (2) and to a lesser extent (1) can be seen in the results from Nayyar et al. (2011)—albeit in the absence of stability information and apparently for anti-symmetric wrinkled patterns only. Our detection of the phenomenon in (3) is new.
The outline of the work is as follows: In Sect. 2 we propose a simple modification of the classical Föppl–von Kármán model accounting for finite in-plane strain; we replace the 2×2 infinitesimal in-plane strain tensor with the 2×2 in-plane Green’s strain tensor in the stored-energy function. An examination of the governing Euler–Lagrange equilibrium equations reveals a geometrically correct nonlinear membrane theory coupled to linear bending. The latter, as in the von Kármán theory, is adequate for the small-amplitude wrinkles expected under very high tension. For purely planar behavior (no wrinkling), this is tantamount to a so-called Saint Venant–Kirchhoff material, which is well known to be inadequate for the general purposes of nonlinear elasticity, cf. Raoult (1986), Ciarlet (1988).
In Sect. 3 we examine the consequences of this from the point of view of mathematical existence. First we justify the use of the Saint Venant–Kirchhoff material for determining the highly stretched planar state: Using general results from Le Dret and Raoult (1995), we show that the quasi-convexification of the minimum energy problem (allowing for well-posed existence), requires no modification of the stored energy function in a large neighborhood of finite (Green) strains: one principal strain is positive while the other principal strain is positive or possibly negative, the permissible magnitude of the latter being not more than that allowed by Poisson contraction. This is certainly reasonable and within the “operating” regime of the problem at hand. Within that regime we can say something about the existence of energy minimizers and their partial regularity for our model. Next we examine the ostensibly singularly perturbed structure of the bending equation; as in the von Kármán model, this reflects the direct dependence of the bending energy on the third power of thickness of the sheet, while the in-plane energy is directly dependent upon the thickness itself. We propose a simple but key idea to get around this difficulty: We divide the bending equation by the squared thickness, and then treat its reciprocal—now appearing in the lower-order terms—as a global bifurcation/continuation parameter. In this way the principal part of the elliptic (biharmonic) operator is left undiminished, while continuation to large values of the new bifurcation parameter (with the macroscopic strain fixed) leads to desired solutions of very fine thickness. We remark that we have already used this idea with great advantage in phase-change problems for solids in the presence of small interfacial energy, cf. Healey and Miller (2007).
In Sect. 4 we discuss our numerical discretization and overall solution strategy. The formulation incorporates several explicit continuation parameters: the reciprocal of the squared thickness of the film, the macroscopic strain, a rescaling parameter controlling the aspect ratio, and Poisson’s ratio. Also noteworthy here is the identification of two classes of solutions—reflection symmetric and anti-symmetric. We solve each of these via distinct boundary value problems on the quarter domain, the latter reduction coming from the fact the both classes of wrinkled solutions have reflection symmetry about the mid-plane perpendicular to the line of action of the imposed macroscopic strain. We emphasize that once such equilibria are found, they are readily extended by symmetry to the entire domain, which is necessary for a careful evaluation of the Hessian associated with the second variation of the energy for stability. In Sect. 5 we present our numerical results. We immediately observe that stable equilibria always come in pairs—one reflection symmetric and the other anti-symmetric. We note the lack of sufficient symmetry in the model to justify this apparent degeneracy. Instead we use an approximate beam-on-elastic foundation analogy to argue that the two different modes asymptotically coincide as the thickness of the film goes to zero. This, in turn, leads to the apparent “asymptotic continuous symmetry” discussed in (3) above.
2 Formulation
In this section we formulate the problem of a highly stretched, thin elastic film, employing a modification of the Föppl–von Kármán model. Let {e 1,e 2,e 3} denote a fixed orthonormal basis for the Euclidean vector space \(\mathbb{E}^{3}\). We assume that the undeformed rectangular sheet, denoted Ω, lies in the plane \(\mathbb{E}^{2} = \operatorname{span}\{ \mathbf{e}_{1},\mathbf {e}_{2}\}\); Ω={x:=x α e α :x 1∈(0,L),x 2∈(0,W)}. Here and throughout we employ summation convention, with repeated Latin indices summing from 1 to 3, and repeated Greek indices summing from 1 to 2. We denote the deformation of the sheet, \(\mathbf{f}:\varOmega\to\mathbb{E}^{3}\), via
where \(\mathbf{u}:\varOmega\to\mathbb{E}^{2}\ \mbox{and } w:\varOmega \to\mathbb{R}\) denote the in-plane displacement and the out-of-plane displacement component, respectively. The deformation gradient is then given by
where ∇(⋅) denotes the surface gradient, I:=e α ⊗e α , and “⊗” denotes the tensor product. This yields the membrane (Lagrangian) strain
and we also define the linear bending strain
where ∇2:=∇∘∇(⋅) denotes the surface second gradient.
As illustrated in Fig. 1, we fix the sheet on the left side of the boundary at x 1=0, and on the right side we prescribe the displacement u(L,x 2)≡εL e 1,ε>0. It is convenient to make the change of variables u′(x)≡u(x)−εx 1 e 1. Henceforth dropping the notation (⋅)′, equations (2.2), (2.3) now take the form


respectively, where the subscript has been added to emphasize the dependence upon the macroscopic strain ε. Accordingly we may now prescribe the homogeneous boundary conditions
As in the Föppl–von Kármán model, we assume an additive decomposition of the stored energy density, in terms of membrane and bending effects, viz., ϒ m +ϒ b , where
with E,ν and h denoting Young’s modulus, Poisson’s ratio and sheet thickness, respectively. In the absence of body forces and tractions (on the top and bottom parts of the boundary), we may normalize (2.8) to
without affecting the formulation. The total (normalized) potential energy of the film is then given by
Note that our problem is independent of Young’s modulus; we make the physically reasonable assumption
Next we define
Clearly N ε is the (in-plane) second Piola–Kirchhoff (P–K) stress tensor, while M is a couple-stress tensor. Smooth fields \(\boldsymbol {\eta}:\varOmega\to \mathbb{E}^{2}\ \mbox{and } \zeta:\varOmega\to\mathbb{R}\) satisfying the respective geometric conditions (2.7) are said to be admissible variations. The first variation of the energy yields the weak form of the equilibrium equations:

for all admissible variations η,ζ. Integration by parts formally delivers the Euler–Lagrange equilibrium equations for (2.10):
where ∇⋅(⋅) denotes the surface divergence. From (2.4), (2.9)2, and (2.12), the equilibrium equations (2.14) take on the more revealing form
where Δ(⋅):=∇⋅(∇(⋅)) denotes the Laplace operator and Δ2(⋅):=Δ∘Δ(⋅) the biharmonic operator. Integration by parts also gives natural boundary conditions, which we list here for the sake of completeness:
where n denotes the outward unit normal to the boundary ∂Ω. In summary, the formal boundary value problem (BVP) comprises the partial differential equations (2.15), the geometric boundary conditions (2.7), the natural boundary conditions (2.16), (2.17), the constitutive relations (2.9), (2.12), and the kinematic relations (2.4), (2.6).
Our model combines a geometrically exact, nonlinear membrane theory, cf. (2.5), (2.6), (2.9)1, with the linearized bending theory of the von Kármán model, cf. (2.4), (2.9)2. Observe that it reduces to the Föppl–von Kármán model when the nonlinear strain term “∇u T∇u” is dropped from (2.3), e.g., cf. Dym and Shames (1973). The differences between the Föppl–von Kármán model and ours arise, not only from the use of the Lagrangian strain (2.3), (2.6) in (2.12)1, (2.17), but perhaps more profoundly in the governing equations (2.15). Observe that (2.15)1 requires the divergence of the “in-plane” first Piola–Kirchhoff stress to vanish, whereas in the classical model we have ∇⋅N=0. The former impacts (2.15)2, generally giving rise to a first-order term (in ∇w), which vanishes identically in the classical case.
3 Mathematical Considerations
We first look for planar solutions of the BVP, i.e.,w≡0, in which case (2.15)2, (2.16), (2.17)3,4 are satisfied identically, while (2.6), (2.7), (2.12)1, (2.15)1, (2.17)1,2 specialize to a rather formidable problem of 2-dimensional nonlinear elasticity (in \(\mathbb{E}^{2}\)). Indeed for ε>0, it’s easy to see that there are no homogeneous solutions satisfying (2.7), and it seems highly unlikely that a closed-form inhomogeneous solution can be found. It’s then natural to contemplate local existence theorems, say, based upon the implicit function theorem, e.g., Valent (1988), and subsequent global continuation methods, cf. Healey and Simpson (1998). However, all such techniques demand sufficient smoothness of solutions that would obviate the expected singularities arising at the four corners of Ω, where prescribed displacements (2.7) and tractions (2.17)1,2 meet.
Another possibility is to employ direct methods of energy minimization in order to obtain the existence of a planar solution. The so-called Saint Venant–Kirchhoff energy density W m (E) does not exhibit unbounded growth as detF↘0 (cf. (2.2), (2.9)1 with w≡0 and \(\mathbf{F} \in L(\mathbb {E}^{2}): = \mathrm{set\ of\ all\ linear\ transformations\ of}\ \mathbb{E}^{2}\ \mathrm{into\ itself}\)). But this is more than acceptable for thin films, since we expect out-of-plane wrinkling in lieu of vanishing local area ratios. Moreover, it simplifies the analysis of the planar problem. On the other hand, the minimization of
with \(\mathbf{E} \in L(\mathbb{E}^{2})\) given by (2.6) (with w≡0), subject to (2.7)1,2, is generally not well posed—the functional is not quasi-convex, cf. Raoult (1986). As such, the minimum of (3.1) will not generally be attained in the expected topology \(\mathbf{u} \in W^{1,4}(\varOmega;\mathbb{R}^{2})\) (i.e., each component u α (x) and its two generalized partial derivatives belong to L 4(Ω), α=1,2).
Fortunately it is known how to “repair” the problem by explicit construction of the quasi-convex envelope of W m (E), cf. Le Dret and Raoult (1995). We need a little extra notation in order to explain this. In view of (2.3) with w≡0, we define Φ(F T F):=W m (E). As shown in that work, the quasi-convex envelope of W m (E) has the general characterization
where \(S_{2}^{ +}\) denotes the set of all positive, symmetric, semi-definite linear transformations of \(\mathbb{E}^{2}\) into itself. We then replace (3.1) with minimization of the relaxed energy
which always attains its minimum under the conditions described above for (3.1). Moreover, the minimum of (3.3) coincides with the infimum of (3.1), and any infimizing sequence for (3.1) has a subsequence converging weakly in \(W^{1,4}(\varOmega;\mathbb{R}^{2})\) to a minimizer of (3.3), cf. Dacorogna (2008).
An explicit formula for (3.2) is provided in Le Dret and Raoult (1995) for the Saint Venant–Kirchhoff density in the 3-dimensional setting. It is revealing to specialize their approach, in part, to our planar, 2-dimensional elasticity model. In particular, a calculation similar to theirs shows that
whenever the principal values of C=F T F, denoted \(\lambda _{1}^{2},\lambda_{2}^{2}\) (squared principle stretches) satisfy
That is, W m (E) coincides with its quasi-convex envelope \(W_{m}^{*}(\mathbf{E})\) within the domain (3.5). For our planar pre-wrinkled state, we expect \(\lambda_{1}^{2} \approx(1 + \varepsilon)^{2}\) with \(\lambda_{2}^{2} \le1\) possibly on some subset of Ω of non-zero measure. In that case the second condition in (3.5) simply requires no more than total Poisson contraction in terms of the principal Green strains. This is completely reasonable and expected for the problem at hand. We note that if a minimizer \(\mathbf {u} \in W^{1,4}(\varOmega;\mathbb{R}^{2})\) of (3.3) verifies (3.5), then by (3.4) and the results of Evans (1986), we see that u, which is easily shown to be a weak solution of (2.13) (with w=ζ≡0), actually satisfies the partial differential equation (pde) (2.15)1 in the strong sense a.e. in Ω. Finally we remark that for non-planar solutions the direct minimization of the energy (2.10) on \((\mathbf{u},w) \in W^{1,4}(\varOmega;\mathbb{R}^{2}) \times H^{2}(\varOmega)\) is well posed due to the convexity in the argument ∇2 w (provided it can be shown that any minimizer is not characterized by w≡0).
Next we take the point of view that a one-parameter family of planar solutions u=u ε ,w≡0 is known. Formal linearization of (2.15)2 then leads to the pde
where, from (2.6), (2.12)1, we have
Nontrivial solution pairs (ε,w) of (3.6), subject to (2.7)3,4, (2.16) and the linearization of (2.17)3,4, yield potential bifurcation points indicating the onset of wrinkling. More pertinent here is the weak form of (3.6), which follows most easily from (2.4), (2.12)2 and (2.13) with η≡0, \(\mathbf{N}_{\varepsilon} = \mathbf{N}_{\varepsilon} ^{o}\):
for all admissible variations ζ. In particular, choosing ζ≡w in (3.8), we arrive at
Since the last two terms in (3.9) are non-negative, we have:
Lemma
Suppose that \(\mathbf{N}_{\varepsilon} ^{o} \in L^{2}(\varOmega,\mathbb{R}^{2 \times 2})\) and
i.e., the second P–K stress is non-compressive almost everywhere in the stretched flat film. Then the only weak solution, w∈H 2(Ω) (i.e., w and each of its first and second generalized partial derivatives belong to L 2(Ω)), satisfying (3.8) is the trivial one w≡0 (no wrinkling). We conclude that a necessary condition for bifurcation is the violation of (3.10), i.e., that \(\mathbf{N}_{\varepsilon} ^{o}\) “sustains compression”.
The proof of the Lemma follows easily from (3.9), (3.10), which immediately yield ∇2 w=0⇒∇w=c (const.) a.e. in Ω. Integration and the boundary conditions (2.7) then imply w≡0.
4 Solution Strategy and Numerical Implementation
Since h 2 is extremely small for thin films, we recognize that (3.6) (or (3.8)) is a singularly perturbed eigenvalue problem. Indeed, the nonlinear pde (2.15)2 is singularly perturbed. Consequently, we generally expect numerical difficulties in realistic models of thin sheets. We avoid this problem here by an approach similar to that employed successfully in Healey and Miller (2007). The first simple step is to divide through by the squared thickness, replacing (2.15)2 with
The key idea is to employ κ as a bifurcation/continuation parameter. The numerical advantage of (4.1) over (2.15)2 is obvious: we leave the well behaved elliptic operator Δ2 w undiminished, while seeking bifurcations in the parameter κ, and use continuation to very large values of κ. Our selection criterion here, employed in concert with this approach, is to choose stable solutions, the latter which we now make precise.
First we define the admissible solution space
In view of (2.9), (2.10), we define an equivalent potential energy functional

where E ε is given by (2.6). For fixed ε,κ>0, we say that (u,w)∈X is a weak equilibrium solution if

for all admissible variations η,ζ, where N ε is defined in (2.12)1. Observe that (4.4) is equivalent to (2.13). In addition, the weak equilibrium solution (u,w) is said to be stable if the second variation of the potential energy evaluated there is positive, i.e.,

for all admissible variations η,ζ, such that η≠0 and/or ζ≠0, where

We employ the formulation (4.3)–(4.6) throughout the remainder of this work.
Obviously our problem is characterized by three explicit, non-negative parameters, ε,ν and κ, each of which is useful in continuation. It is also convenient for the purposes of continuation to have a parametric formulation allowing for variation of the aspect ratio. One way to accomplish this is to rescale the variable e 2⋅x=x 2→x 2/β,β>0, and then work on a fixed domain Ω=(0,L)×(0,W), where L,W are fixed constants. Defining the diagonal transformation
we then arrive at the appropriate formulation, characterized by explicit dependence upon β in (4.3)–(4.6), via the following substitutions:
That is, the expressions on the left of (4.8) are replaced in (4.3)–(4.6) by the respective expressions on the right. In this way, a solution w(x 1,x 2),u(x 1,x 2) of (4.3)–(4.6), for a given fixed value β>0 on the fixed domain (0,L)×(0,W), yields a solution w(x 1,βx 2),u(x 1,βx 2) on the domain (0,L)×(0,W/β).
Problem (4.3)–(4.8) has obvious but important symmetries that we exploit in computing equilibria:
In each case, we solve the problem on the lower half of the domain, say, subject to sets of boundary conditions along x 2=W/2, the latter of which we discuss shortly. In this way we efficiently separate the computation of two distinct families of equilibria. Of less importance, we also expect relevant solutions of each family (4.9) to possess reflection symmetry about the line x 1=L/2, enabling a further reduction to a quarter-domain in each case. However, it’s worth mentioning now that the full equilibrium solution, extended over the entire domain, is required in order to check for stability.
We discretize problem (4.3)–(4.6) via a uniform rectangular grid and employ 4-node rectangular conformal finite elements (e.g., Reddy 2004) as follows: Each corner of a given rectangular element possesses 6 degrees of freedom corresponding to the values of u 1,u 2,w,w,1:=∂w/∂x 1,w,2:=∂w/∂x 2 and w,12:=∂ 2 w/∂x 1 ∂x 2 there. We use a superscript j=1,…,4 to distinguish their values at each of the four corners of the element, respectively, say, counter-clockwise in a consistent way. Let (x c ,y c ) denote the coordinates of the center of a given element, and define the local coordinates (ξ,η), where ξ:=(x 1−x c )/a,η:=(x 2−y c )/b and “2a×2b” denotes the uniform size of each element. Letting (ξ j ,η j ) denote the local coordinates of the jth corner, we introduce the interpolation polynomials
Next we define the nodal variables vector for the element:
Then the displacement field over the element can be approximated via interpolation:
and the required derivatives are readily computed:
We now substitute (4.13) into (4.3) for each rectangular element and then sum, arriving at a finite-dimensional approximation of the total potential energy:

where “N
e
” denotes the total number of elements in the quarter-domain, Ω
i
is the rectangular domain of the ith element, \(\underline{\mathbf{u}} ^{i}\) is the nodal variables vector (4.11) for the ith element, and \(g(\underline{\mathbf{u}} ^{i};\kappa,\varepsilon,\beta,\nu)\) denotes the integrand in (4.3) after the substitution from (4.13). Here  denotes the global nodal “displacement” vector of unknowns, assembled in the usual way, representing the unconstrained degrees of freedom for the system. For both types of solutions (4.9), we work on the quarter-domain and enforce (2.7) along x
1=0. In consonance with (4.4), the problem is unconstrained along x
2=0. The following distinct sets of boundary conditions follow directly from (4.9):
denotes the global nodal “displacement” vector of unknowns, assembled in the usual way, representing the unconstrained degrees of freedom for the system. For both types of solutions (4.9), we work on the quarter-domain and enforce (2.7) along x
1=0. In consonance with (4.4), the problem is unconstrained along x
2=0. The following distinct sets of boundary conditions follow directly from (4.9):

We also impose the following reflection-symmetric boundary conditions for both types in (4.9):
The specifically chosen geometric boundary conditions (4.15) and (4.16) are now clear, given the degrees of freedom associated with our discretization. In particular, accounting for 6 degrees of freedom at each unconstrained node, and accounting for (2.7), (4.15), (4.16), assume a M×N grid on the quarter-domain, i.e., N e =MN, where M is along the length and N along the width. Then for each case in (4.15), the total number of unknowns for the problem is the same, viz.,
i.e.,  in each case (although their precise entries are not the same).
in each case (although their precise entries are not the same).
The vanishing of the total derivative of (4.14) delivers the discrete equilibrium equations

As is typical of any Rayleigh–Ritz method, (4.4) and (4.18) are the same when the former is evaluated according to (4.13) and the admissible variations (η,ζ)≡(u,w) are chosen in the same consistent manner. Specifically, we define the nodal variation vector for a typical element as in (4.11):
Then as in (4.12) we have
and we may compute approximate derivatives as in (4.13). Direct substitution into (4.4) now leads to

for all global variation vectors  , which yields (4.18).
, which yields (4.18).
Observe that  , i.e., (4.18) represents d simultaneous nonlinear equations in the d unknowns,
, i.e., (4.18) represents d simultaneous nonlinear equations in the d unknowns,  , while containing 4 parameters, κ,ε,β,ν, each of which is at our disposal for numerical continuation. The later requires various partial derivatives that are readily obtained from (4.18), e.g.,
, while containing 4 parameters, κ,ε,β,ν, each of which is at our disposal for numerical continuation. The later requires various partial derivatives that are readily obtained from (4.18), e.g.,

Equation (4.22)1 gives the tangent or Jacobian matrix for the symmetry-reduced problems associated with (4.15), (4.16), which is related to the second variation (4.6). But as mentioned previously, (4.5) must be evaluated at a solution for the full problem over the entire domain in the determination of stability. In either of the cases (4.15), together with (4.16), we readily extend the solutions by reflection or rotation via (4.9), and then extend by reflection across the line x
1=L/2. We denote the extended solution by  , where “r” denotes the total number of degrees of freedom for the full problem: Since we now have 4N
e
=4(MN) elements subject only to (2.7), we find that
, where “r” denotes the total number of degrees of freedom for the full problem: Since we now have 4N
e
=4(MN) elements subject only to (2.7), we find that
Imitating (4.14), we obtain the total potential energy for the full problem by summing over the total number of elements, 4N e :

We then obtain the required Hessian for checking stability by repeated differentiation of (4.24) as in (4.22)1:

Evaluated at an equilibrium  , observe that (4.15) is a symmetric, square matrix of size r
2, cf. (4.23). Similar to (4.18)–(4.21), the discretized second variation (4.5) is given by
, observe that (4.15) is a symmetric, square matrix of size r
2, cf. (4.23). Similar to (4.18)–(4.21), the discretized second variation (4.5) is given by

for all global variation vectors  . In view of (4.5) and (4.26), we conclude that the discrete equilibrium
. In view of (4.5) and (4.26), we conclude that the discrete equilibrium  is stable if the Hessian (4.25) is positive definite. Finally, we comment that in lieu of (4.25), the Hessian is easily and more efficiently assembled from the Jacobian (4.22)1 on the quarter-domain via sub-structuring.
is stable if the Hessian (4.25) is positive definite. Finally, we comment that in lieu of (4.25), the Hessian is easily and more efficiently assembled from the Jacobian (4.22)1 on the quarter-domain via sub-structuring.
5 Numerical Results
Referring to Fig. 2, we choose W=10 cm (width) and L=20 cm (length) as the dimensions of the fixed domain Ω. In order to solve (4.18) for the two cases (4.15) on the quarter-domain, our computational strategy is as follows:
-
1.
Fix κ=1/h 2=100, ν=0.45 (Poisson’s ratio) and β=1 (aspect-ratio parameter). For this moderately thick sheet (h=0.1 cm), wrinkling is not an issue: starting from the known solution point
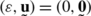 , compute a family of planar solutions (w≡0) of (4.18) with ε as the continuation parameter up to ε=0.1.
, compute a family of planar solutions (w≡0) of (4.18) with ε as the continuation parameter up to ε=0.1. -
2.
Next fix ε=0.1 and continue the family of planar solutions, but now with κ=1/h 2 as the continuation/bifurcation parameter. In the range 100≤κ≤20,000, locate the first few bifurcation points, say κ=κ m ,m=1,…,4, at which the Jacobian (4.22)1 is not invertible. For each of the cases (4.15), this is easily done by tracking the sign of a few of the smallest eigenvalues.
-
3.
Switch to nontrivial (non-planar) bifurcating branches with κ as the bifurcation parameter and compute to very large values of κ (corresponding to very small values of h 2).
-
4.
Extend the solution over the entire domain Ω according to (4.9) (as discussed above (4.23)), and then check for stability via positivity of the full Hessian (4.25). Since the Hessian H is symmetric, this is carried out efficiently via the Cholesky decomposition—its success/failure indicates a stable/unstable equilibrium.
-
5.
Once stable solutions are found for sufficiently small values of the squared thickness, fix κ=1/h 2 and continue solutions in the other three parameters to study robustness of the results. In particular, we are keenly interested in the behavior of wrinkled solutions as the macroscopic strain ε is varied.
Remark
In carrying out steps 1–3 and 5 above, we employ Euler–Newton continuation with pseudo arc-length control, cf. Keller (1987). Except at bifurcation points, the Euler prediction is proportional to the unique tangent to the solution curve; at simple bifurcation points the Euler prediction incorporates a component of the null vector of the Jacobian (4.22)1 to facilitate branch switching.
In Fig. 2 we summarize the results of the calculations resulting from steps 1–3 above, i.e., the bifurcation diagram is given for the first four bifurcating branches in κ=1/h 2 for each of the two problems (4.15). Here the anti-symmetric branches are shown in blue, and the reflection symmetric branches in red. Each of the eight branches is a projection of a “pitchfork” bifurcation. For reasons to be discussed shortly, the calculations throughout this section for the determination of equilibria are carried out on a 70×170 uniform grid on the quarter domain, i.e., N e =11,900, with more refinement in the x 2-direction. The stability check, step 4 above, reveals that the higher bifurcating branches 2–4 (bifurcating at values κ>1) are globally unstable, while the first two branches are “neutrally stable” all along the branches. We discuss this terminology in more detail shortly. In any case, Figs. 3 and 4 each depict three such wrinkled configurations—anti-symmetric and reflections symmetric, respectively—along the first branches at the specific solution points marked on Fig. 2. Note that in each case the three wrinkled configurations represent membrane thicknesses of 0.1, 0.05, and 0.033 mm, respectively, but otherwise corresponding to the same data.
A striking aspect of Fig. 2 is the apparent coincidence of bifurcation points (along the κ-axis) for the “blue” and the “red” branches. This is verified by their computed numerical values. Recall that these solution branches are computed via two distinct reduced problems, cf. (4.15). Of course each is a solution branch of the full problem. We remark that there is no generic explanation for the occurrence of double eigenvalues here based on symmetry. For example, the frequencies of vibration for simply-supported rectangular membranes and plates are “generically” distinct; see e.g., Meirovitch (1967). From the group-theoretic point of view, the irreducible representations of the symmetry group (of a thin rectangular object in 3-space) are all 1-dimensional. Thus, based on symmetry, we should expect a repeated eigenvalue here only in situations for which the parameters are specially “tuned”, cf. Golubitsky and Schaeffer (1985). This is closely related to our terminology above, neutrally stable, in reference to the first two apparently simultaneous branches. In particular, we find that the computed Hessian (4.25) along each branch is positive semi-definite, always possessing one and only one near-zero eigenvalue: along the anti-symmetric branch the near-zero eigenvalue is associated with a reflection symmetric eigenvector and vice versa. We draw this conclusion from the following observation.
We compare the smallest (in magnitude) computed eigenvalue of the Hessian (4.25) along the trivial solution up to the first bifurcation point and then along each of the first two bifurcating branches—anti-symmetric and reflection symmetric—as a function of κ for various grid sizes. The results are summarized in Fig. 5: For a given grid on the entire domain Ω, the two zero eigenvalues eventually depart slightly from zero—sometimes with opposite signs and sometimes together. But as the grid size is increased, the two eigenvalues “stay together at zero” for greater and greater values of κ. For example, for the grid size 140×340, the two eigenvalues are contained in [−5×10−7,5×10−7] for all κ∈[8605,50000].
As discussed in Sect. 3, the inhomogeneity of the planar solution (3.7) renders a direct analysis of the linearized wrinkling problem (3.6) an unlikely possibility. In an effort to understand the occurrence of double bifurcation points, we consider an analogy with the buckling of a beam on an elastic foundation under thrust with free ends, cf. Hetényi (1946). In that case the first buckling mode can be either even or odd (with respect to the mid-span), depending on the magnitude of the bending stiffness and strength of the elastic foundation. But as the modulus of the elastic foundation becomes large in comparison to the bending stiffness, the first buckling loads for the two symmetry types both increase and asymptotically approach the same value. For the sake of analogy, assume that \(\mathbf{N}_{\varepsilon} ^{o}\) in (3.6) has the homogeneous form \(\mathbf{N}_{\varepsilon} ^{o} = T(\varepsilon)\mathbf{e}_{1} \otimes\mathbf{e}_{1} - C(\varepsilon)\mathbf{e}_{2} \otimes\mathbf{e}_{2}\), where T(ε),C(ε)>0 are independent of x. Then assuming a solution of (3.6) of the form w(x 1,x 2)=sin(πx 1/L)v(x 2), we arrive at the beam-on-elastic- foundation equation

In the beam analogy for (5.1), P=O(1/h 2)>0 represents the axial compressive load, k=O(1/h 2)>0 is the foundation modulus, and the bending stiffness of the beam is “1”. As κ=1/h 2 becomes sufficiently large, the first buckling load asymptotically possesses both an even and an odd buckling mode. The buckling load itself also increases in the limit, by a known formula (cf. Hetényi 1946), which is not pertinent here because the presumed homogeneous form for \(\mathbf{N}_{\varepsilon} ^{o}\) is not correct. Nonetheless, from the Lemma in Sect. 3, \(\mathbf{N}_{\varepsilon} ^{o}(\mathbf{x})\) must have principal “compressive” components over some subset of Ω of non-zero measure, over which the behavior of the principal stresses is O(1/h 2), by virtue of (4.1). Thus, we expect similar behavior here in our case, leading to double bifurcation points to within the accuracy of the computations.
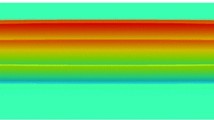
With stable solutions in hand, we now fix a conveniently large value of κ along the first two (simultaneous) bifurcating branches and then continue in the other parameters. In particular, we begin with the macroscopic strain ε. In this way we easily construct more physically relevant bifurcation diagrams in ε>0 for films of a given fine thickness—without directly confronting the singular-perturbation problem (3.6). Such diagrams are presented in Fig. 6 for film thicknesses 0.1 mm and 0.05 mm. In each case the blue curve represents the obtained solutions for our model, valid (the same) for both reflection symmetric and anti-symmetric configurations. All solutions on the blue curves are neutrally stable, as previously discussed above. In Figs. 7, 8, 9, 10 we depict wrinkled configurations—rotationally symmetric and anti-symmetric—corresponding to the marked points on the respective bifurcation diagrams.
Referring to Fig. 6, observe that each blue solution curve is bounded—starting and then terminating again on the ε-axis. This indicates that as the film is increasingly stretched, wrinkles emerge with an amplitude that first increases, reaches a maximum, and decreases, with the wrinkles then disappearing again. This is certainly realistic: As dramatized in the depicted configurations, as the film is increasingly stretched, it eventually approaches a nearly homogeneous, compressive-free state away from the two clamped ends. In contrast, the red curve in each bifurcation diagram depicts the solutions obtained for the classical Föppl–von Kármán model. In each case, observe the unrealistic prediction that a constant increase of wrinkling magnitude occurs as the macroscopic strain is indefinitely increased.
Figure 6 suggests that the isola “region” of macroscopic strains associated with wrinkling increases with decreasing film thickness. This is reinforced by the bifurcation diagram for thickness h=0.082 mm (κ=15,000), shown below in Fig. 11. For example, from Fig. 6(a) we see that there is no wrinkling when, say, ε=0.12 at thickness h=0.1 mm, while from Fig. 11, there is slight wrinkling for that same value of ε when h=0.082 mm. As in the previous bifurcation diagrams, the red curve in Fig. 11 depicts the response for the Föppl–von Kármán model.
The investigation of stable wrinkling for other values of the aspect-ratio parameter β and Poisson’s ratio ν is readily carried out by continuation from any of the above solutions. First we consider varying the aspect ratio at the fixed values h=0.05 mm and ε=0.1: The resulting bifurcation diagram in β (corresponding to the true width W=10/β) is shown in Fig. 12. We present a sampling of such configurations in Fig. 13, as marked along the branch in Fig. 12, in the anti-symmetric case only (since the reflection-symmetric case delivers the identical bifurcation diagram). Observe that wrinkles occur only for a specific range of aspect ratios.
As a further illustration of this behavior, we provide a sequence of bifurcation diagrams in the macroscopic strain ε for various aspect ratios (with h=0.05 mm) in Fig. 13. The diagram in Fig. 6(b) (β=1) should also be included in this sequence. As before the bounded blue curve represents the solutions obtained for our model, while the red curve is that obtained from the Föppl–von Kármán model. Two significant observations here are: (i) wrinkling occurs only within a bounded range of aspect ratios. The disappearance of a bifurcating branch for β≤0.75 and for β≥1.9 (not necessarily sharp bounds) indicates a standard isola-center bifurcation (the “birth” or “death” of a closed loop of bifurcating solutions from a singular point, cf. Golubitsky and Schaeffer 1985). (ii) The Föppl–von Kármán model erroneously predicts bifurcation of wrinkling solutions for β≤0.75 and for β≥1.9.
The same qualitative behavior is preserved in the bifurcation diagrams if we continue to other reasonable values of Poisson’s ratio, as shown in Figs. 15. These too should be viewed together with Fig. 6(b) (ν=0.45).
Finally we return to the discussion above concerning the double bifurcations associated with reflection symmetric and anti-symmetric solutions. As mentioned previously, the bifurcation diagrams given in Fig. 6, but also in Figs. 11, 12, 14, and 15, are valid (identical) for the two types of solutions. This is undoubtedly a nonlinear version of the above argument (5.1) for very large κ=1/h 2. Also, recall that the anti- (reflection) symmetric branches of solutions presented in these figures are neutrally stable, with the Hessian (4.25) always possessing an essentially zero eigenvalue that is associated with a reflection (anti-) symmetric eigenvector. In terms of stability, the two types of wrinkled solutions are equally likely. But these observations strongly suggest more: that there are asymmetrical solutions corresponding to an arbitrary phase shift between the reflection symmetric and the rotational symmetric solutions (for the same data). Indeed we find that our solutions come in “orbits”, as depicted schematically in Fig. 16. We find these by seeking solutions of (4.18) over the entire domain via Euler–Newton continuation along the suspected orbit as follows: For the first Euler step, we start with an anti- (reflection) symmetric solution and add to it a sufficiently small increment of the reflection (anti-) symmetric eigenvector associated with the zero eigenvalue. We then correct via Newton iteration, which we find to successfully converge. The updated full Hessian is then found to have a near-zero eigenvalue. Solutions along an orbit are then obtained by a similar continuation scheme—the first Euler step is always in a small “direction” of the eigenvector associated with the near-zero eigenvalue. In this way we compute an entire family of neutrally stable (and hence equally likely) solutions connecting the reflection symmetric solutions to the anti-symmetric solutions. Note also that the value of the total energy is constant along such an orbit—to within the small tolerance employed in the Newton solver.
Configurations along half of the orbit for h=0.05 mm are shown in Fig. 17. Here ϕ is a convenient phase variable along the orbit, defined so that ϕ=0 and π represent the two “sides” of the blue pitchfork of anti-symmetric solutions, while ϕ=π/2 represents the reflection symmetric solution that is half-way “between” the two. Note that each solution along the quarter orbit “in-between” an anti-symmetric solution and a reflection symmetric solution is neither reflection symmetric nor anti-symmetric.
6 Concluding Remarks
Our results point to the potential dangers in modeling thin-film problems involving large mid-plane strains via the classical Föppl–von Kármán theory. In this paper we show that it leads to unrealistic post-critical behavior, e.g., an indefinite increase in the wrinkling amplitude with increasing macroscopic strain, and it erroneously predicts bifurcation in certain regimes. Indeed the classical theory was devised solely for the purpose of initial post-buckling behavior of thin metallic rectangular panels, with aircraft structures in mind, cf. Von Kármán and Edson (1967). In particular, the in-plane strains are typically quite small in that setting. Our geometrically correct membrane model allows for phenomena not seen in the classical theory, e.g., the appearance and disappearance of bifurcating solutions via an isola-center bifurcation, as demonstrated in Fig. 14. The beautiful existence work due to Berger (1977) on the classical model shows the persistence of an infinity of bifurcation modes as an in-plane compressive load is increased indefinitely—just as in Euler’s elastica. On the other hand, our results here are striking similar to what happens when large compressibility is incorporated into a generalized elastica: Only finitely many bifurcating pitchforks may exist, and the latter can “interact” as parameters are varied, leading to non-bifurcating solutions and/or isola-center bifurcations, cf. Antman and Pierce (1990). Similarly we note that symmetry-breaking isola-center bifurcations occur quite naturally in the inflation of nonlinearly elastic, nominally spherical balloons, cf. Chen and Healey (1991).
The model employed here is crude by the standards of general nonlinear elasticity, and improvements are certainly possible. Obviously a superior in-plane, nonlinear membrane theory can be used such that worries about quasi-convexification of the energy as in Sect. 3 are not an issue. But for the strain regime considered in this problem, our simple, finite-strain model is shown to be rational and performs very well. Also, our model incorporates linear bending; models involving more accurate measures of curvature are well known, e.g., Ciarlet (2005), Steigmann (2013). However, for small-amplitude wrinkling under high tension as observed here in this problem, it seems unlikely that such corrections would have much of an impact on the results.
Our numerical results demonstrating continuous orbits of neutrally stable solutions—connecting reflection symmetric solutions to anti-symmetric solutions—seems to be a new phenomenon. The symmetry of the problem is not rich enough to explain the results. Rather the results appear to be asymptotic in the limit of a vanishingly thin film in the presence of large stretch. We call this asymptotic continuous symmetry, since to within the accuracy of the numerical solver, the problem behaves like one in the presence of a continuous symmetry group.
References
Antman, S.S., Pierce, J.F.: The intricate global structure of buckled states of compressible columns. SIAM J. Appl. Math. 50, 95–419 (1990)
Berger, M.S.: Nonlinearity and Functional Analysis. Academic Press, New York (1977)
Cerda, E., Mahadevan, L.: Geometry and physics of wrinkling. Phys. Rev. Lett. 90, 1–4 (2003)
Cerda, E., Ravi-Chandar, K., Mahadevan, L.: Wrinkling of an elastic sheet under tension. Nature 419, 579–580 (2002)
Chen, Y.-C., Healey, T.J.: Bifurcation to pear-shaped equilibria of pressurized spherical membranes. Int. J. Non-Linear Mech. 26, 279–291 (1991)
Ciarlet, P.G.: Mathematical Elasticity, vol. I. North-Holland, Amsterdam (1988)
Ciarlet, P.G.: An introduction to differential geometry with applications to elasticity. J. Elast. 78–79, 3–201 (2005)
Dacorogna, B.: Direct Methods in the Calculus of Variations, 2nd edn. Springer, New York (2008)
Dym, C.L., Shames, I.H.: Solid Mechanics: A Variational Approach. McGraw-Hill, New York (1973)
Evans, L.C.: Quasiconvexity and partial regularity in the calculus of variations. Arch. Ration. Mech. Anal. 95, 227–252 (1986)
Friedl, N., Rammerstorfer, F.G., Fischer, F.D.: Buckling of stretched strips. Comput. Struct. 78, 185–190 (2000)
Golubitsky, M., Schaeffer, D.G.: Singularities and Groups in Bifurcation Theory. Springer, New York (1985)
Healey, T.J., Miller, U.: Two-phase equilibria in the anti-plane shear of an elastic solid with interfacial effects via global bifurcation. Proc. R. Soc. A, Math. Phys. Eng. Sci. 463, 1117–1134 (2007)
Healey, T.J., Simpson, H.S.: Global continuation in nonlinear elasticity. Arch. Ration. Mech. Anal. 143, 1–28 (1998)
Hetényi, M.: Beams on Elastic Foundation. University Michigan Press, Ann Arbor (1946)
Jacques, N., Potier-Ferry, M.: On mode localization in tensile plate buckling. C. R., Méc. 333, 804–809 (2005)
Keller, H.B.: Numerical Methods in Bifurcation Problems. Tata Institute of Fundamental Research/Springer, Bombay/New York (1987)
Le Dret, H., Raoult, A.: Quasiconvex envelopes of stored energy densities that are convex with respect to the strain tensor. In: Calculus of Variations, Applications and Computations. Pitman Research Notes in Mathematics, vol. 326, pp. 138–146 (1995)
Meirovitch, L.: Analytical Methods in Vibrations. Macmillan, New York (1967)
Nayyar, V., Ravi-Chandar, K., Huang, R.: Stretch-induced stress patterns and wrinkles in hyperelastic thin sheets. Int. J. Solids Struct. 48, 3471–3483 (2011)
Puntel, E., Deseri, L., Fried, E.: Wrinkling of a stretched thin sheet. J. Elast. 105, 137–170 (2011)
Raoult, A.: Non-polyconvexity of the stored energy function of a Saint Venant–Kirchhoff material. Apl. Mat. 31, 417–419 (1986)
Reddy, J.N.: Nonlinear Finite Element Analysis. Oxford University Press, New York (2004)
Steigmann, D.J.: Koiter’s shell theory from the perspective of three-dimensional elasticity. J. Elast. 111, 91–107 (2013)
Valent, T.: Boundary Value Problems of Finite Elasticity. Springer, New York (1988)
Von Kármán, T., Edson, L.: The Wind and Beyond. Little, Brown and Company, Boston (1967)
Acknowledgements
The work of R.-B.C. and T.J.H. was supported in part by the National Science Foundation through grant DMS-0707715 and that of T.J.H. also through NSF grant DMS-1007830. The work of Q.L. was supported in part by China Scholarship Council 2010850685 and by the National Science Foundation of China 61104150. Each of these is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Healey, T.J., Li, Q. & Cheng, RB. Wrinkling Behavior of Highly Stretched Rectangular Elastic Films via Parametric Global Bifurcation. J Nonlinear Sci 23, 777–805 (2013). https://doi.org/10.1007/s00332-013-9168-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-013-9168-3





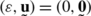 , compute a family of planar solutions (w≡0) of (
, compute a family of planar solutions (w≡0) of (














