Elastic Instability and Surface Wrinkling

Abstract

Hydrodynamics instabilities, such as Bénard–Marangoni convection, Rayleigh–Plateau, Rayleigh–Taylor, and many others, are well known to produce beautiful patterns. Indeed, capillary, viscous, and/or inertial forces could conspire to generate very regular morphologies. In this chapter, we will see that elasticity can also produce complex structures, either regular or fully random, provided that slender objects are used. These objects are usually classified as rods, shells, or sheets. In the classical picture, thin sheets constrained by external forces minimize elastic energy through focalization of deformation in singularities. We will see that, due to geometric constraints, these origami structures cannot always be obtained. In addition, very regular wrinkles with a very large range of wavelength can be observed for deformed sheets, if the sheet is tightly attached on a soft foundation. At the onset, these wrinkles reflect the competition between bending and elastic deformation forces. For large deformations, however, the morphology is surprisingly determined by the nature of the foundation. Fold localization or period-doubling bifurcations are indeed observed for liquid or solid substrate, respectively. Finally, these various studies also highlight the effort of this growing interdisciplinary researcher community to the emergence of a global picture of elastic instability. Interestingly, these wrinkled surfaces appear to be particularly useful for various applications including the design of superhydrophobic surfaces, new non-permanent adhesive, flexible electronic devices, optical devices such as anti-reflective coatings.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

The stability of constrained slender structures is a very old topic, that has started with Galileo, who questioned the stability of a beam supporting a heavy load and solved by Leonhard Euler with the Elastica [1]. With the emergence of new architectural design, this stability problem rapidly becomes a major subject for mechanical engineers. Surprisingly, physicists and engineers have rediscovered the specific problem of thin sheets instability at the end of twentieth century. This re-discovery was triggered by two seminal papers reporting experiments about the formation of regular wrinkles in constrained systems. Tanaka et al. showed that the outer surface of a gel confined in a petri dish swollen by solvent vapors becomes unstable and exhibits periodic structures (Fig. 8.1a) [2]. Bowden et al. have beautifully explained the formation of tiny wrinkles during the thermal evaporation of a metal thin film on a soft foundation (Fig. 8.1b) [3]. They performed a linear stability analysis including the bending of the rigid metal layer and the elastic deformation of the soft foundation that clearly demonstrates the instability of the outer surface.

Fig. 8.1

(Left) ionized acrylamide gel formed in a petri dish allowed to swell in water, (a)–(c) show the evolution of the morphology with time [2]. (Right) optical micrographs showing representative patterns of wrinkles that formed when a nanometric gold layer is evaporated onto warm (110 ^∘C) polydimethylsiloxane. The pattern appears when the sample is cooled to room temperature [3]

From countless examples, it is now crystal clear that the homogeneous (often flat) states of constrained thin sheets are very often unstable. Since the seminal works of Tanaka and Bowden, the final states were broadened in a zoo of complex morphologies made of wrinkles, creases, crumples, folds, and blisters, several morphologies sometimes co-existing in a single experiment. Transition from one morphology to another can be observed depending on various experimental conditions. For instance, by decreasing adhesion, you switch from regular wrinkles to blister. Increasing compression could also reveal nonlinear regimes with increasing complexity. As fluids, thin elastic sheets appear to be very promising systems that bear similarity with classical problems of linear and nonlinear pattern formation such as period-doubling bifurcations. Their study opens new prospects to understand the emergence of complexity, breaking of symmetry and singularities. Even the simple buckling of a sheet shows intrinsic behaviors that raise fundamental questions such as, why do films become folded upon confinement whereas a thick slab of an identical material favors creases? Why does paper sheets crumple into singularities whereas rubber sheets would smoothly wrinkle? Answering these questions (and many others) is important, first for our natural curiosity, and to understand the emergence of complex shapes and patterns in Nature.

Understanding thin sheets behavior is also extremely important for many technological applications, specially for those involving micro-patterning of surfaces. The design of new materials combining extreme mechanics with optical, electronic, or chemical properties is very often achieved with specific coatings on thin sheets. In this case, the failure of the coating, or even the thin sheet itself, should be avoided. The opposite is also true! These complex features can be very interesting for some applications, essentially in micro- and nano-technology. Indeed, understanding how complex patterns emerge spontaneously under featureless forces may inspire efficient methods for tailoring a desired surface pattern to achieve the required property (e.g., reversible superhydrophobicity, flexible electronics).

8.2 Wrinkling in Constrained Free-Sheets

Usually, wrinkles are associated with multilayers, including materials with very contrasted elastic properties. The archetype of these systems that will be discussed in the next section is the rigid/inextensible thin sheet glued on an elastomer or a fluid foundation and subjected to a uniaxial constraint. It is however possible to generate wrinkles in free sheets provided you are using the proper geometrical constraints. The very typical example of this geometrically induced wrinkling is the collapse of a viscous bubble (Fig. 8.2). During the collapse, the shape of the bubble drastically changes from a purely spherical to a flat shape, due to surface tension at the edge of the hole created in the bubble. With this sudden change of morphology, a hoop stress builds that induces the wrinkling of the fluid thin layer (high viscosity slows the relaxation of the wrinkles allowing their visualization) [4, 5].

Fig. 8.2

Image of a collapsing viscous bubble. The bubble loses its axisymmetric shape, small amplitude ripples grow. The inset displays a schematic side view of the essentially conical deflating bubble at the onset of the instability [5]

Geometrical constraints can also be applied on rectangular sheets. Indeed, thin sheets compressed at one edge to follow a periodic sinusoidal profile and free at the other, i.e. a curtain-like morphology (Fig. 8.3), develop a self-similar hierarchy of folds [6, 7]. We will now demonstrate a universal method based on a scaling approach to find the morphology of constrained thin sheets.

Fig. 8.3

Top of a rubber curtain constrained at one edge with an imposed sinusoidal deformation z (0, y) = A(0) sin(q(0)y) and power laws describing the evolution of the wavelength with the distance from the constrained edge [6]

As shown in Fig. 8.3, sheets made of various materials constrained at one edge develop a regular hierarchical pattern of folds that follow simple power laws. These patterns consist of a hierarchy of successive generations of folds whose wavelength gradually increases along x. For the sake of clarity, the structure of the deformed sheet is described by a periodic function z(x, y) = A(x) sin q(x)y, with z the amplitude of out-of-plane deflections, y being parallel to the edge ($q=2\pi /\lambda$). The hierarchical patterns are characterized by the evolution of the average wavelength, λ(x). For rigid sheets, the amplitude of the folds is determined by the compression ratio and the inextensibility of the sheet, $A\sim \lambda \sqrt{\delta }$. Since, inextensibility ensures that

$$ {W}_0={\int}_0^Wds \cos \theta \simeq {\int}_0^Wds\left(1-\frac{1}{2}{\dot{z}}^2\right)\simeq W-\frac{1}{2}W{\left(\frac{A}{\lambda}\right)}^2 $$

and $\delta =\left(W-{W}_0\right)/W$.

The bending energy density related to a fold is thus given by

$$ {u}_b\sim E{h}^3 {\kappa}^2\sim E{h}^3\delta /{\lambda}^2. $$

Since u _b is proportional to 1∕λ ², the membrane adopts the largest possible wavelength compatible with the imposed constraints. The minimization of bending energy is thus the “driving force” toward larger and larger folds and is the source of the observed hierarchy. Figure 8.3 shows that curtains made of various materials with contrasted properties can be sorted in two classes with different exponents ∼ 2 ∕ 3 for “light” sheets and ∼ 1 ∕ 2 for “heavy” sheets (we will see later the meaning of light and heavy). What does determine these exponents, is it related to pure geometry or to deformation energy of the sheet? To increase the wavelength, adjacent folds should merge. Looking carefully a curtain, you would probably observe the merging of two, three, and very rarely fourfolds, some folds remaining almost unaltered. We will however make the assumption, first proposed by mathematicians Jin and Sternberg, that the observed morphology can be described by successive period-doubling transitions constituting the building-blocks of the global pattern [8]. The hierarchy is obtained by stitching these building-blocks. The key feature of a single block element, here after named wrinklon, is its length, L, i.e., the sheet length required to accommodate the λ − 2λ transition. If the energy is also involved (and not only geometry), this length should be determined by material properties, E, h the constraint/compression ratio δ and the wavelength. The power law describing self-similar patterns can be built from this length according to $d\lambda /dx\sim \lambda /L$. To estimate the length of the wrinklon, we use a scaling approach where energetic penalty must be compensates by energetic gain. Close inspection of the wrinklon morphology reveals the occurrence of a curved ridge at the tip of the merging folds (Fig. 8.4). Such curved ridge is characterized by a non-vanishing Gauss curvature. From the Theorema Egregium [9], the sheet around these curved ridge should concentrate on stretching energy (i.e., the surface is no more isometric of a flat surface). The energetic penalty involved into a single λ − 2λ transition should be related to local stretching, the energetic gain being related to the decrease in curvature.

Fig. 8.4

(a) Wrinklon morphology. (b) Origami model of the λ − 2λ transition [6]

The stretching energy can be estimated from the slope of the sheet which determines the strain ε induced by the change of amplitude A − 2A (related to the change of wavelength since inextensibility ensures that $A\sim \sqrt{\delta}\lambda$). The strain given by $\varepsilon \sim {A}^2/{L}^2\sim \delta {\lambda}^2/{L}^2$ yields the stretching energy U _s  ∼ Eh L λ ε ² ∼ Eh δ ² λ ⁵ L ⁻³. The wrinklon length results then from a balance of this stretching energetic penalty and bending energy, U _b  ∼ Eh ³ L λ κ ² which yields $L\left(\lambda \right)\sim {h}^{-1/2}{\delta}^{1/4}{\lambda}^{3/2}$. The scaling for the wavelength describing the whole hierarchical pattern of folds is obtained by the integration of equation $d\lambda /dx\sim \lambda /L$,

$$ \frac{\lambda (x){\delta}^{1/6}}{h}\sim {\left(\frac{x}{h}\right)}^{2/3}. $$

The class of patterns related to “light” curtains, 2/3 exponent, is in close agreement with this scaling model. In addition to yielding the proper exponent, this relation enables the comparison of the data obtained from seemingly disparate systems, over a wide range of lengthscales. Figure 8.5 provides a remarkable collapse of the data measured with paper, fabric, and various plastic sheets. Interestingly, the elastic modulus of the material used to build the sheet does not appear in this relation. This was expected since both stretching and bending energies linearly depend on the elastic modulus.

Fig. 8.5

Master curves, normalized wavelength vs. normalized distance from edge for the “light” (a) and “heavy” (b) curtains [6]

As shown in Fig. 8.3, “heavy” curtains, made of nanometric films of polystyrene on water [7], rubber sheets, and constrained graphene do not follow the 2/3 scaling. Instead, their dynamics obey $\lambda \propto \sqrt{x}$). The main difference between both families is related to the lack or the occurrence of a significant tensile force, T. For all “heavy” curtains, an additional tensile force is acting on the sheet. For graphene sheets, this tension is related to the longitudinal tensile strain induced by thermal manipulations of the compression device [10]. For rubber curtains, the tension is determined by gravity (T ∼ ρ _c ghH, where ρ _c and H are the density and height of the curtain). For compressed nanometric polystyrene films on water, a tensile force is exerted by the surface tension of water at the free edges of the polymer film [7].

The tension per unit width imposes an additional stretching energy U _t  ∼ T α ² Lλ ∼ T δ λ ³ L ⁻¹ where α is the slope of the sheet within the wrinklon (α ∼ A ²/L ²). This energy becomes dominant when U _t  > U _s , that is when T > Eh ² δ/A. Neglecting the stretching term, the total energy of the distorted membrane becomes ${U}_{\mathrm{tot}}={U}_t+{U}_b$. The wrinklon length which minimizes U _tot (balancing tension and bending energies) becomes $L\left(\lambda \right)\sim \frac{\lambda^2}{h}\sqrt{\frac{T}{Eh}}$. As expected, the tensile force increases the length of wrinklons for a given wavelength and can thus be used to tune the energetic penalty associated with the λ − 2λ transitions. Considering the equation $d\lambda /dx\sim \lambda /L$, we obtain the scaling for the wavelength along a heavy sheet

$$ \frac{\lambda (x)}{h}\sim {\left(\frac{Eh}{T}\right)}^{1/4} {\left(\frac{x}{h}\right)}^{1/2}. $$

(8.1)

This scaling is in excellent agreement with the power laws observed for heavy curtains and graphene bilayers (Fig. 8.3). The data of various macroscopic curtains, graphene bilayers, and nanometric polystyrene thin films indeed collapse onto a single master curve without any fitting parameters (see Fig. 8.5) which highlight the universality of our description. Our formalism is thus validated for seven orders of magnitude in thickness from graphene sheets to rubber and fabric curtains.

There is obviously various method to geometrically constrain a free sheet. Consider, for instance, a thin film of PS of nanometric thickness deposited on a water droplet (Fig. 8.6). The edge of the circular sheet is decorated with a set wrinkles [11]. These wrinkles should grow to accommodate the stress arising when a flat sheet is forced to adopt a spherical shape. In fact, the change of shape induces a change in Gaussian curvature and thus a stretching. Since the surface tension exerted by water at the edge is not strong enough to overcome this stretching force, the thin sheet slightly retracts and wrinkles to avoid compression along the edge.

Fig. 8.6

(Left) image of a ultrathin sheet of polystyrene deposited on a water droplet [11]. (Right) sheets confined between two spheres [12]

8.3 Compression of Thin Sheets on a Soft Foundation

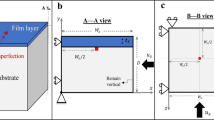
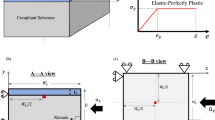
In the previous section, we showed how to generate wrinkles by playing with geometrical constraints applied on a free thin sheet. This method is very powerful to generate hierarchical wrinkles, as shown in Figs. 8.3 and 8.6. In fact constrained free-sheets always tend to develop cascades of wrinkles with an increasing wavelength whatsoever the way geometrical constraints are applied. This natural tendency is directly related to the minimization of bending energy through the curvature (U _b  ∼ κ ² ∼ 1/λ ⁴). Surprisingly, the growth of a pattern made of regular parallel wrinkles with a constant wavelength is far from obvious! The solution is to balance the bending energy with another energy that decreases when curvature increases. This can be achieved by gluing the thin sheet on a soft substrate, able to follow the shape of the constrained sheet. This strategy was successfully applied to fluid [13] and to elastomers [3, 14]. As shown in Fig. 8.7, very regular parallel wrinkles are observed when a rigid sheet deposited on a soft substrate is compressed uniaxially. The wavelength is determined by the elastic properties of the membrane and the foundation (Fig. 8.7). The exact shape of the sheet can be obtained either via variational methods through Euler–Lagrange equation [15–17] or from a linear stability analysis of the homogeneous flat state [2, 3, 13, 15].

Fig. 8.7

(Top) images of wrinkled state of a rigid sheet compressed on water for increasing compression ratios [13]. Uniform wrinkled state and period-doubling morphology observed for compressed sheet deposited on elastomer [14]. (Bottom) evolution of the wrinkles wavelength for fluid (circles) and elastomer (square) foundations [16]

A linear stability analysis for systems consisting in a rigid layer, E _m on top of an elastomer, E _f with E _m  ≫ E _f can be easily achieved. When uniaxially compressed by a factor ($\Delta =L-{L}_0\Big)/{L}_0$), energy can be stored in two ways, (1) as pure compression, the sheet remaining flat, U _c , or (2) as bending of the sheet plus elastic deformation of the soft foundation, U _b , U _f in the wrinkled state. The comparison of these energy yields $\Delta U={U}_b+{U}_f-{U}_c$. The profile of the wrinkled state is periodic ($q=2\pi /\lambda$) and can always be described through a Fourier expansion, y (x) = ∑ A _m cos mqx. For a linear analysis, we only consider single mode, the mean curvature of a sinusoidal profile is < y″ > ∼ A ² q ². We also assume inextensible boundary condition for the rigid sheet which implies that $\Delta ={A}^2{q}^2$. The difference in energy can be written as

$$ \Delta U=\Delta \left({E}_m{h}^3{q}^2+{E}_f\frac{1}{q}-{E}_mh\Delta \right). $$

The flat state becomes unstable if $\Delta U<0$. For each wavenumber q we have thus a critical compression, ${\Delta}_c={h}^2{q}^2+\left({E}_f/{E}_mh\right){q}^{-1}$. Close to the threshold, the observed wrinkles period should correspond to the minimum of ${\Delta}_c$ which yields the following wavelength and critical strain

$$ q={\left(\frac{E_f}{E_m{h}^3}\right)}^{1/3} \lambda =h{\left(\frac{E_m}{E_f}\right)}^{1/3} $$

(8.2)

$$ {\Delta}_c^{\ast }=2{\left(\frac{E_f}{E_m}\right)}^{2/3}. $$

(8.3)

The predicted evolution of the wavelength with the material properties is in very good agreement with observed data for a large variety of experimental systems (Fig. 8.7). A similar method can be used to study the stability of compressed sheets on fluid substrates provided you replace the energy of substrate deformation by the relation U _f  ∼ ρgA ², involving the hydrostatic pressure of the fluid [13, 18]. The wavelength for fluid substrate becomes $\lambda \sim {\left({E}_m{h}^3/\rho g\right)}^{1/4}$ in very good agreement with experimental observations (Fig. 8.7).

Obviously such a linear analysis is only valid very close to the threshold, i.e. when A is infinitely small. This model suggests that above (but close to) the threshold, the wrinkles amplitude should scale as $\sqrt{\Delta}$ with the compression ratio. Figure 8.8 shows that this law remains however valid for unexpectedly large compression ratios, $\Delta \le 0.2$, well above the threshold for this peculiar system, close to 0. 02. This observation highlights the robustness of the single wavelength wrinkled morphology, there is no emergence of super-harmonic modes (nq, with n integer) as expected for classical pattern formation mechanisms [19].

Fig. 8.8

(a) Definitions of the wrinkles amplitudes A0 and A1. (b) Comparison between experimental and theoretical evolutions of A0 and A1 as a function of the compression ratio for polystyrene and PDMS [16]

Close to the threshold for wrinkling, there is no way to discriminate wrinkles on fluid or solid/elastomer substrates. Increasing the compression ratio changes the rules, a drastic modification of morphology is indeed observed with different responses for fluid and elastomers. For fluid substrates, the extra length due to compression concentrates in a single fold, while compressed sheets on elastomers always stay periodic. This difference should reflect the emergence of different nonlinear terms that breaks the symmetry of the wrinkled state. In a similar manner that buckling breaks the symmetry of the homogeneous flat state. For fluids, the nonlinearity essentially arises from the bending energy, through the curvature, $\kappa =\overset{\dot{\mkern6mu}\dot{\mkern6mu}}{y}/\sqrt{1-{\dot{y}}^2}$. This nonlinearity generates a quartic term in the expression of energy that will break the longitudinal symmetry keeping the transversal symmetry of the deformed sheet, i.e., folds up and down are energetically equivalent. As shown by Diamant and Witten, the resulting nonlinear Euler–Lagrange equation describing these systems is reminiscent of the sine-Gordon family equations explaining the growth of solitons [17].

For elastomers, a bifurcation due to the nonlinearities is observed with the emergence of a sub-harmonic mode, q/2 (Fig. 8.8). This bifurcation clearly corresponds to a period-doubling sequence similar to what is observed for Faraday instability of shaken fluid layers, except that this bifurcation refers to time and not space [20]. For the Faraday instability, the period-doubling is usually described with a nonlinear parametric oscillator model. Interestingly, the Euler–Lagrange equation describing the minimization of energy for the compressed sheet on elastomer bears also some resemblance with a parametric oscillator [14].

It should be noticed however that the period-doubling behavior is only observed for elastomer substrates without pre-strain. When the compression is achieved through a pre-stretching of the elastomer slab prior deposition of the thin sheet, the nonlinear elasticity of the PDMS rubber comes into play and other morphology characterized by periodic cusps is observed [21].

8.4 Wrinkling Coupled to Diffusion, Swelling, Thermal Constraints, …

Wrinkles are however not limited to a set of parallel periodic folds, 2D wrinkled patterns can also be produced. Obviously, there is no way to generate 2D morphology from simple uniaxial compression of the thin sheets. We will now consider radial compression, symmetric or not. The simplest method to produce 2D patterns is to apply compression in the rigid sheet along two orthogonal directions. Different morphologies, with periodic nipples, squares, or labyrinthine can be achieved. However, several experimental studies highlight that the resulting morphology strongly depends on the history of deformations, applying two subsequent uniaxial compressions is clearly not the same as applying simultaneously compression along two directions (Fig. 8.9).

Fig. 8.9

SEM and AFM images of surface patterns when compressing an oxidized PDMS film either (a) sequentially or (b) simultaneously [22]

Interestingly, 2D compression stress can be applied through unconventional methods involving, swelling, or surface tension. 2D stress can also be applied by subsequent inflating/deflating of a spherical bump in a microfluidic device (Fig. 8.10) [23]. Swelling can be used in two different ways, either by a direct compression of a confined slab as shown by Tanaka et al. [2], or indirectly, the solvent changing the rheological properties of the foundation [24, 25]. This last method was used to induce wrinkling in bilayers of titanium thin film deposited on polystyrene (PS). Wrinkling was induced by immersing the multilayers in toluene vapors. Toluene is a good solvent of PS, it can swell the polymer layer located below the Ti membrane by diffusing through tiny defects, either resulting from the deposition process or obtained by AFM indentation.

Fig. 8.10

(a) Highly pre-stretched bi-layer system using micro-fluidics. (b) Compressive strain is applied by reducing the oil inside the chamber and a ridge structure emerges on the surface. (c) SEM image of the ridge structure [23]

As shown in Fig. 8.11, immersion of a polystyrene film capped with a thin titanium layer in toluene vapors leads to the formation of wrinkle domains in the metallic membrane with various morphologies. Parallel wrinkles, herringbones, splaying-fan like morphologies, circles, and circles decorated with tiny dots can be observed when the solvent diffuses inside the polymer layer. These metastable patterns emerge spontaneously depending on the geometry of the diffusion front and the layer thicknesses.

Fig. 8.11

(Left) parallel and radial wrinkles morphologies observed when solvent diffuses in the PS layer from an edge or a point-like defect, respectively. (Right) schematic representation of the wrinkle mechanism induced by solvent diffusion. First, the thermal deposition process generates compression in the upper membrane. Subsequently, solvent diffusion triggers the transition from unbuckled to buckled state

For the diffusion assisted wrinkling process, the compressive stress at the origin of the patterns is related to the thermal deposition of the metal film on the polymer substrate. Due to the very high elastic modulus of glassy PS the metal surface while in compression remains flat. The wrinkling instability is then induced by immersing the samples in solvent vapors of the polymer, since swelling induces a drastic decrease of the elastic modulus (Fig. 8.11). Strikingly, the resulting wrinkling patterns do not show the usual labyrinthine morphology [3] (see Fig. 8.1) but are clearly determined by the geometry of the diffusion process (Fig. 8.11). Parallel wrinkles are observed when the solvent diffuses from the edge yielding a linear front. Radial organization of wrinkles arises from point-like diffusion starting at tiny holes randomly distributed in the thin metal layer (i.e., defects resulting from the deposition process of the metallic film). The wrinkles thus always grow preferentially perpendicular to the wavefront. The relevance of molecular diffusion in the observed phenomena is obviously supported by the dynamics of the process that follows the classical Fickian diffusive behavior, distance ∝ t ^1/2.

As a consequence, multilayers made up of low elastic modulus elastomers, such as polydimethylsiloxane (PDMS, E _p  ∼ 10⁶ Pa), buckle with very small critical stresses. It was thus not surprising that metal surfaces deposited by thermal evaporation wrinkle during the deposition process [3]. The PDMS layer, thermally expanded during metal deposition, induces a compressive stress in the rigid membrane when cooled to ambient temperature. In contrast, replacing the elastomer with a high modulus glassy polymer, such as PS, E _p  ∼ 10⁹ Pa, increases the critical stress by one order of magnitude. It could become so large that the thin metal surfaces, while stressed, remain perfectly flat after the thermal deposition. These stressed but flat titanium surfaces can thus be considered as ready to buckle membranes.

The Ti/PS/SiO _x multilayers are however highly sensitive to chemical stimulation thanks to the polymer layer. Indeed, the diffusion of a good solvent in PS leads to a drop of the glass transition temperature together with a drastic decrease of the elastic modulus (e.g., adding 15 % w/w of toluene is enough to obtain elastomeric PS at room temperature). To some extent, we could consider that solvent diffusion is equivalent to a local increase of temperature for the PS layer. Since the formation of wrinkles is fully determined by the critical stress, strongly dependent on polymer elastic modulus, this diffusion process should trigger a transition from unwrinkled to wrinkled state (Fig. 8.11).

The relation between the wavelength and materials properties can be obtained from a scaling energetic approaches, based on a balance of the membrane bending energy with the penalty associated with the deformation of the foundation [26]. For micrometric polymer film thicknesses, the wrinkle wavelength follows the allometric relation λ ∝ (hH _p )^1/2 or λ ^∗ ∝ H _p ^∗1/2 using variables without dimensions, ${\lambda}^{\ast }=\lambda /h$ and ${H}_p^{\ast }={H}_{ p}/h$.

Interestingly, we observe a drastic deviation from the expected behavior for very thin polymer films (nanometric thickness), Fig. 8.12. Instead of a continuous decrease of λ ^∗ with H _p ^∗, a “V shape” curve with a slope reversal is observed. Since the deviation appears for polymer films thinner than 50 nm, we add van der Waals (VDW) interactions between the silicon substrate and the titanium membrane in our model. These interactions cannot be neglected when both surfaces are separated by a distance smaller than 100 nm. The VDW energy (per unit surface area) between two surfaces separated by a distance z is given by $P(z)={A}_H/12\pi {z}^2$ [27]. The Hamaker constant, A _H , corresponding to the interactions of two surfaces, 1 and 2, through a medium 3, can be computed from the dispersive component of the individual surface tensions, γ _i ^D, by using the relation ${A}_{132}\simeq (\sqrt{\gamma_1^D}-\sqrt{\gamma_3^D})(\sqrt{\gamma_2^D}-\sqrt{\gamma_3^D})$ [28]. For two materials of high surface energy separated by a polymer medium, ${A}_H\simeq -4.1{0}^{-19} \mathrm{J}$. For a wrinkled surface with a slowly varying thickness z(x), the corresponding energy can be estimated from a Taylor expansion limited at the second order of P[z(x)] that yields

$$ \underset{0}{\overset{\lambda }{\int }}\frac{1}{2}{\left(\frac{d^2P}{d{z}^2}\right)}_{z={z}_0}{[z(x)-{z}_0]}^2 dx, $$

where z ₀ is the average film thickness.

Fig. 8.12

Evolution of the normalized wavelength, λ ^∗, with the normalized foundation thickness H _p ^∗, for trilayers Ti/PS/SiO _x immersed in toluene vapors. The line corresponds to the solution of Eq. (8.5)

For a sinusoidally wrinkled polymer layer with $z(x)={H}_p+A \sin 2\pi x/\lambda$ and z ₀ = H _p , the total energy of the system per unit surface area can be written as:

$$ {U}_T\simeq \frac{E{h}^3{A}^2}{\lambda^3}+\frac{E_{ p}{\lambda}^3{A}^2}{H_{ p}^3}-\frac{\left|{A}_H\right|{A}^2\lambda }{H_{ p}^4}, $$

(8.4)

where the first term is the bending energy of the upper Ti membrane, the second term is the elastic energy stored in the polymer layer, and the third term is the contribution of the VDW energy. For such very high molecular weight polymer (M _w = 1. 4 × 10⁶ Da), we can consider a purely elastic foundation. Indeed, the time scale of the experiment ( ≃ 100 s) remains very small with respect to the disentanglement time τ _d that determines the transition between elastic and viscous behaviors. Minimizing the total energy with respect to λ ^∗, considering λ ^∗ and H _p ^∗ variables, yields the relation

$$ -\frac{E}{\lambda^{\ast 4}}+\frac{E_p{\lambda}^{\ast 2}}{H_p^{\ast 3}}-\frac{|{A}_H|}{h^3{H}_p^{\ast 4}}=0. $$

(8.5)

The solution of this equation is plotted with the experimental data in Fig. 8.12, showing the good agreement between the model including VDW energy and the experimental results.

Wrinkling from solvent diffusion was also used for other systems [29]. For instance, combining UV exposure and solvent diffusion, a zoo of morphology: flowers, concentrated rings, and labyrinthine patterns can be obtained (Fig. 8.13). It should be noted however that there is no theoretical model to explain the transition between all these rather exotic patterns.

Fig. 8.13

Variety of morphological patterns via swelling-induced surface wrinkling. Optical microscopy images of various wrinkling patterns produced on 500 nm thick PS films with different UVO exposure times from 2–40 min [29]

Combining wrinkling and diffusion provides thus an interesting method to produce complex patterns with tunable dimensions. However this physical method by itself is not suitable as a patterning technique due to the randomness of the wrinkle nucleation events. Indeed, the random distribution of the wrinkled domains is related to the uncontrolled localization of defects in the metal membrane. To solve this problem, we use thicker titanium layers and an AFM tip (Fig. 8.14) to make small holes in the metal layer with a specific geometry. As shown in Fig. 8.14c, this nano-indentation process prior to solvent exposure provides a fine control of the spatial layout of the wrinkled domains. Furthermore, since the wrinkle orientation is determined by the diffusion front, it becomes possible to generate tailor-made wrinkled patterns by tuning the geometry of the carving. Wrinkles initiated at the corners and tips of the engraved area (Fig. 8.14b) exhibit radial orientation while parallel wrinkles develop from the linear parts.

Fig. 8.14

Optical images of wrinkled Si/PS/Ti multilayers, previously patterned with an AFM tip and then exposed to toluene vapor for 2 min. (a) scheme of the patterning method, observed patterns for squares 2 μm (b) and lines 2 μm wide (c). Scale bars correspond to 10 mm [25]

8.5 Conclusions

Playing with materials properties and the way the compression stress is applied, various topography with parallel wrinkles (with a cascade of wavelength, or a superposition of several modes, or the growth of a soliton-like solution), radial wrinkles, chaotic labyrinthine, and many others patterns can be generated. For application purposes, it is usually more convenient to generate in situ the rigid thin sheet on the elastomer by using UV irradiation, for instance. Oxydation of the polymer surface creates a crust that wrinkles when a compression stress is applied. As shown by Eq. (8.2), the thin sheet thickness and thus irradiation time determines the wavelength that could range from hundred of nanometers to centimeters. These surfaces were used for various applications including the design of superhydrophobic surfaces, new non-permanent adhesive [30], flexible electronic devices [31]. Wrinkled surfaces exhibiting sub-micrometric features were also used for optical devices such as anti-reflective coatings, optical cavity [32, 33].