Global dynamics of a generalist predator–prey model in open advective environments

Abstract

This paper deals with a system of reaction–diffusion–advection equations for a generalist predator–prey model in open advective environments, subject to an unidirectional flow. In contrast to the specialist predator–prey model, the dynamics of this system is more complex. It turns out that there exist some critical advection rates and predation rates, which classify the global dynamics of the generalist predator–prey system into three or four scenarios: (1) coexistence; (2) persistence of prey only; (3) persistence of predators only; and (4) extinction of both species. Moreover, the results reveal significant differences between the specialist predator–prey system and the generalist predator–prey system, including the evolution of the critical predation rates with respect to the ratio of the flow speeds; the take-over of the generalist predator; and the reduction in parameter range for the persistence of prey species alone. These findings may have important biological implications on the invasion of generalist predators in open advective environments.

1 Introduction

Many species reside in environments with predominantly unidirectional flow, such as streams or rivers. Despite the flow induced washout, aquatic species can persist in their habitats for many generations (Müller 1982; Vasilyeva and Lutscher 2012). This phenomenon has been termed as the “drift paradox" (Müller 1982; Hershey et al. 1993), which has attracted wide attentions in recent years (Anholt 1995; Cantrell et al. 2020; Cosner 2014; Huang et al. 2016; Lutscher et al. 2010; Speirs and Gurney 2001; Vasilyeva and Lutscher 2010). To explain this paradox, a core question is to study how flow speed affects the survival of individual species. Speirs and Gurney (2001) were the first to propose the persistence mechanism driven by random diffusion, based upon a reaction-diffusion-advection model. Their studies suggested that the persistence of a single species is possible only when the flow speed is slow relative to the diffusion and the stream is long enough. Inspired by this work, a salient insight from the subsequent modeling approaches is that there exists a threshold value of the flow speed, separating population persistence from extinction, which confirms that random diffusive movement can balance the passive movement caused by water flow and in return gives rise to population persistence (Jin et al. 2019; Lou and Lutscher 2014; Lou et al. 2018; Lou 2008; Lutscher et al. 2010, 2005; Vasilyeva and Lutscher 2012; Wang et al. 2019; Wang and Shi 2019).

Community composition in aquatic habitats is shaped by species interactions, such as competition or predation, as well as by hydrological characteristics of the habitat, including flow speed and water temperature, etc. Due to natural causes or human activities, flow speeds in aquatic habitats can change over time, and alter competitive outcomes from one species dominating to coexistence or even to the other species dominating (Lou et al. 2018; Lutscher et al. 2007; Vasilyeva and Lutscher 2012). Hence, it is an important question to explore how flow speeds influence the competitive outcomes and mediate the coexistence of aquatic species. To address this issue at a single trophic level, a reaction-diffusion-advection model for two competing species has been proposed by Lutscher et al. (2007), which suggests that the trade-offs between multiple factors (such as dispersal strategy, advection movement, growth ability, competitive ability, the net loss of individuals at the boundary, and spatial heterogeneity) allow the shift of the competition outcomes (see Hao et al. 2021; Lam et al. 2015; Lou and Lutscher 2014; Lou et al. 2018; Lou and Zhou 2015; Lou 2008; Lutscher et al. 2007; Tang and Zhou 2020; Vasilyeva and Lutscher 2012; Wang et al. 2020; Yan et al. 2022; Zhou et al. 2021; Zhou and Xiao 2018, and the references therein).

Two trophic level systems such as predator-prey interactions can also be easily found in advective environments, for instance, herbivorous zooplankton and phytoplankton in water columns. Hilker and Lewis (2010) modeled predator-prey systems with specialist predators, as well as generalist predators, in advective environments. Their model (Hilker and Lewis 2010) for the prey and the specialist predators, which cannot sustain themselves without the prey, is as follows (see also Dubois 1975):

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{t}=d_{1}N_{xx}-q_{1}N_{x}+r(1-\frac{N}{K})N-aNP,&{} x\in (0,L),\ t>0,\\ P_{t}=d_{2}P_{xx}-q_{2}P_{x}+eaNP-\gamma P,&{} x\in (0,L),\ t>0,\\ d_{1}N_{x}(0,t)-q_{1}N(0,t)=N_{x}(L,t)=0,&{} t>0,\\ d_{2}P_{x}(0,t)-q_{2}P(0,t)=P_{x}(L,t)=0,&{} t>0,\\ N(x,0)=N_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,L],\\ P(x,0)=P_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,L].\\ \end{array}\right. } \end{aligned}$$

(1.1)

Here N(x, t) and P(x, t) are the population densities of the prey and predators at time t and location x, respectively. $d_{i}$ $(i=1,2)$ are the diffusion rates, and the effective advective flow speeds for the prey and predators are denoted by $q_{i}$ $(i=1,2)$. r and K are the intrinsic growth rate and the carrying capacity of the prey species, respectively, a is the predation rate, e is the trophic conversion efficiency, $\gamma$ denotes the mortality rate of the predators, and L is the domain length. $q_{i}$ $(i=1,2)$ are assumed to be non-negative constants, and all the other parameters are positive. Danckwert’s boundary conditions (see Ballyk et al. 1998) are imposed, i.e. no-flux condition at the upstream end $x=0$ and homogeneous Neumann boundary condition at the downstream end $x=L$.

Motivated by the predictions of Hilker and Lewis on (1.1), Nie et al. (2020, 2021) investigated the global dynamics of system (1.1), and they showed that there exist two critical advection rates which divide the dynamics of this system into three scenarios: (1) the extinction of both species; (2) the failed invasion of predators; and (3) the successful invasion of predators in the form of coexistence of two species. Moreover, their numerical results indicate that the random dispersal of both species are favorable to the invasion of specialist predators.

Another predator-prey model in advective environments, where the generalist predator with alternative food sources is involved, was also proposed by Hilker and Lewis (2010):

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{t}=d_{1}N_{xx}-q_1N_{x}+r_{1}(1-\frac{N}{K_{1}})N-aNP,&{} x\in (0,L),\ t>0,\\ P_{t}=d_{2}P_{xx}-q_2P_{x}+r_{2}(1-\frac{P}{K_{2}})P+eaNP,&{} x\in (0,L),\ t>0,\\ d_{1}N_{x}(0,t)-q_1N(0,t)=N_{x}(L,t)=0,&{} t>0,\\ d_{2}P_{x}(0,t)-q_2P(0,t)=P_{x}(L,t)=0,&{} t>0,\\ N(x,0)=N_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,L],\\ P(x,0)=P_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,L],\\ \end{array}\right. } \end{aligned}$$

(1.2)

where $r_{i}>0$ and $K_{i}>0$ $(i=1,2)$ are the intrinsic growth rate and the carrying capacity of the prey and predators, respectively. The other parameters are the same as those in (1.1). Based upon their analysis of traveling wave speeds and numerical simulations, Hilker and Lewis (2010) raised some conjectures about the dynamics of system (1.2) and suggested that four scenarios may occur: (1) coexistence; (2) persistence of prey only; (3) persistence of predator only; and (iv) extinction of both species. Notably, in contrast to the specialist predator-prey system (1.1), there occurs a new phenomenon (i.e. the persistence of predators only) for the generalist predator-prey system (1.2), which is called generalist predator take-over (Hilker and Lewis 2010). The goal of this work is to explore the dynamics of system (1.2) and settle the predictions of Hilker and Lewis.

The rest of this paper is organized as follows. In Sect. 2, we state the main mathematical results. Section 3 is devoted to the numerical studies of system (1.2) and the biological discussions of the main results. In Sect. 4, we present some preliminary results which will be useful in the subsequent sections. In Sect. 5, we give a classification of the global dynamics of system (1.2) in the $q_1-q_2$ plane. In Sect. 6, in order to investigate the influence of the predation rate and the ratio of flow speeds on the global dynamics of system (1.2), we set $q_2=\tau q_1$ and classify the global dynamics of system (1.2) in the $q_1-a$ plane. The proof of Lemma 4.5 is given in Sect. 7 via the comparison principle and uniform persistence theory.

2 Main results

Throughout the paper we make the following assumption:

$$\begin{aligned} d_1, d_2, r_{1},r_{2},K_{1},K_{2},e>0\ \text{ fixed } \text{ and } L=1. \qquad \qquad \qquad \mathrm{(H)} \end{aligned}$$

The corresponding single species models of system (1.2) with $L=1$ are, respectively, given by

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{t}=d_{1}N_{xx}-q_1N_{x}+r_{1}(1-\frac{N}{K_{1}})N,&{} x\in (0,1),\ t>0,\\ d_{1}N_{x}(0,t)-q_1N(0,t)=N_{x}(1,t)=0,&{} t>0,\\ N(x,0)=N_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,1],\\ \end{array}\right. } \end{aligned}$$

(2.1)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{t}=d_{2}P_{xx}-q_2P_{x}+r_{2}(1-\frac{P}{K_{2}})P,&{} x\in (0,1),\ t>0,\\ d_{2}P_{x}(0,t)-q_2P(0,t)=P_{x}(1,t)=0,&{} t>0,\\ P(x,0)=P_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

(2.2)

To determine the dynamics of systems (2.1) and (2.2), we introduce the following linear eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} d\phi _{xx}-q\phi _{x}+m(x)\phi =\mu \phi ,&{} x\in (0,1),\\ d\phi _{x}(0)-q\phi (0)=\phi _{x}(1)=0, \end{array}\right. } \end{aligned}$$

(2.3)

where $d>0,q\ge 0$ are constants and $m(x)\in C([0,1])$. It is well-known that (2.3) admits a principal eigenvalue, denoted by $\mu _{1}(d,q,m)$, which is also simple (see Cantrell and Cosner 2003) such that the corresponding eigenfunction $\phi _{1}(d,q,m)$ can be chosen positive and is uniquely determined by $\max \limits _{x\in [0,1]}\phi _{1}(d,q,m)=1$.

From Theorem 2.1(b) in Lou and Zhou (2015), we know that for $d_{i},r_{i}>0\ (i=1,2)$ fixed, there exists a unique critical value ${q}_{i}^{*}\in \ (0,2\sqrt{d_{i}r_{i}})$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{i},q_i,r_{i})>0,\ \text{ if }\ 0\le q_i<{q}_{i}^{*},\\ \mu _{1}(d_{i},q_i,r_{i})=0,\ \text{ if }\ q_i={q}_{i}^{*},\\ \mu _{1}(d_{i},q_i,r_{i})<0,\ \text{ if }\ q_i>{q}_{i}^{*}. \end{array}\right. } \end{aligned}$$

(2.4)

By virtue of the critical flow speeds $q_1^*$ and $q_2^*$, the threshold dynamics of the single species models (2.1) and (2.2) are given as follows, respectively:

Lemma 2.1

(Lou et al. 2018; Lou and Zhou 2015) Suppose $d_{i},r_{i}, K_i>0$ are fixed. Let N(x, t), P(x, t) be the solution of (2.1) and (2.2) respectively, and $q_{i}^{*}$ is uniquely determined by (2.4). Then

• (i) system (2.1) admits a unique positive steady-state solution $\theta _{1}=\theta _{1}(\cdot ;\ q_1)$, which satisfies $\lim \limits _{t\rightarrow +\infty }N(x,t)=\theta _{1}(\cdot ;\ q_1)$ when $0\le q_1<q_{1}^{*}$, and $\lim \limits _{t\rightarrow +\infty }N(x,t)=0$ provided that $q_1\ge q_{1}^{*}$;

• (ii) system (2.2) admits a unique positive steady-state solution $\theta _{2}=\theta _{2}(\cdot ;\ q_2)$, which satisfies $\lim \limits _{t\rightarrow +\infty }P(x,t)=\theta _{2}(\cdot ;\ q_2)$ when $0\le q_2<q_{2}^{*}$, and $\lim \limits _{t\rightarrow +\infty }P(x,t)=0$ provided that $q_2\ge q_{2}^{*}$.

Lemma 2.1 indicates that $q_1^*$ and $q_2^*$ are the threshold values of the flow speeds for the persistence of prey and predators, respectively. Now we are ready to state our first main result.

Theorem 2.1

Suppose (H) holds, $a>0$ and $q_1, q_2\ge 0$. Then there exist two continuous curves $q_2=q_2^0(q_1)$ and $q_1=q_1^0(q_2)$ such that the solution (N(x, t), P(x, t)) of system (1.2) satisfies

• (A1) $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,0)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if $q_1\ge q_1^*$ and $q_2>q_2^*$;

• (A2) $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(\theta _1,0)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if $0\le q_1<q_1^*$ and $q_2>q_2^0(q_1)$;

• (A3) If $0<a\le \frac{r_1}{K_2}$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0, \theta _2)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ when $0\le q_2<q_2^*$ and $q_1>q_1^0(q_2)$; If $a>\frac{r_1}{K_2}$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0, \theta _2)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if ${\hat{q}}_2\le q_2<q_2^*, q_1>q_1^0(q_2)$ or $0\le q_2<{\hat{q}}_2, q_1\ge 0$;

• (A4) If $0<a\le \frac{r_1}{K_2}$, then system (1.2) is uniformly persistent in the sense that there exists an $\eta >0$, independent of the initial data, such that the solution (N(x, t), P(x, t)) satisfies $\liminf \limits _{t\rightarrow +\infty }N(x,t)\ge \eta$, and $\liminf \limits _{t\rightarrow +\infty }P(x,t)\ge \eta$ for $x\in [0,1]$ when $0\le q_1<q_1^*, q_2^*\le q_2<q_2^0(q_1)$ or $0\le q_2<q_2^*, 0\le q_1<q_1^0(q_2)$; If $a>\frac{r_1}{K_2}$, system (1.2) is uniformly persistent when $0\le q_1<q_1^*, (q_1^0(q_2))^{-1}<q_2<q_2^0(q_1)$. Moreover, in both cases, system (1.2) admits a unique positive steady state.

Here ${\hat{q}}_2$ is uniquely determined by $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}({\hat{q}}_2))=0$, and $(q_1^0(q_2))^{-1}$ denotes the inverse function of $q_1=q_1^0(q_2)$ with $q_2\in [{\hat{q}}_2, q_2^*)$ (see Lemma 5.3). Furthermore, the two critical curves enjoy the following properties:

• (B1) The critical curve $q_2=q_2^0(q_1)$ defined in $q_1\in [0, q_{1}^{*})$ is strictly decreasing with respect to $q_1$ with $q_2^0(0)={\bar{q}}_2$ and $\lim \limits _{q_1\rightarrow q_1^*-}q_2^0(q_1)=q_2^*$, where ${\bar{q}}_2$ is uniquely determined by $\mu _1(d_2, {\bar{q}}_{2}, r_2+eaK_1)=0$ (see Lemma 4.3);

• (B2) If $0<a\le \frac{r_1}{K_2}$, then the critical curve $q_1=q_1^0(q_2)$ is defined in $q_2\in [0, q_2^{*})$ and strictly increasing with respect to $q_2$ with $\lim \limits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*,$ $q_1^0(0)>0$ if $a<\frac{r_1}{K_2}$ and $q_1^0(0)=0$ if $a=\frac{r_1}{K_2}$;

• (B3) If $a>\frac{r_1}{K_2}$, then the critical curve $q_1=q_1^0(q_2)$ is defined in $q_2\in [{\hat{q}}_2, q_2^*)$ and strictly increasing with respect to $q_2$ with $\lim \limits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*$ and $q_1^0({\hat{q}}_2)=0$.

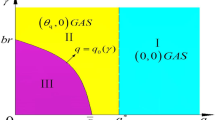
As shown in Theorem 2.1, the dynamics of system (1.2) is more complex in contrast to system (1.1) (see Nie et al. 2020). More precisely, there exist some critical curves such as $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1),\ q_1=q_{1}^{*}$ and $q_2=q_{2}^{*}$ in the $q_1-q_2$ plane, which divide the dynamics of system (1.2) into four scenarios (Fig.  1). If both the prey and predators are subject to large flow speeds, then they will be washed out eventually (Theorem 2.1(A1)). The species with the smaller flow speed may survive alone if the other species experiences a larger flow speed (Theorem 2.1(A2)–(A3)). Only when both species have relatively small flow speeds, they can coexist (Theorem 2.1(A4)).

Fig. 1

Schematic illustration of Theorem 2.1 in the $q_1-q_2$ plane. Here the abbreviation “GAS” denotes “globally asymptotically stable”. $0<a<\frac{r_1}{K_2}$ in (a), $a=\frac{r_1}{K_2}$ in (b) and $a>\frac{r_1}{K_2}$ in (c). In region I, the trivial solution (0, 0) is GAS. The semi-trivial solution $(0,\theta _{2})$ is GAS in region II while the semi-trivial solution $(\theta _{1},0)$ is GAS in region IV. System (1.2) is uniformly persistent in region III, which admits a unique positive steady state

Furthermore, Theorem 2.1 and subsequent numerical simulations (Figs. 4 and 5) also indicate that the dynamics of system (1.2) strongly depends on the predation rate a and the ratio $q_2:q_1$ of flow speeds. To understand the joint influence of the predation rate and the flow speed ratio on the dynamics of system (1.2), we set $q_2=\tau q_1$ and have the following two results:

Theorem 2.2

Suppose (H) holds, $a>0,\ q_2=\tau q_1$ and $q_1\ge 0$. If $0<\tau \le \frac{q_2^*}{q_1^*}$, then there exist two curves $a=a_\tau ^*(q_1)$ with $0\le q_1<q_{1}^{*}$ (defined by Lemma 6.3) and $q_1=\frac{q_{2}^{*}}{\tau }$ such that the solution (N(x, t), P(x, t)) of system (1.2) satisfies

• (i) If $q_1>\frac{q_{2}^{*}}{\tau }$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,0)\ \text{ uniformly } \text{ for }\ x\in [0,1];$

• (ii) If $0\le q_1<q_{1}^{*}$ and $a>a_\tau ^*(q_1)$, or $q_{1}^{*}\le q_1<\frac{q_{2}^{*}}{\tau }$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,\theta _{2})$ uniformly for $x\in [0,1];$

• (iii) If $0\le q_1<q_{1}^{*}$ and $0<a<a_\tau ^*(q_1)$, then system (1.2) is uniformly persistent. Moreover, system (1.2) admits a unique positive steady state.

Fig. 2

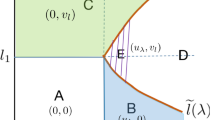
Schematic illustrations of Theorems 2.2 and 2.3 with $q_2=\tau q_1$ and $\frac{r_2}{r_1}<\frac{q_{2}^{*}}{q_{1}^{*}}$ in the $q_1-a$ plane. Here $\tau \le \frac{r_2}{r_1}$ in (a); $\frac{r_2}{r_1}<\tau <\frac{q_2^*}{q_1^*}$ in (b); $\tau = \frac{q_2^*}{q_1^*}$ ( i.e. $q_1^*=\frac{q_2^*}{\tau }$) in (c); and $\tau >\frac{q_2^*}{q_1^*}$ in (d). What each colored region means is similar to Fig. 1

Theorem 2.3

Suppose (H) holds, $a>0,\ q_2=\tau q_1$ and $q_1\ge 0$. If $\tau >\frac{q_2^*}{q_1^*}$, then there exist three curves $a=a_\tau ^*(q_1)$ with $0\le q_1<\frac{q_{2}^{*}}{\tau }$, $a=a_\tau ^{0}(q_1)$ with $\frac{q_{2}^{*}}{\tau }\le q_1<q_{1}^{*}$ (defined by Lemma 6.2) and $q=q_{1}^{*}$ such that the solution (N(x, t), P(x, t)) of system (1.2) satisfies

• (i) If  $q_1\ge q_{1}^{*}$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,0)\ \text{ uniformly } \text{ for }\ x\in [0,1];$

• (ii) If  $\frac{q_{2}^{*}}{\tau }\le q_1<q_{1}^{*}$ and $0<a<a_\tau ^{0}(q_1)$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(\theta _{1},0)$ uniformly for $x\in [0,1];$

• (iii) If  $0\le q_1<\frac{q_{2}^{*}}{\tau }$ and $a>a_\tau ^*(q_1)$, then $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,\theta _{2})$ uniformly for $x\in [0,1];$

• (iv) If  $0\le q_1<\frac{q_{2}^{*}}{\tau }$ and $0<a<a_\tau ^*(q_1)$, or $\frac{q_{2}^{*}}{\tau }\le q_1<q_{1}^{*}$ and $a>a_\tau ^{0}(q_1)$, then system (1.2) is uniformly persistent. Moreover, system (1.2) admits a unique positive steady state.

Theorems 2.2–2.3 are illustrated in Fig. 2.2 (for the case $\frac{r_2}{r_1}<\frac{q_2^*}{q_1^*}$) and Fig. 2.3 (for the case $\frac{r_2}{r_1}>\frac{q_2^*}{q_1^*}$), respectively. These results confirm the vital role of the predation rate and the ratio of flow speeds on the dynamics of system (1.2). To be more specific,

• 1. If the ratio satisfies $0<\tau \le \frac{q_2^*}{q_1^*}$, then only three scenarios can occur (see Figs. 2a–c and 3a, b). That is, if the prey’s flow speed is small (i.e. $0\le q_1<q_{1}^{*}$), then predators can coexist with the prey when the predation rate is also suitably small (i.e. $a<a_\tau ^*(q_1)$), followed by the prey going extinct when the predation rate continues to increase (i.e. $a>a_\tau ^*(q_1)$). The prey is washed out and predators survive alone if the prey takes intermediate flow speeds (i.e. $q_{1}^{*}\le q_1<\frac{q_{2}^{*}}{\tau }$), no matter how large the predation rate is. If the prey’s flow speed is sufficiently large (i.e. $q_1>\frac{q_{2}^{*}}{\tau }$), both the prey and predators are washed out, which is consistent with our intuition.

• 2. If the ratio $\tau >\frac{q_2^*}{q_1^*}$, then there are four scenarios for the generalist predator-prey system (1.2) (see Figs. 2d and 3c, d). For small flow speed satisfying $0\le q_1<\frac{q_{2}^{*}}{\tau }$, the dynamics is similar to the previous case. If the prey’s flow speed is suitably large (i.e. $\frac{q_{2}^{*}}{\tau }\le q_1<q_{1}^{*}$), the critical curve $a=a_\tau ^{0}(q_1)$ distinguishes the following two scenarios: (i) the successful invasion of predators when the predation rate is large, i.e. $a>a_\tau ^{0}(q_1)$, and (ii) the survival of the prey only when $a<a_\tau ^{0}(q_1)$. That is, large predation rate can balance the intermediate flow speed and help predators invade successfully. Both species are washed out when the flow is strong enough (i.e. $q_1\ge q_{1}^{*}$).

Fig. 3

Schematic illustrations of Theorems 2.2 and 2.3 with $q_2=\tau q_1$ and $\frac{r_2}{r_1}>\frac{q_{2}^{*}}{q_{1}^{*}}$ in the $q_1-a$ plane. Here $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$ in (a); $\tau =\frac{q_2^*}{q_1^*}$ in (b); $\frac{q_2^*}{q_1^*}<\tau <\frac{r_2}{r_1}$ in (c); and $\tau \ge \frac{r_2}{r_1}$ in (d). What each colored region indicates is similar to Fig. 1

In summary, as Hilker and Lewis (2010) predicted, the dynamics of system (1.2) is more complex. In sharp contrast to system (1.1) (see Nie et al. 2020), there occurs a new phenomenon (i.e. the persistence of predators only) for the generalist predator-prey system (1.2). Moreover, the range for the prey persistence shrinks because the prey is propagating into the habitat occupied by predators, which leads to a reduced prey growth (see Hilker and Lewis 2010; Nie et al. 2020, and Figs. 2 and 3).

3 Numerical simulations and biological discussions

The goal of this section is to investigate system (1.2) numerically and discuss the biological implications of the main results.

3.1 Numerical simulations

As shown in Theorems 2.1–2.3, the predation rate a and the ratio $\tau =q_2:q_1$ of flow speeds, experienced by predators and prey, play important roles in determining the dynamics of system (1.2). To further understand their joint influence on the dynamics of system (1.2), we next study system (1.2) via a numerical approach. Fix $r_{1}=1,\ r_{2}=0.5,\ K_1=3,\ K_2=2,\ e=0.5,\ L=1$, and vary the parameter values of $d_1, ~d_2, ~a$ to find various locations of the critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1)$ and the number of points where the curve $q_2=\tau q_1$ intersect with two critical curves.

Fig. 4

The numerical bifurcation diagrams on the classification of the global dynamics of system (1.2) are illustrated in terms of the four critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1),\ q_1=q_{1}^{*}$ and $q_2=q_{2}^{*}$ in the $q_1-q_2$ plane. The horizontal axis $q_1$, the flow speed of the prey, ranges from 0 to 0.2, and the vertical axis $q_2$ is the flow speed of the predator ranging from 0 to 1. Here the parameters are taken as follows: $d_1=0.1, d_2=2, r_{1}=1, r_{2}=0.5, K_1=3, K_2=2, e=0.5, L=1$ and $a=0.4, 0.5, 0.6, 0.7$ in (a)-(d) respectively. For different predation rates, the black dashed line $q_2=\tau q_1$ with $\tau =0.95\frac{q_2^*}{q_1^*}$ may have zero, one or two intersections with the critical curve $q_1=q_1^0(q_2)$, which separates persistence of generalist predators only from coexistence

At first, we take $d_1=0.1$, $d_2=2$. By computations, $q_{1}^{*}=0.1801$ and $q_{2}^{*}=0.3638$. Hence, we have $\frac{r_2}{r_1}<\frac{q_2^*}{q_1^*}$ in this case. Taking $a=0.4, 0.5, 0.6, 0.7$ in turns, we observe that the locations of two critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1)$ are changing with respect to the predation rate a in the $q_1-q_2$ plane (see Fig. 4). More precisely, the strictly increasing critical curve $q_1=q_1^0(q_2)$ always passes through the point $(q_{1}^{*}, q_{2}^{*})$, and all the other points on it go to the left with the increase of the predation rate. Similarly, the strictly decreasing critical curve $q_2=q_2^{0}(q_1)$ also passes through the point $(q_{1}^{*}, q_{2}^{*})$, and all the other points on it go upward with the increase of the predation rate. It follows from Proposition 5.4 that two critical curves $q_1=q_1^{0}(q_2)$ and $q_2=q_2^{0}(q_1)$ continuously depend on the predation rate a. Moreover, when a goes to zero, they converge to the curve $q_1=q_1^*$ with $q_2\in [0, q_2^*)$ and $q_2=q_2^*$ with $q_1\in [0, q_1^*)$, respectively. In this case, the unique positive steady state, denoted by $(N_a, P_a)$, of system (1.2) converges to $(\theta _1, \theta _2)$ uniformly for $x\in [0, 1]$ as $a\rightarrow 0+$. If $a\rightarrow +\infty$, two critical curves $q_1=q_1^{0}(q_2)$ and $q_2=q_2^{0}(q_1)$ converge to the curve $q_2=q_2^*$ with $q_1\in [0, q_1^*)$ and $q_1=q_1^*$ with $q_2\in (q_2^*, +\infty )$, respectively, and the unique positive steady state $(N_a, P_a)$ of system (1.2) converges to (0, 0) almost everywhere on [0, 1] as a goes to infinity.

Moreover, we observe that the line $q_2=\tau q_1$ with $\tau =0.95\frac{q_2^*}{q_1^*}\in (\frac{r_2}{r_1}, \frac{q_2^*}{q_1^*})$ is always below the critical curve $q_2=q_2^{0}(q_1)$ without intersections (see Fig. 4), which implies that the semi-trivial steady state $(\theta _1, 0)$ is always unstable (see Lemma 5.2). However, it may cross the critical curve $q_1=q_1^0(q_2)$ zero time, once or twice (see Fig. 4), which means that for different predation rates a, the stability of $(0, \theta _2)$ may change zero time, once or twice as the flow speed $q_1$ changes (see Lemma 5.3). These observations match with Corollary 6.1(i), which classifies the global dynamics of system (1.2) with $q_2=\tau q_1$ and $\frac{r_2}{r_1}<\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$; see also Fig. 2b in the $q_1-a$ plane.

If $\tau >\frac{q_2^*}{q_1^*}$, then it is easy to see that the line $q_2=\tau q_1$ always crosses the critical curve $q_2=q_2^{0}(q_1)$ exactly once, which implies that the stability of $(\theta _1, 0)$ changes exactly once as $q_1$ increases (see Lemma 5.2). From another perspective, by combining Lemma 6.2 with Proposition 6.4, one can conclude that there exists a strictly increasing critical curve $a=a_\tau ^{0}(q_1)$ defined in $q_1\in [\frac{q_2^*}{\tau }, q_1^*)$ in the $q_1-a$ plane, which exactly distinguishes between the stable and unstable regions of $(\theta _1, 0)$, such that $a_\tau ^{0}(\frac{q_{2}^{*}}{\tau })=0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{0}(q_1)=+\infty$. Meanwhile, the line $q_2=\tau q_1$ with $\tau >\frac{q_2^*}{q_1^*}$ may cross the critical curve $q_1=q_1^0(q_2)$ zero time or once, which means the stability of $(0, \theta _2)$ may change zero time or once (see Lemma 5.3). These observations suggest that the classification of the global dynamics of system (1.2) with $q_2=\tau q_1$ and $\tau >\frac{q_{2}^{*}}{q_{1}^{*}}$ looks like Fig. 2d in the $q_1-a$ plane. Similarly, for $\tau \le \frac{r_2}{r_1}$ and $\tau =\frac{q_2^*}{q_1^*}$, the classification of the global dynamics of system (1.2) with $q_2=\tau q_1$ is shown in Fig. 2a, c, respectively.

Secondly, if we take $d_1=2, d_2=0.1$, then $q_{1}^{*}=0.6078$ and $q_{2}^{*}=0.1238$ by some computations. Hence, $\frac{q_2^*}{q_1^*}<\frac{r_2}{r_1}$. Taking $a=0.35, 0.45, 0.5, 0.6$ in turns, we observe a similar phenomena on the locations of two critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1)$, changing with respect to the predation rate a in the $q_1-q_2$ plane (see Fig. 5). Moreover, we observe that the line $q_2=\tau q_1$ with $\tau =1.1\frac{q_2^*}{q_1^*}\in (\frac{q_2^*}{q_1^*}, \frac{r_2}{r_1})$ always crosses the critical curve $q_2=q_2^{0}(q_1)$ exactly once, and it may cross the critical curve $q_1=q_1^0(q_2)$ zero time, once or twice (see Fig. 5). These observations coincide with Corollary 6.1(ii), which classifies the global dynamics of system (1.2) with $q_2=\tau q_1$ and $\frac{q_{2}^{*}}{q_{1}^{*}}<\tau <\frac{r_2}{r_1}$; see also Fig. 3c in the $q_1-a$ plane. Similarly, for $\tau \le \frac{q_2^*}{q_1^*}$ and $\tau \ge \frac{r_2}{r_1}$, the classification of the global dynamics of system (1.2) with $q_2=\tau q_1$ is depicted in Fig. 3a, b, d, respectively.

Fig. 5

The numerical bifurcation diagrams on the classification of the global dynamics of system (1.2) are illustrated in terms of the four critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1),\ q_1=q_{1}^{*}$ and $q_2=q_{2}^{*}$ in the $q_1-q_2$ plane. The horizontal axis $q_1$ denotes the flow speed of the prey ranging from 0 to 0.8, and the vertical axis $q_2$ denotes the flow speed of the predator ranging from 0 to 0.3. Here the parameters are taken as follows: $d_1=2, d_2=0.1, r_{1}=1, r_{2}=0.5, K_1=3, K_2=2, e=0.5, L=1$ and $a=0.35, 0.45, 0.5, 0.6$ in (a)–(d) respectively. For different predation rates, the black dashed line $q_2=\tau q_1$ with $\tau =1.1\frac{q_2^*}{q_1^*}$ may cross the critical curve $q_1=q_1^0(q_2)$ zero time, once or twice

3.2 Biological discussions

As shown by Hilker and Lewis (2010), different prey and predator flow speeds may cause complex dynamics for the predator-prey system in advective environments. In particular, Hilker and Lewis (2010) have discovered that the ratio $\tau =q_2: q_1$ of flow speeds, experienced by predators and prey, plays a vital role in determining the dynamics of the predator-prey system in advective environments. More precisely, for the dimensionless predator-prey model of Hilker and Lewis (2010), if the specialist predators are faster than the prey in the absence of flow and the ratio $\tau =q_2: q_1>1$, then the following scenarios are distinguished (see Fig. 5 of Hilker and Lewis 2010):

• (i) For small flow speeds, the predators catch up to the prey in the upstream direction, and two species coexist eventually.

• (ii) As flow speeds increase, the prey runs away from the predators in the upstream direction, and there is coexistence with a prey run-away rather than a predator catch-up.

• (iii) A further increase of flow speeds causes the wash-out of predators and gives rise to a prey refuge.

• (iv) The result by increasing flow speeds further is the wash-out of both predators and prey.

It is worth highlighting that only (i) and (iv) can occur if the predators and prey take identical flow speeds, which is illustrated in Fig. 4 of Hilker and Lewis (2010).

Similar transition of dynamical behaviors can be observed for generalist predator-prey model as flow speeds vary, see, e.g., Fig. 6 of Hilker and Lewis (2010). Specifically, as shown in Fig. 6 of Hilker and Lewis (2010), if the critical predator flow speed is larger than the critical prey flow speed, denoted by $v^{\ddagger }$ and $v^\star$ respectively there, then the prey extinction and the persistence of the predators occur only for some intermediate flow speeds. This new flow regime can only be observed in the generalist predator-prey system. Nevertheless, the critical predator flow speed $v^{\ddagger }$ is strictly decreasing with respect to the ratio $\tau =q_2: q_1$ of flow speeds. As the ratio $\tau$ increases, the critical predator flow speed $v^{\ddagger }$ may become less than the critical prey flow speed $v^\star$ (see Fig. 6 of Hilker and Lewis (2010)), which will cause (ii) and (iii) to be observed for some intermediate flow speeds. In general, all the results illustrated in Figs. 4–6 of Hilker and Lewis (2010) show us that different prey and predator flow speeds may cause complex dynamics for the predator-prey system in advective environments.

Motivated by these predictions of Hilker and Lewis (2010) on the dynamics of the predator-prey system in advective environments, we studied the dynamics of system (1.2) and discovered that the ratio $\tau$ of flow speeds does play a vital role in determining the dynamics of system (1.2).

If the ratio $\tau$ is small enough such that the two critical flow speeds satisfy $q_1^*<\frac{q_2^*}{\tau }$, then for intermediate flow speeds (i.e. $q_1^*<q_1<\frac{q_2^*}{\tau }$), there appears the new phenomenon of generalist predator take-over (i.e., the extinction of prey and the persistence of generalist predators only, see Hilker and Lewis 2010) in comparison with the specialist predator-prey system (1.1) (see Nie et al. 2020), which is shown in Theorem 2.2(ii), and is also illustrated in Figs. 2a, b and 3a. As mentioned above, this phenomenon has already been depicted in Fig. 6 of Hilker and Lewis (2010) , which is a significant difference between the specialist predator-prey system and the generalist predator-prey system in advective environments.

Meanwhile, as shown in Theorems 2.2(ii) and 2.3(iii), for small flow speeds (i.e. $0\le q_1<\min \{q_1^*,\frac{q_2^*}{\tau }$}), generalist predators can take over by increasing the predation rate a to balance the negative effect of flow speeds regardless of the size of the ratio $\tau$, see also Figs. 1 and 2. That is, there exists a critical curve $a=a_\tau ^*(q_1)$, which separates the coexistence from the persistence of generalist predators alone. This observation indicates that the predation rate also plays an important role in determining the dynamics of system (1.2), which is not mentioned by Hilker and Lewis (2010).

Furthermore, we observe the interesting evolution of the critical curve $a=a_\tau ^*(q_1)$ when the ratio $\tau$ changes (see Figs. 2 and 3). More precisely, if $\frac{r_2}{r_1}<\frac{q_2^*}{q_1^*}$, then the critical curve $a=a_\tau ^*(q_1)$ evolves from Fig. 2a–d as the ratio $\tau$ increases (see Proposition 6.5), for which generalist predators always succeed in invading as long as the flow speed is suitably small (i.e. $0\le q_1<\frac{q_2^*}{\tau }$). Furthermore, for small $\tau$ (i.e. $\tau \le \frac{r_2}{r_1}$), we have ${\dot{a}}_\tau ^{*}(0)=\frac{\tau r_{1}-r_{2}}{r_{2}K_{2}}\le 0$ and $q_1^*<\frac{q_2^*}{\tau }$, which implies that the critical curve $a=a_\tau ^*(q_1)$ may decrease to zero in $q_1\in [0, q_1^*)$ as shown in Fig. 2a (see Proposition 6.5(i)(ii)). Increasing $\tau$ gives rise to ${\dot{a}}_\tau ^{*}(0)=\frac{\tau r_{1}-r_{2}}{r_{2}K_{2}}>0$ and the difference $\frac{q_2^*}{\tau }-q_1^*$ decreasing from positive to negative. In particular, for $\frac{r_2}{r_1}<\tau <\frac{q_2^*}{q_1^*}$, the critical curve $a=a_\tau ^*(q_1)$ may first increase and eventually decrease to zero in $[0, q_1^*)$, and the difference $\frac{q_2^*}{\tau }-q_1^*>0$ goes down (see Corollary 6.1(i) and Fig. 2b). For $\tau =\frac{q_2^*}{q_1^*}$, $\frac{q_2^*}{\tau }$ and $q_1^*$ coincide perfectly, and a sketch of $a=a_\tau ^*(q_1)$ is shown in Fig. 2c. Increasing $\tau$ eventually causes $\frac{q_2^*}{\tau }<q_1^*$, and the critical curve $a=a_\tau ^*(q_1)$ defined in $[0, \frac{q_2^*}{\tau })$ goes to infinity as $q_1$ tends to $\frac{q_2^*}{\tau }$; see Proposition 6.5(iii) for further details. It is worth stressing that similar shrinks of the difference (i.e. $\frac{q_2^*}{\tau }-q_1^*$) between the two critical flow speeds have been described in Figs. 5 and 6 of Hilker and Lewis (2010). However, the influence of the predation rate has been ignored there.

Similarly, if $\frac{r_2}{r_1}>\frac{q_2^*}{q_1^*}$, then the critical curve $a=a_\tau ^*(q_1)$ evolves from Fig. 3a to 3d as the ratio $\tau$ increases (see Proposition 6.5). Under this circumstance, the shape of the critical curve $a=a_\tau ^*(q_1)$ with $q_1\in [0, \frac{q_2^*}{\tau })$ changes dramatically, which can be decreasing first (if $\frac{q_2^*}{q_1^*}<\tau <\frac{r_2}{r_1}$) and eventually increasing to infinity when $q_1$ tends to $\frac{q_2^*}{\tau }$ (see Corollary 6.1(ii) and Fig. 3c). Therefore, there may exist an optimal flow speed $q_1$ for generalist predator take-over, where the critical predation rate $a_\tau ^*(q_1)$ reaches its minimum. This is another striking difference between the specialist predator-prey system and the generalist predator-prey system.

In addition, similar to (iii) mentioned above, a prey refuge may appear conditionally for system (1.2) when the ratio $\tau >\frac{q_2^*}{q_1^*}$. To be more precise, for this case, another strictly increasing critical curve $a=a_\tau ^{0}(q_1)$ in $q_1\in [\frac{q_2^*}{\tau }, q_1^*)$ occurs, satisfying $a_\tau ^{0}(\frac{q_{2}^{*}}{\tau })=0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*-}}a_\tau ^{0}(q_1)=+\infty$ (see Proposition 6.4), under which (i.e. the predation rate $a<a_\tau ^{0}(q_1)$) the prey can persist alone (see Theorem 2.3(ii), Figs. 2d and 3c, d). Moreover, in contrast to the specialist predator-prey system (1.1) (see Nie et al. 2020), the range of prey persistence alone shrinks as the difference $q_1^*-\frac{q_2^*}{\tau }$ decreases, and it is more likely for generalist predators to catch the prey and invade successfully. Recalling that the gap $q_1^*-\frac{q_2^*}{\tau }$ decreases with the decrease of the ratio $\tau$, one concludes that the lower ratio of flow speeds experienced by predators and prey is in favor of the invasion of the predators. These results confirm and extend the predictions of Hilker and Lewis (2010) on the generalist predator-prey system (1.2).

Generally speaking, as Hilker and Lewis predicted about the dynamics of system (1.2), four scenarios may occur for the generalist predator-prey system in open advective environments: (1) coexistence; (2) the persistence of prey only; (3) the persistence of predators only; and (4) the extinction of both species. In particular, it is worth mentioning that scenario (3) can not occur in the specialist predator-prey system (1.1) (see Nie et al. 2020). Biologically speaking, the slower flow speeds and the lower ratio of flow speeds experienced by predators and prey, the more likely it is for generalist predators to invade successfully. Moreover, large predation rate can balance the negative effect of flow speeds and help generalist predators invade successfully. Both species are washed out when the flow is strong enough.

We end this section by mentioning some interesting problems for future investigations. This paper deals with a generalist predator-prey system in open advective environments, i.e. the Danckwert’s boundary conditions (see Ballyk et al. 1998) at the downstream end. A natural question concerns the dynamics of the generalist predator-prey system (1.2) in closed advective environments (i.e. by imposing no-flux conditions at both ends (Lam et al. 2015)). Also, how does the dynamics change if the functional response is Holling type II or other nonlinear ones? We leave these problems for future studies.

4 Preliminaries

In this section, we first present some important results on the linear eigenvalue problem (2.3) and the positive steady states of (2.1) and (2.2).

Lemma 4.1

(Nie et al. 2020) Suppose $d>0,\ q\ge 0$ are constants and $m(x)\in C([0,1])$. Then the principal eigenvalue $\mu _{1}(d,q,m)$ of (2.3) satisfies

$$\begin{aligned} -\mu _{1}(d,q,m)=\inf _{\phi \ne 0,\phi \in H^{1}((0,1))}\frac{q\phi ^{2}(0)+\int _{0}^{1}e^{-\frac{q}{d}x}(d\phi _{x}^{2}-m(x)\phi ^{2})d x}{\int _{0}^{1}e^{-\frac{q}{d}x}\phi ^{2}d x}. \end{aligned}$$

(4.1)

Moreover, it has the following properties:

• (i) $\mu _{1}(d,q,m)$ depends smoothly on parameters d and q;

• (ii) $m_{n}(x)\rightarrow m(x)$ in $L^\infty ((0,1))$ implies $\mu _{1}(d,q,m_{n})\rightarrow \mu _{1}(d,q,m)$;

• (iii) $m_{1}(x)\ge m_{2}(x)$ in [0, 1] implies $\mu _{1}(d,q,m_{1})\ge \mu _{1}(d,q,m_{2})$, the equality holds only if $m_{1}\equiv m_{2}$;

• (iv) $\mu _{1}(d,q,m)$ is strictly decreasing with respect to $q\in [0,+\infty )$, and $\lim \limits _{q\rightarrow +\infty }\mu _{1}(d,q,m)=-\infty$;

• (v) $\lim \limits _{d\rightarrow 0+}\mu _{1}(d,q,m)=-\infty$ if $q>0$, and $\lim \limits _{d\rightarrow +\infty }\mu _{1}(d,q,m)=\int _{0}^{1}m(x)d x-q$ if $q\ge 0$;

• (vi) $\mu _{1}(d,q,0)$ is strictly increasing with respect to $d\in (0, +\infty )$ and $\mu _{1}(d,0,0)=0;$

• (vii) the positive eigenfunction $\phi _{1}(d,q,0)$ depends smoothly on parameters d and q, and $0<(\phi _{1})_{x}<\frac{q}{d}\phi _{1}\ if\ q>0,\ \ \phi _{1}(d,0,0)\equiv 1.$

We denote the principal eigenvalue of a linear operator ${\mathcal {B}}$ by $\lambda _{1}({\mathcal {B}})$ in the subsequent analysis if necessary. It follows from Lemma 2.1 that the unique positive steady state $\theta _{i}(\cdot ;\ q_i)$ for single species system (2.1) or (2.2) exists when $q_i\in [0,q_{i}^{*})$. Next we state the following results in regard to $\theta _{i}(\cdot ;\ q_i)$:

Lemma 4.2

Suppose $0\le q_i<q_{i}^{*}\ (i=1,2)$. Then

• (i) $\frac{K_{i}}{r_{i}}\mu _{1}(d_{i},q_i,r_{i})\phi _{1}(d_{i},q_i,r_{i})\le \theta _{i}(\cdot ;\ q_i)<K_{i}$ for $x\in [0,1]$ provided that $0<q_i<q_{i}^{*}$;

• (ii) $\theta _{i}(\cdot ;\ q_i)$ is continuously differentiable for $q_i\in [0,q_{i}^{*})$, and it is decreasing pointwisely on $x\in [0,1]$ when $q_i$ increases; moreover, $\theta _{i}(\cdot ;\ 0)\equiv K_{i},\ \ \lim \limits _{q_i\rightarrow q_{i}^*-}\theta _{i}(\cdot ;\ q_i)=0$ uniformly for $x\in [0,1]$.

Proof

(i) If $0<q_i<q_{i}^{*}$, then we have $0<\mu _{1}(d_{i},q_i,r_{i})<\mu _{1}(d_{i},0,r_{i})=r_{i}$. Hence, by the upper and lower solution method and the uniqueness of $\theta _{i}$, direct calculations lead to $\frac{K_{i}}{r_{i}}\mu _{1}(d_{i},q_i,r_{i})\phi _{1}(d_{i},q_i,r_{i})\le \theta _{i}(\cdot ;\ q_i)<K_{i}$ on [0, 1].

The results in (ii) can be established by similar arguments as in Lemma 5.4(ii) of Lou et al. (2018). Since the proof is rather standard, we omit it here. $\square$

Next, we derive some a priori estimates on the solutions of system (1.2) with $L=1$. To establish a priori estimates of the steady-state solutions of system (1.2) with $L=1$, we consider

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}N_{xx}-q_1N_{x}+r_{1}(1-\frac{N}{K_{1}})N-aNP=0,&{} x\in (0,1),\\ d_{2}P_{xx}-q_2P_{x}+r_{2}(1-\frac{P}{K_{2}})P+eaNP=0,&{} x\in (0,1),\\ d_{1}N_{x}(0)-q_1N(0)=0,\ N_{x}(1)=0,\\ d_{2}P_{x}(0)-q_2P(0)=0,\ P_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(4.2)

Lemma 4.3

Suppose (H) holds, $a>0$, $q_1, q_2\ge 0$ and (N, P) is a nonnegative solution of (4.2) with $N\not \equiv 0$, $P\not \equiv 0$. Then

• (i) $0\le q_1<q_{1}^{*},\ 0\le q_2<{\bar{q}}_{2},$ where ${\bar{q}}_{2}$ is uniquely determined by $\mu _1(d_2, {\bar{q}}_{2}, r_2+eaK_1)=0$;

• (ii) $0<N<\theta _{1}(\cdot ;q_1)$ and $0<P<K_{2}+\frac{eaK_{1}K_{2}}{r_{2}}$ on [0, 1];

• (iii) $\theta _{2}(\cdot ; q_2)<P$ on [0, 1] provided that $0\le q_2<q_{2}^{*}.$

Proof

By the strong maximum principle, $N>0,\ P>0$ in [0, 1]. Combining with the first equation of (4.2) and Lemma 4.1(iii), we have

$$\begin{aligned} \mu _{1}(d_{1},q_1,r_{1})>\mu _{1}(d_{1},q_1,r_{1}-r_{1}\frac{N}{K_{1}}-aP)=0. \end{aligned}$$

Obviously, by using (2.4) we obtain that $0\le q_1<q_{1}^{*}$.

It follows from the first equation of (4.2) that

$$\begin{aligned}&d_{1}N_{xx}-q_1N_{x}+r_{1}(1-\frac{N}{K_{1}})N\\&>d_{1}N_{xx}-q_1N_{x}+r_{1}(1-\frac{N}{K_{1}})N-aNP=0,\quad x\in (0,1). \end{aligned}$$

Note that

$$\begin{aligned} {\left\{ \begin{array}{ll} d_1(\theta _1)_{xx}-q_1(\theta _1)_{x}+r_1\theta _1(1-\frac{\theta _1}{K_1})=0,&{} x\in (0,1),\\ d_{1}(\theta _{1})_{x}(0)-q_1\theta _{1}(0)=0,\ (\theta _1)_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(4.3)

We obtain that $N<\theta _{1}$ on [0, 1] by the upper and lower solution method and the uniqueness of $\theta _{1}$. From Lemma 2.1, we know that $\theta _{2}$ exists when $0\le q_2<q_{2}^{*}$. By similar arguments as above, we can prove $\theta _{2}<P$ on [0, 1] when $0\le q_2<q_{2}^{*}$.

Furthermore, by Lemma 4.2(i), we have $0<N<K_{1}$ on [0, 1], hence

$$\begin{aligned} \mu _{1}(d_{2},q_2,r_{2}+eaK_{1})>\mu _{1}(d_{2},q_2,r_{2}-r_{2}\frac{P}{K_{2}}+eaN)=0. \end{aligned}$$

Similar arguments as for (2.4) yield that there exists a unique ${\bar{q}}_2\in (0, 2\sqrt{d_2(r_2+eaK_1)})$ such that

$$\begin{aligned} \mu _{1}(d_{2},{\bar{q}}_2,r_{2}+eaK_{1})=0. \end{aligned}$$

By Lemma 4.1(iv), we obtain that $q_2<{\bar{q}}_2.$ Meanwhile, we also have

$$\begin{aligned} \mu _{1}(d_{2},q_2,r_{2}-r_{2}\frac{P}{K_{2}}+eaK_{1})>\mu _{1}(d_{2},q_2,r_{2}-r_{2}\frac{P}{K_{2}}+eaN)=0. \end{aligned}$$

By Lemma 4.1(vi) and (iv), we have

$$\begin{aligned} \mu _{1}(d_{2},q_2,0)=0\ \text{ if }\ q_2=0,\ \ \mu _{1}(d_{2},q_2,0)<0\ \text{ if }\ q_2>0, \end{aligned}$$

(4.4)

which deduce that $r_{2}-r_{2}\frac{P}{K_{2}}+eaK_{1}>0$. That is, $P<K_{2}+\frac{eaK_{1}K_{2}}{r_{2}}$ on [0, 1]. $\square$

Lemma 4.4

Suppose (H) holds, $a>0$ and $q_1, q_2\ge 0$. Then system (1.2) has a unique solution (N(x, t), P(x, t)) defined for all $x\in [0,1]$ and $t>0$, and

$$\begin{aligned} 0<N(x,t)\le C_{2},\ 0<P(x,t)\le C_{3},\ x\in [0,1],\ t>0, \end{aligned}$$

where positive constants $C_{2},\ C_{3}$ are dependent on the initial data $N_{0}(x),\ P_{0}(x).$ Moreover,

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }N(x,t)\le K_1 ~\mathrm {and}~ \limsup \limits _{t\rightarrow +\infty }P(x,t)\le K_{2}+\frac{eaK_1K_{2}}{r_{2}} ~\mathrm {uniformly}~\mathrm {on}~[0,1]. \end{aligned}$$

Proof

It’s standard to show the local existence and uniqueness of solutions to (1.2) (see Smoller 1983). Next we prove the global boundedness. Easily we get that $N(x,t)>0,\ P(x,t)>0$ for all $x\in [0,1],\ t>0$ by using the strong maximum principle of the parabolic equation. Hence,

$$\begin{aligned} {\left\{ \begin{array}{ll} N_{t}<d_{1}N_{xx}-q_1N_{x}+r_{1}N(1-\frac{N}{K_{1}}),&{} x\in (0,1),\ t>0,\\ d_{1}N_{x}(0,t)-q_1 N(0,t)=0,\ N_{x}(1,t)=0,&{} t>0,\\ N(x,0)=N_{0}(x)\ge 0,\not \equiv 0,&{} x\in [0,1]. \end{array}\right. } \end{aligned}$$

(4.5)

Taking $C_{2}=\max \{K_{1},\Vert N_{0}(x)\Vert _{\infty }\}$, we can deduce that $N(x,t)\le C_{2}$ for all $x\in [0,1],\ t>0$ by the application of the comparison principle.

By the equation for P(x, t), we obtain

$$\begin{aligned} P_{t}\le d_{2}P_{xx}-q_2 P_{x}+r_{2}P(1+\frac{eaC_{2}}{r_{2}}-\frac{P}{K_{2}}),\ x\in (0,1),\ t>0.\end{aligned}$$

Similarly, taking $C_{3}=\max \{K_{2}+\frac{eaC_{2}K_{2}}{r_{2}},\Vert P_{0}(x)\Vert _{\infty }\}$, we can deduce that $P(x,t)\le C_{3}$ for all $x\in [0,1],\ t>0.$

It follows from (4.5) that

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }N(x,t)\le K_1~\mathrm {uniformly}~\mathrm {on}~[0,1]. \end{aligned}$$

Hence, for any $\varepsilon >0$, there exists $T_0>0$ large such that $N(x,t)<K_1+\varepsilon$ for all $x\in [0, 1], t\ge T_0.$ By using the equation for P(x, t) again, we have

$$\begin{aligned} P_{t}\le d_{2}P_{xx}-q_2 P_{x}+r_{2}P(1+\frac{ea(K_1+\varepsilon )}{r_{2}}-\frac{P}{K_{2}}),\ x\in (0,1),\ t\ge T_0,\end{aligned}$$

which implies that $\limsup \limits _{t\rightarrow +\infty }P(x,t)\le K_{2}+\frac{eaK_1K_{2}}{r_{2}}$ uniformly on [0, 1]. That is, the solution of system (1.2) is ultimately bounded for all $x\in [0,1]$. $\square$

It follows from Lemma 2.1 that there are three types of nonnegative steady state solutions of (1.2): (i) trivial steady state solution (0, 0); (ii) semi-trivial steady state solution $(\theta _{1}(\cdot ;\ q_1),0)$ exists if $0\le q_1<q_{1}^{*}$ and $(0,\theta _2(\cdot ;\ q_2))$ exists if $0\le q_2<q_{2}^{*}$; (iii) positive solutions (N, P) with $N>0,P>0$ on [0, 1]. For simplicity, we denote $\theta _{1}(\cdot ;\ q_1),\theta _{2}(\cdot ;\ q_2)$ by $\theta _{1}(q_1),\theta _2(q_2)$ or $\theta _{1},\theta _2$, respectively.

The following lemma indicates that the steady state solutions $(0,0), (\theta _{1}(q_1),0)$ and $(0,\theta _2(q_2))$ of system (1.2) are globally asymptotically stable if they are locally asymptotically stable, respectively. And if they are all unstable, then system (1.2) is uniformly persistent.

Lemma 4.5

Suppose (H) holds, $a>0$ and $q_1, q_2\ge 0$. Then the solution (N(x, t), P(x, t)) of system (1.2) satisfies

• (i) $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0,0)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if $q_1\ge q_1^*$ and $q_2>q_2^*$;

• (ii) $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(\theta _1,0)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1})<0$;

• (iii) $\lim \limits _{t\rightarrow +\infty }(N(x,t),P(x,t))=(0, \theta _2)\ \text{ uniformly } \text{ for }\ x\in [0,1]$ if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2})<0$;

• (iv) system (1.2) is uniformly persistent in the sense that the solution (N(x, t), P(x, t)) satisfies

  $$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }N(x,t)\ge \eta ,\ \text{ and } \liminf \limits _{t\rightarrow +\infty }P(x,t)\ge \eta \end{aligned}$$

  for $x\in [0,1]$ if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2})>0$ and $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1})>0$. Moreover, in this case, system (1.2) admits a unique positive steady state.

Since the proof of Lemma 4.5 is exactly similar to Theorems 1.1 and 1.2 of Nie et al. (2020), we postpone its proof to the Appendix. Indeed, by the subsequent Lemmas 5.1–5.3, we conclude that

• (i) if $q_1\ge q_1^*$ and $q_2>q_2^*$, then (0, 0) is locally asymptotically stable;

• (ii) if $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))<0$, then $(\theta _1, 0)$ is locally asymptotically stable;

• (iii) if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))<0$ , then $(0, \theta _2)$ is locally asymptotically stable;

• (iv) if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))>0$ and $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))>0$, then (0, 0), $(\theta _1,0)$ and $(0, \theta _2)$ are all unstable.

Hence, Lemma 4.5 suggests that each of the trivial or semitrivial nonnegative steady state solutions is globally asymptotically stable if it is locally asymptotically stable, respectively. And system (1.2) is uniformly persistent if all of them are unstable.

5 Dynamics of system (1.2) in the $q_1-q_2$ plane

As shown in Lemma 4.5, the global dynamics of system (1.2) is related to the local stability of its nonnegative steady state solutions $(0,0), (\theta _{1}(q_1),0)$ and $(0,\theta _2(q_2))$. To investigate dynamical behavior of system (1.2) in the $q_1-q_2$ plane, we need to figure out the local stability of these trivial and semi-trivial steady state solutions by examining the spectrum of the corresponding linearized operators.

Lemma 5.1

Suppose (H) holds, $a>0$ and $q_1, q_2\ge 0$. The trivial solution (0, 0) of (4.2) is locally asymptotically stable if $q_1\ge q_{1}^{*}$ and $q_2>q_{2}^{*}$, and unstable if $0\le q_1<q_{1}^{*}$ or $0\le q_2<q_{2}^{*}.$

Proof

The linearized operator of (4.2) at (0, 0) is

$$\begin{aligned} L_{0}= \left( \begin{array}{cc} d_{1}\frac{d ^{2}}{d x^{2}}-q_1\frac{d }{d x}+r_1 &{} 0 \\ \ \ 0 &{} d_{2}\frac{d ^{2}}{d x^{2}}-q_2\frac{d }{d x}+r_2 \end{array} \right) \end{aligned}$$

with the boundary conditions $d_1\phi _{x}(0)-q_1\phi (0)=\phi _{x}(1)=0$ and $d_2\psi _{x}(0)-q_2\psi (0)=\psi _{x}(1)=0$. It follows from (2.4) that $\mu _{1}(d_1,q_1,r_1)\le 0$ and $\mu _{1}(d_2,q_2,r_2)<0$ when $q_1\ge q_{1}^{*}$ and $q_2>q_{2}^{*}$, which implies that (0, 0) is locally asymptotically stable when $q_1\ge q_{1}^{*}$ and $q_2>q_{2}^{*}$. Indeed, we can further show that (0, 0) is globally asymptotically stable when $q_1\ge q_{1}^{*}$ and $q_2>q_{2}^{*}$ (see Lemma 4.5(i)). Meanwhile, if $q_1\in [0, q_{1}^{*})$ or $q_2\in [0, q_{2}^{*})$, then we have $\mu _{1}(d_1,q_1,r_1)>0$ or $\mu _{1}(d_2,q_2,r_2)>0$ by (2.4), which implies the instability of (0, 0). $\square$

Lemma 5.2

Suppose (H) holds, $a>0$ and $0\le q_1<q_{1}^{*}$. Then there exists a continuous and strictly decreasing critical curve $q_2=q_2^0(q_1)$ defined in $q_1\in [0, q_{1}^{*})$ such that $(\theta _{1}(q_1),0)$ is locally asymptotically stable if $q_2\in (q_2^{0}(q_1),+\infty )$, and unstable if $q_2\in [0, q_2^{0}(q_1))$. Moreover, $q_2^0(0)={\bar{q}}_2$ and $\lim \limits _{q_1\rightarrow q_1^*-}q_2^0(q_1)=q_2^*.$

Proof

The linearized operator of (4.2) at $(\theta _{1}(q_1),0)$ is given by

$$\begin{aligned} L_{1}= \left( \begin{array}{cc} d_{1}\frac{d ^{2}}{d x^{2}}-q_1\frac{d }{d x}+r_{1}-2\frac{r_{1}}{K_{1}}\theta _{1}(q_1) &{} -a\theta _{1}(q_1) \\ 0\ \ &{} d_{2}\frac{d ^{2}}{d x^{2}}-q_2\frac{d }{d x}+r_{2}+ea\theta _{1}(q_1) \end{array} \right) \end{aligned}$$

with the boundary conditions $d_1\phi _{x}(0)-q_1\phi (0)=\phi _{x}(1)=0$ and $d_2\psi _{x}(0)-q_2\psi (0)=\psi _{x}(1)=0$. It follows from the Riesz-Schauder theory that the eigenvalues of $L_{1}$ consist of the eigenvalues of ${\mathcal {B}}_{1}=d_{1}\frac{d ^{2}}{d x^{2}}-q_1\frac{d }{d x}+r_{1}-2\frac{r_{1}}{K_{1}}\theta _{1}(q_1)$ and ${\mathcal {B}}_{2}=d_{2}\frac{d ^{2}}{d x^{2}}-q_2\frac{d }{d x}+r_{2}+ea\theta _{1}(q_1)$. By the equation for $\theta _1(q_1)$, we notice that

$$\begin{aligned} \mu _{1}(d_1,q_1,r_1-\frac{r_1}{K_1}\theta _1(q_1))=0 \end{aligned}$$

when $q_1\in [0, q_1^*)$. It follows from Lemma 4.1(iii) that all the eigenvalues of ${\mathcal {B}}_{1}$ subjected to the boundary conditions $d_1\phi _{x}(0)-q_1\phi (0)=\phi _{x}(1)=0$ are negative. Therefore, $(\theta _{1}(q_1),0)$ is locally asymptotically stable if $\lambda _{1}({\mathcal {B}}_{2})=\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))<0$, and it is unstable if $\lambda _{1}({\mathcal {B}}_{2})=\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))>0$.

In view of $0<\theta _{1}(q_1)\le K_1$ when $q_1\in [0, q_1^*)$ (see Lemma 4.3), it follows from Lemma 4.1(iii) that

$$\begin{aligned}&\mu _{1}(d_{2},q_2^*,r_{2}+ea\theta _{1}(q_1))>\mu _{1}(d_{2},q_2^*,r_{2})=0 \text{ and } \\&\quad \mu _{1}(d_{2},{\bar{q}}_2,r_{2}+ea\theta _{1}(q_1))\le \mu _{1}(d_{2},{\bar{q}}_2,r_{2}+eaK_1)=0 \end{aligned}$$

when $q_1\in [0, q_1^*)$. Moreover, $\mu _{1}(d_{2},{\bar{q}}_2,r_{2}+ea\theta _{1}(q_1))=0$ iff $q_1=0.$ We conclude that for $q_1\in [0, q_{1}^{*})$, there exists a unique $q_2^0=q_2^0(q_1)\in (q_2^*, {\bar{q}}_2]$ continuously depending on $q_1$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))>0\ \ \text{ if }\ q_2<q_2^{0}(q_1),\\ \mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))=0\ \ \text{ if }\ q_2=q_2^{0}(q_1),\\ \mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))<0\ \ \text{ if }\ q_2>q_2^{0}(q_1). \end{array}\right. } \end{aligned}$$

(5.1)

That is, $(\theta _{1}(q_1),0)$ is locally asymptotically stable if $q_2\in (q_2^{0}(q_1),+\infty )$, and unstable if $q_2\in [0, q_2^{0}(q_1))$.

Next, we study the properties of the critical curve $q_2=q_2^0(q_1)$ with $q_1\in [0, q_{1}^{*})$. By Lemma 4.1(iv), one can easily see that $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))$ is strictly decreasing with respect to $q_2$. Combining Lemma 4.1(iii) with Lemma 4.2(ii), one can conclude that $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))$ is also strictly decreasing with respect to $q_1$. Hence, we can conclude that $q_2^0(q_1)$ is strictly decreasing with respect to $q_1$ in $[0, q_1^*)$ by the implicit function theorem.

Recall that $\mu _{1}(d_{2},q_2^{0}(q_1),r_{2}+ea\theta _{1}(q_1))=0$, and $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1}(q_1))$ is continuous and strictly decreasing with respect to $q_1$. Since $\theta _{1}(0)=K_1$ and $\mu _{1}(d_{2},{\bar{q}}_{2},r_{2}+eaK_1)=0$, we obtain $q_2^0(0)={\bar{q}}_2$ by using the strict monotone property of $\mu _{1}(d_{2},q_2,r_{2}+eaK_1)$ on $q_2$. Similarly, note that $\lim \limits _{q_1\rightarrow q_1^*-}\theta _{1}(q_1)=0$ and $\mu _{1}(d_{2},q_{2}^{*},r_{2})=0$. Let $q_1\rightarrow q_1^*$ in $\mu _{1}(d_{2},q_2^{0}(q_1),r_{2}+ea\theta _{1}(q_1))=0$, then we have $\lim \limits _{q_1\rightarrow q_1^*-}q_2^0(q_1)=q_2^*.$ $\square$

Lemma 5.3

Suppose (H) holds, $a>0$ and $0\le q_2<q_{2}^{*}$.

• (i) If $a\le \frac{r_1}{K_2}$, then there exists a continuous and strictly increasing critical curve $q_1=q_1^0(q_2)$ defined in $q_2\in [0, q_2^{*})$ such that $(0,\theta _{2}(q_2))$ is locally asymptotically stable if $q_1\in (q_1^0(q_2),+\infty )$, and unstable if $q_1\in [0,q_1^0(q_2))$. Moreover, $\lim \limits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*,$ $q_1^0(0)>0$ if $a<\frac{r_1}{K_2}$ and $q_1^0(0)=0$ if $a=\frac{r_1}{K_2}$.

• (ii) If $a>\frac{r_1}{K_2}$, then there exists a unique ${\hat{q}}_2\in (0,q_2^*)$ such that for $q_2\in [0,{\hat{q}}_2)$, $(0,\theta _{2}(q_2))$ is always locally asymptotically stable; for $q_2\in [{\hat{q}}_2, q_2^*)$, there exists a continuous and strictly increasing critical curve $q_1=q_1^0(q_2)$ such that $(0,\theta _{2}(q_2))$ is locally asymptotically stable if $q_1\in (q_1^0(q_2),+\infty )$, and unstable if $q_1\in [0,q_1^0(q_2))$. Moreover, $q_1^0(0)={\hat{q}}_2$ and $\lim \limits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*.$

Proof

The linearized operator of (4.2) at $(0,\theta _{2}(q_2))$ is given by

$$\begin{aligned} L_{2}= \left( \begin{array}{cc} d_{1}\frac{d ^{2}}{d x^{2}}-q_1\frac{d }{d x}+r_{1}-a\theta _{2}(q_2) &{} 0\ \ \\ ea\theta _{2}(q_2) &{} d_{2}\frac{d ^{2}}{d x^{2}}-q_2\frac{d }{d x}+r_{2}-2\frac{r_{2}}{K_{2}}\theta _{2}(q_2) \end{array} \right) \end{aligned}$$

with the boundary conditions $d_1\phi _{x}(0)-q_1\phi (0)=\phi _{x}(1)=0$ and $d_2\psi _{x}(0)-q_2\psi (0)=\psi _{x}(1)=0$. By the equation for $\theta _2(q_2)$, we obtain that

$$\begin{aligned} \mu _{1}(d_2,q_2,r_2-\frac{r_2}{K_2}\theta _2(q_2))=0 \end{aligned}$$

when $q_2\in [0, q_2^*)$. It follows from Lemma 4.1(iii) that all the eigenvalues of ${\mathcal {B}}_{3}$ subjected to the boundary conditions $d_2\psi _{x}(0)-q_2\psi (0)=\psi _{x}(1)=0$ are negative, where ${\mathcal {B}}_{3}=d_{2}\frac{d ^{2}}{d x^{2}}-q_2\frac{d }{d x}+r_{2}-2\frac{r_{2}}{K_{2}}\theta _{2}(q_2)$. Let ${\mathcal {B}}_{4}=d_{1}\frac{d ^{2}}{d x^{2}}-q_1\frac{d }{d x}+r_{1}-a\theta _{2}(q_2)$ with the boundary conditions $d_1\phi _{x}(0)-q_1\phi (0)=\phi _{x}(1)=0$. By similar arguments as in Lemma 5.2, one can easily see that $(0,\theta _{2}(q_2))$ is locally asymptotically stable if $\lambda _{1}({\mathcal {B}}_{4})=\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))<0$, and it is unstable if $\lambda _{1}({\mathcal {B}}_{4})=\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))>0$.

(i) If $a\le \frac{r_1}{K_2}$, then it follows from Lemma 4.1(iii) that for $q_2\in [0, q_2^*)$,

$$\begin{aligned} \mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))\ge \mu _{1}(d_{1},0,r_{1}-aK_2)\ge 0 \end{aligned}$$

(5.2)

based on $0<\theta _{2}(q_2)\le K_2$ on [0, 1]. Moreover, $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))=0$ if and only if $q_2=0$ and $a=\frac{r_1}{K_2}$. On the other hand, we have

$$\begin{aligned} \mu _{1}(d_{1},q_1^*,r_{1}-a\theta _2(q_2))<\mu _{1}(d_{1},q_1^*,r_1)=0. \end{aligned}$$

(5.3)

By Lemma 4.1(iv) together with (5.2) and (5.3), we can deduce that there exists a unique $q_1^0=q_1^0(q_2)\in [0,q_1^*)$ continuously depending on $q_2$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))>0\ \ \text{ if }\ q_1<q_1^0(q_2),\\ \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))=0\ \ \text{ if }\ q_1=q_1^0(q_2),\\ \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))<0\ \ \text{ if }\ q_1>q_1^0(q_2). \end{array}\right. } \end{aligned}$$

(5.4)

That is, $(0,\theta _{2}(q_2))$ is locally asymptotically stable when $q_1\in (q_1^{0}(q_2),+\infty )$, and it is unstable when $q_1\in [0, q_1^{0}(q_2))$. Furthermore, it is easy to see that $q_1^0(0)=0$ if $a=\frac{r_1}{K_2}$, and $q_1^0(0)>0$ if $a<\frac{r_1}{K_2}$. Meanwhile, noting that $\lim \nolimits _{q_2\rightarrow q_2^*-}\mu _{1}(d_{1},q_1^*,r_{1}-a\theta _{2}(q_2))=0$, one can deduce that $\lim \nolimits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*$ by Lemma 4.1(iv). By similar arguments as in Lemma 5.2, we conclude that $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))$ is strictly decreasing with respect to $q_1$ and strictly increasing with respect to $q_2$. It follows from the implicit function theorem that the critical curve $q_1^0(q_2)$ is strictly increasing with respect to $q_2$ in $[0, q_2^*)$. Hence, (i) holds.

(ii) If $a>\frac{r_1}{K_2}$, then it follows from Lemma 4.1(ii) and Lemma 4.2(ii) that $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(0))=\mu _{1}(d_{1},0,r_{1}-aK_2)=r_{1}-aK_2<0$ and $\lim \limits _{q_2\rightarrow q_2^*-}\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))=\mu _{1}(d_{1},0,r_{1})=r_1>0.$ The strict monotonicity of $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))$ with respect to $q_2$ (see Lemmas 4.1(iii) and 4.2(ii)) means that there exists a unique ${\hat{q}}_2\in (0,q_2^*)$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))<0\ \ \text{ if }\ q_2<{\hat{q}}_2,\\ \mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))=0\ \ \text{ if }\ q_2={\hat{q}}_2,\\ \mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))>0\ \ \text{ if }\ q_2>{\hat{q}}_2. \end{array}\right. } \end{aligned}$$

Hence, for $q_2\in [0,{\hat{q}}_2)$, by Lemmas 4.1(iii)(iv) and 4.2(ii), we always have $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(q_2))\le \mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))<\mu _{1}(d_{1},0,r_{1}-a\theta _{2}({\hat{q}}_2))=0$. That is, $(0,\theta _{2}(q_2))$ is always locally asymptotically stable when $q_2\in [0,{\hat{q}}_2)$.

For $q_2\in [{\hat{q}}_2, q_2^*)$, we have $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))\ge 0$, and $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}(q_2))=0$ if and only if $q_2={\hat{q}}_2$. On the other hand, similar arguments yield

$$\begin{aligned} \mu _{1}(d_{1},q_1^*,r_{1}-a\theta _2(q_2))<\mu _{1}(d_{1},q_1^*,r_1)=0. \end{aligned}$$

Combining Lemma 4.1(iv) with the above inequalities, we can deduce that there exists a unique $q_1^0=q_1^0(q_2)\in [0,q_1^*)$ continuously depending on $q_2$ such that (5.4) holds, which implies that $(0,\theta _{2}(q_2))$ is locally asymptotically stable when $q_1\in (q_1^{0}(q_2),+\infty )$, and it is unstable when $q_1\in [0, q_1^{0}(q_2))$.

Furthermore, it is easy to see that $q_1^0({\hat{q}}_2)=0$ since $\mu _{1}(d_{1},0,r_{1}-a\theta _{2}({\hat{q}}_2))=0$ and $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}({\hat{q}}_2))$ is strictly decreasing with respect to $q_1$. The proofs of $\lim \limits _{q_2\rightarrow q_2^*-}q_1^0(q_2)=q_1^*$ and the strict monotonicity of the critical curve $q_1^0(q_2)$ are exactly similar to case (i). Finally, we mention that the strictly increasing curve $q_1=q_1^0(q_2)$ with $q_2\in [{\hat{q}}_2, q_2^*)$ has a unique inverse function defined in $q_1\in [0, q_1^*)$, which is denoted by $(q_1^0(q_2))^{-1}$. $\square$

Theorem 2.1 follows directly from Lemma 4.5 and Lemmas 5.1–5.3, which provides a complete classification on the global dynamics of system (1.2) in the $q_1-q_2$ plane (see Fig. 1). It turns out that there exist four critical curves such as $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1),\ q_1=q_{1}^{*}$ and $q_2=q_{2}^{*}$ in the $q_1-q_2$ plane, which divide the dynamics of system (1.2) into four scenarios (see Fig. 1). Here the critical curve $q_1=q_1^0(q_2)$ separates persistence of generalist predators only from coexistence, and the critical curve $q_2=q_2^{0}(q_1)$ separates persistence of prey only from coexistence. Especially, there occurs the new phenomenon of prey extinction and persistence of generalist predators alone, see also Fig. 1, which is not observed in the specialist predator-prey system (1.1) (see Nie et al. 2020).

Furthermore, it follows from (5.1) and (5.4) that the two critical curves $q_1=q_1^0(q_2),\ q_2=q_2^{0}(q_1)$ are dependent on the predation rate a. To emphasize their dependence on the predation rate a, we denote them by $q_1=q_1^0(q_2, a),\ q_2=q_2^{0}(q_1, a)$ respectively. Next, we investigate the specific influence of the predation rate a on the two critical curves $q_1=q_1^0(q_2, a),\ q_2=q_2^{0}(q_1, a)$ and the corresponding coexistence solutions.

Proposition 5.4

• (i) The critical curve $q_2=q_2^{0}(q_1, a)$ is strictly increasing with respect to a in the sense that $q_2^{0}(q_1, a_1)<q_2^{0}(q_1, a_2)$ in $q_1\in [0, q_1^*)$ if $0<a_1<a_2$. Moreover, it goes exactly to the curve $q_2=q_2^*$ defined in $q_1\in [0, q_1^*)$ as $a\rightarrow 0+$, and goes exactly to the curve $q_1=q_1^*$ defined in $q_2\in (q_2^*, +\infty )$ as $a\rightarrow +\infty .$

• (ii) The critical curve $q_1=q_1^{0}(q_2, a)$ is strictly decreasing with respect to a in the sense that $q_1^{0}(q_2, a_2)<q_1^{0}(q_2, a_1)$ for $q_2$ belonging to the intersection of their domains if $0<a_1<a_2$. Moreover, it goes exactly to the curve $q_1=q_1^*$ defined in $q_2\in [0, q_2^*)$ as $a\rightarrow 0+$, and goes exactly to the curve $q_2=q_2^*$ defined in $q_1\in [0, q_1^*)$ as $a\rightarrow +\infty .$

• (iii) The unique positive steady state (if it exist), denoted by $(N_a, P_a)$, of system (1.2) converges to $(\theta _1, \theta _2)$ uniformly on [0, 1] as $a\rightarrow 0+$, and it converges to (0, 0) almost everywhere on [0, 1] as $a\rightarrow +\infty$.

Proof

(i) Note that $\mu _1(d_2, q_2^{0}(q_1, a_1), r_2+ea_1\theta _1(q_1))=0$ and $\mu _1(d_2, q_2^{0}(q_1, a_2), r_2+ea_2\theta _1(q_1))=0$ in $q_1\in [0, q_1^*)$. By Lemma 4.1(iii), we have

$$\begin{aligned} \mu _1(d_2, q_2^{0}(q_1, a_1), r_2+ea_2\theta _1(q_1))>\mu _1(d_2, q_2^{0}(q_1, a_1), r_2+ea_1\theta _1(q_1))=0 \end{aligned}$$

if $0<a_1<a_2$. Hence, one can easily conclude that $q_2^{0}(q_1, a_1)<q_2^{0}(q_1, a_2)$ in $q_1\in [0, q_1^*)$ by Lemma 4.1(iv).

Let $a\rightarrow 0+$ in $\mu _1(d_2, q_2^{0}(q_1, a), r_2+ea\theta _1(q_1))=0$, then it is easy to see that $\lim \limits _{a\rightarrow 0+}q_2^{0}(q_1, a)=q_2^*$ in $q_1\in [0, q_1^*)$, which implies that the critical curve $q_2=q_2^{0}(q_1, a)$ goes exactly to the curve $q_2=q_2^*$ with $q_1\in [0, q_1^*)$ as $a\rightarrow 0+.$

Next, we claim $\lim \limits _{a\rightarrow +\infty }q_2^{0}(q_1, a)=+\infty$ in $q_1\in [0, q_1^*)$, which means that the critical curve $q_2=q_2^{0}(q_1, a)$ goes exactly to the curve $q_1=q_1^*$ with $q_2\in (q_2^*, +\infty )$ as $a\rightarrow +\infty .$ We prove it by contradiction. If $q_2^{0}(q_1, a)$ is uniformly bounded when $a\rightarrow +\infty$, then one can conclude that $\mu _1(d_2, q_2^{0}(q_1, a), r_2+ea\theta _1(q_1))>0$ for all large a, a contradiction. Hence, (i) holds true.

(ii) can be shown similarly by using $\mu _1(d_1, q_1^{0}(q_2, a), r_1-a\theta _2(q_2))=0$ and Lemma 4.1.

(iii) At last, we investigate the limits of the unique positive steady state to system (1.2) when the predation rate $a\rightarrow 0+$ or $a\rightarrow +\infty$. Clearly, when $a\rightarrow 0+$, Theorem 2.1(A4) and Proposition 5.4(i)(ii) indicate that for $(q_1, q_2)\in [0, q_1^*)\times [0, q_2^*)$, system (1.2) admits a unique positive steady state, denoted by $(N_a, P_a)$. Furthermore, we conclude that $N_a, P_a$ are uniformly bounded by Lemma 4.3 as $a\rightarrow 0+$. Hence, it is easy to see that $(N_a, P_a)\rightarrow (\theta _1, \theta _2)$ uniformly on [0, 1] as $a\rightarrow 0+$.

When $a\rightarrow +\infty$, it follows from Theorem 2.1(A4) and Proposition 5.4(i)(ii) that system (1.2) admits a unique positive steady state $(N_a, P_a)$ only if $q_1\in [0, q_1^*)$ and $q_2>q_2^*$. Next, we claim that $(N_a, P_a)$ converges to (0, 0) almost everywhere on [0, 1] as $a\rightarrow +\infty$. Indeed, by the equation for $N_a$, we have $\mu _1(d_1,q_1, r_1(1-\frac{N_a}{K_1})-aP_a)=0.$ Let ${\tilde{\phi }}_1$ be the corresponding principal eigenfunction to $\mu _1(d_1,q_1, r_1(1-\frac{N_a}{K_1})-aP_a)$. Then it follows from Lemma 4.1 that

$$\begin{aligned} \begin{aligned} 0&=\mu _1(d_1,q_1, r_1(1-\frac{N_a}{K_1})-aP_a)\\&=\frac{-q_1{\tilde{\phi }}_1^{2}(0)-d_1\int _{0}^{1}e^{-\frac{q_1}{d_1}x}({\tilde{\phi }}_1)_{x}^{2}d x +\int _{0}^{1}[r_1(1-\frac{N_a}{K_1})-aP_a]e^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}{\int _{0}^{1}e^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}\\&<\mu _1(d_1,q_1,r_1)-\frac{a\int _{0}^{1}P_ae^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}{\int _{0}^{1}e^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}. \end{aligned} \end{aligned}$$

Clearly, $\mu _1(d_1,q_1,r_1)>0$ since $q_1\in [0, q_1^*)$. Hence,

$$\begin{aligned} 0<\frac{a\int _{0}^{1}P_ae^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}{\int _{0}^{1}e^{-\frac{q_1}{d_1}x}{\tilde{\phi }}_1^{2}d x}<\mu _1(d_1,q_1,r_1), \end{aligned}$$

which implies that $P_a\rightarrow 0$ almost everywhere on [0, 1] as $a\rightarrow +\infty$.

Similarly, let $\phi _2$ be the corresponding principal eigenfunction to $\mu _1(d_2, q_2, r_2)$. Then it follows from the equation for $P_a$ and Lemma 4.1 that

$$\begin{aligned} \begin{aligned} 0&=\mu _1(d_2,q_2, r_2(1-\frac{P_a}{K_2})+eaN_a)\\&=\sup _{\phi \ne 0,\phi \in H^{1}((0,1))}\frac{-q_2\phi ^{2}(0)-d_2\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi _{x}^{2}d x +\int _{0}^{1}[r_2(1-\frac{P_a}{K_2})+eaN_a]e^{-\frac{q_2}{d_2}x}\phi ^{2}d x}{\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi ^{2}d x}\\&\ge \frac{-q_2\phi _2^{2}(0)-d_2\int _{0}^{1}e^{-\frac{q_2}{d_2}x}(\phi _2)_{x}^{2}d x +\int _{0}^{1}[r_2(1-\frac{P_a}{K_2})+eaN_a]e^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}{\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}\\&=\mu _1(d_2,q_2,r_2)+\frac{-\frac{r_2}{K_2}\int _{0}^{1}P_ae^{-\frac{q_2}{d_2}x}\phi _2^{2}d x +ea\int _{0}^{1}N_ae^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}{\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}, \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} 0<\frac{ea\int _{0}^{1}N_ae^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}{\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi _2^{2}d x} \le -\mu _1(d_2,q_2,r_2)+\frac{r_2}{K_2}\frac{\int _{0}^{1}P_ae^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}{\int _{0}^{1}e^{-\frac{q_2}{d_2}x}\phi _2^{2}d x}. \end{aligned}$$

Since the right-hand side of this inequality is uniformly bounded with respect to a, one can conclude that $N_a\rightarrow 0$ almost everywhere on [0, 1] as $a\rightarrow +\infty$. Here $\mu _1(d_2,q_2,r_2)<0$ based on $q_2>q_2^*$. In a word, the unique positive steady state $(N_a, P_a)$ of system (1.2) converges to (0, 0) almost everywhere on [0, 1] as $a\rightarrow +\infty$. The proof is finished. $\square$

6 Dynamics of system (1.2) in the $q_1-a$ plane

Theorem 2.1 and numerical simulations have shown that both the predation rate a and the ratio $\tau =q_2: q_1$ of flow speeds experienced by predators and prey have a significant influence on the dynamical behavior of system (1.2). To understand the joint influence of the predation rate and flow speeds on the dynamics of system (1.2), we set $q_2=\tau q_1$ in this section and investigate the classification on the global dynamics of system (1.2) in the $q_1-a$ plane.

It follows from Lemma 4.5 that nonnegative steady state solutions $(0,0), (\theta _{1}(q_1),0)$ and $(0,\theta _2(\tau q_1))$ of system (1.2) with $q_2=\tau q_1$ are globally asymptotically stable if they are locally asymptotically stable, respectively. And system (1.2) with $q_2=\tau q_1$ is uniformly persistent if they are all unstable. Here $\theta _2(\tau q_1)$ is the unique positive steady state solution to system (2.2) with $q_2=\tau q_1$. Hence, we turn to focus on the classification of the local dynamics of system (1.2) with $q_2=\tau q_1$ in the $q_1-a$ plane by examining the spectrum of the corresponding linearized operators.

At first, by similar arguments as in Lemma 5.1, we have the following result.

Lemma 6.1

Suppose (H) holds, $a>0,\ q_2=\tau q_1$ and $q_1\ge 0$. The trivial solution (0, 0) of (4.2) is locally asymptotically stable if $q_1>\max \{q_{1}^{*}, \frac{q_{2}^{*}}{\tau }\}$ or $q_1=q_{1}^{*}>\frac{q_{2}^{*}}{\tau }$, and unstable if $0\le q_1<\max \{q_{1}^{*}, \frac{q_{2}^{*}}{\tau }\}.$

Lemma 6.2

Suppose (H) holds, $a>0,\ q_2=\tau q_1$ and $0\le q_1<q_{1}^{*}$.

• (i) If $q_1\in [0,\min \{q_{1}^{*},\frac{q_2^*}{\tau }\})$, then $(\theta _{1}(q_1),0)$ is unstable for any $a>0$.

• (ii) If $\tau >\frac{q_{2}^{*}}{q_{1}^{*}}$, then for any $q_1\in [\frac{q_2^*}{\tau },q_{1}^{*})$, there exists a unique $a_\tau ^{0}(q_1)\in [0,+\infty )$ continuously depending on the parameter $q_1$ such that $(\theta _1(q_1),0)$ is locally asymptotically stable if $a\in (0,a_\tau ^{0}(q_1))$, and unstable if $a\in (a_\tau ^{0}(q_1),+\infty )$.

Proof

It follows from similar arguments as in Lemma 5.2 that $(\theta _{1}(q_1),0)$ is locally asymptotically stable if $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _{1}(q_1))<0$, and it is unstable if $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _{1}(q_1))>0$.

(i) If $q_1\in [0,\min \{q_{1}^{*},\frac{q_2^*}{\tau }\})$, then $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _{1}(q_1))>\mu _{1}(d_{2},\tau q_1,r_{2})>0$ for all $a>0$ by using Lemmas 4.1(iii), 4.2(i) and (2.4). Thus, if $q_1\in [0,\min \{q_{1}^{*},\frac{q_2^*}{\tau }\})$, then $(\theta _{1}(q_1),0)$ is unstable for any $a>0.$

(ii) If $a=0$, then it follows from (2.4) that $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _{1}(q_1))=\mu _{1}(d_{2},\tau q_1,r_{2})\le 0$ for $q_1\in [\frac{q_2^*}{\tau },q_{1}^{*})$. Moreover, $\mu _{1}(d_{2},\tau q_1,r_{2})=0$ if and only if $q_1=\frac{q_2^*}{\tau }.$ On the other hand, if $a\rightarrow +\infty$, then it is easy to see that $\mu _{1}(d_{2},\tau q_{1},r_{2}+ea\theta _{1}(q_1))\rightarrow +\infty$ since there exists $\delta >0$ independent of a such that $\theta _{1}(q_1)>\delta$ on [0, 1] when $q_1<q_{1}^{*}$. Since $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))$ is continuous and strictly increasing with respect to a, one can deduce that there exists a unique $a_\tau ^{0}=a_\tau ^{0}(q_1)\in [0,+\infty )$ continuously depending on the parameter $q_1$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))>0\ \ \text{ if }\ a>a_\tau ^{0}(q_1),\\ \mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))=0\ \ \text{ if }\ a=a_\tau ^{0}(q_1),\\ \mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))<0\ \ \text{ if }\ a<a_\tau ^{0}(q_1). \end{array}\right. } \end{aligned}$$

(6.1)

That is, $(\theta _1(q_1),0)$ is locally asymptotically stable if $a\in (0,a_\tau ^{0}(q_1))$, and unstable if $a\in (a_\tau ^{0}(q_1),+\infty )$. $\square$

Lemma 6.3

Suppose (H) holds, $a>0,\ q_2=\tau q_1$ and $0\le q_1<\frac{q_2^*}{\tau }$. Then

• (i) for $0\le q_1<\min \{q_{1}^{*},\frac{q_2^*}{\tau }\}$, there exists a critical curve $a=a_\tau ^{*}(q_1)\in (0,+\infty )$ continuously depending on the parameter $q_1$ such that $(0,\theta _{2}(\tau q_1))$ is locally asymptotically stable if $a\in (a_\tau ^{*}(q_1),+\infty )$, and unstable if $a\in (0,a_\tau ^{*}(q_1))$;

• (ii) if $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$, then $(0,\theta _{2}(\tau q_1))$ is locally asymptotically stable provided that $q_1\in [q_{1}^{*},\frac{q_2^*}{\tau }).$

Proof

Similar arguments as in Lemma 5.3 yield that $(0,\theta _{2}(\tau q_1))$ is locally asymptotically stable if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))<0$, and unstable if $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))>0$.

(i) In view of $0\le q_1<\min \{q_{1}^{*},\frac{q_2^*}{\tau }\}$, there exists $\delta >0$ such that $\min \limits _{x\in [0,1]}\theta _{2}(\tau q_1)>\delta$, and

$$\begin{aligned} \lim \limits _{a\rightarrow 0+}\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))= & {} \mu _{1}(d_{1},q_1,r_{1})>0; \end{aligned}$$

(6.2)

$$\begin{aligned} \lim \limits _{a\rightarrow +\infty }\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))< & {} \lim \limits _{a\rightarrow +\infty }\mu _{1}(d_{1},q_1,r_{1}-a\min \limits _{x\in [0,1]}\theta _{2}(\tau q_1))\nonumber \\ {}= & {} -\infty . \end{aligned}$$

(6.3)

Combining Lemma 4.1(ii)(iii) with (6.2)–(6.3), we obtain that there exists a unique $a_\tau ^{*}=a_\tau ^{*}(q_1)\in (0,+\infty )$ continuously depending on $q_1$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))>0\ \ \text{ if }\ a<a_\tau ^{*}(q_1),\\ \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))=0\ \ \text{ if }\ a=a_\tau ^{*}(q_1),\\ \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))<0\ \ \text{ if }\ a>a_\tau ^{*}(q_1). \end{array}\right. } \end{aligned}$$

(6.4)

Hence, the result (i) holds.

(ii) If $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$, then it follows from Lemma 4.1(iii), $a>0$ and (2.4) that

$$\begin{aligned} \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))<\mu _{1}(d_{1},q,r_{1})\le 0 \end{aligned}$$

when $q_1\in [q_{1}^{*},\frac{q_{2}^{*}}{\tau })$. Therefore, $(0,\theta _{2}(\tau q_1))$ is locally asymptotically stable if $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$ and $q_1\in [q_{1}^{*},\frac{q_{2}^{*}}{\tau })$. $\square$

Theorems 2.2 and 2.3 follow directly from Lemma 4.5 and Lemmas 6.1–6.3, which indicate that the critical curves $q_1=q_{1}^{*}$, $q_1=\frac{q_{2}^{*}}{\tau }$, $a=a_\tau ^{0}(q_1)$ and $a=a_\tau ^*(q_1)$ divide the global dynamics of system (1.2) with $q_2=\tau q_1$ in the $q_1-a$ plane into three or four scenarios (see Figs. 2 and 3). To further investigate the specific classification of global dynamics of system (1.2) in the $q_1-a$ plane, we next investigate the properties of the two critical curves $a=a_\tau ^{0}(q_1)$ and $a=a_\tau ^{*}(q_1)$.

Proposition 6.4

Suppose $\tau >\frac{q_{2}^{*}}{q_{1}^{*}}$. Then the critical curve $a=a_\tau ^{0}(q_1)$ uniquely determined by (6.1) is strictly increasing with respect to $q_1$ in $(\frac{q_{2}^{*}}{\tau },q_{1}^{*})$. Moreover, $a_\tau ^{0}(\frac{q_{2}^{*}}{\tau })=0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{0}(q_1)=+\infty .$

Proof

Since $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))$ is strictly increasing with respect to a (see Lemma 4.1(iii)) and strictly decreasing with $q_1$ (see Lemma 2.5 of Nie et al. 2020 ), we can conclude that $a_\tau ^{0}(q_1)$ is strictly increasing with respect to $q_1\in [\frac{q_{2}^{*}}{\tau },q_{1}^{*})$ by the implicit function theorem.

Recall that $\mu _{1}(d_{2},\tau q_1,r_{2}+ea\theta _1(q_1))$ is continuous and strictly increasing with respect to a. Taking $q_1=\frac{q_{2}^{*}}{\tau }$ in $\mu _{1}(d_{2},\tau q_1,r_{2}+ea_\tau ^{0}(q_1)\theta _1(q_1))=0$, we have $\mu _{1}(d_{2},q_{2}^{*},r_{2}+ea_\tau ^{0}(\frac{q_{2}^{*}}{\tau })\theta _{1}(\frac{q_{2}^{*}}{\tau }))=0$. Since $\theta _{1}(\frac{q_{2}^{*}}{\tau })>0$ on [0, 1] and $\mu _{1}(d_{2},q_{2}^{*},r_{2})=0$, we immediately obtain $a_\tau ^{0}(\frac{q_{2}^{*}}{\tau })=0$.

Next we show that $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{0}(q_1)=+\infty$. Note that $a_\tau ^{0}(q_1)$ is strictly increasing with respect to $q_1$ in $[\frac{q_{2}^{*}}{\tau },q_{1}^{*})$. Suppose that $a_\tau ^{0}(q_1)$ is bounded in $[\frac{q_{2}^{*}}{\tau },q_{1}^{*})$. Then there exists a constant $A<+\infty$ such that $\lim \limits _{q\rightarrow q_{1}^{*}-}a_\tau ^{0}(q_1)=A$. Let $q_1\rightarrow q_{1}^{*}-$ in $\mu _{1}(d_{2},\tau q_1,r_{2}+ea_\tau ^{0}(q_1)\theta _1(q_1))=0$, then we have $\mu _{1}(d_{2},\tau q_{1}^{*},r_{2})=0$ since $\lim \limits _{q_1\rightarrow q_1^*-}\theta _1(q_1)=0$, which contradicts the fact that $\mu _{1}(d_{2},\tau q_{1}^{*},r_{2})<\mu _{1}(d_{2},q_{2}^{*},r_{2})=0$ since $\tau q_{1}^{*}>q_{2}^{*}$. Thus, $\lim \limits _{q\rightarrow q_{1}^{*}-}a_\tau ^{0}(q_1)=+\infty .$ $\square$

Proposition 6.5

The critical curve $a=a_\tau ^{*}(q_1)$ with $q_1\in [0,\min \{q_{1}^{*},\frac{q_2^*}{\tau }\})$ uniquely determined by (6.4) satisfies:

• (i) $a_\tau ^{*}(0)=\frac{r_{1}}{K_{2}}$, and ${\dot{a}}_\tau ^{*}(0)=\frac{\tau r_{1}-r_{2}}{r_{2}K_{2}}$ (‘$\ \dot{\ }$’ denotes $\frac{\mathrm {d}}{\mathrm {d} q}$ or $\frac{\partial }{\partial q}$ from now on);

• (ii) if $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$, then $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{*}(q_1)=0$, and ${\dot{a}}_\tau ^{*}(q_{1}^{*})<0$. Moreover, $a_\tau ^{*}(q_1)\le {\bar{a}}$ for $q_1\in [0,q_{1}^{*})$, where ${\bar{a}}$ is uniquely determined by

  $$\begin{aligned} \mu _{1}(d_{1},q_1,r_{1}-{\bar{a}}\frac{K_{2}}{r_{2}}\mu _{1}(d_{2},\tau q_1,r_{2})\min \limits _{x\in [0,1]}\phi _{1}(d_{2},\tau q_1,r_{2}))=0; \end{aligned}$$

• (iii) if $\tau >\frac{q_{2}^{*}}{q_{1}^{*}}$, then $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}a_\tau ^{*}(q_1)=+\infty$, and $a_\tau ^{*}(q_1)\ge \frac{\mu _{1}(d_{1},q_1,r_{1})}{K_{2}}:={\underline{a}}$ for $q_1\in [0,\frac{q_{2}^{*}}{\tau });$

• (iv) if $\tau =\frac{q_{2}^{*}}{q_{1}^{*}}$, then $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{*}(q_1)>0.$

Proof

(i) It follows from (6.4), Lemmas 4.2(ii) and 4.1(iv) that

$$\begin{aligned} 0=\mu _{1}(d_{1},0,r_{1}-a_\tau ^*(0)\theta _{2}(0))=\mu _{1}(d_{1},0,r_{1}-a_\tau ^*(0)K_{2})=r_{1}-a_\tau ^*(0)K_{2}. \end{aligned}$$

Hence, we immediately have $a_\tau ^{*}(0)=\frac{r_{1}}{K_{2}}$.

In view of $\mu _{1}(d_{1},q_1,r_{1}-a_\tau ^{*}(q_1)\theta _{2}(\tau q_1))=0$, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}({\tilde{\varphi }}_{1})_{xx}-q_1({\tilde{\varphi }}_{1})_{x}+(r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1)){\tilde{\varphi }}_{1}=0,&{} x\in (0,1),\\ d_{1}({\tilde{\varphi }}_{1})_{x}(0)-q_1{\tilde{\varphi }}_{1}(0)=0,\ \ ({\tilde{\varphi }}_{1})_{x}(1)=0, \end{array}\right. } \end{aligned}$$

(6.5)

where ${\tilde{\varphi }}_{1}={\tilde{\varphi }}_{1}(\cdot ;\ d_{1},q_1,r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1))$ is the corresponding principal eigenfunction of $\mu _{1}(d_{1},q_1,r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1))$. Differentiating the Eq. (6.5) with respect to $q_1$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}(\dot{{\tilde{\varphi }}}_{1})_{xx}-q_1(\dot{{\tilde{\varphi }}}_{1})_{x}-({\tilde{\varphi }}_{1})_{x}+(r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1))\dot{{\tilde{\varphi }}}_{1}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -({\dot{a}}_\tau ^{*}(q_1)\theta _{2}(\tau q_1)+\tau a_\tau ^*(q_1){\dot{\theta }}_{2}(\tau q_1)){\tilde{\varphi }}_{1}=0,&{} x\in (0,1),\\ d_{1}(\dot{{\tilde{\varphi }}}_{1})_{x}(0)-q_1\dot{{\tilde{\varphi }}}_{1}(0)-{\tilde{\varphi }}_{1}(0)=0,\ (\dot{{\tilde{\varphi }}}_{1})_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(6.6)

Note that $\theta _{2}(0)=K_{2},\ a_\tau ^{*}(0)=\frac{r_{1}}{K_{2}}$, ${\tilde{\varphi }}_{1}|_{q_1=0}\equiv 1\ \text{ and }\ ({\tilde{\varphi }}_{1})_{x}|_{q_1=0}=0$ (see Lemma 4.1(vii)). Setting $q_1=0$ in (6.6), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}(\dot{{\tilde{\varphi }}}_1|_{q_1=0})_{xx}-{\dot{a}}_\tau ^{*}(0)K_{2}-\frac{\tau r_{1}}{K_{2}}{\dot{\theta }}_{2}(0)=0,&{} x\in (0,1),\\ d_{1}(\dot{{\tilde{\varphi }}}_1|_{q_1=0})_{x}(0)=1,\ (\dot{{\tilde{\varphi }}}_1|_{q_1=0})_{x}(1)=0. \end{array}\right. } \end{aligned}$$

Integrating this equation over (0, 1), we get ${\dot{a}}_\tau ^{*}(0)=-\frac{\tau r_{1}}{K_{2}^{2}}\int _{0}^{1}{\dot{\theta }}_{2}(0)d x-\frac{1}{K_{2}}$.

To calculate $\int _{0}^{1}{\dot{\theta }}_{2}(0)d x$, differentiating the equation of $\theta _{2}(q_2)$ with respect to $q_2$ and setting $q_2=0$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{2}({\dot{\theta }}_{2}(0))_{xx}-r_{2}{\dot{\theta }}_{2}(0)=0,\qquad x\in (0,1),\\ d_{2}({\dot{\theta }}_{2}(0))_{x}(0)=K_{2},\ ({\dot{\theta }}_{2}(0))_{x}(1)=0 \end{array}\right. } \end{aligned}$$

since $\theta _{2}(0)\equiv K_2.$ Integrating this equation over (0, 1), we get $\int _{0}^{1}{\dot{\theta }}_{2}(0)d x=-\frac{K_{2}}{r_{2}}$. Hence, ${\dot{a}}_\tau ^{*}(0)=\frac{\tau r_{1}-r_{2}}{r_{2}K_{2}}.$

(ii) Note that

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}(\phi _{1})_{xx}-q_1(\phi _{1})_{x}+r_{1}\phi _{1}=\mu _{1}(d_{1},q_1,r_{1})\phi _{1},&{} x\in (0,1),\\ d_{1}(\phi _{1})_{x}(0)-q_1\phi _{1}(0)=0,\ (\phi _{1})_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(6.7)

Here $\phi _{1}:=\phi _{1}(\cdot ; d_{1},q_1,r_{1})$ is the principal eigenfunction corresponding to $\mu _{1}(d_{1},q_1,r_{1})$. Multiplying (6.5) by $e^{-\frac{q_1}{d_{1}}x}\phi _{1}$ and (6.7) by $e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}$, integrating over (0, 1) and subtracting the two equations, we obtain

$$\begin{aligned}&\mu _{1}(d_{1},q_1,r_{1})\int _{0}^{1}e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}\phi _{1}d x =a_\tau ^*(q_1)\int _{0}^{1}e^{-\frac{q_1}{d_{1}}x}\theta _{2}(\tau q_1){\tilde{\varphi }}_{1}\phi _{1}d x. \end{aligned}$$

(6.8)

Taking $q_1=q_{1}^{*}$ in (6.8), we get $a_\tau ^*(q_1^*)\int _{0}^{1}e^{-\frac{q_1^*}{d_{1}}x}\theta _{2}(\tau q_1^*){\tilde{\varphi }}_{1}|_{q_1=q_1^*}\phi _{1}|_{q_1=q_1^*}d x=0$ since $\mu _{1}(d_{1},q_1^*,r_{1})=0$. Note that $\theta _{2}(\tau q_1^*)>0$ follows from $\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$, and the principal eigenfunctions ${\tilde{\varphi }}_{1}|_{q_1=q_1^*}>0$ and $\phi _{1}|_{q_1=q_1^*}>0$. We conclude that $a_\tau ^{*}(q_{1}^{*})=0.$

Next we prove that ${\dot{a}}_\tau ^{*}(q_{1}^{*})<0$. Set $q_1=q_{1}^{*}$ in (6.5) and (6.6) . Then we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}({\tilde{\varphi }}_{1}|_{q_1=q_1^*})_{xx}-q_{1}^{*}({\tilde{\varphi }}_{1}|_{q_1=q_1^*})_{x}+r_{1}{\tilde{\varphi }}_{1}|_{q_1=q_1^*}=0,\ x\in (0,1),\\ d_{1}({\tilde{\varphi }}_{1}|_{q_1=q_1^*})_{x}(0)-q_{1}^{*}{\tilde{\varphi }}_{1}|_{q_1=q_1^*}(0)=0,\ \ ({\tilde{\varphi }}_{1}|_{q_1=q_1^*})_{x}(1)=0, \end{array}\right. } \end{aligned}$$

(6.9)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}(\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*})_{xx}-q_{1}^{*}(\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*})_{x} -({\tilde{\varphi }}_1|_{q_1=q_1^*})_{x}\\ \quad +r_{1}\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*} -{\dot{a}}_\tau ^{*}(q_{1}^{*})\theta _{2}(\tau q_{1}^{*}){\tilde{\varphi }}_1|_{q_1=q_1^*}=0,\quad x\in (0,1),\\ d_{1}(\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*})_{x}(0)-q_{1}^{*}\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*}(0)-{\tilde{\varphi }}_1|_{q_1=q_1^*}(0)=0,\ (\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*})_{x}(1)=0. \end{array}\right. }\quad \end{aligned}$$

(6.10)

Multiplying the equation (6.9) by $e^{-\frac{q_{1}^{*}}{d_{1}}x}\dot{{\tilde{\varphi }}}_1|_{q_1=q_1^*}$ and (6.10) by $e^{-\frac{q_{1}^{*}}{d_{1}}x}{\tilde{\varphi }}_1|_{q_1=q_1^*}$, and integrating over (0, 1) yield that

$$\begin{aligned}&-\frac{1}{2}[({\tilde{\varphi }}_1|_{q_1=q_1^*})^{2}(0)+e^{-\frac{q_{1}^{*}}{d_{1}}}({\tilde{\varphi }}_1|_{q_1=q_1^*})^{2}(1)] -\frac{q_{1}^{*}}{2d_{1}}\int _{0}^{1}e^{-\frac{q_{1}^{*}}{d_{1}}x}({\tilde{\varphi }}_1|_{q_1=q_1^*})^{2}d x\\&\quad -\int _{0}^{1}{\dot{a}}_\tau ^{*}(q_{1}^{*})e^{-\frac{q_{1}^{*}}{d_{1}}x}\theta _{2}(\tau q_{1}^{*})({\tilde{\varphi }}_1|_{q_1=q_1^*})^{2}d x=0. \end{aligned}$$

This implies that ${\dot{a}}_\tau ^{*}(q_{1}^{*})<0$ since $\theta _{2}(\tau q_{1}^{*})>0.$

To show that $a_\tau ^*(q_1)$ has an upper bound in $[0, q_{1}^{*})$, we first recall that $\frac{K_{2}}{r_{2}}\mu _{1}(d_{2},\tau q_1,r_{2})\phi _{1}(d_{2},\tau q_1,r_{2})\le \theta _{2}(\tau q_1)$ in $[0, q_{1}^{*})$(see Lemma 4.2(i)). Thus,

$$\begin{aligned}&\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))\\&\quad \le \mu _{1}(d_{1},q_1,r_{1}-a\frac{K_{2}}{r_{2}}\mu _{1}(d_{2},\tau q_1,r_{2})\phi _{1}(d_{2},\tau q_1,r_{2}))\\&\quad \le \mu _{1}(d_{1},q_1,r_{1}-a\frac{K_{2}}{r_{2}}\mu _{1}(d_{2},\tau q_1,r_{2})\min \limits _{x\in [0,1]}\phi _{1}(d_{2},\tau q_1,r_{2})). \end{aligned}$$

By similar arguments as for (6.2)–(6.4), we obtain that there exists a unique ${\bar{a}}\in (0, +\infty )$ such that

$$\begin{aligned} \mu _{1}(d_{1},q_1,r_{1}-{\bar{a}}\frac{K_{2}}{r_{2}}\mu _{1}(d_{2},\tau q_1,r_{2})\min \limits _{x\in [0,1]}\phi _{1}(d_{2},\tau q_1,r_{2}))=0. \end{aligned}$$

Hence, $\mu _{1}(d_{1},q_1,r_{1}-{\bar{a}}\theta _{2}(\tau q_1))\le 0$. Since $\mu _{1}(d_{1},q_1,r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1))=0$, it follows from Lemma 4.1(iii) that $a_\tau ^*(q_1)\le {\bar{a}}.$

(iii) It follows from (6.8) that

$$\begin{aligned} \begin{aligned} \lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}a_\tau ^*(q_1)&=\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}\frac{\mu _{1}(d_{1},q_1,r_{1})\int _{0}^{1}e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}\phi _{1}d x}{\int _{0}^{1}\theta _{2}(\tau q_1)e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}\phi _{1}d x} \\&\ge \lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}\frac{\mu _{1}(d_{1},q_1,r_{1} )}{\max \limits _{x\in [0,1]}\theta _{2}(\tau q_1)}. \end{aligned} \end{aligned}$$

Observe that $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}\theta _{2}(\tau q_1)=0$, and $\mu _{1}(d_{1},\frac{q_{2}^{*}}{\tau },r_{1})>0$ since $\tau >\frac{q_{2}^{*}}{q_{1}^{*}}$. This implies $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}a_\tau ^*(q_1)=+\infty .$

Next we show that $a_\tau ^*(q_1)$ has a lower bound in $[0, \frac{q_{2}^{*}}{\tau })$. Since $\theta _{2}(\tau q_1)\le K_{2}$ in $[0, \frac{q_{2}^{*}}{\tau })$ (see Lemma 4.2(i)), we have

$$\begin{aligned} \begin{aligned} \mu _{1}(d_{1},q_1,r_{1}-a\theta _{2}(\tau q_1))\ge \mu _{1}(d_{1},q_1,r_{1}-aK_{2})=\mu _{1}(d_{1},q_1,r_{1})-aK_{2} \end{aligned} \end{aligned}$$

for $q_1\in [0, \frac{q_{2}^{*}}{\tau })$. Let ${\underline{a}}=\frac{\mu _{1}(d_{1},q_1,r_{1})}{K_{2}}$. Then $\mu _{1}(d_{1},q_1,r_{1}-{\underline{a}}\theta _{2}(\tau q_1))\ge 0$. Note that $\mu _{1}(d_{1},q_1,r_{1}-a_\tau ^*(q_1)\theta _{2}(\tau q_1))=0$. It follows from Lemma 4.1(iii) that $a_\tau ^*(q_1)\ge {\underline{a}}.$

(iv) If $\tau =\frac{q_{2}^{*}}{q_{1}^{*}}$, then $q_{1}^{*}=\frac{q_{2}^{*}}{\tau }$, and we observe that $\mu _{1}(d_{1},q_{1}^{*},r_{1})=0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}\theta _{2}(\tau q_1)=0$.

Next, we claim that $\frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}<0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}\frac{\partial \theta _{2}(\tau q_1)}{\partial q_1}<0.$ Differentiating the Eq. (6.7) with respect to $q_1$, and setting $q_1=q_1^*$, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}({\dot{\phi }}_1|_{q_1=q_1^*})_{xx}-q_{1}^{*}({\dot{\phi }}_1|_{q_1=q_1^*})_{x}+r_{1}{\dot{\phi }}_1|_{q_1=q_1^*}-(\phi _1|_{q_1=q_1^*})_x\\ \quad =\frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}\phi _1|_{q_1=q_1^*},\ x\in (0,1),\\ d_{1}({\dot{\phi }}_1|_{q_1=q_1^*})_{x}(0)-q_{1}^{*}{\dot{\phi }}_1|_{q_1=q_1^*}(0)-\phi _1|_{q_1=q_1^*}(0)=0,\\ ({\dot{\phi }}_1|_{q_1=q_1^*})_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(6.11)

Recall that

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}(\phi _{1}|_{q_1=q_1^*})_{xx}-q_{1}^{*}(\phi _{1}|_{q_1=q_1^*})_{x}+r_{1}\phi _{1}|_{q_1=q_1^*}=0,\ x\in (0,1),\\ d_{1}(\phi _{1}|_{q_1=q_1^*})_{x}(0)-q_{1}^{*}\phi _{1}|_{q_1=q_1^*}(0) =0,\ \ (\phi _{1}|_{q_1=q_1^*})_{x}(1)=0. \end{array}\right. } \end{aligned}$$

(6.12)

Multiplying (6.11) by $e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}|_{q_1=q_1^*}$ and (6.12) by $e^{-\frac{q_1^*}{d_{1}}x}{\dot{\phi }}_1|_{q_1=q_1^*}$, integrating over (0, 1) and subtracting the two equations, we obtain

$$\begin{aligned}&\frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}\int _0^1e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}^2|_{q_1=q_1^*}\mathrm {d}x\\&\quad =-\phi _1^2|_{q_1=q_1^*}(0)-\int _0^1e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}|_{q_1=q_1^*}(\phi _{1}|_{q_1=q_1^*})_{x}\mathrm {d}x. \end{aligned}$$

Hence, we have

$$\begin{aligned} \frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}=\frac{-\phi _1^2|_{q_1=q_1^*}(0)-\int _0^1e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}|_{q_1=q_1^*}(\phi _{1}|_{q_1=q_1^*})_{x}\mathrm {d}x}{\int _0^1e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}^2|_{q_1=q_1^*}\mathrm {d}x}<0\nonumber \\ \end{aligned}$$

(6.13)

by using Lemma 4.1(vii).

Now, we turn to calculate $\lim \limits _{q_1\rightarrow q_{1}^{*}-}\frac{\partial \theta _{2}(\tau q_1)}{\partial q_1}$. To this end, we first apply Crandall–Rabinowitz bifurcation theorem (Crandall and Rabinowitz 1971) to get the expression of $\theta _{2}(\tau q_1)$ near $q_{1}=q_1^*(=\frac{q_{2}^{*}}{\tau })$. Note that $\theta _{2}(\tau q_1)$ is the unique positive solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} d_2u_{xx}-\tau q_1u_{x}+r_2(1-\frac{u}{K_2})u=0, &{} 0<x<1,\\ d_2u_{x}(0)-\tau q_1u(0)=0,\ u_{x}(1)=0 \end{array}\right. } \end{aligned}$$

(6.14)

for $q_{1}\in [0,\frac{q_2^*}{\tau })$. By using similar arguments as in Proposition 2.2 of Yan et al. (2022), we conclude that there exists an $\varepsilon >0$ such that $\theta _{2}(\tau q_1)$ regarded as the bifurcation solution of (6.14) can be described by the $C^1$ curve

$$\begin{aligned} \Gamma _+=\{(q_1(s), u(s)): 0<s<\varepsilon \}=\{(q_1(s), s\psi _1^*+s\Psi (s)): 0<s<\varepsilon \} \end{aligned}$$

near the bifurcation point $(\frac{q_2^*}{\tau }, 0)$, which satisfies $q_1(0)=\frac{q_2^*}{\tau }$, $\Psi (0)=0$, and $\Psi (s)\in Z=\{\psi \in W^{2,p}(0,1): \int _0^1\psi _1^*\psi \mathrm {d}x=0\}.$ Here $\psi _1^*$ is the principal eigenfunction corresponding to $\mu _1(d_2, q_2^*, r_2)$.

Substituting $(q_1(s), u(s))=(q_1(s), s\psi _1^*+s\Psi (s))$ into (6.14), dividing by s, taking the derivative with respect to s at $s=0$ and denoting $\frac{\mathrm {d}}{\mathrm {d}s}='$, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} d_2(\Psi '(0))_{xx}-q_2^*(\Psi '(0))_{x}+r_2\Psi '(0)=\tau q'_1(0)\psi _1^*+\frac{r_2}{K_2}(\psi _1^*)^2, \ \ x\in (0, 1),\\ d_2(\Psi '(0))_{x}|_{x=0}-q_2^*\Psi '(0)|_{x=0}=\tau q'_1(0)\psi _1^*(0), \ (\Psi '(0))_{x}|_{x=1}=0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(6.15)

Recall that $\mu _1(d_2, q_2^*, r_2)=0$ (see (2.4)) and

$$\begin{aligned}&d_2(\psi _1^*)_{xx}-q_2^*(\psi _1^*)_{x}+r_2\psi _1^*=0, \ x\in (0, 1),\nonumber \\&d_2(\psi _1^*)_{x}(0)-q_2^*\psi _1^*(0)=0,\ (\psi _1^*)_{x}(1)=0. \end{aligned}$$

(6.16)

Multiply (6.15) by $e^{-\frac{q_2^*}{d_2}x}\psi _1^*$ and (6.16) by $e^{-\frac{q_2^*}{d_2}x}\Psi '(0)$, integrate over (0, 1) by parts and subtract the two equations to yield

$$\begin{aligned} q'_1(0)=-\frac{r_2}{\tau K_2}\cdot \frac{\int _{0}^1e^{-\frac{q_2^*}{d_2}x}(\psi _1^*)^3\mathrm {d}x}{(\psi _1^*(0))^2+\int _0^1e^{-\frac{q_2^*}{d_2}x}(\psi _1^*)_x\psi _1^*\mathrm {d}x}<0 \end{aligned}$$

(6.17)

by using Lemma 4.1(vii). Hence, we have

$$\begin{aligned} \lim \limits _{q_1\rightarrow q_{1}^{*}-}\frac{\partial \theta _{2}(\tau q_1)}{\partial q_1}=\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}\frac{\partial \theta _{2}(\tau q_1)}{\partial q_1} =\frac{\psi _1^*}{q'_1(0)}. \end{aligned}$$

(6.18)

In view of $\mu _{1}(d_{1},q_{1}^{*},r_{1})=0$ and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}\theta _{2}(\tau q_1)=0$, it follows from (6.8) that

$$\begin{aligned} \begin{aligned} \lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^*(q_1)&=\lim \limits _{q_1\rightarrow q_{1}^{*}-}\frac{\mu _{1}(d_{1},q_1,r_{1})\int _{0}^{1}e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}\phi _{1}d x}{\int _{0}^{1}\theta _{2}(\tau q_1)e^{-\frac{q_1}{d_{1}}x}{\tilde{\varphi }}_{1}\phi _{1}d x}\\&=\frac{\frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}\int _{0}^{1}e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}^2|_{q=q_1^*}d x}{\int _{0}^{1}\lim \limits _{q_1\rightarrow q_{1}^{*}-}\frac{\partial \theta _{2}(\tau q_1)}{\partial q_1}e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}^2|_{q=q_1^*}d x}\\&=\frac{q_1'(0)\frac{\partial \mu _{1}(d_{1}, q_1, r_{1})}{\partial q_1}|_{q_1=q_1^*}\int _{0}^{1}e^{-\frac{q_1^*}{d_{1}}x}\phi _{1}^2|_{q=q_1^*}d x}{\int _{0}^{1}e^{-\frac{q_1^*}{d_{1}}x}\psi _1^*\phi _{1}^2|_{q=q_1^*}d x}>0 \end{aligned} \end{aligned}$$

by using (6.13), (6.17) and (6.18). Here ${\tilde{\varphi }}_{1}|_{q=q_1^*}=\phi _{1}|_{q=q_1^*}$ (see (6.5)). The proof is finished. $\square$

Based on Lemma 6.3 and Proposition 6.5, we can sum up the following conclusions related to the critical curve $a=a_\tau ^*(q_1)$:

Corollary 6.1

Suppose (H) holds, $a>0,\ q_2=\tau q_1$.

• (i) If $\frac{r_{2}}{r_1}<\tau <\frac{q_{2}^{*}}{q_{1}^{*}}$, then ${\dot{a}}_\tau ^{*}(0)>0$. Moreover, ${a}_\tau ^{*}(q_{1}^{*})=0$ and ${\dot{a}}_\tau ^{*}(q_{1}^{*})<0$. Set $a_{M}=\sup \{{a}_\tau ^{*}(q_1):0\le q_1<q_{1}^{*}\}$, then $a_{M}>{a}_\tau ^{*}(0)=\frac{r_{1}}{K_{2}}$ and

  • when $a\in (\frac{r_{1}}{K_{2}},a_{M})$, the stability of $(0,\theta _{2}(\tau q_1))$ changes at least twice in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$;

  • when $0<a<\frac{r_{1}}{K_{2}}$, the stability of $(0,\theta _{2}(\tau q_1))$ changes at least once in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$;

  • when $a>a_{M}$, $(0,\theta _{2}(\tau q_1))$ is always asymptotically stable in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$.

• (ii) If $\frac{q_{2}^{*}}{q_{1}^{*}}<\tau <\frac{r_{2}}{r_1}$, then ${\dot{a}}_\tau ^{*}(0)<0$. Moreover, $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}{a}_\tau ^{*}(q_1)=+\infty$ and $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}{\dot{a}}_\tau ^{*}(q_1)>0$. Set $a_{m}=\inf \{{a}_\tau ^{*}(q_1):0\le q_1<\frac{q_{2}^{*}}{\tau }\}$, then $a_{m}<{a}_\tau ^{*}(0)=\frac{r_{1}}{K_{2}}$ and

  • when $a\in (a_{m},\frac{r_{1}}{K_{2}})$, the stability of $(0,\theta _{2}(\tau q_1))$ changes at least twice in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$;

  • when $a>\frac{r_{1}}{K_{2}}$, the stability of $(0,\theta _{2}(\tau q_1))$ changes at least once in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$;

  • when $0<a<a_{m}$, $(0,\theta _{2}(\tau q_1))$ is always unstable in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$.

By Propositions 6.4–6.5 and Corollary 6.1, we conclude that the two critical curves $a=a_\tau ^{0}(q_1)$ and $a=a_\tau ^{*}(q_1)$ evolve interestingly when the ratio $\tau =q_2:q_1$ changes (see Figs. 2 and 3).

The critical curve $a=a_\tau ^{0}(q_1)$ occurs only when $\tau >\frac{q_2^*}{q_1^*}$, which separates the coexistence from the persistence of prey alone (see Lemma 6.2). Furthermore, it must pass through the point $(\frac{q_2^*}{\tau }, 0)$ and increase to infinity along $q_1\rightarrow q_1^*-$ if it exist (see Proposition 6.4). This implies that $(\theta _1(q_1), 0)$ is always unstable when $\tau \le \frac{q_2^*}{q_1^*}$ (see Figs. 2a–c and 3a, b, and see also Lemma 6.2(i)), and its stability changes exactly once when $\tau >\frac{q_2^*}{q_1^*}$ (see Figs. 2d and 3c, d, and see also Lemma 6.2(ii)).

The shape of the critical curve $a=a_\tau ^*(q_1)$, which separates the coexistence from the persistence of generalist predators alone, is more complicated with the change of the ratio $\tau$. There exist two critical values $\tau =\frac{r_2}{r_1}$ and $\tau =\frac{q_2^*}{q_1^*}$ such that the shape of the curve $a=a_\tau ^*(q_1)$ changes dramatically when $\tau$ crosses $\frac{r_2}{r_1}$ and $\frac{q_2^*}{q_1^*}$. More precisely, ${\dot{a}}_\tau ^{*}(0)=\frac{\tau r_{1}-r_{2}}{r_{2}K_{2}}$ changes from negative to positive when $\tau$ crosses $\frac{r_2}{r_1}$, see Figs. 2 and 3. Meanwhile, if $\tau <\frac{q_2^*}{q_1^*}$, then $a_\tau ^{*}(q_1)$ is well-defined in $[0, q_1^*)$, and $\lim \limits _{q_1\rightarrow q_{1}^{*}-}a_\tau ^{*}(q_1)=0$. If $\tau >\frac{q_2^*}{q_1^*}$, then $a_\tau ^{*}(q_1)$ is well-defined in $[0, \frac{q_2^*}{\tau })$, and $\lim \limits _{q_1\rightarrow \frac{q_{2}^{*}}{\tau }-}a_\tau ^{*}(q_1)=+\infty$ (see Proposition 6.5). Hence, combining with Corollary 6.1, one can conclude that the critical curve $a=a_\tau ^*(q_1)$ evolves from Fig. 2a–d with the increasing of the ratio $\tau$ provided that $\frac{r_2}{r_1}<\frac{q_2^*}{q_1^*}$, and it evolves from Fig. 3a–d with the increasing of the ratio $\tau$ provided that $\frac{r_2}{r_1}>\frac{q_2^*}{q_1^*}$. This implies that for different predation rates a, the stability of the semi-trivial steady state $(0, \theta _2(\tau q_1))$ may change zero times, once or twice as $q_1$ changes.

In general, we observe that the ratio $\tau$ of flow speeds has a significant influence on the shapes of the critical curves $a=a_\tau ^{0}(q_1)$ and $a=a_\tau ^*(q_1)$. Hence, it plays an important role in determining the dynamics of system (1.2). In particular, when the ratio $\tau$ lies between $\frac{q_2^*}{q_1^*}$ and $\frac{r_2}{r_1}$, there exist some suitably predation rates such that the stability of the semitrivial steady state $(0, \theta _2(\tau q_1))$ may change at least twice in $q_1\in [0, \frac{q_{2}^{*}}{\tau })$ (see Corollary 6.1). This is a significant difference between the specialist predator-prey system and the generalist predator-prey system in open advective environments.

Appendix

For completeness and the reader’s convenience, we provide the proof of Lemma 4.5 here via the comparison principle and uniform persistence theory although its proof is exactly similar to Theorems 1.1 and 1.2 of Nie et al. (2020).

Proof of Lemma 4.5

(i) Since the positive solution of (1.2) satisfies $N(x,t)>0$ and $P(x,t)>0$ for $x\in [0,1]$ and $t>0$ (see Lemma 4.4), we have

$$\begin{aligned} N_{t}\le d_{1}N_{xx}-q_1N_{x}+r_{1}N(1-\frac{N}{K_{1}}),\ x\in (0,1),\ t>0. \end{aligned}$$

Let ${\mathcal {N}}(x,t)$ be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {N}}_{t}= d_{1}{\mathcal {N}}_{xx}-q_1{\mathcal {N}}_{x}+r_{1}{\mathcal {N}}(1-\frac{{\mathcal {N}}}{K_{1}}),&{} x\in (0,1),\ t>0,\\ d_{1}{\mathcal {N}}_{x}(0,t)-q_1{\mathcal {N}}(0,t)=0,\ {\mathcal {N}}_{x}(1,t)=0,&{} t>0,\\ {\mathcal {N}}(x,0)=N_{0}(x)\ge 0,\not \equiv 0, &{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

(7.1)

The comparison principle for parabolic equations yields that $N(x, t)\le {\mathcal {N}}(x, t)$ for all $x\in [0,1],\ t>0$. In view of $q_1\ge q_{1}^{*}$, by Lemma 2.1, we conclude that ${\mathcal {N}}(x,t)\rightarrow 0,\ x\in [0,1]$ as $t\rightarrow +\infty$. Thus $\lim \limits _{t\rightarrow +\infty }N(x,t)=0$ uniformly in [0, 1]. Hence for any $\epsilon >0$, there exists $T_{\epsilon }>0$ such that $N(x,t)\le \epsilon$ for all $x\in [0,1],\ t\ge T_{\epsilon }$. Furthermore,

$$\begin{aligned} P_{t}\le d_{2}P_{xx}-q_2P_{x}+(r_{2}+ea\epsilon )P\ \text{ for }\ x\in (0,1),\ t\ge T_{\epsilon }. \end{aligned}$$

Let ${\mathcal {P}}(x, t)$ be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {P}}_{t}=d_{2}{\mathcal {P}}_{xx}-q_2{\mathcal {P}}_{x}+(r_{2}+ea\epsilon ){\mathcal {P}},&{} x\in (0,1),\ t\ge T_{\epsilon },\\ d_{2}{\mathcal {P}}_{x}(0,t)-q_2{\mathcal {P}}(0,t)=0,\ {\mathcal {P}}_{x}(1,t)=0,&{} t\ge T_{\epsilon },\\ {\mathcal {P}}(x,T_{\epsilon })=P(x,T_{\epsilon }),&{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

The comparison principle implies $P(x,t)\le {\mathcal {P}}(x,t)$ for all $x\in [0,1]$, $t\ge T_{\epsilon }$. Since $\mu _{1}(d_{2},q_2,r_{2})<0$ when $q_2>q_{2}^{*}$, we conclude that there exists $\epsilon >0$ sufficiently small such that $\mu _{1}(d_{2},q_2,r_{2}+ea\epsilon )<0$ for $q_2>q_{2}^{*}$. By the method of variable separation we get $\lim \limits _{t\rightarrow +\infty }{\mathcal {P}}(x,t)=0$, $x\in [0,1]$, which implies that $\lim \limits _{t\rightarrow +\infty }P(x,t)=0$ for all $x\in [0,1]$. Thus, the solution (N(x, t), P(x, t)) of system (1.2) converges to (0, 0) uniformly for $x\in [0,1]$ as $t\rightarrow +\infty .$

(ii) Recall that $N(x, t)\le {\mathcal {N}}(x, t)$ for all $x\in [0,1],\ t>0$, where ${\mathcal {N}}(x, t)$ is the solution of (7.1). Observe that the existence of $\theta _1$ means $q_1<q_{1}^{*}$. It follows from Lemma 2.1 that $\lim \limits _{t\rightarrow +\infty }{\mathcal {N}}(x,t)=\theta _{1}$ uniformly for $x\in [0,1]$. This implies that

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }N(x,t)\le \theta _{1}\ \text{ uniformly } \text{ for }\ x\in [0,1]. \end{aligned}$$

(7.2)

Then for any $\epsilon >0$, there exists $T_{1}>0$ such that $N(x,t)<\theta _{1}+\epsilon$ for all $x\in [0,1],\ t\ge T_{1}$. Let $\mathbf{P} (x,t)$ satisfy the following equation,

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {P}_{t}=d_{2}\mathbf {P}_{xx}-q_2\mathbf {P}_{x}+r_{2}\mathbf {P}(1-\frac{\mathbf {P}}{K_{2}})+ea\mathbf {P}(\theta _{1}+\epsilon ),&{} x\in (0,1),\ t\ge T_{1},\\ d_{2}\mathbf {P}_{x}(0,t)-q_2\mathbf {P}(0,t)=0,\ \mathbf {P}_{x}(1,t)=0,&{} t\ge T_{1},\\ \mathbf {P}(x,T_{1})=P(x,T_{1}),&{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

Easily we know that $P(x, t)\le \mathbf{P} (x,t)$ for all $x\in [0,1],\ t\ge T_{1}$ by using the comparison principle. Since $\mu _{1}(d_{2},q_2, r_{2}+ea\theta _1(q_1))<0$, there exists $\epsilon >0$ small enough such that $\mu _{1}(d_{2},q_2, r_{2}+ea(\theta _1(q_1)+\epsilon ))<0$. Similar arguments as in Lemma 2.1 yield that $\lim \limits _{t\rightarrow +\infty }{} \mathbf{P} (x,t)=0,\ x\in [0,1]$, thus $\lim \limits _{t\rightarrow +\infty }P(x,t)=0$ uniformly for $x\in [0,1]$. Therefore, for any $\epsilon >0$, there exists $T_{2}>T_{1}$ such that $P(x,t)\le \epsilon$ for all $x\in [0,1],\ t\ge T_{2}$, which leads to

$$\begin{aligned} N_{t}\ge d_{1}N_{xx}-q_1N_{x}+r_{1}N(1-\frac{N}{K_{1}})-aN\epsilon ,\ x\in (0,1),\ t\ge T_{2}. \end{aligned}$$

Let $\mathbf{N} (x,t)$ be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {N}_{t}= d_{1}\mathbf {N}_{xx}-q_1\mathbf {N}_{x}+r_{1}\mathbf {N}(1-\frac{\mathbf {N}}{K_{1}})-a\mathbf {N}\epsilon ,&{} x\in (0,1),\ t\ge T_{2},\\ d_{1}\mathbf {N}_{x}(0,t)-q_1\mathbf {N}(0,t)=0,\ \mathbf {N}_{x}(1,t)=0,&{} t\ge T_{2},\\ \mathbf {N}(x,T_{2})=N(x,T_{2}), &{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

(7.3)

The comparison principle implies $N(x,t)\ge \mathbf{N} (x,t)$ for all $x\in [0,1],\ t\ge T_{2}$. Noting that $\mu _{1}(d_{1},q_1,r_{1})>0$ based on $q_1<q_{1}^{*}$, we can choose $\epsilon >0$ sufficiently small such that $\mu _{1}(d_{1},q_1,r_{1}-a\epsilon )>0$. Similar arguments as in Lemma 2.1 yield that $\lim \limits _{t\rightarrow +\infty }N(x,t)=\mathbf{N} _{\epsilon }^{*}$ uniformly for $x\in [0,1]$, where $\mathbf{N} _{\epsilon }^{*}$ is the unique positive steady-state solution of (7.3). Just as Lemma 4.2, we can obtain that $0<\mathbf{N} _{\epsilon }^{*}<K_{1}-\frac{aK_{1}\epsilon }{r_{1}}$. Integrating the steady-state system of (7.3) over (0, x), easily we have both $(\mathbf{N} _{\epsilon }^{*})_{x}$ and $(\mathbf{N} _{\epsilon }^{*})_{xx}$ are uniformly bounded in [0, 1]. By $L^{p}$ estimates and Sobolev embedding theorem, we can deduce that $\mathbf{N} _{\epsilon }^{*}\rightarrow \theta _{1}$ as $\epsilon \rightarrow 0$. That is

$$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }N(x,t)\ge \theta _{1}\ \text{ uniformly } \text{ for }\ x\in [0,1]. \end{aligned}$$

(7.4)

It follows from (7.2) and (7.4) that (ii) holds.

(iii) Easily we have

$$\begin{aligned} P_{t}\ge d_{2}P_{xx}-q_2P_{x}+r_{2}P\left( 1-\frac{P}{K_{2}}\right) ,\ x\in (0,1),\ t>0 \end{aligned}$$

since the positive solution of (1.2) satisfies $N(x,t)>0$ and $P(x,t)>0$ for $x\in [0,1]$ and $t>0$. Let ${\hat{P}}(x,t)$ be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{P}}_{t}= d_{2}{\hat{P}}_{xx}-q_2{\hat{P}}_{x}+r_{2}{\hat{P}}(1-\frac{{\hat{P}}}{K_{2}}),&{} x\in (0,1),\ t>0,\\ d_{2}{\hat{P}}_{x}(0,t)-q_2{\hat{P}}(0,t)=0,\ {\hat{P}}_{x}(1,t)=0,&{} t>0,\\ {\hat{P}}(x,0)=P_{0}(x)\ge 0,\not \equiv 0, &{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

The comparison principle for parabolic equations yields that $P(x, t)\ge {\hat{P}}(x, t)$ for all $x\in [0,1],\ t>0$. Observe that the existence of $\theta _2$ means $q_2<q_{2}^{*}$. It follows from Lemma 2.1 that $\lim \limits _{t\rightarrow +\infty }{\hat{P}}(x,t)=\theta _{2}$ uniformly for $x\in [0,1]$. This implies that

$$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }P(x,t)\ge \theta _{2}\ \text{ uniformly } \text{ for }\ x\in [0,1]. \end{aligned}$$

(7.5)

Then for any $\epsilon >0$, there exists $T_{3}>0$ such that $P(x,t)>\theta _{2}-\epsilon$ for all $x\in [0,1],\ t\ge T_{3}$. Let ${\hat{N}}(x,t)$ satisfy the following equation,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{N}}_{t}=d_{1}{\hat{N}}_{xx}-q_1{\hat{N}}_{x}+r_{1}{\hat{N}}(1-\frac{{\hat{N}}}{K_{1}})-a{\hat{N}}(\theta _{2}-\epsilon ),&{} x\in (0,1),\ t\ge T_{3},\\ d_{1}{\hat{N}}_{x}(0,t)-q_1{\hat{N}}(0,t)=0,\ {\hat{N}}_{x}(1,t)=0,&{} t\ge T_{3},\\ {\hat{N}}(x,T_{3})=N(x,T_{3}),&{} x\in [0,1].\\ \end{array}\right. } \end{aligned}$$

It is not hard to know that $N(x,t)\le {\hat{N}}(x,t)$ for all $x\in [0,1],\ t\ge T_{3}$ by using the comparison principle. Since $\mu _{1}(d_1,q_1, r_1-a\theta _2)<0$, we can choose $\epsilon >0$ small enough such that $\mu _{1}(d_{1},q, r_{1}-a(\theta _{2}-\epsilon ))<0$. Similar arguments as in Lemma 2.1 yield that $\lim \limits _{t\rightarrow +\infty }{\hat{N}}(x,t)=0,\ x\in [0,1]$, thus $\lim \limits _{t\rightarrow +\infty }N(x,t)=0$ uniformly for $x\in [0,1]$. Therefore, for any $\epsilon >0$, there exists $T_{4}>T_{3}$ such that $N(x,t)<\epsilon$ for all $x\in [0,1],\ t\ge T_{4}$, which leads to

$$\begin{aligned} P_{t}\le d_{2}P_{xx}-q_2P_{x}+r_{2}P(1-\frac{P}{K_{2}})+eaP\epsilon ,\ x\in (0,1),\ t\ge T_{4}. \end{aligned}$$

Let ${\hat{P}}_{\epsilon }(x,t)$ be the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} ({\hat{P}}_{\epsilon })_{t}= d_{2}({\hat{P}}_{\epsilon })_{xx}-q_2({\hat{P}}_{\epsilon })_{x}+r_{2}{\hat{P}}_{\epsilon }(1-\frac{{\hat{P}}_{\epsilon }}{K_{2}})+ea\epsilon {\hat{P}}_{\epsilon },&{} x\in (0,1),\ t\ge T_{4},\\ d_{2}({\hat{P}}_{\epsilon })_{x}(0,t)-q_2{\hat{P}}_{\epsilon }(0,t)=0,\ ({\hat{P}}_{\epsilon })_{x}(1,t)=0,&{} t\ge T_{4},\\ {\hat{P}}_{\epsilon }(x,0)=P_{0}(x)\ge 0,\not \equiv 0, &{} x\in [0,1].\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(7.6)

The comparison principle implies $P(x,t)\le {\hat{P}}_{\epsilon }(x,t)$ for all $x\in [0,1],\ t\ge T_{4}$. Noting that $\mu _{1}(d_{2},q_2,r_{2})>0$ when $0\le q_2<q_{2}^{*}$, obviously we have that $\mu _{1}(d_{2},q_2,r_{2}+ea\epsilon )>0$. By similar arguments as in Lemma 2.1, we deduce that $\lim \limits _{t\rightarrow +\infty }P(x,t)={\hat{P}}_{\epsilon }^{*}$ uniformly for $x\in [0,1]$, where ${\hat{P}}_{\epsilon }^{*}$ is the steady-state solution of (7.6). Similar to Lemma 4.2, we get $0<{\hat{P}}_{\epsilon }^{*}<K_{2}+\frac{eaK_{2}\epsilon }{r_{2}}$. Integrating the steady-state system of (7.6) over (0, x), easily we have both $({\hat{P}}_{\epsilon }^{*})_{x}$ and $({\hat{P}}_{\epsilon }^{*})_{xx}$ are uniformly bounded in [0, 1]. By $L^{p}$ estimates and Sobolev embedding theorem, we can deduce that ${\hat{P}}_{\epsilon }^{*}\rightarrow \theta _{2}$ as $\epsilon \rightarrow 0$. That is

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }P(x,t)\le \theta _{2}\ \text{ uniformly } \text{ for }\ x\in [0,1]. \end{aligned}$$

(7.7)

It follows from (7.5) and (7.7) that (iii) holds.

(iv) To prove the uniform persistence of system (1.2), let $\Theta (t)$ be the solution semiflow generated by system (1.2) on the state space ${\mathbb {P}}$, where

$$\begin{aligned} {\mathbb {P}}=\{(N,P)\in C[0,1]\times C[0,1]: N\ge 0,\ P\ge 0,\ x\in [0,1]\}. \end{aligned}$$

Define

$$\begin{aligned} {\mathbb {P}}_{0}=\{(N,P)\in {\mathbb {P}}: N(x)\not \equiv 0\ \text{ and }\ P(x)\not \equiv 0\} \end{aligned}$$

and $\partial {\mathbb {P}}_{0}={\mathbb {P}}\setminus {\mathbb {P}}_{0}$. Let

$$\begin{aligned} M_{\partial }=\{(N_{0},P_{0})\in \partial {\mathbb {P}}_{0}: \Theta (t)(N_{0},P_{0})\in \partial {\mathbb {P}}_{0},\ \forall t\ge 0\} \end{aligned}$$

and $\omega ((N_{0},P_{0}))$ be the omega limit set of the forward orbit $\gamma ^{+}((N_{0},P_{0}))=\{\Theta (t)(N_{0},P_{0}): t\ge 0\}$. By the strong maximum principle of the parabolic equation, we conclude that ${\mathbb {P}}_{0}$ is open in ${\mathbb {P}}$ and forward invariant under the dynamics generated by system (1.2), and $\partial {\mathbb {P}}_{0}$ contains steady state points (0, 0), $(\theta _1,0)$ and $(0,\theta _{2}).$

We first claim that

$$\begin{aligned} \cup _{(N_{0},P_{0})\in M_{\partial }}\omega ((N_{0},P_{0}))\subset \{(0,0)\}\cup \{(\theta _{1},0)\}\cup \{(0,\theta _{2})\}. \end{aligned}$$

Indeed, for any given $(N_{0},P_{0})\in M_{\partial }$, we have $\Theta (t)(N_{0},P_{0})\in \partial {\mathbb {P}}_{0},\ \forall t\ge 0$. That is, $N(x,t,(N_{0},P_{0}))\equiv 0\ \text{ or }\ P(x,t,(N_{0},P_{0}))\equiv 0$ for each $x\in [0,1],\ t\ge 0$. Clearly, in the case where $N(x,t,(N_{0},P_{0}))\equiv 0$ for all $x\in [0,1],\ t\ge 0$, $P(x,t,(N_{0},P_{0}))$ satisfies the single species system (2.2). It follows from Lemma 2.1 that either $\lim \limits _{t\rightarrow +\infty }P(x,t)=0$, or $\lim \limits _{t\rightarrow +\infty }P(x,t)=\theta _{2}$, $x\in [0,1]$. In the case where $N(x,\tau _0,(N_{0},P_{0}))\not \equiv 0$ for $x\in [0,1]$ and some $\tau _0>0$, we have $N(x,t,(N_{0},P_{0}))>0$ for all $x\in [0,1],\ t>\tau _0$ by strong maximum principle, which implies that $P(x,t,(N_{0},P_{0}))\equiv 0$ for all $x\in [0,1],\ t>\tau _0$. Thus $N(x,t,(N_{0},P_{0}))$ is the solution of (2.1). By Lemma 2.1 we have that either $\lim \limits _{t\rightarrow +\infty }N(x,t)=0$, or $\lim \limits _{t\rightarrow +\infty }N(x,t)=\theta _1,\ x\in [0,1]$. Hence, $\cup _{(N_{0},P_{0})\in M_{\partial }}\omega ((N_{0},P_{0}))\subset \{(0,0)\}\cup \{(\theta _1,0)\}\cup \{(0,\theta _2)\}.$

We next claim that (0, 0), $(\theta _{1},0)$ and $(0,\theta _{2})$ are uniform weak repellers in the sense that

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }\Vert \Theta (t)(N_{0},P_{0})-(0,0)\Vert \ge \delta _{1}\ \text{ for } \text{ all }\ (N_{0},P_{0})\in {\mathbb {P}}_{0}, \end{aligned}$$

(7.8)

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }\Vert \Theta (t)(N_{0},P_{0})-(\theta _1,0)\Vert \ge \delta _{2}\ \text{ for } \text{ all }\ (N_{0},P_{0})\in {\mathbb {P}}_{0}, \end{aligned}$$

(7.9)

and

$$\begin{aligned} \limsup \limits _{t\rightarrow +\infty }\Vert \Theta (t)(N_{0},P_{0})-(0,\theta _{2})\Vert \ge \delta _{3}\ \text{ for } \text{ all }\ (N_{0},P_{0})\in {\mathbb {P}}_{0}. \end{aligned}$$

(7.10)

In fact, (7.8), (7.9) and (7.10) are equivalent to the linear instability of (0, 0), $(\theta _{1},0)$ and $(0,\theta _{2})$ respectively, which is guaranteed by the conditions $\mu _{1}(d_{1},q_1,r_{1}-a\theta _{2})>0$ and $\mu _{1}(d_{2},q_2,r_{2}+ea\theta _{1})>0$ (see Lemmas 5.1–5.3). For the detailed proof, please see Theorem 4.3 of Nie et al. (2020).

Now we define a continuous function ${\mathcal {D}}:{\mathbb {P}}\rightarrow [0,\infty )$ by

$$\begin{aligned} {\mathcal {D}}((N,P))=\min \limits _{x\in [0,1]}\{\min N(x),\ \min P(x)\}\ \text{ for } \text{ any }\ (N,P)\in {\mathbb {P}}. \end{aligned}$$

It follows from the standard comparison principle that ${\mathcal {D}}^{-1}(0,\infty )\subseteq {\mathbb {P}}_{0}$ and ${\mathcal {D}}$ satisfies that if ${\mathcal {D}}((N,P))>0\ \text{ or }\ (N,P)\in {\mathbb {P}}_{0}\ \text{ with }\ {\mathcal {D}}((N,P))=0$, then ${\mathcal {D}}(\Theta (t)(N,P))>0,\ \forall t>0$. That is, ${\mathcal {D}}$ is a generalized distance function for the semiflow $\Theta (t):{\mathbb {P}}\rightarrow {\mathbb {P}}$ (see Smith and Zhao 2001). It follows from Lemma 4.4 that $\Theta (t)$ is point dissipative on ${\mathbb {P}}$. Obviously, $\Theta (t):{\mathbb {P}}\rightarrow {\mathbb {P}}$ is compact for any $t>0$. By Theorem 2.6 of Magal and Zhao (2005), $\Theta (t):{\mathbb {P}}\rightarrow {\mathbb {P}},\ t\ge 0$ admits a global compact attractor. It follows from $\cup _{\Psi \in M_{\partial }}\omega (\Psi )\subset \{(0,0)\}\cup \{(\theta _{1},0)\}\cup \{(0,\theta _{2})\}$ that any forward orbit of $\Theta (t)$ in $M_{\partial }$ converges to (0, 0), $(\theta _{1},0)$ or $(0,\theta _{2})$. Recalling that (0, 0), $(\theta _{1},0)$ and $(0,\theta _{2})$ are uniform weak repellers (see (7.8) – (7.10)), we conclude that $\{(0,0)\},\ \{(\theta _{1},0)\}\text{ and }\ \{(0,\theta _{2})\}$ are isolated invariant sets in ${\mathbb {P}}$, and

$$\begin{aligned}&W^{S}\{(0,0)\}\cap {\mathcal {D}}^{-1}(0,\infty )=\emptyset ,\ W^{S}\{(\theta _{1},0)\}\cap {\mathcal {D}}^{-1}(0,\infty )\\&\quad =\emptyset \ \text{ and } \ W^{S}\{(0,\theta _{2})\}\cap {\mathcal {D}}^{-1}(0,\infty )=\emptyset . \end{aligned}$$

Here $W^{S}\{(0,0)\}$, $W^{S}\{(\theta _{1},0)\}$ and $W^{S}\{(0,\theta _{2})\}$ are the stable sets of (0, 0), $(\theta _{1},0)$ and $(0,\theta _{2})$, respectively (see Hale and Waltman 1989; Smith and Zhao 2001). Furthermore, no subsets of $\{(0,0)\}\cup \{(\theta _{1},0)\}\cup \{(0,\theta _{2})\}$ form a cycle in $\partial {\mathbb {P}}_0$. By Theorem 3 of Smith and Zhao (2001), there exists $\eta >0$ such that for any $(N_{0},P_{0})\in {\mathbb {P}}_{0},$

$$\begin{aligned} \min \limits _{(N_{0},P_{0})\in \omega ((N,P))}{\mathcal {D}}((N_{0},P_{0}))>\eta . \end{aligned}$$

This implies that for any $(N,P)\in {\mathbb {P}}_{0},\ \liminf \limits _{t\rightarrow +\infty }N(x,t)\ge \eta \ \text{ and }\ \liminf \limits _{t\rightarrow +\infty }P(x,t)\ge \eta ,\ x\in [0,1].$

It follows from Theorem 3.7 and Remark 3.10 of Magal and Zhao (2005) that $\Theta (t):{\mathbb {P}}_0\rightarrow {\mathbb {P}}_0$ admits a global attractor $A_0$. Then by Theorem 4.7 of Magal and Zhao (2005), we conclude that $\Theta (t)$ admits at least one steady-state solution $({\bar{N}}(\cdot ),{\bar{P}}(\cdot ))\in {\mathbb {P}}_0$. Furthermore, we deduce that ${\bar{N}}(\cdot ), {\bar{P}}(\cdot )>0$ by the strong maximum principle (see Protter and Weinberger 1984). Thus, system (1.2) admits at least one positive steady state solution $({\bar{N}}(\cdot ),{\bar{P}}(\cdot ))$. The uniqueness of positive steady state to system (1.2) follows from similar arguments as in Step 3 of Theorem 3.1 of Nie et al. (2020), see also the proof of Lemma 3.3 and Theorem 3.4 of Nie et al. (2015). $\square$