1 Introduction

The question of why individuals disperse has fascinated ecologists and evolutionary biologists for many decades now. Many different models were studied; we focus on reaction-diffusion equations. Starting with the work by Hastings (1983), one robust prediction of these models is that slow diffusion should evolve in temporally constant but spatially variable environments, as long as dispersal is completely random; see also Dockery et al. (1998). The intuitive explanation for this phenomenon is that slower dispersal allows individuals to better track favorable environmental conditions whereas fast dispersal moves individuals away from favorable regions. When individuals can sense and follow gradients in resource distribution, i.e. when movement consists of random (diffusion) and directed (taxis) components, then the situation changes. For a given strength of taxis, faster—but not too fast—dispersal can be beneficial. The intuitive explanation here is that individuals can become ‘too good’ at tracking favorable regions; the population is overcrowded at only the best quality locations and misses other, reasonably beneficial areas. Faster dispersal can help individuals spread out to these regions as well. Too high dispersal rates, however, dilute the positive effect of taxis, and a population only accesses some averaged resource density. Consequently, for a given strength of taxis, some intermediate diffusion rate should be selected. Alternatively, for a given diffusion rate, there are limits to the benefits of taxis upwards resource gradients. The intuitive explanation is that if taxis is too strong, then the population might miss reasonably beneficial areas and fail to exclude a competing population. We refer to Cantrell et al. (2007), Chen et al. (2012), Hambrock and Lou (2009), Lam and Lou (2013) and references therein for more details.

More recently, there is growing interest in modeling and understanding spatial population dynamics in advective environments, i.e. environments where individuals are exposed to unidirectional flow or biased dispersal (McKenzie et al. 2012). Examples include streams and rivers, coastlines with dominant longshore current, lake water columns with gravitational downward pull, and moving environments such as an oasis in the desert, moved by wind, or a favorable climate zone, moved by global warming. We will describe these examples in detail later. Note that the term ‘advection’ was used in a series of works (Belgacem and Cosner 1995; Cantrell et al. 2006; Chen and Lou 2008; Cosner and Lou 2003; Lam 2011, 2012; Lam and Ni 2010) to indicate movement towards better quality habitat, sometimes also named taxis. In this work, we strictly refer to advection as constant, unidirectional bias of movement.

Unidirectional bias in movement will push individuals away from favorable locations, and this effect could be a mechanism that negatively impacts slow dispersers. Unidirectional flow can also induce a net loss of individuals from a given patch. Random dispersal can have the same effect, but slower dispersers should experience smaller loss and, hence, be favored. There are, thus, a number of different effects to consider when exploring the effect of advection on the evolution of dispersal. In this work, we consider several scenarios that explicitly include downstream loss of individuals. Different assumptions about this loss lead to different boundary conditions. In all cases. we show that advection puts slow dispersers at a disadvantage. We begin with an overview of various biological scenarios and resulting boundary conditions in the following section, where we describe our modeling approach.

2 Modeling

We follow the standard modeling framework and consider a system of reaction-diffusion equations for two logistically growing and competing species that differ only in their diffusion rate; (see Dockery et al. 1998). We denote the densities of the two species at time \(t\) and location \(x\) in the bounded interval \([0,L]\) by \(u\) and \(v\), respectively. The equations read

$$\begin{aligned} \begin{aligned} u_t&=d_1 u_{xx}-q u_x+u(r(x)-u-v), \quad 0<x<L, \ t>0, \\ v_t&=d_2 v_{xx}-q v_x+v(r(x)-u-v), \quad 0<x<L, \ t>0. \end{aligned} \end{aligned}$$
(1)

The function \(r(x)\) stands for the quality of the habitat; the population can grow where \(r>0\) and will decline where \(r<0\). Diffusion rates are positive, i.e. \(d_i>0\), and advection points towards larger \(x\), i.e. \(q\ge 0\). Subscripts denote partial derivatives. In analogy with rivers, we call \(x=0\) the upstream end and \(x=L\) the downstream end of the habitat. We have to prescribe boundary conditions at the upstream and downstream end. We motivate several possible choices by different ecological scenarios.

2.1 Periphyton in the water column

Gravity pulls algae in a lake or ocean towards the bottom (advection), whereas buoyancy allows for upward movement (diffusion) (Huisman et al. 2002; Kolokolnikov et al. 2009). The upstream boundary is the water surface, the downstream boundary is the ground. Neither boundary allows individuals to pass through, hence, we impose no-flux conditions for both. Note that the flux in Eq. (1) contains a diffusive and advective component, i.e. we have

$$\begin{aligned} d_1 u_{x}-q u=0 \quad \text {and} \quad d_2v_x-qv=0 \quad \text {for} \quad x\in \{0,L\}. \end{aligned}$$
(2)

We refer to this situation as no-flux/no-flux, or NF/NF for short.

2.2 Stream to lake

Water flow imposes directional bias (advection), buoyancy and turbulence contribute to unbiased movement (diffusion) (Speirs and Gurney 2001). When the stream flows into a freshwater lake, individuals can enter the downstream end of the stream from the lake by diffusion. The flux into the lake is only the advective flux, the diffusive flux into and from the lake balances (Vasilyeva and Lutscher 2011). Hence, we have the downstream condition

$$\begin{aligned} u_x(L)=0, \quad v_x(L)=0. \end{aligned}$$
(3)

Together with the no-flux upstream conditions, we obtain the so-called Danckwerts conditions. We refer to this as no-flux/free-flow or NF/FF for short.

2.3 Stream to ocean

When individuals do not return into the patch after leaving at the downstream end, we obtain hostile downstream conditions:

$$\begin{aligned} u(L)=0, \quad v(L)=0. \end{aligned}$$
(4)

For example, most freshwater organisms die when they reach the ocean. These downstream conditions were originally proposed in Speirs and Gurney (2001). In combination with no-flux upstream conditions as in (2), we refer to this situation as no-flux/hostile or NF/H for short. There is some discussion as to whether a waterfall would create FF or H conditions downstream. Both of these conditions have been derived from a random walk model in terms of leaving probabilities (Lutscher et al. 2006).

2.4 Moving patch

In some situations, there is no directional bias in individual movement, but the environmental conditions shift. For example, an oasis in a desert shifts location as sand dunes are moved by wind (Dahmen et al. 2000; Desai and Nelson 2005). Another example is the poleward shift of temperature isoclines due to global warming (Berestycki et al. 2009; Berestycki and Rossi 2008; Leroux et al. 2013; Potapov and Lewis 2004). If the patch moves at a constant speed then changing to a moving coordinate frame will fix the patch in space and introduce an advective term as in (1). The choice of boundary conditions depends on the quality of the area surrounding the moving patch and the behavior of individuals at the interface between the two (Maciel and Lutscher 2013; Ovaskainen and Cornell 2003). In the extreme case of a hostile exterior, we impose the hostile conditions (4) at the upstream and downstream ends, and we refer to this case as hostile/hostile or H/H.

In general, and including all boundary conditions mentioned so far, we can write Robin-type boundary conditions where we link the flux to the density as

$$\begin{aligned} d_1 u_x-q u&= b_u q u \;\; \text {for}\;\; x=0, \nonumber \\ d_1 u_x-q u&= -b_d q u\;\; \text {for}\;\; x=L. \end{aligned}$$
(5)

Dimensionless parameters \(b_u\) and \(b_d\) measure the rate, relative to flow rate, at which individuals leave the domain at the upstream and downstream conditions, respectively; (see Lutscher et al. 2006) for a detailed derivation. For \(b_d=0\), we have the no-flux conditions (2), for \(b_d=1\), we obtain the free-flow conditions (3) and for \(b_d\rightarrow \infty \), we see hostile conditions (4).

2.5 Rotating mask

Bacteria can be grown in an annulus in a petri dish, and can be exposed to different growth conditions by radiation and protective shading via an opaque mask (Lin et al. 2004). Making this mask rotate will lead, via a change of coordinates as previously mentioned, to effective advection and periodic boundary conditions

$$\begin{aligned} u(0)=u(L),\quad u_x(0)=u_x(L), \quad \text {and} \quad v(0)=v(L),\quad v_x(0)=v_x(L). \end{aligned}$$
(6)

If at least one of \(b_u, b_d\) is positive, then there is a net loss of individuals from the domain. The study of population dynamical consequences of advection-induced loss began with the work in Murray and Sperb (1983). We present the first analysis of advection-induced consequences for the evolution of dispersal. We focus on the NF/H and NF/FF boundary conditions, i.e., advection will induce a net of loss of individuals from the habitat. Our goal is to illustrate that for both scenarios, the unidirectional flow can put slow dispersers at a disadvantage and a higher dispersal rate can evolve. The case of no boundary loss, i.e. NF/NF or periodic conditions is more subtle and will be considered elsewhere.

Our paper is organized as follows: in Sect. 3, we use a spatially implicit approximation of model (1) to gain some insights into the evolutionary dynamics that we can expect and to introduce some notation from the theory of adaptive dynamics. We begin the analysis of the spatially explicit model in Sect. 4, where we study persistence conditions of a single species in an advective environment with boundary loss, and we establish the existence of a critical value for the advection speed. In Sect. 5, we derive a formula for the invasion exponent for general boundary conditions (5) and perform a linear stability analysis of the semi-trivial steady state with NF/FF boundary conditions when the growth rate is a constant or linear function. In Sect. 6, we show that in a homogeneous advective environment with NF/FF boundary conditions, populations with higher dispersal rate will always displace populations with slower dispersal rate. We conclude with a summary and some biological insights, and we list future challenges that emerge from our work.

3 A spatially implicit model

Before we begin the detailed analysis of the infinite-dimensional dynamical system in (1), we use a spatially implicit, two-dimensional approximation to gain some insights into the potential evolutionary dynamics of dispersal and to introduce some of the terminology from the framework of adaptive dynamics that we will use later on. We assume that conditions inside the habitat patch \([0,L]\) are homogeneous, i.e. \(r\) is a constant. We then replace the advection–diffusion operator in (1) with a net loss rate derived from the dominant eigenvalue of the advection–diffusion operator. The underlying idea is that since the advection–diffusion operator will account for net loss from the patch, one replaces this operator with a simple linear death term that captures the average time spent in the patch.

More precisely, instead of system (1) we study the system

$$\begin{aligned} u_t&= -\nu _1 u+u(r-u-v), \nonumber \\ v_t&= -\nu _2 v+v(r-u-v), \end{aligned}$$
(7)

where \(\nu _i:=\nu (d_i)>0\) is the dominant eigenvalue of the advection–diffusion operator, satisfying

$$\begin{aligned} d_i u_{xx}-q u_x=-\nu (d_i) u=-\nu _i u \end{aligned}$$
(8)

on \([0,L]\) with boundary conditions (5). This number can be interpreted as the inverse of the residence time in the patch (Ballyk et al. 1998). Working with the so-derived spatially implicit model has recently been successfully applied to study population (rather than evolutionary) dynamics in a competition model (Vasilyeva 2011; Vasilyeva and Lutscher 2012a, b) and in a predator–prey model (Strohm and Tyson 2012). A more formal derivation via occupancy times was given in Cobbold and Lutscher (2013).

The ecological dynamics of the model in (7) are simple. There are two semi-trivial states \((u^*,0)=(r-\nu _1,0)\), and \((0,v^*)=(0,r-\nu _2)\), provided \(\nu _1<r\), and \(\nu _2<r\), respectively. The linearized growth rate of species \(v\) at \((u^*,0)\) is given by \(\nu _1-\nu _2\). The species can invade the semi-trivial state exactly if this quantity is positive. Mutual invasibility of the semi-trivial states implies stable coexistence of the two species; invasibility without mutual invasibility implies replacement.

To consider the evolution of dispersal, in the sense of adaptive dynamics (Dieckmann 1997), we choose the diffusion rate as the “trait” and assume a monomorphic “resident” population at equilibrium \((u^*,0)\) with trait value \(d_1=d_\mathrm{res}\). A potential mutant with trait value \(d_\mathrm{inv}=d_2\) can invade the resident if the invasion exponent \(\Lambda (d_1,d_2)=\nu _1-\nu _2=\nu (d_1)-\nu (d_2)\) is positive, i.e. if the loss rate from the patch is larger for the resident than for the invading species. Based on the dynamics of the ecological model, the species with the smaller loss rate will invade and replace the species with the larger loss rate; coexistence is impossible. Assuming that the mutant trait value is close to the resident trait value, the selection gradient

$$\begin{aligned} \frac{\partial \Lambda (d_1,d_2)}{\partial d_2}\big |_{d_2=d_1}=\frac{ \partial (\nu (d_1)-\nu (d_2))}{\partial d_2}\big |_{d_2=d_1}=-\nu '(d_1) \end{aligned}$$
(9)

gives the direction of the evolutionary dynamics. If the invasion exponent is negative, then evolution will tend towards smaller dispersal rates, and vice versa. It remains to study how the eigenvalue \(\nu \) in (8) depends on the dispersal parameter \(d\).

As the simplest case where all expressions can be given explicitly, we consider hostile boundary conditions at either end of the domain (denoted as H/H). The dominant eigenvalue of (8) is

$$\begin{aligned} \nu (d)=\frac{q^2}{4d}+\frac{d\pi ^2}{L^2}. \end{aligned}$$
(10)

When \(q=0\), then \(-\nu '(d)=-\pi ^2/L^2<0\), so that evolution will favor smaller dispersal rates. When \(q>0\), then \(-\nu ''(d)>0\) and there is a unique intermediate critical point where \(\nu '(d^*)=0\). This point, given explicitly by \(d^*=\frac{qL}{2\pi }\), is a singular strategy for the adaptive dynamics (Dieckmann 1997). Furthermore, we can calculate that this singular strategy is immune to nearby invasion (a local ESS), it is attainable, it can invade its neighbors, and there is no mutual invasibility nearby (see Dieckmann 1997) for definitions of these terms and mathematical conditions.

More challenging is the case of NF/H conditions. The dominant eigenvalue is now

$$\begin{aligned} \nu =\frac{q^2}{4d}+ dm^2, \end{aligned}$$
(11)

where \(m\) is the smallest positive solution of the transcendental equation \(2dm=-q\tan (mL)\). Geometric considerations show that \(\pi <2Lm<2\pi \) and \(m'(d)<0\). Numerical root finding shows that \(\nu \) is convex for NF/H conditions, just like it was for H/H conditions. Therefore, the conclusion is the same as in the H/H case: there is a unique minimum \(d^*\) for \(\nu \), and this minimum constitutes an ESS that is convergent stable and no mutual invasion occurs nearby.

In the case of NF/FF boundary conditions, we obtain \(\nu \) as in (11), but the defining equation for \(m\) is \(4mdq=-(q^2-4m^2d^2)\tan (mL)\). Figure 1 gives a comparison between the three different scenarios. In the H/H and NF/H case, the eigenvalue has a unique minimum, which turns out to be the local ESS. In the NF/FF conditions, the eigenvalue decreases monotonically to zero as \(d\rightarrow \infty ;\) larger dispersal rates evolve.

Fig. 1
figure 1

The dominant eigenvalue as a function of dispersal rate \(d\) for H/H boundary conditions (dash–dot), for NF/H conditions (dashed) and for NF/FF conditions (solid). Parameters are \(q=1, L=10\)

Full size image

While the ecological and evolutionary dynamics for the spatially implicit model are relatively easy to establish, the corresponding results for the spatially explicit model pose considerable analytical challenges. We need to establish conditions for a single-species steady state when the growth rate \(r\) is not a constant and find the dependence of the invasion exponent or selection gradient on the diffusion rate. It turns out that the dependence of the invasion exponent on the advection rate \(q\) is somewhat easier to determine and yields biologically relevant results. For that reason, we focus on that parameter in the next section and return to the dependence on the diffusion rates later.

4 Persistence of a single species

In this section, we consider the conditions for the existence of a single-species steady state \((u^*(x),0)\) of system (1). For NF/H boundary conditions, this state satisfies the equation

$$\begin{aligned}&d u_{xx}^* - q u_x^*+u^*[r(x)-u^*]=0, \quad 0<x<L, \nonumber \\&d u^*_x(0)-qu^*(0)=u^*(L)=0. \end{aligned}$$
(12)

For NF/FF boundary conditions, it satisfies

$$\begin{aligned}&d u_{xx}^* - q u_x^*+u^* [r(x)-u^*]=0, \quad 0<x<L, \nonumber \\&d u^*_x(0)-q u^*(0)=u_x^*(L)=0. \end{aligned}$$
(13)

Since the single equation for \(u\) in (1) is monotone, existence and uniqueness of a positive steady state for (12) and (13) is equivalent to the zero solution being linearly unstable (see, e.g. Cantrell and Cosner 2003). Hence, we will study conditions for the dominant eigenvalue, denoted as \(\lambda _1=\lambda _1(q)\), of the following problems to be positive:

$$\begin{aligned}&d \phi _{xx} - q \phi _x+\phi r(x)=\lambda \phi ,\quad 0<x<L, \nonumber \\&d\phi _x(0)-q\phi (0)=\phi (L)=0 \end{aligned}$$
(14)

for NF/H boundary conditions and

$$\begin{aligned}&d \phi _{xx} - q \phi _x+\phi r(x)=\lambda \phi ,\quad 0<x<L, \nonumber \\&d\phi _x(0)-q\phi (0)=\phi _x(L)=0 \end{aligned}$$
(15)

for NF/FF boundary conditions.

While \(\lambda _1(q)\) also depends on the function \(r\) and the values of \(d\) and \(L\), we restrict our discussions to its dependence on \(q\). The main result for this section is

Theorem 4.1

Let \(\lambda _1(q)\) denote the dominant eigenvalue of (14) or (15). If \(\lambda _1(0)\le 0\), then \(\lambda _1(q)<0\) for any \(q>0\); If \(\lambda _1(0)>0\), then there exists some \(q^*>0\) such that \(\lambda _1(q)>0\) for \(q<q^*\) and \(\lambda (q)<0\) for \(q>q^*\).

We give the proof of this theorem for the two cases NF/H and NF/FF separately in the following two subsections.

Remark 4.2

When \(r\) is a positive constant, for NF/H conditions, \(\lambda _1(0)>0\) if and only if \(L>\frac{\pi }{2}\sqrt{\frac{d}{r}}\). From Speirs and Gurney (2001), \(q^*\) is the unique positive root of \(L=L_c(q)\) for \(L>\frac{\pi }{2}\sqrt{\frac{d}{r}}\), where

$$\begin{aligned} L_c(q):=\frac{\pi -\arctan \left( \frac{\sqrt{4rd-q^2}}{q} \right) }{\frac{\sqrt{4rd-q^2}}{2d}} \end{aligned}$$
(16)

is a strictly increasing function of \(q\in [0, 2\sqrt{d r})\), with the range \([\frac{\pi }{2}\sqrt{\tfrac{d}{r}}, \infty )\). For NF/FF conditions, similar conclusions can be drawn from the results in Vasilyeva and Lutscher (2011).

For the H/H case, Eq. (26) of Berestycki et al. (2009) gives the critical length as

$$\begin{aligned} L_c^H(q)=\frac{2d\pi }{\sqrt{4rd-q^2}}. \end{aligned}$$

We observe that, \(L_c(q)<L_c^H(q)\) for all \(q\). This result confirms the biological intuition that it is easier for a species to persist when the upstream conditions are no-flux rather than hostile.

Both critical lengths are strictly monotone increasing in \(q\) and approach infinity as \(q\rightarrow 2\sqrt{d r}\). Interestingly, their ratio

$$\begin{aligned} \frac{L_c(q)}{L_c^H(q)}=1-\frac{1}{\pi } \arctan \left( \frac{\sqrt{4d r-q^2}}{q}\right) \end{aligned}$$

is a strictly monotone increasing function of \(q\) and it satisfies

$$\begin{aligned} \lim _{q\rightarrow 0}\frac{L_c(q)}{L_c^H(q)}=\frac{1}{2}, \quad \quad \lim _{q\rightarrow 2\sqrt{d r}}\frac{L_c(q)}{L_c^H(q)}=1. \end{aligned}$$

Hence, increasing advection will lessen the difference between the effects of the no-flux condition and the hostile condition at the upper stream on the persistence of a single species.

Remark 4.3

When the population can persist for \(q=0\), then it can persist for \(q\) in some interval \([0,q^*)\). An upper bound for \(q^*\) can be obtained by considering the eigenvalue problems (14) and (15) with \(r(x)\) replaced by \(r^*=\max r\). This calculation with NF/H conditions was presented in Speirs and Gurney (2001) and for NF/FF conditions in Vasilyeva and Lutscher (2011). In both cases, we find \(q^*<2\sqrt{d\max r}\).

Since the single equation for \(u\) in (1) is monotone and it is of the logistic type, as a consequence of Theorem 4.1 we have

Corollary 4.4

Let \(\lambda _1(0)\) denote the dominant eigenvalue of (14) [or (15)] with \(q=0\).

  1. 1.

    If \(\lambda _1(0)\le 0\), then \(u=0\) is globally asymptotically stable among all solutions of

    $$\begin{aligned} u_t=d u_{xx}-q u_x+u(r-u), \quad 0<x<L, \quad \ t>0, \end{aligned}$$
    (17)

    with non-negative and not identically zero initial data, subject to NF/H boundary conditions (NF/FF boundary conditions, respectively).

  2. 2.

    If \(\lambda _1(0)>0\), then there exists \(q^*>0\) such that for \(q\ge q^{*},\,u=0\) is globally asymptotically stable among all solutions of (17); For \(q<q^*\), there is a unique positive steady state of (12) [(13), respectively], which is globally asymptotically stable.

Part 1 says that for both NF/H and NF/FF boundary conditions, if the population can not persist without advection, then it can not persist with any advection. Part 2 implies that if the population can persist without advection, there exists a critical advection speed such that the population can persist if and only if the advection speed is less than the critical value.

We briefly outline the proof of Part 2: (i) When \(q<q^*\), combining Theorem 3.1 and Proposition 3.1 of Cantrell and Cosner (2003), we see that Eq. (12) has no positive solution and all non-negative solutions of (17) decay exponentially to zero as \(t\rightarrow \infty \). (ii) Since the reaction term in (17) is of logistic type, it is standard to show that any positive steady state of (17), if exists, is linearly stable (Cantrell and Cosner 2003). When \(q=q^*\), we first show that (12) has no positive solution. If (12) had a positive solution for \(q=q^*\), the implicit function theorem would imply that (12) has positive solution for any \(q\) close to \(q^*\), which contradicts our conclusion for the case \(q<q^*\). By the monotone dynamical system theory (Smith 1995) \(u=0\) is globally asymptotically stable. (iii) For \(q>q^*\), by the supersolution and subsolution method Eq. (12) has a unique positive solution which is globally asymptotically stable.

In the following and as well for the rest of the paper, all integrals are definite integrals over the interval \([0,L]\), unless otherwise specified.

4.1 NF/H boundary conditions

For NF/H boundary conditions, Theorem 4.1 follows from the following two results.

Lemma 4.5

The dominant eigenvalue of (14) is a strictly decreasing function of \(q\).

Proof

We use the transformation \(\phi =e^{\alpha x}\psi \), where \(\alpha =q/d\). Then Eq. (14) becomes

$$\begin{aligned} d \psi _{xx}+q\psi _x+r\psi =\lambda _1 \psi \quad 0<x<L,\quad \psi _x(0)=0,\quad \psi (L)=0, \end{aligned}$$
(18)

where \(\psi >0\) is uniquely determined by the normalization \(\int \psi ^2\, dx=1\). By the implicit function theorem, \(\psi \) is a smooth function of \(q\) from \({\mathbb {R}}\) into \(C^2([0,L])\) (Belgacem and Cosner 1995). Now we differentiate with respect to \(q\) and denote \(\frac{\partial }{ \partial q}='\). We obtain

$$\begin{aligned} d \psi '_{xx}+\psi _x + q\psi '_x+r\psi '=\lambda _1'\psi +\lambda _1\psi ' \quad \! 0<x<L, \quad \psi '_x(0)=0, \quad \psi '(L)=0.\nonumber \\ \end{aligned}$$
(19)

Next, we multiply (18) by \(e^{\alpha x} \psi '\) and (19) by \(e^{\alpha x} \psi \), and then integrate and subtract the two equations. We obtain

$$\begin{aligned} d\left[ \psi e^{\alpha x} \psi '_x\big |_0^L-\psi ' e^{\alpha x} \psi _x\big |_0^L\right] +\int e^{\alpha x}\psi \psi _x dx=\lambda _1'\int e^{\alpha x}\psi ^2 dx. \end{aligned}$$
(20)

The boundary terms together with the boundary conditions give

$$\begin{aligned} \psi e^{\alpha x} \psi '_x\big |_0^L-\psi ' e^{\alpha x} \psi _x\big |_0^L=0. \end{aligned}$$
(21)

We integrate the first integral in Eq. (20) by parts and apply \(\psi (L)=0\) to obtain

$$\begin{aligned} \int e^{\alpha x}\psi \psi _x dx=\int e^{\alpha x}\left( \frac{\psi ^2}{2}\right) _x dx= -\frac{\psi ^2(0)}{2}-\frac{q}{d}\int e^{\alpha x}\frac{\psi ^2}{2} dx. \end{aligned}$$
(22)

Therefore, we have

$$\begin{aligned} \lambda _1'=-\frac{\frac{\psi ^2(0)}{2}+\frac{q}{d}\int e^{\alpha x}\frac{\psi ^2}{2} dx}{\int e^{\alpha x}\psi ^2 dx}<0. \end{aligned}$$
(23)

This completes the proof. \(\square \)

Lemma 4.6

Let \(\lambda _1\) denote the dominant eigenvalue of (14). Then, \(\lim _{q\rightarrow \infty } \lambda _1=-\infty \).

Proof

Without loss of generality set \(d=1\). Multiplying (12) by \(e^{q x}\) we can rewrite the equation as

$$\begin{aligned} \left( e^{ q x} \psi _x\right) _x+e^{qx}\psi =\lambda _1 e^{q x}\psi , \quad 0<x<L, \quad \psi _x(0)=\psi (L)=0. \end{aligned}$$

By (18) and the variational characterization of the dominant eigenvalue (e.g. in Cantrell and Cosner 2003) we have

$$\begin{aligned} -\lambda _1=\inf _{\varphi \in S} \frac{\int e^{q x} \left( \varphi _x^2-r\varphi ^2\right) \, dx}{\int e^{q x} \varphi ^2\, dx}, \end{aligned}$$

where \(S=\{\varphi \in C^1([0, L]): \varphi \not \equiv 0, \ \varphi (L)=0\}\). Set \(\psi =e^{(q/2)x} \varphi \). Then

$$\begin{aligned} -\lambda _1&= \inf _{\psi \in S} \frac{\int \left[ (\psi _x -\frac{q}{2}\psi )^2 -r\psi ^2\right] \, dx}{\int \psi ^2\,dx} \\&= \inf _{\psi \in S} \frac{\int \left( \psi _x^2-q\psi \psi _x -r\psi ^2\right) \, dx}{\int \psi ^2\, dx}+\frac{q^2}{4} \\&= \inf _{\psi \in S} \frac{\int \left( \psi _x^2 -r\psi ^2\right) \,dx +\frac{q}{2}\psi ^2(0)}{\int \psi ^2\, dx}+\frac{q^2}{4}\\&\ge \frac{q^2}{4}-\max r. \end{aligned}$$

This completes the proof. \(\square \)

Remark 4.7

The two Lemmas in this subsection also hold in the case of hostile upstream and downstream boundary conditions. The boundary conditions in Eqs. (18) and (19) change to \(\psi (0)=\psi (L)=0\) and \(\psi '(0)=\psi '(L)=0\), respectively. In expressions (22) and (23), the term \(\psi ^2(0)\) vanishes. The set \(S\) is modified to include the zero upstream boundary in its definition.

4.2 NF/FF boundary conditions

For NF/FF boundary conditions, Theorem 4.1 follows from the following two results.

Lemma 4.8

The dominant eigenvalue of (15) is a strictly decreasing function of \(q\).

Proof

We use the transformation \(\phi =e^{\alpha x}\psi \), where \(\alpha =q/d\). Then the equation becomes

$$\begin{aligned} d \psi _{xx}+q\psi _x+r\psi =\lambda _1\psi \quad 0<x<L,\quad \! \psi _x(0)=0,\quad \! d\psi _x(L)=- q\psi (L),\quad \quad \end{aligned}$$
(24)

where \(\psi >0\) is uniquely determined by \(\int \psi ^2\, dx=1\). Now we differentiate with respect to \(q\) and denote \(\frac{\partial }{ \partial q}='\). We obtain

$$\begin{aligned} d \psi '_{xx}+\psi _x + q\psi '_x+r\psi '&= \lambda _1'\psi +\lambda _1\psi ' \quad 0<x<L,\quad \psi '_x(0)=0, \nonumber \\ d\psi '_x(L)&= -q \psi '(L)-\psi (L). \end{aligned}$$
(25)

Next, we multiply (24) by \(e^{\alpha x} \psi '\) and (25) by \(e^{\alpha x} \psi \), and then integrate and subtract the two equations. We obtain

$$\begin{aligned} d\left[ \psi e^{\alpha x} \psi '_x\big |_0^L-\psi ' e^{\alpha x} \psi _x\big |_0^L\right] +\int e^{\alpha x}\psi \psi _x dx=\lambda _1' \int e^{\alpha x}\psi ^2 dx. \end{aligned}$$
(26)

The boundary terms together with the boundary conditions give

$$\begin{aligned} d\left[ \psi (L)\psi '_x(L)e^{\alpha L}-\psi (0)\psi '_x(0)-\psi '(L)\psi _x(L)e^{\alpha L}+\psi '(0)\psi _x(0)\right] =-e^{\alpha L} \psi ^2(L).\nonumber \\ \end{aligned}$$
(27)

We integrate the first integral in Eq. (26) by parts

$$\begin{aligned} \int e^{\alpha x}\psi \psi _x dx=\int e^{\alpha x}\left( \frac{\psi ^2}{2}\right) _x dx= e^{\alpha L} \frac{\psi ^2(L)}{2}-\frac{\psi ^2(0)}{2}-\frac{q}{d}\int e^{\alpha x}\frac{\psi ^2}{2} dx.\nonumber \\ \end{aligned}$$
(28)

Therefore, by (26), (27) and (28) we have

$$\begin{aligned} \lambda _1'=-\frac{e^{\alpha L} \frac{\psi ^2(L)}{2}+\frac{\psi ^2(0)}{2}+\frac{q}{d}\int e^{\alpha x}\frac{\psi ^2}{2} dx}{\int e^{\alpha x}\psi ^2 dx}<0. \end{aligned}$$
(29)

This completes the proof. \(\square \)

Lemma 4.9

Let \(\lambda _1\) denote the dominant eigenvalue of (15). Then, \(\lim _{q\rightarrow \infty } \lambda _1=-\infty \).

Proof

Without loss of generality assume that \(d=1\). By (24) and the variational characterization of the dominant eigenvalue we have

$$\begin{aligned} -\lambda _1=\inf _{\varphi \in S} \frac{\int e^{q x} \left( \varphi _x^2-r\varphi ^2\right) \, dx+q e^{q L} \varphi ^2(L)}{\int e^{q x} \varphi ^2\, dx}, \end{aligned}$$

where \(S=\{\varphi \in C^1([0, L]): \varphi \not \equiv 0\}\). Set \(\psi =e^{(q/2)x} \varphi \). Then

$$\begin{aligned} -\lambda _1&= \inf _{\psi \in S} \frac{\int \left[ (\psi _x -\frac{q}{2}\psi )^2 -r\psi ^2\right] \, dx+q \psi ^2(L) }{\int \psi ^2\, dx} \\&= \inf _{\psi \in S} \frac{\int \left( \psi _x^2-q\psi \psi _x -r\psi ^2\right) \, dx +q \psi ^2(L)}{\int \psi ^2\, dx}+\frac{q^2}{4} \\&= \inf _{\psi \in S} \frac{\int \left( \psi _x^2 -r\psi ^2\right) \, dx +\frac{q}{2}\psi ^2(L)+\frac{q}{2}\psi ^2(0)}{\int \psi ^2\, dx}+\frac{q^2}{4} \\&\ge \frac{q^2}{4}-\max r. \end{aligned}$$

This completes the proof. \(\square \)

Remark 4.10

The two lemmas proved in this subsection also hold in the case of general boundary conditions (5), provided \(b_d>1/2\). In other words, the outflow at the downstream end has to be at least half of the advective flow to make these estimates work. The changes to the proofs above are as follows. The boundary conditions in (24) change to \(d\psi _x(0)=b_u q \psi (0)\) and \(d \psi _x(L)=-b_d q \psi (L)\), whereas the conditions in (25) become

$$\begin{aligned} d\psi '_x(0)=b_u \psi (0) + b_u q \psi '(0), \quad d\psi '_x(L)=-b_d \psi (L) - b_d q \psi '(L). \end{aligned}$$

Evaluating the boundary terms in (26) results in the expression \(-b_d e^{\alpha L}\psi ^2(L)-b_u\psi ^2(0)\). The numerator in (29) becomes

$$\begin{aligned} (b_d-1/2)e^{\alpha L} \psi ^2(L)+(b_u+1/2)\psi ^2(0)+\frac{q}{d}\int e^{\alpha x}\frac{\psi ^2}{2} dx, \end{aligned}$$

which is positive if \(b_d>1/2\).

5 Invasion analysis

In this section, we perform a linear stability analysis of the steady state \((u^*, 0)\); the results shed light onto the global dynamics of our problem as well. The linearized equation for \(v\) decouples [(e.g., modifying the proof of Lemma 5.5 in Chen et al. (2008)], so that we only need to consider the dominant eigenvalue or invasion exponent, denoted as \(\Lambda =\Lambda (d_1, d_2)\), of the linear eigenvalue problem

$$\begin{aligned} d_2 \phi _{xx} - q \phi _x+\phi (r(x)-u^*)=\lambda \phi , \quad 0<x<L, \end{aligned}$$
(30)

with suitable boundary conditions.

Rather than calculating the sign of \(\Lambda \) (which is difficult in general), we calculate the selection gradient, i.e. the derivative \(\frac{\partial \Lambda }{\partial d_2}\) evaluated at \(d_1=d_2\), see (9). The advantage of calculating the selection gradient is that for \(d_1=d_2\), we know that \(\Lambda =0\) so that the dominant eigenfunction is precisely the steady-state profile of the resident species, \(u^*\).

In the following, we frequently use the equality

$$\begin{aligned} d\phi _{xx}-q\phi _x=d\left( e^{\alpha x}\left( e^{-\alpha x} \phi \right) _x\right) _x,\quad \text {where}\quad \alpha =q/d. \end{aligned}$$
(31)

5.1 The selection gradient

Now, let \(u^*\) be the positive steady state with general boundary conditions (5), and let \(\Lambda \) be the dominant eigenvalue of (30) with the same boundary conditions (5) and with corresponding eigenfunction \(\phi \).

We let \('=\frac{\partial }{\partial d_2}\) denote differentiation with respect to \(d_2\). Differentiating (30) and using (31), we obtain with \(\alpha =q/d_2\):

$$\begin{aligned} d_2(e^{\alpha x}(e^{-\alpha x}\phi ')_x)_x + \phi _{xx}+\phi '(r-u^*)=\Lambda '\phi +\Lambda \phi '. \end{aligned}$$
(32)

Multiplying (30) by \(e^{-\alpha x}\phi '\), we get

$$\begin{aligned} d_2\int e^{-\alpha x}\phi '(e^{\alpha x}(e^{-\alpha x}\phi )_x)_x dx + \int e^{-\alpha x}\phi '(r-u^*)\phi dx=\Lambda \int e^{-\alpha x}\phi \phi ' dx.\nonumber \\ \end{aligned}$$
(33)

Similarly, we multiply (32) by \(e^{-\alpha x}\phi \) to get

$$\begin{aligned}&d_2\int e^{-\alpha x}\phi (e^{\alpha x}(e^{-\alpha x}\phi ')_x)_x dx + {\int e^{-\alpha x}\phi \phi _{xx}}\, dx \nonumber \\&\quad + \int e^{-\alpha x}\phi '(r-u^*)\phi dx=\int e^{-\alpha x}\phi (\Lambda '\phi +\Lambda \phi ') dx. \end{aligned}$$
(34)

Integrating by parts and subtracting Eq. (34) from (33), we get

$$\begin{aligned} d_2\left[ \phi '(e^{-\alpha x}\phi )_x\bigg |_0^L -\phi (e^{-\alpha x}\phi ')_x\bigg |_0^L\right] -\int e^{-\alpha x}\phi \phi _{xx} dx=-\Lambda '\int e^{-\alpha x}\phi ^2 dx.\nonumber \\ \end{aligned}$$
(35)

Next, we consider the first boundary term with the general conditions (5).

$$\begin{aligned} d_2\phi '(e^{-\alpha x}\phi )_x\bigg |_0^L&= e^{-\alpha x}\phi '(d_2\phi _x-q\phi )\bigg |_0^L \nonumber \\&= -qe^{-\alpha L}\phi (L)\phi '(L) b_d - q\phi (0)\phi '(0) b_u. \end{aligned}$$
(36)

Differentiating the boundary condition for \(\phi \) at \(x=0\) and \(x=L\) with respect to \(d_2\), we find

$$\begin{aligned} \phi _x+d_2\phi '_x-q\phi '=b_u q\phi ',\quad \mathrm{and}\quad \phi _x+d_2\phi '_x-q\phi '=-b_d q\phi '. \end{aligned}$$
(37)

With these expressions, the second boundary term gives

$$\begin{aligned} d_2\phi (e^{-\alpha x}\phi ')_x\bigg |_0^L =e^{-\alpha L}\phi (L)\left( -b_d q \phi '(L) -\phi _x(L)\right) - \phi (0)\left( b_u q \phi '(0) -\phi _x(0)\right) \!.\nonumber \\ \end{aligned}$$
(38)

Hence, (35) becomes

$$\begin{aligned} e^{-\alpha L}\phi (L)\phi _x(L)-\phi (0)\phi _x(0)-\int e^{-\alpha x}\phi \phi _{xx} dx=-\Lambda ' \int e^{-\alpha x}\phi ^2 dx.\quad \quad \end{aligned}$$
(39)

Finally, we use integration by parts

$$\begin{aligned} \int e^{-\alpha x}\phi \phi _{xx} dx=e^{-\alpha L}\phi (L)\phi _x(L)-\phi (0)\phi _x(0)-\int (e^{-\alpha x}\phi )_x\phi _x dx,\quad \quad \end{aligned}$$
(40)

to obtain our desired formula for the selection gradient.

Lemma 5.1

The selection gradient at the \((u^*,0)\)-steady state of (1) with boundary conditions (5) is given by

$$\begin{aligned} \frac{\partial \Lambda }{\partial d_2}\bigg |_{d_2=d_1}=-\frac{\int (e^{-\alpha x} u^*)_x u^*_x dx}{ \int e^{-\alpha x}(u^*)^2 dx}, \end{aligned}$$
(41)

where \(\alpha =q/d_1\).

5.2 Invasion analysis: NF/FF boundary conditions

Lemma 5.2

Assume that \(r\) is constant and consider NF/FF boundary conditions. Then the selection gradient is positive. In particular, \(v\) can invade the semi-trivial steady state \((u^*,0)\) if and only if \(d_2>d_1\). Higher dispersal rates will evolve.

Proof

For constant \(r\) and NF/FF boundary conditions, we have \(u^*_x>0\) and \(0<u^*<r\) (Vasilyeva and Lutscher 2011). Integrating the steady state equation for \(u^*\), we find

$$\begin{aligned} d_1u^*_x(x) -qu^*(x)+\int _0^x u^*(y)(r-u^*(y))dy=0, \end{aligned}$$
(42)

from which we conclude \(d_1u^*_x-qu^*<0\). Since we evaluate (41) at \(d_1=d_2\), we have \(d_1u^*_x-qu^*=d_1 e^{\alpha x}(e^{-\alpha x}u^*)_x\). Hence, the integral in the numerator of (41) is negative and the claim follows. \(\square \)

Remark 5.3

The claim of the previous lemma is in general false when \(r\) is not a constant. Consider \(q=0\), so that the boundary conditions become NF/NF. It is known that the selection gradient is negative in that case (Hastings 1983). By continuity, the selection gradient is still negative for small enough \(q\).

The claim of the preceding lemma can be generalized to a linearly increasing growth rate and NF/FF boundary conditions. Monotone increasing (or decreasing) growth rates are particularly important for advective systems since they can represent typical patterns along a stream or river. For example, water temperature and nutrient load typically increase downstream. The choice of a linearly increasing function follows (Lutscher et al. 2007) where the single-species and competitive ecological dynamics were studied.

Theorem 5.4

Assume that the growth rate is linear, \(r(x)=r_1 x+r_0,\,r_0, r_1>0\), and that \(q>d_1 r_1/r_0\). Assume that the zero state of

$$\begin{aligned} u_t=d_1 u_{xx}-qu_x+u(r(x)-u), \end{aligned}$$

with NF/FF boundary conditions is linearly unstable. Then the unique positive steady state, \(u^*\), satisfies \(u^*(x)<r(x)\) and \(u^*_x> 0\) in \((0, L)\). In particular, the selection gradient of \(v\) at the semi-trivial state \((u^*,0)\) is positive.

Proof

The statement about the selection gradient follows exactly like in Lemma 5.2, once the two properties of \(u^*\) have been established.

To see that \(u^*<r\), pick any initial condition \(u(x,0)<r(x)\). By monotonicity, the solution to this initial condition will converge to the unique positive steady state \(u^*\). Set \(z(x,t)=u(x,t)-r(x)\). Then

$$\begin{aligned} d_1 z_{xx}-qz_x-uz-z_t=qr_1>0,\quad x\in (0,L) \end{aligned}$$

and \(-z_x(L,t)=r_1>0\) as well as \(d_1 z_x(0)-qz(0)=qr_0-d_1 r_1\). By assumption, the latter boundary expression is also positive so that, by the maximum principle [e.g. Lemma 2.2 in Lieberman (1996)], we have \(z<0\) for \(x\in (0,L)\) and \(t>0\). By letting \(t\rightarrow \infty \) we have \(u^*-r=\lim _{t\rightarrow \infty }z(x,t)\le 0\); i.e. \(u^*\le r\). We further show that \(u^*\not \equiv r\): if \(u^*\equiv r\), then by the equation of \(u^*\) we have \(d_1 r_{xx}-q r_x=0\) in \((0, L),\,d_1 r_x(0)=q r(0)\) and \(r_x(L)=0\). But this is clearly impossible for any (nonzero) linear function \(r\). Hence, \(u^*\le r\) and \(u^*\not = r\). Set \(z^*=u^*-r\). Then \(z^*\le 0,\,z^*\not \equiv 0\) and it satisfies \(d_1 z^*_{xx}-q z_{x}-u^* z^*=q r_1\ge 0\) in \((0, L)\). By the strong maximum principle, \(z^*<0\) in \((0, L)\); i.e. \(u^*<r\) in \((0, L)\).

Since \(u^*<r\), by the equation of \(u^*\) we have \(d_1u^*_{xx}-qu^*_x<0\) in \((0, L)\). Hence, \((e^{-(q/d_1) x} u^*_x)_x<0\), i.e., \(e^{-(q/d_1) x} u^*_x\) is strictly monotone decreasing. Since \(u^*_x(L)=0\), we have \(u^*_x>0\) in \([0, L)\). \(\square \)

6 Evolution of higher dispersal in homogeneous advective environment

Lemma 5.2 suggests that in a homogeneous advective environment with NF/FF boundary conditions, higher dispersal rates will evolve. In this section, we further show that populations with higher dispersal rate not only can prevent the invasion of populations with slower dispersal rate but also can invade and replace populations with slower dispersal rate.

Consider the system

$$\begin{aligned} \left\{ \begin{array}{l} u_t=d_1 u_{xx}-q u_x+u(r-u-v), \quad 0<x<L, \quad \ t>0,\\ v_t=d_2 v_{xx}-q v_x+v(r-u-v),\quad 0<x<L, \quad \ t>0,\\ d_1 u_{x}(0, t)-q u(0, t)=d_2 v_{x}(0, t)-q v(0, t)=0,\\ u_{x}(L, t)=v_{x}(L, t)=0. \end{array}\right. \end{aligned}$$
(43)

Throughout this section, we assume that \(q\) and \(r\) are positive constants.

The main result of this section is

Theorem 6.1

Suppose that \(q, r\) are positive constants. If \(d_1>d_2\), then \((u^*, 0)\), whenever it exists, is globally asymptotically stable.

The proof of this theorem is preceded by a number of lemmas. We begin by considering the eigenvalue problem

$$\begin{aligned}&\tau \phi _{xx}-q \phi _x+ h(x) \phi =\lambda \phi , \quad 0<x<L, \\&\tau \phi _x(0)=q\phi (0), \quad \phi _x(L)=0. \end{aligned}$$

For any \(\tau >0\), let \(\lambda (\tau )\) denote the largest eigenvalue and \(\phi \) the corresponding eigenfunction, uniquely determined by \(\max _{0\le x\le L} \phi (x)=1\).

Lemma 6.2

Suppose \(h(x)>0\) in \((0, L)\). Then \(\lambda (\tau )\) has at most one positive root. Moreover, if \(\lambda (\tau ^*)=0\) for some \(\tau ^*>0\), then \(\frac{\partial \lambda }{\partial \tau }(\tau ^*)>0\).

Proof

By Eqs. (39) and (40),

$$\begin{aligned} \frac{\partial \lambda }{\partial \tau }=-\frac{\int (e^{-\alpha x} \phi )_x \phi _x dx}{ \int e^{-\alpha x}\phi ^2 dx}, \end{aligned}$$
(44)

where \(\alpha =q/\tau \). It is clear that our lemma follows from the following assertion:

Claim If \(\lambda (\tau ^*)=0\) for some \(\tau ^*>0\), then

$$\begin{aligned} \frac{\partial \lambda }{\partial \tau }\Big |_{\tau =\tau ^*}>0. \end{aligned}$$
(45)

It remains to establish (45). To this end, let \(\phi ^*\) denote the eigenfunction corresponding to \(\lambda (\tau ^*)\), uniquely determined by \(\max \phi ^*=1\). As \(\lambda (\tau ^*)=0,\,\phi ^*\) satisfies

$$\begin{aligned}&\tau ^*\phi ^*_{xx}-q\phi ^*_x+ h(x)\phi ^*=0, \quad 0<x<L, \nonumber \\&\tau ^*\phi ^*_{x}(0)-q\phi ^*(0)=\phi ^*_x(L)=0. \end{aligned}$$
(46)

Integrating Eq. (46) from zero to \(x\), we find

$$\begin{aligned} \tau ^* \phi ^*_x(x) -q\phi ^*(x)+\int _0^x \phi ^*(y) h(y) dy=0. \end{aligned}$$
(47)

As \(h>0\) in \((0, L)\), we conclude \(0>\tau ^* \phi ^*_x-q\phi ^*=\tau ^* e^{\alpha ^* x}(e^{-\alpha ^* x}\phi ^*)_x\), where \(\alpha ^*=q/\tau ^*\).

Next we show that \(\phi _x^*>0\) in \([0, L)\). If \(\phi ^*(0)=0\), then by the boundary condition of \(\phi ^*\) at \(x=0,\,\phi ^*_x(0)=0\). By the equation of \(\phi ^*\) and the uniqueness of ODE, we have \(\phi ^*\equiv 0\) in \((0, L)\), which is a contradiction. Hence, \(\phi ^*(0)>0\). This implies that \(\phi _x^*(0)>0\). If \(\phi _x^*>0\) in \([0, L)\) does not hold, there exists some \(x_0\in (0, L)\) such that \(\phi _x^*>0\) in \([0, x_0)\) and \(\phi _x^*(x_0)=0\). Since \(\phi _x^*(L)=0\), there must exist some \(x_1\ge x_0\) such that \(\phi _x^*(x_1)=0\) and \(\phi _{xx}^*(x_1)\ge 0\). By the equation of \(\phi ^*,\,h(x_1)\le 0\), which is a contradiction. Hence, \(\phi _x^*>0\) in \([0, L)\).

Finally, since \((e^{-\alpha ^* x}\phi ^*)_x<0\) and \(\phi _x^*>0\) in \((0, L)\), we see that (45) holds. \(\square \)

Lemma 6.3

If \(d_1>d_2\), then \((u^*, 0)\), whenever it exists, is locally asymptotically stable.

Proof

Let \(h(x)=r-u^*\). Then, \(\lambda (d_1)=0\). Since \(h>0\) in \([0, L]\), the previous lemma asserts that \(d_1\) is the only positive root of \(\lambda (\tau )=0\), and \(\lambda (d_2)>0\) if and only if \(d_2>d_1\). That is, \((u^*,0)\) is stable if \(d_1>d_2\), and unstable if \(d_1<d_2\). \(\square \)

Next, we will show that (43) has no coexistence (positive) steady state. First, we establish the following a priori estimate on any positive steady state of (43).

Lemma 6.4

Let \(u, v\) be any positive steady state of (43). Then \(u_x, v_x>0\) in \([0, L)\) and \(u+v<r\) in \([0, L]\).

Proof

Differentiate the equations of \(u\) and \(v\) we obtain

$$\begin{aligned} \left\{ \begin{array}{l} d_1 u_{xxx}-q u_{xx}+u_x(r-2u-v)-u v_x=0, \quad 0<x<L,\\ d_2 v_{xxx}-q v_{xx}+v_x(r-u-2v)-v u_x=0,\quad 0<x<L, \\ d_1 u_{x}-q u=d_2 v_{x}-q v=0 \quad \text{ at } \ x=0,\\ u_{x}=v_{x}=0 \quad \text{ at } \ x=L. \end{array}\right. \end{aligned}$$
(48)

Set \(w=u_x/u\) and \(z=v_x/v\). Then \(w\) and \(z\) satisfy

$$\begin{aligned} \left\{ \begin{array}{l} d_1 w_{xx}+(2d_1 u_x/u-q) w_x-uw-vz=0, \quad 0<x<L,\\ d_2 z_{xx}+(2 d_2 v_x/v-q) z_x-uw-vz=0,\quad 0<x<L, \\ w(0)=q/d_1>0, \ z(0)=q/d_2>0, \ w(L)=z(L)=0. \end{array}\right. \end{aligned}$$
(49)

We first show that \(u(L)+v(L)\not =r\). To this end, we argue by contradiction: suppose that \(u(L)+v(L)=r\). By the boundary condition \(u_x(L)=v_x(L)=0\) and equations of \(u\) and \(v\), we obtain \(u_{xx}(L)=v_{xx}(L)=0\). That is, \(w_x(L)=z_x(L)=0\). As \(w(L)=z(L)=0\), by the uniqueness of ODEs we obtain \(w=z=0\) in \([0, L]\), i.e., both \(u\) and \(v\) are positive constants. However, this contradicts boundary conditions at \(x=0\). Hence, it suffices to consider two cases: (i) \(u(L)+v(L)>r\); (ii) \(u(L)+v(L)<r\).

Case (i) By the equations of \(u, v\) and the boundary conditions \(u_x(L)=v_x(L)=0\), there exists some \(\delta >0\) such that \(u_{xx}>0\) and \(v_{xx}>0\) for \(L-\delta \le x\le L\). Hence, \(u_x<0\) and \(v_x<0\) in \([L-\delta , L)\). Since \(u_x(0)>0\) and \(v_x(0)>0,\,u_x\) and \(v_x\) must have some root in \((0, L-\delta )\). Without loss of generality, we may assume that there exists some \(x_1\in (0, L-\delta )\) such that \(u_x(x_1)=0,\,v_x(x_1)\le 0,\,u_x<0\) and \(v_x<0\) in \((x_1, L)\). Recall that \(w=u_x/u\) in \((x_1, L)\). Choose \(x_2\in (x_1, L)\) such that \(w(x_2)=\min _{x_1\le x\le L} w(x)\). Hence, \(w(x_2)<0,\,w_{x}(x_2)=0\), and \(w_{xx}(x_2)\ge 0\). By the equation of \(w\) we obtain \(z(x_2)>0\), which is a contradiction. This rules out Case (i).

Case (ii) By the equations of \(u, v\) and the boundary conditions \(u_x(L)=v_x(L)=0\), there exists some \(\delta >0\) such that \(u_{xx}<0\) and \(v_{xx}<0\) for \(L-\delta \le x\le L\). Hence, \(u_x>0\) and \(v_x>0\) in \([L-\delta , L)\). Suppose that there exists some \(x_3\in (0, L-\delta )\) such that \(u_x(x_3)=0\) and \(u_x>0\) in \((x_3, L)\). Choose \(x_4\in (x_3, L)\) such that \(w(x_4)=\max _{x_3\le x\le L} w(x)\). Hence, \(w(x_4)>0,\,w_{x}(x_4)=0\), and \(w_{xx}(x_4)\le 0\). By the equation of \(w\) we obtain \(z(x_4)<0\). Hence, as \(v_x>0\) in \([L-\delta , L]\), there exists some \(x_5\in (x_4, L-\delta )\) such that \(z(x_5)=0,\,z>0\) in \((x_5, L)\). Choose \(x_6\in (x_5, L)\) such that \(z(x_6)=\max _{x_5\le x\le L} z(x)\). Hence, \(z(x_6)>0,\,z_{x}(x_6)=0\), and \(z_{xx}(x_6)\le 0\). By the equation of \(z\) we obtain \(w(x_6)<0\), which is a contradiction as \(u_x>0\) in \((x_3, L)\). Hence, \(u_x>0\) in \([0, L)\). Similarly, \(v_x>0\) in \([0, L)\). Furthermore, \(u(x)+v(x)\le u(L)+v(L)<r\) for any \(x\in [0, L]\). This completes the proof. \(\square \)

Let \(u^*, v^*\) denote any positive steady state of system (43). Consider the eigenvalue problem

$$\begin{aligned}&\tau \phi _{xx}-q \phi _x+\phi (r-u^*-v^*)=\lambda \phi , \quad 0<x<L,\\&\tau \phi _x(0)=q\phi (0), \quad \phi _x(L)=0. \end{aligned}$$

For any \(\tau >0\), let \(\lambda _1(\tau )\) denote the largest eigenvalue of the above eigenvalue problem.

Lemma 6.5

The dominant eigenvalue \(\lambda _1(\tau )\) has at most one positive root.

Proof

It follows from Lemmas 6.2 and 6.4. \(\square \)

Lemma 6.6

Suppose that \(d_1\not =d_2\). Then system (43) has no positive steady state.

Proof

Let \(u^*, v^*\) denote any positive steady state of system (43). Then \(u^*, v^*\) satisfy

$$\begin{aligned} \left\{ \begin{array}{l} d_1 u^*_{xx}-q u^*_x+u^*(r-u^*-v^*)=0, \quad 0<x<L,\\ d_2 v^*_{xx}-q v^*_x+v^*(r-u^*-v^*)=0,\quad 0<x<L,\\ d_1 u^*_{x}(0)-q u^*(0)=d_2 v^*_{x}(0)-q v^*(0)=0,\\ u^*_{x}(L)=v^*_{x}(L)=0. \end{array}\right. \end{aligned}$$
(50)

Hence, \(\lambda _1(d_1)=\lambda _1(d_2)=0\). By Lemma 6.5, \(d_1=d_2\), which is a contradiction. \(\square \)

By the maximum principle for cooperative systems (Protter and Weinberger 1984) and standard theory for parabolic equations, if the initial conditions of (43) are non-negative and not identically zero, system (43) has a unique positive smooth solution, which exists for all time, and it defines a smooth dynamical system on \(C([0, L])\times C([0, L])\) (Cantrell and Cosner 2003; Smith 1995). The stability of steady states of (43) is understood with respect to the topology of \(C([0, L])\times C([0, L])\). The following result is a consequence of the maximum principle and the structure of (43); e.g., modifying the proof of Theorem 3 (Cantrell et al. 2010).

Theorem 6.7

System (43) is a strongly monotone dynamical system, i.e., conditions

  1. (a)

    \(u_1(x, 0)\ge u_2(x, 0)\) and \(v_1(x, 0)\le v_2(x, 0)\) for all \(x\in (0, L)\) and

  2. (b)

    \((u_1(x, 0), v_1 (x, 0))\not \equiv (u_2(x, 0), v_2(x, 0))\)

imply \(u_1(x, t)>u_2(x, t)\) and \(v_1(x, t)<v_2(x, t)\) for all \(x\in [0, L]\) and \(t>0\).

The following result is a consequence of Theorem 6.7 and the theory of strongly monotone dynamical system (Hsu et al. 1996; Smith 1995):

Theorem 6.8

If system (43) has no positive steady state, then one of the semi-trivial steady states is unstable and the other one is globally asymptotically stable.

Proof of Theorem 6.1

Assume that \(d_1>d_2\) and that the semi-trivial state \((u^*,0)\) exists. If the semi-trivial steady state \((0, v^*)\) also exists, Theorem 6.1 follows from Theorem 6.8, Lemmas 6.3 and 6.6. If \((0, v^*)\) does not exist, the solution of the single species equation

$$\begin{aligned}&V_t=d_2 V_{xx}-q V_x+ V(r-V),\quad 0<x<L, \ t>0, \nonumber \\&d_2 V_{x}(0, t)-q V(0, t)=0, \quad V_{x}(L, t)=0 \end{aligned}$$
(51)

satisfies \(V(x,t )\rightarrow 0\) uniformly in \(x\) as \(t\rightarrow \infty \). Let \((u(x,t), v(x,t))\) denote the solution of (43) with \(v(x,0)=V(x,0)\). Since \(u(x,t)>0,\,v(x, t)\) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} v_t\le d_2 v_{xx}-q v_x+ v(r-v),\quad 0<x<L, \ t>0,\\ d_2 v_{x}(0, t)-q v(0, t)=0, \quad v_{x}(L, t)=0. \end{array}\right. \end{aligned}$$
(52)

By the comparison principle for parabolic equations (Protter and Weinberger 1984), \(v(x,t)\le V(x,t)\) for any \(x\in [0, L]\) and \(t\ge 0\). Hence, \(v(x,t )\rightarrow 0\) uniformly in \(x\) as \(t\rightarrow \infty \), which in turn implies that \(u(x,t)\rightarrow u^*\) uniformly in \(x\) as \(t\rightarrow \infty \). This convergence together with Lemma 6.3 shows that \((u^*, 0)\) is globally asymptotically stable in \(C([0, L])\times C([0, L])\) norm. \(\square \)

7 Discussion

For a randomly dispersing population in a spatially variable but temporally constant environment, evolution favors lower dispersal rates since these allow for better tracking of resources (Dockery et al. 1998; Hastings 1983). In streams and other advective environments, an externally imposed movement bias transports individuals “downstream” and thereby potentially away from resources and even out of a given domain. This phenomenon occurs in the gastrointestinal tract (Ballyk et al. 1998; Boldin 2008), in wandering oases (Dahmen et al. 2000; Desai and Nelson 2005), in the water column of lakes (Huisman et al. 2002; Kolokolnikov et al. 2009), in climate change models (Leroux et al. 2013; Potapov and Lewis 2004), and in rivers (Speirs and Gurney 2001; Vasilyeva and Lutscher 2011). Our work shows that in the presence of advection, slower dispersers are often at a disadvantage, and intermediate or higher dispersal rates may evolve. Dispersal rates can be linked to various physiological aspects of organisms, for example buoyancy (to counteract the gravitational downward pull in the water column), physical strength and body size (to move greater distances against the flow and to withstand higher flow rates) or flagella (to self-propell in liquid media).

The direction of evolution of dispersal depends crucially on boundary conditions and the profile of the growth rate. The effect of boundary conditions can be observed clearly by applying the framework of adaptive dynamics to the spatially implicit model (7), i.e. by studying the selection gradient. When the diffusion rate is small, the selection gradient is positive since increasing diffusion increases the chances of individuals to stay in the domain longer and reproduce. When the diffusion rate is large, the selection gradient is positive only if diffusion does not lead to loss across the boundary, i.e. in the NF/FF case. With at least one hostile boundary, the selection gradient becomes negative. High diffusion rates imply high loss rates, and consequently diminished chances for an invading population to become established. In the latter case, a critical point for the evolutionary dynamics is an ESS. Since it is also a critical point for the linearized population growth rate [see (9)], evolution maximizes the density-independent growth rate in that case. In the former case, there is no critical point of the evolutionary dynamics.

In the spatially explicit model, the sign of the selection gradient is given by the sign of the integral

$$\begin{aligned} \int _0^L (e^{-\alpha x} u^*)_x \cdot u^*_x \, dx, \end{aligned}$$

where \(\alpha =q/d_1\). With NF/FF conditions and constant growth rate, the steady state profile \(u^*(x)\) is monotone, and this integral expression is positive. Further analysis in Theorem 6.1 shows that the population with larger diffusion rate will take over the other. The spatially implicit and explicit models agree in their predictions.

Hostile downstream conditions, however, force \(u^*\) to be hump-shaped, and the sign of the integral is not clear. The effect of dispersal-induced loss from the domain can be seen, for example, in the critical domain length. The expression in (16) has a local minimum with respect to \(d\) and increases to infinity as \(d\) increases while all other parameters are held constant. The corresponding expression for the critical length with free-flow conditions downstream is monotone decreasing with dispersal rate, see formula (2.4) in Vasilyeva and Lutscher (2011).

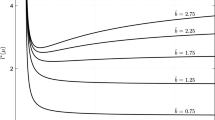
Since the spatially implicit model suggests that intermediate dispersal rates should evolve, we evaluated the selection gradient (41) for the spatially explicit system numerically to compare it to the prediction of the spatially implicit model; see Fig. 2. We find, indeed, that the selection gradient is positive for small dispersal parameter and negative for large dispersal parameter. This observation leads us to conjecture that there is an intermediate dispersal rate that constitutes a local (and maybe even global) ESS in the spatially explicit model. The proof of this conjecture remains a challenge for the future.

Fig. 2
figure 2

Selection gradient (41) for two sets of boundary conditions in the spatially explicit model. When the selection gradient is positive, larger dispersal rates can evolve, when it is negative, smaller rates will invade. The curve for H/H boundary conditions is not defined for \(d>0.02\) since the system has no semi-trivial steady state above this value. Parameters are \(L=10. q=1\), as in the previous figure, and \(r=1\)

Full size image

Among all possible growth rates, monotone functions are of particular interest in river environments, since many external influences are (roughly) monotone (e.g. temperature downstream, nutrient load). We showed that for a linearly increasing growth rate and free-flow boundary conditions, higher dispersal rates evolve. At this point, we can only speculate about the effects of different boundary conditions. Hostile downstream conditions, for example, would put the highest risk of washout from the domain in the same location as the best growth conditions. High dispersal rates would contribute to boundary loss and move individuals upstream, where growth conditions are less favorable. Both factors should prevent high dispersal rates. A monotone decreasing growth function, however, could lead to higher dispersal rates (assuming that upstream conditions are no-flux), so that the drift to downstream, low-growth regions could be avoided. A number of analytical challenges arise from these questions. For example, the steady state \(u^*\) is in general not bounded by \(r\) (but this property was a crucial argument in several of our proofs).

Several open questions remain also in terms of the adaptive dynamics framework. For example, we were not able to completely characterize the trait space, i.e. the set of all \(d\) that allow the resident population to persist, given fixed \(q\) and \(r(x)\). It is, thus, not clear whether evolutionary suicide could occur. Mathematically speaking, the challenge is to determine the behavior of the function \(d\rightarrow \lambda _1(d,r)\). Under which conditions is it monotone? When does it have a single extremum? An answer of these questions would also shed light onto whether evolution maximizes the population growth rate (Metz et al. 2008). Specifically, if \(\lambda _1(d)\) has a critical point, is that point a critical point for the adaptive dynamics? And is it an ESS?

Finally, for the spatially implicit model, it is easy to show that lack of mutual invasibility implies replacement of species. Since our spatially explicit system is a strongly monotone dynamical system, monotone dynamical system theory ensures that if it has no coexistence state, then lack of mutual invasibility does guarantee replacement; i.e., one of the semi-trivial steady states is globally asymptotically stable. We were able to show that no coexistence state is possible for NF/FF boundary condition and constant \(r\) (Lemma 6.6), but the general case is yet unclear. For some Lotka-Volterra competition models with random dispersal, a counter example exists (Hutson et al. 2002).