1 Introduction

In the past decade, a number of modeling studies explored conditions and mechanisms for population persistence and spread in habitats with unidirectional flow. Most obviously, such environments represent streams and rivers (Speirs and Gurney 2001; Pachepsky et al. 2005; Vasilyeva and Lutscher 2010; Sarhad et al. 2014; Samia and Lutscher 2012), but similar models describe population dynamics in the face of climate change (Potapov and Lewis 2004; Berestycki et al. 2009), sinking phytoplankton species (Huisman et al. 2002), as well as bacteria in the gut (Ballyk et al. 1998; Boldin 2008). In the context of streams and rivers, the question of persistence in the presence of downstream advection dates back to ecological investigations of the “drift paradox” (Müller 1982).

Two salient insights from these modeling studies are that (1) unbiased, random movement may prevent wash-out and allow a population to persist locally, and that (2) a benthic phase, sheltered from the downstream transport, greatly enhances the ability of a population to persist locally. In either case, it is clear that high fecundity aids persistence.

All of these studies considered a population with aquatic life stages only. However, a key feature of the life cycle of many stream insects is the separation into (at least) two stages: aquatic larvae and winged adults. Only during the aquatic stages are individuals exposed to downstream drift. In fact, the earliest proposed and most widely accepted mechanism for population persistence in the face of advection is that adult upstream flight conter-acts larval downstream drift (Müller 1954). This mechanism was tested in several empirical studies (Madsen et al. 1974; Williams and William 1993; MacNeale et al. 2005): there is clear evidence that several species of stoneflies and caddisflies do bias their dispersal during the adult stage in the upstream direction. Moreover, often bias is strongest in dispersing gravid females. We are aware of only one theoretical study that considers the effect of multiple dispersal modes on the persistence of stream populations (Lutscher et al. 2010). These authors found that dispersal bias, while not necessary for persistence, can significantly increase chances of persistence.

In this paper, we present and analyze a novel mathematical model for a population of stream insects with two distinct, non-overlapping life-cycle stages: an aquatic larval stage and a winged adult stage. The model is in the form of an impulsive reaction–advection–diffusion equation, where the partial differential equation describes the downstream drift of the larval stage and an integral operator represents the outcome of dispersal through adult flight. The advection–diffusion operator gives a reasonably accurate, yet mathematically tractable description of transport in streams and rivers while the integral operator allows us to accommodate a wide variety of empirically determined dispersal patterns. In our analysis of this continuous–discrete hybrid model, we focus on two fundamental question of spatial ecology: spreading and travelling wave speeds (for an unbounded domain) and the critical habitat size (for a bounded domain). We express our results in terms of key biological and hydrological parameters such as flow speed, motility of the organisms, adult dispersal patterns, and population dynamics characteristics. This work builds on and generalizes the work by Lutscher et al. (2010) by considering nonlinear dynamics and the reaction–advection–diffusion equation explicitly, and the work by Lewis and Li (2012) by introducing advection and a non-local impulse.

In Sect. 2, we formulate the model in detail. In Sect. 3, we undertake some preliminary analysis and introduce the notions of weak and local persistence, spreading speeds and travelling wave speed. In Sect. 4, we analyze the linear model on an unbounded domain. We give an explicit solution, a condition for weak persistence, compute the upstream and downstream travelling wave speeds, and formulate the local persistence conditions in terms of minimum upstream and downstream travelling wave speeds. In Sect. 5, we study the nonlinear model on an unbounded domain, formally connecting the upstream and downstream spreading speed for the nonlinear model to the minimum upstream and downstream travelling wave speeds. In Sect. 6, we focus on the finite domain case, using the average dispersal success (ADS) approach, to obtain an approximate expression for the critical domain size. Furthermore, in Sect. 7, we connect our model to empirical work, estimate parameter values, and use numerics to illustrate the accuracy of the ADS approach. We finish with a discussion.

2 Model formulation

We formulate a mixed continuous–discrete model for a single population of a stream insect species (e.g. stoneflies, mayflies) with two distinct, non-overlapping developmental stages. During the aquatic larval stage at the beginning of the season, individuals grow, compete and mature. During the winged adult stage in the second part of the season, individuals emerge from the water, disperse and deposit eggs that develop into larvae at the beginning of the next season; see Fig. 1. This winged stage is typically very short, adult mayflies do not feed.

Fig. 1
figure 1

Diagram showing the life cycle of a stonefly. Larvae are present at ‘0’, develop into nymphs that drift down the stream or river. At ‘\(\tau \)’ the winged adults emerge and fly to deposit eggs

Full size image

We denote the density of the larval population at time t and location x during season n as \(u_n(x,t).\) Larvae are transported by diffusion (with rate \(d>0\)) and drift (with speed \(q\ge 0\)), and experience possibly density-dependent death according to some positive function f. The equation describing the larval density during a season of length \(\tau \) is

$$\begin{aligned} \frac{\partial u_n}{\partial t} = d\frac{\partial ^2 u_n}{\partial x^2}-q\frac{\partial u_n}{\partial x}-f(u_n),\quad u_n(x,0)=u_{n,0}, \end{aligned}$$
(2.1)

for \(0\le t\le \tau .\) We assume that mortality \(f(u)=\alpha u+f_1(u)\) consists of a constant background mortality rate \(\alpha >0\) and an additional density-dependent mortality source \(f_1(u)\) that satisfies \(f_1\ge 0,f_1(0)=f_1'(0)=0.\) When we consider a very long river, Eq. (2.1) is valid for \(x\in \mathbb {R}.\) When we consider a short river, say of length L,  we impose boundary conditions on the interval \(x\in [0,L].\) In general, we formulate these conditions in terms of the flux as

$$\begin{aligned} du_x-qu= & {} a_1 u,\quad x=0,\nonumber \\ du_x-qu= & {} -a_2 u, \quad x=L, \end{aligned}$$
(2.2)

where \(a_i\ge 0.\) The sign condition ensures that no individuals enter the domain at either boundary; individuals may or may not leave the domain. A typical choice for the upstream condition is zero flux, so \(a_1=0\) (Vasilyeva and Lutscher 2011; Lou and Lutscher 2013). Downstream, conditions could be hostile (\(a_2\rightarrow \infty \)) or ‘free flow’ (\(a_2=q\)), see Lutscher et al. (2006) for a detailed derivation of these conditions. We denote the solution operator of Eq. (2.1) by \(Q_\tau ,\) i.e. \(u_n(x,\tau )=Q_\tau [u_{n,0}].\)

To describe dispersal of adult insects by flight we employ a dispersal kernel, K,  that gives the probability density function of the signed dispersal distances. Specifically, if u is the density of individuals at the beginning of the winged stage, then the density at the end of the winged stage is given by the convolution

$$\begin{aligned} (K*u)(x)=\int _{-\infty }^\infty K(x-y)u(y)dy \end{aligned}$$
(2.3)

(Lutscher et al. 2010). Naturally, we require \(K\ge 0\) and \(\int _{-\infty }^\infty K(x) dx=1.\) We do not require K to be symmetric so as to accommodate potentially upstream-biased adult flight.

Dispersal of adults on a bounded domain may or may not be described by a convolution as in (2.3). We will assume that individuals move as if the domain were infinite, but die when they land outside of the favorable patch [0, L]. In this case, the domain of integration for the convolution is simply truncated to [0, L] (Kot and Schaffer 1986; Lutscher et al. 2005). More generally, when individual dispersal behavior changes at the boundary of the domain, dispersal probabilities depend on initial and final location and not only on distance. Those dispersal scenarios are discussed in more detail by Van Kirk and Lewis (1999) and Musgrave and Lutscher (2013). In the case of a bounded domain, we write the adult density after dispersal as

$$\begin{aligned} \int _0^L \bar{K}(x,y)u(y)dy. \end{aligned}$$
(2.4)

We still require that \(\bar{K}\) be positive, but since individuals may leave the domain during dispersal, we only have the integral inequality \(\int _0^L \bar{K}(x,y)dx\le 1.\)

To describe egg deposition and survival until the larval stage, we consider a differentiable function \(g=g(u).\) We require \(g(0)=0,\) with \(g(u),g'(u)>0,g''(u)<0\) for \(u>0,\) and \(g(u)<u\) for large enough u. The Beverton–Holt function satisfies the requirements for g,  but an Allee effect or the Ricker function are excluded.

Combining the equations above on the infinite domain, we arrive at the following model within and between seasons

$$\begin{aligned} \frac{\partial u_n}{\partial t}= & {} d\frac{\partial ^2 u_n}{\partial x^2}-q\frac{\partial u_n}{\partial x}-f(u_n),\quad 0\le t\le \tau ,\quad u_n(x,0)=u_{n,0}(x)\nonumber \\ u_{n+1,0}(x)= & {} g\left( \int _{-\infty }^\infty K(x-y)(u_n(y,\tau ))dy \right) \end{aligned}$$
(2.5)

The discrete updating function from the beginning of one season to the next is

$$\begin{aligned} u_{n+1,0}=Q[u_{n,0}]:=g(K*Q_\tau [u_{n,0}]). \end{aligned}$$
(2.6)

On a bounded domain, boundary conditions are added to the reaction–advection–diffusion equation, and the domain of integration in the convolution integral is replaced by [0, L].

We will frequently study the linearization of model (2.5) at zero, which is given by

$$\begin{aligned} \frac{\partial u_n}{\partial t}= & {} d\frac{\partial ^2 u_n}{\partial x^2}-q\frac{\partial u_n}{\partial x}-\alpha u_n, \end{aligned}$$
(2.7)
$$\begin{aligned} u_{n+1,0}(x)= & {} \rho \int _{-\infty }^\infty K(x-y)u_n(y,\tau )dy, \end{aligned}$$
(2.8)

where \(\rho =g'(0)>0.\) The first equation is valid for \(0\le t\le \tau ,\) and uses initial conditions \( u_n(x,0)=u_{n,0}(x).\)

3 Preliminary analysis and definitions

We note that all three parts of the model satisfy a comparison principle.

Lemma 3.1

Assume \(v_0, w_0\) are non-negative continuous functions on \(\mathbb {R}\) and \(v_0(x)\le w_0(x)\) for all \(x\in \mathbb {R}.\) We denote by v(x, t) and w(x, t) the solutions of (2.1) with initial conditions \(v_0\) and \(w_0.\) Then we have

  1. 1.

    \(v(x,t)\le w(x,t)\) for all \(x\in \mathbb {R},0<t\le \tau ,\)

  2. 2.

    \((K*v_0)(x)\le (K*w_0)(x)\) for all \(x\in \mathbb {R},\) and

  3. 3.

    \(g(v_0(x))\le g(w_0(x))\) for all \(x\in \mathbb {R}.\)

The proof of this lemma follows from the comparison principle for reaction–diffusion equations, from the non-negativity of K and from the monotonicity assumption on g. This lemma implies that the next-generation operator Q in (2.6) has the same monotonicity property. Obviously, the same is true for the linearized model.

On an unbounded spatial domain we can consider spatially constant solutions to (2.6). If we start with a constant positive profile \(u_0(x,0)=g(U_0)\) then the solution \(u_n(x,0)\) of (2.5) remains spatially constant, and satisfies:

$$\begin{aligned} \frac{d U_n}{d t}= & {} -\alpha U_n -f_1(U_n) ,\quad 0\le t \le \tau \nonumber \\ U_{n+1}(0)= & {} g(U_n(\tau )). \end{aligned}$$
(3.1)

Lewis and Li (2012) calculated the solutions to this model explicitly in the special case where \(f_1(U)=\gamma U^2.\) In general, the differential equation in (3.1) defines a map \(U\mapsto F(U),\) where F(U) is the solution at time \(\tau \) of the differential equation with initial condition U. We have \(F(0)=0\), \(F(U)>0\) if \(U>0\), \(F(U)<U\), and F is strictly monotone increasing. Furthermore, \(F'(U)\le F'(0)=\exp (-\alpha \tau ).\)

Next, we consider the function \(H(U)=g(F(U))\) with g as in Sect. 2. By the properties of F and g, H is strictly increasing, and we find

$$\begin{aligned} H(0)=0,\quad H'(0)=g'(0)F'(0)=\rho e^{-\alpha t},\quad \frac{H(U)}{U}\le \frac{g(U)}{U}, \end{aligned}$$

and the latter expression is less than unity for large U. Hence, we have the following observation about the non-spatial model (3.1).

Lemma 3.2

(cf. Lewis and Li 2012)

  1. 1.

    If \(g'(0)\le e^{\alpha \tau }\) and \(U_0> 0\), then \( U_{n+1}\le U_n\) and \(\lim _{n\rightarrow \infty } U_n=0\).

  2. 2.

    If \(g'(0)>e^{\alpha \tau }\) then there exists a unique \(U^*>0\) with \(H(U^*)=U^*.\)

  3. 3.

    If \(g'(0)>e^{\alpha \tau }\) and \(0< U_0<U^*\), then \( U_{n+1}> U_n\) and \(\lim _{n\rightarrow \infty } U_n=U^*\).

With this lemma, we can establish a necessary condition for non-extinction in the nonlinear spatial model (2.5). The proof of the following proposition follows from the comparison principle in Lemma 3.1.

Proposition 3.3

Suppose \(g'(0)\le e^{\alpha \tau }\). Let \(u_n(x,0)\) be a solution of (2.5), with bounded, non-negative initial condition \(u_0(x,0)\). Then \(u_n(x,0)\rightarrow 0\) uniformly in x.

In our analysis of (2.6) we will use classical concepts of persistence, spreading speeds and travelling wave speeds. Given an initial population of \(n_0\) individuals, introduced locally, so that the density is nonzero on a bounded set and zero outside that set, we say that the population is weakly uniformly persistent (sensu Freedman and Moson 1990) if

$$\begin{aligned} \liminf _{n\rightarrow \infty }\sup _{x\in \mathbb {R}} u_n(x,0)>\varepsilon . \end{aligned}$$
(3.2)

Because of movement bias, however, a weakly persistent population on an infinite domain could be transported away from any point faster than it can grow at that point. This scenario is illustrated in Figure 1(b) in Byers and Pringle (2006) and discussed in more detail in Lutscher et al. (2010).

For a definition of local persistence, we require that a population remains bounded below at some fixed location. In other words, there exist \(\varepsilon >0\) and \(x\in \mathbb {R}\), such that for all sufficiently large n, we have \(u_n(x,0)>\varepsilon \). In particular, we define the population to be locally persistent if

$$\begin{aligned} \sup _{x\in \mathbb {R}} \liminf _{n\rightarrow \infty } u_n(x,0)>\varepsilon . \end{aligned}$$
(3.3)

However, on an infinite domain, it is much more practical to formulate this persistence condition in terms of upstream and downstream spreading speeds. Namely, a population persists if its spreading speeds in both directions are positive; see also Lutscher et al. (2010). We need to consider spreading speeds in both directions, since a net bias in either direction could cause the spreading speed in either direction to be positive or negative.

More formally, given initial conditions that are nonzero on a bounded set, and zero outside of that set, the upstream spreading speed is defined by

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x<-(c_*^++\varepsilon )t} u_n(x,0)=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{-(c_*^+-\varepsilon )t<x<0} |u_n(x,0)-U^*|=0 \end{aligned}$$

for \(0<\varepsilon \le c_*^+\) where \(\varepsilon \ll 1\). Roughly speaking, if an observer moves upstream (to the left) faster than the upstream spreading speed, the observer sees the un-invaded steady state. On the other hand, if the observer moves upstream slower than the upstream spreading speed, the observer sees the carrying capacity steady state \(u=U^*\). The downstream spreading speed is defined analogously by

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x>(c_*^-+\varepsilon )t} u_n(x,0)=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{0<x<(c_*^--\varepsilon )t} |u_n(x,0)-U^*|=0 \end{aligned}$$

for \(0<\varepsilon \le c_*^-\) where \(\varepsilon \ll 1\), and has a similar interpretation, with the observer moving downstream (to the right).

The advantage of formulating persistence in terms of upstream and downstream spreading speeds is that the spreading speeds are linearly determined and given by associated minimum traveling wave speeds, and these are straightforward to calculate. A traveling wave moving upstream at speed \(c^+\) takes the form \(u_{n+1}(x,0)=u_n(x+c^+,0)\) where \(\lim _{x\rightarrow -\infty }u_n(x,0)=0\) and \(\lim _{x\rightarrow \infty }u_n(x,0)=U^*\) (nonlinear system) or \(\lim _{x\rightarrow \infty }u_n(x,0)=\infty \) (linear system). A traveling wave moving downstream at speed \(c^-\) takes the form \(u_{n+1}(x,0)=u_n(x-c^-,0)\) where \(\lim _{x\rightarrow -\infty }u_n(x,0)=U^*\) (nonlinear system) or \(\lim _{x\rightarrow -\infty }u_n(x,0)=\infty \) (linear system) and \(\lim _{x\rightarrow \infty }u_n(x,0)=0\). We give the formal connection between spreading speeds and traveling wave speeds in Theorem 5.2.

4 Linear dynamics on the unbounded domain

In this section, for the linear model (2.7, 2.8), we study conditions for persistence according to our definitions, and we derive the dispersion relation between the speed of a traveling wave and its steepness at the leading edge.

Equation (2.7) possesses the explicit solution:

$$\begin{aligned} u_n(x,\tau )=\int _{-\infty }^\infty e^{-\alpha \tau }\Gamma _{q\tau , 2d\tau }(x-y)u_n(y,0)dy, \end{aligned}$$
(4.1)

where \(\Gamma _{q\tau , 2d\tau }\) denotes the Gaussian distribution with mean \(q\tau \) and variance \(2d\tau \)

$$\begin{aligned} \Gamma _{q\tau , 2d\tau }(x)=\frac{1}{2\sqrt{\pi d \tau }}\exp \left( -\frac{(x-q\tau )^2}{4d\tau }\right) . \end{aligned}$$
(4.2)

Substituting this solution into the second equation, we get the iteration scheme:

$$\begin{aligned} u_{n+1}(x,0)=\rho e^{-\alpha \tau } (K*\Gamma _{q\tau , 2d\tau })*u_n(x,0). \end{aligned}$$
(4.3)

Hence, the linearized model on the unbounded domain is equivalent to an integrodifference equation with a convolution of two kernels. Such a model with various combinations of mechanistically derived kernels was studied in the context of the drift paradox by Lutscher et al. (2010).

We begin by deriving a sufficient condition for extinction of the population.

Proposition 4.1

The condition \(\rho < e^{\alpha \tau }\) is a sufficient condition for extinction for model (2.7, 2.8).

Proof

First, if \(u_0(x,0)= U_0\) is a constant, then \(u_n(x,t)\) is spatially constant, for any n and t. Thus, \(u_n(x,t)=U_n(t)\) solves the iteration

$$\begin{aligned} \frac{dU_n}{dt}= & {} -\alpha U_n,\quad 0<t<\tau ,\nonumber \\ U_{n+1}(0)= & {} \rho U_n(\tau ). \end{aligned}$$

The explicit solution of this iteration is

$$\begin{aligned} U_n(t)=e^{-\alpha t} (\rho e^{-\alpha \tau })^{n-1} U_0,\quad 0\le t\le \tau . \end{aligned}$$
(4.4)

This iteration converges to zero exactly if \(\rho < e^{\alpha \tau }\).

Now, assume \(u_0(x,0)\) is some non-negative function, bounded above by a constant \(U_0\). By the comparison principle in Lemma 3.1, the solution \(u_n(x,t)\) is bounded above by the solution \(U_n(t),\) for all \(x\in \mathbb {R}.\) Therefore, the extinction condition holds. \(\square \)

The reverse of the above inequality is sufficient for a spatially constant function \(u_0(x,0)= U_0\) to grow. In the linear system, growth will be geometric, while in the associated nonlinear system, growth will move the population towards the carrying capacity \(U^*,\) which is defined as the unique positive spatially constant fixed point for Eq. (2.6).

The inequality, \(\rho >e^{\alpha \tau },\) is clearly a necessary condition for persistence for spatially non-constant functions. Whether it is also sufficient depends on the definition of persistence. It turns out that it is a sufficient condition for weak persistence, but not local persistence.

Lemma 4.2

Solutions to Eq. (4.3) with \(\rho >e^{\alpha \tau }\) and initial data nonzero on a bounded set are weakly persistent in the sense of Eq. (3.2). In other words, there exists some \(\varepsilon >0\) such that for all \(n>n^*\) there exists \(x_n\in \mathbb {R}\) such that \(u_n(x_n,0)>\varepsilon \).

A proof is given in the Appendix. By way of contrast, an example where the condition \(\rho >e^{\alpha \tau }\) is not sufficient for local persistence is given in Example 4.3, below.

To investigate the issue of local persistence on an infinite domain, we determine the upstream and downstream travelling wave speeds for the linear system. First, we consider a fixed profile at the beginning of the larval stage, traveling upstream with some constant speed, \(c^+\). Thus, we assume a solution of the form \(u_{n+1}(x,0)=u_n(x+c^+,0)\). In our linear model, we use the exponential ansatz \(u_n(x,0)=e^{sx},\) where \(s>0\).

Thus, we have

$$\begin{aligned} e^{sx+sc^+}=\rho \int _{-\infty }^\infty K(x-y)u_n(y,\tau )dy, \end{aligned}$$
(4.5)

where

$$\begin{aligned} u_n(y,\tau )=e^{-\alpha \tau }\frac{1}{2\sqrt{\pi d\tau }}\int _{-\infty }^\infty e^{-\frac{(y-z-q\tau )^2}{4d\tau }} e^{sz}dz. \end{aligned}$$
(4.6)

From the change of variables \(w=y-z-q\tau \), we obtain

$$\begin{aligned} u_n(y,\tau )=e^{-\alpha \tau +sy-sq\tau -d\tau s^2}. \end{aligned}$$
(4.7)

Inserting this expression into (4.5) and using another change of variables, we can cancel the term \(e^{sx}\) from both sides of the equation and obtain the dispersion relation

$$\begin{aligned} e^{sc^+}=\rho e^{-\alpha \tau -sq\tau +d\tau s^2}M(-s), \end{aligned}$$
(4.8)

where M is the moment generating function of kernel K,  i.e. \(M(s)=\int K(x)e^{sx}dx\). Taking logarithms, we can define the upstream speed as a function of the steepness of the profile as

$$\begin{aligned} c^+(s)=\frac{\ln (\rho M(-s))-\alpha \tau }{s}-q\tau +d\tau s. \end{aligned}$$
(4.9)

For the downstream travelling wave speed \(c^-\), we make the corresponding ansatz \(u_n(x,0)=e^{-sx},\) where \(s>0\). Accordingly, we obtain the downstream speed as

$$\begin{aligned} c^-(s)=\frac{\ln (\rho M(s))-\alpha \tau }{s}+q\tau +d\tau s. \end{aligned}$$
(4.10)

If dispersal during the adult state is unbiased, then K is symmetric and so is M. Then, the only difference in the expressions for \(c^+\) and \(c^-\) is in the sign of larval drift q.

The local persistence condition, in terms of minimum travelling wave speeds, therefore takes the form

$$\begin{aligned} \inf _{s>0}c^+(s)> 0 \quad \mathrm{and}\quad \inf _{s>0}c^-(s)> 0. \end{aligned}$$
(4.11)

We equate the minimum travelling wave speeds of this linear system to the spreading speeds of the nonlinear system in Theorem 5.2. We finish this section by deriving an explicit persistence condition in the following special case.

Example 4.3

Suppose K(x) is a Gaussian distribution with mean \(\mu \) and variance \(\sigma ^2,\) denoted by \(\Gamma _{\mu ,\sigma ^2}\) as in (4.2). When \(\mu \) and q are of opposite sign, then adult dispersal and larval dispersal are biased in opposite directions. The moment generating function is \(M(s)=\exp (\mu s+\frac{1}{2}\sigma ^2s^2)\). Substituting M(s) into (4.9) and (4.10), we obtain

$$\begin{aligned} c^\pm (s)=\frac{\ln (\rho )-\alpha \tau }{s}+\left( \frac{\sigma ^2}{2}+d\tau \right) s\mp \left( \mu +q\tau \right) . \end{aligned}$$
(4.12)

Note that if the extinction condition is satisfied, i.e. \(\ln \rho -\alpha \tau <0,\) then \(c^\pm (s)\rightarrow -\infty \) as \(s\rightarrow 0^+\). Thus, in this case, the infimum in (4.11) is undefined, and the population does not spread. Similarly, when \(\rho =e^{\alpha \tau }\), the infimum in (4.11) is zero and the population does not spread either.

From now on, we assume \(\rho > e^{\alpha \tau }\). We observe that \(c^\pm (s)\) approach infinity as \(s\rightarrow 0^+\) and \(s\rightarrow \infty \). Thus, \(c^\pm (s)\) attain a minimum on \((0,\infty )\). Since \(c^+(s)\) and \(c^-(s)\) differ only by a constant, this minimum occurs at the same point, say \(s^*>0\). Setting the derivative of either function to zero, we get the unique critical point

$$\begin{aligned} s^*=\sqrt{\frac{{\ln (\rho )}-\alpha {\tau }}{\sigma ^2/2+d{\tau }}}. \end{aligned}$$
(4.13)

Thus, the upstream and downstream spreading speeds are given by

$$\begin{aligned} c^\pm (s^*)=2\sqrt{\left( \ln (\rho )-\alpha \tau \right) \left( \frac{\sigma ^2}{2}+d\tau \right) }\mp \left( {\mu }+q\tau \right) . \end{aligned}$$
(4.14)

We note that \(c^+(s^*)>0\) and \(c^-(s^*)>0\) are each equivalent to \(\rho >e^{\alpha \tau }e^\frac{(\mu +q\tau )^2}{2(\sigma ^2+2\tau d)}.\) Thus, the population spreads in both directions exactly when

$$\begin{aligned} \rho >e^{\alpha \tau }e^\frac{(\mu +q\tau )^2}{2(\sigma ^2+2d\tau )}. \end{aligned}$$
(4.15)

This condition is, in general, stronger than the non-extinction condition \(\rho >e^{\alpha \tau }.\) The two conditions are equal only if \(\mu =-q\tau ,\) i.e. the upstream dispersal bias and the downstream drift precisely compensate each other. In that case, the upstream and downstream speeds are equal. All else being equal, the minimal per capita growth rate required for spread in both directions increases with the total net displacement by directed movement (given by \(|\mu +q\tau |\)) and decreases with the total amount of random movement (given by \(\sigma ^2+d\tau \)).

5 Nonlinear model on unbounded domain

We now return to the nonlinear model (2.5) on the unbounded domain and use the theory developed in Weinberger (1982) to prove the existence and linear determinacy of the upstream and downstream spreading speed, and the equivalence of these spreading speeds with the minimum travelling wave speeds in the upstream and downstream directions. Most applications of Weinberger (1982) focus on the case where spreading speeds are identical in both direction, but the theory also applies to the case where there are different speeds in different directions, as illustrated in Li et al. (2009).

For the remainder of this section, we assume that the condition \(g'(0)> e^{\alpha \tau }\) holds. We define B as the set of non-negative continuous functions on \(\mathbb {R}\) that are bounded by \(U^*,\) the fixed point of the map H above. To apply Weinberger’s spreading speed theory, we establish the basic facts about our solution operator Q in (2.6), namely Hypotheses (3.1) in Weinberger (1982). These are

H1:

\(Q[u]\in B\) for all \(u\in B\);

H2:

Q commutes with \(T_y\) where \(T_y[u](x)=u(x-y)\);

H3:

there are constants \(0\le \pi _0<\pi _1\le \pi _+\) such that \(Q[\beta ]>\beta \) for \(\beta \in (\pi _0,\pi _1)\), \(Q[\pi _0]=\pi _0\), \(Q[\pi _1]=\pi _1\), if \(\pi _1<\infty \);

H4:

\(u\le v\) implies \(Q[u]\le Q[v]\);

H5:

\(u_n\rightarrow u\) uniformly on each bounded interval implies that \(Q[u_n]\rightarrow Q[u]\) pointwise.

By the comparison Lemma 3.1, operator Q leaves B invariant so H1 is satisfied. To evaluate H2, observe that Q commutes with all translations of the real line. It is clear that operator \(Q_\tau \) commutes with all translations. For the convolution, we see this fact from the change of variables

$$\begin{aligned} \int _{-\infty }^\infty K(x-y-z)v(z)dz=\int _{-\infty }^\infty K(x-s)v(s-y)ds \end{aligned}$$

and for the map g that is applied pointwise, it is clear. The properties in H3,

$$\begin{aligned} Q[0]=0, \quad Q[U^*]=U^*,\quad \mathrm{and}\quad Q[U]>U\quad \mathrm{for}\quad U\in (0,U^*), \end{aligned}$$

are clear from the properties of the function H,  defined previously. By the comparison Lemma 3.1, operator Q is also order preserving, so that H4 is satisfied.

The time-\(\tau \)-map \(Q_\tau \) of the reaction–advection–diffusion equation is compact in B in the topology of uniform convergence on every bounded interval. In addition:

Lemma 5.1

The convolution operator \(u\mapsto K*u\) is compact in B.

A proof is given in the Appendix. Because g is continuous, the above two results are sufficient to make Q (2.6) compact in B in the topology of uniform convergence on every bounded interval.

Altogether, by applying the results from Weinberger (1982), we find the following result.

Theorem 5.2

The rightward and leftward spreading speeds \(c_*^\pm \) exist for model (2.5). For every \(c>c_*^+\) (\(c>c_*^-\)) there exists a rightward (leftward) traveling wave of speed c. Furthermore, the system is linearly determined, i.e. \(c_*^\pm =\inf _{s>0}c^\pm (s)\), see (4.11).

6 Critical domain size

In this section, we explore the dynamics of our model on the bounded domain [0, L]. Depending on the choice of boundary conditions in (2.2) and dispersal kernel, individuals may leave the domain but cannot enter. Since we have excluded an Allee effect from the dynamics of our model, we have the classical set-up of the critical patch-size problem. We expect there to be a minimum value \(L^*,\) below which the population will go extinct, and above which it will persist.

The larval drift model (2.1) on the bounded domain [0, L] and with boundary conditions in (2.2) is well defined in some appropriate function space, for example the space of square integrable functions on [0, L]. In analogy with the solution on the unbounded domain, we denote its solution with initial condition \(u_{n,0}\) as \(u_n(x,\tau )=\bar{Q}_\tau [u_{n,0}].\) Accordingly, the next-generation map is

$$\begin{aligned} u_{n+1,0}(x)=g\left( \int _0^L \bar{K}(x,y) \bar{Q}_\tau [u_{n,0}](y) dy\right) . \end{aligned}$$
(6.1)

We assume that \(\bar{K}\) is a continuous function that is bounded below by some positive constant. Then the next-generation operator is positive and completely continuous on the space of square-integrable functions. To define its derivative, we consider the Green’s function, \({\bar{G}},\) of the linearization of the advection–diffusion equation on the bounded domain [0, L], namely

$$\begin{aligned} \frac{\partial {\bar{G}}}{\partial t}=d\frac{\partial ^2 {\bar{G}}}{\partial x^2}-q\frac{\partial {\bar{G}}}{\partial x}-\alpha {\bar{G}},\quad {\bar{G}}(x,y,0)=\delta (x-y), \end{aligned}$$
(6.2)

with boundary conditions

$$\begin{aligned} d\frac{\partial {\bar{G}}}{\partial x}-q {\bar{G}} = a_1 {\bar{G}}, \quad x=0, \quad d\frac{\partial {\bar{G}}}{\partial x}-q {\bar{G}} = - a_2 {\bar{G}}, \quad x=L. \end{aligned}$$
(6.3)

Then the solution \({\bar{G}}(x,y,\tau )\) is the linearization of \(\bar{Q}_\tau \) at zero (Lewis and Li 2012). Using the chain rule, the Fréchet derivative of the operator in (6.1) at zero is given by

$$\begin{aligned} \phi \mapsto \rho \int _0^L \int _0^L \bar{K}(x,y) {\bar{G}}(y,z,\tau )dy \phi (z) dz=:\rho \int _0^L {\widehat{K}}(x,z)\phi (z) dz. \end{aligned}$$
(6.4)

Under the assumptions in this paper, this Fréchet derivative is a superpositive operator, i.e. it has a simple dominant eigenvalue with positive eigenfunction, and no other eigenfunction is positive (Krasnosel’skii 1964; Lutscher and Lewis 2004). The critical domain size is given when the dominant eigenvalue of this operator equals unity.

In general, it is impossible to derive an exact explicit expression for the critical domain size. In the special case where \(\tau =0,\) and \(\bar{K}\) is a truncated Laplace kernel, such an explicit expression is available (Kot and Schaffer 1986). Even when the kernel is a convolution of two Laplace kernels, an expression can be obtained through the reduction of the integral equation to a differential equation (Jin and Lewis 2011). Since in our case such a reduction, and therefore explicit expression, is impossible, we look for an explicit but approximate expression for the dominant eigenvalue and the critical domain size.

We find the desired approximate expression for the dominant eigenvalue by using the average dispersal success approximation for integral operators (Van Kirk and Lewis 1997; Lutscher and Lewis 2004; Fagan and Lutscher 2006) and related ideas for partial differential equations (Vasilyeva and Lutscher 2012; Cobbold and Lutscher 2013). Indeed, spatial averaging shows that to first order, the dominant eigenvalue \(\lambda \) of the linearized operator in (6.4) is given by \(\lambda \approx \rho {\widehat{S}},\) where

$$\begin{aligned} {\widehat{S}}=\frac{1}{L}\int _0^L\int _0^L {\widehat{K}}(x,z)dx dz \end{aligned}$$
(6.5)

is the average dispersal success (ADS) of kernel \({\widehat{K}}.\) When \({\widehat{K}}\) is symmetric, then this approximation presents an upper bound of the dominant eigenvalue and is therefore a conservative estimate of population growth or extinction.

To calculate the ADS for \({\widehat{K}}\), we use Fubini’s theorem and obtain

$$\begin{aligned} \lambda \approx \rho \frac{1}{L}\int _0^L\int _0^L\int _0^L \bar{K}(x,z) {\bar{G}}(z,y,\tau )dz dy dx=\rho \frac{1}{L}\int _0^L s_{K}(z)r_{G}(z)dz, \end{aligned}$$
(6.6)

where \(s_K(y)=\int _0^L \bar{K}(x,y)dx\) is the dispersal success function for \(\bar{K}\), and \(r_G(x)=\int _0^L {\bar{G}}(x,y,\tau )dy\) is the redistribution function for \({\bar{G}}\) (Lutscher and Lewis 2004).

The redistribution function \(r_G(x)\) denotes the density of individuals at the end of the aquatic stage, given that they were initially distributed in a spatially uniform manner. The dispersal success function \(s_K(y)\) denotes the probability that an individual dispersing from the point y, \(0\le y \le L\), remains in the domain [0, L] after dispersal. Formula (6.6) has a nice interpretation in this two-stage process. Given a uniform initial density of individuals, function \(r_G\) indicates where individuals move to during the first, aquatic dispersal phase, and function \(s_K\) indicates from where those individuals manage to stay in the domain during the second, airborne dispersal phase. Dispersal success is high if the locations where individuals frequently settle after the first phase coincide with locations where recruitment into the domain is high in the second phase.

For a given kernel \(\bar{K},\) the dispersal success function can be evaluated in a straightforward manner, but since \({\bar{G}}\) is given only indirectly as the Green’s function of a differential operator, we now derive an approximation to \(r_G\) in terms of the underlying differential equation.

We start by noting that \(r_G(x)=u(x,\tau )\), where u(x, t) is the solution of the linear reaction–diffusion–advection equation (2.7) with boundary conditions (2.2) and initial value \(u(x,0)=1\). Indeed,

$$\begin{aligned} u(x,\tau )=\int _0^L {\bar{G}}(x,y,\tau ) u(y,0)dy=\int _0^L {\bar{G}}(x,y,\tau )\cdot 1 dy=r_G(x). \end{aligned}$$
(6.7)

Assuming that \(\tau \) is large enough (which reflects the fact that the larval stage is the longest stage of the life cycle) and that the spectral gap between the first and second eigenvalue of equation (2.7) with boundary conditions (2.2) is large enough, we can approximate \(r_G(x)\) by \(e^{\lambda _1\tau }\phi _1(x)\), where \(\lambda _1\) is the principal eigenvalue of (2.7) with boundary conditions (2.2), and \(\phi _1(x)\) is the corresponding positive eigenfunction with average equal to unity. In the following, we give a few examples of \(r_G\) and \(s_K.\)

6.1 Hostile boundary conditions

When the boundary conditions for the reaction–advection–diffusion equations are hostile, we can calculate the approximate redistribution function explicitly. Hostile boundary conditions result when \(a_{1,2}\rightarrow \infty \) in conditions (6.3). The resulting eigenvalue problem

$$\begin{aligned} \lambda _1 \phi _1=d\phi _1''-q\phi _1'-\alpha \phi _1,\quad \phi _1(0)=\phi _1(L)=0 \end{aligned}$$
(6.8)

is best solved by using the transformation \(v(x)=w(x)\exp (qx/(2d)).\) We find

$$\begin{aligned} \lambda _1=-\left( \frac{\pi ^2 d}{L^2} + \frac{q^2}{4d} +\alpha \right) ,\quad \phi _1(x)=A_1 e^{\frac{qx}{2d}}\sin (\pi x/L). \end{aligned}$$
(6.9)

We determine \(A_1\) by scaling the average of \(\phi _1\) to unity, and we obtain the approximate expression

$$\begin{aligned} r_G(x)\approx e^{\lambda _1\tau }\phi _1= e^{\lambda _1\tau } \frac{\frac{q^2 L^2}{4\pi d^2} + \pi }{e^{\frac{qL}{2d}}+1}e^{\frac{qx}{2d}}\sin (\pi x/L). \end{aligned}$$
(6.10)

6.2 Danckwerts boundary conditions

We calculate this eigenfunction for zero flux upstream and free-flow downstream conditions, i.e. \(a_1=0\), \(a_2=q.\) Using Prop. 2.1 from Vasilyeva and Lutscher (2011), we find

$$\begin{aligned} \phi _1(x)=A_1e^{\frac{q}{2d}x}\cos \left( \theta _1x\right) +B_1e^{\frac{q}{2d}x}\sin \left( \theta _1x\right) , \end{aligned}$$
(6.11)

where \(\theta _1=\frac{\sqrt{-4d(\lambda _1+\alpha )-q^2}}{2d}\), and \(A_1, B_1\) are constants. From the condition that the expression under the root be positive, we obtain the bound \(\lambda <-(q^2/(4d)+\alpha ).\) In fact, solving for \(\lambda _1\), we find the analogous expression to (6.9) as

$$\begin{aligned} \lambda _1=-\left( \theta _1^2 d + \frac{q^2}{4d} +\alpha \right) . \end{aligned}$$
(6.12)

The boundary conditions impose the conditions of the coefficients

$$\begin{aligned} B_1=\frac{q}{2\theta _1d}A_1,\quad \mathrm{and}\quad \tan (\theta _1L)=\frac{2d\theta _1q}{4d^2\theta _1^2-q^2}. \end{aligned}$$
(6.13)

The latter equality defines a sequence of eigenvalues for (2.7, 2.2), and in particular \(\lambda _1.\) We normalize the eigenfunction so that its average equals unity and arrive at

$$\begin{aligned} \phi _1(x)=\frac{e^{\frac{qx}{2d}}\left( \cos (\theta _1x)+\frac{q}{2\theta _1d}\sin (\theta _1x)\right) }{\frac{1}{L}\int _0^Le^{\frac{qx}{2d}} \left[ \cos (\theta _1x)+\frac{q}{2\theta _1d}\sin (\theta _1x)\right] dx}. \end{aligned}$$
(6.14)

6.3 Normal distribution for adult flight

When the adult dispersal stage is modeled by a Normal distribution with mean \(\mu \) and variance \(\sigma ^2,\) we have

$$\begin{aligned} K(x)=\frac{1}{2\sigma \sqrt{\pi }}\exp \left( -\frac{(x-\mu )^2}{2\sigma ^2}\right) . \end{aligned}$$
(6.15)

The dispersal success function of this kernel can be written in terms of the so-called error function

$$\begin{aligned} s_K(x)=\frac{1}{2}\left[ \mathrm{erf}\left( \frac{x-\mu }{\sigma \sqrt{2}}\right) - \mathrm{erf} \left( \frac{x-\mu -L}{\sigma \sqrt{2}}\right) \right] . \end{aligned}$$
(6.16)

6.4 Laplace distribution for adult flight

We can also describe adult flight by a possibly shifted, asymmetric Laplace kernel

$$\begin{aligned} K(x)=\left\{ \begin{array}{ll} A e^{b_1(x-{\bar{x}})}, &{} x<{\bar{x}}\\ Ae^{-b_2 (x-{\bar{x}})},&{} x\ge {\bar{x}}, \end{array}\right. \end{aligned}$$
(6.17)

where \(b_{1,2}>0\) and \(A=\frac{b_1b_2}{b_2+b_1}.\) When \({\bar{x}}=0,\) this kernel can be derived from a process of random movement and constant settling (Lutscher et al. 2005). The mean, variance and skewness of this kernel are

$$\begin{aligned} \mu =\frac{1}{b_2}-\frac{1}{b_1}+{\bar{x}},\quad \sigma ^2=\frac{1}{b_2^2} + \frac{1}{b_1^2},\quad \gamma _1=2\frac{b_1^3-b_2^3}{(b_1^2+b_2^2)^{3/2}}. \end{aligned}$$
(6.18)

The dispersal success function can be calculated explicitly as follows:

  1. (a)

    if \({\bar{x}}<-L\) then

    $$\begin{aligned} s_K(z)=-\frac{A}{b_2}e^{b_2(z+{\bar{x}})}(e^{-b_2L}-1),\quad 0\le z\le L; \end{aligned}$$
    (6.19)
  2. (b)

    if \(-L\le {\bar{x}}\le 0\), then

    $$\begin{aligned} s_K(z)= \left\{ \begin{array}{ll} -\frac{A}{b_2}e^{b_2(z+{\bar{x}})}(e^{-b_2L}-1),&{} 0\le z\le - {\bar{x}} \\ A\left( \frac{1-e^{-b_1(z+{\bar{x}})}}{b_1}+\frac{1-e^{-b_2(L-z-{\bar{x}})}}{b_2}\right) , &{} -{\bar{x}}\le z\le L, \end{array}\right. \end{aligned}$$
    (6.20)

We explore some of these formulas and their sensitivity with respect to parameter values in the next section.

7 Parameters and numerical results

To illustrate some of our results, we find parameter estimates (for the linear model) for stoneflies (Plecoptera) from the literature. The hydrological conditions for Broadstone Stream in southeast England are reported by Speirs and Gurney (2001). This 750m long stream moves with average speed \(\hat{q}=4\) km/day. Citing work by Townsend and Hildrew (1976), about relative abundance of stoneflies in drift and benthos, Speirs and Gurney argue that the effective drift velocity for stoneflies should be only 0.01 % of the flow speed, so that \(q=0.4 ~\hbox {m}\)/day. The diffusion coefficient is much harder to estimate; Speirs and Gurney use \(d=0.021\) km\(^2\)/day for simulations.

A single female stonefly can lay several hundred or even a few thousand eggs. Assuming a 50/50 sex-ratio, we choose \(\rho =1000.\) The death rate (\(\alpha \)) is strongly dependent on conditions. Low oxygen levels can induce high mortality in stoneflies. Main predators are fish, but those are absent from Broadstone Stream. We consider values of \(\alpha \) that result in the (non-spatial) basic reproduction number \(R_0=\rho e^{-\alpha \tau }\) to be in the range [1.0015, 2.5]. Accordingly, \(\alpha \in [0.03,0.0345],\) which corresponds to between 0.1 and 0.25 % survival probability during a 200-day drift period.

For adult dispersal, we use the data from MacNeale et al. (2005), who marked, released and recaptured 190 stoneflies. Specifically, their histogram of dispersal distances is the basis of Fig. 2. We used least squares to fit a Gaussian kernel and a generalized Laplace kernel to this histogram. The resulting mean and variance of the Gaussian kernel are \(\mu =-172~\hbox {m}\) and \(\sigma ^2=28079~\hbox {m}^2\).

Fig. 2
figure 2

Comparison of the histogram from MacNeale et al. (2005) with two different (scaled) distributions. Parameters for the Gaussian kernel (6.15) and the generalized Laplace kernel (6.17) were obtained by minimizing the sum of squared differences with the histogram

Full size image

7.1 Persistence and average dispersal success

The boundary conditions for the drift stage of the population have a profound effect on the persistence conditions when the domain is short. We obtain a rough estimate for the required growth rate \(\rho \) by setting \(\lambda =1\) in (6.5) and find the condition \(\rho >1/{\widehat{S}}.\) When boundary conditions are hostile at the upstream and downstream end, the average dispersal success is extremely low (\({\widehat{S}}\sim 10^{-35}\)) so that the population cannot persist despite its high reproductive output. With Danckwerts boundary conditions, the ADS is much higher (\({\widehat{S}}=0.0017\)) and the population can easily persist, given its high reproductive output. The average dispersal success for hostile boundary conditions is highly sensitive to domain length, much more so than for Danckwerts conditions. For example, increasing the length of the stream to 10 km increases the ADS for hostile conditions to \({\widehat{S}}\sim 10^{-4}\) so that persistence of the species is possible with \(\rho >1900,\) which seems to be within the possible range. For Danckwerts conditions, we find \({\widehat{S}}=0.0024\) for those values. (All of these calculations refer to \(\alpha =0.03.)\)

We illustrate the redistribution function and dispersal success function for this case in Fig. 3. The redistribution function for hostile conditions is highest near the center of the domain. Towards the boundaries, the risk of boundary loss increases. For the Danckwerts conditions, the redistribution function is higher at the downstream end since individuals get transported there but only leave the domain by advection and not by diffusion. The dispersal success function with negative \(\mu \) and smaller \(\sigma ^2\) is shifted to the upstream end (left); and has a long plateau because of the relatively smaller variance (solid line). For larger variance and zero mean, we see a symmetric function with a smaller plateau in the middle (dashed).

For comparison, Speirs and Gurney (2001) considered the population without adult flight stage. They used zero flux boundary conditions upstream and hostile conditions downstream; a situation somewhere in between our two cases. They found that the population can easily persist. The rescaling of the advection speed according to benthic residence time (see above) is crucial for persistence in both cases. Without a benthic refuge where stoneflies are not transported downstream, the population cannot persist, irrespective of the boundary conditions.

Fig. 3
figure 3

Left panel the redistribution functions for hostile boundary conditions (solid) as in (6.10) and for Danckwerts conditions (dashed) as in (6.14). Parameters are \(\tau =200\) days, \(L=10\) km, \(d=0.021~\hbox {km}^2\)/day, \(q=0.4~\hbox {m}\)/day, \(\alpha =0.03\). Right panel the dispersal success function for a a Gaussian dispersal kernel as in (6.16). Parameters are \(L=10\) km, \(\mu =-172~\hbox {m}\), \(\sigma ^2=28079~\hbox {m}^2\) (solid) and \(\mu =0~\hbox {m}\), \(\sigma ^2=280790~\hbox {m}^2\) (dashed)

Full size image

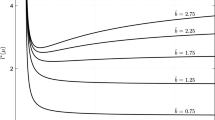
To explore the effect of different parameters on persistence, we chose to vary each parameter uniformly around its mean value by \(\pm \)20 % and performed a sensitivity analysis based on Latin hypercube sampling and partial rank correlation coefficients (PRCC), after visually inspecting that the relationship between each of the parameters and the average dispersal success is monotone (Marino et al. 2008). For the chosen values, we find that \({\widehat{S}}\) is most sensitive to domain length (positive) and to mortality and time in drift (negative), see Fig. 4.

Fig. 4
figure 4

Tornado plot of PRCCs, showing the sensitivity of the average dispersal success \({\widehat{S}}\) to all parameters with Danckwerts boundary conditions. Mean parameter values are varied by \(\pm \)20 %, \(N=1000\) samples were generated for the Latin hypercube sample. Mean values are as in the previous figure. Here \(\sigma ^2\) is the variance of the dispersal kernel, \(\mu \) is the shift of the dispersal kernel, \(\alpha \) is the mortality rate in the water, q is the advection speed, d is the diffusion coefficient, L is the domain size and \(\tau \) is the length of time in the aquatic phase

Full size image

If the population can persist, solutions will approach a positive impulsive periodic orbit. Population levels decline throughout the year due to death and increase sharply once a year due to births. The shape of the spatial distribution depends on the boundary conditions for the drift stage and the shape of the dispersal kernel. In Fig. 5, we chose Danckwerts’ boundary conditions and a Gaussian dispersal kernel. At the end of the drift phase, the upstream end (\(x=0\)) is lowest, and the density profile is increasing downstream. At the beginning of the next drift phase, the population decreases downstream since adult flight and egg deposition are biased upstream.

Fig. 5
figure 5

Dynamics of a population approaching a stable impulsive periodic orbit. Danckwerts’ boundary conditions and a Gaussian dispersal kernel are used. Time is in days, space is in meters. Parameters are as in the text with \(\alpha =0.0345\). Population reproduction is modeled by a scaled Beverton–Holt function \(g(u)=1000u/(1+1000u)\)

Full size image

7.2 Population spread

When a population can persist on a bounded domain, it can spread upstream and downstream on the infinite domain. When adult dispersal is unbiased, the downstream spread rate (\(c^-\)) is higher than the upstream rate (\(c^+\)), since water flow takes individuals downstream. As the upstream bias of adult flight increases (\(\mu <0\)), the downstream rate decreases and the upstream rate increases. At the estimated value \(\mu =-172~\hbox {m}\), both speeds are positive so that the population can persist and spread in both directions. When adult dispersal is biased downstream (\(\mu >0\)) the upstream speed can eventually decrease to zero so that the population cannot spread upstream. The left panel in Fig. 6 illustrates these observations for the Gaussian kernel, using the explicit formula in Example 4.3.

Fig. 6
figure 6

Upstream and downstream spread rates (\(c^\pm \) in meters per generation) according to formula (4.14) as a function of bias of adult flight (\(\mu ,\) left panel) and effective drift velocity (q,  right panel). Fixed parameters are \(\tau =200\) days, \(d=0.021~\hbox {km}^2\)/day, \(q=0.4~\hbox {m}\)/day, \(\alpha =0.0345\), \(\mu =-172~\hbox {m}\), \(\sigma ^2=28079~\hbox {m}^2\)

Full size image

Similarly, as we increase the effective drift speed (q), the upstream speed will decrease and the downstream speed will increase. At the estimated value \(q=0.4\hbox {m}\)/d, both speeds are positive, and the population can persist and spread. Increasing downstream transport by a factor of about 4 will decrease the upstream speed below zero so that the population cannot persist (see right panel in Fig. 6).

Figure 7 shows how the population spreads in both directions after a local introduction in the center of the domain. For this scenario, we chose the same set-up as in Fig. 5.

Fig. 7
figure 7

A population spreads upstream and downstream from a small initial inoculation. The domain is 100 km long, the initial population is distributed over 2 km at the center of the domain. Danckwerts boundary conditions and a Gaussian dispersal kernel are used with parameters as above

Full size image

8 Discussion

This paper focuses on a mathematical model for persistence of river organisms with multiple life stages, one in the drift, and the other on the river bank. While each life stage has dispersal, the first stage dispersal is driven by water flow and the second is driven by flight, possibly with an upstream bias. The result is a nonlinear dynamical system, given by an impulsive reaction–advection–diffusion equation with non-local impulse in space. The model extends earlier work by Lutscher et al. (2010) where linear integrodifference equations were used to describe the same process. Our mathematical analysis of the model builds on earlier work by Lewis and Li (2012) on the behaviour of impulsive reaction diffusion equation with a local, rather than nonlocal, impulse in space. However, the deeper mathematical foundations for the analysis can be found in Weinberger (1982).

Our definitions of weak versus local persistence on an infinite domain allow us to distinguish between populations that persist in the system, but not at any fixed location (weak persistence), versus populations that persist at a fixed location because they maintain a toe hold there (local persistence). We connect the issue of local persistence in the infinite domain to having positive upstream and downstream spreading speeds. These speeds, in turn, are connected to the minimum travelling wave speeds for the linearized operator, in upstream and downstream directions using the theory of Weinberger (1982). On the other hand, we would expect that a species that persists only weakly is at risk of being washed out of the system when the domain size becomes finite. However, the details of such outcomes depend crucially on the boundary conditions for the finite domain. When these are applied it is possible to use dispersal success theory (Lutscher and Lewis 2004) to analyze outcomes.

When our model is calibrated to the stone fly populations we observe that that either weak or local persistence is possible on an infinite domain, depending on parameter values, and, likewise, populations may or not persist on a finite domain, depending on the parameters. Hence, an investigation on how individual parameter values affect persistence is a useful undertaking. As shown in Fig. 4, the average dispersal success in the river has varying sensitivity to the model parameters, but increases to stream length (L) have the largest positive effects and increases to mortality rates (\(\alpha \)) or development times (\(\tau \)) have the largest negative effects on dispersal success. By way of contrast, adult flight has a key role in determining local persistence of the population, as illustrated explicitly in the persistence formula (4.15) in Example 4.3. There are two mechanisms to decrease the requirements on the minimum reproductive output for local persistence according to (4.15). Upstream bias in adult flight implies that \(\mu \) and q are of opposite signs, so that increasing \(\mu \) decreases the right hand side of (4.15), at least as long as \(|\mu |<q\tau .\) Variance in adult dispersal, on the other hand, acts similarly to diffusion during the aquatic dispersal phase in that the population is spread over a larger region, thereby enhancing upstream movement, and there by persistence.

In this work, drift and diffusion rates in the flow were scaled by the fraction of time that the larvae were in the flow versus residing on the benthos. An alternative approach that could be used for future work would involve an additional compartment for organisms on the benthos, with movement of individuals back and forth between benthic and advection–diffusion compartments. This kind of approach has been used successfully before, for example by Pachepsky et al. (2005) in their extension of the Speirs and Gurney (2001) original reaction–diffusion–advection model for the drift paradox. An even more general approach would involve a stage-structured impulsive reaction–diffusion–advection system of equations. This would allow for insects with overlapping generations as described by the stage-structured model. Currently such theory is lacking, but could be developed in a straightforward way, based on Roger Lui’s extensions (Lui 1989a, b) of the work by Weinberger (1982).