Abstract
Organisms inhabiting river systems contend with downstream biased flow in a complex tree-like network. Differential equation models are often used to study population persistence, thus suggesting resolutions of the ‘drift paradox’, by considering the dependence of persistence on such variables as advection rate, dispersal characteristics, and domain size. Most previous models that explicitly considered network geometry artificially discretized river habitat into distinct patches. With the recent exception of Ramirez (J Math Biol 65:919–942, 2012), partial differential equation models have largely ignored the global geometry of river systems and the effects of tributary junctions by using intervals to describe the spatial domain. Taking advantage of recent developments in the analysis of eigenvalue problems on quantum graphs, we use a reaction–diffusion–advection equation on a metric tree graph to analyze persistence of a single population in terms of dispersal parameters and network geometry. The metric graph represents a continuous network where edges represent actual domain rather than connections among patches. Here, network geometry usually has a significant impact on persistence, and occasionally leads to dramatically altered predictions. This work ranges over such themes as model definition, reduction to a diffusion equation with the associated model features, numerical and analytical studies in radially symmetric geometries, and theoretical results for general domains. Notable in the model assumptions is that the zero-flux interior junction conditions are not restricted to conservation of hydrological discharge.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
Organisms associated with streams and rivers may be redistributed by flow that is strongly biased downstream. These include macroinvertebrates (Waters 1972; Rader 1997), algae and diatoms (Ameziane et al. 2003; Robson et al. 2008), riparian plants (Levine 2003), and even non-living organic matter (Newbold 1992). In the absence of counteracting processes, a population subjected to directionally-biased redistribution will see its average location shifted downstream, eventually being washed out into habitats such as lakes or estuaries where conditions do not support survival or reproduction. The problem of explaining how populations persist in the face of downstream biased flow has been termed the “drift paradox” (Müller 1954; Waters 1972; Müller 1982; Hershey et al. 1993; Williams and Williams 1993).
Hypothesized resolutions to the drift paradox generally emphasize compensatory upstream movements [the so-called colonization cycle, Müller (1954)], or suggest that drifting individuals represent a surplus that would not otherwise contribute to local persistence (Waters 1972). Over the past decade, these hypothesized mechanisms have been formalized mathematically (e.g. Speirs and Gurney 2001; Lutscher et al. 2005; Pachepsky et al. 2005). A key idea is that populations must have the ability to invade upstream in order to persist (Lutscher et al. 2010). Once that necessary condition is met, persistence is determined by the interplay of the size of the habitable river domain, population dispersal characteristics, and ecological interactions (see also Lutscher et al. 2006, 2007; Hilker and Lewis 2010; Kolpas and Nisbet 2010).
With the aim of presenting analytically tractable models, the geometric structure of the river system is commonly modeled by the real line or a finite length interval (e.g., the models cited above). In this simple interval geometry, population persistence can be easily related to the length of the habitable river domain and population dispersal via the principle eigenvalue of an appropriately linearized system of equations. Typically, the principle eigenvalue characterizes growth rate away from the zero (extinction) steady state, leading to a critical domain size. This approach follows a long tradition in ecological modeling dating back to early invasion models Fisher (1937) and persistence models (Skellam 1951; see also Cantrell and Cosner 2003).
Unlike the simple geometry of an interval spatial domain, real river systems exhibit a branching tree-like (“dendritic”) network structure. Drawing valid conclusions about complex river networks from models with interval geometries is problematic. Dendritic network geometries in themselves may lead to changes in population dynamics and viability (Cuddington and Yodzis 2002; Fagan 2002; Goldberg et al. 2010), while tributary dependent features, including non-uniform headwater conditions and longitudinal changes in habitable cross-sectional areas, may alter persistence conditions (Fausch et al. 2002; Grant et al. 2007). Although these previous models address aspects of network complexity, they artificially discretize habitat so that population dynamics are restricted to network nodes. Previous work modelling population dynamics locally in river segments using differential equations in continuous domains (e.g. intervals) suggests that network branches should be considered as continuous primary habitat in order to connect local river segment dynamics to global river network dynamics. The lack of an appropriate modeling framework for branching river networks has been identified as a major hindrance to understanding the influences of spatial structure and variability on ecological dynamics (Grant et al. 2007).
The theory of quantum graphs provides a framework that can overcome the geometric limitations of interval river models. Quantum graphs pair a metric graph, which allows continuous representations of the spatial domain on a branching network, with a differential operator (Kuchment 2004, 2008). Metric graph branches (the graph “edges”) are identified with continuous intervals; functions and operators are defined along these intervals. This structure supports differential equation models on the graph, with junction conditions determining how solutions merge and split at branch junctions (the graph “vertices”).
Quantum graph models have been extensively applied to quantum systems [see Kuchment (2004, 2008) for surveys, and Exner et al. (2008) for a collection of recent work] and to mathematical studies of diffusion on networks [Kostrykin et al. (2008) has numerous references]. Potential applications in biology have been noted (Carlson 2006; Maury et al. 2009; Nicaise 1985; Sherwin et al. 2003), but the literature here is more sporadic and undeveloped. Population dynamics in rivers is typically modeled using extensions of reaction–diffusion–advection (RDA) partial differential equations, which are parabolic initial value problems. While some work has explored related mathematical issues (von Below 1989), the problems of adapting quantum graph concepts to model the impact of branching network structure in rivers has only recently been addressed in Ramirez (2012). This work extended a ‘jump-settlement’ integro-differential equation model introduced in Lutscher et al. (2005) to a network spatial domain using the mathematical theory of quantum graphs. Ramirez (2012) takes advantage of the quantum graph structure by allowing for edge dependent movement parameters and cross-sectional areas while introducing bounds for the critical growth rate in terms of edge-wise parameters, subgraph monotonicity, and upstream boundary condition types. However, as identified in Ramirez (2012), further work is necessary to track how the topological and geometric features of a network interact with movement parameters to affect persistence.
Our current work focuses on an RDA equation in a quantum graph with global constants for diffusion and advection rates. This choice includes a minimum number of parameters, which aids in isolating the effects of network geometry on persistence. Population persistence is characterized in the standard fashion by examining the principle eigenvalue for a linear differential equation that approximates dynamics near the zero steady state. As we will show, persistence results for the RDA model are easily translated over to the jump-settlement integro-differential model.
A notable deviation here from the Ramirez (2012) model is that we interpret cross-sectional area as a habitable area rather than a physical cross-sectional area of a river segment. As a result, our zero-flux interior junction conditions are not restricted to conservation of hydrological discharge, which allows for a broader range of junction behavior and greater interactions between network geometry and movement parameters in estimating persistence outcomes. Another simple (but important) distinction is that we use population density per unit volume (rather than per unit length) which leads us to more easily identify the role of a self-adjoint Laplacian. For our simpler model we are able to establish necessary and sufficient conditions for persistence, characterizing the critical growth rate in terms of the principal eigenvalue of this Laplacian. Moreover, our estimates on the principal eigenvalue are sensitive to global geometric features. We go on to identify radial trees as an important class of examples which we use for both numerical and theoretical studies.
In addition to tracking local edge-wise data as in Ramirez (2012), we track how global geometric features of networks affect persistence. The distribution of habitable domain is much richer in networks than in interval models, capturing a wider array of features of an actual river system, thereby producing richer relationships between dispersal parameters, volume distribution, and principal eigenvalues. Our results shed light on these complex relationships and highlight key differences with interval models.
Although the focus here is on river ecology, the analyses are relevant to a wide range of problems in science involving movement in continuous spatial networks, including predator-prey dynamics on plants (Cuddington and Yodzis 2002), signal propagation in nerve networks (Brette et al. 2007), and nutrient or drug delivery in body vessels (Leitner et al. 2010).
1.2 Summary of results
Quantum graph models of river networks support a wide range of population persistence studies by incorporating such key features as realistic river system geometries, various headwater boundary conditions, and variation of habitable cross-sectional areas. This class of models is rich enough to support detailed numerical work, but tractable enough for interesting analysis. This paper provides an extensive analysis for models with constant diffusion coefficients and advection speeds.
Section 2 introduces the basic quantum graph framework, with RDA equations describing population dynamics along river segments. At segment junctions solutions are required to be continuous and balance incoming and outgoing flows of population, but are not restricted to hydrological conservation of discharge since sectional areas represent habitable areas rather than channel cross sections, and advection represents a directional bias, rather than strictly hydrologic flow speed. Upstream and downstream boundary conditions either exclude return to the system from the outside, or balance advective inflow with diffusive outflow. Because the diffusion coefficient and advection speed are assumed constant, the original reaction–diffusion–advection model may be reduced to a related diffusion equation. This reduction brings along technical tools such as the maximum principle, positivity preservation, and principle eigenvalue analysis. Extending the conditions seen in interval models, population persistence is characterized by a simple condition relating the principle eigenvalue, population growth rate, advection speed and diffusion coefficient.
Section 3 treats radial tree models, for which all model parameters depend only on the distance to the outflow boundary. For these models, eigenfunctions and eigenvalues have simple descriptions in terms of transfer matrix functions, reducing population persistence studies to simple numerical root finding exercises. Numerical studies show that distribution of habitable volume away from a lethal boundary, length structure, and advection speed emerge as important interacting factors in determining persistence while unusual volume distribution can make total volume a poor predictor of population persistence. As such parameters are varied, interval models either underestimate or overestimate persistence relative to the tree model. Although broad parameter ranges are used to aid in the identification of relationships which may otherwise be too subtle to detect, included within is an example which places emphasis on parameter ranges that are realistic in actual river networks. We also consider a radial tree which has an infinite length downstream root branch and recover a persistence condition which coincides with the limiting process of increasing the root branch length to infinity.
Section 4 treats general stream geometries. In this general setting one cannot expect simple formulas for persistence determining eigenvalues. We do provide explicit upper and lower bounds linking persistence with geometric data for quite general river geometries. These bounds feature sensitivity to global data (e.g., volume distribution and distances from headwater boundaries to downstream boundary) in addition to local data (e.g., edge lengths and edge cross sections). A numerical study shows that these bounds track the behavior of principal eigenvalues for radial trees. The form of the bounds suggest that certain trends which appear in radial trees extend to general geometries.
Section 5 relates persistence analysis of the RDA model to persistence analysis of the jump-settlement integro-differential equation (IDE) model introduced in Lutscher et al. (2005) and applied to networks in Ramirez (2012). In particular, a simple formula relates the principal eigenvalue for the RDA model to the principal eigenvalue of the IDE model. A persistence condition for the IDE model is given in terms of the principal eigenvalue of the RDA model.
The paper concludes with a discussion of the results. Proofs for some of the Sects. 2 and 3 results appear in an appendix.
2 RDA models for river networks
2.1 The basic model
The starting point for the network model is a single-species reaction–diffusion–advection (RDA) equation
describing the dynamics of a population residing in a river or stream segment (Speirs and Gurney 2001; Cantrell and Cosner 2003). The function \(u(t,x)\) represents the population density per unit of river volume at time \(t\) and position \(x\). Population movement is modeled with a combination of diffusion and downstream-biased transport (advection). The diffusion coefficient \(D > 0\) captures movement without a preferential direction at the population scale, such as benthic crawling, swimming, or redistribution by river turbulence. The downstream advection speed \(V \ge 0\) captures the downstream population drift, which can differ from the rate of the river current due to organism behavior. The function \(F\) handles birth and death processes.
This work considers population persistence, asking if the linearized model
with intrinsic growth rate \(r > 0\) describes a small population density which is increasing or decreasing. Previous work (Speirs and Gurney 2001; Jin and Lewis 2011; Lutscher et al. 2007) has often modeled the spatial domain by a finite interval, in which case (2.2) is supplemented by boundary conditions.
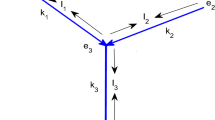
A tree network river model extends this local description by considering multiple river segments whose interactions are mediated by interior junction conditions. As a graph, the river network is a (finite) binary tree. In the network model, river segments are called edges (or branches), and are identified with intervals. Tree vertices with a single incident edge are called boundary vertices. For river modeling, junctions where three segments meet are called interior vertices (see Fig. 1a). In this work all networks will be trees, so the terms will be used interchangeably.
RDA in (directed) rooted metric tree graphs. Each edge (branch) \(e_j\) of the tree is associated with a real interval \([a_j,b_j]\) with length \(l_j=b_j-a_j\) (a). The natural distance function \(d\) on the tree is used to define a global function \(X\) in terms of the root vertex \(w_d\), which provides local coordinates for each edge. Note that \(X\) increases toward the root to zero, in the direction of \(V\) (b). For computations around a junction \(w\), we use the conventions and labels in a
If \(-X\) denotes the distance from the root vertex, then \(X\), which increases in the downstream direction (see Fig. 1b), is a convenient choice of local coordinates for the river segments. With \(A_e\) denoting the habitable cross-sectional area (see Fig. 1a) of the river segment \(e\), the downstream population flux on segment \(e\) is \(A_e(V_eu_e - D_e\frac{\partial u_e}{\partial X}) \). Numbering of the segments meeting at a junction provides a useful alternative notation. Consider an interior junction where two upstream segments (or network edges) \(e_1,e_2\) join the downstream segment \(e_0\) (see Fig. 1a) . Balancing the incoming and outgoing population flux at a junction \(w\) leads to the condition
Population density is assumed continuous at interior junctions, so
If the spatial domain consists of finite length river segments, the tree model will include a single downstream boundary, or root vertex, and multiple upstream boundary vertices. The lethal boundary condition
will be used to model population outflow at upstream or downstream boundary vertices when organisms that cross these boundaries cannot return to the system, as when the river empties into an estuary or flows over a dam. Other upstream boundary conditions include the zero flux condition
which balances advective inflow and diffusive outflow of the population.
Some simplifying assumptions are adopted throughout this work. The cross sectional river (habitat) areas \(A_e\) for segments \(e\) are assumed to be constant along each river segment, although they may vary from segment to segment. The diffusion coefficient \(D\) and advection speed \(V\) are constant throughout the entire model river domain.
As in the single river segment models, some basic properties of solutions to (2.2) on trees may be established by elementary integrations. First, consider the rate of change of the total population. Solutions of (2.2) with the boundary conditions (2.5), (2.6) and junction conditions (2.3), but without the intrinsic growth term \((r = 0)\), should describe nonincreasing populations. Integration over one edge \(e = [a_e,b_e]\) gives
Suppose an interior junction has incident edges \([a_j,b_j]\) for \(j = 0,1,2\), with \([a_0,b_0]\) being the downstream edge (see Fig. 1a). Adding the boundary terms from (2.7) for this junction, the zero flux condition (2.3) gives
The upstream boundary terms (2.6) also vanish. In particular, if (2.6) holds at all upstream boundary vertices, and the lethal condition \(u(v) = 0\) holds at the root vertex, then summing (2.7) over the edges of the tree gives the rate of change in total population,
where \(w_d\) is the root vertex and \(A_d\) denotes the sectional area assigned to the downstream root edge. As expected, the population change is controlled by the root boundary term, which is negative if the population is positive.
A second integral calculation emphasizes the role of the junction and boundary conditions. Still assuming \(r=0\), multiply (2.2) by \(u_e\) and integrate over the edge \(e\) to get
Adding the boundary terms at an interior junction, using (2.3), and using the continuity of \(u\) at interior junctions yields
At upstream boundary vertices \(a_e\) where (2.6) holds there is a contribution
For each interior vertex \(w\), define the incident sectional area difference
Let \(A\) denote the piecewise constant function given by \(A_e\) on edge \(e\). Suppose (2.3) applies at all interior junctions, (2.6) holds at all upstream boundary vertices, and the lethal condition (2.5) holds at the downstream boundary vertex. Summing (2.9) over the edges of the tree \(\fancyscript{T}\) leads to
where \(\varSigma _{a}\) is the sum over interior vertices and \(\varSigma _b\) is the sum over upstream boundary vertices.
Notice that if the habitable area in the two upstream branches at the junctions equals that in the adjacent downstream branches, that is \(A_0 = A_1 + A_2\), all terms on the right in (2.11) are nonpositive, with \(B(w) = 0\). In the following analysis this condition will be extended to allow
maintaining the sign condition at each interior vertex. The assumption (2.12) allows strictly less habitable upstream area. Such a situation could result from longitudinal increases in external hydrological inputs, or from simple changes in benthic habitat. If \(A_j\) is interpreted as a habitable area, the assumption (2.12) could thus be decoupled from the physical sectional areas. Since \(A_j\) is interpreted as habitable area (not necessarily the physical sectional area) and \(V\) is interpreted as a directional bias (rather than being restricted to river flow velocity), (2.12) is not necessarily the allowance of a nonconservative hydrological relation.
2.2 Reduction of the RDA model to a diffusion equation
While the above integral calculations are suggestive, a more careful analysis of (2.2) will provide detailed model predictions, including sharp results on population persistence. This analysis involves a reduction of the RDA model to a related diffusion equation, with an eigenvalue analysis of the corresponding Laplace operator. Because \(V\) and \(D\) are constant throughout the modeled river domain, (2.2) can be reduced to a diffusion equation by a change of variables, which facilitates use of the maximum principle and the development of uniform estimates. If \(-X\) denotes the distance from the root vertex, and if \(u_e(t,X) = \exp (\frac{VX}{2D})U_e(t,X)\) satisfies (2.2), then \(U_e\) satisfies
If \(\fancyscript{T}\) has no infinite length edges, populations \(u\) will persist if and only if solutions \(U\) persist.
This change of variables leaves \(U\) continuous at the junctions. The boundary vertex conditions (2.6) become
while the interior junction conditions (2.3) become
Using these modified vertex conditions, the analysis is simplified further by temporarily dropping the constant \(r - V^2/(4D)\), putting the focus on the diffusion equation \(\partial U/\partial t = D \partial ^2 U/\partial X^2 \) .
The diffusion equation and (2.13) will be solved using eigenfunction expansions. Setting up the appropriate technical machinery, introduce the Hilbert space \(L^2(\fancyscript{T})\), with an inner product given by summing edge integrals,
To treat the diffusion equation with a variety of boundary vertex conditions, denote by \(L\) the differential operator acting by
subject to (2.15) at interior vertices, the downstream boundary vertex condition \(U(w_d) = 0\), and either (2.14) or \(U(w) = 0\) at upstream boundary vertices. When (2.12) holds at each interior vertex, the corresponding operators are denoted by \({L_{m}}\),
and the corresponding diffusion equations with admissible vertex conditions are written as
As with (2.11), integration by parts leads to an expression for the bilinear form of the operators \(L\),
with \(\varSigma _{a}\) again denoting the sum over interior vertices, and \(\varSigma _b\) denoting the sum over those upstream boundary vertices where (2.14) applies. If (2.12) holds, then
Since \(\langle Lf,g\rangle = \langle f, Lg \rangle \) by (2.19), the operator \(L\) is formally self adjoint. Since \(\fancyscript{T}\) has finitely many edges, some routine care (Kuchment 2004) about the domain of \(L\) makes the operator self adjoint with compact resolvent on \(L^2(\fancyscript{T})\). The spectrum thus consists of a sequence of eigenvalues \(\{ \lambda _n \}\) of finite multiplicity, with \( \lambda _n \rightarrow -\infty \). The eigenvalue sequence is comparable to \(-n^2\), and there is an orthonormal basis \(\{ \phi _n \}\) of corresponding eigenfunctions. Every eigenfunction \(\phi _n\) vanishes at the root vertex, so the derivative \(\phi _n^{\prime }\) is not everywhere 0, forcing
Bringing back the constant \(r - V^2/(4D)\), solutions to (2.13) and (2.18) satisfying the vertex conditions for \(t > 0\) may be constructed by expansions with the eigenfunctions of \(L\). If \(U(0,\cdot ) = \sum _n c_n \phi _n \in L^2(\fancyscript{T})\), then the solution of (2.13) will be
2.3 Properties of solutions and a persistence condition
Pointwise estimates for solutions and their derivatives may be obtained with the aid of the following lemma. Together with the eigenfunction expansion (2.21), Lemma 1 shows that if \(U(0,\cdot )\in L^2(\fancyscript{T})\) with edge restrictions \(U_e\), then the solutions \(U_e (t,X)\) of (2.13) and (2.18) are continuous in \((t,X)\) for \( t > 0\). Let \(R_{max}\) be the maximum distance from the root \(w_d\) to a point of \(\fancyscript{T}\), while \(A_{min} = \min _j A_j\). The proofs of the results in this subsection are relegated to an appendix.
Lemma 1
Suppose \(\phi _n\) is an eigenfunction of \(L_m\) with eigenvalue \(\lambda _n\) and \(\Vert \phi _n \Vert = 1\). For all \(w \in \fancyscript{T}\)
When (2.12) holds, the diffusion equation (2.18) satisfies a maximum principle. For a domain \(\varOmega = [0,t_1] \times \fancyscript{T}\), let \(\partial \varOmega \subset \varOmega \) denote the set of points \((t,x)\) with \(t=0,\,t=t_1\), or with \(x\) a boundary vertex of \(\fancyscript{T}\), and let \(\partial \varOmega _0 \) denote the set with \(t=0\) or with \(x\) a boundary vertex. The interior of \(\varOmega \) is \(\varOmega {\setminus } \partial \varOmega \).
Proposition 1
Suppose \(U\) is a solution to \(\partial U/\partial t = D \partial ^2 U/\partial X^2 \) on the interior of \(\varOmega \) with continuity, (2.15), and (2.12) holding at interior vertices. Assume that \(U(t,w_d) = 0\), but relax the previous boundary vertex conditions and assume simply that \(U\) extends continuously to \(\varOmega \). Then the minimum and maximum values of \(U\) are achieved on \(\partial \varOmega _0\).
Proposition 2
Suppose \(U\) is a solution to (2.18). If \(U\) is continuous and nonnegative for \(t=0\), then \(U \ge 0\) for all \(t > 0\).
In addition to the parameter \(r - \frac{V^2}{4D}\), growth or decay of solutions to (2.13) depends on the principle eigenvalue \(\lambda _1\) of \(L\), which varies with the spatial domain. This dependence has an elementary description when the tree \(\fancyscript{T}\) is a single edge of length \(l\). Assume the lethal condition at the downstream boundary, while the upstream boundary condition is \(DU^{\prime }(w) - \frac{V}{2} U(w) = 0\) in downstream oriented coordinates. An eigenfunction \(\phi \) must be a multiple of \( D\cos (x\sqrt{\lambda /D } ) + \frac{V}{2} \sqrt{ \frac{D}{\lambda }}\sin (x \sqrt{\lambda /D })\), and the lethal condition at \(x = l\) means the principle eigenvalue \(\lambda _1 = -\lambda \) is given by the smallest positive solution of
The principle eigenvalue varies continuously from \(\lambda _1 = - \pi ^2D/(4l^2)\) as \(D/(Vl) \rightarrow \infty \), to \(\lambda _1 = - \pi ^2D/l^2\) as \(D/(Vl) \rightarrow 0\), approaching a lethal upstream condition.
Proposition 3
The operator \({L_{m}}\) has a nonnegative eigenfunction \(\phi _1 \) with eigenvalue \(\lambda _1\). Any such \(\phi _1\) is strictly positive except at a lethal boundary vertex.
Proposition 4
The eigenspace for the principle eigenvalue \(\lambda _1\) of \({L_{m}}\) has dimension one.
Theorem 1
Suppose a population \(U\) satisfies (2.13) with the admissible vertex conditions of (2.17), that is
If \(r - \frac{V^2}{4D} < |\lambda _1 | \) the population will not persist. In particular the population will not persist if \(r - \frac{V^2}{4D} \le 0\). If \(r - \frac{V^2}{4D} \ge |\lambda _1 | \) a continuous positive initial population will persist.
This theorem extends to river networks the conditions for population persistence seen in interval models (Speirs and Gurney 2001). If \(r \le \frac{V^2}{4D} \), no population can persist, regardless of the size of the habitable domain. (This result is also consistent with Lutscher et al. (2005) and (Ramirez 2012) when mapped to the jump-settlement IDE model; see Sect. 5 below.) This minimum growth rate represents the upstream invasion criterion in an infinite system (described by Lutscher et al. 2005, 2010). If this minimal growth rate condition is met, population persistence is then constrained geometrically, which is the critical domain size problem (of Skellam 1951; Speirs and Gurney 2001; Lutscher et al. 2005; Pachepsky et al. 2005; Lutscher et al. 2010, among others). It is important to note that Theorem 1 does not necessarily hold without assumption (2.12) since \(\lambda _1\) is no longer guaranteed to be negative and therefore \(r - \frac{V^2}{4D} \le 0\) does not rule out persistence (see Sect. 3.2).
3 Radial tree models
The theoretical and numerical analysis of persistence conditions for river networks is greatly simplified if a tree symmetry assumption is added to the model (2.13). A rooted tree is said to be radial if all tree features, including edge lengths, sectional areas, and boundary conditions depend only on the distance to the root. For example, Fig. 1a is radial if \(a_1=a_2,\,A_1=A_2\), and the boundary conditions at \(a_1\) and \(a_2\) are the same. Radial trees support radial functions and radial solutions to (2.13), which are the focus of this section. More extensive treatments of radial tree function theory are in Carlson (1997, 2000), and Naimark and Solomyak (2000).
Radial tree calculations make use of the global function \(X\), with \(-X\) being the distance to the root (see Fig. 1b). This places the root vertex, assumed to have degree 1, at \(X=0\). Assume there are \(N-1\) subsequent bifurcation levels (see Fig. 1a) at \(X_{N-1} < \cdots < X_1 < 0\), with the upstream boundary vertices at \(X_N\). For \(n = 1,\dots ,N\), the edge lengths at level \(n\) are \(l_n = |X_{n} - X_{n-1}|\). Suppose \(U\) is a radial function whose restriction to \([X_{n},X_{n-1}]\) is \(U_n\).
Sectional areas for edges incident on an interior vertex may vary with the bifurcation level, but in each case \(A_1 = A_2\). The interior junction conditions (2.15) can now be written as a simplified derivative jump condition
while the zero flux condition (2.14) at upstream boundary vertices is
Radial solutions of (2.13) coincide with solutions computed for the interval \([X_N,0]\) in case \(A_0 = A_1 + A_2 = 2A_1\) at each interior vertex. In this case the parameters of (3.1) have the values \(\alpha _n = 0\) and \(\beta _n = 2\), while the sum of the cross sectional areas at a distance \(X\) from the root vertex is constant, independent of \(X\). To establish the claim, suppose \(U(X)\) is a solution of (2.13) on the interval \([X_N,0]\) with lethal or no flux boundary conditions at the endpoints. The corresponding radial function on the radial tree obviously satisfies (2.13) on each edge. At each \(X_n\) the function is continuous, with a continuous derivative, so the conditions (3.1) are satisfied. This identification also extends to integrals of radial population densities and other radial functions over the tree.
Returning to the general conditions (3.1) for a radial tree, Theorem 1 shows that population persistence is controlled by the principle eigenvalue \(\lambda _1\) for the operator \(L_m\). By Proposition 3 this eigenspace has a positive eigenfunction. In the radial tree case the operator \(L_m\) commutes with the tree automorphisms which interchange the subtrees below each interior junction. Averaging the positive eigenfunction over these automorphisms will result in a positive radial eigenfunction with the same eigenvalue, so the \(\lambda _1\) eigenfunction is radial.
3.1 Transfer matrices
The behavior of radial eigenfunctions for \(L\) may be described by using transfer matrices to propagate the initial conditions of solutions of the eigenvalue equation. These transfer matrices are products of monodromy matrices, which propagate initial data across the edges, with jump matrices, which propagate data across interior junctions. The elementary form of these matrices makes them useful for both theoretical and numerical analyses of eigenvalue problems, including the calculation of \(\lambda _1\).
Any eigenfunction of the operator \(L\) will satisfy an equation \(y^{\prime \prime }- (\lambda /D)y=0\) on each interval \([X_{n},X_{n-1}]\). For notational simplicity, consider the case \(D=1\),
Radial eigenfunctions are continuous and satisfy (3.1) at each interior junction. For notational convenience, let \(\omega = \sqrt{-\lambda }\), the square root taken with \(\omega > 0\) if \(- \lambda > 0\).
If the initial data for a solution of (3.3) is \(y(0),y^{\prime }(0)\), the solution on the root edge is
so initial data at 0 is mapped to corresponding data at \(X\) by
In particular if
then at \(X_1 = -l_1\),
Continuity of solutions and (3.1) imply
This process continues across each interior \(X_n\). In terms of the monodromy matrices
and the jump matrices
the solution at \(X_N\) is given by the transfer matrix \(T_N(\lambda )\),
where
Consider the problem of computing \(\lambda _1\) for a radial tree. Although the transfer matrix is complicated for a general radial tree, straightforward numerical methods can be used to compute \(\lambda _1\) for trees with large numbers of edges. Since the lethal condition \(u(w_d) = 0\) holds at the root vertex, initial data for the \(\lambda _1\) eigenfunction \(y\) may be taken as \(y(0) = 0,\,y^{\prime }(0) = 1\). Returning to an arbitrary diffusion constant, the propagated data at \(X_N\) will satisfy the boundary conditions (3.2) at the upstream boundary if \(Dy^{\prime }(X_N^+) - \frac{V}{2}y(X_N) = 0\). In terms of matrix elements \(T_N[i,j]\), this leads to the equation
The principle eigenvalue is the smallest root of (3.5). The problem formulation is similar if the lethal headwater condition replaces (3.2). In that case \(\lambda \) is an eigenvalue when \((0,1)^T\) is an eigenvector of \(T_N\), which occurs when \(T_N[1,2](\lambda {/}D) = 0\).
3.2 Numerical examples
The transfer matrix method from Sect. 3 facilitates computations of principal eigenvalues in radial trees given changes in tree geometry and movement parameters. Yet even within the class of radial trees, geometry is determined by a large quantity of information, particularly the edge lengths and cross sectional areas at each level of the tree. This makes finding simple analytical rules relating general changes in geometry to the principal eigenvalue difficult. Instead, we use our machinery to conduct numerical experiments that explore the sensitivity to changes in geometry and movement parameters for trees described by particular themes. Specifically, the focus is on geometries where all cross sections and edge lengths are, respectively, scalings of the root cross section and root edge length. Headwater boundary conditions are fixed identically as (3.2) while the root is always considered lethal for all results below. In addition, interior junction conditions are those of the operator \(L\), dropping the condition (2.12) from \({L_{m}}\), that \(B(w)V\ge 0\). In this case, the principal eigenvalue \(\lambda _1\) for \(L\) is no longer assured to be strictly negative. Moreover, to extend the discussion of persistence analysis to \(L\) for numerical examples in this subsection, it is assumed that the stability of (2.21) is still determined by the principal eigenvalue \(\lambda _1\) for \(L\) [see (3.6) below].
Let \(r\) be the linearized growth rate in (2.2), and set
From (2.21), persistence thus requires
and \(-\varLambda _1\) is the critical obstruction for the growth rate to overcome to ensure persistence. Equivalently, \(\varLambda _1\) is the principal eigenvalue associated with (2.13) when \(r=0\). In this sense, \(\varLambda _1\) is the most important metric in terms of population dynamics. However, the spectral shift, \(V^2/4D\), separating \(\lambda _1\) and \(\varLambda _1\), is invariant to changes in domain geometry. Therefore \(\lambda _1\), which is sensitive to geometric variation as well as movement parameters \(V\) and \(D\), is a more precise indicator of how geometry interacts with \(V\) and \(D\) to affect persistence. For these reasons, both plots for \(\lambda _1\) and \(\varLambda _1\) are included in many of the figures.
Since the trees are radial, the lengths and sectional areas are described by the level \(n=1,2,\dots ,N\) of a tree with \(N\) branching levels. Edges with branching level \(n\) have endpoints with bifurcation indices \(n-1\) and \(n\), so the root edge has branching level \(n=1\), the two edges upstream of the bifurcation at \(X_1\) have branching level \(n=2\), and so on (e.g., Fig. 1b presents a radial tree with 3 branching levels). The areas \(A_n\) and lengths \(l_n\) are given by
This type of exponential scaling occurs in natural river networks (Rodriguez-Iturbe and Rinaldo 2001) and there are known trends for actual values of \(\eta \) and for \(\zeta \) if \(A\) is considered to be the physical cross-sectional area of a river segment. In this case, since \(V\) is globally constant, hydrological conservation of discharge implies that \(\zeta =1/2\). Our model considers \(A\) more generally, as a habitable area, of which the physical cross section is a special case and is consistent with the choice \(\zeta =1/2\). Horton’s Law implies that \(\eta \) is near 1/2 (Rodriguez-Iturbe and Rinaldo 2001).
The numerical examples below primarily serve to provide insight into how the geometry and topology of networks affect persistence. In addition, they are meant to probe for characteristic interactions between movement parameters and network structure, with emphasis on the influence of advection on junction behavior. Physically realistic parameter ranges of \(\zeta ,\,\eta ,\,V\), and \(D\) may be too small for numerical analyses to detect relationships which are subtle in those ranges. For this reason, the following studies ignore physically realistic parameter ranges in favor of larger ranges, with the exception of the analysis in Fig. 5, which imposes Horton’s law on \(\eta \) and uses actual river data for \(V\) (interpreted as hydrologic flow in this example) and \(D\).
The information given in (3.7) determines the total volume of a tree:
Note that \(\zeta \le 1/2\) corresponds to a class of trees which fall under the assumption (2.12) on \({L_{m}}\): \(\zeta \le 1/2\) if and only if \(B(w)\ge 0\). Also note that \(\lambda _1\) is invariant to a uniform rescaling of areas. Indeed, the transfer matrix only depends on areas in terms of \(\alpha _n\) and \(\beta _n\), which in this context are given by \(\alpha _n= (\zeta ^{-1}/2) -1\) and \(\beta _n=\zeta ^{-1}\). Therefore \(\lambda _1\) is independent of \(A_1\), so it can be assumed without loss of generality that \(A_1=1\). A normalized diffusion constant \(D=1\) is also used.
Figure 2 plots \(\lambda _1\) and \(\varLambda _1\), respectively, against variations in tree geometry which increase total volume. Figure 2a and b consider changes which increase the levels of branching \(N\) of the tree while Fig. 2c and d consider a continuous variation in \(\zeta \) for a tree fixed at \(N\) levels.
Sensitivity of persistence to variations in tree geometry which increase total volume. Plot curves are included for various advection speeds \(V\). a, b Plot \(\lambda _1\) and \(\varLambda _1\), respectively, against an increase in the levels of branching \(N\) of the tree for \(\zeta =1/3, \eta =1\), and \(l_1=1\). c, d Plot \(\lambda _1\) and \(\varLambda _1\), respectively, against an increase in \(\zeta \) for \(N=5,\,l_1=1\), and \(\eta =1\)
Figure 2 plots show that \(\lambda _1\) and hence \(\varLambda _1\) increase monotonically with an increase in the distance from the tree root to the upstream boundary, analogous to increasing length in the interval model, and decrease with increasing advection. Increases in the distance from root to upstream boundary also increases total volume. Similarly, this is true for increases in the area relation \(\zeta \), yet total volume does not emerge as a good indicator for \(\lambda _1\) since \(\lambda _1\) is invariant to a uniform rescaling of areas. By uniformly rescaling sectional areas (for each \(N\) or \(\zeta )\), Fig. 2 plots are also volume-fixing plots. Changes in the area relation alter the slope over which \(\lambda _1\) and \(\varLambda _1\) increase at different advection levels (Fig. 1c, d), suggesting the distribution of volume in the tree can be quite important.
In Fig. 2c, increasing the area relation \(\zeta \) past 1/2 at higher advection speeds (e.g. \(V=9)\) results in a positive, increasing \(\lambda _1\). In (c), though not shown in the plot, \(\lambda _1\rightarrow V^2/4D\) as \(\zeta \rightarrow \infty \). Equivalently, \(\varLambda _1\rightarrow 0\) as \(\zeta \rightarrow \infty \). This could suggest that \(\varLambda _1<0\) for the operator \(L\), i.e. without the restriction that \(\zeta \le 1/2\). This differs from the operator \(L_m\) but does not break the physical model. Indeed, \(\varLambda _1<0\) still corresponds to decay when growth rate \(r=0\), which is expected, since the total population should not grow or even stay constant in the presence of a lethal root condition. Note that a positive \(\lambda _1\) represents an important deviation from interval models, in that \(r<V^2/4D\) no longer guarantees extinction.
To further explore how the distribution of volume influences persistence, Fig. 3 features plots for \(\lambda _1\) and \(\varLambda _1\) in trees where geometric features are altered but the total volume is fixed at 1. Rather than fixing volume by uniformly rescaling the sectional areas, \(\zeta ,\,\eta \), and \(l_1\) are covaried which, in contrast to Fig. 2, leads to a broad range of length structures across changes in \(N\) and \(\zeta \). The volume is fixed at 1 by setting \(\eta =1/\zeta \) and adjusting \(l_1\).
Sensitivity of persistence to variation in tree geometry when total volume is fixed at 1. Plots are included for various advection speeds \(V\). a, b Plot \(\lambda _1\) and \(\varLambda _1\), respectively, against an increase in the number of branching levels \(N\), for \(\zeta =1/3,\,\eta =3\), and \(l_1(N)=1/(2^N -1)\). c, d Plot \(\lambda _1\) and \(\varLambda _1\), respectively, against a continuous change in \(\zeta \), for a 5 level tree, with \(\eta =1/\zeta \) and \(l_1=1/31\)
Though volume is fixed at 1, Fig. 3a shows a more rapid increase in \(\lambda _1\) as \(N\) increases than in Fig. 2a at all advection speeds. In Fig. 2a all tree edges have length 1 for all \(N\), while in Fig. 3a, the longest edges are always the upstream boundary edges which grow to \(3^7/(2^8 -1)\approx 8.57\) at \(N=8\). Also noteworthy is that the volume contained in the collection of the upstream most edges is \(2^{N-1}/(2^N -1)>1/2\) for all \(N\), and therefore the upstream most edges combined, contain more than half of the volume of the tree at each \(N\). This suggests that although there is a trade off with the area decay equaling length growth in the upstream direction, the area decay does not significantly shift the distribution of volume towards the lethal root as \(N\) increases. This allows the benefit of the maximum edge length increase to dominate, bringing \(\lambda _1\) near zero. Figure 3b shows that the critical obstruction to growth rate is still highly influenced by \(V\).
Figure 3c features \(N=5\) level trees which at one extreme, \(\zeta =1/4\), have long upstream edges with little sectional area \((l=81/31\) and \(A=1/81\) for upstream most edges). When \(\zeta =1\), edge lengths and sectional areas are uniform with \(l=1/31\) and \(A=1\). Figure 3c highlights an interesting interaction of \(V\) with \(\zeta \), especially at higher \(V\). For \(\zeta \le 1/2\), decreasing \(\zeta \) toward 1/4, increases \(\lambda _1\) toward zero, and hence favors persistence at all \(V\). In this range it is clear that the benefit of the exponentially increasing edge lengths is dominating over the hindrance of exponentially decaying areas. However at \(V=27\), there is a reverse in this relationship, \(\lambda _1\) begins to increase with increasing \(\zeta \), to the point that it becomes positive and continues to grow quickly as \(\zeta \rightarrow 1\). This indicates that volume distribution (exponentially increasing areas) is dominating over length structure effects. A similar interaction between \(V\) and \(\zeta \) is evident in Fig. 4c below.
As in Fig. 2c, \(\lambda _1\) becomes positive but is bounded above strictly by \(V^2/4D\) (not shown), so that \(\varLambda _1\) is strictly smaller than zero. When advection is fully accounted for in Fig. 3d, \(\varLambda _1\) decreases with \(V\) as expected and the local minimum in \(\lambda _1\) in Fig. 3c is less dramatic.
In order to more fully describe the effects of network structure on persistence, we compare results for river networks to persistence criteria from interval models. Adding domain in a tree may involve adding branching levels with potentially different habitat features. It is therefore useful to choose several different ways to compare changes in the habitable domain between tree and interval models.
There are three scenarios we consider for comparing trees with interval models: (1) \(vol(N)\) corresponds to an interval model with length equal to \(vol(\fancyscript{T}(N))\) (3.8) at each \(N\). (2) \(len(N)\) corresponds to an interval of length equal to the distance from the root vertex to the upstream boundary in \(\fancyscript{T}(N)\) at each \(N\). (3) \(len^{*}(N)\) corresponds to an interval of length equal to the total length of \(\fancyscript{T}(N)\) (i.e. the sum of the lengths of all edges) at each \(N\). There is a constant cross sectional area in the interval models, and without loss of generality, it is normalized to 1.
For \(\zeta =1/3,\,l_1=1\), and \(\eta =1\), the lengths of the interval models at each \(N\) are
These interval models are plotted alongside tree models in Fig. 4a and b. Figure 4c and d plot an \(N=5\) tree against \(\zeta \in (1/3,1/2)\). Volume is fixed at \(\sum _{n=1}^5(2/3)^{n-1}=211/81\), which is the volume of the \(N=5\) tree from Fig. 4a. This is accomplished by setting \(l_1(\zeta )=(211/81)(1/\sum _{n=1}^5(2\zeta )^{n-1})\) and \(\eta =1\). Thus all edges of the tree at each \(\zeta \) have a common length \(l(\zeta )\) which decrease as \(\zeta \) increases.
Tree models versus interval models. The notation tree denotes a tree with \(N\) branching levels, \(\zeta =1/3,\,\eta =1\), and \(l_1=1\). The lengths of the intervals at each branching level correspond to the three interval models \(vol,\,len\), and \(len^{*}\) given in (3.9). a uses advection speed \(V=1\), while b uses \(V=9\). c illustrates the effect of \(V\) on tree and \(vol\). Volume is fixed as \(\zeta \) changes, in a manner such that \(\zeta =1/3\) corresponds to the \(N=5\) tree in a and b and \(\zeta =1/2\) corresponds to \(vol\) in a and b
The results in Fig. 4a and b show that interval models can either overestimate or underestimate persistence relative to the tree model, depending on advection speed. In Fig. 4a, \(vol\) underestimates persistence while \(len\) and \(len^{*}\) overestimate persistence. In Fig. 4b, \(vol\), as well as \(len\) and \(len^{*}\) underestimate persistence relative to the tree. The interval model \(len\), commonly used for the length of a river segment does not give a good approximation for trees with area relation \(\zeta =1/3\) at either advection speed, while \(len^{*}\) is an even worse approximation.
The most interesting result is that the interval model \(vol\) produces smaller eigenvalues than tree at \(V=1\) but larger eigenvalues at \(V=9\). As in the previous results above, this suggests there is some interaction between advection speed \(V\) and the area condition \(\zeta \). Figure 4c provides an illustration of this interaction. Recall that when \(\zeta =1/2\), the eigenvalue problem in a radial tree is equivalent to that in an interval of length equal to the distance from root to upstream boundary in the tree. Figure 4c connects tree and \(vol\) via a continuous change in \(\zeta \) from 1/3 to 1/2, showing that at \(V=1,\,\lambda _1\) decreases with increasing \(\zeta \) while at \(V=9,\,\lambda _1\) increases with increasing \(\zeta \). This explains the ‘switch’ of \(vol\) and tree from Fig. 4a to b: at ‘low’ advection, transitioning continuously from the tree to the interval model hurts persistence, while at ‘high’ advection the opposite happens. This phenomena also suggests that there should be at least one advection speed where \(vol\) and tree coincide. The intermediate advection speed \(V=3.5\) shows a specific case when \(\lambda _1\) is essentially constant for a range of \(\zeta \). Although Fig. 4c with \(V=3.5\) achieves near equality of \(vol\) and tree in particular for \(N=5\), numerical results confirm that \(vol\) and tree essentially coincide for \(1\le N \le 8\) with \(V=3.5\) (not shown). Figure 4d shows that the constancy of the \(V=3.5\) curve begins to break down for \(\zeta >1/2\). As \(\zeta \) increases, the uniform edge length \(l(\zeta )\) decreases which eventually dominates volume distribution effects, resulting in decreasing \(\lambda _1\). This also holds when \(V=9\) for sufficiently large \(\zeta \) (not shown).
The three figures suggest an interesting interaction between advection and the area relation. Examination of the downstream transport across a junction sheds light on this. Heuristically, if the downstream transport is decreased across a junction, this should reduce the portion of the population which die at the lethal root, corresponding to an increase in \(\lambda _1\). Suppose \(\phi \) is a nonnegative eigenfunction for \(\lambda _1\), only vanishing at the root. At a junction \(w\), the jump Eq. (3.1) yields
with the subscripts 0 and 1 denoting, respectively, the edges downstream and upstream of \(w\), as in Fig. 1a. The jump Eq. (3.10) compares the downstream transport into and out of the junction \(w\), respectively, \(\phi _1 ^{\prime }(w)\) and \(\phi _0 ^{\prime }(w)\). Note, for \(\zeta =1/2\), these are the same. If \(V=0\), then the difference is controlled by \(\zeta \) alone. However, for \(V>0\), the last term in (3.10) is positive for \(\zeta < 1/2\) and negative for \(\zeta > 1/2\). Though \(\phi \) depends on \(\zeta ,\,V\), edge lengths, and \(w\), Fig. 2c (3.10) suggest that \(V\) amplifies the effect of \(\zeta \) in increasing or decreasing \(\phi _0 ^{\prime }(w)\) relative to \(\phi _1 ^{\prime }(w)\). At all \(V,\,\lambda _1\) increases with increasing \(\zeta \) and the rate of increase is amplified by \(V\). As \(\zeta \) increases, the downstream sectional area is decreased relative to the sum of the two upstream sectional areas. We interpret this amplification as due to increased ‘congestion’ at junctions as \(\zeta \) increases. Figures 3c and 4c are less straightforward to interpret within this context, because unlike Fig. 2c, the length structures vary with \(\zeta \). Figure 3c suggests that \(V\) amplifies the effect of decreasing edge lengths as \(\zeta \) is increased. The \(V=27\) curve indicates that the congestion dominates the length structure for sufficiently large \(\zeta \). Figure 4c would indicate that \(V\) determines whether or not decreasing downstream transport dominates decreasing edge lengths.
Concluding our numerical analysis of persistence in radial networks are a set of parameterized examples. Literature estimates provide values for \(V\) and \(D\) and the physically realistic \(\eta =1/2\) (Horton’s Law) scaling of branch lengths is imposed (Rodriguez-Iturbe and Rinaldo 2001). Persistence is tracked continuously for \(\zeta \in [1/3, 2/3]\) in a radial tree, with \(\zeta =1/2\) consistent with the interpretation that \(A\) is a physical cross-section of a river segment and that discharge is conserved. We begin with parameter values that are inspired by stonefly and plankton populations in Broadstone Stream as described in Speirs and Gurney (2001). The upstream most branches are taken to be the length of Broadstone Stream, 750 m. Advection speed \(V\) is a depth averaged hydrologic flow speed (4,300 m/day) which is rescaled to an ‘effective velocity’ for the stonefly by the (unitless) fraction of time \((10^{-4})\) the stonefly spends in the water column. The diffusion rate necessary for persistence in the stonefly population is estimated by Speirs and Gurney (2001) to be \(D=0.6\) m\(^2\hbox {/day}\) (r.m.s. \(\approx \)1 m). Cross-sectional area units are ignored since the unitless area relation provides the sole influence of area on persistence.
The stonefly and plankton populations are extreme cases, for interval domains and trees, in the following sense: \(V\) and \(D\) are both either very small (stonefly) or very large (plankton). More specifically, in the stonefly case the estimated \(D\) is so small that geometry is not a factor, while in the plankton case \(V\) is so large that persistence requires likely implausible values of \(D\). For the stonefly, numerical trials show that \(r\ge V^2/4D\) is necessary and sufficient for persistence, which makes the system comparable to an infinitely long interval geometry. Indeed, for both the 750 m interval and the tree, \(-\varLambda _1\approx V^2/4D\) (i.e., \(\lambda _1\approx 0)\). This is due to \(D\) being very small relative to even the shortest stream segment (750 m; see eigenvalue bounds (4.3) and (4.8) in Sect. 4). For the estimated intrinsic growth rate for stoneflies \(r=0.03\) day\(^{-1}\) (Speirs and Gurney 2001), the population will persist for \(D\approx 1.5\) but not for \(D=0.6\), in either the interval or tree. In the tree case \(\zeta \) has no discernible effect. The plankton population, with an estimated growth rate of \(r=1\) day\(^{-1}\), can persist in a large tree only for extremely large \(D\) near \(5\times 10^6\) (r.m.s \( \approx \)3,200 m). This is due to the fact that, assuming (2.12) (e.g. \(\zeta \le 1/2)\), Theorem 1 states that persistence requires \(D\ge V^2/4r\approx 4.6 \times 10^6\). In previous plots (e.g., Fig. 2d), the effect of \(\zeta >1/2\) has shown to alter this estimate, but not by more than an order of magnitude. We computed that in a five level tree with root branch length 12,000 and upstream branches 750, persistence is possible for \(D=5\times 10^6\) and geometry is a factor in determining persistence; the critical growth rate goes from \(r\approx 1.1\) to \(r\approx 0.9\) as \(\zeta \) goes from 1/3 to 2/3. Since it is unclear what mechanisms would be able to lead to such large diffusion rates, we argue that persistence would still be extremely unlikely in a river network, regardless of geometry.
It is worth noting that the stonefly result is not consistent with the estimate in Speirs and Gurney (2001) that suggests that persistence is possible when \(D = 0.6\) in a 750 m stream. In fact, for any length interval and any tree with \(\zeta \le 1/2\), persistence requires \(r\ge 0.077\) when \(D=0.6\) (by Theorem 1). On the interval, Speirs and Gurney (2001) predict that plankton with the parameters we use will not persist for any diffusion rate. This is consistent with the bound provided by Eq. (4.6) (applicable for \(\zeta \le 1/2)\), for \(R_{max} = 750\) since \(\sigma _{max}\in [1,5]\) for \(\zeta \in [1/3,1/2]\). However, in the five level tree system with \(R_{max} = 23{,}250\) (longest branch at 12,000), (4.6) does not rule out persistence.
In order to treat some less extreme cases, we propose two hypothetical populations whose \(D\)’s and effective \(V\)’s lie somewhere between the stonefly and plankton populations. Let population \(S\) be an adjustment of the stonefly population which has a larger effective velocity \(V=10^{-3}\times 4{,}300=4.3\) and a larger \(D\) in the neighborhood of 50 (r.m.s \(\approx \)10). This population could represent a more active benthic macroinvertebrate such a mayfly of the genus Baetis. Let population \(P\) be an adjustment of the plankton population which has a lower effective velocity \(V=10^{-1}\times 4{,}300= 430\) and a lower \(D\) in the neighborhood of \(5\times 10^{4}\) (r.m.s. \(\approx \)320), perhaps mimicking a situation described in Speirs and Gurney (2001) where individual cells spend a large proportion of time near the slower-flowing benthic boundary layer.
Analysis of persistence using empirically inspired parameter values. In each plot, the three lower \(y\)-axis tick marks correspond to \(-V^2/4D\): for \(V = 4.3\) and \(D = 60, 50, 40\) in a, \(-V^2/4D = -0.077,-0.092, -0.116\), respectively; For \(V = 430\) and \(D = 6\times 10^4, 5\times 10^4, 4\times 10^4\) in b, \(-V^2/4D = -0.77,-0.92, -1.16\), respectively
Figure 5 considers both populations \(S\) (Fig. 5a) and \(P\) (Fig. 5b) in a three level tree with upstream branches 750, doubling each level to the root branch at 3,000 while \(\zeta \) varies continuously in \([1/3,2/3]\). Figure 5a shows that this range of \(D\) is still too small for geometry to be a factor for population \(S\) when \(\zeta <1/2\), with the system still comparable to an infinitely long interval since \(-\varLambda _1 \approx V^2/4D\). However, for \(\zeta >1/2\), the geometry becomes a factor in determining persistence, decreasing \(-\varLambda _1\) slightly below \(V^2/4D\). Figure 5b illustrates that the persistence of the \(P\) population is affected by \(\zeta \) over the entire range of \(\zeta \), as \(-\varLambda _1\) ranges from above to below \(V^2/4D\) as \(\zeta \) increases from 1/2 to 2/3. The critical growth rates are in the neighborhood of 0.1 and 1, respectively, for the \(S\) and \(P\) populations, depending on \(D\) and \(\zeta \). Not pictured is a trial for an additional population with effective velocity \(V=10^{-2}\times 4{,}300= 43\) and \(D\) near \(5\times 10^{3}\) (r.m.s. \(\approx \)100) which qualitatively mimics Fig. 5b, with \(-\varLambda _1\) approximately an order of magnitude smaller so that critical growth rates are near 0.1.
3.3 Radial tree analyses
In some cases, analysis of radial trees provides interesting theoretical results for our population models on tree networks. Two problems are considered here. The first problem uses a diffusion only, lethal boundary example with junction condition \(A_0 = A_1 = A_2\) to show that trees can grow arbitrarily large without bringing \(\lambda _1\) close to zero. In this case population persistence is strongly affected by the sectional area assumption. The second problem uses a modified spatial structure, adding a half-line root edge and eliminating the downstream boundary. With the \(A_0 = A_1 + A_2\) junction condition, the transition from population extinction to persistence in bounded subdomains occurs at \(r - \frac{V^2}{4D} = 0\).
3.3.1 The area condition \(A_0 = A_1 = A_2\)
The rate of growth of habitable area when junctions are passed can have a significant impact on population persistence. The model considered here assumes an unchanging area \(A_0 = A_1 = A_2\) at each interior junction. The edge lengths are uniformly bounded, the lethal condition \(u(w) = 0\) holds at all boundary vertices, and population movement will be by diffusion alone, so \(V = 0\). As noted earlier, if the sectional area grows by \(A_0 = A_1 + A_2\) at each interior junction, then radial solutions on a radial tree coincide with solutions computed for the interval \([X_N,0]\). If the lethal boundary condition applies at both ends of the interval, the principle eigenvalue \(\lambda _1\) for \(L=\partial _x^2\) will approach zero if the length is sufficiently large. In contrast, the principle eigenvalue for the \(A_0 = A_1 = A_2\) model will be bounded away from zero, independent of the tree size.
The argument makes use of explicit computations with the transfer matrix of (3.4) in case all edges have the same length. After a rescaling one can assume that \(l_n = |X_{n} - X_{n-1}| = 1\) for all \(n\). Use the abbreviations \(c(\omega ) = \cos (\omega )\) and \(s(\omega ) = \sin (\omega )/\omega \) to write
Then
The characteristic polynomial for \(JM\) is
Letting \(b =\left( \frac{\beta + 2}{2}\right) c(\omega ) - \alpha s(\omega )\), the eigenvalues are
with eigenvectors
When the eigenvectors are independent, \(JM\) may be diagonalized,
If \(\varDelta = s(\omega )[\sigma _+ - \sigma _- ]\), then
Theorem 2
Suppose \(\fancyscript{T}\) is a rooted radial binary tree with edge lengths \(0 < l_n \le 1\). Assume the sectional area condition \(A_0 = A_1 = A_2\) at each interior vertex, the lethal condition \(u(v) = 0\) at all boundary vertices, and (3.1) with \(V = 0\) at the interior vertices. Then, independent of the number \(N\) of branching levels, the principle eigenvalue \(\lambda _1\) satisfies
where \(\omega _0 \simeq 0.34\) is the smallest positive solution of
Proof
As noted above, the principle eigenvalue is negative, with a radial eigenfunction. Suppose first that the edge lengths are all \(l_n = 1\). Since there is no advection term, the jump matrix is
and
Since a principle eigenfunction \(y\) satisfies the lethal condition at all boundary vertices, the initial data at the root vertex may be chosen as \(y(0) = 0,\,y^{\prime }(0) = 1\). Propagating this initial data by (3.4) gives
Multiplying both sides by \(J\) leads to the conclusion that at the principle eigenvalue \(\lambda _1\) the matrix \((JM)^N\) has \([0, 1]\) as an eigenvector.
The matrix \(JM\) has real entries for \(\omega \) real, so for \(\omega \ge 0\) the eigenvalues are either real or a conjugate pair. At \(\omega = 0\) the eigenvalues of \(JM(\omega )\) are \(\sigma _+(0) =1\) and \(\sigma _-(0) = 1/2\). Since the determinant of \(JM\) is 1/2 for all \(\omega \), the eigenvalues will be real and satisfy \(\sigma _+(\omega ) > 1{/}\sqrt{2},\,\sigma _-(\omega ) < 1{/}\sqrt{2}\) until the first value of \(\omega \) with \(\sigma _+(\omega ) = \sigma _-(\omega ) = 1{/}\sqrt{2}\). Using (3.11), this occurs at the smallest positive value \(\omega _0\) with
If \(0 \le \omega < \omega _0\) the eigenvalues of \((JM)^N\) are \(\sigma _{\pm }^N(\omega )\), which are distinct. Thus any eigenvector of \((JM)^N\) is an eigenvector of \(JM\). If \(JM\) has [0,1] as a eigenvector , then \(\sin (\omega )/\omega = 0\), or \(\omega = m\pi ,\,m= 1,2,3,\dots \). Thus \((JM)^N\) does not have [0,1] as a eigenvector if \(0 \le \omega < \omega _0\), establishing the result when the edge lengths are all 1.
To see that shrinking the edges will raise the magnitude of the principle eigenvalue, suppose \(\fancyscript{T}\) is a radial tree with edges of length one, while \(\fancyscript{T}_1\) is the same tree with edge lengths reduced to \(l_n \le 1 \). Let \(\mu _1\) be the principle eigenvalue for \(\fancyscript{T}_1\), with normalized radial eigenfunction \(y_1,\,\int _{\fancyscript{T}_1} y_1^2 = 1\). Let \(X\) and \(T\) be the distances to the root in \(\fancyscript{T}\) and \(\fancyscript{T}_1\) respectively.
Map \(\fancyscript{T}_1\) to \(\fancyscript{T}\) with a smooth increasing function \(X = \phi (T)\), which satisfies \(X_n = \phi (T_n)\) and \(\phi ^{\prime }(T) \ge 1\). Further require \(\phi ^{\prime }(T_n) = 1\), so the coordinate change will maintain the interior junction conditions. Define the function
The principle eigenvalue of \(\fancyscript{T}_1\) will be estimated using a Rayleigh quotient.
For each edge \(e\) of \(\fancyscript{T}\) with coordinate \([X_{n},X_{n-1}]\) and corresponding edge \(e_1\) of \(\fancyscript{T}_1\) with coordinate \([T_{n},T_{n-1}]\), the change of variables gives
and
Since \(\phi ^{\prime } \ge 1\) everywhere, these edgewise integral equalities lead to
finishing the proof. \(\square \)
3.3.2 Infinite root edge
Spatial domains in river systems have been modeled with the lethal condition at the downstream boundary (Jin and Lewis 2011; Speirs and Gurney 2001), as well as a zero derivative condition (Hilker and Lewis 2010) intended to minimize the effect of a distant boundary. For the next radial tree analysis the tree model is extended by appending a half line to the downstream vertex of \(\fancyscript{T}\). In this model the finite tree \(\fancyscript{T}\) represents the spatial domain of interest, while the appended half-line describes an arguably more realistic coupling of the domain \(\fancyscript{T}\) to the total river system, providing for outflow and diffusive return to \(\fancyscript{T}\) while avoiding artificial boundary effects. A new feature is that population persistence within the domain \(\fancyscript{T}\) is the concern, rather than persistence in the entire model river system.
The presence of the appended half line in the model of the total river system complicates the analysis of (2.2) by eigenfunction expansions. Rather than pursuing the generalized eigenfunction expansion methods, the model is simplified by assuming the area conditions \(A_0 = A_1 + A_2\) at each interior vertex, with the usual vertex conditions. Recall that in this case radial solutions of (2.2) coincide with solutions computed for a half line; transfer matrices are not needed. With this simplification it is possible to solve and analyze the associated diffusion equation directly. This analysis will show population persistence in \(\fancyscript{T}\) if \(r - \frac{V^2}{4D} > 0\), while the population in \(\fancyscript{T}\) will decay to zero if \(r - \frac{V^2}{4D} < 0\).
Theorem 3
Assume that either the lethal or zero flux conditions hold at the upstream boundary vertices. Suppose \(u(0,X)\) is radial, with \(|u(0,X)| \le M \exp (\frac{V}{2D}X)\). If \(r - \frac{V^2}{4D} < 0\), then the population density \(u(t,X)\) converges to zero uniformly on compact subsets of \(0 \le X < \infty \) as \(t \rightarrow \infty \).
If \(r - \frac{V^2}{4D} > 0\), assume in addition that \(u(0,X)\) is bounded and nonnegative for \(X \ge 0\), with \(\int _0^{\infty } u(0,X) \ dX > 0\). Then \(u(t,X) \rightarrow \infty \) as \(t \rightarrow \infty \) uniformly on compact subsets of \(0 < X < \infty \).
The proof of Theorem 3 is included in the appendix. For related mathematical work, see Gaveau et al. (1993) and Okada (1993) (and references therein), which include some explicit heat kernels and decay estimates for various trees and other graphs, in the context of zero advection \((V=0)\).
4 Principle eigenvalues bounds for general rivers
Theorem 1 establishes the expected link between persistence of the river population and the principle eigenvalue \(\lambda _1\) of the operator \({L_{m}}\). The previous section treated the persistence problem for radial tree models, where both theoretical and numerical studies are relatively simple. The problem becomes more complex for realistic geometries, where the river bifurcation patterns, varying with edge lengths and sectional areas, are both nonsymmetric and highly variable. Given a particular river geometry, one can resort to numerical modeling for predictions regarding population persistence, but this still leaves open the problem of describing, in a general way, how population persistence depends on such parameters as \(D,\,V\), size of the tree, sectional area, and boundary vertex conditions.
This section addresses the problem by developing explicit upper and lower bounds for the principle eigenvalue \(\lambda _1\) of the operator \({L_{m}}\). While the estimates are quite general, they are most effective when the tree model is sufficiently similar to the radial tree. The sectional areas should satisfy \(A_0 \sim A_1 + A_2\) at interior junctions, and the distances \(R\) from the downstream vertex to the upstream vertices should be similar (in a radial tree, these distances are all equal). These assumptions will give a linear river volume growth as a function of the distance from the downstream boundary. The bounds developed below then support the validity of interval models (2.23),
Notice in particular that the \(A_0 = A_1 = A_2\) case developed for Theorem 2, with its unusual \(\lambda _1\) behavior, had an exponentially increasing habitable river volume distribution.
The key tool for developing upper and lower bounds is the variational formula
for functions \(f\) in the domain of \({L_{m}}\). This well known result may be derived using an eigenfunction expansion. By (2.20)
To develop a lower bound for \(|\lambda _1|\), consider the family \(\varGamma \) of simple paths \(\gamma \) joining the upstream boundary vertices \(w_u\) to the downstream boundary vertex \(w_d\). Give each path \(\gamma \) a weight \(W_\gamma \) equal to the sectional area of the edge incident on \(w_u\). When \(A_0 = A_1 + A_2\) at each interior vertex, the sectional area \(A_e\) of each edge \(e\) in \(\fancyscript{T}\) is equal to the sum of the weights of the paths \(\gamma \in \varGamma \) containing \(e\). For a general river, \(A_e\) will be compared to the sum of path weights using
Recall that \(R_{max}\) denotes the distance from the downstream boundary vertex \(w_d\) to the most distant upstream boundary vertex.
Theorem 4
Suppose the condition \(A_0 \ge A_1 + A_2 \) holds at each interior vertex. Then the magnitude of the principle eigenvalue \(\lambda _1\) for \({L_{m}}\) has the lower bound
Proof
Recall that functions in the domain of \({L_{m}}\) satisfy the downstream vertex condition \(u(w_d) = 0\), and that \(\lambda _1 < 0\). Suppose a simple path \(\gamma \) has length \(l_{\gamma }\), and \(f:\fancyscript{T}\rightarrow \mathbb R \) is a continuous, piecewise \(C^1\) function with \(f(w_d) = 0\). If the restriction of \(f^2\) to \(\gamma \) has a maximum at \(y\), then by the Cauchy–Schwarz inequality
Since \(A_0 \ge A_1 + A_2\) for each interior vertex, each edge area has the bounds
If \(\Vert f \Vert = 1\) then
Apply this inequality and (4.2) to an eigenfunction \(\phi \) for the principle eigenvalue with \(\Vert \phi \Vert = 1\) to get
\(\square \)
The lower bound (4.3) can be used to obtain an estimate on \(V,\,R_{min}\), and \(\sigma _{max}\), such that for any diffusion rate \(D\), the population can not persist. By (4.3) and Theorem 1, if
the population will not persist. For fixed \(V,\,R_{min}\), and \(\sigma _{max},\,F(D)\) has a minimum at \(D^{*}:=(V R_{max} \sqrt{\sigma _{max}})/2\), with \(F(D^{*})=V/(\sqrt{\sigma _{max}}R_{max})\). Therefore, if \(r< F(D^{*})\), i.e.,
the population will not persist [see (Speirs and Gurney 2001) p. 1232, for a similar estimation in an interval domain].
Upper bounds for \(|\lambda _1| \) are obtained from (4.1) by choosing explicit trial functions \(g\) in the domain of \({L_{m}}\) for the Rayleigh quotient,
As an illustration, suppose an edge \(e = [a_e,b_e]\) in \(\fancyscript{T}\) has maximal length \(l_{max}\). Using the trial function \(g\) which is zero except on the edge \(e\), where \(g(x) = 1 - \cos (2\pi (x - a_e)/(b_e - a_e))\), an elementary calculation gives the crude but broadly applicable estimate
In addition to showing that \(\lambda _1 \rightarrow 0\) as \(l_{max} \rightarrow \infty \), this estimate provides an upper bound for \(|\lambda _1|\) which is independent of the advection speed \(V\)
More care in the construction of a trial function will produce a better estimate. Relative to the distance \(R\) from the downstream boundary vertex \(w_d\), define the volume distribution function
The next estimate is motivated by the radial case, when edge lengths depend only on the distance from \(w_d\). If in addition \(A_0 = A_1 + A_2\) at all interior vertices, then \(\rho \) is a linear function of \(R\). As noted above, the behavior is quite different if \(A_0 = A_1 = A_2\) at all interior vertices, when \(\rho \) grows exponentially with \(R\) if the edge lengths are equal.
For a general river, let \(R_{min}\) denote the distance from the downstream boundary vertex \(w_d\) to the nearest upstream boundary vertex.
Theorem 5
The magnitude of the principle eigenvalue for \(L_m\) has the upper bound
Proof
Some auxiliary functions will help provide the estimate. Start with
Next, pick a vertex \(w\) and an incident edge \(e\) of length \(l_e\). On \(e\) use the local coordinate \(x\) given by the distance from the vertex \(w\). Define the function \(f_{(w,e,\alpha )} \) to be 0 at every point of \(\fancyscript{T}\) not in \(e\). For points in \(e\) define
In terms of the local coordinate \(x\) on \(e\)
For any given \(\alpha \) and \(\epsilon > 0\) there is a \(\beta > 0\) such that
Consider the initial trial function
This function is continuous at the interior vertices. By adding suitably chosen functions \(f_{w,e,\alpha }\) the function \(g\) may be adjusted to lie in the domain of \(L_m\) with a negligible change in the Rayleigh quotient from (4.7). Since \(0 \le g \le 1\) at all points, \(g^2(R) \ge 1/2\) for \(R_{min}/4 \le R \le 3R_{min}/4\), and \(g\) vanishes at all boundary vertices, simple estimates using (4.7) give (4.9). \(\square \)
Theorem 5 may be applied to those subtrees of \(\fancyscript{T}\) consisting of the vertices and edges upstream of an edge \(e\). In this case \(g\) is extended by zero beyond the subtree.
For \({L_{m}}\) [i.e. assuming (2.12)], Theorem 1 states that persistence requires (and is assured for) \(r\ge |\varLambda _1|=|\lambda _1|+V^2/4D\). Upper and lower bounds on \(|\lambda _1|\) therefore provide ranges for \(r\) which either guarantee persistence or extinction. Increases in either lower bound (4.3) or upper bound (4.9) therefore suggest reductions in the potential for persistence. Cursory examination of Eqs. (4.3) and (4.9) shows that increasing \(V\) or \(D\) increases (4.9) while increasing \(D\) increases (4.3). Decreasing \(R_{max}\) while holding \(1/\sigma _{max}\) constant (e.g. shrinking tree edges without altering topology) also increases (4.3). In (4.9), decreasing the distance from root to nearest upstream boundary, \(R_{min}\), increases the upper bound.
However, both bounds highlight features such as \(\sigma _{max},\,\rho \), and the sectional area difference \(B(w)\) that are absent in interval models, but which may have significant impact as demonstrated in Theorem 2. The lower bound (4.3) depends inversely on \(\sigma _{max}\), which has a minimum of 1 when trees satisfy \(B(w)=0\) at all junctions, and increases as \(B(w)\) is increased at any junction. The upper bound (4.9) increases with increasing \(B(w)\), while the term \(\rho (3 R_{min}/4)-\rho (R_{min}/4)\) in the denominator suggests that the distribution of volume with respect to the lethal root is an important persistence indicator. For example, if most of the volume of the tree is concentrated within a radius \(R_{min}/4\) of the lethal root \(w_d\), then \(\rho (R_{min}/4)\approx \rho (3R_{min}/4)\), and the upper bound will be very large. It is worth noting that (4.3) and (4.9) are sensitive to global features of tree networks, such as \(R_{min},\,R_{max},\,\rho \), and \(\sum _a B(v)\). This is in contrast to the eigenvalue bounds available in Ramirez (2012) which detect edgewise features.
Numerical comparison of bounds in Eqs. (4.3) and (4.9) with explicit principal eigenvalues for radial trees further highlights the bounds’ properties (Fig. 6). Both upper and lower bounds track the general behavior of the principal eigenvalues for the radial trees, specifically a decrease with increasing branching levels \(N\). The bounds and radial eigenvalues also converge as branching level increases. This concordance of behavior is not necessarily expected given that the bounds cover such a broad range of non-radial geometries. The upper and lower bounds comfortably bound eigenvalues for the radial trees in our example, although it is unclear how deviations from the radial cases approach the bounds. The upper bound most exceeds both radial cases at lower \(N\), partially due to its discounting the persistence-enhancing effects of diffusion in favor of persistence-reducing ones. The upper bound provides a closer approximation to eigenvalues from radial trees with lethal upstream boundaries, as there are more lethal points for individuals moving by diffusion to encounter. However, it is unclear whether this effect is general to non-radial cases. The lower bound considers the persistence-enhancing effect of \(\sigma _{max}>1\) (Fig. 3c), but not the possible persistence-reducing effects of \(B(w)>0\) (Fig. 2c). For the radial trees in Fig. 6, \(\zeta =1/3\) gives \(\sigma _{max}(N)=(3/2)^{N-1}\), so that lower bound (4.3) (proportional to \(\sigma _{max}^{-1}(N))\) decreases fast with \(N\). The fact that there is such a comfortable bound around the radial eigenvalues highlights their broad range of applicability to general, non-radial tree geometries with variable cross-sectional area relations and either lethal or zero flux conditions at upstream boundaries.
An example of upper and lower bounds in Eqs. (4.9) and (4.3) compared to eigenvalues for radial trees. The notation tree and lethal tree denote trees with \(N\) branching levels, with \(\zeta =1/3,\,\eta =1,\,l_1=1\), and the lethal root condition. At upstream boundaries, tree uses the zero flux condition while lethal tree uses the lethal condition. In a, upper and lower bounds are presented for \(|\lambda _1|\), respectively, Eqs. (4.9) and (4.3), along with \(|\lambda _1|\) for example radial trees. In b, similar results are presented for \(|\varLambda _1|\). For both a and b, \(V=D=1\)
5 Application of RDA model to a jump-settlement IDE model
As mentioned in the introduction, the emphasis on population persistence in networks in the current article is centered on how geometric and topological features of networks affect persistence. Due to this emphasis, the number of movement parameters is reduced to a (globally) constant advection rate \(V\) and diffusion rate \(D\) in the simple RDA model. In this section, it is shown that the RDA model adapts naturally to an integro-differential equation (IDE) model involving two additional movement parameters. The purpose of this section is to relate the principal eigenvalue \(\lambda _1\) of our current model to persistence in the IDE model, namely to the dominant eigenvalue \(\nu _1\) of the corresponding integral operator.
Lutscher et al. (2005) proposed a novel derivation of an IDE from a population model which breaks the population into two parts: a ‘stationary’ population \(u\) in the benthos and a ‘moving’ population \(w\) in the drift. The organisms jump from the benthos with rate \(\mu \) and settle back to the benthos at rate \(\sigma \). The equations describing this mechanism are as follows:
Here, \(G\) is a movement (differential) operator, e.g. \(D\varDelta - V \nabla \) (diffusion-advection), while \(F\) encodes birth and death processes (as in Sect. 2). A separation of time scales argument is used in Lutscher et al. (2005) to derive the following IDE from (5.1):
The ‘dispersal kernel’ \(k\) in (5.2) is interpreted as the probability that a benthic organism which jumps at a point \(y\) will settle back to the benthos at a point \(x\) in the domain \(\fancyscript{T}\). The second and third terms on the right hand side of (5.2) represent emigration (out of the benthos) and immigration (into the benthos), respectively. Linearizing \(F\) around zero, persistence in the (5.2) model requires \(F^{\prime }(0)\ge \mu (1-\nu _1)\), where \(\nu _1\) is the dominant (positive) eigenvalue satisfying (Lutscher et al. 2005)
Note that if \(F^{\prime }(0)\ge \mu \), persistence is guaranteed independent of \(\nu _1\). The interesting case is when \(F^{\prime }(0)<\mu \), in which case persistence depends on \(\nu _1\).
The derivation of (5.2) in Lutscher et al. (2005) assumes that the dynamics of movement \((w)\) occur much faster than population dynamics in the benthos \((u)\). In particular, it relies on setting \(\epsilon = \mu / \sigma \), rescaling \(w\) and \(G\) appropriately, and letting \(\epsilon \rightarrow 0\) [see Lutscher et al. (2005) for the complete derivation]. The derivation assumes the invertibility of the operator \({\fancyscript{L}}:= -(G/\sigma ) + 1\), in which case the dispersal kernel \(k\) is the Green’s function associated to \({\fancyscript{L}}\) and thus the integral operator defined by \(k\) is the inverse of the differential operator \({\fancyscript{L}}\):
Ramirez (2012) has extended (5.2) to the case when \(\fancyscript{T}\) is a tree graph, providing a derivation of (5.2) which maintains the property that \(k\) is the Green’s function for \({\fancyscript{L}}\). In particular, that (5.4) holds for the graph case and that the principal eigenvalue of \({\fancyscript{L}}\) is the reciprocal of the dominant eigenvalue of (5.3), follows from results in Proposition 2 in Ramirez (2012).
Provided here is an equivalent formulation which connects the IDE to our self-adjoint Laplacian \({L_{m}}\) and its corresponding resolvent operator. Let \(X\) be defined as the negative of the distance to the root (as in Fig. 1b) and let \(q(X):=\exp [VX/2D]\) be considered as a multiplication operator on \(L^{2}(\fancyscript{T})\), where \(\fancyscript{T}\) denotes the tree graph domain. We assume \(\hbox {dom}(G)\), and hence \(\hbox {dom}(\mathcal{L })\), satisfies (2.3), (2.4), and (2.12). The change of variables used in Sect. 2.2 to reduce (2.2) to (2.13) is used similarly here to conclude
In the following, the operator inverses of \({\fancyscript{L}}\) and related differential operators on \(\fancyscript{T}\) will be expressed as integral operators. If \(I\) is an integral operator on \(\fancyscript{T}\) with kernel \(k\), then \(\psi =I f\) is expressed edgewise as
where \(X\) and \(Y\) provide local coordinates for edges \(a\) and \(b\), respectively, and the sum is over all edges \(b\) of \(\fancyscript{T}\). For the remainder of this section, we will adopt the following shorthand for (5.6):
It has been shown in Sect. 2 that the eigenvalues of \({L_{m}}\) satisfy \(\lambda _n<0\) and thus \(-P^2\) is not an eigenvalue of \((-{L_{m}}/\sigma )\). In this case, \(-P^2\) is in the resolvent set of \((-{L_{m}}/\sigma )\) and \((-{L_{m}}/\sigma ) + P^2\) is invertible. (We note that if \(\lambda _n < V^2/4D\) for the operator \(L\) (2.16), as conjectured in Sect. 3, then \(-\lambda _n/\sigma > -V^2/4D\sigma > -P^2\) and \((-L/\sigma ) +P^2\) is also invertible.) Define \(L_{1}:=(-{L_{m}}/\sigma ) +P^2\). Then, following from results in Kostrykin and Schrader (2006), for \(f\in L^{2}(\fancyscript{T})\),
where \(K\) is the Green’s function for \(L_{1}\).
Note that \(q^{-1}g\in L^{2}(\fancyscript{T})\) if and only if \(g\in L^2 (\fancyscript{T})\) and that \(h\in \hbox { dom}(L_1)\) if and only if \(qh\in \hbox { dom}({\fancyscript{L}})\). From (5.5), (5.8), and the invertibility of the multiplication operator \(q,\,{\fancyscript{L}}=q\circ L_{1}\circ q^{-1}\) and for \(g\in L^{2}(\fancyscript{T})\),
Setting \(k_{ab}(X,Y)=q(X)K_{ab}(X,Y)q^{-1}(Y)\), we recover (5.4) with \(k\) as the Green’s function for \({\fancyscript{L}}\).
We can simplify the analysis of (5.2) in the same vein as in Sect. 2.2 by observing that
for \(u_e(t,X)=q(X) U_e(t,X)\). Note that \(U\) will persist if and only if \(u\) persists. After linearizing \(F\), (5.2) can be reduced to the following equation in the \(U\) variable:
Moreover, if \(\phi \) is an eigenfunction for \({\fancyscript{L}}^{-1}\) with eigenvalue \(\nu \), then \({\fancyscript{L}}^{-1}\phi =\nu \phi \) if and only if \(L_{1}^{-1}\varPhi =\nu \varPhi \) for \(\phi =q\varPhi \). Thus \(\varPhi \) is an eigenfunction for \(L_{1}^{-1}\), with eigenvalue \(\nu \), from which it follows that \(\varPhi \) is also an eigenfunction for \(L_{1}\) with eigenvalue \(1/\nu \) \((\nu \ne 0)\). An elementary computation further shows that \(\varPhi \) is an eigenfunction for \({L_{m}}\). Therefore analysis of (5.4) can be replaced with analysis of following eigenvalue problem,
where \(\varPhi \) is an eigenfunction for \({L_{m}}\). A general solution to (5.11) is now easily written in terms of the eigenbasis \(\{\varPhi _n \}\) associated to \({L_{m}}\) and the eigenvalues \(\nu _{n}\) of (5.12):
where the coefficients \(c_n\) are determined by the initial condition \(U(0,\cdot )\in L^{2}(\fancyscript{T})\). There is a simple relationship between \(\nu _n\) and \(\lambda _n\). From (5.5) and (5.9), we have
Since \(\lambda _n < 0 < V^2/4D\), for all \(n\), it follows that \(0< \nu _n < 1\) for all \(n\) and since \(\lambda _n\rightarrow -\infty \) monotonically, \(\nu _n \rightarrow 0\) monotonically. In particular \(\nu _1\in (0,1)\) is the positive dominant eigenvalue of (5.12). Combining this with (5.13) and using the same argument as in the proof of Theorem 1, we recover that \(F^{\prime }(0)\ge \mu (1-\nu _1)\) is necessary and sufficient for zero steady-state persistence in (5.2). Using (5.14), this persistence condition is written in terms of \(\lambda _1\) as
Note that if the network is increased enough, e.g. the root edge is increased to infinity, then by Sect. 4 results, \(\lambda _1\rightarrow 0\) and the population will not persist, regardless of habitat geometry if
which recovers the Lutscher et al. (2005) condition and is consistent with Theorem 3 in Ramirez (2012).
Let \(\varLambda _1\) be as defined in Sect. 3, i.e., \(\varLambda _1=\lambda _1- V^2/4D\) (equivalently, \(\varLambda _1\) is the principal eigenvalue of \(G=D\varDelta - V \nabla )\). Then (5.14) and (5.15), respectively, are written in terms of \(\varLambda _1\) as
The relationships (5.14) and (5.15) reduce analysis of the IDE model (5.2) to the study of the principal eigenvalue of the self-adjoint Laplace operator \({L_{m}}\). These formulas [along with (5.17) and (5.18)] allow Sect. 3 analytical and numerical results, concerning the effects of graph geometry on persistence, to translate via simple formulas to the IDE model. It is unknown whether these relationships hold if \({L_{m}}\) is relaxed to \(L\). The eigenvalue bounds in Sect. 4 can similarly be rewritten, using (5.14), to become bounds on the critical growth rate in the IDE model. Another benefit of the formulation provided above is that, via (5.14) and (5.13), the evolution of the zero solution in the IDE model is written in terms of \(\lambda _n\) and \(\varPhi _n\), the eigenvalues and eigenfunctions for \({L_{m}}\), respectively. This isolates \({L_{m}}\), a very simple self-adjoint elliptic operator, as a useful component to persistence in the IDE model and suggests that it could play an important role in further investigations of the IDE model, including transient behavior and multi-species models.
6 Discussion
River networks feature a complex geometry with important variations in segment lengths, habitat volume distribution, and junction behavior. The relationships between this rich collection of geometric features and persistence were initially investigated using a quantum graph population model in Ramirez (2012), with this novel approach substantially extending the theory of population persistence in river systems and yielding results differentiating persistence estimates for network models from interval models. However, tracking the effects of variance in network structure on persistence remains largely undeveloped. The results of our current paper further demonstrate quantum graph models can incorporate crucial geometric features (both edge-wise and global), with subsequent eigenvalue analysis in numerical trials, analytic examples, and eigenvalue bounds relating changes in these geometric features to persistence outcomes.
This work has explored a variety of features as potential substitutes for the domain length of interval models. Features such as distances from the root to the nearest or farthest upstream boundary \((R_{min}\) and \(R_{max}\), respectively), and the length of the longest edge in the network \((l_{max})\) are the closest network analogues to domain size in interval models. Although the results of Sects. 3 and 4 show that an increase in any of these measures is beneficial to persistence, the extent of this benefit is modified by other geometric features such as volume distribution. Numerical results show that relying on interval models can lead to overestimates or underestimates of persistence in a network (Fig. 4). This fact was previously identified by Ramirez (2012), however, our numerical trials have demonstrated that advection speed and area relation are important mitigating factors in these estimates.
The distribution of habitat volume arises as a novel geometric factor effecting persistence in the models presented here. Total volume by itself may be a poor indicator of persistence, as discussed in Sect. 3 and evident from Eqs. (2.14) and (2.15). When the population is largely distributed in habitat far from a lethal boundary, contact with that boundary is reduced, increasing persistence potential. Increasing the relative edge lengths or habitable areas in upstream edges while fixing total volume increases persistence potential [Figs. 2c, 3c, (4.9)].
Beyond the length structure of network segments, network junction conditions alter the persistence inhibiting influence of advection speed in ways not observed in interval models. Although faster advection is always worse for persistence in the numerical results, this effect is dampened when the sectional area upstream of a junction exceeds the downstream area (Figs. 2d, 3d). This suggests that junctions can become “congested”, hindering the downstream transport towards the lethal root. Moreover, the principle eigenvalue \(\lambda _1\) can achieve positive values for an area relation sufficiently larger than 1/2 (e.g. Fig. 2c), meaning that the persistence criteria \(r<V^2/4D\) (Theorem 1) no longer implies extinction. It is plausible that the “congestion” at junctions is an additional contributor to the resolution of the drift paradox: whereas a positive upstream invasion speed sufficiently bounds persistence in interval models, junction behavior presents a deviation from this criterion in river networks.
The parameterized examples of the stonefly and plankton represent extreme cases of advection, diffusion, and intrinsic growth rates. In these cases geometry, whether considered as an interval or a tree network, has little effect on persistence outcomes. In Fig. 5, we feature two hypothetical populations \(S\) and \(P\), which have rates that lie in a range between those estimated for the stonefly and plankton. Figure 5a shows an effect of geometry on population \(S\) only for large \(\zeta \), as diffusion is still fairly minimal relative to system length. Population \(P\) in Fig. 5b is qualitatively similar to Fig. 2d, in that the likelihood of persistence increases monotonically with \(\zeta \). The area relation is a mitigating factor in determining the critical growth rate in these examples, although the effect of \(\zeta \) on \(\varLambda _1\) in Fig. 5a and b is much more subtle than in Figs. 2d and 3d, which emphasizes the need for a model to cast a wide net for possible interactions that may otherwise go undetected in numerical simulations. Notably, the parameterized examples maintain the result that \(\zeta >1/2\) can alter the persistence requirement \(r\ge V^2/4D\).
The analyses here are restricted to cases where population growth and movement parameters are constant across the network. This strategy allowed us to isolate the impact of geometric features and explore interactions between geometry, movement parameters, and persistence outcomes. More realistic (tactical) models would allow growth rates and movement parameters to vary edgewise, potentially with advection speeds proportional to the cross-sectional areas. In addition to adding parameters, this poses other analytical difficulties, particularly since our analysis made use of a reduction from the RDA equation to the associated diffusion equation. This reduction may not be available when movement parameters vary. Still, such features could lead to important effects on persistence, as quite complex outcomes have been observed in discrete space tree models where parameters vary with branching level (Goldberg et al. 2010). Increased heterogeneity in growth rates and movement parameters might provide some plausible paths to persistence for high advection populations like plankton. In a continuous network model, results have shown that variance in movement parameters across branches can allow for local persistence in upstream sub-networks (Ramirez 2012), while further work is necessary to link the effects of this variance with global geometric features.
Many of the analyses presented here hold across a wide range of tree geometries, yet others are focused on radial trees. Non-radial trees are more realistic representations of actual river networks in terms of geometry and allow for junction and headwater boundary conditions which do not agree across levels in the network. For example, some headwater boundaries may be most appropriately modeled with the lethal condition (e.g. a headwater edge that connects to a stream disturbed by deforestation or agriculture) while others fit the zero-flux condition. The eigenvalue bounds provided for general geometries (Sect. 5) are sensitive to global network features, in contrast to similar types of bounds in Ramirez (2012) which are restricted to detecting local edgewise features. Bounds which only detect edgewise features have certain disadvantages. For example, such bounds cannot distinguish the length structure of a two level tree, whose three edges each have length 1, from an interval of length 1. The Sect. 4 bounds, (4.3) and (4.9), are sensitive to the benefits to persistence the tree offers \((R_{min}=R_{max}=2)\) in comparison to the interval \((R_{min}=R_{max}=1)\). On the other hand, the bounds in Ramirez (2012) have an advantage in that they extend to nonconstant movement parameters across edges, yielding, for example, interesting results for upstream refuge. The structure of the bounds (4.3) and (4.9) suggest that certain trends which appear in radial trees extend to general geometries, but the extent to which precise conclusions about non-radial trees can be drawn from radial trees is unclear.
Graphical models also present a basis for studying the consequences of network geometry on more complex ecological models, such as the ‘jump-settlement’ benthos-drift model (e.g. Lutscher et al. 2005; Ramirez 2012) and various multi-species models (e.g. Ballyk et al. 1998; Lutscher et al. 2007; Hilker and Lewis 2010). Analysis in these models is routinely reduced to studying eigenvalues as was done here, although with a greater number of parameters determining outcomes. Persistence in the jump-settlement model can be reduced to studying the principal eigenvalue associated to a reaction–diffusion–advection equation describing the drift population, which would include parameters describing the exchange between the benthos and the drift, as described in Sect. 5. Persistence and stability in consumer-resource and competitive interactions is also a principal eigenvalue analysis, which features a dependence on species specific growth rates and movement parameters.
We expect network eigenvalue analysis to reveal important consequences of geometry on species interactions. The structure of spatial networks can alter encounter rates between predators and prey and hence stability (Cuddington and Yodzis 2002); these dynamics could be further complicated in the framework presented here if, for example, each species has its own area relation. Differences in habitable areas among tree edges could also influence species interactions in advective systems where prey or weak competitors find spatial refuges near headwater boundaries (Levine 2003; Lutscher et al. 2007; Auerbach and Poff 2011). As network geometry appears to constrain patterns of biodiversity in discrete-patch models (e.g. Muneepeerakul et al. 2007; Padgham and Webb 2010; Auerbach and Poff 2011; White and Rashleigh 2012), it is important to understand how species interactions and other biodiversity influencing processes operate in network models that acknowledge the continuous nature of river landscapes.
References
Ameziane T, Dauta A, Le Cohu R (2003) Origin and transport of phytoplankton in a large river: the Garonne, France. Arch Hydrobiol 156:385–404
Auerbach DA, Poff NL (2011) Spatiotemporal controls of simulated metacommunity dynamics in dendritic networks. J Am Benthol Soc 30:235–251
Ballyk M, Dung L, Jones DA, Smith HL (1998) Effects of random motility on microbial growth and competition in a flow reactor. SIAM J Appl Math 59:573–596
von Below J (1989) A maximum principle for semilinear parabolic network equations. Differential Equations with Applications in Biology, Physics, and Engineering (Leibnitz), pp 37–45. Lecture Notes Pure Applied Mathematics (1991) 133. Dekker, New York
Brette R, Rudolph M, Carnevale T, Hines M, Beeman D, Bower JM, Diesmann M, Morrison A, Goodman PH, Harris FC, Zirpe M, Natschlager T, Pecevski D, Ermentrout B, Djurfeldt M, Lansner A, Rochel O, Vieville T, Muller E, Davison AP, El Boustani S, Destexhe A (2007) Simulation of networks of spiking neurons: a review of tools and strategies. J Comput Neurosci 23:349–398
Cantrell RS, Cosner C (2003) Spatial ecology via reaction–diffusion equations. Wiley, New York
Carlson R (1997) Hill’s equation for a homogeneous tree. Electron J Differ Equ 23:1–30
Carlson R (2000) Nonclassical Sturm-Liouville problems and Schrodinger operators on radial trees. Electron J Differ Equ 71:1–24
Carlson R (2006) Linear network models related to blood flow. In: Quantum graphs and their applications. Contemp Math. AMS 415:65–80
Cuddington K, Yodzis P (2002) Predator-prey dynamics and movement in fractal environments. Am Nat 160:119–134
Exner P, Keating J, Kuchment P, Sunada T, Teplyaev A (2008) Analysis on graphs and its applications, vol 77. PSUM. AMS, Providence, Rhode Island, USA
Fagan WF (2002) Connectivity, fragmentation, and extinction risk in dendritic metapopulations. Ecology 83:3243–3249
Fausch KD, Torgersen CE, Baxter CV, Li HW (2002) Landscapes to riverscapes: bridging the gap between research and conservation of stream fishes. BioScience 52:483–498
Fisher RA (1937) The wave of advance of advantageous genes. Ann Eugen 7:355–369
Gaveau B, Okada M, Okada T (1993) Explicit heat kernels on graphs and spectral analysis. In: Fornaess JE (ed) Several Complex Varibales, (Proceedings of the Mittag-Leffler Institute, Stockholm, 1987-88), Princeton Math Notes, Vol. 38. Princeton University Press, pp. 364–388
Goldberg EE, Lynch HJ, Neubert MG, Fagan WF (2010) Effects of branching spatial structure and life history on the asymptotic growth rate of a population. Theor Ecol 3:137–152
Grant EHC, Lowe WH, Fagan WF (2007) Living in the branches: population dynamics and ecological processes in dendritic networks. Ecol Lett 10:165–175
Hershey AE, Pastor J, Peterson BJ, Kling GW (1993) Stable isotopes resolve the drift paradox for baetis mayflies in an arctic river. Ecology 74:2315–2325
Hilker FM, Lewis MA (2010) Predator-prey systems in streams and rivers. Theor Ecol 3:175–193
Jin Y, Lewis MA (2011) Seasonal influences on population spread and persistence in streams: critical domain size. SIAM J Appl Math 71(4):1241–1262
Kolpas A, Nisbet RM (2010) Effects of demographic stochasticity on population persistence in advective media. Bull Math Biol 72:1254–1270
Kostrykin V, Potthoff J, Schrader R (2008) Contraction semigroups on metric graphs. In: Analysis on graphs and its applications, vol 77, pp 423–458. PSUM. AMS, Providence, Rhode Island, USA
Kostrykin V, Schrader R (2006) Laplacians on metric graphs. In: Berkolaiko G, Carlson R, Fulling SA, Kuchment P (eds) Quantum graphs and their applications. Contemp Math, vol 415. AMS, Providence, pp 65–80
Kuchment P (2004) Quantum graphs: I. Some basic structures. Waves Random Media 14(1):S107–S128
Kuchment P (2008) Quantum graphs: an introduction and a brief survey. In: Exner P, Keating JP, Kuchment P, Sunada T, Teplyaev T (eds) Analysis on graphs and its applications. PSUM, vol 77. AMS, Providence, pp 291–312
Leitner D, Klepsch S, Kniess A, Schnepf A (2010) The algorithmic beauty of plant roots—an l-system model for dynamic root growth simulation. Math Comput Model Dyn Syst 16:575–587
Levine JM (2003) A patch modeling approach to the community-level consequences of directional dispersal. Ecology 84:1215–1224
Lutscher F, Lewis MA, McCauley E (2006) Effects of heterogeneity on spread and persistence in rivers. Bull Math Biol 68:21–29
Lutscher F, McCauley E, Lewis MA (2007) Spatial patterns and coexistence mechanisms in systems with unidirectional flow. Theor Pop Biol 71:267–277
Lutscher F, Nisbet RM, Pachepsky E (2010) Population persistence in the face of advection. Theor Ecol 3:271–284
Lutscher F, Pachepsky E, Lewis MA (2005) The effect of dispersal patterns on stream populations. SIAM J Appl Math 65:1305–1327
Maury B, Salort D, Vannier C (2009) Trace theorem for trees and application to the human lungs. Netw Heterog Media 4:469–500
Müller K (1954) Investigations on the organic drift in north Swedish streams. Rep Inst Freshw Res 34:133–148
Müller K (1982) The colonization cycle of freshwater insects. Oecologia 52:202
Muneepeerakul R, Weitz JS, Levin SA, Rinaldo A, Rodriguez-Iturbe I (2007) A neutral metapopulation model of biodiversity in river networks. J Theor Biol 245:351–363
Naimark K, Solomyak M (2000) Eigenvalue estimates for the weighted Laplacian on metric trees. Proc Lond Math Soc 80(3):690–724
Newbold JD (1992) Cycles and spirals of nutrients 1. Hydrological and ecological principles. In: Calow P, Petts G (eds) The rivers handbook. Blackwell Scientific, Oxford, pp 379–408
Nicaise S (1985) Some results on spectral theory over networks applied to nerve impulse transmission. In: Brezinski C, Draux A, Magnus AP, Maroni P, Ronveaux A (eds) Polynomes orthogonaux et applicationes. Lecture Notes Mathematics, vol 1171. Springer, Berlin, pp 532–541
Okada T (1993) Asymptotic behavior of skew conditional heat kernels on graph networks. Can J Math 45(4):863–878
Pachepsky E, Lutscher F, Nisbet RM, Lewis MA (2005) Persistence, spread and the drift paradox. Theor Pop Biol 67:61
Padgham M, Webb JA (2010) Multiple structural modifications to dendritic ecological networks produce simple responses. Ecol Model 221:2537–2545
Rader RB (1997) A functional classification of the drift: traits that influence invertebrate availability to salmonids. Can J Fish Aquat Sci 54:1211–1234
Ramirez JM (2012) Population persistence under advection–diffusion in river networks. J Math Biol 65:919–942
Robson BJ, Matthews TG, Lind PR, Thomas NA (2008) Pathways for algal recolonization in seasonally-flowing streams. Freshw Biol 53:2385–2401
Rodriguez-Iturbe I, Rinaldo A (2001) Fractal river basins: chance and self-organization. Cambridge University Press, Cambridge
Sherwin S, Franke V, Peiro J, Parker K (2003) One-dimensional modeling of a vascular network in space-time variables. J Eng Math 47:217–250
Skellam JG (1951) Random dispersal in theoretical populations. Biometrika 38:196–218
Speirs DC, Gurney WSC (2001) Population persistence in rivers and estuaries. Ecology 82:1219–1237
Strauss w (2008) Partial differential equations. Wiley, New York
Waters TF (1972) The drift of stream insects. Annu Rev Entomol 17:253–272
White D, Rashleigh B (2012) Effects of stream topology on ecological community results from neutral models. Ecol Model 231:20–24
Williams DD, Williams NE (1993) The upstream/downstream movement paradox of lotic invertebrates: quantitative evidence from a welsh mountain stream. Freshw Biol 30:199–218
Acknowledgments
The research of J. Sarhad and K. E. Anderson was supported by the National Science Foundation under Grant No. DMS-1122726. Two anonymous reviews provided comments that greatly enhanced the quality of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Section 2 proofs
Proof
(Proof of Lemma 1)
Begin with some estimates for functions \(f\) in the domain of \(L_m\), which are continuous with \(f(w_d) = 0\). Let \(w \in \fancyscript{T}\), and let \(\gamma \) be a simple path of length \(d(w_d,w)\) joining the root vertex \(w_d\) and the point \(w\), with vertices \(w_d= w_0,w_1,\dots ,w_{N-1}\) along the path. Let \(w_N = w\). Start with
By the Cauchy–Schwarz inequality,
or replacing \(\gamma \) in the last integral by \(\fancyscript{T}\),
Applying (2.20) with \(f = \phi _n\) gives
If \(A_j \ge A_{min} > 0\), then (7.1) gives the desired estimate. \(\square \)
Proof
(Proof of Proposition 1)
It suffices to treat the maximum case. Treating \(V > 0\) first, use the local coordinate function \(X\), where \(-X\) is the distance from the root vertex \(w_d\). For \(\epsilon >0\) and \(G(X)=\exp [VX/2D]\), consider \(F\) defined edgewise by \(F_e(t,X) = U_e(t,X) + \epsilon G(X)\). The boundary condition \(U(t,w_d) = U(t,0) = 0\) means \(F(t,0) = \epsilon > 0\), so a maximum of \(F\) is nonnegative. \(G\) and its \(X\)-derivatives are continuous at junctions, so no edge indexing of these derivatives at a junction is required.
A standard method (Strauss 2008, p. 43) rules out a maximum for \(F(t_0,w)\) when \(0 < t_0 < t_1\) and \(w\) is interior to an edge. If such a maximum existed, then
so
Since \(U\) satisfies the diffusion equation one has the contradictory assertion
and this maximum cannot exist.
Extending this argument, suppose \(0 < t_0 < t_1,\,w\) is an interior vertex, and \(F\) has a maximum at \((t_0,w)\). Then
An elementary calculation shows that \(G\), and therefore \(F\), satisfies (2.15) at \(w\). Using \(F(t_0,w)\ge 0\) and (2.12) gives
The left hand side of (7.3) is a sum of three nonpositive terms, so
and the maximality of \(F(t_0,w)\) implies
The argument starting with (7.2) above now shows \(F\) can not attain a maximum at \((t_{0},w)\) when \(w\) is an interior vertex.
Similar ideas rule out a maximum for \(F\) when \(t =t_1\), since then
which leads to a contradiction as before.
Having now established
the proof for \(V > 0\) is finished by noting that for all \(\epsilon > 0\) and some constant \(C \ge 0\)
When \(V=0\), the auxiliary function \(G(X)=\exp (X)\) can be used. The function \(F=U+\epsilon G\) does not satisfy (2.15), but
which still forces \(\partial F_{j}/\partial X =0\) for \(j=0,1,2\) and the proof follows as before. \(\square \)
Proof
(Proof of Proposition 2)
Suppose \(U\) is negative somewhere. Since the eigenvalues of \(L_m\) are strictly negative, Lemma 1 implies that \(U \rightarrow 0\) uniformly as \(t \rightarrow \infty \). Thus there is a global negative minimum at some point \(U(t_0,w)\). The maximum principle implies \(w\) is an upstream boundary vertex. But the upstream boundary vertex conditions are \(\frac{V}{2}U = D\partial U/\partial X \), meaning that \(U\) decreases as one moves out from the vertex, which is impossible since \(U(t_0,w)\) is minimal. \(\square \)
Proof
(Proof of Proposition 3)
Pick a nonnegative initial function \(U(0,\cdot ) \) which is in the domain of \({L_{m}}\), and is not orthogonal to some eigenfunction of \({L_{m}}\) with eigenvalue \(\lambda _1\). Let \(U(t,\cdot )\) be the solution of (2.18) with this initial value. Proposition 2 and an eigenfunction expansion for \(U\) show that \(e^{-\lambda _1t}U\) is a nonnegative function which converges, as \(t \rightarrow \infty \) to a nontrivial eigenfunction \(\phi _1\) with eigenvalue \(\lambda _1\).
Since \(\phi _1 \ge 0\), any point \(x_0 \in \fancyscript{T}\) with \(\phi _1(x_0) = 0\) is a global minimum. If \(x_0\) is interior to an edge, then \(\phi _1 ^{\prime }(x_0) = 0 \) by calculus. If \(x_0\) is a boundary vertex with nonlethal condition, then \(\phi _1^{\prime }(x_0) = 0 \) by the boundary condition (2.14). If \(x_0\) is an interior vertex then in outward pointing local coordinates \(\phi _1^{\prime }(x_0) \ge 0 \) for each edge incident on \(x_0\). Since \(\phi _{1}(x_{0})=0\), the junction condition (2.15) gives \(\phi _1^{\prime }(x_0) = 0 \) on each incident edge.
Since the eigenfunction \(\phi _1\) is a solution to the linear equation \(\phi _1^{\prime \prime } = \lambda _1\phi _1\) on each edge, \(\phi _1\) is the zero function, first on any closed edge containing \(x_0\), then on any adjacent edge. Since \(\fancyscript{T}\) is connected, if \(\phi _1\) vanishes at any point except a lethal vertex, then it is zero everywhere. \(\square \)
Proof
(Proof of Proposition 4)
Suppose \(\psi \) is an eigenfunction with eigenvalue \(\lambda _1\) which is orthogonal to the nonnegative eigenfunction \(\phi _1\) of Proposition 3. Since \(\phi _1\) is strictly positive except at lethal vertices \(w\), where \(\frac{\partial \phi _1}{\partial X}(w) \not = 0\), there is an \(\alpha > 0\) such that \(\psi + \alpha \phi _1 \ge 0\). If \(\alpha _1\) is the smallest possible \(\alpha \), there will be a lethal vertex \(w\) with \((\psi + \alpha _1\phi _1)^{\prime }(w) = 0\) or a point \(x_0\) which is not a lethal vertex where \((\psi + \alpha _1\phi _1)(x_0) = 0\). As in Proposition 3 this forces \((\psi + \alpha _1\phi _1)(x)= 0\) for all \(x \in \fancyscript{T}\). Since \(\psi \) and \(\phi _1\) are orthogonal, \(\psi =0\).
\(\square \)
Proof
(Proof of Theorem 1)
Using an expansion in eigenfunctions of \(L_m\), suppose \(U(0,\cdot ) = \sum _n c_n \phi _n\). Then the solution of (2.24) is
Recall that \(\lambda _n < 0\) for all \(n\). If \(r - \frac{V^2}{4D} < |\lambda _1 | \), then \(r - \frac{V^2}{4D} + \lambda _n < 0\) for all \(n\), and the estimate (2.22) implies that all solutions converge uniformly to 0 as \(t \rightarrow - \infty \).
In the other direction, suppose \(r - \frac{V^2}{4D} \ge |\lambda _1| \). By Proposition 3 any positive initial population \(U(0,\cdot )\) will not be orthogonal to \(\phi \). The solution \(U(t,\cdot )\) of (2.13) will be nonnegative, with the \(\lambda _1\) component dominant as \(t \rightarrow \infty \), so the population survives. \(\square \)
1.2 Proof of Theorem 3
The analysis starts in the same manner for both zero flux and lethal conditions at the upstream boundary. The half line has coordinate \(0 \le X < \infty \), with \(X=0\) representing the upstream boundary position, and \(X = X_1\) being the position of the downstream boundary vertex for \(\fancyscript{T}\). As before, the original model Eq. (2.2) may be reduced to the diffusion equation
by using the substitution
For notational convenience, the zero flux condition (2.14) is abbreviated as
Following Strauss (2008, p. 60), the solution for (7.5) is constructed by extending \(F\) and the resulting solution to (7.5) on the whole line so that
satisfies the desired boundary condition at \(X = 0\). When the lethal boundary condition is desired, the odd extension \(F(-X) = -F(X)\) is used. In the zero flux case, \(F^{\prime }(X) - \theta F(X)\) should have an odd extension given by
An integration by parts shows that \(W_X(0) - \theta W(0) = 0\).
First consider \(W(t,X)\) when \(\delta < 0\) in (7.6). If \(W(t,X)\) is bounded, then solutions \(u(t,X)\) of (2.2) will converge to zero uniformly on compact subsets of \([0,\infty )\) as \(t \rightarrow \infty \). Suppose the initial function \(F(X)\) is bounded for \(X \ge 0\). If the upstream boundaries are lethal, the extension \(F(-X) = -F(X)\) is also bounded, and the averaging of the heat kernel implies solutions \(W(t,X)\) of (7.7) are also bounded. Alternatively, if the zero flux condition holds at the upstream boundary, and \(|F(X)| \le M\) for \(X \ge 0\), the simple estimate
shows that the extension of \(F\) by (7.8) is bounded for all \(X \in \mathbb R \). Again, \(W(t,X)\) is bounded, so the population does not persist.
The proof that the population does persist when \(\delta > 0\) will be based on an asymptotic expansion of \(W(t,X)\) as \(t \rightarrow \infty \).
Proposition 5
Suppose \(F:\mathbb R \rightarrow \mathbb R \) satisfies the moment conditions
Then as \(t \rightarrow + \infty \) solutions \(W(t,X)\) of (7.7) satisfy
the estimate holding uniformly for \(X\) bounded.
Proof
For \(s \ge 0 \) use the low order Taylor expansion \(\exp (-s) = 1 - s + R_1(s)\), where \( 0 \le R_1(s) \le s^2/2\). Then
with
\(\square \)
A simple assumption will insure the hypotheses of Proposition 5 are satisfied.
Lemma 2
For some constant \(C > 0\), suppose
Extend \(F\) to \(-\infty < X < \infty \) using either (7.8) or \(F(-X) = -F(X)\). Then
so that \(|F(X)|\) has all moments finite. In addition,
Proof
The results are immediate if \(F(-X) = -F(X)\), so assume the extension (7.8) is used. The conclusion (7.11) follows from
The claim (7.12) follows by changing the order of integration,
Thus
\(\square \)
By (7.12) the \(t^{-1/2}\) coefficient vanishes in (7.9). To establish the nonvanishing of the \(t^{-3/2}\) coefficient, consider
when \(\int _0^{\infty } F > 0\). In the lethal boundary case the last integrand of (7.13) is \(2yF(y)\), so (7.13) is negative for \(X > 0\). For the zero flux case, start with the calculation
The second computation is
and (7.13) is again negative.
If \(\delta > 0\) the slow decay of \(W(t,X)\) as \(t \rightarrow \infty \) is outmatched by the factor \(e^{\delta t}\) in (7.6), and \(u(t,X) \rightarrow \infty \). Note that a bounded population in the original model implies the exponential decay (7.10) for the initial data of the diffusion equation. In the context of the original model (2.2), this analysis completes the proof of Theorem 3.
Rights and permissions
About this article
Cite this article
Sarhad, J., Carlson, R. & Anderson, K.E. Population persistence in river networks. J. Math. Biol. 69, 401–448 (2014). https://doi.org/10.1007/s00285-013-0710-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-013-0710-6
Keywords
- Quantum graphs
- Reaction–diffusion–advection equation
- Principal eigenvalues
- Population persistence
- River ecology