Abstract
We introduce the concept of generalized Cayley graphs of semigroups and discuss their fundamental properties, and then study a special case, the universal Cayley graphs of semigroups so that some general results are given and the universal Cayley graph of a  -partial order of complete graphs with loops is described.
-partial order of complete graphs with loops is described.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and preliminaries
The investigation and characterization of digraphs that are Cayley graphs of certain algebraic structures have a long history, documented for example in Maschke’s Theorem from 1896 about groups of genus zero, that is, groups G which possess systems A of generating elements, such that the Cayley graphs Cay(G,A) are planar. A modern presentation of this can be found in [16]. Stimulated by the rich results of research on the Cayley graphs of groups, the Cayley graphs of semigroups have also been considered by many authors, see, for example, [1, 5–8, 13, 14, 18]. Some of the earliest references on this subject are [2, 19, pp. 93–101]. The Cayley graphs of semigroups are closely related to the finite state automata and have many valuable applications (see the survey [11] and Sect. 2.4 of the book [4]). In addition, similar questions concerning divisibility graphs and power graphs of semigroups were considered in [9, 10], respectively.
If S is a semigroup, and T is a nonempty subset of S, the so-called connection set, then the Cayley graph Cay(S,T) of S relative to T is usually defined as the graph with vertex set S and edge set E(Cay(S,T)) consisting of those ordered pairs (x,y), where xt=y for some t∈T, see [1, 5, 8, 12–14]. Note that in all of these articles the Cayley graph is defined by right translations which is quite usual. But at the same time, in some other articles, the Cayley graph is defined by left translations, see, for example, [6, 7, 11, 18].
However, the reflection of algebraic properties of S may depend strongly on the choice of left actions or right actions. Evidently, for a given semigroup S and a fixed subset T of S, the Cayley graphs Cay(S,T) defined by left actions and by right actions may not be the same. In order to unify these two cases, and to get more applications, we shall generalize the definition of Cayley graphs of semigroups in the present paper.
As we can see in [1, 5–8, 11–14, 18], when studying Cayley graphs of semigroups, at least the following three basic aspects are of significance: (1) to describe the Cayley graph of a given semigroup; (2) given a Cayley graph of a semigroup, to determine the structure or study the properties of this semigroup; and (3) to find or construct a semigroup whose Cayley graph is a given graph. Our work on generalized Cayley graphs of semigroups will follow a similar line.
In Sect. 1 of the present paper, we introduce the notion of generalized Cayley graphs of semigroups. Some fundamental properties of generalized Cayley graphs are discussed in Sect. 2. At last, in Sect. 3, we focus on a special case, the universal Cayley graphs of semigroups so that some general results are given. Here we give some fundamental concepts and simple facts for preliminaries. As Example 1.4 below shows, the generalized Cayley graphs of a given semigroup may include more universal classes of graphs than the usual Cayley graphs.
Recall that if S is an ideal of a semigroup T, then we call T an ideal extension of S. For any semigroup T, let
Now we present the main definition of this paper, which generalizes the Cayley graph of a semigroup S relative to a subset of S to that relative to a relation on T 1 with T an ideal extension of S.
Definition 1.1
Let T be an ideal extension of a semigroup S and ρ⊆T 1×T 1. The Cayley graph Cay(S,ρ) of S relative to ρ is defined as the graph with vertex set S and edge set E(Cay(S,ρ)) consisting of those ordered pairs (a,b), where xay=b for some (x,y)∈ρ.
We also call the Cayley graphs defined in this way the generalized Cayley graphs, in order to distinguish them from the usual ones. Some examples are displayed below.
Example 1.2
If T is a nonempty subset of a semigroup S, then generalized Cayley graph Cay(S,T×{1}) is actually the usual Cayley graph Cay(S,T) of S relative to T defined by the left actions, while generalized Cayley graph Cay(S,{1}×T) is precisely the usual Cayley graph Cay(S,T) of S relative to T defined by the right actions.
Example 1.3
Assume that S is a semigroup. Let ω l =S 1×{1} (the left universal relation on S 1), ω r ={1}×S 1 (the right universal relation on S 1) and ω=S 1×S 1 (the universal relation on S 1). Then the generalized Cayley graphs Cay(S,ω l ), Cay(S,ω r ) and Cay(S,ω) are called left universal, right universal and universal Cayley graphs of S, respectively.
Example 1.4
Let N be the semigroup of all natural numbers with the usual multiplication, and S the ideal of N consisting of all nonnegative even integers. Then on the one hand, for any subset T of S, the usual Cayley graph Cay(S,T) can not contain any edge (a,b) such that b is not divided by 4. But on the other hand, there are indeed such edges in the generalized Cayley graph Cay(S,N×N).
In what follows, we give some simple facts for preliminaries. Assume that S is a semigroup and a∈S. Then L(a)=S 1 a, R(a)=aS 1 and J(a)=S 1 aS 1 is the principal left ideal, principal right ideal and principal ideal generated by a, respectively. The next lemma is a direct consequence of Definition 1.1.
Lemma 1.5
Let T be an ideal extension of a regular semigroup S and ρ⊆T 1×T 1. Then the following statements hold:
-
(1)
if a,b∈S such that (a,b)∈E(Cay(S,ρ)), then J(a)⊇J(b);
-
(2)
there is a relation ρ 0⊆S×S such that Cay(S,ρ) is a subgraph of Cay(S,ρ 0).
Throughout the paper, graphs are directed graphs without multiple edges, but possibly with loops, or digraphs in terms of [1, 14]. For a graph Γ, denote by V(Γ) and E(Γ) its vertex set and edge set, respectively. For any a∈V(Γ), Let
Let T be an ideal extension of a semigroup S and ρ⊆T 1×T 1. If a,b∈S such that (a,b)∈E(Cay(S,ρ)), then by Definition 1.1, there exists (x,y)∈ρ such that xay=b. Let
and set
We call ρ(a)1 the ρ-class of a. It is evident that (a,b)∈E(Cay(S,ρ)) if and only if b∈ρ(a). So by (1.1), we obtain
The next lemma will be used repeatedly later.
Lemma 1.6
Let T be an ideal extension of a semigroup S, ρ⊆T 1×T 1 and a,b∈S. If ρ 1(a)⊇ρ 1(b) and a≠b, then (a,b)∈E(Cay(S,ρ)).
Proof
Assume that ρ 1(a)⊇ρ 1(b) and a≠b. By (1.3), b∈ρ 1(b)⊆ρ 1(a)=ρ(a)∪{a}. Since a≠b, we have that b∈ρ(a). By (1.2), there exists (x,y)∈ρ such that xay=b. Hence by Definition 1.1, (a,b)∈E(Cay(S,ρ)) as required. □
As usual, a directed graph without loops and multiple edges is called simple. Note that although generalized Cayley graphs defined in the present paper have no multiple edges, they may have loops, and so they don’t have to be simple. Sometimes, we shall equate two graphs each of which is isomorphic to the other one. That is, if Γ 1⋍Γ 2, then we may identify Γ 1 with Γ 2.
We use standard terminology of graph theory following, for example, [17]. For semigroup theory, we refer the reader to [3, 15, 20].
2 Fundamental properties of generalized Cayley graphs of semigroups
The aim of this section is to discuss in general the fundamental properties of generalized Cayley graphs of semigroups by introducing some new concepts such as ‘I-compatible’ and ‘stable’. A necessary and sufficient condition is given in Theorem 2.2 for a relation on a semigroup to be I-compatible, and the semigroup whose generalized Cayley graph is a chain of complete graphs with loops is characterized in Theorem 2.10.
Let us begin by introducing the first new notion of this section.
Definition 2.1
Let T be a semigroup and ρ⊆T×T. If that (a,b),(c,d)∈ρ for any a,b,c,d∈T always implies (ca,bd)∈ρ, then we call ρ inversely compatible, or briefly, I-compatible.
For example, if T is a semigroup with A and B subsemigroups of T, then it is clear that ρ=A×B is I-compatible. Particularly, if S is a semigroup, then S×{1}, S 1×{1}, {1}×S, {1}×S 1, S×S and S 1×S 1 are all I-compatible.
Suppose that S and T are semigroups. A mapping ϕ:S⟶T is called an anti-homomorphism if ϕ(ab)=ϕ(b)ϕ(a) for all a,b∈S. Furthermore, if ϕ is a bijection, then we call ϕ an anti-isomorphism, or say that S is anti-isomorphic to T.
For characterizing the I-compatibility, suppose that T is a semigroup and ρ⊆T×T, and let
If a,b∈l ρ , then exist c,d∈T such that (a,c),(b,d)∈ρ. If ρ is I-compatible, then (ba,cd)∈ρ which means that ba∈l ρ and cd∈r ρ . Thus both l ρ and r ρ are subsemigroups of T.
Now ρ⊆l ρ ×r ρ . It is evident that the mapping ρ⟶l ρ , (a,b)↦a is an onto anti-homomorphism. Let \(l_{\rho}^{*}=l_{\rho}\). For any \(a,b\in l_{\rho}^{*}\), define a∗b=ba. Then \((l_{\rho}^{*}, \ast)\) is a semigroup anti-isomorphic to l ρ . We call \((l_{\rho}^{*}, \ast)\) the anti-semigroup of l ρ . The anti-semigroup of a subsemigroup of a semigroup T is called a anti-subsemigroup of T. Thus \((l_{\rho}^{*}, \ast)\) is a anti-subsemigroup of T. Now, \(\rho\longrightarrow l_{\rho}^{*}\), (a,b)↦a is an onto homomorphism. Of course, the mapping ρ⟶r ρ , (a,b)↦b is also an onto homomorphism. So ρ is a subdirect product of \(l_{\rho}^{*}\) and r ρ .
Conversely, assume that ρ is a subdirect product of \((l_{\rho}^{*}, \ast)\), an anti-subsemigroup of T, and l ρ , a subsemigroup of T. Then ρ is a subsemigroup of the direct product \(l_{\rho}^{*}\times r_{\rho}\). Thus for any (a,b),(c,d)∈ρ, we have that (ca,bd)=(a∗c,bd)=(a,b)(c,d)∈ρ. It follows that ρ is I-compatible.
Summarizing the above arguments, we obtain
Theorem 2.2
Assume that T is a semigroup and ρ⊆T×T. Then ρ is I-compatible if and only if there exist an anti-subsemigroup A and a subsemigroup B such that ρ is the subdirect product of A and B.
Let us turn our attention to the second new notion of this section.
Definition 2.3
Let Γ be a graph. If that (a,b),(b,c)∈E(Γ) for a,b,c∈V(Γ) always implies that (a,c)∈E(Γ), then Γ is said to be edge-transitive.
The relation of the above two notions is indicated in
Proposition 2.4
Assume that T is an ideal extension of a semigroup S. If ρ⊆T 1×T 1 is I-compatible, then Cay(S,ρ) is edge-transitive.
Proof
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1 is I-compatible. If (a,b),(b,c)∈E(Cay(S,ρ)), then there exist (x,y),(x 0,y 0)∈ρ such that b=xay and c=x 0 by 0. Thus
where (x 0 x,yy 0)∈ρ by the assumption that ρ is I-compatible. It follows that (a,c)∈E(Cay(S,ρ)). Therefore, Cay(S,ρ) is edge-transitive and the proof is complete. □
Corollary 2.5
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1 is I-compatible. If (a,b)∈E(Cay(S,ρ)), then ρ(a)⊇ρ(b) and ρ 1(a)⊇ρ 1(b).
Proof
Suppose that (a,b)∈E(Cay(S,ρ)) and that ρ is I-compatible. Together with (1.2) and Definition 1.1, we obtain that b∈ρ(a). According to Proposition 2.4, Cay(S,ρ) is edge-transitive. Now, for any c∈ρ(b), (b,c)∈E(Cay(S,ρ)). It follows that (a,c)∈E(Cay(S,ρ)), that is, c∈ρ(a). Therefore, ρ(a)⊇ρ(b). By (1.3), ρ 1(b)=ρ(b)∪{b}. It follows that ρ(a)⊇ρ 1(b). Hence ρ 1(a)⊇ρ(a)⊇ρ 1(b) and the proof is complete. □
To obtain the converse implication of Corollary 2.5, we introduce the third new concept of this section as follows.
Definition 2.6
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1. An element a of S is called stable under ρ if a∈ρ(a). If all elements of S are stable under ρ, then S is called stable under ρ.
It is clear that a is stable under ρ if and only if ρ(a)1=ρ(a). For example, it is easy to show that if S is a regular semigroup or a monoid, then S is stable under ω l , ω r and ω, respectively. Combining Lemma 1.6 and Corollary 2.5, one may easily deduce
Proposition 2.7
Assume that T is an ideal extension of a semigroup S. If ρ⊆T 1×T 1 is I-compatible and S is stable under ρ, then for any a,b∈S the following conditions are equivalent:
-
(1)
(a,b)∈E(Cay(S,ρ));
-
(2)
ρ(a)⊇ρ(b);
-
(3)
ρ 1(a)⊇ρ 1(b).
In what follows, we shall characterize semigroups whose generalized Cayley graphs are some special graphs.
Let (Y,≥) be a partially ordered set. For any a∈Y, set
Recall that for any a,b∈Y, a,b are called comparable if a≥b or b≥a. We call (Y,≥) a totally ordered set if a,b are comparable for all a,b∈Y. Also we call the total order ≥ a linear order. The relation graph of a linear order is called a linear graph. It is easily seen that a graph Γ is a linear graph if and only if the following conditions are satisfied: (1) Γ does not contain multiple edges; (2) for any a∈V(Γ), (a,a)∈E(Γ); (3) for any a,b∈V(Γ), (a,b)∈E(Γ) or (b,a)∈E(Γ); (4) if a≠b∈V(Γ) and (a,b)∈E(Γ), then \((b,a)\ \bar{\in}\ E(\varGamma )\); (5) Γ is edge-transitive. The next lemma characterizes semigroups whose Cayley graphs are linear graphs.
Lemma 2.8
Assume that T is an ideal extension of a semigroup S and that ρ⊆T 1×T 1 is I-compatible such that S is stable under ρ. Then the following conditions are equivalent:
-
(1)
Cay(S,ρ) is a linear graph;
-
(2)
There exists a linear order ≥ on S such that for any a∈S, ρ(a)=a↓;
-
(3)
There exists a linear order ≥ on S such that for any a∈S, ρ 1(a)=a↓.
Proof
Assume that T is an ideal extension of a semigroup S and ρ⊇T 1×T 1 is I-compatible such that S is stable under ρ. Then by Proposition 2.4 and (1.4) Cay(S,ρ) is edge-transitive and for any a∈S, \(\rho ^{1}(a)=\rho(a)=\overrightarrow{a}\).
(1) ⇒ (2). Suppose that Cay(S,ρ) is a linear graph. Then define an order ≥ on S by that a≥b if and only ρ(a)⊇ρ(b). It is clear that ≥ is reflexive and transitive. Assume that a≥b and b≥a. Then ρ(a)⊇ρ(b) and ρ(b)⊇ρ(a). Thus ρ(a)=ρ(b). By Proposition 2.7, (b,a)∈E(Cay(S,ρ)) and (a,b)∈E(Cay(S,ρ)). Since Cay(S,ρ) is a linear graph, we have a=b. Therefore ≥ is anti-symmetric and furthermore it is a partial order. For any a,b∈S, (a,b)∈E(Cay(S,ρ)) or (b,a)∈E(Cay(S,ρ)). It follows from Proposition 2.7 that ρ(a)⊇ρ(b) or ρ(b)⊇ρ(a). That is, a≥b or b≥a, which means that ≥ is a total order. By (2.2) and Proposition 2.7, for any a∈S, \(a\downarrow=\{b\in S|a\geq b\}=\{b\in S|\rho (a)\supseteq\rho (b)\}=\{b\in S|(a,b)\in E(\mathrm{Cay}(S,\rho))\}=\overrightarrow{a}=\rho(a)\), as required.
(2) ⇒ (1). Assume that ≥ is a linear order on S such that for any a∈S, ρ(a)=a↓. Then for any a∈S, a≥a. It follows that a∈a↓=ρ(a) which means that (a,a)∈E(Cay(S,ρ)). For any a,b∈S, a≥b or b≥a. It follows that b∈a↓=ρ(a) or a∈b↓=ρ(b). That is, (a,b)∈E(Cay(S,ρ)) or (b,a)∈E(Cay(S,ρ)). Thus by Proposition 2.7, ρ(a)=ρ(b) which deduce that a↓=b↓. Hence a≥b and b≥a. Since ≥ is anti-symmetric, we have a=b. Therefore, Cay(S,ρ) is a linear graph.
(2) ⇔ (3). This is trivial because ρ 1(a)=ρ(a) for every a∈S by the assumption that S is stable under ρ, and so the lemma is proved. □
A complete graph with loops are defined as a graph Γ with the edge set E(Γ)={(x,y)|x,y∈V(Γ)}. Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1. If ρ 1(a)=ρ 1(b) for all a,b∈S, then S is called ρ-simple. It is easy to check that S is ρ-simple if and only if for every a∈S, ρ 1(a)=S. For example, if T is an ideal extension of a simple (rep. left simple, right simple) semigroup S, then S is ω- (resp., ω l -, ω r -) simple. The next lemma uses the concept ‘ρ-simple’ to characterize semigroups whose Cayley graphs are complete graphs with loops.
Lemma 2.9
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1 is an I-compatible relation such that S is stable under ρ. Then the following conditions are equivalent:
-
(1)
Cay(S,ρ) is a complete graph with loops;
-
(2)
S is ρ-simple.
Proof
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1 is I-compatible such that S is stable under ρ. Then the conditions of Proposition 2.7 are satisfied.
(1) ⇒ (2). Suppose that Cay(S,ρ) is a complete graph with loops. Then for any a,b∈S, (a,b)∈E(Cay(S,ρ)) and (b,a)∈E(Cay(S,ρ)). According to Proposition 2.7, ρ 1(a)=ρ 1(b) which means that S is ρ-simple.
(2) ⇒ (1). Assume that S is ρ-simple. Then for any a,b∈S, ρ 1(a)=ρ 1(b). Again, by Proposition 2.7, (a,b)∈E(Cay(S,ρ)) and (b,a)∈E(Cay(S,ρ)). It is shown that Cay(S,ρ) is a complete graph with loops. □
Together with Proposition 2.7, Lemmas 2.8 and 2.9, we can easily prove the main theorem of this section:
Theorem 2.10
Assume that T is an ideal extension of a semigroup S and ρ⊆T 1×T 1 is an I-compatible relation such that S is stable under ρ. Then the following conditions are equivalent:
-
(1)
Cay(S,ρ) is a chain of complete graph with loops;
-
(2)
S is a chain of ρ-simple semigroups.
3 Universal Cayley graphs of semigroups
In this section, we concentrate on the special case ρ=ω, that is, we shall investigate the universal Cayley graph Cay(S,ω) of a semigroup S, where ω is the universal relation on S
1. The main results of this section are Theorems 3.9 and 3.13. The former establishes the connection between a completely regular semigroup and a semilattice of complete graphs with loops, and the latter generalizes Theorem 3.9 and characterizes the nonidempotent-trivial  -partial order of complete graphs with loops by means of a new construction similar with Clifford semigroups, so called semigroup-partially-ordered sets of semigroups which we define in Definition 3.11.
-partial order of complete graphs with loops by means of a new construction similar with Clifford semigroups, so called semigroup-partially-ordered sets of semigroups which we define in Definition 3.11.
Observing that ω is I-compatible and S is stable under ω, and that for any a∈S, ω 1(a)=ω(a)=J(a), the principal ideal of a, according to Proposition 2.7, we get the following result.
Lemma 3.1
For any semigroup S, the following conditions are equivalent:
-
(1)
(a,b)∈E(Cay(S,ω));
-
(2)
J(a)⊇J(b).
As a consequence of this lemma or Lemma 2.9, we have
Lemma 3.2
Assume that S is a semigroup. Then Cay(S,ω) is a complete graph with loops if and only if S is simple.
Let us turn our attention to universal Cayley graphs of semilattices.
The relation graph of the inverse relation ≥ of the natural order ≤ on a semilattice is called a semilattice graph. It is easily seen that a graph Γ is a semilattice graph if and only if the following conditions are satisfied: (1) for any a∈V(Γ), (a,a)∈E(Γ); (2) for any a,b∈V(Γ), \(\overrightarrow{a}\cap\overrightarrow{b}\neq\emptyset\) and it has an initial element, that is to say, there exists \(c\in \overrightarrow{a}\cap\overrightarrow{b}\) such that (c,d)∈E(Γ) for all \(d\in \overrightarrow{a}\cap\overrightarrow{b}\).
Lemma 3.3
If S is a semilattice, then Cay(S,ω) is a semilattice graph. Actually, Cay(S,ω) is exactly the relation graph of inverse relation ≥ of the natural order ≤ on S.
Proof
If for a,b∈S, a≥b, then b≤a which implies that ab=b. Thus b∈J(a) and J(b)⊆J(a). By Lemma 3.1, (a,b)∈E(Cay(S,ω)).
Conversely, if (a,b)∈E(Cay(S,ω)), then by Lemma 3.1 again, J(b)⊆J(a). Thus we have b∈J(a) which implies that b=xay=xya for some x,y∈S 1. Thus b≤a, or equivalently, a≥b.
Now we have proved that a≥b if and only if (a,b)∈E(Cay(S,ω)). So, Cay(S,ω) is exactly the relation graph of ≥ on S, and Cay(S,ω) is a semilattice graph. □
Remark 3.4
The converse of Lemma 3.3 is not true. For example, we consider the null semigroup with three elements 0,a,b. Evidently, J(0)={0}, J(a)={0,a} and J(b)={0,b}. So the Cay(S,ω) is a semilattice graph, but S is not a semilattice.
Lemma 3.5
For a semilattice graph Γ, there is a semilattice S such thatCay(S,ω)=Γ.
Proof
Since Γ is a semilattice graph, then there is a semilattice (S,≤) such that Γ is the relation graph of the inverse relation ≥ of the relation ≤. For any a,b∈S, define multiplication by ab=a∧b, the greatest lower bound of a and b in (S,≤). Then S becomes a semigroup which is a semilattice. By Lemma 3.3, Cay(S,ω) is exactly the relation graph of ≥ on S, where ≥ is the inverse relation of the natural order ≤ on S. That is, Cay(S,ω)=Γ, as required. □
To describe further the properties of universal Cayley graphs of semigroups, we require some new concepts which we introduce as follows.
A partially ordered set (Y,≥) is called a strong partially ordered set if for any α,β∈X, there is γ∈Y such that α≥γ and β≥γ. If (Y,≥) is a partially ordered set, and Y is a semigroup such that for any α,β∈Y, α,β≥αβ, then we call the semigroup Y a partially ordered semigroup, and we call the partially ordered set Y a semigroup-partially-ordered set. If B is a partially ordered semigroup which is also a band (i.e., an idempotent semigroup), then we call B a band-partially-ordered set or a partially ordered band. If (Y,≥) is a partially ordered set, Y is a semigroup, T is an ideal extension of Y and ρ⊆T
1×T
1 such that for any α∈Y, ρ
1(α)=α↓ where by α↓ we denote the set {β|α≥β}, then we call the semigroup Y a ρ-semigroup, and we call the partially ordered set Y a ρ-partially-ordered set. In particular, if ρ=S
1×S
1 (rep. S
1×{1}, {1}×S
1), then a ρ-partially-ordered set or ρ-semigroup is called a  -partially-ordered set or
-partially-ordered set or  -semigroup (rep.
-semigroup (rep.  -partially-ordered set or
-partially-ordered set or  -semigroup,
-semigroup,  -partially-ordered set or
-partially-ordered set or  -semigroup).
-semigroup).
It is clear that a semilattice with its natural order is a  -partially-ordered set, a
-partially-ordered set, a  -partially-ordered set is a semigroup-partially-ordered set, and a semigroup-partially-ordered set is a strong partially ordered set. The relation graph of a strong partially ordered set (rep. semigroup-partially-ordered set,
-partially-ordered set is a semigroup-partially-ordered set, and a semigroup-partially-ordered set is a strong partially ordered set. The relation graph of a strong partially ordered set (rep. semigroup-partially-ordered set,  -partially-ordered set, etc.) is called a strong partially ordered graph (rep. semigroup-partially-ordered graph,
-partially-ordered set, etc.) is called a strong partially ordered graph (rep. semigroup-partially-ordered graph,  -partially-ordered graph, etc.). From definitions, it is easy to deduce
-partially-ordered graph, etc.). From definitions, it is easy to deduce
Lemma 3.6
If
Y
is a
 -semigroup, then Cay(Y,ω) is precisely the relation graph of the partially ordered set
Y. Conversely, if
Y
is a partially-ordered graph as the universal Cayley graph of a semigroup, then
Y
is a
-semigroup, then Cay(Y,ω) is precisely the relation graph of the partially ordered set
Y. Conversely, if
Y
is a partially-ordered graph as the universal Cayley graph of a semigroup, then
Y
is a
 -partially-ordered graph.
-partially-ordered graph.
Now we are ready to analyze the characteristics of the universal Cayley graph of a semigroup.
According to Lemma 3.1, we know that (a,b)∈E(Cay(S,ω)) if and only if J(a)⊇J(b), and that (a,b),(b,a)∈E(Cay(S,ω)) if and only if J(a)=J(b). Denoted by J
a
the  -class of a element a is S, as in [3]. Thus, (a,b)∈E(Cay(S,ω)) if and only if J
b
≤J
a
(see (2.1.3) of [3]), and (a,b),(b,a)∈E(Cay(S,ω)) if and only if
-class of a element a is S, as in [3]. Thus, (a,b)∈E(Cay(S,ω)) if and only if J
b
≤J
a
(see (2.1.3) of [3]), and (a,b),(b,a)∈E(Cay(S,ω)) if and only if  . Since
. Since  is an equivalence relation on S, S is decomposed into a union of all distinguished
is an equivalence relation on S, S is decomposed into a union of all distinguished  -classes each of which is in correspondence with a complete subgraph with loops of Cay(S,ω). Suppose that J
b
<J
a
and that Γ
α
,Γ
β
are the complete subgraphs with loops of Cay(S,ω), which correspond with J
a
and J
b
respectively. Then for any a′∈Γ
α
and b′∈Γ
β
,
-classes each of which is in correspondence with a complete subgraph with loops of Cay(S,ω). Suppose that J
b
<J
a
and that Γ
α
,Γ
β
are the complete subgraphs with loops of Cay(S,ω), which correspond with J
a
and J
b
respectively. Then for any a′∈Γ
α
and b′∈Γ
β
,  . From this and Lemma 3.1, it follows that (a′,b′)∈E(Cay(S,ω)) but \((b',a')\bar{\in} E(\mathrm{Cay}(S,\omega))\).
. From this and Lemma 3.1, it follows that (a′,b′)∈E(Cay(S,ω)) but \((b',a')\bar{\in} E(\mathrm{Cay}(S,\omega))\).
Define a relation on V(Cay(S,ω)) by setting a∼b if and only if
It is clear that a∼b if and only if  . Thus ∼ is an equivalence on V(Cay(S,ω)), and for every a∈S, the ∼-class [a] of a is exactly J
a
, the
. Thus ∼ is an equivalence on V(Cay(S,ω)), and for every a∈S, the ∼-class [a] of a is exactly J
a
, the  -class of a. Now we define the quotient graph Cay(S,ω)/∼ of Cay(S,ω) as the graph with vertex set V(Cay(S,ω))/∼ and the edge set
-class of a. Now we define the quotient graph Cay(S,ω)/∼ of Cay(S,ω) as the graph with vertex set V(Cay(S,ω))/∼ and the edge set
Immediately, we have that  , and that E(Cay(S,ω)/∼)={(J
a
,J
b
)|J
b
≤J
a
)}. It is trivial that for any a,b∈S, J(ab)⊆J(a) and J(ab)⊆J(b). Thus ([a],[ab])∈E(Cay(S,ω)/∼) and ([b],[ab])∈E(Cay(S,ω)/∼). It follows that Cay(S,ω)/∼ is a strong partially ordered graph.
, and that E(Cay(S,ω)/∼)={(J
a
,J
b
)|J
b
≤J
a
)}. It is trivial that for any a,b∈S, J(ab)⊆J(a) and J(ab)⊆J(b). Thus ([a],[ab])∈E(Cay(S,ω)/∼) and ([b],[ab])∈E(Cay(S,ω)/∼). It follows that Cay(S,ω)/∼ is a strong partially ordered graph.
If the quotient graph Γ/∼ of a graph Γ respective to ∼ is a strong partially ordered graph (resp. semigroup-partially-ordered graph,  -partially-ordered graph, semilattice graph, etc.), then we call Γ a strong partial order (resp. semigroup-partial order,
-partially-ordered graph, semilattice graph, etc.), then we call Γ a strong partial order (resp. semigroup-partial order,
 -partial-order, semilattice, etc.) of complete graphs with loops. A strong partial order Γ of complete graphs Γ
α
with loops is called nonidempotent-trivial if Γ
α
is trivial (i.e., |V(Γ
α
)|=1) for every nonidempotent α of Y. In terms of these terminologies and in light of the above arguments, we obtain the following lemma, which characterizes the fundamental property of the universal Cayley graph of a semigroup.
-partial-order, semilattice, etc.) of complete graphs with loops. A strong partial order Γ of complete graphs Γ
α
with loops is called nonidempotent-trivial if Γ
α
is trivial (i.e., |V(Γ
α
)|=1) for every nonidempotent α of Y. In terms of these terminologies and in light of the above arguments, we obtain the following lemma, which characterizes the fundamental property of the universal Cayley graph of a semigroup.
Lemma 3.7
For any semigroup S, Cay(S,ω) is a strong partial order of complete graphs with loops.
For further discussion, we need the following lemma.
Lemma 3.8
For any completely regular semigroup S, Cay(S,ω) is a semilattice of complete graphs with loops.
Proof
Assume that S is a completely regular semigroup S. By Lemma 3.7, Cay(S,ω) is a strong partial order of complete graphs with loops. In light of [3], S is a semilattice Y of completely simple semigroups S
α
, that is S=⋃
α∈Y
S
α
. Each S
α
is actually a  -class of S. The quotient graph Cay(S,ω)/∼ is exactly the relation graph of the inverse relation ≥ of the semilattice (Y,≤), thus it is a semilattice graph. Therefore, Cay(S,ω) is a semilattice of complete graphs with loops. □
-class of S. The quotient graph Cay(S,ω)/∼ is exactly the relation graph of the inverse relation ≥ of the semilattice (Y,≤), thus it is a semilattice graph. Therefore, Cay(S,ω) is a semilattice of complete graphs with loops. □
Based on Lemma 3.8, the next theorem characterizes completely the universal Cayley graphs of completely regular semigroups:
Theorem 3.9
The following statements are valid:
-
(1)
if S is a completely regular semigroup, then Cay(S,ω) is a semilattice of complete graphs with loops;
-
(2)
if Γ is a semilattice of complete graphs with loops, then there is a (commutative) completely regular semigroup such that Cay(S,ω)=Γ.
Proof
First, (1) follows from Lemma 3.8 directly.
Second, to prove (2), suppose that Γ is a semilattice Y of complete graphs Γ α with loops. It is obvious that for any α∈Y, there is an (Abelian) group G α such that |G α |=|V(Γ α )|. The identity element of G α is denoted by 1 α . Obviously, G α is a simple semigroup. So from Lemma 3.2, it follows that Cay(G α ,ω)=Γ α .
For any α∈Y, define a mapping as follows: ϕ α,α :G α ⟶G α ,a↦a; and for any α>β∈Y, define a mapping as follows: ϕ α,β :G α ⟶G β ,a↦1 β . It is verified that for α≥β≥γ, ϕ α,β ∘ϕ β,γ =ϕ α,γ . Consequently, ({G α } α∈Y ,{ϕ α,β } α≥β ) is a strong semilattice of all groups G α ’s.
Let \(S=\dot{\bigcup}_{\alpha \in Y} G_{\alpha}\), the disjoint union of G α . Define a composition on S as follows: for a∈G α ,b∈G β , ab=(a)ϕ α,αβ (b)ϕ β,αβ . Then S is a (commutative) Clifford semigroup which is of course completely regular. For any a∈G α , J(a)=G α . For any a∈G α ,b∈G β , J(a) and J(b) are comparable if and only if α and β are comparable. Furthermore, J(a)⊇J(b) if and only if α≥β. Thus by Lemma 3.1, Cay(S,ω)=Γ, as required. □
To generalize the result of Theorem 3.9, we need
Lemma 3.10
Let
Γ
be the relation graph of a partially ordered set (Y,≥). Then there is a composition on
Y
such that
Y
becomes a semigroup and Cay(Y,ω)=Γ
if and only if (Y,≥) is a
 -partially-ordered set.
-partially-ordered set.
Proof Necessity.
If Y is a semigroup such that Cay(Y,ω)=Γ, then for any a∈Y, \(J(a)=\omega ^{1}(a)=\omega (a)=\overrightarrow{a}=a\downarrow\). Thus (Y,≥) is a  -partially-ordered set.
-partially-ordered set.
Sufficiency. Assume that (Y,≥) is  -partially-ordered set. Then Y is a semigroup and for any a∈Y, \(J(a)=a\downarrow =\overrightarrow{a}\). Thus for any a,b∈Y, (a,b)∈E(Cay(Y,ω)) if and only if J(a)⊇J(b), if and only if a↓⊇b↓, if and only if a≥b. Then Cay(Y,ω) is just the relation graph of ≥, that is, Cay(Y,ω)=Γ. □
-partially-ordered set. Then Y is a semigroup and for any a∈Y, \(J(a)=a\downarrow =\overrightarrow{a}\). Thus for any a,b∈Y, (a,b)∈E(Cay(Y,ω)) if and only if J(a)⊇J(b), if and only if a↓⊇b↓, if and only if a≥b. Then Cay(Y,ω) is just the relation graph of ≥, that is, Cay(Y,ω)=Γ. □
Also, we need the following construction, which is similar to that of Clifford semigroups.
Definition 3.11
Let (Y,≥) be a semigroup-partially-ordered set, {S α } α∈Y a class of semigroups. If for any α≥β∈Y, there is a homomorphism ϕ α,β :S α ⟶S β satisfying the following conditions:
-
(1)
\(\phi _{\alpha,\alpha}=i_{S_{\alpha}}\), the identity mapping;
-
(2)
ϕ α,β ∘ϕ β,γ =ϕ α,γ (with mapping notations on the right of the variables).
then ({G α } α∈Y ,{ϕ α,β } α≥β ) is called a semigroup-partially-ordered set Y of semigroups S α ’s.
It is routine to verify the next lemma.
Lemma 3.12
With the same notations as in Definition 3.11, let \(S=\dot{\bigcup}_{\alpha \in Y} S_{\alpha}\), the disjoint union of G α , and define a composition on S as follows: for a∈S α ,b∈S β , a∗b=(a)ϕ α,αβ (b)ϕ β,αβ . Then (S,∗) is a semigroup.
Evidently, the composition ∗ in Definition 3.12 restricted to S α coincides with the original one of S α if and only if α is an idempotent of the semigroup Y. If Y and S α ’s are all commutative semigroups, then so is S.
Now we are ready to prove the following theorem, which generalizes Theorem 3.9, describes the basic properties of the universal Cayley graph of an arbitrary semigroup and characterizes the  -partial order of complete graphs with loops.
-partial order of complete graphs with loops.
Theorem 3.13
The following statements hold:
-
(1)
For any semigroup S, Cay(S,ω) is a strong partial order of complete graphs with loops, and for each a∈S and all b∈J(a), (a,b)∈E(Cay(S,ω));
-
(2)
Let Γ be a nonidempotent-trivial
 -partial order
Y
of complete graphs with loops. Then there is a semigroup
S
such that Cay(S,ω)=Γ. Moreover, if
Y
is a commutative semigroup, then
S
can be chosen to be commutative.
-partial order
Y
of complete graphs with loops. Then there is a semigroup
S
such that Cay(S,ω)=Γ. Moreover, if
Y
is a commutative semigroup, then
S
can be chosen to be commutative.
Proof
From Lemmas 3.7 and 3.1, (1) follows. To prove (2), let Γ be a  -partial order (Y,≥) of complete graphs Γ
α
’s with loops. For any α∈Y, it cleat that there is a simple monoid (in fact, an Abelian group) S
α
such that |S
α
|=|V(Γ
α
)|, and by Lemma 3.2, Cay(S
α
,ω)=Γ
α
. In light of Lemma 3.12, we obtain a semigroup \((S=\dot{\bigcup}_{\alpha \in Y} S_{\alpha},\ast)\). If Y is a commutative semigroup, then S can be chosen to be commutative since all S
α
’s can be chosen to be commutative.
-partial order (Y,≥) of complete graphs Γ
α
’s with loops. For any α∈Y, it cleat that there is a simple monoid (in fact, an Abelian group) S
α
such that |S
α
|=|V(Γ
α
)|, and by Lemma 3.2, Cay(S
α
,ω)=Γ
α
. In light of Lemma 3.12, we obtain a semigroup \((S=\dot{\bigcup}_{\alpha \in Y} S_{\alpha},\ast)\). If Y is a commutative semigroup, then S can be chosen to be commutative since all S
α
’s can be chosen to be commutative.
Denote by X the set of all idempotents of Y. For any a∈S, there exists a unique α∈Y such that a∈S
α
. If α∈X, then the composition ∗ restricted in S
α
coincides with the original one of S
α
. Since S
α
is a simple monoid, S
α
∗a∗S
α
=S
α
by Corollary 3.1.2 of [3]. If α∈Y∖X, then Γ
α
is trivial by the assumption. Thus S
α
is trivial, in effect, S
α
={1
α
}={a}. So whether α is in X or not, we have S
α
⊆J(a). Since Y is a  -partially-ordered set, J(α)=α↓={β|α≥β}. It follows that \(J(a)=\bigcup _{\alpha \geq\beta}S_{\beta}=\{b|(a,b)\in E(\varGamma )\}=\overrightarrow{a}\). Thus we have Cay(S,ω)=Γ as required. □
-partially-ordered set, J(α)=α↓={β|α≥β}. It follows that \(J(a)=\bigcup _{\alpha \geq\beta}S_{\beta}=\{b|(a,b)\in E(\varGamma )\}=\overrightarrow{a}\). Thus we have Cay(S,ω)=Γ as required. □
References
Arworn, Sr., Knauer, U., Chiangmai, N.N.: Characterization of digraphs of right (left) zero unions of groups. Thai J. Math. 1(1), 131–140 (2003)
Dénes, J.: Connections between transformation semigroups and graphs. In: Theory of Graphs. Gordon & Breach, New York (1967)
Howie, J.M.: Fundamentals of Semigroup Theory. Clarendon, Oxford (1995)
Kelarev, A.V.: Graph Algebras and Automata. Dekker, New York (2003)
Kelarev, A.V.: On Cayley graphs of inverse semigroups. Semigroup Forum 72, 411–418 (2006)
Kelarev, A.V.: On undirected Cayley graphs. Australas. J. Combin. 25, 73–78 (2002)
Kelarev, A.V., Praeger, C.E.: On transitive Cayley graphs of groups and semigroups. Eur. J. Comb. 24(1), 59–72 (2003)
Kelarev, A.V., Quinn, S.J.: A combinatorial property and Cayley graphs of semigroups. Semigroup Forum 66, 89–96 (2003)
Kelarev, A.V., Quinn, S.J.: A combinatorial property and power graphs of semigroups. Comment. Math. Univ. Carol. 45(1), 1–7 (2004)
Kelarev, A.V., Quinn, S.J.: Directed graphs and combinatorial properties of semigroups. J. Algebra 251(1), 16–26 (2002)
Kelarev, A., Ryan, J., Yearwood, J.: Cayley graphs as classifiers for data mining: The influence of asymmetries. Discrete Math. 309, 5360–5369 (2009)
Panma, S., Knauer, U., Arworn, S.: On transitive Cayley graphs of right (left) groups and of Clifford semigroups. Thai J. Math. 2(1), 183–195 (2004)
Panma, S., Knauer, U., Arworn, S.: On transitive Cayley graphs of strong semilattices of right (left) groups. Discrete Math. 309(17), 5393–5403 (2009)
Panma, S., Chiangmai, N.N., Knauer, U., Arworn, S.: Characterizations of Clifford semigroup digraphs. Discrete Math. 306(12), 1247–1252 (2006)
Petrich, M., Reilly, N.: Completely Regular Semigroups. Wiley, New York (1999)
White, A.T.: Graphs, Groups and Surfaces. Amsterdam, Elsevier (2001)
Wilson, R.J.: Introduction to Graph Theory, 3rd edn. Longman, New York (1982)
Yang, D., Gao, X.: D-saturated property of the Cayley graphs of semigroups. Semigroup Forum 80, 174–180 (2010)
Zelinka, B.: Graphs of semigroups. Čas. Pěst. Mat. 106, 407–408 (1981)
Zhu, Y.: On (n,m)-semigroups. Semigroup Forum (2011). doi:10.1007/s00233-011-9360-4
Acknowledgements
The author thanks Tom Hall for his help and also Andrei Kelarev for guidance and valuable suggestions. The work was supported by National Natural Foundation of China (No. 10571005) and Shandong Province Natural Science Foundation ZR2011AM005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Thomas E. Hall.
Rights and permissions
About this article
Cite this article
Zhu, Y. Generalized Cayley graphs of semigroups I. Semigroup Forum 84, 131–143 (2012). https://doi.org/10.1007/s00233-011-9368-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00233-011-9368-9




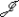 -partial order
Y
of complete graphs with loops. Then there is a semigroup
S
such that Cay(S,ω)=Γ. Moreover, if
Y
is a commutative semigroup, then
S
can be chosen to be commutative.
-partial order
Y
of complete graphs with loops. Then there is a semigroup
S
such that Cay(S,ω)=Γ. Moreover, if
Y
is a commutative semigroup, then
S
can be chosen to be commutative. -partial order of complete graphs with loops
-partial order of complete graphs with loops