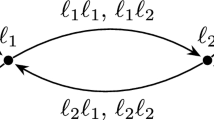Directed graphs of inner translations of semigroups

Abstract

A mapping $\alpha :S\rightarrow S$ is called a Cayley function if there exist an associative operation $\mu :S\times S\rightarrow S$ and an element $a\in S$ such that $\alpha (x)=\mu (a,x)$ for every $x\in S$. The aim of the paper is to give a characterization of Cayley functions in terms of their directed graphs. This characterization is used to determine which elements of the centralizer of a permutation on a finite set are Cayley functions. The paper ends with a number of problems.

1 Introduction

Let S be a set equipped with a binary operation, say:

Both the rows and columns of this table can be viewed as full transformations on S. For example, the row of 1 induces the map $\lambda _2$ and the column of 2 induces the map $\rho _1$ as follows:

$$\begin{aligned} \rho _1=\left( \begin{array}{cccc} 0&{}1&{}2&{}3\\ 0&{}1&{}0&{}1 \end{array} \right) , \quad \lambda _2=\left( \begin{array}{cccc} 0&{}1&{}2&{}3\\ 0&{}0&{}2&{}0 \end{array} \right) . \end{aligned}$$

Observe that $\lambda _1\rho _2=\rho _2\lambda _1$. In fact, one may check that in the Cayley table above, every row commutes with every column. Saying that the rows of $(S,\cdot )$ commute with its columns is just another way of saying that $(S,\cdot )$ is a semigroup (see [5]). This simple observation prompts an approach to a study of semigroups. However, before outlining the approach, we introduce some terminology and notation, and recall some facts.

Let S be a semigroup. For a fixed $a\in S$, the mapping $\lambda _a:S\rightarrow S [\rho _a:S\rightarrow S$] defined by $\lambda _a(x)=ax [\rho _a(x)=xa$] is called a left [right] inner translation of S. If S is a finite group, then $\lambda _a$ is a regular permutation on S, that is, $\lambda _a$ is a product of disjoint cycles of the same length. If S is an infinite group, then $\lambda _a$ is a formal product of disjoint cycles of the same (possibly infinite) length (see [21, Definition 3.2] and [24, Definition 1.1]). The converse is also true, that is, if $\alpha$ is a regular permutation on a set S, then there is a group with universe S such that $\alpha$ is a left inner translation of the group S [28]. The same facts are true for right inner translations.

Let $\alpha$ be a transformation on a set S. Following [30], we say that $\alpha$ is a Cayley function on S if there is a semigroup with universe S such that $\alpha$ is an inner translation of the semigroup S. Note that $\alpha$ is a left inner translation of a semigroup $(S,\cdot )$ if and only if $\alpha$ is a right inner translation of the semigroup $(S,*)$, where for all $a,b\in S, a*b=b\cdot a$.

We now describe an approach to a study of semigroups prompted by the observation that in any semigroup, the mappings induced by the rows of the Cayley table (left inner translations) commute with the mappings induced by the columns (right inner translations). Let S be any set.

• 1. Find the Cayley functions on S.

• 2. Given a Cayley function $\alpha$ on S, find all transformations on S that commute with $\alpha$, that is, describe the centralizer of $\alpha$ in the full transformation monoid T(S) on S.

• 3. Given a Cayley function $\alpha$ on S, find all Cayley functions on S that commute with $\alpha$.

• 4. Find pairs $\{\alpha ,\beta \}$ of Cayley functions on S such that $\alpha$ and $\beta$ occur as left inner translations of the same semigroup $(S,\cdot )$.

• 5. Let $G_S$ be the simple graph whose vertices are the Cayley functions on S and the edges are pairs $\{\alpha ,\beta \}$ such that $\alpha$ and $\beta$ occur as left inner translations of the same semigroup $(S,\cdot )$. We will call the graph $G_S$ the common semigroup graph of S. Identify the maximal cliques of the common semigroup graph $G_S$.

• 6. Let $H_S$ be the simple graph whose vertices are the Cayley functions on S and the edges are pairs $\{\alpha ,\beta \}$ such that:

  • $\{\alpha ,\beta \}$ is an edge in the common semigroup graph $G_S$, and

  • there exists a clique C of size |S| in $G_S$ such that $\alpha$ and $\beta$ commute with every element of C.

  Identify the maximal cliques of the graph $H_S$.

The solution of problem 1 tells us which mappings can appear as rows or columns in the Cayley table of a semigroup. The solution of problem 2 gives us the candidates for the rows of the Cayley table of a semigroup provided a given mapping appears as a column. Problems 3 and 4 are steps toward solving problems 5 and 6.

Regarding problem 5, suppose that $(S,\cdot )$ is a semigroup. The left inner translations $\lambda _a$ of S, where $a\in S$, form a clique in the common semigroup graph $G_S$. Hence, the solution of problem 5 would give us the candidates (the vertices of a maximal clique of $G_S$) from which the rows of the Cayley table of a semigroup can be selected. The same analysis applies to columns.

Regarding problem 6, suppose that we have the Cayley table of a semigroup $(S,\cdot )$. Then the rows of the table form a clique, say $C_1$, in the common semigroup graph $G_S$, and the columns also form a clique, say $C_2$, in $G_S$. Moreover, $|C_1|=|C_2|=|S|$ and each Cayley function in $C_1$ commutes with each Cayley function in $C_2$. Therefore, the rows [columns] of the Cayley table of $(S,\cdot )$ are contained in a maximal clique of the graph $H_S$. Therefore, the solution of problem 6 would give us the candidates (the vertices of a pair of maximal cliques in $H_S$) from which the Cayley table of a semigroup can be constructed. In other words, it would provide us with a tool to devise a method for building the Cayley tables of semigroups. In the process we might gain a deeper understanding of transformations and the Cayley tables of semigroups.

The current status of the solutions of these problems is as follows. Algebraic descriptions of transformations $\alpha$ that are Cayley functions (in terms of properties of powers of $\alpha$) have been provided in [8, 9, 11, 30]. The problem of describing the centralizer of a given transformation took longer, but it has been fully solved; the final stage was [6], but this is just the last step in a long process [1–4, 14–23, 25–27] (not claiming exhaustiveness). Given that problems 1 and 2 have been solved, one might think that problem 3 follows straightforwardly. This is not the case, though. One of the reasons is that while the description of the centralizers is geometric in nature, the available descriptions of the Cayley functions are not, thus making it difficult to combine the two results.

Hence, this paper has two goals. The first is to provide a geometric characterization of the Cayley functions, which can be connected to the existing geometric descriptions of centralizers. The second is to describe the Cayley functions that commute with a finite permutation. That is, we solve problem 3 in a special case. In other words, we describe the candidates for the rows of the Cayley table of a finite semigroup when one of its columns is a permutation. This is the part of the paper containing the most delicate considerations.

Any $\alpha :S\rightarrow S$ can be represented by a directed graph $D_\alpha$ with S as the set of vertices such that $x\rightarrow y$ is an arc in $D_\alpha$ if and only if $\alpha (x)=y$. A directed graph representing some transformation on its set of vertices is called a functional digraph. We will characterize the functional digraphs that represent Cayley functions. As a result, we will obtain a visual criterion for a transformation $\alpha$ on a set S to be a Cayley function: look at the digraph of $\alpha$ and see if it has desired properties.

To obtain a complete characterization of digraphs that represent Cayley functions, we first need to describe functional digraphs. We provide such a description in Sect. 2 (Propositions 2.5 and 2.6). Transformations on a set S can be divided into two types: those that have the so called stabilizer and those that do not. In Sect. 3, we characterize the functional digraphs that represent transformations with stabilizers (Theorem 3.10). In Sect. 4, we characterize the digraphs that represent Cayley functions (Theorems 4.6 and 4.10). Finally, in Sect. 5, we apply our characterization to centralizers of finite permutations (Theorem 5.6). We illustrate our results with examples and figures. We conclude the paper with a list of open problems (Sect. 6).

For the remainder of the paper, we fix a non-empty set S and denote by T(S) the set of all transformations on S (mappings $\alpha :S\rightarrow S$).

2 Functional digraphs

A directed graph (or a digraph) is a pair $D=(S,\rho )$ where S is a non-empty set of vertices (not necessarily finite), which we denote by V(D), and $\rho$ is a binary relation on S. Any pair $(x,y)\in \rho$ is called an arc of D, which we will write as $x\rightarrow y$. A vertex x is called an initial vertex in D if there is no $y\in S$ such that $y\rightarrow x$; it is called a terminal vertex in D if there is no $y\in S$ such that $x\rightarrow y$.

A digraph D is called a functional digraph if there is $\alpha \in T(S)$ such that for all $x,y\in S, x\rightarrow y$ is an arc in D if and only if $\alpha (x)=y$. If such an $\alpha$ exists, then it is unique, and we will write $D=D_\alpha$ and refer to D as the digraph that represents $\alpha$. In this section, we describe functional digraphs.

Let D be a digraph and let $\ldots ,x_{-1},x_0,x_1,\ldots$ be pairwise distinct vertices of D. Consider the following sub-digraphs of D:

$$\begin{aligned}&x_0\rightarrow x_1\rightarrow \cdots \rightarrow x_{k-1}\rightarrow x_0 \end{aligned}$$

(2.1)

$$\begin{aligned}&x_0\rightarrow x_1\rightarrow \cdots \rightarrow x_m \end{aligned}$$

(2.2)

$$\begin{aligned}&x_0\rightarrow x_1\rightarrow x_2\rightarrow \cdots \end{aligned}$$

(2.3)

$$\begin{aligned}&\cdots \rightarrow x_2\rightarrow x_1\rightarrow x_0 \end{aligned}$$

(2.4)

$$\begin{aligned}&\cdots \rightarrow x_{-1}\rightarrow x_0\rightarrow x_1\rightarrow \cdots \end{aligned}$$

(2.5)

We call (2.1)–(2.5), respectively: a cycle of length $k (k\ge 1$), written $(x_0\,x_1\ldots \, x_{k-1})$; a chain of length m, written $[x_0\,x_1\ldots \, x_m] (m\ge 0$); a right ray, written $[x_0\,x_1\,x_2\ldots \rangle$; a left ray, written $\langle \ldots \, x_2\,x_1\,x_0]$; and a double ray, written $\langle \ldots \, x_{-1}\,x_0\,x_1\ldots \rangle$.

Definition 2.1

Let $D_\alpha$ be a functional digraph, where $\alpha \in T(S)$. A right ray $[x_0\,x_1\,x_2\ldots \rangle$ in $D_\alpha$ is called a maximal right ray if $x_0$ is an initial vertex of $D_\alpha$.

Definition 2.2

Let $D_\alpha$ be a functional digraph, where $\alpha \in T(S)$.

• A left ray $L=\langle \ldots \,x_2\,x_1\,x_0]$ in $D_\alpha$ is called an infinite branch of a cycle C [double ray W] in $D_\alpha$ if $x_0$ lies on C [W] and $x_1$ does not lie on C [W]. We will refer to any such L as an infinite branch in $D_\alpha$.

• A chain $P=[x_0\,x_1\ldots \,x_m]$ of length $m\ge 1$ in $D_\alpha$ is called a finite branch of a cycle C [double ray W, maximal right ray R, infinite branch L] in $D_\alpha$ if $x_0$ is an initial vertex of $D_\alpha , x_m$ lies on C [W, R, L] and $x_{m-1}$ does not lie on C [W, R, L]. If $x_m$ lies on an infinite branch $L=\langle \ldots \,y_2\,y_1\,y_0]$, we also require that $x_m\ne y_0$. We will refer to any such P as a finite branch in $D_\alpha$.

By a branch in $D_\alpha$ we will mean a finite or infinite branch in $D_\alpha$. Note that all branches of a maximal right ray R or an infinite branch L are finite. In other words, we only consider infinite branches of cycles and double rays.

Definition 2.3

Let $\alpha \in T(S), x\in S$. The subgraph of $D_\alpha$ induced by the set

$$\begin{aligned} \{y\in S: \alpha ^k(y)=\alpha ^m(x) \hbox { for some integers } k,m\ge 0\} \end{aligned}$$

is called the component of $D_\alpha$ containing x. The components of $D_\alpha$ correspond to the connected components of the underlying undirected graph of $D_\alpha$.

Definition 2.4

Let $\{D_i\}_{i\in I}$ be a collection of digraphs $D_i=(S_i,\rho _i)$. By the join of the digraphs $D_i$, denoted $\bigsqcup _{i\in I}D_i$, we mean the digraph $D=(S,\rho )$ such that $S=\bigcup _{i\in I}S_i$ and $\rho =\bigcup _{i\in I}\rho _i$. (That is, $x\rightarrow y$ is an arc in the join D if and only if $x\rightarrow y$ is an arc in some $D_i$.) If the index set I is finite, say $I=\{1,2,\ldots ,m\}$, we will write $D_1\sqcup D_2\sqcup \cdots \sqcup D_m$ for $\bigsqcup _{i\in I}D_i$.

The following two propositions, proved in [6, Propositions 2.10 and 2.13], describe the functional digraphs. (The first characterization of functional digraphs is due to F. Harary [10, Theorem 2].)

Proposition 2.5

Let $D_\alpha$ be a functional digraph. Then for every component A of $D_\alpha$, exactly one of the following three conditions holds:

• (a) A has a unique cycle but not a double ray or right ray;

• (b) A has a double ray but not a cycle; or

• (c) A has a maximal right ray but not a cycle or double ray.

Proposition 2.6

Let $D_\alpha$ be a functional digraph. Then for every component A of $D_\alpha$:

• (1) if A has a (unique) cycle C, then A is the join of C and its branches;

• (2) if A has a double ray W, then A is the join of W and its branches;

• (3) if A has a maximal right ray R but not a double ray, then A is the join of R and its (finite) branches.

Suppose that a component A of $D_\alpha$ has a right ray R but not a double ray. It is then clear by Proposition 2.6 that A is the join of its maximal right rays. We will say that such a component A is of type $rro$ (“right rays only”).

Figure 1 presents a component of a digraph that contains a cycle (necessarily unique). The cycle has two infinite and three finite branches. The infinite branch on the right has one finite branch. Figure 2 presents a component of a digraph that contains a double ray. The double ray in the middle has one infinite and three finite branches. The infinite branch has one finite branch and extends to the second double ray of the component. Figure 3 presents a component of a digraph that contains a maximal right ray but not a double ray (type $rro$). The maximal right ray in the middle has five (necessarily) finite branches.

Fig. 1

A functional digraph component with a cycle

Fig. 2

A functional digraph component with a double ray

Fig. 3

A functional digraph component of type $rro$

3 Transformations with stabilizers

In this section, we describe the functional digraphs representing transformations that have the so called stabilizer.

Let $\alpha \in T(S)$. We denote by ${{\mathrm{im}}}(\alpha )$ the image of $\alpha$. For an integer $n>0$, we denote by $\alpha ^n$ the nth power of $\alpha$, that is, the composition of $\alpha$ with itself n times. As usual, $\alpha ^0$ denotes the identity transformation ${{\mathrm{id}}}_S$ on S.

Definition 3.1

Let $\alpha \in T(S)$. The stable image of $\alpha$, denote ${{\mathrm{sim}}}(\alpha )$, is a subset of S defined by

$$\begin{aligned} {{\mathrm{sim}}}(\alpha )=\{x\in S:x\in {{\mathrm{im}}}(\alpha ^n)\hbox { for every } n\ge 0.\}. \end{aligned}$$

(See [12, p. 42], where ${{\mathrm{sim}}}(\alpha )$ is called the stable range of $\alpha$.)

Remark 3.2

If $\alpha \in T(S)$, then:

• ${{\mathrm{sim}}}(\alpha )$ consists of the vertices of $D_\alpha$ that lie on cycles, double rays, or infinite branches;

• ${{\mathrm{sim}}}(\alpha )=\emptyset$ if and only if each component of $D_\alpha$ is of type $rro$.

Definition 3.3

Following [30], we define the stabilizer of $\alpha \in T(S)$ as the smallest integer $s\ge 0$ such that ${{\mathrm{im}}}(\alpha ^s)={{\mathrm{im}}}(\alpha ^{s+1})$. If such an s does not exist, we say that $\alpha$ has no stabilizer.

Remark 3.4

If $\alpha \in T(S)$, then:

• the stabilizer of $\alpha$ is the smallest integer $s\ge 0$ such that $\alpha ^s(x)\in {{\mathrm{sim}}}(\alpha )$ for every $x\in S$;

• $\alpha$ has the stabilizer $s=0$ if and only if ${{\mathrm{im}}}(\alpha )={{\mathrm{sim}}}(\alpha )=S$, which happens if and only if each component A of $D_\alpha$ is either the join of a cycle C and the infinite branches of C or the join of a double ray W and the infinite branches of W;

• if $\alpha$ has the stabilizer s, then ${{\mathrm{sim}}}(\alpha )={{\mathrm{im}}}(\alpha ^s)$.

The transformations represented by the digraphs in Figs. 1 and 2 have stabilizers 2 and 4, respectively. If $\alpha$ is the transformation represented by the digraph in Fig. 3, then ${{\mathrm{sim}}}(\alpha )=\emptyset$ and the stabilizer of $\alpha$ does not exist.

Example 3.5

A transformation may have a non-empty stable image and no stabilizer. Let $S=\{\ldots ,x_{-1},x_0,x_1,\ldots \}\cup \{y_1,y_2,\ldots \}\cup \{z_1,z_2,\ldots \}$. Consider $\alpha \in T(S)$ represented by the digraph in Fig. 4. Then ${{\mathrm{sim}}}(\alpha )=\{\ldots ,x_{-1},x_0,x_1,\ldots \}\cup \{y_1,y_2,\ldots \}$ but $\alpha$ has no stabilizer because of the increasing lengths of the finite branches of the double ray $\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$.

Fig. 4

The digraph of $\alpha$ from Example 3.5

For the rest of this section, our goal is to characterize the digraphs of transformations with stabilizers.

Lemma 3.6

Let $\alpha \in T(S)$ such that $\alpha$ has the stabilizer s. Suppose $[x_0\,x_1\ldots \,x_s]$ is a chain in $D_\alpha$ such that $x_s$ does not lie on a cycle. Then $\alpha$ has a left ray $\langle \ldots \, y_2\,y_1\,x_s]$.

Proof

We will construct a sequence $y_0,y_1,y_2,\ldots$ of elements of S such that $y_0=x_s$ and for every $n\ge 0$,

• (a) $[y_n\ldots \,y_0]$ is a chain in $D_\alpha$, and

• (b) $y_n\in {{\mathrm{sim}}}(\alpha )$.

Let $y_0=x_s$. Then $[y_0]$ is a chain in $D_\alpha$ and $y_0=x_s=\alpha ^s(x_0)\in {{\mathrm{sim}}}(\alpha )$ (see Remark 3.4). Let $n\ge 0$ and suppose we have constructed vertices $y_0=x_s,y_1,\ldots ,y_n$ that satisfy (a) and (b). Since ${{\mathrm{sim}}}(\alpha )={{\mathrm{im}}}(\alpha ^s)={{\mathrm{im}}}(\alpha ^{s+1})$, we have $y_n\in {{\mathrm{im}}}(\alpha ^{s+1})$. Thus, there are $z_0,\ldots ,z_s,z_{s+1}$ in S such that

$$\begin{aligned} z_0\rightarrow \cdots \rightarrow z_s\rightarrow z_{s+1}=y_n. \end{aligned}$$

Let $y_{n+1}=z_s$. Then

$$\begin{aligned} y_{n+1}=z_s\rightarrow z_{s+1}=y_n\rightarrow y_{n-1}\rightarrow \cdots \rightarrow y_0. \end{aligned}$$

Note that $y_{n+1}\notin \{y_n,\dots ,y_0\}$ since otherwise $x_s=y_0$ would lie on a cycle. Thus $[y_{n+1}\,y_n\ldots \,y_0]$ is a chain in $D_\alpha$ and $y_{n+1}=z_s=\alpha ^s(z_0)\in {{\mathrm{sim}}}(\alpha )$.

The sequence $y_0=x_s,y_1,y_2,\ldots$ that satisfies (a) and (b) for every $n\ge 0$ has been constructed. But then $\langle \ldots \, y_2\,y_1\,x_s]$ is a left ray in $D_\alpha$. $\square$

The following lemma states that the digraph of a transformations with stabilizer cannot have a component of type $rro$ (see the paragraph after Proposition 2.6 and Figure 3).

Lemma 3.7

Let $\alpha \in T(S)$ with stabilizer s. Then for every component A of $D_\alpha , A$ has a (unique) cycle or a double ray.

Proof

Suppose that a component A of $D_\alpha$ does not have a cycle. Select any $x_0\in A$. Since A has no cycle, $[x_0\,x_1\,x_2\ldots \rangle$, where $x_1=\alpha (x_0), x_2=\alpha (x_1),\ldots$, is a right ray in A. By Lemma 3.6, A has a left ray $\langle \ldots \, y_2\,y_1\,x_s]$. For every $n\ge 0, y_n\notin \{x_{s+1},x_{s+2},\ldots \}$ since otherwise A would have a cycle. Hence $\langle \ldots \, y_2\,y_1\,x_s\,x_{s+1}\,x_{s+2}\ldots \rangle$ is a double ray in A. $\square$

The converse of Lemma 3.7 is not true, that is, not every $\alpha \in T(S)$ such that every component of $D_\alpha$ has a cycle or a double ray has the stabilizer (see Example 3.5).

Definition 3.8

Let $\alpha \in T(S)$. A finite branch $[x_0\,x_1\ldots \,x_m]$ in $D_\alpha$ is called a twig in $D_\alpha$ if $x_m\in {{\mathrm{sim}}}(\alpha )$ (that is, $x_m$ lies on a cycle, double ray, or infinite branch) and $x_p\notin {{\mathrm{sim}}}(\alpha )$ for every $p\in \{0,\ldots ,m-1\}$.

Example 3.9

Not every finite branch is a twig. Let $S=\{\ldots ,x_{-1},x_0,x_1,\ldots \}\cup \{y_1,y_2,\ldots \}\cup \{z_1,\ldots ,z_5\}$, and consider $\alpha \in T(S)$ with the digraph in Figure 5. Then $[z_1\,z_2\,y_1\,x_0]$ is a branch in $D_\alpha$ but not a twig, while $[z_1\,z_2\,y_1]$ and $[z_3\,z_4\,z_5\,x_2]$ are twigs.

Fig. 5

The digraph of $\alpha$ from Example 3.9

Theorem 3.10

Let $\alpha \in T(S)$. Then $\alpha$ has the stabilizer if and only if:

• (1) every component of $D_\alpha$ has a unique cycle or a double ray, and

• (2) there is an integer $M\ge 0$ such that every twig in $D_\alpha$ has length $\le M$.

Proof

Suppose $\alpha$ has the stabilizer, say s. Then (1) holds by Lemma 3.7. To prove (2), suppose to the contrary that such an integer M does not exist. Then there is a twig in $D_\alpha$ of length greater than s, say $[x_0\ldots \,x_s\ldots \,x_m]$ with $m>s$. Since s is the stabilizer of $\alpha$, we have $x_s=\alpha ^s(x_0)\in {{\mathrm{sim}}}(\alpha )$ (see Remark 3.4), which contradicts the definition of a twig. We have proved (2).

Conversely, suppose that $\alpha$ satisfies (1) and (2). Let s be the smallest value of M from (2). We claim that ${{\mathrm{im}}}(\alpha ^s)={{\mathrm{im}}}(\alpha ^{s+1})$. Let $z\in {{\mathrm{im}}}(\alpha ^s)$. Suppose to the contrary that $z\notin {{\mathrm{sim}}}(\alpha ^{s+1})$. Then, by (1), Proposition 2.6, and the fact that $z\in {{\mathrm{im}}}(\alpha ^s), D_\alpha$ has a finite branch $[x_0\ldots \,x_k\ldots \,x_{k+s}=z\ldots \,x_t]$, where $k\ge 0, t\ge k+s$, and $x_t$ lies on a cycle or double ray. Consider the smallest $p\in \{0,\ldots ,t\}$ such that $x_p\in {{\mathrm{sim}}}(\alpha )$ and note that $p\le k+s$. (Indeed, if $p>k+s$, then $[x_0\ldots \,x_{k+s}\ldots \,x_p]$ would be a twig of length $p>s$, which is impossible.) But then $z=x_{k+s}=\alpha ^{k+s-p}(x_p)\in {{\mathrm{sim}}}(\alpha )$, which is a contradiction. Thus $z\in {{\mathrm{sim}}}(\alpha )$, and so $z\in {{\mathrm{im}}}(\alpha ^{s+1})$ by the definition of ${{\mathrm{sim}}}(\alpha )$. We proved that ${{\mathrm{im}}}(\alpha ^s)\subseteq {{\mathrm{im}}}(\alpha ^{s+1})$. Since the reverse inclusion is obvious, it follows that ${{\mathrm{im}}}(\alpha ^s)={{\mathrm{im}}}(\alpha ^{s+1})$.

We claim that s is the stabilizer of $\alpha$. The claim is clearly true if $s=0$. Suppose $s>0$. Then $D_\alpha$ has a twig $[x_0\ldots \,x_s]$. Suppose to the contrary that there exists $p, 0\le p<s$ such that ${{\mathrm{im}}}(\alpha ^{p})={{\mathrm{im}}}(\alpha ^{p+1})$. Then $x_{p}=\alpha ^{p}(x_0)\in {{\mathrm{im}}}(\alpha ^{p})$. But ${{\mathrm{im}}}(\alpha ^{p})={{\mathrm{im}}}(\alpha ^{p+1})={{\mathrm{im}}}(\alpha ^{p+2})=\cdots$, which implies that $x_{p}\in {{\mathrm{im}}}(\alpha ^n)$ for every $n\ge 0$. Thus $x_{p}\in {{\mathrm{sim}}}(\alpha )$, which is a contradiction since $p<s$ and $[x_0\ldots \,x_s]$ is a twig. The claim has been proved, which concludes the proof of the theorem. $\square$

It follows from Theorem 3.10 and its proof that if $\alpha \in T(S)$ has the stabilizer s, then

$$\begin{aligned} s=\hbox { the smallest } M\ge 0 \hbox { such that every twig in } D_\alpha \hbox { has length } \le M. \end{aligned}$$

(3.1)

4 Cayley functions

Let S be a set. Recall that a transformation $\alpha \in T(S)$ is called a Cayley function if there is a binary operation $*$ on S such that $(S,*)$ is a semigroup and $\alpha$ is an inner translation of the semigroup S; that is, there exists $a\in S$ such that for every $x\in S, \alpha (x)=a*x$.

The purpose of this section is to characterize the digraphs of the Cayley functions. To do this, we will use the algebraic description of the Cayley functions given in [30].

Definition 4.1

Suppose $\alpha \in T(S)$ has the stabilizer s. If $s>0$, we define the subset $\Omega _\alpha$ of S by:

$$\begin{aligned} \Omega _\alpha =\{a\in S: \alpha ^s(a)\in {{\mathrm{sim}}}(\alpha ) \hbox { but } \alpha ^{s-1}(a)\notin {{\mathrm{sim}}}(\alpha )\}. \end{aligned}$$

If $s=0$, we define $\Omega _\alpha$ to be S.

Remark 4.2

If $\alpha \in T(S)$ has the stabilizer $s>0$, then $\Omega _\alpha$ consists of the initial vertices of the twigs of length s in $D_\alpha$.

For example, for $\alpha$ defined in Example 3.9, $\Omega _\alpha =\{z_3\}$. The following result is due to Zupnik [30, Theorems 1–3].

Theorem 4.3

Let $\alpha \in T(S)$. Then $\alpha$ is a Cayley function if and only if exactly one of the following conditions holds:

• (a) $\alpha$ has no stabilizer and there exists $a\in S$ such that $\alpha ^n(a)\notin {{\mathrm{im}}}(\alpha ^{n+1})$ for every $n\ge 0$;

• (b) $\alpha$ has the stabilizer s such that $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is one-to-one and there exists $a\in \Omega _\alpha$ such that $\alpha ^m(a)=\alpha ^n(a)$ implies $\alpha ^m=\alpha ^n$ for all $m,n\ge 0$; or

• (c) $\alpha$ has the stabilizer s such that $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is not one-to-one and there exists $a\in \Omega _\alpha$ such that:

  • (i) $\alpha ^m(a)=\alpha ^n(a)$ implies $m=n$ for all $m,n\ge 0$; and

  • (ii) For every $n\ge s$, there are pairwise distinct elements $y_1,y_2,\ldots$ of S such that $\alpha (y_1)=\alpha ^n(a), \alpha (y_k)=y_{k-1}$ for every $k\ge 2$, and if $n>0$ then $y_1\ne \alpha ^{n-1}(a)$.

Conditions (a)–(c) of Theorem 4.3 correspond to Theorems 1–3 of [30], respectively. The slight difference in phrasing is due to the fact that for transformations $\alpha$ with stabilizer s, Zupnik uses the set

$$\begin{aligned} B_\alpha =\{b\in S: \alpha ^n(b)\in {{\mathrm{im}}}(\alpha ^s) \hbox { if and only if } n\ge s-1\} \end{aligned}$$

(although he does not specify exactly what that means when $s=0$), while we use the set $\Omega _\alpha$ from Definition 4.1. The set $\Omega _\alpha$ is more natural for our purposes than $B_\alpha$ since if $s>0$, then $\Omega _\alpha$ consists of the initial vertices of the twigs in $D_\alpha$ of length s, whereas $B_\alpha =\{\alpha (a):a\in \Omega _\alpha \}$; that is, $B_\alpha$ consists of the vertices that come after the initial vertices of such twigs.

Lemma 4.4

Let $\alpha \in T(S)$. Then $\alpha |_{{{\mathrm{sim}}}(\alpha )}$ is one-to-one if and only if $D_\alpha$ does not have an infinite branch.

Proof

($\Rightarrow$) We will prove the contrapositive. Suppose $D_\alpha$ has an infinite branch L. Then L is an infinite branch of a cycle or double ray. Suppose $L=\langle \ldots \,y_2\,y_1\,x_i]$ is an infinite branch of a cycle $C=(x_0\ldots \,x_{k-1})$. Then $y_1,x_{i-1}\in {{\mathrm{sim}}}(\alpha )$ with $y_1\ne x_{i-1}$ (since $y_1$ does not lie on C) and $\alpha (y_1)=\alpha (x_{i-1})=x_i$, which implies that $\alpha |_{{{\mathrm{sim}}}(\alpha )}$ is not one-to-one. An argument in the case when L is an infinite branch of a double ray is similar.

($\Leftarrow$) Suppose $D_\alpha$ does not have an infinite branch. Let $x,y\in {{\mathrm{sim}}}(\alpha )$ be such that $\alpha (x)=\alpha (y)$. Then x and y are vertices of the same component of $D_\alpha$, say A. By Proposition 2.5, A has a unique cycle or a double ray (since a component of type $rro$ has no vertices that belong to ${{\mathrm{sim}}}(\alpha )$). Suppose A has a cycle C. Then, since $x,y\in {{\mathrm{sim}}}(\alpha )$ and $D_\alpha$ does not have an infinite branch, x and y must lie on C. Thus $\alpha (x)=\alpha (y)$ since, clearly, $\alpha$ restricted to the vertices of C is one-to-one. If A has a double ray, we prove that $\alpha (x)=\alpha (y)$ in a similar way. Hence $\alpha |_{{{\mathrm{sim}}}(\alpha )}$ is one-to-one. $\square$

Lemma 4.5

Let $\alpha \in T(S)$ be a Cayley function. Then every component of $D_\alpha$ has a unique cycle or a double ray if and only if $\alpha$ has the stabilizer.

Proof

Suppose every component of $D_\alpha$ has a unique cycle or a double ray. Suppose to the contrary that $\alpha$ has no stabilizer. Then, by Theorem 4.3, there is $a\in S$ such that $\alpha ^n(a)\notin {{\mathrm{im}}}(\alpha ^{n+1})$ for every $n\ge 0$. Let A be the component of $D_\alpha$ containing a. Suppose A has a unique cycle, say C. Then, by Proposition 2.6, A is the join of C and its branches. It follows that there is an integer $k\ge 0$ such that $\alpha ^k(a)$ lies on C. But then $\alpha ^k(a)\in {{\mathrm{im}}}(\alpha ^{k+1})$, which is a contradiction. If A has a double ray, we obtain a contradiction by a similar argument. Hence $\alpha$ has the stabilizer.

The converse follows from Theorem 3.10. $\square$

If $\alpha \in T(S)$, then the digraph $D_\alpha$ has exactly one of the following features:

• $D_\alpha$ has a component of type $rro$;

• every component of $D_\alpha$ has a unique cycle or a double ray, and $D_\alpha$ does not have an infinite branch; or

• every component of $D_\alpha$ has a unique cycle or a double ray, and $D_\alpha$ has an infinite branch.

We will characterize the digraphs of Cayley functions considering each of the above three cases.

Theorem 4.6

Let $\alpha \in T(S)$ be such that $D_\alpha$ has a component of type $rro$. Then $\alpha$ is a Cayley function if and only if $D_\alpha$ has a component A of type $rro$ such that:

• (1) A is the join of a maximal right ray $R=[x_0\,x_1\,x_2\ldots \rangle$ and its branches;

• (2) for every $i\ge 1$, if $[y_0\,y_1\ldots \,y_m=x_i]$ is a branch of R, then $m\le i$.

Proof

Suppose $\alpha$ is a Cayley function. Then $\alpha$ has no stabilizer by Lemma 4.5. Hence, by Theorem 4.3, there is $a\in S$ such that such that $\alpha ^n(a)\notin {{\mathrm{im}}}(\alpha ^{n+1})$ for every $n\ge 0$. Let A be the component of $D_\alpha$ containing a, and note that A is of type $rro$ (see the proof of Lemma 4.5). Let $x_0=a$ and $x_i=\alpha (x_{i-1})$ for every $i\ge 1$. Then $x_0$ is an initial vertex of $D_\alpha$ (since $x_0=a\notin {{\mathrm{im}}}(\alpha )$) and $x_0,x_1,x_2,\ldots$ are pairwise distinct (since A has no cycle). Thus $R=[x_0\,x_1\,x_2\ldots \rangle$ is a maximal right ray in A. By Proposition 2.6, A is the join of R and its branches, that is, (1) is satisfied. To prove (2), suppose to the contrary that for some $i\ge 1$, there is a branch $[y_0\,y_1\ldots \,y_m=x_i]$ of R with $m>i$. Then

$$\begin{aligned} \alpha ^i(a)=\alpha ^i(x_0)=x_i=y_m=\alpha ^m(y_0)\in {{\mathrm{im}}}(\alpha ^m)\subseteq {{\mathrm{im}}}(\alpha ^{i+1}), \end{aligned}$$

which is a contradiction. Hence (2) is satisfied.

Conversely, suppose that $D_\alpha$ has a component A of type $rro$ such that (1) and (2) are satisfied. Then $\alpha$ has no stabilizer by Theorem 3.10. Let $a=x_0$. Suppose to the contrary that there is $n\ge 0$ such that $\alpha ^n(a)\in {{\mathrm{im}}}(\alpha ^{n+1})$. Then $x_n=\alpha ^n(x_0)=\alpha ^n(a)=\alpha ^{n+1}(y)$ for some $y\in S$. Clearly y does not lie on R. Thus, by Proposition 2.6, there is a finite branch $[y_0\ldots \,y_k=y\ldots \,y_m=x_i]$ of R with $0\le k<m$. By (2), we have $m\le i$. Since $\alpha ^{n+1}(y)=x_n$, we must have $n\ge i$. Thus

$$\begin{aligned} \alpha ^{n-i}(x_i)=x_n=\alpha ^{n+1}(y)=\alpha ^{n+1}(y_k)=\alpha ^{n-m+k+1}(\alpha ^{m-k}(y_k))=\alpha ^{n-m+k+1}(x_i), \end{aligned}$$

which implies $n-i=n-m+k+1$. Thus $k+1=m-i\le 0$ (since $m\le i$), which is a contradiction. We have proved that $\alpha ^n(a)\notin {{\mathrm{im}}}(\alpha ^{n+1})$ for every $n\ge 0$. Hence $\alpha$ is a Cayley function by Theorem 4.3. $\square$

Example 4.7

Consider components $A_1$ and $A_2$ in Fig. 6. By Theorem 4.6, any transformation $\alpha _1$ whose digraph has component $A_1$ is a Cayley function, whereas any transformation $\alpha _2$ whose only component of type $rro$ is $A_2$ is not a Cayley function. Also, any $\alpha$ that has the component presented in Fig. 3 is a Cayley function.

Fig. 6

A Cayley function (left) and not a Cayley function (right) (see Theorem 4.6)

Definition 4.8

Let $\alpha \in T(S)$ and let $\mathbb N=\{0,1,2,\ldots \}$. We define $\mathrm {sup}_b(\alpha ),\mathrm {sup}_t(\alpha )\in \mathbb N\cup \{\infty \}$ by

$$\begin{aligned} \mathrm {sup}_b(\alpha )&=\sup \{m: m=0 \hbox { or } m \hbox { is the length of a finite branch in } D_\alpha \}, \nonumber \\ \mathrm {sup}_t(\alpha )&=\sup \{m:m=0 \hbox { or } m \hbox { is the length of a twig in } D_\alpha \}. \end{aligned}$$

(4.1)

Lemma 4.9

Let $\alpha \in T(S)$ be such that every component of $D_\alpha$ has a unique cycle or a double ray, and $D_\alpha$ does not have an infinite branch. Then $\mathrm {sup}_b(\alpha )=\mathrm {sup}_t(\alpha )$.

Proof

Since every twig is a finite branch (see Definition 3.8), $\mathrm {sup}_t(\alpha )\le \mathrm {sup}_b(\alpha )$ in any $D_\alpha$. To prove $\mathrm {sup}_b(\alpha )\le \mathrm {sup}_t(\alpha )$, it suffices to show that if $D_\alpha$ has a finite branch of length m, then $D_\alpha$ has a twig of length $k\ge m$. Let $P=[y_0\ldots \,y_m]$ be a finite branch of length m, and let A be the component of $D_\alpha$ containing P. If A has a unique cycle, then every finite branch in A is a twig (since $D_\alpha$ has no infinite branches and a component with a cycle does not have a double or right ray), so a desired twig of length at least m is P itself. Suppose A has a double ray, say W. Then ${{\mathrm{sim}}}(\alpha )\cap A=V(W)$ since $D_\alpha$ has no infinite branches. Thus, if $y_m$ lies on W, then again P itself is a desired twig. Suppose $y_m$ does not lie on W (which is possible since $y_m$ may lie on a maximal right ray). Then, by Proposition 2.6, there is a finite branch $P_1=[y_0\ldots \,y_m\ldots \,y_k]$ such that $k>m$ and $y_k$ lies on W. Thus $P_1$ is a twig of length bigger than m. Hence $\mathrm {sup}_b(\alpha )\le \mathrm {sup}_t(\alpha )$. $\square$

Lemma 4.9 is not true if $D_\alpha$ has an infinite branch. Let

$$\begin{aligned} S=\{\ldots \,x_{-1}\,x_0,x_1,\ldots \}\cup \{y_1,y_2,\ldots \}\cup \{z_1,z_2,\ldots \}, \end{aligned}$$

and consider $\alpha \in T(S)$ with digraph in Figure 7. Note that ${{\mathrm{sim}}}(\alpha )=\{\ldots ,x_{-1},x_0,x_1,\ldots \}\cup \{y_1,y_2,\ldots \}$. We have $\mathrm {sup}_b(\alpha )=\infty$ since for every $n\ge 1, [z_n\,y_n\ldots \,y_1\,x_0]$ is a finite branch (of the double ray $\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$), but $\mathrm {sup}_t(\alpha )=1$ since the only twigs in $D_\alpha$ are $[z_1\,y_1],[z_2\,y_2], [z_3\,y_3],\ldots \,$.

Fig. 7

A transformation $\alpha$ with $\mathrm {sup}_t(\alpha )<\mathrm {sup}_b(\alpha )$

Theorem 4.10

Let $\alpha \in T(S)$ be such that every component of $D_\alpha$ has a unique cycle or a double ray, and $D_\alpha$ does not have an infinite branch. Then $\alpha$ is a Cayley function if and only if the following conditions are satisfied:

• (1) $s=\mathrm {sup}_b(\alpha )$ is finite;

• (2) if $s>0$ and $D_\alpha$ has a double ray, then some double ray in $D_\alpha$ has a branch of length s;

• (3) if $D_\alpha$ does not have a double ray, then there are integers $1\le k_1<k_2<\ldots <k_p, p\ge 1$, such that:

  • (a) $\{k_1,\ldots ,k_p\}$ is the set of the lengths of the cycles in $D_\alpha$;

  • (b) $k_i$ divides $k_p$ for every $i\in \{1,\ldots ,p\}$; and

  • (c) if $s>0$, then some cycle of $D_\alpha$ of length $k_p$ has a branch of length s.

Proof

Suppose $\alpha$ is a Cayley function. By Lemma 4.5, $\alpha$ has the stabilizer, say $s_1$. By (3.1), $s_1=\mathrm {sup}_t(\alpha )$, and so $s_1=\mathrm {sup}_b(\alpha )=s$ by Lemma 4.9. Thus (1) holds since the stabilizer of any transformation is finite by definition. By Lemma 4.4, $\alpha |_{{{\mathrm{sim}}}(\alpha )}$ is one-to-one, and so $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is one-to-one since ${{\mathrm{sim}}}(\alpha )={{\mathrm{im}}}(\alpha ^s)$ (see Remark 3.4).

Suppose that $s>0$ and that $D_\alpha$ has a double ray, say $W=\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$. By Theorem 4.3, there is $a\in \Omega _\alpha$ such that for all $m,n\ge 0$, if $\alpha ^m(a)=\alpha ^n(a)$ then $\alpha ^m=\alpha ^n$. Then a is the initial point of some twig P in $D_\alpha$ of length s (see Remark 4.2). Suppose to the contrary that no double ray in $D_\alpha$ has a branch of length s. Then P must be a branch of some cycle $(y_0\ldots \,y_{k-1}), k\ge 1$. Thus $\alpha ^s(a)=\alpha ^{s+k}(a)$, and so $\alpha ^s=\alpha ^{s+k}$. But then $x_s=\alpha ^s(x_0)=\alpha ^{s+k}(x_0)=x_{s+k}$, which is a contradiction, as W is a double ray. Hence some double ray of $D_\alpha$ must have a branch of length s, which proves (2).

Suppose $D_\alpha$ does not have a double ray. Then each component of $D_\alpha$ has a unique cycle. Let $a\in \Omega _\alpha$ be as in the proof of (2) (but here we do not assume that $s>0$). Then there is a cycle $C=(y_0\ldots \,y_{k-1})$ in $D_\alpha$ such that, for some j, either $a=y_j$ (if $s=0$) or C has a branch $[a\ldots \,y_j]$ of length s (if $s>0$). In either case, $\alpha ^s(a)=\alpha ^{s+k}(a)$, and so $\alpha ^s=\alpha ^{s+k}$. Let $(x_0\ldots \,x_{t-1})$ be any cycle in $D_\alpha$, and let $i\in \{0,\ldots ,t-1\}$ be such that $\alpha ^s(x_i)=x_0$. Then

$$\begin{aligned} x_k=\alpha ^k(x_0)=\alpha ^k(\alpha ^s(x_i))=\alpha ^{s+k}(x_i)=\alpha ^s(x_i)=x_0. \end{aligned}$$

It follows that $k\equiv 0\!\!\pmod t$, that is, t divides k. We have proved that the set of the lengths of the cycles in $D_\alpha$ is bounded above by k, and so it is finite, say $\{k_1,k_2,\ldots ,k_p\}$ with $1\le k_1<k_2<\ldots <k_p=k$. We have also proved that each $t=k_i$ divides $k=k_p$ and that C has a branch of length s (if $s>0$). Thus (3) holds.

Conversely, suppose that (1)–(3) are satisfied. Then, by (1), (3.1), and Lemma 4.9, $s=\mathrm {sup}_b(\alpha )$ is the stabilizer of $\alpha$. As in the proof of the first part, $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is one-to-one.

Suppose $D_\alpha$ has a double ray. Then, by (2), there is $a\in \Omega _\alpha$ such that $\alpha ^s(a)$ lies on some double ray. Then, for all $m,n\ge 0$, if $\alpha ^{m}(a)=\alpha ^n(a)$ then $m=n$, and so $\alpha ^n=\alpha ^m$.

Suppose $D_\alpha$ does not have a double ray. Then, by (3), there is $a\in \Omega _\alpha$ such that $\alpha ^s(a)$ lies on a cycle C of length $k_p$. Suppose $\alpha ^{m}(a)=\alpha ^n(a)$, where $m,n\ge 0$. We may assume that $m\ge n$. Then $m\equiv n\!\!\pmod {k_p}$, that is, $m=n+qk_p$ for some $q\ge 0$. If $n<s$ (which is possible only if $s>0$), then $\alpha ^m(a)=\alpha ^n(a)$ implies $m=n$, so $\alpha ^m=\alpha ^m$. Suppose $n\ge s$, and let $x\in S$. Since s is the stabilizer of $\alpha$ and $n\ge s, \alpha ^n(x)$ lies on some cycle of $D_\alpha$. Let $C_1=(x_0\ldots \,x_{k_i})$ be the cycle such that $\alpha ^n(x)=x_j$ for some j. By (3), $k_p=rk_i$ for some $r\ge 1$. Thus

$$\begin{aligned} \alpha ^m(x)=\alpha ^{n+qk_p}(x)=\alpha ^{n+qrk_i}(x)=\alpha ^{qrk_i}(\alpha ^n(x))=\alpha ^{qrk_i}(x_j)=x_j=\alpha ^n(x), \end{aligned}$$

which implies $\alpha ^m=\alpha ^n$ since x was an arbitrary element of S. Hence $\alpha$ is a Cayley function by Theorem 4.3. $\square$

Example 4.11

Consider transformations $\alpha$ and $\beta$ whose digraphs are presented in Figs. 8 and 9, respectively. Then $\alpha$ is a Cayley function, while $\beta$ is not a Cayley function (since $s=3$ and (2) of Theorem 4.10 is not satisfied). If we remove the component with the double ray from Fig. 8, the resulting transformation will not be a Cayley function since (3) of Theorem 4.10 will not be satisfied. If we remove the component with the double ray from Fig. 9, the resulting transformation will be a Cayley function.

Fig. 8

A Cayley function described by Theorem 4.10

Fig. 9

Not a Cayley function (see Theorem 4.10)

It is of interest to apply Theorem 4.10 to permutations. Let ${{\mathrm{Sym}}}(S)$ be the set of permutations on S, that is, bijections from S to S. Let $\alpha \in {{\mathrm{Sym}}}(S)$. Then $\alpha$ is an inner translation of a group with universe S if and only if $D_\alpha$ is either a join of disjoint double rays or a join of cycles of the same length [28, Theorem 2]. The following is an immediate corollary of Theorem 4.10.

Corollary 4.12

Let $\alpha \in {{\mathrm{Sym}}}(S)$. Then $\alpha$ is a Cayley function if and only if exactly one of the following conditions holds:

• (a) $D_\alpha$ has a double ray; or

• (b) $D_\alpha$ is a join of cycles, and there are integers $1\le k_1<k_2<\ldots <k_p, p\ge 1$, such that

  • (i) $\{k_1,\ldots ,k_p\}$ is the set of the lengths of the cycles in $D_\alpha$;

  • (ii) $k_i$ divides $k_p$ for every $i\in \{1,\ldots ,p\}$.

Example 4.13

Let $S=\{1,2,\ldots ,11\}$. Consider

$$\begin{aligned} \alpha =(1\,2\,3\,4\,5\,6)(7\,8\,9)(10\,11) \text{ and } \beta =(1\,2\,3\,4)(5\,6\,7\,8)(9\,10\,11) \end{aligned}$$

in T(S). Then $\alpha$ is a Cayley function, while $\beta$ is not a Cayley function.

The last case to consider is when $D_\alpha$ has no component of type $rro$ but it does have an infinite branch.

Theorem 4.14

Let $\alpha \in T(S)$ be such that every component of $D_\alpha$ has a unique cycle or a double ray, and $D_\alpha$ has an infinite branch. Then $\alpha$ is a Cayley function if and only if the following conditions are satisfied:

• (1) $s=\mathrm {sup}_t(\alpha )$ is finite;

• (2) $D_\alpha$ has a double ray $W=\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$ such that for some $x_i$:

  • (a) if $s>0$ then W has a finite branch at $x_i$ of length s; and

  • (b) W has an infinite branch at each $x_j$ with $j>i$.

Proof

Suppose $\alpha$ is a Cayley function. By Lemma 4.5, $\alpha$ has the stabilizer, say $s_1$. By (3.1), $s_1=\mathrm {sup}_t(\alpha )=s$, and so (1) holds since the stabilizer of any transformation is finite by definition. By Lemma 4.4, $\alpha |_{{{\mathrm{sim}}}(\alpha )}$ is not one-to-one, and so $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is not one-to-one since since ${{\mathrm{sim}}}(\alpha )={{\mathrm{im}}}(\alpha ^s)$. Thus, there exists $a\in \Omega _\alpha$ such that (i) and (ii) of Theorem 4.3 hold. Let A be the component of $D_\alpha$ containing a. Suppose to the contrary that A has a cycle, say $C=(x_0\ldots \,x_{k-1})$. Then, by Proposition 2.6, $\alpha ^p(a)=x_j$ for some j and $p\ge 0$, and so $\alpha ^{k+p}(a)=\alpha ^k(\alpha ^p(a))=\alpha ^k(x_j)=x_j=\alpha ^p(a)$. Thus $k+p=p$ by (i) of Theorem 4.3, which is a contradiction.

Hence A has a double ray, and so ${{\mathrm{sim}}}(\alpha )\cap V(A)$ consists of the vertices x of A such that x lies on some double ray in A. Thus, since $\alpha ^s(a)\in {{\mathrm{sim}}}(\alpha )$, there is a double ray $W=\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$ in A such that $\alpha ^s(a)=x_i$ for some i. If $s>0$, then $[a\,\alpha (a)\,\alpha ^2(a)\ldots \,\alpha ^s(a)=x_i]$ is a finite branch of W of length s (by the definition of $\Omega _\alpha$). Let $j>i$ and note that $x_j=\alpha ^n(a)$ for $n=s+j-i$. By (ii) of Theorem 4.3, there is a left ray $L=\langle \ldots \,y_2\,y_1\,\alpha ^n(a)=x_j]$ in A such that $y_1\ne \alpha ^{n-1}(a)=x_{j-1}$. Hence $y_1$ does not lie on W, and so L is an infinite branch of W at $x_j$. We have proved (2).

Conversely, suppose (1) and (2) are satisfied. Then, by (1) and (3.1), $s=\mathrm {sup}_t(\alpha )$ is the stabilizer of $\alpha$. By Lemma 4.4, $\alpha |_{{{\mathrm{im}}}(\alpha ^s)}$ is not one-to-one. Let $W=\langle \ldots \,x_{-1}\,x_0\,x_1\ldots \rangle$ be a double ray from (2). If $s>0$, then W has a finite branch $[y_0\ldots \,y_s=x_i]$. Set $a=y_0$ if $s>0$, and $a=x_i$ if $s=0$. In either case, $a\in \Omega _\alpha$. For all $m,n\ge 0$, if $\alpha ^m(a)=\alpha ^n(a)$ then $m=n$ since a is in a component of $D_\alpha$ that does not have a cycle. Let $n\ge s$. We want to prove that there are pairwise distinct elements $y_1,y_2,\ldots$ of S such that $\alpha (y_1)=\alpha ^n(a), \alpha (y_k)=y_{k-1}$ for every $k\ge 2$, and if $n>0$ then $y_1\ne \alpha ^{n-1}(a)$. If $n=s$, then we can take $y_1=x_{i-1}, y_2=x_{i-2},\ldots \,$. Suppose $n>s$. Then $\alpha ^n(a)=x_j$ for $j=i+n-s>i$. By (2b), W has an infinite branch $\langle \ldots \,z_2\,z_1\,x_j]$, and we can take $y_1=z_1,y_2=z_2,\ldots \,$. Hence $\alpha$ is a Cayley function by Theorem 4.3. $\square$

For example, the transformation with digraph in Fig. 10 is a Cayley function (with $s=4$).

Fig. 10

A Cayley function described by Theorem 4.14

Let $\alpha \in T(S)$ be such that every component of $D_\alpha$ has a unique cycle or a double ray. By Theorems 4.10 and 4.14, if $\alpha$ is a Cayley function, then either every component of $D_\alpha$ has at most one double ray or some component of $D_\alpha$ has infinitely many double rays. So, transformations with digraphs in Figs. 2, 4, 5, and 7 are not Cayley functions.

5 The solution of problem 3 for finite permutations

Let S be a non-empty set. For a transformation $\alpha \in T(S)$, the centralizer $C(\alpha )$ of $\alpha$ in T(S) is defined by $C(\alpha )=\{\beta \in T(S):\alpha \beta =\beta \alpha \}$. Elements of $C(\alpha )$, for an arbitrary $\alpha \in T(S)$, were characterized in [6]. In this section, we initiate the study of the following problem: given $\alpha \in T(S)$, which transformations $\beta \in C(\alpha )$ are Cayley functions? We show how our description of Cayley functions can be used to solve this problem in the special case when S is finite and $\alpha$ is a permutation. As will be clear by the end of this section, problem 3 is very difficult, even with graph descriptions of the centralizers and Cayley functions.

For the remainder of this section, S will denote a finite non-empty set. The following theorem is [6, Corollary 6.4]. We agree that if $(y_0\ldots \,y_{m-1})$ is a cycle and i is an integer, then $y_i$ means $y_r$ where $r\equiv i\pmod m$ and $0\le r<m$.

Theorem 5.1

Let $\alpha \in {{\mathrm{Sym}}}(S)$ and $\beta \in T(S)$. Then $\beta \in C(\alpha )$ if and only if for every cycle $\sigma =(x_0\ldots \,x_{k-1})$ in $\alpha$, there exists a cycle $\theta =(y_0\ldots \,y_{m-1})$ in $\alpha$ such that m divides k and $\beta$ wraps $\sigma$ around $\theta$ at some $y_t$, that is, $\beta (x_i)=y_{t+i}\,$ for every $i\in \{0,1,\ldots ,k-1\}$.

Let $\alpha \in {{\mathrm{Sym}}}(S)$ and let $\mathcal {C}_\alpha$ be the set of cycles in $\alpha$ (including the 1-cycles). For $\beta \in C(\alpha )$, we define a transformation $\psi _\beta$ on $\mathcal {C}_\alpha$ by

$$\begin{aligned} \psi _\beta (\sigma )=\hbox { the unique } \theta \in \mathcal {C}_\alpha \hbox { such that } \beta \hbox { wraps } \sigma \hbox { around } \theta . \end{aligned}$$

Note that $\psi _\beta$ is well defined by Theorem 5.1, that is, $\psi _\beta \in T(\mathcal {C}_\alpha )$, and that the vertices of the digraph $D_{\psi _\beta }$ are the cycles in $\alpha$.

The following lemma, which we will use implicitly in the subsequent arguments, follows immediately from the definition of $\psi _\beta$ and Theorem 5.1.

Lemma 5.2

Let $\alpha \in {{\mathrm{Sym}}}(S)$ and $\beta \in C(\alpha )$. Suppose that A is a component of $D_{\psi _\beta }$ with cycle $(\sigma _0\,\sigma _1\ldots \, \sigma _{k-1})$, and that Z is the set of all elements $x\in S$ such that x is in some $\sigma \in A$. Then:

• (1) the cycles $\sigma _0,\sigma _1,\ldots ,\sigma _{k-1}$ have the same length;

• (2) for every $x\in Z, \beta (x)\in Z$, that is, $\beta |_Z\in T(Z)$;

• (3) if $\sigma ,\theta \in A$ with $\psi _\beta (\sigma )=\theta$, then for every x in $\sigma , \beta (x)$ is in $\theta$;

• (4) if $x\in Z$ is not in any $\sigma _i$, then x does not lie on any cycle of $D_{\beta |_Z}$.

Lemma 5.3

Let $\alpha \in {{\mathrm{Sym}}}(S)$ and $\beta \in C(\alpha )$. Suppose that A is a component of $D_{\psi _\beta }$ with cycle $(\sigma _0\,\sigma _1 \ldots \, \sigma _{k-1})$, each $\sigma _i$ having length p. Let Z be as in Lemma 5.2 and let $\sigma _0=(x_0\,x_1 \ldots \, x_{p-1})$. Then:

• (1) $\beta ^k(x_0) = x_l$ for some $l\in \{0,1,\ldots ,p-1\}$;

• (2) every cycle in $D_{\beta |_Z}$ has length $\frac{kp}{\gcd (p,l)}$.

Proof

Since $(\sigma _0\,\sigma _1 \ldots \, \sigma _{k-1})$ is a cycle in $D_{\psi _\beta }, \psi _\beta ^k(\sigma _0)=\sigma _0$. Hence $\beta ^k(x_0)$ is in $\sigma _0$, and so $\beta ^k(x_0)=x_l$ for some l. This proves (1).

To prove (2), recall that $\beta |_Z\in T(Z)$ by Lemma 5.2. Let t be the smallest positive integer such that $\beta ^t(x_0)=x_0$. Then $\psi _\beta ^t(\sigma _0)=\sigma _0$, and hence $t=ku$ for some integer u. As $\alpha$ and $\beta$ commute, we have

$$\begin{aligned} x_0= & {} \beta ^t(x_0)=\beta ^{ku}(x_0)=\beta ^{k(u-1)}(x_l)=\beta ^{k(u-1)}(\alpha ^l(x_0))\\= & {} \alpha ^l\beta ^{k(u-1)}(x_0)=\dots =\alpha ^{lu}(x_0). \end{aligned}$$

The smallest positive integer u for which $\alpha ^{lu}(x_0)=x_0$ is $\frac{p}{\gcd (p,l)}$. Hence $D_{\beta |_Z}$ contains a cycle of length $t=ku=\frac{kp}{\gcd (p,l)}$.

We will show that every cycle in $D_{\beta |_Z}$ has length $\frac{kp}{\gcd (p,l)}$. Let $x\in Z$. If x is not a vertex of any $\sigma _i$, then x is not a vertex of any cycle of $D_{\beta |_Z}$ by Lemma 5.2.

Suppose that x is a vertex of $\sigma _0$, say $x=x_i$. Since $\beta ^k\in C(\alpha )$ and $\beta ^k(x_0)=x_l$, we have $\beta ^k(x_i)=x_{i+l}$ by Theorem 5.1. We can renumber the vertices of $\sigma _0$ in such a way that $x_i$ becomes $x_0$. Then, by the foregoing argument, we obtain a cycle $(x\ldots )$ in $D_{\beta |_Z}$ of length $\frac{kp}{\gcd (p,l)}$.

Suppose that x is a vertex of $\sigma _m$ with $m\ne 0$. Renumber the vertices of $\sigma _0,\sigma _1,\ldots ,\sigma _{k-1}$ in such a way that for each $i, \sigma _i=(x^i_0\ldots ), x=x^m_0$, and $\beta ^i(x^0_0)=x^i_0$. We have already shown that $\beta ^k(x^0_0)=x^0_l$. Thus, since $\beta ^m\in C(\alpha )$,

$$\begin{aligned} \beta ^k(x^m_0)=\beta ^k(\beta ^m(x^0_0))=\beta ^m(\beta ^k(x^0_0))=\beta ^m(x^0_l)=x^m_l. \end{aligned}$$

Hence, by the foregoing argument, we obtain a cycle $(x\ldots )$ in $D_{\beta |_Z}$ of length $\frac{kp}{\gcd (p,l)}$. Since we have considered all possible cycles in $D_{\beta |_Z}$, (2) follows.

Remark 5.4

Let Z and $\sigma _0,\sigma _1,\ldots , \sigma _{k-1}$ be as in Lemma 5.3, and let $x\in Z$. By the proof of Lemma 5.3, we have:

• (1) if x is not in any $\sigma _i$, then x does not lie on any cycle of $D_{\beta |_Z}$;

• (2) if x is in some $\sigma _i$, then $D_{\beta |_Z}$ has a cycle $(x\ldots )$ of length $\frac{kp}{\gcd (p,l)}$, where $l\in \{0,1,\ldots ,p-1\}$ is such that $\beta ^k(x)=\alpha ^l(x)$.

Lemma 5.5

Let $\alpha \in {{\mathrm{Sym}}}(S)$ and $\beta \in C(\alpha )$. Suppose that A is a component of $D_{\psi _\beta }$ with cycle $(\sigma _0\,\sigma _1 \ldots \, \sigma _{k-1})$. Let Z be as in Lemma 5.2. Assume that the maximum length of a branch in A is s (with $s=0$ if A has no branches). Then:

• (1) if $s=0$, then $D_{\beta |_Z}$ has no branches;

• (2) if $s>0$, then every branch in $D_{\beta |_Z}$ has length at most s, and there exists a branch in $D_{\beta |_Z}$ of length s.

Proof

If A has no branches, then every element of Z lies on some cycle in $D_{\beta |_Z}$ by Remark 5.4. This shows the first assertion.

To prove (2), suppose that $s>0$ and let $[\theta _0\,\theta _1\ldots \,\theta _m=\sigma _i]$ be a branch in A, so $m \le s$. Let x be in $\theta _j$, where $j\in \{0,1 \ldots , {m-1}\}$. Since $m\le s$, we have $\psi _\beta ^s(\theta _j)=\sigma _{i+s-m+j}$, and so $\beta ^s(x)$ is in $\sigma _{i+s-m+j}$. Thus, by Remark 5.4, $\beta ^s(x)$ lies on a cycle in $D_{\beta |_Z}$. Hence every branch in $D_{\beta |_Z}$ has length at most s.

Now let $[\theta _0\,\theta _1\ldots \,\theta _s=\sigma _i]$ be a branch of A whose length realizes the maximum value s. Let x be in $\theta _0$. Then $\beta ^s(x)$ is in $\sigma _i$ (since $\psi _\beta (\theta _0)=\sigma _i$) and for every $u\in \{0,1,\ldots ,s-1\}, \beta ^u(x)$ is in $\theta _u$ (since $\psi _\beta (\theta _0)=\theta _u$), and so $\beta ^u(x)$ does not lie on any cycle of $D_{\beta |_Z}$ by Remark 5.4. Thus $[x\,\beta (x)\,\beta ^2(x)\ldots \beta ^s(x)]$ is a branch in $D_{\beta |_Z}$ of length s. $\square$

With Theorem 4.10 and the lemmas of this section, we obtain the following characterization.

Theorem 5.6

Let $\alpha ,\beta \in T(S)$, where S is finite, $\alpha$ is a permutation, and $\beta \in C(\alpha )$. Suppose that $\{A_1,A_2,\ldots ,A_t\}$ is the set of components of $D_{\psi _\beta }$ and $s=\mathrm {sup}_b(\psi _\beta )$. Let M be the set of numbers of the form $\frac{k_ip_i}{\gcd (p_i,l_i)}, 1\le i\le t$, where $k_i$ is the length of the cycle $C_i$ in $A_i, p_i$ is the length of each cycle of $\alpha$ that occurs in $C_i$, and $l_i$ is the unique number in $\{0,1,\ldots ,p_i-1\}$ such that $\beta ^{k_i}(x)=\alpha ^{l_i}(x)$, where x is any element of any cycle of $\alpha$ that occurs in $C_i$. Then $\beta$ is a Cayley function if and only if the following conditions are satisfied:

• (1) the largest element m of M is a multiple of every element of M;

• (2) if $s>0$, then some component $A_r$ of $D_{\psi _\beta }$ such that $\frac{k_rp_r}{\gcd (p_r,l_r)}=m$ has a branch of length s.

Proof

Suppose that $\beta$ is a Cayley function. By Lemma 5.3, M is the set of the lengths of cycles in $D_\beta$. Thus (1) follows from Theorem 4.10. Suppose that $s>0$. By Lemma 5.5, $s=\mathrm {sup}_b(\beta )$, and so, by Theorem 4.10 and the foregoing observation about M, some cycle C of $D_\beta$ of length m has a branch of length s. By Lemma 5.3 and its proof, there exists a component $A_r$ of $D_{\psi _\beta }$ such that $m=\frac{k_rp_r}{\gcd (p_r,l_r)}$ and all vertices of C are contained in Z, where Z is as in Lemma 5.2 (with $A=A_r$). Finally, by Lemma 5.5, $A_r$ has a branch of length s.

Conversely, suppose that conditions (1) and (2) are satisfied. We have already observed that $s=\mathrm {sup}_b(\beta )$ and that M is the set of the lengths of cycles in $D_\beta$. Thus, 3(a) and 3(b) of Theorem 4.10 hold by (1). By Lemmas 5.3 and 5.5, $D_\beta$ has a cycle of length m with a branch of length s. Hence 3(c) of Theorem 4.10 holds, and so $\beta$ is a Cayley function. $\square$

Theorem 5.6 enables us to decide if a given $\beta \in C(\alpha )$ is a Cayley function by analyzing the components of the digraph of $\psi _\beta$ and the corresponding numbers from the set M.

Example 5.7

Let $S=\{x_0,x_1,x_2,x_3,y_0,y_1,z_0,z_1,w_0,w_1\}$. Consider

$$\begin{aligned} \alpha =(x_0\,x_1\,x_2\,x_3)(y_0\,y_1)(z_0\,z_1)(w_0\,w_1)\in {{\mathrm{Sym}}}(S). \end{aligned}$$

Let $\theta =(x_0\,x_1\,x_2\,x_3), \sigma _1=(y_0\,y_1), \sigma _2=(z_0\,z_1)$, and $\sigma _3=(w_0\,w_1)$.

Let $\beta \in C(\alpha )$ such that $D_{\psi _\beta }$ is given in Figure 11, $\beta (x_0)=y_0, \beta (y_0)=y_0, \beta (z_0)=w_1$, and $\beta (w_0)=z_0$. (Note that the remaining values of $\beta$ are determined uniquely by Theorem 5.1.) The components of $D_{\psi _\beta }$ and the corresponding numbers from M are:

• $A_1=\{\theta ,\sigma _1\}$ with $\frac{k_1p_1}{\gcd (p_1\!,l_1)}=\frac{1\cdot 2}{\gcd (2,0)}=1$,

• $A_2=\{\sigma _2,\sigma _3\}$ with $\frac{k_2p_2}{\gcd (p_2,l_2)}=\frac{2\cdot 2}{\gcd (2,1)}=4$.

Thus $M=\{1,4\}$ with $m=4$, and so (1) of Theorem 5.6 holds. However, we have $s=1$ and $A_2$, which is the only component with the corresponding number equal to $m=4$, does not have a branch of length s. Hence (2) of Theorem 5.6 does not hold, and so $\beta$ is not a Cayley function.

Fig. 11

Digraph $D_{\psi _\beta }$ from Example 5.7

Now consider $\gamma \in C(\alpha )$ such that $D_{\psi _\gamma }$ is given in Fig. 12, $\gamma (x_0)=x_2, \gamma (y_0)=z_0, \gamma (z_0)=w_1$, and $\gamma (w_0)=z_0$. The components of $D_{\psi _\gamma }$ and the corresponding numbers from M are:

• $A_1=\{\theta \}$ with $\frac{k_1p_1}{\gcd (p_1\!,l_1)}=\frac{1\cdot 4}{\gcd (4,2)}=2$,

• $A_2=\{\sigma _1,\sigma _2,\sigma _3\}$ with $\frac{k_2p_2}{\gcd (p_2,l_2)}=\frac{2\cdot 2}{\gcd (2,1)}=4$.

Thus $M=\{2,4\}$ with $m=4$, and so (1) of Theorem 5.6 holds. Further, we have $s=1$ and $A_2$, whose corresponding number is $m=4$, has a branch of length s. Hence (2) of Theorem 5.6 also holds, and so $\gamma$ is a Cayley function.

Fig. 12

Digraph $D_{\psi _\gamma }$ from Example 5.7

6 Problems

In this paper, we have solved a special case of problem 3 of the approach outlined on page 2. The solution for the case of finite permutations opens some natural questions.

Problem 6.1

Let $\sigma$ be a permutation on a finite set S. Describe the Cayley idempotents that commute with $\sigma$. Describe the Cayley permutations $\delta$ of S such that $\sigma \delta$ and $\delta \sigma$ are Cayley permutations.

Moving from permutations to idempotents, the following problem is also natural.

Problem 6.2

Find the Cayley functions on a finite set that commute with a given Cayley idempotent.

The main open question regarding the content of this paper is problem 3 in its full generality.

Problem 6.3

Describe the Cayley functions on a set S that commute with a given Cayley function on S.

Problem 4 of the approach does not need the solution of problem 3, and hence can be immediately attempted. Recall that the size of the image of a transformation on S is called its rank.

Problem 6.4

Characterize the pairs $\{\alpha ,\beta \}$ of Cayley functions on S such that $\alpha$ and $\beta$ occur as left inner translations of the same semigroup (possibly with some constrains added, such as pairs of permutations, idempotents, or maps of a given rank).

The ultimate goal is to carry out all steps of the approach outlined on page 2.

Problem 6.5

Carry out the steps 3–6 of the approach on page 2 for some special types of maps (permutations, idempotents, maps of a fixed maximum rank) on a finite set.

Problem 6.6

Carry out the steps 3–6 of the approach for all Cayley functions on an arbitrary set.

Other problems about Cayley functions present themselves.

Problem 6.7

Characterize the ordered pairs $(\alpha ,\beta )$ of Cayley functions on S such that in the same semigroup $(S,\cdot ), \alpha =\lambda _a$ and $\beta =\rho _a$ for some $a\in S$.

Problem 6.8

Given a Cayley function $\alpha$ on S, find all Cayley functions $\beta$ on S such that $\alpha \beta$ and $\beta \alpha$ are Cayley functions.

If $\alpha$ and $\beta$ occur as left inner translations of the same semigroup, then the semigroup generated by $\alpha$ and $\beta$ consists of Cayley functions. The converse is not necessarily true.

Problem 6.9

Find the pairs of Cayley functions [permutations, idempotents, functions of a given rank] that generate a semigroup of Cayley functions.

Let S be a semigroup. A left translation of S is a transformation $\lambda$ on S such that $\lambda (xy)=(\lambda (x))y$ for all $x,y\in S$; similarly, a right translation of S is a transformation $\rho$ on S such that $\rho (xy)=x(\rho (y))$ for all $x,y\in S$. A left translation $\lambda$ and a right translation $\rho$ of S form a linked pair $(\lambda ,\rho )$ if $x(\lambda (y))=(\rho (x))y$ for all $x,y\in S$. For every $a\in S$, the pair of inner translations $(\lambda _a,\rho _a)$ is a linked pair. (See [7, page 10].) The following problem is a generalization of Problem 6.7.

Problem 6.10

Characterize the pairs $(\alpha ,\beta )$ of transformations on a set S such $(\alpha ,\beta )$ is a linked pair for some semigroup with universe S.

We can also replace inner translations of a semigroup with endomorphisms of a semigroup or some other algebraic structure.

Problem 6.11

Describe the transformations $\alpha$ on a set S such that $\alpha$ is an endomorphism of some semigroup [group, inverse semigroup, completely regular semigroup, band, partially ordered set, etc.] with universe S.

Some research along these lines has already been done [29].

In this paper, we deal with full transformations on a set S, but analogous problems can also be considered for partial injective transformations on S. A partial injective transformation $\alpha$ on a set S is said to be a Vagner-Preston function if there exists an inverse semigroup with universe S such that $\alpha$ appears in the Vagner-Preston representation of S (see [13, Theorem 5.1.7]).

Problem 6.12

Describe Vagner-Preston functions and their digraphs. For Vagner-Preston functions, solve problems analogous to those problems posed above for which an analogous version makes sense and is not trivial.