Introduction

Cell membrane is a key component of the cell and membrane protein is the most important part of cell membrane. Membrane protein plays a key role in physiology and biology, such as a carrier to transport materials into or out of the cells and as receptors of some hormone or chemical substance, and membrane protein is a kind of important drug target (Ding et al. 2012). Therefore, accurately and rapidly identifying the functional types of membrane proteins will be helpful for disease treatment and drug design, because the knowledge about the type of a query membrane protein has a close relationship with its functions.

According to some previous studies (Chou and Shen 2007; Huang and Yuan 2013), membrane proteins are mainly divided into the following eight functional types: single-pass type I, single-pass type II, single-pass type III, single-pass type IV, multipass, lipid-anchor, GPI-anchor, and peripheral membrane proteins.

Although the functional type of a membrane protein may be determined by carrying out various biochemical experiments, these approaches by purely doing experiments are both time consuming and expensive. In the post-genomic age, the gap between the newly found membrane protein sequences and the information of their types is becoming increasingly wide (Wang and Li 2012). Therefore, to bridge such a gap, it is urgent to develop an effective and rapid computational method to identify the functional types of membrane proteins.

In the past several years, many efforts have been made in identifying the functional types of membrane proteins, such as Chou and Elrod (1999) predicted the functional types of membrane proteins based on the covariant discriminant algorithm (CDA) and amino acid composition (AAC); Wang et al. (2005), by using supervised locally linear embedding (SLLE) technique and pseudo amino acid composition (PseAAC) with k-nearest neighbor (KNN) algorithm to identify membrane proteins’ types, achieved a success rate of 82.3 % by jackknife test; Shen et al. (2006) predicting membrane protein types by hybridizing pseudo amino acid composition with fuzzy k-nearest neighbor (FKNN) algorithm, achieved a success rate of 85.6 % by jackknife test and 95.7 % by independent dataset test; and Pu et al. (2007) predicting membrane proteins types based on sequence information and evolution information, obtained 92.3 % success rate, and many others.

Although the aforementioned methods have their own advantages and did play a key role in stimulating the development of this field, they were only focused on identifying which type it belongs to for a query membrane protein (Xiao et al. 2013). In fact, there are many membrane proteins that have more than one function or functional type (Xiao et al. 2013). Those proteins should not escape our eyes because they may have some unique biological functions worthy of our special notice (Glory and Murphy 2007; Smith 2008).

In the paper, a new method by hybridizing various pseudo amino acid compositions was proposed to identify the functional types of human membrane proteins. A multi-label classifier called multi-label k-nearest neighbor (ML-KNN) was introduced, which is derived from classical KNN algorithm. Finally, a promising result was obtained, which indicated that the method is useful, and it may be used in identifying other attributes of proteins.

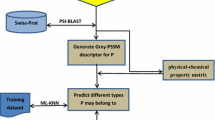
According to a recent comprehensive review (Chou 2011), to establish a powerful and efficient predictor for a protein system, the following procedures should be considered: (1) establish or select a valid benchmark dataset to train and test the predictor; (2) formulate the protein sequences using an effective mathematic that can truly reflect the intrinsic correlation with the target to be predicted; (3) develop or introduce a powerful algorithm (or engine) to operate the prediction; and (4) properly perform cross-validation tests to objectively evaluate the anticipated accuracy of the predictor. We describe the processes in detail.

Materials and Methods

Benchmark Datasets

All of the membrane protein sequences used in the current study were collected from the UniProtKB database released on 04-Apr 16, 2014 at website http://www.uniprot.org/. In order to obtain a high quality and well-defined dataset, the following procedures should be considered: (1) only human membrane protein sequences were collected; (2) sequences annotated with “fragment” were removed; (3) sequences with less than 50 amino acid residues were also removed to avoid the influence of fragment; (4) to reduce the redundancy and homology bias, the program named CD-HIT was used to remove those proteins that have more than 60 % (not 25 %, because some types data too little) pairwise sequence identity to any other protein in the same subset.

Finally, we obtained 3,166 different human membrane protein sequences covered in eight different functional types, which can be formulated as

$$S = S_{1} \cup S_{2} \cup S_{3} \cup S_{4} \cup S_{5} \cup S_{6} \cup S_{7} \cup S_{8},$$
(1)

where \(S_{1}\) represents the functional type of “single-pass type I”, \(S_{2}\) for “single-pass type II”, and so forth. The symbol \(\cup\) represents the “union” in the set theory. For convenience, the numbers from 1 to 8 were used to represent the 8 subsets. A detailed information about the benchmark dataset are listed in Table 1.

Table 1 Detail of benchmark dataset of human membrane proteins
Full size table

Because some membrane proteins may simultaneously belong to two or more functional types, it is instructive to introduce the concept of “virtual protein” (Xiao et al. 2013; Chou et al. 2011, 2012) as briefed below. If a protein possesses two different functional types, it will be counted as two virtual proteins; if it possesses three functional attributes, it will be counted as three virtual proteins, and so forth. Thus, the number of total virtual proteins can be formulated as (Xiao et al. 2013; Lin et al. 2013)

$$N(\text {vir})\;\; = \;\;N(\text{seq})\; + \;\sum\limits_{m = 1}^{M} {(m\; - \;1)N(m)}$$
(2)

where \(N(\text {vir})\) is the number of total virtual proteins, \(N(\text {seq})\) is the number of total different protein sequences investigated, \(N(1)\) is the number of membrane proteins with one functional type, \(N(2)\) is the number of membrane proteins with two different functional types, and so forth, while \(M\) is the number of total functional types of membrane proteins investigated.

According to Eq. (2), the virtual membrane proteins investigated in the current study can be calculated by the following formulation:

$$\begin{gathered} N(\text{ vir}) = N(\text {seq}) + (1-1) \times 3069 +(2-1) \times 93 + (3 -1) \times 4 \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {} & {} & { = 3166 + 0 + 93 + 8} \\ \end{array} = \;3267. \hfill \\ \end{gathered}$$
(3)

As we can see from Eqs. (2,  3), the number of total virtual membrane proteins is generally greater than the number of different membrane proteins. When and only when all of the membrane proteins belong to one functional type, the two (i.e., virtual proteins and different proteins) will be the same (Lin et al. 2013).

Feature Extraction

In order to develop an effective predictor for identifying the functional types of human membrane proteins based on the sequence information, one of the most important things is to formulate the protein sequence with an efficient mathematical expression that can truly reflect the intrinsic correlation with the target to be predicted (Xiao et al. 2013; Chou 2011). However, it is not an easy work to realize this because this kind of correlation is usually deeply hidden or “buried” into piles of complicated sequences (Xiao et al. 2013).

As is well known, the most straightforward method is to formulate the protein sequence using its entire amino acid composition. For a protein sequence \(P\) with \(L\) amino acids, it can be expressed as

$$P = R_{1} R_{2} R_{3} \cdots R_{L},$$
(4)

where \(R_{1}\) is the first residue of the sequence, \(R_{2}\) is the second residue, and so forth. Each of the residues belongs to the 20 native amino acids. In order to identify its attribute(s), the sequence similarity search-based tools, such as BLAST (Zhang et al. 1997; Wootton and Federhen 1993), were utilized to search the protein database for those proteins that have high sequence similarity to the query protein \(P\). Then, the attribute(s) of the proteins thus found were used to deduce the attribute(s) for the query \(P\). However, this kind of straightforward sequential model, although quite intuitive and has the ability to contain the entire sequence information, failed to work when the query protein \(P\) did not have significant sequence similarity to any attribute-known proteins.

Thus, to overcome the above difficulty, various discrete models were proposed in a hope to enhance the power of the predictor.

Amino Acid Composition (AAC)

Among the various discrete models, the simplest one is the AAC-discrete model that represents the protein sample using its AAC (Nakashima et al. 1986). According to the AAC-discrete model, the protein \(P\) can be formulated as (Chou 1995)

$$P\;\; = \;\;[f_{1} f_{2} f_{3} \cdots f_{20} ]^{\text{T}},$$
(5)

where \(f_{i} (i\;\; = \;\;1,2, \ldots ,20)\) represents the normalized occurrence frequencies of the 20 native amino acids in the protein and T stands for the transposing operator. However, as we can see from Eq. (5), if only the AAC-discrete model was used to represent the protein sequence \(P\), all of the sequence-order information would be lost.

In order to avoid completely losing the sequence-order information, a new model was proposed to replace the simple amino acid composition that is pseudo amino acid composition (PseAAC) (Chou 2001).

Since the concept of PseAAC was proposed by Chou in 2001, it has been widely recognized and used by many investigators to identify various attributes of proteins, such as identifying subcellular location of proteins (Xiao et al. 2005; Shen and Chou 2007; Li and Li 2008; Park and Kanehisa 2003), predicting subcellular location of apoptosis proteins (Chen and Li 2007; Jian et al. 2008; Lin et al. 2009), predicting enzyme classes or subclasses (Zhou et al. 2007; Chou and Elrod 2003), identifying the functional types of antimicrobial peptides (Xiao et al. 2013; Khosravian and Kazemi 2013), and among many others.

Chou’s Pseudo Amino Acid Composition (CPseAAC)

According to the concept of Chou’s pseudo amino acid composition, a protein sequence can be represented by a \(20\; + \;\lambda\) dimension vector. The first 20 elements represent the amino acid composition, and the latter \(\lambda\) elements represent the sequence-order information. The sequence-order information can be indirectly represented by the following equation:

$$\delta_{\theta } \;\; = \;\;\frac{1}{L\; - \;\theta }\sum\limits_{i\; = \;1}^{L\; - \;\theta } {\varOmega (R_{i} ,R_{i\; + \;\theta} )} ,\;(\theta \;\; = \;\;1,2, \ldots ,\lambda \begin{array}{*{20}c} {\;{\text{and}}\begin{array}{*{20}c} {\;\lambda < L} \\ \end{array} } \\ \end{array} ),$$
(6)

where L denotes the length of the protein sequence and \(\delta_{\theta }\) is called the \(\theta {\text{th}}\) correlation factor which harbors the sequence-order information between all the \(\theta\) most contiguous residues. The correlation function \(\varOmega (R_{i} ,R_{i\; + \;\theta} )\) is defined by

$$\varOmega (R_{i} ,R_{i\; + \;\theta} ) = \frac{1}{3}\left\{ {[F(R_{i\; + \;\theta} )\; - \;F(R_{i} )]^{2} \; + \;[G(R_{i\; + \;\theta} )\; - \;G(R_{i} )]^{2} \; \quad+ \;[H(R_{i\; + \;\theta} )\; - \;H(R_{i} )]^{2} } \right\},$$
(7)

where \(F(R_{i} )\), \(G(R_{i} )\) and \(H(R_{i} )\) are the evaluated values of hydrophobicity, hydrophilicity, and mass, respectively. There are also three types of values that can be used. Before we use these values, a standard conversion should be conducted using Eq. (4) of Huang and Yuan (2013). The numerical values of the three physical–chemical properties for each of the 20 native amino acids can be obtained from (Shen and Chou 2008).

Then a sample protein \(P\) can be represented as

$$P\;\; = \;\;[x_{1} ,x_{2} , \ldots ,x_{20} ,x_{20\; + \;1} , \ldots ,x_{20\; + \;\lambda } ]^{T} \begin{array}{*{20}c} {} & {\lambda < L} \\ \end{array}$$
(8)

where

$$ x_{u} \;\; = \;\;\left\{ \begin{gathered} \frac{{f_{u} }}{{\sum\limits_{i\; = \;1}^{20} {f_{i} \; + \;w\sum\limits_{\theta\; = \;1}^{\lambda } {\delta_{\theta} } } }},\;(1 \le u \le 20) \hfill \\ \frac{{w\delta_{u\; - \;20} }}{{\sum\limits_{i\; = \;1}^{20} {f_{i} \; + \;w\sum\limits_{\theta\; = \;1}^{\lambda } {\delta_{\theta} } } }},\;(20\; + \;1 \le u \le 20\; + \;\lambda ;\;\lambda < L) \hfill \\ \end{gathered} \right. $$
(9)

where \(w\) is the weight factor, \(f_{i} (i\;\; = \;\;1,2, \ldots ,20)\) represents the normalized occurrence frequencies of the 20 native amino acids in the sample protein P, and \(\delta_{\theta}\) is the \(\theta\)-tier sequence-correlation factor, computed according to Eq. (6). In this study, we choose \(w\;\; = \;\;0.05\),  \(\lambda = 20\) after careful consideration of easy handling; they can be assigned other values, of course, but the impact on the result would be small.

Information Entropy (IE)

Shannon proposed that any information is redundant, and redundant size is related with the occurrence probability or uncertainty of each symbol such as numbers, letters, or words among the information. The information entropy for a system can be defined as

$$H\;\; = \; - \sum\limits_{i\; = 1}^{20} {f(i)\log_{2} f(i)}$$
(10)

where \(f(i)(i\;\; = \;\;1,2, \ldots ,20)\) represents the occurrence probability of amino acid \(i\). The information entropy \(H\) is a measured value of the amount of information. For example, for the digital sequence \(P\;\, = \;\;100100011010010\), the information entropy \(H\) is obtained as given below:

$$\left\{ \begin{gathered} P(0)\;\; = \;\;{\raise0.7ex\hbox{$9$} \!\mathord{\left/ {\vphantom {9 {15}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${15}$}}\;\; = \;\;0.6 \hfill \\ P(1)\;\; = \;\;{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {15}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${15}$}}\;\; = \;\;0.4 \hfill \\ {{H}}\;\; = \; - (0.6\; \times \;\log_{2} 0.6\; + \;0.4\; \times \;\log_{2} 0.4)\;\; = \,\;0.971. \hfill \\ \end{gathered} \right.$$
(11)

Distribution (D)

According to Zou et al. (2013), based on the different physiochemical properties, the 20 native amino acids can be divided into 3 groups. In this study, the following eight different physiochemical properties were utilized: secondary structure, solvent accessibility, normalized van der Waals volume, hydrophobicity, charge, polarizability, polarity, and surface tension (Zou et al. 2013) (listed in Table 2). The descriptor called distribution was utilized to describe the global composition of each of those properties. In this study, five distributions were assigned—position percentage of first, 25, 50, 75, and 100 % residue occurrence in the entire sequence. Therefore, the distribution \(D_{x}\) for the descriptor \(E_{i}\) is calculated as below (Saravanan and Lakshmi 2013):

$$E_{i} 1D_{x} = \frac{{P_{1} }}{L},$$
(12)
$$E_{i} 25D_{x} = \frac{{P_{25} }}{L},$$
(13)
$$E_{i} 50D_{x} = \frac{{P_{50} }}{L},$$
(14)
$$E_{i} 75D_{x} = \frac{{P_{75} }}{L},$$
(15)
$$E_{i} 100D_{x} \;\; = \;\;\frac{{P_{100} }}{L}(i\;\; = \;\;1,2, \ldots ,8;\;x\;\; = \;\;1,2,3),$$
(16)

where \(P_{1}\), \(P_{25}\), \(P_{50}\), \(P_{75}\), \(P_{100}\) indicate the position of first occurrence of \(x\), and positions of 25, 50, 75, 100 % occurrence of \(x\), respectively.

Table 2 Details of the physiochemical descriptor
Full size table

We give an example to explain in detail the distribution in the following. Assuming that there is a protein sequence, its amino acid composition is AEAAAEAEEAAAAAEAEEEAAEEAEEEAAE, which has 16 alanines and 14 glutamic acids. The first, 25, 50, 75, and 100 % of A are located in the first, 5th, 12th, 20th, and 29th residue. The D descriptor for A is 1/30 = 0.0333, 5/30 = 0.1667, 12/30 = 0.4000, 20/30 = 0.6667, 29/30 = 0.9667. Similarly, the D descriptor for E is 0.0667, 0.2667, 0.6000, 0.7667, 1.0000. Overall, the D descriptor for this sequence is D = (0.0333, 0.1667, 0.4000, 0.6667, 0.9667, 0.0667, 0.2667, 0.6000, 0.7667, 1.0000).

Position-Specific Scoring Matrix (PSSM)

The position-specific scoring matrix (PSSM) is often used to describe the sequence evolution information of protein. A protein sequence \(P\) with \(L\) amino acid residues can be formulated by an L  ×  20  matrix, it can be expressed as follows:

$$P_{\text{PSSM}}^{(0)} = \left[ {\begin{array}{*{20}c} {n_{1,1}^{(0)} } & {n_{1,2}^{(0)} } & \cdots & {n_{1,20}^{(0)} } \\ {n_{2,1}^{(0)} } & {n_{2,2}^{(0)} } & \cdots & {n_{2,20}^{(0)} } \\ \vdots & \vdots & \vdots & \vdots \\ {n_{L,1}^{(0)} } & {n_{L,2}^{(0)} } & \cdots & {n_{L,20}^{(0)} } \\ \end{array} } \right]$$
(17)

where \(n_{i,j}^{(0)}\) stands for the initial score of amino acid residues during the evolution process the \(i \text {-th}\;(i\; = \;1,2, \ldots ,L)\) sequential position has been changed into type \(j(j = 1,2, \ldots ,20)\) amino acid. The numbers 1, 2, …, 20, respectively, represent the 20 native amino acid types based on the alphabetical order considering only their single character codes (Chou et al. 2012). We can obtain the L × 20 scores in Eq. (17) using PSI-BLAST (Schäffer et al. 2001) to search the UniProtKB/Swiss-Prot database (Boutet et al. 2007; UniPort Consortium 2008). There is an important problem to be noticed, when only Eq. (17) was used directly, because the data have a significant variation, it gives inaccurate results; in order to solve the problem, we should make each element in Eq. (17) change from 0 to 1, and thus a standard conversion was performed. Through the conversion, Eq. (17) will become this

$$P_{\text{PSSM}}^{(1)} = \left[ {\begin{array}{*{20}c} {n_{1,1}^{(1)} } & {n_{1,2}^{(1)} } & \cdots & {n_{1,20}^{(1)} } \\ {n_{2,1}^{(1)} } & {n_{2,2}^{(1)} } & \cdots & {n_{2,20}^{(1)} } \\ \vdots & \vdots & \vdots & \vdots \\ {n_{L,1}^{(1)} } & {n_{L,2}^{(1)} } & \cdots & {n_{L,20}^{(1)} } \\ \end{array} } \right]$$
(18)

where

$$n_{i,j}^{(1)} \; = \;\frac{1}{{1\; + \;{\text e}^{{ - n_{i,j}^{(0)} }} }}$$
(19)

After getting the PSSM matrix, we compute the average replaced possibility for all 20 types of amino acids, and finally 20 features are obtained. It can be formulated as (Zou et al. 2013)

$$P^{\prime}_{\text{PSSM}} = \left[ {\overline{{E_{1} }} ,\overline{{E_{2} }} , \ldots ,\overline{{E_{20} }} } \right]^{\text T}$$
(20)

where T is the symbol of transpose operator

$$\overline{{E_{j} }} \; = \;\frac{1}{L}\sum\limits_{i\; = \;1}^{L} {n_{i,j}^{(1)} }$$
(21)

where \(\overline{{E_{j} }}\) represents the average score of the amino acid residues in the protein sequence being changed to amino acid type \(j\) during the evolution process.

Prediction Engine

In this study, the ML-KNN classifier was adopted to perform the prediction, which is derived from the classical KNN algorithm. The detailed description about how the classifier works is clearly described in Zhang and Zhou (2007), and hence there is no need for repeating it here. The predictor established in this study can be used to predict the functional types of both singleplex and multiplex human membrane proteins.

Performance Metrics

It is worthy to point out that for a multi-label learning system like the current system, which is different from the classical single-label learning system, the existing metrics, which were used to evaluate the quality of a predictor on a single-label system would fail to work when a multi-label learning system like this is faced. The metrics will be much more complicated for a multi-label learning system. We now describe the metrics used in multi-label system in the following section.

For a multi-label learning system containing \(N\) protein sequences, which belong to \(M\) functional types, \(L\) is the label set that contains all of the possible functional types concerned. Thus, the \(i{\text -{th}}\) sequence \(P_{i}\) and its corresponding functional type(s) can be expressed by

$$\{ P_{i} ,L_{i} \} (i = 1,2, \ldots ,N)$$
(22)

where \(L_{i}\) is the subset that includes all class label (s) for the \(i{\text -{th}}\) protein. Obviously, we have

$$L_{1} \cup L_{2} \cup \ldots \cup L_{N} \subseteq L\; = \;\{ l_{1} ,l_{2} , \ldots l_{M} \}$$
(23)

where \(l_{i} (i = 1,2, \ldots ,M)\) corresponds to the label for the \(i{\text -{th}}\) functional type. In this study, the value of \(N\) is 3,166, the value of \(M\) is 8. Assume that \(L_{i}^{*}\) is the all predicted label(s) for the \(i{\text -{th}}\) sample. Thus, the following five metrics can be used to measure the prediction quality of the multi-label system:

$$\left\{ \begin{aligned} &{\text{Absolute}}-{\text{False}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\frac{{\left\| {L_{i} \cup L_{i}^{*} } \right\| - \left\| {L_{i} \cap L_{i}^{*} } \right\|}}{M}} \right)} \hfill \\ &{\text{Accuracy}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\frac{{\left\| {L_{i} \cap L_{i}^{*} } \right\|}}{{\left\| {L_{i} \cup L_{i}^{*} } \right\|}}} \right)} \hfill \\ &{\text{Precision}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\frac{{\left\| {L_{i} \cap L_{i}^{*} } \right\|}}{{\left\| {L_{i}^{*} } \right\|}}} \right)} \hfill \\ &{\text{Recall}}= \frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {\frac{{\left\| {L_{i} \cap L_{i}^{*} } \right\|}}{{\left\| {L_{i} } \right\|}}} \right)} \hfill \\ &{\text{Absolute true}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\Delta (L_{i} ,L_{i}^{*} )} \hfill \\ \end{aligned} \right.$$
(24)

where \(N\) is the number of different membrane proteins, \(M\) is the total number of functional types, here \(N = 3,166\) and \(M = 8\). The symbol \(\cup\) and \(\cap\) represent “union” set theory and intersection, respectively. ∥ ∥ is the operator acting on the set therein to count the number of its elements, and

$$\left\{ {\begin{array}{ll} {\Delta (L_{i} ,L_{i}^{*} )=1,\quad {\rm if\; all\; the\; labels\; in\; L_i\; are\; identified\; to\; those\; in\; L_{i}^{*}}} \\ {\Delta (L_{i} ,L_{i}^{*} )=0, \quad {\rm otherwise}} \\ \end{array} } \right.$$
(25)

Among the five evaluation measures, the rate of absolute-false is opposite to those of the other four. As can be easily seen from Eq. (22), when the multi-labels for all of the samples are correctly predicted, i.e., \(L_{i} \; \equiv \;L_{i}^{*}\) or \(\left\| {L_{i} \; \cup \;L_{i}^{*} } \right\|\; = \;\left\| {L_{i} \; \cap \;L_{i}^{*} } \right\|\) \((i = 1,2, \ldots ,N)\), the rate of absolute-false equals to 0. When each of \(P\) \((i = 1,2, \ldots ,N)\) is predicted completely wrong, i.e., belonging to all the possible categories except its own category or categories; i.e., \(L_{i} \; \cup \;L_{i}^{*} \; = \;L\) and \(L_{i} \; \cap \;L_{i}^{*} \; = \;\emptyset\), or \(\left\| {L_{i} \; \cup \;L_{i}^{*} } \right\|\; = \;M\) and \(\left\| {L_{i} \; \cap \;L_{i}^{*} } \right\|\; = \;0\), the rate of absolute-false is equal to 1. Therefore, the lower the absolute-false is, the better the prediction quality will be. However, for the other four metrics, the meanings of their rates are just opposite; i.e., the higher their rates are, the better the prediction quality will be.

Results and Discussion

In statistical prediction, it is meaningless to simply say the success rate of a predictor without specifying what methods and benchmark dataset were utilized to test its accuracy (Wu et al. 2012). As is well known, there are three methods that are often used to examine the quality of a predictor: they are jackknife test, sub-sampling test, and independent dataset test, respectively. Among the three approaches, the jackknife test was considered as the least but most objective one, yielding a unique result for a given benchmark dataset, and hence it has been widely recognized and increasingly used to examine the power of various predictors. Therefore, the jackknife test was also adopted in this study to evaluate the quality of the predictor.

However, even though the jackknife test method has been used, the same predictor may also generate obviously different results for different benchmark datasets. The reason is that the more stringent a benchmark dataset in excluding homologous and high similarity sequences, the more difficult it becomes for a predictor to achieve a high overall success rate (Chou and Shen 2010). Also, the more the number of subsets a benchmark dataset covers, the more difficult it is to achieve a high overall success rate.

In this study, the results obtained are listed in Table 3. As we can see from Table 3, comparing the other two methods, the combination of D + PSSM provides better results; the overall absolute-true is 73.94 %, while the absolute-false is 6.48 %, i.e., the overall absolute-false rates are very low, while the absolute-true rates are quite higher; all of these results are indeed promising, indicating that the method is useful in identifying the functional types of membrane proteins.

Table 3 The results obtained by jackknife test with ML-KNN algorithm in the benchmark dataset
Full size table

Now, let us consider that a benchmark dataset consists of two subsets with each containing the same number of proteins. The overall success rate in identifying their attribute categories by random assignment would be 1/2 = 50 %; however, when the protein samples distributed among the eight different types are completely random, the overall success rate by random assignments would be 1/8 = 12.5 %; if the assignments are weighted as its sizes of subsets (Table 1), then the overall success rate would be:

$$\left( {605^{2} + 195^{2} + 25^{2} + 27^{2} + 1444^{2} + 251^{2} + 83^{2} + 6377^{2} } \right)/3267^{2} \; \approx \;27.79\;\%$$
(26)

Apparently, even the overall success rate by the worst solution in the benchmark dataset is overwhelmingly higher than the completely randomized rate and weighted randomized rate, so the models presented in this paper are indeed very encouraging (Huang and Yuan 2013).

Conclusion

Although many investigators made efforts in identifying the functional types of membrane proteins, it is still a challenge in this area with the explosion of newly found protein sequences entering into protein databanks. In this study, a new method by fusing various pseudo amino acid compositions was proposed, and the results obtained indicate that the new method has a very high potential for becoming a useful high-throughput tool for identifying the functional types of membrane proteins (Xiao et al. 2013). We hope it may play a key complementary role to the existing predictors in this area. In the future, we will investigate other methods for the sake of enhancing the powerful of the prediction.

Since user-friendly and publicly accessible web-servers provide direction for developing practically more useful models, simulated methods, or predictors (Chou and Shen 2009), we shall make efforts in our future work to provide a web server for the method presented in this study.