Introduction

Almost all living cells are enclosed by membranes which are composed of mainly lipids and proteins that play various roles (Chou and Elrod 1999); for instance, membranes define cell boundaries, maintaining the essential differences between the cytosol and the extracellular environment, and some of them offer the skeleton for the lipid bilayer membrane. Membrane proteins can be mainly divided into eight types (Chou and Shen 2007b): (1) single-pass type I membrane, (2) single-pass type II membrane, (3) single-pass type III membrane, (4) single-pass type IV membrane, (5) multipass membrane, (6) lipid-anchor membrane, (7) GPI-anchor membrane and (8) peripheral membrane.

Knowledge about the type of a particular membrane protein is very helpful because this kind of information is highly correlated with its function (Nanni and Lumini 2008). Between 20 and 35 % of genes encode membranes, whereas only 1 % of proteins are membrane proteins whose 3D structures are known (Nanni and Lumini 2008). Determining the membrane protein type through multifarious biochemical experiments is not only resource-intensive but time-consuming, so developing automated methods for efficiently and accurately identifying the types of given proteins is highly desired.

The prediction of membrane protein type is similar to the problem of subcellular localization. Several different types of subcellular localization predictors have been proposed in the last decade or so (Chou and Shen 2006, 2007a, 2008, 2010b; Chou et al. 2011, 2012; Shen and Chou 2007, 2009, 2010a, 2010b; Wu et al. 2011, 2012; Xiao et al. 2011b, 2011c). Also, a series of classifiers and methods have been developed to identify membrane protein sequences (Chen and Li 2013; Chou and Cai 2005; Chou and Shen 2007b; Nanni and Lumini 2008). All of them can only deal with membrane protein sequences in which one sequence belongs to only one type. To the best of our knowledge, no predictor can handle the problem that one membrane sequence belongs to two or more than two types. But these types of protein are also very important because they may have some special biological significance. Considering the fact that several predictors which can deal with protein subcellular localization with both single and multiple sites have been established, it is urgent and meaningful to develop methods or predictors which are able to handle membrane protein sequences with single and multiple types.

In this article, we adopt a multilabel algorithm named ML_KNN, whose basic consideration is a multilabel-based K-nearest neighbor algorithm (KNN) derived from the common K-nearest neighbor algorithm (Zhang and Zhou 2007) and pseudo–amino acid composition which has proven to be a very efficient tool in representing protein sequences to compose this new classifier. Application to a rigorous benchmark data set shows that this prediction model performs well, as an initial study on this new topic.

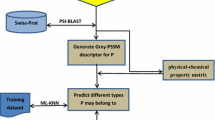
According to a comprehensive review (Chou 2011) and as demonstrated by a series of recent publications (Chen et al. 2012, 2013; Lin et al. 2012; Wang et al. 2011; Xiao et al. 2011a, 2012), to establish a really useful statistical predictor for a protein system, we need to consider the following procedures: (1) construct or select a valid benchmark data set to train and test the predictor, (2) formulate the protein samples with an effective mathematical expression that can truly reflect their intrinsic correlation with the attribute to be predicted, (3) introduce or develop a powerful algorithm (or engine) to operate the prediction and (4) properly perform cross-validation tests to objectively evaluate the anticipated accuracy of the predictor. Below, we describe how to deal with these steps.

Materials and Methods

Data Set

The protein data set was taken from the UniprotKB/Swiss-Prot database at (http://www.ebi.ac.uk/uniprot/) released in June 2012. The detailed procedures are as follows: (1) open the Web site at http://www.uniprot.org/; (2) click the button “Advanced,” select “Subcellular Location” for “Fields,” type in “single-pass type I membrane” for “Term” and select “Experimental” for “Confidence”; (3) click the button “Add&Search,” select “or” and repeat step 2 with the only difference being that each of the following terms is typed in once in order until all of them are used: “single-pass type II membrane,” “single-pass type III membrane,” “single-pass type IV membrane,” “multipass membrane protein,” “lipid-anchor,” “GPI-anchor,” “peripheral membrane protein”; (4) click the button “Add&Search,” choose “and,” select “Fragment(yes/no)” for “Field” and choose “no”; (5) click the button “Add&Search,” choose “and,” select “Sequence Length” for “Field” and choose the sequence length “≥50.”

CD-HIT software (Huang et al. 2010; Li and Godzik 2006; Niu et al. 2010) was used to exclude those sequences which have more than 80 % sequence identity to any others in the same membrane type group.

The information of this benchmark data set is listed in Table 1.

Table 1 Detail of the benchmark data set derived from Swiss-Prot database according to the procedures described in “Data Set”
Full size table

Feature Extraction

Chou’s Pseudo–Amino Acid–Based Features

One of the most efficient methods to engender the sample of a query protein P is the pseudo–amino acid composition (Chou 2001, 2011; Shen and Chou 2008), which has been widely applied to predict a myriad of protein attributes (Esmaeili et al. 2010; Fan and Li 2012; Georgiou et al. 2009; Hayat and Khan 2012; Jiang et al. 2008; Khosravian et al. 2013; Mei 2012; Mohabatkar 2010; Mohabatkar et al. 2011, 2013; Mohammad Beigi et al. 2011; Nanni et al. 2012a, 2012b; Niu et al. 2012; Xiao et al. 2006a, 2006b; Zhang et al. 2008; Zia Ur and Khan 2012). In this study, we also adapted this method to construct the query proteins.

The model can be divided into two parts. One part is just its amino acid composition, which includes 20 discrete numbers, each of them representing the normalized occurrence frequencies of one of the native amino acids in protein P. The other part is the pseudo–amino acid composition part, which takes advantage of the information from the sequence order effect. The steps are shown below.

Suppose a protein including l amino acid residues:

$$ P = [Q_{1} ,Q_{2} ,Q_{3} ,Q_{4} \ldots ,Q_{L} ] $$
(1)

The sequence-order information can be indirectly represented by the following equations

$$ \left\{ \begin{aligned} \delta_{1} = & \frac{1}{L - 1}\sum\limits_{i = 1}^{L - 1} {\Upomega (Q_{i} ,Q_{i + 1} )} \\ \delta_{2} = & \frac{1}{L - 2}\sum\limits_{i = 1}^{L - 2} {\Upomega (Q_{i} ,Q_{i + 2} )} \\ \delta_{3} = & \frac{1}{L - 3}\sum\limits_{i = 1}^{L - 3} {\Upomega (Q_{i} ,Q_{i + 3} ),\;\eta < L} \\ \delta_{4} = & \frac{1}{L - 4}\sum\limits_{i = 1}^{L - 4} {\Upomega (Q_{i} ,Q_{i + 4} )} \\ & \cdots \\ \delta_{\eta } = & \frac{1}{L - \eta }\sum\limits_{i = 1}^{L - \eta } {\Upomega (Q_{i} ,Q_{i + \eta } )} \\ \end{aligned} \right. $$
(2)

In Eq. (2) the correlation function is defined by

$$ \Upomega (Q_{i} ,Q_{j} ) = \frac{1}{3}\{ [F(Q_{j} ) - F(Q_{i} )]^{2} + [G(Q_{j} ) - G(Q_{i} )]^{2} + [H(Q_{j} ) - H(Q_{i} )]^{2} \} $$
(3)

where F(Q i ), G(Q i ) and H(Q j ) are the values of hydrophobicity, hydrophilicity and mass, respectively. There are also three types of value that can be used. Before we use these values, a standard conversion described by the following should be conducted:

$$ \left\{ \begin{aligned} F(i) = & \frac{{F^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{F^{0} (i)}}{20}} }}{{\sqrt {\frac{{\sum\limits_{i = 1}^{20} {\left[ {F^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{F^{0} (i)}}{20}} } \right]^{2} } }}{20}} }} \\ G(i) = & \frac{{G^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{G^{0} (i)}}{20}} }}{{\sqrt {\frac{{\sum\limits_{i = 1}^{20} {\left[ {G^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{G^{0} (i)}}{20}} } \right]^{2} } }}{20}} }} \\ H(i) = & \frac{{H^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{H^{0} (i)}}{20}} }}{{\sqrt {\frac{{\sum\limits_{i = 1}^{20} {\left[ {H^{0} (i) - \sum\limits_{i = 1}^{20} {\frac{{H^{0} (i)}}{20}} } \right]^{2} } }}{20}} }} \\ \end{aligned} \right. $$
(4)

where F 0(i) is the original hydrophobicity value of the ith amino acid, G 0(i) is the original hydrophilicity value of the ith amino acid and H 0(i) is the original mass value of the ith amino acid side chain. These data were achieved from the Web server PseACC (Shen and Chou 2008). We use numbers 1–20 to denote the 20 native amino acids according to the order of their three-letter names: Ala (A), Arg (R), Asn (N), Asp (D), Cys (C), Gln (Q), Glu (E), Gly (G), His (H), Ile (I), Leu (L), Lys (K), Met (M), Phe (F), Pro (P), Ser (S), Thr (T), Trp (W), Tyr (Y), Val (V).

Then, a sample protein P can be represented as

$$ P = \left[ \begin{gathered} q_{1} \hfill \\ \vdots \hfill \\ q_{20} \hfill \\ q_{20 + 1} \hfill \\ \vdots \hfill \\ q_{20 + \eta } \hfill \\ \end{gathered} \right] $$
(5)

where

$$ q_{k} = \left\{ \begin{gathered} \frac{{t_{k} }}{{\sum\limits_{i = 1}^{20} {t_{i} + \mu \sum\limits_{j = 1}^{\eta } {\delta_{j} } } }},\;(1 \le k \le 20) \hfill \\ \frac{{\mu \delta_{k - 20} }}{{\sum\limits_{i = 1}^{20} {t_{i} + \mu \sum\limits_{j = 1}^{\eta } {\delta_{j} } } }},\;(20 + 1 \le k \le 20 + \eta ) \hfill \\ \end{gathered} \right. $$
(6)

where μ is the weight factor, which was set at 0.5 (Chou 2005; Chou and Cai 2005) and 0.05 (Chou 2001); \( t_{i} (i = 1,2, \ldots ,20) \) represents the normalized occurrence frequencies of the 20 amino acids in the sample protein P; and δ j is the j-tier sequence-correlation factor, computed according to Eq. (2). In this article, we chose μ = 0.05, η = 20 after careful consideration of easy handling; they can be assigned other values, of course, but the impact on the result would be small.

Algorithms for Classification

ML_KNN

In this article, we follow the notations used by Zhang and Zhou (2007). Define ℑ = Hd as the input vector space, \( {\mathbb{C}} = \{ 1,2,3, \ldots ,C\} \) as the set of C possible labels and \( {\mathbb{Z}} = \{ (q_{i} ,t_{i} ),1 \le i \le N\} \) as a train set in which \( q_{i} \in \Im ,t_{i} \subseteq {\mathbb{C}} \), using \( {\mathbb{Z}} \) to train the multilabel classifier. Usually, the learning model will output a real valued vector based on the function \( g:\;\Im \times {\mathbb{C}} \Rightarrow {\rm H} \). Considering q i and its corresponding label set t i , g(*,*) has the character of \( g(q_{i} ,c_{1} ) < g(q_{i} ,c_{2} ) \) when any \( c_{1} \notin t_{1} \;and\;c_{2} \in t_{2} \). Apparently, the result yields larger values for labels belonging to t i rather than those not belonging to t i . On the side, we use rank g (q i ,c) to represent the ranking function derived from g(q i ,c) which outputs the rank of c(\( {c \in {\mathbb{C}}} \)). Clearly, the larger value of g(q i ,c) corresponds with the higher rank of c. The multilabel classifier t(*) can also be computed by g(*,*) as \( t(q_{i} ) = \{ c|g(q_{i} ,c) > u(q_{i} ),c \in {\mathbb{C}}\} \), where u(*) is a threshold function usually set to 0 for easy handling.

The KNN used here is considered in the multilabel way (Zhang and Zhou 2007). Considering an instance q and its corresponding label set \( C^{\prime} \subseteq {\mathbb{C}} \), let \( \overrightarrow {{f_{q} }} \) be the full category vector for q, in which its jth component, \( \overrightarrow {{f_{q} (j)}} (j \in {\mathbb{C}}) \), takes the value of 0 if \( j \notin C^{\prime} \) and 1 otherwise. Moreover, we use L(q) to represent the set of K-nearest neighbors of q computed in the training set, so an element counting vector can be set as

$$ \overrightarrow {{N_{q} (j)}} = \sum\limits_{d \in L(q)} {\overrightarrow {{f_{d} (j)}} } ,\;\;\;\;j \in {\mathbb{C}} $$
(7)

where \( \overrightarrow {{N_{q} (j)}} \) computes the number of neighbors of q associated with the jth label.

As for each test vector p, its K-nearest neighbor, L(p), is computed first. Let G 0 j represent the fact that p has no label j and G 1 j otherwise. In addition, let \( F_{i}^{j} (i \in \{ 0,1,2,3, \cdots ,K\} ) \) express the fact that there are exactly i examples that have label j among the K-nearest neighbors of p. Thus, given the element counting vector \( \overrightarrow {{N_{p} }} \), the category vector \( \overrightarrow {{f_{p} (j)}} \) can be determined as follows:

$$ \overrightarrow {{f_{p} (j)}} = \mathop {\arg \hbox{max} }\limits_{{a \in \{ 0,1\} }} \;P\left[ {G_{j}^{a} |F_{{\overrightarrow {{N_{p} (j)}} }}^{j} } \right],\;j \in {\mathbb{C}} $$
(8)

According to the Bayesian rule, Eq. (8) can be represented by

$$ \overrightarrow {{f_{p} (j)}} = \mathop {\arg \hbox{max} }\limits_{{a \in \{ 0,1\} }} \;P(G_{j}^{a} )P(F_{{\overrightarrow {{N_{p} (j)}} }}^{j} |G_{j}^{a} ) $$
(9)

The prior probabilities, \( P(G_{j}^{a} )\,(j \in {\mathbb{C}},a \in \{ 0,1\} ) \), and the posterior probabilities, \( P(F_{i}^{j} |G_{j}^{a} )\,(i \in \{ 0,1, \ldots ,K\} ) \), are needed to determine the category vector; and these data can be taken directly from the training set.

Pseudocode and more details of KNN can be viewed in Zhang and Zhou (2007). The source code of ML_KNN can be downloaded at http://cse.seu.edu.cn/people/zhangml/Resources.htm#codes.

Evaluation measures

Given a multilabel test data set, \( \chi = \left\{ {(x_{i} ,X_{i} )\,1 \le i \le n} \right\} \), based on the definition in the previous section, the following popular multilabel evaluation metrics (Schapire and Singer 2000; Zhang 2006, 2009; Zhang et al. 2009; Zhang and Zhou 2007) are used:

  1. (1)

    Hamming Loss:

$$ {\text{Hamming\_loss }}\chi (t) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\frac{1}{C}|t(x_{i} )\Updelta X_{i} |} $$
(10)

\( \Updelta \) represents the symmetric difference between two data sets

  1. (2)

    One-Error:

$$ {\text{one\_error }}\chi (g) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left[ {\left[ {\mathop {\arg \hbox{max} }\limits_{{c \in {\mathbb{C}}}} g(x_{i} ,c)} \right] \notin X_{i} } \right]} $$
(11)
  1. (3)

    Coverage:

$$ {\text{coverage }}\chi (g) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\mathop {\hbox{max} }\limits_{{c \in X_{i} }} {\text{rank}}_{g} (x_{i} ,c) - 1} $$
(12)
  1. (4)

    Ranking Loss:

$$ \begin{gathered} {\text{ranking\_loss }}\chi (g) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\frac{1}{{|X_{i} ||\mathop {X_{i} }\limits^{\_\_\_} |}}\left| {RA(x_{i} )} \right|} ,\;{\text{where}} \hfill \\ RA(x_{i} ) = \left\{ {(t_{1} ,t_{2} )|g(x_{i} ,t_{1} ) \le g(x_{i} ,t_{2} ),\;(t_{1} ,t_{2} ) \in X_{i} \times \mathop {X_{i} }\limits^{\_\_\_} } \right\} \hfill \\ \end{gathered} $$
(13)
  1. (5)

    Average Precision:

$$ \begin{aligned} {\text{average\_prec }}\chi (g) = & \frac{1}{n}\sum\limits_{i = 1}^{n} {\frac{1}{{|X_{i} |}}\sum\limits_{{c \in X_{i} }} {AP(x_{i} )} } ,\;{\text{where}} \\ AP(x_{i} ) = & \frac{{\left| {\{ c'|{\text{rank}}_{g} (x_{i} ,c') \le {\text{rank}}_{g} (x_{i} ,c),\;c' \in X_{i} \} } \right|}}{{{\text{rank}}_{g} (x_{i} ,c)}} \\ \end{aligned} $$
(14)

In all, Hamming loss evaluates the times that an instance-label pair is misclassified; one-error evaluates the times that the top-ranked label is not in the set of proper labels of the instance; coverage evaluates the number of steps needed, on the average, to move down the label list in order to cover all the proper labels attached to an instance; ranking loss examines the average fraction of label pairs that are reversely ordered for the instance; average precision evaluates the average fraction of labels which are ranked above a particular label \( h \in X \) and really are in X. Note that, for the first four metrics, the smaller the better and, for the last one, the larger the better performance.

Results and Discussion

In statistical prediction, the following three cross-validation methods are often used to examine a predictor for its effectiveness in practical application: independent data set test, subsampling test and jackknife test. However, of the three test methods, the jackknife test is deemed the least arbitrary that can always yield a unique result for a given benchmark data set, as elaborated in Chou and Shen (2010a) and demonstrated by equations 28–30 in Chou (2011). Accordingly, the jackknife test has been widely recognized and increasingly used by investigators to examine the quality of various predictors (Chen and Li 2013; Esmaeili et al. 2010; Mohabatkar 2010; Sahu and Panda 2010; Sun et al. 2012; Zhao et al. 2012; Zia Ur and Khan 2012). However, to reduce the computational time, we adopted the fivefold cross-validation in this study as done by many investigators with SVM as the prediction engine.

Tables 2, 3, 4, 5 and 6 provide the test results based on different K numbers. For each K number, fivefold cross-validation is performed on the data set, and the performances (mean ± standard deviation) out of five independent runs are presented. As the tables show, for each evaluation measurement, ↓ represents the smaller the better and ↑ represents the larger the better. The K number of the multilabel-based KNN classifier is the most important parameter that may directly affect the predicted result. Thus, it is meaningful to see how prediction is influenced by the parameter K on the membrane data set used. The parameter K was increased from 1 to 20 with a step of 1. The overall values are estimated by the method of fivefold cross-validation. It is quite clear that the differences between results of each multilabel evaluation metric are negligible (Fig. 1). This fact indicates that no matter which K number is chosen, the prediction result is highly robust and dependable. Considering the fact that it is a new study focusing on this very topic, the performance is quite encouraging in comparison with the performance of similar methods applied in other biometric data sets (Zhang 2006, 2009).

Table 2 Performance of each compared algorithm (mean ± SD) on membrane protein data under K (1–4)
Full size table
Table 3 Performance of each compared algorithm (mean ± SD) on membrane protein data under K (5–8)
Full size table
Table 4 Performance of each compared algorithm (mean ± SD) on membrane protein data under K (9–12)
Full size table
Table 5 Performance of each compared algorithm (mean ± SD) on membrane protein data under K (13–16)
Full size table
Table 6 Performance of each compared algorithm (mean ± SD) on membrane protein data under K(17–20)
Full size table
Fig. 1
figure 1

Prediction results on the membrane data set using fivefold cross-validation under different K: (a) Hamming loss, (b) one-error, (c) coverage, (d) ranking loss, (e) average precision

Full size image

Conclusions

Prediction of membrane protein type is a meaningful and challenging task. Even though several models have been proposed, to the best of our knowledge, there is no algorithm to deal with proteins with multiple membrane types. However, those proteins are still important owing to the fact that they may represent some special biological significance worth our attention.

In this study, a new model for predicting membrane proteins with single or multiple types was proposed. The predictor is applicable in annotating membrane protein types. The prediction results are listed in Tables 2, 3, 4, 5 and 6, which are sufficiently good for initial research. We also presented the performances of the algorithm using different K numbers in order to investigate the impact of parameter K on the prediction performance. In the future, we will investigate other types of algorithm for the sake of improving the performance of the prediction.

Since user-friendly and publicly accessible web-servers represent the future direction for developing practically more useful models, simulated methods or predictors (Chou and Shen 2009), we shall make efforts in our future work to provide a web-server for the method presented in this article.