1 Introduction

In a wide range of natural phenomena and industrial applications, fluid flows are driven by means of buoyancy effects resulted from density gradients, which are produced sometimes by combined temperature and concentration variations. This phenomenon of the combined heat and mass transfer is usually called double-diffusive flow. Due to the applied and academic interest in this field, there has been a wide range of mostly theoretical studies for more than a decade Mojtabi and Charrier-Mojtabi [1]. Recently, the in progress state of art of the combined heat and mass transfer in porous media has been summarised by Nield and Bejan [2].

The combined heat and mass transfer in a porous enclosure was studied numerically and analytically by Trevisan and Bejan [3] using Darcy formulation. Extensive efforts were implemented to examine the non-Darcian influences on the thermosolutal free convection in porous cavities such as employing Darcy–Brinkman’s model to study the viscous effects of the boundaries Goyeau et al. [4], also using the generalised porous media model which allows to examine the influence of porosity variation in non-Darcy regime Nithiarasu et al. [5], and finally comparing the effects of Darcy, viscous, inertial, and combined viscous-inertial drag on double-diffusive flow Karimi-Fard et al. [6]. Recently, the effect of tilting the porous cavities on the combined natural heat and mass transfer through them was investigated numerically by Al-Farhany and Turan [7]. The results revealed that increasing the inclination angle affects the vortex strength negatively.

Regarding to the combined heat and mass transfer in porous media subjected to rotation, studying such field has been motivated by its wide range of practical applications in engineering and geophysics. Chemical and food processing industries, centrifugal casting and solidification of metals, geophysical problems, petroleum industries, biomechanics applications, in addition to rotating machinery are just few examples of its engineering applications Vadasz [8]. Three-dimensional fluid flow in a rotating square channel occupied by a heterogeneous porous medium was studied analytically Vadasz [9] and numerically Havstad and Vadasz [10] using Darcy formulation. The data has confirmed the ability of inducing a mainstream flow along the channel by means of the secondary circulation resulted from the locally varying permeability. Vadasz [11, 12] examined analytically the Coriolis effects on natural convection induced by gravity in a long rotating porous box but with applying different thermal boundary conditions. The results revealed that there was a secondary circulation in the plane perpendicular to the leading natural convection plane and it was motivated by the Coriolis forces. The natural convection induced by centrifugal acceleration in a narrow porous layer subjected to rotation was examined analytically by Vadasz [13–15] for an axis of rotation attached to the porous layer, distant from the porous layer, and located within the porous layer, respectively. The results indicated that displacing the porous layer away from the axis of rotation has a destabilizing effect, while placing the rotation axis within the porous layer has produced a stabilising influence in the part of the layer located to the left of the axis of rotation and a destabilising effect to the right part of it. The combined centrifugally and gravity driven free convection in a narrow porous layer located far away from the axis of rotation studied analytically by Vadasz and Govender [16] using Darcy law, where it was found that increasing the value of gravity Rayleigh number had a stabilising influence on the flow field. In his analytical investigation for Coriolis influence on gravitational induced convection, Vadasz [17] found that heat transfer is retarded by rotation for both overstable and stationary convection. However, it was noticed that heat transfer at overstable convection is enhanced by rotation just within a limited range of small parameters including Prandtl number. Motivated by the work of Vadasz [17], Straughan [18] examined analytically the thermal instability in a Darcian porous medium rotating around an axis perpendicular to the porous layer, where results of nonlinear energy was derived for thermal convection. An analytical investigation was presented by Malashetty et al. [19] for the thermal convection in a rotating horizontal porous layer cooled from above and heated from below using Darcy formulation and the thermal local non-equilibrium model. They found that the rotation has a retarding influence on heat transfer rates. More recently, Bhadauria et al. [20] investigated analytically the rotation effect on the combined heat and mass transfer in a saturated porous layer subjected to vertical temperature and concentration differences. It was found that increasing the rotation strength has a negative influence on the onset of convection in addition to its role in reducing both the heat and mass transfer rate.

The aim of the current paper is to present a comprehensive numerical study for the fluid flow induced by means of the combined natural heat and mass transfer in the fully developed flow region of a rotating square channel occupied by a saturated porous medium. The Coriolis effects are presented in terms of stream-functions, isotherms, and iso-concentration patterns in addition to the average values of Nusselt and Sherwood numbers.

2 Mathematical formulation

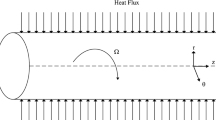
A long rotating channel of a square cross section and occupied by isotropic, homogeneous, and saturated porous medium, as shown in Fig. 1 is assumed to carry an incompressible fluid flow within it. The channel is assumed to be rotating around the vertical axis, while the flow is considered steady and fully developed; hence all the dependent variables remain constant along the axial direction except the pressure, which has a constant gradient. All lateral walls are considered impermeable with keeping the horizontal walls insulated for both temperature and concentration, while the left and right vertical walls are maintained at a uniform temperature and concentration (T h & c h ) and (T c & c c ), respectively.

Fig. 1
figure 1

The geometrical shape of the studied problem

Full size image

To avoid overestimation in heat or mass transfer due to using Darcy model compared to models include Forchheimer and Brinkman extensions as noticed by Beckermann et al. [21] and Karimi-Fard et al. [6], the generalised model is employed to simulate the momentum equations, which is capable of detecting the porosity influence on flow characteristics, Nithiarasu et al. [5]. Both the solid and fluid phases are assumed to be in local thermal equilibrium with each other. The flow is assumed to be driven by a combined buoyancy effect, resulted from both temperature and concentration gradients with neglecting the buoyancy forces resulted from the transverse and longitudinal centrifugal acceleration. The Soret and Dufour effects have been neglected with assuming all the fluid properties to be constant everywhere of the flow field except the fluid density in the buoyancy term, which is considered changeful according to the Boussinesq approximation as:

$$\rho_{f} = \rho_{0} \left[ {1 - \beta_{T} (T - T_{0} ) - \beta_{c} (c - c_{0} )} \right]$$
(1)

where β T  = −(1/ρ 0)(∂ρ/∂T) p,c is the coefficient of thermal expansion, while β c  = −(1/ρ 0)(∂ρ/∂c) p,T represents the coefficient of concentration expansion. Thus, the dimensional forms of the conservation equations of mass, momentum, energy, and species are:

$${\nabla } \cdot v = 0$$
(2)
$$\frac{{\rho_{f} }}{{\varepsilon^{2} }}({\mathbf{v}} \cdot \nabla ){\mathbf{v}} = - \nabla p_{r} + \frac{{\mu_{f} }}{\varepsilon }\nabla^{2} {\mathbf{v}} - \frac{{\mu_{f} }}{K}{\mathbf{v}} - \rho_{f} \frac{{c_{F} }}{\sqrt K }\left| {\mathbf{v}} \right|{\mathbf{v}} + \left( {\rho_{f} - \rho_{0} } \right)g\nabla (e_{g} \cdot {\mathbf{x}}) - \frac{{2\rho_{f} \omega }}{\varepsilon }e_{\omega } \times {\mathbf{v}}$$
(3)
$$({\mathbf{v}} \cdot \nabla )T = \alpha_{e} \nabla^{2} T$$
(4)
$$({\mathbf{v}} \cdot \nabla )c = D_{m} \nabla^{2} c$$
(5)

where c F represents the form-drag coefficient and it is incorporated through using Ergun’s correlation c F  = 1.75/(150 ε 3)1/2, p r  = p − ρ 0 g(e g ·x) − ρ 0 ω 2(e ω  × x)·(e ω  × x)/2 is the reduced pressure generalised to include the constant components of the gravity in addition to the centrifugal terms. This assumption and its derivation is detailed in Vadasz and Govender [22]. Also, α e refers to the effective thermal diffusivity of the porous medium in terms of mean thermal conductivity k m divided by the specific heat capacity of the fluid (ρcp) f . The mean thermal conductivity accounts for the overall thermal conductivity of both the fluid and solid phases k m  = εk f  + (1 − ε)k s . So, the effective thermal diffusivity can be computed as:

$$\alpha_{e} = \frac{{\varepsilon \,k_{f} + (1 - \varepsilon )\,k_{s} }}{{(\rho \,cp)_{f} }} = \varepsilon \,\alpha_{f} + (1 - \varepsilon )\frac{{\,k_{s} }}{{(\rho \,cp)_{f} }}$$
(6)

Moreover, D m  = εD represents the effective mass diffusivity of the substance within the porous medium. Above governing equations can be written in their detailed dimensionless forms as:continuity equation:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(7)

X-momentum equation:

$$\frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}} \right) = - \frac{{\partial P_{r} }}{\partial X} + \frac{1}{\varepsilon }\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) - \frac{U}{Da} - \frac{1.75}{{\sqrt {150\,\varepsilon^{3} } }}\frac{{\left| {\mathbf{V}} \right|\,U}}{{\sqrt {Da} }}\, - \frac{1}{\varepsilon \,Ek}W$$
(8)

Y-momentum equation:

$$\frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}} \right) = - \frac{{\partial P_{r} }}{\partial Y} + \frac{1}{\varepsilon }\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) - \frac{V}{Da} - \frac{1.75}{{\sqrt {150\,\varepsilon^{3} } }}\frac{{\left| {\mathbf{V}} \right|\,V}}{{\sqrt {Da} }}\, + \,\frac{Ra}{\Pr }\,(\theta + N\,C)$$
(9)

Z-momentum equation:

$$\frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial W}{\partial X} + V\frac{\partial W}{\partial Y}} \right) = 1 + \frac{1}{\varepsilon }\left( {\frac{{\partial^{2} W}}{{\partial X^{2} }} + \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right) - \frac{W}{Da} - \frac{1.75}{{\sqrt {150\,\varepsilon^{3} } }}\frac{{\left| {\mathbf{V}} \right|\,W}}{{\sqrt {Da} }}\, + \frac{1}{\varepsilon \,Ek}U$$
(10)

energy equation:

$$U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{1}{\Pr }\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(11)

concentration equation:

$$U\frac{\partial C}{\partial X} + V\frac{\partial C}{\partial Y} = \frac{1}{Sc}\left( {\frac{{\partial^{2} C}}{{\partial X^{2} }} + \frac{{\partial^{2} C}}{{\partial Y^{2} }}} \right)$$
(12)

The non-dimensional parameters employed in Eqs. (7)–(12) are:

$$\left. \begin{aligned} & X = \frac{x}{a},\quad Y = \frac{y}{a},\quad Z = \frac{z}{a}, \\ & U = \frac{a}{{\nu_{f} }}u,\quad V = \frac{a}{{\nu_{f} }}v,\quad W = \frac{a}{{\nu_{f} }}w, \\ & P_{r} = \frac{{a^{2} }}{{\rho_{f} \nu_{f}^{2} }}p_{r} ,\quad \theta = \frac{{T - T_{c} }}{{T_{h} - T_{c} }},\quad C = \frac{{c - c_{c} }}{{c_{h} - c_{c} }},\quad \\ & Ra = \frac{{g\beta_{T} \Delta Ta^{3} }}{{\nu_{f} \alpha_{e} }},\quad \Pr = \frac{{\nu_{f} }}{{\alpha_{e} }},\quad Sc = \frac{{\nu_{f} }}{{D_{m} }}, \\ & N = \frac{{\beta_{c} \Delta c}}{{\beta_{T} \Delta T}},\quad Da = \frac{K}{{a^{2} }},\quad Ek = \frac{{\nu_{f\,} }}{{2\omega a^{2} }} \\ \end{aligned} \right\}$$
(13)

The rates of heat and mass transfer at the walls are computed by means of the average values of Nusselt and Sherwood numbers, respectively, as:

$$Nu = \frac{1}{a}\int\limits_{0}^{a} { - \frac{\partial \theta }{\partial Y}dy}$$
(14)
$$Sh = \frac{1}{a}\int\limits_{0}^{a} { - \frac{\partial C}{\partial Y}dy}$$
(15)

Eventually, the dimensionless forms of the boundary conditions employed to solve the aforementioned equations are:

$$\left. {\begin{array}{*{20}l} {U = V = W = 0,\quad \theta = C = 1} \hfill & {at\;X = 0;} \hfill \\ {U = V = W = 0,\quad \theta = C = 0} \hfill & {at\;X = 1;} \hfill \\ {U = V = W = 0,\quad \frac{\partial \theta }{\partial Y} = \frac{\partial C}{\partial Y} = 0} \hfill & {at\;Y = 0\& 1} \hfill \\ \end{array} } \right\}$$
(16)

3 Solution procedure

Equations (7)–(12) have been discretised and transformed into linear algebraic forms by using the finite volumes method. The hybrid differencing approximation of Spalding [23] has been employed to represent the convection terms which appear in the discretised forms of the governing equations. By implementing this scheme, either second-order accuracy solution at low Peclet numbers or highly stable solution at its high values have been ensured. The problem of pressure–velocity coupling has been solved according to the PISO algorithm of Issa [24]. For solving the resulted discretised algebraic equations, tri-diagonal matrix algorithm (TDMA) has been used. In order to predict the probably steep gradients of velocity, temperature and concentration at the channel walls more precisely, the mesh has been refined near the walls boundaries symmetrically about both X = 0.5 and Y = 0.5 by implementing the form of Havstad and Vadasz [10]. Convergence has been measured in terms of the maximum change allowed in each variable during any iteration, where the maximum change allowed for convergence check is 10−6. An in-house FORTRAN code was developed for solving the current problem and validated with some of the previous investigations related to the present study. Figure 2 represents the comparison of average Nusselt or Sherwood number computed by the current code with the work of Karimi-Fard et al. [6] for the double-diffusive flow by using various porous media models. Figure 3 shows the comparison with the work of Nithiarasu et al. [5] for the variation of mean Sherwood with the buoyancy ratio by using the generalized model of fluid flow via porous media. The computed results by the current code have been in a good agreement with the earlier studies, although there were small variances due to the difference in the numerical techniques used in the current code and the previous investigations.

Fig. 2
figure 2

The variation of average Nusselt or Sherwood number with Darcy number for various porous media models at Pr = 1.0, Ra = 105, N = 1.0, and Sc = 1.0

Full size image
Fig. 3
figure 3

The variation of average Sherwood number with the buoyancy ratio N at ε = 0.6, Pr = 1.0, Ra × Da = 200, and Le = 1.0

Full size image

4 Results

In the current section, the resulted data are presented in terms of the streamlines, isotherms or iso-concentrations, and the contours of the main velocity component within the secondary plane in addition to the average values of Nusselt or Sherwood number and for a wide range of non-dimensional parameters used. These dimensionless parameters are the Darcy–Rayleigh number (100 ≤ Ra* ≤ 10,000), Darcy number (10−6 ≤ Da ≤ 10−4), the buoyancy ratio (−10 ≤ N ≤ 8), and Ekman number (10−7 ≤ Ek ≤ 10−3), while the values Prandtl and Schmidt numbers are maintained constant and equal to 1.0, hence, both the thermal and solutal fields were assumed to be identical.

Firstly, the rotation effects on the flow and heat or mass transfer patterns are shown in Fig. 4a–f for Ra* = 1,000, Da = 10−5, and N = 1.0 for various values of Ekman number. In general, the strength of the secondary circulation decreases with reducing Ekman number, or in other words by increasing the rotation rate, hence, the heat and mass transfer strength is affected and reduced with increasing the rotation level. This outcome is due to the increasing mainstream velocity with enhancing the rotation rate and for a specific range of Ekman number as shown in Fig. 4a–c, which will cause an obvious increase in the U-velocity components by means of Coriolis effect in the X-direction, and hence it will affect the entire secondary flow and heat and mass transfer. However, with enhancing the rotation rate further; its impact on the main velocity component is reversed, where the mainstream velocity tends to decrease considerably with reducing Ekman number as it is clear from Fig. 4d–f. This reversal in trend is a consequence of the vanishing of the secondary flow at extreme rotation levels, and accordingly, the induced mainstream velocity will be reduced significantly.

Fig. 4
figure 4

The effect of rotation strength on streamlines (left), W-velocity (middle), and isotherms or concentration (right) at ε = 0.6, Da = 10−5, Pr = 1.0, Sc = 1.0, Ra = 108, N = 1.0, and for Ekman number values (from top to bottom) of a Ek = 10−4, b Ek = 10−5, c Ek = 3 × 10−6, d Ek = 2 × 10−6, e Ek = 10−6, and f Ek = 7 × 10−7

Full size image

The mutual influence of medium permeability and the rotation rate is shown in Fig. 5 for different values of both Darcy and Ekman numbers at N = 1.0. In accordance to expectations, lessening Darcy number or Ekman number or both of them reduces the rates of heat and mass transfer. However, it is also observed that at high values of permeability or Darcy number, the effects of rotation on the rates heat and mass transfer are promoted considerably with decreasing Ekman number, while they are hardly detected at the lower levels of Darcy number. This result is due to the fact that reducing Darcy number or the medium permeability means increasing the resistance of the solid matrix to the fluid flow through it, and hence decreasing the strength of the mainstream flow which leads to reducing the negative impact of Coriolis effect on the secondary flow and heat and mass transfer within the transverse plane.

Fig. 5
figure 5

The effect of varying Darcy number with changing the Ekman number on the values of average Nusselt or Sherwood number at ε = 0.6, Ra = 108, Pr = 1.0, Sc = 1.0, and N = 1.0

Full size image

Figure 6 shows the combined effect of the buoyancy ratio and Ekman number on the average values of Nusselt and Sherwood numbers at Ra* = 1,000 and Da = 10−4. The effect of amplifying the buoyancy effects on the rates of heat and mass transfer is quite obvious. At low rotation levels and with increasing the absolute value of the buoyancy ratio within the range of (−2 ≥ N ≥ 0), the values of both Nusselt and Sherwood numbers are enhanced considerably, while with increasing the rotation levels, its influence vanishes gradually until the transport phenomenon of both heat and mass tend to occur approximately by pure conduction at the extreme levels of rotation as it was noted before in Fig. 4f of the isotherms and iso-concentrations patterns.

Fig. 6
figure 6

The effect of buoyancy ratio variation with changing Ekman number on the values of average Nusselt or Sherwood at ε = 0.6, Da = 10−4, Ra* = 1,000, Pr = 1.0, Sc = 1.0

Full size image

Eventually, the computed values of Nusselt or Sherwood number were fitted to the power law proposed earlier by Trevisan and Bejan [3] and reconfirmed later by Goyeau et al. [4] after modifying it to include the rotation effect as follow:

$$Nu,\;Sh = 1 + C_{1} \;Ek^{{C_{2} }} \;\left( {Ra*\left| {N + 1} \right|} \right)^{{C_{3} }}$$
(17)

It is clear that Lewis number has been dropped from the above correlation because it is equal to 1.0 due to our earlier assumption that both the thermal and solutal boundary layers are identical and both Prandtl and Schmidt numbers are equal to 1.0; hence, above correlation is valid for both Nusselt and Sherwood numbers. Also, this correlation can be used for any value of buoyancy ratio even N = −1. Hundreds of simulations were run to cover the entire range of the independent variables, which were Darcy number, Darcy–Rayleigh number, Ekman number, and the buoyancy ratio. A statistical program (SPSS version 16.0) was used to arrive at the coefficients of this correlation equation. The computed data was divided into sub ranges in order to get the best fitting for them, where the data was divided firstly according to the level of Darcy number, and then according to the rotation level. The determined coefficients of above correlation and the proportion of variance R 2 are listed in Table 1 according to range of the used data, where they are valid for 100 ≤ Ra* ≤ 10,000 and −10 ≤ N ≤ 8.

Table 1 The correlation coefficients and the proportion of variance R 2
Full size table

It is quite obvious that the effect of Darcy number on the exponent C 3 is similar to what was suggested earlier by Goyeau et al. [4], where its value at low Darcy numbers was expected to be close to 0.5, and then it decreases with increasing Darcy number. Also, it is noticeable that Coriolis effect on the heat and mass transfer rates is not significant at the moderate levels of rotation, but it becomes more dominant when the rotation rates increase as it is clear from the values of the exponent C 2. The correlated data was plotted with the computed data in order to examine the deviation between them for different values of Ra*|N + 1| and Ek as it is shown in Figs. 7, 8 and 9 for Darcy number of 10−4, 10−5, and 10−6, respectively. It is clear that the correlated data are in a good agreement with the computed at the moderate levels of rotation, but it deviates quite obviously at the extreme rates of rotation and especially at the lower values of Ra*|N + 1|. Also, it is noticeable that the correlated values of Nusselt number have the best agreement with the calculated data at the lowest Darcy number Da = 10−6. However, it cannot be said that reducing Darcy number value increases the matching of the correlated values with the computed data because it is clear that the agreement for Da = 10−4 is better than it for Da = 10−5. This fact can indicate the difficulty of finding a single and universally valid correlation that covers the entire domain of computed data vis-a-vis the Darcy number and meanwhile has a predictable trend of the agreement between the correlated data and computed values.

Fig. 7
figure 7

The computed and correlated values of average Nusselt or Sherwood number versus Ra*|N + 1| at Da = 10−4 for different values of Ekman number

Full size image
Fig. 8
figure 8

The computed and correlated values of average Nusselt or Sherwood number versus Ra*|N + 1| at Da = 10−5 for different values of Ekman number

Full size image
Fig. 9
figure 9

The computed and correlated values of average Nusselt or Sherwood number versus Ra*|N + 1| at Da = 10−6 for different values of Ekman number

Full size image

5 Conclusions

Numerical study for the double-diffusive flow in a long rotating porous channel has been presented. The temperature and concentration at the vertical walls are maintained constant at high and low values, while both horizontal walls are kept insulated. The generalised model has been used to simulate the momentum equations with employing the Boussinesq approximation for the density variation. Moreover, both the fluid and solid phases are assumed to be at a local thermal equilibrium. Computations are carried out for a wide range of dimensionless parameters like Darcy–Rayleigh number (100 ≤ Ra* ≤ 10,000), Darcy number (10−6 ≤ Da ≤ 10−4), the buoyancy ratio (−10 ≤ N ≤ 8), and Ekman number (10−7 ≤ Ek ≤ 10−3), with keeping the values of the medium porosity, Prandtl and Schmidt numbers constant at ε = 0.6, Pr = 1.0, and Sc = 1.0, respectively. The results reveal that the rotation has a negative impact on the secondary circulation, and hence, the heat and mass transport is reduced considerably with increasing the rotation strength. In addition, the mainstream velocity increases significantly with decreasing Ekman number at the lower and moderate levels of rotation, while it starts to decrease noticeably at the extreme rates of rotation as a result of the vanishing of the secondary flow. Furthermore, the rotation seems to have a dominant role at high levels of porous medium permeability, where it reduces the strength of the secondary flow, and hence the rates of heat and mass transfer. However, this role is reduced gradually with decreasing the medium permeability, but does not completely vanish. Eventually, the computed values of Nusselt or Sherwood number were fitted to a power law of Ekman number, Darcy–Rayleigh number, and buoyancy ratio, where the correlated data is found to be in a good agreement with the computed values at the moderate levels of rotation, but it deviates quite obviously at the extreme rates of rotation and especially at the lower values of Ra*|N + 1|.