1 Introduction

Fluid flow over and through the porous media has encountered great importance in the diverse fields of science and engineering. The porous media (such as rocks, paper, sponge, wood, beach sand, human lung, bones, etc.) is described as a composition of solid material with interconnected voids (pores) through which the fluid can flow [36]. Porous materials are adapted for various industrial, biomedical/bioengineering applications such as food processing, storage of grains, spread of underground pollutants, filtration and sedimentation, geological and geothermal systems, groundwater/oil flow, drug delivery systems, transport of biological and brain tissues, medical imaging, drug delivery, and many more [24, 27, 32, 38, 43, 48, 50, 53]. The broad range of porous media applications always fascinates the researchers to explore the underlying physics. Specifically, the use of porous cylinders/obstacles/blocks of various cross-sections (circular, square, rectangular, triangular, etc.) in heat exchangers [11], heat pipes [39], and solar collectors [5] is getting popularity for improving their performance and new applications. In addition to this, semi-circular porous obstacles play an important role in biomechanics applications as these kinds of obstacles appear in blood flow through stenosed arteries where stenoses or cholesterol clogs behave like semi-circular porous obstacles [6, 20,21,22]. These stenoses create hindrance to the blood flow from the heart to the other parts of the body and it may lead to various cardiovascular diseases such as heart attacks and strokes etc. Additionally, the semi-circular porous cylinders are being used in the cooling applications of electronic devices, CPUs, and server rooms, etc. Nowadays, some novel designs of heat exchangers are also using semi-circular porous obstacles specifically for low Reynolds number applications. Internal fouling of the large pipelines due to the vegetation may be considered as semi-circular porous obstacles. Therefore, by keeping in mind the vast and preceding applications of porous cylinders (semi-circular), we aimed to investigate the fluid flow past a semi-circular permeable cylinder attached to the bottom channel wall. Before discussing our problem at length, we have reviewed the relevant available literature to the best of our knowledge.

The fluid flow within porous media is initially approximated by Darcy’s law [36] which reveals the linear dependency between the flow rate and pressure gradient. Further developments in the flow through porous media lead to the formation of Forchheimer [1, 41] and Brinkman equations [17, 33]. The Forchheimer equation is applicable to high flow velocity inside porous media whereas the Brinkman equation considers the boundary effects because these effects are not acknowledged in Darcy’s law. Many researchers have been studied the transport mechanism of fluid flow inside or outside the porous media [3, 40, 46]. Besides this, a group of studies are also dedicated to explore the flow characteristics over porous cylindrical obstacles of various cross-sections including circular [8, 14, 45, 55, 56] and non-circular sections [13, 23, 26, 42, 51, 54]. Further, these studied can be partitioned into the unconfined [8, 13, 14, 51, 54,55,56] and confined [23, 26, 42, 45] flow domain. In this context, the flow through a porous cylinder (circular) has been examined by Bhattacharyya et. al. [8]. They observed that the drag coefficient reduces with the enhancement in Re and it rises with the decrease in Da. In another study, Yu et. al. investigated the wake structure at the rear part of the porous cylinder (circular) [55] and porous sphere [56]. They concluded that the recirculation size decays with the rise in Da and the recirculating wakes initially appear within the porous media for some values of Da. Recently, Ebrahimi et. al. [14] explored the fluid flow characteristics of an oscillating permeable circular cylinder and found that the oscillating cylinder leads to the increment in drag coefficient in comparison to the stationary cylinder. The aforementioned studies are concerned about the unconfined flow domain. Although in most of the realistic applications e.g. chemical filters, heat exchangers, and solar collectors, the fluid flow is highly influenced by the channel wall. Within this framework, Shahsavari et. al. [45] examined the impact of confinement ratio on the flow characteristics for the case of the circular porous cylinder and concluded that the drag force is increased by enlarging the confinement of the channel.

Apart from the permeable circular cylinders, several numerical studies have been performed for the flow field around the non-circular porous cylinders (square, rectangular, triangular, etc.) [13, 23, 26, 42, 51, 54] in an unconfined/confined flow domain. In this direction, the behavior of the recirculating zones at the rear part of the porous cylinder (square) was investigated by Yu et. al. [54] for \(10^{-6}\le Da \le 10^{-1}\) and \(1\le Re \le 50.\) They observed that at low Darcy number \((Da=10^{-6}),\) wake behavior seems like a solid cylinder but at high value of Darcy number \((Da=10^{-1}),\) all the recirculating wakes disappear. Then, a pair of detached wakes has been noticed for \(Da=7\times 10^{-3}\) and \(Re=21.\) The length of the detached wakes increases as Re increases from 21 to 30 and after that, it continuously decreases and finally disappears at \(Re=42.\) In the continuation, Dhinakaran et. al. [13] examined the flow attributes past a square permeable cylinder and identified that the wake length and drag coefficient are enhanced by diminishing Darcy number. Valipour et. al. [51] altered the orientation of the square permeable cylinder and showed the decrement in the pressure coefficient with the increment in Darcy number. The flow field over multiple rectangular porous blocks attached to the channel wall has been explored by Huang et. al. [26] and they observed that the recirculation zones are contracted as Da rises with a significant increase in pressure drop. In another study, Rong et. al. [42] inspected the flow characteristics across a porous enveloped square obstacle located in a channel and observed the complex influence of governing parameters. Their results suggested that for \(Da>10^{-4},\) drag coefficient has decreased with the increment in Da but it has increased with the increment in \(\epsilon\).

In addition to the above-mentioned literature, various studies have been performed related to the fluid flow from an impermeable semi-circular cylinder confined in a channel [18,19,20,21,22, 29]. Kiya and Arie [29] studied the viscous flow over the semi-circular and semi-elliptical obstacles attached to a plane wall for \(0.1\le Re \le 100.\) They observed the vortices both at the front and rear part of the obstacle and investigated the influence of Re on drag and pressure coefficient. In a partially blocked channel (by cylinders or obstacles), the blockage ratio is an important parameter which is the ratio of channel width blocked by the obstacle. In this direction, Griffith et. al. [19] investigated the wake behavior and stability of the flow in a two-dimensional channel partially blocked by a semi-circular obstacle by varying the values of Reynolds number \((25 \le Re \le 300)\) and blockage ratio. The blockage ratio has been varied from 0.05 to 0.9 by adjusting the radius of the obstacle. Further, Griffith et. al. extended their work by exploring the axisymmetric steady [20] and pulsatile [21] fluid flow through a circular tube constricted by semi-circular bumps as an idealization of stenosed arteries. In addition to semi-circular obstacles, Griffith et. al. [22] numerically investigated the flow through an axisymmetric sinuous stenoses for \(1\le Re\le 400.\) There are numerous studies [30, 31, 47, 52] which examine the fluid flow from a semi-circular solid cylinder placed in between the channel.

An inspection of the aforementioned resources suggests that the shape of the permeable cylinder clearly influences the flow attributes. Additionally, most of the above-mentioned numerical studies are related to the fluid flow over circular and rectangular porous cylinders followed by the other shapes. Surprisingly, the fluid flow across the confined semi-circular porous cylinder is missing from the literature. Therefore, the current study is focused on the fluid flow through a semi-circular permeable cylinder attached to the bottom channel wall. The porosity \((\epsilon )\) and permeability \((\kappa )\) are the main characteristics of the porous medium where the former represents the void space in the porous media and the latter defines the interconnectedness of the voids. The Darcy number is defined as the dimensionless permeability to represent the governing flow through the porous cylinder and the Reynolds number is the governing parameter for the flow outside the porous cylinder. These parameters have been non-dimensionalized by using the diameter of the semi-circular obstacle (D) and the free stream velocity \((U_\infty )\). In addition to the above parameters, blockage ratio \((\beta )\) is also used in the current study as the ratio of diameter (D) of the semi-circular cylinder to the channel height (H). Usually, the researchers define the blockage ratio as the ratio of the height of the obstacle to the channel height. But, in our case, we have used the diameter of the porous cylinder as a length scale and therefore the value of \(\beta\) is sometimes larger than unity. The present study intends to find the non-trivial effects of fluid flow across semi-circular porous cylinder by varying Reynolds number \((0.01\le Re \le 40)\), Darcy number \((10^{-6}\le Da \le 10^{-1}),\) blockage ratio of channel \((0.1667 \le \beta \le 1.5)\) and porosity \((0.1\le \epsilon \le 0.9)\). The range of the Reynolds number in the present study is chosen by considering the applications related to the flow in oil reservoirs and aquifers, water seepage in walls and river banks, and marine related applications to study the sinking porous aggregates [2, 25, 28]. There are numerous implementations of the considered range of the Darcy number \((10^{-6}\le Da \le 10^{-1})\) such as blood clots, wire cramps, copper powder (hot compacted), cigarette, hair left , highly fractured rocks, oil reservoir rocks, beach sand, and cloth etc. [9, 36, 57,58,59] . The streamlines contours and vorticity contours are determined for the governing parameters. Also, the prominent output parameters as pressure coefficient and drag coefficient are computed.

Fig. 1
figure 1

(a) Schematic representation of the confined fluid flow across a porous semi-circular cylinder (b) Grid structure

Full size image

2 Problem description and mathematical modeling

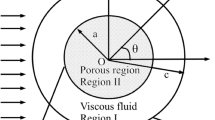
The two-dimensional flow of Newtonian and incompressible fluid over a confined porous semi-circular cylinder is investigated. The fluid enters into the channel with a uniform inlet velocity \((U_\infty ),\) as indicated in Fig. 1(a). The semi-circular porous cylinder (of diameter D) has been affixed to the base wall of the rectangular channel of height H, at the distance \(L_{in}\) from the inlet and \(L_{out}\) from the outlet. The following assumptions have been employed for the simplification of the considered problem:

  • The fluid flow is steady and laminar.

  • The physicochemical fluid properties (density and viscosity) are constant.

  • The porous media is homogeneous and isotropic.

  • The porous configuration having uniform permeability \((\kappa )\) and porosity \((\epsilon )\).

  • The viscosity of fluid inside porous cylinder \((\mu _e)\) and flow viscosity outside the porous cylinder \((\mu _f)\) are equal.

The uniform inlet velocity \((U_\infty )\) and the cylinder diameter (D) have been used as the velocity and length scales for the non-dimensionlization of velocity and distances, respectively. \(\rho\) denotes the density of the fluid. The scaling variable \(\rho U^2_\infty\) has been taken for the non-dimensionalization of pressure (p) and P denotes the dimensionless pressure. The porosity \((\epsilon )\) of the cylinder is determined as the volume fraction of void space in the porous cylinder [4] and defined as

$$\begin{aligned} \epsilon = {\left\{ \begin{array}{ll} 0<\epsilon <1, \quad \text {inside the porous cylinder,}\\ 1, \quad \text {outside the porous cylinder} \\ \end{array}\right. } \end{aligned}$$

\(\mathbf{U} =(U,V)\) is the dimensionless velocity vector where U and V are the velocity components in the X and Y direction, respectively. A single domain-approach [7] has been implemented to govern the flow field in the channel, i.e., a single set of Eqs. (1)–(3) is used to supervise the flow both inside and outside the porous cylinder. Therefore, U denotes the fluid velocity outside the porous cylinder and the Darcy velocity (superficial velocity) inside the cylinder [36]. The dimensionless parameters used in the present study are the blockage ratio \((\beta )\), Reynolds number (Re),  and the Darcy number (Da). The blockage ratio of the channel is defined as \(\beta =\frac{D}{H}\) and varied from \(0.1667 (8.34\%)\) to \(1.5 (75\%)\) by adjusting the height of the channel. The Reynolds number (Re) in the current study is determined as

$$\begin{aligned} Re(\text {Reynolds number})= & {} \frac{\rho U_\infty D}{\mu _f} \end{aligned}$$

where \(\mu _f\) is the dynamic viscosity of the fluid. The diameter (D) of the cylinder has been used as the length scale for the Reynolds number. The Darcy number (Da) is the dimensionless permeability \((\kappa )\) of the porous cylinder and it is non-dimensionalized by D,  and defined as

$$\begin{aligned} Da(\text {Darcy number})= & {} \frac{\kappa }{D^2}. \end{aligned}$$

In the fluid region (outside porous cylinder), Da \(\rightarrow\) \(\infty\).

The fluid flow in the channel is supervised by Darcy-Brinkman-Forchheimer model [12] to incorporate the inertial and viscous effects in porous media. The governing dimensionless equations are provided as follows:

Continuity equation

$$\begin{aligned} \frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0 \end{aligned}$$
(1)

Momentum equations

$$\begin{aligned} \begin{aligned} \frac{1}{\epsilon ^2}\bigg (U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}\bigg )=- \frac{\partial P}{\partial X}+ \frac{\mu _e}{\epsilon \mu _f Re}\bigg ( \frac{\partial ^2 U}{\partial X^2}+\frac{\partial ^2 U}{\partial Y^2}\bigg )-\frac{1}{Re Da} U - \frac{F}{\sqrt{Da}} |\overrightarrow{U}| U\\ \end{aligned} \end{aligned}$$
(2)
$$\begin{aligned} \begin{aligned} \frac{1}{\epsilon ^2}\bigg (U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}\bigg )=- \frac{\partial P}{\partial Y}+\frac{\mu _e}{\epsilon \mu _f Re}\bigg ( \frac{\partial ^2 V}{\partial X^2}+\frac{\partial ^2 V}{\partial Y^2}\bigg )-\frac{1}{Re Da} V - \frac{F}{\sqrt{Da}} |\overrightarrow{U}| V \end{aligned} \end{aligned}$$
(3)

where, \(|\overrightarrow{U}|=\sqrt{U^2+V^2}\) and \(F=\frac{1.75}{\sqrt{150}} \frac{1}{\epsilon ^{3/2}}\) is the Forchheimer inertial coefficient [15, 49]. The fluid viscosity inside \((\mu _e)\) and outside \((\mu _f)\) of the porous cylinder are assumed to be equal. Finally, for the completion of our problem, the subsequent dimensionless boundary conditions have been undertaken:

  • At the inlet: the uniform velocity inlet profile is applied as \(U=1\) and \(V=0.\)

  • On the top and bottom wall: no slip boundary condition is implemented as \(U=0\) and \(V=0.\)

  • At the outlet: zero relative pressure is used at the outlet boundary i.e., \(P=0\).

  • At the porous-fluid interface: pressure and velocity continuity is implemented at interface [7, 8, 34].

The solution of the Eqs. (1)–(3) characterizes the flow field with regards to the velocity components U,  V,  and pressure, P. Further, these quantities have been post processed to obtain the significant engineering parameters such as pressure coefficient \((C_P)\) and drag coefficient \((C_D).\)

Drag coefficient\((C_D)\): The dimensionless drag force employed by the fluid on the permeable cylinder is referred as the drag coefficient and it is computed by using the succeeding formula:

$$\begin{aligned} C_D= & {} \frac{ 4 F_D}{ \rho U_{\infty }^2 D} \end{aligned}$$

where \(F_D\) is the total drag force (per unit length of the cylinder) exerted by the fluid on the semi-circular cylinder. It has been calculated by integrating the total stress in the \(x-\) direction [16] over the curved surface of the semi-circular porous cylinder.

Pressure coefficient\((C_P)\): The non-dimensionalized pressure difference in the form of pressure coefficient is defined as:

$$\begin{aligned} C_P=\frac{2(p_s-p_{\infty })}{ \rho U_\infty ^2}. \end{aligned}$$

Here, \(p_s\) and \(p_\infty\) denote the local surface pressure and reference pressure, respectively.

3 Methodology

The obtained governing mathematical equations bounded with the imposed boundary conditions are being solved by using COMSOL Multiphysics (FEM based commercial software). The non-uniform triangular elements are used to discretize the flow domain, as indicated in Fig. 1(b). The parallel direct linear solver (PARDISO) has been used for solving the resulting system of non-linear equations.

Table 1 Domain optimization
Full size table
Table 2 Grid optimization
Full size table

The domain size and grid structure of the problem strongly affects the authenticity and reliability of the numerical findings. Therefore, it is important to make the provident selection of these parameters.

3.1 Domain independence test

The domain independence test has been performed at extreme values of Re,  Da,  \(\epsilon\) and \(\beta ,\) as shown in Table 1. The inlet length \((L_{in})\) has been optimized by varying \(L_{in}\) as 20H, 30H, 40H and by fixing \(L_{out}=50H.\) A detailed inspection of the results suggests that the change in the values of \(C_D\) by varying \(L_{in}\) is negligible \((<0.1\%).\) Therefore, it is safe to choose \(L_{in}=30H\) among the values of \(L_{in}\) for all values of the governing parameters. Subsequently, the outlet length \((L_{out})\) is optimized by varying \(L_{out}\) as 30H, 40H and 50H. While optimizing \(L_{out},\) we have taken the optimized value of \(L_{in}.\) The relative error in the values of \(C_D\) is found to be less than \(0.01\%.\) Hence, in the present study, \(L_{in}=L_{out}=30H\) has been considered for all the numerical computations.

3.2 Grid independence test

After optimizing the domain size, we move further for the grid optimization, as shown in Table 2. An adequately fine grid is intended in the proximity of a porous semi-circular cylinder for resolving the steep velocity and pressure gradients. For this purpose, we have done the grid independence study for three distinct grids namely G1, G2 and G3 by varying the element size \((\delta /D)\) and number of elements \((n_p)\) in the proximity of the porous cylinder. Again, the drag coefficient has been computed at uttermost values of the considered parameters and a negligible difference (\(< 1\%\)) has been observed in \(C_D.\) Therefore, the grid G1 is adequate for the present study. Furthermore, convergence criterion of \(10^{-6}\) has been used in this study [44].

4 Results and discussion

The proposed study explores the fluid flow characteristics for the flow across a semi-circular porous cylinder attached to the bottom channel wall. The obtained numerical results are analyzed for the chosen range of parameters as Reynolds number (\(0.01\le Re \le 40\)), Darcy number (\(10^{-6}\le Da \le 10^{-1}\)), blockage ratio \((0.1667 \le \beta \le 1.5),\) and porosity (\(0.1 \le \epsilon \le 0.9\)). The streamline and vorticity profiles are plotted to show the flow field (Figs. 3, 4, 5, 6, 7 and 8). The engineering parameters such as pressure coefficient \((C_P)\) and drag coefficient \((C_D)\) are calculated to describe their functional dependence on \(Re,Da,\epsilon\) and \(\beta .\)

Fig. 2
figure 2

Comparison of drag coefficient with the literature [13] at \(Da= 10^{-4}\) for different values of Re.

Full size image

4.1 Validation of results

Before discussing the new findings for the flow across a semi-circular porous cylinder, it is important to validate the numerical approach used here. For this purpose, we have reproduced the numerical results of Dhinakaran et. al. [13] for the flow over a square porous cylinder at \(Da=10^{-4}\) for different values of Re and presented in Fig. 2. The reproduced results show a good agreement with Dhinakaran et. al. [13], as seen in Fig. 2. Hence the adopted methodology is trustworthy for further investigation.

Fig. 3
figure 3

Streamlines contours at \(\beta =0.1667\)

Full size image
Fig. 4
figure 4

Streamlines contours at \(\beta =0.5\)

Full size image
Fig. 5
figure 5

Streamlines contours at \(\beta =1.5\)

Full size image

4.2 Streamlines contours

The streamline contours in the proximity of a confined semi-circular porous cylinder are represented in Figs. 3, 4 and 5 at various combinations of governing parameters (\(\beta ,\epsilon ,Re,Da\)). For the comparison purpose, a similar length scale has been used for all the streamline profiles. Figure 3 represents the streamline profiles for \(\beta =0.1667 (8.35\%)\) by varying \(\epsilon ,\) Re and Da. This figure is divided into three sections based on porosity \((\epsilon =0.1,0.5,0.9).\) The streamline profiles of the first section show that at \(Da=10^{-6},\) streamlines do not pass across the porous cylinder for any value of Re and follow the fluid/porous interface. Thus, the porous cylinder acts as the solid cylinder at the above conditions and similar results are reported in the literature [55]. Additionally, the recirculation zones have been seen at the front and rear part of the cylinder for \(Da=10^{-6}\) and \(Re=0.01.\) These recirculation zones may appear due to the interplay between the no-slip boundary condition and the curvature of the porous cylinder. As per Moffatt’s analysis, these eddies may appear as the angle of the intersection of the cylinder and the channel wall is less than the critical angle \(({146.3}^\circ ).\) In our case, the angle of intersection is \({90}^\circ ,\) and hence, there are two sets of eddies at the front and rear part of the cylinder for low Reynolds number [35, 37]. As we increase Re from 0.01 to 40,  by keeping other parameters constant, the decrease in the front recirculation zone has been observed and the rear recirculation zone increases with the increase in Re at other constant parameters. It can happen due to the domination of viscous forces to inertial forces and the influence of body geometry (semi-circular porous cylinder). Further increasing the value of Da from \(10^{-6}\) to \(10^{-3},\) the streamlines start penetrating the porous cylinder with ease. It has adhered that as the permeability increases, the flow through the porous cylinder increases and this may be the reason for the disappearance of front recirculation zones. The detachment of the recirculation zone has been observed at \(Re=20\) and this similar kind of behavior is reported by Yu et. al. [55, 56]. As Re is further increased to 40,  the detached wake is shifted towards the cylinder. Furthermore, at \(Da=10^{-1},\) the more fluid is passing through the porous cylinder as permeability is increased. Here, the flow field behaves like a rectangular channel flow without any obstacle (porous cylinder). In the second section \((\epsilon =0.5)\) of the Fig. 3, the streamline profiles are almost similar to \(\epsilon =0.1\) except for \(Da=10^{-3}\) and \(Re=20,40.\) The rear recirculation zones start to penetrate partially into the porous cylinder and the flow separation starts within the cylinder itself. It may be due to the additional influence of porosity and permeability at higher values of Re. Further, the size of the recirculation zone is increased as Re increases from 20 to 40. Subsequently, in the third section \((\epsilon =0.9)\) of Fig. 3, similar flow behavior is observed except for \(Da=10^{-3}\) and \(Re=0.01,1.\) At these conditions, increase in the value of porosity leads to the formation of front and rear recirculation zones similar to \(Da=10^{-6}.\)

Figure 4 represents the streamline profiles for \(\beta =0.5({25\%})\) by varying \(\epsilon ,Re\) and Da. Similar to Fig. 3, the front recirculation zones are observed at \(Da=10^{-6}\) for all values of \(\epsilon\) and Re. But the size of front recirculation zones seems to be smaller than Fig. 3. We already know that the formation of recirculation zones suppresses due to the increase in blockage ratio. Hence, this phenomenon affects the rear recirculation zone and it shows some complex behavior because of the multiple governing parameters. Specifically, at \(Da=10^{-6},\) the size of the recirculation zone decreases for \(Re=0.01,1\) and increases for \(Re=20,40,\) as compared to \(\beta =0.1667.\) Furthermore, the right shift of the recirculation zone is observed at \(Da=10^{-3}\) and \(\epsilon =0.5,0.9\) due to the influence of the blockage ratio. Subsequently, Fig. 5 exhibits the streamline contours for \(\beta =1.5 ({75\%})\) and it can be observed that all the recirculation zones vanish except for \(Da=10^{-6}\) and \(Re=20,40.\) This happens due to the high value of the blockage ratio. Additionally, it is seen that the porosity effect is negligible for \(\beta =1.5.\)

By comparing Figs. 3, 4 and 5, it is observed that the porous cylinder acts as a solid cylinder at the lowest value of Da for all the values of other parameters \((Re,\epsilon ,\beta )\). The front recirculation zone appearing at \(Da=10^{-6},\) shrinks as \(\beta\) is increased from 0.1667 to 0.5 and it vanishes at \(\beta =1.5.\) Moreover, the rear recirculation zone shows a complex behavior with the increment in blockage ratio. As \(\beta\) is increased from 0.1667 to 0.5,  the rear recirculation zone is decreased for \(Re=0.01,0.1\) and increased for \(Re=20,40.\) Further, for \(\beta =1.5,\) the size of rear recirculation zones is reduced as compared to \(\beta =0.5\) and 0.1667. The porosity has a considerable impact on the flow properties for \(\beta =0.1667\) and 0.5 whereas its effect is almost insignificant for \(\beta =1.5.\)

Fig. 6
figure 6

Vorticity contours at \(\beta =0.1667\)

Full size image
Fig. 7
figure 7

Vorticity contours at \(\beta =0.5\)

Full size image
Fig. 8
figure 8

Vorticity contours at \(\beta =1.5\)

Full size image

4.3 Vorticity contours

Figures 6, 7 and 8 represent the vorticity contours in the proximity of semi-circular porous cylinder by varying the values of \(\beta ,\epsilon ,Re\) and Da. In Fig. 6 vorticity contours are shown for \(\beta =0.1667\) at various combinations of other governing parameters. In the first section \((\epsilon =0.1)\) of this figure, at \(Da=10^{-6},\) the vorticity contours are failed to diffuse inside the porous cylinder at each value of Reynolds number. It happens because of the solid behavior of permeable cylinder at low Darcy number \((Da=10^{-6})\). It is also observed that three vorticity zones are appearing at the top, front, and rear part of the cylinder. The presence of recirculation zones can be noticed in the streamline profiles (Fig. 3) corresponding to the front and rear vorticity zones. The high magnitude vorticity occurs in the top vorticity zone as compared to the other two zones. It is also observed that the top vorticity zone increases and shifts towards the front of the cylinder as Re increases. Due to the shifting of the top zone, the front zone has been reduced with the augmentation in Re. Simultaneously, the size of the rear vorticity zone increases with Re and leads to the rise in the size of the rear recirculation zone as seen in corresponding streamline profiles (Fig. 3). Furthermore, by increasing the value of Da from \(10^{-6}\) to \(10^{-3},\) the vorticity contours start to diffuse inside the porous cylinder for all the values of Re. The top vorticity zone elongates and shifts towards the rear portion of the cylinder as the value of Re is enhanced. On the other hand, the front and rear vorticity zones penetrate inside the permeable cylinder as a consequence of the raised permeability of the cylinder. Further at \(Da=10^{-1},\) the diffusion of vorticity contours inside the cylinder is more than the previous cases \((Da=10^{-6},10^{-3}).\) Additionally, the decrement in the size of vorticity zones has been observed. For this reason, the recirculation zones appearing at the front and rear part of the cylinder vanish in the corresponding streamline profiles. Moreover, two additional vorticity zones appear at the front and rear part of the cylinder and this may be due to the result of the complex interplay among the considered parameters. In the second section \((\epsilon =0.5)\) of the Fig. 6, for \(Da=10^{-6}\), the behavior of vorticity contours is almost similar to \(\epsilon =0.1.\) But the effect of porosity can be easily seen for \(Da=10^{-3},10^{-1}.\) At \(Da=10^{-3},\) in addition to the front and rear vorticity zones, the top vorticity zone also starts to diffuse inside the porous cylinder and this may be due to the increased value of porosity. Similarly, the penetration of recirculation zones is also noticed in corresponding streamline profiles (Fig. 3). Further at \(Da=10^{-1},\) the size of all the vorticity zones has decreased as comparative to \(\epsilon =0.1.\) This may lead to the more straight streamline contours for \(\epsilon =0.5\) than \(\epsilon =0.1.\) In the third section \((\epsilon =0.9)\) of the Fig. 6, a distinct behavior of vorticity contours has been observed at \(Da=10^{-1}.\) Here the size of all the vorticity zones has been further decreased as compared to \(\epsilon =0.5.\) Hence, the corresponding streamline contours are more straight in Fig. 3.

Figure 7 represents the vorticity contours for \(\beta =0.5\) for various combinations of \(\epsilon ,Re\) and Da. Here, the size of all the vorticity zones has been decreased and the magnitude of maximum vorticity has been increased for all the values of \(\epsilon ,Re,\) and Da as compared to \(\beta =0.1667\). The increase in the vorticity magnitude is due to the increase in blockage ratio. Moreover, the trend of vorticity contours concerning \(\epsilon ,Re,\) and Da is similar to \(\beta =0.1667.\)

Subsequently in Fig. 8 vorticity contours are shown for \(\beta =1.5\). This figure has been plotted at \(200\%\) zoom due to the relatively small vorticity zones as compared to Figs. 6 and 7. In the first section of Fig. 8, for \(Da=10^{-6}\) and \(Re=0.01,\) an additional vorticity zone is observed near the top channel wall due to the high blockage ratio. Moreover, at this blockage ratio, the channel wall is sufficiently close to the semi-circular porous cylinder and therefore the passage for the fluid flow outside the porous cylinder is very narrow which leads to high velocity in this narrow zone. Due to this reason, the maximum vorticity is observed at the top channel wall. Additionally, by increasing the value of Re from 0.01 to 40,  the size of this vorticity zone increases. Furthermore, at \(Da=10^{-3},\) the fluid starts to penetrate inside the cylinder and therefore the fluid flow in the narrow zone has been reduced. As a result, the velocity in the narrow zone reduces which leads to the reduction in vorticity magnitude at the top channel wall. The size of the top vorticity zone increases with the rise in Re similar to \(Da=10^{-6}.\) By further increasing the value of Da from \(10^{-3}\) to \(10^{-1},\) the vorticity magnitude on the top channel wall again decreases as the fluid flow in the narrow zone has been comparatively decreased. A distinct behavior of vorticity contours has been observed for \(\epsilon =0.5\) and \(Da=10^{-1}.\) Here all the vorticity zones appearing at the surface of the porous cylinder almost vanish and vorticity contours are more smooth as compared to \(\beta =0.1667\) and \(\beta =0.5.\) By further increasing the value of \(\epsilon\) from 0.5 to 0.9 for the same Darcy number, these vorticity contours become more straight. The remaining trend of vorticity contours with \(\epsilon ,Re\) and Da is similar to the previous blockage ratios \((\beta =0.1667,0.5)\).

By comparing Figs. 6, 7 and 8, it is observed that at \(Da=10^{-6},\) the size of all the vorticity zones decreases as \(\beta\) increases from 0.1667 to 1.5 at constant value of \(\epsilon\) and Re. Additionally, the top vorticity zone at the surface of the porous cylinder bends towards the bottom channel wall with the increment in \(\beta .\) Moreover, the magnitude of maximum vorticity appearing at the surface of the porous cylinder has increased with the increment in \(\beta .\) At \(Da=10^{-3},\) the behavior of vorticity contours with blockage ratio is similar to \(Da=10^{-6}.\) Further at \(Da=10^{-1}\) and \(\epsilon =0.5,\) the size of all the vorticity zones appearing at the surface of the porous cylinder decreases as \(\beta\) is increased from 0.1667 to 0.5. By further increasing the value of blockage ratio to 1.5,  these zones almost vanish due to the high blockage ratio. As we increase the value of porosity to 0.9 at the same Darcy number \((Da=10^{-1}),\) the front vorticity zone vanishes as \(\beta\) increases from 0.1667 to 0.5. At the highest value of blockage ratio \((\beta =1.5),\) all the vorticity zones disappear and the vorticity contours are almost straight.

Fig. 9
figure 9

Variation of pressure coefficient \((C_P)\) on the curved surface at \(\beta =0.1667\) with Re, Da and \(\epsilon :\) (a)Re=0.01 (b)Re=1 (c) Re=20 (d)Re=40

Full size image
Fig. 10
figure 10

Variation of pressure coefficient \((C_P)\) on the curved surface at \(\beta =0.5\) with Re, Da and \(\epsilon :\) (a)Re=0.01 (b)Re=1 (c) Re=20 (d)Re=40

Full size image
Fig. 11
figure 11

Variation of pressure coefficient \((C_P)\) on the curved surface at \(\beta =1.5\) with Re, Da and \(\epsilon :\) (a)Re=0.01 (b)Re=1 (c) Re=20 (d)Re=40

Full size image

4.4 Pressure coefficient \((C_P)\)

Figures 9, 10 and 11 represent the variation in \(C_P\) on the curved surface of the porous cylinder by varying the values of \(\beta , Re,Da\) and \(\epsilon .\) The \(x-axis\) of these figures represents the curved length of the semi-circular cylinder. In Fig. 9, pressure coefficient is plotted for \(\beta =0.1667.\) Here, at \(Re=0.01,\) the pressure coefficient attains the maximum value between the points A and B,  and the minimum value between the points B and C for \(Da=10^{-6}\) and \(Da=10^{-3}\) at \(\epsilon =0.1\). Further, for \(Da=10^{-1}\) and \(\epsilon =0.1,\) the lowest and highest values of \(C_P\) are obtained at the points A and C, respectively. Moreover, a complex trend of \(C_P\) \((\text {for } Re=0.01,\epsilon =0.1)\) with Da has been observed such as the value of pressure coefficient is decreasing with the increase in Da (for constant \(\epsilon\)) at the front part of the cylinder whereas the reverse trend has been observed for the rear part of the cylinder. It may happen due to the increment in Da which leads to the increased penetration of the fluid inside the permeable cylinder and hence pressure distribution at the front of the cylinder decreases. On the other hand, due to the interplay between the flow inside and outside of the porous cylinder, \(C_P\) has increased with Da at the rear part of the cylinder. Furthermore, the influence of porosity is more prominent at \(Da=10^{-1}\) rather than the other values of Da. At \(Da=10^{-1},\) \(C_P\) increases with \(\epsilon\) in the proximity of the point A but it decreases with \(\epsilon\) near the point C. As we move away from these points, \(C_P\) shows an inverse relationship with porosity at the front portion of the cylinder and it shows the direct relationship with porosity at the rearward portion of the cylinder.

Further, by increasing the value of Re from 0.01 to 1, a similar trend of \(C_P\) has been observed. Although the values of pressure coefficient have been increased as compared to \(Re=0.01\) at constant values of Da and \(\epsilon .\) It is noticed that all these pressure coefficient curves are converging at some point near B (between A and B). By increasing the value of Re from 1 to 40, these converging points are segregated based upon Da and move towards the point A. Moreover, the values of the pressure coefficient are increasing with the increase in Re at constant values of Da and \(\epsilon .\) It happens because the inertial forces become dominant by increasing the value of Re,  which results in the increment of pressure coefficient. Furthermore, a similar trend of \(C_P\) with Da and \(\epsilon\) has been observed for \(Re=20,40.\)

In Fig. 10, \(C_P\) is plotted for increased value of \(\beta =0.5\) and it is observed that \(C_P\) has decreased with the increase in \(\beta .\) The respective trend of \(C_P\) with Re, Da and \(\epsilon\) remains similar to Fig. 9. Similarly, Fig 11 represents the pressure coefficient for \(\beta =1.5\) and it depicts that the pressure coefficient has been further decreased as compared to \(\beta =0.5\) at constant values of other parameters (Re, Da and \(\epsilon )\). In Fig. 11, for \(Re=0.01,\) as we move over the edge of the porous cylinder starting from A, initially \(C_P\) has almost negligible variation with Da and \(\epsilon .\) But after that \(C_P\) decreases with the decrement in Da at constant value of \(\epsilon .\) Additionally, \(C_P\) increases as the value of \(\epsilon\) increases at \(Da=10^{-3},10^{-1}.\) By further enhancing Re from 0.01 to 40,  \(C_P\) shows a direct relationship with Re. Whereas, the similar trend of pressure coefficient with Da and \(\epsilon\) is observed for \(Re=0.01\) to \(Re=40\).

Overall, from the Figs. 9, 10 and 11, it is observed that \(C_P\) shows an inverse relationship with \(\beta\) for all the values of Da, Re,  and \(\epsilon .\) Additionally, the trend of \(C_P\) over the edge of the porous cylinder remains similar at \(\beta =0.1667,0.5.\) But for \(\beta =1.5,\) a distinct trend has been observed for all the values of Re.

Fig. 12
figure 12

Drag coefficient by varying Re,  Da and \(\beta\) (a) \(\epsilon =0.1\) (b) \(\epsilon =0.5\) (c) \(\epsilon =0.9\)

Full size image

4.5 Drag coefficient \((C_D)\)

The drag coefficient \((C_D)\) has been plotted in Fig. 12 at various combinations of \(\epsilon ,Re,Da\) and \(\beta .\) Here, the drag coefficient shows the classical inverse relationship with Re for the constant value of Darcy number, blockage ratio, and porosity [10] and it can be visualized from Fig. 12. In Fig. 12(a), drag coefficient has been represented for \(\epsilon =0.1\) by varying Re, Da and \(\beta .\) It has been noticed that \(C_D\) decreases with the increment in Da. It happens as the value of Da increases, the permeability of the porous cylinder increases and it allows more fluid to penetrate the permeable cylinder. Due to the increased flow through the cylinder, it experiences less drag. Additionally, it is noticed that \(C_D\) has been increased by increasing the blockage ratio at any value of Re. This can be explained as \(\beta\) increases, the distance of the channel wall from the cylinder decreases, and therefore porous cylinder experiences more drag force from the incoming flow. Further, for \(\beta =1.5,\) there is a significant rise in \(C_D\) with decreasing Da. But, this variation is seen to be less prominent for \(\beta =0.5\) and 0.1667.

Subsequently, Fig. 12(b) shows the variation in \(C_D\) for \(\epsilon =0.5.\) Here, it has observed that the values of \(C_D\) almost coincides at \(Da=10^{-6}\) and \(Da=10^{-3}\) for \(\beta =0.5,0.1667.\) The remaining trend of \(C_D\) with Re, Da and \(\epsilon\) is similar to Fig. 12(a). Further, in Fig. 12(c) \((\epsilon =0.9\)), a distinct trend is observed at \(Da=10^{-6},10^{-3}\) and \(\beta =0.5,0.1667\) as \(C_D\) increases with the increase in Da. It may happen due to complex influence of \(\beta ,Da\) and highest value of porosity \((\epsilon =0.9).\) Overall, it can be noticed from the Fig. 12 that the effect of porosity is prominent for \(\beta =0.5\) and \(\beta =0.1667\) at \(Da=10^{-6},10^{-3}\) rather than other governing parameters.

5 Conclusions

The present paper intends to observe the influences of \(Re,\beta ,Da,\) and \(\epsilon\) for the flow across a semi-circular porous cylinder attached to a channel wall. The streamlines profiles, vorticity profiles, pressure coefficient \((C_P)\), and drag coefficient \((C_D)\) have been represented for the chosen range of governing parameters. The interaction of the governing parameters shows an entangle behavior on the flow properties. The porous cylinder imitates a solid cylinder at the lowest value of Da i.e. \(Da=10^{-6}\) irrespective of the values of other governing parameters. Further enhancement in Da induces a rise in the permeability of the porous cylinder and therefore, more amount of fluid travels through the permeable cylinder. Whereas at \(Da=10^{-1},\) the flow field looks like a channel flow without any obstacle. The impact of \(\epsilon\) on the flow field is negligible at \(Da=10^{-6}\) and this influence is intensifying with Da. Furthermore, the diffusion of vorticity contours inside the cylinder has been observed with an incrementation of Da and \(\epsilon\). Subsequently, a complex influence of \(\beta\) has been observed on the flow patterns. The magnitude of maximum vorticity magnifies and the size of the vorticity zones diminishes with the enhancement in \(\beta\). The Darcy number exhibits a complex impact on the pressure coefficient distribution and the values of the drag coefficient. The influence of porosity on the pressure coefficient becomes prominent with the augmentation in Darcy number. Additionally, \(C_P\) declines and \(C_D\) rises with the increment in the blockage ratio.