1 Introduction

The thermal management of the electronic devices and power sources became the challenging issue in the last decade because of both, miniaturization and heat transfer rate increasing. The various cooling solutions have been proposed using both the single and two-phase heat transfer. Since this paper deals with the single phase heat transfer of water, only these cooling solutions will be considered.

The advantage of the single-phase microchannel heat sink, is based on an increase the heat transfer coefficient as the hydraulic diameter is deceasing. Also the channel walls are acting as the fins that increase the heat transfer area. For the case of the microchannel heat sinks, the investigations are made for single layer arrangement [1–6] and double layer arrangement [7, 8]. The research has been made experimentally and numerically although the analytical solution based on a porous model has been announced [9]. The fractal branching microchannel heat sink was investigated in [10]. Also, the viscous dissipation effect and the slip flow regime were considered for rectangular microchannel heat sinks [11, 12]. In addition, the review chapters on micro-heat sinks might be found in [13, 14].

Contrary to the microchannel heat sink, Soliman et al. [15] presented the results for the numerical modeling made on microtube heat sink. The constant property laminar heat transfer of the water through the microtubes is considered. It was found that proposed heat sink have higher thermal resistance and requires lower pumping power compared to the microchannel heat sink for the same Re and hydraulic diameter. On the other hand, based on the unit pumping power, the microtube heat sink can dissipate slightly larger heat rate than the microchannel heat sink.

Besides, Ryu et al. [16] have presented the numerical analysis of the manifold microchannel heat sink. It is concluded that this heat sink has better performances than the classical microchannel heat sink, lower thermal resistance and more uniform temperature distribution for the same pumping power. The optimization of the heat sink geometric parameters is done to obtain the best heat transfer characteristics.

For the microchannel heat sinks with large length to diameter ratio and uniform inlet velocity feeding of the channels, the fluid flow and thermal regime are fully developed for almost the total channel length. As the heat transfer coefficient is lower in this case, another option is to induce flow instabilities and consequently to establish developing fluid flow and heat transfer along the channel.

Sung and Mudawar [17] analyzed the hybrid jet impingement microchannel heat sink in turbulent heat transfer and fluid flow. It was shown that the vorticity has the large influence on a zone outside the impingement jet. The stronger attachment of the fluid flow to the heated surface for higher Re is observed. It was also proposed the improved design of the heat sink based on the optimized analysis that lowers the temperature distribution of the heated surface.

Following this review of the cooling solutions used for electronic and high power devices, the microtube heat sink with impingement jet is analyzed. To extend the benefits from the fluid flow attachment to the tube wall, the inlet impingement jet is tangentially positioned to the microtube.

2 Problem description and numerical details

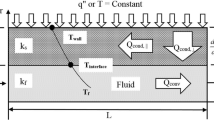
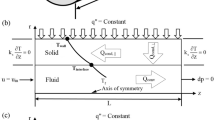
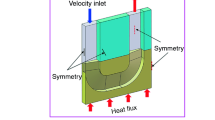
The microtube heat sink assembly proposed for numerical analysis is presented in the Fig. 1 and dimensions are given in Table 1. It might be observed that feeding of the microtube heat sink is realized through the gaps on the top surface of the heat sink. The cross section of the microtube with the inlet channel is presented in the Fig. 2. It can be noticed that the microtube is thermally and hydrodynamically symmetrical with respect to the boundary positioned at the half-length of the microtube. So, only the left part of the microtube is analyzed. Lelea et al. [18] and Lelea [19, 20] have analyzed numerically and experimentally the laminar heat transfer and fluid flow of the water through the single microtube and concluded that conventional theories are applicable to the microtubes with diameters down to 100 μm. Also the Reynolds analogy might be applied for different fluid flow configurations as mentioned in [21–23]. For the phenomena occurring in this case, the set of the Navier-Stokes equations can be used, as follows:

Fig. 1
figure 1

The microtube heat sink assembly with tangential impingement jet

Full size image
Fig. 2
figure 2

The single microtube geometry

Full size image

The conservation of mass

$$ {\frac{{\partial \left( {\rho \cdot u_{i} } \right)}}{{\partial x_{i} }}} = 0 $$
(1)

The conservation of momentum

$$ {\frac{{\partial \left( {u_{i} \cdot \rho \cdot u_{j} } \right)}}{{\partial x_{i} }}} = - {\frac{\partial p}{{\partial x_{i} }}} + {\frac{\partial }{{\partial x_{i} }}}\left( {\mu {\frac{{\partial u_{j} }}{{\partial x_{i} }}}} \right) $$
(2)

The conservation of energy

$$ {\frac{{\partial \left( {\rho \cdot c_{\text{p}} \cdot u_{i} \cdot T} \right)}}{{\partial x_{i} }}} = {\frac{\partial }{{\partial x_{i} }}}\left( {k{\frac{\partial T}{{\partial x_{i} }}}} \right) $$
(3)

For the micro-tube heat sink presented in this paper, the following boundary conditions are settled:

Table 1 The geometry, thermal and flow conditions of the micro-tube heat sink
Full size table

  • The fluid flow is stationary, incompressible and laminar;

  • The fluid properties were considered as temperature dependent with following equations:

    • Dynamic viscosity:

      $$ {{\upmu}}\left( t \right) = 2.6412018\; \times 10^{ - 4} + 0.0014009 \times {\text{e}}^{{ - {\frac{t}{31.0578605}}}} $$

    • Density:

      $$ {{\uprho}}\left( t \right) = 1000.0 \times \left( {1 - {\frac{t + 288.9414}{{508929.2 \times \left( {t + 68.12963} \right)}}} \times \left( {t - 3.9863} \right)^{2} } \right) $$

    • Thermal conductivity:

      $$ k\left( t \right) = - 0.58166 + 6.355 \times 10^{ - 3} \times T - 7.964 \times 10^{ - 6} \times T^{2} $$

    • Specific heat:

      $$ c_{\text{p}} \left( t \right) = 8958.9 - 40.535 \times T + 0.11243 \times T^{2} - 1.014 \times 10^{ - 4} \times T^{3} $$

  • The viscous dissipation is neglected because of the low flow rates;

  • The uniform velocity field and the constant temperature are imposed at the channel inlet, while at the outlet the partial derivates of the velocity and temperature in the stream-wise direction are vanishing;

  • The conjugate heat transfer between the solid and fluid flow is considered and the no-slip velocity conditions at the solid–fluid interface;

The conjugate heat transfer procedure, implies the continuity of the temperature and heat flux at the solid–liquid interface defined as,

$$ x = R_{i} :T_{\text{s}} |_{R + } = T_{\text{f}} |_{R - } $$
$$ k_{\text{s}} \left( {{\frac{{\partial T_{\text{s}} }}{\partial x}}} \right)_{R + } = k_{\text{f}} \left( {{\frac{{\partial T_{\text{f}} }}{\partial x}}} \right)_{R - } $$
$$ y = R_{i} :T_{\text{s}} |_{R + } = T_{\text{f}} |_{R - } $$
$$ k_{\text{s}} \left( {{\frac{{\partial T_{\text{s}} }}{\partial y}}} \right)_{R + } = k_{\text{f}} \left( {{\frac{{\partial T_{\text{f}} }}{\partial y}}} \right)_{R - } $$

Also at the inlet cross-section:

$$ y = R_{i} + h_{\text{ch}} ;\quad R_{i} - b_{\text{ch}} < x < R_{i} ; \quad 0 < {\text{z}} < l_{\text{ch}} /2 $$
$$ M = M_{\text{in}} \;\;{\text{and}}\;\;T = T_{\text{in}} $$

All the outer surfaces of the heat sink are insulated except the bottom one in contact with the chip:

$$ y = - \left[ {H - \left( {D_{\text{i}} + h_{\text{ch}} } \right) + R_{i} } \right] ; \quad - w_{\text{m}}/2 < x < w_{\text{m}}/2 ; \quad 0 < z < L/2 $$
$$ q = k_{\text{s}} {\frac{\partial T}{\partial y}} $$

At the outlet of the microtube the following boundary conditions are prescribed:

$$ z = L/2 $$
$$ {\frac{\partial v}{\partial z}} = 0 ; \quad {\frac{\partial w}{\partial z}} = 0 ; \quad {\frac{\partial u}{\partial z}} = 0 ; \quad {\frac{\partial T}{\partial z}} = 0 $$

At the symmetry boundaries:

$$ z = 0 $$
$$ {\frac{\partial v}{\partial z}} = 0 ; \quad {\frac{\partial w}{\partial z}} = 0 ; \quad {\frac{\partial u}{\partial z}} = 0 ; \quad {\frac{\partial T}{\partial z}} = 0 $$
$$ x = \pm w_{\text{m}} /2 $$
$$ {\frac{\partial v}{\partial x}} = 0 ; \quad {\frac{\partial w}{\partial x}} = 0 ; \quad {\frac{\partial u}{\partial x}} = 0 ; \quad {\frac{\partial T}{\partial x}} = 0 $$

The set of the partial differential equations along with the boundary conditions are solved using the Fluent commercial solver [24] with methods described in [25]. The Simple algorithm is used for the velocity-pressure coupling solution and second order upwind scheme for equations discretization. The under-relaxation factors are used for pressure field (α = 0.3) and momentum conservation (α = 0.7). The convergence criterion is defined as:

$$ R^{\varphi } = {\frac{{\sum {_{{{\text{cells}},P}} } \left| {\sum {_{\text{nb}} }\ a_{\text{nb}} \cdot \phi_{\text{nb}} + b - a_{p} \phi_{p} } \right|}}{{\sum {_{{{\text{cells}},P}} \left| {a_{p} \phi_{p} } \right|} }}} $$
(4)

The residuals for velocity components and continuity equation were 10−5 and for temperature field 10−8. Three different grids have been used to test the grid sensitivity, 1 (414 cells at each cross-section, 200 subdivisions in axial direction with total of 82,800 cells), 2 (646,250,161,500) and 3 (1,020,313,319,260). In Fig. 3 is presented the temperature distribution at the centerline of the heat sink bottom surface for these three grids. A difference between the grids 2 and 3 is about 1.5% along the axial direction, so the grid nr. 2 is used for further calculations.

Fig. 3
figure 3

Grid independence test

Full size image

3 Results and discussion

The results obtained for velocity, pressure and temperature filed are used to calculate the main heat sink parameters like thermal resistance and pumping power. The thermal resistance is calculated as:

$$ R = {\frac{{T_{\max } - T_{\text{in}} }}{q}} $$
(5)

while the pumping power is defined as:

$$ {{\Uppi}} = M \cdot {\frac{\Updelta p}{\rho }} $$
(6)

The pressure difference is calculated as a difference between the average values at the inlet and outlet cross-sections:

$$ \Updelta p = p_{\text{in}} - p_{\text{out}} $$
(7)

Also the Re is defined as:

$$ \text{Re} = {\frac{4 \cdot (M/2)}{\pi \cdot D \cdot \mu }} $$
(8)

In the Fig. 4 the temperature distribution is presented along the heated surface for circular impingement jet heat sink and classic heat sink with front inlet cross-section, and low pumping power Π = 0.003 W. It can be observed that maximum temperature is lower for the jet impingement microtube heat sink (T = 313.21 K for constant fluid properties and T = 311.13 for variable fluid properties) against the classic heat sink (T = 324.14 K). On the hand, the temperature difference along the heated surface is higher for the classic microtube heat sink (ΔT = 19.2 K) than the jet impingement microtube heat sink (ΔT = 9.6 K for constant fluid properties and ΔT = 7.8 K for variable fluid properties). In the jet impingement region the temperature is almost constant, while in the outside region the temperature variation exhibits almost the boundary layer behavior. It means that for very low pumping powers or mass flow rates, the jet zone impingement has negligible influence on outside region toward the microtube outlet cross-section.

Fig. 4
figure 4

The temperature distribution at the bottom heat sink surface along the fluid flow for Π = 0.003 W and two different configurations

Full size image

In the Fig. 5, the temperature distribution along the centerline of the heated surface is presented for two arrangements and higher pumping power. Once again the jet impingement configuration has both lower maximum temperature (T = 304.84 K for constant fluid properties and T = 304.39 for variable fluid properties) and lower temperature difference (ΔT = 2.5 K for constant fluid properties and ΔT = 2.23 K for variable fluid properties) against the classic microtube heat sink (T = 312.82 K) and (ΔT = 9.8 K). In this case temperature behavior of the jet impingement heat sink has two separate zones outside the jet impingement region, each one with variation similar to boundary layer behavior. This means that the swirl flow created in the jet impingement zone has the impact on a downstream portion of the microtube.

Fig. 5
figure 5

The temperature distribution of a bottom heat sink surface along the fluid flow for Π = 0.055 W and two different configurations

Full size image

In the Fig. 6, the thermal resistance versus pumping power is presented. Following these observations, it is obvious the thermal resistance for jet impingement microtube heat sink is lower than the thermal resistance of the classic microtube heat sink for the whole range of the pumping power.

Fig. 6
figure 6

Thermal resistance R versus pumping power for three different cases

Full size image

The fluid viscosity distribution at the outlet cross-section for various mass flow rates is presented in the Fig. 7. For the low flow rates and higher outlet temperatures there is a large variation of viscosity along the cross-section. As it is expected the lower viscosity is observed near the tube wall. For the higher mass flow rates the swirl flow creates the higher mixing of the fluid and more uniform viscosity.

Fig. 7
figure 7

The viscosity distribution at the outlet cross section of the microtube for various mass flow rates

Full size image

The similar conclusion might be outlined for a density distribution at the outlet cross-section. For lower mass flow rates and higher temperatures the variations in fluid density is observed from tube wall to the axis. Contrary to one that might expect, the portions of the fluid with higher density are not pushed toward the tube wall because of the lower variations in fluid density (Fig. 8).

Fig. 8
figure 8

The density distribution at the outlet cross section of the microtube for various mass flow rates

Full size image

In Figs. 9 and 10, the fluid path lines for two different mass flow rates are presented. It is observed that for the low flow rates the swirl flow is created without mixing. The flow behavior is similar to the boundary layer one, except for the inlet portion of the tube. For the higher flow rates the swirl flow created by the tangential fluid inlet, increases the fluid mixing and heat transfer coefficient.

Fig. 9
figure 9

The axial velocity path lines for single microtube mass flow rate M = 10 × 10−5 kg/s

Full size image
Fig. 10
figure 10

The axial velocity path lines for single microtube mass flow rate M = 80 × 10−5 kg/s

Full size image

4 Conclusions

The numerical modeling of the tangential jet impingement microtube heat sink is presented. The obtained results for temperature and velocity fields are used for performance evaluation against the classic microtube heat sink, in terms of thermal resistance and pumping power. It is concluded that both, lower peak temperature and lower temperature difference are associated to jet impingement heat sink. Therefore an additional effort regarding the inlet manifold is fully justified considering the thermal benefits.

On the other hand, the fluid viscosity has a great influence on a temperature and velocity field and thermal parameters of the heat sink. This observation is valid for the lower flow rates and higher temperatures. Due to the small variations in fluid density, the portions of the fluid with higher density are not pushed toward the tube wall.