Parametric analysis of axial wall conduction in a microtube subjected to two classical thermal boundary conditions

Abstract

Heat transfer in laminar flow microtube is numerically explored with an objective of discriminating conjugate heat transfer process experienced in a microtube under two different thermal conditions. Two classical thermal conditions – constant heat flux and constant wall temperature – are imposed separately on the outer surface of a microtube. Wide parametric variations are considered in this study, for the two thermal conditions, albeit the problem under consideration being very classical from both geometry and thermal condition point of view. The parametric variations considered in this work include wall thickness, wall conductivity and coolant flow rate. An expression for Nusselt number in terms of radial (or transverse) and axial conduction number is presented and validated against existing theoretical correlation as well as reported experimental data for both circular and non-circular channels. Dominance of axial conduction over radial (or transverse) conduction is explored and it is found that the effect of wall material on conjugate heat transfer plays an important role. Additionally, it is also observed that with the increase in coolant flow rate, the ratio of radial to axial conduction number increases for both thermal boundary conditions.

1 Introduction

One of the greatest challenges in thermal engineering is to enhance the local as well as average heat transfer rate while the temperature difference is limited by the practical conditions. Miniaturization of heat transfer devices increases the heat transfer coefficient due to the higher surface area to volume ratio. In recent times, there has been rapid progress in the development of microchannel-based heat exchangers, thanks to developments in micromachining technology [1]. Miniaturization leads to the flow being mostly laminar in nature along micro-ducts. Laminar flow finds many applications in mini/microchannel-based heat sinks and microfluidic energy devices. Therefore, convection forced by laminar flow in ducts is a fundamental problem of great importance in the design of different energy systems such as heat sink, heat exchangers, etc.

For a constant wall heat flux (hereafter referred to as “q′′”) applied on the outer surface of a circular tube, there exists a difference in wall temperature between two axial locations where temperature is higher towards the outlet. Axial temperature difference in solid wall results in axial back conduction. In a conventional size tube, the thickness of the tube can be negligible compared with the inner diameter. Hence, the potential for axial conduction is limited by the axial temperature gradient in wall temperature. Secondly, the magnitude of heat conduction is negligible compared with the amount of heat carried away by fluid through convection. Therefore, the phenomenon of axial conduction will not have much influence on overall heat transfer of the system. Unlike conventional tubes, microtubes will have higher or of the same order of wall thickness compared to its inner radius. Therefore, there exists an additional source (of higher solid cross-sectional area) for axial back conduction in a microtube solid wall in addition to the axial temperature gradient.

Maranzana et al [2] defined a dimensionless number called axial conduction number (M) and suggested that effect of axial wall conduction is negligible if M < 0.01. Later, this number was further modified by Li et al [3] by including temperature difference (between inlet and outlet) in solid (ΔT_s) and fluid (ΔT_f) regions. They found that with increase in wall thickness over hydraulic diameter, it leads to higher discrepancy in overall heat transfer. The results also show that for low values of Reynolds number, the wall conduction effect can lead to higher values. Later on, Rahimi and Mehryar [4] showed that ending length is not a function of tube or channel length physically by comparing results to axial conduction number M [2]. Results show that this ending length depends on flow conditions, tube geometry and thermal conductivity of wall and the suggested correlation provides better accuracy compared with other numerical results.

Many correlations based on experimental results have been proposed in literature to predict thermal performance of conventional as well as microchannels/microtubes. Stephan and Preuβer [5] proposed Nusselt number correlations for both constant wall heat flux and constant wall temperature for the range of 0.7 < Pr < 7 or RePrD/L < 33.

Peng and Peterson [6] conducted experimental study on single-phase forced convective heat transfer in a rectangular microchannel (D_h ~ 0.133–0.367 mm) using water as the working fluid. Based on experimental data, they derived a correlation for laminar convective heat transfer. Choi et al [7] performed experimental study on laminar flow heat transfer in a microtube by varying hydraulic diameter (3–81.2 μm), tube length (24–52 mm) and Reynolds number (20–25,000). Liu et al [8] experimentally investigated forced convective heat transfer in quartz microtubes with inner diameter of 242, 315 and 520 μm and proposed a correlation for constant wall heat flux. Results obtained from proposed correlation for Nusselt number were found to be in good agreement with the classical laminar correlations at a lower Re.

It can be assumed that correlations based on experimental study proposed in [2,3,4,5,6,7,8] already include axial conduction effect. However, these experiment-based correlations are limited for particular test arrangement conducted during the experimental investigation. Lin and Kandlikar [9] performed theoretical analysis and proposed a new correlation for Nusselt number that includes axial wall conduction effect on local wall and fluid temperature. This correlation is compared to various experimental analyses and found to be in good agreement with experimental data. This result also shows that for higher conductivity channel material, or thicker channel walls, effects of axial wall conduction are not negligible. Though the correlation proposed by Lin and Kandlikar [9] is improvised over older correlations, still conduction effect in radial/transverse direction is missing, which is included in the present work. From this discussion it is found that many correlations of Nusselt number with or without axial conduction number were proposed but few of them included temperature gradient in their correlations.

Secondly, correlations proposed in [2,3,4,5,6,7,8] also reveal that main affecting parameters that lead to axial wall conduction effect are solid wall thickness to inner radius ratio (δ_sf), solid wall to coolant liquid conductivity ratio (k_sf) and coolant flow rate (Re). Considering these parameters, Moharana et al [10] performed a numerical study on conjugate heat transfer in a rectangular microchannel and demonstrated that the actual thermal boundary condition experienced at the solid–fluid interface in a square microchannel (engraved on a solid substrate) is different from the applied/imposed thermal condition.

The results indicate that magnitude of heat flux distribution at the solid–fluid interface is more near the inlet region, and hence heat flux distribution decreases neat the outlet. Observing this, Duryodhan et al [11] used an inclined channel instead of flat channels for redistribution of heat flux. They found that axial wall conduction effect weakens in diverging type of microchannels. Similarly, Sahar et al [12] demonstrated effect of hydraulic diameter and channel aspect ratio in a rectangular microchannel. They found that channel aspect ratio does not affect heat transfer coefficient. However, Moharana and Khandekar [13] find that on changing the aspect ratio with different wall materials, the effect of conjugate heat transfer can be observed. This also indicates that the dominance of axial wall conduction increases with high conductive material.

The situation is slightly different in microtubes compared with non-circular channels (square/rectangular), where it is a one-dimensional phenomenon at any axial location. Recently, the effect of axial wall conduction combined with rarefaction and viscous dissipation was observed by Sen and Darici [14]. The result clearly indicates that fluid properties significantly affect heat transfer performance. Considering this, Zhai et al [15] demonstrated effects of axial wall conduction by varying Peclet number (Pe), wall to fluid thermal conductivity ratio (k_sf) and solid wall thickness to tube inner radius ratio (δ_sf). Results indicate that axial wall conduction lowers local Nu_z along tube length relative to variable parameters under q′′.

Based on this discussion, wall thickness and material conductivity are found to be important parameters that control overall heat transfer process. However, numerous numerical studies related to conjugate heat transfer have been performed in different designs of microchannels. Most of them focused on parameters such as channel cross-section aspect ratio, shapes of microchannel structure, Reynolds number, etc. [16,17,18,19]. Very few studies dealing with finding optimum parameters such as channel aspect ratio, material, thickness, etc. are available in existing literature.

Additionally, many numerical/experimental studies do exist in the literature that deal with the study of conjugate heat transfer or axial back conduction in microtube subjected to either constant wall heat flux [20, 21] or constant wall temperature [22,23,24] on its outer surface. Conjugate heat transfer effect is not limited to microtubes/microchannels only. It is equally applicable to thick-walled conventional size ducts/pipes. Microtubes/microchannels also fall under the thick-walled system. Darıcı et al [25] and Ates et al [26] explored the conjugate heat transfer effect in thick-walled pipes for hydrodynamically and thermally developing laminar flow. Parametric variations considered in these works are wall thickness ratio, wall-to-fluid thermal conductivity ratio, wall-to-fluid thermal diffusivity ratio and Peclet number. It is observed that heat transfer characteristics are strongly dependent on these parameter values.

The literature presented earlier reveals that conjugate heat transfer situation arises due to the presence of axial temperature gradient. However, the order of this axial temperature gradient is not reported anywhere. Next, existing correlations for Nusselt number hardly explore the axial temperature gradient. Considering this, a mathematical expression for data reduction of average Nusselt number is proposed that fulfils all these criteria. A detailed theoretical and numerical investigation is undertaken by considering the wide parametric variation of factors affecting the thermal performance of microtube subjected to either constant wall temperature (henceforth T) or constant wall heat flux (henceforth q′′) on its outer surface, and a direct comparison is presented for better clarity. The details are elaborated next.

2 Method and validation

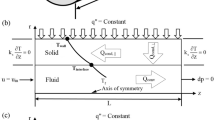
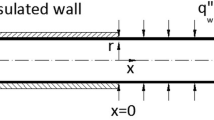
To expose the effect induced by axial wall conduction on overall heat transfer in a microtube, the outer surface is separately subjected to two different thermal boundary conditions: constant wall heat flux q′′ or constant wall temperature T. Schematic presentation of computational domain of microtube is shown in figure 1.

Figure 1

Schematic presentation of computational domain of microtube.

The heat flux within the wall by means of conduction is coupled with convective heat transfer from solid–fluid interface to the fluid. Such tendency of heat transfer is defined as “conjugate heat transfer”. Ideally, conduction heat transfer should be radially towards the solid–fluid interface. However, here due to the presence of axial wall conduction, conduction occurs ‘bi-directionally’ (see figure 1).

Total thermal resistance offered by microtube is given as follows:

$$ {\text{R}}_{\text{total}} = {\text{R}}_{{{\text{cond}},\parallel }} + {\text{R}}_{{{\text{cond}}, \bot }} + {\text{R}}_{\text{conv}} . $$

(1)

Conduction thermal resistance in axial direction is given as

$$ {\text{R}}_{{{\text{cond}},\parallel }} = {\text{R}}_{\text{total}} - {\text{R}}_{{{\text{cond}}, \bot }} - {\text{R}}_{\text{conv}} . $$

(2)

Total conductive and convective thermal resistances as defined by Chai et al [27] are given as

$$ {\text{R}}_{{{\text{cond}}, \bot }} = \frac{{{\bar{\text{T}}}_{\text{a}} - {\bar{\text{T}}}_{\text{i}} }}{\text{Q}},\quad {\text{R}}_{\text{conv}} = \frac{{{\bar{\text{T}}}_{\text{i}} - {\bar{\text{T}}}_{\text{f}} }}{\text{Q}},\quad {\text{R}}_{\text{total}} = \frac{{{\text{T}}_{ \hbox{max} } - {\text{T}}_{\text{in}} }}{\text{Q}}, $$

(3)

where ${\bar{\text{T}}}_{\text{a}}$, ${\bar{\text{T}}}_{\text{i}}$ and ${\bar{\text{T}}}_{\text{f}}$ are average temperature of the surface at the thermal condition imposed, solid–fluid interface and bulk, respectively. T_in is bulk temperature at inlet, and T_max is maximum temperature within the microchannel/microtube. Using Eq. (3) in Eq. (2) gives

$$ {\text{R}}_{{{\text{cond}},\parallel }} = \frac{{{\text{T}}_{ \hbox{max} } - {\text{T}}_{\text{in}} }}{\text{Q}} - \frac{{{\bar{\text{T}}}_{\text{a}} - {\bar{\text{T}}}_{\text{i}} }}{\text{Q}} - \frac{{{\bar{\text{T}}}_{\text{i}} - {\bar{\text{T}}}_{\text{f}} }}{\text{Q}}, $$

(4)

$$ {\text{R}}_{{{\text{cond}}, \, \parallel }} = \frac{{\left( {{\text{T}}_{ \hbox{max} } - {\text{T}}_{\text{in}} } \right) - \left( {{\bar{\text{T}}}_{\text{a}} - \frac{{{\text{T}}_{\text{in}} + {\text{T}}_{\text{out}} }}{2}} \right)}}{\text{Q}}. $$

(5)

Equation (5) can also be used to calculate axial conduction resistance by measuring the fluid temperature at channel inlet and outlet, temperature of the surface at which thermal condition is imposed and at the outlet plane of the solid domain. It can be noted that maximum temperature within the solid domain will always occur at the outlet plane. In an experimental study, fluid inlet and outlet temperature can be measured comfortably. From energy balance

$$ {\text{Q}}_{\text{cond}} = {\text{Q}}_{{{\text{cond}},\parallel }} + {\text{Q}}_{{{\text{cond}}, \bot }} = {\text{Q}}_{\text{conv}} $$

(6)

where

$$ Q_{cond, \bot } = - k_{s} A_{surf} \frac{dT}{dy} = k_{s} A_{surf} \frac{{\bar{T}_{a \, } - \bar{T}_{\text{i}} }}{{\delta_{s} }}, $$

(7)

$$ Q_{cond,\parallel } = k_{s} A_{cs} \frac{{T_{w,out} - T_{w,in} }}{L}, $$

(8)

$$ Q_{conv} = \dot{m}c_{p} \left( {T_{b,out} - T_{b,in} } \right) = \rho A_{cf} Uc_{p} \left( {T_{b,out} - T_{b,in} } \right) $$

(9)

where k_s, A_surf, A_cs, A_cf, h and L are thermal conductivity of wall material, surface area of solid–fluid interface, cross-sectional area of solid wall, cross-sectional area of fluid domain, heat transfer coefficient and length of microchannel/microtube, respectively. Nusselt number with axial wall conduction can be derived from Eqs. (7)–(9):

$$ Nu = \frac{{{\text{Convective}}\;{\text{heat}}\;{\text{transfer}}}}{{{\text{Conductive}}\;{\text{heat}}\;{\text{transfer}}}} $$

(10)

$$ Nu = \frac{{Q_{conv} }}{{{\text{Q}}_{cond} }} = \frac{{Q_{conv} }}{{Q_{radial} + Q_{axial} }} = \frac{1}{{\frac{{Q_{radial} }}{{Q_{conv} }} + \frac{{Q_{axial} }}{{Q_{conv} }}}} = \frac{1}{R + M} $$

(11)

where R is radial/transverse conduction number and M is axial conduction number. Using Eqs. (7)–(9) in Eq. (11), we get

$$ Nu = \frac{1}{{\frac{{\left( {k_{s} A_{surf} \frac{{\bar{T}_{a \, } - \bar{T}_{i} }}{{\delta_{s} }}} \right)}}{{\dot{m}c_{p} \left( {T_{b,out} - T_{b,in} } \right)}} - \frac{{\left( {k_{s} A_{cs} \frac{{T_{w,out} - T_{{w,\text{in} }} }}{L}} \right)}}{{\dot{m}c_{p} \left( {T_{b,out} - T_{b,in} } \right)}}}} $$

(12)

$$ Nu = \frac{1}{{k_{sf} \frac{S}{{A_{cf} }}\frac{{\left( {\bar{T}_{a \, } - \bar{T}_{i} } \right)}}{{\left( {T_{b,out} - T_{b,in} } \right)}}\frac{{D_{h} }}{\text{Pe}} - k_{sf} \frac{{A_{cs} }}{{A_{cf} }}\frac{{\left( {T_{w,out} - T_{{w,\text{in} }} } \right)}}{{\left( {T_{b,out} - T_{b,in} } \right)}}\frac{1}{\text{Pe}}\frac{{D_{h} }}{L}}} . $$

(13)

Equation (13) can be used for microchannels of any shape carved on a solid substrate. Here, S is conduction shape factor, which is defined as the ratio of surface area of applied/experienced heat flux to thickness of the wall. Nusselt number for different geometries considered in this work as in table 1 is calculated using Eq. (13), which requires value of S, which can be obtained from table 1.

Table 1 Conduction shape factor for different geometries.

Graphical method [28] is used for calculation of conduction shape factor S of straight and wavy microchannels where M is number of heat-flow lanes, N is the number of temperature increments between inner and outer surfaces, n is the number of curvilinear-square plots and L_c is total curve length of vertical wavy solid–fluid interface, which can be calculated by the least-square method to fit a continuous piecewise linear function.

2.1 Validation

Many correlations are available in the literature for predicting average Nusselt number that is developed based on experimental data. The expression for average Nusselt number given in Eq. (13) is validated by direct comparison to selected experimental results reported in the open literature.

2.1a Comparison to experimental data: So far, many experimental studies do exist in the literature related to heat transfer in microchannels and some of them are considered in the present study for validation. For example, Tso and Mahulikar [29] experimentally studied heat transfer in a circular microchannel using water as the coolant. The test section consists of multiple circular microchannels (d = 0.729 ± 0.027 mm) drilled in an aluminium plate. Experimental data reported in [29] are used in Eq. (13) to calculate average Nu and are compared to reported experimental average Nu, as shown in figure 2. Figure 2 shows a good agreement between the reported and predicted value of average Nu using Eq. (13).

Figure 2

Variation of average Nu with Re in a circular microchannel.

Validity of Eq. (13) for the non-circular channel is verified by comparison to experimental data reported in Sui et al [30], which deals with heat transfer in a wavy microchannel with a rectangular cross-section.

The available data presented by Sui et al [30] are found to be insufficient for predicting average Nu using Eq. (13). Therefore, to demonstrate the accuracy and reliability of Eq. (13), numerical study has been performed in a copper-based wavy microchannel exactly as considered in [30]. Desired data from this simulation are used in Eq. (13) for predicting average Nu. Average Nu is also calculated completely based on this numerical simulation. The reported experimental test piece (25 × 25 × 69.5 mm³) contains 60 parallel wavy (wavelength 2.5 mm, amplitude 259 μm) rectangular cross-section microchannels (205 μm × 404 μm) and here we assume that performance of every wavy microchannel is the same. Considering this, we numerically investigated heat transfer performance using water flow in a single wavy microchannel.

Figure 3 presents a comparison between average Nu obtained from numerical simulation, predicted using Eq. (13), and experimental Nu reported by Sui et al [30]. It is clearly depicted in figure 3 that the present numerical result and the prediction using Eq. (13) are in good agreement with the experimental data by Sui et al [30].

Figure 3

Variation of average Nu with Re in a wavy microchannel.

2.1b Comparison with existing correlations: Based on an experimental study on laminar flow heat transfer, Stephan and Preuβer [5] proposed a correlation for predicting average Nusselt number in circular tube subjected to constant T. Peng and Peterson [6] had proposed a similar correlation for the noncircular channel (subjected to q′′) based on their experimental study. The proposed correlation (both for circular and non-circular (see Eq. (13))) is validated against these two correlations and presented in figure 4 for Pr = 6.99, where average Nu varies with Flow Re. The required data for the proposed correlation are obtained from simulation of the exact condition. The proposed correlation is found to be in good agreement to that of Stephan and Preuβer [5] and Peng and Peterson [6].

Figure 4

Variation of average Nu with Re.

Thus, from this validation it can be concluded that the proposed correlation can be used for predicting average Nu in both circular as well as non-circular microchannels with either q′′ or T boundary conditions. The only limitation of Eq. (13) is that it is dependent on the axial temperature gradient, which is not possible to obtain precisely in any experimental work. However, the advantage of the proposed correlation is that calculation of convective heat transfer coefficient or heat flux at the solid–fluid interface is not required to obtain average Nu.

Next, to indicate the influence of axial conduction on microtube heat transfer, a detailed numerical investigation is performed and presented. Impact of conjugate heat transfer in terms of axial as well as radial thermal resistance is presented, which has never been explored in the available literature.

3 Numerical simulation

Considering angular symmetry, a two-dimensional simulation is carried out for which the computational domain in consideration is presented in figure 1. Unlike conventional circular tubes, the wall thickness of a microtube (δ_s) is of the order of or higher than its inner radius (represented here as δ_f). Therefore, while the thickness of the microtube (δ_s) is varied from 0.2 to 2 mm, the inner radius (δ_f) and the length of the microtube are maintained at constant values of 0.2 and 60 mm, respectively, such that the solid to fluid thickness ratio (δ_sf = δ_s/δ_f) varies from 1 to 10. The outer surface of the microtube is subjected to either q′′ or T separately. The cross-sectional faces of the solid wall are assumed to be adiabatic. Water is used as the coolant, which enters the inlet of the microtube at the ambient temperature of 300 K where the velocity of water at the inlet is assumed to be constant in the radial direction from the centre of the tube up to the inner radius. The inlet velocity of the fluid is varied such that the flow Re varies from 100 to 500. The conductivity of the solid wall (k_s) is varied such that the solid to fluid conductivity ratio (k_sf = k_s/k_f) varies from 2.26 to 646. The simulations were performed for a wide range of parameters as presented in table 2.

Table 2 Range of parameters considered in simulations.

Secondly, straight and wavy microchannels are also studied, where channel height (δ_f) and average channel width (ω_f or a) are kept constant at 0.9 and 0.6 mm, respectively, while amplitude (A) is varied. Thus, with the presence of different expansion factors, performance of a raccoon microchannel is different from that of a wavy microchannel even for both channels having equal waviness. If we compare both microchannels, width (ω_f or a) and height (δ_f) of the straight channel are the same as average width (ω_f or a) and height (δ_f) of the wavy microchannel. Thus, the microchannel cross-section is rectangular for all three microchannels. Additionally, to study the conjugate effect on overall heat transfer, substrate thickness (H) of all microchannels is varied from 1.8 to 5.4 mm, while channel height (δ_f) is kept constant at 0.9 mm. Variation of substrate thickness in dimensionless form is represented by δ_sf (ratio of δ_s to δ_f) where δ_s = H − δ_f (see figure 5). Thus, the channel aspect ratios (δ_f /ω_f) of straight and wavy microchannels remain constant at 1.5 throughout this study. However, channel aspect ratio varies along the length of the raccoon microchannel except at inlet (z = 0) and outlet (z = L), where it is 1.5.

Figure 5

Schematic diagram of (a) straight microchannel (SMC) and (b) wavy microchannel (WMC).

3.1 Governing equation and boundary condition

For this purpose, following assumptions are adopted:

• 1. The flow is steady, laminar and incompressible.

• 2. The Knudsen number is less than 0.01, namely the continuum flow regime. Therefore, the microscale thermal and fluidic system cannot take into account the effects of slip flow and temperature jump at the wall.

• 3. Viscous dissipation in the liquid domain is found to be small enough to be neglected for the range of parameters considered in the present study [22, 31, 32].

• 4. Constant thermo-physical properties of fluid (variation with temperature is negligible).

• 5. Heat loss by natural convection or radiation to ambient is neglected.

Thus the 2-D steady Navier–Stokes and energy equations are solved in ANSYS-Fluent^@ to describe the flow and heat transfer in the whole region. Based on the aforementioned assumptions the problem to be investigated is axisymmetric and the governing equations, i.e. continuity, Navier–Stokes and energy equations, are as follows.

For liquid domain:

$$ \nabla .\vec{u} = 0, $$

(14)

$$ \vec{u}\nabla \vec{u} = - \frac{1}{\rho }\nabla p + \frac{\mu }{\rho }\nabla^{2} \vec{u}, $$

(15)

$$ \vec{u}.\nabla T = \left( {\frac{k}{{\rho C_{p} }}} \right).\nabla^{2} T. $$

(16)

For solid domain:

$$ \nabla^{2} T = 0. $$

(17)

The associated boundary conditions are as follows:

$$ \frac{{\partial {\text{T}}}}{{\partial {\text{z}}}} = 0\;{\text{at}}\;{\text{z}} = 0\;{\text{and}}\;{\text{z}} = {\text{L}}\;{\text{and}}\;\updelta_{\text{f}} \le {\text{r}} \le (\updelta_{\text{f}} +\updelta_{\text{s}} ). $$

(18)

For a fully heated microtube

$$ q^{\prime \prime } \;{\text{or}}\;T = {\text{constant}}\;{\text{at}}\;r = \delta_{s} + \delta_{f} \left( {0 \le z \le L} \right), $$

(19)

$$ - {\text{k}}_{\text{s}} \frac{{\partial {\text{T}}}}{{\partial {\text{r}}}} = {\text{h}}({\text{T}} - {\text{T}}_{\text{f}} )\;{\text{at}}\;{\text{r}} =\updelta_{\text{f}} , $$

(20)

$$ u = \bar{u}\;{\text{at}}\;z = 0, $$

(21)

$$ u = 0\;{\text{at}}\;r = \delta_{f} , $$

(22)

$$ p = 0\;{\text{at}}\;z = L, $$

(23)

$$ \frac{{\partial {\text{T}}}}{{\partial {\text{r}}}} = 0,\;\frac{{\partial {\text{u}}}}{{\partial {\text{r}}}} = 0\;{\text{at}}\;{\text{r = 0}} . $$

(24)

A structured rectangular elements mesh is used for discretization and standard grid independence test procedure is adopted to select suitable mesh size for every geometry under consideration. The standard SIMPLE algorithm is employed to solve the governing differential equation of pressure–velocity coupling. A second-order discretization scheme is used for the pressure equation and second-order upwind scheme is used to solve both momentum and energy equations. The residual criteria for continuity, momentum and energy equations are taken to be 10⁻⁶, 10⁻⁶ and 10⁻⁹, respectively.

3.2 Grid independence check

As multiple microchannel geometries (see figures 1 and 5) are considered in this work, the suitable grid size of each microchannel geometry may be different. For this purpose, extensive grid convergence study is performed for each microchannel geometry to find suitable mesh size for each microchannel geometry. For demonstration, microtubes, straight and wavy microchannels with wall thickness to channel height/inner radius ratio δ_sf = 1 are considered and detailed geometrical dimensions of the microchannels are presented in table 3. The optimum finer mesh is selected to capture high fluxes (gradients) near solid–fluid interfaces and fluid region.

Table 3 Overall geometric dimensions of the microchannels shown in figure 5.

Table 4 presents different grids considered for straight, wavy and raccoon channels at Reynolds number of 100. Relative error (e%) [17] is calculated using

$$ {\text{e}}\% = \left| {\frac{{{\text{J}}_{1} - {\text{J}}_{2} }}{{{\text{J}}_{1} }}} \right| \times 100 $$

(14)

where J_i (i = 1, 2) represents parameter of interest, i.e. Nusselt number, pressure drop, etc. Here, J₁ is value of the parameter acquired from the finest grid, whereas J₂ represents value of the parameters obtained from other grids.

Table 4 Effect of grid size on average Nusselt number and pressure drop.

For attaining higher order accuracy in numerical results, convergence study is carried out and five suitable choices of grid size are made for all geometries and their grid numbers are shown in table 4. For the straight microchannel, it can be observed that local Nusselt number along the channel length is found to vary by 0.98% and pressure drop varies by less than 1.69% when shifted from the first grid (no. 1) to last grid (no. 5). Hence, grid no. 4 is selected with maximum error percentage within 0.65% for this study. Similarly, for the other two geometries (wavy and raccoon), grid no. 3 is suitably selected, which is highlighted (bold) in their relevant sections of table 4, as it reveals the best trade-off between both accuracy and CPU time.

3.3 Data reduction

The axial coordinate z in non-dimensional form is defined as

$$ z^{*} = \frac{z}{L}. $$

(26)

The non-dimensional local heat flux at the solid–fluid interface is defined as

$$ \phi = \frac{{q^{\prime\prime}_{e} }}{{q^{\prime\prime}_{i} }}. $$

(27)

Here $q^{\prime\prime}_{e}$ is the heat flux value experienced at the solid–fluid interface for either q′′ or T condition imposed on the outer surface of the tube, and $q^{\prime\prime}_{i}$ is the ideal/theoretical heat flux expected locally at the solid–fluid interface along the tube length. From energy balance between the outer surface and the interface, $q^{\prime\prime}_{i} = q^{\prime\prime}_{s} (1 + \delta_{sf} )$ where $q^{\prime\prime}_{s}$ is the heat flux on the outer surface of the tube that is (i) applied (constant along the length of the tube) in the case of q′′ condition and (ii) experienced (varying along the length of the tube) in the case of T condition. The dimensionless bulk and wall temperatures are given by

$$ \varTheta_{w} = \frac{{(T_{w} - T_{fi} )}}{{(T_{bo} - T_{bi} )}}, \, \varTheta_{f} = \frac{{(T_{f} - T_{fi} )}}{{(T_{bo} - T_{bi} )}} $$

(28)

where T_bi and T_bo are the bulk temperature at the tube inlet and outlet, respectively; T_b is the bulk temperature at any axial location and T_w is the wall temperature at the same location. Local Nusselt number and local heat transfer coefficient are given by

$$ Nu_{z} = \frac{{h_{z} \cdot D}}{{k_{f} }}, \, h_{z} = \frac{{q^{\prime\prime}_{i} }}{{(T_{w} - T_{f} )}}, $$

(29)

respectively. The average Nusselt number over total channel length is given by

$$ Nu = \frac{1}{L}\int\limits_{0}^{L} {Nu_{z} dz} . $$

(30)

3.4 Validation of numerical results

The numerical results of local Nusselt number are validated using Lee and Garimella [33] and Perkins et al [34] correlations obtained using water flow in a single microtube of 0.4 mm diameter and 60 mm length; q′′ of 45 kW/m² is imposed at the outer surface of microtube. It can be seen in figure 6 that numerical predictions are in good agreement with the correlations and theoretical value (Nu_th) in the fully developed region.

Figure 6

Axial variation of local Nusselt number.

4 Results and discussion

The parametric variations considered in this study are described in section 3, and also presented in table 2. Overall, the effect of flow Re, microtube wall thickness and its material on axial back conduction is explored with the help of axial variation of bulk temperature, heat flux and wall temperature at the solid–fluid interface. The complete study described earlier is carried out distinctly for two separate thermal conditions on the outer surface of the tube: q′′ and T.

4.1 Parametric study of axial wall conduction effect in microtube

This section highlights parameters that govern heat flow in an axial direction causing axial wall conduction. The parameters included in this study are radial/transverse conduction number (R), axial conduction number (M), axial conductive thermal resistance (R_cond,||), convective thermal resistance (R_conv), tube wall thickness to inner radius ratio (δ_sf), wall material thermal conductivity (k_sf) and flow Re.

The wall thickness of microtube is usually higher than the tube inner radius. In such a scenario, wall thermal resistance becomes an important factor that controls the overall heat transfer process. Considering this, effect of axial conductive thermal resistance (R_cond,||) is directly compared to a convective thermal resistance (R_conv) at different k_sf, δ_sf and Re for both q′′ and T on the outer surface of microtube and the results are listed in tables 5 and 6, respectively. Here, convective thermal resistance is inversely proportional to axial conductive thermal resistance. Hence, under ideal thermal condition, lower convective resistance always offers higher axial thermal resistance.

Table 5 Axial conduction and convective thermal resistance at different δ_sf, k_sf for (a) Re = 100 and (b) Re = 500 at q′′.

Table 6 Axial conduction and convective thermal resistance at different δ_sf, k_sf for (a) Re = 100 and (b) Re = 500 at T.

Table 5 presents a comparison between R_cond,|| and R_conv for different k_sf, δ_sf and Re for a microtube subjected to q′′. The results show that convective heat transfer in the microtube is lower at high k_sf (~337 to 646) compared with low k_sf values (~19 to 60.7) for all values of δ_sf and Re. This happens because a higher temperature gradient is observed at the solid–fluid interface; this allows more heat transfer towards the axial direction, causing low R_cond,||. Secondly, for Re = 500, thermal resistance is found to be almost independent of material properties as no significant change is observed with change in k_sf. Also, convective thermal resistance (R_conv) increases with increase in δ_sf. The negative sign indicates that convective thermal resistance decreases with an increase in immediate higher k_sf whereas for axial thermal resistance (R_cond,||), the negative sign indicates dominance of axial wall conduction.

For T boundary condition, convective thermal resistance does not make any impact on conduction heat transfer as the outer surface temperature remains unchanged. With the increase in δ_sf, the solid–fluid interface moves away from the outer surface. Thus, the decrease in solid–fluid interface temperature with respect to applied condition is limited due to convection to moving fluid. From table 6, it is clear that with increasing δ_sf, R_conv decreases for all k_sf. This happens because low conductive material offers higher thermal resistance. Thus, limited fall in temperature at the solid-fluid interface is observed. With increasing k_sf, the fall in interface temperature with respect to applied condition is relatively higher. This induces negative sign in percentage reduction in both R_conv and R_cond,||.

To explore the insight mechanism of heat transfer within the wall of microtube, radial/transverse conduction number (R) and axial conduction number (M) are computed and their combined effect is presented in figure 7 in terms of the ratio R/M. Overall heat conduction through the solid wall consists of both axial as well as radial/transverse conduction between the outer surface and the solid–fluid interface. Theoretically, at constant Nu, radial conduction number (R) decreases with increasing axial conduction number (M) and vice versa. This is indicated mathematically in Eq. (13). For ideal performance of microtubes it is necessary that axial conduction number (M) should be minimum possible. Figure 7 shows the influence of conduction parameters over a range of k_sf, δ_sf and Re for both q′′ and T.

Figure 7

Influence of conduction parameters with varying k_sf.

It can be observed in figure 7 that at low k_sf, ratio R/M attains the highest value. This happens because low conductive material (k_sf = 2.26) offers higher axial thermal resistance; thus M attains a very small value, which increases the value of R/M. As k_sf increases, R/M starts decreasing and attains lower values and with further increase in k_sf, R/M attains constant value for all k_sf, δ_sf and Re. This is because a higher conductivity material offers lower thermal resistance, which results in higher temperature gradient (in solid region) between inlet and outlet regions. Thus, it allows more heat conduction in the axial direction, resulting in higher M. Additionally, the value of R at any k_sf is always found to be greater than that of M for both q′′ and T boundary conditions. Secondly, it can be seen that ratio R/M attains higher value for T boundary condition compared with q′′ boundary condition, which means that with T boundary condition (see figure 7(c) and (d)), M values for all k_sf, δ_sf and Re attain lower values compared with q′′ boundary condition (see figure 7(a) and (b)).

Again, it is also observed that with increase in δ_sf, the potential of heat flow within the wall in axial direction increases, which results in an increase in the magnitude of M and decrease in the magnitude of R in the same proportion. This indicates the dominance of axial wall conduction. Additionally, the relative difference of R/M increases for T boundary condition compared with q′′ boundary condition. This indicates that with increase in δ_sf, dominance of axial wall conduction is found to be higher for T boundary condition compared with q′′ boundary condition. It is also observed that with an increase in Re, R/M attains higher values compared with low Re for both q′′ and T boundary conditions. Thus, it can be said that higher Re reduces the dominance of axial wall conduction.

Combined effects of radial conduction number (R) and axial conduction number (M) are presented in figure 8. The value of Nu obtained using Eq. (13) is directly compared with the numerical Nu average calculated using Eq. (30). To visualize the impact of tube material on overall heat transfer, average Nusselt number predicted for varying k_sf (over a broad range) at different flow Re is presented in figure 8(a) and (b) for q′′ and T, respectively. The prediction of Nu using Eq. (13) for different parameters is almost the same as the prediction using Eq. (30), which is based on present numerical simulation. For the case of q′′, the deviation between the two predictions using Eqs. (13) and (30) increases with increasing δ_sf, and decreases with increasing Re (see figure 8(a)). For the case of applied T, the deviation between the two predictions using Eqs. (13) and (30) increases with increasing δ_sf, and Re (see figure 8(b)). Maximum deviation is within 6.42% and 3.62%, respectively, for constant wall heat flux (figure 8(a)) and T (figure 8(b)). Overall it can be concluded that, at higher δ_sf, the percentage difference between predicted Nu using Eqs. (13) and (30) increases marginally.

Figure 8

Average Nusselt number varying with k_sf.

The effect of solid conductivity can be seen prominently in figure 8. For q″, average Nu increases as k_sf is decreased from a higher value (see figure 8(a)). However, beyond a threshold value of k_sf, the average Nu starts to decrease with further increase in the value of k_sf. Thus, there exists an optimum k_sf at which average Nu is maximum. This can be attributed to higher radial thermal resistance compared with axial thermal resistance when k_sf value decreases below the threshold value. However, the scenario is different for T as shown in figure 8(b), where average Nu attains higher value at low k_sf and decreases with increasing k_sf. Again, beyond a threshold value of k_sf, Nu remains almost constant or increases by a marginal value for all set of δ_sf. However, with increasing tube thickness, thermal resistance in radial direction increases, which results in low Nu for all k_sf for both thermal boundary conditions.

Again, for any value of k_sf and δ_sf, the magnitude of average Nu increases with increasing flow Re. This is due to increase in thermal entry length with increasing flow Re. This phenomenon is true for both thermal conditions of q″ and T. Secondly, for q″, the average Nu decreases with increasing wall thickness irrespective of any value of k_sf, and Re, which can be seen in figure 8(a). However, for T, average Nu increases with increasing wall thickness (see figure 8(a)), which is exactly opposite of what happens in case of q″. This is because higher wall thickness causes higher axial back conduction in solid wall, which leads towards isothermal wall temperature at the solid interface rather than q″, though q″ is applied on the outer surface. Overall, it can be concluded that higher wall thickness decreases overall heat transfer rate when q″ is applied while it increases overall heat transfer when T is applied.

Similarly, the variation of average Nu for straight and wavy microchannels as a function of k_sf is presented in figure 9. At low k_sf, average Nu in both straight and wavy microchannels attains lower value for all δ_sf and Re. With further increase in k_sf, Nu increases and attains the highest value for both straight and wavy microchannels at k_sf = 22 and 60.6, respectively. Beyond these values of k_sf, average Nu in straight microchannel starts decreasing with increase in k_sf for all δ_sf and Re while in wavy microchannel it varies negligibly. Additionally, Nu obtained using Eq. (13) is compared to numerical simulation and it is found that for all k_sf there is a good agreement for low δ_sf in straight microchannel and little deviation is observed for higher δ_sf while for wavy microchannel a good match is found for all k_sf, δ_sf and Re.

Figure 9

Variation of average Nu for straight and wavy microchannels as a function of k_sf for q′′.

From this discussion, it can be recommended that use of wall materials of relatively high conductivity in thick-walled tube or channel (e.g. copper) induces axial wall conduction. Therefore, a material with relatively lower wall conductivity is better in thick-walled tube/channel from the axial wall conduction point of view.

4.2 Effect of wall to fluid conductivity ratio and tube wall thickness to inner radius ratio

The flux experienced at the solid–fluid interface actually decides the overall heat transfer process as it influences the local wall and fluid temperature, which in turn decides the local heat transfer coefficient and local Nusselt number. Therefore, the main parameters of interest for this study at the solid–fluid interface are (a) peripheral averaged local heat flux, (b) local bulk temperature and (c) peripheral averaged local wall temperature. Considering angular symmetry (and two-dimensional study to simulate this condition), the values of flux and wall temperature at different axial location points are considered. Similarly, the bulk temperature is calculated along the radial line. These parameters help us in concluding/predicting the degree to which the axial back conduction in the solid domain influences the local Nusselt number. The conductivity ratio (k_sf) is defined as the ratio of thermal conductivity of the microtube wall material (k_s) to that of the working fluid (k_f).

The axial variation of dimensionless wall heat flux (ϕ) is presented in figures 10 and 11 for q″ and T boundary condition, respectively, at different Re, k_sf, and δ_sf. Among a wide range of k_sf values considered in this study, only three representative values of k_sf, including the extreme lower and higher value (k_sf = 2.26 and 646), are reported in figures 10, 11, 12, 13, 14 and 15. As the thickness of the solid wall increases, the heated boundary (outer surface) moves away from the actual solid–fluid interface. Ideally, the dimensionless local heat flux at the solid–fluid interface throughout the length of the microtube should be equal to unity as per the definition used in Eq. (27). This implies that the thermal condition at the solid–fluid interface should have been exactly the same as that imposed on the outer surface of the tube. Any deviation from the ideal value of unity indicates that the thermal condition (either q″ or T) at the interface is not the same as that of the corresponding imposed condition on the outer surface. This deviation occurs because of axial flow of heat by conduction in the annular space between the outer surface and the solid–fluid interface, i.e. along the solid wall, called axial wall/back conduction. The direction of this heat flow will be towards the inlet of the microtube.

Figure 10

Axial variation of dimensionless local heat flux (at the solid–fluid interface) for q′′.

Figure 11

Axial variation of dimensionless local heat flux (at the solid–fluid interface) for T.

Figure 12

Axial variation of dimensionless wall and bulk temperature for q′′.

Figure 13

Axial variation of dimensionless wall and bulk temperature for T.

Figure 14

Axial variation of local Nusselt number for q′′.

Figure 15

Axial variation of local Nusselt number for T.

It can be observed in figure 10(a)–(c) that the dimensionless local heat flux (ϕ) at the interface is uniform and equal to unity almost throughout the length irrespective of the value of flow Re and δ_sf. This corresponds to k_sf = 2.26, the lowest value among all. The value of ϕ corresponding to k_sf = 646 (see figure 10(d)–(f)) can be found to be completely deviating from the ideal value of unity throughout the length of the microtube. This indicates that with increasing conductivity of the solid (i.e. k_sf), the resistance to axial heat conduction towards the inlet reduces; thus the heat flux near the inlet becomes more than unity, while it becomes less than unity near the outlet. Secondly, it can be observed that for a given solid material (i.e. k_sf) and the relative wall thickness (δ_sf), the deviation in the value of ϕ from its ideal value of unity decreases at any axial location. This can be explained as follows: the higher the flow Re, the more the amount of heat transfer by convective heat transfer process. Thus, there is less opportunity for conduction of heat due to decrease in the slope of the axial wall temperature. Finally, it can be observed that for a given k_sf and Re, the deviation in the value of ϕ from its ideal value of unity increases with increasing wall thickness (δ_sf). This is because of decrease in the thermal resistance to axial heat conduction with increasing wall thickness. At this junction it can be concluded that lower k_sf, and δ_sf, and higher Re are favourable to experience ideal heat flux value at the solid–fluid interface when q′′ is imposed on the outer surface of the tube.

Figure 11 presents the equivalent information for a microtube subjected to T condition imposed on its outer surface as in figure 10 for q′′. Ideally, there is no axial temperature gradient. and thus little possibility for axial wall conduction. The basic difference here from that of constant wall heat flux is that some amount of heat flux will be experienced at the outer surface of the microtube, which is used to define the dimensionless heat flux (ϕ) as described in section 3.3. Here, it can be observed that there is hardly any effect of Re, k_sf and δ_sf except near the inlet.

Figures 12 and 13 show the axial variation of dimensionless wall and bulk temperature as a function of k_sf, Re and δ_sf corresponding to constant q′′ and T condition, respectively, on the outer surface of the microtube. For q′′ applied on outer surface of the tube, the bulk temperature varies linearly between the inlet and the outlet. As per Eq. (28), the limiting values of Θ_f are 0 and 1, between which the value of Θ_b varies linearly. Again, the difference between the wall and the bulk temperature remains constant in the thermally developed region. This occurs when the wall thickness of the tube is negligible compared with its inner radius. In such case, there is no opportunity for axial back conduction along the solid wall. A similar phenomenon for axial variation of bulk and wall temperature can be found in figure 12(a), which corresponds to lower k_sf (= 2.26) and Re (= 100). With increasing Re, the thermal development length increases, which can be observed in figure 12(b) and (c). Again, with increasing Re, the fluid outlet temperature decreases as the same amount of heat is added by applying q′′ on the outer surface of the tube. This makes the difference in fluid outlet and fluid inlet temperatures smaller; thus, the value of wall temperature Θ_w (as defined in Eq. (28)) increases. Secondly, it is important to observe in figure 12(a)–(c) that there is no effect of wall thickness, i.e. δ_sf, which is varied from 1 to 10.

When the k_sf value is further increased to 646, a drastic change is observed, which is seen in figure 12(d)–(f). Here, the effect of wall thickness δ_sf starts to dominate. With increase in wall thickness (i.e. δ_sf), the wall temperature near the inlet increases while it decreases near the outlet; thus, the wall temperature is flattened. This implies that the axial wall conduction distorts the thermal condition experienced at the solid–fluid interface. The thermal condition experienced at the solid–fluid interface is closer to the isothermal wall temperature, rather than the constant wall heat flux applied. This can be supported by the axial variation of bulk temperature, which deviates away from its linearity with increasing δ_sf. This deviated axial variation of bulk temperature at higher δ_sf is closer to the bulk temperature of a situation of applied constant T.

Next, it can be observed in figure 13(d) that axial wall temperature is isothermal except only near the inlet, which is due to the effect of inlet. Therefore, it can be concluded that the condition experienced at the solid–fluid interface is exactly the same as that applied on the outer surface of the microtube. With increasing flow Re, the thermal development length increases, which can be seen in figure 13(e) and (f). Secondly, there is no effect of microtube wall thickness. As the k_sf value decreases, the wall temperature deviates from isothermal condition. Also, the bulk temperature approaches towards linearity. Additionally, the wall thickness starts to show its effect, which is more at lower flow Re. This can be observed in figure 13(a)–(c).

The combined effect of local heat flux, bulk and wall temperature can be found in the value of Nusselt number, which is defined in Eq. (29), consisting of these three in dimensionless form. The fully developed Nusselt number values are 3.66 and 4.36, respectively, for constant T and q′′ conditions [35]. Fully developed Nu value is expected to be close to 3.66 corresponding to the situation shown in figure 15(d)–(f). The axial variation of local Nusselt number corresponding to figures 10 and 12 is presented in figure 14, and corresponding to figures 11 and 13 is presented in figure 15. The values of 3.66 and 4.36 anticipated above based on figures 10, 11, 12 and 13 are found to be accurate in the corresponding situation in figures 14 and 15, where the two limiting fully developed Nu values are represented by horizontal dashed line.

5 Summary and conclusion

Conjugate heat transfer in single-phase laminar developing flow in microtube is studied numerically to find the basic difference in conjugate heat transfer process experienced in a microtube subjected to two different thermal conditions (q″ and T) imposed on its outer surface. Water at 300 K enters the microtube and flows through it. The cross-sectional faces of the tube are considered to be adiabatic. The effects of wall thickness, wall material conductivity and flow rate on the axial wall conduction of the microtube are studied. Dimensionless variables considered in this study are (i) solid wall thickness to inner radius ratio (δ_sf ∼ 1 to 10), solid wall to working fluid conductivity ratio (k_sf ~2.2 to 646) and flow Re (100–500). An expression for Nusselt number is presented, which includes both radial (or transverse) and axial wall conduction effects. Additionally, conjugate heat transfer effect in the straight and wavy microchannels is also studied and comparison between numerical simulation and the generalized expression for Nusselt number is presented.

The outcomes of this study are as follows:

• 1. An equation (Eq. (13)) is presented for calculating Nu of any geometry of microchannel subjected to either q′′ or T boundary condition.

• 2. The present study reveals that with Re ≥ 500, the performance of microtube is independent of wall thickness and tube material effect. Thus, axial wall effect can be neglected in such cases.

• 3. In today’s scenario, most of the single-phase laminar flow analysis is performed for the purpose of heat transfer enhancement. Considering this, a variety of complex shape designs (ribs and cavity, twisted microtube, wavy passage, fins, etc.) has been proposed by the various researchers. Keeping the pressure loss in mind, the Reynolds number cannot be increased; thus, in such conditions, axial wall conduction effect cannot be neglected.

• 4. For q′′ condition, it is found that with increasing conductivity of the microtube wall material, the axial back conduction dominates; thus, it distorts the heat flux at the solid–fluid interface. The axial variation of wall temperature is flattened and it becomes closer to isothermal wall temperature.

• 5. For T condition, it is found that the behaviours are exactly opposite to those observed in case of constant wall heat flux. Axial wall conduction starts to dominate for low-wall-conductivity material, and the effect of tube thickness gets prominently observed. With increasing flow Re, the situation resembles that of q′′ experienced at the solid–fluid interface.

• 6. It is found that for q′′, there exists an optimum-wall-conductivity material for which the average Nusselt number over the channel length is maximum. However, no such observation is found in case of constant wall heat flux condition, where it is found that the average Nusselt number over the channel length continuously decreases with increasing wall material conductivity.

From this work as well as previous works in this field, it has already been established that conjugate effects influence overall heat transfer, including local wall temperature, bulk temperature and Nusselt number, in both circular and non-circular mini/micro- as well as conventional channel/ducts. Therefore, it is now high time to include conjugate effects in textbooks on heat transfer/convective heat transfer in the relevant section. This will enable budding researchers in this field not committing any mistakes in experimental/numerical study to devote some time in exploring this phenomenon at a later stage of their research.