The conjugate heat transfer of the partially heated microchannels

Abstract

In this paper, the conjugate heat transfer of the water flow inside the microtube (D _i/D _o = 0.1/03 and 0.1/0.5 mm) was investigated. The laminar regime was considered with Re up to 200, input heat transfer rate of Q ₀ = 0.1 W and variable thermophysical properties of the water. Two different cases of the partial joule heating were considered for the tube wall. In the first case the tube wall was heated near the inlet of the tube (upstream heating) while, in the second case, the outlet portion of the wall was heated (downstream heating). In order to investigate the influence of the tube material on the heat transfer behavior and limits of the axial conduction inside the wall, three different tube wall materials were considered, stainless steel (k = 15.9 W/m K), silicon (k = 189 W/m K) and copper (k = 398 W/m K).

1 Introduction

The microchannel heat transfer and fluid flow has gained the interest in the last decade due to the downsizing of the thermal devices used in various fields of everyday life. The cooling of the VLSI devices, biomedical applications, micro-heat-exchangers are some of the examples where the fundamentals of the microchannel heat transfer and fluid flow are essential for a proper design of these devices.

It has to be stated that the first microchannel fluid flow experiment was made by Poiseuille [1] in 1870 on a glass tube with internal diameter ranging from 29 to 140 μm with a water as the working fluid and non-heating working conditions. Based on these results, the well-known relation for the volume flow rate was established and extended lately to the macrochannels.

Tuckerman and Pease [2] have increased the interest on microchannel heat transfer phenomena with the microchannel heat sink used for the cooling of the VLSI devices. Wu and Little [3, 4] have made the microchannel heat transfer and fluid flow experiments used for designing the Joule–Thomson micro-refrigerator. The working fluid in their research was nitrogen and inner diameters of the tubes were from 100 to 300  μm. Their heat transfer and hydrodynamic results shown differences against the conventional results for macrotubes. In the following years, large amount of work have been done in order to explain these discrepancies. Sobhan and Garimella [5] have presented the intuitive review of these papers.

Morini [6] has also presented the review on a single-phase microchannel heat transfer, indicated some of the reasons for a large dispersion of the experimental results. Both gas and liquid flows have been considered.

In the recent years, Lelea et al. [7], have made the experimental research on microtube heat transfer and fluid flow with inner diameters between 100 and 500 μm for laminar regime of the water flow. These results have shown the good agreement with the conventional theories even for the entrance region of the tube. Tiselj et al. [8] have presented the experimental research on microchannel heat transfer and fluid flow of water through the multichannel configuration with triangular cross-section of the channels. The hydraulic diameter was 160  μm and low Re number range (3.2–64) considering the axial conduction in the tube wall. The results are also in good agreement with conventional theories, confirmed also with the numerical modeling using the conventional set of the Navier–Stokes equations. Lee et al. [9] have investigated the laminar fluid flow of the water through the multichannel configuration of the rectangular cross-section with a hydraulic diameter from 318 to 903 μm. Their experimental and numerical results shown that, classical continuum theory can be applied for microchannels, considered in their study. On the other hand, the entrance and boundary effects have to be carefully analyzed in the case of theoretical approach.

Bahrani et al. [10] analyzed the influence of the surface roughness on laminar convective heat transfer and developed the analytical model for estimating this behaviour. The authors found that surface roughness may increase the thermal performance and pressure drop of the microtube. At the same time the convective heat transfer coefficient slightly increases by increasing the wall roughness.

The outcome of the research reports mentioned above, is that special attention has to be paid to macroscale phenomena that are amplified at the microscale. For example, due to a high heat transfer rate, the temperature variable fluid properties have to be considered. Lelea [11] has investigated the influence of the temperature dependent fluid viscosity on Po number. On the other hand, the small diameter and large length of the tube can result in viscous heating even in the case of liquid flow, as presented in [12].

On the other hand, the axial conduction through the tube wall has to be considered in the case of the microchannel heat transfer due to the high ratio between the inner and outer tube diameter, unusual in the case of the macrochannels. Maranzana et al. [13] have analyzed the influence of the axial conduction in the tube wall on microchannel heat transfer. The fluid flow between the parallel plates as well as the fluid flow in the counter flow heat exchanger was considered. It was found that the axial conduction has the influence on heat transfer parameters as far as the axial conduction number M, defined in this study, is higher than 10⁻². In this case the total length of the tube was heated. However, in industrial or laboratory applications, the heating length is not always equal to the total length of the tube.

For this reason, in the present research two cases were considered: the upstream heating where the first half of the tube was heated and downstream heating where the second half of the tube was heated. As the tube material has the great impact on axial conduction through the tube wall, three different materials are considered, stainless steel, silicon and copper. The axial conduction through the tube wall is decreasing as the Re number is increasing, so the low Re number regime is considered. Moreover, in this paper, the axial conduction influence was analyzed through the input and outlet heat transfer ratio that in fact is the microchannel heat balance or heat losses.

2 Numerical details

In order to discuss the axial conduction influence, the velocity and temperature distributions were numerically solved taking into account the temperature variation of the fluid properties, procedure described in [7, 11].

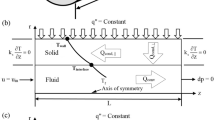
The computational domain is presented in Fig. 1, as follows:

• The fluid flow domain defined at r = 0, R _i and z = 0, L

• The temperature field domain defined at r = 0, R _o and z = 0, L

The outer portion of the tube has two parts, the heated and insulated part. So, as shown in Fig. 2, the respective insulated part was included in the numerical domain. The following set of partial differential equations is used to describe the phenomena, taking into account the variable thermophysical properties of the water

Fig. 1

The calculation domain

Fig. 2

The heating positions

Continuity equation

$$ \frac{{\partial (\rho (T)u)}}{{\partial z}} + \frac{1}{r}\frac{{\partial (r \rho (T) v)}}{{\partial r}} =0 $$

(1)

Momentum equation

$$\frac{{\partial (\rho (T)vu)}}{{\partial r}} + \frac{{\partial (\rho (T)uu)}}{{\partial z}} = - \frac{{{\rm d}p}} {{{\rm d}z}} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({\mu (T)r\frac{{\partial u}}{{\partial r}}} \right)} $$

(2)

Energy equation

$$ \frac{{\partial (\rho (T)c_{p} (T)vT)}}{{\partial r}} + \frac{{\partial (\rho (T) c_{p} (T)uT)}}{{\partial z}} = {\left[ {\frac{1}{r}\frac{\partial}{{\partial r}}{\left({k(T) r\frac{{\partial T}}{{\partial r}}} \right)} + \frac{\partial}{{\partial z}}{\left({k(T)\frac{{\partial T}}{{\partial z}}} \right)}} \right]} $$

(3)

At the inlet of the tube, the uniform velocity and temperature field is considered, while at the exit the temperature gradient is equal to zero.

The boundary conditions are

$$ \begin{array}{ll} z = 0, \quad 0 < r < R_{\rm o}:& u = u_{\rm 0}, \quad T = T_w = T_{\rm 0}\\ 0 < z < L_{\rm tot} :& r = 0,\quad\frac{{\partial u}}{{\partial r}} = 0{,} \quad \frac{{\partial T}}{{\partial r}} = 0{,} \quad v = 0\\ & r = R_i, \quad u = v = 0 \end{array} $$

The Joule heating of the tube wall can be expressed either by the uniform heat generation through the tube wall or by the uniform heat flux imposed on the outer surface of the wall. For the latter case, the boundary condition is defined as,

$$ \begin{aligned} r &= R_{\rm o} :\quad\quad q_{\rm o} = k_{\rm s} \frac{{\partial T}}{{\partial r}} \quad (\hbox{for the heated portion of the tube})\\ k_{\rm s} \frac{{\partial T}}{{\partial r}} &= 0 \qquad\qquad (\hbox{for the insulated portion of the tube}) \end{aligned} $$

where q _o is the heat flux based on the outer heat transfer area of the tube wall.

$$ z = L_{\rm tot}, 0 < r < R_o:\quad \frac{{\partial T}}{{\partial z}} = 0 $$

The conjugate heat transfer procedure, implies the continuity of the temperature and heat flux at the solid–liquid interface defined as,

$$ \begin{aligned} r &= R_{\rm i} : T_{\rm s} |_{\rm Ri+} = T_{\rm f} |_{\rm Ri-}\\ k_{\rm s} {\left({\frac{{\partial T_{\rm s}}}{{\partial r}}} \right)}_{{R_{\rm i} +}} &= k_{\rm f} {\left({\frac{{\partial T_{\rm f}}}{{\partial r}}} \right)}_{{Ri-}} \end{aligned} $$

The partial differential equations (1)–(3) together with boundary conditions, are solved using the finite volume method described in [14].

First, the parabolic flow field condition is considered and the velocity field is solved. The temperature field, as a conjugate heat transfer problem, was then solved as the elliptic problem using the obtained velocity field. The fluid flow regime is considered to be a steady-state laminar flow with variable fluid properties. In order to evaluate fluid properties (density, viscosity and thermal conductivity), the subroutines from Computer package PROPATH v. 10.2 are used in the present code.

As a consequence of the temperature dependent fluid properties, iterative procedure is needed to obtain the convergence of the fluid properties (viscosity, thermal conductivity, density and specific heat capacity) through the successive solution of the flow and temperature field.

A tube wall and water flow inside the tube, are considered as one domain and harmonic mean values for the thermal conductivity are calculated at the solid–liquid interface [14]

$$ k_{\rm m} = {\left({\frac{{1 - f}}{{k_{\rm s}}} + \frac{\rm f}{{k_{\rm f}}}} \right)}^{{- 1}} $$

The viscosity in the solid region was set to a very large value, in order to handle discontinuities between these two domains.

In order to test the grid sensitivity, two grids have been used. The coarser one with 250 cells in radial direction and 400 cells in axial direction and finer grid with 500 and 800 cells in z- and r- direction, respectively. Differences obtained for Po and Nu were smaller than 0.1%, so the coarser grid has been used for further calculations.

Although the numerical model was verified with microtube experimental results in [7] and [11], additional validation was made with experimental results of Piva and Pagliarini [15]. In this work, the axial conduction in the copper tube wall was used to simulate the exponential boundary conditions H5. The comparison is presented in Fig. 3 for copper tubes with D _i/D _o = 10/12 mm, total length of L _tot = 750 mm, water as the working fluid with Re = 611 and heat transfer rate Q = 9.89 W. The good agreement between the experimental and numerical results is observed.

Fig. 3

The code validation with experimental results presented in [15]

3 Results and discussion

The microtube conjugate heat transfer analysis was made for two values of the wall thickness D _i/D _o = 0.1/0.3 and 0.1/0.5 mm and three different tube materials, stainless steel (k = 15.9 W/m K), silicon (k = 198 W/m K) and copper (k = 398 W/m K). In order to investigate the axial conduction behaviour in the tube wall, the low Re range was considered Re < 200. The input heat transfer rate was constant for all the runs Q ₀ = 0.1 W.

As it was stated in Faghri and Sparrow [16], in the case of simultaneous wall and fluid axial conduction, the heat transfer coefficient is a function of three unknowns Q, T _wand T _b each of them function of axial distance. So, the main issue is how to estimate the tube wall axial conduction influence on fluid flow and thermal characteristics.

In Faghri and Sparrow [16], the non-dimensional parameter was defined as the measure of this influence:

$$\ I = \frac{{k_{\rm s} \delta}}{{k_{\rm f} R}} $$

(4)

Cotton and Jackson [17] demonstrated that the effect of wall conduction is defined with the following parameter:

$$ I = \frac{{k_{\rm s}}}{{k_{\rm f}}} {\left[ {\frac{\delta}{{D_{\rm i}}} {\left({1 + \frac{\delta}{{D_{\rm i}}}} \right)}} \right]} \frac{1}{{Pe^{2}}} $$

(5)

More recently, Maranzana et al. [13] defined the axial conduction parameter for two dimensional micochannel fluid flow

$$ I = \frac{{r^{2} {\rm NTU}}}{{Bi}} $$

(6)

Chiou [18] have defined the following conductance number as the parameter for the estimation of the wall axial conduction:

$$ I = \frac{{A_{\rm s}}}{{A_{\rm f}}} \frac{{D_{\rm i}}}{L}\frac{1}{{Pe}} \frac{{k_{\rm s}}}{{k_{\rm f}}} $$

(7)

From the relations presented above, it is obvious that wall axial conduction depends on thermal conductivity ratio k _s/k _f, Peand diameters ratio D _e/D _i. The question is what is the practical implication of the axial conduction in the tube wall. For instance, one might be interested in the heat losses and consequently in the overall input and output heat transfer rate ratio. So, in Figs. 4, 5, 6 and 7 the ratio Q/Q ₀ versus Re has been presented, where Q is calculated from

$$ Q = {\mathop m\limits^.} c_{p} \left(T_{\rm out} - T_{\rm in} \right) $$

(8)

From Fig. 4, one can conclude that in the case of the downstream heating, D _i/D _o = 0.1/0.3 mm and for the entire range of Re, there is no axial conduction inside the tube wall, considering that the input heat transfer rate is equal to the output convective heat transfer rate. In the case of the larger diameter ratio D _i/D _o = 0.1/0.5 mm (Fig. 5) and downstream heating, only for the copper tubes and very low Re <  50, the output heat transfer rate is 12% lower than the input value.

Fig. 4

The heat transfer rate ratio versus Re for downstream heating and diameter ratio D _i/D _o = 0.1/0.3 mm

Fig. 5

The heat transfer rate ratio versus Re for downstream heating and diameter ratio D _i/D _o = 0.1/0.5 mm

In the case of the upstream heating (Figs. 6, 7), except for the stainless steel tubes, the heat losses are obvious for all other cases. In the case of the silicon tubes, Q/Q ₀ is decreasing to 0.9 for D _i/D _o = 0.1/0.3 mm, and to 0.75 for D _i/D _o = 0.1/0.5 mm.

Fig. 6

The heat transfer rate ratio versus Re for upstream heating and diameter ratio D _i/D _o = 0.1/0.3 mm

Fig. 7

The heat transfer rate ratio versus Re for upstream heating and diameter ratio D _i/D _o = 0.1/0.5 mm

The highly conducted copper tubes facilitate the axial conduction in the tube wall resulting in heat losses of almost 25% for D _i/D _o = 0.1/0.3 mm and 55% for D _i/D _o = 0.1/0.5 mm.

It is obvious that Q/Q ₀, depends on the heating position. Apparently, in the case of the downstream heating the wall axial conduction is inactive and the question is if this is the correct prediction. The answer on this uncertainty, one may find from the graph presenting the local heat flux distribution along the fluid flow. The heat flux is calculated at the fluid–solid interface and can be expressed as,

$$ q = - k_{\rm f} {\left({\frac{{\partial T}}{{\partial r}}} \right)}_{{r = R_{\rm i}}} $$

(9)

Although the graph in Fig. 4 indicated the no-axial conduction case for the copper tube with D _i/D _o = 0.1/0.3 mm and downstream heating, from Fig. 8 it is clear that axial conduction exists for the silicon and copper tubes. The explanation can be found from Fig. 9 where the heat flux versus axial distance was presented for the copper tube. It can be seen that heat flux generated in the upstream section, described by surface 0BC is equal to the heat flux loss in the downstream section described by surface BDE.

Fig. 8

The heat flux variation versus axial distance for the downstream heating, diameter ratio D _i/D _o = 0.1/0.3 mm and Re = 12.95

Fig. 9

The heat flux variation versus axial distance for the downstream heating, diameter ratio D _i/D _o = 0.1/0.3 mm, Re = 12.95 and copper tube

The same conclusion can be outlined from the local heat flux distribution for the silicon tube. In the case of the stainless steel tube, the heat flux is equal to zero in the upstream section and in the range of the input heat flux in the downstream section.

In the case of the tubes with larger wall thickness D _i/D _o = 0.1/0.5 mm and lower Re = 12.95, the heat flux generated in the upstream section is not equal to the heat flux dispersed in the downstream section (Fig. 10), as a consequence the heat loss is about 12%. As the Re is increasing (Fig. 11), the heat transfer phenomena, is approaching the no-axial conduction case.

Fig. 10

The heat flux variation versus axial distance for the downstream heating, diameter ratio D _i/D _o = 0.1/0.5 mm and Re = 12.95

Fig. 11

The heat flux variation versus axial distance for the downstream heating, diameter ratio D _i/D _o = 0.1/0.5 mm and Re = 202.85

In the case of the upstream heating and stainless steel tubes (Figs. 6, 7) the Q/Q ₀ = 1. The same conclusion can be found from Figs. 12 and 13, where heat flux is equal to the input value in the upstream region and equal to zero in the downstream portion of the tube. In the case of the silicon tubes, the input and output heat flux are almost equal as the Re >  50. It is also observed that heat flux decreases from input value at the entrance, to zero at the end of the heated portion. This is especially obvious for the case of the greater thickness of the tube wall. As the heat flux is vanishing along the non-heated part of the tube, it is plausible to expect that heat might be dispersed through the inlet part of the tube wall. As the Re is increasing to Re = 53.53 and 202.85, the heat losses are lower and consequently the heat flux is approaching the input value.

Fig. 12

The heat flux variation versus axial distance for the upstream heating, diameter ratio D _i/D _o = 0.1/0.5 mm and Re = 12.95

Fig. 13

The heat flux variation versus axial distance for the upstream heating, diameter ratio D _i/D _o = 0.1/0.5 mm and Re = 202.85

As the thermal conductivity is larger, the latter phenomena is more obvious. From Figs. 6 and 7, the output heat transfer rate is decreasing to 75% of the input heat transfer rate for D _i/D _o = 0.1/0.3 mm and to 45% for D _i/D _o = 0.1/0.5 mm. At higher D _i/D _o = 0.1/0.5  mm and lower Re = 12.95, even the entrance value of the heat flux is considerably lower than the input value.

In Fig. 14 the local variation of the wall and bulk temperature along the tube has been presented for low Re = 12.95. In this case a difference between the bulk and wall temperature is very small, so these distributions are overlapping for specific tube material and heating position. The temperature variation in the case of the stainless steel tubes, is the one of no-axial conduction phenomena, with the inlet and maximum allowable temperature in the non-heated and heated sections, respectively. For the silicon tubes and upstream heating, as a consequence of heat losses, the outlet temperature is lower than the maximum temperature like in the case of the no-axial conduction.

Fig. 14

The wall and bulk temperature variation versus axial distance for various tube materials, Re = 12.95 and diameter ratio D _i/D _o =  0.1/0.5 mm

As it was shown earlier, in the case of downstream heating, a part of the heat transfer rate was dispersed upstream, so the heat rate was not lost through the outer part of the tube. Consequently, the outlet temperature of the silicon tube is the same as in the case of no-axial conduction phenomena.

Finally, for highly conducted copper tubes and upstream heating, the outlet temperature is considerably lower (t _b = 34°C) compared to the no-axial conduction case temperature (t _b = 49°C). The outlet temperature in the case of the downstream heating is slightly lower (t _b = 47°C) than the no-axial conduction temperature (t _b = 49°C).

For higher Re = 202.85, the axial conduction is almost negligible for the silicon and copper tubes, so the outlet temperatures are the same as in the case of stainless steel tubes (Fig. 15). At the same time, the temperature exhibits the same linear variation as noted in the no-axial conduction case.

Fig. 15

The wall and bulk temperature variation versus axial distance for copper tube, Re = 202.85 and diameter ratio D _i/D _o = 0.1/0.5 mm

In Figs. 16 and 17 the local Nu versus non-dimensional axial distance is presented, in order to compare it with the case of the heat transfer and fluid flow through the tubes without the wall axial conduction. Only the heated portion of the tube was considered due to the fact that in the non-heated portion, the H5 exponentially thermal boundary condition is established, that is not relevant to this analysis. Two different values of Re are considered, Re  = 12.95 (Fig. 16) and Re = 202.85 (Fig. 17).

Fig. 16

Relation of local value of Nu to non-dimensional axial distance for copper tube, upstream heating and Re = 12.95

Fig. 17

Relation of local value of Nu to non-dimensional axial distance for copper tube, downstream heating and Re = 202.85

First of all, the local Nu distribution has the same behavior, regardless of the tube wall thickness, material and Re, depending only on a heating position. Also, after the entrance region in the so-called fully developed flow the local value of Nu is in the range of the well-known value Nu = 4.36. There are sharp changes only near the end of the heating section.

It is also observed, that in the fully developed region, the local Nu is increasing for the lower Re  = 12.85. In this case, the higher temperature difference implies the temperature dependent thermal conductivity. In order to verify the latter phenomena, the local Nu value versus non-dimensional axial distance is presented for the case of heating, cooling and constant thermal conductivity (Fig. 18). As the opposite of the heating case, in the case of cooling, the local Nu is decreasing and for k = const it remains constant in the fully developed region at Nu = 4.36.

Fig. 18

Relation of local value of Nu to non-dimensional axial distance, for three different modes of the input heat transfer rate, Re = 12.95, upstream heating and SUS304

4 Conclusions

The conjugate heat transfer of the partially heated microchannels was analyzed numerically, considering the heat losses defined by the heat transfer rate ratio Q/Q ₀. Influence of the heating position, tube material, wall thickness and Re upon the thermal parameters has been considered and the following conclusions were outlined:

• The wall axial conduction has the negligible influence on thermal characteristics of the stainless steel tubes, regardless of the heating position, wall thickness or Re.

• In the case of the upstream heating, the heat is dispersed through the tube wall in the upstream section of the fluid flow so the Q/Q ₀ = 1 for all the cases except for copper tube of D _i/D _o = 0.1/0.5  mm and low Re = 12.85.

• The local Nu exhibits the usual distribution as for the non-axial conduction case, except the slightly increasing behaviour (decreasing in the case of cooling) in the fully developed region at low Re, due to the thermal conductivity variations.

• Except the abrupt decreasing of the local Nu at the end of the heating section, the local Nu in the fully developed region has the usual value Nu = 4.36.