On the Co-orbital Motion in the Three-Body Problem: Existence of Quasi-periodic Horseshoe-Shaped Orbits

Abstract

Janus and Epimetheus are two moons of Saturn with very peculiar motions. As they orbit around Saturn on quasi-coplanar and quasi-circular trajectories whose radii are only 50 km apart (less than their respective diameters), every four (terrestrial) years the bodies approach each other and their mutual gravitational influence lead to a swapping of the orbits: the outer moon becomes the inner one and vice-versa. This behavior generates horseshoe-shaped trajectories depicted in an appropriate rotating frame. In spite of analytical theories and numerical investigations developed to describe their long-term dynamics, so far very few rigorous long-time stability results on the “horseshoe motion” have been obtained even in the restricted three-body problem. Adapting the idea of Arnol’d (Russ Math Surv 18:85–191, 1963) to a resonant case (the co-orbital motion is associated with trajectories in 1:1 mean motion resonance), we provide a rigorous proof of existence of 2-dimensional elliptic invariant tori on which the trajectories are similar to those followed by Janus and Epimetheus. For this purpose, we apply KAM theory to the planar three-body problem.

1 Introduction

In the framework of the planetary three-body problem (two bodies orbiting a more massive one), the co-orbital motion is associated with trajectories in 1:1 mean-motion resonance. In other words, the planets share the same orbital period. This problem possesses a very rich dynamics which is related to the five famous “Lagrange” configurations.¹ This resonance has been extensively studied since the discovery of Jupiter’s “Trojan” asteroids whose trajectories librate around one of the $L_4$ and $L_5$ equilibria with respect to the Sun and the planet. Since then, other co-orbital objects have been discovered in the Solar System and particularly in the system of Saturn’s satellites which presently holds five pairs of co-orbital moons: Calypso and Telesto, which are co-orbital with Tethys, Helene and Polydeuces, co-orbital with Dione, and the pair Janus-Epimetheus.

Fig. 1

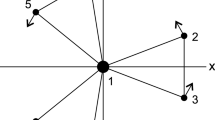
a, b Schematic representation of the orbital motion of the co-orbital moons of Saturn. The average values of the semi-major axes are rescaled to 1 while the moons’ radial excursions are exaggerated by a factor of 200. The trajectories of Helene, Polydeuces, Calypso, and Telesto are seen in frames that rotate respectively with Dione and Tethys. Polydeuces’ and Helene’s trajectories (respectively Calypso’s and Telesto’s trajectories) describe a tadpole shape that surrounds the Lagrange points $L_4$ and $L_5$ with respect to the Sun and Dione (respectively Tethys)

As displayed in Fig. 1, the trajectories of Calypso and Telesto (resp. Helene and Polydeuces) in the rotating reference frame with Tethys (resp. Dione) describe a tadpole shape which corresponds to a small deformation of the Lagrange equilateral configurations $L_4$ or $L_5$ with respect to Saturn and Tethys. This “tadpole” motion, which is also characteristic of Jupiter’s Trojans, has been extensively investigated in recent decades especially long-term stability of these asteroids (see [20, 31]).

Fig. 2

Schematic representation of the Saturn-Janus-Epimetheus trajectories which are depicted in an appropriate rotating frame that rotates with the moons’ average mean-motion. They describe a horseshoe shape whose radial amplitude is about 80 km for Epimetheus (red curve) and 20 km for Janus (blue curve). Starting from the configuration A where Janus, Saturn, and Epimetheus are aligned and the latter is the outer moon, Janus catches up with Epimetheus and a close encounter occurs: due to their mutual gravitational interaction the inner moon shifts towards the outer one and vice-versa (configuration B). More precisely, without overtaking Epimetheus, Janus decelerates and “falls” towards the outer orbit. Likewise, Epimetheus accelerates as it becomes the inner moon and moves away from Janus until another aligned configuration is reached (configuration C). Next, Epimetheus catches up with Janus, a close encounter occurs, and another orbital exchange takes place (configuration D). It takes about 4 years between each orbital exchange and about 8 years for Janus and Epimetheus to cover all their horseshoe-shaped trajectories (which corresponds to 4000 revolutions around Saturn)

Regarding Janus and Epimetheus, as Fig. 2 shows, they exhibit a horseshoe-shaped trajectory. As they orbit around Saturn (in about 17 h) on quasi-coplanar and quasi-circular trajectories whose radii are only 50 km apart (less than their respective diameters), their mean orbital frequency is slightly different (the inner body being a little faster than the outer one). Thus, the bodies approach each other every four terrestrial years and their mutual gravitational influence leads to a swapping of the orbits: the outer moon becomes the inner one and vice-versa. This behavior generates the horseshoe trajectories depicted in an appropriate² rotating frame. This surprising dynamics of the Janus-Epimetheus co-orbital pair was confirmed by Voyager 1’s flyby in 1981 (see [1]).

Actually, the two moons exchange their orbits after a relatively close approach whose minimal distance is larger than 10000 km, which is too far apart to get in their respective Hill’s sphere³ whose radius is around 150 km. Hence, the gravitational influence of the planet dominates the orbital dynamics of Janus and Epimetheus while their mutual interaction remains only a perturbation.

Summarizing, we look for coplanar, low eccentricity co-orbital trajectories which mimic the behavior of these satellites. Contrarily to the tadpole orbits (Helene, Polydeuces, Calypso, and Telesto as in Fig. 1 and also Jupiter’s Trojans) where the difference of mean longitudes oscillates around $\pm 60^\circ$ (see Sect. 2.3), for the considered horseshoe trajectories this quantity oscillates around $180^\circ$ with a large amplitude, larger than $312^\circ$ (see Sects. 2.3 and 4.4 for details).

From a theoretical point of view, using a suitable approximation of the restricted three-body problem (RTBP)⁴ and without available observations, Brown [7] was the first to consider “horseshoe” orbits which encompass $L_4$, $L_3$, $L_5$ equilibria and predicted that they were possible solutions of the system. Subsequently, some horseshoe orbits and families of orbits of this kind have been found numerically in the planar RTBP with respect to the Sun and Jupiter by Rabe [29] followed by numerous other authors.

Several analytical theories have been developed to describe the long-term dynamics of the Janus-Epimetheus co-orbital pair and, more generally, of horseshoe motions in the three-body problem.

One approach, elaborated by Spirig and Waldvogel [35], lies in the description of the two moon dynamics by matching two adapted approximations: the outer one where the moons do not interact when they are apart and the inner one where the mutual gravitational influence dominates during the close encounter. As we have seen, from an astronomical point of view this is not relevant with the observed motions of the Janus and Epimetheus. From a mathematical point of view, and this is central in the present paper, the reasoning followed by Spirig and Waldvogel [35] does not lie in classical setting of the implicit function theorem or KAM theory where we need to consider a perturbation of a unique integrable system.

Another approach, which is followed in the present paper, is precisely based on the introduction of a unique integrable approximation associated with the co-orbital resonance. This kind of global model was introduced in the late seventies. In the context of the restricted problem (RTBP) by tacking the mass ratio between the secondary and the primary small enough, Garfinkel [17] develops an approximation adapted to quasi-circular orbits in co-orbital resonance in order to study the behavior of the Trojan asteroids. Following the same idea, Yoder et al. [36] give a less accurate approximation of the co-orbital resonance but applicable to the situation of two comparable moons such as Janus and Epimetheus.⁵ Going back to the framework of the restricted problem (RTBP), the most detailed numerical exploration of horseshoe dynamics has been carried out in Dermott and Murray [13, 14]. Focusing on quasi-circular trajectories, they provide some general properties such as heuristic estimates of the horseshoe orbit lifetime and the relative width of the tadpole and horseshoe domain.

In spite of these analytical theories as well as the indications provided by some numerical investigations (see [3, 25]), so far very few rigorous long-time stability results have been obtained on the “horseshoe motion”, even in the restricted three-body problem.

Cors and Hall [10] studied the persistence of these trajectories in the three-body problem with the help of a Hamiltonian formulation of the planetary problem by introducing several small quantities (the mass of the moons, the radii difference, and the minimum angular separation between the moons) whose relative sizes are determined in order to explore the horseshoe dynamics. Their approximation of the dynamics in the co-orbital resonance retains terms up to a given order in the expansion of the perturbation which correspond to the mutual interaction between the moons. An important feature in Cors and Hall [10] is that their approximation is valid for an area in phase space composed of orbits where the mutual distance at closest approach of the satellites is comparable to $\varepsilon ^\alpha$ for $0<\alpha <1/5$ with the ratio $\varepsilon$ of the moons’ masses to the central body’s mass. This allows one to get results on the existence of horseshoe-shaped orbits over times of order $\varepsilon ^{\alpha -2}$.

After completion of the present work, Cors et al. [11] published an article about the existence of quasi-periodic horseshoe trajectories. The authors use Cors and Hall [10] approximation to give a computer-assisted proof for the existence of 4-dimensional Lagrangian tori associated with co-orbital orbits where there are close approaches of the satellites. Even if some details of the proof are omitted in this paper, this promising work provides normalizing transformations of the considered Hamiltonian designed to prove the existence of invariant tori.

Going back to the strategy of Garfinkel [17], Yoder et al. [36], Dermott and Murray [13, 14], a Hamiltonian formalism adapted to the study of the motion of two planets in co-orbital resonance was developed in Robutel and Pousse [33]. This yields a global integrable 1:1-resonant normal form which was specified in Robutel et al. [32] where estimates on the required averaging process are given (and also some stability results). In particular, this model is valid for any orbits in 1:1 resonance provided the mutual distance at closest approach is reduced by $\varepsilon ^{1/3}$, which corresponds to Hill’s sphere, and its domain of definition includes the $L_3$, $L_4$ and $L_5$ equilibria. A drawback to this method is that the action-angle variables in this integrable approximation are not explicit. Nevertheless, we can compute asymptotic estimates on the frequencies of trajectories close to orbits homoclinic to the hyperbolic equilibrium $L_3$ (see Fig. 2).

In the present paper, our goal is to prove the existence of invariant tori on which the trajectories are similar to those followed by Janus and Epimetheus and for this purpose we apply KAM theory with the latter integrable approximation in co-orbital resonance.

In his seminal article, Arnol’d [2] proved rigorously the existence of quasi-periodic motions in the planar planetary three-body problem. This has been extended to the spatial N-body problem by Féjoz [16] and Chierchia and Pinzari [9]. Going back to the spatial three-body problem, Biasco et al. [6] proved the existence of lower dimensional invariant tori while Chenciner and Llibre [8] and Lei [23] proved the existence of quasi-periodic almost-collisional orbits.

Assuming that the planets never experience close encounters, Arnol’d first considered two uncoupled Kepler problems as the integrable part of the Hamiltonian. In order to get Kolmogorov non-degeneracy of the frequency map, he added a suitable approximation of the secular part of the perturbation.⁶

In the co-orbital resonance, KAM theory has already been applied: in the restricted three-body problem, Leontovich [24] proved the existence of quasi-periodic tadpole trajectories. His reasonings are based on a fourth degree expansion of the Hamiltonian around Lagrange equilateral configurations which yields a Kolmogorov non-degenerate integrable Hamiltonian. Unfortunately, this method is only relevant in the neighborhood of the equilateral equilibria and does not fit trajectories that encompass the $L_4$, $L_3$, and $L_5$ equilibria such as the horseshoe orbits.

As discussed before, in our context the mutual interaction of the moons remains a perturbation of the main force which comes from the central attractor. As a consequence, the planetary three-body problem studied by Arnol’d is also relevant for modeling Janus and Epimetheus’ trajectories around Saturn.

We would like to use KAM theory in order to prove the existence of quasi-periodic trajectories whose main features are those of the observed satellite’s trajectories but our context is tricky : unlike Arnol’d’s situation that relies on non-resonant Kepler orbits, we are strictly in 1:1 resonance which prevents of use the secular perturbation in order to get a non-degeneracy.

In order to prove the existence of quasi-periodic horseshoe orbits, we replace the previous secular perturbation by the integrable 1:1-resonant normal form introduced by Robutel and Pousse [33]. Since the action-angle variables in the integrable approximation are not explicit, it is very tricky to check Kolmogorov’s non-degeneracy condition as in Arnol’d’s article. However, it is possible to look at weaker non-degereracy conditions, like those stated by Pöschel [28] to prove the persistence of lower dimensional normally elliptic invariant tori in the context of non-linear partial differential equations.⁷ This latter result was already applied in celestial mechanics by Biasco et al. [6] to prove the existence of 2d elliptic invariant tori for the three-body planetary problem in a non-resonant case (while co-orbital trajectories are resonant). In our context, we will follow the same scheme of proof and, as a consequence, we give a rigorous proof of 2-dimensional tori associated with horseshoe like motions. Our main theorem (Theorem 2.1) is stated at the end of Sect. 2.

Actually, it is certainly possible to compute higher order normal forms with a computer-assisted proof in order to check Kolmogorov’s non-degeneracy condition in our setting and ensure the existence of Lagrangian invariant tori.

In Sect. 2, we specify the characteristics of the quasi-periodic orbits we want to obtain. In Sect. 3, some useful notations are introduced. In Sect. 4, we describe the different steps of our reduction scheme in order to build an integrable approximation associated with the horseshoe motion. Section 5 is dedicated to the application of KAM theory. Finally, Sect. 6 is devoted to extensions, comments, and prospects.

Appendix A concerns the proof of the technical propositions and lemmas used in our reasonings.

2 2d Co-orbital Tori and Horseshoe Trajectories in the Planetary Problem

2.1 Canonical heliocentric coordinates

We consider two planets of respective masses ${\varepsilon }m_1$ and ${\varepsilon }m_2$ orbiting in a plane around a central body (the Sun or a star) of mass $m_0$, ${\varepsilon }$ being an arbitrarily small positive parameter. We assume that the three bodies are only influenced by their mutual gravitational interaction. Without loss of generality, we assume the gravitational constant to be equal to 1 and set

$$\begin{aligned} 0< m_1\leqslant m_2. \end{aligned}$$

Using heliocentric coordinates [22] and rescaling both action variables and time (see formore details [32]), the Hamiltonian of the three-body problem reads

(2.1)

where “” and “$\left\| \,\cdot \, \right\|$” are respectively the Euclidean scalar product and norm.

In these expressions, the canonical variable $\mathbf{r} _j$ corresponds to the heliocentric position of planet j while $\tilde{\mathbf{r}} _j$, the conjugated variable of $\mathbf{r} _j$, is associated with the rescaled barycentric linear momentum of the same body. The mass parameters ${\widehat{m}}_j$ and $\mu _j$ are defined by

$$\begin{aligned} {\widehat{m}}_j = \frac{m_0 m_j}{m_0+{\varepsilon }m_j} \quad \text{ and } \quad \mu _j = m_0+\varepsilon m_j. \end{aligned}$$

The Hamiltonian ${{\mathcal {H}} }$, which is an analytical function in the domain

$$\begin{aligned} {{\mathcal {D}}} = \left\{ (\tilde{\mathbf{r}} _1,\mathbf{r} _1,\tilde{\mathbf{r}} _2,\mathbf{r} _2)\in {\mathbb {R}}^8\ \text {such that}\ \mathbf{r} _1\ne \mathbf{r} _2 \right\} , \end{aligned}$$

possesses two components: ${{\mathcal {H}} }_K$, which describes the unperturbed Keplerian motion of the two planets (the motion of a body of mass ${\widehat{m}}_j$ around a fixed center of mass $m_0+{\varepsilon }m_j$), and ${{\mathcal {H}} }_P$, which models the perturbations due to the gravitational interaction between the two planets and the fact that the heliocentric frame is not a Galilean one.

Finally, the planetary Hamiltonian ${{\mathcal {H}} }$ is invariant under the action of the symmetry group SO(2) associated with the rotations around the vertical axis. This property is equivalent to the fact that the total angular momentum, that is ${\tilde{{{\mathcal {C}}}}}(\tilde{\mathbf{r}} _j, \mathbf{r} _j) = \sum _{j\in \{1,2\}} \tilde{\mathbf{r}} _j \times \mathbf{r} _j$ (where “$\times$” is the vectorial product), is preserved.

2.2 Poincaré complex variables.

In order to define a canonical coordinate system related to the elliptic elements $(a_j,e_j,\lambda _j,\varpi _j)$ (respectively the semi-major axis, the eccentricity, the mean longitude, and the longitude of the pericenter of the planet j), we use Poincaré’s complex variables $(\Lambda _j,\lambda _j,x_j,{\widetilde{x} }_j)_{j\in \{ 1,2\} }\in ({\mathbb {R}}\times {{\mathbb {T}}}\times {{\mathbb {C}}}\times {{\mathbb {C}}})^2$:

$$\begin{aligned} \begin{aligned} \Lambda _j = {\widehat{m}}_j\sqrt{\mu _ja_j}, \quad x_j= \sqrt{\Lambda _j}\sqrt{1-\sqrt{1-e_j^2}}\exp (i\varpi _j), \quad \text{ and }\quad {\widetilde{x} }_j = -i{\overline{x} }_j. \end{aligned} \end{aligned}$$

This coordinate system has the advantage of being regular when the eccentricities tend to zero. Consequently, the product $\tilde{\Upsilon }= (\tilde{\Upsilon }_1,\tilde{\Upsilon }_2)$ of analytic symplectic transformations

$$\begin{aligned} \tilde{\Upsilon }_j(\Lambda _j,\lambda _j,x_j,{\widetilde{x} }_j )=(\tilde{\mathbf{r}} _j ,\mathbf{r} _j ) \quad (j\in \{1,2\}) \end{aligned}$$

yields the new Hamiltonian

$$\begin{aligned} \begin{aligned} {\tilde{H} }(\Lambda _j,\lambda _j,x_j,{\widetilde{x} }_j)&={\tilde{H} }_K(\Lambda _1,\Lambda _2) +{\tilde{H} }_P(\Lambda _j,\lambda _j,x_j,{\widetilde{x} }_j) \\ \text{ where } \quad {{\mathcal {H}} }_K(\tilde{\mathbf{r}} _j,\mathbf{r} _j)&={\tilde{H} }_K (\Lambda _1,\Lambda _2) = -\sum _{j\in \, \{1,2\}} \frac{1}{2}\frac{\mu _j^2{\widehat{m}}_j^3}{\Lambda _j^2}. \end{aligned} \end{aligned}$$

${\tilde{H} }$ is analytic on the domain $\tilde{\Upsilon }^{-1}({{\mathcal {D}}} ) \subset ({\mathbb {R}}\times {{\mathbb {T}}}\times {{\mathbb {C}}}\times {{\mathbb {C}}})^2$.

2.3 The 1:1 resonance

In the limit of the Keplerian approximation, two planets are in co-orbital resonance, or 1:1 mean-motion resonance, when their two orbital frequencies are equal. According to the third Kepler law, the exact resonance occurs when $(\Lambda _1,\Lambda _2) = (\Lambda _{1,0},\Lambda _{2,0})$ with

$$\begin{aligned} \begin{aligned}&\frac{\partial {\tilde{H} }_K }{\partial \Lambda _1}(\Lambda _{1,0},\Lambda _{2,0}) = \frac{\partial {\tilde{H} }_K }{\partial \Lambda _2}(\Lambda _{1,0},\Lambda _{2,0}) = \upsilon _0 >0, \\&\quad \text{ that } \text{ is } \quad \, \frac{\mu _1^2{\widehat{m}}_1^3}{(\Lambda _{1,0})^3} =\frac{\mu _2^2{\widehat{m}}_2^3}{(\Lambda _{2,0})^3} =\upsilon _0, \\&\quad \text{ where } \quad \Lambda _{j,0} ={\widehat{m}}_j \sqrt{\mu _j a_{j,0}} \quad \text{ and } \quad a_{j,0} = \mu _j^{1/3}\upsilon _0^{-2/3} \end{aligned} \end{aligned}$$

(2.2)

are respectively the exact-resonant action and semi-major axis of the planet j.

In order to construct a coordinate system adapted to the co-orbital resonance, let us introduce the symplectic transformation

$$\begin{aligned} \Upsilon ({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) = (\Lambda _1,\lambda _1,x_1,{\widetilde{x} }_1,\Lambda _2,\lambda _2,x_2,{\widetilde{x} }_2) \end{aligned}$$

such that

$$\begin{aligned} \begin{aligned} {\mathbf{Z} }= \begin{pmatrix} Z_1\\ Z_2 \end{pmatrix} = \begin{pmatrix} 1 &{} 0\\ 1 &{} 1 \end{pmatrix} \begin{pmatrix} \Lambda _1-\Lambda _{1,0}\\ \Lambda _2-\Lambda _{2,0} \end{pmatrix},&\quad \varvec{\zeta }= \begin{pmatrix} \zeta _1\\ \zeta _2 \end{pmatrix} = \begin{pmatrix} 1 &{} -1\\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} \lambda _1 \\ \lambda _2 \end{pmatrix},\\ {\mathbf{x} }= \begin{pmatrix} x_1\\ x_2 \end{pmatrix},&\quad {\widetilde{\mathbf{x}} }= -i\overline{{\mathbf{x} }}. \end{aligned} \end{aligned}$$

In these variables, the planetary Hamiltonian becomes

$$\begin{aligned} \begin{aligned} H({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} })&= H_K({\mathbf{Z} }) + H_P({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }),\\ \text{ where }\quad H_K({\mathbf{Z} })&= - \frac{{\widehat{m}}_1^3\mu _1^2}{2(\Lambda _{1,0} + Z_1)^2} - \frac{{\widehat{m}}_2^3\mu _2^2}{2(\Lambda _{2,0} + Z_2 - Z_1 )^2} \text{ and } H_P = {\tilde{H} }_P\circ \Upsilon , \end{aligned} \end{aligned}$$

which yields a zero frequency $\partial _{Z_1} H_K ({\mathbf{0} })$ at the origin. Hence, the temporal evolution of the angles $\zeta _j$ and variables $x_j$ satisfy the relation

$$\begin{aligned} {\dot{\zeta }}_2 = \upsilon _0 + {{\mathcal {O}}} (\left\| {\mathbf{Z} } \right\| ) + {{\mathcal {O}}} ({\varepsilon }), \quad {\dot{\zeta }}_1 = {{\mathcal {O}}} (\left\| {\mathbf{Z} } \right\| )+ {{\mathcal {O}}} ({\varepsilon }), \quad \text{ and } \quad \dot{x}_j = {{\mathcal {O}}} ({\varepsilon }) \end{aligned}$$

where ${\varepsilon }$ is the small parameter associated with the planetary masses (see Sect. 2.1).

As a consequence, these variables evolve at different rates: $\zeta _2$ is a “fast” angle with a frequency of order 1, $\zeta _1$ undergoes “semi-fast” variations at a frequency of order $\sqrt{{\varepsilon }}$ (in the resonant domain, ${\mathbf{Z} }$ is at most of order $\sqrt{\varepsilon }$ as it is shown in Sect. 4.4), while the variables $(x_j)_{j\in \{1,2\}}$ related to the eccentricities are associated with the “slow” degrees of freedom evolving on a timescale of order ${\varepsilon }$ (secular variations of the orbits).

A classical way to reduce the problem in order to study the semi-fast and secular dynamics of the co-orbital resonance is to average the Hamiltonian over the fast angle $\zeta _2$ to get a resonant normal form. We shall prove, in Sect. 4.2, that there exists a symplectic transformation $\overline{\Upsilon }$ close to the identity and defined on a domain that will be specified later, such that

and

$\overline{H} _P$ is the averaged perturbation which depends only on the semi-fast and slow variables while the remainder $H_*$ is supposed to be small with respect to $\overline{H} _P$. More precisely, the sizes of $\overline{H} _P$ and $H_*$ increase simultaneously with the distance to the singularity associated with the planetary collision. We showed in Robutel et al. [32] that the remainder is negligible compared to $\overline{H} _P$ as long as the distance to the singularity is less than a quantity of order ${\varepsilon }^{1/3}$, which will be assumed from the Sect. 4. In addition, properties regarding the transformation $\overline{\Upsilon }$ and the remainder $H_*$ will be stated in Sect. 4.2. More precisely, the averaging process will be iterated until the fast component is exponentially small with respect to ${\varepsilon }$.

2.3.1 D’Alembert rule and averaged Hamiltonian’s dynamics.

The Hamiltonian H, which is analytic on a suitable domain, can be expanded in Taylor series in a neighborhood of ${\mathbf{x} }={\widetilde{\mathbf{x}} }={\mathbf{0} }$ as

$$\begin{aligned} H({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) = \sum _{(k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }) \in {{\mathscr {D}}}} f_{k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }}({\mathbf{Z} },\zeta _1)x_1^{p_1}x_2^{p_2}{\widetilde{x} }_1^{{\widetilde{p} }_1}{\widetilde{x} }_2^{{\widetilde{p} }_2}\exp (i k\zeta _2) \end{aligned}$$

(2.3)

$$\begin{aligned} \text{ where }\quad {{\mathscr {D}}}=\left\{ (k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} })\in {{\mathbb {Z}}}\times {{\mathbb {N}}}^2\times {{\mathbb {N}}}^2\,/\, k + p_1 + p_2 - {\widetilde{p} }_1-{\widetilde{p} }_2 = 0\right\} \end{aligned}$$

(2.4)

is known as the D’Alembert rule which is equivalent to the conservation of the angular momentum ${\tilde{{{\mathcal {C}}}}}(\tilde{\mathbf{r}} _j, \mathbf{r} _j)$. From this relation follows a key property of the averaged Hamiltonian that reads

Indeed, the D’Alembert rule still holds after averaging (see [33]) and the Taylor expansion of the averaged Hamiltonian $\overline{H}$, which does not depend on the angle , is even in the slow variables . Moreover, this propriety is equivalent to the fact that the quantity

(2.5)

is an integral of the averaged motion. As a consequence, the set

is an invariant manifold for the flow of $\overline{H}$. On this “quasi-circular” manifold, the dynamics is controlled by the one-degree of freedom Hamiltonian .

2.4 Semi-fast dynamics and horseshoe domain

The phase portrait of the integrable Hamiltonian is displayed in Fig. 3. This figure being extensively described in Robutel and Pousse [33], we will limit ourselves to present what will be useful thereafter.

Fig. 3

Phase portrait of the Hamiltonian in the coordinates . The units and the parameter are chosen such that , $m_0=1$, $\upsilon _0 = 2\pi$, ${\varepsilon }m_1 = 10^{-3}$, ${\varepsilon }m_2 = 3 \times 10^{-4}$. The blue area corresponds to tadpole or Trojan orbits while the red one corresponds to horseshoe orbits. See Sect. 2.4 for more details

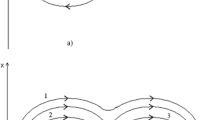
Two elliptic fixed points are present on this phase portrait. These points, labelled by $L_4$ or $L_5$, coincide with the Lagrange equilateral equilibria, which are linearly stable as long as the planetary masses are small enough.⁸ They are surrounded by periodic orbits (blue domains) that correspond to semi-fast deformations of Lagrange configurations (the tadpole orbits of Fig. 1). In the center of the phase portrait, the fixed point labelled by $L_3$ represents the unstable Euler configuration for which the three bodies are aligned and the Sun is between the two planets. Its stable and unstable manifolds, which coincide (red curve), bound the two previous domains. Outside these separatrices lie the horseshoe orbits (red region). Contrarily to the tadpole orbits for which the variation of does not exceed $156^\circ$, along a horseshoe trajectory the difference of the mean-longitudes oscillate around $180^\circ$ with a very large amplitude of at least $312^\circ$ (see Sect. 4.4). It is on this region, more precisely close to the outer edge of the separatrix, that we will focus in the next sections.

Fig. 4

Phase portrait of the considered Hamiltonian $\tilde{{\mathscr {H}} }_1(Z_1, \zeta _1)=- {\varepsilon }B(1+\delta )$. It approximates the one of the Hamiltonian $\overline{H} ({\mathbf{Z} }, \zeta _1,{\mathbf{0} }, {\mathbf{0} })$, which is depicted in Fig. 3, in the $L_3$-separatrix region. The units and the parameter are the same as in Fig. 3. In this approximation, the $L_1$ and $L_2$ fixed points as well as their separatrices have disappeared while $\{\zeta _1 = 0\}$ became a singularity. For $\delta =0$, the separatrix divides the phase portrait in two distinct dynamics: the two tadpole trajectory domains for $\delta <0$, which are surrounded by the separatrix, and the horseshoe trajectories for $\delta >0$ (grey trajectory)

The outer part of the horseshoe domain is bounded by the separatrices associated with $L_1$ and $L_2$ (beige and brown curves). Beyond these manifolds, the top and the bottom light grey areas correspond to non-resonant dynamics where the angle evolves slowly but in a monotonous way. The singularity that corresponds to the collision between the planets is located at and is separated from the previous regions by the stable and unstable manifolds originated at $L_1$ and $L_2$. It is shown in Robutel et al. [32] that the distance between the singularity and these structures is of order ${\varepsilon }^{1/3}$. As mentioned above, in this case, the remainder $H_*$ is at least as large as the perturbation, and this part of the phase portrait is not necessarily relevant. But this is not a problem since, in the following, we will work only in the vicinity of the $L_3$-separatrix.

2.5 2d co-orbital tori

In Sect. 4.3, we shall introduce a linear transformation that uncouple the fast and semi-fast dynamics. Moreover, we shall approximate the semi-fast dynamics in the $L_3$-separatrix region (the two domains surrounded by the separatrix and its outer neighborhood; see Fig. 4) by a simple Hamiltonian proportional to

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(Z_1,\zeta _1) = -A Z_1^2 + {\varepsilon }B {{\mathcal {F}} }(\zeta _1) \end{aligned}$$

where the coefficients A, B, and the $2\pi$-periodic real function ${{\mathcal {F}} }$ will be defined later. With the previous notations, the separatrix is defined by the level curve $\tilde{{\mathscr {H}} }_1(Z_1,\zeta _1) = h_0 = -{\varepsilon }B$ while those given by $\tilde{{\mathscr {H}} }_1(Z_1,\zeta _1) = h_\delta = -{\varepsilon }B(1+\delta )$ with $\delta >0$ are the horseshoe orbits surrounding the latter. As a consequence, for each $2\pi /\nu _\delta$-periodic trajectory of the differential system associated with the Hamiltonian $\tilde{{\mathscr {H}} }_1$, there exists a $2\pi$-periodic real function $F_\delta$ such that the parametric representation of the latter trajectory reads

$$\begin{aligned} \zeta _1(t) = F_\delta (\nu _\delta t)\, , \quad Z_1(t) = - \frac{\nu _\delta F_\delta '(\nu _\delta t)}{2A}. \end{aligned}$$

(2.6)

Moreover, the function $F_\delta$ parametrizing a horseshoe orbit of energy $h_\delta$ satisfies

$$\begin{aligned} - \frac{\nu _\delta ^2\left( F_\delta '(\nu _\delta t)\right) ^2}{4A} + {\varepsilon }B {{\mathcal {F}} }\left( F_\delta (\nu _\delta t)\right) = -{\varepsilon }B(1+\delta ) \quad \text{ with } \quad \delta >0. \end{aligned}$$

(2.7)

The smaller $\delta$ is, the closer to the separatrix the orbit is.

In the same way the fast dynamics will be approached by a quadratic integrable Hamiltonian ${{\mathscr {H}} }_2(Z_2)$ (see Sect. 4.3). Hence we are led to consider the Hamiltonian system linked to

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(Z_1,\zeta _1) +{{\mathscr {H}} }_2(Z_2). \end{aligned}$$

(2.8)

Consequently the phase space is foliated in 2-dimensional tori invariant under the Hamiltonian flow linked to (2.8). Hence, we choose as reference tori the 2d tori that are parametrized in the original variables by

$$\begin{aligned} \left\{ \begin{aligned}&\lambda _1(\varvec{\theta }) = c_1 + \theta _2 + (1 - \kappa ) F_\delta (\theta _1 ) \\&\lambda _2(\varvec{\theta }) = c_2 + \theta _2 - \kappa F_\delta ( \theta _1) \\&\Lambda _1(\varvec{\theta }) = c_3 + \sqrt{\varepsilon }G_\delta (\theta _1)\\&\Lambda _2(\varvec{\theta }) = c_4 - \sqrt{\varepsilon }G_\delta (\theta _1) \\&x_j(\varvec{\theta }) = 0 \end{aligned}\right. \end{aligned}$$

(2.9)

with $\varvec{\theta }\in {{\mathbb {T}}}^2$ and $\sqrt{{\varepsilon }}G_\delta = -\nu _{\delta }F'_\delta /2A$. These objects will be called 2d co-orbital tori. In the expression (2.9), the function $F_\delta$ and the frequency $\nu _\delta$ parametrize respectively the semi-fast horseshoe orbits and frequency as in (2.6) and (2.7), while the $c_j$ are real constant coefficients and $\kappa = m_1/(m_1+m_2)$. On each torus, the flow is linear with the frequency

$$\begin{aligned} \dot{\varvec{\theta }} = \varvec{\omega }= (\nu _\delta ,\upsilon ) \quad \text{ where } \nu _\delta \sim d_1{\frac{\sqrt{\varepsilon }}{\ln \delta }} \text{ and } \upsilon \sim d_2 \end{aligned}$$

for some constants $d_1>0$ and $d_2>0$ when $\delta$ goes to zero.

By an application of KAM theory, we would like to continue the 2d co-orbital tori under the flow of the three-body problem carrying quasi-periodic trajectories with two frequencies: a semi-fast one, corresponding to the averaged motion, and a fast one. But to this end, the knowledge of the semi-fast dynamics is not enough, it is also necessary to control the dynamics in the directions that are normal to the 2d co-orbital tori. These normal directions will be called secular directions. Hence, we will consider the Hamiltonian

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(Z_1, \zeta _1) + {{\mathscr {H}} }_2(Z_2) + \tilde{{\mathscr {Q}} }(\zeta _1,{\mathbf{x} }, {\widetilde{\mathbf{x}} }) \end{aligned}$$

where $\tilde{{\mathscr {Q}} }$ is a suitable approximation of the secular dynamics, which is quadratic in the eccentricity variables thanks to the conservation of the D’Alembert rule given by (2.4).

$\tilde{{\mathscr {Q}} }$ characterizes the linear stability of the ${\mathrm C}_0$-manifold in the normal directions $({\mathbf{x} },{\widetilde{\mathbf{x}} })$ via the derived variational equations in the eccentricity variables. However, as $\tilde{{\mathscr {Q}} }$ is $\zeta _1$-dependent, the variational equations are time-dependent along a 2d co-orbital tori which prevents to express their solutions in a close form. Hence, we shall transform our system of canonical coordinates in order to uncouple the semi-fast and secular dynamics, and express the Hamiltonian in a suitable normal form.

2.6 Reduction to a suitable normal form

In the horseshoe region, the semi-fast angle $\zeta _1$ does not evolve in a monotonous way which prevents to remove directly the $\zeta _1$-dependency via a second averaging process.

Using the classical integral formulations (see Sect. 4.4), we will build semi-fast action-angle variables adapted to horseshoe trajectories. Hence we shall prove that there exists a canonical transformation

$$\begin{aligned} \Psi : (J_1, Z_2, \phi _1, \zeta _2, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) \longmapsto ({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) \end{aligned}$$

such that the considered Hamiltonian reads

$$\begin{aligned} \begin{aligned}&{{\mathscr {H}} }_1(J_1) + {{\mathscr {H}} }_2(Z_2) + {{\mathscr {Q}}}(J_1,\phi _1, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) \\&\text{ where } \quad {{\mathscr {H}} }_1(J_1) = \tilde{{\mathscr {H}} }_1(Z_1(J_1, \phi _1), \zeta _1(J_1, \phi _1)),\\&\frac{{\mathrm {d}}{{\mathscr {H}} }_1}{{\mathrm {d}}J_1}(J_1) = \nu _{\delta (J_1)}, \quad \text{ and } \quad {{\mathscr {Q}}}(J_1,\phi _1, {\mathbf{x} },{\widetilde{\mathbf{x}} }) = \tilde{{\mathscr {Q}} }(\zeta _1(J_1,\phi _1), {\mathbf{x} }, {\widetilde{\mathbf{x}} }). \end{aligned} \end{aligned}$$

However, it gives rise to an important drawback: the expressions of the semi-fast dynamics are no longer explicit which bring additional difficulties in our forthcoming application of KAM theory.

Then, we will proceed to a second averaging process (over the semi-fast angle $\phi _1$ in that case) in order to reject the $\phi _1$-dependency in a general remainder. The method is based on asymptotic expansions as the trajectory gets closer to the separatrix. For the sake of simplicity, as $\delta$ tends to zero, we constrain the energy shift $\delta$ by the relation ${\varepsilon }^{2{\hat{{\mathrm q }}}}\leqslant \delta \leqslant {\varepsilon }^{\hat{{\mathrm q }}}$ for some exponent ${\hat{{\mathrm q }}}>0$. We shall prove that there exists a symplectic transformation

close to identity and such that, in these variables, the considered Hamiltonian becomes

and ${{\mathscr {H}} }_*$ is supposed to be small with respect to $\overline{{\mathscr {Q}} }$. More precisely, we will iterate the averaging process until the semi-fast component ${\mathscr {H}}^\dagger _*={{\mathscr {H}} }_* - \overline{{\mathscr {H}}_*}$, where

is exponentially small with respect to ${\varepsilon }$.

Finally, from the secular Hamiltonian $\overline{{\mathscr {H}} }$ that reads

we shall deduce the linear stability of the 2d co-orbital tori considered in the formulas (2.9). Indeed, from the conservation of the D’Alembert rule given by (2.4) and of the integral given by (2.5), we will control the remainder $\overline{{\mathscr {H}}_*}$ that reads

and obtain the spectrum of the second order terms in the eccentricities, that is

The spectrum being simple with purely imaginary eigenvalues associated with the two secular frequencies

$$\begin{aligned} \varvec{\Omega }= (g_1, g_2)= {{\mathcal {O}}} \left( {\varepsilon },\, \frac{{\varepsilon }}{\left| \ln {\varepsilon } \right| }\right) , \end{aligned}$$

then we will prove that the considered 2d co-orbital tori are normally elliptic. As a consequence, we will consider the normal form

where $({\mathbf{z} }, {\widetilde{\mathbf{z}}} )$ are the eccentricity variables that diagonalize the secular Hamiltonian $\overline{{\mathscr {Q}} }+ \overline{{\mathscr {H}}_*}$.

2.7 2d tori for the full Hamiltonian in the horseshoe domain

Now, let us see how the quasi-periodic orbits associated with the horseshoe region can be built in the full problem, and what will they look like.

As described above, we will develop an integrable approximation of the problem which will enable us to uncouple the fast, semi-fast, and secular dynamics. It will be proved that, if we choose a horseshoe orbit which lies on the quasi-circular manifold ${\mathrm C}_0$ and is close enough to the $L_3$-separatrix, its two frequencies (fast and semi-fast) are respectively of order $(1,\, \sqrt{{\varepsilon }}/\left| \ln {\varepsilon } \right| )$ while it is normally elliptic along the two transversal directions with frequencies of order $({\varepsilon },\, {\varepsilon }/\left| \ln {\varepsilon } \right| )$. This yields four different timescales that will prevent the occurrence of small divisors for ${\varepsilon }$ small enough. As a consequence, we will take advantage of this property, which will be used to fulfill the Melnikov condition on the frequency map required to apply Pöschel [28]’s theorem, to get 2-dimensional tori associated with the horseshoe orbits in the three-body problem.

Theorem 2.1

There exists a real number ${\varepsilon }_{*}>0$ such that for all ${\varepsilon }$ with $0<{\varepsilon }<{\varepsilon }_{*}$, the Hamiltonian flow linked to the planetary Hamiltonian ${{\mathcal {H}} }$ given by (2.1) admits an invariant set which is an union of 2-dimensional ${{\mathscr {C}}}^{\infty }$ invariant tori carrying quasi-periodic trajectories. These tori are close, in ${{\mathscr {C}}}^{0}$-topology, to the 2d co-orbital tori introduced above.

The quasi-periodic trajectories that come from this application of KAM theory can be described as follows:

$$\begin{aligned} \left\{ \begin{aligned} \lambda _1(\varvec{\theta })&= c_1 + \theta _2 + (1 - \kappa ) F_\delta ( \theta _1) + f_1(\varvec{\theta }; {\varepsilon }) \\ \lambda _2(\varvec{\theta })&= c_2 + \theta _2 - \kappa F_\delta ( \theta _1) + f_2(\varvec{\theta }; {\varepsilon }) \\ \Lambda _1(\varvec{\theta })&= c_3 + \sqrt{{\varepsilon }} G_\delta ( \theta _1) + f_3(\varvec{\theta }; {\varepsilon }) \\ \Lambda _2(\varvec{\theta })&= c_4 + \sqrt{{\varepsilon }} G_\delta ( \theta _1) + f_4(\varvec{\theta }; {\varepsilon }) \\ x_j(\varvec{\theta })&= f_{5,j}(\varvec{\theta }; {\varepsilon })\, \end{aligned}\right. \end{aligned}$$

where $\dot{\varvec{\theta }} = \varvec{\omega }= ( \nu _\delta ,\upsilon )$ and $f_j$ are small perturbative terms. Indeed, there exists $C\geqslant 1$ independent of the small parameters of the problem such that:

$$\begin{aligned} \left\| f_1 \right\| \leqslant C {\varepsilon }^{\gamma _1},\quad \left\| f_2 \right\| \leqslant C {\varepsilon }^{\gamma _1}, \quad \left\| f_3 \right\| \leqslant C {\varepsilon }^{\gamma _2}, \quad \left\| f_4 \right\| \leqslant C{\varepsilon }^{\gamma _2}, \quad \left\| f_{5,j} \right\| \leqslant C {\varepsilon }^{\gamma _3} \end{aligned}$$

for the supremum norm on our domain with real exponents $\gamma _j$ such that

$$\begin{aligned} 7/40< \gamma _1< \gamma _2<\gamma _3 < 3/4. \end{aligned}$$

In this expression, the functions $F_\delta$ and $G_\delta$ parametrize the semi-fast horseshoe orbits as in (2.9).

3 Notations

In order to apply KAM theory, we need an integrable approximation of the Hamiltonian of the problem associated with the horseshoe motion and whose frequency map satisfies non-degeneracy properties.

Before going further, let us introduce some useful notations.

First of all, the vector (0, 0) will be denoted ${\mathbf{0} }$ while ${\mathrm E }(x)$ will denote the floor function of a real number x.

Moreover, for ${\mathbf{z} }\in {{\mathbb {C}}}^n$, ${{\,\mathrm{Re}\,}}({\mathbf{z} })\in {\mathbb {R}}^n$, ${{\,\mathrm{Im}\,}}({\mathbf{z} })\in {\mathbb {R}}^n$ are the vectors corresponding respectively to the real part and the imaginary part of ${\mathbf{z} }$. Finally, the magnitude $\left| \,\cdot \, \right|$ of the complex vector ${\mathbf{z} }$ is the supremum norm of the magnitude on each complex coordinate, that is

$$\begin{aligned} \left| {\mathbf{z} } \right| = \sup _{j\in \{1, \ldots , n\}} \left| z_j \right| . \end{aligned}$$

3.1 Complex domains and norms

Let ${{\mathcal {D}}}$ a subset of ${{\mathbb {C}}}^n$ and f a function in ${{\mathscr {C}}}({{\mathcal {D}}} , {{\mathbb {C}}}^m)$. Then, we will denote $\left\| f \right\| _{{{\mathcal {D}}} }$ the supremum norm of f on the domain ${{\mathcal {D}}}$ such that

$$\begin{aligned} \left\| f \right\| _{{{\mathcal {D}}} }= \sup _{{\mathbf{z} }\in {{\mathcal {D}}} } \left| f({\mathbf{z} }) \right| . \end{aligned}$$

Now, let ${{\mathcal {U}} }$ a subset of ${\mathbb {R}}^n$. We will define its associate complexified domain of width $r>0$ such that

$$\begin{aligned} {{\mathcal {B}}}_r{{\mathcal {U}} }= \left\{ {\mathbf{z} }\in {{\mathbb {C}}}^n \,/\,\exists {\mathbf{x} }_0 \in {{\mathcal {U}} } \text{ such } \text{ that } \left| {\mathbf{z} }- {\mathbf{x} }_0 \right| \leqslant r \right\} ={\displaystyle {\bigcup \limits _{{\mathbf{x} }_0\in {{\mathcal {U}} }}}}{{\mathcal {B}}}_r\{{\mathbf{x} }_0\} \end{aligned}$$

where for a real vector ${\mathbf{x} }_0\in {\mathbb {R}}^n$, ${{\mathcal {B}}}_r\{{\mathbf{x} }_0\}$ is the complex closed ball of radius $r>0$ centered on ${\mathbf{x} }_0$. Hence, we will denote

$$\begin{aligned} {{\mathcal {B}}}_r^n = {{\mathcal {B}}}_r\{{\mathbf{0} }_n\} \end{aligned}$$

the closed ball of radius $r>0$ centered on the origin in ${{\mathbb {C}}}^n$.

Let ${{\mathcal {U}} }$ a subset of ${{\mathbb {T}}}^n$. We will define its associated complexified domain of width s such that

$$\begin{aligned} {{\mathcal {V}}} _s {{\mathcal {U}} }= \left\{ {\mathbf{z} }\in {{\mathbb {C}}}^{n}/{{\,\mathrm{Re}\,}}({\mathbf{z} }) \in {{\mathcal {U}} }, \quad \left| {{\,\mathrm{Im}\,}}({\mathbf{z} }) \right| \leqslant s \right\} . \end{aligned}$$

For an interval ${{\mathcal {S}} }= \left[ a, b\right] \subset {{\mathbb {R}}}$ and a set ${\hat{{{\mathcal {I}} }} }\subset {{\mathbb {T}}}^2$, if $\rho >0$ and $\sigma >0$, we define the complex domain ${\hat{{{\mathcal {K}} }}}_{\rho ,\sigma }$ as follows:

$$\begin{aligned} {\hat{{{\mathcal {K}} }}}_{\rho ,\sigma }= {{\mathcal {B}}}_\rho {{\mathcal {S}} }\times {{\mathcal {B}}}^1_\rho \times {{\mathcal {V}}} _\sigma {\hat{{{\mathcal {I}} }} }\times {{\mathcal {B}}}^4_{\sqrt{\rho \sigma }}. \end{aligned}$$

For $0<p\leqslant 1$, we also consider the domains

$$\begin{aligned} {\hat{{{\mathcal {K}} }}}_p = {\hat{{{\mathcal {K}} }}}_{p\rho , p\sigma } \end{aligned}$$

and define the supremum norm on these latter as follows:

$$\begin{aligned} \left\| \,\cdot \, \right\| _p=\left\| \,\cdot \, \right\| _{{\hat{{{\mathcal {K}} }}}_{p\rho , p\sigma }}. \end{aligned}$$

We will need to consider the case of anisotropic analyticity widths where for $\varvec{\rho }=(\rho _1, \rho _2)\in {\mathbb {R}}_+^*\times {\mathbb {R}}_+^*$ and $\varvec{\sigma }=(\sigma _1, \sigma _2)\in {\mathbb {R}}_+^*\times {\mathbb {R}}_+^*$. The complex domain ${{\mathcal {K}} }_{\varvec{\rho }, \varvec{\sigma }}$ is defined as follows:

$$\begin{aligned} {{\mathcal {K}} }_{\varvec{\rho }, \varvec{\sigma }} = {{\mathcal {B}}}_{\rho _1}{{\mathcal {S}} }\times {{\mathcal {B}}}^1_{\rho _2} \times {{\mathcal {V}}} _{\sigma _1}{{\mathbb {T}}}\times {{\mathcal {V}}} _{\sigma _2}{{\mathbb {T}}}\times {{\mathcal {B}}}^4_{\sqrt{\rho _2\sigma _2}} \end{aligned}$$

and its restriction ${{\mathcal {K}} }_{\varvec{\rho },\varvec{\sigma },r}$, such as

$$\begin{aligned} {{\mathcal {K}} }_{\varvec{\rho }, \varvec{\sigma },r} = {{\mathcal {B}}}_{\rho _1}{{\mathcal {S}} }\times {{\mathcal {B}}}^1_{\rho _2} \times {{\mathcal {V}}} _{\sigma _1}{{\mathbb {T}}}\times {{\mathcal {V}}} _{\sigma _2}{{\mathbb {T}}}\times {{\mathcal {B}}}^4_r \end{aligned}$$

for $0<r\leqslant \sqrt{\rho _2\sigma _2}$. Thus, for $0<p\leqslant 1$, we also consider the domains

$$\begin{aligned} {{\mathcal {K}} }_p= {{\mathcal {K}} }_{p\varvec{\rho }, p\varvec{\sigma }} \quad \text{ and } \quad {{\mathcal {K}} }_{p,r}= {{\mathcal {K}} }_{p\varvec{\rho }, p\varvec{\sigma }, r} \end{aligned}$$

with the supremum norms

$$\begin{aligned} \left\| \, \cdot \, \right\| _p = \left\| \, \cdot \, \right\| _{{{\mathcal {K}} }_p} \quad \text{ and } \quad \left\| \, \cdot \, \right\| _{p,r}= \left\| \, \cdot \, \right\| _{{{\mathcal {K}} }_{p,r}}. \end{aligned}$$

Finally, for $1\leqslant k\leqslant +\infty$ and a given function $f\in {{\mathscr {C}}}^{k}({{\mathcal {U}} },{{\mathbb {C}}}^m)$ where ${{\mathcal {U}} }$ is a compact set in ${{\mathbb {C}}}^n$, we define the ${{\mathscr {C}}}^{k}$-norm $\left\| f \right\| _{{{\mathscr {C}}}^{k}}$ on ${{\mathcal {U}} }$ such that

$$\begin{aligned} \left\| f \right\| _{{{\mathscr {C}}}^{k}} = \sup _{p \leqslant k}\left\| \frac{\partial ^{p} f}{\partial z_1^{p_1} \ldots \partial z_n^{p_n}} \right\| _{{\mathcal {U}} }\end{aligned}$$

(3.1)

with $(p_j)_{j\in \{1,\ldots ,n\}} \in {{\mathbb {N}}}^n$ and $p = \sum _{j=1}^n p_j$.

3.2 Estimates

In the sequel we do not attempt to obtain estimates with particularly sharp constants. Actually, we suppress all constants and use the notation

to indicate respectively that

$$\begin{aligned} x<Cy, \quad Cx<y, \quad \text{ and } \quad x=Cy \end{aligned}$$

with some constant $C\geqslant 1$ independent of the small parameters of the problem.

3.3 Derivatives

Let us now introduce several simplified notations about the derivatives. Let a function f(z) with $z\in {{\mathbb {C}}}$, we will denote

$$\begin{aligned} f'(z) = \frac{{\mathrm {d}}f}{{\mathrm {d}}z}(z) \quad \text{ and } \quad f^{(l)}(z) = \frac{{\mathrm {d}}^lf}{{\mathrm {d}}z^l} (z). \end{aligned}$$

Let $f({\mathbf{w} },{\mathbf{x} },{\mathbf{y} }, {\mathbf{z} })$ a multi-variable function of ${{\mathbb {C}}}^8$ with ${\mathbf{w} }= (w_1,w_2)$, ${\mathbf{x} }= (x_1,x_2)$, ${\mathbf{y} }= (y_1,y_2)$, and ${\mathbf{z} }= (z_1,z_2)$. Then, we will denote the partial derivatives

$$\begin{aligned} \partial _{w_1}f= & {} \frac{\partial f}{\partial w_1},\quad \partial _{w_1}^l f = \frac{\partial ^l f}{\partial w_1^l},\\ \partial _{\mathbf{w} }f= & {} (\partial _{w_j}f)_{j\in \{1,2\}},\quad \partial _{\mathbf{w} }\partial _{\mathbf{x} }f= \left( \frac{\partial ^2f}{\partial w_j\partial x_k }\right) _{j,k\in \{1,2\}},\\ \partial _{{\mathbf{w} }}^2 f= & {} \partial _{{\mathbf{w} }}\partial _{{\mathbf{w} }}= \left( \frac{\partial ^2f}{\partial w_j\partial w_k}\right) _{j,k\in \{1,2\}},\quad \partial _{({\mathbf{z} },{\mathbf{w} })} f= (\partial _{{\mathbf{z} }}f,\partial _{{\mathbf{w} }}f), \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \partial _{({\mathbf{z} },{\mathbf{w} })}^2f&= \partial _{({\mathbf{z} },{\mathbf{w} })}\partial _{({\mathbf{z} },{\mathbf{w} })}f= \begin{pmatrix} \partial _{{\mathbf{z} }}\partial _{\mathbf{z} }f &{} \partial _{{\mathbf{z} }}\partial _{{\mathbf{w} }} f\\ \partial _{{\mathbf{w} }}\partial _{{\mathbf{z} }} f &{} \partial _{{\mathbf{w} }}\partial _{\mathbf{w} }f \end{pmatrix}. \end{aligned} \end{aligned}$$

Finally, the differential of the function f will be denoted

$$\begin{aligned} {\mathrm {d}}f = (\partial _{\mathbf{w} }f, \partial _{\mathbf{x} }f, \partial _{\mathbf{y} }f, \partial _{\mathbf{z} }f) \quad \text{ and } \quad {\mathrm {d}}^lf= \underbrace{{\mathrm {d}}{\mathrm {d}}\ldots {\mathrm {d}}}_{l}f. \end{aligned}$$

3.4 Hamiltonian flow

The Hamiltonian flow at a time t generated by an auxiliary function $g({\mathbf{w} },{\mathbf{x} },{\mathbf{y} },{\mathbf{z} })$ will be denoted $\Phi _t^g({\mathbf{w} },{\mathbf{x} },{\mathbf{y} },{\mathbf{z} })$. By introducing the Poisson bracket of the two real functions $f({\mathbf{w} },{\mathbf{x} },{\mathbf{y} },{\mathbf{z} })$ and $g({\mathbf{w} },{\mathbf{x} },{\mathbf{y} },{\mathbf{z} })$, such as

then the Hamiltonian flow satisfies

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}t}(f\circ \Phi ^g_t) = \left\{ f,g\right\} \circ \Phi _t^g \end{aligned}$$

and thus the Taylor expansions

$$\begin{aligned} f\circ \Phi _1^g&= f + \int _0^1\left\{ g,f\right\} \circ \Phi _s^g {\mathrm {d}}s\quad \text{ and } \quad \end{aligned}$$

(3.2)

$$\begin{aligned} f\circ \Phi _1^g&= f + \left\{ g,f\right\} + \int _0^1(1-s)\left\{ g,\left\{ g,f\right\} \right\} \circ \Phi _s^g {\mathrm {d}}s . \end{aligned}$$

(3.3)

4 Reduction of the Hamiltonian

The main goal of this section is to reduce the planetary Hamiltonian $H({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) = H_K({\mathbf{Z} }) +H_P({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} })$ defined in Sect. 2.3 to the sum of two terms: an integrable Hamiltonian associated with horseshoe trajectories written in terms of action variables and a remainder whose size is controlled. Several steps are necessary.

4.1 A collisionless domain

First of all, let us define a complexified domain excluding the collision manifold where the sizes of the Keplerian and perturbation parts will be estimated.

For an arbitrary fixed $\hat{\Delta }>0$, independent of the small parameters of the problem, we define the set ${\hat{{{\mathcal {I}} }} }$ by

$$\begin{aligned} {\hat{{{\mathcal {I}} }} }= \left\{ \varvec{\zeta }\in {{\mathbb {T}}}^2/\left| \zeta _1 \right| \geqslant \hat{\Delta }\right\} \end{aligned}$$

where “$\left| \,\cdot \, \right|$” denotes the usual distance over the quotient space ${{\mathbb {T}}}={\mathbb {R}}/2\pi {{\mathbb {Z}}}$. Remark that the condition on $\zeta _1$ can also be considered with the real variable $\zeta _1\in [\hat{\Delta }, 2\pi -\hat{\Delta }]$ since there exists an unique real representative in this segment for an angle $\zeta _1$ with a modulus lowered by $\hat{\Delta }$. Hence, ${\hat{{{\mathcal {I}} }} }$ has the structure of a cylinder in ${\mathbb {R}}\times {{\mathbb {T}}}$.

If we assume that the planets are on circular exact-resonant orbits (${\mathbf{Z} }={\mathbf{x} }= {\widetilde{\mathbf{x}} }= {\mathbf{0} }$; see Sect. 2.3), the fixed quantity $\hat{\Delta }$ corresponds to the minimal angular separation between the two planets which yields to a minimal distance given by $\displaystyle \Delta = 2 \min (a_{1,0}, a_{2,0})\sin (\hat{\Delta }/2)$. Thus, with the notations of Sect. 3, for an arbitrary $\hat{\Delta }>0$ independent of the small parameters of the problem, $\rho >0$ and $\sigma >0$ small enough that will be specified in the sequel, we can define a complex domain of holomorphy

$$\begin{aligned} {\hat{{{\mathcal {K}} }}}_{\rho ,\sigma }= {{\mathcal {B}}}^2_{\rho } \times {{\mathcal {V}}} _{\sigma }{\hat{{{\mathcal {I}} }} }\times {{\mathcal {B}}}^4_{\sqrt{\rho \sigma }} \end{aligned}$$

that excludes the collision manifold. In this setting, it will be possible to estimate the size of the transformations and the functions involved in our resonant normal form constructions.

Hence, we set out the following

Lemma 4.1

(Estimates on $H_K$ and $H_P$). Assuming that

the Hamiltonian H is analytic in the domain ${\hat{{{\mathcal {K}} }}}_{\rho _0,\sigma _0}$ and satisfies:

(4.1)

4.2 First averaging

In the first step of the reduction scheme, we average the Hamiltonian H over the fast angle $\zeta _2$ in order to reject the $\zeta _2$-dependency in an exponentially small remainder. This reduction is provided by the following

Theorem 4.1

(First averaging theorem). For

$$\begin{aligned} 1/7<\beta < 1/2,\quad (\rho , \sigma ) = \sigma _0({\varepsilon }^\beta , 1), \end{aligned}$$

and ${\varepsilon }$ small enough (i.e. ), there exists a canonical transformation

(4.2)

and such that

(4.3)

with the following estimates:

(4.4)

(4.5)

for

and

$$\begin{aligned} \alpha = \frac{1 - 2\beta }{5}. \end{aligned}$$

Moreover, the size of the transformation $\overline{\Upsilon }$ is given by

(4.6)

The remainder $H^\dagger _*$ being exponentially small on ${\hat{{{\mathcal {K}} }}}_{1/3}$, we choose to drop it for the moment in order to focus our reduction on the averaged Hamiltonian given by

At last, we have the following crucial property.

Lemma 4.2

(D’Alembert rule in the Averaged Problem). We choose the transformation $\overline{\Upsilon }$ such as the D’Alembert rule, given by (2.4), is preserved (see Lemma A.1). Equivalently, the quantity

(4.7)

associated with the angular momentum ${\tilde{{{\mathcal {C}}}}}(\tilde{\mathbf{r}} _j, \mathbf{r} _j)$, is a first integral of the averaged Hamiltonian $\overline{H}$.

Furthermore, if a general function f, which does not depend on the fast angle , satisfies the D’Alembert rule, then there exists a set of function $(f_{(j,k)})_{j,k\in \{1,2\}}$ such that

(4.8)

This implies that in the expansion of $\overline{H}$ in the neighborhood of the total degree in , , , in the monomials appearing in the associated Taylor series is even. Hence, the quasi-circular manifold defined as follows:

is invariant by the flow of the Hamiltonian $\overline{H}$. For more details on the topology of ${\mathrm C}_0$, see the phase portrait and its description in Sect. 2.4.

4.3 The reduction of $\overline{H}$

In the second step, we perform some reductions in order to get a more tractable expression of the Hamiltonian $\overline{H}$. It mainly consists in an expansion of the Hamiltonian in a suitable domain and at an appropriate degree.

First of all, regarding the eccentricities, a polynomial expansion of degree two in is enough to control the dynamics along the secular directions (i.e. the directions transversal to ${\mathrm C}_0)$.

For the action variables , it is natural to expand in the neighborhood of the exact-resonant actions $(\Lambda _{1,0},\Lambda _{2,0})$ given in the formula (2.2), that is . Thus, $\overline{H} _P$ is truncated at degree zero while it is necessary to keep the second order for the Keplerian part.

However, coming from the fact that when with

$$\begin{aligned} {\mathbf{Z} }_\star = \begin{pmatrix} \Lambda _{1,0}-\Lambda _{1,\star }\\ \Lambda _{1,0}+\Lambda _{2,0} -(\Lambda _{1,\star }+\Lambda _{2,\star }) \end{pmatrix} \quad \text{ and } \quad \Lambda _{j,\star } = {\widehat{m}}_j\mu _j^{1/2}m_0^{1/6}\upsilon _0^{-1/3}, \end{aligned}$$

the two associated semi-major axes are both equal to the same value given by $a_\star = m_0^{1/3}\upsilon _0^{-2/3}$. Consequently, it is much more convenient to center the expansion of $\overline{H} _P$ at . This shift generates only small additional terms, as the difference between $\Lambda _{j,0}$ and $\Lambda _{j,\star }$ satisfies the inequalities . Remark that the reduced mass ${\widehat{m}}_j$ can be replaced by $m_j$ which only adds small terms to the remainder of order from $H_K$ and of order ${\varepsilon }^2$ from $\overline{H} _P$.

Finally, in order to uncouple the fast and semi-fast action variable and , we introduce a new set of action-angle variables via the linear transformation $\tilde{\Psi }$ given by

$$\begin{aligned} \tilde{\Psi }: \quad \Bigg \{ \begin{array}{ccc} {\hat{{{\mathcal {K}} }}}_{1/6} &{}\longrightarrow &{} {\hat{{{\mathcal {K}} }}}_{1/3} \\ ({\mathbf{I} },{\varvec{\varphi }},{\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) &{}\longmapsto &{}(I_1 +\kappa I_2, I_2,\varphi _1, \varphi _2-\kappa \varphi _1, {\mathbf{w} },{\widetilde{{\mathbf{w} }} }) \end{array} \end{aligned}$$

where

$$\begin{aligned} \kappa =\frac{m_1}{m_1+m_2}\leqslant \frac{1}{2} \end{aligned}$$

and such that

$$\begin{aligned} {\hat{{{\mathcal {K}} }}}_{1/18}\subseteq \tilde{\Psi }({\hat{{{\mathcal {K}} }}}_{1/6})\subseteq {\hat{{{\mathcal {K}} }}}_{1/4}\;. \end{aligned}$$

(4.9)

All of these successive transformations and estimation of the generate remainder are summarized in the following

Theorem 4.2

(Hamiltonian reduction). Under the assumptions of Theorem 4.1, we have the following assertions:

• (1) in the coordinates $({\mathbf{I} },{\varvec{\varphi }}, {\mathbf{w} },{\widetilde{{\mathbf{w} }} })$ the averaged Hamiltonian $\tilde{{\mathscr {H}} }=\overline{H} \circ \tilde{\Psi }- H_{K}({\mathbf{0} })$ can be written

  $$\begin{aligned} \tilde{{\mathscr {H}} }({\mathbf{I} }, \varphi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = \tilde{{\mathscr {H}} }_1(I_1,\varphi _1) + {{\mathscr {H}} }_2(I_2)&+ \tilde{{\mathscr {Q}} }(\varphi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) + \tilde{{\mathscr {R}} }({\mathbf{I} }, \varphi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) \nonumber \\ \end{aligned}$$

  (4.10)

  where

  $$\begin{aligned} \tilde{{\mathscr {H}} }_1(I_1,\varphi _1)= & {} \upsilon _0 \left( -AI_1^2 + {\varepsilon }B{{\mathcal {F}} }(\varphi _1)\right) ,\quad {{\mathscr {H}} }_2(I_2) = \upsilon _0 \left( I_2-E I_2^2\right) ,\\ \tilde{{\mathscr {R}} }({\mathbf{I} }, \varphi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} })= & {} \tilde{{\mathscr {R}} }_0({\mathbf{I} }, \varphi _1)+ \sum _{j,k\in \{1, 2\}} \tilde{{\mathscr {R}} }_{(j,k)}({\mathbf{I} }, \varphi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} })w_j{\widetilde{w} }_k,\\ \tilde{{\mathscr {Q}} }(\phi _1,{\mathbf{w} },{\widetilde{{\mathbf{w} }} })= & {} \sum _{j,k\in \{1, 2\}} \tilde{{\mathscr {Q}} }_{(j,k)}(\phi _1)w_j{\widetilde{w} }_k\\&= i{\varepsilon }\upsilon _0 D\bigg ( \frac{{\tilde{{\mathcal {A}}}}(\varphi _1)}{m_1}w_1{\widetilde{w} }_1 + \frac{{\tilde{{{\mathcal {B}}}}}(\varphi _1)}{\sqrt{m_1m_2}} w_1{\widetilde{w} }_2 \\&\quad + \frac{{{\,\mathrm{conj}\,}}({\tilde{{{\mathcal {B}}}}})(\varphi _1)}{\sqrt{m_1m_2}} {\widetilde{w} }_1 w_2 + \frac{{\tilde{{\mathcal {A}}}}(\varphi _1)}{m_2}w_2{\widetilde{w} }_2 \bigg ), \end{aligned}$$

  with

  $$\begin{aligned} \begin{aligned}&{{\mathcal {F}} }(\varphi _1) =\frac{2}{3} \left( \cos \varphi _1 - {{\mathcal {D}}} (\varphi _1)^{-1}\right) ,\\&{\tilde{{\mathcal {A}}}}(\varphi _1) = \frac{{{\mathcal {D}}} (\varphi _1)^{-5}}{4}\left( 5\cos 2\varphi _1 - 13 + 8\cos \varphi _1\right) - \cos \varphi _1, \\&{\tilde{{{\mathcal {B}}}}}(\varphi _1) = e^{-2i\varphi _1}- \frac{{{\mathcal {D}}} (\varphi _1)^{-5}}{8}\left( e^{-3i\varphi _1} + 16 e^{-2i\varphi _1} - 26e^{-i\varphi _1} + 9 e^{i\varphi _1}\right) ,\\&{{\,\mathrm{conj}\,}}({\tilde{{{\mathcal {B}}}}})(\varphi _1) \text{ is } \text{ the } \text{ complex } \text{ conjugate } \text{ of } {\tilde{{{\mathcal {B}}}}}(\varphi _1), \\&{{\mathcal {D}}} (\varphi _1) = \sqrt{2-2\cos \varphi _1}, \end{aligned} \end{aligned}$$

  (4.11)

  and the parameters:

  $$\begin{aligned} \begin{aligned} A&= \frac{3}{2}\upsilon _0^{1/3}m_0^{-2/3}\left( \frac{1}{m_1} + \frac{1}{m_2}\right) , \quad B= \frac{3}{2}\upsilon _0^{-1/3}m_0^{2/3} D,\\ D&= \frac{m_1m_2}{m_0},\quad E = \frac{3}{2}\upsilon _0^{1/3}m_0^{-2/3}(m_1 + m_2)^{-1}. \end{aligned} \end{aligned}$$

  (4.12)

• (2) The remainder $\tilde{{\mathscr {R}} }$ is bounded by the threshold

  

  and, if we assume $\beta >1/3$, we can ensure

  

Remark 4.1

On the domain ${\hat{{{\mathcal {K}} }}}_{1/6}$, the size of the remainder $\tilde{{\mathscr {R}} }$ is larger than the one provided by the first averaging given by (4.4).

As a consequence, the averaged Hamiltonian $\tilde{{\mathscr {H}} }$ possesses three components. The first one describes the dynamics on the quasi-circular manifold ${\mathrm C}_0$. It is composed of the integrable Hamiltonian ${{\mathscr {H}} }_2$ and the mechanical system $\tilde{{\mathscr {H}} }_1$, respectively associated with the fast and the semi-fast variations. The second component $\tilde{{\mathscr {Q}} }$ which is of order two in eccentricity and depends of the semi-fast angle described the main part of the secular behavior along the two normal-directions. At last, we have the remainder $\tilde{{\mathscr {R}} }$ whose shape and size are controlled on the domain ${\hat{{{\mathcal {K}} }}}_{1/6}$.

4.4 The mechanical system $\tilde{{\mathscr {H}} }_1$

In the third step, we focus our efforts on the semi-fast dynamics in order to build an action-angle coordinate system valid for the horseshoe trajectory region. According to Theorem 4.2, the semi-fast component of the Hamiltonian is given by the following mechanical system:

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(I_1, \varphi _1) = \upsilon _0\left( -AI_1^2 + {\varepsilon }B {{\mathcal {F}} }(\varphi _1)\right) \end{aligned}$$

where the real function ${{\mathcal {F}} }$ is defined on $]0,2\pi [$ by (4.11) and A, B are two positive constants given by (4.12). As

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(-I_1, \varphi _1) = \tilde{{\mathscr {H}} }_1(I_1, \varphi _1) \quad \text{ and } \quad \tilde{{\mathscr {H}} }_1(I_1, \pi -\varphi _1) = \tilde{{\mathscr {H}} }_1(I_1, \pi + \varphi _1), \end{aligned}$$

the study of the Hamiltonian $\tilde{{\mathscr {H}} }_1$ and its flow can be reduced to ${\mathbb {R}}_+\times ]0,\pi ]$. As

$$\begin{aligned} {{\mathcal {F}} }(\varphi _1) = -1 + \frac{7}{24}(\varphi _1 - \pi )^2 +{{\mathcal {O}}} _4(\varphi _1-\pi ), \end{aligned}$$

the point of coordinates $(0,\pi )$ is a hyperbolic fixed point whose energy level equals $h_0 = {\varepsilon }\upsilon _0 B {{\mathcal {F}} }(\pi ) = -{\varepsilon }\upsilon _0B$.

With these notations, the horseshoe orbits that we are interested in are the level curves of $\tilde{{\mathscr {H}} }_1$ which fulfill the relation

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(I_1, \varphi _1) = h_\delta = - {\varepsilon }\upsilon _0 B(1+\delta ) \quad \text{ with } \quad \delta >0. \end{aligned}$$

Fig. 5

Phase portrait of the mechanical system $\tilde{{\mathscr {H}} }_1(I_1,\varphi _1)$ depicted in the domain ${\mathbb {R}}_+\times ]0,\pi [$ (the entire phase portrait is represented in Fig. 4). $\delta =0$ corresponds to the separatrix (black curve) that surrounds the tadpole domain ($\delta <0$) while $\delta >0$ corresponds to the horseshoe trajectories (grey curves). The grey region represents the horseshoe trajectories such as $\delta ^* \leqslant \delta \leqslant 2\delta ^*$ where adapted action-angle variables are built

Along a $h_\delta$-level curve, the action $I_1$ can be expressed as a function of $\varphi _1$ for $\varphi _{1,\delta }^{\min } \leqslant \varphi _1 \leqslant \pi$, where $\varphi _{1,\delta }^{\min }$ is the angle corresponding in one of the two intersections of the level curve with the axis $I_1 = 0$ (see Fig. 5). This angle, which is also the minimal value of $\varphi _1$ along a $h_\delta$-level curve, verifies

$$\begin{aligned} \varphi _{1,\delta }^{\min } = 2 \arcsin \left( \frac{\sqrt{2} -1}{2}\right) - c_0\delta + {{\mathcal {O}}} (\delta ^2) \quad \text{ where } \quad 1/4< c_0 <1/3. \end{aligned}$$

(4.13)

By symmetry reasons, the amplitude of variation of $\varphi _1$ around $\pi$, for a given value of $h_\delta$, is greater than $2\pi - 2\varphi _{1,\delta }^{\min } > 312^\circ$.

When $\delta >0$, the orbit of energy $h_\delta$ is periodic and the corresponding period is given by the expression

$$\begin{aligned} \begin{aligned} T_\delta&= \frac{2}{\upsilon _0 \sqrt{{\varepsilon }A B}}\int _{\varphi _{1,\delta }^{\min }}^\pi \frac{{\mathrm {d}}\varphi _1}{\sqrt{U_\delta (\varphi _1)}} \quad \text{ with } \quad \\ U_\delta (\varphi _1)&={\varepsilon }^{-1}AB^{-1}( I_1(\varphi _1))^2 = 1 + \delta + {{\mathcal {F}} }(\varphi _1). \end{aligned} \end{aligned}$$

As the orbit approaches the separatrix ($\delta$ tends to zero), its period $T_\delta$ tends to infinity. More precisely,

Lemma 4.3

(Semi-fast Frequency). if $0<\delta ^*$ is small enough (), then for all $\delta \in [\delta ^*, 2\delta ^* ]$ the asymptotic expansions of the semi-fast frequency and of its first derivative read

$$\begin{aligned} \nu _\delta = 2\pi T_\delta ^{-1} = \frac{\upsilon _0 \sqrt{{\varepsilon }}K}{\left| \ln \delta \right| }\left( 1 + \hat{h}_0(\delta )\right) \quad \text{ and } \quad \nu '_\delta = \frac{\upsilon _0\sqrt{{\varepsilon }}K}{\delta \left| \ln \delta \right| ^2}\left( 1 + \hat{h}_1(\delta )\right) \end{aligned}$$

(4.14)

where $(\hat{h}_j)_{j\in \{0,1\}}$ are analytic functions over $[\delta ^*, 2\delta ^* ]$ that satisfy the relations

We define a subset of the horseshoe region in order to build the adapted action-angle variables. Thus, let us consider the domain ${{\mathfrak {D}}} _{*}$ defined as

$$\begin{aligned} {{\mathfrak {D}}} _{*} = \left\{ \begin{array}{c}(I_1,\varphi _1) \in {\mathbb {R}}\times ]0,2\pi [ \quad \text{ such } \text{ that } \quad \tilde{{\mathscr {H}} }_1(I_1,\varphi _1) = h_\delta \\ \text{ with }\quad \delta ^* \leqslant \delta \leqslant 2\delta ^* \end{array}\right\} . \end{aligned}$$

(4.15)

This set, which corresponds to the grey region in Fig. 5, contains the horseshoe orbits of the mechanical system which are close to the separatrix.

In this domain we can build a system of action-angle variables denoted $(J_1,\phi _1)$ such that

$$\begin{aligned} \begin{aligned} {{\mathscr {H}} }_1(J_1)&= \tilde{{\mathscr {H}} }_1\circ {{\mathfrak {F}}}(J_1, \phi _1) =h_\delta \quad \text{ and } \quad {{\mathscr {H}} }_1'(J_1) = \nu _\delta \\&\text{ where } \quad {{\mathfrak {F}}}=({{\mathfrak {F}}}_1,{{\mathfrak {F}}}_2) :\ \Bigg \{ \begin{array}{ccc} {{\mathfrak {F}}}^{-1}\!\left( {{\mathfrak {D}}} _{*} \right) &{}\longrightarrow &{} {{\mathfrak {D}}} _{*}\\ (J_1,\phi _1) &{}\longmapsto &{}(I_1, \varphi _1) \end{array}\\&\mathrm{with}\quad {{\mathfrak {F}}}^{-1}\!\left( {{\mathfrak {D}}} _{*} \right) ={{\mathcal {S}} }_{*}\times {{\mathbb {T}}}\ ;\ {{\mathcal {S}} }_{*}=\left[ a, b\right] \subset {{\mathbb {R}}}. \end{aligned} \end{aligned}$$

(4.16)

If we restrict our attention to an arbitrary energy level corresponding to a fixed shift of energy $\delta$ that belongs to the segment $\left[ \delta ^* , 2\delta ^*\right]$, the transformation in action-angle variables can be defined explicitly by the classical integral formulation:

$$\begin{aligned} \begin{aligned} J_1&= 4 \sqrt{{\varepsilon }BA^{-1}} \int _{\varphi _{1,\delta }^{\min }}^\pi \sqrt{U_\delta (s)} {\mathrm {d}}s \quad \text{ and } \quad \phi _1 = -\frac{\nu _\delta }{2\upsilon _0 \sqrt{{\varepsilon }AB}}\int _{\varphi _{1,\delta }^{\min }}^{\varphi _1} \frac{{\mathrm {d}}s}{\sqrt{U_\delta (s)}}\, \end{aligned} \end{aligned}$$

where $\delta$ and $\varphi _{1,\delta }^{\min }$ are functions of $(I_1,\varphi _1)$.

As we look for a complex domain of holomorphy for the integrable Hamiltonian ${{\mathscr {H}} }_1$, we have the following

Theorem 4.3

(Semi-fast holomorphic extension). For $\delta ^*$ small enough (), the transformation ${{\mathfrak {F}}}$ can be extended holomorphically over ${{\mathcal {B}}}_{\hat{\rho }_1}{{\mathcal {S}} }_{*}\times {{\mathcal {V}}} _{\hat{\sigma }_1} {{\mathbb {T}}}$ with $\hat{\rho }_1 = \sqrt{{\varepsilon }}(\delta ^*)^{{\hat{p} }}$ and $\hat{\sigma }_1 =(\delta ^*)^{{\hat{p} }}$ for some positive exponent ${\hat{p} }$. Moreover, the extended function is C-Lipschitz with .

Remark 4.2

Rough estimates lead to ${\hat{p} }=11/2$ which is far to be optimal. Moreover, without loss of generality, we can assume that $\delta ^*$ is small enough that in the domain ${{\mathcal {B}}}_{\hat{\rho }_1}{{\mathcal {S}} }_{*}$ there is a diffeomorphism between $J_1$ and $\delta$. We will also use the notations $h_\delta$, $\nu _\delta$, $\nu '_\delta$ for the energy and the frequency on the complex domain ${{\mathcal {B}}}_{\hat{\rho }_1}{{\mathcal {S}} }_{*}$. From a more general point of view, the polynomial link between the energy shift $\delta ^*$ and the analyticity widths is arbitrary and certainly not optimal. Another possibility would be to leave these quantities independent during the calculations and to fix them at the end, in view of the constraints obtained.

4.5 The Hamiltonian in semi-fast action-angle variables

Going back to the averaged Hamiltonian $\tilde{{\mathscr {H}} }$ considered in (4.10), the introduction of action-angle variables of the mechanical system leads to the following expressions.

Theorem 4.4

(Semi-fast action-angle variables). With the notations of Sect. 3, for $\delta ^*$ small enough () there exists a canonical transformation

$$\begin{aligned}&\Psi : \quad \Bigg \{ \begin{array}{ccc} {{\mathcal {K}} }_{\varvec{\rho },\varvec{\sigma }} &{}\longrightarrow &{} {\hat{{{\mathcal {K}} }}}_{1/6}\\ ({\mathbf{J} },{\varvec{\phi }},{\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) &{}\longmapsto &{} ({\mathbf{I} },{\varvec{\varphi }},{\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) \end{array}\nonumber \\&\quad \text{ where } \quad (I_1,\varphi _1,I_2, \varphi _2) = ({{\mathfrak {F}}}(J_1,\phi _1), J_2,\phi _2) \end{aligned}$$

and

Then, the transformed Hamiltonian ${{\mathscr {H}} }= \tilde{{\mathscr {H}} }\circ \Psi$ is analytic, satisfies the D’Alembert rule, and reads

$$\begin{aligned} \begin{aligned} {{\mathscr {H}} }({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = {{\mathscr {H}} }_1(J_1) + {{\mathscr {H}} }_2(J_2)&+ {{\mathscr {Q}}}(J_1, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} })+ {{\mathscr {R}} }({\mathbf{J} }, \phi _1,{\mathbf{w} },{\widetilde{{\mathbf{w} }} }) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {{\mathscr {H}} }_1(J_1)= & {} h_{\delta },\quad {{\mathscr {H}} }_1'(J_1) = \nu _{\delta }, \quad {{\mathscr {H}} }_1''(J_1) = -\frac{\nu _{\delta }' \nu _{\delta }}{{\varepsilon }\upsilon _0 B}, \\ {{\mathscr {H}} }_2(J_2)= & {} \upsilon _0 \left( J_2-E J_2^2\right) ,\\ {{\mathscr {R}} }({\mathbf{J} }, \phi _1,{\mathbf{w} },{\widetilde{{\mathbf{w} }} })= & {} {{\mathscr {R}} }_0(J_1, \varphi _1) + \sum _{ j,k\in \{1,2\}} {{\mathscr {R}} }_{(j,k)}({\mathbf{J} }, \phi _1,{\mathbf{w} },{\widetilde{{\mathbf{w} }} })w_j{\widetilde{w} }_k,\\ {{\mathscr {Q}}}(J_1,\phi _1,{\mathbf{w} },{\widetilde{{\mathbf{w} }} })= & {} \sum _{j,k \in \{1,2\}} {{\mathscr {Q}}}_{(j,k)}(J_1, \phi _1)w_j{\widetilde{w} }_k\\= & {} i{\varepsilon }\upsilon _0 D\bigg ( \frac{{\mathcal {A}}(J_1,\phi _1)}{m_1}w_1{\widetilde{w} }_1 + \frac{{{\mathcal {B}}}(J_1,\phi _1)}{\sqrt{m_1m_2}} w_1{\widetilde{w} }_2\\&+ \frac{{{\,\mathrm{conj}\,}}({{\mathcal {B}}})(J_1,\phi _1)}{\sqrt{m_1m_2}} {\widetilde{w} }_1 w_2 + \frac{{\mathcal {A}}(J_1,\phi _1)}{m_2}w_2{\widetilde{w} }_2 \bigg ) \end{aligned}$$

with ${\mathcal {A}}= {\tilde{{\mathcal {A}}}}\circ {{\mathfrak {F}}}_2$ and ${{\mathcal {B}}}= {\tilde{{{\mathcal {B}}}}}\circ {{\mathfrak {F}}}_2$. Moreover, the following bounds are satisfied:

(4.17)

and

Remark 4.3

In the complex domain ${{\mathcal {K}} }_{\varvec{\rho }, \varvec{\sigma }}$, there exists a diffeomorphism between the shift of energy $\delta$ and the semi-fast action $J_1$.

4.6 Second averaging

In the fourth step, we average the Hamiltonian ${{\mathscr {H}} }$ over the semi-fast angle $\phi _1$ in order to reject the $\phi _1$-dependency up to an exponentially small remainder.

Up to now, $\delta$ and ${\varepsilon }$ were two independent small parameters. However, in order to simplify the calculations in the following we link the bounds in energy level to ${\varepsilon }$ such that

$$\begin{aligned} \delta ^* = {\varepsilon }^{\hat{{\mathrm q }}} \end{aligned}$$

(4.18)

where ${\hat{{\mathrm q }}}$ is a positive exponent that will be determined in the sequel. Hence, the analyticity widths of the considered domain of holomorphy ${{\mathcal {K}} }_{\varvec{\rho }, \varvec{\sigma }}$ are equal to

Then, using the notations of Sect. 3 we restrict the domain of holomorphy of the Hamiltonian ${{\mathscr {H}} }$ to the complex domains ${{\mathcal {K}} }_{p}= {{\mathcal {K}} }_{p\varvec{\rho }, p\varvec{\sigma }}$ for $0<p\leqslant 1$ with

where the following bounds on the semi-fast frequency are valid:

for any $\delta \in \left[ \delta ^* ,2\delta ^*\right]$ (or equivalently for any $J_*\in {{\mathcal {S}} }_{*}$) and for $J_1\in {{\mathcal {B}}}_{\rho _1}{{\mathcal {S}} }_{*}$ there exists $J_*\in {{\mathcal {S}} }_{*}$ such that

The latter estimates come from (4.17) which allows to bound ${{\mathscr {H}} }''_1$. Consequently, we have

(4.19)

uniformly over ${{\mathcal {K}} }_p$.

In this setting, one can normalize once again the Hamiltonian in order to eliminate the semi-fast angle $\phi _1$ according to the following

Theorem 4.5

(Second averaging theorem). For

$$\begin{aligned} {\mathrm q }= \frac{3\beta - 1}{15} \quad \text{ with } \quad 4/9<\beta < 1/2 \end{aligned}$$

(4.20)

and ${\varepsilon }$ small enough , there exists a canonical transformation

such that ${{\mathscr {H}} }\circ \overline{\Psi }= \overline{{\mathscr {H}} }+ {\mathscr {H}}^\dagger _*$ where

is the secular Hamiltonian with

and ${\mathscr {H}}^\dagger _*$ is the remainder that contains the -dependency such that

Moreover, for $0<p<7/12$ the choice for ${\mathrm q }$ given in (4.20) yields the following upper bounds:

(4.21)

(4.22)

and

(4.23)

Finally, we can bound the size of the transformation by

The remainder ${\mathscr {H}}^\dagger _*$ being exponentially small, we drop it for the moment in order to focus on the secular Hamiltonian $\overline{{\mathscr {H}} }$.

Remark 4.4

In the same way as in the Remark 4.3, on the complex domain ${{\mathcal {K}} }_{p}$ there exists a diffeomorphism between the shift of energy and the semi-fast action .

4.7 The normal frequencies

In the fifth step, we focus our effort on the secular dynamics. From the estimates of the previous theorem, the main part of the secular dynamics is given by $\overline{{\mathscr {Q}} }$ whose coefficients ${\overline{ {\mathcal {A}}}}$ and ${\overline{{{\mathcal {B}}}}}$ are the result of the averaging of ${\tilde{{\mathcal {A}}}}\circ {{\mathfrak {F}}}_2$ and ${\tilde{{{\mathcal {B}}}}}\circ {{\mathfrak {F}}}_2$ with respect to the semi-fast angle $\phi _1$. The action-angle transformation ${{\mathfrak {F}}}$ being not explicit, we perform the average with respect to the initial angle $\varphi _1 = {{\mathfrak {F}}}_2(J_1, \phi _1)$. More specifically, we consider the average at a semi-fast action $J_*\in {{\mathcal {S}} }_{*}$, hence on a level curve corresponding to such that

(4.24)

From these expressions, we deduce the asymptotic expansion of the pure imaginary eigenvalues of $(\overline{{\mathscr {Q}} }_{(j,k)}(J_*))_{j,k\in \{1, 2\}}$ that we denote for $j\in \{1,2\}$ where and correspond to the main part of the two secular frequencies. Hence, we have the following

Theorem 4.6

(Secular frequencies). The asymptotic expansions of the main part of the secular frequencies as tends to zero (with our definition of ${{\mathfrak {D}}} _*$ given by (4.15)) are given by

(4.25)

where

Then, we need to reduce the quadratic part

(4.26)

to a diagonal form for for some $0<p<7/12$. Since we link the shift in energy with the mass ratio ${\varepsilon }$ via a power law as in (4.18), the differences between the coefficients of and $(\overline{{\mathscr {Q}} }_{(j,k)}(J_*))_{j,k\in \{1,2\}}$ for are negligible with respect to the eigenvalues (4.25). Indeed, the estimates (4.21) of Theorem 4.5 together with the mean value theorem provide the following:

In the same way, the estimates (4.22) imply that the coefficients $({{\mathscr {F}} }_{(j,k)})_{j,k\in \{1, 2\}}$ are of size ${\varepsilon }^{2-2\beta }$ and thus, are also negligible with respect to the eigenvalues (4.25) over ${{\mathcal {B}}}_*$. Consequently, for all , the main part of the eigenvalues in the quadratic form (4.26) are given by the eigenvalues of for some $J_*\in {{\mathcal {S}} }_*$.

We denote by the eigenvalues of (4.26) for . Since these quantities are perturbation of and , which are different for ${\varepsilon }$ small enough, the spectrum of (4.26) is simple. On the real domain ${{\mathcal {B}}}_*\cap {{\mathbb {R}}}^2$, the angular momentum given by (4.7) being an integral of ${{\mathscr {H}} }\circ \overline{\Psi }$ considered in Theorem 4.5, the manifold ${\mathrm C}_0$ is normally stable. These two properties imply that the two perturbed frequencies are also purely imaginary numbers, or equivalently is real, for .

In the complex domain ${{\mathcal {B}}}_*$, we have

Consequently, as , for $\varepsilon$ small enough we have

(4.27)

on the complex domain ${{\mathcal {B}}}_*$.

Since the spectrum is simple, there exists a symplectic transformation which is linear with respect to , and diagonalizes the quadratic form (4.26). In the same way, the eigenspaces of (4.26) are close to those of which correspond to a non-singular transformation depending of and . Hence, we have the following

Theorem 4.7

(Diagonalization). With the notations of Sect. 3, for

(which is strictly smaller that $\sqrt{\rho _2\sigma _2}$ with the considered values of $\beta$), there exists $0<p<7/12$ and a canonical transformation

which is linear with respect to ${\mathbf{z} }$ and ${\widetilde{\mathbf{z}}}$ with

such that the secular Hamiltonian $\overline{{\mathscr {H}} }\circ \Xi = \check{{\mathscr {H}} }+ \check{{{\mathscr {R}} }}$ reads

(4.28)

As a consequence, we set out the following

Corollary 4.1

Taking into account the exponentially small remainders in Theorems 4.1 and 4.5, the planetary Hamiltonian ${{\mathcal {H}} }$ given in (2.1) reads

5 Application of a Pöschel Version of KAM Theory

As said in the introduction, we apply Pöschel version of KAM theory for the persistence of lower dimensional normally elliptic invariant tori [28]. More precisely we implement a formulation of Pöschel’s theorem [28] given in Proposition 2.2 of Biasco et al. [6], which is a summary of Theorems A, B and Corollary C in Pöschel [28] for the finite-dimensional case. In the co-orbital case, we have to be cautious about the dependance with respect to the small parameter ${\varepsilon }$ of the constants involved in these statements. Indeed, some quantities, such as the analyticity width with respect to the semi-fast angle, are singular in our problem.

For the sake of clarity, we will now try to be as close as possible to the notations used in Biasco et al. [6]. Pöschel’s theorem requires a parametrized normal form that can be written in our case as

$$\begin{aligned} {\mathrm N }({\mathbf{y} },{\mathbf{z} },{\widetilde{\mathbf{z}}} ;\varvec{\xi }) = \sum _{j=1,2} \omega _j(\varvec{\xi }) y_j + \sum _{j=1,2} i\Omega _j(\varvec{\xi })z_j{\widetilde{z}} _j \end{aligned}$$

(5.1)

where $\varvec{\omega }$ are the internal frequencies, which depends on the 2d parameter $\varvec{\xi }$ belonging a complex set $\Pi$ defined later and $\varvec{\Omega }$ are the normal or secular frequencies. The 2d tori given by the quasi-circular manifold ${\mathrm C}_0 = \{{\mathbf{z} }={\widetilde{\mathbf{z}}} ={\mathbf{0} }\}$ are invariant under the flow of the normal form given by (5.1) and are normally elliptic.

Let us now consider the Hamiltonian

$$\begin{aligned} {\mathrm H }({\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi }) = {\mathrm N }({\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi }) + {\mathrm P }({\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi }) \end{aligned}$$

(5.2)

with

$$\begin{aligned} \left\{ \begin{aligned} \omega _j(\varvec{\xi })&= {{\mathscr {H}} }_j'(\xi _j) + \partial _{\Gamma _j} {{\mathscr {F}} }_0(\varvec{\xi }) \\ \Omega _j(\varvec{\xi })&= g_j(\varvec{\xi }) \end{aligned}\right. \end{aligned}$$

and

$$\begin{aligned} {\mathrm P }({\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi }) = \check{{\mathrm H }}(\varvec{\xi }+ {\mathbf{y} }, \varvec{\psi }, {\mathbf{z} }, {\widetilde{\mathbf{z}}} )-{\mathrm N }({\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi })- \check{{\mathscr {H}} }(\varvec{\xi },{\mathbf{0} }, {\mathbf{0} }), \end{aligned}$$

(5.3)

$\check{{\mathrm H }}$ and $\check{{\mathscr {H}} }$ being respectively the planetary Hamiltonian considered in the corollary 4.1 and the integrable approximation of Theorem 4.7.

We will need estimates on the Lipschitz norm of a function f defined over the domain $\Pi$:

$$\begin{aligned} \left| f \right| _\Pi ^{\mathrm{Lip}} = \sup \limits _{\varvec{\xi }\ne \varvec{\xi }'\in \Pi } \frac{\left| f(\varvec{\xi }) - f(\varvec{\xi }') \right| }{\left| \varvec{\xi }- \varvec{\xi }' \right| }\, . \end{aligned}$$

Hence $\left| f \right| _\Pi ^{\mathrm{Lip}}\leqslant \left\| {\mathrm {d}}f \right\| _\Pi$ for a differentiable function. Especially, we consider the upper bound:

$$\begin{aligned} \vert \varvec{\omega }\vert _\Pi ^{\mathrm{Lip}} + \vert \varvec{\Omega }\vert _\Pi ^{\mathrm{Lip}} \leqslant M. \end{aligned}$$

Moreover, Pöschel reasoning requires that the internal frequency map $\varvec{\omega }$ is a diffeomorphism onto its image $\varvec{\omega }(\Pi )$ (more precisely $\Pi ={{\mathcal {B}}}^2_\rho$ where $\rho$ is determined in Proposition A.4). Thus, we consider the following upper bound:

$$\begin{aligned} \vert \varvec{\omega }^{-1} \vert _\Pi ^{\mathrm{Lip}} \leqslant L. \end{aligned}$$

In order to ensure the persistence of normally elliptic tori, we have to check Melnikov’s condition for multi-integers of length bounded by

$$\begin{aligned} K_0 = 16L M . \end{aligned}$$

More precisely, we have to prove the existence of a constant $\gamma _0>0$ such that

(see Proposition A.1 for more details).

The planetary Hamiltonian ${\mathrm H }$ defined in (5.2) is analytic over the domain

$$\begin{aligned} D({\bar{r}},{\bar{s}}) = \left\{ ({\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ) \in {{\mathbb {C}}}^8\ /\ \left| {\mathbf{y} } \right|< {\bar{r}}^2, \, \varvec{\psi }\in {{\mathcal {V}}} _{{\bar{s}}}{{\mathbb {T}}}^2,\,\left| ({\mathbf{z} },{\widetilde{\mathbf{z}}} ) \right| < {\bar{r}}\right\} \end{aligned}$$

(5.4)

such that $0< {\bar{r}}<r$ and . The thresholds of Proposition 2.2 in Biasco et al. [6] concern the size of the perturbation ${\mathrm P }$ measured using the norm of its associated Hamiltonian vector field $X_{\mathrm P }$. More precisely, on the domain $D({\bar{r}},{\bar{s}})$, we consider the following norms:

$$\begin{aligned} \begin{aligned} \left\| X_{\mathrm P } \right\| _{{\bar{r}}, D({\bar{r}},{\bar{s}})}&= \sup \limits _{D({\bar{r}},{\bar{s}})\times \Pi } \left( \vert \partial _{{\mathbf{y} }} {\mathrm P }\vert + \frac{1}{{\bar{r}}^2}\vert \partial _{\varvec{\psi }} {\mathrm P }\vert + \frac{1}{{\bar{r}}}\left( \vert \partial _{{\mathbf{z} }} {\mathrm P }\vert +\vert \partial _{{\widetilde{\mathbf{z}}} } {\mathrm P }\vert \right) \right) , \\ \left\| X_{\mathrm P } \right\| _{{\bar{r}}, D({\bar{r}},{\bar{s}})}^{\mathrm{Lip}}&= \sup \limits _{D({\bar{r}},{\bar{s}})} \left( \vert \partial _{{\mathbf{y} }} {\mathrm P }\vert _\Pi ^{\mathrm{Lip}} + \frac{1}{{\bar{r}}^2}\vert \partial _{\varvec{\psi }} {\mathrm P }\vert _\Pi ^{\mathrm{Lip}} + \frac{1}{{\bar{r}}}\left( \vert \partial _{{\mathbf{z} }} {\mathrm P }\vert _\Pi ^{\mathrm{Lip}} +\vert \partial _{{\widetilde{\mathbf{z}}} } {\mathrm P }\vert _\Pi ^{\mathrm{Lip}} \right) \right) \end{aligned} \end{aligned}$$

where, for a function f defined over $D({\bar{r}},{\bar{s}})\times \Pi$, we define

$$\begin{aligned} \vert f \vert _\Pi ^{\mathrm{Lip}} = \sup \limits _{\varvec{\xi }\ne \varvec{\xi }'\in \Pi } \frac{\left\| f(\,\cdot \,;\varvec{\xi }) - f(\,\cdot \,;\varvec{\xi }') \right\| _{D({\bar{r}},{\bar{s}})}}{\vert \varvec{\xi }- \varvec{\xi }'\vert }, \end{aligned}$$

hence $\vert f \vert _\Pi ^{\mathrm{Lip}}\leqslant \vert \vert \partial _{\varvec{\xi }} f\vert \vert _{D({\bar{r}},{\bar{s}})\times \Pi }$ for a differentiable function.

Now, we can state the theorem which ensures the existence of invariant tori.

Theorem 5.1

With the previous notations, there exists a large enough parameter $\tau >0$ such that for $\gamma \in ] 0, \gamma _0/2]$, if

(5.5)

where $a= \tau +1$, $b= 2\tau +4$, and $c>0$ is a constant depending only on $\tau$, then the following holds. There exists a non-empty Cantor set of parameters $\Pi _{*} \subset \Pi$ (more precisely, the measure of its complement $\Pi \backslash \Pi _{*}$ goes to zero with $\gamma$) and a Lipschitz continuous family of tori embedding

$$\begin{aligned} \mathbf{T}: \quad \Bigg \{ \begin{array}{ccc} {{\mathbb {T}}}^2\times \Pi _{*} &{} \longrightarrow &{} D_{ {\bar{r}}} \\ (\varvec{\theta }, \varvec{\xi }) &{} \longmapsto &{} ( {\mathbf{y} }(\varvec{\theta }, \varvec{\xi }), \varvec{\psi }(\varvec{\theta }, \varvec{\xi }),{\mathbf{z} }(\varvec{\theta }, \varvec{\xi }), {\widetilde{\mathbf{z}}} (\varvec{\theta }, \varvec{\xi })) \end{array} \end{aligned}$$

with

$$\begin{aligned} D_{{\bar{r}}}=]-{\bar{r}}^2,{\bar{r}}^2[\times ]-{\bar{r}}^2,{\bar{r}}^2[\times {{\mathbb {T}}}^2\times {{\mathcal {B}}}^4_{{\bar{r}}} \text{ and } {\widetilde{\mathbf{z}}} (\varvec{\theta }, \varvec{\xi })=-i{{\bar{{\mathbf{z} }}}}(\varvec{\theta }, \varvec{\xi }), \end{aligned}$$

a Lipschitz homeomorphism $\varvec{\omega }_{*}$ on $\Pi _{*}$ such that, for any $\varvec{\xi }\in \Pi _{*}$, the image $\mathbf{T}({{\mathbb {T}}}^2,\varvec{\xi })$ is a real-analytic (elliptic) ${\mathrm H }$-invariant 2-dimensional torus, on which the flow linked to ${\mathrm H }$ is analytically conjugated to the linear flow $\varvec{\theta }\mapsto \varvec{\theta }+\varvec{\omega }_{*}t$. Moreover, the embedding $\mathbf{T}({{\mathbb {T}}}^2,\varvec{\xi })$ for $\varvec{\xi }\in \Pi _{*}$ is $\epsilon /\gamma$-close to the torus $\{\varvec{\Gamma }+\varvec{\xi }={\mathbf{z} }={\widetilde{\mathbf{z}}} =\mathbf{0}\}$ with the notations of the Corollary 4.1.

Remark 5.1

The previous theorem corresponds to Proposition 2.2 in Biasco et al. [6] but we have to specify the dependance with respect to the parameters which appear in threshold (5.5) since these constants goes to zero in our case. This is obtained by going back to the original paper of Pöschel [28] where the exponent “a” comes from Corollary C, the exponent “b” is defined below formula (6) and (17) of Pöschel [28], finally the parameter $\tau$ is defined in formula (22).

As it was specified above, we have to be cautious with the fact that the involved constants degenerate when ${\varepsilon }$ goes to zero. This is overcome by constraining ${\varepsilon }$ to be inside an interval $[{\varepsilon }_0/2, {\varepsilon }_0]$ for any arbitrary ${\varepsilon }_0>0$ and in Sect. A.11, we prove that the main threshold (5.5) is satisfied if ${\varepsilon }_0$ is small enough ().

Consequently, for mass ratio ${\varepsilon }$ small enough, we find the desired quasi-periodic horseshoe orbits.

6 Extensions, Comments and Prospects

As we have seen, the obtained quasi-periodic motions suffer two limitations: they correspond to 2-dimensional tori but not Lagrangian tori in this 4-degree of freedom system and they are close to the $L_3$-separatrix.

Concerning the first item, our initial goal was to obtain Lagrangian tori following the reasonings of Herman and Féjoz in the N-body planetary problem with large gaps between the planets [16]. To ensure the existence of Lagrangian invariant tori, we have to prove that the frequency map associated with the Hamiltonian $\check{{\mathscr {H}} }$, introduced in Theorem 4.7, satisfies R$\ddot{\mathrm{u}}$ssmann non-degeneracy condition (i.e. its image should not be included in any hyperplane of ${\mathbb {R}}^4$). Hence, we have to consider the map ${\mathrm F }(\varvec{\Gamma })=(\varvec{\omega }(\varvec{\Gamma }), \check{\varvec{\Omega }}(\varvec{\Gamma }))$ with:

where are the normal frequencies associated with the averaged quadratic part $\left( \overline{{\mathscr {Q}} }_{(j,k)}(\Gamma _1)\right) _{j,k\in \{1,2\}}$, that are introduced in Theorem 4.6. The functions $\check{f}_j$ are small quantities generated by the remainder $\left( {{\mathscr {F}} }_{(j,k)}(\varvec{\Gamma }, {\mathbf{0} }, {\mathbf{0} }))\right) _{j,k\in \{1,2\}}$. If we consider the approximate frequency map

we can prove that

$$\begin{aligned} \mathrm{det}({\mathrm F }_0,\partial _{\Gamma _2}{\mathrm F }_0,\partial _{\Gamma _1}{\mathrm F }_0,\partial ^2_{\Gamma _1}{\mathrm F }_0)\ne 0. \end{aligned}$$

But our approach does not give enough control on the remainder $(\partial _{\Gamma _j}{{\mathscr {F}} }_0(\varvec{\Gamma }) , \check{f}_j(\varvec{\Gamma }))$ to ensure the same property on the complete frequency map ${\mathrm F }(\varvec{\Gamma })$. Hence we don’t have enough information in our approximation which has to be refined in order to prove R$\ddot{\mathrm{u}}$ssmann non-degeneracy condition for Lagrangian tori. We believe that a possible way to overcome this issue would be to consider an integrable approximation truncated at higher order in semi-fast action. Indeed in this case, the integrable approximation would not be a mechanical system as in Medvedev et al. [26]. From a more general point of view, estimates that may be useful in our context can certainly be found in the work of Biasco and Chierchia [4, 5] where a general KAM theory of secondary Lagrangian tori is studied in the case of a perturbed mechanical system.

We can also consider a nearly-invariant Lagrangian tori where the solutions are almost quasi-periodic for a very long time. More specifically, the horseshoe orbits which are $\varepsilon$-close to the $L_3$-separatrix have four frequencies (fast, semi-fast and two normal frequencies) which are respectively of order $(1, \sqrt{{\varepsilon }}/\left| \ln {\varepsilon } \right| , {\varepsilon }, {\varepsilon }/\left| \ln {\varepsilon } \right| )$. These four different timescales, which prevent the occurrence of small divisors for ${\varepsilon }$ small enough, allows to reduce the secular Hamiltonian $\check{{\mathscr {H}} }$ introduced in Theorem 4.7 to a Birkhoff normal form up to an arbitrary order. Using Theorem 5.5 of Giorgilli et al. [20] or Proposition 1 of Delshams and Gutiérrez [12], it is possible to get the following statement.

Theorem 6.1

The estimates (4.27) and Theorem 4.7 ensure that for an arbitrary $L\in {{\mathbb {N}}}^*$, there exists ${\varepsilon }_L>0$ such that for any ${\varepsilon }<{\varepsilon }_L$ we have

(6.1)

for any $(l_1,l_2)\in {{\mathbb {Z}}}^2$ of length $0<\left| l_1 \right| + \left| l_2 \right| \leqslant L$.

Hence, if we impose

then for any ${\varepsilon }<{\varepsilon }_L$ and $p'<p$ small enough, there exists a canonical transformation

with

such that the transformed secular Hamiltonian

is reduced in a Birkhoff normal form up to order L in .

As a consequence, we have

where ${\mathrm N }^{(s)}$ is a homogeneous polynomial of degree s in and while the remainder ${\mathrm R }_*^{(L+1)}$ is of order $L+1$ in and .

By using the action-angle variables $(\Theta _j,\theta _j)_{j\in \{1,\ldots ,4\}}$ such that

we obtain a nearly-invariant Lagrangian tori over polynomially long times with respect to $\varepsilon$ at any order. Actually, in view of estimates (6.1), we can certainly push these reasonings in order to obtain a time of stability of order ${\varepsilon }^{\ln {{\varepsilon }}}$.

Another possible direct extension of our work comes from the fact that our reasonings are valid in the vicinity of the separatrices arising from $L_3$. Actually, we have considered orbits which surround these separatrices but we can also consider orbits which are inside one of these loops (see Fig. 3). In that case, the frequencies have the same order as in the present paper and the same strategy would certainly allows to ensure the existence of quasi-periodic tadpole orbits which are far from the equilateral Lagrange configurations.

Concerning prospects, in this paper we have shown the existence of invariant tori which are polynomially (with respect to ${\varepsilon }$) close to the $L_3$-separatrix. This is only a trick that leads us to derive the frequency map, which is, in this case, close to the one evaluated at the $L_3$ equilibrium. Actually our mechanical approximation, defined in Sect. 4.4, is valid well beyond this separatrix: numerical simulations show that this kind of model is able to approach accurately Janus-Epimetheus actual motion (see [34]). Thus, it would be interesting to build quasi-periodic trajectories with initial conditions close to those of these satellites.

Another natural extension of our result would be to consider the spatial three-body problem. Using Jacobi reduction, which allows one to eliminate inclinations and ascending nodes for a given value of the angular momentum (see [30]), the spatial problem can be reduced to a four degrees of freedom Hamiltonian system as it is the case for the planar case. Once reduced, the spatial problem should have properties that are similar to those of the Hamiltonian studied in the present paper.

Appendix A. Proofs

1.1 Theorem 4.1: Estimates on $H_K$, $H_P$

By the real analyticity of the transformation in Poincaré resonant complex variable $\tilde{\Upsilon }\circ \Upsilon$, there exists $\rho _0>0$ and $\sigma _0>0$ such that the differential of its complex extension,

$$\begin{aligned} \tilde{\Upsilon }\circ \Upsilon : \quad \Bigg \{ \begin{array}{ccc} {\hat{{{\mathcal {K}} }}}_{\rho _0, \sigma _0} &{}\longrightarrow &{} {{\mathbb {C}}}^8 \\ ({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) &{}\longmapsto &{}(\tilde{\mathbf{r}} _1, \mathbf{r} _1, \tilde{\mathbf{r}} _2, \mathbf{r} _2 )\, , \end{array} \end{aligned}$$

admits a norm uniformly bounded on the collisionless domain ${\hat{{{\mathcal {K}} }}}_{\rho _0, \sigma _0}$ (defined in Sect. 4.1) by a constant $C>0$ independent of ${\varepsilon }$.

In the following, we will denote $D_{\rho _0,\sigma _0}$ the image of ${\hat{{{\mathcal {K}} }}}_{\rho _0, \sigma _0}$ by the transformation $\tilde{\Upsilon }\circ \Upsilon$.

Hence, as $\left\| ({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) \right\| _{{\hat{{{\mathcal {K}} }}}_{\rho _0,\sigma _0}} \leqslant \rho _0 + \sigma _0 + 2\sqrt{\rho _0\sigma _0}$ then

$$\begin{aligned} \left\| \mathbf{r} _j - {{\,\mathrm{Re}\,}}(\mathbf{r} _j) \right\| _{D_{\rho _0,\sigma _0}} \leqslant C(\rho _0 + \sigma _0 + 2\sqrt{\rho _0\sigma _0}) . \end{aligned}$$

Thus, one has

$$\begin{aligned} \begin{aligned} \left\| \mathbf{r} _1 - \mathbf{r} _2 \right\| _{D_{\rho _0,\sigma _0}}&\geqslant \left\| {{\,\mathrm{Re}\,}}(\mathbf{r} _1) - {{\,\mathrm{Re}\,}}(\mathbf{r} _2) \right\| _{D_{\rho _0,\sigma _0}} - \sum _{j\in \{1,2\}}\left\| \mathbf{r} _j - {{\,\mathrm{Re}\,}}(\mathbf{r} _j) \right\| _{D_{\rho _0,\sigma _0}} \\&\geqslant \Delta - 8C\sigma _0 \geqslant \frac{\Delta }{2} \end{aligned} \end{aligned}$$

since $\rho _0<\sigma _0$ and where $\hat{\Delta }$ is an arbitrary fixed value on ${{\mathbb {T}}}$ such that the minimum distance $\Delta$ between two planets in circular motion is reached (see Sect. 4.1 for more details).

Consequently, and

as $\Delta$ (resp. $\hat{\Delta }$) does not depend on the small parameter ${\varepsilon }$.

Finally, since then there exists a constant $c>0$ such that

$$\begin{aligned} c\leqslant \left\| \Lambda _{1,0} + Z_1 \right\| _{{{\mathcal {K}} }_{\rho _0, \sigma _0}} \quad \text{ and } \quad c\leqslant \left\| \Lambda _{2,0} + Z_2-Z_1 \right\| _{{{\mathcal {K}} }_{\rho _0, \sigma _0}} \end{aligned}$$

which implies that

1.2 Theorem 4.1: First Averaging Theorem

First of all, we define an iterative lemma of averaging. Let us introduce some notations: $(\xi _k)_{k\in \{1,2,3\}}$ are given positive numbers such that

$$\begin{aligned} 0<\xi _1< \rho , \quad 0< \xi _2<\sigma , \quad 0<\xi _{3}<\sqrt{\rho \sigma } \end{aligned}$$

and, for $0\leqslant r\leqslant 1$, we denote ${\hat{{{\mathfrak {K}} }} }_r$ the domain such as

$$\begin{aligned} {\hat{{{\mathfrak {K}} }} }_r={{\mathcal {B}}}^2_{\rho -r\xi _1}\times {{\mathcal {V}}} _{\sigma -r\xi _2}{\hat{{{\mathcal {I}} }} }\times {{\mathcal {B}}}^4_{\sqrt{\rho \sigma } - r\xi _{3}} . \end{aligned}$$

Hence, we set out the following

Lemma A.1

(First iterative lemma). Let $\rho ^-$, $\sigma ^-$, $\xi _1$, $\xi _2$ be fixed positive real numbers that depend on the small parameter ${\varepsilon }$ and

$$\begin{aligned} \begin{aligned} \rho ^+&= \rho ^- - \xi _1>0,\quad \sigma ^+ = \sigma ^- - \xi _2>0, \\ \xi _{3}&= \sqrt{\rho ^-\sigma ^-} - \sqrt{\rho ^+\sigma ^+} . \end{aligned} \end{aligned}$$

(A.1)

Let $H^-$ be a Hamiltonian of the form

$$\begin{aligned} \begin{aligned} H^-({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} })&= H_K({\mathbf{Z} }) + \overline{H} _P({\mathbf{Z} }, \zeta _1, {\mathbf{x} }, {\widetilde{\mathbf{x}} })\\&\quad + {H_{*}^{0,-}}({\mathbf{Z} }, \zeta _1, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) + {H_{*}^{1,-}}({\mathbf{Z} }, \varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) \end{aligned} \end{aligned}$$

which is analytic on the domain ${\hat{{{\mathfrak {K}} }} }_0^-={\hat{{{\mathcal {K}} }}}_{\rho ^-, \sigma ^-}$ and such that

$$\begin{aligned} {\overline{H} _{*}^{1,-}}({\mathbf{Z} }, \zeta _1, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) = \frac{1}{2\pi }\int _0^{2\pi } {H_{*}^{1,-}}({\mathbf{Z} }, \zeta _1, \zeta _2, {\mathbf{x} }, {\widetilde{\mathbf{x}} }){\mathrm {d}}\zeta _2 =0 . \end{aligned}$$

Let $\eta ^-$, $(\mu _l^-)_{l\in \{0,1,2,3\}}$ be fixed positive real numbers, which depend on ${\varepsilon }$, such that

$$\begin{aligned} \begin{aligned} \left\| {H_{*}^{1,-}} \right\| _{{\hat{{{\mathfrak {K}} }} }_0^-}\leqslant \eta ^-, \quad \left\| {H_{*}^{0,-}} \right\| _{ {\hat{{{\mathfrak {K}} }} }_0^-}\leqslant \mu _0^- \end{aligned} \end{aligned}$$

(A.2)

and

$$\begin{aligned} \begin{aligned}&\left\| \partial _{{\mathbf{Z} }}\big (\overline{H} _P + {H_{*}^{0,-}}\big ) \right\| _{ {\hat{{{\mathfrak {K}} }} }_0^-}\leqslant \mu _1^-,&\quad&\left\| \partial _{\varvec{\zeta }}\big (\overline{H} _P +{H_{*}^{0,-}}\big ) \right\| _{{\hat{{{\mathfrak {K}} }} }_0^-}\leqslant \mu _2^-,&\\&\left\| \partial _{({\mathbf{x} },{\widetilde{\mathbf{x}} })}\big (\overline{H} + {H_{*}^{0,-}}\big ) \right\| _{ {\hat{{{\mathfrak {K}} }} }_0^-}\leqslant \mu _3^- .&\end{aligned} \end{aligned}$$

If we assume that

(A.3)

then there exists a canonical transformation

(A.4)

and such that, in the new variables, the Hamiltonian $H^+= H^- \circ \overline{\Upsilon }^+$ can be written

$$\begin{aligned} \begin{aligned} H^+&= H_K + \overline{H} _P + {H_{*}^{0,-}} + H_*^+ \\&= H_K + \overline{H} _P + {H_{*}^{0,+}} + {H_{*}^{1,+}} \end{aligned} \quad \text{ with } \quad \left\{ \begin{array}{l} {H_{*}^{0,+}} = {H_{*}^{0,-}} + \overline{H} _{*}^+ \\ {H_{*}^{1,+}} = H_*^+ - \overline{H} _*^+ \end{array} \right. \end{aligned}$$

and

Furthermore, we have the thresholds

$$\begin{aligned} \begin{aligned} \left\| {H_{*}^{1,+}} \right\| _{{\hat{{{\mathfrak {K}} }} }_1^-}\leqslant \eta ^+ , \quad \left\| {H_{*}^{0,+}} \right\| _{ {\hat{{{\mathfrak {K}} }} }_1^-}\leqslant \mu _0^+ , \end{aligned} \end{aligned}$$

(A.5)

and

$$\begin{aligned} \begin{aligned}&\left\| \partial _{{\mathbf{Z} }}\big (\overline{H} _P + {H_{*}^{0,+}}\big ) \right\| _{ {\hat{{{\mathfrak {K}} }} }_1^-}\leqslant \mu _1^+ ,&\quad&\left\| \partial _{\varvec{\zeta }}\big (\overline{H} _P + {H_{*}^{0,+}}\big ) \right\| _{{\hat{{{\mathfrak {K}} }} }_1^-}\leqslant \mu _2^+ ,&\\&\left\| \partial _{({\mathbf{x} }, {\widetilde{\mathbf{x}} })}\big (\overline{H} _P + {H_{*}^{0,+}}\big ) \right\| _{ {\hat{{{\mathfrak {K}} }} }_1^-}\leqslant \mu _3^+,&\end{aligned} \end{aligned}$$

(A.6)

with the following quantities:

(A.7)

Proof

We define $\overline{\Upsilon }^+:{\hat{{{\mathfrak {K}} }} }_1^-\longrightarrow {\hat{{{\mathfrak {K}} }} }_0^-$ that is the time-one map of the Hamiltonian flow generated by the auxiliary function $\chi ^+$, i.e. $\overline{\Upsilon }^+=\Phi _1^{\chi ^+}$ with

$$\begin{aligned} {\chi ^+}({\mathbf{Z} },\varvec{\zeta }, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) = \frac{2\pi }{\upsilon _0}\int _0^1 s {H_{*}^{1,-}}({\mathbf{Z} },\zeta _1, \zeta _2 + 2\pi s, {\mathbf{x} }, {\widetilde{\mathbf{x}} }){\mathrm {d}}s \end{aligned}$$

such that

(A.8)

Thus, in the new variables, the Hamiltonian reads

with the remainder

that is given by the Eqs. (3.2) and (3.3) while $(*)$ is equal to zero by (A.8).

We have to estimate the size of $H_*^+$ to prove the thresholds (A.5) and (A.6). Firstly, by the conditions (A.2), we have as $\upsilon _0={{\mathcal {O}}} (1)$. One then applies the Cauchy inequalities to obtain the partial derivatives

and deduces the estimates on the Poisson brackets

(by the threshold given by (4.1) and the mean value theorem),

(as (A.1) implies that $(\xi _{3})^2 \geqslant \xi _1 \xi _2$), and

As a consequence, the remainder of the transformation $\overline{\Upsilon }^+$ is bounded such that

where $\theta ^+$ is given by (A.7). Moreover, taking into account that $\overline{\chi }^+=0$ (given by (A.8)), we have

$$\begin{aligned} \overline{H} _{*}^+({\mathbf{Z} }, \zeta _1, {\mathbf{x} }, {\widetilde{\mathbf{x}} }) = \frac{1}{2\pi } \int _0^{2\pi } \int _0^1 s \left\{ {\chi ^+},{H_{*}^{1,-}}\right\} \circ \Phi _s^{\chi ^+}({\mathbf{Z} }, \zeta _1, \tau , {\mathbf{x} }, {\widetilde{\mathbf{x}} }) {\mathrm {d}}s {\mathrm {d}}\tau \end{aligned}$$

and therefore

Hence, if we denote ${H_{*}^{0,+}} = {H_{*}^{0,-}} + \overline{H} _{*}^+$ and ${H_{*}^{1,+}} = H_*^+ - \overline{H} _*^+$ then the triangle inequality gives the estimates (A.5) and (A.6) (together with the Cauchy inequalities for the last).

Finally, by the Eq. (3.2) and the Cauchy inequalities, we can estimate the size of the transformation $\overline{\Upsilon }^+$. Hence, the condition (A.3) provides the following estimates

which yields (A.4). $\quad \square$

Now, in order to prove Theorem 4.1, one applies a first time Lemma A.1. Thus, we define the following

$$\begin{aligned} (\xi _1, \xi _2, \xi _3) = \frac{\sigma _0}{3}({\varepsilon }^\beta , 1, {\varepsilon }^{\beta /2}) \quad \text{ for } \quad 1/7<\beta <1/2 \end{aligned}$$

such that ${\hat{{{\mathfrak {K}} }} }_r = {\hat{{{\mathcal {K}} }}}_{1-\frac{r}{3}}$ for $0\leqslant r\leqslant 1$. By Theorem 4.1 and the notations of Lemma A.1, the Hamiltonian H is analytical on ${\hat{{{\mathcal {K}} }}}_1$ and of the form

$$\begin{aligned} H({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) = H_K({\mathbf{Z} }) + \overline{H} _P({\mathbf{Z} },\zeta _1,{\mathbf{x} },{\widetilde{\mathbf{x}} }) + \big [H_P - \overline{H} _P\big ]({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) \end{aligned}$$

with

Hence, the condition (A.3) is fulfilled and Lemma A.1 provides the existence of the transformation $\overline{\Upsilon }^{0}: {\hat{{{\mathcal {K}} }}}_{2/3} \longrightarrow {\hat{{{\mathcal {K}} }}}_{1}$ such that

$$\begin{aligned} H^{0}=H\circ \overline{\Upsilon }^{0}= H_K + \overline{H} _P + H_{*}^{0,0} + H_{*}^{1,0} \end{aligned}$$

with the following thresholds:

(A.9)

and

Moreover, by the Eq. (3.2) and the Cauchy inequalities, one has:

Then, we apply iteratively Lemma A.1 to reduce the fast component of the Hamiltonian until an exponentially small size with respect to ${\varepsilon }$. To do so, let s be a non-zero integer such that $s = {\mathrm E }({\varepsilon }^{-\alpha }) + 1$ where

$$\begin{aligned} \alpha = \frac{1-2\beta }{5} \quad \text{ for } \quad 1/7<\beta <1/2 . \end{aligned}$$

We define

$$\begin{aligned} (\xi _1, \xi _2, \xi _3) = \frac{\sigma _0}{3s}({\varepsilon }^\beta , 1, {\varepsilon }^{\beta /2}) \end{aligned}$$

as well as the sequences $(\rho ^{j})_{j\in \{0,1,\ldots ,s\}}$, $(\sigma ^{j})_{j\in \{0,1,\ldots ,s\}}$ with

$$\begin{aligned} (\rho ^{j}, \sigma ^{j}) = \frac{2s-j}{3s} (\rho ,\sigma ) \quad \text{ for } \quad j\in \{1,\ldots ,s\} \end{aligned}$$

such that ${\hat{{{\mathfrak {K}} }} }^j_r = {\hat{{{\mathcal {K}} }}}_{\frac{2}{3}-\frac{j + r}{3s}}$ for $0\leqslant r\leqslant 1$.

Replacing the notation $^-$ and $^+$ of Lemma A.1 by $^{j-1}$ and $^{j}$ and assuming that for all $0< j\leqslant s$ the following condition (associated with (A.3)) is fulfilled:

(A.10)

an iterative application of Lemma A.1 to the Hamiltonian $H^{0}$ provides a sequence of canonical transformations $(\overline{\Upsilon }^{j})_{j\in \{1,\ldots ,s\}}$ such that $H^0\circ \overline{\Upsilon }^{1}\circ \cdots \circ \overline{\Upsilon }^{s}$ is equal to the Hamiltonian of the formula (4.3) with

In order to complete the proof, let us consider $n\in \{1,\ldots ,s\}$ such that the sequences $(\eta ^{j})_{j\in \{1,\ldots ,n\}}$ and $(\mu _l^{j})_{j\in \{1,\ldots , n\}}$ satisfy the following induction hypothesis:

$$\begin{aligned} \eta ^{j}\leqslant \eta ^{j-1}\exp (-1) \quad \text{ and } \quad \mu _l^{j} - \mu _l^{j-1} \leqslant \frac{\mu _l^{0}}{s} \quad (l\in \{1,2,3\}) . \end{aligned}$$

For $n=1$, as $0<\alpha<1/7<\beta <1/2$, (A.10) is satisfied and implies that

for and

for .

For a fixed integer n, $(\eta ^j)_{j\in \{0,\ldots ,n\}}$ is decreasing while

$$\begin{aligned} \mu _l^{n} \leqslant \mu _l^{n-1} + \frac{\mu _l^{0}}{s} \leqslant \cdots \leqslant \mu _l^{0} + n\frac{\mu _l^{0}}{s} \leqslant 2 \mu _l^{0}\quad (l\in \{1,2,3\}), \end{aligned}$$

then the induction is immediate. Indeed, (A.10) is satisfied and implies that

As a consequence, we have

which prove (4.5). Likewise,

and then proves (4.4).

At last, and in the same way as for the first application of Lemma A.1, for each transformation $\overline{\Upsilon }^j$ with $j\in \{1, \ldots , s\}$, the Eq. (3.2) and Cauchy inequalities lead to

Consequently, the size of the transformation $\overline{\Upsilon }$ is dominated by that of the transformation $\overline{\Upsilon }^{0}$ which provides the estimates (4.6) and yields (4.2).

1.3 Lemma 4.2: D’Alembert rule in the Averaged Problem

The D’Alembert rule, given by (2.4), derives from the preservation of the angular momentum denoted ${\tilde{{{\mathcal {C}}}}}= \sum _{j\in \{1,2\}} \tilde{\mathbf{r}} _j \times \mathbf{r} _j$. By the transformation in the resonant Poincaré complex variables $\tilde{\Upsilon }\circ \Upsilon$, we have ${{\mathcal {C}}}({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) = {\tilde{{{\mathcal {C}}}}}\circ \tilde{\Upsilon }\circ \Upsilon ({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) = Z_2 + ix_1{\widetilde{x} }_1 + ix_2{\widetilde{x} }_2$. ${\tilde{{{\mathcal {C}}}}}$ being an integral of the motion, it turns out that

$$\begin{aligned} 0 = \{{\tilde{{{\mathcal {C}}}}}, {{\mathcal {H}} }\} = \{ {{\mathcal {C}}}, {{\mathcal {H}} }\circ \tilde{\Upsilon }\circ \Upsilon \} = \{ {{\mathcal {C}}}, H \} . \end{aligned}$$

(A.11)

Injecting the expansion (2.3) in (A.11) we get

$$\begin{aligned} \begin{aligned} 0&= \{ {{\mathcal {C}}}, \sum _{(k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }) \in {{\mathscr {D}}}}\quad f_{k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }}({\mathbf{Z} },\zeta _1)x_1^{p_1}x_2^{p_2}{\widetilde{x} }_1^{{\widetilde{p} }_1}{\widetilde{x} }_2^{{\widetilde{p} }_2}\exp (i k\zeta _2) \} \\&= - i \quad \sum _{(k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }) \in {{\mathscr {D}}}} \quad ( k + p_1 -{\widetilde{p} }_1 + p_2 - {\widetilde{p} }_2 ) f_{k,{\mathbf{p} },{\widetilde{{\mathbf{p} }} }}({\mathbf{Z} },\zeta _1)x_1^{p_1}x_2^{p_2}{\widetilde{x} }_1^{{\widetilde{p} }_1}{\widetilde{x} }_2^{{\widetilde{p} }_2}\exp (i k\zeta _2) . \end{aligned} \end{aligned}$$

As a consequence, one has

$$\begin{aligned} k + p_1 -{\widetilde{p} }_1 + p_2 - {\widetilde{p} }_2 = 0. \end{aligned}$$

In order to prove Lemma 1, it only needs to be shown that the expression of ${\overline{{{\mathcal {C}}}}}= {{\mathcal {C}}}\circ \overline{\Upsilon }$ is equal to . As the averaging transformation $\overline{\Upsilon }$ is generated by the composition of the transformations $(\Phi _1^{\chi ^{j}})_{j\in \{0,\ldots ,s\}}$ (see Sect. A.2), the result holds if $\{ {\mathcal \chi ^{j}} , {\overline{{{\mathcal {C}}}}}\} = 0$.

At first iteration, the generating function $\chi ^{0}$ reads

$$\begin{aligned} \chi ^{0}({\mathbf{Z} },\varvec{\zeta },{\mathbf{x} },{\widetilde{\mathbf{x}} }) = \frac{2\pi }{\upsilon _0}\int _0^1 s \left[ H_P - \overline{H} _P\right] _{({\mathbf{Z} },\zeta _1,\zeta _2 + 2\pi s,{\mathbf{x} },{\widetilde{\mathbf{x}} })} {\mathrm {d}}s . \end{aligned}$$

As $H_P$ satisfies the D’Alembert rule, one has

$$\begin{aligned} \{ \chi ^{0} , {{\mathcal {C}}}\} = \frac{2\pi }{\upsilon _0}\int _0^1 s\{ H_P - \overline{H} _P, {{\mathcal {C}}}\}{\mathrm {d}}s = 0 , \end{aligned}$$

which leads to: ${{\mathcal {C}}}\circ \Phi _1^{\chi ^{0}} = {{\mathcal {C}}}$. The same holds true for the other iterations.

Finally, let a real function f that satisfies the D’Alembert rule and does not depend on the fast angle . Hence, the total degree in , , , in the monomials appearing in the Taylor expansion of f in neighborhood of is even. As a consequence f can be decomposed such as $f= f_0 +f_2$ with the properties (4.8).

1.4 Theorem 4.2: Reduction

The Hamiltonian of Theorem 4.2 is obtained by a suitable expansion of the averaged Hamiltonian $\overline{H}$ in the neighborhood of the quasi-circular manifold ${\mathrm C}_0$.

First of all, by Lemma 4.2, $\overline{H}$ and $\overline{H} _*$ can be decomposed respectively such as

Regarding the eccentricities, a polynomial expansion of $\overline{H}$ of the degree two with respect to provides

The size of the remainder involved in this approximation is estimated thanks to the mean value theorem applied on the function $g_{(j,k)}$ for together with the bound (4.1) of Theorem 4.1. Hence, this yields

Now, we consider the expansion of $\overline{H}$ with respect to the exact resonant action . The Keplerian part can be written:

where the quadratic form $\tilde{ Q }$ reads

and its approximation

The application of the Taylor formula on the function $g(t)= H_K(t{\mathbf{Z} })$ for $(t,{\mathbf{Z} })\in [0,1]\times {{\mathcal {B}}}^2_{\rho /3}$ leads to

and, together with the bound (4.1), provides the estimates

Regarding the estimate of $R^3_K$, as

$$\begin{aligned} {\widehat{m}}_j = m_j + {{\mathcal {O}}} ({\varepsilon }), \quad \mu _j = m_0 + {{\mathcal {O}}} ({\varepsilon }), \end{aligned}$$

(A.12)

then ${\tilde{A}}- A = {{\mathcal {O}}} ({\varepsilon })$ and ${\tilde{\kappa }}- \kappa = {{\mathcal {O}}} ({\varepsilon })$ provide the following bound:

In the case of the the perturbation part, one can split $\overline{H} _{P,0}$ and $(\overline{H} _{P,(j,k)})_{1\leqslant j,k,\leqslant 2}$ in the sum of three terms as follows:

and

where

and

$$\begin{aligned} \left( G_{(j,k)}\right) _{1\leqslant j,k\leqslant 2} = i{\varepsilon }\frac{m_1m_2}{\sqrt{m_0}} \begin{pmatrix} \displaystyle \frac{A_0}{m_1a_{1,0}^{1/2}} &{} \displaystyle \frac{B_0}{\sqrt{m_1m_2}(a_{1,0}a_{2,0})^{1/4}} \\ \displaystyle \frac{{{\,\mathrm{conj}\,}}(B_0)}{\sqrt{m_1m_2}(a_{1,0}a_{2,0})^{1/4}} &{} \displaystyle \frac{A_0}{m_1a_{1,0}^{1/2}}\end{pmatrix} \end{aligned}$$

with

With similar reasonings as for the eccentricities, we use the mean value theorem to evaluate the remainder in the truncation at order 0 of $\overline{H} _{P,0}$ and $(\overline{H} _{P,(j,k)})_{1\leqslant j,k,\leqslant 2}$. Hence, this yields

Moreover the following estimates:

are obtained with the approximation of the formula (A.12).

Finally, in order to get a more tractable expression, one can shift the perturbation parts to

with $\Lambda _{j,\star } = {\widehat{m}}_j \mu _j^{1/2}m_0^{1/6}\upsilon _0^{-1/3}$ where the two associated semi-major axes are both equal to the same value given by $a_\star = m_0^{1/3} \upsilon _0^{-2/3}$. This yields

$$\begin{aligned} G_0= {\varepsilon }\upsilon _0B {{\mathcal {F}} }+ R^4_{P,0} \quad \text{ and } \quad G_{(j,k)} = \tilde{{\mathscr {Q}} }_{(j,k)} + R^4_{P,(j,k)} \end{aligned}$$

with the following thresholds:

that are estimated thanks to the bound .

As a consequence,

Lemma A.2

The averaged Hamiltonian can be written

with such that

$$\begin{aligned} \begin{aligned} R_0&= R_K^2 + R_{P,0}^2 + R_K^3 + R_{P,0}^3 + R_{P,0}^4 + \overline{H} _{*,0}\\ R_{(j,k)}&= R_{P,(j,k)}^1 + R_{P,(j,k)}^2 + R_{P,(j,k)}^3 + R_{P,(j,k)}^4 + \overline{H} _{*,(j,k)} \end{aligned} \end{aligned}$$

and

Moreover, if we assume $\beta >1/3$, we can ensure that

Remark that this last bound comes from the threshold

that is obtained by application of the Cauchy inequalities.

In order to uncouple the fast and semi-fast degrees of freedom, we perform the symplectic linear transformation which diagonalizes the quadratic form Q. This leads to the Hamiltonian $\tilde{{\mathscr {H}} }$ and its remainder $\tilde{{\mathscr {R}} }= R\circ \tilde{\Psi }$. The inclusions (4.9) are ensured since $\kappa \leqslant 1/2$.

1.5 Lemma 4.3: Semi-fast Frequency

Let us first prove the expression (4.13) which gives the lower bound of $\varphi _1$ along a $h_\delta$-level curve.

A straightforward calculation shows that $\varphi _{1,\delta }^{\min }$ is given by the smallest positive root of the polynomial equation $4X^3 -(5+3\delta )X +1 =0$, where $X = \sin (\varphi _{1,\delta }^{\min }/2)$. It follows that $\varphi _{1,\delta }^{\min }$ is an analytic function of $\delta$ in a neighborhood of 0, which satisfies

$$\begin{aligned} \varphi _{1,\delta }^{\min }= 2 \arcsin \left( \frac{\sqrt{2} -1}{2}\right) - \frac{3(\sqrt{2} -1) }{(3\sqrt{2} -2)\sqrt{1+2\sqrt{2}}}\delta + {{\mathcal {O}}} (\delta ^2). \end{aligned}$$

In order to prove the relations (4.14), let us begin to derive an asymptotic expansion of the integral ${{\mathcal {I}} }_\delta = {\int }_{\varphi _{1,\delta }^{\min }}^\pi \displaystyle \frac{{\mathrm {d}}\varphi }{\sqrt{U_\delta (\varphi )}}$ involved in the expression (4.4). ${{\mathcal {I}} }_\delta$ can be splitted in three different terms:

$$\begin{aligned} \begin{aligned}&{{\mathcal {I}} }_\delta = {{\mathcal {I}} }_\delta ^{1} + {{\mathcal {I}} }_\delta ^{2} + {{\mathcal {I}} }_\delta ^{3} \quad \text{ with } \quad \\&{{\mathcal {I}} }_\delta ^{1} = \int _{\varphi _{1,\delta }^{\min }}^\frac{\pi }{3} \frac{{\mathrm {d}}\varphi }{\sqrt{U_\delta (\varphi )}}, \quad {{\mathcal {I}} }_\delta ^{(2)} = \int _{\frac{\pi }{3}}^{\pi }\frac{{\mathrm {d}}\varphi }{\sqrt{U_\delta ^0(\varphi )}} \quad \text{ and } \quad \\&{{\mathcal {I}} }_\delta ^{3} = \int _{\frac{\pi }{3}}^{\pi } \left( \frac{1}{\sqrt{U_\delta (\varphi )}} - \frac{1}{\sqrt{U_\delta ^0(\varphi )}} \right) {\mathrm {d}}\varphi \\&\text{ where } \quad U_\delta ^0(\varphi ) = \delta + \frac{7}{24}(\varphi -\pi )^2 . \end{aligned} \end{aligned}$$

As $U_\delta (\varphi _{1,\delta }^{\min }) =0$, Taylor formula leads to

$$\begin{aligned} \begin{aligned} {{\mathcal {I}} }_\delta ^{1}&= \left( \frac{\pi }{3} - \varphi _{1,\delta }^{\min }\right) \int _0^1 \frac{{\mathrm {d}}u}{\sqrt{u}\sqrt{G_\delta (u)}}\quad \text{ where } \quad \\ G_\delta (u)&= \int _0^1 {{\mathcal {F}} }'\left( \varphi _{1,\delta }^{\min }+ \left( \frac{\pi }{3} - \varphi _{1,\delta }^{\min }\right) uv \right) {\mathrm {d}}v . \end{aligned} \end{aligned}$$

As $G_\delta (u) > G_\delta (1)$ and $G_0(1) >1$ and if $\delta >0$ is small enough, one has

As a consequence, ${{\mathcal {I}} }_\delta ^{1}$ is analytic with respect to $\delta$.

The integral expression ${{\mathcal {I}} }_\delta ^{2}$ can be calculated explicitly as

$$\begin{aligned} {{\mathcal {I}} }_\delta ^{2} = \sqrt{\frac{24}{7}} \mathrm{arcsinh}\left( \sqrt{\frac{7}{54}}\frac{\pi }{\sqrt{\delta }} \right) = \sqrt{\frac{6}{7}} \vert \ln \delta \vert + {\mathscr {I}}_\delta ^{2} \end{aligned}$$

where ${\mathscr {I}}_\delta ^{2}$ is analytic in $\delta$.

All that remains is to estimate the size of ${{\mathcal {I}} }_\delta ^{3}$ and of its first derivative. First of all, $U_\delta$ being an infinitely differentiable function of $\varphi \in [\pi /3, \pi ]$ satisfying the additional relations:

$$\begin{aligned} U_\delta (\pi ) = 1 + \delta + {{\mathcal {F}} }(\pi ) = \delta , \quad \frac{{\mathrm {d}}U_\delta }{{\mathrm {d}}\varphi }(\pi ) = \frac{{\mathrm {d}}^3 U_\delta }{{\mathrm {d}}\varphi ^3}(\pi )=0 \quad \text{ and } \quad \frac{{\mathrm {d}}^2 U_\delta }{{\mathrm {d}}\varphi ^2}(\pi )=\frac{7}{12} , \end{aligned}$$

Taylor formula leads to From the inequalities

that hold for $(\delta ,\varphi ) \in [\delta ^*,2\delta ^*]\times [\pi /3,\pi ]$, one can derive the following relations:

It follows that ${{\mathcal {I}} }_\delta ^{3}$ is analytic on $[\delta ^*,2\delta ^*]$ and that its first derivative is bounded by

As a consequence

$$\begin{aligned} T_\delta = \frac{2\pi }{\upsilon _0 \sqrt{{\varepsilon }}K} \left| \ln \delta \right| \left[ 1 + g(\delta ) \right] \end{aligned}$$

with and . As

$$\begin{aligned} \nu _\delta = \frac{\upsilon _0 \sqrt{{\varepsilon }}K}{\vert \ln \delta \vert } \left[ 1 - g(\delta ) + \frac{ g(\delta )^2}{1+ g(\delta )}\right] , \end{aligned}$$

we get the expressions (4.14).

1.6 Theorem 4.3: Semi-fast Holomorphic Extension

We consider the mechanical system

$$\begin{aligned} \tilde{{\mathscr {H}} }_1(I_1, \varphi _1) = \upsilon _0\left( -AI_1^2 + {\varepsilon }B {{\mathcal {F}} }(\varphi _1)\right) \end{aligned}$$

where A, B are two positive constants and the real function ${{\mathcal {F}} }$ is defined on $]0,2\pi [$ by (4.11).

On the domain ${{\mathfrak {D}}} _*$, defined as

$$\begin{aligned} {{\mathfrak {D}}} _* = \left\{ \begin{array}{c}(I_1,\varphi _1) \in {\mathbb {R}}\times ]0,2\pi [ \quad \text{ such } \text{ that } \quad \tilde{{\mathscr {H}} }_1(I_1,\varphi _1) = h_\delta \\ \text{ with }\quad \delta ^* \leqslant \delta \leqslant 2\delta ^* \end{array}\right\} \end{aligned}$$

for some $\delta ^*>0$, we can build a system of action-angle variables denoted $(J_1,\phi _1)$ such that

$$\begin{aligned} {{\mathscr {H}} }_1(J_1)= \tilde{{\mathscr {H}} }_1\circ {{\mathfrak {F}}}(J_1, \phi _1) =h_\delta \quad \text{ and } \quad {{\mathscr {H}} }_1'(J_1) = \nu _\delta . \end{aligned}$$

The transformation in action-angle variables, which will be denoted ${{\mathfrak {G}}}$, satisfies

$$\begin{aligned} {{\mathfrak {G}}}: \quad \Bigg \{ \begin{array}{ccc} {{\mathfrak {D}}} _{*} &{}\longrightarrow &{} {{\mathcal {S}} }_*\times {{\mathbb {T}}}\\ (I_1,\varphi _1) &{}\longmapsto &{} (J_1, \phi _1) \end{array} \end{aligned}$$

with ${{\mathcal {S}} }_* = \left[ a, b\right]$ for some $a< 0 <b$. We also denote ${{\mathfrak {F}}}={{{\mathfrak {G}}}}^{-1}$ the inverse of the action-angle transformation as in (4.16).

We rewrite the Hamiltonian in a suitable form for the complex extension,

$$\begin{aligned} \begin{aligned} \tilde{{\mathscr {H}} }_1(I_1, \varphi _1)&=-{\varepsilon }\upsilon _0 B(1+{\mathrm h }(I_1, \varphi _1))\\ \text{ with } \quad {\mathrm h }(I_1, \varphi _1)&= \frac{A}{{\varepsilon }B}I_1^2-1-{{\mathcal {F}} }(\varphi _1 ), \end{aligned} \end{aligned}$$

and the transformation ${{{\mathfrak {G}}}}$ can be defined explicitly by a classical integral formulation. The action is given by

$$\begin{aligned} \begin{aligned} J_1&= 4 \sqrt{{\varepsilon }\frac{B}{A}}\left( \pi -\varphi _{(I_1,\varphi _1)}^{\min }\right) \int _{0}^{1}\sqrt{{{\mathcal {U}} }^\pi _{(I_1, \varphi _1) }(x)} {\mathrm {d}}x\\ \text{ with } \quad {{\mathcal {U}} }^{\theta }_{(I_1,\varphi _1)}(x)&= 1 + {{\mathcal {F}} }\left( (1-x)\varphi _{(I_1,\varphi _1)}^{\min } + x\theta \right) + {\mathrm h }(I_1, \varphi _1) \end{aligned} \end{aligned}$$

where $\varphi _{(I_1,\varphi _1)}^{\min }={{\mathcal {F}} }^{-1}(-1-{\mathrm h }(I_1,\varphi _1))$ and $J_{1}$ is the action linked to an energy curve corresponding to an arbitrary shift of energy $\delta \in ]\delta ^* ,2\delta ^* [$. The lower angle $\varphi _{(I_1,\varphi _1)}^{\min }$ is well defined since ${{\mathcal {F}} }'(\varphi _0^{\min })\ne 0$ where $\varphi _0^{\min }=2\arcsin \left( \frac{\sqrt{2} -1}{2}\right)$ is the minimal value of the angle $\varphi _1$ along the separatrix hence ${{\mathcal {F}} }(\varphi _0^{\min })=-1$, consequently ${{\mathcal {F}} }^{-1}$ is analytic around $-1$. Concerning the angle $\phi _1$, we have to consider the time of transit from the point $( 0,\varphi _{(I_1,\varphi _1)}^{\min })$ to $(I_1,\varphi _1)$ which is given by

$$\begin{aligned} \begin{aligned} \tau (I_1,\varphi _1)&=\frac{2}{\sqrt{{\varepsilon }AB}}\left( \varphi _1 -\varphi _{(I_1,\varphi _1)}^{\min }\right) \int _{0}^{1} \frac{{\mathrm {d}}x}{\sqrt{{{\mathcal {U}} }^{\varphi _1}_{(I_1,\varphi _1)}(x)}}\\&\text{ and }\quad \phi _1 =\displaystyle \frac{\pi }{2}\frac{\tau (I_1,\varphi _1)}{\tau (I_1,\pi )} . \end{aligned} \end{aligned}$$

Now, we look for the complex domain of holomorphy of the integrable Hamiltonian ${{\mathscr {H}} }_1$. We first consider the complex domain

$$\begin{aligned} D_{*,\hat{\rho }} = \left\{ (I_1,\varphi _1 )\in {{\mathbb {C}}}^2 / \exists (I_1^*,\varphi _1^*)\in {{\mathfrak {D}}} _{*} \text{ with: } \begin{array}{l} \left| I_1 - I_1^* \right| \leqslant \sqrt{{\varepsilon }} \hat{\rho }\\ \left| \varphi _1 - \varphi _1^* \right| \leqslant \hat{\rho }\end{array}\right\} \end{aligned}$$

for $\hat{\rho }>0$ and ${\varepsilon }$ small enough (, ).

In order to disentangle the dependance of the complex domain $D_{*,\hat{\rho }}$ with respect to $\delta ^*$ and ${\varepsilon }$, we perform the following scalings:

$$\begin{aligned} I_1 =\sqrt{{\varepsilon }}{\hat{I}} _1 \quad \text{ and } \quad J_1 =\sqrt{{\varepsilon }} \hat{J } _1 \quad \text{ for } \quad ({\hat{I}} _1,\varphi _1)\in {\hat{{{\mathfrak {D}}} }}_{*} \end{aligned}$$

with

$$\begin{aligned} {\hat{{{\mathfrak {D}}} }}_{*} = \left\{ \begin{array}{c}({\hat{I}} _1,\varphi _1) \in {\mathbb {R}}\times ]0,2\pi [ \quad \text{ such } \text{ that } \quad {\hat{{\mathrm h }} }({\hat{I}} _1,\varphi _1) = \delta \\ \text{ with }\quad \delta ^* \leqslant \delta \leqslant 2\delta ^* \end{array}\right\} \end{aligned}$$

for the real analytic function

$$\begin{aligned} {\hat{{\mathrm h }} }({\hat{I}} _1, \varphi _1)=\frac{A}{B}{\hat{I}} _1^2-1-{{\mathcal {F}} }(\varphi _1), \end{aligned}$$

and we consider the complex extension ${\hat{D}}_{*,\hat{\rho }} = {{\mathcal {B}}}_{\hat{\rho }}{\hat{{{\mathfrak {D}}} }}_{*}$ with

$$\begin{aligned} {\hat{D}}_{*,\hat{\rho }} = \left\{ ({\hat{I}} _1,\varphi _1 )\in {{\mathbb {C}}}^2 / \exists ({\hat{I}} _1^*,\varphi _1^*)\in {\hat{{{\mathfrak {D}}} }}_{*} \text{ with: } \begin{array}{l} \left| {\hat{I}} _1 - {\hat{I}} _1^* \right| \leqslant \hat{\rho }\\ \left| \varphi _1 - \varphi _1^* \right| \leqslant \hat{\rho }\end{array}\right\} \end{aligned}$$

where $\hat{\rho }>0$ is small enough ().

Likewise, we have the following real analytic functions:

$$\begin{aligned} \hat{J } _1({\hat{I}} _1, \varphi _1) = 4 \sqrt{\frac{B}{A}}\left( \pi -\hat{\varphi {}} _{({\hat{I}} _1,\varphi _1)}^{\min }\right) \displaystyle \int _{0}^{1}\sqrt{{\hat{{{\mathcal {U}} }} }^\pi _{({\hat{I}} _1, \varphi _1)}(x)} {\mathrm {d}}x \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \begin{aligned} {\hat{{{\mathcal {U}} }} }^{\theta }_{({\hat{I}} _1,\varphi _1)}(x)\!&=\! 1\! +\! {{\mathcal {F}} }\left( (1-x)\hat{\varphi {}} _{({\hat{I}} _1,\varphi _1)}^{\min }\! + x\theta \right) \! + {\hat{{\mathrm h }} }({\hat{I}} _1, \varphi _1),\\ \hat{\varphi {}} _{({\hat{I}} _1,\varphi _1)}^{\min }\!\!&=\! {{\mathcal {F}} }^{-1}(-1 - {\hat{{\mathrm h }} }({\hat{I}} _1, \varphi _1)), \end{aligned} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \phi _1 ({\hat{I}} _1,\varphi _1)= \displaystyle \frac{\pi }{2} \frac{\varphi _1 -\hat{\varphi {}} _{({\hat{I}} _1,\varphi _1)}^{\min }}{\pi -\hat{\varphi {}} _{({\hat{I}} _1,\varphi _1)}^{\min }} \frac{\displaystyle \int _{0}^{1}\frac{{\mathrm {d}}x}{\sqrt{{\hat{{{\mathcal {U}} }} }^{\varphi _1}_{({\hat{I}} _1, \varphi _1)}(x)}}}{\displaystyle \int _{0}^{1}\frac{{\mathrm {d}}x}{\sqrt{{\hat{{{\mathcal {U}} }} }^{\pi }_{({\hat{I}} _1, \varphi _1)}(x)}}}. \end{aligned}$$

Hence we consider the transformation

$$\begin{aligned} {\hat{{{\mathfrak {G}}}}}: \quad \Bigg \{ \begin{array}{ccc} {\hat{{{\mathfrak {D}}} }}_{*} &{}\longrightarrow &{} {{\hat{{{\mathcal {S}} }}} }_* \times {{\mathbb {T}}}\\ ({\hat{I}} _1,\varphi _1) &{}\longmapsto &{} ( \hat{J } _1, \phi _1) \end{array} \end{aligned}$$

with

$$\begin{aligned} {{\hat{{{\mathcal {S}} }}} }_* = \left[ \frac{a}{\sqrt{{\varepsilon }}}, \frac{b}{\sqrt{{\varepsilon }}}\right] \quad \text{ for } \text{ some } \quad a<0 <b \end{aligned}$$

which corresponds to the action-angle variables for the mechanical system

$$\begin{aligned} \hat{{\mathscr {H}} }_1({\hat{I}} _1, \varphi _1) = \upsilon _0\left( -A {\hat{I}} _1^2 + B {{\mathcal {F}} }(\varphi _1)\right) \end{aligned}$$

and its inverse mapping will be denoted ${\hat{{{\mathfrak {F}}}}}={\hat{{{\mathfrak {G}}}}}^{-1}$. Moreover, these transformations are independent of $\varepsilon$.

By classical theorem of complex analysis, ${\hat{{{\mathfrak {F}}}}}$ (resp. ${\hat{{{\mathfrak {G}}}}}$) can be extended in a unique way to a map F (resp. G) holomorphic on a complex set

$$\begin{aligned} \begin{aligned} {{\mathcal {B}}}_r{{\hat{{{\mathcal {S}} }}} }_*\times {{\mathcal {V}}} _{s}{{\mathbb {T}}}= \left\{ \begin{array}{c} ( \hat{J } _1,\phi _1 )\in {{\mathbb {C}}}^2\, / \, \exists \hat{J } _1^*\in {{\hat{{{\mathcal {S}} }}} }_* \quad \text{ such } \text{ that } \quad \\ \left| \hat{J } _1- \hat{J } _1^* \right| \leqslant r ,\quad {{\,\mathrm{Re}\,}}(\phi _1)\in {{\mathbb {T}}}\\ \text{ and }\quad \left| {{\,\mathrm{Im}\,}}(\phi _1) \right| \leqslant s \end{array}\right\} \end{aligned} \end{aligned}$$

and G holomorphic over the set ${\hat{D}}_{*,\hat{\rho }}$ for some $r>0$, $s>0$ and $\hat{\rho }>0$ small enough. We want to compute a lower bound on the analyticity widths r, s. For $\hat{\rho }>0$, we denote

$$\begin{aligned} \left\| \hat{J } _1 \right\| _{\hat{\rho }} =\sup \limits _{{\hat{D}}_{*,\hat{\rho }}} \left| \hat{J } _1( {\hat{I}} _1,\varphi _1) \right| , \quad \left\| \phi _1 \right\| _{\hat{\rho }} = \sup \limits _{{\hat{D}}_{*,\hat{\rho }}}\left| \phi _1({\hat{I}} _1,\varphi _1) \right| , \end{aligned}$$

moreover, we consider

$$\begin{aligned} {\tilde{M}} =\left\| \hat{J } _1 \right\| _{\hat{\rho }} +\left\| \phi _1 \right\| _{\hat{\rho }} . \end{aligned}$$

Finally, since the real mapping ${\hat{{{\mathfrak {G}}}}}$ is symplectic, it is non-degenerate at each point of the domain ${\hat{{{\mathfrak {D}}} }}_{*}$ and we denote

$$\begin{aligned} {\tilde{L}} =\sup \limits _{{\hat{{{\mathfrak {D}}} }}_{*}} \left| {\mathrm {d}}{\hat{{{\mathfrak {G}}}}}^{-1}_{({\hat{I}} _1,\varphi _1)} \right| . \end{aligned}$$

By a standard application of the Lipschitz inverse function theorem (see [18]), we obtain the main estimate of this section.

Theorem A.1

Suppose that U is an open subset of a Banach space $(E,\vert \vert .\vert \vert )$ and that $g : U\rightarrow E$ is a Lipschitz mapping with constant $K<1$.

Let $f(x)=x+g(x)$. If the closed ball ${{\mathcal {B}}}_\varepsilon \{x\}$ centered at $x\in E$ of radius $\varepsilon$ is contained in U, then

$$\begin{aligned} {{\mathcal {B}}}_{(1-K )\varepsilon }\{f (x)\}\subseteq f({{\mathcal {B}}}_\varepsilon \{x\})\subseteq {{\mathcal {B}}}_{(1+K )\varepsilon } \{f (x)\} . \end{aligned}$$

The mapping f is a homeomorphism of U onto $f^{-1} (U)$, the inverse mapping $f^{-1}$ is a Lipschitz mapping with constant $(1- K)^{-1}$ and f(U) is an open subset of E.

More precisely, we use Theorem 4.1 and Cauchy inequalities applies on G which yields

Theorem A.2

With the previous notations, if

then G admits an inverse mapping F which is holomorphic on ${{\mathcal {B}}}_{r}{{\hat{{{\mathcal {S}} }}} }_* \times {{\mathcal {V}}} _s{{\mathbb {T}}}$ and F is C-Lipschitz with .

Hence, in order to estimate the analyticity widths in action-angle variables for the considered mechanical system, we have to compute the dependance w.r.t. the quantity $\delta ^*$ of the analyticity width $\hat{\rho }$ in the original variables $({\hat{I}} _1,\varphi _1)$, the upper bounds ${\tilde{L}}$ on the real domain ${\hat{{{\mathfrak {D}}} }}_{*}$ and ${\tilde{M}}$ on the complex domain $D_{*,\hat{\rho }}$. In order to bound ${\tilde{L}}$, we use the fact that ${\hat{{{\mathfrak {G}}}}}$ is symplectic on the real domain ${\hat{{{\mathfrak {D}}} }}_{*}$, hence the coefficients of the Jacobian matrix linked to ${\mathrm {d}}{\hat{{{\mathfrak {G}}}}}^{-1}$ are given by the derivatives of ${\hat{{{\mathfrak {G}}}}}$ that we estimate by an application of Cauchy inequalities over $D_{*,\hat{\rho }}$. We obtain

Concerning the quantities $\hat{\rho }$ and ${\tilde{M}}$ on the complex domain $D_{*,\hat{\rho }}$, rough estimates ensure that if we choose the analyticity width for $\delta ^*$ small enough (), we can ensure the upper bound

Plugging these estimates in the latter theorem ensure that G admits an inverse mapping F which is holomorphic on ${{\mathcal {B}}}_r{{\hat{{{\mathcal {S}} }}} }_*\times {{\mathcal {V}}} _s{{\mathbb {T}}}$ for

Going back to the initial variables, if we denote $F=(F_1,F_2)$, then the extended transformation in action-angle coordinates in the complex plane is given by

$$\begin{aligned} (\sqrt{{\varepsilon }} F_1(J_1/\sqrt{{\varepsilon }}, \phi _1), F_2(J_1/\sqrt{{\varepsilon }}, \phi _1)) \end{aligned}$$

and we obtain the analyticity widths of Theorem 4.3.

Moreover, F is C-Lipschitz with and the distance to the real domain of the image is bounded by $\sqrt{{\varepsilon }}(\delta ^{*})^{{\hat{p} }-1/2}$ for $I_1$ and by $(\delta ^{*})^{{\hat{p} }-1/2}$ for $\varphi _1$ hence these quantities are bounded by $\sqrt{{\varepsilon }} (\delta ^*)^5$ and $(\delta ^*)^5$ for ${\hat{p} }= 11/2$.

1.7 Theorem 4.4: Semi-fast Action-Angle variables

The existence of the transformation $\Psi$ is immediate by application of Lemma 4.3 to the averaged Hamiltonian $\tilde{{\mathscr {H}} }$ considered in (4.3).

Finally, the two last thresholds in (4.17) are deduced by an application of the Cauchy inequalities.

1.8 Theorem 4.5: Second Averaging Theorem

In the same way as for the First Averaging Theorem, we define firstly an iterative lemma of averaging. Let us introduce some notations: $(\xi _k)_{k\in \{1,\ldots , 5\}}$ are given positive numbers such that

$$\begin{aligned} 0<\xi _j< \rho _j, \quad 0< \xi _{2+j}<\sigma _j \quad \text{ for } j\in \{1,2\}\text{, } \quad 0<\xi _{5}<\sqrt{\rho _2\sigma _2}, \end{aligned}$$

and for $0\leqslant r\leqslant 1$, we denote ${{\mathfrak {K}} }_r$, the domain such as

$$\begin{aligned} {{\mathfrak {K}} }_r={{\mathcal {B}}}_{\rho _1-r\xi _1}{{\mathcal {S}} }_*\times {{\mathcal {B}}}^1_{\rho _2-r\xi _2}\times {{\mathcal {V}}} _{\sigma _1-r\xi _3}{{\mathbb {T}}}\times {{\mathcal {V}}} _{\sigma _2-r\xi _4}{{\mathbb {T}}}\times {{\mathcal {B}}}^4_{\sqrt{\rho _2\sigma _2} - r\xi _{5}}. \end{aligned}$$

Moreover, we will consider $\nu _0$ a lower bound for the semi-fast frequency ${{\mathscr {H}} }'_1$ on the complex domain ${{\mathcal {K}} }_p$ and according to (4.19), we can choose

with our polynomial dependence of $\delta ^*$ with respect to $\varepsilon$.

Hence, we set out the following:

Lemma A.3

(Second iterative lemma). Let $\varvec{\rho }^{-}$, $\varvec{\sigma }^{-}$, $(\xi _k)_{k\in \{1,\ldots ,4\}}$ be fixed positive real numbers that depend on the small parameter ${\varepsilon }$ and

$$\begin{aligned} \begin{aligned}&\varvec{\rho }^{+} =\varvec{\rho }^- - (\xi _1,\xi _2),&\quad&\varvec{\sigma }^{+} = \varvec{\sigma }^- - (\xi _3,\xi _4), \\&\xi _{5}= \sqrt{\rho _2^-\sigma _2^-} - \sqrt{\rho _2^{+}\sigma _2^{+}}&\text{ such } \text{ as } 0<\rho _j^{+}\text{, } 0 < \sigma _j^{+} \text{ for } j\in \{1,2\}\text{. } \end{aligned} \end{aligned}$$

Let ${{\mathscr {H}} }^{-}$ be a Hamiltonian of the form

$$\begin{aligned} \begin{aligned} {{\mathscr {H}} }^{-}({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) =&{{\mathscr {H}} }_1(J_1) + {{\mathscr {H}} }_2(J_2) + \overline{{\mathscr {Q}} }(J_1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} })\\ +&{{\mathscr {H}} }_{*}^{0,-}({\mathbf{J} }, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) + {{\mathscr {H}} }_{*}^{1,-}({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) \end{aligned} \end{aligned}$$

with ${{\mathscr {H}} }_*^{l,-} = {{\mathscr {H}} }_{*,0}^{l,-} + \sum _{j,k\in \{1,2\}} {{\mathscr {H}} }_{*,(j,k)}^{l,-}w_j{\widetilde{w} }_k$ for $l\in \{0,1\}$ (given by (4.8)), which satisfies the D’Alembert rule, is analytic on the domain ${{\mathfrak {K}} }^{-}_0={{\mathcal {K}} }_{\varvec{\rho }^{-}, \varvec{\sigma }^{-}}$ and such that

$$\begin{aligned} {\overline{{\mathscr {H}} }_{*}^{1,-}}({\mathbf{J} }, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = \frac{1}{2\pi }\int _0^{2\pi } {{{\mathscr {H}} }_{*}^{1,{-}}}({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }){\mathrm {d}}\phi _1 =0. \end{aligned}$$

Let $(\eta _l^{-})_{l\in \{0,2\}}$ and $(\mu _{l,m}^{-})_{l\in \{0,2\},m\in \{0,1,2\}}$ be fixed positive real numbers, which depend on ${\varepsilon }$, such that:

$$\begin{aligned} \begin{aligned}&\left\| {{{\mathscr {H}} }_{*,0}^{1,{-}}} \right\| _{{{\mathfrak {K}} }_0^{-}}\leqslant \eta _0^{-} ,&\quad&\left\| {{{\mathscr {H}} }_{*,(j,k)}^{1,{-}}} \right\| _{{{\mathfrak {K}} }_0^{-}}\leqslant \eta _2^{-} ,&\\&\left\| {{{\mathscr {H}} }_{*,0}^{0,{-}}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{0,0}^{-} ,&\quad&\left\| {{{\mathscr {H}} }_{*,(j,k)}^{0,{-}}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{2,0}^{-} ,&\end{aligned} \end{aligned}$$

(A.13)

and

$$\begin{aligned} \left\| \partial _{J_m}{{\mathscr {H}} }_{*,0}^{0,{-}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{0,m}^{-},\quad \left\| \partial _{J_m}{{\mathscr {H}} }_{*,(j,k)}^{0,{-}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{2,m}^{-} \quad (m\in \{1,2\}). \end{aligned}$$

If we assume that

(A.14)

then there exists a canonical transformation

and such that, in the new variables, the Hamiltonian ${{\mathscr {H}} }^{+}= {{\mathscr {H}} }^{-} \circ \overline{\Psi }^{+}$ satisfies the D’Alembert rule and can be written

$$\begin{aligned} \begin{aligned} {{\mathscr {H}} }^{+}&= {{\mathscr {H}} }_1 + {{\mathscr {H}} }_2 + \overline{{\mathscr {Q}} }+ {{{\mathscr {H}} }_{*}^{0,{-}}} + {{\mathscr {H}} }_*^{+}\\&= {{\mathscr {H}} }_1 + {{\mathscr {H}} }_2 + \overline{{\mathscr {Q}} }+ {{{\mathscr {H}} }_{*}^{0,{+}}} + {{\mathscr {H}} }_{*}^{1,+} \end{aligned} \quad \text{ with } \quad \left\{ \begin{array}{l} {{{\mathscr {H}} }_{*}^{0,{+}}} = {{\mathscr {H}} }_{*}^{0,{-}} + \overline{{\mathscr {H}} }_{*}^{+} \\ {{{\mathscr {H}} }_{*}^{1,{+}}} = {{\mathscr {H}} }_*^{+} - \overline{{\mathscr {H}} }_*^{+} \end{array} \right. \end{aligned}$$

such that for $l\in \{0,1\}$ (given by (4.8)) and

Furthermore, we have the thresholds

$$\begin{aligned} \begin{aligned}&\left\| {{{\mathscr {H}} }_{*,0}^{1,{+}}} \right\| _{{{\mathfrak {K}} }_0^{-}}\leqslant \eta _0^{+} ,&\quad&\left\| {{{\mathscr {H}} }_{*,(j,k)}^{1,{+}}} \right\| _{{{\mathfrak {K}} }_0^{-}}\leqslant \eta _2^{+} ,&\\&\left\| {{{\mathscr {H}} }_{*,0}^{0,{+}}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{0,0}^{+} ,&\quad&\left\| {{{\mathscr {H}} }_{*,(j,k)}^{0,{+}}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{2,0}^{+} ,&\end{aligned} \end{aligned}$$

(A.15)

and

$$\begin{aligned} \left\| \partial _{J_m}{{\mathscr {H}} }_{*,0}^{0,{+}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{0,m}^{+},\quad \left\| \partial _{J_m}{{\mathscr {H}} }_{*,(j,k)}^{0,{+}} \right\| _{ {{\mathfrak {K}} }_0^{-}}\leqslant \mu _{2,m}^{+}\quad (m\in \{1,2\}), \end{aligned}$$

(A.16)

with the following quantities:

(A.17)

for $m\in \{1,2\}$ and

$$\begin{aligned} \begin{aligned} \gamma _0^+&= \frac{\eta _0^-}{\xi _1\xi _3} , \quad \gamma _2^+= \eta _2^-\left( \frac{1}{\xi _1\xi _3} + \frac{1}{(\xi _5)^2}\right) ,\quad \theta _0^+ = \frac{\mu _{0,1}^-}{\xi _3} + \gamma _0^+ ,\\ \theta _1^+&= \frac{\left\| \overline{{\mathscr {Q}} }_{(j,k)} \right\| _{{{\mathfrak {K}} }^-_0}}{\xi _1\xi _3}+ \frac{\mu _{2,1}^-}{\xi _3} ,\\ \theta _2^+&= \frac{\left\| \overline{{\mathscr {Q}} }_{(j,k)} \right\| _{{{\mathfrak {K}} }^-_0}}{(\xi _5)^2} + \frac{\mu _{2,0}^-}{(\xi _5)^2} + \gamma _2^+ . \end{aligned} \end{aligned}$$

(A.18)

Proof

We define $\overline{\Psi }^+:{{\mathfrak {K}} }_1^-\longrightarrow {{\mathfrak {K}} }_0^-$ as the time-one map of the Hamiltonian flow generated by some auxiliary function ${\chi ^+}$, i.e. $\overline{\Psi }^+=\Phi _1^{\chi ^+}$ with

$$\begin{aligned} {\chi ^+}({\mathbf{J} },\phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = \frac{2\pi }{{{\mathscr {H}} }_1'(J_1)}\int _0^1 s {{{\mathscr {H}} }_{*}^{1,-}}({\mathbf{J} },\phi _1+ 2\pi s, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }){\mathrm {d}}s \end{aligned}$$

such that the following properties are satisfied:

$$\begin{aligned} \begin{aligned}&\left\{ \chi ^+,{{\mathscr {H}} }_1\right\} + {{\mathscr {H}} }_*^{1,-} = 0,\\&\overline{\chi }^+({\mathbf{J} }, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = \frac{1}{2\pi }\int _0^{2\pi } \chi ^+({\mathbf{J} }, \phi _1,{\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) {\mathrm {d}}\phi _1 = 0,\\&\text{ and } \quad \chi ^+ = \chi _0^+ + \sum _{1\leqslant j,k\leqslant 2}\chi ^+_{(j,k)}w_j{\widetilde{w} }_k \quad \text{(given } \text{ by } \quad (4.8)). \end{aligned} \end{aligned}$$

(A.19)

Thus, for the same reason as in Lemma A.1, the Hamiltonian can be written

$$\begin{aligned} {{\mathscr {H}} }^+ = {{\mathscr {H}} }^-\circ \overline{\Psi }^+ = {{\mathscr {H}} }_1 + {{\mathscr {H}} }_2 + \overline{{\mathscr {Q}} }+ {{\mathscr {H}} }_{*}^{0,-} + \underbrace{{{{\mathscr {H}} }_{*}^{1,-}} + \left\{ {\chi ^+},{{\mathscr {H}} }_1\right\} }_{(*)} +{{\mathscr {H}} }^+_* \end{aligned}$$

with

$$\begin{aligned} {{\mathscr {H}} }_*^+ = \int _0^1 \left\{ {\chi ^+},\overline{{\mathscr {Q}} }+{{\mathscr {H}} }_{*}^{0,-}+ s{{\mathscr {H}} }_{*}^{1,-}\right\} \circ \Phi _s^{\chi ^+} {\mathrm {d}}s \end{aligned}$$

and $(*)$ is equal to zero by (A.19).

Then, in order to estimate the size of the remainder ${{\mathscr {H}} }_*^+$, the thresholds (A.13) provide

while the Cauchy inequalities imply the following:

as well as the following estimates on the Poisson brackets:

and

as $1 \leqslant \frac{\sqrt{\rho _2^- \sigma _2^-}}{\xi _5} \leqslant \frac{\rho _2^- \sigma _2^-}{(\xi _5)^2}$. Consequently, the remainder of the transformation $\overline{\Psi }^+$ is bounded such that

where $\gamma _0^+$, $\gamma _2^+$, $\theta _0^+$,$\theta _1^+$ and $\theta _2^+$ are defined in (A.17). Moreover by taking into account that $\overline{\chi }^+=0$ (given by (A.19)), we deduce the following:

Hence, if we denote ${{{\mathscr {H}} }_{*}^{0,+}} = {{{\mathscr {H}} }_{*}^{0,-}} + \overline{{\mathscr {H}} }_{*}^+$ and ${{{\mathscr {H}} }_{*}^{1,+}} = {{\mathscr {H}} }_*^+ - \overline{{\mathscr {H}} }_*^+$ then the triangle inequality gives the estimates (A.15) and (A.16) (together with the Cauchy inequalities for the last).

Finally, in the same way as for Lemma A.1, the conditions (A.14) provide the estimates on the size of the transformation $\overline{\Psi }^+$ which yields (A.17) and (A.18). $\quad \square$

Now, in order to prove Theorem 4.5, one applies iteratively Lemma A.3 to the Hamiltonian ${{\mathscr {H}} }$ that can be written:

$$\begin{aligned} \begin{aligned} {{\mathscr {H}} }({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) =&\, {{\mathscr {H}} }_1(J_1) + {{\mathscr {H}} }_2(J_2) + \overline{{\mathscr {Q}} }(J_1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) \\ +&\,{{\mathscr {H}} }^{0,0}_*({\mathbf{J} }, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) +{{\mathscr {H}} }^{1,0}_*({\mathbf{J} }, \phi _1,{\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {{\mathscr {H}} }^{0,0}_*= & {} {{\mathscr {H}} }^{0,0}_{*,0} + \sum _{j,k\in \{1,2\}} {{\mathscr {H}} }^{0,0}_{*,(j,k)}w_j{\widetilde{w} }_k = \overline{{\mathscr {R}} },\\ {{\mathscr {H}} }^{1,0}_*= & {} {{\mathscr {H}} }^{1,0}_{*,0} + \sum _{j,k\in \{1,2\}} {{\mathscr {H}} }^{1,0}_{*,(j,k)}w_j{\widetilde{w} }_k = {{\mathscr {R}} }-\overline{{\mathscr {R}} }+ {{\mathscr {Q}}}- \overline{{\mathscr {Q}} },\\&\text{ and } \quad \overline{{\mathscr {R}} }({\mathbf{J} }, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) = \frac{1}{2\pi }\int _0^{2\pi } {{\mathscr {R}} }({\mathbf{J} }, \phi _1, {\mathbf{w} }, {\widetilde{{\mathbf{w} }} }) d\phi _1 , \end{aligned}$$

with the following thresholds:

Moreover, by reducing the domain of analyticity to ${{\mathcal {K}} }_{5/6}$, one can apply the Cauchy inequalities and obtain the followings:

In the same way as in the proof of Theorem 4.5, let s a non-zero integer such that $s = {\mathrm E }({\varepsilon }^{-{\mathrm q }}) + 1$ where

$$\begin{aligned} {\mathrm q }= \frac{3\beta -1}{15} \quad \text{ for } \quad 4/9< \beta <1/2. \end{aligned}$$

We define

as well as the sequences $\left( \varvec{\rho }^{j}\right) _{j\in \{0,1,\ldots ,s\}}$,$\left( \varvec{\sigma }^{j}\right) _{j\in \{0,1,\ldots ,s\}}$ with

$$\begin{aligned} (\varvec{\rho }^{j}, \varvec{\sigma }^{j}) = \left( \frac{5}{6} - \frac{j}{4s}\right) (\varvec{\rho },\varvec{\sigma }) \quad \text{ for } \quad j\in \{0,\ldots ,s\} \end{aligned}$$

such that ${{\mathfrak {K}} }^{j}_r = {{\mathcal {K}} }_{\frac{5}{6}-\frac{j+r}{4s}}$ for $0\leqslant r\leqslant 1$.

Replacing the notation $^-$ and $^+$ by $^{j-1}$ and $^{j}$ and assuming that for all $0<j\leqslant s$ the following conditions (associated with (A.14)) are fulfilled:

then an iterative application of Lemma A.3 to the Hamiltonian ${{\mathscr {H}} }$ provides a sequence of canonical transformations $\left( \overline{\Psi }^{j}\right) _{j\in \{1,\ldots ,s\}}$ such that ${{\mathscr {H}} }\circ \overline{\Psi }= \overline{\Psi }^{1}\circ \overline{\Psi }^{2}\circ \cdots \circ \overline{\Psi }^{s}$ is equal to the Hamiltonian $\overline{{\mathscr {H}} }+ {\mathscr {H}}^\dagger _*$ with ${{\mathscr {F}} }= {{\mathscr {H}} }_{*}^{0,s}$ and ${\mathscr {H}}^\dagger _* = {{\mathscr {H}} }_{*}^{1,s}$.

For the same reasons as in the proof of Theorem 4.1, for all $n\in \{1,\ldots , s\}$, the sequences $\left( \eta _l^{j}\right) _{j\in \{1,\ldots ,n\}}$ and $\left( \mu _{l,m}^{j}\right) _{j\in \{1,\ldots , n\}}$ must satisfy the following induction hypothesis:

$$\begin{aligned} \begin{aligned}&\eta _l^{j}\leqslant \eta _l^{j-1}\exp (-1) ,&\quad&\mu _{l,m}^{j} - \mu _{l,m}^{j-1} \leqslant \frac{\mu _{l,m}^{0}}{s},&\end{aligned} \end{aligned}$$

(A.20)

for $l\in \{0,2\}$ and $m\in \{0,1,2\}$.

For $n=1$, (A.20) is fulfilled as $4/9<\beta < 1/2$ and . Moreover,

imply that

for and

for ($m\in \{0,1,2\}$).

For a fixed integer n, the induction is immediate since the sequences $\left( \eta _l^{j}\right) _{j\in \{0,\ldots ,n\}}$ are decreasing such that $\displaystyle \frac{\eta _0^{n}}{\eta _2^{n}} \leqslant \frac{\eta _0^{0}}{\eta _2^{0}}$ while $\displaystyle \mu _{l,m}^{n} \leqslant 2 \mu _{l,m}^{0}$.

Hence, this proves the hypothesis (A.20) up to s and consequently that

which provide (4.23) and a part of the thresholds (4.21) and (4.22). The missing thresholds of (4.22) are deduced by using the Cauchy inequalities in a restricted domain ${{\mathcal {K}} }_p$ with $0<p<7/12$.

Finally, the Eq. (3.2) as well as the Cauchy inequalities provide the size of the transformation $\overline{\Psi }$ on ${{\mathcal {K}} }_p$:

and in the same way

Remark that as $\chi ^{j}$ does not depend on $\phi _2$ for all $j\in \{1,\ldots ,s\}$ then . This yields ${{\mathcal {K}} }_{5/12} \subseteq \overline{\Psi }({{\mathcal {K}} }_{7/12}) \subseteq {{\mathcal {K}} }_{9/12}$ for .

1.9 Theorem 4.6: Secular Frequencies

We denote by $f(J,\phi )$ a regular function on ${\mathbb {R}}\times {{\mathbb {T}}}$ and by ${\tilde{f}}(\varphi )$ the real function satisfying the relation ${\tilde{f}} \circ {{\mathfrak {F}}}_2 = f$. Using these notations, the average of f at $J_*\in {{\mathcal {S}} }_*$ reads

(A.21)

As ${\tilde{{\mathcal {A}}}}(2\pi - \varphi ) = {\tilde{{\mathcal {A}}}}(\varphi )$ and ${\tilde{{{\mathcal {B}}}}}(2\pi - \varphi ) = {{\,\mathrm{conj}\,}}({\tilde{{{\mathcal {B}}}}}(\varphi ))$, the expressions of ${\overline{ {\mathcal {A}}}}(J_*)$ and ${\overline{{{\mathcal {B}}}}}(J_*)$ given by (4.24) follow.

The asymptotic expansions of ${\overline{ {\mathcal {A}}}}(J_*)$ and ${\overline{{{\mathcal {B}}}}}(J_*)$ have now to be derived. As ${\tilde{{\mathcal {A}}}}(\pi ) = 7/8$, it follows from Lemma 2 and (A.21) that

The main part of the integral involved in the previous expressions can be computed as follows:

As and because , the two last integrals are respectively and . It turns out that

and .

For the same reasons, we also have

where the real coefficients $C_{\mathcal {A}}$ and $C_{{\mathcal {B}}}$ are bounded by

$$\begin{aligned} -28< C_{\mathcal {A}}<-27 \quad \text{ and } \quad 16< C_{{\mathcal {B}}}< 17. \end{aligned}$$

This provides all that is needed for deriving the asymptotic expansion of the secular frequencies and . Indeed, these frequencies are given by where $\lambda _j$ are the two roots of the polynomial

$$\begin{aligned} \lambda ^2 - \frac{m_1+m_2}{m_1m_2}{\overline{ {\mathcal {A}}}}(J_*) \lambda - \frac{{\overline{{{\mathcal {B}}}}}(J_*)^2-{\overline{ {\mathcal {A}}}}(J_*)^2}{m_1m_2} . \end{aligned}$$

At this point, Theorem 4.6 is deduced from an asymptotic expansion of the $\lambda _j$, from which it follows that the coefficients $c_2$ involved in (4.25) satisfy the relations

$$\begin{aligned} -90< c_2 = 2(C_{\mathcal {A}}- C_{{\mathcal {B}}}) < - 86. \end{aligned}$$

1.10 Theorem 4.7: Diagonalization

By the discussion that precedes Theorem 4.7, as the spectrum of (4.26) is simple, there exists a symplectic transformation $\check{\Psi }$ which is linear with respect to , and diagonalizes the quadratic form (4.26).

In the general case the diagonalizing transformation is generated by a function which can be written

where are of order 1 over the considered domain.

Using Cauchy inequalities to bound the derivatives of $\chi$ in order to control the variation of the angles associated with under the considered transformation, we obtain the upper bounds

since .

Finally, by Lemma 4.2 the Taylor expansion reads

Together with the estimates (4.22) of Theorem 4.5, this provides the threshold (4.28) on .

1.11 Theorem 5.1: Application of a Pöschel version of KAM Theory

As it was specified in Sect. 5, from now on, we constrain ${\varepsilon }$ to be inside an interval $[{\varepsilon }_0/2, {\varepsilon }_0]$ for an arbitrary ${\varepsilon }_0>0$.

Let us consider the frequency map linked to the Hamiltonian $\check{{\mathscr {H}} }$ (see Theorem 4.7) that is denoted $(\varvec{\omega }(\varvec{\Gamma }), \varvec{\Omega }(\varvec{\Gamma }))$ with $\omega _j = {{\mathscr {H}} }'_j + \partial _{\Gamma _j} {{\mathscr {F}} }_0$ and $\Omega _j = g_j$, and the following thresholds:

that are deduced from and the bounds (4.22) and (4.27). Moreover, we have the following thresholds on the derivatives:

with ${{\mathscr {E}}} _1= \upsilon _0K^2B^{-1}$ and ${{\mathscr {E}}} _2 = -2E\upsilon _0$ (that are not equal to zero) from the bounds (4.22) and the mean value theorem. Consequently the eigenvalues of ${\mathrm {d}}\varvec{\omega }$ are small perturbations of $\displaystyle \frac{{{\mathscr {E}}} _1}{{\varepsilon }_0^{{\mathrm q }}\left| \ln {{\varepsilon }_0} \right| ^4}$ and ${{\mathscr {E}}} _2$. We also ensure that ${\mathrm {d}}\varvec{\omega }$ is inversible with the eigenvalues $\lambda _1(\varvec{\Gamma })$, $\lambda _2(\varvec{\Gamma })$ such that

Hence, $\varvec{\omega }$ is a local diffeomorphism.

In order to apply Pöschel version of KAM theory for the persistence of lower dimensional normally elliptic invariant tori [28], we must consider a domain where the internal frequency map $\varvec{\omega }$ is a diffeomorphism. Hence, we set out the following

Lemma A.4

For ${\varepsilon }\in [{\varepsilon }_0/2,{\varepsilon }_0]$, the internal frequency map $\varvec{\omega }$ is a diffeomorphism from $\Pi = {{\mathcal {B}}}^2_{\rho }$ onto its image provided by

Moreover, we have the upper bounds

(A.22)

Proof

We consider $\varvec{\omega }_0=\varvec{\omega }- \varvec{\omega }({\mathbf{0} })$ where $\varvec{\omega }_0$ is holomorphic on the closed ball ${{\mathcal {B}}}_{\rho _1}^2$ with . Then, we define

$$\begin{aligned} \begin{aligned} \tilde{\varvec{\omega }}_0=&({\mathrm {d}}\varvec{\omega }({\mathbf{0} }))^{-1}\varvec{\omega }_0 - {{\,\mathrm{Id}\,}}\quad \text{ such } \text{ that } \quad {\mathrm {d}}\tilde{\varvec{\omega }}_0 = ({\mathrm {d}}\varvec{\omega }({\mathbf{0} }))^{-1}({\mathrm {d}}\varvec{\omega }- {\mathrm {d}}\varvec{\omega }({\mathbf{0} })). \end{aligned} \end{aligned}$$

Hence, since the highest eigenvalue of $({\mathrm {d}}\varvec{\omega }({\mathbf{0} }))^{-1}$ satisfies for ${\varepsilon }$ small enough with ${{\mathscr {E}}} _2 \ne 0$. Furthermore, by the mean value theorem as well as the Cauchy inequalities, we can ensure that on the closed ball ${{\mathcal {B}}}^2_{\widetilde{\rho }}$ such that then

Consequently, the application:

$$\begin{aligned} \hat{\varvec{\omega }}_0 = {{\,\mathrm{Id}\,}}+ \tilde{\varvec{\omega }}_0 \end{aligned}$$

is a diffeomorphism from ${{\mathcal {B}}}^2_{\widetilde{\rho }}$ to $\tilde{\varvec{\omega }}_0({{\mathcal {B}}}^2_{\widetilde{\rho }})$ by the fixed point theorem. Moreover, $\hat{\varvec{\omega }}({\mathbf{0} }) = {\mathbf{0} }$ yields

$$\begin{aligned} {{\mathcal {B}}}^2_{\widetilde{\rho }/2} \subset \hat{\varvec{\omega }}_0({{\mathcal {B}}}_{\widetilde{\rho }}^2) \subset {{\mathcal {B}}}^2_{3\widetilde{\rho }/2} \end{aligned}$$

and $\hat{\varvec{\omega }}_0^{-1}$ is a Lipschitz mapping with a constant 2.

Now, as $\varvec{\omega }= \varvec{\omega }({\mathbf{0} }) + {\mathrm {d}}\varvec{\omega }({\mathbf{0} }) \hat{\varvec{\omega }}_0$, we consider

$$\begin{aligned} \varvec{\omega }^{-1}({\mathbf{y} }) = \hat{\varvec{\omega }}_0^{-1}\left( ({\mathrm {d}}\varvec{\omega }({\mathbf{0} }))^{-1}({\mathbf{y} }- \varvec{\omega }({\mathbf{0} }))\right) . \end{aligned}$$

If $({\mathrm {d}}\varvec{\omega }({\mathbf{0} }))^{-1}({\mathbf{y} }- \varvec{\omega }({\mathbf{0} }))\in {{\mathcal {B}}}^2_{\widetilde{\rho }/2}$, then there exists

(as ). Hence, we have determined $\varvec{\omega }^{-1}$ over ${{\mathcal {B}}}_{\hat{\rho }}\{\varvec{\omega }({\mathbf{0} })\}$.

Finally for $({\mathbf{y} }, {\mathbf{y} }') \in ({{\mathcal {B}}}_{\hat{\rho }}\{\varvec{\omega }({\mathbf{0} })\})^2$, we have

as ${\mathrm {d}}\hat{\varvec{\omega }}_0^{-1}$ is 2-Lispshitz and . Hence, as then

Consequently, $\varvec{\omega }$ is a diffeomorphism from ${{\mathcal {B}}}^2_\rho$ onto its image and the estimates (A.22) are ensured (by the estimates (4.22)). $\quad \square$

By the notations of Sect. 5, with $\vert f \vert _\Pi ^{\mathrm{Lip}}\leqslant \vert \vert {\mathrm {d}}f\vert \vert _\Pi$ for a differentiable function and the upper bounds (A.22) ensure

A property needed to apply the Pöschel results on the persistence of normally elliptic tori is to ensure Melnikov’s condition for multi-integers of length bounded by $K_0 = 16L M$. This is the content of the following

Proposition A.1

Let

we have, for ${\varepsilon }\in [{\varepsilon }_0/2,{\varepsilon }_0]$ with ,

Proof

First of all, for $\varvec{\xi }\in \Pi$ we have the followings:

(A.23)

that are deduced from (4.19) and (4.27). As a consequence, with ${\varepsilon }\in [{\varepsilon }_0/2, {\varepsilon }_0]$, for $\varvec{\xi }\in \Pi$:

$$\begin{aligned} \vert \Omega _1(\varvec{\xi })\vert \geqslant \gamma _0,\quad \vert \Omega _2(\varvec{\xi })\vert \geqslant \gamma _0,\quad \vert \Omega _1(\varvec{\xi }) - \Omega _2(\varvec{\xi })\vert \geqslant \gamma _0. \end{aligned}$$

For $({\mathbf {k}},{\varvec{l}})\in {{\mathbb {Z}}}^2\times {{\mathbb {Z}}}^2$ with $0<\left| {\mathbf {k}} \right| \leqslant K_0$ and $\left| {\varvec{l}} \right| \leqslant 2$ we have

since $4/9< \beta < 1/2$. Especially, for a large enough constant $C>0$, we have

deduced from (A.23) with and $k_2 \ne 0$. Likewise, if $k_2=0$ then for a large enough constant $C>0$, we have

with . $\quad \square$

The Hamiltonian ${\mathrm H }$ defined in (5.2) is analytic over the domain $D({\bar{r}},{\bar{s}})$ defined in (5.4) with $0<{\bar{r}}< r$ and .

With the estimates given in Proposition A.1, it remains to check the thresholds of the Proposition 2.2 in Biasco et al. [6] which become here the threshold (5.5) of Theorem 5.1 and has to be satisfied for a small enough bound ${\varepsilon }_0$ on the mass ratio.

We decompose the perturbation (5.3) in ${\mathrm P }={\mathrm P }_1 + {\mathrm P }_2 + {\mathrm P }_3 + {\mathrm P }_4$ with

$$\begin{aligned} \begin{aligned} {\mathrm P }_1({\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi })&=\sum _{j\in \{1,2\}} \Big ({{\mathscr {H}} }_j(\xi _j +y_j)-{{\mathscr {H}} }_j(\xi _j)- \omega _j (\varvec{\xi })y_j \Big )+ {{\mathscr {F}} }_0(\varvec{\xi }+{\mathbf{y} })-{{\mathscr {F}} }_0(\varvec{\xi }),\\ {\mathrm P }_2({\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi })&= \sum _{j\in \{1,2\}} i \big (g_j(\varvec{\xi }+{\mathbf{y} })- g_j(\varvec{\xi })\big ) z_j{\widetilde{z}} _j,\\ {\mathrm P }_3({\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi })&=\check{{{\mathscr {R}} }}(\varvec{\xi }+{\mathbf{y} },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ), \quad \text{ and } \quad {\mathrm P }_4({\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ; \varvec{\xi })=\check{{\mathscr {H}} }_{*}(\varvec{\xi }+{\mathbf{y} },\varvec{\psi },{\mathbf{z} }, {\widetilde{\mathbf{z}}} ). \end{aligned} \end{aligned}$$

With the estimates of Theorem 4.5 together with Taylor formula, since ${\mathrm P }_1$, ${\mathrm P }_2$ (resp. ${\mathrm P }_3$) are of order 2 in $y_i$, $z_j{\widetilde{z}} _j$ (resp. of order 4 in $z_j$, ${\widetilde{z}} _j$). Likewise, with the corollary 4.1, $\varvec{\psi }$ appears only in ${\mathrm P }_4$ which is exponentially small. As a consequence, we obtain for ${\varepsilon }\in [{\varepsilon }_0/2,{\varepsilon }_0 ]$ that

hence

for some positive exponents p and $p'$ (remark that $p=p'$ can be chosen). We need

and we choose ${\bar{r}}= r_0{\varepsilon }_0^{d}$ for a small enough constant $r_0>0$ and a large enough exponent d which ensure

Then,

is ensured for small enough ${\varepsilon }_0 <{\varepsilon }_*$ and the main threshold (5.5) is satisfied. Hence, we can find quasi-periodic horseshoe orbits for mass ratio $0<{\varepsilon }<{\varepsilon }_*$.