Abstract
In this paper, we use a quantitative structure–retention relationship (QSRR) method to predict the retention times of polychlorinated biphenyls (PCBs) in comprehensive two-dimensional gas chromatography (GC×GC). We analyse the GC×GC retention data taken from the literature by comparing predictive capability of different regression methods. The various models are generated using 70 out of 209 PCB congeners in the calibration stage, while their predictive performance is evaluated on the remaining 139 compounds. The two-dimensional chromatogram is initially estimated by separately modelling retention times of PCBs in the first and in the second column (1 t R and 2 t R, respectively). In particular, multilinear regression (MLR) combined with genetic algorithm (GA) variable selection is performed to extract two small subsets of predictors for 1 t R and 2 t R from a large set of theoretical molecular descriptors provided by the popular software Dragon, which after removal of highly correlated or almost constant variables consists of 237 structure-related quantities. Based on GA-MLR analysis, a four-dimensional and a five-dimensional relationship modelling 1 t R and 2 t R, respectively, are identified. Single-response partial least square (PLS-1) regression is alternatively applied to independently model 1 t R and 2 t R without the need for preliminary GA variable selection. Further, we explore the possibility of predicting the two-dimensional chromatogram of PCBs in a single calibration procedure by using a two-response PLS (PLS-2) model or a feed-forward artificial neural network (ANN) with two output neurons. In the first case, regression is carried out on the full set of 237 descriptors, while the variables previously selected by GA-MLR are initially considered as ANN inputs and subjected to a sensitivity analysis to remove the redundant ones. Results show PLS-1 regression exhibits a noticeably better descriptive and predictive performance than the other investigated approaches. The observed values of determination coefficients for 1 t R and 2 t R in calibration (0.9999 and 0.9993, respectively) and prediction (0.9987 and 0.9793, respectively) provided by PLS-1 demonstrate that GC×GC behaviour of PCBs is properly modelled. In particular, the predicted two-dimensional GC×GC chromatogram of 139 PCBs not involved in the calibration stage closely resembles the experimental one. Based on the above lines of evidence, the proposed approach ensures accurate simulation of the whole GC×GC chromatogram of PCBs using experimental determination of only 1/3 retention data of representative congeners.

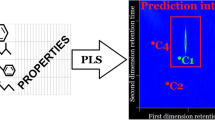
Agreement between experimental two-dimensional GCxGC chromatogram of 139 polychlorinated biphenyls and the one predicted by PLS-1 regression based on 237 molecular descriptors
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Polychlorinated biphenyls (PCBs) are harmful persistent pollutants ubiquitously present in the environment and are well known to undergo bio-accumulation throughout the food chain [1–5].
Routine monitoring of PCBs can be carried out by capillary gas chromatography (GC) normally coupled to electron capture or mass spectrometry detection [6, 7]. PCB separation can be efficiently improved by means of comprehensive two-dimensional gas chromatography (GC×GC) [8–10], to offer enhanced peak capacity, sensitivity, and selectivity [11].
Recently, several approaches have been proposed to predict retention in GC×GC [12–16] with the aim of simplifying the separation optimisation which is more difficult than that of conventional GC. Some of these models [12–14] were generated by using as input data solute retention indices or retention factors measured directly on the primary and secondary columns. These quantities were combined with fluid mechanical calculations to predict retention times in both GC×GC dimensions. Seeley and co-workers [15, 16] proposed a less sophisticated method applicable under the assumption that retention indices of solutes in the stationary phases are independent of column dimensions, carrier gas flow and temperature programme. This approach, which does not require preliminary knowledge of temperature dependence of retention factors or retention indices, rather than the conventional two-dimensional chromatogram generates a two-dimensional “retention diagram” showing the retention order and spacing in both dimensions similar to that found in the experimental GC×GC chromatogram. Retention data from standard single-column temperature-programmed separations were initially used as the model inputs [15], while later the “retention diagram” was entirely built by using descriptors of both solutes and interfaced stationary phases taken from the literature [16].
In this paper, we explore the possibility of predicting the retention times of PCBs in GC×GC using a quantitative structure–retention relationship (QSRR) method. In the last decades, QSRRs of a large variety of solutes in many different one-dimensional chromatographic systems have been established [17, 18]. The possibility of deducing retention on the basis of molecular structure of solutes, which is one of the objectives of QSRR methods, can be helpful in the optimisation stage of chromatographic separations as an alternative to less efficient non-systematic empirical methods. The first step of QSRR analysis is the identification of a set of molecular descriptors that will constitute the independent variables of a multivariate regression model providing as a response the retention time (or a retention-related parameter). According to the well-known linear solvation energy relationship (LSER) model [19], the solvatochromic properties of solutes can be successfully considered as retention predictors both in GC and liquid chromatography [17, 18]. In a GC×GC context, Seeley et al. [16], as anticipated above, generated a “retention diagram” using as input data a set of descriptors for the target solutes and stationary phases obtained by the LSER method. Arey et al. [20] showed that first- and second-dimension retention indices of diesel fuel hydrocarbons estimated by GC×GC can be modelled by means of solvatochromic descriptors. Poole and Poole [21] using the LSER method investigated the degree of orthogonality within 32 GC capillary columns aimed at finding the most suitable combination for GC×GC separation. It must be noted that although solvatochromic descriptors of nearly 4,000 compounds have been determined [22], these quantities are not available for most chemicals of analytical interest. QSRR methodology, on the other hand, can nowadays rely on various professional software packages able to provide several classes of theoretical molecular descriptors, permitting to quickly collect a large quantity of structure-related properties. In particular, various kinds of theoretical molecular descriptors have been already used to quantify the influence of structure on the retention of PCBs in single-column GC [23–29].
In this paper, we analyse the GC×GC retention data of PCBs published by Focant et al. [8]. The same data set was previously investigated by Ren et al. [30] who actually modelled by QSRR only the retention time of PCBs in the first column. As preliminary knowledge of the degree of orthogonality of the two interfaced GC systems is only partial, we test various regression methods able to both independently and simultaneously providing the retention times of PCBs in the first and in the second dimension (1 t R and 2 t R, respectively). In the first stage of this investigation, we combine multilinear regression (MLR) with genetic algorithm (GA) variable selection to extract two suitable sets of molecular descriptors from the large number provided by the popular software Dragon [31] with the aim of independently modelling 1 t R and 2 t R. The molecular descriptors incorporated into the two separate GA-MLR models giving 1 t R and 2 t R are simultaneously considered as the input variables of an artificial neural network (ANN) with two output neurons with the aim of producing through a single calibration procedure the peak coordinates in the GC×GC chromatogram and accounting for possible interaction and non-linearity effects within the data set. Partial least squares (PLS) regression, which does not require preliminary variable selection and can both independently and simultaneously provide 1 t R and 2 t R, is finally applied.
Method
Data set
Experimental conditions used to collect the PCB retention data analysed here can be found in the original paper [8]. In the present study, the 209 objects (the PCB congeners) of the dataset were partitioned into a calibration set (70 data samples), used to generate the QSRR retention model, and a test (or prediction) set (139 data samples), that served to finally evaluate its generalisation ability. The calibration set was designed by means of the Kennard–Stone [32] algorithm applied to the two-dimensional space defined by 1 t R and 2 t R, which allows generation of a subset of uniformly spaced PCBs over the GC×GC chromatogram (Fig. 1).
Molecular descriptors
Molecular geometries of various PCBs are generated assuming standard bond lengths and angles. The adopted conformation of each compound, defined by the magnitude of the torsion angle φ between the planes of two benzene rings, was that corresponding to the minimum energy according to B3LYP density functional calculations carried out by Dorofeeva et al. [33]. In particular, neglecting small deviations, φ was set to 38° and 60° for PCB congeners with none or one chlorine atom in the ortho-position, respectively, and 90° for all the remaining cases.
The software Dragon [31] was used to compute the molecular descriptors from PCB geometries. For those conformers exhibiting axial chirality (atropoisomery), the geometries of both enantiomers were generated and, to account for the fact that these are present in PCB commercial standard mixtures used in conventional (non-chiral) GC as racemates, the values of the molecular descriptors of enantiomers, when different, were averaged. The version of Dragon utilised in this work provides 1,664 descriptors classified as zero- (0D), one- (1D), two- (2D) and three-dimensional (3D) descriptors depending on the fact they are computed from the chemical formula, the substructure list representation, the molecular graph or the geometrical representation of the molecule, respectively [34]. In this investigation, a preliminary rough variable selection was carried out by removing among the large set provided by Dragon those descriptors with little variance, and, by retaining only one descriptor, randomly selected, among groups of highly correlated descriptors (r > 0.9). After this procedure, we identify 237 molecular descriptors belonging to various classes (collected in Table 1) that will be considered in further analysis.
Multilinear regression combined with genetic algorithm variable selection
Owing to simple statistical bases and easy interpretation of the resulting models, MLR is the most widely applied regression method in QSRR analyses [17, 18]. According to MLR modelling, the response variable y is expressed as a linear combination of descriptors X i :
where a i is the regression coefficient and a 0 is the intercept.
In this paper, the 237 molecular descriptors that remained after removal of highly correlated and almost constant quantities were subjected to GA variable selection aimed at finding a small descriptor subset with appropriate explanatory ability. GA [35, 36] is a stochastic optimisation method inspired by genetics and Darwinian theory based on the evolution of a starting random population of models that through mutation, cross-over, and selection after a number of generations finally provides an optimal or near optimal solution. Each population individual (chromosome) is a binary vector in which each position (gene) encodes the presence or absence of a descriptor in the model by 1 or 0, respectively. According to biological evolution rules, the chance for a given chromosome of being preserved in the next generation is evaluated by a fitness function that measures how well a solution fits the considered problem. In this investigation, we select those molecular descriptors independently influencing 1 t R and 2 t R. To this end, the fitness function associated to each chromosome was the % of leave-one-out cross-validated variance explained by the MLR model corresponding to that chromosome, which response was 1 t R or 2 t R. This (or the related determination coefficient Q 2loo-cv ) is the quantity maximised in the evolution process. GA-MLR analysis is performed here using the programme package V-PARVUS 2008 [37]. In each calculation, a starting random population of 100 chromosomes is subjected to 50 evolution cycles or evolution process is stopped before if no improvement of the fitness function is observed after five cycles. Probability of mutation is set to 1% and elitism, which gives the number of the best chromosomes of each generation that are passed unchanged to the next one, is set to 2%.
Artificial neural network regression
An ANN consists of interconnected single processing units called neurons [35, 38]. Among the different kinds of ANNs, feed-forward multi-layer networks are the most widely used in chemistry and to establish quantitative structure–property relationships, in particular. Neurons are generally organised in three layers: one input layer which collects the external input (the descriptors in regression applications), one output layer providing the network response (here two neurons giving 1 t R and 2 t R) and one hidden layer with an adjustable number of neurons fully connected to both input and output neurons. Information that flows only from input to output neurons is modulated by weights associated to each connection. The input neurons do no calculation but simply distribute the external variables to the hidden neurons where the weighted signals are summed, added to a bias value and the result is transformed by an activation function providing an output signal for each hidden neuron. These are in turn sent to the output neuron(s) that after analogue computation gives the network “answer”. In the network learning step, a number of input/output pairs (training set) are processed and weights and biases are iteratively optimised to produce the best agreement between target and computed responses. Training process is commonly carried out using the error back-propagation learning algorithm which can sometimes suffer from slow convergence. This limitation can be overcome by learning algorithms, as the quasi-Newton method [39], that incorporate second order information about the shape of error surface. To avoid over-fitting, the network was optimised by evaluating its capability of modelling a suitable number of data samples (validation set) not used in the training stage.
To this end, the Kennard–Stone algorithm [32] was applied to the 70 samples of the calibration set projected in the space of 1 t R and 2 t R and 50 PCBs to be used in ANN training were extracted, while the 20 unselected compounds were put in the validation set. The final model was tested on the 139 PCB congeners of the prediction set not involved in previous variable selection and ANN optimisation stages. In this work, ANN analysis was carried out using the JavaNNS neural network simulator [40].
Partial least squares regression
PLS regression [41, 42] is particularly useful to handle a large number of descriptors even in the presence of co-linearity and noise. It is based on the identification of a relatively small number of linear combinations of the original variables, considered as approximations of underlying factors (also known as latent variables) strongly correlated with the response(s). When several response variables must be modelled two approaches can be used: the so-called PLS-1 algorithm computes the responses one at a time while the PLS-2 algorithm provides all responses in a single calibration procedure. In PLS-1 the matrix of independent variables is decomposed to identify the factors more correlated with a given response, while in PLS-2 the matrices of dependent variables and responses (X and Y, respectively) are simultaneously decomposed and couples of Y and X factors are used to build the model in place of regression of Y onto X. The X factors are sequentially extracted according to the decreasing order of the covariance with the response, in the case of PLS-1, or with Y factors, in the case of PLS-2. This procedure is iteratively repeated until the next factor does not improve the model performance, usually evaluated by cross-validation.
Results and discussion
GA-MLR modelling
GA-MLR analysis was carried out to find two appropriate subsets of molecular descriptors among the large number provided by Dragon able to separately encode the effect of PCB structure on 1 t R and 2 t R. A preliminary GA-MLR exploration of the data suggested that a quite good modelling of 1 t R could be obtained including only four descriptors into the MLR model. Incorporation of a fifth descriptor, as expected, was seen to produce a non-negligible increase of the determination coefficient in calibration (R 2), but did not result in a comparable improvement of predictive performance as measured by Q 2loo-cv . After a large number of GA-MLR runs with different starting chromosome populations, the set of descriptors providing the highest Q 2loo-cv was finally selected (Table 2). As to 2 t R accurate modelling required five descriptors (given in Table 2), although model performance was slightly worse as compared with that of the four-dimensional relationship providing 1 t R, but did not increase sensitively after the addition of a sixth descriptor. For both relationships, values of the regression coefficients, their standard deviations, the standardised regression coefficients and statistical significance of each descriptor according to t test are given in Table 3. Table 4 displays the descriptive and predictive performance of the MLR models, quantified by usual statistical indexes, R 2, standard error in calibration (SEC), Q 2loo-cv , determination coefficient of external prediction (Q 2), standard error in leave-one-out cross-validation (SEPval) and external prediction (SEPtest). In the same table, we also report the average absolute relative error in calibration and prediction (aae(%)cal and aae(%)test, respectively) defined as follows:
where t′R is the computed or predicted retention time, t R is the corresponding experimental value and the sum is extended over the n samples of the calibration or prediction set.
ANN modelling
In a preliminary stage of ANN modelling, we consider all the nine molecular descriptors previously selected by GA-MLR as the network inputs. The network was optimised by evaluating through trial-and-error the effect of typical ANN features, namely the learning rule and duration, the number of hidden neurons, the form of the activation function and the kind of variable scaling, on the validation error. After a number of trials, in which initial weights were randomly generated between −0.1 and 0.1, an acceptably low validation error was obtained using a 9-8-2 network having the hyperbolic tangent as the activation function of the hidden neurons. This network was trained with quasi-Newton learning algorithm for 46 epochs and input variables were subjected to a range scaling between −1 and 1. Before applying this model to the PCBs of the external prediction set we attempted to reduce its complexity by removing possible redundant input variables. To this end, we followed a stepwise procedure using the method of weight zeroing proposed by Nord and Jacobbson [43] to evaluate the relative importance of ANN inputs. According to this approach, the influence of a given descriptor to define the network response can be related to the deterioration of model performance when the effect of that variable is removed by zeroing the corresponding weights. The importance of a given descriptor is quantified by (SECx-zeroed -SECfull)·σ x , where SECfull and SECx-zeroed are standard errors provided by the full network and the network in which weights associated to the corresponding input are zeroed, respectively, and σ x is the standard deviation of the variable of interest. In each step of the iterative variable elimination, after the less important variable has been removed the network is re-optimised with respect to the number of hidden neurons and the number of learning epochs. Stepwise variable elimination is terminated before an unacceptable worsening of validation error is observed. Using the above strategy, four molecular descriptors (RDF055m, Mor14m, EEig10x, and EEig15x) were removed. The reduced ANN model was finally calibrated with a 5-6-2 network learned for 102 epochs; its descriptive and predictive performance is displayed in Table 4. As compared with MLR, ANN comparably or slightly better models 1 t R and 2 t R. It must be noted that, while all calibration data were used to build the MLR models, update of network weights could benefit from more limited chemical information, as a number of calibration data (20 out to 70) served to optimise the ANN-based model. Although the ANN model computes the two retention times in a single calibration procedure and utilises a reduced descriptor set, its performance is substantially comparable to that of MLR, which is recommended according to a parsimony criterion. In summary, simulation of the two-dimension GC×GC chromatogram of PCBs appears as a linear problem, while resorting to higher computational flexibility offered by ANN seems unjustified.
PLS modelling
PLS regression does not require preliminary variable selection and can model the retention times in the two dimensions of a GC×GC chromatogram both in two separate one-response steps, in which retention time in one dimension is modelled (PLS-1), or in a single two-response step (PLS-2). In the circumstance of correlated responses PLS-2 regression, in which the target properties are simultaneously calibrated, is recommended. When the responses are independent, PLS-2 models can require many factors, whereas PLS-1 provides less complex and usually more precise models [42]. In the PLS application presented here, the two response variables are expected to be uncorrelated if the separation mechanisms in the two interfaced columns are truly independent [21]. In the circumstance that a clear understanding of this aspect is lacking, it cannot be known in advance whether PLS-1 works better than PLS-2 or not. Both PLS-1 and PLS-2 were performed on the autoscaled variables. The optimal number of latent factors was found by means of leave-one-out cross-validation procedure, by examining the influence of PLS model complexity on Q 2loo-cv . Maximum of Q 2loo-cv in PLS-1 modelling of 1 t R was observed for 15 latent factors, whereas 19 and 23 latent variables are required to maximise Q 2loo-cv in PLS-1 modelling of 2 t R and PLS-2 regression, respectively. However, in these last two cases, the increase of Q 2loo-cv passing from a 15-latent-variable model to the one with the optimal complexity was relatively small. Therefore, we finally choose 15 latent variables also in these cases. The performance of PLS-1 and PLS-2 models in calibration and prediction is illustrated in Table 4. These results reveal that PLS-1 regression provides a slightly better predictive capability than PLS-2 modelling, although the difference between the PLS-1 and PLS-2 models becomes smaller if the number of latent variables in the PLS-2 model is increased up to 23. If compared with GA-MLR counterparts, the PLS-1 models for 1 t R and 2 t R exhibit a noticeably better descriptive and predictive performance, which is not unexpected as PLS regression incorporates all the chemical information encoded by the 237 molecular descriptors, while in MLR models retention times are related to a small set of selected descriptors.
Comparison of various QSRR approaches
Figure 2 displays the sequential steps followed in the generation and validation of each model, while Table 4 summarises both descriptive and predictive performance of the various approaches. These results reveal that 1 t R is always better modelled than 2 t R regardless of the kind of regression method. It must be remarked that although a relatively small number of PCBs have been used in calibration (about 1/3 of all congeners), prediction of 1 t R is very good and comparable or better than that of retention times of PCBs in one-dimensional GC under less severe cross-validation conditions [24–29]. Generally, all the 209 congeners are used to generate the model and predictive performance is evaluated by leave-one-out cross-validation [24–27] or by testing the model on a number of data samples extracted from the calibration set, after these have been already used in variable selection and model building [28, 29]. In this work, the various models are tested on really unknown data samples, as the 139 PCBs of the prediction set have not been involved in any previous model generation stage. Ren et al. [30], who analysed the same data set investigated in the present work, even though they did not model 2 t R, used 155 PCBs to calibrate a four-dimensional MLR model for 1 t R successively tested on the remaining 37 PCBs giving resolved peaks. These authors obtained a model for 1 t R with a noticeably worse descriptive and predictive performance (R 2 = 0.976, Q 2 = 0.975) than those generated in the present work, for which R 2 and Q 2 values are greater than 0.998 and 0.995, respectively. Better predictive performance of our models is also witnessed by the lower average absolute error, ranging between 0.7% and 1.3% (Table 4), than that (about 3%) obtained by Ren and co-workers. On chromatographic level such improvement seems considerable: first of all, model generation requires collection of a relatively small number of retention data. Moreover, the low prediction error can prevent incorrect peak assignment of almost co-eluting PCBs.
Modelling of 2 t R provided by the various approaches is not as good as that of 1 t R, and the results seem to be more dependent on the regression method. In this connection, it must be noted that residuals are seen to be always quite homogenously distributed around zero, which suggests the absence of systematic errors, but the variability range of deviations was seen to be influenced by the kind of regression method, as witnessed by the aae(%) values reported in Table 4. In other terms, the kind of regression method apparently influences the model precision. As expected, we found that precision increases if a greater number of calibration data are employed, or decreases if size of calibration set is diminished, but we always obtained a quite uniform residual distribution and did not detect outlier points. It should be also noted that even a moderate change in the size of calibration data set can modify the pool of variables selected by GA-MLR and relative importance of original descriptors within PLS latent variables, but the alternative best models generated with a given regression method, if built using the same calibration set, were seen to exhibit substantially comparable performances. Based on the whole of statistical parameters collected in Table 4, PLS-1 is the statistical method providing both the best descriptive and predictive performance and, for this reason, will be discussed in more detail. Figures 3 and 4 display the agreement between experimental 1 t R and 2 t R values, respectively, and the corresponding values computed or predicted by PLS-1. Trends of calibration and prediction error of 1 t R and 2 t R are shown in Figs. 5 and 6, respectively. Calibration residuals for both 1 t R and 2 t R are within ±1%. It can be observed that prediction residuals for 1 t R are within ±1.5% with the exception of about dozen cases, but the maximum absolute error does not exceed 3.7%. Prediction errors for 2 t R are within ±7%, but absolute relative error of most of the PCBs (excepting less than twenty cases) is lower than 3%. Figure 7 displays a comparison between the computed GC×GC chromatogram of the 70 PCBs congeners of the calibration set and the experimental one. As a consequence of excellent performance of PLS-1 in calibration, computed coordinates of PCBs in the two-dimensional chromatogram are almost superimposed to the corresponding experimental ones. Figure 8 shows the agreement between the experimental chromatogram of the 139 PCBs belonging to the test set and the predicted one. Even if simulation of the two-dimensional chromatogram in prediction, as expected, is not as good as in calibration, the result is promising anyway. Differences between predicted and expected coordinates of PCBs in the two-dimensional chromatogram are mainly located along the second dimension, as a consequence of greater error on 2 t R. As the chromatogram consists of a large number of peaks and many PCBs almost co-elute, the observed prediction error does not allow unequivocal assignment of chromatographic peak to PCB structure, excepting those analytes giving isolated peaks, but the overall qualitative feature of the experimental GC×GC chromatogram is nicely reproduced by the PLS-1 model. It must be remarked that, according to QSRR approach, the proposed methods evaluate only the effect of solute structure on the peak coordinates of PCBs within the GC×GC chromatogram, but are incapable of predicting changes in the retention times due to changes of separation conditions (column and/or temperature programme variations) in one or both dimension. However, experimental effort required to optimise GC×GC separation by exploring dependence of chromatogram resolution from the separation conditions may be highly reduced, as the proposed method allows accurate simulation of the full two-dimensional chromatogram of PCBs using retention data of about 1/3 congeners.
Conclusions
In this paper, we evidence that the experimental GC×GC chromatogram of PCBs can be accurately predicted using a QSRR model calibrated with retention data of about 1/3 of the congeners collected under the same separation conditions. The effect of structure on retention time in both dimensions can be successfully encoded by theoretical molecular descriptors quickly available by means of various computational methods. The regression methods that have been compared in this investigation (MLR, PLS-1, PLS-2, and ANN) exhibit quite similar performances and retention in the second dimension is always slightly worse modelled as compared with that in the first dimension. Probably, the effect of molecular structure on the retention time in the second GC column is only partially established as a consequence of very rapid analysis and great compression of retention times. Based on predictive performance, PLS-1 seems to slightly prevail on the other regression methods. PLS-1 modelling, apart from providing lower prediction residuals than the other investigated regression methods, can work on the full matrix of theoretical descriptors without the need of preliminary variable selection. ANN coupled to a suitable variable selection method and PLS-2, although in this specific case exhibit a little worse performance than PLS-1, are promising tools able to provide the two-dimensional chromatogram in a single calibration procedure and may be advantageous in the circumstance that the interfaced columns of the GC×GC system are less dissimilar than those investigated in this work.
References
Gdaniec-Pietryka M, Wolska L, Namieśnik J (2007) Trends Anal Chem 26:1005–1012
Sun P, Basu I, Hites RA (2006) Environ Sci Technol 40:1178–1183
Riget F, Dietz R, Vorkamp K, Johansen P, Muir D (2004) Sci Total Environ 331:29–52
Thomas GO, Wilkinson M, Hodson S, Jones KC (2006) Environ Pollut 141:30–41
Donato F, Magoni M, Bergonzi R, Scarcella C, Indelicato A, Carasi S, Apostoli P (2006) Chemosphere 64:1562–1572
Cochran JW, Frame GM (1999) J Chromatogr A 843:323–368
Mydlová-Memersheimerová J, Tienpont B, David F, Krupčík J, Sandra P (2009) J Chromatogr A 1216:6043–6062
Focant JF, Sjödin A, Patterson DG Jr (2004) J Chromatogr A 1040:227–238
Korytár P, Leonards PEG, de Boer J, Brinkman UATH (2002) J Chromatogr A 958:203–218
Harju M, Danielsson C, Haglund P (2003) J Chromatogr A 1019:111–126
Dallüge J, Beens J, Brinkman UATH (2003) J Chromatogr A 1000:69–108
Beens J, Tijssen R, Blomberg J (1998) J Chromatogr A 822:233–251
Vendeuvre C, Bertoncini F, Thiébaut D, Martin M, Hennion MC (2005) J Sep Sci 28:1129–1136
Lu X, Kong H, Li H, Ma C, Tian J, Xu G (2005) J Chromatogr A 1086:175–184
Seeley JV, Seeley SK (2007) J Chromatogr A 1172:72–83
Seeley JV, Libby EM, Hill Edwards KA, Seeley SK (2009) J Chromatogr A 1216:1650–1657
Héberger K (2007) J Chromatogr A 1158:273–305
Kaliszan R (2007) Chem Rev 107:3212–3246
Vitha M, Carr PW (2006) J Chromatogr A 1126:143–194
Arey JS, Nelson RK, Xu L, Reddy CM (2005) Anal Chem 77:7172–7182
Poole SK, Poole CF (2008) J Sep Sci 31:1118–1123
Abraham MH (2000) Database of general solvation model molecular descriptors. University College, London
Krawczuk A, Voelkel A, Lulek J, Urbaniak R, Szyrwińska K (2003) J Chromatogr A 1018:63–71
Gramatica P, Navas N, Todeschini R (1998) Chemom Intell Lab Syst 40:53–63
Liu SS, Liu Y, Yin DQ, Wang XD, Wang LS (2006) J Sep Sci 29:296–301
Ghavami R, Sadeghi F (2009) Chromatographia 70:851–868
Jäntschi L, Bolboacă SD, Diudea MV (2007) Int J Mol Sci 8:1125–1157
Hasan MN, Jurs PC (1988) Anal Chem 60:978–982
Robbat A Jr, Xyrafas G, Marshall D (1988) Anal Chem 60:982–985
Ren Y, Liu H, Yao X, Liu M (2007) Anal Bioanal Chem 388:165–172
Talete SRL (2006) DRAGON version 5.4 for windows (Software for molecular descriptor calculations) http://www.talete.mi.it/
Kennard RW, Stone LA (1969) Technometrics 11:137–148
Dorofeeva OV, Novikov VP, Moiseeva NF, Yungman VS (2005) J Struct Chem 46:237–242
Todeschini R, Consonni V (2000) Handbook of molecular descriptors. Wiley-VCH, Weinheim
Leardi R (ed) (2003) Nature-Inspired methods in chemometrics: genetic algorithms and artificial neural networks (data handling in science and technology, vol 23). Elsevier, Amsterdam
Wehrens R, Buydens LMC (1998) Trends Anal Chem 17:193–203
Forina M, Lanteri S, Armanino C, Casolino C, Casale M, Oliver P, V-PARVUS (2008) Dip chimica e tecnologie farmaceutiche ed alimentari, University of Genova http://www.parvus.unige.it
Zupan J, Gasteiger J (1999) Neural networks in chemistry and drug design. Wiley-VCH, Weinheim
Derks EPPA, Buydens LMC (1998) Chemom Intell Lab Syst 41:171–184
Copyright ©1996–2001 JavaNNS Group, Wilhelm-Schickard-Institute for Computer Science (WSI), University of Tübingen, Germany
Wold S, Sjöström M, Eriksson L (2001) Chemom Intell Lab Syst 58:109–130
Martens H, Naes T (1993) Multivariate calibration. Wiley, Chichester
Nord LI, Jacobsson SP (1998) Chemom Intell Lab Syst 44:153–160
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
D’Archivio, A.A., Incani, A. & Ruggieri, F. Retention modelling of polychlorinated biphenyls in comprehensive two-dimensional gas chromatography. Anal Bioanal Chem 399, 903–913 (2011). https://doi.org/10.1007/s00216-010-4326-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00216-010-4326-z