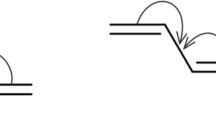1 Introduction

The bond length alternation (BLA) in linear polyenes is a well-known phenomenon, a rather basic problem in Quantum Chemistry, and it has been studied using a wide variety of theoretical methods [1,2,3,4,5,6,7]. The understanding of the electronic factors that govern its magnitude still deserves attention. The simplest description of these π-electron systems consists in double bonds connected by single bonds, according to the Lewis qualitative picture [8]. It is known that the contrast between short and long bonds decreases with the polyene size: while the CC bond is very short in ethylene, the assumed double bonds are significantly longer in larger polyenes [9].

The most natural and routinely used theoretical entrance to the problem starts from the self-consistent field (SCF) optimization of a Slater determinant. Linear polyenes cannot be considered as highly correlated systems, and they have a large gap at the Fermi level, especially the small polyenes studied hereafter. Starting from the SCF solution seems therefore a relevant strategy. However, the SCF approximation systematically overestimates the BLA [10]. Electron correlation has therefore an important effect on a property of the weakly correlated ground state. Indeed, complete active space self-consistent field (CASSCF) calculations involving all π electrons in all π valence molecular orbitals (MOs) predict a reduced value of the BLA [5]. Using a strongly localized bond MO formulation, reference [5] attributed the decrease of the BLA from SCF to CASSCF to a decrease of the effective energy of the charge transfer (CT) components. The present paper follows a similar strategy but proceeds to both analytical derivations and exhibits the role of σ bond electrons and analyses of the coefficients of the wave function at various levels of treatment. It will be shown that the decrease of BLA obtained when using multi-determinantal methods must be attributed to an increased electron delocalization between the electron pairs located on double bonds and a decrease of the effective energy of inter-bond charge transfer components of the wave function.

The BLA is indeed governed by the magnitude of the charge transfer coefficients between adjacent double bonds, but these coefficients are strongly affected by dynamic polarization, involving both π and σ bonds. The dynamic polarization is brought by single excitations on the inter-bond CT determinants. We will show how these excitations stabilize the effective energies of the CT determinants. The single determinant SCF method treats part of the inter-bond delocalization owing to the molecular orbital optimization, but it underestimates its magnitude as this correlation effect is missing. The dynamic polarization is indeed a correlation effect, and it takes into account the fluctuation of the electric field, a phenomenon which cannot be taken into account in SCF treatments, since mean-field methods only capture static polarization. In the SCF solution the delocalization is ruled by the Brillouin’s theorem, which kills the interaction between the reference and the singly excited determinants. As shown on different problems, the way to correct the delocalization of SCF MOs is complex, requiring to introduce 2hole-1particle or 1hole-2particle excitations [11]. Our strategy differs from the standard one which starts from the SCF solution and then introduces double excitations. We start from a Lewis-type reference function free from any inter-bond delocalization. To build this function, we determine strongly localized (on the double bonds) bonding and antibonding MOs from unitary transformations of the canonical CASSCF ones. The Lewis-type reference belongs to the π active space. We then treat delocalization and correlation on an equal footing, by using a method proposed by one of us and coworkers in the context of a semi-empirical Hamiltonian, namely the perturbative configuration interaction from localized orbitals (PCILO) method [12,13,14]. One may note that this method is here employed in the ab initio context, as already done for the evaluation of the cyclic-delocalization energy (or aromatic contribution to the energy of benzene [15] and in reference [5].

The aims of this article are (i) to show the origin of the error of the single determinant SCF procedure, (ii) to understand the mechanisms responsible for the improvement of the valence full-π CASSCF method, (iii) to highlight the role of dynamic polarization taking place in the inter-bond charge transfer components and finally (iv) to construe the distinct effects of σ and π electrons. Analytical derivations and numerical calculations, respectively, presented in Sects. 2 and 3 are here joined to demonstrate the role of dynamic polarization on the BLA structural impact. The smallest all-trans polyenes butadiene, hexatriene and octatetraene have been chosen to numerically illustrate this demonstration.

2 Analytical development

2.1 Motivating features

Let us present abruptly, in Table 1, the impact of electron correlation on the BLA of the studied polyenes. The BLA is here defined as the difference between the long and short bond lengths (see Sect. 3.1 for computational details). The results reported have been obtained at different levels of treatments, namely SCF, CASSCF of the π electrons in the π valence MOs (full-π valence CAS), and post-CAS treatment introducing the 1hole-1particle excitations on the top of this CAS.

Table 1 Optimal BLA (in Å) of the three studied polyenes at SCF, full-π valence CASSCF and CASSCF + single excitations
Full size table

One sees that the correlation reduces the BLA value by about 35%. This is the phenomenon we want to address in the present work.

2.2 Strongly Localized approach

For a sake of simplicity, we shall restrict the following presentation to the simplest system of four π orbitals housing four electrons, i.e., butadiene. Since the key delocalization process takes place in the π electronic system, the CAS(4,4)SCF calculation involving the four π electrons in the four valence π MOs provides an appropriate ground state wave function and an optimal mono-electronic π valence space. The space spanned by the 4 optimized active MOs and the CASSCF function are of course invariant under unitary transforms among the space of active MOs. Using the DoLo procedure, [16, 17] strongly localized bond MOs (SLMOs), noted 1 (between atoms A and B), 2 (between atoms C and D), and their antibonding counterparts 1\(^{*}\) and 2\(^{*}\) have been generated. They are linear combinations of the atom-supported orthogonal orbitals (OAOs) noted a, b, c, d, respectively, centered on atoms A, B, C and D. The SLMOs are related to the OAOs by the following relations

$$\begin{gathered} 1 = (a + b)/\sqrt 2 \hfill \\ 2 = (c + d)/\sqrt 2 \hfill \\ \end{gathered}$$
(1)

which are bonding, and their antibonding counterparts

$$\begin{gathered} 1^{*} \, = \, (a - b)/\sqrt 2 \hfill \\ 2^{*} \,= \, (c - d)/\sqrt 2 \hfill \\ \end{gathered}$$
(2)

Such orbitals are depicted in Fig. 1. This strategy provides a Lewis-type zero-order function as recently discussed in references [5, 15]. It is worth noting that these SLMOs are different from the single determinant SCF localized ones which exhibit large delocalization tails from one bond to the other. Orthogonalization tails of SLMOs on atoms belonging to the next bond are of weak amplitude.

Fig. 1
figure 1

π bonding and antibonding SLMOs, determined from the set of CAS(4,4)SCF MOs for butadiene

Full size image

The Lewis picture corresponds to a strongly localized closed-shell determinant that will be used as reference:

$$\Phi_{0} = \left| {\Pi_{i} i\overline{i.} \Pi_{I} I\overline{I} } \right|$$
(3)

where the i’s are the doubly occupied σ MOs and the I’s are π SLMOs. One should note that thanks to the demixing between bonding and antibonding active orbitals, the SLMOs are much more localized than the SCF MOs, which are obtained by rotation between the SCF occupied MOs and the SCF unoccupied MOs separately. A Fock operator can be defined in this set of MOs

$$F_{0} = h + \sum\limits_{i} {2J{}_{i} - K_{i} + \sum\limits_{I} {} } 2J_{I} - K_{I}^{{}}$$
(4)

where h is the mono-electronic operator, J and K are, respectively, the Coulomb and exchange operators. The energy of the reference is:

$$E_{0} = \left\langle {\Phi_{0} } \right|H\left| {\Phi_{0} } \right\rangle .$$
(5)

where H is the Born-Oppenheimer Hamiltonian.

2.3 First-order interacting space and first-order wave function

The CAS function can be expressed as a linear combination of the reference and excited determinants |K > , obtained from \(\Phi_{0}\) by different excitations.

$$\Psi_{0} = C_{0} \Phi_{0} + \sum\nolimits_{K \ne 0}^{{}} {\left| K \right\rangle C_{K} }$$
(6)

Due to the bi-electronic character of the Hamiltonian, only singly and doubly excited determinants have to be considered in the expression of the total energy, provided that the coefficients are exact. From the eigen-equation relative to \(\Phi_{0},\) the energy writes:

$$E = E_{0} + (\sum\nolimits_{K \ne 0}^{{}} {\left\langle 0 \right|} H\left| K \right\rangle C_{K} )/C_{0}$$
(7)

Among the various contributions to the energy, the π delocalization energy may be defined, according to Eq. (7) as

$$E{}_{{{\text{deloc}}}} = (\sum\nolimits_{I,J^{*}}^{{}} {\left\langle 0 \right|} H\left| {\Phi_{I \to J^{*}} } \right\rangle C_{I \to J^{*}} )/C_{0}$$
(8)

The on-bond single excitations have a negligible effect since the bonds are nonpolar. If the bond MO I is defined on the two OAOs a and b,

$$\left\langle {\Phi_{0} } \right|H\left| {\Phi_{1 \to 1^{*}} } \right\rangle = (F_{aa} - F_{bb} )/2 \approx 0.$$
(9)

The singly excited determinants that play an important role are the inter-bond charge transfer determinants, such as:

$$\Phi_{I \to J^{*}} = a_{J^{*}}^{ + } a_{I} \Phi_{0}$$
(10)

that interacts with the reference through

$$\left\langle {\Phi_{0} } \right|H\left| {\Phi_{I \to J^{*}} } \right\rangle = F_{IJ^{*}}^{{}}$$
(11)

In larger polyenes this hopping integral between SLMOs is very small except between adjacent MOs. The delocalization energy will be given by:

$$E_{{{\text{deloc}}}} = \sum\limits_{I,J^{*}} {} \left\langle {\Phi_{0} } \right|H\left| {\Phi_{I \to J^{*}} } \right\rangle C_{I \to J^{*}} \cong (F_{IJ^{*}} )C_{I \to J^{*}}$$
(12)

The matrix element is fixed, and correlation effects change the coefficients of the CT determinants.

At the first order of the Möller–Plesset perturbation theory, the coefficients of these CT determinants are:

$$C_{I \to J^{*}} = \left\langle {\Phi_{0} } \right|H\left| {\Phi_{I \to J^{*}} } \right\rangle /(\left\langle {\Phi_{0} } \right|H\left| {\Phi_{0} } \right\rangle - \left\langle {\Phi_{I \to J^{*}} } \right|H\left| {\Phi_{I \to J^{*}} } \right\rangle ) = F_{IJ^{*}} /(F_{II} - F_{J^{*}J^{*}} )$$
(13)

In full generality the Möller–Plesset second-order delocalization energy is given by

$$E_{deloc}^{(2)MP} = \sum\limits_{I,J^{*}} {F_{IJ^{*}}^{2} /(F_{II} - F_{J^{*}J^{*}} )}$$
(14)

Equation (14) suggests that the delocalization energy (in absolute value) increases when the BLA decreases, since this geometry variation, shortening the BC bond and lengthening the AB and CD bonds, increases the numerator and decreases the denominator. If one uses an Epstein Nesbet zero-order Hamiltonian, the denominator introduces an important hole-particle attraction integral JIJ\(^{*}\) (and a negligible inter-bond exchange integral KIJ\(^{*}\)),

$$E_{{{\text{deloc}}}}^{{\text{(2)EN}}} = \sum\limits_{I,J^{*}} {} (F_{IJ^{*}} )^{2} /(F_{II} - F_{J^{*}J^{*}} + J_{IJ^{*}} )$$
(15)

The most important double excitations are:

(i) intra-bond double excitations \(II \to I^{*}I^{*}\), contributing by

$$E_{{\text{Intra - bond}}} = \sum\limits_{I} {K_{II^{*}} } C_{II \to I^{*}I^{*}} \approx \sum\limits_{I} {\frac{{K_{II^{*}}^{2} }}{{2\left( {F_{II} - F_{I^{*}I^{*}} } \right)}}}$$
(16)

where \(K_{II^{*}}\) is an exchange integral, \(K_{II^{*}} = (J_{aa} - J_{ab} )/2\), if a and b are the two OAOs spanning the bond I. This excitation tends to lengthen the double bonds as the magnitude of the numerator increases, while that of the denominator decreases with the distance between the centers. In this sense these excitations may contribute to reduce the BLA and their impact has to be numerically checked.

(ii) inter-bond double excitations \(IJ \to I^{*}J^{*}\) may have important amplitudes if I and J are on neighbor bonds. They involve 3 types of determinants, namely.

  • \(I\overline{J} \to I^{*}\overline{J ^{*}}\), which contribute by \(2(II ^{*},JJ ^{*})C_{{I\overline{J} \to I ^{*}\overline{J ^{*}} }}\)

    where the bi-electronic integral is a dipole–dipole interaction \((II ^{*},JJ ^{*})\).

  • \(I\overline{J} \to J ^{*}\overline{I ^{*}}\) is a crossed excitation and involves a very weak interaction \((IJ ^{*},JI ^{*})\) with the reference,

  • \(IJ \to I ^{*}J ^{*}\) (same spin excitations) which interacts with the reference through \((II ^{*},JJ ^{*}) - (IJ ^{*},JI ^{*})\)

The sum of these contributions may be called inter-bond correlation. The total energy involving only the π energy corrections may be written as:

$$E = E_{0} + E_{{{\text{deloc}}{.}}} +E_{{\text{Intra - bond}}} + E_{{\text{Inter - bond}}}$$
(17)

It is relevant to identify the physical content of the SCF single determinant wave function

$$\Phi_{0}^{^{\prime}} = \left| {\prod_i i\overline{i}.\prod_I I^{\prime}\overline{I} ^{\prime}} \right|$$
(18)

where the localized MOs I’ have delocalization tails from one bond to the other, contrarily to the Lewis reference. Due to the single determinant constraint of the HF-SCF method, the energy minimization of this function only proceeds through orbitals delocalization in order to satisfy the Brillouin’s theorem [18, 19]. This delocalization cancels the interactions between the SCF determinant and its singly -excited determinants. If one starts from the strongly localized function \(\Phi_{0}\) to go to the SCF function \(\Phi_{0}^{^{\prime}}\), the energy stabilization can be assimilated to the perturbative contribution of the inter-bond CT determinants (Eqs. 14 and 15). As it will be shown in the following, doubly excited determinants will stabilize these charge transfer components and qualitatively change their contribution to the correlated wave function.

2.4 Dynamic polarization of CT components.

It is important to consider the interaction between a CT determinant \(\left| {\Phi_{I \to J^{*}} } \right\rangle\) and the determinant obtained from it by a single excitation \(k \to l^{*}\),\(a_{l^{*}}^{ + } a_{k} \left| {\Phi_{I \to J^{*}} } \right\rangle\). Hereafter, the orbitals k and l may be indifferently of π or of σ symmetry. \(\left| {\Phi_{I \to J^{*}} } \right\rangle\) defines a new Fock operator FIJ\(^{*}\), which differs from the Fock operator of the reference by the following relation

$$F^{IJ^{*}} = F_{0} - J_{I} + J_{J^{*}}$$

if one neglects the less important exchange operators. FIJ\(^{*}\) takes into account the modification of the electric field created by the \(I \to J^{*}\) excitation

$$\left\langle {a_{l^{*}}^{ + } a_{k} \Phi_{I \to J^{*}} } \right|H_{{}} \left| {\Phi_{I \to J^{*}} } \right\rangle = \left\langle {l^{*}} \right|F^{IJ^{*}} \left| k \right\rangle$$

A special attention may be paid to the excitations giving the largest interactions. If one works with localized bond MOs and their antibonding counterpart, the matrix element \(\left\langle {l^{*}} \right|F^{0} \left| k \right\rangle\) is zero if the k and l MOs are not of the same σ/π symmetry. The important corrections concern the bonding to antibonding excitations on the same bond, since the kk\(^{*}\) distribution defines a strong on-bond dipole. Then the matrix element

$$\left\langle {a_{k^{*}}^{ + } a_{k} \Phi_{I \to J^{*}} } \right|H_{{}} \left| {\Phi_{I \to J^{*}} } \right\rangle = \left\langle {k^{*}} \right| - J_{I} + J_{J^{*}} \left| k \right\rangle$$

represents the interaction between the transition dipole kk\(^{*}\) and the dipole J\(^{*}\)J\(^{*}\)-II. From the determinant \(a_{k^{*}}^{ + } a_{k} \Phi_{I \to J^{*}}\) one may return to \(\Phi_{I \to J^{*}}\), with the same interaction,

$$\left\langle {\Phi_{I \to J^{*}} } \right|H_{{}} \left| {a_{k^{*}}^{ + } a_{k} \Phi_{I \to J^{*}} } \right\rangle = \left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle$$

and one gets a third-order correction to the coefficient of this determinant

$$C_{I \to J*}^{(3)} \leftarrow \frac{{\left\langle {\Phi_{I \to J^{*}} } \right|H\left| {a_{k^{*}}^{ + } a_{k} \Phi_{I \to J^{*}} } \right\rangle \left\langle {a_{k^{*}}^{ + } a_{k} \Phi_{I \to J^{*}} } \right|H\left| {\Phi_{I \to J^{*}} } \right\rangle }}{{(F_{II} - F_{J^{*}J^{*}} )(F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} )}}C_{I \to J^{*}}^{(1)}$$

One may sum the contributions from the various MOs k and write

$$C_{I \to J^{*}}^{(3)} = \sum\limits_{k \ne I,J} {} \frac{{\left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle^{2} }}{{(F_{II} - F_{J^{*}J^{*}} + J_{IJ^{*}} )(F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} )}}C_{I \to J^{*}}^{(1)}$$

One may write the third-order corrected coefficient of the CT determinant as

$$C_{I \to J^{*}}^{(1 + 3)} = (1 + \sum\limits_{k \ne I,J} {} \frac{{\left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle^{2} }}{{(F_{II} - F_{J^{*}J^{*}} + J_{IJ^{*}} )(F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} )}})C_{I \to J^{*}}^{(1)}$$

or, replacing 1 + d by (1-d)−1.

$$C_{I \to J^{*}}^{(1 + 3)} = (1 - \sum\limits_{k \ne I,J} {} \frac{{\left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle^{2} }}{{(F_{II} - F_{J^{*}J^{*}} + J_{IJ^{*}} )(F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} )}})^{ - 1} C_{I \to J^{*}}^{(1)}$$

An elementary algebraic derivation leads to the modified expression of the CT coefficient

$$C_{I \to J^{*}}^{(1 + 3)} = \frac{{F_{IJ^{*}}^{{}} }}{{F_{II} - F_{J^{*}J^{*}} + J_{IJ^{*}} - \sum\limits_{k} {\frac{{\left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle^{2} }}{{(F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} )}}} }}$$

This is more than a mathematical approximation, and one may demonstrate that it is the result of a converging series of contributions consisting in back and forth movements from the CT determinant to the polarizing doubly excited determinants. One finally sees that the contribution of the dynamic polarization contribution results in the decrease of the effective energies of the CT determinants, and more precisely as an increase of the hole-particle attraction:

$$J_{IJ^{*}}^{{{\text{eff}}}} = J_{IJ^{*}} - \sum\limits_{k} {\frac{{\left\langle k \right| - J_{I} + J_{J^{*}} \left| {k^{*}} \right\rangle^{2} }}{{\left( {F_{II} + F_{kk} - F_{J^{*}J^{*}} - F_{k^{*}k^{*}} } \right)}}}$$

These analytical derivations can receive a graphical representation in terms of Feynman diagrams (see Fig. 2).

Fig. 2
figure 2

Diagrammatic representation of the effect of the single excitations on the effective energy of CT determinants

Full size image

3 Numerical results at SCF, CASSCF and post-CAS levels and discussion

3.1 Computational details

In a first subsection, we will focus on butadiene for which we will present a detailed analysis of the results. In a second subsection, our interpretation will be extended to hexatriene and octatetraene larger polyenes. Ideal planar geometries have been considered, the CH bond length being 1.085 Å, and all angles between close C–C–C and C–C–H atoms have been kept equal to 120°. In hexatriene and octatetraene all short (long) bond lengths are kept identical. Ground state energies and wave functions as functions of BLA have been calculated imposing the constraint that the sum of the short and long bond lengths takes the reasonable value of (2x 1.4 Å), i.e., l(C=C) + l(C–C) = 2.8 Å. The BLA is defined as the difference between long and short bond lengths which vary symmetrically around 1.4 Å. Using nonlinear regression (cubic spline) of the energy curves, the optimal BLA, i.e., the BLA at the energy minimum, has been determined at different levels of correlation. The corresponding wave functions have then been analyzed at these precise points to provide insights on the factors governing the BLA. For the largest molecules the various levels of correlation that have been studied are: (i) strongly localized Lewis determinant (built from unitary transformations of the active π CASSCF orbitals), (ii) single reference SCF \(\Phi_{0}^{^{\prime}}\), (iii) CASSCF (involving all π electrons in all π orbitals) and (iv) CAS + S in which all singly excited determinants on the top of the CAS have been added to the configuration interaction. In the simplest case of butadiene, we have also studied the Lewis (\(\Phi_{0}\)) reference plus double excitations (\(\Phi_{0}\) + Dπ) and plus single and double ones (\(\Phi_{0}\) + SDπ) remaining in the π active space, the CAS(4,4) + SD and the CAS(10,10) where all valence σ and π orbitals located on the carbon–carbon bonds and their electrons have been added to the active space, and finally the CAS(10,10) + S. Calculations have been performed using the MOLCAS 7.8 [20,21,22] and CASDI [23, 24] codes. Relativistic correlation consistent atomic natural orbitals (ANO-RCC [25]) basis sets were used for all atoms; for C a (14s9p4d) set is contracted to [3s2p1d] and for H a (8s4p) set is contracted to [2s1p].

3.2 Butadiene

3.2.1 Dramatic impact of correlation on BLA

Table S1 reports the ground state energies for different BLA computed using strongly localized MOs for the reference \(\Phi_{0}\)(Lewis),\(\Phi_{0}\) + Dπ,\(\Phi_{0}\) + SDπ, \(\Phi ^{\prime}_{0}\)(SCF), \(\Phi ^{\prime}_{0}\) + SD, the CAS(4,4)SCF, CAS(4,4) + S, CAS(4,4) + SD, CAS(10,10)SCF and CAS(10,10) + S levels. Table 2 reports the BLA (in Å) at the minimum of energy of these various levels of calculations. The Lewis function \(\Phi_{0}\) exhibits a very strong BLA (0.200 Å). The SCF function incorporates the delocalization through MO mixings (essentially due to interactions between the reference and the singly excited determinants) inducing a reduction of the BLA to 0.147 Å. If one adds only the double excitations to the Lewis reference \(\Phi_{0}\), labeled \(\Phi_{0}\) + Dπ in Table 2, the BLA is reduced (0.171 Å), which shows that the intra-bond π double excitations on the Lewis function are partly responsible for the BLA reduction. Moreover, adding the singles to this space (\(\Phi_{0}\) + SD) the BLA is submitted to a major reduction and falls to 0.133 Å.

Table 2 Butadiene: optimized BLA (in Å) obtained at different levels of calculations (see text). The ground state energy + 155 a.u. at the minimum is given in parenthesis
Full size table

The CAS(4,4)SCF energy is minimal (-155.084717 a.u.) for a significantly smaller BLA of 0.114 Å. When adding the 1 h-1p excitations to the CAS, i.e., at the CAS + S level, the minimal energy is E = −155.169375 a.u. and the BLA is further decreased to 0.099 Å. The BLA obtained by adding single and double excitations (CAS + SD) is in between (0.109 Å). However, this last value may suffer from size-consistency defect as the norm of the CAS components of the wave function is reduced to 0.86 instead of 0.95 for the CAS + S. Indeed, the Davidson correction applied to the CAS + SD results decreases the BLA to 0.103 Å.

Augmenting the active space to the σCC valence MOs, CAS(10,10), gives a further reduction of the BLA (0.097 Å), with a minimal energy of -155.162200 a.u. Adding the single excitations on the top of this wave function leads to an additional reduction of the BLA (0.084 Å). The role of the σ bonds will be analyzed in Sect. 3.3.

3.2.2 Physics in the π valence space

3.2.2.1 Leading contributions

Table 3 reports the coefficients in intermediate normalization, i.e., divided by C0, of the largest (or having a qualitative role in the researched factors) determinants in the various calculated wave functions, i.e., (i) the coefficient of the 4 inter-bond charge transfer singly excited determinants such  as \({\pi }_{1}\to {\pi }_{2}^{*}\), noted CCT, (ii) the coefficient of intra-bond doubly excited determinant such as \({\pi }_{1}\overline{{\pi }_{1}}\to {\pi }_{1}^{*}\overline{{\pi }_{1}^{*}}\) and noted CINTRA, and (iii) the coefficients of the inter-bond doubly excited determinant noted CINTER. Among these determinants, we could distinguish those resulting from excitations such as \({\pi }_{1}\overline{{\pi }_{2}}\to {\pi }_{1}^{*}\overline{{\pi }_{2}^{*}}\), i.e., keeping the same spin on the double bond from those involving different spins such that \({\pi }_{1}\overline{{\pi }_{2}}\to {\pi }_{2}^{*}\overline{{\pi }_{1}^{*}}\). Table 3 only reports the largest coefficients CINTER that have the same spins on each double bond. One may note that as for a sake of comparison with further calculations we have also reported the values (in bold) obtained for the optimal BLA (0.099 Å) obtained at the CAS(4,4) + S level. Detailed analyses reported hereafter have been performed for this value of the BLA.

Table 3 Butadiene: coefficients of the most important determinants (see text) for different BLA (in Å) at different levels of calculations. The last column refers to a CASSCF involving the 2 π bonds and the 3 CC σ bonds
Full size table

A first observation concerns the evolution of these coefficients as a function of the BLA. As expected from equations 12, 13 and 16, all coefficients increase when the BLA decreases.

It is worth analyzing the coefficients of the determinants in the CAS(4,4) calculations. The largest excited coefficients (Table 3) are those of intra-bond double excitations, followed by those of the CT components. One may notice that the sensitivity to the BLA is larger for the CT components than for the intra-bond double excitations. Going from BLA = 0.16 to 0.08 Å, the CT coefficients increase by 13%, while those of the double excitations only increase by 7%.

The coefficients of the inter-bond double excitations are reported in Tables 3 and S2. From the analysis of the interactions with the reference, reported in section II, one might expect that the largest coefficient would concern the determinant \(\Phi_{{1\overline{2} \to 1^{*}\overline{2} ^{*}}}\) obtained from the reference through the \({\pi }_{1}\overline{{\pi }_{2}}\to {\pi }_{1}^{*}\overline{{\pi }_{2}^{*}}\) excitation since it interacts with the reference through a strong dipole–dipole interaction (π1π1\(^{*}\),π2π2\(^{*}\)). Oppositely the determinants \(\Phi_{{1\overline{2} \to 2^{*}\overline{1} ^{*}}}\) obtained from the reference through the \({\pi }_{1}\overline{{\pi }_{2}}\to {\pi }_{2}^{*}\overline{{\pi }_{1}^{*}}\) excitations only interact with the reference through the very small (π1π2\(^{*}\),π2π1\(^{*}\)) integral, interaction between two weak product (or overlap) distributions. Surprisingly the largest coefficient concerns the \({\pi }_{1}\overline{{\pi }_{2}}\to {\pi }_{2}^{*}\overline{{\pi }_{1}^{*}}\) excitations. The reason is that these determinants may also be obtained from the reference through the products of two CT single excitations π1π2\(^{*}\) of α spin and π2π1\(^{*}\) of β spin. The second-order contribution to the coefficient of this determinant, involving the sequence \(\Phi_{0} \to \Phi_{1 \to 2^{*}} (or{\kern 1pt} \,\Phi_{{\overline{2} \to \overline{1^{*}} }} ) \to \Phi_{{1\overline{2} \to 2^{*}\overline{1^{*}} }}\), is larger than the first-order one. The second-order coefficient of \(\Phi_{{1\overline{2} \to 2^{*}\overline{1^{*}} }}\) can be evaluated as \(C_{{{\text{Inter}}}} = - 2C_{CT} F_{12^{*}} /2\Delta E(\pi_{1} \to \pi_{1}^{*} )^{(3)} = - C_{CT} F_{12^{*}} /\Delta E(\pi_{1} \to \pi_{1}^{*} )^{(3)}\). since the doubly excited determinant consists in the product of two intra-bond triplets, as recalled by the superscript (3) in the above equation. Comparatively one should remember that \(C_{CT} \approx - F_{12^{*}} /\Delta E(\pi_{1} \to \pi_{2}^{*} )\) so that the coefficient of the doubly excited determinant may be estimated to be \(C_{CT}^{2} \Delta E(\pi_{1} \to \pi_{2}^{*} )/\Delta E(\pi_{1} \to \pi_{1}^{*} )^{(3)}\). Now one should remember that the excitation energy to the π intra-bond to π\(^{*}\) triplet state is about 4 eV, while the inter-bond CT excitation is close to 9 eV, which results in a significant enhancement of the coefficient of \(\Phi_{{1\overline{2} \to 2^{*}\overline{1^{*}} }}\). And consistently the variation of the amplitude of these excitations when decreasing the BLA is approximately the square of the variation of CT coefficients (31% for the variation of the CINTER/C0 when going from 0.16 to 0.08 Å BLA and 27% for the variation of the square of the CT coefficients for the CAS(4,4) + S).

3.2.2.2 Interpretation: role of dynamic polarization on inter-bond CT components in the π valence space

Our purpose is to understand which are the doubly excited determinants responsible for the increase of the coefficients of the inter-bond CT determinants (πi→πj\(^{*}\) CT). The coefficients of the intra-bond doubly excited determinants are indeed large, but their interactions with the π→π\(^{*}\) CT imply weak inter-bond overlap distributions, for instance

$$\left\langle {\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|} \right|H\left| {\left| {{\text{core}}.1^{*}\overline{1^{*}} 2\overline{2} } \right|} \right\rangle = (2^{*}1^{*},11^{*}) \approx 0$$
(19)

The largest interactions with the CT determinants involve the doubly excited determinants which are obtained by an intra-bond single excitation on the top of the CT determinant, such as \(\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2^{*}} } \right|\) obtained by a \(\overline{\pi}_2\)→\(\overline{\pi}_2\)\(^{*}\) excitation on \(\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|\). This determinant is doubly excited with respect to \(\Phi_{0}\) and interacts with it, but the interaction

$$\left\langle {\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2^{*}} } \right|} \right|H\left| {\Phi_{0} } \right\rangle = (12^{*},22^{*})$$
(20)

implies the negligible 12\(^{*}\) distribution. On the contrary the interaction between the doubly excited determinant and the CT determinant is large, since it consists in the interaction between a transition dipole and a dipole

$$\left\langle {\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|} \right|H\left| {\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2^{*}} } \right|} \right\rangle = \left\langle 2 \right|J_{2^{*}} - J_{1} \left| {2^{*}} \right\rangle$$
(21)

The operator J2\(^{*}\)—J1 represents the deviation of the electric field created by the CT distribution (AB)+ (CD)− from the mean field. In the integral \(\left\langle 2 \right|J_{2^{*}} - J_{1} \left| {2^{*}} \right\rangle\) the first operator does not contribute, due to local symmetry reasons, since the distribution 22\(^{*}\) is antisymmetric with respect to the center of this bond, while J2\(^{*}\) is symmetric. One may develop the other integral in terms of atomic bi-electronic integrals and one obtains

$$\left\langle 2 \right|J_{1} \left| {2^{*}} \right\rangle = (J_{bc} - J_{ad} )/4$$
(22)

which is a positive and large quantity. The physical role of this excited determinant is to polarize the π2 bond between atoms C and D in the direction of the hole created on bond AB by the charge transfer excitation from AB to CD. This interaction increases the charge on atom C and decreases that on D.

Of course the π bond 1 between atoms A and B is also subject to a polarization effect in the CT state, and the process passes through the interaction between the CT determinant and a π1→π1\(^{*}\)excitation on \(\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|\), leading to the determinant \(\left| {{\text{core}}.2^{*}\overline{1^{*}} 2\overline{2} } \right|\). The interaction is

$$\left\langle {\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|} \right|H\left| {\left| {{\text{core}}.2^{*}\overline{1^{*}} 2\overline{2} } \right|} \right\rangle = \left\langle 1 \right|J_{2^{*}} - J_{1} \left| {1^{*}} \right\rangle$$
(23)

the same operator J2\(^{*}\)—J1 is now acting on the 11\(^{*}\) dipolar distribution. The contribution passes through the J2\(^{*}\) operator, and

$$\left\langle 1 \right|J_{2^{*}} \left| {1^{*}} \right\rangle = - (J_{{{\text{bc}}}} - J_{{{\text{ad}}}} )/4$$
(24)

the same quantity as for the polarization of the CD bond. Now the singly occupied π orbital of the AB bond is polarized toward the atom A by the field created by the negatively charged CD bond. One may write the mixing between the 1→2\(^{*}\) CT determinant \(\left| {{\text{core}}.2^{*}\overline{1} 2\overline{2} } \right|\) and the doubly excited determinant \(\left| {{\text{core}}.2^{*}\overline{1^{*}} 2\overline{2} } \right|\) as a relaxation of the MO 1 in the CT determinant, leading to \(\left| {{\text{core}}.2^{*}\overline{1}^{\prime\prime}2\overline{2} } \right|\), with

$$1^{\prime\prime} = 1 - \frac{{\left\langle 1 \right|J_{2^{*}} \left| {1^{*}} \right\rangle }}{{\Delta E{}_{{1\overline{1} \to 2^{*}\overline{1 ^{*}}}}^{{}} }}1^{*}$$
(25)

the denominator being an excitation energy from the reference to the doubly excited determinant. The numerator is negative, the mixing coefficient between 1 and 1\(^{*}\) is positive, and thanks to our definition of 1\(^{*}\) the coefficient of I” is increased on A and decreased on B. In the 1→2\(^{*}\) CT component the electron remaining on bond 1 is polarized in direction of atom A, far from the negatively charged CD bond. This is of course a dynamic process, impossible to be kept in a static treatment. These mechanisms fall as special cases in our general development about dynamic polarization of CT components, they dress the energy of the 1→2\(^{*}\) CT determinant by the excitations k→k\(^{*}\) = \(\overline{1} \to \overline{1^{*}}\) and by k→k\(^{*}\) = 2→2\(^{*}\).

3.3 Polarization of σ bond electrons

Dynamic polarization of CT components also concerns the σ bonds, their electrons also feel the fluctuation of the electric field created by the delocalization of the π electrons. Indeed, one can see in Table 3 that the CAS + S increases the coefficient of the inter-bond CT determinants by 14%. As a consequence, the off-diagonal density matrix elements between orbitals b and c are increased, resulting in an enhancement of the π bond index of the assumed single bond and therefore in a reduction of the BLA. In contrary the coefficients of the intra-bond doubly excited determinants decrease. This increase of the CT coefficients decreases when the BLA is reduced.

In a second approach one enlarges the active space of CASSCF treatment to the three σ CC bonding MOs and their valence antibonding counterparts. This iterative procedure starts from the localized orbitals, and the resulting additional active MOs are strongly localized on bond AB for σ1 and σ1\(^{*}\), on bond CD for σ2 and σ2\(^{*}\), and on bond BC for σc and σc\(^{*}\). The optimal BLA for the CAS(10,10)SCF in Table 2, is 0.097 Å, i.e., very close to that of the CAS(4,4) + S. This enlarged CASSCF treatment only runs on processes involving valence σ CC MOs, while the CAS(4,4) + S and CAS(4,4) + SD consider all inactive MOs, including the σ CH bond MOs which run on semi-active double excitations, and in CAS(4,4) + SD on inactive double excitations which are not considered in the CAS(4,4) + S treatment.

In order to analyze the effect of the different σ orbitals, calculations with either frozen σCH (+ core) or σCC MOs have been performed. According to the results presented in Table 4, the impact of σCH (+ core) MOs is very limited. Table S2 that shows the variation of the most important coefficients for BLA = 0.099 confirms this result.

Table 4 Butadiene: optimal BLA value in Å for different sets of kept MOs (all the others were frozen or deleted) and different level of excitations, using CAS(4/4)SCF MO. In all cases, the active space contains the 4 π orbitals. Numbers below the BLA are the difference to the BLA obtained at the CAS(4,4)SCF level
Full size table

As the σCC are responsible for the main effects of the dynamic polarization acting on the π electrons, a further analysis will consist in introducing these MOs in the active space, which leads to a CAS(10,10)SCF. Among the various excitations, we will distinguish the single and double excitations by proceeding through different calculations. Starting from the CAS(10,10)SCF MOs, strongly localized π and σ MOs will be generated through unitary transforms. Then CAS(4,4) + 1h-1p and CAS(4,4) + 2h-2p calculations will be performed. Comparisons between the coefficients of the most important determinants can be performed from the results appearing in Table 5. The main conclusions are the following:

  • The largest coefficients out of the minimal CAS are the intra-bond closed-shell excitations, (σi→σi\(^{*}\))2 (lines 5 and 6), and the double excitations coupling transition dipoles in both the σ and π systems in the same double bond (σi→σi\(^{*}\)).(πi→πi\(^{*}\)) (line 7, 9 and 10). They all tend to stretch the double bonds.

  • Since our σ bond MOs are now strongly localized, the inter-bond σ CT determinants have important coefficients, (0.036, line 8).

  • The doubly excited determinants which are obtained by an intra-bond single (σi→σi\(^{*}\)) excitation on the top of the π CT determinants, responsible for the dynamic polarization of these π CT determinants (lines 13 and 15) have important coefficients; the largest one, 0.015, concerns the single excitation on the central σ bond, σc→σc\(^{*}\), acting on π CT determinant, and obtained from the reference by the (σc→σc\(^{*}\)).(πi→πj\(^{*}\)) excitations. This is an expected result since the central CC bond is in the very middle of the (AB)+ (CD)− dipole.

  • Interestingly, one may notice the occurrence of determinants (line 19) which introduce the response of the π electrons to the fluctuation of the σ population, introduced by the σ CT components between adjacent bonds. The corresponding determinants are obtained from the reference by (σi→σj\(^{*}\)).(πk→πk\(^{*}\)) excitations.

Table 5 Butadiene (BLA 0.099 Å): largest coefficients of the singly and doubly excited determinants from the reference Φ0 and within the CAS(10,10)SCF. This CAS involves π and σCC valence active MOs. π 1 and σ1 are relative to the AB bond, π2 and σ2 are relative to the CD bond, σc is the BC central bond. Columns 2 and 3 concern truncated CIs, limited to the CAS(4,4) and 1hole-1particle or 2hole-2particle excitations within the active MOs of the CAS(10,10)SCF
Full size table

One should remember that CAS(4,4)+S and CAS(4,4)+SD involve more excitations than the CAS extended to the CC bonds, and they introduce excitations to non-valence MOs and include the dynamic polarization of the CH bonds, which might be of the same order of magnitude as that of the σ CC bonds. In order to estimate the relative contributions of the CH versus CC bonds to the dynamic polarization, we have frozen the CH bonding and antibonding MOs as well as the core orbitals in the post-CAS treatments. As one can see in Table S2, the ratio CCT/C0 increases from 0.152 to 0.166 at the CAS(4,4)+S when the “CH+Core” are frozen, while it raises to 0.174 when all the occupied MOs are allowed to contribute to the polarization. The most relevant information concerns the value of the BLA calculated at different levels and reported in Table 4. One sees that starting from the CASSCF (4,4) which gives a value of 0.114 for the BLA, adding the singles of the CH only lets this value untouched (0.113) while adding only the CC reduces this value to 0.103. Treating simultaneously all valence MOS does not change this value.

One may wonder whether the correlation implying non-valence MOs may affect the BLA. Actually in the 1→2\(^{*}\) CT determinant, the CD bond 2 is negatively charged and a relaxation of its MOs toward diffuse MOs might also contribute to the stabilization of this ionic component. We have performed a CAS+S calculation restricting the singles to those involving non-valence MOs (Table 4). The impact on the BLA is negligible, so that we may conclude that most of the dynamic polarization takes place in the valence space.

3.4 Hexatriene and Octatetraene

The same methodology has been used on the next linear polyenes, hexatriene and octatetraene in their all-trans conformation. Tables S3 and S4 report the ground state energies for different BLA computed using strongly localized MOs SCF, CAS(Full π)SCF and CAS(Full π)) + S levels of calculations. The optimal BLA and most important coefficients obtained at different levels of calculations for hexatriene appear in Tables 6 and 7, those for octatetraene in Tables 8 and 9. For hexatriene the calculated optimal BLA values are 0.140 Å at the SCF level, 0.108 Å at the CAS(6,6)SCF level and reach the weakest BLA value, (BLA = 0.093 Å) when one adds the 1 h-1p excitations on the CAS(6,6). For octatetraene the corresponding values are 0.137 Å at the SCF level, 0.104 Å at the CAS(8,8)SCF level, and 0.089 Å when on adds the 1h-1p excitations. The BLA decreases when the polyene length increases at all levels of treatments. While a variation of ~ 0.01 Å is obtained at the various levels of calculations presented in Table 1 between butadiene and octatetraene, the relative variation (difference of BLA/ mean values of BLA) is stronger at the CAS(full π) + S level (0.018 at SCF, 0.021 at CAS(Full π) and 0.027 at CAS(full π) + S).

Table 6 Hexatriene: optimal BLA value in Å for different MO frosts and different levels of calculations, using CAS(6/6)SCF MOs. Numbers below the BLA are the difference to the BLA obtained at the CAS(6,6)SCF level
Full size table
Table 7 Hexatriene: ground state coefficients of the most important determinants for CAS(6,6)SCF and CAS(6,6) + S calculations for the optimal BLA (= 0.092 Å) obtained at the CAS(6,6) + S level. σc is the σ bond between the C and D atoms
Full size table
Table 8 Octatetraene: optimal BLA value in Å obtained at different levels of calculations, using CAS(8/8)SCF MOs
Full size table
Table 9 Octatetraene: ground state coefficients of the most important determinants for CAS(8,8)SCF and CAS(8,8) + S calculations for the geometry of the minimum energy of the octatetraene model at the CAS(8,8) + S level (BLA = 0.089)
Full size table

For the same bond alternation and the same level of treatment the coefficients of the CT excitations between adjacent double bonds, reported in Tables 7 and 9 are almost constant, and very close or identical to those obtained for butadiene, with the same increase by the addition of the 1hole-1particle excitations. The coefficients of the central to external bond excitations and those of the external to central bonds are almost identical, and the side effects arē very weak. The long-range charge transfers, 1→3\(^{*}\) in both hexatriene and octatetraene, and 1→4\(^{*}\) in octatetraene are more strongly affected by addition of the dynamic polarization. Going from CAS to CAS + S increases the coefficients of the CT between adjacent bonds by 20%, between second-neighbor bonds by 30% and those relative to 3rd-neighbor bonds by 47%. Two factors may explain these trends. The first one may be the strength of the dipole associated to the CT, for instance 1→4\(^{*}\) CT component implies the strong dipolar operator J4*—J1. Another factor contributes to this increase, namely the fact that the long-range CT are not essentially obtained by a direct jump from one bond to a remote bond, but by propagation of the hole or the particle, in processes such (1→2*)→(1→3*)→(1→4*) (particle propagation) or (3→4\(^{*}\))→(2→4\(^{*}\))→(1→4\(^{*}\)) (hole propagation). At each of these steps a dynamic polarization takes place and in the third-order contribution to the 1→4\(^{*}\) coefficient each denominator is lowered by the dynamic polarization, so that the amplitude of the effect is more and more pronounced.

4 Conclusion

This work illustrates limits of mean-field calculations and identifies their drawbacks on the paradigmatic problem of BLA of linear polyenes. In the single determinant SCF treatment, a single set of doubly occupied MOs is optimized. A VB-type reading of this wave function is possible but (i) the combinations of the VB components are fixed by the MO delocalization and (ii) important correlation effects are missing, for instance the preference for neutrality or for the intra-atomic Hund’s rule satisfaction [26]. In a valence CASSCF function, the function is spanned on all possible orthogonal valence bond components, introducing much flexibility. Nevertheless, we must not forget two limitations of this practice (beyond the neglect of the short-range electron–electron avoidance, i.e., of the Coulomb cusp):

  • The CASSCF uses a unique set of valence MOs to describe the various components of the CAS function, while each of these components would require MOs appropriate to its associated electric field. This remark has led to the so-called breathing orbital valence bond (BOVB) method [27], which optimizes specifically the valence orbitals of each VB component. In their ground state the linear polyenes are not highly correlated and the single determinant SCF function should be a good entrance in the wave function building, a CASSCF description does not seem to be required. As shown in the present work, the full-π valence CASSCF treatment incorporates part of the component-specific relaxation of the valence MOs, the 1hole-1particle excitations on the top of the leading configurations which remain in the CAS introduce the largest part of dynamic polarization effects.

  • As the active space is limited to a subset of electrons and MOs, the numerous inactive electrons remain treated in a mean-field approximation. Their dynamic response to the fluctuation of the field created by the active electrons should be considered, and this can be done at a reasonable computational cost by performing a CAS + 1hole-1particle CI. Enlarging the CAS to its maximum tractable size is not the best solution, since in principle dynamic polarization concerns all the inactive electrons. Those of all σ CC and CH bonds react to the fluctuation of the electric field of the π electrons. It is certainly preferable to start from a moderate-size active space and to add the full response of the inactive electrons at a rather low-cost treatment than to enlarge the CAS.

It is interesting to note the relation of this typical organic chemistry problem with an apparently totally different coordination chemistry one. In transition-metal binuclear magnetic complexes where two unpaired electrons occupy two atom-centered 3d type orbitals, it seems reasonable to treat the singlet–triplet gap starting from a CASSCF of 2 electrons in 2 orbitals and then to add the configurations which, according to a perturbative expansion, may contribute to the energy gap. The classes of excitations involving either 2h-1p or 1h-2p happen to play an unexpected important role [28]. It has been shown that they contribute to an increase of the delocalization between the metals and the ligands by revising the spatial extent of the magnetic orbitals [11]. The effect passes through the dynamic polarization of the LMCT determinants, which is already true in mono-radicals, such as CuCl2 [29], and it is observed as well in organic radicals such as phenyl or diradicals as xylylenes [30].

The mean-field approximation underlying MOs descriptions faces severe limitations and must frequently be overcome by accessing correlated treatments. Understanding multi-configurational wave functions sometimes requires tedious analyzes but produces an intelligibility of the physical factors governing a property. In our opinion, it is much easier to understand the correlation effects using localized MOs or atom-supported orbitals, as is done in valence bond treatments, than using delocalized symmetry-adapted MOs [26]. Understanding qualitatively the physics taking place in the valence space, inside a limited CAS and beyond, is not only intellectually satisfying, but it also opens the route to the conception of computational tools which remain close to the minimum level of treatment of the key physical effects. Quantum chemistry as a science is not limited to furnishing numbers, it must in principle provide explanations, identify physical effects, predict trends, possibly laws [31] and produce methods. It is in this spirit that Fernand Spiegelman has practiced this discipline throughout his career. The recognition of the essentially local character of the electronic interactions which we exploited here is certainly at the basis of his fruitful developments of the DFTB method [32, 33].