An adaptive finite element DtN method for the elastic wave scattering problem

Abstract

Consider the scattering of an incident wave by a rigid obstacle, which is immersed in a homogeneous and isotropic elastic medium in two dimensions. Based on a Dirichlet-to-Neumann (DtN) operator, an exact transparent boundary condition is introduced and the scattering problem is formulated as a boundary value problem of the elastic wave equation in a bounded domain. By developing a new duality argument, an a posteriori error estimate is derived for the discrete problem by using the finite element method with the truncated DtN operator. The a posteriori error estimate consists of the finite element approximation error and the truncation error of the DtN operator, where the latter decays exponentially with respect to the truncation parameter. An adaptive finite element algorithm is proposed to solve the elastic obstacle scattering problem, where the truncation parameter is determined through the truncation error and the mesh elements for local refinements are chosen through the finite element discretization error. Numerical experiments are presented to demonstrate the effectiveness of the proposed method.

1 Introduction

A basic problem in classical scattering theory is the scattering of time-harmonic waves by a bounded and impenetrable medium, which is known as the obstacle scattering problem. It has played a crucial role in diverse scientific areas such as radar and sonar, geophysical exploration, medical imaging, and nondestructive testing. Motivated by these significant applications, the obstacle scattering problem has been widely studied for acoustic and electromagnetic waves. Consequently, a great deal of results are available concerning its solution [18, 41, 42]. Recently, the scattering problems for elastic waves have received ever-increasing attention due to the important applications in seismology and geophysics [3, 38, 39]. For instance, they are fundamental to detect the fractures in sedimentary rocks for the production of underground gas and liquids. Compared with acoustic and electromagnetic waves, elastic waves are less studied due to the coexistence of compressional waves and shear waves that have different wavenumbers [16, 36].

The obstacle scattering problem is usually formulated as an exterior boundary value problem imposed in an open domain. The unbounded physical domain needs to be truncated into a bounded computational domain for the convenience of mathematical analysis or numerical computation. Therefore, an appropriate boundary condition is required on the boundary of the truncated domain to avoid artificial wave reflection. Such a boundary condition is called the transparent boundary condition (TBC) or non-reflecting boundary condition. It is one of the important and active subjects in the research area of wave propagation [6, 19,20,21,22,23,24]. Since Berenger proposed a perfectly matched layer (PML) technique to solve the time-dependent Maxwell equations [7], the research on the PML has undergone a tremendous development due to its effectiveness and simplicity. Various constructions of PML have been proposed and studied for a wide range of scattering problems on acoustic and electromagnetic wave propagation [5, 10, 15, 27, 30, 44]. The basic idea of the PML technique is to surround the domain of interest by a layer of finite thickness fictitious medium that attenuates the waves coming from inside of the computational domain. When the waves reach the outer boundary of the PML region, their values are so small that the homogeneous Dirichlet boundary conditions can be imposed.

A posteriori error estimates are computable quantities which measure the solution errors of discrete problems. They are essential in designing algorithms for mesh modification which aim to equidistribute the computational effort and optimize the computation. The a posteriori error estimates based adaptive finite element methods have the ability of error control and asymptotically optimal approximation property [2]. They have become a class of important numerical tools for solving differential equations, especially for those where the solutions have singularity or multiscale phenomena. Combined with the PML technique, an efficient adaptive finite element method was developed in [11] for solving the two-dimensional diffraction grating problem, where the medium has a one-dimensional periodic structure and the model equation is the two-dimensional Helmholtz equation. It was shown that the a posteriori error estimate consists of the finite element discretization error and the PML truncation error which decays exponentially with respect to the PML parameters such as the thickness of the layer and the medium properties. Due to the superior numerical performance, the adaptive PML method was quickly extended to solve the two- and three-dimensional obstacle scattering problems [10, 12] and the three-dimensional diffraction grating problem [4], where either the two-dimensional Helmholtz equation or the three-dimensional Maxwell equations were considered. Although the PML method has been developed to solve various elastic wave propagation problems in engineering and geophysics soon after it was introduced [14, 17, 25, 35], the rigorous mathematical studies were only recently done for elastic waves because of the complex of the model equation [8, 13, 33, 34].

As a viable alternative, the finite element DtN method has been proposed to solve the obstacle scattering problems [29, 32, 40], the diffraction grating problems [31, 45], and the open cavity scattering problem [47], respectively, where the transparent boundary conditions are used to truncate the domains. In this new approach, the layer of artificial medium is not needed to enclose the domain of interest, which makes is different from the PML method. The transparent boundary conditions are based on nonlocal Dirichlet-to-Neumann (DtN) operators and are given as infinite Fourier series. Since the transparent boundary conditions are exact, the artificial boundary can be put as close as possible to the scattering structures, which can reduce the size of the computational domain. Numerically, the infinite series need to be truncated into a sum of finitely many terms by choosing an appropriate truncation parameter N. It is known that the convergence of the truncated DtN map could be arbitrarily slow to the original DtN map in the operator norm. The a posteriori error analysis of the PML method cannot be applied directly to the DtN method since the DtN map of the truncated PML problem converges exponentially fast to the DtN map of the untruncated PML problem. To overcome this issue, a duality argument had to be developed to obtain the a posteriori error estimate between the solution of the scattering problem and the finite element solution. Comparably, the a posteriori error estimates consist of the finite element discretization error and the DtN truncation error, which decays exponentially with respect to the truncation parameter N. The numerical experiments demonstrate that the adaptive DtN method has a competitive behavior to the adaptive PML method. Recently, an interesting adaptive finite element method was developed for the diffraction grating problem [48]. The method combines the PML and few-mode DtN truncations so that those Fourier modes which cannot be well absorbed by the PML can pass through the boundary without reflections.

In this paper, we present an adaptive finite element DtN method and carry out its mathematical analysis for the elastic wave scattering problem. The goal is threefold: (1) prove the exponential convergence of the truncated DtN operator; (2) give a complete a posteriori error estimate; (3) develop an effective adaptive finite element algorithm. This paper significantly extends the work on the acoustic scattering problem [29], where the Helmholtz equation was considered. Apparently, the techniques differ greatly from the existing work because of the complicated transparent boundary condition associated with the elastic wave equation.

Specifically, we consider a rigid obstacle which is immersed in a homogeneous and isotropic elastic medium in two dimensions. The Helmholtz decomposition is utilized to formulate the exterior boundary value problem of the elastic wave equation into a coupled exterior boundary value problem of the Helmholtz equation. By using a Dirichlet-to-Neumann (DtN) operator, an exact transparent boundary condition, which is given as a Fourier series, is introduced to reduce the original scattering problem into a boundary value problem of the elastic wave equation in a bounded domain. The discrete problem is studied by using the finite element method with the truncated DtN operator. Based on the Helmholtz decomposition, a new duality argument is developed to obtain an a posteriori error estimate between the solution of the original scattering problem and the discrete problem. The a posteriori error estimate consists of the finite element approximation error and the truncation error of the DtN operator which is shown to decay exponentially with respect to the truncation parameter. The estimate is used to design the adaptive finite element algorithm to choose elements for refinements and to determine the truncation parameter N. Since the truncation error decays exponentially with respect to N, the choice of the truncation parameter N is not sensitive to the given tolerance. Numerical experiments are presented to demonstrate the effectiveness of the proposed method.

The paper is organized as follows. In Sect. 2, the elastic wave equation is introduced for the scattering by a rigid obstacle; a boundary value problem is formulated by using the transparent boundary condition; the corresponding weak formulation is discussed. In Sect. 3, the discrete problem is considered by using the finite element approximation with the truncated DtN operator. Section 4 is devoted to the a posteriori error analysis and serves as the basis of the adaptive algorithm. In Sect. 5, we discuss the numerical implementation of the adaptive algorithm and present two numerical examples to illustrate the performance of the proposed method. The paper is concluded with some general remarks and directions for future work in Sect. 6.

2 Problem formulation

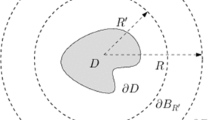
Consider a two-dimensional elastically rigid obstacle D with Lipschitz continuous boundary $\partial D$, as seen in Fig. 1. Denote by $\nu =(\nu _1, \nu _2)^\top$ and $\tau =(\tau _1, \tau _2)^\top$ the unit normal and tangent vectors on $\partial D$, where $\tau _1=\nu _2$ and $\tau _2=-\nu _1$. The exterior domain ${\mathbb {R}}^2{\setminus }{{\overline{D}}}$ is assumed to be filled with a homogeneous and isotropic elastic medium with a unit mass density. Let $B_R=\{{\varvec{x}}=(x, y)^\top \in {\mathbb {R}}^2: |\varvec{x}|<R\}$ and $B_{{\hat{R}}}=\{{\varvec{x}}\in {\mathbb {R}}^2: |{\varvec{x}}|<{\hat{R}}\}$ be the balls with radii R and ${\hat{R}}$, respectively, where $R>{\hat{R}}>0$. Denote by $\partial B_R$ and $\partial B_{{\hat{R}}}$ the boundaries of $B_R$ and $R_{{\hat{R}}}$, respectively. Let ${\hat{R}}$ be large enough such that ${{\overline{D}}}\subset B_{{\hat{R}}}\subset B_R$. Denote by $\Omega =B_R{\setminus }{{\overline{D}}}$ the bounded domain where the boundary value problem will be formulated.

Fig. 1

Schematic of the elastic wave scattering problem

Let the obstacle be illuminated by an incident wave ${\varvec{u}}^{\mathrm{inc}}$, which can be either a point source or a plane wave. The displacement of the total field ${\varvec{u}}$ satisfies the two-dimensional elastic wave equation

$$\begin{aligned} \mu \Delta {\varvec{u}}+(\lambda +\mu )\nabla \nabla \cdot {\varvec{u}} +\omega ^2 {\varvec{u}}=0\quad \text {in}\,{\mathbb {R}}^2{\setminus }{\overline{D}}, \end{aligned}$$

(2.1)

where $\omega >0$ is the angular frequency and $\lambda , \mu$ are the Lamé constants satisfying $\mu>0, \lambda +\mu >0$. Since the obstacle is assumed to be rigid, the displacement of the total field vanishes on the boundary of the obstacle, i.e.,

$$\begin{aligned} {\varvec{u}}=0\quad \text {on}\,\partial D. \end{aligned}$$

(2.2)

The scattered field is defined as ${\varvec{u}}^s={\varvec{u}}-{\varvec{u}}^{\mathrm{inc}}$ and it is required to satisfy the Kupradze–Sommerfeld radiation condition

$$\begin{aligned} \lim _{r\rightarrow \infty }r^{1/2}(\partial _r{\varvec{u}}^s_{\mathrm{p}} -\mathrm{i}\kappa _1 {\varvec{u}}^s_{\mathrm{p}})=0,\quad \lim _{r\rightarrow \infty }r^{1/2}(\partial _r{\varvec{u}}^s_{\mathrm{s}} -\mathrm{i}\kappa _2{\varvec{u}}^s_{\mathrm{s}})=0,\quad r=|{\varvec{x}}|, \end{aligned}$$

(2.3)

where

$$\begin{aligned} {\varvec{u}}^s_{\mathrm{p}} =-\frac{1}{\kappa _1^2}\nabla \nabla \cdot {\varvec{u}}^s,\quad {\varvec{u}}^s_{\mathrm{s}} =\frac{1}{\kappa _2^2}{} \mathbf{curl}\mathrm{curl} {\varvec{u}}^s, \end{aligned}$$

are the compressional and shear wave components of ${\varvec{u}}^s$, respectively. Here

$$\begin{aligned} \kappa _1=\frac{\omega }{(\lambda +2\mu )^{1/2}},\quad \kappa _2=\frac{\omega }{\mu ^{1/2}} \end{aligned}$$

are knowns as the compressional wavenumber and the shear wavenumber, respectively. Clearly we have $\kappa _1<\kappa _2$ since $\mu>0, \lambda +\mu >0$. Given a vector function ${\varvec{u}}=(u_1, u_2)^\top$ and a scalar function u, the scalar and vector curl operators are defined by

$$\begin{aligned} \mathrm{curl}{\varvec{u}}=\partial _x u_2 -\partial _y u_1,\quad \mathbf{curl}u=(\partial _y u, -\partial _x u)^\top . \end{aligned}$$

For any solution ${\varvec{u}}$ of (2.1), we introduce the Helmholtz decomposition

$$\begin{aligned} {\varvec{u}}=\nabla \phi +\mathbf{curl}\psi , \end{aligned}$$

(2.4)

where $\phi , \psi$ are called the scalar potential functions. Substituting (2.4) into (2.1), the corresponding potential functions $\phi ^s, \psi ^s$ for the scattered field ${\varvec{u}}^s$ satisfy the Helmholtz equations

$$\begin{aligned} \Delta \phi ^s+\kappa _1^2\phi ^s=0,\quad \Delta \psi ^s+\kappa _2^2\psi ^s=0\quad \text {in}\, \mathbb R^2{\setminus }{{\overline{D}}}. \end{aligned}$$

(2.5)

Taking the dot product of (2.2) with $\nu$ and $\tau$, respectively, we get

$$\begin{aligned} \partial _{\nu } \phi ^s-\partial _{\tau }\psi ^s=f_1, \quad \partial _{\nu }\psi ^s+\partial _{\tau }\phi ^s=f_2 \quad \text {on}\,\partial D, \end{aligned}$$

(2.6)

where $f_1=-{\varvec{u}}^{\mathrm{inc}}\cdot \nu$ and $f_2=-{\varvec{u}}^{\mathrm{inc}}\cdot \tau$.

In addition, the potential functions $\phi ^s, \psi ^s$ satisfy the Sommerfeld radiation conditions

$$\begin{aligned} \lim _{r\rightarrow \infty }r^{1/2}(\partial _r \phi ^s-\kappa _1\phi ^s)=0,\quad \lim _{r\rightarrow \infty }r^{1/2}(\partial _r \psi ^s-\kappa _2 \psi ^s)=0. \end{aligned}$$

(2.7)

By the Helmholtz decomposition, it can be shown that the boundary value problems (2.1)–(2.3) and (2.5)–(2.7) are equivalent. The result is stated in the following lemma and the proof can be found in [38].

Lemma 2.1

Let ${\varvec{u}}^s$ be the scattered field corresponding to the solution of the boundary value problem (2.1)–(2.3). Then $\phi ^s=-\kappa _1^{-2}\nabla \cdot {\varvec{u}}^s, \psi ^s=\kappa _2^{-2}\mathrm{curl}{\varvec{u}}^s$ are the solutions of the coupled boundary value problem (2.5)–(2.7). Conversely, if $\phi ^s, \psi ^s$ are the solutions of the boundary value problem (2.5)–(2.7), let ${\varvec{u}}^s =\nabla \phi ^s+\mathbf{curl}\psi ^s$, then ${\varvec{u}}={\varvec{u}}^s+{\varvec{u}}^{\mathrm{inc}}$ is the solution of the boundary value problem (2.1)–(2.3).

Denote by $L^2(\Omega )$ the usual Hilbert space of square integrable functions. Let $H^1(\Omega )$ be the standard Sobolev space equipped with the norm

$$\begin{aligned} \Vert u\Vert _{H^1(\Omega )}=\Big (\Vert u\Vert ^2_{L^2(\Omega )}+\Vert \nabla u\Vert ^2_{L^2(\Omega )} \Big )^{1/2}. \end{aligned}$$

Define $H^1_{\partial D}(\Omega )=\{u\in H^1(\Omega ): u=0 \text { on }\partial D\}$. For any function $u\in L^2(\partial B_R)$, it admits the Fourier series expansion

$$\begin{aligned} u(R, \theta )=\sum _{n\in {\mathbb {Z}}}{\hat{u}}_n(R) e^{\mathrm{i}n\theta },\quad {\hat{u}}_n(R)=\frac{1}{2\pi }\int _0^{2\pi }u(R,\theta ) e^{-\mathrm{i}n\theta }\mathrm{d}\theta . \end{aligned}$$

The trace space $H^s(\partial B_R), s\in {\mathbb {R}}$ is defined by

$$\begin{aligned} H^s(\partial B_R)=\{u\in L^2(\partial B_R): \Vert u\Vert _{H^s(\partial B_R)}<\infty \}, \end{aligned}$$

where $H^s(\partial B_R)$ norm is given by

$$\begin{aligned} \Vert u\Vert _{H^s(\partial B_R)}=\Big (2\pi \sum _{n\in \mathbb {Z}}(1+n^2)^s|{\hat{u}}_n(R)|^2 \Big )^{1/2}. \end{aligned}$$

Let ${\varvec{H}}^1(\Omega )=H^1(\Omega )^2$ and $\varvec{H}^1_{\partial D}(\Omega )=H^1_{\partial D}(\Omega )^2$ be the Cartesian product spaces equipped with the corresponding 2-norms of $H^1(\Omega )$ and $H^1_{\partial D}(\Omega )$, respectively. Throughout the paper, we take the notation of $a\lesssim b$ to stand for $a\le C b$, where C is a positive constant whose value is not required but should be clear from the context.

The elastic wave scattering problem (2.2)–(2.3) is formulated in the open domain ${\mathbb {R}}^2{\setminus }{{\overline{D}}}$, which needs to be truncated into the bounded domain $\Omega$. An appropriate boundary condition is required on $\partial B_R$.

Define a boundary operator on $\partial B_R$ as follows

$$\begin{aligned} {\mathscr {B}}{\varvec{v}}=\mu \partial _r {\varvec{v}} +(\lambda +\mu )\nabla \cdot {\varvec{v}} {\varvec{e}}_r, \end{aligned}$$

where ${\varvec{e}}_r$ is the unit outward normal vector on $\partial B_R$. It is shown in [38] that the scattered field ${\varvec{u}}^s$ satisfies the transparent boundary condition on $\partial B_R$:

$$\begin{aligned} {\mathscr {B}} {\varvec{u}}^s =({\mathscr {T}}{\varvec{u}}^s)(R, \theta ) :=\sum _{n\in {\mathbb {Z}}}M_n{\varvec{u}}^s_n(R) e^{\mathrm{i}n\theta },\quad {\varvec{u}}^s(R,\theta ) =\sum _{n\in \mathbb Z}{\varvec{u}}^s_n(R) e^{\mathrm{i}n\theta }, \end{aligned}$$

(2.8)

where ${\mathscr {T}}$ is called the Dirichlet-to-Neumann (DtN) operator and $M_n$ is a $2\times 2$ matrix whose entries are given in (A.4) and (A.6). By a simple calculation, the total field ${\varvec{u}}$ satisfies the transparent boundary condition

$$\begin{aligned} {\mathscr {B}}{\varvec{u}}={\mathscr {T}}{\varvec{u}}+{\varvec{g}}\quad \text {on}\,\partial B_R, \end{aligned}$$

(2.9)

where ${\varvec{g}}:={\mathscr {B}}{\varvec{u}}^\mathrm{inc}-{\mathscr {T}}{\varvec{u}}^{\mathrm{inc}}$.

Based on the transparent boundary condition (2.9), the variational problem for (2.1)–(2.3) is to find ${\varvec{u}}\in {\varvec{H}}_{\partial D}^{1}(\Omega )$ such that

$$\begin{aligned} b({\varvec{u}}, {\varvec{v}})=\int _{\partial B_R} {\varvec{g}}\cdot \overline{{\varvec{v}}}\mathrm{d}s \quad \forall {\varvec{v}}\in {\varvec{H}}^{1}_{\partial D}(\Omega ), \end{aligned}$$

(2.10)

where the sesquilinear form $b: {\varvec{H}}_{\partial D}^1(\Omega )\times {\varvec{H}}_{\partial D}^1(\Omega )\rightarrow {\mathbb {C}}$ is defined as

$$\begin{aligned} b({\varvec{u}}, {\varvec{v}})&=\mu \int _{\Omega }\nabla {\varvec{u}}:\nabla \overline{\varvec{v}}\mathrm{d}{\varvec{x}} +(\lambda +\mu )\int _{\Omega }\left( \nabla \cdot {\varvec{u}} \right) \left( \nabla \cdot \overline{{\varvec{v}}}\right) \mathrm{d}{\varvec{x}}\nonumber \\&\quad -\omega ^2 \int _{\Omega } {\varvec{u}}\cdot \overline{{\varvec{v}}} \mathrm{d}{\varvec{x}}- \int _{\partial B_R}{\mathscr {T}}{\varvec{u}}\cdot \overline{{\varvec{v}}}\mathrm{d}s. \end{aligned}$$

(2.11)

Here $A:B=\mathrm{tr}(AB^\top )$ is the Frobenius inner product of square matrices A and B.

Following [38], we may show that the variational problem (2.10) has a unique weak solution ${\varvec{u}}\in {\varvec{H}}_{\partial D}^1(\Omega )$ for any frequency $\omega$ and the solution satisfies the estimate

$$\begin{aligned} \Vert {\varvec{u}}\Vert _{{\varvec{H}}^1(\Omega )}\lesssim \Vert \varvec{g}\Vert _{{\varvec{H}}^{-1/2}(\partial B_R)} \lesssim \Vert \varvec{u}^{\mathrm{inc}}\Vert _{{\varvec{H}}^1(\Omega )}. \end{aligned}$$

(2.12)

It follows from the general theory in [1] that there exists a constant $\gamma >0$ such that the following inf-sup condition holds

$$\begin{aligned} \sup _{0\ne {\varvec{v}}\in {\varvec{H}}_{\partial D}^1(\Omega )} \frac{|b({\varvec{u}},{\varvec{v}})|}{\Vert \varvec{v}\Vert _{{\varvec{H}}^1(\Omega )}}\ge \gamma \Vert \varvec{u}\Vert _{{\varvec{H}}^1(\Omega )} \quad \forall \varvec{u}\in {\varvec{H}}_{\partial D}^1(\Omega ). \end{aligned}$$

3 The discrete problem

In the variational problem (2.10), the DtN operator ${\mathscr {T}}$ is given as an infinite series. In computation, the infinite series needs to be truncated into a finite sum. Given a sufficiently large N, we define the truncated DtN operator

$$\begin{aligned} {\mathscr {T}}_N {\varvec{u}}=\sum \limits _{|n|\le N}M_n\varvec{u}_n(R) e^{\mathrm{i}n\theta }. \end{aligned}$$

(3.1)

Hence ${\varvec{g}}$ also needs to be approximated as ${\varvec{g}}_N={\mathscr {B}}{\varvec{u}}^\mathrm{inc}-{\mathscr {T}}_N{\varvec{u}}^{\mathrm{inc}}$. Using (3.1), we have the truncated problem: find ${\varvec{u}}_N\in {\varvec{H}}_{\partial D}^1(\Omega )$ such that

$$\begin{aligned} b_N({\varvec{u}}_N, {\varvec{v}}) =\int _{\partial B_R} {\varvec{g}}_N\cdot \overline{{\varvec{v}}}\mathrm{d}s \quad \forall {\varvec{v}}\in {\varvec{H}}^1_{\partial D}(\Omega ), \end{aligned}$$

(3.2)

where the sesquilinear form $b_N:{\varvec{H}}_{\partial D}^1(\Omega )\times {\varvec{H}}_{\partial D}^1(\Omega )\rightarrow {\mathbb {C}}$ is defined as

$$\begin{aligned} b_N({\varvec{u}}, {\varvec{v}})&=\mu \int _{\Omega }\nabla {\varvec{u}}:\nabla \overline{ {\varvec{v}}}\mathrm{d}{\varvec{x}} +(\lambda +\mu )\int _{\Omega }\left( \nabla \cdot {\varvec{u}} \right) \left( \nabla \cdot \overline{{\varvec{v}}}\right) \mathrm{d}{\varvec{x}} \nonumber \\&\quad -\omega ^2 \int _{\Omega } {\varvec{u}}\cdot \overline{{\varvec{v}}}\mathrm{d}{\varvec{x}} -\int _{\partial B_R}{\mathscr {T}}_N{\varvec{u}}\cdot \overline{{\varvec{v}}}\mathrm{d}s. \end{aligned}$$

(3.3)

Let us consider the discrete problem of (2.10) by using the finite element approximation. Let ${\mathcal {M}}_h$ be a regular triangulation of $\Omega$, where h denotes the maximum diameter of all the elements in ${\mathcal {M}}_h$. For simplicity, we assume that the boundary $\partial D$ is polygonal and ignore the approximation error of the boundary $\partial B_R$, which allows us to focus on deducing the a posteriori error estimate. Thus any edge $e\in {\mathcal {M}}_h$ is a subset of $\partial \Omega$ if it has two boundary vertices.

Let $\Omega _h:=\cup _{K\in {\mathcal {M}}_h} K$ and $\tilde{\varvec{V}}_h\subset {\varvec{H}}^{1}(\Omega _h)$ be a conforming finite element space, i.e.,

$$\begin{aligned} \tilde{{\varvec{V}}}_h:= \left\{ {\varvec{v}}\in C(\overline{\Omega _h})^2: {\varvec{v}}|_{K}\in P_m(K)^2 \text { for any } K\in {\mathcal {M}}_h\right\} , \end{aligned}$$

where m is a positive integer and $P_m(K)$ denotes the set of all polynomials of degree no more than m. Introduce an isoparametric-equivalent finite element space

$$\begin{aligned} {\varvec{V}}_h:=\left\{ {\varvec{v}}({\varvec{F}}^{-1}({\varvec{x}})): {\varvec{x}}\in {\varvec{F}}(\Omega _h),\,{\varvec{v}}\in \tilde{{\varvec{V}}}_h \right\} , \end{aligned}$$

where ${\varvec{F}} \in \tilde{{\varvec{V}}}_h$ is a one-to-one continuous mapping constructed in [37]. We refer to [9, 37] for more details about the construction and properties of ${\varvec{F}}$. The finite element approximation to the variational problem (2.10) is to find ${\varvec{u}}^h\in {\varvec{V}}_{h, \partial D}$ such that

$$\begin{aligned} b({\varvec{u}}^h, {\varvec{v}}^h) =\int _{\partial B_R} {\varvec{g}}\cdot \overline{{\varvec{v}}^h}\mathrm{d}s\quad \forall {\varvec{v}}^h\in {\varvec{V}}_{h,\partial D}, \end{aligned}$$

(3.4)

where ${\varvec{V}}_{h,\partial D}=\{{\varvec{v}}\in \varvec{V}_h: {\varvec{v}}=0\text { on }\partial D\}$.

The truncated finite element approximation to the variational problem (3.2) is to find $\varvec{u}_N^h\in {\varvec{V}}_{h, \partial D}$ such that

$$\begin{aligned} b_N({\varvec{u}}^h_N, {\varvec{v}}^h) =\int _{\partial B_R} {\varvec{g}}_N\cdot \overline{{\varvec{v}}^h}\mathrm{d}s \quad \forall {\varvec{v}}^h\in {\varvec{V}}_{h, \partial D}. \end{aligned}$$

(3.5)

Following the argument in [28, 38], we may show that for sufficiently large N the variational problem (3.2) is well-posed. Moreover, for sufficiently small h, the discrete inf-sup condition of the sesquilinear form $b_N$ may be established by following the approach in [43]. Based on the general theory in [1], the truncated variational problem (3.5) can be shown to have a unique solution ${\varvec{u}}_N^h\in {\varvec{V}}_h$. The details are omitted since our focus is the a posteriori error estimate.

4 The a posteriori error analysis

For any triangular element $K\in {\mathcal {M}}_h$, we denote by $h_K$ its diameter. Let ${\mathcal {B}}_h$ denote the set of all the edges of K. For any edge $e\in {\mathcal {B}}_h$, let $h_e$ be its length. For any interior edge e which is the common side of triangular elements $K_1, K_2\in {\mathcal {M}}_h$, we define the jump residual across e as

$$\begin{aligned} J_e=-\left( \mu \nabla {\varvec{u}}_N^h|_{K_1}\cdot \varvec{\nu } _1+(\lambda +\mu )\nabla \cdot {\varvec{u}}_N^h|_{K_1} \varvec{\nu }_1+\mu \nabla {\varvec{u}}_N^h|_{K_2}\cdot \varvec{\nu }_2+(\lambda +\mu ) \nabla \cdot {\varvec{u}}_N^h|_{K_2}\varvec{\nu }_2\right) , \end{aligned}$$

where $\varvec{\nu }_j$ is the unit outward normal vector on the boundary of $K_j, j=1,2$. For any boundary edge $e\subset \partial B_R$, we define the jump residual

$$\begin{aligned} J_e=2\left( {\mathscr {T}}_N{\varvec{u}}_N^h +{\varvec{g}}_N -\mu (\nabla {\varvec{u}}_N^h\cdot {\varvec{e}}_r) -(\lambda +\mu )(\nabla \cdot {\varvec{u}} _N^h){\varvec{e}}_r\right) . \end{aligned}$$

For any triangular element $K\in {\mathcal {M}}_h$, denote by $\eta _K$ the local error estimator which is given by

$$\begin{aligned} \eta _K=h_K\Vert {\mathscr {R}}{\varvec{u}}_N^h\Vert _{{\varvec{L}}^2(K)} +\left( \frac{1}{2}\sum \limits _{e\in \partial K} h_e \Vert J_e\Vert ^2_{{\varvec{L}}^2(e)}\right) ^{1/2}, \end{aligned}$$

where ${\mathscr {R}}$ is the residual operator defined by

$$\begin{aligned} {\mathscr {R}}{\varvec{u}}=\mu \Delta {\varvec{u}} +(\lambda +\mu )\nabla \left( \nabla \cdot {\varvec{u}}\right) +\omega ^2\varvec{u }. \end{aligned}$$

For convenience, we introduce a weighted norm $|\!\Vert \cdot |\!\Vert _{{\varvec{H}}^{1}(\Omega )}$ which is given by

$$\begin{aligned} |\!\Vert {\varvec{u}}|\!\Vert ^2_{{\varvec{H}}^{1}(\Omega )} =\mu \int _{\Omega } |\nabla {\varvec{u}}|^2\mathrm{d}{\varvec{x}} +(\lambda +\mu )\int _{\Omega }|\nabla \cdot {\varvec{u}}|^2\mathrm{d}{\varvec{x}} +\omega ^2 \int _{\Omega } |{\varvec{u}}|^2\mathrm{d}{\varvec{x}}. \end{aligned}$$

(4.1)

It can be verified for any ${\varvec{u}}\in \varvec{H}^1(\Omega )$ that

$$\begin{aligned} \min \left( \mu , \omega ^2\right) \Vert {\varvec{u}}\Vert ^2_{\varvec{H}^{1}(\Omega )} \le |\!\Vert {\varvec{u}}|\!\Vert ^2_{\varvec{H}^1(\Omega )} \le \max \left( 2\lambda +3\mu , \omega ^2\right) \Vert {\varvec{u}}\Vert ^2_{{\varvec{H}}^{1}(\Omega )}, \end{aligned}$$

(4.2)

which implies that the two norms $\Vert \cdot \Vert _{\varvec{H}^1(\Omega )}$ and $|\!\Vert \cdot |\!\Vert _{{\varvec{H}}^1(\Omega )}$ are equivalent.

Now we state the main result of this paper.

Theorem 4.1

Let ${\varvec{u}}$ and ${\varvec{u}}_N^h$ be the solutions of the variational problems (2.10) and (3.5), respectively. Then for sufficiently large N, the following a posteriori error estimate holds:

$$\begin{aligned} |\!\Vert {\varvec{u}}-{\varvec{u}}_N^h |\!\Vert _{{\varvec{H}}^{1}(\Omega )}\lesssim \left( \sum _{K\in {\mathcal {M}}_h} \eta ^2_{K}\right) ^{1/2} + N\bigg (\frac{\hat{R}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

We point out that the a posteriori error estimate consists of two parts: the first part arises from the finite element discretization error; and the second part comes from the truncation error of the DtN operator. Apparently, the DtN truncation error decreases exponentially with respect to N since $\hat{R}<R$.

In the rest of the paper, we shall prove the a posteriori error estimate in Theorem 4.1. First, we present the result on trace regularity for functions in $H^1(\Omega )$. The proof can be found in [29].

Lemma 4.2

For any $u\in H^{1}(\Omega )$, the following estimates hold:

$$\begin{aligned} \Vert u\Vert _{H^{1/2}(\partial B_R)}\lesssim \Vert u\Vert _{H^{1}(\Omega )}, \quad \Vert u\Vert _{H^{1/2}(\partial B_{\hat{R}})}\lesssim \Vert u\Vert _{H^{1}(\Omega )}. \end{aligned}$$

Let $\varvec{\xi }={\varvec{u}}-{\varvec{u}}_N^h$, where ${\varvec{u}}$ and ${\varvec{u}}_N^h$ are the solutions of the problems (2.10) and (3.5), respectively. Combining (4.1), (2.11), and (3.3), we have from straightforward calculations that

$$\begin{aligned} |\!\Vert \varvec{\xi }|\!\Vert ^2_{{\varvec{H}}^{1}(\Omega )}= & {} \mu \int _{\Omega } \nabla \varvec{\xi }:\nabla \overline{\varvec{\xi }} \mathrm{d}{\varvec{x}} +(\lambda +\mu )\int _{\Omega }\left( \nabla \cdot \varvec{\xi } \right) \left( \nabla \cdot \overline{\varvec{\xi }}\right) \mathrm{d}{\varvec{x}} +\omega ^2 \int _{\Omega } \varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}{\varvec{x}}\nonumber \\= & {} \Re b(\varvec{\xi }, \varvec{\xi })+2\omega ^2 \int _{\Omega }|\varvec{\xi }|^2\mathrm{d}{\varvec{x}} +\Re \int _{\partial B_R}{\mathscr {T}}\varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}s\nonumber \\= & {} \Re b(\varvec{\xi }, \varvec{\xi })+\Re \int _{\partial B_R}\left( {\mathscr {T}} -{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}s +2\omega ^2 \int _{\Omega }|\varvec{\xi }|^2\mathrm{d}{\varvec{x}}\nonumber \\&+\Re \int _{\partial B_R}{\mathscr {T}}_N \varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}s, \end{aligned}$$

(4.3)

which is the error representation formula.

In the following, we discuss the four terms in (4.3) one by one. Lemma 4.5 presents the a posteriori error estimate for the truncation of the DtN operator on the scattered field ${\varvec{u}}^s$. Lemma 4.6 gives the a posteriori error estimate for the total field ${\varvec{u}}$ on both of the finite element approximation and DtN operator truncation.

Lemma 4.3

Let $0<\kappa _1<\kappa _2$ and $0<{\hat{R}}<R$. For sufficiently large |n|, the following estimate holds for $j=1, 2$:

$$\begin{aligned} \left| \frac{H_{n}^{(j)}(\kappa _1 R)}{H_{n}^{(j)}(\kappa _1 {\hat{R}})}-\frac{H_{n}^{(j)}(\kappa _2 R)}{H_{n}^{(j)}(\kappa _2 {\hat{R}})}\right| \le \frac{\kappa _2\left( \kappa _2-\kappa _1\right) }{|n|-1} \left( R^2-{\hat{R}}^2\right) \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}, \end{aligned}$$

where $H_n^{(1)}$ and $H_n^{(2)}$ are the Hankel functions of the first and second kind with order n, respectively.

Proof

Since the Hankel functions of the first and second kind are complex conjugate to each other, we only need to show the proof for the Hankel function of the first kind.

Let $J_n$ and $Y_n$ be the Bessel functions of the first and second kind with order n, respectively. Since $J_{-n}(z)=(-1)^n J_n(z), Y_{-n}(z)=(-1)^nY_n(z)$, it suffices to show the result for positive n. For a fixed $z>0$, they admit the following asymptotic properties [46]:

$$\begin{aligned} J_n(z)\sim \frac{1}{\sqrt{2\pi n}}\left( \frac{ez}{2n}\right) ^n,\qquad Y_n(z)\sim -\sqrt{\frac{2}{\pi n}}\left( \frac{ez}{2n}\right) ^{-n},\quad n\rightarrow \infty . \end{aligned}$$

(4.4)

Define $S(z)=J_n(z)/Y_n(z)$. A simple calculation yields

$$\begin{aligned} \frac{H_n^{(1)}(zR)}{H_n^{(1)}(z{\hat{R}})}= & {} \frac{J_n(zR)+\mathrm{i}Y_n(zR)}{J_n(z\hat{R})+\mathrm{i}Y_n(z{\hat{R}})} =\frac{Y_n(zR)}{Y_n(z{\hat{R}})}\frac{1-\mathrm{i}\frac{J_n(zR)}{Y_n(zR)}}{1-\mathrm{i}\frac{J_n(z{\hat{R}})}{Y_n(z{\hat{R}})}}\nonumber \\= & {} \frac{Y_n(zR)}{Y_n(z{\hat{R}})}\frac{1-\mathrm{i}S_n(zR)}{1-\mathrm{i}S_n(z{\hat{R}})}=\frac{Y_n(zR)}{Y_n(z{\hat{R}})}+\mathrm{i}\frac{Y_n(zR)}{Y_n(z{\hat{R}})}\frac{S_n(z{\hat{R}})-S_n(zR)}{1-\mathrm{i}S_n(z{\hat{R}})}.\nonumber \\ \end{aligned}$$

(4.5)

By (4.4)–(4.5), we have

$$\begin{aligned} S_n(z)=\frac{J_n(z)}{Y_n(z)}\sim \frac{\frac{1}{\sqrt{2\pi n}} \left( \frac{ez}{2n}\right) ^n}{-\sqrt{\frac{2}{\pi n}}\left( \frac{ez}{2n}\right) ^{-n}} = -\frac{1}{2}\left( \frac{ez}{2n}\right) ^{2n}, \qquad n\rightarrow \infty . \end{aligned}$$

and

$$\begin{aligned}&\left| \frac{H_{n}^{(1)}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 {\hat{R}})}-\frac{H_{n}^{(1)}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 {\hat{R}})}\right| \le \left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}-\frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\frac{S_n(\kappa _1 {\hat{R}})}{1-\mathrm{i}S_n(\kappa _1 {\hat{R}})}\right| \\&\quad +\left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\frac{S_n(\kappa _1 R)}{1-\mathrm{i}S_n(\kappa _1 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\frac{S_n(\kappa _2 {\hat{R}})}{1-\mathrm{i}S_n(\kappa _2 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\frac{S_n(\kappa _2 R)}{1-\mathrm{i}S_n(\kappa _2 {\hat{R}})}\right| . \end{aligned}$$

It is easy to verify that

$$\begin{aligned} \left| \frac{S_n(z R)}{1-\mathrm{i}S_n(z {\hat{R}})}\right| \le \left( \frac{ezR}{2n}\right) ^{2n},\quad \left| \frac{S_n(z {\hat{R}})}{1-\mathrm{i}S_n(z {\hat{R}})}\right| \le \left( \frac{ez{\hat{R}}}{2n}\right) ^{2n} \end{aligned}$$

and

$$\begin{aligned} \frac{Rz Y^\prime _n(z R)}{Y_n(z R)} \sim \frac{z^2 R^2}{2(n-1)}-n,\quad \frac{Y_n(z R)}{Y_n(z {\hat{R}})}\sim \left( \frac{{\hat{R}}}{R}\right) ^{|n|}. \end{aligned}$$

Combining the above estimates, we have for $R>{\hat{R}}$ and $\kappa _2>\kappa _1$ that

$$\begin{aligned}&\left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\frac{S_n(\kappa _1 {\hat{R}})}{1-\mathrm{i}S_n(\kappa _1 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\frac{S_n(\kappa _1 R)}{1-\mathrm{i}S_n(\kappa _1 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\frac{S_n(\kappa _2 {\hat{R}})}{1-\mathrm{i}S_n(\kappa _2 {\hat{R}})}\right| \\&\quad +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\frac{S_n(\kappa _2 R)}{1-\mathrm{i}S_n(\kappa _2 {\hat{R}})}\right| \le 2\left( \frac{e\kappa _2 R}{2n}\right) ^{2n}\left( \left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\right| \right) . \end{aligned}$$

Define $F(z)=Y_n(z R)/Y_n(z {\hat{R}})$. By the mean value theorem, there exits $\xi \in (\kappa _1, \kappa _2)$ such that

$$\begin{aligned} F(\kappa _1)-F(\kappa _2)= & {} F'(\xi )(\kappa _1-\kappa _2)\\= & {} \frac{R Y'_n(\xi R) Y_n(\xi {\hat{R}})- {\hat{R}} Y_n(\xi R) Y'_n(\xi {\hat{R}})}{Y_n(\xi {\hat{R}})^2}(\kappa _1-\kappa _2)\\= & {} \left( \frac{R\xi Y'_n(\xi R)}{Y_n(\xi R)}-\frac{{\hat{R}}\xi Y'_n(\xi {\hat{R}})}{Y_n(\xi {\hat{R}})}\right) \frac{Y_n(\xi R)}{Y_n(\xi {\hat{R}})}\frac{\kappa _1-\kappa _2}{\xi }\\\sim & {} \frac{\xi \left( \kappa _1-\kappa _2\right) }{2(n-1)} \left( R^2-{\hat{R}}^2\right) \frac{ Y_n(\xi R)}{Y_n(\xi {\hat{R}})}. \end{aligned}$$

Therefore,

$$\begin{aligned} \left| \frac{H_{n}^{(1)}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 {\hat{R}})}-\frac{H_{n}^{(1)}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 {\hat{R}})}\right|\le & {} \left| \frac{\xi \left( \kappa _1-\kappa _2\right) }{2(n-1)} \right| \left| \left( R^2-{\hat{R}}^2\right) \frac{Y_n(\xi R)}{Y_n(\xi {\hat{R}})}\right| \\&\quad +2\left( \frac{e\kappa _2 R}{2n}\right) ^{2n}\left( \left| \frac{Y_n(\kappa _1 R)}{Y_n(\kappa _1 {\hat{R}})}\right| +\left| \frac{Y_n(\kappa _2 R)}{Y_n(\kappa _2 {\hat{R}})}\right| \right) \\\le & {} \frac{\kappa _2\left( \kappa _2-\kappa _1\right) }{|n|-1} \left( R^2-{\hat{R}}^2\right) \left( \frac{{\hat{R}}}{R}\right) ^{|n|}, \end{aligned}$$

which completes the proof. $\square$

Remark 4.4

In the proof of Lemma 4.3, we use the asymptotic properties of the Bessel functions (4.4) for the case when z is fixed and $n\rightarrow \infty$. It is worth mentioning that the truncation number should be increased with respect to $\kappa _2 R$ in order to keep the term $Y_n(z)$ dominating in $H_n^{(1)}(z)$, which is a technique issue. The result may be improved by making a more sophisticated analysis on the Bessel functions.

Lemma 4.5

Let ${\varvec{u}}^s\in {\varvec{H}}^1(\Omega )$ be the scattered field corresponding to the solution of the variational problem (2.10). For any ${\varvec{v}}\in \varvec{H}^1(\Omega )$, the following estimate holds:

$$\begin{aligned} \left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}}^s\cdot \overline{{\varvec{v}}}\,ds \right| \lesssim N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )} \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

Proof

Recalling the Helmholtz decomposition $\varvec{u}^s=\nabla \phi ^s+\mathbf{curl}\psi ^s$, we have from the Fourier series expansions in (A.1) that

$$\begin{aligned} \phi _n^s(R)=\frac{H_n^{(1)}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 {\hat{R}})}\phi _n^s({\hat{R}}), \quad \psi _n^s(R)=\frac{H_n^{(1)}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 {\hat{R}})}\psi ^s_n({\hat{R}}). \end{aligned}$$

Comparing the Fourier coefficients of ${\varvec{u}}$ and $\phi , \psi$ in the Helmholtz decomposition gives

$$\begin{aligned} {\varvec{u}}^s_n(R)= & {} \begin{bmatrix} \alpha _{1n}(R) &{} \frac{\mathrm{i}n}{R}\\ \frac{\mathrm{i}n}{R} &{} -\alpha _{2n}(R) \end{bmatrix} \begin{bmatrix} \phi _n^s(R)\\ \psi ^s_n(R) \end{bmatrix}\\= & {} \begin{bmatrix} \alpha _{1n}(R) &{} \frac{\mathrm{i}n}{R}\\ \frac{\mathrm{i}n}{R} &{} -\alpha _{2n}(R) \end{bmatrix} \begin{bmatrix} \frac{H_n^{(1)}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 {\hat{R}})} &{} 0\\ 0 &{} \frac{H_n^{(1)}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 {\hat{R}})} \end{bmatrix} \begin{bmatrix} \phi _n^s({\hat{R}})\\ \psi ^s_n({\hat{R}}) \end{bmatrix}\\= & {} \begin{bmatrix} \alpha _{1n}(R) &{} \frac{\mathrm{i}n}{R}\\ \frac{\mathrm{i}n}{R} &{} -\alpha _{2n}(R) \end{bmatrix} \begin{bmatrix} \frac{H_n^{(1)}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 {\hat{R}})} &{} 0\\ 0 &{} \frac{H_n^{(1)}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 {\hat{R}})} \end{bmatrix} \begin{bmatrix} -\alpha _{2n}({\hat{R}}) &{} -\frac{\mathrm{i}n}{{\hat{R}}}\\ -\frac{\mathrm{i}n}{{\hat{R}}} &{} \alpha _{1n}({\hat{R}}) \end{bmatrix} \frac{{\varvec{u}}^s_n({\hat{R}})}{\Lambda _n({\hat{R}})}\\= & {} -\frac{1}{\Lambda _n({\hat{R}})}\begin{bmatrix} A_{11} &{} A_{12}\\ A_{21} &{} A_{22} \end{bmatrix}{\varvec{u}}^s_n({\hat{R}}), \end{aligned}$$

where $\alpha _{jn}, \Lambda _n$ is given in (A.5) and

$$\begin{aligned} A_{11}= & {} \frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}\alpha _{1n}(R)\alpha _{2n}({\hat{R}}) -\frac{n^2}{R {\hat{R}}}\frac{H_n^{(1)}(\kappa _2 R)}{H_n^{(1)}(\kappa _2 {\hat{R}})},\\ A_{12}= & {} \frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}\alpha _{1n}(R)\frac{\mathrm{i}n}{{\hat{R}}} -\frac{\mathrm{i}n}{R}\alpha _{1n}({\hat{R}}) \frac{H_n^{(1)}(\kappa _2 R)}{H_n^{(1)}(\kappa _2 {\hat{R}})},\\ A_{21}= & {} \frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}\alpha _{2n}({\hat{R}})\frac{\mathrm{i}n}{R} -\frac{\mathrm{i}n}{{\hat{R}}}\alpha _{2n}(R) \frac{H_n^{(1)}(\kappa _2 R)}{H_n^{(1)}(\kappa _2 {\hat{R}})},\\ A_{22}= & {} \frac{H_n^{(1)}(\kappa _2 R)}{H_n^{(1)}(\kappa _2 {\hat{R}})}\alpha _{1n}({\hat{R}})\alpha _{2n}(R) -\frac{n^2}{R {\hat{R}}}\frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}. \end{aligned}$$

By Lemma 4.3 and (A.7), we have

$$\begin{aligned} \left| A_{11}\right|\le & {} \left| \frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}\right| \left| \alpha _{1n}(R)\alpha _{2n}({\hat{R}})-\frac{n^2}{R {\hat{R}}}\right| +\frac{n^2}{R {\hat{R}}}\left| \frac{H_n^{(1)}(\kappa _1 R)}{H_n^{(1)}(\kappa _1 {\hat{R}})}-\frac{H_n^{(1)}(\kappa _2 R)}{H_n^{(1)}(\kappa _2 {\hat{R}})}\right| \\\le & {} \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}\left| \left( \frac{\kappa _1^2 R}{2(n-1)}-\frac{n}{R}\right) \left( \frac{\kappa _2^2 {\hat{R}}}{2(n-1)}-\frac{n}{{\hat{R}}}\right) -\frac{n^2}{R {\hat{R}}}\right| \\&\quad +\frac{n^2}{R {\hat{R}}} \frac{\kappa _2\left( \kappa _2-\kappa _1\right) }{|n|-1} \left( R^2-{\hat{R}}^2\right) \bigg (\frac{\hat{R}}{R}\bigg )^{|n|}\\\le & {} \kappa _2\left( \kappa _2-\kappa _1\right) \left( R^2-{\hat{R}}^2\right) \frac{2|n|}{R {\hat{R}}} \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|} \lesssim |n| \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}, \end{aligned}$$

Similarly, it can be shown that

$$\begin{aligned} |A_{ij}| \lesssim |n| \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|} ,\quad i,j=1, 2. \end{aligned}$$

The details are omitted for brevity.

Combining the above estimates and Lemma A.1, we obtain

$$\begin{aligned} \left| {\varvec{u}}^{s}_n(R)\right| \lesssim |n| \bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}\left| {\varvec{u}}^{s}_n({\hat{R}})\right| . \end{aligned}$$

(4.6)

It follows from (A.6)–(A.7) that

$$\begin{aligned}&\left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}}^s\cdot \overline{{\varvec{v}}}\mathrm{d}s \right| \nonumber \\&\quad =\bigg | 2\pi R\sum \limits _{|n|>N}\bigg \{ \Big [\Big (-\frac{\mu }{R}+\frac{\omega ^2}{\Lambda _n}\alpha _{2n}(R)\Big ) u_n^{s, r}(R)+\mathrm{i}n\Big (-\frac{\mu }{R}+\frac{\omega ^2}{\Lambda _n} \frac{1}{R}\Big )u_n^{s,\theta }(R)\Big ]\overline{v_n^{r}(R)}\nonumber \\&\qquad +\Big [-\mathrm{i}n\Big (-\frac{\mu }{R}+\frac{\omega ^2}{ \Lambda _n}\frac{1}{R}\Big )u_n^{s, r}(R)+\Big (-\frac{\mu }{R}+\frac{\omega ^2}{ \Lambda _n }\alpha _{1n}(R)\Big ) u_n^{s, \theta }(R) \Big ]\overline{v_n^{\theta }(R)}\bigg \} \bigg |\nonumber \\&\quad \lesssim \sum \limits _{|n|>N}\Big [ \sqrt{|n|} \big (|u_n^{s, r}(R)|+ |u_n^{s, \theta }(R)| \big )\Big ] \Big [ \sqrt{|n|} \big ( |\overline{v_n^r(R)}|+ |\overline{v_n^\theta (R)}| \big )\Big ]\nonumber \\&\quad \lesssim \bigg (\sum \limits _{|n|>N}\Big [ |n|\big (|u_n^{s, r}(R)|^2+ |u_n^{s, \theta }(R)|^2\big )\Big ]\bigg )^{1/2}\nonumber \\&\qquad \times \bigg (\sum \limits _{|n|>N}\Big [ |n|\big (|v_n^r(R)|^2+ |v_n^\theta (R)|^2\big )\Big ]\bigg )^{1/2}. \end{aligned}$$

(4.7)

Substituting (2.12) and (4.6) into (4.7) and using Lemma 4.2, we obtain

$$\begin{aligned}&\left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}}^s\cdot \overline{{\varvec{v}}}\mathrm{d}s \right| \\&\quad \lesssim \Bigg (\sum \limits _{|n|>N}\bigg [ |n|^3\bigg (\frac{\hat{R}}{R}\bigg )^{2|n|} \big ( |u_n^{s, r}(\hat{R})|^2+ |u_n^{s, \theta }(\hat{R})|^2 \big )\bigg ]\Bigg )^{1/2} \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1/2}(\partial B_R)}\\&\quad \lesssim \max _{|n|>N}\bigg (|n|\bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}\bigg ) \Vert {\varvec{u}}^s\Vert _{{\varvec{H}}^{1/2}(\partial B_{{\hat{R}}})}\Vert {\varvec{v}}\Vert _{ {\varvec{H}}^{1/2}(\partial B_{R})}\\&\quad \lesssim \max _{|n|>N}\bigg (|n|\bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}\bigg ) \Vert {\varvec{u}}^s\Vert _{{\varvec{H}}^{1}(\Omega )} \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}(\Omega )}\\&\quad \lesssim \max _{|n|>N}\bigg (|n|\bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}\bigg ) \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )} \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}(\Omega )}, \end{aligned}$$

which completes the proof by noting that $|n|\left( \frac{\hat{R}}{R}\right) ^{|n|}$ is decreasing for sufficiently large |n|.

$\square$

In Lemma 4.5, it is shown that the truncation error of the DtN operator on the scattered field decay exponentially with respect to the truncation parameter N. The result implies that N can be small in practice.

Lemma 4.6

Let ${\varvec{v}}$ be any function in ${\varvec{H}}_{\partial D}^{1}(\Omega )$, we have

$$\begin{aligned}&\left| b(\varvec{\xi }, {\varvec{v}})+\int _{\partial B_R} \left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{{\varvec{v}}}\mathrm{d}s\right| \\&\quad \lesssim \left( \left( \sum \limits _{K\in {\mathcal {M}}_h}\eta _{K}^2\right) ^{1/2} + N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )}\right) \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

Proof

For any function ${\varvec{v}}$ in ${\varvec{H}}_{\partial D}^{1}(\Omega )$ and ${\varvec{v}}^h$ in ${\varvec{V}}_{h, \partial D}$, we have

$$\begin{aligned}&b(\varvec{\xi }, {\varvec{v}}) +\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{{\varvec{v}}}\mathrm{d}s \\&\quad = b({\varvec{u}}, {\varvec{v}})-b_N^h({\varvec{u}}_N^h, {\varvec{v}}^h) +b_N^h({\varvec{u}}_N^h, {\varvec{v}}^h)-b({\varvec{u}}_N^h, {\varvec{v}}) +\int _{\partial B_R}({\mathscr {T}}-{\mathscr {T}}_N)\varvec{\xi }\cdot \overline{{\varvec{v}}}\mathrm{d}s\\&\quad =\int _{\partial B_R}{\varvec{g}}_N\cdot \big (\overline{{\varvec{v}}} -\overline{{\varvec{v}}^h}\big )\mathrm{d}s -b_N^h({\varvec{u}}_N^h, {\varvec{v}}-{\varvec{v}}^h) \\&\qquad + \int _{\partial B_R}\left( {\varvec{g}}-{\varvec{g}}_N\right) \cdot \overline{{\varvec{v}}}\mathrm{d}s +\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}} \cdot \overline{{\varvec{v}}}\mathrm{d}s. \end{aligned}$$

For any ${\varvec{v}}^h\in {\varvec{V}}_{h, \partial D}$, it follows from the integration by parts that

$$\begin{aligned}&-b_N({\varvec{u}}_N^h, {\varvec{v}}-{\varvec{v}}^h) +\int _{\partial B_R}{\varvec{g}}_N\cdot \left( \overline{{\varvec{v}}}-\overline{{\varvec{v}}^h}\right) \mathrm{d}s \\&\quad = -\sum \limits _{K\in {\mathcal {M}}_h}\left\{ \mu \int _{K} \nabla {\varvec{u}}_N^h:\nabla \big (\overline{\varvec{v}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}{\varvec{x}} +(\lambda +\mu )\int _{K} \big (\nabla \cdot {\varvec{u}}_N^h\big ) \nabla \cdot \big (\overline{\varvec{v}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}{\varvec{x}}\right\} \\&\qquad -\sum \limits _{K\in \mathcal M_h}\left\{ -\omega ^2\int _{K}{\varvec{u}}_N^h\cdot \big (\overline{{\varvec{v}}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}{\varvec{x}} -\int _{\partial B_R\cap \partial K} \big ({\mathscr {T}}_N{\varvec{u}}_N^{h}+{\varvec{g}}_N\big )\cdot \big (\overline{{\varvec{v}}}-\overline{{\varvec{v}}^h} \big ) \mathrm{d}s\right\} \\&\quad = \sum \limits _{K\in {\mathcal {M}}_h} \left\{ -\int _{\partial K}\left[ \mu \nabla {\varvec{u}}_N^h\cdot \varvec{\nu } +(\lambda +\mu )(\nabla \cdot {\varvec{u}}_N^h)\varvec{\nu }\right] \cdot \big (\overline{{\varvec{v}}}-\overline{{\varvec{v}}^h}\big ) \mathrm{d}s \right. \\&\qquad \left. +\int _{\partial B_R\cap \partial K}\big ({\mathscr {T}}_N{\varvec{u}}_N^{h}+{\varvec{g}}_N\big )\cdot \big (\overline{{\varvec{v}}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}s\right\} \\&\qquad +\sum \limits _{K\in {\mathcal {M}}_h}\int _{K} \left[ \mu \Delta {\varvec{u}}_N^h +(\lambda +\mu )\nabla \nabla \cdot {\varvec{u}}_N^h+\omega ^2{\varvec{u}} _N^h\right] \cdot \big ( \overline{\varvec{v}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}{\varvec{x}} \\&\quad = \sum \limits _{K\in {\mathcal {M}}_h}\left[ \int _{K}\mathscr {R}{\varvec{u}}_N^h \cdot \big ( \overline{\varvec{v}}-\overline{{\varvec{v}}^h}\big )\mathrm{d}{\varvec{x}} +\sum \limits _{e\in \partial K}\frac{1}{2}\int _{e}J_e \cdot \big (\overline{{\varvec{v}}}-\overline{{\varvec{v}}^h}\big )\mathrm{ds} \right] . \end{aligned}$$

We take ${\varvec{v}}^h=\Pi _h {\varvec{v}}\in {\varvec{V}}_{h, \partial D}$, where $\Pi _h$ is the Clément-type interpolation operator and has the following interpolation estimates (cf. [12]):

$$\begin{aligned} \Vert {\varvec{v}}-\Pi _h {\varvec{v}}\Vert _{{\varvec{L}}^2(K)}\lesssim h_K \Vert \nabla {\varvec{v}}\Vert _{{\varvec{L}}^2({\tilde{K}})},\quad \Vert {\varvec{v}}-\Pi _h{\varvec{v}}\Vert _{{\varvec{L}}^2(e)}\lesssim h_e^{1/2}\Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}({\tilde{K}}_e)}. \end{aligned}$$

Here ${\tilde{K}}$ is the union of all the triangular elements in ${\mathcal {M}}_h$, which have nonempty intersection with the element K, and ${\tilde{K}}_e$ is the union of $\{{\tilde{K}}: e\subset K\in {\mathcal {M}}_h\}$. It follows from the definitions of ${\varvec{g}}$ and ${\varvec{g}}_N$ that

$$\begin{aligned} \int _{\partial B_R}\big ({\varvec{g}}-{\varvec{g}}_N\big )\cdot \overline{{\varvec{v}}}\mathrm{d}s= & {} \int _{\partial B_R}\left[ \left( {\mathscr {B}}{\varvec{u}}^\mathrm{inc}-{\mathscr {T}}{\varvec{u}}^{\mathrm{inc}}\right) -\left( {\mathscr {B}}{\varvec{u}}^\mathrm{inc}-{\mathscr {T}}_N{\varvec{u}}^{\mathrm{inc}}\right) \right] \cdot \overline{{\varvec{v}}}\mathrm{d}s\\= & {} \int _{\partial B_R} \left( {\mathscr {T}}_N-{\mathscr {T}}\right) {\varvec{u}}^{\mathrm{inc}} \cdot \overline{{\varvec{v}}}\mathrm{d}s. \end{aligned}$$

By Lemma 4.5, we have

$$\begin{aligned}&\left| \int _{\partial B_R}\left( {\varvec{g}}-{\varvec{g}}_N\right) \cdot \overline{ {\varvec{v}}}\mathrm{d}s +\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}} \cdot \overline{{\varvec{v}}}\mathrm{d}s\right| \\&\quad = \left| \int _{\partial B_R} \left( {\mathscr {T}}-{\mathscr {T}}_N\right) {\varvec{u}}^s\cdot \overline{\varvec{{\varvec{v}}}} \mathrm{d}s\right| \lesssim N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )} \Vert {\varvec{v}}\Vert _{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

The proof is completed by combining the above estimates. $\square$

The following lemma is to estimate the last term in (4.3).

Lemma 4.7

For any $\delta >0$, there exists a positive constant $C(\delta )$ independent of N such that

$$\begin{aligned} \Re \int _{\partial B_R}{\mathscr {T}}_N\varvec{\xi }\cdot \overline{ \varvec{\xi }}\mathrm{d}s\le C(\delta ) \Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2( B_R{\setminus } \overline{B_{{\hat{R}}}} )} +\bigg (\frac{R}{{\hat{R}}}\bigg )\delta \Vert \varvec{\xi }\Vert ^2_{{\varvec{H}}^{1}(B_R{\setminus } \overline{B_{{\hat{R}}}})}. \end{aligned}$$

Proof

Using (3.1), we get from a simple calculation that

$$\begin{aligned} \Re \int _{\partial B_R}{\mathscr {T}}_N\varvec{\xi }\cdot \overline{ \varvec{\xi }}\mathrm{d}s = 2\pi R\,\Re \sum \limits _{|n|\le N }\left( M_n\varvec{\xi }_n\right) \cdot \overline{\varvec{\xi }_n}. \end{aligned}$$

Denote $\hat{M}_n=(M_n+M_n^*)/2$. Then $\Re \left( M_n\varvec{\xi }_n\right) \cdot \overline{\varvec{\xi }_n}=\big (\hat{M}_n\varvec{\xi } _n\big )\cdot \overline{\varvec{\xi }_n}$. It is shown in [38] that $\hat{M}_n$ is negative definite for sufficiently large |n|, i.e., there exists $N_0>0$ such that $\big (\hat{M}_n\varvec{\xi }_n\big )\cdot \overline{\varvec{\xi } _n}\le 0$ for any $|n|>N_0$. Hence

$$\begin{aligned} \Re \int _{\partial B_R}{\mathscr {T}}_N\varvec{\xi }\cdot \overline{ \varvec{\xi }}\mathrm{d}s =2\pi R\sum \limits _{|n|\le \min (N_0, N)}\big (\hat{M}_n\varvec{\xi }_n\big )\cdot \overline{\varvec{\xi }_n} +2\pi R\sum \limits _{N\ge |n|>\min (N_0, N)}\big (\hat{M}_n\varvec{\xi }_n\big )\cdot \overline{\varvec{\xi }_n}\qquad \nonumber \\ \end{aligned}$$

(4.8)

Here we define

$$\begin{aligned} \sum \limits _{N>|n|>\min (N_0, N)}\big (\hat{M}_n\varvec{\xi } _n\big )\cdot \overline{\varvec{\xi }_n} =0, \quad N_0>N. \end{aligned}$$

Since the second part in (4.8) is non-positive, we only need to estimate the first part which consists of finite terms. Moreover we have

$$\begin{aligned} \Re \int _{\partial B_R}{\mathscr {T}}_N\varvec{\xi }\cdot \overline{ \varvec{\xi }}\mathrm{d}s\le & {} 2\pi R\sum \limits _{|n|\le \min (N_0, N)}\big (\hat{M}_n\varvec{\xi }_n\big )\cdot \overline{\varvec{\xi }_n} \nonumber \\\le & {} C \sum \limits _{|n|\le \min (N_0, N)}|\varvec{\xi }_n|^2\le C\Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2(\partial B_R)}. \end{aligned}$$

(4.9)

Consider the annulus

$$\begin{aligned} B_R{\setminus } B_{\hat{R}}=\{(r, \theta ): \hat{R}<r<R,\,0<\theta <2\pi \}. \end{aligned}$$

For any $u\in H^{1}(B_R{\setminus }\overline{B_{\hat{R}}})$ and $\delta >0$, it follows from the Cauchy–Schwarz inequality that

$$\begin{aligned}&(R-{\hat{R}})|u(R)|^2 = \int _{{\hat{R}}}^{R} |u(r)|^2\mathrm{d}r+\int _{{\hat{R}}}^{R}\int _{r}^{R}\frac{\mathrm{d}}{\mathrm{d}t}|u(t)|^2\mathrm{d}t\mathrm{d}r\\&\qquad \le \int _{{\hat{R}}}^{R}|u(r)|^2\mathrm{d}r+(R-{\hat{R}})\int _{{\hat{R}}}^{R} 2|u(r)||u'(r)|\mathrm{d}r \\&\qquad =\int _{{\hat{R}}}^{R} |u(r)|^2\mathrm{d}r+(R-{\hat{R}})\int _{{\hat{R}}}^{R}2\frac{|u(r)|}{\sqrt{\delta }}\sqrt{ \delta }|u'(r)|\mathrm{d}r\\&\qquad \le \int _{{\hat{R}}}^{R}|u(r)|^2\mathrm{d}r+\delta ^{-1}(R-{\hat{R}})\int _{{\hat{R}}}^{R}|u(r)|^2 \mathrm{d}r +\delta (R-{\hat{R}})\int _{{\hat{R}}}^{R}|u'(r)|^2\mathrm{d}r, \end{aligned}$$

which gives

$$\begin{aligned} |u(R)|^2\le \left[ \delta ^{-1}+(R-{\hat{R}})^{-1}\right] \int _{{\hat{R}}}^{R}|u(r)|^2 \mathrm{d}r +\delta \int _{{\hat{R}}}^{R}|u'(r)|^2\mathrm{d}r. \end{aligned}$$

(4.10)

On the other hand, we have

$$\begin{aligned} \Vert \nabla u\Vert ^2_{{\varvec{L}}^2(B_R{\setminus } \overline{B_{{\hat{R}}}} )}= & {} 2\pi \sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R}\Big ( r|u_n'(r)|^2+\frac{n^2}{r}|u_n(r)|^2\Big )\mathrm{d}r, \end{aligned}$$

(4.11)

$$\begin{aligned} \Vert u\Vert _{L^{2}(B_R{\setminus } \overline{B_{{\hat{R}}}})}^2= & {} 2\pi \sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R}r|u_n(r)|^2\mathrm{d}r. \end{aligned}$$

(4.12)

Using (4.10)–(4.12), we have for any $u\in H^{1}(B_R{\setminus } \overline{B_{{\hat{R}}}} )$ that

$$\begin{aligned}&\Vert u\Vert ^2_{L^2(\partial B_R)} = 2\pi R\sum \limits _{n\in {\mathbb {Z}}}|u_n(R)|^2 \nonumber \\&\quad \le 2\pi R\left[ \delta ^{-1}+(R-{\hat{R}})^{-1}\right] \sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R}|u_n(r)|^2 \mathrm{d}r \nonumber \\&\qquad +2\pi R\delta \sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R}| u'_n(r)|^2\mathrm{d}r \nonumber \\&\quad \le 2\pi \left[ \delta ^{-1}+(R-{\hat{R}})^{-1}\right] \bigg (\frac{R}{{\hat{R}}}\bigg )\sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R} r|u_n(r)|^2\mathrm{d}r \nonumber \\&\qquad +2\pi \delta \bigg (\frac{R}{{\hat{R}}}\bigg )\sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R} \Big (r|u'_n(r)|^2 +\frac{n^2}{r}|u_n(r)|^2\Big )\mathrm{d}r\nonumber \\&\quad = 2\pi \left[ \delta ^{-1}+(R-{\hat{R}})^{-1}\right] \bigg (\frac{R}{{\hat{R}}}\bigg )\Vert u\Vert ^2_{L^2( B_R{\setminus } \overline{B_{{\hat{R}}}} )} +\delta \bigg (\frac{R}{{\hat{R}}}\bigg )\Vert \nabla u\Vert ^2_{L^2( B_R{\setminus } \overline{B_{{\hat{R}}}} )}\nonumber \\&\quad \le C(\delta ) \Vert u\Vert ^2_{L^2(B_R{\setminus } \overline{B_{{\hat{R}}}} )}+\bigg (\frac{R}{{\hat{R}}}\bigg )\delta \Vert \nabla u\Vert ^2_{L^2( B_R{\setminus } \overline{B_{{\hat{R}}}} )}. \end{aligned}$$

(4.13)

Therefore, combining (4.9) and (4.13) yields

$$\begin{aligned} \Re \int _{\partial B_R}{\mathscr {T}}_N\varvec{\xi }\cdot \overline{ \varvec{\xi }}\mathrm{d}s\le & {} C\Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2(\partial B_R)} \le C(\delta ) \Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2(B_R{\setminus } \overline{B_{{\hat{R}}}} )} +\bigg (\frac{R}{{\hat{R}}}\bigg )\delta \int _{\Omega }|\nabla \varvec{\xi }| \mathrm{d}{\varvec{x}}\\\le & {} C(\delta ) \Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2( B_R{\setminus } \overline{B_{{\hat{R}}}} )} +\bigg (\frac{R}{{\hat{R}}}\bigg )\delta \Vert \varvec{\xi }\Vert ^2_{{\varvec{H}}^{1}(B_R{\setminus } \overline{B_{{\hat{R}}}} )}, \end{aligned}$$

which completes the proof. $\square$

To estimate the third term on the right hand side of (4.3), we consider the dual problem

$$\begin{aligned} b({\varvec{v}}, {\varvec{p}})=\int _{\Omega } {\varvec{v}}\cdot \overline{\varvec{\xi }}\mathrm{d}{\varvec{x}}, \quad \forall {\varvec{v}}\in {\varvec{H}}^{1}_{\partial D}(\Omega ). \end{aligned}$$

(4.14)

It is easy to check that ${\varvec{p}}$ is the solution of the following boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu \Delta {\varvec{p}}+(\lambda +\mu )\nabla \nabla \cdot {\varvec{p}}+\omega ^2{\varvec{p}} = -\varvec{\xi } \quad &{}\text {in }\Omega ,\\ {\varvec{p}}=0 \quad &{}\text {on }\partial D,\\ {\mathscr {B}}{\varvec{p}}={\mathscr {T}}^{*}{\varvec{p}} \quad &{} \text {on }\partial B_R, \end{array}\right. } \end{aligned}$$

(4.15)

where ${\mathscr {T}}^*$ is the adjoint operator to the DtN operator ${\mathscr {T}}$. Letting ${\varvec{v}}=\varvec{\xi }$ in (4.14), we obtain

$$\begin{aligned} \Vert \varvec{\xi }\Vert ^2_{{\varvec{L}}^2(\Omega )} =b(\varvec{\xi }, {\varvec{p}})+\int _{\partial B_R}\left( {\mathscr {T}} -{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s -\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s.\nonumber \\ \end{aligned}$$

(4.16)

To evaluate (4.16), we need to explicitly solve system (4.15), which is very complicate due to the coupling of the compressional and shear wave components. We consider the Helmholtz decomposition to the boundary value problem (4.15). Let

$$\begin{aligned} \varvec{\xi }=\nabla \xi _1+\mathbf{curl}\xi _2, \end{aligned}$$

(4.17)

where $\xi _j, j=1, 2$ has the Fourier series expansion

$$\begin{aligned} \xi _j(r, \theta )=\sum _{n\in {\mathbb {Z}}}\xi _{jn}(r) e^{\mathrm{i}n\theta },\quad \hat{R}<r<R. \end{aligned}$$

Meanwhile, we assume that

$$\begin{aligned} \varvec{\xi }(r,\theta )=\sum \limits _{n\in {\mathbb {Z}}}\left( \xi _n^{r}(r) {\varvec{e}}_r +\xi _n^{\theta }(r){\varvec{e}}_{\theta }\right) e^{\mathrm{i}n\theta }. \end{aligned}$$

(4.18)

Using the Fourier series expansions and the Helmholtz decomposition, we get

$$\begin{aligned} \varvec{\xi } (r,\theta )= & {} \sum \limits _{n\in {\mathbb {Z}}}\left[ \xi _n^{r}(r){\varvec{e}}_r +\xi _n^{\theta }(r){\varvec{e}}_{\theta }\right] e^{\mathrm{i}n\theta }=\nabla \xi _1+\mathbf{curl}\xi _2\\= & {} \sum \limits _{n\in {\mathbb {Z}}} \left[ \xi '_{1n}(r){\varvec{e}}_r+\frac{\mathrm{i}n}{r}\xi _{1n}(r){\varvec{e}}_{\theta } +\frac{\mathrm{i}n}{r}\xi _{2n}(r){\varvec{e}}_r-\xi '_{2n}(r) {\varvec{e}}_{\theta }\right] e^{\mathrm{i}n\theta }\\= & {} \sum \limits _{n\in {\mathbb {Z}}}\left[ \Big (\xi '_{1n}(r)+\frac{\mathrm{i}n}{r}\xi _{2n}(r)\Big ){\varvec{e}}_r +\Big (\frac{\mathrm{i}n}{r}\xi _{1n}(r)-\xi '_{2n}(r)\Big ){\varvec{e}}_{\theta }\right] e^{\mathrm{i}n\theta }, \end{aligned}$$

which shows that the Fourier coefficients $\xi _{1n}, \xi _{2n}$ satisfy

$$\begin{aligned} \xi '_{1n}(r)+\frac{\mathrm{i}n}{r}\xi _{2n}(r)=\xi _n^{r}(r),\quad \frac{\mathrm{i}n}{r}\xi _{1n}(r)-\xi '_{2n}(r) =\xi _n^{\theta }(r), \quad&r\in ({\hat{R}}, R). \end{aligned}$$

Lemma 4.8

The system for the Fourier coefficients

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi '_{1n}(r)+\frac{\mathrm{i}n}{r}\xi _{2n}(r)=\xi _n^{r}(r), \quad &{} r\in ({\hat{R}}, R),\\ \frac{\mathrm{i}n}{r}\xi _{1n}(r)-\xi '_{2n}(r) =\xi _n^{\theta }(r), \qquad &{} r\in ({\hat{R}}, R),\\ \xi _{1n}(R)=0,\quad \xi _{2n}(R)=0,\quad &{} r=R, \end{array}\right. } \end{aligned}$$

(4.19)

has a unique solution given by

$$\begin{aligned} \xi _{1n}(r)= & {} -\frac{1}{2}\int _{r}^{R} \left[ \left( \frac{r}{t}\right) ^n +\left( \frac{t}{r}\right) ^n\right] \xi _n^r(t)\mathrm{d}t +\frac{\mathrm{i}}{2}\int _{r}^{R}\left[ \left( \frac{r}{t}\right) ^n -\left( \frac{t}{r}\right) ^n\right] \xi _n^{\theta }(t)\mathrm{d}t, \end{aligned}$$

(4.20)

$$\begin{aligned} \xi _{2n}(r)= & {} \frac{\mathrm{i}}{2}\int _{r}^{R} \left[ \left( \frac{t}{r}\right) ^n -\left( \frac{r}{t}\right) ^n\right] \xi _n^r(t)\mathrm{d}t -\frac{1}{2}\int _{r}^{R}\left[ \left( \frac{r}{t}\right) ^n +\left( \frac{t}{r}\right) ^n\right] \xi _n^{\theta }(t)\mathrm{d}t. \nonumber \\ \end{aligned}$$

(4.21)

Proof

Denote

$$\begin{aligned} A_n(r)=\begin{bmatrix} 0 &{} -\frac{\mathrm{i}n}{r}\\ \frac{\mathrm{i}n}{r} &{} 0\end{bmatrix}. \end{aligned}$$

By the standard theory of the first order differential system, the fundamental solution $\Phi _n(r)$ is

$$\begin{aligned} \Phi _n(r)= & {} e^{\int _{{\hat{R}}}^r A_n(\tau )\mathrm{d}\tau }=\exp \left( \begin{bmatrix} 0 &{} -\mathrm{i}n\ln \frac{r}{{\hat{R}}}\\ \mathrm{i}n\ln \frac{r}{{\hat{R}}} &{} 0 \end{bmatrix}\right) \\= & {} \begin{bmatrix} \frac{1}{\sqrt{2}} &{} \frac{\mathrm{i}}{\sqrt{2}}\\ \frac{\mathrm{i}}{\sqrt{2}} &{} \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \left( \frac{r}{{\hat{R}}}\right) ^n &{} 0\\ 0 &{} \left( \frac{r}{{\hat{R}}}\right) ^{-n} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} &{} -\frac{\mathrm{i}}{\sqrt{2}}\\ -\frac{\mathrm{i}}{\sqrt{2}} &{} \frac{1}{\sqrt{2}} \end{bmatrix}. \end{aligned}$$

The inverse of $\Phi _n$ is

$$\begin{aligned} \Phi _n^{-1}(r)= \begin{bmatrix} \frac{1}{\sqrt{2}} &{} \frac{\mathrm{i}}{\sqrt{2}}\\ \frac{\mathrm{i}}{\sqrt{2}} &{} \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} \left( \frac{r}{{\hat{R}}}\right) ^{-n} &{} 0\\ 0 &{} \left( \frac{r}{{\hat{R}}}\right) ^{n} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} &{} -\frac{\mathrm{i}}{\sqrt{2}}\\ -\frac{\mathrm{i}}{\sqrt{2}} &{} \frac{1}{\sqrt{2}} \end{bmatrix}. \end{aligned}$$

Using the method of variation of parameters, we let

$$\begin{aligned} (\xi _{1n}(r),\xi _{2n}(r))^\top =\Phi _n(r)C_n(r), \end{aligned}$$

where the unknown vector $C_n(r)$ satisfies

$$\begin{aligned} C_n^\prime (r)= & {} \Phi _n^{-1}(r)(\xi _n^r(r), \xi _n^{\theta }(r))^\top \nonumber \\= & {} \frac{1}{2} \begin{bmatrix} \left[ \left( \frac{r}{{\hat{R}}}\right) ^{-n}+\left( \frac{r}{{\hat{R}}}\right) ^n\right] \xi _n^r(r) +\mathrm{i}\left[ \left( \frac{r}{{\hat{R}}}\right) ^{n}-\left( \frac{r}{{\hat{R}}}\right) ^{-n} \right] \xi _n^{\theta }(r)\\ \mathrm{i}\left[ \left( \frac{r}{{\hat{R}}}\right) ^{-n}-\left( \frac{r}{{\hat{R}}}\right) ^n\right] \xi _n^r(r) +\left[ \left( \frac{r}{{\hat{R}}}\right) ^{-n}+\left( \frac{r}{{\hat{R}}}\right) ^{n}\right] \xi _n^{\theta }(r) \end{bmatrix}. \end{aligned}$$

(4.22)

Using the boundary condition yields

$$\begin{aligned} (\xi _{1n}(R), \xi _{2n}(R))^\top =\Phi _n(R)C_n(R)=(0,0)^\top , \end{aligned}$$

which implies that $C_n(R)=(0, 0)^\top$. Then

$$\begin{aligned} C_n(r)=-\int _{r}^{R}C_n^\prime (t)\mathrm{d}t. \end{aligned}$$

(4.23)

Combining (4.22) and (4.23), we have

$$\begin{aligned} C_n(r)=-\frac{1}{2}\begin{bmatrix} \int _{r}^{R}\left[ \left( \frac{t}{{\hat{R}}}\right) ^{-n}+\left( \frac{t}{{\hat{R}}} \right) ^{n}\right] \xi _n^{r}(t)\mathrm{d}t +\mathrm{i}\int _{r}^{R}\left[ \left( \frac{t}{{\hat{R}}}\right) ^{n}-\left( \frac{t}{{\hat{R}}} \right) ^{-n}\right] \xi _n^{\theta }(t)\mathrm{d}t\\ \mathrm{i}\int _{r}^{R}\left[ \left( \frac{t}{{\hat{R}}}\right) ^{-n}-\left( \frac{t}{{\hat{R}}} \right) ^{n}\right] \xi _n^{r}(t)\mathrm{d}t +\int _{r}^{R}\left[ \left( \frac{t}{{\hat{R}}}\right) ^{n}+\left( \frac{t}{{\hat{R}}} \right) ^{-n}\right] \xi _n^{\theta }(t)\mathrm{d}t. \end{bmatrix}. \end{aligned}$$

Substituting $C_n(r)$ into the general solution, we obtain

$$\begin{aligned} \xi _{1n}(r)= & {} -\frac{1}{2}\left( \frac{r}{{\hat{R}}}\right) ^n\int _{r}^{R}\left( \frac{t}{{\hat{R}}} \right) ^{-n}\xi _n^{r}(t)\mathrm{d}t +\frac{\mathrm{i}}{2}\left( \frac{r}{{\hat{R}}}\right) ^n\int _{r}^{R}\left( \frac{t}{{\hat{R}}} \right) ^{-n} \xi _n^{\theta }(t)\mathrm{d}t\\&\qquad -\frac{1}{2}\left( \frac{r}{{\hat{R}}}\right) ^{-n}\int _{r}^{R}\left( \frac{t}{{\hat{R}}} \right) ^{n}\xi _n^{r}(t)\mathrm{d}t -\frac{\mathrm{i}}{2} \left( \frac{r}{{\hat{R}}}\right) ^{-n}\int _{r}^{R}\left( \frac{t}{{\hat{R}}}\right) ^{n} \xi _n^{\theta }(t)\mathrm{d}t\\ \xi _{2n}(r)= & {} -\frac{\mathrm{i}}{2}\left( \frac{r}{{\hat{R}}}\right) ^n\int _{r}^{R}\left( \frac{t}{{\hat{R}}} \right) ^{-n} \xi _n^{r}(t)\mathrm{d}t +\frac{\mathrm{i}}{2} \left( \frac{r}{{\hat{R}}}\right) ^{-n}\int _{r}^{R}\left( \frac{t}{{\hat{R}}}\right) ^{n} \xi _n^{r}(t)\mathrm{d}t\\&\qquad -\frac{1}{2}\left( \frac{r}{{\hat{R}}}\right) ^{n}\int _{r}^{R}\left( \frac{t}{{\hat{R}}} \right) ^{-n}\xi _n^{\theta }(t)\mathrm{d}t-\frac{1}{2} \left( \frac{r}{{\hat{R}}}\right) ^{-n}\int _{r}^{R}\left( \frac{t}{{\hat{R}}}\right) ^{n} \xi _n^{\theta }(t)\mathrm{d}t, \end{aligned}$$

which completes the proof. $\square$

Let ${\varvec{p}}$ be the solution of the dual problem (4.15). Then ${\varvec{p}}$ satisfies the following boundary value problem in $B_R{\setminus }{{\overline{B}}}_{\hat{R}}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu \Delta {\varvec{p}}+(\lambda +\mu )\nabla \nabla \cdot {\varvec{p}} +\omega ^2 {\varvec{p}}=-\varvec{\xi } \quad &{} \text {in}\, B_R{\setminus }\overline{B_{{\hat{R}}}}, \\ {\varvec{p}}({\hat{R}},\theta )={\varvec{p}}({\hat{R}}, \theta ) \quad &{} \text {on}\, \partial B_{{\hat{R}}},\\ {\mathscr {B}}{\varvec{p}}={\mathscr {T}}^{*}{\varvec{p}} \quad &{} \text {on}\,\partial B_R. \end{array}\right. } \end{aligned}$$

(4.24)

Introduce the Helmholtz decomposition for ${\varvec{p}}$:

$$\begin{aligned} {\varvec{p}}=\nabla q_1+\mathbf{curl} q_2, \end{aligned}$$

(4.25)

where $q_j, j=1, 2$ admits the Fourier series expansion

$$\begin{aligned} q_j(r, \theta )=\sum \limits _{n\in {\mathbb {Z}}}q_{jn}(r)e^{\mathrm{i}n\theta }. \end{aligned}$$

Let $\xi _{jn}, j=1, 2$ be the solution of the system (4.19). Consider the second order system for $q_{jn}, j=1, 2$:

$$\begin{aligned} {\left\{ \begin{array}{ll} q''_{jn}(r)+\frac{1}{r}q'_{jn}(r)+\big (\kappa _j^2-\left( \frac{n}{R} \right) ^2\big )q_{jn}(r) =c_j\xi _{jn}(r),\quad &{} r\in ({\hat{R}}, R),\\ q_{jn}({\hat{R}})=q_{jn}({\hat{R}}),\quad &{} r={\hat{R}},\\ q'_{jn}(R)=\overline{\alpha _{jn}} q_{jn}(R),\quad &{} r=R, \end{array}\right. } \end{aligned}$$

(4.26)

where $c_1=-1/(\lambda +2\mu ), c_2=-1/\mu ,$ and $\alpha _{jn}$ is given in (A.5). The boundary condition $q'_{jn}(R)=\overline{\alpha _{jn}} q_{jn}(R)$ comes from (A.2), i.e., $q_j$ satisfies the boundary condition

$$\begin{aligned} \partial _r q_j={\mathscr {T}}_j^* q_j:=\sum _{n\in \mathbb Z}\overline{\alpha _{jn}} q_{jn}(R)e^{\mathrm{i}n\theta }\quad \text {on}\,\partial B_R, \end{aligned}$$

where ${\mathscr {T}}_j^*$ is the adjoint operator to the DtN operator ${\mathscr {T}}_j$.

Lemma 4.9

The boundary value problem (4.24) and the second order system (4.26) are equivalent under the Helmholtz decomposition (4.25).

Proof

It suffices to show if the Fourier coefficients $q_{jn}$ satisfy the second order system (4.26), then ${\varvec{p}}=\nabla q_1+\mathbf{curl}q_2$ is the solution of (4.24).

In the polar coordinates, we let

$$\begin{aligned} {\varvec{p}}(r, \theta )=\sum _{n\in {\mathbb {Z}}}(p_n^r(r)\varvec{e}_r + p_n^\theta (r){\varvec{e}}_\theta )e^{\mathrm{i}n\theta },\quad r\in ({\hat{R}}, R). \end{aligned}$$

(4.27)

It follows from the Helmholtz decomposition that

$$\begin{aligned} p_n^{r}(r)=q'_{1n}(r)+\frac{\mathrm{i}n}{r}q_{2n}(r),\quad p_n^{\theta }(r)=\frac{\mathrm{i}n}{r}q_{1n}(r)-q'_{2n}(r). \end{aligned}$$

(4.28)

Using (4.27)–(4.28), we have from a straightforward calculation that

$$\begin{aligned} {\mathscr {B}}{\varvec{p}}= & {} \big (\mu \partial _r{\varvec{p}}+(\lambda +\mu )\nabla \cdot {\varvec{p}} {\varvec{e}}_r\big ) |_{r=R} \\= & {} \sum \limits _{n\in {\mathbb {Z}}} \Big [(\lambda +2\mu )q''_{1n}(R)+(\lambda +\mu )\frac{1}{R}q'_{1n}(R) -(\lambda +\mu )\frac{n^2}{R^2}q_{1n}(R)\Big ]e^{\mathrm{i}n\theta }{\varvec{e}}_r\\&+\sum \limits _{n\in {\mathbb {Z}}}\Big [\mu \frac{\mathrm{i}n}{R}q'_{1n}(R)-\mu \frac{\mathrm{i}n}{R^2}q_{1n}(R)\Big ] e^{\mathrm{i}n\theta }{\varvec{e}}_{\theta } \\&+\sum \limits _{n\in {\mathbb {Z}}}\Big [\mu \frac{\mathrm{i}n}{R}q'_{2n}(R)-\mu \frac{\mathrm{i}n}{R^2}q_{2n}(R)\Big ] e^{\mathrm{i}n\theta }{\varvec{e}}_{r}+\sum \limits _{n\in {\mathbb {Z}}}-\mu q''_{2n}(R)e^{\mathrm{i}n\theta }{\varvec{e}}_{\theta }. \end{aligned}$$

On the other hand, it is easy to verify that

$$\begin{aligned} {\mathscr {T}}^{*}{\varvec{p}}= & {} \sum \limits _{n\in {\mathbb {Z}}} \left\{ \Big [\overline{M_{11}^{(n)}} p_n^r(R) +\overline{M_{21}^{(n)}} p_n^{\theta }(R)\Big ]{\varvec{e}}_r +\Big [\overline{M_{12}^{(n)}} p_n^r(R) +\overline{M_{22}^{(n)}} p_n^{\theta }(R)\Big ]{\varvec{e}}_{\theta }\right\} e^{{ \mathrm i}n\theta }\\= & {} \sum \limits _{n\in {\mathbb {Z}}}\left\{ \overline{M_{11}^{(n)}} \Big [q'_{1n}(R)+\frac{\mathrm{i}n}{R}q_{2n}(R)\Big ] +\overline{M_{21}^{(n)}} \Big [\frac{\mathrm{i}n}{R}q_{1n}(R)-q'_{2n}(R)\Big ]\right\} {\varvec{e}}_r e^{\mathrm{i}n\theta }\\&\quad +\sum \limits _{n\in {\mathbb {Z}}} \left\{ \overline{M_{12}^{(n)}} \Big [q'_{1n}(R)+\frac{\mathrm{i}n}{R}q_{2n}(R)\Big ] +\overline{M_{22}^{(n)}} \Big [\frac{\mathrm{i}n}{R}q_{1n}(R)-q'_{2n}(R)\Big ]\right\} {\varvec{e}}_{\theta } e^{\mathrm{i}n\theta }, \end{aligned}$$

where $M_{ij}^{(n)}, i,j=1, 2$ are given in (A.4).

Using the boundary condition $q'_{jn}(R)=\overline{\alpha _{jn}} q_{jn}(R)$, we get

$$\begin{aligned}&\left( \mu \frac{\mathrm{i}n}{R}-\overline{M_{12}^{(n)}}\right) q'_{1n}(R)-\left( \overline{M_{22}^{(n)}} \frac{\mathrm{i}n}{R} +\mu \frac{\mathrm{i}n}{R^2}\right) q_{1n}(R)\\&\quad = \left( \mu \frac{\mathrm{i}n}{R}-\mathrm{i}n\frac{\mu }{R}+\omega ^2\frac{\mathrm{i}n}{R}\frac{1}{\overline{\Lambda _n(R)}} \right) q'_{1n}(R)\\&\qquad -\left( -\frac{\mu }{R}\frac{\mathrm{i}n}{R}+\omega ^2\frac{\mathrm{i}n}{R}\frac{\overline{\alpha _{1n}}}{\overline{\Lambda _n(R)}} +\mu \frac{\mathrm{i}n}{R^2}\right) q_{1n}(R)\\&\quad = \omega ^2 \frac{\mathrm{i}n}{R}\frac{1}{\overline{\Lambda _n(R)}}\left( q'_{1n}(R)-\overline{ \alpha _{1n}} q_{1n}(R)\right) =0 \end{aligned}$$

and

$$\begin{aligned}&\left( \mu \frac{\mathrm{i}n}{R}+\overline{M_{21}^{(n)}}\right) q'_{2n}(R)-\left( \overline{M_{11}^{(n)}} \frac{\mathrm{i}n}{R}+\mu \frac{\mathrm{i}n}{R^2}\right) q_{2n}(R)\\&\quad = \left( \mu \frac{\mathrm{i}n}{R}-\mathrm{i}n\frac{\mu }{R}+\mathrm{i}n\frac{\omega ^2}{R}\frac{1}{\overline{\Lambda _n(R)}}\right) q'_{2n}(R)\\&\qquad -\left( \mu \frac{\mathrm{i}n}{R^2}-\frac{\mu }{R}\frac{\mathrm{i}n}{R}+\omega ^2\frac{\mathrm{i}n}{R}\frac{\overline{\alpha _{2n}}}{\overline{\Lambda _n(R)}} \right) q_{2n}(R)\\&\quad = \mathrm{i}n\frac{\omega ^2}{R}\frac{1}{\overline{\Lambda _n(R)}}\left( q'_{2n}(R)-\overline{\alpha _{2n}}q_{2n}(R)\right) =0. \end{aligned}$$

Since $q_{2n}$ satisfies the second order equation

$$\begin{aligned} q''_{2n}(r)+\frac{1}{r}q'_{2n}(r)+\left( \kappa _2^2-\left( \frac{n}{r} \right) ^2\right) q_{2n}(r)=-\frac{1}{\mu }\xi _{2n},\quad r\in ({\hat{R}}, R), \end{aligned}$$

we obtain from the boundary condition $\xi _{2n}(R)=0$ that

$$\begin{aligned}&-\mu q''_{2n}(R)-\left( \overline{M_{12}^{(n)}}\frac{\mathrm{i}n}{R}q_{2n}(R)-\overline{M_{22}^{(n)}}q'_{2n}(R)\right) \\&\quad = -\mu q''_{2n}(R)-\frac{\mathrm{i}n}{R}\left( \mathrm{i}n\frac{\mu }{R} -\omega ^2 \frac{\mathrm{i}n}{R}\frac{1}{\overline{\Lambda _n(R)}}\right) q_{2n}(R) +\left( -\frac{\mu }{R}+\omega ^2 \frac{\overline{\alpha _{1n}}}{\overline{\Lambda _n(R)}}\right) q'_{2n}(R)\\&\quad = \xi _{2n}(R)+\mu \kappa _2^2 q_{2n}(R) +\omega ^2\left( \frac{\mathrm{i}n}{R}\right) ^2\frac{1}{\overline{\Lambda _n(R)}} q_{2n}(R) +\omega ^2\frac{\overline{\alpha _{1n}}}{\overline{\Lambda _n(R)}} q'_{2n}(R)\\&\quad =\xi _{2n}(R)+\frac{\omega ^2}{\overline{\Lambda _n(R)}}\left( \left( \frac{n}{R} \right) ^2 q_{2n}(R) -\overline{\alpha _{1n}}\overline{\alpha _{2n}} q_{2n}(R) -\left( \frac{n}{R}\right) ^2 q_{2n}(R)+\overline{\alpha _{1n}} q'_{2n}(R)\right) \\&\quad = \xi _{2n}(R)+\omega ^2\frac{\overline{\alpha _{1n}}}{\overline{ \Lambda _n(R)}} \left( -\overline{\alpha _{2n}} q_{2n}(R)+q'_{2n}(R)\right) =0. \end{aligned}$$

Similarly, combining the equation

$$\begin{aligned} q''_{1n}(r)+\frac{1}{r}q'_{1n}(r)+\left( \kappa _1^2-\left( \frac{n}{r} \right) ^2\right) q_{1n}(r)=-\frac{1}{\lambda +2\mu }\xi _{1n}(r),\quad r\in ({\hat{R}}, R) \end{aligned}$$

and the boundary condition $\xi _{1n}(R)=0$, we have

$$\begin{aligned}&(\lambda +2\mu )q''_{1n}(R)+(\lambda +\mu ) \frac{1}{R}q'_{1n}(R) -(\lambda +\mu )\frac{n^2}{R^2}q_{1n}(R)\\&\qquad -\overline{M_{11}^{(n)}}q'_{1n}(R) -\frac{\mathrm{i}n}{R}\overline{M_{21}^{(n)}}q_{1n}(R)\\&\quad =(\lambda +2\mu )\left[ -\frac{1}{\lambda +2\mu }\xi _{1n}(R)-\frac{1}{R} q'_{1n}(R)-\left( \kappa _1^2 -\left( \frac{n}{R}\right) ^2\right) q_{1n}(R)\right] \\&\qquad +\left( \frac{\lambda +2\mu }{R}-\omega ^2\frac{\overline{\alpha _{2n}}}{ \overline{\Lambda _n(R)}}\right) q'_{1n}(R)\\&\qquad +\left( -(\lambda +2\mu )\left( \frac{n}{R}\right) ^2 +\omega ^2\frac{1}{\overline{\Lambda _n(R)}}\left( \frac{n}{R}\right) ^2\right) q_{1n}(R)\\&\quad = -\xi _{1n}(R)-\omega ^2\frac{\overline{\alpha _{2n}}}{\overline{ \Lambda _n(R)} }q'_{1n}(R)+\left( -\omega ^2 +\omega ^2\frac{1}{\overline{\Lambda _n(R)}}\left( \frac{n}{R}\right) ^2\right) q_{1n}(R)\\&\quad = -\xi _{1n}(R)-\frac{\omega ^2}{\overline{\Lambda _n(R)}}\left( \overline{ \alpha _{2n}}q'_{1n}(R) +\left( \frac{n}{R}\right) ^2 q_{1n}(R) -\overline{\alpha _{1n}\alpha _{2n}} q_{1n}(R) \right. \\&\qquad \left. -\left( \frac{n}{R} \right) ^2 q_{1n}(R)\right) \\&\quad = -\xi _{1n}(R) -\frac{\omega ^2}{\overline{\Lambda _n(R)}}\overline{\alpha _{2n}} \left[ q'_{1n}(R) -\overline{\alpha _{1n}} q_{1n}(R)\right] =0. \end{aligned}$$

Hence we prove that $\mathscr {B}{\varvec{p}}={\mathscr {T}}^*{\varvec{p}}$ on $\partial B_R$.

Moreover, we get from the Helmholtz decomposition that

$$\begin{aligned}&\mu \Delta {\varvec{p}}+(\lambda +\mu )\nabla \nabla \cdot {\varvec{p}}+\omega ^2 {\varvec{p}} \\&\quad = \nabla \left( (\lambda +2\mu )\Delta q_1+\omega ^2 q_1\right) +\mathbf{curl}\left( \mu \Delta q_2+\omega ^2 q_2\right) \\&\quad = -\nabla \xi _1-\mathbf{curl}\xi _2=-\varvec{\xi }, \end{aligned}$$

which completes the proof. $\square$

Based on Lemma 4.8 and Lemma 4.9, we have the asymptotic properties of the solution to the dual problem (4.24) for large |n|.

Theorem 4.10

Let ${\varvec{p}}$ be the solution of (4.24) and admit the Fourier series expansion

$$\begin{aligned} {\varvec{p}}(r,\theta )=\sum \limits _{n\in Z} \left( p_n^r(r){\varvec{e}}_r +p_n^{\theta }(r){\varvec{e}}_{\theta }\right) e^{\mathrm{i}\,n\theta }. \end{aligned}$$

For sufficient large |n|, the Fourier coefficients $p_n^r, p_n^{\theta }$ satisfy the estimate

$$\begin{aligned} |p_n^r(R)|^2+|p_n^{\theta }(R)|^2\lesssim & {} n^2\bigg (\frac{{\hat{R}}}{R}\bigg )^{2|n|+2}\left( |p_n^r({\hat{R}})|^2+|p_n^{\theta } ({\hat{R}})|^2\right) \\&+\frac{1}{|n|^2}\left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}^2+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}^2\right) , \end{aligned}$$

where $\xi _n^r, \xi _n^\theta$ are the Fourier coefficients of $\varvec{\xi }$ in the polar coordinates and are given in (4.18).

Proof

It follows from straightforward calculations that the second order systems (4.26) have a unique solution, which is given by

$$\begin{aligned} q_{1n}(r)= & {} \beta _{1n}(r)q_{1n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{r}tW_{1n}(r,t) \xi _{1n}(t)\mathrm{d}t \nonumber \\&\qquad +\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R}t \beta _{1n}(t)W_{1n}({\hat{R}}, r)\xi _{1n}(t)\mathrm{d}t , \end{aligned}$$

(4.29)

$$\begin{aligned} q_{2n}(r)= & {} \beta _{2n}(r)q_{2n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{r}t W_{2n}(r,t) \xi _{2n}(t)\mathrm{d}t \nonumber \\&\qquad +\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R}t \beta _{2n}(t)W_{2n}({\hat{R}}, r)\xi _{2n}(t)\mathrm{d}t , \end{aligned}$$

(4.30)

where

$$\begin{aligned} \beta _{jn}(r)=\frac{H_n^{(2)}(\kappa _j r)}{H_n^{(2)}(\kappa _j {\hat{R}})},\quad W_{jn}(r,t)=H_n^{(1)}(\kappa _j r)H_n^{(2)}(\kappa _j t)-H_n^{(1)}(\kappa _j t)H_n^{(2)}(\kappa _j r). \end{aligned}$$

Taking the derivative of (4.29)–(4.30) with respect to r gives

$$\begin{aligned} q'_{1n}(r)= & {} \beta '_{1n}(r)q_{1n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{r}t\partial _r W_{1n}(r,t)\xi _{1n}(t)\mathrm{d}t \nonumber \\&\qquad +\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R} t \beta _{1n}(t)\partial _t W_{1n}({\hat{R}}, r)\xi _{1n}(t)\mathrm{d}t, \end{aligned}$$

(4.31)

$$\begin{aligned} q'_{2n}(r)= & {} \beta '_{2n}(r)q_{2n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{r}t\partial _r W_{2n}(r,t)\xi _{2n}(t)\mathrm{d}t\nonumber \\&\qquad +\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R} t \beta _{2n}(t)\partial _t W_{2n}({\hat{R}}, r)\xi _{2n}(t)\mathrm{d}t. \end{aligned}$$

(4.32)

Evaluating (4.29)–(4.30) and (4.31)–(4.32) at $r=R$ and $r={\hat{R}}$, respectively, we may verify that

$$\begin{aligned} q_{1n}(R)= & {} \beta _{1n}(R)q_{1n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R}t \beta _{1n}(R) W_{1n}({\hat{R}}, t)\xi _{1n}(t)\mathrm{d}t,\\ q_{2n}(R)= & {} \beta _{2n}(R)q_{2n}({\hat{R}})+\frac{\mathrm{i}\pi }{4}\int _{{\hat{R}}}^{R}t \beta _{2n}(R) W_{2n}({\hat{R}}, t)\xi _{2n}(t)\mathrm{d}t,\\ q'_{1n}({\hat{R}})= & {} \beta '_{1n}({\hat{R}}) q_{1n}({\hat{R}})+\frac{1}{{\hat{R}}}\int _{{\hat{R}}}^{R} t \beta _{1n}(t) \xi _{1n}(t)\mathrm{d}t,\\ q'_{2n}({\hat{R}})= & {} \beta '_{2n}({\hat{R}}) q_{2n}({\hat{R}})+\frac{1}{{\hat{R}}}\int _{{\hat{R}}}^{R} t \beta _{2n}(t) \xi _{2n}(t)\mathrm{d}t. \end{aligned}$$

It follows from the Helmholtz decomposition that

$$\begin{aligned} p_n^{r}(r)=q'_{1n}(r)+\frac{\mathrm{i}n}{r}q_{2n}(r), \quad p_n^{\theta }(r)=\frac{\mathrm{i}n}{r}q_{1n}(r)-q'_{2n}(r). \end{aligned}$$

(4.33)

Evaluating (4.33) at $r=R$, noting $\beta '_{jn}(R)=\overline{\alpha _{jn}(R)}$ and $q'_{jn}(R)=\overline{\alpha _{jn}(R)} q_{jn}(R)$, we obtain

$$\begin{aligned} \begin{bmatrix} p_n^{r}(R) \\ p_n^{\theta }(R) \end{bmatrix}=U_n(R) \begin{bmatrix} q_{1n}({\hat{R}}) \\ q_{2n}({\hat{R}}) \end{bmatrix}+\frac{\mathrm{i}\pi }{4}U_n(R) \begin{bmatrix} \int _{{\hat{R}}}^{R} t W_{1n}({\hat{R}}, t)\xi _{1n}(t)\mathrm{d}t\\ \int _{{\hat{R}}}^{R} t W_{2n}({\hat{R}}, t)\xi _{2n}(t)\mathrm{d}t \end{bmatrix}, \end{aligned}$$

(4.34)

where

$$\begin{aligned} U_n(R)=\begin{bmatrix} \overline{\alpha _{1n}(R)} &{} \frac{\mathrm{i}n}{R}\\ \frac{\mathrm{i}n}{R} &{} -\overline{\alpha _{2n}(R)} \end{bmatrix} \begin{bmatrix} \beta _{1n}(R) &{} 0 \\ 0 &{} \beta _{2n}(R) \end{bmatrix}. \end{aligned}$$

Similarly, evaluating (4.33) at $r={\hat{R}}$ and noting $\beta '_{jn}({\hat{R}})=\overline{\alpha _{jn}({\hat{R}})}$ yield that

$$\begin{aligned} \begin{bmatrix} p_n^{r}({\hat{R}}) \\ p_n^{\theta }({\hat{R}}) \end{bmatrix}=K_n({\hat{R}}) \begin{bmatrix} q_{1n}({\hat{R}}) \\ q_{2n}({\hat{R}}) \end{bmatrix}+ \begin{bmatrix} \eta _1\\ \eta _2 \end{bmatrix}, \end{aligned}$$

(4.35)

where

$$\begin{aligned} K_n({\hat{R}})=\begin{bmatrix} \overline{\alpha _{1n}({\hat{R}})} &{} \frac{\mathrm{i}n}{{\hat{R}}}\\ \frac{\mathrm{i}n}{{\hat{R}}} &{} -\overline{\alpha _{2n}({\hat{R}})} \end{bmatrix}, \end{aligned}$$

and

$$\begin{aligned} \eta _{1n}=\frac{1}{{\hat{R}}}\int _{{\hat{R}}}^{R} t \beta _{1n}(t)\xi _{1n}(t)\mathrm{d}t,\quad \eta _{2n}=-\frac{1}{{\hat{R}}}\int _{{\hat{R}}}^{R} t \beta _{2n}(t)\xi _{2n}(t)\mathrm{d}t. \end{aligned}$$

Solving (4.35) for $q_{1n}({\hat{R}}), q_{2n}({\hat{R}})$ in terms of $p_n^r({\hat{R}}), p_n^{r}({\hat{R}})$ gives

$$\begin{aligned} \begin{bmatrix} q_{1n}({\hat{R}}) \\ q_{2n}({\hat{R}}) \end{bmatrix}=\frac{V_n({\hat{R}})}{\overline{\Lambda _n({\hat{R}})}} \begin{bmatrix} p_n^{r}({\hat{R}})-\eta _{1n}\\ p_n^{\theta }({\hat{R}})-\eta _{2n} \end{bmatrix}, \end{aligned}$$

(4.36)

where

$$\begin{aligned} \Lambda _n({\hat{R}})=\left( \frac{n}{{\hat{R}}}\right) ^2-\alpha _{1n}({\hat{R}})\alpha _{2n}({\hat{R}}),\quad V_n({\hat{R}})=\begin{bmatrix} -\overline{\alpha _{2n}({\hat{R}})} &{} -\frac{\mathrm{i}n}{{\hat{R}}}\\ -\frac{\mathrm{i}n}{{\hat{R}}} &{} \overline{\alpha _{1n}({\hat{R}})} \end{bmatrix}. \end{aligned}$$

Substituting (4.36) into (4.34) yields

$$\begin{aligned} \begin{bmatrix} p_n^{r}(R) \\ p_n^{\theta }(R) \end{bmatrix}= & {} \frac{U_n(R) V_n({\hat{R}})}{\overline{\Lambda _n({\hat{R}})}} \begin{bmatrix} p_n^{r}(\hat{R}) \\ p_n^{\theta }(\hat{R}) \end{bmatrix}+\frac{\mathrm{i}\pi }{4}U_n(R) \begin{bmatrix} \int _{{\hat{R}}}^{R} t W_{1n}({\hat{R}}, t) \xi _{1n}(t)\mathrm{d}t\\ \int _{{\hat{R}}}^{R} t W_{2n}({\hat{R}}, t) \xi _{2n}(t)\mathrm{d}t \end{bmatrix}\nonumber \\&-\frac{U_n(R)V_n({\hat{R}})}{\overline{\Lambda _n({\hat{R}})}} \begin{bmatrix} \eta _{1n} \\ \eta _{2n} \end{bmatrix}. \end{aligned}$$

(4.37)

Following the proofs in Lemmas 4.5 and A.1, we may similarly show that for sufficiently large |n|

$$\begin{aligned} \left| \frac{U_n(R) V_n({\hat{R}})}{\overline{\Lambda _n({\hat{R}})}}\right| \lesssim |n|\bigg (\frac{{\hat{R}}}{R}\bigg )^{|n|}. \end{aligned}$$

For fixed t and sufficiently large |n|, using (4.20) and (4.21), we may easily show

$$\begin{aligned} |\xi _{1n}(t)|\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \int _{t}^{R}\left( \frac{r}{t}\right) ^{|n|}\mathrm{d}r, \end{aligned}$$

(4.38)

$$\begin{aligned} |\xi _{2n}(t)|\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \int _{t}^{R}\left( \frac{r}{t}\right) ^{|n|}\mathrm{d}r . \end{aligned}$$

(4.39)

By (4.38)–(4.39) and

$$\begin{aligned} W_{jn}({\hat{R}}, t) \sim -\frac{2\mathrm{i}}{\pi |n|}\left[ \bigg (\frac{t}{{\hat{R}}}\bigg )^{|n|} -\bigg (\frac{{\hat{R}}}{t}\bigg )^{|n|}\right] ,\quad \beta _{jn}(t) \sim \bigg (\frac{{\hat{R}}}{t}\bigg )^{|n|}, \end{aligned}$$

we get

$$\begin{aligned} \left| \int _{{\hat{R}}}^{R} t W_{jn}({\hat{R}}, t)\xi _{jn}(t)\mathrm{d}t\right|\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \\&\quad \frac{1}{|n|} \int _{{\hat{R}}}^{R}t\left( \frac{t}{{\hat{R}}}\right) ^{|n|}\int _{t}^{R}\left( \frac{r}{t} \right) ^{|n|}\mathrm{d}r\mathrm{d}t\\= & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \frac{1}{|n|(|n|+1)}\\&\qquad \times \int _{{\hat{R}}}^{R}t\left( \frac{1}{{\hat{R}}}\right) ^{|n|}\left( R^{|n|+1}-t^{|n|+1}\right) \mathrm{d}t\\\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \frac{1}{|n|^2}\bigg (\frac{R}{{\hat{R}}}\bigg )^{|n|} \end{aligned}$$

and

$$\begin{aligned} \left| \frac{1}{{\hat{R}}}\int _{{\hat{R}}}^{R} t \beta _{jn}(t)\xi _{jn}(t)\mathrm{d}t\right|\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \\&\quad \int _{{\hat{R}}}^{R} t \bigg (\frac{{\hat{R}}}{t}\bigg )^{|n|}\int _{t}^{R}\left( \frac{r}{t}\right) ^{|n|} \mathrm{d}r\mathrm{d}t\\= & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \frac{1}{1+|n|}\\&\qquad \times \int _{{\hat{R}}}^{R} \bigg (\frac{{\hat{R}}}{t}\bigg )^{|n|}\frac{R^{|n|+1}-t^{|n|+1}}{t^{|n|-1}} \mathrm{d}t\\\lesssim & {} \left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}\right) \frac{1}{|n|^2}\bigg (\frac{R}{{\hat{R}}}\bigg )^{|n|}. \end{aligned}$$

Substituting the above estimates into (4.37), we obtain

$$\begin{aligned} |p_n^r(R)|^2+|p_n^{\theta }(R)|^2\lesssim & {} n^2\bigg (\frac{{\hat{R}}}{R}\bigg )^{2|n|+2}\left( |p_n^r({\hat{R}})|^2+|p_n^{\theta } ({\hat{R}})|^2\right) \\&+\frac{1}{|n|^2}\left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}^2+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}^2\right) , \end{aligned}$$

which completes the proof. $\square$

Using Theorem 4.10, we may estimate the last term in (4.16).

Lemma 4.11

Let ${\varvec{p}}$ be the solution of the dual problem (4.24). For sufficiently large N, the following estimate holds

$$\begin{aligned} \left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi } \cdot \overline{ {\varvec{p}}}\mathrm{d}s\right| \lesssim \frac{1}{N}\Vert \varvec{\xi }\Vert ^2_{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

Proof

Using the definitions of the DtN operators ${\mathscr {T}}$, $\mathscr {T}_N$ and following the discussion in (4.7), we have

$$\begin{aligned}&\left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s \right| \le 2\pi R\sum \limits _{|n|>N} \left| \left( M_n \varvec{\xi }_n(R)\right) \cdot \overline{{\varvec{p}}}_n(R)\right| \nonumber \\&\quad \lesssim 2\pi R \sum \limits _{|n|>N} |n| \left( |\xi _n^r(R)|+|\xi _n^{\theta }(R)|\right) \left( |p_n^r(R)|+|p_n^{\theta }(R)|\right) \nonumber \\&\quad = 2\pi R \sum \limits _{|n|>N} \frac{|n|}{|n|^{3/2}(1+n^2)^{1/4}} (1+n^2)^{1/4}\nonumber \\&\quad \times \left( |\xi _n^r(R)|+|\xi _n^{\theta }(R)|\right) |n|^{3/2}\left( |p_n^r(R)|+|p_n^{\theta }(R)|\right) \nonumber \\&\quad \lesssim \frac{1}{N} \left[ \sum \limits _{|n|>N}(1+n^2)^{1/2}\left( |\xi _n^r(R)|+|\xi _n^{\theta } (R)|\right) ^2\right] ^{1/2}\nonumber \\&\quad \times \left[ \sum \limits _{|n|>N} |n|^3 \left( |p_n^r(R)|+|p_n^{\theta }(R)|\right) ^2\right] ^{1/2} \nonumber \\&\quad \lesssim N^{-1} \Vert \varvec{\xi }\Vert _{H^{1/2}(\partial B_R)} \left[ \sum \limits _{|n|>N} |n|^3 \left( |p_n^r(R)|^2+|p_n^{\theta }(R)|^2\right) \right] ^{1/2}\nonumber \\&\quad \lesssim N^{-1} \Vert \varvec{\xi }\Vert _{H^{1}(\Omega )} \left[ \sum \limits _{|n|>N} |n|^3 \left( |p_n^r(R)|^2+|p_n^{\theta }(R)|^2\right) \right] ^{1/2}. \end{aligned}$$

(4.40)

Following [29], we let $t\in [{\hat{R}}, R]$ and assume, without loss of generality, that t is closer to the left endpoint ${\hat{R}}$ than the right endpoint R. Denote $\zeta =R-{\hat{R}}$. Then we have $R-t\ge \frac{\zeta }{2}$. Thus

$$\begin{aligned} |\xi _n^{(r, \theta )}(t)|^2= & {} \frac{1}{R-t}\int _{R}^{t}\left( (R-s)|\xi _n^{(r, \theta )}(s)|^2\right) ' \mathrm{d}s\\= & {} \frac{1}{R-t}\int _{R}^{t}\left( -|\xi _n^{(r, \theta )}(s)|^2+2\left( R-s\right) \Re \big (\xi _n^{(r, \theta )\prime } (s) \overline{\xi _n^{(r, \theta )}(s)}\big )\right) \mathrm{d}s \\\le & {} \frac{1}{R-t}\int _{t}^{R}|\xi _n^{(r, \theta )}(s)|^2\mathrm{d}s +2\int _{{\hat{R}}}^{R} |\xi _n^{(r, \theta )}(s)||\xi _n^{(r, \theta )\prime }(s)|\mathrm{d}s, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert \xi _n^{(r, \theta )}\Vert ^2_{L^{\infty }([{\hat{R}}, R])}\le & {} \frac{2}{\zeta }\Vert \xi _n^{(r, \theta )}\Vert ^2_{L^{2}([{\hat{R}}, R])} +2\Vert \xi ^{(r, \theta )}_{n}\Vert _{L^2([{\hat{R}}, R])}\Vert \xi ^{(r, \theta )\prime }_{n}\Vert _{L^2([{\hat{R}}, R])}\\\le & {} \left( \frac{2}{\zeta }+|n|\right) \Vert \xi _n^{(r, \theta )}\Vert ^2_{L^2([{\hat{R}}, R])} +|n|^{-1}\Vert \xi _n^{(r, \theta )\prime }\Vert ^2_{L^2([{\hat{R}}, R])}. \end{aligned}$$

Using Lemma 4.10 and the Cauchy–Schwarz inequality, we get

$$\begin{aligned}&\sum \limits _{|n|>N} |n|^3 \left( |p_n^r(R)|^2+|p_n^{\theta }(R)|^2\right) \\&\quad \lesssim \sum \limits _{|n|>N} |n|^3 \left\{ n^2\bigg (\frac{{\hat{R}}}{R}\bigg )^{2|n|+2}\left( |p_n^r({\hat{R}})|^2+|p_n^{\theta } ({\hat{R}})|^2\right) \right. \\&\qquad \left. +\frac{1}{|n|^2}\left( \Vert \xi _n^r\Vert _{L^{\infty }([{\hat{R}}, R])}^2+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}^2\right) \right\} \\&\quad \lesssim \sum \limits _{|n|>N} |n|^5 \bigg (\frac{{\hat{R}}}{R}\bigg )^{|2n|}\left( |p_n^r({\hat{R}})|^2+|p_n^{\theta } ({\hat{R}})|^2\right) \\&\qquad +\sum \limits _{|n|>N} |n|\left( \Vert \xi _n^{r}\Vert _{L^{\infty }([{\hat{R}}, R])}^2+\Vert \xi _n^{\theta }\Vert _{L^{\infty }([{\hat{R}}, R])}^2 \right) \\&\quad {:=} I_1+I_2. \end{aligned}$$

Noting that the function $t^{4} e^{-2t}$ is bounded on $(0, +\infty )$, we have

$$\begin{aligned}&I_1\lesssim \max \limits _{|n|>N}\left( n^{4}\bigg (\frac{{\hat{R}}}{R}\bigg )^{|2n|}\right) \sum \limits _{|n|>N} |n|\left( |p_n^r({\hat{R}})|^2+|p_n^{\theta }({\hat{R}})|^2\right) \\&\quad \lesssim \Vert {\varvec{p}}\Vert _{H^{1/2}(\partial B_{{\hat{R}}})}^2 \lesssim \Vert \varvec{\xi }\Vert _{H^{1}(\Omega )}^2, \end{aligned}$$

where the last inequality uses the stability of the dual problem (4.24). For $I_2$, we can show that

$$\begin{aligned} I_2\lesssim & {} \sum \limits _{|n|>N} \left[ |n|\left( \frac{2}{\zeta }+|n|\right) \left( \Vert \xi _n^r\Vert _{L^{2}([{\hat{R}}, R])}^2 +\Vert \xi _n^{\theta }\Vert _{L^{2}([{\hat{R}}, R])}^2 \right) \right. \\&\quad \left. + \left( \Vert \xi _n^{r\prime }\Vert _{L^{2}([{\hat{R}}, R])}^2 +\Vert \xi _n^{\theta \prime }\Vert _{L^{2}([{\hat{R}}, R])}^2 \right) \right] \\\le & {} \sum \limits _{|n|>N} \left[ \left( \frac{2}{\zeta }|n|+n^2\right) \Vert \varvec{\xi }_n\Vert _{L^{2}([{\hat{R}} , R])}^2 + \Vert \varvec{\xi }_n^\prime \Vert _{L^{2}([{\hat{R}}, R])}^2\right] . \end{aligned}$$

On the other hand, a simple calculation yields

$$\begin{aligned} \Vert \xi _n^{(r, \theta )}\Vert ^2_{H^{1}( B_R{\setminus } \overline{B_{{\hat{R}}}} )}= & {} 2\pi \sum \limits _{n\in {\mathbb {Z}}} \int _{{\hat{R}}}^{R} \left[ \left( r+\frac{n^2}{r}\right) |\xi _n^{(r, \theta )}(r)|^2+r|\xi _n^{(r, \theta )\prime } (r)|^2\right] \mathrm{d}r \\\ge & {} 2\pi \sum \limits _{n\in {\mathbb {Z}}}\int _{{\hat{R}}}^{R} \left[ \left( {\hat{R}}+\frac{n^2}{R}\right) |\xi _n^{(r, \theta )}(r)|^2 +{\hat{R}} |\xi _n^{(r, \theta )\prime }(r)|^2\right] \mathrm{d}r. \end{aligned}$$

It is easy to note that

$$\begin{aligned} \frac{2}{\zeta }|n|+n^2\lesssim {\hat{R}}+\frac{n^2}{R}. \end{aligned}$$

Combining the above estimates, we obtain

$$\begin{aligned} I_2\lesssim \Vert \varvec{\xi }\Vert ^2_{H^{1}(B_R{\setminus } B_{\hat{R}})}\le \Vert \varvec{\xi }\Vert ^2_{H^{1}(\Omega )}, \end{aligned}$$

which gives

$$\begin{aligned} \sum \limits _{|n|>N}|n|^3 \left( |p_n^{r}(R)|+|p_n^{\theta }(R)|\right) ^2\lesssim \Vert \varvec{\xi }\Vert ^2_{H^{1}(\Omega )}. \end{aligned}$$

Substituting the above inequality into (4.40), we get

$$\begin{aligned} \left| \int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s \right| \lesssim \frac{1}{N}\Vert \varvec{\xi }\Vert ^2_{{\varvec{H}}^{1}(\Omega )}, \end{aligned}$$

(4.41)

which completes the proof. $\square$

Now, we are ready to present the proof of Theorem 4.1.

Proof

By Lemma 4.6 and Lemma 4.7, we obtain

$$\begin{aligned} |\!\Vert \varvec{\xi }|\!\Vert ^2_{{\varvec{H}}^{1}(\Omega )}&= \Re b(\varvec{\xi }, \varvec{\xi })+\Re \int _{\partial B_R} \left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}s \\&\quad +2\omega ^2 \int _{\Omega } \varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}{\varvec{x}} +\Re \int _{\partial B_R} {\mathscr {T}}_N\varvec{\xi }\cdot \overline{\varvec{\xi }}\mathrm{d}s\\&\le C_1\left[ \bigg (\sum \limits _{K\in {\mathcal {M}}_h} \eta ^2_K\bigg )^{1/2} + N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^{\mathrm{inc}}\Vert _{{\varvec{H}}^{1}(\Omega )} \right] \Vert \varvec{\xi }\Vert _{{\varvec{H}}^{1}(\Omega )}\\&\quad +\left( C_2+C(\delta )\right) \Vert \varvec{\xi }\Vert ^2_{{\varvec{L}} ^2(\Omega )} +\bigg (\frac{R}{ {\hat{R}}}\bigg )\delta \Vert \varvec{\xi }\Vert ^2_{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

Using (4.2) and choosing $\delta$ such that $\frac{R}{{\hat{R}}}\frac{\delta }{\min (\mu , \omega ^2)}<\frac{1}{2}$, we get

$$\begin{aligned} |\!\Vert \varvec{\xi }|\!\Vert ^2_{{\varvec{H}}^{1}(\Omega )}&\le 2C_1\left[ \bigg (\sum \limits _{K\in {\mathcal {M}}_h} \eta ^2_{K}\bigg )^{1/2} + N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^{\mathrm{inc}}\Vert _{{\varvec{H}}^{1}(\Omega )} \right] \Vert \varvec{\xi }\Vert _{{\varvec{H}}^{1}(\Omega )}\nonumber \\&\quad +2\left( C_2+C(\delta )\right) \Vert \varvec{ \xi }\Vert ^2_{{\varvec{L}} ^2(\Omega )}. \end{aligned}$$

(4.42)

It follows from (4.2), (4.16), Lemmas 4.6 and 4.11 that we have

$$\begin{aligned} \Vert \varvec{\xi }\Vert ^{2}_{{\varvec{L}}^2(\Omega )}= & {} b(\varvec{\xi }, {\varvec{p}}) +\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s -\int _{\partial B_R}\left( {\mathscr {T}}-{\mathscr {T}}_N\right) \varvec{\xi }\cdot \overline{ {\varvec{p}}}\mathrm{d}s\\\lesssim & {} \left[ \bigg (\sum \limits _{K\in {\mathcal {M}}_h} \eta ^2_{K}\bigg )^{1/2} + N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^{\mathrm{inc}}\Vert _{{\varvec{H}}^{1}(\Omega )} \right] \Vert \varvec{\xi }\Vert _{H^{1}(\Omega )}+\frac{1}{N} \Vert \varvec{\xi }\Vert ^2_{H^{1}(\Omega )}. \end{aligned}$$

Substituting the above estimate into (4.42) and taking sufficiently large N such that

$$\begin{aligned} \frac{2\left( C_2+C(\delta )\right) }{N}\frac{1}{\min (\mu , \omega ^2)}<1, \end{aligned}$$

we obtain

$$\begin{aligned} |\!\Vert {\varvec{u}}-{\varvec{u}}_N^h |\!\Vert _{{\varvec{H}}^{1}(\Omega )}\lesssim \bigg (\sum \limits _{K\in {\mathcal {M}}_h} \eta ^2_{K}\bigg )^{1/2} + N\bigg (\frac{{\hat{R}}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )} . \end{aligned}$$

which completes the proof of theorem. $\square$

5 Implementation and numerical experiments

In this section, we discuss the algorithmic implementation of the adaptive finite element DtN method and present two numerical examples to demonstrate the effectiveness of the proposed method.

5.1 Adaptive algorithm

Based on the a posteriori error estimate from Theorem 4.1, we use the FreeFem [26] to implement the adaptive algorithm of the linear finite element formulation. It is shown in Theorem 4.1 that the a posteriori error estimator consists of two parts: the finite element discretization error $\epsilon _h$ and the DtN truncation error $\epsilon _N$ which depends on the truncation number N. Explicitly

$$\begin{aligned} \epsilon _h = \left( \sum \limits _{T\in {\mathcal {M}}_h} \eta ^2_{T}\right) ^{1/2}, \quad \epsilon _N =N\bigg (\frac{\hat{R}}{R}\bigg )^{N} \Vert {\varvec{u}}^\mathrm{inc}\Vert _{{\varvec{H}}^{1}(\Omega )}. \end{aligned}$$

(5.1)

In the implementation, we choose $\hat{R}, R$, and N based on (5.1) to make sure that the finite element discretization error is not polluted by the DtN truncation error, i.e., $\epsilon _N$ is required to be very small compared to $\epsilon _h$, for example, $\epsilon _N\le 10^{-8}$. For simplicity, in the following numerical experiments, ${\hat{R}}$ is chosen such that the obstacle is exactly contained in the disk $B_{{\hat{R}}}$, and N is taken to be the smallest positive integer such that $\epsilon _N\le 10^{-8}$. The algorithm is shown in Table 1 for the adaptive finite element DtN method for solving the elastic wave scattering problem.

Table 1 The adaptive finite element DtN method for the elastic wave scattering problem

5.2 Numerical experiments

We report two examples to demonstrate the performance of the proposed method. The first example is a disk and has an analytical solution; the second example is a U-shaped obstacle which is commonly used to test numerical solutions for the wave scattering problems. In each example, we plot the magnitude of the numerical solution to give an intuition where the mesh should be refined, and also plot the actual mesh obtained by our algorithm to show the agreement. The a posteriori error is plotted against the number of nodal points to show the convergence rate. In the first example, we compare the numerical results by using the uniform and adaptive meshes to illustrate the effectiveness of the adaptive algorithm.

Example 1

This example is constructed such that it has an exact solution. Let the obstacle $D=B_{0.5}$ be a disk with radius 0.5 and take $\Omega =B_{1}{\setminus } {\overline{B}}_{0.5}$, i.e., $\hat{R}=0.5, R=1$. If we choose the incident wave as

$$\begin{aligned} {\varvec{u}}^{\mathrm{inc}}({\varvec{x}}) = - \frac{\kappa _1 H_0^{(1)'}(\kappa _1 r)}{r}\begin{pmatrix} x\\ y \end{pmatrix} -\frac{\kappa _2 H_0^{(1)'}(\kappa _2 r)}{r}\begin{pmatrix} y\\ -x \end{pmatrix},\quad r=(x^2+y^2)^{1/2}, \end{aligned}$$

then it is easy to check that the exact solution is

$$\begin{aligned} {\varvec{u}}({\varvec{x}}) = \frac{\kappa _1 H_0^{(1)'}(\kappa _1 r)}{r}\begin{pmatrix} x\\ y \end{pmatrix} +\frac{\kappa _2 H_0^{(1)'}(\kappa _2 r)}{r}\begin{pmatrix} y\\ -x \end{pmatrix}, \end{aligned}$$

where $\kappa _1$ and $\kappa _2$ are the compressional wave number and shear wave number, respectively.

In Table 2, numerical results are shown for the adaptive mesh refinement and the uniform mesh refinement, where $\text {DoF}_h$ stands for the degree of freedom or the number of nodal points of the mesh ${\mathcal {M}}_h$, $\epsilon _h$ is the a posteriori error estimate, and $e_h=\Vert {\varvec{u}}-{\varvec{u}}_N^h\Vert _{{\varvec{H}}^1(\Omega )}$ is the a priori error. It can be seen that the adaptive mesh refinement requires fewer $\text {DoF}_h$ than the uniform mesh refinement to reach the same level of accuracy, which shows the advantage of using the adaptive mesh refinement. Figure 2 displays the curves of $\log e_h$ and $\log \epsilon _h$ versus $\log \text {DoF}_h$ for the uniform and adaptive mesh refinements with $\omega =\pi , \lambda =2, \mu =1$, i.e., $\kappa _1=\pi /2, \kappa _2=\pi$. It indicates that the meshes and the associated numerical complexity are quasi-optimal, i.e., $\Vert {\varvec{u}}-{\varvec{u}}_N^h\Vert _{{\varvec{H}}^1(\Omega )} =O\big (\text {DoF}_h^{-1/2}\big )$ holds asymptotically. Figure 3 plots the magnitude of the numerical solution and an adaptively refined mesh with 15,407 elements. We can see that the solution oscillates on the edge of the obstacle but it is smooth away from the obstacle. This feature is caught by the algorithm. The mesh is adaptively refined around the obstacle and is coarse away from the obstacle.

Table 2 Comparison of numerical results using adaptive mesh and uniform mesh refinements for Example 1

Fig. 2

Quasi-optimality of the a priori and a posteriori error estimates for Example 1

Fig. 3

The numerical solution of Example 1. (Left) the magnitude of the numerical solution; (right) an adaptively refined mesh with 15,407 elements

Example 2

This example does not have an analytical solution. We consider a compressional plane incident wave ${\varvec{u}}^\mathrm{inc}({\varvec{x}}) ={\varvec{d}} e^{\mathrm{i}\,\kappa _1 {\varvec{x}}\cdot {\varvec{d}}}$ with the incident direction ${\varvec{d}}=(1,0)^\top$. The obstacle is U-shaped and is contained in the rectangular domain $\left\{ {\varvec{x}}\in \mathbb R^2: -2<x<2.2, -0.7<y<0.7\right\}$. Due to the problem geometry, the solution contains singularity around the corners of the obstacle. We take $R=3, {\hat{R}}=2.31$. Figure 4 shows the curve of $\log \epsilon _h$ versus $\log \text {DoF}_h$ at different frequencies $\omega =1, \pi , 2\pi$. It demonstrates that the decay of the a posteriori error estimates is $O\big (\text {DoF}_h^{-1/2}\big )$. Figure 5 plots the contour of the magnitude of the numerical solution and its corresponding mesh by using the parameters $\omega =\pi , \lambda =2, \mu =1$. Again, the algorithm does capture the solution feature and adaptively refines the mesh around the corners of the obstacle where the solution displays singularity.

Fig. 4

Quasi-optimality of the a posteriori error estimates with different frequencies for Example 2

Fig. 5

The numerical solution of Example 2. (Left) The contour plot of the magnitude of the solution; (right) an adaptively refined mesh with 12,329 elements

6 Conclusion

In this paper, we present an adaptive finite element DtN method for the elastic obstacle scattering problem. Based on the Helmholtz decomposition, a new duality argument is developed to obtain the a posteriori error estimate. It does not only take into account of the finite element discretization error but also includes the truncation error of the DtN operator. We show that the truncation error decays exponentially with respect to the truncation parameter. The a posteriori error estimate for the solution of the discrete problem serves as a basis for the adaptive finite element approximation. Numerical results show that the proposed method is accurate and effective. This work provides a viable alternative to the adaptive finite element PML method to solve the elastic obstacle scattering problem. The method can be applied to solve many other wave propagation problems where the transparent boundary conditions are used for open domain truncation. Future work includes extending our analysis to the adaptive finite element DtN method for solving the three-dimensional elastic obstacle scattering problem, where a more complicated transparent boundary condition needs to be considered.

Appendix A. Transparent boundary conditions

In this section, we show the transparent boundary conditions for the scalar potential functions $\phi ^s, \psi ^s$ and the displacement of the scattered field ${\varvec{u}}^s$ on $\partial B_R$.

In the exterior domain ${\mathbb {R}}^2{\setminus }{{\overline{B}}}_R$, the solutions of the Helmholtz equations (2.5) have the Fourier series expansions in the polar coordinates:

$$\begin{aligned} \phi ^s(r,\theta )=\sum _{n\in {\mathbb {Z}}}\frac{H^{(1)}_n(\kappa _1 r)}{H_{n}^{(1)} (\kappa _1 R)} \phi ^s_n(R)e^{\mathrm{i}n\theta },\quad \psi ^s(r,\theta )=\sum _{n\in {\mathbb {Z}}}\frac{H^{(1)}_n(\kappa _2 r)}{H_{n}^{(1)}(\kappa _2 R)}\psi ^s_n(R)e^{\mathrm{i}n\theta }, \end{aligned}$$

(A.1)

where $H_n^{(1)}$ is the Hankel function of the first kind with order n. Taking the normal derivative of (A.1), we obtain the transparent boundary condition for the scalar potentials $\phi ^s, \psi ^s$ on $\partial B_R$:

$$\begin{aligned} \partial _r\phi ^s= & {} {\mathscr {T}}_1\phi ^s:=\sum \limits _{n\in {\mathbb {Z}}} \frac{\kappa _1 H_n^{(1)'}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 R)} \phi ^s_n(R)e^{\mathrm{i}n\theta },\nonumber \\ \partial _r \psi ^s= & {} {\mathscr {T}}_2 \psi ^s:=\sum \limits _{n\in {\mathbb {Z}}} \frac{\kappa _2 H_n^{(1)'}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 R)} \psi ^s_n(R)e^{\mathrm{i}n\theta }. \end{aligned}$$

(A.2)

The polar coordinates $(r, \theta )$ are related to the Cartesian coordinates ${\varvec{x}}=(x, y)$ by $x=r\cos \theta , y=r\sin \theta$ with the local orthonormal basis $\{{\varvec{e}}_r, \varvec{e}_\theta \}$, where ${\varvec{e}}_r=(\cos \theta , \sin \theta )^\top , {\varvec{e}}_\theta =(-\sin \theta , \cos \theta )^\top$.

Define a boundary operator for the displacement of the scattered wave

$$\begin{aligned} {\mathscr {B}} {\varvec{u}}^s =\mu \partial _r {\varvec{u}}^s +(\lambda +\mu )(\nabla \cdot {\varvec{u}}^s) \varvec{e}_r\quad \text {on}\,\partial B_R. \end{aligned}$$

Based on the Helmholtz decomposition (2.5) and the transparent boundary condition (A.2), it is shown in [38] that the scattered field ${\varvec{u}}$ satisfies the transparent boundary condition

$$\begin{aligned} {\mathscr {B}}{\varvec{u}}^s =({\mathscr {T}}{\varvec{u}}^s)(R, \theta ):=\sum _{n\in {\mathbb {Z}}}M_n{\varvec{u}}^s_n(R) e^{\mathrm{i}n\theta }\quad \text {on}\,\partial B_R, \end{aligned}$$

(A.3)

where

$$\begin{aligned} {\varvec{u}}^s(R, \theta )=\sum _{n\in {\mathbb {Z}}}{\varvec{u}}^s_n(R) e^{\mathrm{i}n\theta }=\sum _{n\in {\mathbb {Z}}}\big (u_n^{s, r}(R)\varvec{e}_r + u_n^{s, \theta }(R){\varvec{e}}_\theta \big ) e^{\mathrm{i}n\theta } \end{aligned}$$

and $M_n$ is a $2\times 2$ matrix defined by

$$\begin{aligned} M_n=\begin{bmatrix} M_{11}^{(n)} &{} M_{12}^{(n)}\\ M_{21}^{(n)} &{} M_{22}^{(n)} \end{bmatrix} =\frac{1}{\Lambda _n(R)}\begin{bmatrix} N_{11}^{(n)} &{} N_{12}^{(n)}\\ N_{21}^{(n)} &{} N_{22}^{(n)} \end{bmatrix}. \end{aligned}$$

(A.4)

Here

$$\begin{aligned} \Lambda _n(R)=\left( \frac{n}{R}\right) ^2-\alpha _{1n}(R)\alpha _{2n}(R), \quad \alpha _{jn}(R)=\frac{\kappa _j H_n^{(1)'}(\kappa _j R)}{H_{n}^{(1)}(\kappa _j R)}, \end{aligned}$$

(A.5)

and

$$\begin{aligned} N_{11}^{(n)} =&\mu \left( \frac{n}{R}\right) ^2\Big (\alpha _{2n}(R)-\frac{1}{R}\Big ) -\alpha _{2n}(R)\bigg [(\lambda +2\mu )\frac{\kappa _1^2 H_{n}^{(1)''}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 R))}\\&\qquad +(\lambda +\mu )\Big (\frac{1}{R}\alpha _{1n}(R)-\left( \frac{n}{R} \right) ^2\Big )\bigg ], \\ N_{12}^{(n)}=&\mu \frac{\mathrm{i}n}{R}\alpha _{1n}(R)\Big (\alpha _{2n}(R)-\frac{1}{R}\Big ) -\frac{\mathrm{i}n}{R} \bigg [(\lambda +2\mu )\frac{\kappa _1^2 H_{n}^{(1)''}(\kappa _1 R)}{H_{n}^{(1)}(\kappa _1 R))}\\&\qquad +(\lambda +\mu )\Big (\frac{1}{R}\alpha _{1n}(R)-\left( \frac{n}{R} \right) ^2\Big )\bigg ],\\ N_{21}^{(n)} =&-\mu \frac{\mathrm{i}n}{R}\alpha _{2n}(R)\Big (\alpha _{1n}(R)-\frac{1}{R}\Big ) +\mu \frac{\mathrm{i}n}{R}\frac{\kappa _2^2 H_{n}^{(1)''}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 R)},\\ N_{22}^{(n)} =&\mu \left( \frac{n}{R}\right) ^2 \Big (\alpha _{1n}(R)-\frac{1}{R}\Big ) -\mu \alpha _{1n}(R)\frac{\kappa _2^2 H_{n}^{(1)''}(\kappa _2 R)}{H_{n}^{(1)}(\kappa _2 R)}. \end{aligned}$$

The matrix entries $N_{ij}^{(n)}, i,j=1, 2$ can be further simplified. Recall that the Hankel function $H_n^{(1)}(z)$ satisfies the Bessel differential equation

$$\begin{aligned} z^2 H_n^{(1)''}(z)+z H_n^{(1)'} (z)+(z^2-n^2) H_{n}^{(1)}(z)=0. \end{aligned}$$

We have from straightforward calculations that

$$\begin{aligned} N_{11}^{(n)}&=-\alpha _{2n}(R)\Bigg [(\lambda +2\mu )\bigg [-\frac{1}{R^2} \Big (\kappa _j R \frac{H^{(1)'}_n(\kappa _j R)}{H^{(1)}_n(\kappa _j R)}+\left( (\kappa _j R)^2-n^2\right) \Big )\bigg ]\\&\qquad +(\lambda +\mu )\left( \frac{1}{R}\alpha _{1n}(R)-\left( \frac{n}{R} \right) ^2\right) \Bigg ] +\mu \left( \frac{n}{R}\right) ^2\left( \alpha _{2n} (R)-\frac{1}{R}\right) \\&\quad =-\alpha _{2n}(R)\Bigg [-\left( \frac{\lambda +2\mu }{R}\right) \alpha _{1n} (R)-(\lambda +2\mu )\kappa _1^2\\&\qquad +(\lambda +2\mu )\left( \frac{n}{R}\right) ^2 +\left( \frac{\lambda +\mu }{R}\right) \alpha _{1n}(R)\\&\qquad -(\lambda +\mu )\left( \frac{n}{R}\right) ^2\Bigg ] +\mu \left( \frac{n}{R}\right) ^2\left( \alpha _{2n}(R)-\frac{1}{R}\right) \\&=-\frac{\mu }{R}\left[ \left( \frac{n}{R}\right) ^2-\alpha _{1n}(R)\alpha _{2n} (R)\right] +\alpha _{2n}(R)\omega ^2\\&= -\frac{\mu }{R}\Lambda _n(R)+\alpha _{2n}(R)\omega ^2,\\ N_{12}^{(n)}&= -\frac{\mathrm{i}n}{R}\Bigg [(\lambda +2\mu )\bigg [-\frac{1}{R^2}\Big (\kappa _j R \frac{H^{(1)'}_n(\kappa _j R)}{H^{(1)}_n(\kappa _j R)}+\left( (\kappa _j R)^2-n^2\right) \Big )\bigg ]\\&\qquad +(\lambda +\mu )\left( \frac{1}{R}\alpha _{1n}(R)-\left( \frac{n}{R} \right) ^2\right) \Bigg ] \\&\qquad +\frac{\mathrm{i}n\mu }{R}\alpha _{1n}(R)\alpha _{2n}(R)-\mu \frac{\mathrm{i}n}{R^2}\alpha _{1n}(R)\\&= -\frac{\mathrm{i}n}{R}\left[ -\frac{\mu }{R}\alpha _{1n}(R)+\mu \left( \frac{n}{R}\right) ^2 -(\lambda +2\mu )\kappa _1^2\right] \\&\qquad +\frac{\mathrm{i}n\mu }{R}\alpha _{1n}(R)\alpha _{2n}(R)-\frac{\mathrm{i}n}{R^2}\mu \alpha _{1n}(R)\\&= -\frac{\mathrm{i}n\mu }{R}\Lambda _n(R)+\frac{\mathrm{i}n}{R}\omega ^2,\\ N_{21}^{(n)}&= -\mu \frac{\mathrm{i}n}{R}\alpha _{2n}(R)\alpha _{1n}(R)+\frac{\mathrm{i}n\mu }{R^2}\alpha _{2n}(R) \\&\qquad +\mu \frac{\mathrm{i}n}{R}\left( \frac{-1}{R^2}\right) \left( R\alpha _{2n}(R)+(\kappa _2 R)^2-n^2\right) \\&= -\mu \frac{\mathrm{i}n}{R}\alpha _{1n}(R)\alpha _{2n}(R)+\frac{\mathrm{i}n\mu }{R^2}\alpha _{2n}(R) -\mu \frac{\mathrm{i}n}{R^2}\alpha _{2n}(R)-\frac{\mathrm{i}n\mu }{R}\kappa _2^2+\mathrm{i}\mu \left( \frac{n}{R}\right) ^3\\&= \frac{\mathrm{i}\mu n}{R}\Lambda _n(R)-\frac{\mathrm{i}n}{R}\omega ^2,\\ N_{22}^{(n)}&= \mu \left( \frac{n}{R}\right) ^2\alpha _{1n}(R)-\frac{\mu }{R}\left( \frac{n}{R} \right) ^2-\mu \alpha _{1n}(R)\frac{-1}{R^2}\left( R\alpha _{2n}(R)+(\kappa _2 R)^2-n^2\right) \\&=\mu \left( \frac{n}{R}\right) ^2\alpha _{1n}(R)-\frac{\mu }{R}\left( \frac{n}{R }\right) ^2+\frac{\mu }{R}\alpha _{1n}(R)\alpha _{2n}(R)\\&\qquad +\alpha _{1n}(R)\mu \kappa _2^2-\mu \left( \frac{n}{R}\right) ^2\alpha _{1n}(R)\\&=-\frac{\mu }{R}\left( \left( \frac{n}{R}\right) ^2-\alpha _{1n}(R)\alpha _{2n} (R)\right) +\alpha _{1n}(R)\omega ^2\\&=-\frac{\mu }{R}\Lambda _n(R)+\alpha _{1n}(R)\omega ^2. \end{aligned}$$

Substituting the above into (A.3), we obtain

$$\begin{aligned} {\mathscr {B}}{\varvec{u}}^s&= {\mathscr {T}}{\varvec{u}}^s =\sum \limits _{n\in {\mathbb {Z}}}\frac{1}{\Lambda _n}\bigg \{ \Big [\Big (-\frac{\mu }{R}\Lambda _n(R)+\alpha _{2n}(R)\omega ^2\Big ) u_n^{s, r}(R) \nonumber \\&\quad +\Big (-\frac{\mathrm{i}n\mu }{R}\Lambda _n(R)+\frac{\mathrm{i}n}{R}\omega ^2\Big ) u_n^{s, \theta }(R)\Big ] {\varvec{e}}_r \nonumber \\&\quad + \Big [\Big (\frac{\mathrm{i}\mu n}{R}\Lambda _n(R)-\frac{\mathrm{i}n}{R}\omega ^2 \Big )u_n^{s, r}(R) \nonumber \\&\quad +\Big (-\frac{\mu }{R}\Lambda _n(R)+\alpha _{1n}(R)\omega ^2 \Big )u_n^{s, \theta }(R)\Big ]{\varvec{e}}_{\theta } \bigg \} e^{\mathrm{i}n\theta }. \end{aligned}$$

(A.6)

Lemma A.1

Let $z>0$. For sufficiently large |n|, $\Lambda _n(z)$ admits the following asymptotic property

$$\begin{aligned} \Lambda _n(z)=\frac{1}{2}(\kappa _1^2+\kappa _2^2)+{\mathcal {O}}\Big (\frac{1}{|n|}\Big ). \end{aligned}$$

Proof

Using the asymptotic expansions of the Hankel functions [46]

$$\begin{aligned} \frac{H_n^{(1)'}(z)}{H_n^{(1)}(z)}=-\frac{|n|}{z}+\frac{z}{2|n|}+{\mathcal {O}} \Big (\frac{1}{|n|^2}\Big ), \end{aligned}$$

we have

$$\begin{aligned} \alpha _{jn}(z)=\frac{\kappa _j H_n^{(1)'}(\kappa _j z)}{H_{n}^{(1)}(\kappa _j z)}=-\frac{|n|}{z}+\frac{\kappa ^2_j z}{2|n|}+{\mathcal {O}} \Big (\frac{1}{|n|^2}\Big ). \end{aligned}$$

(A.7)

A simple calculation yields that

$$\begin{aligned} \Lambda _n(z)=\left( \frac{n}{z}\right) ^2-\alpha _{1n}(z)\alpha _{2n}(z)=\frac{1}{2 }(\kappa _1^2+\kappa _2^2)+{\mathcal {O}}\Big (\frac{1}{|n|}\Big ), \end{aligned}$$

which completes the proof.$\square$