Interpolation properties of generalized plane waves

Abstract

This paper is aimed at developing new shape functions adapted to the scalar wave equation with smooth (possibly vanishing) coefficients and investigates the numerical analysis of their interpolation properties. The interpolation is local, but high order convergence is shown with respect to the size of the domain considered. The new basis functions are then implemented in a numerical method to solve a scalar wave equation problem with a mixed boundary condition. The main theoretical result states that any given order of approximation can be achieved by an appropriate choice of parameters for the design of the shape functions. The convergence is studied with respect to the size of the domain, which is referred to in the literature as $h$-convergence.

1 Introduction

This paper focuses on the design of Generalized Plane Waves (GPW) to approximate smooth solutions $u\in \mathcal C^\infty (\Omega )$ of the model problem

$$\begin{aligned} -\Delta u + \beta u = 0, \quad \text { in } \Omega \subset {\mathbb {R}}^2, \end{aligned}$$

(1)

where $\beta$ is in $\mathcal C^\infty (\Omega )$. This time-harmonic equation, generally called the scalar wave equation, models for instance the acoustic pressure describing the behavior of sound in matter or a polarized electromagnetic wave propagating in an isotropic medium. If $\beta =-\omega ^2$, $\omega \in {\mathbb {R}}$, the equation is the classical Helmholtz equation and is still the subject of recent research, see for instance [27]. If $\beta <0$ is non constant, this is a simple model of wave propagation in an inhomogeneous medium. If $\beta >0$, it models an absorbing medium and the partial differential equation is coercive. The applications considered here include both propagative and absorbing media, as well as smooth transitions in between them, i.e. respectively $\beta >0$, $\beta <0$ and $\beta =0$.

Several types of numerical methods are used for the simulation of wave propagation. Classical finite element methods applied to such problems are known to be polluted by dispersion, see [1]. An alternative is to consider approximation methods based on shape functions that are local solutions of the homogeneous equation: this justifies the development of Trefftz-based methods, first introduced in [32], that rely on solutions of the homogeneous governing domain equation: information about the problem is embedded in the finite basis. The present work originated from the idea of applying such a method to a problem modeled by (1) in which the coefficient is likely to vanish: shape functions adapted to this problem are here designed and studied. See the previous work [22] for the physical motivation of the problem. We refer to [29] and references therein for more recent developments of these Trefftz-based methods, and to [12, 17] for applications linked to one specific method, the so-called Ultra Weak Variational Formulation (UWVF). The method coupling the latter to the adapted shape functions is the topic of [22], and the present work includes numerical results for the $h$ convergence of the coupled method.

The novelty in the present lies in the fact that the shape functions, called Generalized Plane Waves (GPWs), are selected from a smooth coefficient $\beta$ of the governing domain Eq. (1). This work can be compared to recent progress that focus on non polynomial methods for smooth varying coefficients, see for instance [3, 31]. The design of shape functions adapted to smooth and possibly vanishing coefficients, that is the core of this work, starts from mimicking the equation

$$\begin{aligned} (-\Delta + \beta )e^{\imath \omega \overrightarrow{k} \cdot \overrightarrow{x}} =\left( -(\imath \omega \Vert \overrightarrow{k} \Vert )^2-\omega ^2\right) e^{\imath \omega \overrightarrow{k} \cdot \overrightarrow{x}} = 0, \end{aligned}$$

where $\imath =\sqrt{-1}$. It shows that classical plane waves functions $e^{\imath \omega \overrightarrow{k} \cdot \overrightarrow{x}}$ are exact solutions of (1) when $\beta =-\omega ^2$ is constant and negative.

The case of a piecewise constant coefficient is addressed for example in [5, 11], and the more general case of a smooth coefficient is generally approximated by a piecewise constant coefficient. A very simple extension of classical plane waves for a positive or negative constant coefficient would be to consider at a point $\overrightarrow{g}=(x_0,y_0)\in {\mathbb {R}}^2$ the shape function

$$\begin{aligned} \varphi (x,y)=\exp \left( \sqrt{{\mathrm{sgn}}\left( \beta \left( \overrightarrow{g}\right) \right) }\sqrt{\left| \beta \left( \overrightarrow{g}\right) \right| }\left( (x-x_0)\cos \theta + (y-y_0) \sin \theta \right) \right) ,\quad \end{aligned}$$

(2)

where the parameter $\theta$ represents the direction of the plane wave. Indeed, the case $\beta \left( \overrightarrow{g}\right) <0$ corresponds to the classical plane wave whereas the case $\beta \left( \overrightarrow{g}\right) >0$ corresponds to a purely imaginary wavenumber. This choice will provide a tool to extend the interpolation results cited previously. Note that if the coefficient $\beta \left( \overrightarrow{g}\right) <0$ goes to zero then the corresponding classical plane waves functions, generated by equi-spaced directions $\theta$, tend not to be independent anymore.

To address the general case of a smooth coefficient, the idea developed in the present work is to design approximate solutions of the governing equation, in the form of exponential of polynomials: the GPWs. Typically, in the case $\beta (x,y)=x$ the Airy functions $Ai$ and $Bi$ are exact solutions; however, in the general case there is no exact analytic solution known. Indeed, as was explained in Section 2.1 of [22], no exponential of a polynomial can solve a generic scalar wave equation. It is then natural to generalize the classical plane waves by approximate solutions. A parameter $q$ will describe the order of this approximation. The explicit design of those GPWs is the first concern of this paper. It is key to prove the interpolation property.

The desired interpolation property aims at approximating any smooth solution of Eq. (1) using a basis of GPWs. It is the second concern of this paper. The goal of the theoretical part of this paper is to prove high order approximation properties on such sets of basis functions, provided that a sufficient number of basis functions is used with respect to the approximation parameter $q$. It will be stated with more precision in Theorem 1, and can be announced/summarized as follows.

Claim

Assume $n\in {\mathbb {N}}$, standing for an interpolation parameter and $\overrightarrow{g}=(x_0,y_0)$, standing for a point in a bounded domain $\Omega$. Suppose that the coefficients of the Taylor expansion

$$\begin{aligned} \forall \overrightarrow{m}&= (x,y)\in \Omega , \beta \left( \overrightarrow{m}\right) \\&= \sum _{0\le i+j < n+1 } \frac{{{\partial }_{x}}^i {{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{i!j!} (x-x_0)^i(y-y_0)^j +O\left( \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1}\right) \end{aligned}$$

are given, where $\beta$ is the coefficient of the scalar wave equation (1). Consider a smooth solution $u\in \mathcal C^{n+1}(\Omega )$ of Eq. (1). There exists a linear combination of GPWs $u_a$ which is an approximation of order $n+1$ of $u$ in the following sense: there is a constant $C_{\Omega }$ such that for all $\overrightarrow{m}\in {\mathbb {R}}^2$

$$\begin{aligned} \left\{ \begin{array}{l} \left| u\left( \overrightarrow{m}\right) -u_a\left( \overrightarrow{m}\right) \right| \le C_{\Omega } \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \left\| u \right\| _{\mathcal C^{n+1}}\!,\\ \left\| \nabla u\left( \overrightarrow{m}\right) -\nabla u_a\left( \overrightarrow{m}\right) \right\| \le C_{\Omega } \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n} \left\| u \right\| _{\mathcal C^{n+1}}\!. \end{array} \right. \end{aligned}$$

Note that this result is local; it is stated at a given point $\overrightarrow{g}\in {\mathbb {R}}^2$. Theorem 1 specifies a sufficient number of GPWs to achieve an arbitrarily high order of convergence. It can be related to what is called in the literature Hermitte-Birkhoff interpolation thanks to GPWs, see [30].

Also note that in the literature of finite element or plane wave numerical methods, such a result is referred to as $h$-convergence as it provides a rate of convergence with respect to $h$ if $\left| \overrightarrow{m}-\overrightarrow{g}\right| \le h$. It is opposed to the $p$-convergence which focuses on the convergence with respect to the number of basis functions. A first glance at the $p$-version is proposed following the proof of the Theorem.

There are two main approaches in proving such interpolation results for Helmholtz equation that have been developed in the literature. One of them is based on Vekua theory, which was first translated into English in [14] for functions in ${\mathbb {R}}^2$. A more recent introduction to the topic can be found in [2]. Theoretical studies based on this technical tool can be found in [25], and more recently in [28]. In the latter, the case of the Helmholtz equation with constant coefficient is explicitly studied and interpolation properties are obtained with explicit dependence with respect to the parameters. However, even if this theory is powerful, in the case of a smooth coefficient it gives no explicit estimates with respect to the different parameters. The second main stream method relies on Taylor expansions, and was proposed in [5]. Since the design of solutions developed in this paper is based on Taylor expansions as well, this second approach will be the one followed here.

Section 2 describes precisely the design process of the GPWs. The approximation property is obtained subject to constraints on the function’s coefficients. Then a set of approximated functions is obtained by specifying these constraints, mimicking the classical plane wave functions. The notion of a GPW is made precise in Definition 1. Section 3 focuses on the main approximation result of the paper, namely Theorem 1. This theorem states a theoretical framework to obtain the approximation properties presented in the previous claim. Its proof relies on fundamental properties of the GPWs. Section 4 presents a series of numerical validations of Theorem 1. It considers two different normalizations of the GPWs. The numerical test cases are chosen to consider problems linked with reflectometry, a radar diagnostic technique for fusion plasma, see [22] for more details.

Notation. The complex number $\sqrt{-1}$ is denoted by $\imath$. The symbol $l\in [\![n,m]\!]$ stands for the statement: $l\in {\mathbb {N}}$ such that $n\le l \le m$. The symbol $\mathcal C^n$ represents the set of functions whose derivatives up to the order $n$ exist and are continuous.

2 Design of the generalized plane waves

A GPW is designed as a function $\varphi = e^{P}$, where $P$ is a complex polynomial in two variables, which satisfies locally an approximated version of the governing Eq. (1): $(-\Delta +\beta )e^P\approx 0$. This section is split into two parts: a first one dedicated to the design of a GPW as an approximate solution to the scalar wave Eq. (1), and a second one dedicated to the construction of a basis of such approximate solutions. While the design process depends on a single approximation order denoted $q$, the construction of a basis depends on two additional parameters: the number $p$ of basis functions as well as a normalization parameter denoted $N$.

Definition 1 states a precise definition of a GPW.

2.1 An approximate solution

Since the design process is local, denote by $\overrightarrow{g}=(x_0,y_0)$ a point in ${\mathbb {R}}^2$. Consider a complex polynomial

$$\begin{aligned} P(x,y)=\sum _{i=0}^{\mathrm{d}P} \sum _{j=0}^{\mathrm{d}P-i} \lambda _{i,j} (x-x_0)^i (y-y_0)^j, \end{aligned}$$

(3)

together with the associated function $\varphi = e^{P}$. In order for $\varphi$ to be a GPW, its image by the operator $-\Delta + \beta$ has to be small. Since $\beta$ is not constant but smooth, $P$ will be designed to ensure that

$$\begin{aligned} (-\Delta + \beta ) e^{P} =\big (-({{\partial }_{{x}^{2}}}P + ({{\partial }_{x}}P)^2 +{{\partial }_{{y}^{2}}}P + ({{\partial }_{y}}P)^2) + \beta \big ) e^{P} \quad \text {is}\,\,\,locally \text { small. } \end{aligned}$$

To simplify the notation, define the polynomial $P_\Delta = {{\partial }_{{x}^{2}}}P + ({{\partial }_{x}}P)^2 +{{\partial }_{{y}^{2}}}P + ({{\partial }_{y}}P)^2$, so that $(-\Delta + \beta ) e^{P} = (-P_\Delta + \beta ) e^P$. Since $e^P$ is locally close to $e^{\lambda _{0,0}}\ne 0$, the idea is to set $-P_\Delta +\beta$ to be small.

The design of the GPW is then performed by setting the coefficients of $P$ to match the Taylor expansions of $P_\Delta$ and $\beta$: introducing an approximation parameter $q\in {\mathbb {N}}$, $q\ge 1$, the design process described in this paper is be based on the local equation

$$\begin{aligned} -P_\Delta (x,y) + \beta (x,y) = O \left( \Vert (x,y)-(x_0,y_0)\Vert ^q\right) . \end{aligned}$$

(4)

The specific case $q=1$ corresponds to the simplest generalization of plane waves described previously in (2). Indeed, in that case (4) is reduced to only one equation, reading for $\mathrm{d}P\ge 2$

$$\begin{aligned} - 2\lambda _{2,0} - \lambda _{1,0}^2 - 2\lambda _{0,2} -\lambda _{0,1}^2 + \beta \left( \overrightarrow{g}\right) = 0. \end{aligned}$$

So setting

$$\begin{aligned} (\lambda _{1,0},\lambda _{0,1}) = \sqrt{\text {sgn} \beta \left( \overrightarrow{g}\right) } \sqrt{\left| \beta \left( \overrightarrow{g}\right) \right| } (\cos \theta , \sin \theta ) \end{aligned}$$

together with $\lambda _{0,2} = \lambda _{2,0} = 0$ corresponds to the shape function described in (2) and is sufficient to satisfy the approximation property (4) for $q=1$. In the general case $q\ge 1$, the procedure includes choosing the degree of the polynomial and giving an explicit expression to compute the coefficients of the polynomial. These two choices are not independent. A precise analysis of Eq. (4) leads to choosing the degree of $P$ such that the computation of the coefficients appears to be straightforward.

Consider now the coefficients of $P$ as unknowns in the general case $q > 1$. In order to solve to ensure that Eq. (4) holds, consider a system described by:

• $N_{un} = \frac{(\mathrm{d}P+1)(\mathrm{d}P+2)}{2}$ unknowns, namely the coefficients of $P$,

• $N_{eq} = \frac{q(q+1)}{2}$ equations, corresponding to the cancellation of the terms of degree lower than $q$ in the Taylor expansion of $\beta -P_\Delta$.

As a result the system is overdetermined if $\mathrm{d}P+1< q$, and in such a case the existence of a solution is not guaranteed. The idea is then to find the smallest value of $\mathrm{d}P\ge q-1$ that would provide an invertible system.

The case $\mathrm{d}P = q-1$ provides a square, but generally not invertible system. For instance consider the case $q=2$ and $\mathrm{d}P = 1$. Then (4) is reduced to three equations reading

$$\begin{aligned} \left\{ \begin{array}{l} - \lambda _{1,0}^2 -\lambda _{0,1}^2 + \beta \left( \overrightarrow{g}\right) = 0, \\ {{\partial }_{x}}\beta \left( \overrightarrow{g}\right) = 0, \\ {{\partial }_{y}}\beta \left( \overrightarrow{g}\right) = 0. \end{array}\right. \end{aligned}$$

Since no unknowns appear in the second and third equations this system obviously has no solution in the general case.

The case $\mathrm{d}P = q$ is more intricate than the next one, since the $q$ equation stemming from the terms of degree $q-1$ have no linear term. In a such case, the system is underdetermined however there is no straightforward way to obtain an invertible system, because of the nonlinearity. For instance consider the case $\mathrm{d}P = q=2$. Then (4) is reduced to three equations reading

$$\begin{aligned} \left\{ \begin{array}{l} - 2\lambda _{2,0} - \lambda _{1,0}^2 - 2\lambda _{0,2} -\lambda _{0,1}^2 + \beta (\overrightarrow{g}) = 0, \\ - 4 \lambda _{2,0} \lambda _{1,0}+ {{\partial }_{x}}\beta (\overrightarrow{g}) = 0, \\ - 4 \lambda _{0,2} \lambda _{0,1}+ {{\partial }_{y}}\beta (\overrightarrow{g}) = 0. \end{array}\right. \end{aligned}$$

This system is underdetermined, however for a general coefficient $\beta$ it has no obvious solution because of the nonlinearity: finding a solution corresponds to computing non vanishing roots of a polynomial of degree $4$ in two variables $(\lambda _{1,0},\lambda _{0,1})$. So the case $\mathrm{d}P = q$ does not—in general—lead to a convenient invertible system.

As for the case $\mathrm{d}P = q+1$, the system is underdetermined and the number of additional equations to be imposed to get a square system is $N_{un}-N_{eq}=2q+3$. Moreover, since

$$\begin{aligned} \beta (x,y)&= \sum _{ (i,j) \slash 0\le i+j \le q-1 } \frac{ {{\partial }_{x}}^i{{\partial }_{y}}^j\beta (x_0, y_0)}{i!j!} (x-x_0)^i (y-y_0)^j\\&+ O\left( \Vert (x,y)-(x_0,y_0) \Vert ^q \right) , \end{aligned}$$

then the $N_{eq}$ equations of the system that come from (4) actually reads

$$\begin{aligned} \forall (i,j) \text { s.t. } 0&\le i+j \le q-1,\nonumber \\ \frac{{{\partial }_{x}}^i {{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{i!j!}&=(i+2)(i+1)\lambda _{i+2,j}+ (j+2)(j+1) \lambda _{i,j+2}\nonumber \\ \displaystyle&\quad +\sum _{k=0}^{i} \sum _{l=0}^{j} (i-k+1)(k+1) \lambda _{i-k+1,j-l} \lambda _{k+1,l}\nonumber \\ \displaystyle&\quad +\sum _{k=0}^{j} \sum _{l=0}^{i} (j-k+1)(k+1) \lambda _{i-l,j-k+1} \lambda _{l,k+1}. \end{aligned}$$

(5)

As a consequence, to obtain an invertible system the choice proposed in this paper is to fix the set of coefficients $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$. Thus this choice corresponds to the $2q+2$ additional constraints that, together with Eq. (5), form a square system. The next result states the existence and uniqueness of a solution to this square system.

Proposition 1

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$ and the approximation parameter $q\in {\mathbb {N}}$ is such that $q\ge 1$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$ and consider the complex unknowns $\left\{ \lambda _{i,j}, 0\le i+j \le q+1 \right\}$. The system described by (5) together with the additional constraints of fixing the elements of $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$ has a unique solution, given by

$$\begin{aligned} \forall (i,j) \text { s.t. } 0&\le i+j \le q-1,\nonumber \\ \lambda _{i+2,j}&= \frac{1}{(i+2)(i+1)}\Bigg (\frac{{{\partial }_{x}}^i {{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{i!j!} - (j+2)(j+1) \lambda _{i,j+2}\nonumber \\&\quad -\sum _{k=0}^{i} \sum _{l=0}^{j} (i-k+1)(k+1) \lambda _{i-k+1,j-l} \lambda _{k+1,l}\nonumber \\&\quad -\sum _{k=0}^{j} \sum _{l=0}^{i} (j-k+1)(k+1) \lambda _{i-l,j-k+1} \lambda _{l,k+1}\Bigg ). \end{aligned}$$

(6)

Proof

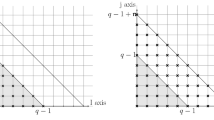
For any given set of coefficients $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$, the existence and uniqueness of a solution to (5) stems directly from the induction relation (6). See Fig. 1.$\square$

Fig. 1

For a given $(i_0,j_0)$, the left part of the figure shows the contributions from $P_\Delta$ to the $x^{i_0}y^{j_0}$ term in $\beta -P_\Delta$. The right part shows that $\lambda _{i_0+2,j_0}$ can be explicitly expressed as long as $\lambda _{k,l}$ are known for all $k\le i_0+1$ and $l\le \mathrm{d}P-2-k$

As a direct consequence of Proposition 1, the choice $\mathrm{d} P = q+1$ provides an invertible system to compute the coefficients of $P$. Thanks to the preceding study, this choice $\mathrm{d} P = q+1$ is actually the smallest value of $\mathrm{d} P$ providing such an invertible system.

Note that for $\mathrm{d} P > q+1$, the system’s equations are still described by (5). However there are more unknowns that in the previous case, namely $\mathrm{d} P = q+1$. More precisely there are $N_{un}-N_{eq}= \frac{(\mathrm{d} P+1)(\mathrm{d} P+2)- q(q+1)}{2}$ extra unknowns: again fixing $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$ uniquely defines the set of coefficients $\left\{ \lambda _{i,j}, 0\le i + j \le q+1 \right\}$ since the induction formula (6) still holds. But the remaining coefficients $\left\{ \lambda _{i,j}, q+1<i+j \le \mathrm{d} P \right\}$ do not appear in the equations: they need to be computed even if they are not involved in the approximation Eq. (4).

Consequently from now on the polynomial $P$ will be of degree $q+1$. The following result summarizes how to design a GPW, providing $2q+1$ degree of freedom to do so.

Corollary 1

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$ and the approximation parameter satisfies $q\in {\mathbb {N}}$ such that $q\ge 1$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider a given set of complex numbers $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$, and the corresponding coefficients $\left\{ \lambda _{i,j}, 0\le i+j \le q+1 \right\}$ computed by the induction formula (6). The function $\varphi (x,y)= \exp \sum _{0\le i+j \le q+1} \lambda _{i,j}(x-x_0)^i (y-y_0)^j$ satisfies $(-\Delta + \beta (x,y) ) \varphi (x,y) = O(\Vert (x,y)-(x_0,y_0) \Vert ^q)$.

The explicit choice for the set of coefficients $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$ that will lead to the explicit definition of a GPW will include a parameter meant to generate not only one, but a set of independent GPWs at a single point $\overrightarrow{g}$.

2.2 A set of approximate solutions

The construction of a set of approximate solutions will take advantage of the degrees of freedom available to design an approximate solution, provided by Corollary 1. Inspired by the construction of classical plane waves, the general design procedure proposed in this paper involves two parameters:

• a parameter $\theta$ corresponding to the direction of the wave,

• a parameter $N\ne 0$ , where $-\imath N$ can be interpreted as the local wave number of the wave.

These parameters are used to set $(\lambda _{1,0},\lambda _{0,1})=N (\cos \theta ,\sin \theta )$. It justifies the name given to the new shape functions: generalized plane waves. Varying $\theta$ then provides different functions $\varphi$, only as long as $N\ne 0$.

The additional constraints that correspond the coefficients $\big \{\lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \big \}$ will be fixed in the following way to give a precise definition of a GPW.

Definition 1

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$, the approximation parameter satisfies $q\in {\mathbb {N}}$ such that $q\ge 1$, $\theta \in {\mathbb {R}}$ and $N\in {\mathbb {C}}$ such that $N\ne 0$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. A generalized plane wave adapted to the operator $-\Delta +\beta$ is a function $\varphi =\exp \sum _{ 0\le i+j\le q+1} \lambda _{i,j}(x-x_0)^i (y-y_0)^j$ whose coefficients satisfy the induction formula (6) together with the additional constraints

• $\lambda _{0,0}=0$,

• $(\lambda _{1,0},\lambda _{0,1})=N (\cos \theta ,\sin \theta )$,

• $\lambda _{i,j}=0$ for $i\in \{0,1\}$ and $1<i+j\le q+1$.

The first item prevents any blow up of the shape function linked to the exponential, since then $\varphi \left( \overrightarrow{g}\right) = e^{\lambda _{0,0}}$ is independent of $\overrightarrow{g}$ and $\beta$, while the second item mimics classical plane waves. The last item is the simplest possible choice and is meant to simplify both the numerical computations—by a substantial decrease of basic operations necessary to evaluate a shape function—and the analysis of the method.

Remark 1

(Other possible choices) Other choices to obtain an invertible system would give the same theoretical results. For instance choosing to fix $\{ \lambda _{i,j},j\in \{0,1\},i\in [\![ 0, q+1-j ]\!]\}$ is possible as well. But numerically, as will be seen later on, there is no evidence of the lack of symmetry with respect to the two space variables.

The condition $N\ne 0$ is mandatory to define a set of linearly independent shape functions: they then form a basis of an approximation space $\mathcal E_{\overrightarrow{g}} (N,p,q)$, where $p$ is the dimension of the space and $q$ the order of approximation in (4).

Definition 2

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$, the approximation parameter satisfies $q\in {\mathbb {N}}$ such that $q\ge 1$, $p \in {\mathbb {N}}$ such that $p\le 3$ and $N\in {\mathbb {C}}$ such that $N\ne 0$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider then for all $l \in [\![1,p]\!]$

• $\theta _l=2\pi (l-1)/p$ a direction, all directions being equi-spaced,

• $(\lambda _{1,0}^l,\lambda _{0,1}^l)=N (\cos \theta _l,\sin \theta _l)$ the corresponding coefficients of the degree one terms,

• $\varphi _l$ the corresponding generalized plane wave as introduced in Definition 1.

The set of $p$ shape functions adapted to the operator $-\Delta + \beta$, denoted $\mathcal E_{\overrightarrow{g}} (N,p,q)$, is defined by $\mathcal E_{\overrightarrow{g}} (N,p,q) = \left\{ \varphi _l \right\} _{l\in [\![1,p]\!]}$.

The parameter $N$ is then the main degree of freedom to be fixed to compute explicitly the approximation space $\mathcal E_{\overrightarrow{g}} (N,p,q)$.

Finally, the explicit design of a set of GPWs at a point $\overrightarrow{g} =(x_0,y_0)$ can be summarized by the following steps:

• 1. fix $p\in {\mathbb {N}}$, $p\ge 3$, the number of functions, and compute for all $l\in [\![1,p]\!]$: $\theta _l=2\pi (l-1)/p$ the direction of each function,

• 2. fix $N\in {\mathbb {C}}$, $N\ne 0$, and compute for all $l\in [\![1,p]\!]$: $(\lambda _{1,0}^l,\lambda _{0,1}^l)=N (\cos \theta _l,\sin \theta _l)$,

• 3. fix $q\in {\mathbb {N}}$, $q\ge 1$, the order of approximation, and compute for all $l\in [\![1,p]\!]$ the set of coefficients of each function $\left\{ \lambda _{i,j}^l, 0\le i+ j \le q+1 \right\}$ according to Corollary 1,

• 4. for all $l\in [\![1,p]\!]$ define $\varphi _l=\exp \sum _{ 0\le i+j\le q+1} \lambda _{i,j}^l (x-x_0)^i (y-y_0)^j$;

the desired set of GPWs is $\{\varphi _l\}_{l\in [\![1,p]\!] }$.

3 Interpolation

The interpolation properties of the set $\mathcal E_{\overrightarrow{g}} (N,p,q)$ are proved in Theorem 1. This section is devoted to the proof of this result, which states that, in order to approximate to a given order $n+1$ the solution of the scalar wave Eq. (1) around a point $\overrightarrow{g}$, a number $p=2n+1$ of basis functions together with a approximation parameter $q=n+1$ are sufficient. The gradient of the solution is then approximated to the order $n$.

The proof of this main theorem relies on a fundamental property of the GPWs, which is first proved and commented.

3.1 A fundamental property of a generalized pane wave

Since the design and the interpolation study are based on different Taylor expansions, the derivatives of the shape function $\varphi$ are important quantities. Moreover, only two coefficients among the set $\left\{ \lambda _{i,j}, i\in \{0,1\}, j \in [\![ 0, q+1-i ]\!] \right\}$ are non-zero to define a GPW. So it is natural to express the other coefficients with respect to those two. Both

• the coefficients $\lambda _{i,j}$s defining a shape function $\varphi$

• the derivatives of $\varphi$

can actually be expressed as polynomials in two variables with respect to $(\lambda _{1,0},\lambda _{0,1})$. The coefficients of these polynomials depend on the indices $i$, $j$, the GPW parameter $N$ and the derivatives of $\beta$ evaluated at $\overrightarrow{g}$. They do not depend on $\theta$, and this is crucial to prove Theorem 1.

Proposition 2 states this fundamental property of the derivatives of a generalized pane wave, and its proof relies on the intermediate Lemma 1. These result strongly use the fact that for a GPW: $\lambda _{1,0}^2+\lambda _{0,1}^2= N^2$.

Lemma 1

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$, the approximation parameter satisfies $q\in {\mathbb {N}}$ such that $q\ge 1$, $\theta \in {\mathbb {R}}$ and $N\in {\mathbb {C}}$ such that $N\ne 0$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider a GPW adapted to the operator $-\Delta +\beta$: $\varphi =\exp \sum _{ 0\le i+j\le q+1} \lambda _{i,j}(x-x_0)^i (y-y_0)^j$.

Then each coefficient of the set $\{\lambda _{i,j}, 0\le i+j\le q+1\}$ can be described as polynomials in two variables in $(\lambda _{1,0},\lambda _{0,1})$ as follows.

$$\begin{aligned} \left\{ \begin{array}{l} \forall i\ge 2\\ \lambda _{i,j}~\mathrm{is }\ \mathrm{a }\ \mathrm{polynomial }\ \mathrm{of }\ \mathrm{total }\ \mathrm{degree }\ \mathrm{at }\ \mathrm{most }\ i-2 . \end{array} \right. \end{aligned}$$

(7)

The coefficients of these polynomials depend on the indices $i$, $j$, the GPW parameter $N$ and the derivatives of $\beta$ evaluated at $\overrightarrow{g}$. They do not depend on $\theta$.

The following proof relies on a close examination of the induction formula (5), considered as polynomial in two variables, namely $(\lambda _{1,0},\lambda _{0,1})$. The idea is to track the terms with higher degree.

Proof

Because of the null coefficients, the induction formula (6) for $i=0$ and $i=1$ reads

$$\begin{aligned} \left\{ \begin{array}{rll} \lambda _{2,0} &{}\displaystyle = \frac{1}{2}\left( \beta \left( \overrightarrow{g}\right) - (\lambda _{1,0})^2-(\lambda _{0,1})^2\right) ,&{}\\ \displaystyle \lambda _{2,j} &{}\displaystyle = \frac{1}{2} \frac{{{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{j!} &{} \forall j>0,\\ \displaystyle \lambda _{3,0} &{}\displaystyle = \frac{1}{6} \left( {{\partial }_{x}}\beta \left( \overrightarrow{g}\right) -4\lambda _{2,0} \lambda _{1,0}\right) , &{}\\ \lambda _{3,j}&{}\displaystyle = \frac{1}{6} \left( \frac{{{\partial }_{x}}{{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{j!} -4\lambda _{2,j} \lambda _{1,0}\right) &{} \forall j>0. \end{array}\right. \end{aligned}$$

(8)

Then (7) for $i=2$ stems from the choice of $(\lambda _{1,0},\lambda _{0,1})$ in the GPW definition. Indeed for $j=0$ the sum $(\lambda _{1,0})^2+(\lambda _{0,1})^2$ does not depend on $(\lambda _{1,0},\lambda _{0,1})$ themselves but only on $N$. Afterwards (7) for $i=3$ is clear from (8).

Now set $i\ge 2$ and suppose that the statement (7) holds true for all $\tilde{i} \in [\![ 3,i+1 ]\!]$. Then, isolating $\lambda _{i+2,j}$ in (5), the higher possible degree of each term is

• ${i-2}$ for the term in $\lambda _{i,j+2}$,

• $(i-1)+1$ for the term in $\lambda _{i+1,j}\lambda _{1,0}$,

• $(i-k-1)+(k-1)$ for the terms in $\lambda _{i-k+1,j-l}\lambda _{k+1,l}$ with $k\ne 0$ and $k\ne i$,

• $(i-2)+1$ for the term in $\lambda _{i,j+1}\lambda _{0,1}$,

• $(i-l-2)+(l-2)$ for the term in $\lambda _{i-l,j-k+1}\lambda _{l,k+1}$ with $l\ne 0$ and $l\ne i$, note that $\lambda _{i-l,j-k+1}\lambda _{l,k+1}=0$ with $l\ne 1$ and $l\ne i-1$ because of null coefficients.

As a consequence the terms with higher degree appearing in the expression of $\lambda _{i+2,j}$ have degree at most equal to $i$. It completes the proof of (7) for $i>2$ by induction.

The dependence of the polynomial expressions with respect to the different parameters is clear through the previous induction proof: the $i$, $j$ and $\beta$ terms appear explicitly in the induction formula (6), while the $N$ appears in the expression of $\lambda _{2,0}$ of (8) since $N^2 = \lambda _{1,0}^2 + \lambda _{0,1}^2$. The parameter $\theta$ does not appear anywhere. $\square$

Proposition 2

Assume $\overrightarrow{g}=(x_0,y_0)$ is a point in ${\mathbb {R}}^2$, the approximation parameter satisfies $q\in {\mathbb {N}}$ such that $q\ge 1$, $\theta \in {\mathbb {R}}$ and $N\in {\mathbb {C}}$ such that $N\ne 0$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider a GPW adapted to the operator $-\Delta +\beta$: $\varphi =\exp \sum _{ 0\le i+j\le q+1} \lambda _{i,j}(x-x_0)^i (y-y_0)^j$. Then for all $(i,j) \in {\mathbb {N}}^2$ such that $i+j\le q+1$ the difference

$$\begin{aligned} R_{i,j} : = {{\partial }_{x}}^i{{\partial }_{y}}^j \varphi \left( \overrightarrow{g}\right) - (\lambda _{0,1})^j (\lambda _{1,0})^i \end{aligned}$$

(9)

can be expressed as a complex polynomial with respect to the two variables $\lambda _{1,0}$ and $\lambda _{0,1}$. such that

• its total degree satisfies $\mathrm{d} R_{i,j} \le i-2$,

• its coefficients only depend on $i$, $j$, $N$ and on the derivatives of $\beta$ but do not depend on $\theta$.

Remark 2

Since $(\lambda _{1,0})^2+(\lambda _{0,1})^2$ is fixed, none of the polynomial expressions that occur in Proposition 2 can be unique. For instance, any occurrence of $(\lambda _{1,0})^2$ could be replaced by $N^2-(\lambda _{0,1})^2$ which would change the term of higher degree. This is the reason why $R_{i,j}$ is not unique: see Sect. 3.2 for a different point of view. However, formula (6) from Proposition 1 gives an explicit procedure for the computation of all $\lambda _{i,j}$s: this is the crucial point that will be used for practical implementation.

One could have expected the degree of $R_{i,j}$ to be smaller than $i+j-1$. The fact that it does actually not depend on $j$ is due to the choice of the coefficients $\{ \lambda _{i,j},i\in \{0,1\},i+j> 1\}$ to be zero. The fact that it is smaller than $i-2$ is due to the fact that the degree of $\lambda _{2,j}$ is $0$, since $(\lambda _{1,0})^2+(\lambda _{0,1})^2=N^2$ is constant with respect to $\lambda _{0,1}$ and $\lambda _{1,0}$. See Definition 1.

Proof

Applying the chain rule introduced in ‘Bivariate version’ in Appendix to the GPW $\varphi$ one gets for all $(i,j) \in {\mathbb {N}}^2$,

$$\begin{aligned} {{\partial }_{x}}^i{{\partial }_{y}}^j \varphi \left( \overrightarrow{g}\right) = i!j!\sum _{\mu =1}^{i+j} \sum _{s=1}^{i+j} \sum _{p_s((i,j),\mu )} \prod _{l=1}^s \frac{(\lambda _{i_l,j_l})^{k_l}}{k_l!}, \end{aligned}$$

where $p_s((i,j),\mu )$ is the set of partitions of $(i,j)$ with length $\mu$:

$$\begin{aligned}&\left\{ (k_l,(i_l,j_l))_{l\in [\![ 1,s ]\!]}:k_l\in {\mathbb {N}}^*, 0\prec (i_1,j_1)\prec \dots \prec (i_l,j_l), \right. \\&\qquad \left. \sum _{l=1}^s k_l = \mu ,\sum _{l=1}^s k_l(i_l,j_l) = (i,j) \right\} . \end{aligned}$$

See ‘Bivariate version’ in Appendix for a definition of this ordering relation. Now consider such a partition to be given and focus on the degree of the corresponding product term, namely $\prod _{l=1}^s (\lambda _{i_l,j_l})^{k_l}$. Thanks to Lemma 1 one can split this product into different terms regarding their degree as polynomials with respect to $(\lambda _{1,0}\lambda _{0,1})$. As a result, since $Deg \ \prod _{l=1}^s (\lambda _{i_l,j_l})^{k_l}=\sum _{l=1}^s k_l Deg\ \lambda _{i_l,j_l}$, this quantity is also at most equal to

$$\begin{aligned} \sum _{i_l=0,j_l=1} k_l j_l+\sum _{i_l=1,j_l=0} k_l i_l+\sum _{i_l=2} k_l\cdot 0+\sum _{i_l\ge 3} k_l (i_l-2) , \end{aligned}$$

(10)

where the two first sums contain at most one term each.

Obviously the leading term in ${{\partial }_{x}}^i{{\partial }_{y}}^j \varphi \left( \overrightarrow{g}\right)$ is $(\lambda _{0,1})^j(\lambda _{1,0})^i$, it corresponds to the partition $(i,j)=j(0,1)+i(1,0)$. Indeed, as long as a partition contains at least one term such that $i_l\ge 2$, the resulting degree computed from (10) will contain at least one term $k_l\cdot 0$ or $k_l(i_l-2)$, and any of them is at most $k_l(i_l+j_l)-2$; as a consequence the degree computed in (10) is then strictly lower than $\sum _{l=1}^s k_l(i_l+j_l)-2= i+j-2$.

Since the product term corresponding to the partition $j(0,1)+i(1,0)$ is $(\lambda _{0,1})^j(\lambda _{1,0})^i/(j!i!)$ it proves both the polynomial nature of $R_{i,j}$ and its degree.

The claim concerning the coefficients of $R_{i,j}$ directly stems from the same property of the coefficients of $\lambda _{i,j}$s from Lemma 1. $\square$

3.2 A more algebraic viewpoint

This paragraph presents a more algebraic point of view on Remark 2.

Suppose $N\in {\mathbb {C}}$ is such that $N\ne 0$, and consider $\{ \lambda _{i,j}\}$ the coefficient of any given GPW defined with the parameters $N$ and a fixed $\theta$. The value of $(\lambda _{1,0},\lambda _{0,1})$ gives that the polynomial $P_{N}$ defined as $P_N=(\lambda _{1,0})^2+(\lambda _{0,1})^2-{N}^2$ satisfies $P_{N}=0$ independently of $\theta$. From then on, considering other quantities as polynomials in two variables in $(\lambda _{0,1},\lambda _{1,0})$ is in fact computing in the quotient ring ${\mathbb {C}} [\lambda _{1,0},\lambda _{0,1}] /(P_{N})$ of ${\mathbb {C}} [\lambda _{1,0},\lambda _{0,1}]$ modulo the ideal generated by $P_{N}$. For instance, the system (8) reads

$$\begin{aligned} \left\{ \begin{array}{rll} \lambda _{2,0} &{}\displaystyle =\frac{\beta \left( \overrightarrow{g}\right) -{N}^2}{2}&{} (P_{N}), \\ \displaystyle \lambda _{2,j} &{}\displaystyle = \frac{{{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{2(j!)}&{} (P_{N}),\ \forall j>0,\\ \displaystyle \lambda _{3,0}&{}\displaystyle = \frac{{{\partial }_{x}}\beta \left( \overrightarrow{g}\right) -2\lambda _{1,0}(\beta \left( \overrightarrow{g}\right) -{N}^2) }{6} &{}(P_{N}),\\ \displaystyle \lambda _{3,j}&{}\displaystyle = \frac{{{\partial }_{x}}{{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{6(j!)}+2 \frac{{{\partial }_{y}}^j \beta \left( \overrightarrow{g}\right) }{j!} \lambda _{1,0}&{} (P_{N}),\ \forall j>0. \end{array}\right. \end{aligned}$$

Of course in this quotient ring, each equivalence class has an infinite number of elements, and all the computations of the previous subsection are performed on elements of these classes. Thus any equality applies to all the elements of the same class. Note that since the ring considered here is the ring of polynomials in two variables, there is no such thing as the Euclidean division. As a result there is nothing like a canonical element of a class used for computations. One can easily see that for $q\ge 4$

$$\begin{aligned} {{\partial }_{x}}^4{{\partial }_{y}}\varphi \left( \overrightarrow{g}\right)&= (\lambda _{1,0})^4 (\lambda _{1,0}) +2{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) \left( (\lambda _{1,0})^2 - (\lambda _{0,1})^2\right) +2{{\partial }_{x}}\beta \left( \overrightarrow{g}\right) \lambda _{0,1}\lambda _{1,0}\\&+\, 2{{\partial }_{x}}{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) \lambda _{1,0}+(-3{{\partial }_{y}}^2\beta \left( \overrightarrow{g}\right) +{{\partial }_{x}}\beta \left( \overrightarrow{g}\right) )\lambda _{0,1}-{{\partial }_{y}}^3\beta \left( \overrightarrow{g}\right) \\&+ \,{{\partial }_{x}}^2{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) ,= (\lambda _{1,0})^4 (\lambda _{1,0}) +2{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) \left( (\lambda _{1,0})^2 + (\lambda _{0,1})^2\right) \\&+\,2{{\partial }_{x}}\beta \left( \overrightarrow{g}\right) \lambda _{0,1}\lambda _{1,0}+ 2{{\partial }_{x}}{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) \lambda _{1,0}+(-3{{\partial }_{y}}^2\beta \left( \overrightarrow{g}\right) \\&+\,{{\partial }_{x}}\beta \left( \overrightarrow{g}\right) )\lambda _{0,1}-{{\partial }_{y}}^3\beta \left( \overrightarrow{g}\right) + {{\partial }_{x}}^2{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) -2N^2{{\partial }_{y}}\beta \left( \overrightarrow{g}\right) \!, \end{aligned}$$

which gives two possible $R_{4,1}\in {\mathbb {C}}[\lambda _{1,0},\lambda _{0,1}]$ satisfying (9) in Proposition 2.

3.3 Theoretical result

This subsection focuses on the interpolation property of the set of basis functions $\mathcal E_{\overrightarrow{g}} (N,p,q)$. The sketch of the proof is inspired by the one developed by Cessenat and Després [5], but it is adapted to the generalized plane wave basis functions.

This proof requires the definition of two matrices, ${\mathsf {M}}_n$ and ${\mathsf {M}}_n^C$, containing the derivatives of classical and generalized plane waves.

Definition 3

Assume $N\in {\mathbb {C}}$ is such that $N\ne 0$, $n\in {\mathbb {N}}$ is such that $n>0$, $q\in {\mathbb {N}}$ such that $q\ge n+1$ and $\overrightarrow{g}=(x_0,y_0)\in {\mathbb {R}}^2$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. For all $l\in {\mathbb {N}}$ such that $1\le l\le 2n+1$ consider the direction $\theta _l=2\pi (l-1)/(2n+1)$, the corresponding GPW $\varphi _l$, $\kappa =-\imath N\in {\mathbb {C}}^*$ and the function

$$\begin{aligned} e_l(x,y)=e^{\imath \kappa \left( (x-x_0)\cos \theta _l + (y-y_0) \sin \theta _l\right) }, \end{aligned}$$

which is a classical plane wave if $N \in \imath {\mathbb {R}}$. The $(n+1)(n+2)/2\times (2n+1)$ matrices ${\mathsf {M}}_n^C$ and ${\mathsf {M}}_n$ are defined as follows: for all $(k_1,k_2)\in {\mathbb {N}}^2$, such that $k_1+k_2\le n$

$$\begin{aligned} \left\{ \begin{array}{l} \left( {\mathsf {M}}_n^C \right) _{\frac{(k_1+k_2)(k_1+k_2+1)}{2}+k_2+1,l} = \frac{{{\partial }_{x}}^{k_1}{{\partial }_{y}}^{k_2}e_l \left( \overrightarrow{g}\right) }{k_1 ! k_2!}, \\ \left( {\mathsf {M}}_n \right) _{\frac{(k_1+k_2)(k_1+k_2+1)}{2}+k_2+1,l} =\frac{{{\partial }_{x}}^{k_1}{{\partial }_{y}}^{k_2}\varphi _l \left( \overrightarrow{g}\right) }{k_1 ! k_2!} . \end{array} \right. \end{aligned}$$

Their $l$th columns contain respectively the Taylor expansion coefficients of the functions $e_l$ and $\varphi _l$.

For instance, one has ${\mathsf {M}}_1= \begin{pmatrix} \varphi _1 \left( \overrightarrow{g}\right) &{}\quad \varphi _2\left( \overrightarrow{g}\right) &{}\quad \varphi _3 \left( \overrightarrow{g}\right) \\ {{\partial }_{x}}\varphi _1 \left( \overrightarrow{g}\right) &{}\quad {{\partial }_{x}}\varphi _2\left( \overrightarrow{g}\right) &{}\quad {{\partial }_{x}}\varphi _3 \left( \overrightarrow{g}\right) \\ {{\partial }_{y}}\varphi _1 \left( \overrightarrow{g}\right) &{}\quad {{\partial }_{y}}\varphi _2\left( \overrightarrow{g}\right) &{}\quad {{\partial }_{y}}\varphi _3 \left( \overrightarrow{g}\right) \end{pmatrix}$, ${\mathsf {M}}_1^C\!=\!\begin{pmatrix} 1&{}1&{}1\\ \imath \kappa \cos \theta _1&{}\quad \! \imath \kappa \cos \theta _2 &{}\quad \! \imath \kappa \cos \theta _3\\ \imath \kappa \sin \theta _1 &{}\quad \! \imath \kappa \sin \theta _2 &{}\quad \! \imath \kappa \sin \theta _3 \end{pmatrix}$ and

$$\begin{aligned} {\mathsf {M}}_2= \begin{pmatrix} \varphi _1 \left( \overrightarrow{g}\right) &{}\quad \! \varphi _2\left( \overrightarrow{g}\right) &{}\quad \! \varphi _3 \left( \overrightarrow{g}\right) &{}\quad \! \varphi _4\left( \overrightarrow{g}\right) &{}\quad \! \varphi _5 \left( \overrightarrow{g}\right) \\ {{\partial }_{x}}\varphi _1 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}\varphi _2\left( \overrightarrow{g}\right) &{} \quad \! {{\partial }_{x}}\varphi _3 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}\varphi _4\left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}\varphi _5 \left( \overrightarrow{g}\right) \\ {{\partial }_{y}}\varphi _1 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{y}}\varphi _2\left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{y}}\varphi _3 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{y}}\varphi _4\left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{y}}\varphi _5 \left( \overrightarrow{g}\right) \\ {{\partial }_{x}}^2\varphi _1 \left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{x}}^2\varphi _2\left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{x}}^2\varphi _3 \left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{x}}^2\varphi _4\left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{x}}^2\varphi _5 \left( \overrightarrow{g}\right) /2 \\ {{\partial }_{x}}{{\partial }_{y}}\varphi _1 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}{{\partial }_{y}}\varphi _2\left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}{{\partial }_{y}}\varphi _3 \left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}{{\partial }_{y}}\varphi _4\left( \overrightarrow{g}\right) &{}\quad \! {{\partial }_{x}}{{\partial }_{y}}\varphi _5 \left( \overrightarrow{g}\right) \\ {{\partial }_{y}}^2\varphi _1 \left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{y}}^2\varphi _2\left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{y}}^2 \varphi _3 \left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{y}}^2\varphi _4\left( \overrightarrow{g}\right) /2 &{}\quad \! {{\partial }_{y}}^2 \varphi _5 \left( \overrightarrow{g}\right) /2 \end{pmatrix}. \end{aligned}$$

The rank of the matrix ${\mathsf {M}}_n^C$ is computed in Lemma 2, which profits from the fact that the result proved by Cessenat and Després [5] for $\kappa >0$ is actually still valid for $\kappa \in {\mathbb {C}}^*$. The proof of Theorem 1 relies on Lemma 3 that explicits the link between the matrix ${\mathsf {M}}_n^C$ and the corresponding matrix ${\mathsf {M}}_n$ built with the generalized plane waves.

Lemma 2

Assume $N\in {\mathbb {C}}$ is such that $N\ne 0$, $n\in {\mathbb {N}}$ is such that $n>0$ and $\overrightarrow{g}=(x_0,y_0)\in {\mathbb {R}}^2$. Finally suppose $\beta \in \mathcal C^{0}$ at $\overrightarrow{g}$. There are two matrices: a rectangle matrix ${\mathsf {P}}_n\in {\mathbb {C}}^{(2n+1)\times (n+1)(n+2)/2}$ only depending on $\beta \left( \overrightarrow{g}\right)$ and a square invertible matrix ${\mathsf {S}}_n \in {\mathbb {C}}^{(2n+1) \times (2n+1)}$ only depending on the directions $\theta _l$ such that ${\mathsf {S}}_n={\mathsf {P}}_n \cdot {\mathsf {M}}_n^C$ and $rk({\mathsf {S}}_n)=2n+1$. Moreover $rk({\mathsf {M}}_n^C)=2n+1$.

Proof

Consider ${\mathsf {M}}_n^C$ to be the matrix introduced in Definition 3 so that for all $(k_1,k_2)\in {\mathbb {N}}^2$, such that $k_1+k_2\le n$ since $e_l \left( \overrightarrow{g} \right) = 1$

$$\begin{aligned} \left( {\mathsf {M}}_n^C \right) _{\frac{(k_1+k_2)(k_1+k_2+1)}{2}+k_2+1,l} = \frac{{{\partial }_{x}}^{k_1} {{\partial }_{y}}^{k_2}e_l\left( \overrightarrow{g}\right) }{k_1 ! k_2!} = \frac{(\imath \kappa )^{k_1+k_2}}{k_1 ! k_2!} \cos ^{k_1} \theta _l \sin ^{k_2} \theta _l. \end{aligned}$$

Define for all $k\in [\![0,n]\!]$

$$\begin{aligned} ({\mathsf {S}}_n)_{n\pm k+1,l}=\frac{1}{(\imath \kappa )^k}\left( \partial _x\pm \imath \partial _y \right) ^k e_l\left( \overrightarrow{g}\right) =\frac{k!}{(\imath \kappa )^k}\sum _{s=0}^{k}\frac{(\pm \imath )^s{{\partial }_{x}}^{(k-s)} {{\partial }_{y}}^{s}e_l\left( \overrightarrow{g}\right) }{(k-s)! s!}. \end{aligned}$$

Thanks to the definition of ${\mathsf {M}}_n^C$ one can check that

$$\begin{aligned} ({\mathsf {S}}_n)_{n\pm k+1,l}=\frac{k!}{(\imath \kappa )^k}\sum _{s=0}^{k}(\pm \imath )^s ({\mathsf {M}}_n^C)_{\frac{((k-s)+s)((k-s)+s+1)}{2}+s+1,l}, \end{aligned}$$

so that ${\mathsf {S}}_n$ is a $(2n+1)\times (2n+1)$ matrix that is a linear transform of ${\mathsf {M}}_n^C$. More precisely, define ${\mathsf {P}}_n$ as a $(2n+1)\times \frac{(n+1)(n+2)}{2}$ matrix such that

$$\begin{aligned} ({\mathsf {P}}_n)_{n\pm k +1,\frac{k(k+1)}{2}+s+1}=k!(\pm \imath )^s\!/\!(\imath \kappa )^k. \end{aligned}$$

Then ${\mathsf {S}}_n={\mathsf {P}}_n\cdot {\mathsf {M}}_n^C$. As a consequence, $rk({\mathsf {M}}_n^C)\ge rk({\mathsf {S}}_n)$.

The rank of ${\mathsf {S}}_n$ is now to be evaluated thanks to the definition of the plane waves $e_l$. Since $e_l(x,y)=e^{(\imath \kappa )\left( (x-x_0)\cos \theta _l + (y-y_0) \sin \theta _l\right) }$ then

$$\begin{aligned} \left( \partial _x\pm \imath \partial _y \right) ^k e_l = (\imath \kappa )^k (\cos \theta _l \pm \imath \sin \theta _l)^k e_l. \end{aligned}$$

Consider that $z_l=\cos \theta _l + \imath \sin \theta _l=(\cos \theta _l - \imath \sin \theta _l)^{-1}$ because $|z_l|=1$, and since $e_l\left( \overrightarrow{g}\right) =1$ it yields

$$\begin{aligned} \left( \partial _x\pm \imath \partial _y \right) ^k e_l \left( \overrightarrow{g}\right) = (\imath \kappa )^k(z_l)^{\pm k}e_l \left( \overrightarrow{g}\right) = (\imath \kappa )^k(z_l)^{\pm k} \Rightarrow ({\mathsf {S}}_n)_{n\pm k+1,l}=(z_l)^{\pm k}. \end{aligned}$$

Thus ${\mathsf {S}}_n$’s columns are proportional to the one of a Vandermonde matrix and

$$\begin{aligned} det \ {\mathsf {S}}_n = \prod _{i=1}^n z_i^{-n}\prod _{i<j}(z_i-z_j). \end{aligned}$$

From the choice of $\theta _l$s, for all $i\ne j$: $z_i\ne z_j$ so that ${\mathsf {S}}_n$ is invertible and $rk({\mathsf {M}}_n^C)\ge rk({\mathsf {S}}_n)=2n+1$. Since

$$\begin{aligned} rk\left( {\mathsf {M}}_n^C\right) \le \min \left( 2n+1, \frac{(n+1)(n+2)}{2}\right) =2n+1 \end{aligned}$$

the proof is then completed. $\square$

Lemma 3

Assume $N\in {\mathbb {C}}$ is such that $N\ne 0$, $n\in {\mathbb {N}}$ is such that $n>0$, $q\in {\mathbb {N}}$ is such that $q\ge n+1$ and $\overrightarrow{g}=(x_0,y_0)\in {\mathbb {R}}^2$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider $\mathcal E_{\overrightarrow{g}} (N,p,q)$ introduced in Definition 2, together with ${\mathsf {M}}_n$ and ${\mathsf {M}}_n^C$ introduced in Definition 3. Then there is a lower triangular matrix ${\mathsf {L}}_n$, whose diagonal coefficients are all equal to $1$ and whose other coefficients are linear combinations of the derivatives of $\beta$ evaluated at $\overrightarrow{g}$, such that

$$\begin{aligned} {\mathsf {M}}_n=L_n\cdot {\mathsf {M}}_n^C. \end{aligned}$$

(11)

As a consequence $rk({\mathsf {M}}_n)=rk({\mathsf {M}}_n^C)$ and both $\Vert {\mathsf {L}}_n\Vert$ and $\Vert ({\mathsf {L}}_n)^{-1}\Vert$ are bounded by a constant only depending on $N$ and $\beta$.

The following proof is straightforward considering the feature of the derivatives of $\varphi _l$ described in Proposition 2.

Proof

From (9) there exists a polynomial $R_{i,j}\in {\mathbb {C}}[X,Y]$ with $Deg\ R_{i,j}\le i-2$ such that

$$\begin{aligned} \forall (i,j) \in {\mathbb {N}}^2,\,\,{{\partial }_{x}}^{i}{{\partial }_{y}}^{j}\varphi _l \left( \overrightarrow{g}\right) = {{\partial }_{x}}^{i}{{\partial }_{y}}^{j}e_l \left( \overrightarrow{g}\right) + R_{i,j} \left( {{\partial }_{x}}e_l \left( \overrightarrow{g}\right) ,\,\,{{\partial }_{y}}e_l \left( \overrightarrow{g}\right) \right) .\quad \quad \end{aligned}$$

(12)

The coefficients of $R_{i,j}$ do not depend on the basis function considered, but only depends on $\beta$ and its derivatives evaluated at $\overrightarrow{g}$. By construction of the classical plane wave $e_l$, one has

$$\begin{aligned} \left\{ \begin{array}{rl} {{\partial }_{x}}^{k}{{\partial }_{y}}^{m}e_l \left( \overrightarrow{g}\right) &{}=\left( {{\partial }_{x}}e_l \left( \overrightarrow{g}\right) \right) ^k\left( {{\partial }_{y}}e_l \left( \overrightarrow{g}\right) \right) ^m,\\ &{}= (\imath \kappa )^{k+m} \cos ( \theta )^k (i\sin (\theta ))^m. \end{array} \right. \end{aligned}$$

The numbering of the rows in matrices ${\mathsf {M}}_n^C$ and ${\mathsf {M}}_n$ is set up such that the derivatives of smaller order appear higher in the matrix, which proves (11). Indeed (12) shows that any coefficient of ${\mathsf {M}}_n$ is the sum of the corresponding coefficient in ${\mathsf {M}}_n^C$ plus a linear combination—whose coefficients do not depend on the column that is considered but only on $\beta$ and its derivatives evaluated at $\overrightarrow{g}$—of terms that appear higher in the corresponding column of ${\mathsf {M}}_n$.

The rank of ${\mathsf {M}}_n$ is then equal to the rank of ${\mathsf {M}}_n^C$, and $\Vert {\mathsf {L}}_n\Vert$ and $\Vert ({\mathsf {L}}_n)^{-1}\Vert$ do only depend on the coefficients of $R_{i,j}$. As a result they do not depend on the basis functions but only on the parameter $N$, the coefficient $\beta$ and its derivatives at $\overrightarrow{g}$. $\square$

The hypothesis of the following theorem give a sufficient condition on the relation between the parameters $p$ and $q$ to achieve a high order interpolation.

Theorem 1

Assume $\Omega \subset {\mathbb {R}}^2$ is a bounded domain, $N\in {\mathbb {C}}$ is such that $N\ne 0$, $n\in {\mathbb {N}}$ is such that $n>0$, $q\ge n+1$, $p=2n+1$ and $\overrightarrow{g}=(x_0,y_0)\in \Omega$. Finally suppose $\beta \in \mathcal C^{q-1}$ at $\overrightarrow{g}$. Consider that $u$ is a solution of scalar wave Eq. (1) which belongs to $\mathcal C^{n+1}$. Consider then $\mathcal E_{\overrightarrow{g}} (N,p,q)$ introduced in Definition 2. Then there are a function $u_a\in Span\ \mathcal E_{\overrightarrow{g}} (N,p,q)$ depending on $\beta$ and $n$, and a constant $C(N,\Omega ,n)$ depending on $N$, $\beta$ and $n$ such that for all $\overrightarrow{m}\in {\mathbb {R}}^2$

$$\begin{aligned} \left\{ \begin{array}{l} \left| u\left( \overrightarrow{m}\right) -u_a\left( \overrightarrow{m}\right) \right| \le C(N,\Omega ,n) \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \left\| u \right\| _{\mathcal C^{n+1}(\Omega )},\\ \left\| \nabla u\left( \overrightarrow{m}\right) -\nabla u_a\left( \overrightarrow{m}\right) \right\| \le C(N,\Omega ,n) \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n} \left\| u \right\| _{\mathcal C^{n+1}(\Omega )}. \end{array} \right. \end{aligned}$$

(13)

Note that it provides an upper bound for the best approximation property of the function space $\mathcal E_{\overrightarrow{g}} (N,p,q)$:

$$\begin{aligned}&\max \left\{ \Vert u - \varphi \Vert _{L^\infty \left( \left| \overrightarrow{m}-\overrightarrow{g}\right| \le h\right) }, \varphi \in Span \mathcal E_{\overrightarrow{g}} (N,p,q)\right\} \\&\quad \le C(N,\Omega ,n) \left\| u \right\| _{\mathcal C^{n+1}(\Omega )} h^{n+1}. \end{aligned}$$

The behavior of the constant $C(N,\Omega ,n)$ as $N$ goes to zero is commented in Sect. 3.4. It suggests the need for a parameter $N$ that is bounded away from zero, see Sect. 4.1.

Proof

The idea of the proof is to look for $u_a= \sum _{l=1}^{2n+1} {\mathsf {X}}_l \varphi _l$ by fitting its Taylor expansion to the one of $u$. This will be done by solving a linear system concerning the unknowns $({\mathsf {X}}_l)_{l\in [\![1,2n+1]\!]}$.

Since $u$ belongs to $\mathcal C^{n+1}$ and for all $l\in [\![1,2n+1]\!]$ the basis function $\varphi _l$ belongs to $\mathcal C^\infty$, their Taylor expansions read: there is a constant $C$ such that for all $\overrightarrow{m}=(x,y) \in \Omega$

$$\begin{aligned} \left| u(x,y) - \sum _{m=0}^n \sum _{k_1+k_2=m} {\mathsf {B}}_{k_1k_2}x^{k_1} y^{k_2} \right|&\le C \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \Vert u\Vert _{\mathcal C^{n+1}},\\ \left| \varphi _l(x,y) - \sum _{m=0}^n \sum _{k_1+k_2=m} {\mathsf {M}}^l_{k_1k_2}x^{k_1} y^{k_2} \right|&\le C \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \Vert \varphi _l\Vert _{\mathcal C^{n+1}}, \end{aligned}$$

where for the sake of simplicity ${\mathsf {M}}^l_{k_1k_2}$ stands for the term ${{\partial }_{x}}^{k_1} {{\partial }_{y}}^{k_2} \varphi _l /(k_1!k_2!)$, which is the definition of $({\mathsf {M}}_n)_{\frac{(k_2+k_1)(k_2+k_1+1)}{2}+k_2+1,l}$. In the same way, define a vector ${\mathsf {B}}_n$: ${\mathsf {B}}_{k_1,k_2}$ stands for the Taylor coefficient of $u$, which is the definition of the coefficient $({\mathsf {B}}_n)_{\frac{(k_2+k_1)(k_2+k_1+1)}{2}+k_2+1}$. Note that at every point $\overrightarrow{g}$ in $\Omega$, there is a constant $C=C_{\overrightarrow{g}}$ such that the two previous estimates hold. This constant $C_{\overrightarrow{g}}$ depends continuously on $\overrightarrow{g}$, through the derivatives of $\beta$ evaluated at $\overrightarrow{g}$. Since $\Omega$ is compact, the constant $C = \max _{\overrightarrow{g}\in \Omega } C_{\overrightarrow{g}}$ is finite. The system to be solved is then

In order to study the system’s matrix, the equations depending on $(k_1,k_2)$ have to be numbered: they will be considered with increasing $m=k_1+k_2$, and with decreasing $k_1$ for a fixed value of $m$. Defining the corresponding vector ${\mathsf {B}}_n\in {\mathbb {C}}^{\frac{(n+1)(n+2)}{2}}$, together with the unknown ${\mathsf {X}}^n=({\mathsf {X}}_1,{\mathsf {X}}_2,\ldots ,{\mathsf {X}}_{2n+1})\in {\mathbb {C}}^{2n+1}$, the system now reads

$$\begin{aligned} \left\{ \begin{array}{l} \text {Find } {\mathsf {X}}^n \in {\mathbb {C}}^{2n+1} \text { such that}\\ {\mathsf {M}}_n \cdot {\mathsf {X}}^n = {\mathsf {B}}_n \end{array} \right. \end{aligned}$$

where ${\mathsf {M}}_n\in {\mathbb {C}}^{\frac{(n+1)(n+2)}{2}\times (2n+1)}$ is the matrix from Definition 3.

Since the system is not square, there is a solution if and only if ${\mathsf {B}}_n\in Im({\mathsf {M}}_n)$. The following points are steps toward the proof of existence of such a solution.

(i) The technical point is to prove that $\underline{rk({\mathsf {M}}_n)=2n+1}$. It is straightforward from Lemmas 3 and 2.

(ii) Build subset ${\mathfrak {K}} \subset {\mathbb {C}}^{\frac{(n+1)(n+2)}{2}}$ such that $\underline{Im({\mathsf {M}}_n)\subset {\mathfrak {K}}\,\,\mathrm{and}\,\, {\mathsf {B}}_n\in {\mathfrak {K}}}$. Such a subspace ${\mathfrak {K}}$ can be built from the fact that the basis functions are designed to fit the Taylor expansion of the scalar wave equation: for all $l\in [\![ 1,2n+1]\!]$, for all $(k_1,k_2)\in [\![ 0,n-2]\!]^2$ such that $k_1+k_2\le n-2$, the element of the $l$th column of ${\mathsf {M}}_n$ satisfy

$$\begin{aligned}&(k_1+1)(k_1+2)({\mathsf {M}}_n)_{k_1+2,k_2} +(k_2+1)(k_2+2)({\mathsf {M}}_n)_{k_1,k_2+2}\\&\quad =\sum _{i=0}^{k_1}\sum _{j=0}^{k_2} \frac{{{\partial }_{x}}^{i} {{\partial }_{y}}^{j} \beta \left( \overrightarrow{g}\right) }{i!j!} ({\mathsf {M}}_n)_{k_1-i,k_2-j} . \end{aligned}$$

This is clear from the design of the GPWs, since for all the basis functions $\varphi _l$, all the terms of order smaller than $q$ in the Taylor expansion of $(-\Delta +\beta )\varphi _l=(-P_{\Delta ,l}+\beta )\varphi _l$ vanish. So define

$$\begin{aligned} {\mathfrak {K}}&:= \left\{ (C_{k_1,k_2}) \in {\mathbb {C}}^{\frac{(n+1)(n+2)}{2}}, \forall (k_1,k_2)\in {\mathbb {N}}^2, k_1+k_2\le n-2, \right. \nonumber \\&\qquad \quad \left. (k_1+1)(k_1+2)C_{k_1+2,k_2}+(k_2+1)(k_2+2)C_{k_1,k_2+2}\right. \nonumber \\&\qquad \quad \left. =\sum \limits _{i=0}^{k_1}\sum \limits _{j=0}^{k_2}\frac{{{\partial }_{x}}^{i} {{\partial }_{y}}^{j} \beta \left( \overrightarrow{g}\right) }{i!j!}C_{k_1-i,k_2-j} \right\} \end{aligned}$$

(14)

With $q\ge n+1$, it is then straightforward to see that $Im({\mathsf {M}}_n)\subset {\mathfrak {K}}$. The fact that ${\mathsf {B}}_n\in {\mathfrak {K}}$ simply stems from plugging the Taylor expansions of $u$ and $\beta$ into scalar wave equation.

(iii) The dimension of ${\mathfrak {K}}$ defined by (14) is $\underline{\mathrm{dim} {\mathfrak {K}} = 2n+1}$. Indeed, one can check—using the same numbering as previously for the equations—that ${\mathfrak {K}}$ is defined by $n(n-1)/2$ linearly independent relations on ${\mathbb {C}}^{\frac{(n+1)(n+2)}{2}}$, so that its dimension is $(n+1)(n+2)/2-n(n-1)/2$.

As a result of points (i), (ii), and (iii), $Im({\mathsf {M}}_n)$ there is a solution to the system ${\mathsf {M}}_n \cdot {\mathsf {X}}^n = {\mathsf {B}}_n$.

As a consequence, consider a solution ${\mathsf {X}}^n$ to the system ${\mathsf {M}}_n \cdot {\mathsf {X}}^n = {\mathsf {B}}_n$, and define $u_a= \sum _{l=1}^{2n+1} {\mathsf {X}}_l \varphi _l$. Thanks to that definition and to the Taylor expansions of $u$ and the $\varphi _l$s it yields

$$\begin{aligned} \left| u\left( \overrightarrow{m}\right) -u_a\left( \overrightarrow{m}\right) \right| \le C \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \left( \left\| u \right\| _{\mathcal C^{n+1}}+\left\| u_a \right\| _{\mathcal C^{n+1}}\right) . \end{aligned}$$

Moreover one has the identity ${\mathsf {X}}^n=({\mathsf {S}}_n)^{-1} {\mathsf {P}}_n ({\mathsf {L}}_n)^{-1}{\mathsf {B}}_n$, where $({\mathsf {S}}_n)^{-1} {\mathsf {P}}_n$ is bounded from above by $\sup _{l\in [\![1,2n+1]\!]} \Vert e_l \Vert _{\mathcal C^{n+1}}$, see Lemma 2, $({\mathsf {L}}_n)^{-1}$ is bounded from above by a constant depending only on $\beta$ and its derivatives from Lemma 3, and ${\mathsf {B}}_n$ is bounded by $\Vert u\Vert _{\mathcal C^{n+1}}$. Since for all $l\in [\![1,2n+1]\!]$ it yields $|{\mathsf {X}}_l|\le C(N,\Omega ,n)\Vert u\Vert _{\mathcal C^{n+1}}$, it turns out to be the first part of (13):

$$\begin{aligned} \left| u\left( \overrightarrow{m}\right) -u_a\left( \overrightarrow{m}\right) \right| \le C(N,\Omega ,n)(2n+2) \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{n+1} \left\| u \right\| _{\mathcal C^{n+1}} . \end{aligned}$$

At last, the second part of (13) stems from taking the Taylor Lagrange formula of the gradient of $u-u_a$, up to the order $n$, since

$$\begin{aligned} \displaystyle \sum _{m=0}^n \sum _{k_1+k_2=m}\left( {\mathsf {B}}_{k_1k_2}(x\!-\!x_0)^{k_1} (y\!-\!y_0)^{k_2} \!-\! \sum _{l=1}^{2n+1}\left( {\mathsf {X}}_l{\mathsf {M}}^l_{k_1k_2}(x\!-\!x_0)^{k_1} (y-y_0)^{k_2}\right) \right) =0. \end{aligned}$$

That is: for all $\overrightarrow{m}=(x,y)\in \Omega$ there are $\zeta _1$, $\zeta _2$ in ${\mathbb {R}}^2$ on the segment line between $\overrightarrow{m}$ and $\overrightarrow{g}$ such that

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {{\partial }_{x}}(u - u_a)(x,y) = \sum _{l=0}^{n} \frac{{{\partial }_{x}}^{l+1}{{\partial }_{y}}^{n-l}(u-u_a)(\zeta _1)}{l!(n-l)!} (x-x_0)^{l} (y-y_0)^{n-l},\\ \displaystyle {{\partial }_{y}}(u - u_a) (x,y)= \sum _{l=0}^{n} \frac{{{\partial }_{x}}^{l}{{\partial }_{y}}^{n-l+1}(u-u_a)(\zeta _2)}{l!(n-l)!} (x-x_0)^{l} (y-y_0)^{n-l} \end{array} \right. \end{aligned}$$

which indeed leads to the desired inequality. $\square$

3.4 Comments on the asymptotic behavior of $C(N,\Omega ,n)$

Consider first the behavior of this constant with respect to $N$. Because the Taylor expansion actually reads

$$\begin{aligned}&(u - u_a)(x,y) = \sum _{j=0}^q \left( \frac{{{\partial }_{x}}^j{{\partial }_{y}}^{q-j} u\left( \overrightarrow{g}\right) }{j!(q-j)!} - \sum _{l=1}^p {\mathsf {X}}_l \frac{{{\partial }_{x}}^j{{\partial }_{y}}^{q-j} \varphi _l\left( \overrightarrow{g}\right) }{j!(q-j)!} \right) \nonumber \\&\quad (x-x_0)^{j} (y-y_0)^{q-j}+ O\left( \left| \overrightarrow{m}-\overrightarrow{g}\right| ^{q+1} \right) , \end{aligned}$$

one can see that if $c_{N,\overrightarrow{g}} = \sum _{l=1}^p {\mathsf {X}}_l \sum _{j=0}^q\frac{{{\partial }_{x}}^j{{\partial }_{y}}^{q-j} \varphi _l\left( \overrightarrow{g}\right) }{j!(q-j)!}$ blows up when $N$ goes to zero, then so does $C(N,\Omega ,n)$.

Since ${\mathsf {X}}^n$ satisfies ${\mathsf {S}}_n \cdot {\mathsf {X}}^n = {\mathsf {P}}_n ({\mathsf {L}}_n)^{-1} {\mathsf {B}}_n$, one can describe the asymptotic behavior of the ${\mathsf {X}}_l$s with respect to $N$ as follows. The matrix of this system doesn’t depend on $N$, but only on $p$. Now consider the right hand side of this system:

• the vector ${\mathsf {B}}_n$ only depends on $u$ and $n$,

• thanks to Proposition 2, the matrix ${\mathsf {L}}_n$ has a lower triangular block structure: particularly the $n$ diagonal square blocs of increasing size $k\times k$ for $k$ from $1$ to $n+1$ are identity blocs, while the sub-diagonal rectangle blocs of size $(k+1)\times k$ for $k$ from $1$ to $n$ are zero blocs, and the rest of the sub-diagonal coefficients are polynomials with respect to $N^2$,

• the inverse $({\mathsf {L}}_n)^{-1}$ shares this sparse structure with ${\mathsf {L}}_n$ and the same dependence with respect to $N$,

• by construction the only non zero blocs of the matrix ${\mathsf {P}}_n$ are row blocs, each element of such a bloc having the same modulus $1\!/\!N^k$, particularly for the first and last rows of ${\mathsf {P}}_n$ which first $\frac{n(n+1)}{2}$ terms are zero while the last $n+1$ terms are respectively $n ! (\pm \imath )^s\!/\!N^n$ for $s$ from $0$ to $n$.

It yields that the right hand side behaves as $1\!/\!N^n$ as $N$ goes to zero, see Fig. 2 for an illustration of these different structures. As a result the coefficients ${\mathsf {X}}_l$s behave as $1\!/\!N^n$ as $N$ goes to zero as well. As opposed to Proposition 2, a result concerning the lowest degree term of ${{\partial }_{x}}^j{{\partial }_{y}}^{q-j} \varphi$ as polynomials with respect to $(\lambda _{1,0},\lambda _{0,1})$ would provide an explicit estimate for $C(N,\Omega ,n)$ as $N$ goes to zero.

Fig. 2

Profile of matrices $P_n$ and $L_n$ for $n=4$. All white blocs are zeros. Left row bloc structure of the $P_n$ matrix. For $k$ from $0$ to $n$, the rows $n\pm k+1$ contain a $1\times (k+1)$ non zero bloc. These non zero blocs are represented in sky blue. As stated in the definition of $P_n$, every non zero element on the row $n\pm k +1$ behaves asymptotically as $1/N^k$ as $N$ goes to zero. Right bloc structure of the $L_n$ matrix. The diagonal blocs are identity blocs of increasing size $k$, they are represented in sky blue. The sub-diagonal blocs of size $k\times (k+1)$ are zeros, so they are represented in white. The rest of the sub-diagonal coefficients, represented on midnight blue, are polynomials with respect to $N^2$ (color figure online)

Consider now the behavior of the constant $C(N,\Omega ,n)$ with respect to the local number of basis functions, $p=2n+1$. The only direct dependence with respect to $p$ stems from the matrix ${\mathsf {S}}_n$, more precisely from its determinant. Indeed, it is clear to see that

$$\begin{aligned} \left| \det {\mathsf {S}}_n \right| = \prod _{j=2}^p \prod _{i=1}^{j-1} \left( \exp \frac{2\imath \pi (i-1)}{p} - \exp \frac{2\imath \pi (j-1)}{p} \right) = \prod _{l=1}^{\frac{p-1}{2} }\left( \sin \frac{2\pi l}{p} \right) ^p. \end{aligned}$$

In order to get a first estimate, one can consider that the convergence will be driven by the terms such that $l\!/\!p \le 100$ and simply bound the other terms by 1. Then from Stirling’s approximation

$$\begin{aligned} \displaystyle \prod _{l=1}^{p/100 }\sin \frac{2\pi l}{p} \approx 2\pi \prod _{l=1}^{p/100 } \frac{ l}{p} \approx 2\pi \sqrt{2\pi \frac{p}{100}} \frac{1}{(100e)^{\frac{p}{100}}}, \end{aligned}$$

so that $\displaystyle \left| \det {\mathsf {S}}_n \right| \le C \left( \frac{p}{100}\right) ^{p/2} \frac{1}{(100e)^{\frac{p^2}{100}}}$. This first estimate is encouraging since in the plane wave literature, and especially for applications linked to the UWVF, the $hp$-convergence seems more attractive than the $h$-convergence, see for instance [18, 20].

4 Numerical validation

In order to validate the Theorem 1, each of the numerical validation case is computed, for a given value of $n$, setting $q=n+1$ and $p=2n+1$. The test case considered is $\beta (x,y)=x-1$, to approximate the exact solution $u_e(x,y)=Airy(x)e^{\imath y}$. See [22] for the physical motivation of this test case: its main interest is that the coefficient vanishes along the line $x=1$, which represents a plasma cut-off that reflects incoming waves.

First a discussion addresses the choice of the normalization parameter $N$ to design the basis functions, introduced in Definition 1.

Of course since the theoretical results give local approximation properties, the validation procedure itself will be local as well. As stated in the theorem $u_e$ can be approximated by a function $u_a$ that belongs to the approximation space $\mathcal E_{\overrightarrow{g}} (N,p,q)$, space that is built with the previously discussed normalizations.

The idea is to follow the error $\max \left| u_e-u_a\right|$ on disks with decreasing radius $h$ in order to observe the order of convergence with respect to $h$. Several different cases are proposed to validate the theoretical order of convergence, and additional cases concern the behavior of the basis functions with respect to the cut-off.

4.1 Two families of generalized plane waves

Two different choices of the normalization parameter $N$ will be considered in this paper. A first choice is comprised of setting $N=\sqrt{\mathrm{sgn} \beta \left( \overrightarrow{g}\right) }\sqrt{\left| \beta \left( \overrightarrow{g}\right) \right| }$, see Definition 4. It gives a direct generalization of a classical plane waves, since in this case $\beta \left( \overrightarrow{g}\right) <0$, so that $\sqrt{-\beta \left( \overrightarrow{g}\right) }$ is the local wave number. However, this choice is local since $N$ does depend on $\overrightarrow{g}\in \Omega$, and cannot be used if $\beta \left( \overrightarrow{g}\right) =0$: it is a classical problem in low frequency regime , see [15, 21]. To overcome this limitation and consider the stationary limit case, a second possibility is to choose one constant and non zero value for $N$: it will not depend on $\overrightarrow{g}$ anymore.

The first type of shape functions corresponds to a local choice since it does depend on $\overrightarrow{g}\in {\mathbb {R}}^2$.

Definition 4

The $\beta$-normalization for GPWs is defined by choosing $N=\sqrt{\mathrm{sgn} \beta \left( \overrightarrow{g}\right) }\sqrt{\left| \beta \left( \overrightarrow{g}\right) \right| }$ in Definition 1, which means setting

• 1. $(\lambda _{1,0},\lambda _{0,1})=\sqrt{\mathrm{sgn} \beta \left( \overrightarrow{g}\right) }\sqrt{\left| \beta \left( \overrightarrow{g}\right) \right| } (\cos \theta ,\sin \theta )$.

• 2. $\{ \lambda _{i,j},0\le i+j\le q+1,i+j\ne 1\}$ are set to zero.

Remark 3

(Back to classical Plane Waves from the $\beta$-normalization) The fact that the quantity $(\lambda _{1,0})^2+(\lambda _{0,1})^2$ is equal to $\beta \left( \overrightarrow{g}\right)$ however gives that the value of $\beta \left( \overrightarrow{g}\right)$ does actually never appear in the expression of the other coefficients explicitly, but only in product terms involving $\lambda _{1,0}$ or $\lambda _{0,1}$. One can easily check by induction that each one of the terms that are summed in formula (6) contains at least one derivative of $\beta$. Indeed (8) proves it for $\lambda _{i,j}$, $i=2$ and $3$, and the induction is then clear for $i\ge 3$ thanks to (6).

As a consequence, for $\beta =-\omega ^2<0$ and for any $q\ge 1$, all the coefficients $\lambda _{i,j}$ such that $i>1$ are actually zero, which means that the corresponding function $\varphi =\exp \sum _{ 0\le i+j\le q+1} \lambda _{i,j}(x-x_0)^i (y-y_0)^j$ is nothing more than a classical plane wave.

As already remarked, it is also obvious that for $q=1$ this new shape function is again nothing more than a classical plane wave as long as $\beta <0$. This case $q=1$ corresponds to the classical fact of approximating a smooth coefficient by its piecewise constant value at the center of the cells.

The fact is that since the terms $(\lambda _{1,0},\lambda _{0,1})$ of the $\beta$-normalization are proportional to the square root of $\beta$, they will vanish when $\beta =0$. Note that the approximation properties of classical place waves do not deteriorate as their wave number goes to zero, see [26, Section 3.4] . However, numerical results show that it causes severe damaging to the conditioning of the discrete UWVF problem if $\beta$ tends to zero. Moreover the theoretical estimate displayed in Sect. 3.4 justifies the need for a second normalization to ensure the desired interpolation property. As a consequence, a second normalization is considered, with a global choice of $N$ independent from $\overrightarrow{g}\in {\mathbb {R}}^2$.

Definition 5

The constant-normalization for GPW is defined by choosing $N=\imath$ in Definition 1, which means setting

• 1. $(\lambda _{1,0},\lambda _{0,1})=\imath (\cos \theta ,\sin \theta )$.

• 2. $\{ \lambda _{i,j},0\le i+j\le q+1,i+j\ne 1\}$ are set to zero.

Remark 4

(Classical Plane Waves and the constant-normalization) In order to balance Remark 3, note that since the constant-normalization does not depend on $\beta$ it arises that for $\beta =-\omega ^2\ne -1$ the term $\beta \left( \overrightarrow{g}\right)$ appears in higher order terms. For instance it is clear that $\lambda _{2,0}=(1+ \beta \left( \overrightarrow{g}\right) )/2$. As a consequence, neither when $\beta (\ne -1)<0$ is constant nor when $q=1$ the shape function designed from the constant-normalization can be a classical plane wave.

4.2 In the propagative zone

The point $\overrightarrow{g}=(-3,1)$ is in the propagative zone. Then concentric disks are centered on $\overrightarrow{g}$ with radius $h=1/2^k$, increasing the value of $k$. Following the theorem, the expected order of convergence is $n+1$.

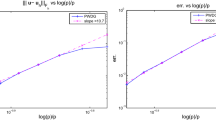
Figure 3 displays computed convergence results that fit perfectly the theoretical result. A set of $p=11$ classical Plane Waves is used as a control case, since $p=11$ is the higher number of basis functions used with both normalizations of the GPWs. As expected, since both normalizations satisfy $N\ne 0$ away from the cut-off, the orders of convergence observed are close to $n+1$. No significant difference is observed between the two types of normalization.

Fig. 3

Convergence results in the propagative zone, computed at $(-3,1)\in {\mathbb {R}}^2$ with different basis functions. Comparison between classical Plane Waves and Generalized Plane Waves for both $\beta$ and constant normalizations. Some of the associated orders of convergence are also provided. In the legend, $beta$ and $CST$ respectively refer to the $\beta$ and constant normalizations, while $n$ is the parameter introduced in Theorem 1: in each case the expected order of convergence is $n+1$. $PW$ refers to the classical Plane Waves

Note that machine precision is reached in the higher order cases.

4.3 In the non propagative zone

The point $\overrightarrow{g}=(2,1)$ is in the non propagative zone. Again concentric disks are centered on $\overrightarrow{g}$ with radius $h=1/2^k$, increasing the value of $k$, and the expected order of convergence is $n+1$. There is no classical Plane Wave that can be computed here since $\beta \left( \overrightarrow{g}\right) >0$.

Figure 4 displays computed convergence results that fit perfectly the theoretical result as well. As was observed in the propagative case, since both normalizations satisfy $N\ne 0$, the orders of convergence observed are equal or slightly higher than the theoretical order $n+1$. Still no significant difference appears between the two types of normalization.

Fig. 4

Convergence results in the non-propagative zone, computed at $(2,1)\in {\mathbb {R}}^2$ with different basis functions. Comparison between Generalized Plane Waves for $\beta$ and constant normalizations. Some of the associated orders of convergence are also provided. In the legend, $beta$ and $CST$ respectively refer to the $\beta$ and constant normalizations, while $n$ is the parameter introduced in Theorem 1: in each case the expected order of convergence is $n+1$

Again machine precision is reached in the higher order cases.

4.4 Along the cut-off: $\beta =0$

The point $\overrightarrow{g}=(1,1)$ lies exactly on the vanishing line of $\beta$. Then again concentric disks are centered on $\overrightarrow{g}$ with radius $h=1/2^k$, increasing the value of $k$. Both classical Plane Waves and GPWs with $\beta$-normalization would provide only one function since they correspond to $N=\beta \left( \overrightarrow{g}\right) =0$. As to the GPWs with constant-normalization, the theoretical results show that their interpolation property holds along the cut-off as well as anywhere else in the domain.

As Figs. 3, 4 and 5 displays results that fit perfectly the theoretical result. The orders of convergence observed are again slightly better than $n+1$. It is an example of efficient approximation of the exact solution $u_e$ along the cut-off.

Fig. 5

Convergence results computed at $(1,1)\in {\mathbb {R}}^2$ where $\beta (1,1)=0$ using Generalized Plane Waves with the constant-normalization. Some of the associated orders of convergence are also provided. In the legend, $n$ is the parameter introduced in Theorem 1: in each case the expected order of convergence is $n+1$

4.5 Toward the cut-off: $\beta \rightarrow 0$

Since $\beta (x=1,y)=0$, it is interesting to look at what happens with the $\beta$-normalization along this line. Again the value of $h$ is $h=1/2^k$, increasing the value of $k$. The point $\overrightarrow{g}_h=[1-h,1]$ remains in the propagative zone. Then disks are here centered on a point $\overrightarrow{g}_h$ that stands at a distance $h$ from the line $x=1$, still with radius $h$. As a result all the disks are tangent to the cut-off line defined by $x=1$. Classical Plane Waves are compared to the $\beta$-normalization with the same number of basis functions. Even if this test case does not correspond to the theoretical result proved in the present work, it is of significant interest for further inclusion of the GPWs to plane wave methods.

Figure 6 show that the $\beta$ normalized Generalized plane waves give a high order approximation of $u$ even getting closer to the vanishing line $x=1$, as long as $h$ is not too small. Note first that there seem to be a significant difference between the classical and generalized plane waves, as the error obtained with the classical plane waves rapidly reaches a threshold which is seven orders of magnitude bigger than with the GPWs. However it is obvious that, as the parameter $n$ increases, the minimum error obtained with the $\beta$-normalized GPWs increases. It justifies the use of the constant-normalization for further applications.

Fig. 6

Convergence results toward $\beta =0$, computed at $(1-h,1)\in {\mathbb {R}}^2$. Comparison between Classical Plane Waves and Generalized Plane Waves with the $\beta$-normalization. Some of the associated orders of convergence are also provided. In the legend, $beta$ and $PW$ respectively refer to the $\beta$ normalization and classical Plane Waves, while $n$ is the parameter introduced in Theorem 1: in each case the expected order of convergence is $n+1$, and $p$ is the number of classical Plane Waves

Another possibility is to compare the influence of two parameters: the size of the disk $h$ and the distance $d$ between $\overrightarrow{g}$ and the line $x=1$. In this case, the error $e=\max |u_e-u_a|$ depends on both parameters, so one can write $e(h,d)$. Figure 7 displays the error computed for $h$ and $d$ convergence with the $\beta$-normalization. The $h$ convergence is clearly damaged for decreasing values of $d$. This is linked to the low frequency limit when $\beta$ goes to zero. However, looking at the $h$ convergence with $d=h$, one can see that the error $e(h,h)$ converges as the error $e(h,1/2)$ until $h=1/2^5$.

Fig. 7

Error computed on a disk of radius $h$ centered at $(1-d;1)\in {\mathbb {R}}^2$. The approximation is computed with $\beta$-normalized basis functions and with $n=5$

5 Conclusion

A procedure to design a set of generalized plane waves that are locally approximate solution of the scalar wave equation has been successfully developed, the novelty being to consider smooth and non constant coefficients. It is to be noted that the design procedure is still valid as the coefficient vanishes. Both theoretical and numerical results evidence the high order approximation property of the GPWs, corresponding to $h$-convergence.

The design procedure could easily be generalized to many differential operators, as described in [23]. Moreover a natural idea would be to extend the generalization process from the phase to the amplitude of plane waves, by considering a looking for a shape function as $\varphi = Qe^P$ where $P$ and $Q$ are two polynomials.

Appendix: Chain rule in dimension 1 and 2

For the sake of completeness, this section is dedicated to describing the formula to derive a composition of two functions, in dimensions one and two. A wide bibliography about this formula is to be found in [24]. It is linked to the notion of partition of an integer or the one of a set. The 1D version is not actually used in this work but is displayed here as a comparison with a 2D version, mainly concerning this notion of partition.

1.1 A.1 Faa Di Bruno formula

Faa Di Bruno formula gives the $m$th derivative of a composite function with a single variable. It is named after Francesco Faa Di Bruno, but was stated in earlier work of Louis F.A. Arbogast around 1800, see [8].

If $f$ and $g$ are functions with sufficient derivatives, then

$$\begin{aligned} \frac{d^m}{dx^m}f(g(x)) = m!\sum f^{(\sum _k b_k)} (g(x)) \prod _{k=1}^{m} \frac{1}{b_k!}\left( \frac{g^{(k)}(x)}{k!} \right) ^{b_k}, \end{aligned}$$

where the sum is over all different solutions in nonnegative integers $(b_k)_{k\in [\![1,m]\!]}$ of $\sum _k k b_k = m$. These solutions are actually the partitions of $m$.

1.2 A.2 Bivariate version

The multivariate formula has been widely studied, the version described here is the one from [7] applied to dimension $2$. A linear order on ${\mathbb {N}}^2$ is defined by: $\forall (\mu ,\nu )\in \left( {\mathbb {N}}^2\right) ^2$, the relation $\mu \prec \nu$ holds provided that

• 1. $\mu _1+\mu _2<\nu _1+\nu _2$; or

• 2. $\mu _1+\mu _2=\nu _1+\nu _2$ and $\mu _1<\nu _1$.

If $f$ and $g$ are functions with sufficient derivatives, then

$$\begin{aligned} {{\partial }_{x}}^i {{\partial }_{y}}^j f(g(x,y))&=i!j! \sum _{1\le \mu \le i+j} f^{\mu }(g(x,y))\\&\quad \times \sum _{s=1}^{i+j} \sum _{p_s((i,j),\mu )} \prod _{l=1}^s \frac{1}{k_l!}\left( \frac{1}{i_l!j_l!} {{\partial }_{x}}^{i_l}{{\partial }_{y}}^{j_l} (g(x,y))\right) ^{k_l}, \end{aligned}$$

where the partitions of $(i,j)$ are defined by the following sets: $\forall \mu \in [\![1,i+j]\!]$, $\forall s\in [\![1,i+j]\!]$, $p_s((i,j),\mu )$ is equal to

$$\begin{aligned}&\bigg \{ (k_1,\ldots ,k_s;(i_1,j_1),\cdots ,(i_s,j_s)):k_i>0,0\prec (i_1,j_1)\prec \cdots \prec (i_s,j_s),\nonumber \\&\quad \sum _{l=1}^s k_l=\mu ,\sum _{l=1}^s k_li_l=i,\sum _{l=1}^s k_lj_l=j\bigg \}. \end{aligned}$$

See [13] for a proof of the formula interpreted in terms of collapsing partitions.