Dynamic analysis and chaos suppression in a fractional order brushless DC motor

Abstract

This paper investigates the dynamic properties and chaos control in a fractional order brushless DC (BLDC) motor. The fractional order model of the brushless DC motor has been derived from its integer order model. Then the qualitative properties of the fractional order BLDC motor are derived. Bifurcation analysis of the BLDC motor with the fractional order has been also discussed. Fractional order chaos control in the BLDC motor is achieved using sliding mode control, robust control and extended back-stepping control.

1 Introduction

Chaos is defined as an aperiodic long-time behavior arising in a deterministic dynamical system that exhibits a sensitive dependence on initial conditions [1]. It is well known that chaotic behavior may lead to undesirable effects and may need to be controlled in electrical systems and many engineering applications. Control of chaotic systems in science and engineering is an important research area in the control literature[1].

In [2], Li et al. studied the bifurcation and chaos control in a permanent-magnet synchronous motor (PMSM). In [3], Jing et al. studied the complex dynamics and properties of the permanent-magnet synchronous motor (PMSM). In [4], Jabli et al. discussed the bifurcation and chaos control of a PI-controlled induction motor.

Fractional order calculus is developed from ordinary calculus and it is a generalization of the integration and differentiation to the non-integer (fractional) order generalization operator $aD_t^q$ in which aand t are limits and q is the order of the operator. This operator is a notation for both the fractional derivatives and fractional integrals in a single expression [5]. Two general fractional order integral/differential operations are commonly discussed, viz. Caputo and Riemann–Liouville (R–L) fractional operators. Physically, the R–L fractional operator has initial value problem [6]. Thus, the Caputo fractional operator is more practical than the R–L fractional operator.

Fractional order models of real dynamical objects and processes have applications in various fields of science and technology [7]. Even though synchronization has been implemented in many chaotic systems with integer derivatives [1], only few works have been reported on fractional order chaotic systems due to complexity in fractional order models of chaotic systems [8].

In this paper, we investigate the chaotic oscillations in a fractional order brushless DC motor. Brushless DC motors have wide applications in aerospace industries [9] and robotics [10]. Chaotic oscillations in an integer order brushless DC motor was controlled using sliding mode control [11]. Modeling and analysis of brushless DC motors (BLDC motors) have been extensively discussed in the literature [12–15].

In this paper, we first discuss the dynamics of the fractional order BLDC motor. We investigate the bifurcation diagrams of the BLDC motor for various system parameters. Fractional order of the chaotic systems close to their integer order models exhibits larger Lyapunov exponents. As discussed in [16], we control chaos of the BLDC motor in the nearest fractional order of the system. Chaos control in the fractional order BLDC motor is achieved with sliding mode control [17–20], robust control [21] and extended back-stepping control [22].

2 Chaotic dynamics of brushless DC motor

The dimensionless mathematical model of the BLDC motor has been studied in [12–15]. BLDC motor is described by the 3-D dynamics

$$\begin{aligned} \dot{x}= & {} v_\mathrm{q} -x-yz+\rho z \nonumber \\ \dot{y}= & {} v_\mathrm{d} -\delta y+xz \nonumber \\ \dot{z}= & {} \sigma (x-z)+\eta xy-T_\mathrm{L} \end{aligned}$$

(1)

The BLDC system (1) exhibits chaotic oscillations when $v_\mathrm{q} =0.168, \rho =60, v_\mathrm{d} =20.66, \delta =0.875, \eta =0.26, T_\mathrm{L} =0.53$ and $\sigma =4.55.$

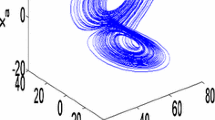
Figure 1 shows the chaotic state portrait of the BLDC system (1) for the initial conditions $x(0)=3.63, y(0)=56.02$ and $z(0)=0.29.$ Figure 2 shows the time series of the states of the BLDC system (1).

Fig. 1

3D state portrait of BLDC motor (1)

Fig. 2

Uncontrolled state oscillations of BLDC motor (1)

3 Fractional order BLDC motor

The fractional order model of BLDC motor system is derived from (3) with the Caputo fractional order definition, which is defined as

$$\begin{aligned} D_t^q f(t)=\frac{1}{\Gamma (1-q)}\int \limits _{t_0}^t {\frac{\dot{f}(\tau )}{(t-\tau )^{q}}\mathrm{d}\tau } \end{aligned}$$

(2)

where $\alpha$ is the order of the system, $t_0$ and t are limits of the fractional order equation, and $\dot{f}(t)$ is integer order calculus of the function.

For numerical calculations, we use Caputo-Riemann-Liouville fractional derivative [23, 24]. Thus, the equation (2) is modified as

$$\begin{aligned} _{(t-L)}D_t^\alpha f(t)=\mathop {\lim }\limits _{h\rightarrow 0} \left\{ {h^{-\alpha }\sum _{j=0}^{N(t)} {b_j \left( {f(t-jh} \right) } } \right\} \end{aligned}$$

(3)

Theoretically fractional order differential equations use infinite memory. Hence when we want to numerically calculate or simulate the fractional order equations we have to use finite memory principal, where L is the memory length and h is the time sampling as $N(t)=\min \left\{ {\left[ {\frac{t}{h}} \right] ,\left[ {\frac{L}{h}} \right] } \right\}$and $b_j =\left( {1-\frac{a+\alpha }{j}} \right) b_{j-1} .$

Applying these fractional order approximations in to the integer order BLDC motor system (1) yields the fractional order BLDC motor model described by (4),

$$\begin{aligned} \begin{array}{l} D^{q_x }x=v_\mathrm{q} -x-yz+\rho z \\ D^{q_y }y=v_\mathrm{d} -\delta y+xz \\ D^{q_z }z=\sigma (x-z)+\eta xy-T_\mathrm{L} \\ \end{array} \end{aligned}$$

(4)

where $q_x ,q_y ,q_z$ are the fractional orders of the BLDC motor system.

The parameter values in the system (4) are taken as $v_\mathrm{q} =0.168,\rho =60, v_\mathrm{d} =20.66, \delta =0.875, \eta =0.26, T_\mathrm{L} =0.53$ and $\sigma =4.55.$

Figure 3 shows the 3-D state portrait of the fractional order BLDC motor (4).

Fig. 3

3D state portraits of the fractional order BLDC motor (4) for $q_x =q_y =q_z =0.98$

4 Qualitative properties of the fractional order BLDC motor

In this section, we analyze the fractional order BLDC motor (4) system for various properties of chaotic behavior like Lyapunov exponents, bifurcation with parameters, bifurcation with fractional orders and bicoherence [25].

4.1 Lyapunov exponents

The Jacobian matrix of the fractional order BLDC system (4) is given by,

$$\begin{aligned} J=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {-1}&{} {-z}&{} {\rho -y} \\ z&{} {-\delta }&{} x \\ {\sigma +\eta y}&{} {\eta x}&{} {-\sigma z} \\ \end{array} }} \right] \end{aligned}$$

(5)

The initial conditions are chosen as $x(0)=3.63, y(0)=56.02$ and $z(0)=0.29.$

The parameter values for the system (4) to exhibit chaotic oscillations are taken as $v_\mathrm{q} =0.168, \rho =60, v_\mathrm{d} =20.66, \delta =0.875, \eta =0.26, T_\mathrm{L} =0.53$ and $\sigma =4.55.$

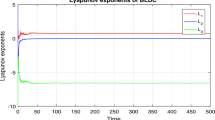
The Lyapunov exponents of the fractional order system are $L_1 =0.560208,L_2 =0$ and $L_3 =-6.989981.$ Figure 4 shows the Lyapunov exponents of the fractional order BLDC system (4).

Also, the Kaplan–Yorke dimension of the fractional order system (4) is calculated as

$$\begin{aligned} D_{\mathrm{KY}} =2+\frac{L_1 +L_2 }{|L_3 |}=2.0802 \end{aligned}$$

(6)

which is fractional.

Fig. 4

Lyapunov exponents of the fractional order BLDC motor

Fig. 5

Bifurcation plot versus. a Load torque. b $\eta$

4.2 Bifurcation and bicoherence

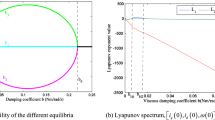
Here we investigate the bifurcation of the attractor for various parameters. The fractional order of the system are kept as $q_x =q_y =q_z =0.98.$ By fixing all the other parameters, $T_\mathrm{L}$ is varied and the behavior of the fractional order system (5) is investigated. The bifurcation plot for various states versus load $T_\mathrm{L}$is given by Fig. 5a. Figure 5b shows the bifurcation of the attractor for the parameter $\eta$. Figure 6 shows the bifurcation of the attractor for the fractional order BLDC motor parameter $\sigma$.

The parameter $\sigma$plays an important role in the chaotic behavior of the BLDC motor. When $\sigma =3.9$, the fractional order BLDC motor shows the period 1 of its chaotic behavior as shown in Fig. 7a. For $\sigma =4.05,$ the fractional system shows the period 2 of the chaotic oscillation as shown in Fig. 7b. When $\sigma =4.10$, period 3 of the chaotic oscillation is exhibited as shown in Fig. 7c. For $\sigma =4.20,$ the system shows period 4 of its oscillation as in Fig. 7d . For $\sigma =4.30$the system goes in to the chaotic oscillation state showing the entry into the positive Lyapunov exponent as shown in Fig. 7e. When $\sigma =4.40$, the fractional order BLDC motor system exhibits the second scroll as shown in Fig. 7f. Figures 7g, h show the complete chaotic attractor for $\sigma =4.50$ and $\sigma =4.55.$. Generally speaking, when the system’s biggest Lyapunov exponents is larger than zero, and the points in the corresponding bifurcation diagram are dense, the chaotic attractor will be found to exist in this system. From the Lyapunov exponents and bifurcation diagrams in figures, a conclusion can be obtained that chaos exist in the fractional order system (4) when selecting a certain range of parameters. Next the individual state responses are studied in detail by varying the parameters.

Fig. 6

Bifurcation plot versus $\sigma$

The bifurcation of the fractional order BLDC motor with the fractional orders $q_x ,q_y ,q_z$generally mentioned as q are shown in Fig. 8a–l. It can be clearly seen that the system (4) shows large Lyapunov exponents when the fractional order is close to 1 and hence the controllers designed in fractional order close to 1 are more efficient and effective than the integer order controllers. The fractional order BLDC motor shows chaotic oscillations when the order is $0.93\le q\le 0.98.$ The chaotic oscillations show periodic behaviour when the order of the system is $q\le 0.92$ and completely loses the positive Lyapunov exponent when the order is $q\le 0.90$.

Fig. 7

3D phase portraits of the fractional order BLDC motor

Fig. 8

Phase portraits for the fractional order q

The bicoherence or the normalized bispectrum is a measure of the amount of phase coupling that occurs in a signal or between two signals. Both bicoherence and bispectrum are used to find the influence of a nonlinear system on the joint probability distribution of the system input. Phase coupling is the estimate of the proportion of energy in every possible pair of frequency components $f_1 ,f_2 ,f_3 ,\ldots ,f_n .$ Bicoherence analysis is able to detect coherent signals in extremely noisy data, provided that the coherency remains constant for sufficiently long times, since the noise contribution falls off rapidly with increasing N. The auto bispectrum of a chaotic system is given by Pezeshki [25]. He derived the auto bispectrum with the Fourier coefficients.

$$\begin{aligned} B(\omega _1 ,\omega _2 )=E[A(\omega _1 )A(\omega _2 )A^{*}(\omega _1 +\omega _2 )] \end{aligned}$$

(7)

where $\omega _n$ is the radian frequency and A is the Fourier coefficients of the time series. The normalized magnitude spectrum of the bispectrum known as the squared bicoherence is given by

$$\begin{aligned} b(\omega _1 ,\omega _2 )=\left| {B(\omega _1 ,\omega _2 )} \right| ^{2}/P(\omega _1 )P(\omega _2 )P(\omega _1 +\omega _2 ) \end{aligned}$$

(8)

$P(\omega _1 )$and $P(\omega _2 )$ are the power spectrums at $f_1$ and $f_2$. Figure 9a–c shows the bicoherence plots of the fractional order BLDC motor.

Fig. 9

Bicoherence plots of the fractional order BLDC motor. a X, b X–Y, c X–Y–Z

5 Stability properties of the fractional order brushless DC motor

The Lyapunov stability of the fractional order brushless DC motor system (4) cannot be directly established as the first derivative of the Lyapunov function yields a complex dynamical fractional order equation. Hence, we derive the following as an alternative to investigate Lyapunov stability.

Lemma 1

If $s\left( t \right)$ is a continuous and derivable function, then for any time instant$t\ge t_0$,

$$\begin{aligned} \frac{1}{2}D_t^\alpha s^{2}(t)\le s(t)\times D_t^\alpha s(t)\quad \forall \alpha \in (0,1) \end{aligned}$$

(9)

Proof

To prove that expression (9) is true we start with

$$\begin{aligned} s(t)D_t^\alpha s(t)-\frac{1}{2}D_t^\alpha s^{2}(t)\ge 0 \quad \forall \alpha \in (0,1) \end{aligned}$$

(10)

By Definition

$$\begin{aligned}&D_t^\alpha s(t)=\frac{1}{\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{\dot{s}(\tau )}{(t-\tau )^{\alpha }}\mathrm{d}\tau } \end{aligned}$$

(11)

$$\begin{aligned}&\frac{1}{2}D_t^\alpha s^{2}(t)=\frac{1}{\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{s(\tau )\cdot \dot{s}(\tau )}{(t-\tau )^{\alpha }}} \mathrm{d}\tau \end{aligned}$$

(12)

Modifying (12),

$$\begin{aligned} \frac{1}{\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{s(t)\cdot \dot{s}(\tau )-s(\tau )\dot{s}(\tau )}{(t-\tau )^{\alpha }}} \mathrm{d}\tau \ge 0 \end{aligned}$$

(13)

Let us assume,

$$\begin{aligned} S(\tau )=s(t)-s(\tau ) \quad \mathrm{and} \quad \dot{S}(\tau )=-\dot{s}(\tau ) \end{aligned}$$

(14)

Substitute (14) in (13)

$$\begin{aligned} \frac{1}{\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{S( \tau )\dot{S}(\tau )}{(t-\tau )^{\alpha }}} \mathrm{d}\tau \ge 0 \end{aligned}$$

(15)

Integration (15) by parts

$$\begin{aligned}&\frac{1}{\Gamma (1-\alpha )}(t-\tau )^{-\alpha }\cdot \frac{1}{2}S^{2}(\tau )-\int \limits _{t_0 }^t \frac{1}{2}S^{2}(\tau )\cdot \nonumber \\&\quad \times \left( {\frac{\alpha (t-\tau )^{-\alpha -1}}{\Gamma (1-\alpha )}} \right) \le 0 \end{aligned}$$

(16)

$$\begin{aligned}&\left[ {\frac{S^{2}(\tau )}{2\Gamma (1-\alpha )(t-\tau )^{\alpha }}} \right] _{\tau =t}-\left[ {\frac{S^{2}(t_0 )}{2\Gamma (1-\alpha )(t-t_0 )^{\alpha }}} \right] \nonumber \\&\quad -\frac{1}{2}\frac{\alpha }{\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{S^{2}(\tau )}{(t-\tau )^{\alpha +1}}\mathrm{d}\tau \le 0} \end{aligned}$$

(17)

Solving first term of (17) for $\tau =t$

$$\begin{aligned} \begin{array}{l} \mathop {\lim }\limits _{\tau \rightarrow t} \frac{S^{2}(\tau )}{2\Gamma (1-\alpha )(t-\tau )^{\alpha }}=\frac{1}{2\Gamma (1-\alpha )}\mathop {\lim }\limits _{\tau \rightarrow t} \frac{\left[ {\begin{array}{l} s^{2}(t)+s^{2}(\tau ) \\ -2s(t)\cdot s(\tau ) \\ \end{array}} \right] ^{2}}{\left( {t-\tau } \right) ^{\alpha }} \\ =\frac{1}{2\Gamma (1-\alpha )}\mathop {\lim }\limits _{\tau \rightarrow t} \left[ {\frac{{\begin{array}{l} -2s(t)\dot{s}(\tau )+ \\ 2s(\tau )\cdot \dot{s}(\tau ) \\ \end{array}}}{-\alpha \left( {t-\tau } \right) ^{\alpha -1}}} \right] =0 \\ \end{array} \end{aligned}$$

(18)

Equation (18) can be rewritten as

$$\begin{aligned} \frac{S^{2}(t_0 )}{2\Gamma (1-\alpha )(t-t_0 )^{\alpha }}+\frac{\alpha }{2\Gamma (1-\alpha )}\int \limits _{t_0 }^t {\frac{S^{2}(\tau )}{(t-\tau )^{\alpha +1}}\mathrm{d}\tau \ge 0}\nonumber \\ \end{aligned}$$

(19)

which clearly holds as $\alpha$ lies between 0 $\le \tau \le$ 1, the L.H.S of the Eq. (19) will always be a positive value. This completes the proof. $\square$

6 Chaos suppression of the fractional order BLDC motor

The control goal of this paper is to design suitable controllers for suppression of chaotic oscillations in the fractional order BLDC motor (4). We investigate three control methods, viz. sliding mode control [17–20], robust control [21] and extended back-stepping control [22] for chaos control of the system.

6.1 Sliding mode control

We define the fractional order BLDC motor with fractional order sliding mode controllers as

$$\begin{aligned} D^{q_x }x= & {} v_\mathrm{q} -x-yz+\rho z+u_x \nonumber \\ D^{q_y }y= & {} v_\mathrm{d} -\delta y+xz+u_y \nonumber \\ D^{q_z }z= & {} \sigma (x-z)+\eta xy-T_\mathrm{L} +u_z \end{aligned}$$

(20)

where $u_x ,u_y$and $u_z$ are sliding controllers to be designed.

The sliding surfaces for the three state variables are defined as follows.

$$\begin{aligned} s_x= & {} [D^{q_x }+\lambda _x ]\left[ {\int \limits _0^t {x(\tau )\mathrm{d}\tau } } \right] =x+\lambda _x \int \limits _0^t {x(\tau )\mathrm{d}\tau } \nonumber \\ s_y= & {} [D^{q_y }+\lambda _y ]\left[ {\int \limits _0^t {y(\tau )\mathrm{d}\tau } } \right] =y+\lambda _y \int \limits _0^t {y(\tau )\mathrm{d}\tau } \nonumber \\ s_z= & {} [D^{q_z }+\lambda _z ]\left[ {\int \limits _0^t {z(\tau )\mathrm{d}\tau } } \right] =z+\lambda _z \int \limits _0^t {z(\tau )\mathrm{d}\tau } \end{aligned}$$

(21)

The fractional derivatives of the sliding surface (21) is given by,

$$\begin{aligned} D^{q_x }s_x= & {} D^{q_x }x+\lambda _x x \nonumber \\ D^{q_y }s_y= & {} D^{q_y }y+\lambda _y y \nonumber \\ D^{q_z }s_z= & {} D^{q_z }z+\lambda _z z \end{aligned}$$

(22)

By the definitions of the reaching law[20], we set the controlled fractional order system as,

$$\begin{aligned} D^{q_x }x= & {} -\eta _x \hbox {sgn}(s_x )-K_x s_x \nonumber \\ D^{q_y }y= & {} -\eta _y \hbox {sgn}(s_y )-K_y s_y \nonumber \\ D^{q_z }s_z= & {} -\eta _z \hbox {sgn}(s_z )-K_z s_z \end{aligned}$$

(23)

Comparing (22) and (23) and solving with (20),

$$\begin{aligned}&v_\mathrm{q} -x-yz+\rho z+u_x =-\eta _x \hbox {sgn}(s_x )-K_x s_x \nonumber \\&v_\mathrm{d} -\delta y+xz+u_y =-\eta _y \hbox {sgn}(s_y )-K_y s_y \nonumber \\&\sigma (x-z)+\eta xy-T_\mathrm{L} +u_z =-\eta _z \hbox {sgn}(s_z )-K_z s_z \end{aligned}$$

(24)

From Eq. (24), the controller can be derived as follows.

$$\begin{aligned} u_x= & {} -v_\mathrm{q} +x+yz-\rho z-\eta _x \hbox {sgn}(s_x )-K_x s_x \nonumber \\ u_y= & {} -v_\mathrm{d} +\delta y-xz-\eta _y \hbox {sgn}(s_y )-K_y s_y \nonumber \\ u_z= & {} -\sigma (x-z)-\eta xy+T_\mathrm{L} -\eta _z \hbox {sgn}(s_z )-K_z s_z \end{aligned}$$

(25)

The stability of the controller (25) can be proved using the Lyapunov function

$$\begin{aligned} V(s_x ,s_y ,s_z )=\frac{1}{2}(s_x^2 +s_y^2 +s_z^2 ) \end{aligned}$$

(26)

The first derivative of the Lyapunov function (26) can be given by,

$$\begin{aligned} \dot{V}=s_x \dot{s}_x +s_y \dot{s}_y +s_z \dot{s}_z \end{aligned}$$

(27)

Using Lemma 1, we find that

$$\begin{aligned} \dot{V}&\le s_x [-\eta _x \hbox {sgn}(s_x )-K_x s_x ]+s_y [-\eta _y \hbox {sgn}(s_y )-K_y s_y ] \nonumber \\&\quad +s_z [-\eta _z \hbox {sgn}(s_z )-K_z s_z ] \end{aligned}$$

(28)

Simplifying (28),

$$\begin{aligned} \dot{V}\le -\eta _x \left| {s_x } \right| -\eta _y \left| {s_y } \right| -\eta _z \left| {s_z } \right| -K_x s_x^2 -K_y s_y^2 -K_z s_z^2\nonumber \\ \end{aligned}$$

(29)

Hence, $\dot{V}$ is a negative definite function. Thus, we infer that the closed-loop system is asymptotically stable and is valid for any bounded initial conditions where $K_{x} , K_{y} ,K_{z}$ are positive constants.

For numerical simulations the fractional order system (20) with the controller (25) are implemented in LabVIEW.

Figure 10 shows the controlled states of the system (4) at $t=70$ s.

Fig. 10

Controlled states of the fractional order BLDC motor (control in action at $t=70$ s)

6.2 Robust control

We derive a robust controller [21] for chaos suppression of the fractional order BLDC motor by introducing controllers to the states X and Z.

We define the brushless DC motor with the robust controllers as

$$\begin{aligned} D^{q_x }x= & {} v_\mathrm{q} -x-yz+\rho z+u_x \nonumber \\ D^{q_y }y= & {} v_\mathrm{d} -\delta y+xz \nonumber \\ D^{q_z }z= & {} \sigma (x-z)+\eta xy-T_\mathrm{L} +u_z \end{aligned}$$

(30)

Let $x^{*},y^{*},z^{*}$denote the equilibrium points. Then the control errors can be defined as

$$\begin{aligned} e_x= & {} x-x^{*} \nonumber \\ e_y= & {} y-y^{*} \nonumber \\ e_z= & {} z-z^{*} \end{aligned}$$

(31)

The fractional derivative of the errors (31) are obtained as follows.

$$\begin{aligned} D^{q_x }e_x= & {} v_\mathrm{q} -(e_x +x^{*})-(e_y +y^{*})(e_z +z^{*})\nonumber \\&+\rho (e_z +z^{*})+u_x \nonumber \\ D^{q_y }e_y= & {} v_\mathrm{d} -\delta (e_y +y^{*})+(e_x +x^{*})(e_z +z^{*}) \nonumber \\ D^{q_z }e_z= & {} \sigma ((e_x +x^{*})-(e_z +z^{*}))\nonumber \\&+\eta (e_x +x^{*})(e_y +y^{*})-T_\mathrm{L} +u_z \end{aligned}$$

(32)

For any equilibrium point, the fractional order BLDC motor system can be given by

$$\begin{aligned}&D^{q_x }x=v_\mathrm{q} -x^{*}-y^{*} z^{*}+\rho z^{*} \nonumber \\&D^{q_y }y=v_\mathrm{d} -\delta y^{*}+x^{*} z^{*} \nonumber \\&D^{q_z }z=\sigma (x^{*}-z^{*})+\eta x^{*} y^{*}-T_\mathrm{L} \end{aligned}$$

(33)

Simplifying (32), we obtain

$$\begin{aligned} D^{q_x }e_x= & {} v_\mathrm{q} -e_x -x^{*}-e_y (e_z +z^{*})-e_z (y^{*}-\rho )\nonumber \\&-z^{*}(y^{*}-\rho )+u_x \nonumber \\ D^{q_y }e_y= & {} v_\mathrm{d} -\delta (e_y +y^{*})+e_x (e_z +z^{*})+x^{*}(e_z +z^{*}) \nonumber \\ D^{q_z }e_z= & {} e_x (\sigma +\eta e_y +\eta y^{*})+x^{*}(\sigma +\eta e_y +\eta y^{*})\nonumber \\&-\sigma (e_z +z^{*})-T_\mathrm{L} +u_z \end{aligned}$$

(34)

At the equilibrium point $x^{{^{*}}}=0,y^{{^{*}}}=0,z^{{^{*}}}=0,$ the equation (34) simplifies to

Fig. 11

Stabilized states of the fractional order BLDC motor (control in action at $t=80s)$

$$\begin{aligned} D^{q_x }e_x= & {} v_\mathrm{q} -e_x -e_y e_z +\rho e_z +u_x \nonumber \\ D^{q_y }e_y= & {} v_\mathrm{d} -\delta e_y +e_x e_z \nonumber \\ D^{q_z }z= & {} \sigma e_x +\eta e_x e_y -\sigma e_z -T_\mathrm{L} +u_z \end{aligned}$$

(35)

From Eq. (35), for the system to be asymptotically stable, the controller can be defined as,

$$\begin{aligned} u_x= & {} -v_\mathrm{q} +e_x +e_y e_z -\rho e_z -k_x e_x \nonumber \\ u_z= & {} -\sigma e_x -\eta e_x e_y +\sigma e_z +T_\mathrm{L} -k_z e_z \end{aligned}$$

(36)

The stability of the controller (36) can be proved using the Lyapunov function

$$\begin{aligned} V=\frac{1}{2}(e_x^2 +e_y^2 +e_z^2 ) \end{aligned}$$

(37)

The first derivative of the Lyapunov function can be given by

$$\begin{aligned} \dot{V}=e_x \dot{e}_x +e_y \dot{e}_y +e_z \dot{e}_z \end{aligned}$$

(38)

Using Lemma 1, we find that

$$\begin{aligned}&\dot{V}\le e_x D^{q_x }e_x +e_y D^{q_y }e_y +e_z D^{q_z }e_z \end{aligned}$$

(39)

$$\begin{aligned}&\dot{V}\le -K_x e_x^2 -K_y e_y^2 -K_z e_z^2 \end{aligned}$$

(40)

From (40), it is evident that the designed controller is globally asymptotically stable.

Figures 11 and 12 shows the stabilized states and the errors respectively.

Fig. 12

Dynamics of the errors (control in action at $t=80$ s)

Fig. 13

Stabilized states of the fractional order BLDC motor tracking the smooth periodic function (control in action $t=45$ s)

7 Extended back-stepping control

The third control is about using an extended back-stepping control [22] to stabilize the states of the fractional order BLDC motor.

In this control scheme, the states of the fractional order BLDC motor are forced to follow a periodic function. The fractional order system with the controllers are defined by

$$\begin{aligned} D^{q_x }x&=v_\mathrm{q} -x-yz+\rho z+u_x \nonumber \\ D^{q_y }y&=v_\mathrm{d} -\delta y+xz+u_y \nonumber \\ D^{q_z }z&=\sigma (x-z)+\eta xy-T_\mathrm{L} +u_z \end{aligned}$$

(41)

The control errors for the chaos suppression of the fractional order BLDC motor (41) are defined as follows.

$$\begin{aligned} e_x= & {} x-x_\mathrm{d} \nonumber \\ e_y= & {} y-y_\mathrm{d} \nonumber \\ e_z= & {} z-z_\mathrm{d} \end{aligned}$$

(42)

where $x_\mathrm{d} =f(t),y_\mathrm{d} =k_x e_x ,z_\mathrm{d} =k_y e_x +k_z e_y$ and f(t) is a smooth periodic function of time.

The fractional derivatives of (42) are calculated as the fractional order error dynamics

$$\begin{aligned} D^{q_x }e_x= & {} D^{q_x }x-D^{q_x }f_x (t) \nonumber \\ D^{q_y }e_y= & {} D^{q_y }y-k_x D^{q_x }e_x \nonumber \\ D^{q_z }e_z= & {} D^{q_z }z-k_y D^{q_x }e_x -k_z D^{q_y }e_y \end{aligned}$$

(43)

Using (41) and (43), we find the following.

$$\begin{aligned} D^{q_x }e_x= & {} v_\mathrm{q} -x-yz+\rho z+u_x -D^{q_x }f_x (t) \nonumber \\ D^{q_y }e_y= & {} v_\mathrm{d} -\delta y+xz+u_y -k_x D^{q_x }e_x \nonumber \\ D^{q_z }e_z= & {} \sigma (x-z)+\eta xy-T_\mathrm{L} +u_z -k_y D^{q_x }e_x -k_z D^{q_y }e_y\nonumber \\ \end{aligned}$$

(44)

We define the controllers for chaos suppression of the fractional order BLDC motor as

$$\begin{aligned} u_x= & {} -v_\mathrm{q} +x+yz-\rho z+D^{q_x }f_x (t)-k_1 e_x \nonumber \\ u_y= & {} -v_\mathrm{d} +\delta y-xz+k_x D^{q_x }e_x -k_2 e_y \nonumber \\ u_z= & {} -\sigma (x-z)-\eta xy+T_\mathrm{L} +k_y D^{q_x }e_x +k_z D^{q_y }e_y -k_3 e_z\nonumber \\ \end{aligned}$$

(45)

To analyze the stability of the designed control algorithm, we use Lyapunov stability theory. We take the Lyapunov function as

$$\begin{aligned} V=\frac{1}{2}\left( {e_x ^{2}+e_y ^{2}+e_z ^{2}} \right) \end{aligned}$$

(46)

The first derivative of the Lyapunov function is derived as

$$\begin{aligned} \dot{V}=[e_x (t)\dot{e}_x (t)+e_y (t)\dot{e}_y (t)+e_z (t)\dot{e}_z (t)] \end{aligned}$$

(47)

Using Lemma 1, we find that

$$\begin{aligned} \dot{V}\le -k_1 e_x ^{2}(t)-k_2 e_y ^{2}(t)-k_3 e_z ^{2}(t) \end{aligned}$$

(48)

Since $\dot{V}$ is a negative definite function, we conclude that the closed-loop system is stable and is valid for any bounded initial conditions.

Figure 13 shows the stabilized states of the closed-loop BLDC system tracking the smooth periodic function. For numerical simulations, we use the smooth periodic function $f(t)=35\sin 0.57t.$ Also, we take the initial conditions as $x(0)=3.63, y(0)=56.02$ and $z(0)=15.09.$

8 Conclusion

In this paper, we derived new results for the fractional order brushless DC motor. First, we discussed the dynamic properties of the fractional order brushless DC motor such as bifurcation with parameters, bifurcation with fractional orders, Lyapunov exponents, and bicoherence. Next, we achieved chaos control and stabilization of the fractional order brushless DC motor with three control schemes (sliding mode control, robust control and extended back-stepping control). The fractional order controller stability is established using Lyapunov stability theorem through a modified fractional order Lyapunov first derivative. Numerical simulations are established to illustrate the mail results for the fractional order brushless DC motor. As future work, we plan to investigate the fractional order controllers for fractional order brushless DC motor with other methods such as super-twisting and terminal sliding mode control, etc.