1 Introduction

Various electromechanical systems such as dynamo [1], driven double pendulum [2], driven triple pendulum [3], inverted pendulum [4], beam coupled with an oscillator [5], and electromechanical transducer [6] have attracted focus due to their interesting dynamics. However, the brushless DC motor (BLDCM) has been of the most studied electromechanical systems. Especially relating to chaos theory, Hemati studied the equilibria and dynamic characteristics (chaos) of a class of motors from their compact form [7]. Similar to the BLDCM model, the synchronous reluctance motor drive (SynRM) model exhibited Hopf bifurcation via one of its input [8].

Hemati has non-dimensionalized the BLDCM [9]. In most studies, the BLDCM model has been non-dimensionalized [10] since it possesses many parameters. While the aim was to make the analysis easier, the richness of the dynamics was hidden. As a result, the BLDCM has been often compared to the Lorenz system [9]. In real life, this comparison has not been useful due to bifurcation in the real system design.

For reference, the BLDCM or the general permanent magnet synchronous motor (PMSM) has also been studied in terms of control with linear control feedback [11], global control [12], dynamic surface control [13].

Furthermore, for synchronization, single-variable coupling [14], various coupling terms and linearization of error dynamics [15], the backstepping design, and the Gerschgorin's theorem method [16] were used.

The bifurcation analysis for these models of BLDCM, including both fractional-order [17] and integer-order [18, 19] have been conducted; however, the methods like Lyapunov exponents or bifurcation diagram are non-rigorous.

Besides the self-excited chaos, the hidden chaos was investigated. The hidden chaos was first reported in the original BLDCM [20, 21] and then in the modified model of PMSM.

The hidden chaos has proven dangerous in multistability in the BLDCM as investigated by Faradja and Qi [21] and adopted for plasma system study by Yang et al. [22] and unmanned aerial vehicles by Bi et al. [23].

Besides traditional bifurcation techniques, other mechanisms to explain dynamics in the BLDCM were investigated, like energy-based methods using Casimir functions and Kolmogorov systems [24], using generalized Hamiltonian functions explained the onset of different dynamical behaviors such as sink, limit cycle, chaos [25].

While traditional bifurcation studies use non-dimensionalized models and energy-based methods refer more to force and energy, the studies on the dynamics of BLDCM, however, are still lacking some insight. Studies of the effects of individual parameters of BLDCM have not been conducted in general. A few exceptional studies exist. Gao systematically studied the permanent-magnet sizing effect [26], compared in that study with the motor torque constant with the same dimension as the permanent magnet flux. Recently, Faradja and Qi considered the bifurcation with the direct-axis voltage as the bifurcation parameter [27]. The BLDCM possesses design parameters such as the viscous damping coefficient (Table 1).

Table 1 Categorization of literature on dynamics of PMSM/BLDCM
Full size table

To the best of our knowledge, bifurcation of the BLDCM with the viscous damping parameter has not been analyzed. It should be considered that the non-dimensionalization has introduced other problems. For example, it is impossible to obtain chaos with a real motor with the chosen parameters because some real parameters will be abnormally negative, as illustrated by Li et al. [10] and Singh et al. [28].

The paper's main finding is that the bifurcation contribution of the damping coefficient in the overall system dynamics is highly complex, even in a real context. Both non-rigorous and rigorous methods are used.

The paper is organized as follows. The model of the BLDCM is described in Sect. 2. The bifurcation analysis exposing the pitchfork and Hopf bifurcation are detailed in Sect. 3. Section 4 deals with the illustration of the different scenarios of bifurcation. The paper is concluded in Sect. 5.

2 Model description of BLDCM

The non-salient-pole (or smooth air gap) BLDCM model in the rotating frame (d-q) obtained after a Park transformation comprises differential equations for three state variables [9] is expressed as follows:

$$ \begin{aligned} \frac{{di_{q} }}{dt} & = \left( { - Ri_{q} - nL\omega i_{d} - nk_{t} \omega + v_{q} } \right)/L, \\ \frac{{di_{d} }}{dt} & = \left( { - Ri_{d} + nL\omega i_{q} + v_{d} } \right)/L, \\ \frac{d\omega }{{dt}} & = \left( {nk_{t} i_{q} - b\omega - T_{L} } \right)/J, \end{aligned} $$
(1)

where \(i_{q}\) the quadrature-axis current, \(i_{d}\) the direct-axis current, \(\omega\) rotor velocity; \(t\) is the elapsed time; for the parameters, \(R\) is the winding resistance matrix with \(L = \tfrac{3}{2}L_{a}\), \(L_{a}\) the self-inductance of the winding, \(n\) the number of permanent-magnet pole pairs, \(k_{t} = \sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}} k_{e} ,\;\) \(k_{e}\) the coefficient of motor torque, \(J\) the moment of inertia, \(b\) the damping coefficient; for the input variables, \(v_{q}\) and \(v_{d}\) are the voltages across the quadrature axis and direct axis, respectively, and \(T_{L}\) the external torque. This model describes a smooth air-gap machine where the variation of reluctance in the air gap \(L_{g}\) is zero.

The following assumptions are made: \(v_{q} = 0\) and \(T_{L} = 0\).

The divergence of the BLDCM model is \(\nabla V = - \left( {{{2R} \mathord{\left/ {\vphantom {{2R} L}} \right. \kern-\nulldelimiterspace} L} + {b \mathord{\left/ {\vphantom {b J}} \right. \kern-\nulldelimiterspace} J}} \right)\), so the system is dissipative when all parameters have sound meanings under the condition \(\nabla V < 0\). Hence, the volume in phase space shrinks exponentially to zero. Also, the energy of the system will become nulled with the absence of inputs. The existence of the damping coefficient in the gradient shows the importance of this parameter.

3 Bifurcation analysis with damping coefficient

We now consider the viscous damping coefficient as the bifurcation parameter. The equilibrium number changes with parametric conditions under the stated assumptions. With the assumptions stated above, the equilibria are obtained. Settingthen the three equilibria are

$$ \begin{aligned} &- Ri_{q} - nL\omega i_{d} - nk_{t} \omega = 0,\\ &- Ri_{d} + nL\omega i_{q} + v_{d} = 0,\; {\text{and}}\;nk_{t} i_{q} - b\omega = 0, \end{aligned} $$
$$ \begin{aligned} E_{1} & = \left[ {0,\frac{{v_{d} }}{R},0} \right],\\ E_{2,3} &= \left[ { \pm \frac{1}{{n^{2} k_{t} L}}\sqrt \Delta ,\; - \frac{{bR + k_{t}^{2} n^{2} }}{{k_{t} Ln^{2} }},\; \pm \frac{1}{nbL}\sqrt \Delta } \right] \end{aligned} $$
(2)

where

$$ \Delta = - bR^{2} \left( {b - b_{p} } \right)\;{\text{and}}\;b_{p} = - {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} {R^{2} }}} \right. \kern-\nulldelimiterspace} {R^{2} }}. $$

Therefore, the BLDCM undergoes pitchfork bifurcation when the damping coefficient takes the value

$$ b_{p} = - {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} {R^{2} }}} \right. \kern-\nulldelimiterspace} {R^{2} }}. $$
(3)

At this value, the number of equilibrium points changes from three for \(b < b_{p}\) to one for \(b > b_{p}\). The occurrence of pitchfork bifurcation is thus observed. The first equilibrium can be saddle-node or sink except when its stability cannot be determined by eigenvalues rather by the center manifold theorem. The equilibria are also found in [27].

For the other equilibria, the characteristic polynomial is written as

$$ \begin{aligned} P(\lambda ) & = \lambda^{3} + \frac{2JR + bL}{{JL}}\lambda^{2} + \frac{{ - Jk_{t}^{2} Rn^{2} - Jk_{t} Ln^{2} v_{d} + LRb^{2} }}{{JL^{2} b}}\lambda \\ & \quad - \frac{{2k_{t}^{2} n^{2} R + 2k_{t} v_{d} Ln^{2} + 2bR^{2} }}{{JL^{2} }} \\ \end{aligned} $$
(4)

The study of the stability of this characteristic polynomial requires that

$$ \frac{2JR + bL}{{JL}} > 0, $$
(5)

meaning that \(2JR + bL > 0\). Then we also have

$$ \frac{{ - Jk_{t}^{2} Rn^{2} - Jk_{t} Ln^{2} v_{d} + LRb^{2} }}{{JL^{2} b}} > 0. $$
(6)

And finally,

$$ - \frac{{2k_{t}^{2} n^{2} R + 2k_{t} v_{d} Ln^{2} + 2bR^{2} }}{{JL^{2} }} > 0. $$
(7)

Based on these three conditions, we have

$$ b < b_{P} $$
(8)

with

$$ b_{p} = - {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {k_{t}^{2} n^{2} R + k_{t} v_{d} Ln^{2} } \right)} {R^{2} }}} \right. \kern-\nulldelimiterspace} {R^{2} }} $$

The condition of Eq. (8) relates the stability of the symmetric equilibria to pitchfork bifurcation. This value \(b_{P}\) is the critical value for the occurrence of pitchfork bifurcation. Inequalities (7) and (8) are necessary conditions for the stability of the symmetric equilibria.

The sufficient condition is drawn from the Routh-Hurwitz table. If the characteristic polynomial in Eq. (4) is \(s^{3} + As^{2} + Bs + C = 0\), the sufficient condition is \((AB - C)/A > 0\). Hence,

$$ \begin{aligned} \textstyle \frac{{ - 2J^{2} k_{t}^{2} R^{2} n^{2}-2v_{d} J^{2} k_{t} LRn^{2}+Jk_{t}^{2} LRbn^{2}+v{}_{d}JKL^{2} bn^{2}+4JLR^{2} b^{2} + L^{2} Rb^{3} }}{{2JLb\left( {k_{t}^{2} Rn^{2} + Lv_{d} k_{t} n^{2} + bR^{2} } \right)}}> 0. \end{aligned} $$
(9)

This inequality is essential. Considering the real case scenario with positive parameters, this inequality shows complexity with the bifurcation using the mechanical parameter. Pravin analyzed the possibility of obtaining real roots from cubic equations [29].

For Hopf bifurcation, three conditions are needed: (1) nonhyperbolicity, (2) transversality condition, and (3) non-genericity.

For the first condition of nonhyperbolicity, it is supposed from Eq. (9) that there is an eigenvalue \(\lambda = \theta j\), then the critical value is obtained from

$$ \textstyle\frac{{ - 2J^{2} k_{t}^{2} R^{2} n^{2} - 2v_{d} J^{2} k_{t} LRn^{2} + Jk_{t}^{2} LRbn^{2} + v{}_{d}JKL^{2} bn^{2} + 4JLR^{2} b^{2} + L^{2} Rb^{3} }}{{2JLb\left( {k_{t}^{2} Rn^{2} + Lv_{d} k_{t} n^{2} + bR^{2} } \right)}} = 0. $$
(10)

Equation (10) possesses three roots:

$$ b_{H0} = - \frac{{b_{dc1} }}{2} - \frac{{b_{dc2} }}{{2b_{dc1} }} - \frac{4JR}{{3L}} - \sqrt 3 \left( {\frac{{b_{dc2} }}{{2b_{dc1} }} - \frac{{b_{dc1} }}{2}} \right)j, $$
(11a)
$$ b_{H1} = - \frac{{b_{dc1} }}{2} - \frac{{b_{dc2} }}{{2b_{dc1} }} - \frac{4JR}{{3L}} + \sqrt 3 \left( {\frac{{b_{dc2} }}{{2b_{dc1} }} - \frac{{b_{dc1} }}{2}} \right)j, $$
(11b)
$$ b_{H2} = b_{dc1} + \frac{{b_{dc2} }}{{b_{dc1} }} - \frac{4JR}{{3L}}, $$
(11c)

with

$$ \begin{aligned} b_{dc1} & = \sqrt[3]{{\left[ {\sqrt {\left( {b_{dc4} - \frac{{64J^{3} R^{3} }}{{27L^{3} }} + b_{dc3} } \right)^{2} - b_{dc2}^{3} } } \right] + b_{dc4} - \frac{{64J^{3} R^{3} }}{{27L^{3} }} + b_{dc3} }}, \\ b_{dc2} & = \frac{{16J^{2} R^{2} }}{{9L^{2} }} - \frac{{b_{dc5} }}{R}, \, b_{dc3} = \frac{{2J^{2} k_{t}^{2} R^{2} n^{2} + 2Lv_{d} J^{2} k_{t} Rn^{2} }}{{2L^{2} R}}, \\ b_{dc4} & = 2Jb_{dc5} , \, b_{dc5} = \frac{{JRk_{t}^{2} Ln^{2} + Jv_{d} k_{t} L^{2} n^{2} }}{{3L^{2} }}. \\ \end{aligned} $$

The analysis of the stability with complex roots must consider the real case scenario. The three roots in Eq. (11) are real for specific conditions. According to Pravin [29], if the numerator of the polynomial in Eq. (10) is written as

$$ b^{3} + B_{2} b^{2} + B_{1} b + B_{0} , $$

then the three roots are real when the following conditions are fulfilled

$$ \left( {2B_{2}^{3} - 9B_{2} B_{1} + 27B_{0} } \right)^{2} \le 4\left( {B_{2}^{2} - 3B_{1} } \right), $$
(12a)
$$ \left( {B_{2}^{2} - 3B_{1} } \right) \ge 0. $$
(12b)

For the first condition (12a), we obtain

$$ \begin{gathered} \frac{{108J^{3} k_{t}^{6} }}{{L^{3} }} + \frac{{6372J^{4} k_{t}^{4} R^{2} n^{4} }}{{L^{4} }} - \frac{{13824J^{5} k_{t}^{2} R^{4} n^{2} }}{{L^{5} }}\hfill \\ \, + \frac{{6372J^{4} k_{t}^{2} v_{d}^{2} n^{4} }}{{L^{2} }} + \frac{{108J^{3} k_{t}^{3} v_{d}^{3} n^{6} }}{{R^{3} }} \hfill \\ \, + \frac{{324J^{3} k_{t}^{5} v_{d} n^{6} }}{{L^{2} R}} + \frac{{324J^{3} k_{t}^{4} v_{d}^{2} n^{6} }}{{LR^{2} }} + \frac{{12744J^{4} k_{t}^{3} Rv_{d} n^{4} }}{{L^{3} }}\hfill \\ \, - \frac{{13824J^{5} k_{t} R^{3} v_{d} n^{2} }}{{L^{4} }} \le 0. \hfill \\ \end{gathered} $$
(13)

By solving the corresponding equation with respect to \(v_{d}\), we get

$$ v_{d1} = - \frac{{k_{t} R}}{L}, $$
(14a)
$$ v_{d2} = - \frac{{R\left( {59JR^{2} + 2k_{t}^{2} Ln^{2} + 11\sqrt {33} JR^{2} } \right)}}{{2k_{t} L^{2} n^{2} }}, $$
(14b)
$$ v_{d3} = - \frac{{R\left( {59JR^{2} + 2k_{t}^{2} Ln^{2} - 11\sqrt {33} JR^{2} } \right)}}{{2k_{t} L^{2} n^{2} }} $$
(14c)

The second condition (14b) implies that

$$ \frac{{16J^{2} R^{2} }}{{L^{2} }} - \frac{{3Jk_{t}^{2} n^{2} }}{L} - \frac{{3Jk_{t} v_{d} n^{2} }}{R} \ge 0, $$
(15)

so that \(v_{d} \le v_{d4} {\text{ with }}\)

$$ v_{d4} = {{\left( { - 3Lk_{t}^{2} Rn^{2} + 16JR^{3} } \right)} \mathord{\left/ {\vphantom {{\left( { - 3Lk_{t}^{2} Rn^{2} + 16JR^{3} } \right)} {3k_{t} L^{2} n^{2} }}} \right. \kern-\nulldelimiterspace} {3k_{t} L^{2} n^{2} }}. $$
(16)

It is straightforward to observe that \(v_{d2} < v_{d1} , \, v_{d3} > v_{d1} \;{\text{and}}\;v_{d1} < v_{d4}\). Therefore the polynomial possesses three roots when

$$ v_{d} \le v_{d2} . $$
(17)

When the number of pole pairs is extremely high,

$$ v_{{d_{4} }} = - k_{t} R/L. $$
(18)

We now test the second condition, i.e., the transversality condition. We recall the characteristic polynomial again in another format

$$ \begin{aligned} P(\lambda ) = & \quad \lambda^{3} + \frac{{2JLR + bL^{2} }}{{JL^{2} }}\lambda^{2} \hfill \\ & + \frac{{LRb^{2} - Jk_{t}^{2} Rn^{2} - Jk_{t} Ln^{2} k_{t} v_{d} }}{{JL^{2} b}}\lambda \hfill \\ & - \frac{{2k_{t}^{2} n^{2} R + 2k_{t} v_{d} Ln^{2} + 2bR^{2} }}{{JL^{2} }}. \end{aligned} $$
(19)

The polynomial is thus derived for the damping coefficient with the eigenvalue being a function of the same parameter,

$$ \begin{aligned} & 3\lambda^{2} d\lambda + 2\frac{{2JLR + bL^{2} }}{{JL^{2} }}\lambda d\lambda \hfill \\ & \quad + \frac{{ - Jk_{t}^{2} Rn^{ 2} - Jk_{t} Ln^{2} k_{t} v_{d} + LRb^{2} }}{{JL^{2} b}}d\lambda \\ & \quad { + }\frac{{\lambda^{2} }}{J}db - \frac{{2R^{2} }}{{JL^{2} }}db + \frac{R\lambda }{{JL}}db \hfill \\ & \quad + \frac{{Jk_{t}^{2} Rn^{2} + Jk_{t} Ln^{2} v_{d} }}{{JL^{2} b^{2} }}\lambda db. \\ \end{aligned} $$
(20)

Extracting the ratio of change of the eigenvalue with respect to the bifurcation parameter, and using the conjugate of the complex denominator yield

$$ \frac{d\lambda }{{db}} = - \frac{{\left( { - \frac{{\theta^{2} }}{J} - \frac{{2R^{2} }}{{JL^{2} }} + \frac{R\theta j}{{JL}} + \frac{{Jk_{t}^{2} Rn^{2} + Jk_{t} Ln^{2} v_{d} }}{{JL^{2} b^{2} }}\theta j} \right)\left( { - 2\theta^{2} - 2\frac{{2JLR + bL^{2} }}{{JL^{2} }}\theta j} \right)}}{{\left( { - 2\theta^{2} + 2\frac{{2JLR + bL^{2} }}{{JL^{2} }}\theta j} \right)\left( { - 2\theta^{2} - 2\frac{{2JLR + bL^{2} }}{{JL^{2} }}\theta j} \right)}}. $$
(21)

The real part of the change of the eigenvalue becomes

$$ {\text{Re}} \left( {\frac{d\lambda }{{db}}} \right) = \frac{{2J^{2} k_{t}^{2} R^{2} n^{2} + 2v_{d} J^{2} k_{t} LRn^{2} + Jk_{t}^{2} LRbn^{2} + v_{d} Jk_{t} L^{2} bn^{2} + JL^{3} b^{2} \theta^{2} + 4JLR^{2} b^{2} + L^{2} Rb^{3} }}{{2\theta^{2} + 2\left( {\frac{{2JLR + bL^{2} }}{{JL^{2} }}} \right)^{2} }}. $$
(22)

The transversality condition is fulfilled when

$$ {\text{Re}} \left( {\frac{d\lambda }{{db}}} \right) \ne 0, $$
(23)

which means

$$ v_{d} \ne - \frac{{J^{2} k_{t}^{2} Rn^{2} + 2RJLb^{2} + L^{2} b^{3} }}{{J^{2} k_{t} Ln^{2} }}, $$
(24a)
$$ R \ne 0, $$
(24b)
$$ R \ne - \frac{{J^{2} k_{t} Ln^{2} v_{d} + L^{2} b^{3} }}{{J^{2} k_{t}^{2} n^{2} + 2JLb^{2} }}. $$
(24c)

Remark 1

This value \(v_{d} = v_{d2}\) from Eq. (14b) is significant for two-dimensional bifurcation combining \(v_{d} {\text{ and }}b\) as it determines the critical value beyond which there is no Hopf bifurcation. In fact, at this value \(b_{H1} = b_{H2}\), Hopf bifurcation may exist without chaos. This value also has an impact on transient chaos. It determines the critical value of transient chaos.

By increasing or decreasing the value, the duration of transient chaos decreases. So it becomes the single point where permanent chaos occurs. We have thus the single-value permanent chaos. Chaos occurs only at those parameter values in the 2D plane. At the values \(b = b_{H1} \, \) [Eq. (11b)] and \(b = b_{H2}\) [Eq. (11c)], the non-hyperbolicity condition is satisfied.

The third condition, i.e., non-genericity, of the Hopf bifurcation can be applied through the center manifold theorem with the viscous damping coefficient. For these two positive points \(b = b_{H1} \, \) [Eq. (11b)] and \(b = b_{H2}\) [Eq. (11c)], we apply the center manifold theorem and the normal form theory developed by Faradja and Qi [27] to obtain non-zero first Lyapunov coefficients at both values. We have supercritical Hopf bifurcation at both points. Equilibria \(E_{2}\) and \(E_{3}\) are stable, then unstable, then stable again before they disappear.

So the damping coefficient values exist for which the eigenvalues produce the conditions for Hopf bifurcation.

Although the motor is an electromechanical device, we easily notice that the occurrence of Hopf bifurcation is conditioned by a special relationship between two electrical parameters. Equation (24) also shows the combined impact of the mechanical ratio \(b/J\) and the electrical damping ratio \(R/L\).

4 Illustration and discussion

We now illustrate the bifurcation with the damping coefficient as the bifurcation parameter. Given the parameters

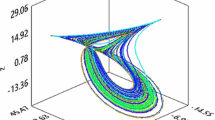
$$ \begin{aligned} k_{t} & = 0.031\;{\text{N}} \cdot {\text{m/A}},\;n = 4,\;L = 14.25 \times 10^{ - 3} \;{\text{H}},\\ R &= 0.9\;\Omega ,\;J = 4.7 \times 10^{ - 5} \;{\text{kgm}}^{2} , \end{aligned} $$

when \(v_{d} = - 27{\text{ V}}\) we have \(b_{H1} = {0}{\text{.007758974260878}}\) and \(b_{H2} = { 0}{\text{.014528633351044}}\) while \(b_{H0} = - {0}{\text{.034161291822448}}\). For these two positive points \(b_{H1}\) and \(b_{H2}\) in Eq. (11), we apply the center manifold theorem and normal form theory and obtain non-zero first Lyapunov coefficients at both values. We have supercritical Hopf bifurcation at both points. Equilibria \(E_{2}\) and \(E_{3}\) are stable, then unstable, then stable again before they disappear. In Fig. 1a, the equilibrium \(E_{1}\) is unstable (in cyan color) and stable (in black). Then equilibrium \(E_{2}\) is unstable (in red) and stable (in magenta). And finally, equilibrium \(E_{3}\) is unstable (in blue) and stable (in green color).

Fig. 1
figure 1

Evolution of dynamical behaviors (Color figure online)

Full size image

Chaos exists only between the two critical values \(b_{H1}\) [Eq. (11b)] and \(b_{H2}\) [Eq. (11c)] as shown as Fig. 1a, b, where \(\left( {L_{1} ,L_{2} ,L_{3} } \right) = \left( { + ,0, - } \right)\). Both symmetric equilibria are saddle fulfilling the Shilnikov condition. Beyond that region, the symmetric equilibria are still saddle, but they do not satisfy the Shilnikov theorem.

We illustrate below the different scenario with the different critical values.

4.1 Case of the first bifurcation point

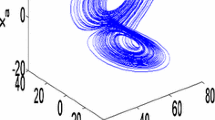
The system has the first Hopf bifurcation at \(b_{H1}\) [Eq. (11b)]. Around the equilibria \(E_{2}\) and \(E_{3}\), the limit cycle is observed, as illustrated in Fig. 2. Far from \(E_{2}\) and \(E_{3}\), it has the non-Shilnikov self-excited chaos (Fig. 3).

Fig. 2
figure 2

Limit cycle of Hopf bifurcation

Full size image
Fig. 3
figure 3

Non-Shilnikov self-excited chaos

Full size image

4.2 Case between two Hopf bifurcation points

Then, consider the value between \(b_{H1}\) and \(b_{H2}\). We observe the Shilnikov self-excited chaos even when starting from the symmetrical equilibria, as shown in Fig. 4. The trajectory starts almost as stable, then starts oscillating almost periodically and then ends chaotic, which is the opposite for scenarios with transient chaos.

Fig. 4
figure 4

Shilnikov self-excited chaos

Full size image

4.3 Case for the second Hopf bifurcation point

At \(b_{H2}\) [Eq. (11c)] the BLDCM exhibits a limit cycle near equilibria in Fig. 5 and non-Shilnikov self-excited chaos far from the equilibria (Fig. 6). Coexistence of different dynamical behaviors is experimented. The family of limit cycles to illustrate the Hopf bifurcation is also illustrated in 3D (Fig. 7).

Fig. 5
figure 5

Limit cycle of Hopf bifurcation

Full size image
Fig. 6
figure 6

Non-Shilnikov self-excited chaos

Full size image
Fig. 7.
figure 7

3D family of limit cycles

Full size image

4.4 Exceptional case when inductance and moment of inertia are equal

Exceptions for the condition of Hopf bifurcation are also tested. For example, when \(J = L\), the Hopf bifurcation does not occur, as illustrated in Fig. 8. This case is fundamental in the analogy relationship between electromechanical quantities and mechanical quantities. Inductance and moment of inertia are equivalent when electrical quantities are related to mechanical rotational quantities.

Fig. 8
figure 8

Special case for the parameters

Full size image

4.5 Exceptional case when bifurcation parameter is more than a certain margin

Illustratively in Fig. 9, when \(v_{d} \ge - {{k_{t} R} \mathord{\left/ {\vphantom {{k_{t} R} L}} \right. \kern-\nulldelimiterspace} L}\) [Eq. (14a)], we have the only equilibrium as predicted.

Fig. 9
figure 9

Another special case

Full size image

4.6 Case for a single bifurcation point

For the critical value conditions \(v_{d} = v_{d2}\) [Eq. (14b)], the BLDCM has a point where there is only one bifurcation value for the damping coefficient. Around the value, we find transient chaos, as is illustrated in Fig. 10, which depicts the change in the transient time as there are slight changes around the critical value \(v_{d} = v_{d2}\). When \(v_{d} = v_{d2}\), we observe Hopf bifurcation and coexistence of the limit cycle (Fig. 10e, f) and chaos (Fig. 10g, h). There are so many dynamical behaviors around this point because it is an exceptional point whereby two Hopf bifurcation points are combined into a single bifurcation point.

Fig. 10
figure 10figure 10

Particular case \(v_{d} = v_{d2}\)

Full size image
Fig. 11
figure 11

Evolutionary bifurcation diagram

Full size image

From Eq. (3), by fixing \(v_{d}\), pitchfork bifurcation happens if \(b = b_{p}\) when \(b_{p} = - {{\left( {n^{2} Lk_{t} v_{d} + Rn^{2} k_{t}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {n^{2} Lk_{t} v_{d} + Rn^{2} k_{t}^{2} } \right)} {R^{2} }}} \right. \kern-\nulldelimiterspace} {R^{2} }}\). Three equilibrium points exist when \(b < b_{p}\). With \(v_{d} = - 50{\text{ V}}\), \(b_{p} = 0.4192\;{\text{N}} \cdot {\text{m/rad/s,}}\;b_{H1} = 0.005\;{\text{N}} \cdot {\text{m/rad/s}}\;{\text{and}}\;b_{H2} = 0.028\;{\text{N}} \cdot {\text{m/rad/s}}\). There are also two switching points, excepted to be homoclinic bifurcation points, depicting switching between symmetric equilibria.

Moreover, comparatively \(b_{H1}\) and \(b_{H2}\) (Figs. 11 and 12a), the evolutionary bifurcation diagram and the evolutionary graph of the Lyapunov exponents are similar.

Figure 12b is the reduced range of the viscous damping coefficients b values from Fig. 12a. There exist points \(b_{H1} = 0.005\;{\text{N}} \cdot {\text{m/rad/s}}\) and \(b_{H2} = 0.028\;{\text{N}} \cdot {\text{m/rad/s}}\) where the maximum \(L_{1} = 0\), the other two LEs are negative. This condition gives rise to limit cycles. Chaos exists in the range between \(b_{H1} = 0.005\;{\text{N}} \cdot {\text{m/rad/s}}\) and \(b_{H2} = 0.028\;{\text{N}} \cdot {\text{m/rad/s}}\).

Comparing with the bifurcation with direct-axis v oltage, it is evident that the bifurcation with the damping coefficient gives more complexity. The damping coefficient is very influential as it participates in the definition of the dissipativity of the BLDCM model.

5 Conclusion

The BLDCM model was analyzed to focus on the viscous damping coefficient, which is a mechanical design parameter. The impact of this parameter was first found in the dissipativity of the system. The pitchfork bifurcation was identified. The onset of the Hopf bifurcation proved the impact of this parameter on the complexity of the overall dynamics. This type of bifurcation occurs twice with real positive parameters. The different scenarios for dynamical behaviors were illustrated. The chaos, limit cycle and stability were checked. Besides, transient features near the single Hopf bifurcation point were observed. The observation is that when the parameter is closer to the unique Hopf point, the transient time gets longer. Evolutionary bifurcation diagrams and Lyapunov exponents support the theoretical results that were found from rigorous methods.

This study also may suggest that parameters that define dissipativity of a system can have a greater impact on the overall dynamics than a parameter that does not contribute to the dissipativity.

Fig. 12
figure 12

Variation of Lyapunov exponents with the viscous damping coefficient

Full size image