Complementary Monopolies with asymmetric information

Abstract

We investigate how asymmetric information on final demand affects strategic interaction between a downstream monopolist and a set of upstream monopolists, who independently produce complementary inputs. We study an intrinsic private common agency game in which each supplier i independently proposes a pricing schedule contract to the assembler, specifying the supplier’s payment as a function of the assembler’s purchase of input i. We provide a necessary and sufficient equilibrium condition. A lot of equilibria satisfy this condition but there is a unique Pareto-undominated Nash equilibrium from the suppliers’ point of view. In this equilibrium, there are unavoidable efficiency losses due to excessively low sales of the good. However, suppliers may be able to limit these distortions by implicitly coordinating on an equilibrium with a rigid (positive) output in bad demand circumstances.

1 Introduction

This paper investigates how asymmetric information on final demand affects strategic interaction when a set of upstream monopoly firms independently provide complementary inputs to the better informed downstream monopolist (complementary monopolies setup¹). In particular, we identify unavoidable efficiency losses generated by excessive cumulative input rates² and we analyze whether input suppliers are able to mitigate these problems.

These questions are not new but they are now more crucial than they were at the time when Cournot (1838) wrote the Chapter IX of his Recherches sur les Principes Mathématiques de la Théorie des Richesses on the “mutual relations of producers”. Whereas Cournot considered copper and zinc suppliers selling to competitive producers of brass, modern examples include a wide range of situations, like for instance: Microsoft and Intel selling respectively chip and operative system to computer makers (HP, Lenovo, Dell.); Boeing buying jet engines to General Electric and avionics to Honeywell. Indeed, as products become more and more sophisticated, input complementarities also become more pervasive. For example, in the biotech industry, modern vaccines incorporate numerous inputs with corresponding third-party proprietary rights attached. In the aviation industry, Laussel (2008) refers that Airbus has no less than 15.000 suppliers among which 600 suppliers are providing parts of planes equipment. Lemley and Shapiro (2006) or Gerardin et al. (2008) refer that modern smartphones incorporate thousands of inputs, whose licenses are held by a fairly large number of firms.³

Over two centuries, the economics literature has identified two sources of inefficiency arising within complementary monopolies setups: (i) coordination failures among input suppliers, and (ii) double marginalization. First, as follows from the seminal work of Cournot (1838), the fact that input suppliers set their prices independently (without accounting for the impact of such decisions on other suppliers) leads to inefficiently low output production. Second, as long as upstream firms exert some degree of bargaining power, they do not account for the effect of their pricing decisions on the downstream firms’ profits, leading to the well-known double marginalization problem (Spengler 1950). The two effects result in price (output) levels which are greater (smaller) than the ones which would follow from joint profit maximization.

While in a complete information setup, the adoption of sophisticated pricing strategies (e.g. nonlinear pricing strategies like two-part tariffs⁴) is able to eliminate the two distortions described above⁵, we conclude this is no longer the case when the downstream firm is better informed about demand than input suppliers. Intuitively, if the suppliers used truthful strategies which are optimal in the full information case, the assembler would misreport (underestimate) the consumers’ willingness to pay for the good in order to reduce the payments due to the suppliers. Thus, under asymmetric information, nonlinear pricing strategies are no more able to restore joint profit maximization of the vertical chain (each supplier ends up setting an excessively high price for its input, in an attempt to reduce the assembler’s informational rent).

Some first insights on the answers to these questions may be drawn from a general paper by Martimort and Stole (2009a) on private common agency games.⁶ The authors model competition in nonlinear price schedules between two firms (the principals), each selling one good to a privately informed consumer (the agent) with the two goods ranging from perfect complements to perfect substitutes. Their model may be alternatively interpreted as a game between two upstream firms and a informed downstream monopolist and, in the perfect complements case, this boils down to our own complementary monopolies model. The authors show that the equilibrium sales level is smaller than the one which would maximize the suppliers’ joint profits. However, they only look at the differentiable equilibrium⁷, whereas we find that, at least in the perfect complements case, this is only one among a lot of possible equilibria.

More precisely, we consider a game in which each input supplier independently offers to the assembler a nonlinear pricing schedule which specifies the payment required for any given quantity of input purchases. Then, the assembler observes the true demand, deciding whether he accepts or rejects all the suppliers’ proposals. Formally, the game we analyze here is an intrinsic private common agency game.⁸

In line with the common agency theory, we look for the Nash equilibrium of the intrinsic private common agency game described above. We find a necessary and sufficient condition for the assembler’s equilibrium sales function (which defines equilibrium sales as a function of the realized value of the demand parameter). This condition is twofold. First, it implies a ceiling on the sales level, which is below the level that maximizes the suppliers’ aggregate expected profits (leading to unavoidable efficiency losses). Second, it includes a sub-condition, which defines a set of admissible sales functions. The latter are such that either (i) the equilibrium sales level increases with the demand unknown parameter or (ii) it is constant over an interval (bunching) of demand realizations. While the second sub-condition is not new for public common agency screening games (see, in particular, Martimort, Semenov and Stole, 2018 (hereafter, MSS, 2018) and Martimort and Stole 2015), it is a new result for private common agency games. Moreover, in our case, we need to impose an original restriction on the set of equilibrium sales functions (the ceiling on sales mentioned earlier) so that not all the sales functions satisfying the condition in MSS (2018) constitute an equilibrium in the present paper.

Nonetheless, this paper shows that a lot of equilibria satisfy our necessary and sufficient condition, including regular (differentiable) equilibria, semi-regular equilibria, constant equilibria, step-function equilibria, and hybrid equilibria. However, those equilibria are not all equivalent from the suppliers’ point of view. We show that there is a unique Pareto-undominated Nash equilibrium. This equilibrium is such that, in the best demand states, sales are strictly increasing with the demand intercept. In the worst demand circumstances, two cases may arise: (i) when the domain of possible demand realizations is large enough, the market is not covered, (ii) when the range of possible demand realizations is sufficiently narrow, suppliers prefer to have a rigid (and strictly positive) level of sales, mitigating the underprovision inefficiencies associated with the assembler’s informational rent. Although in the last case, there is less flexibility to adjust sales to the demand circumstances, suppliers benefit from selecting the most favorable equilibrium contract (as if they were implicitly coordinating on a strictly positive output level).

The possibility of bunching at the bottom arising in our setup also looks like an extension to an incomplete information framework of the type of equilibrium with fixed output (in the negotiation phase) proposed by Spulber (2017) to restore allocative efficiency in an upstream–downstream framework with complementary monopolies.⁹ Indeed, our equilibrium output level tends in the limit toward a constant one when the ex ante uncertainty on demand vanishes. However, differently from Spulber (2017), in our case, the efficiency losses are unavoidable since the constant output level remains too low to maximize the joint profits of the vertical structure.

The paper is organized as follows. In Sect. 2, we present the baseline model. In Sect. 3, we analyze the assembler’s decisions and, in Sect. 4, we look at the suppliers’ optimization problems. In Sect. 5, we characterize the equilibrium sales functions. In Sect. 6 we review the possible equilibria, identifying which equilibria are Pareto-dominated from the supplier’s perspective. Finally, in Sect. 7, we conclude. All the missing proofs are presented in Appendix.

2 The model

Consider a downstream monopoly firm (the “assembler”) that manufactures/ assembles a good from n complementary parts. The latter are supplied by n independent upstream firms (the “subcontractors” or “suppliers”). We assume perfect complementarity among components, meaning that one unit of the good requires one unit of each component part. The set of suppliers is denoted by N. The assembler’s and the suppliers constant marginal costs are normalized to zero.¹⁰

For the sake of simplicity, the good’s final demand is supposed to be linear, with:

$$\begin{aligned} D(P)=\theta -\ P\Leftrightarrow P=\theta -Q, \end{aligned}$$

(1)

where $\theta$ stands for the consumers’ willingness to pay for the final product, P stands for the price in the downstream market and $Q\in \left[ 0,q_{\max }\right]$ represents the sales in the downstream market (i.e. the assembler’s output). The value of $\theta$ is assumed to be private information of the assembler.¹¹ Each subcontractor has the same prior on $\theta ,$ represented by a cumulative distribution function $F( \cdot )$ and a strictly positive density function f everywhere on $[\underline{\theta },\overline{\theta }]$. We make the classical assumption that the inverse hazard rate, $h(\theta )=\frac{1-F(\theta )}{f(\theta )},$ is non-increasing in $\theta .$ This assumption is satisfied by all the usual distributions (e.g. uniform, exponential, normal, binomial, Poisson).

Assumption 1

$h^{\prime }(\theta )\le 0.$

We analyze here a two-stage game between the assembler and the suppliers. In the first stage, each of the n subcontractors independently offers a upper-hemi-continuous tariff (pricing schedule) $T_{i}: [0,q_{\max }]\rightarrow \mathbb {R} ,$ i.e. each supplier promises to supply $q_{i}\in [0,q_{\max }]$ units of input i to the assembler in exchange for a payment¹²$T_{i}(q_{i}).$ We denote by $\mathbf {T} =\{T_{1}( \cdot ),T_{2}( \cdots ), \ldots ,T_{n}( \cdot )\}$ the array of (arbitrary) pricing schedules offered by the set of all suppliers and we denote by $T_{-i}$ the array of (arbitrary) pricing schedules offered by all suppliers except supplier i,  with $\mathbf {T}=\left( \mathbf {T}_{-i} ,T_{i}( \cdot )\right)$.

In equilibrium, the pricing schedule $T_{i}( \cdot )$ is chosen by each supplier i to maximize its own expected profit. Then, in the second stage, the assembler learns the realized value of $\theta$ and, given the tariffs $T_{i}( \cdot )$ proposed by the n suppliers, it accepts or rejects all the subcontractors’ proposals. If it rejects them, it does not produce and it earns zero profits. If it accepts them, it chooses, after learning the realized value of $\theta ,$ to produce the output level Q and to buy the quantities of input $q_{i}$ ($i=1,2, \ldots ,n$) which maximize its profits.

From a formal point of view, the IO problem we are looking at here corresponds to a common agency game in which the suppliers (the principals) simultaneously and independently attempt to influence the assembler’s (agent’s) second-period choice of input and output levels. This influence is exerted through the decision on the pricing schedules which are only restricted here to be upper-hemi-continuous. Actually, the standard model in which the suppliers first choose the prices of the inputs and the downstream monopolist then fixes its price or output level is nothing else than a common agency model in which the pricing schedules are constrained to be linear.

It is worth noting that the common agency game studied in this paper has two key features. First, it is an intrinsic common agency game because the assembler either contracts with all suppliers or with none of them. Second, it is private since each principal contracts on a different observed variable chosen by the downstream firm. It differs from a public common agency game where each principal would offer a contract in which the suppliers’ payments would all depend on the same variable, such as a “royalty contract” in which all payments depend on the downstream firm’s final sales. We implicitly assume here that the sales level is not publicly observable or not contractible or both. Hence, as currently observed in practice, the contract between the downstream firm and each supplier i specifies payments which are only conditional on the quantity of input i which is bought by the assembler to supplier i (not on the amount of input actually used).¹³

Let $\mathbf {q}=\{q_{1},q_{2}, \ldots ,q_{n}\}$ be the vector of input levels. Assumption 2 states that the assembler must buy at least the quantities of input required to produce the intended output level but he is free to buy greater quantities. When doing so, it does not bear any storage or disposal costs.

Assumption 2

(Free disposal): The set of admissible inputs and output levels is

$$\begin{aligned} \Delta =\{Q\in [0,q_{\max }],\mathbf {q}\in [0,q_{\max }]^{n}:Q \le q_{i},i=1,2, \ldots ,n\}. \end{aligned}$$

Let now $\mathbf {T}^{*}=\{T_{1}^{*}( \cdot ), T_{2}^{*}( \cdot ), \ldots ,T_{n}^{*}( \cdot )\}$ be the array of equilibrium tariffs functions and $\mathbf {T} _{-i}^{*}$ the array of equilibrium tariff functions of suppliers other than i. In line with standard common agency theory, we will focus our attention on the pure-strategy perfect Bayesian equilibrium¹⁴, whose formal definition is presented below:

Definition 1

An equilibrium of this game is an array of equilibrium tariff functions $\mathbf {T}^{*}$, a function $Q^{*}$ and an array of functions $\mathbf {q}^{*}=\left( q_{1}^{*}, \ldots ,q_{n}^{*} \right)$, such that, for any $i=1,2, \ldots ,n$:

• (i)
  $$\begin{aligned} \{Q^{*}(\theta ,\mathbf {T}),\mathbf {q}^{*}(\theta ,\mathbf {T})\}\in \arg \max _{\{Q,\mathbf {q}\}\in \Delta }\left[ (\theta -Q)Q-\sum _{j=1}^{n} T_{j}(q_{j})\right] , \end{aligned}$$
• (ii)
  $$\begin{aligned} T_{i}^{*}( \cdot )\in \arg \max _{T_{i}( \cdot )}E[T_{i}(q_{i}^{*}(\theta ,\mathbf {T}_{-i}^{*},T_{i}))] \end{aligned}$$

  subject to

  $$\begin{aligned} \Pi \left( \theta ,Q^{*}(\theta ,\mathbf {T}_{-i}^{*},T_{i}),\mathbf {q} ^{*}(\theta ,\mathbf {T}_{-i}^{*},T_{i}),\mathbf {T}_{-i}^{*} ,T_{i}\right) \ge 0,\forall \theta \in \left[ \underline{\theta },\overline{\theta }\right] , \end{aligned}$$

  where $\Pi ( \cdot )$ denotes the assembler’s profit.

We denote respectively by $Q(\theta )$ and $q(\theta )$ an arbitrary output function and an array of arbitrary input functions.

The functions $Q(\theta )$ and $q(\theta )$ are implementable in the downstream firm’s problem iff there exists an array of tariff functions T such that $Q(\theta )=Q^{*}(\theta ,T)$ and $q(\theta )=q^{*} (\theta ,T)$ for all $\theta \in [\underline{\theta },\overline{\theta }],$ i.e. iff $Q(\theta )$ and $q(\theta )$ maximize the assembler’s profit for some T.

The equilibrium output function $Q^{e}(\theta )$ and the input functions $q^{e}(\theta )$ corresponding to an equilibrium $\{T^{*},Q^{*},q^{*}\}$ are such that $Q^{e}(\theta )=Q^{*}(\theta ,T^{*})$ and $q^{e} (\theta )=q^{*}(\theta ,\mathbf{T}^{*}),$ for all $\theta \in [\underline{\theta },\overline{\theta }],$ where $Q^{*}(\theta ,\mathbf{T}^{*})$ and $q^{*}(\theta ,\mathbf{T}^{*})$ are specified in Definition 1.

As far as concerns the equilibrium properties, it is important to note that part (i) of Definition 1 states that, given the realized value of $\theta$ and the pricing schedules previously selected by the n suppliers, the assembler chooses, in the second stage of the game, the sales and the input levels which maximize its profit.

Part (ii) in Definition 1 implies that each supplier i chooses, in the first stage of the game, the pricing schedule which maximizes its expected profit given the pricing schedules of the $n-1$ other suppliers, subject to the (participation) constraint that the assembler’s profit should not be negative for any realization of $\theta$. Then, at this stage of the game, there is a Nash equilibrium in pricing schedules between the n suppliers.

In the standard principal–agent model, one usually uses the Mirrlees (1971) trick¹⁵ to have the principal choosing the agent’s action which maximizes its own profit for each possible value of an unknown parameter (in our case, $\theta$) and implement it via a contract T instead of selecting directly the optimal T. Martimort and Stole (2009a) have shown that, under pricing schedules, the same trick may be used despite the existence of several suppliers: each individual supplier behaves as would do a monopolist supplier facing a downstream firm, i.e. each supplier maximizes with respect to $q_{i}$ an indirect profit function $\Pi (q_{i},\theta ,\mathbf {T}_{-i}),$ which depends only on $q_{i}$, $\theta$ and the pricing schedules of the other suppliers.¹⁶ More precisely, the indirect profit function $\Pi (q_{i},\theta ,,\mathbf {T}_{-i})$ is defined as

$$\begin{aligned} \Pi (q_{i},\theta ,\mathbf {T}_{-i})&=\underset{Q,\ \mathbf {q}_{-i}}{\max } \left( \theta -Q\right) Q-\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}), \end{aligned}$$

(2a)

$$\begin{aligned} s.t.\ \ Q&\le q_{j},\ \forall j=1,2, \ldots ,n, \end{aligned}$$

(2b)

where $\mathbf {q}_{-i}\in [0,q_{\max }]^{n-1}$ is the vector of input quantities of all the other suppliers besides supplier i. It is important to note that the influence of $q_{i}$ on the agent’s (assembler’s) indirect profit comes here from the constraint on the sales level.

Indeed, we can define

$$\begin{aligned} \{\overline{Q}(q_{i},\theta ,\mathbf {T}_{-i}),\overline{\mathbf {q}}_{-i} (q_{i},\theta ,\mathbf {T}_{-i}))\}&=\underset{Q,\mathbf {q}_{-i}}{\arg \max } \left\{ \left( \theta -Q\right) Q -\sum _{j=1,j\ne i}^{n}T_{j}(q_{j})\right\} , \end{aligned}$$

(3a)

$$\begin{aligned} s.t.\ Q&\le q_{j},\ j=1,2,.,i, \ldots ,n, \end{aligned}$$

(3b)

so that the functions $\overline{Q}(q_{i},\theta ,\mathbf {T}_{-i})$ and $\overline{\mathbf {q}}_{-i}(q_{i},\theta ,\mathbf {T}_{-i})$ show respectively how the sales level and the quantities of inputs bought to other suppliers $j\ne i$ actually depend on the quantity of input $q_{i}.$ This is a necessary step in order to analyze supplier i’s optimization problem since these functions show the influence of i’s choice of $q_{i}$ on the output level as well as on the other suppliers’ input levels.

We may equivalently write the indirect utility function as

$$\begin{aligned} \Pi (q_{i},\theta ,\mathbf {T}_{-i})=\left( \theta -\overline{Q}(q_{i} ,\theta ,\mathbf {T}_{-i})\right) \overline{Q}(q_{i},\theta , \mathbf {T}_{-i})-\sum _{j=1,j\ne i}^{n}T_{j} (\overline{q}_{j}(q_{i},\theta ,\mathbf {T}_{-i})). \end{aligned}$$

This will be useful when we shall come to supplier $i^{\prime }$s optimization problem. After making use of Mirrlees (1971) trick, this problem will indeed amount to determine the equilibrium input function $\widetilde{q}_{i}$ which maximizes supplier $i^{\prime }$s expected profit.

3 Assembler’s decisions

In the second stage of the game, as also follows from Definition 1, upon accepting the suppliers’ offers, the assembler chooses the quantity Q of output and the quantities of inputs $q_{j} (j=1,2, \ldots ,n)$, which, given the n suppliers’ contracts $\mathbf {T}$, maximize its profits for the realized value $\theta$ of the demand shock.

Hence, we can define as follows the assembler’s optimal output and input choices:

$$\begin{aligned} \{Q^{*}(\theta ,\mathbf {T}),\mathbf {q}^{*}(\theta ,\mathbf {T}))\}&=\underset{Q,\mathbf {q}}{\arg \max }\left\{ \left( \theta -Q\right) Q-\sum _{j=1}^{n}T_{j}(q_{j})\right\} , \end{aligned}$$

(4a)

$$\begin{aligned} \mathrm{s}.\mathrm{t}.\ Q&\le q_{j},\ j=1,2,.,i, \ldots ,n. \end{aligned}$$

(4b)

Remark that the equilibrium sales level can never be greater than the level $\frac{\theta }{2}$ which would maximize the assembler’s profit if it could buy the n inputs at zero marginal prices. Otherwise, deviating toward sales equal to $\frac{\theta }{2}$ would be feasible, allowing the assembler to obtain greater gross profits, while paying (at most) the same global price for the inputs.¹⁷

Let $\Pi ^{A}(\theta ,\mathbf {T})$ denote the maximum of the assembler’s profit with respect to Q and $\mathbf {q},$ given the n suppliers’ contracts (as specified in equation (5) below). In order to prepare the way for the analysis of the supplier i’s optimization problem, let

$$\begin{aligned} \widehat{q}_{i}(\theta ,\mathbf {T})=\arg \underset{q_{i}}{\max }\Pi (q_{i}, \theta ,\mathbf {T}_{-i})-T_{i}(q_{i}), \end{aligned}$$

so that, straightforwardly,

$$\begin{aligned} q_{i}^{*}(\theta ,\mathbf {T})=\widehat{q}_{i}(\theta ,\mathbf {T}) \end{aligned}$$

and

$$\begin{aligned} \Pi ^{A}(\theta ,\mathbf {T})=\max _{q_{i}}\Pi (q_{i}, \theta ,\mathbf {T}_{-i})-T_{i}(q_{i}) \end{aligned}$$

(5)

Moreover we can check that $\overline{Q}(q_{i}(\theta ,\mathbf {T}), \theta ,\mathbf {T}_{-i}) = Q^{*}(\theta ,\mathbf {T})$ and $\overline{q}_{-i}(q_{i}(\theta ,\mathbf {T}),\theta ,\mathbf {T}_{-i})) = q_{-i}^{*}(\theta ,\mathbf {T}).$

The lemma below is standard but important since it shows that the Envelope Theorem applies to the assembler’s profit function, which constitutes an essential step for using afterwards the Mirrlees trick to solve the suppliers’ problems.

In Lemma 1, we derive the conditions which an output function and an array of input functions$\{Q(\theta ),\mathbf {q}(\theta )\}$ must satisfy in order to be implementable. For the sake of simplicity, let us denote $\Pi ^{A}(\theta ,T)$ simply by $\Pi ^{A}\left( \theta \right)$.

Lemma 1

• (a) Q is non-decreasing and thus almost everywhere differentiable in $\theta ,$

• (b) $\Pi ^{A}$ is continuous in $\theta$ and $\frac{\partial \Pi ^{A}(\theta )}{\partial \theta }=Q(\theta )\ge 0.$

From Lemma 1 we know that the assembler earns its lowest profit in the worst market conditions (i.e. when the realized value of the market size parameter equals $\underline{\theta }$). Moreover, in the second stage, the assembler’s minimum possible profit from contracting with the subcontractors should not be negative, otherwise it would prefer not to produce. Consequently, condition (iii) in Definition 1 corresponds to the assembler’s participation constraint (i.e. the individual rationality condition for the downstream firm) amounts to

$$\begin{aligned} \Pi ^{A}(\underline{\theta })\ge 0. \end{aligned}$$

(6)

Note also that the absolute continuity of $\Pi ^{A}$ implies that we can now write $\Pi ^{A}(\theta )$ as¹⁸

$$\begin{aligned} \Pi ^{A}(\theta )=\Pi ^{A}(\underline{\theta }) +\int _{\underline{\theta }}^{\theta }Q(s)\mathrm{d}s, \end{aligned}$$

(7)

where the term $\Pi ^{A}(\underline{\theta })$ represents the equilibrium profit in the worst market circumstances ($\theta =\underline{\theta }).$ The second term results from the assembler’s incentive compatibility constraints, which guarantee the assembler’s incentives to reveal the true value of $\theta .$ Hence, the term $\int _{\underline{\theta }}^{\theta }Q(s)\mathrm{d}s$ corresponds to an informational rent.

From (7) follows that, for a realized value of $\theta ,$ the assembler’s rent is an increasing function of Q(s), $s<\theta .$ In other words, when the assembler produces more in the bad circumstances there is a larger benefit to the assembler in good circumstances. This is because the assembler’s incentive to misreport a small demand realization is stronger the greater is Q(s) for some $s<\theta$: in order to ensure truthful reporting this has to be counterbalanced by a smaller aggregate input price.

In light of the definition of $\Pi ^{A}(\theta )$, we find that expression (7) is equivalent to the following necessary condition: in order for some $\{Q(\theta ),q(\theta )\}$ to maximize the assembler’s profit, i.e. to be implementable, there must exist an array $\mathbf {T}$ of tariff functions such that, for all $\theta \in \left[ \underline{\theta },\overline{\theta }\right]$:

$$\begin{aligned} \sum _{j=1}^{n}T_{j}(q_{j}(\theta ))=\left[ \theta -Q(\theta )\right] Q(\theta )-\Pi ^{A}(\underline{\theta })-\int _{\underline{\theta }}^{\theta }Q(s)\mathrm{d}s. \end{aligned}$$

(8)

This condition follows from the Envelope Theorem and it will allow us to eliminate the supplier i’s price schedule from $i^{\prime }$s expected profit. Hence, we can now move to the study of the suppliers’ optimization problems.

4 Suppliers’ optimization problems

In the first stage, supplier i ’s equilibrium tariff should maximize its expected profit (corresponding to the expected payments received from the assembler in exchange of the purchase of quantities $q_{i}(\theta )$ of input i):

$$\begin{aligned} \int _{\underline{\theta }}^{\overline{\theta }}T_{i}(q_{i}(\theta )) f(\theta )\mathrm{d} \theta ,\ \forall i\in N, \end{aligned}$$

subject to the assembler’s incentive compatibility and participation constraints. Regarding the latter, recall that, in equilibrium, in the worst demand circumstances $(\theta =\underline{\theta }),$ we must have $\Pi ^{A}(\underline{\theta })=0,$ since otherwise any supplier could reach a larger expected profit by demanding a larger payment from the assembler, without violating its participation constraint. This follows from the fact that we are considering a model with complementary upstream monopolies and therefore the assembler either accepts all the contracts or rejects them all (choosing not to produce in the last case).

Using now the famous Mirrlees (1971) trick, i.e. substituting for $T_{i} (q_{i}(\theta ))$ its value from equation (8), the equilibrium input function $\widetilde{q}_{i}$ must maximize the expected profit of each supplier, given the tariff functions $\mathbf {T}_{-i}$ of the other suppliers¹⁹, i.e.:

$$\begin{aligned} \widetilde{q}_{i}^{*}\in \ \underset{\widetilde{q}_{i}}{\arg \max } \ \int _{\underline{\theta }}^{\overline{\theta }}\left[ \begin{array}{c} \left( \theta -\overline{Q}(\widetilde{q}_{i}(\theta ),\theta , \mathbf {T}_{-i})\right) \overline{Q}(\widetilde{q}_{i}(\theta ), \theta ,\mathbf {T}_{-i})\\ -\sum _{j=1,i\ne j}^{n}T_{j}(\overline{q}_{j}(\widetilde{q}_{i} (\theta ),\theta ,\mathbf {T}_{-i})))-\Pi ^{A}\left( \theta \right) \end{array} \right] f(\theta )\mathrm{d}\theta , \end{aligned}$$

(9)

subject to the assembler’s incentive compatibility constraint (7) and the participation constraint (6).²⁰

Expression (9) implies that, for each $\theta ,$ supplier i’s profit equals the aggregate profit of the vertical structure minus the assembler’s payments to the other suppliers and the assembler’s informational rent.

Notice that, contrary to what happens in the one principal–one agent model, the expected profit of principal i still depends on the tariffs of the other principals. It is also important to remark that a supplier i cannot directly influence the sales level (nor the quantities purchased of the other inputs) since, under the free disposal assumption, the tariff $T_{i}$ does not depend on them but only on its supply of input i. This makes a substantial difference with the public common agency game in which contracts (“royalty” ones) depend directly on the level of sales of the downstream firm. The indirect influence of $q_{i}$ on Q and $\mathbf {q}_{-i}$ is described by (3a) in Sect. 2.

Integrating by parts supplier i’s maximand and accounting for (7), we obtain the equivalent condition that $\widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i})$ should maximize $\pi _{i}(q_{i},\theta ,\mathbf {T}_{-i})$, corresponding to supplier $i^{\prime }$s adjusted profit. Formally:

$$\begin{aligned} \widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i}) \in \underset{q_{i}}{\ \arg \max }\pi _{i}(q_{i}, \theta , \mathbf {T}_{-i}), \end{aligned}$$

(10)

where

$$\begin{aligned} \pi _{i}(q_{i},\theta ,\mathbf {T}_{-i})=\left( \theta -h(\theta ) -\overline{Q}(q_{i},\theta ,\mathbf {T}_{-i})\right) \overline{Q}(q_{i},\theta ,\mathbf {T}_{-i}) -\sum _{j=1,i\ne j}^{n}T_{j}(\overline{q}_{j}(q_{i} ,\theta ,\mathbf {T}_{-i}))). \end{aligned}$$

(11)

Notice that $\widetilde{q}_{i}^{*}(\theta ,T_{-i})$ does not depend on $T_{i}$. This follows from the usual result allowing for the elimination of $T_{i}$ from the supplier i’s optimization problem, i.e. the Mirrlees’ Trick. If there exist a tariff $T_{i}$ which implements $\widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i})$, then for this tariff, we must have $\widetilde{q}_{i}^{*}(\theta , \mathbf {T}_{-i})=q_{i}^{*}(\theta , \mathbf {T}_{-i},T_{i}).$

Equation (11) points out that in order to estimate the benefits from a given output level Q conditional on $\theta ,$ the supplier must subtract from its direct profit the term $h(\theta )Q,$ since $h(\theta )$ is the marginal increase in the assembler’s informational rent for realizations of the demand parameter greater than $\theta$, resulting, from a marginal increase of Q at $\theta .$ For any $\theta ^{\prime } >\theta$, the assembler’s incentives to misreport consumers’ willingness to pay for the final good (the unknown demand parameter $\theta$) are larger the larger is $Q\left( \theta \right)$. Accordingly, maintaining a truthful reporting of $\theta$ by the assembler requires supplier i to reduce its financial demands.

Given our characterization of $\pi _{i}(q_{i},\theta , \mathbf {T}_{-i}),$ we can now define $\Pi _{i}^{S}(\theta , \mathbf {T}_{-i}),$ corresponding to the maximum of supplier’s i indirect adjusted profit as follows:

$$\begin{aligned} \Pi _{i}^{S}(\theta ,\mathbf {T}_{-i})=\underset{q_{i}}{\max } \pi _{i}(q_{i} ,\theta ,\mathbf {T}_{-i}) \end{aligned}$$

(12)

and we shall check later that the unconstrained solution of this problem satisfies the assembler’s incentive compatibility constraint derived in Lemma 1, i.e. $\frac{\partial Q(\theta )}{\partial \theta } \ge 0$. In the following, for the sake of notational simplicity, we shall write $\Pi _{i} ^{S}(\theta ,\mathbf {T}_{-i})$ as $\Pi _{i}^{S}(\theta )$.

We are now in position to prove a very useful result: at equilibrium, the assembler is induced to buy only the quantities of inputs which are necessary to manufacture the equilibrium output level corresponding to the amount of its final sales. The intuition is that supplier i’ s preferred sales level is never greater than the sales level which would maximize the assembler’s profit absent any constraint on the quantity of input i²¹: by selecting a supply of input i equal to its preferred sales level, supplier i induces the assembler to select the latter.

Lemma 2

The equilibrium sales and input functions must be such that $q_{i}^{e} (\theta )=Q^{e}(\theta )$, $\forall i=1,2, \ldots ,n.$

Remark 1

The equilibrium sales $Q^{e}(\theta )$ is never greater than $\frac{\theta -h(\theta )}{2}$, $\forall \theta \in \left[ \underline{\theta }, \overline{\theta }\right]$ such that $\frac{\theta -h(\theta )}{2}\ge 0$.

The above remark points toward an important difference with the public common agency game where the payments are conditional on the sales level. In the latter model, contrary to the present one, equilibrium sales levels above $\frac{\theta -h (\theta )}{2}$ may constitute an equilibrium due to decreasing tariffs: smaller levels of sales may be “punished” by requiring greater payments to suppliers $j\ne i$²², dissuading a joint deviation toward them by supplier i and the assembler. Under free disposal, it is no more possible to “punish” small out-of-equilibrium sales levels by requiring greater payments since the assembler always buys greater input quantities than required for production if this allows it to pay a smaller price to suppliers²³, so that a joint deviation by a supplier i and the assembler is profitable.

Corollary 1

At equilibrium,

• (i)
  $$\begin{aligned} Q^{e}(\theta )&=\arg \underset{Q}{\max }\left( \theta -h(\theta )-Q\right) Q-\sum _{j=1,i\ne j}^{n}T_{j}(Q),\\ \Pi _{i}^{S}(\theta )&=\underset{Q}{\max }\pi _{i}(Q,\theta , \mathbf {T}_{-i})=\left( \theta -h(\theta )-Q\right) Q -\sum _{j=1,i\ne j}^{n}T_{j}(Q). \end{aligned}$$

• (ii) Condition (8) becomes

  $$\begin{aligned} \sum _{j=1}^{n}T_{j}(Q^{e}(\theta ))=\left[ \theta -Q^{e}(\theta )\right] Q^{e}(\theta )-\Pi ^{A}(\underline{\theta }) -\int _{\underline{\theta }}^{\theta }Q^{e}(s))\mathrm{d}s. \end{aligned}$$

  (13)

Lemma 3 shows that the Envelope Theorem applies both to (i) each supplier’s adjusted profit function and to (ii) the assembler’s profit function.

Lemma 3

$\Pi _{i}^{S}(\theta )$ is absolutely continuous in $\theta ,$ a.e. differentiable and $\frac{\partial \Pi _{i}^{S}(\theta )}{\partial \theta } =\left[ 1-h^{\prime }(\theta )\right] Q^{e}(\theta )$, $\forall i\in N.$

Given the absolute continuity of $\Pi _{i}^{S}(\theta ),$ we now obtain

$$\begin{aligned} \Pi _{i}^{S}(\theta )=\Pi _{i}^{S}\left( \underline{\theta }\right) +\int _{\underline{\theta }}^{\theta }\left( \left[ 1-h^{\prime }(s)\right] Q^{e}(s)\right) \mathrm{d}s, \end{aligned}$$

(14)

and hence it follows that, if $Q^{e}(\theta )$ is an equilibrium sales function which maximizes supplier i’s expected profits, then the tariff functions of all principals $j\ne i$ must satisfy condition (15):

$$\begin{aligned} \underset{i=1,j\ne i}{\sum ^{n}}T_{i}(Q^{e}(\theta ))= & {} \left[ \theta -h(\theta )-Q^{e}(\theta )\right] Q^{e}(\theta )\nonumber \\&-\int _{\underline{\theta }}^{\theta }(1-h^{\prime }(s))Q^{e}(s)\mathrm{d}s -\Pi _{i}^{S}\left( \underline{\theta }\right) . \end{aligned}$$

(15)

Put otherwise, this defines the condition that an array $\mathbf {T}$ of tariff functions must satisfy for, all $\theta \in \left[ \underline{\theta } ,\overline{\theta }\right] ,$ so that $Q^{e}(\theta )$ constitutes a solution of supplier i’s optimization problem, i.e. it defines the condition on $\mathbf {T}$ for $Q^{e}(\theta )$ to be implementable in this problem.

In order to obtain this condition, we have applied nothing else than Mirrlees trick to the principal i’s problem (12): We use the Envelope Theorem to obtain a condition which the aggregate transfer function of all other principals $j\ne i$ must satisfy if principal i is to (indirectly) select a sales function $Q^{e}(\theta )$.²⁴

There are n such conditions (one for each supplier i). Now, summing up over these n conditions, we obtain the following necessary condition on the aggregate transfer function of all principals:

$$\begin{aligned}&(n-1)\underset{i=1}{\sum ^{n}}T_{i}(Q^{e}(\theta ))\nonumber \\&\quad = n\left[ \left[ \theta -h(\theta )-Q^{e}(\theta )\right] Q^{e}(\theta )-\int _{\underline{\theta }}^{\theta }((1-h^{\prime }(s)) Q^{e}(s))\mathrm{d}s\right] -\sum _{i=1}^{n}\left[ \Pi _{i}^{S} \left( \underline{\theta }\right) \right] . \end{aligned}$$

(16)

In light of this result, we are now able to study the properties of equilibrium sales functions.

5 Equilibrium sales functions

When applying the Envelope Theorem to the assembler and to the suppliers payoff functions, we obtained respectively conditions (15) and (16) Taken together, these conditions allow us to eliminate the pricing schedules and to derive a condition which an equilibrium sales function (defining equilibrium sales for different realizations of the demand parameter) must necessarily satisfy. This condition is based on the concept of virtual aggregate profit²⁵ of the vertical structure, which can be formally defined as follows:

Definition 2

The virtual aggregate profit of the vertical structure, V(Q, s),  is defined as:

$$\begin{aligned} V(Q,s)=\left[ s-nh(s)-Q\right] Q, \end{aligned}$$

(17)

with the partial derivative $V_{s}(Q,s)=(1-nh^{\prime }(s))Q.$

Proposition 1

A non-decreasing function $Q^{e}(\theta ),$ is an equilibrium sales function if and only if, for $\forall \theta \in \left[ \underline{\theta },\overline{\theta }\right]$,

• (i)
  $$\begin{aligned} Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2},\ \forall \theta \in \left[ \underline{\theta },\overline{\theta }\right] \, \mathrm{such}\,\mathrm{that}\, \frac{\theta -h(\theta )}{2}\ge 0; \end{aligned}$$

  (18)
• (ii)
  $$\begin{aligned} \int _{\underline{\theta }}^{\theta }V_{s}(Q^{e}(s),s)\mathrm{d}s=V(Q^{e} (\theta ),\theta )-V(Q^{e}(\underline{\theta }),\underline{\theta }). \end{aligned}$$

  (19)

Proposition 1 above fully characterizes the set of equilibrium sales functions and, given Lemma 2, it also characterizes the set of equilibrium input functions of our model. Any such function $Q^{e}(\theta )$, the array of input functions $\mathbf {q}^{e} (\theta )$ where $q_{i}^{e}(\theta )=Q^{e} (\theta )$, $i=1,2, \ldots ,n,$ and any $n-$tuple of tariffs which implements them in the assembler’s and the n suppliers’ optimization problems²⁶ constitute an equilibrium of the game following Definition 1.

Condition (19) is close to the general characterization obtained by MSS (2018) for public intrinsic common agency games, which amounts mutatis mutandis to state that the equilibrium allocation (here the sales function) is a pointwise maximizer of the virtual surplus²⁷.

More precisely, a sales function is an equilibrium one only if a fictitious agent, with payoff function $V(Q^{e}(\widehat{\theta }),\theta )$ would truthfully report the value of $\theta .$ An equilibrium sales function is necessarily an incentive-compatible one for this fictitious problem. Formally:

$$\begin{aligned} \theta =\arg \underset{\widehat{\theta }}{\max } \ V(Q^{e}(\widehat{\theta }),\theta ). \end{aligned}$$

(20)

This incidentally answers the question: what does the vertical structure maximize? This is of course a reminiscent of Slade (1994) who found in the oligopoly case “necessary and sufficient conditions for Nash equilibria of static and state-space games to be observationally equivalent to single optimization problems”.

While in the public intrinsic common agency game studied by MSS (2018), condition (19) is necessary and sufficient, in the case of our (specific) private intrinsic common agency game, it is only necessary.²⁸ Indeed, the private nature of our common agency game together with our free disposal assumption leads to the additional condition (18), absent in MSS, that, for each $\theta ,$ equilibrium sales are bounded above by the critical value $\frac{\theta -h(\theta )}{2}$.

The necessity of (18) is shown in Remark 1. The necessity of (19) is established from (13) and (16) in an original way, i.e. by generalizing the Mirrlees’ Trick to a common agency framework. We apply it first, as usual, to the agent’s problem. Then, we use again the Envelope Theorem to each of the principals problems in order to finally eliminate the transfer functions. To prove the sufficiency of (18) and (19), we show that if these two conditions hold, there must exist price schedules which implement the equilibrium sales and input functions both in the assembler’s and in each supplier’s problems.

Corollary 2 shows that $Q^{e}(\theta )$ is non-decreasing as assumed before: Over any given interval where it is differentiable, either it is constant (bunching) or equal to a flexible sales level $Q^{D}\left( \theta \right) ,$ which is specified as follows

$$\begin{aligned} Q^{D}(\theta )=\frac{1}{2}(\theta -nh(\theta )). \end{aligned}$$

Note that $Q^{D}\left( \theta \right)$ is weakly increasing in $\theta$, since $h^{\prime }(\theta )\le 0,$ by Assumption 1.

The “maximal output level”²⁹ which maximizes for a given $\theta$ the virtual aggregate profit of the vertical structure subject to the only constraint $Q\in \left[ 0,q_{\max }\right]$, is $Q^{\max } (\theta )=\max \{0,Q^{D}(\theta )\}$.

Corollary 2

For $\theta \in [\underline{\theta },\overline{\theta }]$ an equilibrium output function $Q^{e}(\theta )$ is, at any point $\theta$ of differentiability (almost everywhere), either such that $Q^{e\prime }(\theta )=0$ or such that the output level is equal to $Q^{D}\left( \theta \right)$, specified above. Given Assumption 1, $Q^{e}(\theta )$ is non-decreasing in $\theta$.

We are now able to prove an intermediate result³⁰ which will be very useful in the subsequent analysis.

Lemma 4

The virtual aggregate profit function $V(Q^{e}(\theta ),\theta )$ is continuous w.r.t. $\theta$ over $\left[ \underline{\theta }, \overline{\theta }\right]$.

The previous results show that, at equilibrium, the virtual aggregate profit is a continuous non-decreasing function of the private information parameter $\theta$ (monotonicity follows from the Envelope Theorem). More importantly, for any value of this parameter, equilibrium output either is increasing (and it maximizes the virtual aggregate profit) or it is constant over an interval (bunching). Moreover, there may be bunching both at the right and at the left of any point of discontinuity of the equilibrium sales function.

A lot of equilibria do satisfy the conditions in Proposition 1. In the following section, we present a systematic characterization of the possible equilibrium configurations. We start with continuous equilibria, in which the equilibrium sales are a continuous function of $\theta .$ Later on, we address discontinuous equilibria.

Even before looking at the equilibria configurations, it is worth noting that a close examination of the virtual surplus function (17)—of which the equilibrium output function is a pointwise maximizer according to (20)—and of the “maximal output function”—which maximizes the virtual surplus function over the whole range $\left[ 0,q_{\max }\right]$— already suggests that inefficiencies are going to exist at equilibrium. Moreover, these inefficiencies tend to be the more severe the greater is the number of suppliers.

Each supplier, when designing its pricing schedule knows from the assembler’s incentive compatibility constraints that larger output levels for “bad” realized values of the demand parameter result in larger profits left to the assembler for better demand realizations. Accounting for this effect, the equilibrium pricing schedules are not truthful, inducing the choice of output levels below the optimal ones (except for the “best” realized value of the demand parameter). Moreover this inefficiency is all the more severe as the number of suppliers is itself greater. Each supplier (when trying to reduce the informational rents left to the assembler) designs pricing schedules which overvalue its marginal cost. At the same time, each supplier signals to the other suppliers that it would ask more money for any output increase, reducing even more the other suppliers’ desired sales level. Thus, uncoordinated attempts to reduce the assembler’s rents result in cumulative inefficiencies.

6 Equilibria characterization

6.1 Continuous Equilibria

The simplest continuous equilibrium is the constant equilibrium sales one. This is an equilibrium such that the equilibrium sales are constant over $\left[ \underline{\theta }, \overline{\theta }\right] ,\$i.e. $Q^{e}\left( \theta \right) =Q_{0}$, $\forall \theta \in \left[ \underline{\theta }, \overline{\theta }\right] .$ The equilibrium sales function in a constant equilibrium is (trivially) continuous. Any positive output $Q_{0}\le \frac{\underline{\theta }-h(\underline{\theta })}{2}$ obviously satisfies the conditions (18) and (19) of Proposition 1.

These equilibria are like bootstrap ones: each supplier selects the constant output level because the other ones do it as well. They are implementable via simple pricing schedules such that $T(Q)=Q_{0}(\underline{\theta }-Q_{0})$, $\forall Q\le Q_{0}$ and T(Q) very large for all $Q>Q_{0}$.³¹

When the n suppliers select this type of pricing schedule, the assembler has no better choice that $Q(\theta )=Q_{0}$ for all $\theta$. Similarly, a supplier i cannot do better than choosing $Q(\theta )=Q_{0}$ when the $n-1$ other ones select this type of pricing schedule.

From (7), it is easy to compute the assembler’s profit conditional on $\theta$

$$\begin{aligned} \Pi ^{A}(\theta )=Q_{0}(\theta -\underline{\theta }), \end{aligned}$$

and its expected profit is $E_{\theta }[\Pi ^{A}(\theta )] =(E_{\theta }[\theta ]-\underline{\theta })Q_{0}.$

The expected true aggregate profit of the vertical structure equals

$$\begin{aligned} E_{\theta }[(\theta -Q_{0})Q_{0}]=E_{\theta }[\theta ]Q_{0}-Q_{0}^{2}. \end{aligned}$$

Hence, the ex ante expected aggregate profit of suppliers, $\sum _{i=1}^{n}E\left[ \Pi _{i}^{S}\right] ,$ is

$$\begin{aligned} \sum _{i=1}^{n}E\left[ \Pi _{i}^{S}\right]&=E_{\theta }[\theta ]Q_{0} -Q_{0}^{2}-\left( E_{\theta }[\theta ]-\underline{\theta }\right) Q_{0}\\&=\left( \underline{\theta }-Q_{0}\right) Q_{0}. \end{aligned}$$

Since $Q_{0}\le \frac{\underline{\theta }-h(\underline{\theta })}{2},$ the ex ante aggregate profit of suppliers are positive. Maximizing $\sum _{i=1} ^{n}E\left[ \Pi _{i}^{S}\right]$ with respect to $Q_{0},$ it is easy to see that the best constant equilibrium sales level from the suppliers’ point of view is such that $Q_{0}=\frac{\underline{\theta }-h(\underline{\theta })}{2}$ and $\sum _{i=1}^{n}E\left[ \Pi _{i}^{S}\right] =\frac{\underline{\theta }^{2} -h(\underline{\theta })^{2}}{4}.$ A greater sales level (for instance equal to $\frac{\underline{\theta }}{2}$), which would potentially yield greater aggregate profits to suppliers, cannot be implemented under free disposal. An individual supplier would indeed benefit from deviating to a smaller sales level (for instance $\frac{\underline{\theta }-h(\underline{\theta })}{2})$ unless the other suppliers impose a punishment on the assembler for buying quantities of input smaller than $\frac{\underline{\theta }}{2}.$ Such a punishment is impossible under free disposal since the assembler would optimally choose to purchase input quantities $\frac{\underline{\theta }}{2}$ while using smaller ones $\frac{\underline{\theta }-h(\underline{\theta })}{2}.$

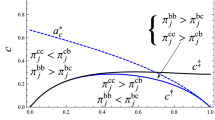
The next continuous equilibrium we analyze is the continuously differentiable (or regular) equilibrium. In this case, the corresponding sales function is given by $Q^{D}(\theta )$ and equilibrium sales are strictly increasing in $\theta ,$ meaning that output is larger in better states of demand, as represented in Fig. 1:

Fig. 1

Regular equilibrium

Notice that $Q^{D}(\theta )=\frac{\theta -nh(\theta )}{2} \le \frac{\theta -h(\theta )}{2}$, $\forall \theta \in \left[ \underline{\theta },\overline{\theta }\right]$.

An obvious necessary condition for the existence of a regular equilibrium is that the equilibrium flexible output $Q^{D}(\theta )$ must be nonnegative for all $\theta \in \left[ \underline{\theta }, \overline{\theta }\right]$, i.e. that the market is covered. Given that, by Assumption 1, $\theta -nh(\theta )$ is non-decreasing in $\theta ,$ this amounts to the condition $\underline{\theta }-nh(\underline{\theta })\ge 0.$ As the number of independent suppliers increases, this condition becomes more difficult to satisfy. For instance, in the case of an uniform distribution, it requires that $\underline{\theta } \ge \frac{n}{n+1}\overline{\theta }.$ So it’s natural to consider as well semi-regular equilibria (Figs. 2, 3 and 4).

Semi-regular equilibria are continuous equilibria in which the equilibrium sales are: (i) constant over some interval and (ii) given by $Q^{D}(\theta )$ over some other intervals, as in Figs. 2, 3 and 4.

Fig. 2

Semi-regular equilibrium (I)

Fig. 3

Semi-regular equilibrium (II)

Fig. 4

Semi-regular equilibrium (III)

Fig. 5

One-step-function equilibrium

Fig. 6

Hybrid equilibrium

Fig. 7

$Q_{C}\left( \theta \right)$ (in dash) vs $Q_{H}\left( \theta \right)$ (solid line)

The continuity of the semi-regular equilibrium functions wrt $\theta$ together with the results in Corollary 2 imply that only three types of semi-regular equilibria are possible. The first type is such that $Q^{e}(\theta )=Q_{1}\le \frac{\underline{\theta } -h(\underline{\theta })}{2}$, $\forall \theta \in \left[ \underline{\theta },x\right]$ and $Q^{e} (\theta )=Q^{D}(\theta )$, $\forall \theta \in \left[ x,\overline{\theta }\right]$. The second one is such that $Q^{e}(\theta )=Q^{D}(\theta )$, $\forall \theta \in \left[ \underline{\theta },x\right]$, and $Q^{e}(\theta )=Q_{1}$, $\forall \theta \in \left[ x,\overline{\theta }\right]$. The third one is such that $Q^{e}(\theta )=Q_{1}\le \frac{\underline{\theta } -h(\underline{\theta } )}{2}$, $\forall \theta \in \left[ \underline{\theta },x_{1}\right]$, $Q^{e} (\theta )=Q^{D}(\theta )$, $\forall \theta \in \left[ x_{1},x_{2}\right]$ and $Q^{e}(\theta )=Q_{2}$, $\forall \theta \in \left[ x_{2}, \overline{\theta }\right] .$ Among semi-regular equilibrium, the maximal equilibrium has attracted much attention. We now present below a natural example of the maximal equilibrium when there is a uniform distribution of $\theta$ between 0 and 1.

Example 1

When $\theta \$is uniformly distributed over $\left[ 0,1\right]$, any maximal equilibrium is the following semi-regular equilibrium (type I) which satisfies:

• (i) $Q^{e}(\theta )=0$ for all $\theta \in [0,\frac{n}{n+1}],$

• (ii) $Q^{e}(\theta ) =\frac{(n+1)\theta -n}{2}$ for all $\theta \in \left[ \frac{n}{n+1},1\right] ,$

• (iii) $\sum _{i=1}^{n}T_{i}(Q) =\frac{n(Q-Q^{2})}{n+1}$, $\forall Q\in \left[ 0,\frac{1}{2}\right]$.

Such an equilibrium is supported by many extensions of the contracts outside the equilibrium sales range (i.e. for $Q>\frac{1}{2}$), for instance $T_{i}(Q)=\frac{Q-Q^{2}}{n+1}$ or the constant $T_{i}(Q)=\frac{1}{4(n+1)}.$

The second result in Example 1 shows that the equilibrium level of final sales is a decreasing function of n for $\theta \in \left[ 0,1\right] .$ The coordination failure is, as usual, all the more severe as the number of suppliers increases. The third result is specially interesting. First it shows that the marginal input price is larger than the marginal cost. Second, it shows that, for any positive sales level, the input price paid by the assembler to each supplier is decreasing with the number of subcontractors. This is of course a reminiscent of the similar result obtained in a model where subcontractors compete in linear prices, following from the strategic complementary in the suppliers’ prices (see Laussel 2008).

Remark 2

In the context of Example 1, we obtain that the ex ante expected profit of the assembler, $E\left[ \Pi ^{A}\right]$, is equal to

$$\begin{aligned} E\left[ \Pi ^{A}\right] =\frac{1}{12(n+1)^{2}}, \end{aligned}$$

(21)

whereas, the expected profit of subcontractor i,  denoted $E\left[ \Pi _{i}^{S}\right] ,$ is

$$\begin{aligned} E\left[ \Pi _{i}^{S}\right] =\frac{1}{6(n+1)^{2}}. \end{aligned}$$

(22)

Interestingly, the values given by equations (21) and (22) are exactly identical to those obtained in a model with no uncertainty ($\theta =1$ with probability 1), independent upstream firms only and linear prices (see Laussel 2008).

6.2 Discontinuous equilibria

A $n-$step-function equilibrium is an equilibrium in which $\left[ \underline{\theta },\overline{\theta }\right]$ is divided in $n+1$ intervals $[x_{j},x_{j+1})$ such that $Q^{e}(\theta )=Q_{j}$, $\forall \theta \in [x_{j},x_{j+1}],$ with $Q_{j+1}>Q_{j}$, $x_{0}=\underline{\theta }$ and $x_{n+1}=\overline{\theta }.$ From Proposition 1, $Q_{j+1} \le \frac{x_{j}-h(x_{j})}{2}$, $\forall j$. In an n-step-function equilibrium, with $n>0$, the equilibrium sales function is discontinuous. More precisely, in an n-step equilibrium, the equilibrium sales function shows a number n of upward jumps as the parameter $\theta$ increases from $\underline{\theta }$ to $\overline{\theta }$ and the level of sales is constant over each interval. Figure 5 illustrates the equilibrium output function in the case of a one-step-function equilibrium.

Corollary 3

From Lemma 4, an $n-$step equilibrium is such that at each point $x_{i}$, $i\ge 1$, $i\le n,$ the condition $V(Q_{i-1},x_{i})=V(Q_{i},x_{i})$ must hold or, equivalently, $x_{i}-nh(x_{i})=Q_{i-1}+Q_{i}.$ Since the function $\theta -nh(\theta )$ is increasing in $\theta$ and it takes its maximum $\overline{\theta }$ at $\theta =\overline{\theta },$ it follows that all successive output pairs must satisfy the sufficient condition $Q_{i-1}+Q_{i}\le \overline{\theta }.$

A hybrid equilibrium is a discontinuous equilibrium such that $\left[ \underline{\theta },\overline{\theta }\right]$ is divided in $n+1$ (a finite number) intervals $[x_{j},x_{j+1})$, so that (i) there is at least one interval over which $Q^{e}(\theta )$ takes a constant value, (ii) there is at least one interval over which $Q^{e}(\theta )=Q^{D}(\theta )$ (iii) there is at least one $x_{j}$ such that $\underset{\theta \uparrow x_{j}}{\lim }Q^{e}(\theta )<\underset{\theta \downarrow x_{j}}{\lim }Q^{e} (\theta )$. Put otherwise, a hybrid equilibrium is a mix of a step-function and a regular (or semi-regular) equilibrium. Given the continuity results in Lemma 4, there cannot be a discontinuity between a strictly increasing segment and a constant segment of the equilibrium output function. Figure 6 illustrates one possible case of a hybrid output equilibrium (the conditions $Q_{j+1}\le \frac{x_{j}-h(x_{j})}{2}$, $\forall j,$ need to hold):

6.3 Equilibria selection

The previous analysis shows that there are a large number of equilibria as long as there are more than one supplier. When $n>1,$ as we argued in the constant equilibrium sales case, the suppliers may implicitly coordinate on a lot of different equilibria by choosing the corresponding pricing schedules. Hence, we investigate here the equilibria which are Pareto-dominated from the suppliers’ point of view. The first steps will be to show that semi-regular equilibria of type (II) and type (III) and discontinuous equilibria are indeed Pareto-dominated (see Lemmas 5 and 6, respectively) allowing us to restrict our attention to regular equilibria and semi-regular equilibria of type (I).

At this point, it is worthwhile to derive simple expressions for the expected aggregate suppliers’ profits $E[\Pi ^{S}]$.

Remark 3

The equilibrium expected aggregate suppliers’ profits is

$$\begin{aligned} E[\Pi ^{S}]=E\left[ (\theta -h(\theta )-Q^{e}(\theta ))Q^{e}(\theta )\right] , \end{aligned}$$

(23)

or, equivalently,

$$\begin{aligned} E[\Pi ^{S}]=V(Q^{e}(\overline{\theta }),\overline{\theta }) +\int _{\underline{\theta }}^{\overline{\theta }}Q^{e}(\theta ) \left[ (n-1)-n(1-h^{\prime }(\theta ))F(\theta )\right] \mathrm{d}\theta . \end{aligned}$$

(24)

From (23), the expected aggregate suppliers’ profit equals the expected virtual surplus in the case $n=1$, i.e. when there is only one supplier. The intuition is that, would all suppliers act cooperatively, they would maximize joint expected profits, which are equal to the expected virtual surplus for $n=1,$ as a result of Eq. (9).

Lemma 5 shows that from the suppliers’ point of view, a constant level of sales $Q^{D}\left( x\right)$ over $(x,\overline{\theta }]$ is inefficiently low. The optimal output level from the suppliers’ point of view is indeed given by the value of $Q^{D}(\theta )$ when $n=1$, i.e. $\frac{1}{2}(\theta -h(\theta ))$. Replacing $Q^{D}\left( x\right)$ for each $\theta \in (x, \overline{\theta }]$ by the greater, though still sub-optimal, flexible sales level $Q^{D}\left( \theta \right)$ unambiguously raises suppliers’ aggregate profits.³²

Lemma 5

Let us consider $x\in \left[ \underline{\theta },\overline{\theta }\right]$. For any arbitrary sales function $\xi \left( \theta \right)$, an equilibrium such that the sales function is given by $\xi \left( \theta \right)$, $\forall \theta \in [\underline{\theta },x],$ and $Q^{D}\left( x\right)$, $\forall \theta \in (x,\overline{\theta }],$ is Pareto-dominated by an equilibrium such that the sales function is given by $\xi \left( \theta \right)$, $\forall \theta \in [\underline{\theta },x],$ and $Q^{D} \left( \theta \right)$, $\forall \theta \in (x,\overline{\theta }]$.

It is also possible to show that hybrid equilibria are Pareto-dominated because, over the discontinuity range $\left[ x_{0},x_{1}\right]$, it is always better to switch to a flexible sales level $Q^{D}(\theta )$ rather than to stick to the two constant output levels $Q^{D}\left( x_{0}\right)$ and $Q^{D} \left( x_{1}\right)$. To this end, for any arbitrary sales function $\xi \left( \theta \right)$, let us consider an equilibrium sales function $Q_{H}\left( \theta \right)$ such that

$$\begin{aligned} Q_{H}\left( \theta \right) =\left\{ \begin{array}{ccc} \xi \left( \theta \right) &{} \qquad if &{} \underline{\theta }\le \theta<x_{0},\\ Q^{D}\left( x_{0}\right) &{}\qquad if &{} x_{0}\le \theta<x,\\ Q^{D}\left( x_{1}\right) &{} \qquad if &{} x\le \theta<x_{1},\\ \xi \left( \theta \right) &{}\qquad if &{} x_{1}\le \theta <\overline{\theta }, \end{array}\right. \end{aligned}$$

(25)

with $\underline{\theta }<x_{0}<x<x_{1}<\overline{\theta }.$

Lemma 6 shows that such step-wise function is Pareto-dominated by a sales function $Q_{C}\left( \theta \right)$ which is identical to $Q_{H}\left( \theta \right)$ except for the fact that it is continuous between $x_{0}$ and $x_{1}$

$$\begin{aligned} Q_{C}\left( \theta \right) =\left\{ \begin{array}{ccc} \xi \left( \theta \right) &{} \qquad if &{} \underline{\theta }\le \theta<x_{0},\\ Q^{D}\left( \theta \right) &{}\qquad if &{} x_{0}\le \theta<x_{1},\\ \xi \left( \theta \right) &{}\qquad if &{} x_{1}\le \theta <\overline{\theta }. \end{array}\right. \end{aligned}$$

(26)

Figure 7 illustrates the behavior of $Q_{H}\left( \theta \right)$ in the solid line and $Q_{C} \left( \theta \right)$, in the dashed line (note that the two coincide when $\underline{\theta }\le \theta <x_{0}$ or $x_{1}\le \theta <\overline{\theta }$).

In order to prove that all hybrid equilibria are Pareto-dominated by equilibria regularized in the way described by (26), we now introduce a new condition on the distribution of types.³³

Assumption 3

For almost all $\theta \in \left[ \underline{\theta }, \overline{\theta }\right]$,

$$\begin{aligned} (1-nh^{\prime }(\theta ))(1-h^{\prime }(\theta ))\ge (n-1) h(\theta )h\text {''}(\theta ). \end{aligned}$$

(27)

Assumption 3, which means that the hazard rate should not be too convex, is identical, mutatis mutandis,³⁴ to Assumption 1 (p. 1174) in MSS (2018).³⁵

To derive it, they use Amador and Bagwell (2013) results on optimal delegation. In their framework, it is a sufficient condition for the existence of a floor equilibrium in a public common agency game. We use it in Lemma 6 to rule out any discontinuous equilibrium.³⁶ The proof is much simpler than the one from Amador and Bagwell (2013). The purpose of Assumption 3 is also more intuitive in the present framework.

Lemma 6

Under Assumptions 1 and 3, an equilibrium such that the sales function is given by $Q_{H}\left( \theta \right)$ defined in (25) is Pareto-dominated by an equilibrium such that the sales function is given by $Q_{C}(\theta )$ in (26).

Lemma 6 implies that all discontinuous equilibria are Pareto-dominated. Given Lemmas 5 and 6, a flexible sales function $Q^{D}\left( \theta \right)$ Pareto-dominates all other equilibrium sales functions except possibly for bad realizations of the demand parameter. Accordingly, in what follows, we shall only consider either (i) regular equilibria, with

$$\begin{aligned} Q^{R}\left( \theta \right) =Q^{D}\left( \theta \right) , \ \forall \theta \in \left[ \underline{\theta },\overline{\theta }\right] , \end{aligned}$$

(28)

or (ii) semi-regular equilibria in which the equilibrium sales function is increasing for the highest values of $\theta$ (being constant for low $\theta -values$),

$$\begin{aligned} Q^{SR}\left( \theta \right) =\left\{ \begin{array}{ccc} Q^{D}\left( \theta ^{SR}\right) &{} \mathrm{if} &{} \underline{\theta } \le \theta \le \theta ^{SR},\\ Q^{D}\left( \theta \right) &{} \mathrm{if} &{} \theta ^{SR}<\theta \le \overline{\theta }. \end{array}\right. \end{aligned}$$

(29)

We now need to study how these equilibria are Pareto-ranked from the point of view of the suppliers. To do so, notice that, from a formal point of view, a regular equilibrium is simply a semi-regular equilibrium, with $\theta ^{SR}=\underline{\theta }$. Hence, ranking the equilibria in (28) and (29) amounts to determine the value of $\theta ^{SR}$, or equivalently, the corresponding level of sales $Q^{D}\left( \theta ^{SR}\right) ,$ which constitutes the minimum equilibrium sales level that maximizes the suppliers’ expected aggregate profit.

Given Assumption 1, the function $Q^{D}(\theta )$ is invertible. Let then $\Theta =\left( Q^{D}\right) ^{-1}$.

Proposition 2

• (i) Sufficiency:

  If Assumptions 1 and 3 hold, the best, Pareto-undominated, Nash equilibrium sales function is defined by (29) and

  $$\begin{aligned} Q^{D}(\theta ^{SR})=\max \left\{ \frac{\underline{\theta } -h(\underline{\theta })}{2},0\right\} , \end{aligned}$$

  (30)

  or, equivalently,

  $$\begin{aligned} \theta ^{SR}=\max \left\{ \Theta \left( \frac{\underline{\theta } -h(\underline{\theta })}{2}\right) ,\Theta (0)\right\} . \end{aligned}$$

  (31)

• (ii) Necessity:

  The best, Pareto-undominated, Nash equilibrium sales function is defined by (29) and (30) only if (27) holds for almost all $\theta \in [\max \{\Theta (\frac{\underline{\theta }-h(\underline{\theta })}{2}),\Theta (0)\}, \overline{\theta }].$

The necessity part of Proposition 2 is completely original. The intuition is the following: if there exists some sub-interval in the range of values of $\theta$ where the sales level is given by $Q^{D}(\theta )$ (the regular part of the equilibrium sales function) and over which (27) does not hold, it is clear from the proof of Lemma 6 that one could always construct a (discontinuous) deviation over this sub-interval which would satisfy Proposition 1 and Pareto-dominate the equilibrium considered in Proposition 2.

According to Proposition 2, bunching optimally occurs in bad circumstances. The best equilibrium from the suppliers’ point of view is (i) either the maximal equilibrium in which the market is not served when the consumers’ willingness to pay for the good is small (bunching at the zero output level) or (ii) an output floor equilibrium in which the sales level is a positive constant for bad realizations of the demand parameter (bunching at a floor output level). The former (resp. latter) case obtains when $\underline{\theta }$ is small (resp. great) enough so that $\underline{\theta }-h(\underline{\theta })<0$ (resp. $\underline{\theta }-h(\underline{\theta } )>0$). Put otherwise, the maximal equilibrium is Pareto-optimal iff the range of realized values of the demand parameter is large enough.

Example 2

In the uniform distribution case:

• (i) $Q^{D}(\theta ^{SR})=0$ and $\theta ^{SR}=\frac{n\overline{\theta }}{n+1}$ when $\overline{\theta } \ge 2\underline{\theta },$

• (ii) $Q^{D}(\theta ^{SR})=\frac{2\underline{\theta } -\overline{\theta }}{2}$ and $\theta ^{SR}=\frac{2\underline{\theta } +(n-1)\overline{\theta }}{n+1}$ when $\overline{\theta } \le 2\underline{\theta }$.

The sales level at which bunching occurs is a result of a trade-off between two opposite forces.³⁷ On one hand, a regular sales function allows a flexible adjustment of the level of sales to the circumstances. On the other one, it implies an inefficiently low level of sales, especially in bad circumstances. The flexibility argument has little bearing when the ex ante uncertainty on $\theta$ is small and bunching (at a positive level) always occurs (the interval over which it occurs being an increasing function of the number of suppliers). Moreover, when the number of suppliers tends to infinity, the floor equilibrium implies a constant equilibrium output in all circumstances.

When ex ante uncertainty is large, bunching at a positive level never occurs though it would be all the more profitable as the number of suppliers increases. The key of this apparent paradox is again free disposal: suppliers would collectively benefit from a floor sales level, but under free disposal, there is no way to dissuade each of them to individually deviate toward a smaller level of input sales.³⁸

7 Conclusion

This paper investigates how asymmetric information on final demand affects strategic interaction between the assembler and a set of upstream monopoly firms, who independently provide complementary inputs to the better informed assembler. To this end, we propose an intrinsic private common agency game. In the first stage, each of the suppliers maximizes its own expected profit by independently proposing a payment contract (price schedule) to the assembler. In the second stage, the assembler learns the realized value of the uncertain demand parameter, choosing whether to accept or reject all the subcontractors’ proposals.

We are able to derive a condition which a sales function satisfies if and only if it is an equilibrium one. We find that this necessary and sufficient equilibrium condition depends on the virtual aggregate profit of the vertical structure (which is always smaller than the true aggregate profit for any number of suppliers larger than one) and it also implies a ceiling on the sales level in each circumstance. This allows us to make the point that, in a setup with asymmetric information, coordination failures always lead to some efficiency losses, even when upstream firms rely on nonlinear pricing schemes.

We also find that a lot of equilibria satisfy the necessary and sufficient equilibrium condition, including regular (differentiable), semi-regular, constant, step-function and hybrid equilibria. However these equilibria are not all equivalent from the point of view of suppliers. In this respect, we find that there is a unique Pareto-undominated Nash equilibrium. In this equilibrium, for the best demand states, sales are increasing with the unknown demand parameter. However, for the worst demand circumstances, two situations are possible, depending on the extent of ex ante demand asymmetry. When the latter is important, we find that the market is not covered in the worst demand states. In other words, a severe form of inefficiency arises in these circumstances. Differently, when the domain of admissible values of the demand parameter is small enough, suppliers can mitigate (without eliminating) the underprovision problem. More precisely, they can implicitly coordinate on an equilibrium with a rigid (and strictly positive) output in bad circumstances (above the regular one). In other words, inefficiency does not preclude full market coverage in this case. However, it remains a problem in the sense that the level of the final sales remains excessively low.

Our results on pricing schedules can be compared with Martimort and Stole (2009a), who also deal with pricing schedules in private common agency games, not necessarily restricted to perfectly complementary inputs. In particular, when the domain of admissible values of the demand parameter is not too wide, we find that suppliers have incentives to implicitly coordinate on a semi-regular equilibrium with bunching at the bottom. This possibility was not analyzed by Martimort and Stole (2009a) since they exclusively studied differentiable equilibria. We show that, by coordinating on this equilibrium, suppliers mitigate (without completing eliminating, though) some inefficiency losses resulting from the interplay of asymmetric information and suppliers’ non-cooperative behavior. While this is not new for public common agency games (see MSS, 2018), this is a new result for a private common agency game.

At a more substantial level, our paper confirms and extends Spulber’s (2017) results on complementary monopolies to a context with private information. In our model bunching at the bottom arises when ex ante uncertainty is small enough, allowing suppliers to partially restore efficiency. In the limit, when uncertainty vanishes, we obtain exactly Spulber’s result: the equilibrium output level tends toward the constant output level that maximizes aggregate suppliers’ profits.

In the future, it would also be interesting to develop an extended version of this model to analyze how asymmetric information on demand may affect suppliers’ incentives to make investments to improve the quality of their inputs (with uncertain impact on final demand).³⁹ It would also be interesting to investigate whether non-regular equilibria, such as the ones derived in this paper, can be obtained as limits of equilibria arising when inputs are imperfect complements. This remains an open question since, in the present state of knowledge, the perfect complementarity case is the only one in which one has been able to characterize all the possible equilibria of the game. Under imperfect complementarity of inputs, only the regular, differentiable, equilibria have been characterized so far (see Martimort and Stole 2009a). Indeed, when the inputs are imperfect complements, the problem becomes more complex: when trying to characterize the equilibria of the game, it becomes impossible to fully eliminate from each supplier’s problem its own pricing schedules. Accordingly, when characterizing the equilibria of the underlying common agency game, one needs to develop new methods that allow us to account for the degree of inputs complementarity, as well as for the relationship between the final downstream sales and each input levels (for each supplier and its rivals as well).⁴⁰ These new sources of strategic interaction (both among suppliers and between them and the assembler) may significantly affect the properties of the equilibria, constituting an interesting question for future research.

Appendices

APPENDIX

1.1 Proof of Lemma 1

• (a) suppose that $\theta ^{\prime }>\theta ;$ from revealed preference it must be that

  $$\begin{aligned} (\theta -Q(\theta ))Q(\theta )-\sum _{i=1}^{n}T_{i}(q_{i}(\theta ))\ge (\theta -Q(\theta ^{\prime }))Q(\theta ^{\prime })-\sum _{i=1}^{n}T_{i}(q_{i} (\theta ^{\prime })) \end{aligned}$$

  and

  $$\begin{aligned} (\theta ^{\prime }-Q(\theta ^{\prime }))Q(\theta ^{\prime })-\sum _{i=1}^{n} T_{i}(q_{i}(\theta ^{\prime }))\ge (\theta ^{\prime }-Q(\theta ))Q(\theta ) -\sum _{i=1}^{n}T_{i}(q_{i}(\theta )), \end{aligned}$$

  implying $\left( \theta -\theta ^{\prime }\right) (Q\left( \theta \right) )-Q\left( \theta ^{\prime }\right) )\ge 0$.

• (b) $\Pi ^{A}$ is convex as a supremum of convex (linear here) functions. It is also continuous at the endpoints of the domain $\left[ \underline{\theta },\overline{\theta }\right]$. It is hence absolutely continuous⁴¹ in $\theta .$ Suppose that $\theta ^{\prime }>\theta ;$ from the above “revealed preference” inequalities we obtain $\left( \theta ^{\prime }-\theta \right) Q\left( \theta ^{\prime }\right) \ge \Pi ^{A}(\theta ^{\prime })-\Pi ^{A}(\theta )\ge \left( \theta ^{\prime } -\theta \right) Q\left( \theta \right) )$, so that, dividing throughout by $\left( \theta ^{\prime }-\theta \right)$ and letting $\theta ^{\prime }$ tend toward $\theta$, we obtain $\frac{\partial \Pi ^{A}(\theta )}{\partial \theta } =Q(\theta ) \ge 0$. $\square$

1.2 Proof of Lemma 2

Suppose on the contrary that $\overline{Q}(\widetilde{q}_{i}^{*} (\theta ,\mathbf {T}_{-i}),\theta ,\mathbf {T}_{-i})<\widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i}),$ where $\widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i})$ is defined by (10), i.e. maximizes supplier i’s adjusted profit.

Let $\{Q^{A}(\theta ),\mathbf {q}_{-i}^{A}(\theta )\}$ be solution of the assembler’s problem (3a) in which the constraint $Q\le q_{i}$ has been deleted.⁴² Since, at the solution of (3a), this constraint does not bind, $\overline{Q}(\widetilde{q}_{i}^{*} (\theta ,\mathbf {T}_{-i}),\theta ,\mathbf {T}_{-i})=Q^{A}(\theta )$ and $\overline{\mathbf {q}}_{-i}(\widetilde{q}_{i}^{*}(\theta ,\mathbf {T} _{-i}),\theta ,\mathbf {T}_{-i})=\mathbf {q}_{-i}^{A}(\theta )$ do not depend on $q_{i}$ and the corresponding supplier’s adjusted profit equals

$$\begin{aligned} \left( \theta -Q^{A}(\theta )-h(\theta )\right) Q^{A}(\theta )-\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}^{A}(\theta )). \end{aligned}$$

(33)

Let us on the other hand consider the solution to the problem of maximizing supplier i’s adjusted profit when i is able to select directly $Q(\theta )$ and $\mathbf {q}_{-i}(\theta )$:⁴³

$$\begin{aligned} \{Q^{S}(\theta ),\mathbf {q}_{-i}^{S}(\theta )\}&=\underset{Q,\mathbf {q}_{-i}}{\arg \max } \left( \theta -Q-h(\theta )\right) Q-\sum _{j=1,j\ne i}^{n} T_{j}(q_{j}),\nonumber \\ s.t.\ \ Q&\le q_{j},\ \forall j\ne i. \end{aligned}$$

(34)

From revealed preferences,

$$\begin{aligned}&\left( \theta -Q^{A}(\theta )\right) Q^{A}(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}^{A}(\theta ))\\&\quad \ge \left( \theta -Q^{S}(\theta )\right) Q^{S}(\theta )-\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}^{S}(\theta )), \end{aligned}$$

and

$$\begin{aligned}&\left( \theta -h(\theta )-Q^{S}(\theta )\right) Q^{S}(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}^{S}(\theta ))\\&\quad \ge \left( \theta -h(\theta )-Q^{A} (\theta )\right) Q^{A}(\theta )-\sum _{j=1,j \ne i}^{n}T_{j}(q_{j}^{A} (\theta )). \end{aligned}$$

This implies

$$\begin{aligned} h(\theta )(Q^{A}(\theta )-Q^{S}(\theta ))\ge & {} 0\Leftrightarrow Q^{S}(\theta ) \le Q^{A}(\theta )=\overline{Q}(\widetilde{q}_{i}^{*} (\theta ,\mathbf {T}_{-i}),\theta ,\mathbf {T}_{-i})\\< & {} \widetilde{q}_{i}^{*}(\theta ,\mathbf {T}_{-i}). \end{aligned}$$

Let us show that the supplier i may reach a greater profit than (33) simply by choosing to sell a quantity of input i equal to $Q^{S}(\theta )$ instead of the quantity $\widetilde{q}_{i}^{*} (\theta ,\mathbf {T}_{-i}).$

This is obviously the case when the solution $\overline{Q}(Q^{S} (\theta ),\theta )$ of the assembler’s problem (3a) under the constraint $Q\le Q^{S}(\theta )$ is such that $\overline{Q}(Q^{S} (\theta ),\theta ,\mathbf {T}_{-i})=Q^{S}(\theta )$.⁴⁴ Let us show that it must indeed be the case that $\overline{Q}(Q^S(\theta ),\theta ,\mathbf T _-i) =Q^S(\theta )$. Suppose on the contrary that the solution of the assembler’s problem (3a) under the constraint $Q\le Q^S(\theta )$ implies a sales level $Q^\prime (\theta )<Q^S(\theta )$. It must then be that

$$\begin{aligned}&\left( \theta -Q^{\prime }(\theta )\right) Q^{\prime }(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(\overline{q}_{j}(Q^{\prime }(\theta ),\theta ))\\&\quad >\left( \theta -Q^{S}(\theta )\right) Q^{S}(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(\overline{q}_{j}(Q^{S}(\theta ),\theta )). \end{aligned}$$

But, since $h(\theta )\ge 0$ and $Q^{\prime }(\theta )<Q^{S}(\theta ),$ were this true, it should be that

$$\begin{aligned}&\left( \theta -h(\theta )-Q^{\prime }(\theta )\right) Q^{\prime }(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(\overline{q}_{j}(Q^{\prime }(\theta ),\theta ))\\&\quad >\left( \theta -h(\theta )-Q^{S}(\theta )\right) Q^{S}(\theta ) -\sum _{j=1,j\ne i}^{n}T_{j}(\overline{q}_{j}(Q^{S}(\theta ),\theta )). \end{aligned}$$

This contradicts (34).

To conclude, supplier i is always able to induce the assembler to select the output and input levels $\{Q^{S}(\theta ),\mathbf {q}_{-i}^{S} (\theta )\}$ by choosing to supply a quantity $Q^{S}(\theta )$ of input i. Then, either $Q^{S}(\theta )<Q^{A}(\theta )$, in which case supplier i clearly obtains greater (adjusted) profits than at $\{Q^{A}(\theta ),\mathbf {q}_{-i}^{A} (\theta )\},$ or $Q^{S}(\theta )=Q^{A}(\theta ),$ in which case an infinitesimal cost of producing input i is enough to ensure that supplier i is better off when supplying a quantity of input i equal to $Q^{S}(\theta )$. $\square$

1.3 Proof of Remark 1

Suppose that $Q(\theta )>\frac{\theta -h(\theta )}{2}>0.$ Obviously $q_{j} (\theta )\ge Q(\theta ).$ Suppose now instead that the supplier i chooses a supply level $q_{i}(\theta )=\frac{\theta -h(\theta )}{2\ }$ and show that it is better off. Indeed, under the constraint $Q\le \frac{\theta -h(\theta )}{2},$ the solution $\overline{Q}(\frac{\theta -h(\theta )}{2},\theta ,\mathbf {T}_{-i})$ of the assembler’s problem (3a) is either $=\frac{\theta -h(\theta )}{2}$ or $<\frac{\theta -h(\theta )}{2}$ so that either

• 1. $\overline{Q}(\frac{\theta -h(\theta )}{2},\theta ,\mathbf {T}_{-i}) =\frac{\theta -h(\theta )}{2}$, and then the supplier i’s adjusted profit is greater than the profit obtained at $Q(\theta )>\frac{\theta -h(\theta )}{2}$ since (i) for $\forall Q(\theta )\ne \frac{\theta -h(\theta )}{2}$, $(\frac{\theta -h(\theta )}{2})^{2}>\left( \theta -h(\theta )-Q(\theta )\right) Q(\theta )$ and (ii) in order to produce a quantity of output $\frac{\theta -h(\theta )}{2}<Q(\theta )$, the assembler does not need greater quantities of inputs other than i and pays accordingly at most the same aggregate transfer $\sum _{j=1,j\ne i}^{n}T_{j}(q_{j}(\theta ))$ to suppliers $j\ne i.$

• 2. or $\overline{Q}(\frac{\theta -h(\theta )}{2},\theta ,\mathbf {T}_{-i}) <\frac{\theta -h(\theta )}{2},$ in which case, by the same argument as in Lemma 2, the supplier i’s adjusted profit must be greater at $\overline{Q} (\frac{\theta -h(\theta )}{2},\theta ,\mathbf {T}_{-i})$ than at $\frac{\theta -h(\theta )}{2}$ and thus strictly greater than at any $Q(\theta )>\frac{\theta -h(\theta )}{2}$. $\square$

1.4 Proof of Lemma 3

Let $\tau =\theta -h(\theta ).$ Define now

$$\begin{aligned} \widehat{\pi }_{i}(\tau ,q)=\left( \tau -Q\right) Q -\sum _{j=1,i\ne j}^{n} T_{j}(Q). \end{aligned}$$

and

$$\begin{aligned} \widehat{\Pi }_{i}^{S}(\tau )=\underset{q}{\max } \widehat{\pi }_{i}(\tau ,q). \end{aligned}$$

Since $\widehat{\pi }_{i}$ is linear in $\tau$, $\widehat{\Pi }_{i}^{S}(\tau )$ is convex in $\tau$ as a supremum of convex (linear) functions, hence absolutely continuous⁴⁵ (AC). By assumption 1, $\tau (\theta )$ is invertible so that $\Pi _{i}^{S}(\theta )=\widehat{\Pi }_{i}^{S}(\tau (\theta ))$ is AC and a.e. differentiable. $\square$

1.5 Proof of Proposition 1

• (a) Necessity

From Lemma 2, $Q^{e}(\theta )=q_{i}^{e}(\theta )$, $\forall i=1,2, \ldots ,n.$ Moreover from Remark 1, it must be that $Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2}.$ On the other hand, we already know that a non-decreasing output function $Q^{e}(\theta ) ($and the input functions $q_{i}^{e}(\theta )=Q^{e}(\theta ))$ solve respectively the Assembler’s Problem (4a) and the Suppliers’ Problems (9) only if the payment schedules, $T_{i}$, are defined by equations (13) and (15).

Substituting in (16) $\sum T_{i}(Q^{e} \left( \theta \right) )$ for its value from (8) and rearranging we obtain:

$$\begin{aligned} 0=\left[ V\left( \theta ,Q\left( \theta \right) \right) -\int _{\underline{\theta }}^{\theta }\left( 1-nh^{\prime } \left( s\right) \right) Q\left( s\right) \mathrm{d}s\right] -\sum _{i=1}^{n}\Pi _{i}^{s}\left( \underline{\theta }\right) . \end{aligned}$$

Evaluating the previous condition at $\theta =\underline{\theta },$ we obtain:

$$\begin{aligned} V\left( \underline{\theta },Q\left( \underline{\theta }\right) \right) =\sum _{i=1}^{n}\Pi _{i}^{s}\left( \underline{\theta }\right) . \end{aligned}$$

Given that $V_{s}(Q(s),s)=(1-nh^{\prime }(s))Q(s),$ the result in Proposition 1 must hold.

• (b) Sufficiency

Let us consider the implementation of a non-decreasing sales function $Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2} \le \frac{\theta }{2}$ when the assembler solves the associate problem $\underset{Q}{\max }\Psi (\theta ,Q)=(\theta -Q)Q -\overline{T(}Q).$ Since $\frac{\partial ^{2}\Psi (\theta ,Q)}{\partial Q\partial \theta }=1>0$, $\Psi (\theta ,Q)$ has increasing differences or is supermodular (see Topkis 1998 or Amir 2005). Therefore, the version of the single-crossing property called CS$^{+}$ in (Fudenberg and Tirole 1991, ch. 7.3.1, p. 259) is here satisfied. Then, there exists $\overline{T}( \cdot )$ such that $\left( Q^{e}( \cdot ),\overline{T}( \cdot )\right)$ is incentive-compatible for this associate problem. Notice that condition (13) where $\sum _{i=1}^{n}T_{i}(Q^{e}(\theta ))$ is replaced by $\overline{T}(Q^{e}(\theta ))$ is necessary in the associate problem as well as in the original one. From condition (13) for any $\theta ^{\prime } >\theta ,$ we have:

$$\begin{aligned} \overline{T}(Q(\theta ^{\prime }))-\overline{T}(Q^{e}(\theta )) =\int _{\theta }^{\theta ^{\prime }}(s-2Q(s))Q^{\prime }(s)\mathrm{d}s, \end{aligned}$$

from what we deduce that $Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2} \le \frac{\theta }{2}$ implies that any transfer function $\overline{T}$ which implements a non-decreasing sales function $Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2}$ in the associate problem must be non-decreasing in Q.

Consider now in the original problem the tariff functions $T_{i}(q_{i} )=\frac{1}{n}\overline{T}(q_{i})$, $i=1,2, \ldots ,n.$ Let us now show that they implement the non-decreasing sales and input functions $q_{i}^{e} (\theta )=Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2}\le \frac{\theta }{2}$, $i=1,2, \ldots ,n.$ Suppose on the contrary that there exist $q_{i}(\theta ^{\prime })=q(\theta ^{\prime })\le \frac{\theta ^{\prime }-h(\theta ^{\prime })}{2},i=1,2, \ldots ,n,$ which gives a strictly greater profit to the assembler, i.e.

$$\begin{aligned} (\theta -\widetilde{q})\widetilde{q}-\overline{T}(q(\theta ^{\prime })) >(\theta -Q^{e}(\theta ))Q^{e}(\theta )-\overline{T}(Q^{e}(\theta )), \end{aligned}$$

where $\widetilde{q}\in [0,q(\theta ^{\prime })]$.⁴⁶ Since $\overline{T}$ is non-decreasing, it follows that

$$\begin{aligned} (\theta -\widetilde{q})\widetilde{q}-\overline{T}(\widetilde{q}) >(\theta -Q^{e}(\theta ))Q^{e}(\theta )-\overline{T}(Q^{e}(\theta )), \end{aligned}$$

contradicting the fact that $\overline{T}$ implements $Q^{e}(\theta )$ in the associate problem.

Using now condition (13), where $\sum _{i=1}^{n}T_{i}(Q^{e}(\theta ))$ is replaced by $\overline{T}(Q^{e}(\theta )),$ together with condition (19), we obtain

$$\begin{aligned} \frac{n-1}{n}\overline{T}(Q^{e}(\theta ))= & {} \left[ \theta -h(\theta )-Q^{e} (\theta )\right] Q^{e}(\theta )\nonumber \\&-\int _{\underline{\theta }}^{\theta }(1-h^{\prime }(s))Q^{e}(s)\mathrm{d}s -\frac{1}{n}V(Q^{e}(\underline{\theta }),\underline{\theta }). \end{aligned}$$

(35)

Notice that the definition of the virtual profits implies that $\sum _{i=1} ^{n}\Pi _{i}^{s}\left( \underline{\theta }\right) =V(Q^{e}(\underline{\theta }),\underline{\theta }).$ Given that the tariff functions are identical for all, the $\Pi _{i}^{s} \left( \underline{\theta }\right)$ are identical as well $\forall i=1,2, \ldots ,n.$ It follows that (35) implies

$$\begin{aligned} \frac{n-1}{n}\overline{T}(Q^{e}(\theta ))= & {} \left[ \theta -h(\theta )-Q^{e} (\theta )\right] Q^{e}(\theta )\nonumber \\&-\int _{\underline{\theta }}^{\theta }(1-h^{\prime }(s))Q^{e}(s)\mathrm{d}s -\Pi _{i} ^{s}\left( \underline{\theta }\right) ,\ i=1,2, \ldots ,n, \end{aligned}$$

(36)

which is the necessary (first-order) condition(15) for each principal i. It remains to verify the global second order conditions for each principal i’s problem. We can apply the same proof strategy as in the agent’s case. Consider the associate problem for principal $i: \underset{Q}{\max }\Gamma _{i}(Q,\theta ) =\left( \theta -Q-h(\theta )\right) Q-\frac{n-1}{n}\overline{T}(Q).$ Since the single-crossing property ($\hbox {CS}^{+}$) is here obviously satisfied (i.e. $\frac{\partial ^{2}\Gamma _{i}(\theta ,Q)}{\partial Q\partial \theta }=1-h^{\prime }(\theta )>0$), not only the local second order conditions (35) are satisfied for the associate problem but also the global ones.

Consider now in the original problem the tariff functions $T_{j}(q_{j} )=\frac{1}{n}\overline{T}(q_{j})$, $j\ne i.$ We now show that $\sum _{j\ne i}\frac{1}{n}\overline{T}(q_{j})$ implements the non-decreasing sales and input functions $q_{i}^{e}(\theta )=Q^{e}(\theta )\le \frac{\theta -h(\theta )}{2}\le \frac{\theta }{2}.$ Suppose on the contrary that there exists $q_{i}(\theta ^{\prime })\le \frac{\theta ^{\prime }-h(\theta ^{\prime })}{2},$ which gives a strictly greater profit to supplier i and remembering that the function $\overline{T}$ is increasing, we must have

$$\begin{aligned} (\theta -h(\theta )-\widehat{q})\widehat{q}-\frac{n-1}{n}\overline{T} (\widehat{q})>(\theta -h(\theta )-Q^{e}(\theta ))Q^{e}(\theta )-\frac{n-1}{n}\overline{T}(Q^{e}(\theta )), \end{aligned}$$

where $\widehat{q}\in [0,q_{i}(\theta ^{\prime })]$.⁴⁷ But this contradicts the optimality of $Q^e(\theta )$ for supplier i in the corresponding associate problem. $\square$

Proof of Corollary 2

The proof is straightforward. Indeed differentiating (19) with respect to $\theta ,$ one obtains $V_{s}( \cdot )=V_{Q}Q^{e\prime }(\theta )+V_{s}( \cdot )$, implying $V_{Q}Q^{e\prime }(\theta )=0.$ Given that $V_{Q}=\theta -nh(\theta )-2Q^{e}(\theta ),$ and given $Q^{D}\left( \theta \right)$, then $V_{Q}Q^{e\prime }(\theta )=0$ implies

$$\begin{aligned} 2\left[ Q^{D}(\theta )-Q^{e}(\theta )\right] Q^{e\prime }(\theta )=0, \end{aligned}$$

yielding the results in the preceding Corollary. $\square$

1.1 Proof of Lemma 4

Given (17), $V(Q^{e}(\theta ),\theta )$ is obviously continuous at any $\theta$ where $Q^{e}(\theta )$ is continuous. So we only have to consider the values of $\theta$ at which $Q^{e}\left( \theta \right)$ is discontinuous. Let $\widetilde{\theta }$ be such a point. Since from Lemma 1, the equilibrium sales function is a.e. differentiable, points of discontinuity are isolated and it is right and left continuous with $\underset{\theta \downarrow \widetilde{\theta }}{\lim }Q^{e}(\theta )=Q^{+}(\widetilde{\theta })> \underset{\theta \uparrow \widetilde{\theta }}{\lim }Q^{e}(\theta )=Q^{-}(\widetilde{\theta }).$ From (19), $\underset{\theta \downarrow \widetilde{\theta }}{\lim }V(Q^{e}(\theta ),\theta )-V(Q^{e} (\underline{\theta }),\underline{\theta })=V(Q^{+} (\widetilde{\theta }),\widetilde{\theta } )-V(Q^{e}(\underline{\theta }), \underline{\theta })=\underset{\theta \uparrow \widetilde{\theta }}{\lim } V(Q^{e}(\theta ),\theta )-V(Q^{e} (\underline{\theta }),\underline{\theta }) =V(Q^{-}(\widetilde{\theta }),\widetilde{\theta }) -V(Q^{e}(\underline{\theta }),\underline{\theta }).$ It follows that $V(Q^{+}(\widetilde{\theta }),\widetilde{\theta })=V(Q^{-} (\widetilde{\theta }),\widetilde{\theta }).$ Notice in addition that, since $Q^{D}(\widetilde{\theta })=\arg \underset{Q}{\max }V(Q, \widetilde{\theta }),$ it must be that $Q^{-}(\widetilde{\theta })<Q^{D}(\widetilde{\theta })<Q^{+}(\widetilde{\theta })$. $\square$

1.2 Proof of Example 1

An equilibrium output function maximizing the virtual aggregate surplus function has already been shown to be given by $Q^{D}(\theta )$, where here $Q^{D}(\theta )= \frac{(n+1)\theta -n}{2}.$ The assembler’s and subcontractor j’s first-order conditions are respectively over $(\frac{n}{n+1} ,1]:(\theta -2Q\left( \theta \right) )=\sum _{i=1}^{n}T_{i}^{\prime } (Q^{e}(\theta ))$ and $2\theta -1-2Q\left( \theta \right) =\sum _{i=1,i\ne j}^{n}T_{i}^{\prime }(Q^{e}(\theta )).$ Subtracting the second from the first we obtain $1-\theta =T_{j}^{\prime }(Q^{e} (\theta )).$ Using (ii) we can express $\theta$ as a function of Q,  with

$$\begin{aligned} \theta =\frac{2Q+n}{n+1}, \end{aligned}$$

and substitute this value for $\theta .$ We obtain $T_{j}^{\prime } (Q)=\frac{1-2Q}{n+1}$ and then integrating with respect to Q, we obtain $T_{j}(Q)=K_{j}+\frac{Q-Q^{2}}{n+1}$, $\forall Q\in \left[ 0,\frac{1}{2}\right]$, where $K_{j}$ is a constant. From the assembler’s participation constraint and suppliers optimization behavior, $\sum _{j=1}^{n}K_{j}=0.$ It is easy to see that choosing $Q=0$ maximizes the assembler’s profit for $\theta \in \left[ 0,\frac{n}{n+1}\right] .$ It follows that $\sum _{j=1} ^{n}T_{j}(Q)=\frac{n(Q-Q^{2})}{n+1}$. $\square$

1.3 Proof of Remark 2

From equation (7) we obtain

$$\begin{aligned} \Pi ^{A}(\theta )&=\int _{\frac{n}{n+1}}^{\theta }Q^{e}(\theta )\mathrm{d}\theta =\frac{\left[ \theta -n(1-\theta )\right] ^{2}}{4(1+n)}\nonumber \\ \text {for all }\theta&\in \left[ \frac{n}{n+1},1\right] \text { and }\Pi ^{A}(\theta )=0\text { otherwise,} \end{aligned}$$

(37)

so that the ex ante expected profit of the assembler, $E\left[ \Pi ^{A}\right] ,$ is equal to

$$\begin{aligned} E\left[ \Pi ^{A}\right] =\int _{\frac{n}{n+1}}^{1} \frac{\left[ \theta -n(1-\theta )\right] ^{2}}{4(1+n)} \mathrm{d}\theta =\frac{1}{12(n+1)^{2}}. \end{aligned}$$

(38)

The profit of subcontractor i,  for all $\theta \in \left[ \frac{n}{n+1},1\right] ,$ is easily obtained from $T_{i}(Q)=\frac{Q-Q^{2} }{n+1},$ by setting $Q=\frac{(n+1)\theta -n}{2},$ implying:

$$\begin{aligned} \Pi _{i}^{S}(\theta )=\frac{\left[ 2-\theta +n(1-\theta )\right] \left[ \theta -n(1-\theta )\right] }{4(n+1)}, \end{aligned}$$

for all $\theta \in \left[ \frac{n}{n+1},1\right]$ and $\Pi _{i}^{S} (\theta )=0$ otherwise. The expected profit of subcontractor i,  denoted $E\left[ \Pi _{i}^{S}\right]$, is

$$\begin{aligned} E\left[ \Pi _{i}^{S}\right] =\int _{\frac{n}{n+1}}^{1}\frac{(2-\theta +n(1-\theta ))(\theta -n(1-\theta ))}{4(n+1)}\mathrm{d}\theta =\frac{1}{6(n+1)^{2}}, \end{aligned}$$

(39)

yielding the results in Remark 2. $\square$

1.4 Proof of Corollary 3

Let us write the condition (19) respectively at some $\theta \in (x_{i},x_{i+1}]$ and at $x_{i}:$

$$\begin{aligned} \int _{\underline{\theta }}^{\theta }V_{s}^{\prime }(Q(s),s)\mathrm{d}s =V(Q_{i}, \theta )-V(Q(\underline{\theta }),\underline{\theta }), \end{aligned}$$

(40)

and

$$\begin{aligned} \int _{\underline{\theta }}^{x_{i}}V_{s}^{\prime }(Q(s),s)\mathrm{d}s =V(Q_{i-1}, x_{i})-V(Q(\underline{\theta }),\underline{\theta }). \end{aligned}$$

(41)

In the equation above, we consider that $\left[ \underline{\theta } ,\overline{\theta }\right]$ is divided in $n+1$ intervals $[x_{j},x_{j+1} )$ such that $Q(\theta )=Q_{j}$, $\forall \theta \in (x_{j},x_{j+1}],$ with $Q_{j+1}>Q_{j}$, $x_{0}=\underline{\theta }$ and $x_{n+1}=\overline{\theta }.$ Subtracting (41) from (40) we obtain

$$\begin{aligned} \int _{x_{i}}^{\theta }V_{s}^{\prime }(Q_{i},s)\mathrm{d}s =V(Q_{i},\theta ) -V(Q_{i-1} ,x_{i}). \end{aligned}$$

The LHS equals $V(Q_{i},\theta )-V(Q_{i},x_{i})$ so that we conclude that $V(Q_{i-1},x_{i})=V(Q_{i},x_{i})$. $\square$

1.5 Proof of Remark 3

• (i) Let us first derive (23). Notice first that substituting in (15) $\sum T_{i}(Q\left( \theta \right) )$ for its value from (8), accounting for $\Pi ^{A} (\underline{\theta })=0,$ and rearranging we obtain an expression which, evaluated at $\theta =\underline{\theta }$, yields

  $$\begin{aligned} {\displaystyle \sum \limits _{i=1}^{i=n}} \Pi _{i}^{S}(\underline{\theta })=\Pi ^{S}(\underline{\theta }) =V(Q^{e} (\underline{\theta }),\underline{\theta }). \end{aligned}$$

  Let us now consider the expected aggregate suppliers’ profit $E[\Pi ^{S}].$ From equation (14) in the paper, and the above result, we obtain

  $$\begin{aligned} E[\Pi ^{S}]= & {} V(Q^{e}(\underline{\theta }),\underline{\theta }) +nE\left[ \int _{\underline{\theta }}^{\theta }(1-h^{\prime } (s))Q^{e}(s)\mathrm{d}s\right] \\= & {} V(Q^{e}(\underline{\theta }),\underline{\theta })+(n-1)E \left[ \int _{\underline{\theta }}^{\theta }Q^{e}(s)\mathrm{d}s\right] \\&+\,E\left[ \int _{\underline{\theta }}^{\theta }(1-nh^{\prime } (s))Q^{e}(s)\mathrm{d}s\right] . \end{aligned}$$

Using now equation (7) and condition (19 ), it turns out that

$$\begin{aligned} E[\Pi ^{S}]=E\left[ V(Q^{e}(\theta ),\theta \right] +(n-1)E\left[ \Pi ^{A}(\theta )\right] . \end{aligned}$$

(42)

Moreover, introducing in (42) $E\left[ \Pi ^{A}\right] =E[(\theta -Q^{e}(\theta ))Q^{e}(\theta )]-E[\Pi ^{S}]$ and using the definition of $V(Q(\theta ),\theta ),$ we obtain:

$$\begin{aligned} E[\Pi ^{S}]=E\left[ (\theta -h(\theta ) -Q^{e}(\theta ))Q^{e}(\theta )\right] . \end{aligned}$$

(43)

• (ii) Let us now derive (24).

From the condition (19), we can write

$$\begin{aligned} \left[ (\theta -h(\theta )-Q^{e}(\theta ))Q^{e}(\theta )\right]= & {} V(Q^{e}(\overline{\theta }),\overline{\theta }))\\&-\int _{\theta }^{\overline{\theta }}(1-nh^{\prime }(s)) Q^{e}(s)\mathrm{d}s+(n-1)h(\theta )Q^{e}(\theta ). \end{aligned}$$

Integrating both sides between $\underline{\theta }$ and $\overline{\theta },$ and then integrating the RHS by parts, we obtain (24). $\square$

1.6 Proof of Lemma 5

Let us denote by $Q_{1}\left( \theta \right)$ the first equilibrium output function and by $Q_{2}\left( \theta \right)$ the second equilibrium output function described in Lemma 5.

Given (43), the difference $E\left[ \Pi ^{S}(Q_{2}(\theta ),\theta )\right] -E\left[ \Pi ^{S}(Q_{1}(\theta ),\theta )\right]$ between the expected aggregate suppliers’ profits under equilibrium output functions $Q_{2}(\theta )$ and $Q_{1}(\theta )$ equals

$$\begin{aligned} \int _{x}^{\overline{\theta }}\left( \theta -h(\theta )-Q^{D} \left( \theta \right) \right) Q^{D}\left( \theta \right) f(\theta )\mathrm{d}\theta -\int _{x}^{\overline{\theta }}\left( \theta -h(\theta )-Q^{D} \left( x\right) \right) Q^{D}\left( x\right) f(\theta )\mathrm{d}\theta . \end{aligned}$$

(44)

Since $\frac{\theta -h(\theta )}{2}=\arg \underset{Q}{\max }\Pi ^{S} (Q,\theta )>Q^{D}(\theta )=\frac{\theta -nh(\theta )}{2} >Q^{D} \left( x\right)$, $\forall \theta \in (x,\overline{\theta }],$ the concavity of $\Pi ^{S}(Q,\theta )$ with respect to Q implies that $\Pi ^{S}(Q^{D}(\theta ),\theta )>\Pi ^{S} (Q^{D}(x),\theta )$, $\forall \theta \in (x,\overline{\theta }]$, so that (44) is $>0$. $\square$

1.7 Proof of Lemma 6

Let us consider the difference between the expected aggregate suppliers’ profit under the equilibrium output functions $Q_{C}(\theta )$ and $Q_{H}(\theta )$, which, given (24), is

$$\begin{aligned}&E\left[ \Pi ^{S}(Q_{C}(\theta ),\theta )\right] -E\left[ \Pi ^{S} (Q_{H}(\theta ),\theta )\right] \\&\quad = \int _{x_{0}}^{x_{1}}Q^{D}\left( \theta \right) g(\theta )\mathrm{d}\theta -\left[ \int _{x}^{x_{1}}Q^{D}(x_{1})g(\theta )\mathrm{d}\theta +\int _{x_{0}}^{x}Q^{D}(x_{0})g(\theta )\mathrm{d}\theta \right] \\&\quad = \int _{x_{0}}^{x_{1}}Q^{D}\left( \theta \right) g(\theta ) \mathrm{d}\theta -[Q^{D}(x_{1})(G(x_{1})-G(x))+Q^{D}(x_{0})(G(x)-G(x_{0}))], \end{aligned}$$

where $g(\theta )=(n-1)-n(1-h^{\prime }(\theta ))F(\theta )$ and $G(\theta )=\int _{\underline{\theta }}^{\theta }g(s)\mathrm{d}s.$

Now, integrating by parts, $\int _{x_{0}}^{x_{1}}Q^{D}\left( \theta \right) g(\theta )\mathrm{d}\theta =Q^{D}(x_{1})G(x_{1})-Q^{D}(x_{0})G(x_{0}) -\int _{x_{0} }^{x_{1}}Q^{D\prime }(\theta )G(\theta )\mathrm{d}\theta ,$ so that

$$\begin{aligned}&E\left[ \Pi ^{S}(Q_{C}(\theta ),\theta )\right] -E\left[ \Pi ^{S}(Q_{H} (\theta ),\theta )\right] \\&\quad =(Q^{D}(x_{1})-Q^{D}(x_{0}))G(x) -\int _{x_{0}}^{x_{1}}Q^{D\prime }(\theta )G(\theta )\mathrm{d}\theta \\&\quad =\int _{x_{0}}^{x_{1}}Q^{D\prime }(\theta )(G(x)-G(\theta ))\mathrm{d}\theta . \end{aligned}$$

Let now $z=\frac{\theta -nh(\theta )}{2}.$ From Assumption 1, this is a monotone increasing function so that there is an inverse function $\Theta (z).$ On the other hand, $\mathrm{d}\theta =\frac{2}{1-nh^{\prime } (\theta )}\mathrm{d}z.$ Remembering that $Q^{D\prime }(\theta )=\frac{1}{2} (1-nh^{\prime }(\theta ))$ a simple change of variables leads to

$$\begin{aligned} E\left[ \Pi ^{S}(Q_{C}(\theta ),\theta )\right] -E\left[ \Pi ^{S}(Q_{H}(\theta ),\theta )\right] =\int _{z_{0}}^{z_{1}}\left( G\left( \Theta \left( \frac{z_{0}+z_{1}}{2}\right) \right) -G(\Theta (z))\right) \mathrm{d}z, \end{aligned}$$

(45)

where $z_{i}=\frac{x_{i}-nh(x_{i})}{2}$, $i=0,1$ and $\Theta (\frac{z_{0} +z_{1}}{2})=x$⁴⁸.

Now, the next step is to prove the concavity of $G(\Theta (z))$ with respect to z. It turns out that:

$$\begin{aligned}&\frac{d^{2}G(\Theta (z))}{\mathrm{d}z^{2}}\\&\quad =\frac{2n}{(1-nh^{\prime }(\theta ))} \left[ -(1-nh^{\prime }(\theta ))(1-h^{\prime }(\theta ))f(\theta ) +h\text {''}(\theta )(n-1)(1-F(\theta ))\right] \\&\quad =\frac{2nf(\theta )}{(1-nh^{\prime }(\theta ))} \left[ -(1-nh^{\prime }(\theta ))(1-h^{\prime }(\theta )) +h\text {''}(\theta )(n-1)h(\theta )\right] . \end{aligned}$$

From Assumptions 1 and 3, this is negative and accordingly $G(\Theta (z))$ is concave with respect to z.

This is enough to show that the RHS of (45) is positive. From the concavity of $G(\Theta (z))$ with respect to z,

$$\begin{aligned} \int _{z_{0}}^{\frac{z_{0}+z_{1}}{2}}\left( G\left( \Theta \left( \frac{z_{0} +z_{1}}{2}\right) \right) -G(\Theta (z))\right) dz \ge \frac{dG\left( \Theta \left( \frac{z_{0}+z_{1}}{2}\right) \right) }{dz} \frac{1}{8}(z_{1}-z_{0})^{2}, \end{aligned}$$

and

$$\begin{aligned} \int _{\frac{z_{0}+z_{1}}{2}}^{z_{1}}\left( G\left( \Theta \left( \frac{z_{0} +z_{1}}{2}\right) \right) -G(\Theta (z))\right) dz \ge -\frac{dG\left( \Theta \left( \frac{z_{0}+z_{1}}{2}\right) \right) }{dz} \frac{1}{8}(z_{1}-z_{0})^{2}, \end{aligned}$$

so that $\int _{z_{0}}^{z_{1}}(G(\Theta (\frac{z_{0}+z_{1}}{2}))-G(\Theta (z)))dz\ge 0$. $\square$

1.8 Proof of Proposition 2

Given (23) and (29), the suppliers’ aggregate expected profits may be written along a semi-regular equilibrium as

$$\begin{aligned}&\int _{\underline{\theta }}^{\theta ^{SR}}(\theta -h(\theta ) -Q^{D}(\theta ^{SR}))Q^{D}(\theta ^{SR})f(\theta )\mathrm{d}\theta \\&\quad +\int _{\theta ^{SR}}^{\overline{\theta }}(\theta -h(\theta ) -Q^{D}(\theta ))Q^{D}(\theta )f(\theta )\mathrm{d}\theta . \end{aligned}$$

Their derivative with respect to $\theta ^{SR}$ is easily obtained as:

$$\begin{aligned} \frac{1-nh^{\prime }(\theta ^{SR})}{2} \int _{\underline{\theta }}^{\theta ^{SR}} (\theta -h(\theta )-2Q^{D}(\theta ^{SR}))f(\theta )\mathrm{d}\theta . \end{aligned}$$

Remember the constraint $Q(\theta )\le \frac{\theta -h(\theta )}{2}$, $\forall \theta \in \left[ \underline{\theta },\overline{\theta }\right]$.

For any $\theta ^{SR}$ such that the previous constraint is satisfied, i.e. $Q^{D}(\theta ^{SR})=\frac{\theta ^{SR} -nh(\theta ^{SR})}{2}\le \frac{\underline{\theta } -h(\underline{\theta })}{2},$ the above derivative is strictly positive. Letting now $\theta ^{c}$ be such that $\frac{\theta ^{c}-nh(\theta ^{c})}{2}=\frac{\underline{\theta }-h(\underline{\theta })}{2}$⁴⁹, the solution of our problem is $\theta ^{SR}=\theta ^c$ whenever the nonnegativity of sales constraint is satisfied, i.e. $\frac{\theta ^c-nh(\theta ^c)}{2}>0.$ Otherwise it has to be such that $\theta ^{SR}=\Theta (0),$ where $\Theta (0)-nh(\Theta (0))=0:$ the optimal sales level is zero for all $\theta \in \left[ \underline{\theta },\Theta (0)\right]$.

The necessity part of the Proposition is straightforward. Suppose that (27) does not hold over some interval $\left[ \theta _{0},\theta _{1}\right] .$ Then the equilibrium sales function which is identical to the semi-regular (or regular) one defined in Proposition 2 except that $Q(\theta )=Q^{D}(\theta _{0})$, $\theta \in \left[ \theta _{0},x\right] ,$ and $Q(\theta )=Q^{D} (\theta _{1})$, $\theta \in \left[ x,\theta _{1}\right] ,$ where $x-nh(x)=\frac{\theta _{0}-nh(\theta _{0})+\theta _{1}-nh(\theta _{1})}{2}$, strongly Pareto-dominates the original one.⁵⁰$\square$