Input price, bargaining power, and a multi-input-multi-product firm

Abstract

This paper investigates conditions under which the downstream firm can benefit from cost disadvantages arose from upstream sector. We consider a vertically related industry consisting of two upstream firms (a specific input supplier and a common input supplier) and one multi-product downstream firm. The downstream firm produces two vertically differentiated products and sells either in two separate markets or in one market. Findings identify a situation under the view that both downstream firms’ profits and consumer surplus are increasing with the input production cost or the bargaining power of upstream firms, which depends on whether the common input supplier has market power. Specifically, in the one market case, we shed light on the importance of the marginal product of the common input of the high-quality product for both the downstream firm’s profit and consumer surplus improving. Moreover, we check the robustness of our findings for extension by considering horizontal product differentiation, price competition, using the specific input for two products, and bilateral bargaining. Our main findings still hold.

1 Introduction

Multi-input-multi-product firms are popular in many business sectors, such as the electronics, chemical, pharmaceutical, and bicycle industries. As a prime example of a multi-input-multi-product firm, Giant is the largest global bicycle manufacturer, producing both high-end and low-end bicycles. For both quality levels of bicycles, the bicycle derailleur as the key component is almost always provided by Shimano, which is the largest bicycle component supplier in the world.¹ However, Giant needs to source additional components for its higher-priced bicycles, such as high-end carbon cranks and shock absorbers.² Empirical studies provide much supporting evidence for these types of firms. Bernard et al. (2010) spotlight the importance of multi-product firms by looking at U.S. manufacturing firms, while Manova and Yu (2017) conclude that multi-product firms allocate activity across products, which is in line with a product hierarchy based on quality.

Various studies in the theoretical literature explore the topic of multi-product firms, such as Ottaviano and Thisse (2011) and Arya and Mittendorf (2010), who focus on strategic interactions among products.³ Our work closely relates to Kopel et al. (2016), Kopel et al. (2017), Kitamura et al. (2018) and Laussel and Resende (2019)⁴; especially Kopel et al. (2016) who analyze a sourcing strategy of a multi-input-multi-product firm that produces two independent final products, showing that such a firm might manufacture in-house even if the marginal production cost exceeds the per-unit input price. In other words, a downstream firm’s sourcing strategy for a specific input can deviate from its cost comparison.

In the present paper, we study conditions under which the downstream firm can benefit from cost disadvantages arising from the upstream sector. In vertically related markets, a common belief is that upstream firms act as the sole input suppliers toward the downstream firms, and they exploit their monopoly power to raise input prices, which unambiguously reduce a downstream firm’s profit and consumer surplus. However, we show that there are situations that do no hold for the widely accepted view that a downstream firm’s profits and consumer surplus are decreasing with cost disadvantage arising from the upstream sector.

To elaborate further, we consider a vertically related industry consisting of two upstream firms (a specific input supplier and a common input supplier) and one multi-product downstream firm selling two different qualities products either in two separate markets or in one market. Producing high- and low-quality products requires β units and one unit of common inputs sold by a monopolistic supplier respectively. In addition, a high-quality product requires a specific input that is complementary to the common input, which also sold by a monopolist supplier. We assume that the specific input supplier-downstream firm pair bargains over a linear wholesale price with bargaining power. In doing so, we show that the downstream firm may benefit from an increase in the cost of the specific input or bargaining power of the specific upstream firm when the two products sell either in two separate markets or in one market.

The intuition behind the result runs as follows. An increase in a specific input price decreases the output of the high-quality products. We name it as the “input production cost effect”, which is unprofitable to the downstream firm. On the other hand, when the common input supplier has market power, the lower output of the high-quality product leads to a lower derived demand and a lower price of the common inputs. A lower common input price is profitable to the high-quality product, which we name as the “complementary effect”. A lower common input price is also profitable to the low-quality product, which we name as the “multi-product effect”. When two products compete in the same market, an increase in a specific input’s price alleviates the cannibalization. Hence, the multi-product downstream firm reallocates the outputs of two products, which may raise the price of the common input. Under this environment, the marginal product of the common input of the high-quality product is crucial, because when the marginal product of the common input is large, the downstream firm benefits from cost disadvantages of the upstream sector.

Even though our study is close to Kopel et al. (2016), we still differ from them in various ways. First, we emphasize whether the downstream firm can benefit from the cost disadvantage of the specific input supplier, which depends on whether the common input supplier has market power. We show when the common input market structure is perfect competition that an increase in specific input price is detrimental to the downstream firm’s profit. In addition, we provide policy implication, showing that the consumer surplus improving along with a higher specific input cost may be attainable.

Second, in the one market case, we provide new insights that an increase in specific input price alleviates cannibalization effect leading the multi-product firm to reallocate the outputs of two products. This affects the equilibrium price of specific input through the marginal product of the common input of the high-quality product, thereby obtaining the downstream firm’s profit and improving consumer surplus, which are not discussed in Kopel et al. (2016). We also check the robustness of our findings for extension by considering horizontal product differentiation, price competition, and using the specific input for two products. Moreover, we further consider bilateral bargaining in which the downstream firm simultaneously and independently bargains with the two suppliers for generalization. We demonstrate that our main findings still hold.

This study also relates to past works in the literature like Kimmel (1992), Zhao (2001) and Wang and Zhao (2010), who study the effects of cost reduction on a firm’s profitability. However, they consider the impact of cost reduction in a Cournot oligopoly model and ignore the importance of a multi-input-multi-product firm. In this present research, we apply the Nash bargaining approach to discuss the impacts of bargaining power on a downstream firm’s profit, such as done by Chen (2003) and Yoshida (2018). However, they do not apply to the multi-input-multi-product firm.

The remainder of this paper runs as follows. Section 2 introduces the model and examines the equilibrium under two separate markets. Section 3 analyzes equilibrium under one market. Section 4 extends the model settings to check if the results are still robust. Section 5 concludes the paper.

2 Two separate markets

This study considers a multi-product firm that produces two differentiated-quality final products, designated 1 and 2. Product 1’s quality $q_{1} = 1$, and product 2’s quality $q_{2} = q$, where q < 1. Following the example of Giant’s high-end and low-end bicycles, we assume that producing one unit of the high-quality final product 1 requires one unit of a specific input, A, and β units of a common input, B, where β denotes the marginal product of the common input. Producing one unit of low-quality final product 2 requires just one unit of the common input. The firm purchases the inputs from two independent suppliers.

Producing input A bears a marginal cost c, while the marginal cost for input B is 0.⁵ The per-unit price of input A (B) is w_A (w_B), where w_A is determined by Nash bargaining between the multi-product firm and the upstream firm A. Assume that $\phi \left( {1 - \phi } \right)$ represents the bargaining power of upstream firm A (downstream firm), where $\phi \in \left[ {0, 1} \right]$. For simplicity, we further assume that a monopolistic supplier determines the input price of common input B, and the supplier has full bargaining power.⁶ Figure 1 summarizes the organizational structure in the two separate markets.

Fig. 1

Organizational structure in the two separate markets

In this section, we apply a vertically differentiated product model to the case of two separate markets, 1 and 2. A consumer purchases at most either one unit of the product or none. Hence, the indirect utility of consumer θ in each market is respectively expressed as $U_{i} = \theta q_{i} - p_{i}$, $i = 1, 2$. Accordingly, we present the index of the marginal consumer in each market, who has the same utilities from purchasing the product and not purchasing it, respectively by $\theta_{1} = \frac{{p_{1} }}{{q_{1} }}$ and $\theta_{2} = \frac{{p_{2} }}{{q_{2} }}$, where $q_{1} = 1$ and $q_{2} = q$. For simplicity, we assume that consumers in each market are uniformly distributed over zero to one with a density of one. Therefore, we derive the inverse demand functions in market 1 and market 2 as $p_{1} = \left( {1 - x_{1} } \right)$ and $p_{2} = q\left( {1 - x_{2} } \right)$, respectively, where $x_{1}$ $\left( {p_{1} } \right)$ and $x_{2}$ $\left( {p_{2} } \right)$ are the outputs (prices) of the two markets.⁷

The game structure under the two separate markets is specified as follows. In the first stage, the upstream firm A bargains over its input price,${ }w_{A}$, with the downstream firm, and the upstream firm B determines $w_{B}$ simultaneously. In the second stage, given the input prices, the downstream multi-product firm determines its outputs. We derive the sub-game perfect equilibrium by backward induction.

In the second stage, the multi-product firm determines its outputs in the two separate markets. The profit function of the multi-product firm is:

$$\pi^{D} \equiv \pi_{1}^{D} + \pi_{2}^{D} = \left( {p_{1} - w_{A} - \beta w_{B} } \right)x_{1} + \left( {p_{2} - w_{B} } \right)x_{2} .$$

(1)

The first-order conditions of (1) lead to:

$$\frac{{\partial \pi^{D} }}{{\partial x_{1} }} = \left( {1 - x_{1} - w_{A} - \beta w_{B} } \right) - x_{1} = 0,$$

(2a)

$$\frac{{\partial \pi^{D} }}{{\partial x_{2} }} = \left[ {q\left( {1 - x_{2} } \right) - w_{B} } \right] - qx_{2} = 0.$$

(2b)

The equilibrium output levels are:

$$x_{1} = \frac{{1 - w_{A} - \beta w_{B} }}{2},$$

(3a)

$$x_{2} = \frac{{q - w_{B} }}{2q}.$$

(3b)

From the above, it is clear to see that $\frac{{\partial x_{1} }}{{\partial w_{A} }} = \frac{ - 1}{2} < 0$, $\frac{{\partial x_{1} }}{{\partial w_{{\varvec{B}}} }} = \frac{ - \beta }{2} < 0$, and $\frac{{\partial x_{2} }}{{\partial w_{B} }} = \frac{ - 1}{{2q}} < 0$. In other words, an increase in the input prices decreases the outputs.

In the first stage, the upstream firm A bargains over its input price, $w_{A}$, with the downstream firm. Hence, the generalized Nash bargaining product is⁸:

$$U_{A} = \left( {\pi^{A} - 0} \right)^{\phi } \left( {\pi^{D} - \pi_{2}^{D} } \right)^{1 - \phi } ,$$

(4)

where $\pi^{A} \equiv \left( {w_{A} - c} \right)x_{1}$, and ${ }\pi_{2}^{D} \equiv \left( {p_{2} - w_{B} } \right)x_{2}$. By differentiating (4) with respect to $w_{A}$ and letting it equal zero, we thus obtain:

$$\phi \left( {1 - 2w_{A} - \beta w_{B} + c} \right) - 2\left( {1 - \phi } \right)\left( {w_{A} - {\text{c}}} \right) = 0.$$

(5)

From (5), it is clear that the wholesale price of input A equals the marginal cost of supplier A when $\phi = 0$—that is, $w_{A}^{*} = c$. On the other hand, supplier A determines the monopoly wholesale price on the input market A when $\phi = 1$.

Supplier B’s objective function is:

$$\pi^{B} = \beta w_{B} x_{1} + w_{B} x_{2} .$$

(6)

By differentiating (6) with respect to $w_{B}$, we can derive the first-order condition for profit maximization as follows:

$$\begin{aligned} \frac{{\partial \pi^{B} }}{{\partial w_{B} }} & = \left( {\frac{{\partial \pi^{B} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B} }}} \right) + \left( {\frac{{\partial \pi^{B} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B} }}} \right) + \frac{{\partial \pi^{B} }}{{\partial w_{B} }} \\ & = \frac{{ - 2w_{B} \left( {1 + \beta^{2} q} \right) + q\left( {1 + \beta } \right) - \beta qw_{A} }}{2q} = 0. \\ \end{aligned}$$

(7)

Using (5) and (7), the comparative static effects are as follows:

$$\frac{{\partial w_{A}^{*} }}{\partial c} = \frac{{2\left( {1 + q\beta^{2} } \right)\left( {2 - \phi } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} > 0,$$

(8a)

$$\frac{{\partial w_{B}^{*} }}{\partial c} = \frac{{ - q\beta \left( {2 - \phi } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} < 0.$$

(8b)

From the above, we find that the two input prices are strategic substitutes. We establish these results as the following lemma.

Lemma 1

When products are sold to separate markets, an increase in the specific input production cost c raises the equilibrium price of the specific input, but lowers the equilibrium price of the common input for any $\phi$ and $\beta$.

The intuition behind the above lemma is quite straightforward. An increase in supplier A’s marginal cost increases input A’s equilibrium price. However, it lowers input B’s price for any $\phi$ and $\beta$, because these two input prices are strategic substitutes.

We further analyze the impact of the input production cost to the downstream firm’s profit. From (3a) and (3b), we derive that $x_{1}$ is a function of $w_{A}$ and $w_{B}$, and $x_{2}$ is a function of $w_{B}$. By substituting equilibrium outputs into (1), we can re-write the objective function of the downstream firm as: $\pi^{D} \left( {x_{1} \left( {w_{A} ,w_{B} } \right),x_{2} \left( {w_{B} } \right),w_{A} ,w_{B} } \right)$. By differentiating $\pi^{D}$ with respect to c and using the envelope theorem ($\partial \pi^{D} /\partial x_{1}$) = ($\partial \pi^{D} /\partial x_{2}$) = 0, we derive:

$$\begin{aligned} \frac{{d\pi^{D} }}{dc} & = \left( {\frac{{\partial \pi^{D} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A} }} + \frac{{\partial \pi^{D} }}{{\partial w_{A} }}} \right)\frac{{\partial w_{A}^{*} }}{\partial c} + \left( {\frac{{\partial \pi^{D} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B} }} + \frac{{\partial \pi^{D} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B} }} + \frac{{\partial \pi^{D} }}{{\partial w_{B} }}} \right)\frac{{\partial w_{B}^{*} }}{\partial c} \\ & = \left( {\underbrace {{\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A} }}\frac{{\partial w_{A}^{*} }}{\partial c}}}_{{{\text{input production cost effect}}\left( - \right)}} + \underbrace {{\frac{{\partial \pi_{1}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c}}}_{{{\text{complementary effect}}\left( + \right)}}} \right) + \underbrace {{\frac{{\partial \pi_{2}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c}}}_{{{\text{multi}} - {\text{product effect}}\left( + \right)}}. \\ \end{aligned}$$

(9)

The first term is denoted as the input production cost effect, which is $\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A} }}\frac{{\partial w_{A}^{*} }}{\partial c} = \left( { - x_{1} } \right)\frac{{2\left( {1 + q\beta^{2} } \right)\left( {2 - \phi } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} < 0$. It implies that an increase in the marginal cost of a specific input raises the production cost, thus leading to lower output and profit from product 1. The second term is denoted as a complementary effect due to requiring multiple inputs for manufacturing product 1, which is $\frac{{\partial \pi_{1}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c} = \left( {\beta x_{1} } \right)\frac{{q{\upbeta }\left( {2 - \phi } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} > 0$. It implies that an increase in the marginal cost of a specific input lowers the derived demand of the common input, which lowers the input price and benefits the profits from product 1. By summarizing these two effects, we realize the impact of the specific input production cost to the profit from product 1, which is $\left( {\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A} }}\frac{{\partial w_{A}^{*} }}{\partial c} + \frac{{\partial \pi_{1}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c}} \right) = - x_{1} \frac{{\left( {2 - \phi } \right)\left( {2 + q\beta^{2} } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} < 0$. It shows that the benefit from a lower common input price is not enough to compensate for the reduction of product 1’s profit due to an increase in the input production cost of a specific input. The third term is $\frac{{\partial \pi_{2}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c} = \left( {x_{2} } \right)\frac{{q{\upbeta }\left( {2 - \phi } \right)}}{{q\beta^{2} \left( {4 - \phi } \right) + 4}} > 0$. The lower input price of a common input is also favorable to make product 2, which is denoted as a positive multi-product effect. All these three effects determine how the input production cost influences the downstream firm’s profit.

It is worth noting when the specific input production cost is large enough—that is, $\overline{c} < c \le c_{1}$—that the positive effect from reducing input B’s price is significant and dominates the negative effect from increasing input A’s price. As a result, the higher the specific input production cost is, the higher is the downstream firm’s profit for any $\phi$ and $\beta$. Kopel et al. (2016) also find this result when $\beta = 1$. In other words, their result is a special case of our model and also relates to Kitamura et al. (2018), who only consider a single final product composed of two complementary inputs. Under their setting, the multi-product effect vanishes. Thus, they demonstrate that an increase in the input production cost leads to lower profit of the downstream firm. However, this is not true for a multi-product downstream firm due to an extra positive multi-product effect.

We further find that $\overline{c}$ decreases with $q$ and $\phi$. An increase in product 2’s quality implies a larger market share of product 2. Therefore, the multi-product effect is intensified by the expansion of the market size of product 2, which is easier to compensate for the reduction of product 1’s profit. Furthermore, since the bargaining power of the specific input supplier increases, the price of the specific input increases substantially. Therefore, the derived demand for the common input falls significantly, leading the input price to drastically drop. Therefore, the multi-product firm’s profit is more likely to increase with the specific input supplier’s cost when $\phi$ is higher.⁹

We now analyze the impacts of the bargaining power between supplier A and the downstream firm to the profit of the multi-product firm. It is commonly believed that a supplier with higher bargaining power is harmful to the downstream firm since the higher bargaining power increases the input price. However, this is not true in this paper. From comparative static effects, we derive¹⁰:

$$\frac{{\partial w_{A}^{*} }}{\partial \phi } = \frac{{4\left( {1 + q\beta^{2} } \right)\left[ {\left( {1 - c} \right)\left( {q\beta^{2} + 2} \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }} > 0,$$

(10a)

$$\frac{{\partial w_{B}^{*} }}{\partial \phi } = \frac{{ - 2{\upbeta }q\left[ {\left( {1 - c} \right)\left( {q\beta^{2} + 2} \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }} < 0.$$

(10b)

From the above, we find that the price of input A increases when the price of input B decreases with the bargaining power. Making use of the above results, we further differentiate $\pi^{D}$ with respect to $\phi$¹¹:

$$\frac{{d\pi^{D} }}{d\phi } = \left( {\underbrace {{\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A} }}\frac{{\partial w_{A}^{*} }}{\partial \phi }}}_{\left( - \right)} + \underbrace {{\frac{{\partial \pi_{1}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial \phi }}}_{\left( + \right)}} \right) + \underbrace {{\frac{{\partial \pi_{2}^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial \phi }}}_{\left( + \right)}.$$

(11)

From (11), we see there are still three effects to determine the impacts of input production cost on the downstream firm’s profit, which is similar to (9). It shows that the downstream firm can benefit from a higher bargaining power of the specific input supplier for any $\beta$ as long as the marginal cost of a specific input is high enough, because the positive multi-product effect increases with the marginal cost of specific input.¹² We thus obtain the following proposition.

Proposition 1

When the products are sold to the separate markets, an increase in the bargaining power of the specific upstream firm may raise the downstream firm’s profit if the production cost and the bargaining power of a specific input supplier are large enough—that is, $c_{\phi } < c \le c_{1} {\text{and}} \overline{\phi } < \phi \le 1$ for any $\beta$.

This is of great interest, because it goes against the conventional wisdom that the high bargaining power of the upstream firm is harmful to the downstream firm. We show that this is not true for a multi-input-multi-product firm. We find that ${ }\frac{{\partial c_{\phi } }}{\partial q} = \frac{ - 16\beta }{{\left( {q\beta^{2} + 4} \right)^{2} }} < 0$. It implies that Proposition 1 is more likely to be supported when product 2’s quality increases. The intuition is that the market size of product 2 expands when product 2’s quality increases, which strengthens the positive multi-product effect. Therefore, as product 2’s quality increases, an increase in the bargaining power of the specific input supplier enhances the possibility that the downstream firm’s profit rises.

This result stands in line with the finding in Yoshida (2018), who assumes a vertically related industry consisting of one upstream and two downstream firms with different marginal costs. That study shows that the inefficient downstream firm may benefit from an increase in the bargaining power of the upstream firm. However, we consider a vertically related industry composed of two upstream firms with complementary inputs and one downstream firm in this paper. The model setting and intuition in Yoshida (2018) are quite different from this paper.

The above result also relates to the finding by Kopel et al. (2016), but we provide a more general analysis. We point out that as long as increasing a specific input price decreases the common input price, it is possible to raise the downstream firm’s profit, providing key insights for the vital influence of the market power of the common input supplier on the downstream firm’s profit. On the contrary, if there is perfect competition in the common input market, then a higher specific input price is detrimental to the downstream firm’s profit, in which the complementary effect and multi-product effect vanish.

We now extend the analysis to consumer surplus and provide the industry policy implications. The consumer surplus from two separate markets are $CS_{1} = \mathop \smallint \nolimits_{{\theta_{1} }}^{1} \left( {\theta - p_{1} } \right)d\theta = \frac{{x_{1}^{2} }}{2}$ and $CS_{2} = \mathop \smallint \nolimits_{{\theta_{2} }}^{1} \left( {\theta q - p_{2} } \right)d\theta = \frac{{qx_{2}^{2} }}{2}$, respectively. Therefore, it shows that $CS_{1} = CS_{1} \left( {x_{1} \left( {w_{A} \left( c \right),w_{B} \left( c \right)} \right)} \right)$ and $CS_{2} = CS_{2} \left( {x_{2} \left( {w_{B} \left( c \right)} \right)} \right)$. The effect of a raising input production cost on the consumer surplus is:

$$\frac{{dCS_{1} }}{dc} = \underbrace {{\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A} }}\frac{{\partial w_{A} }}{\partial c}}}_{( - )} + \underbrace {{\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B} }}\frac{{\partial w_{B} }}{\partial c}}}_{\left( + \right)} = \frac{{ - x_{1} \left( {2 - \phi } \right)\left( {2 + q\beta^{2} } \right)}}{{2\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]}} < 0,$$

(12a)

$$\frac{{dCS_{2} }}{dc} = \underbrace {{\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B} }}\frac{{\partial w_{B} }}{\partial c}}}_{( + )} = \frac{{x_{2} q\beta \left( {2 - \phi } \right)}}{{2\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]}} > 0.$$

(12b)

It is interesting to note that $\frac{{d\left( {CS_{1} + CS_{2} } \right)}}{dc} = \frac{{\left( {2 - \phi } \right)}}{{2\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]}}\left[ { - x_{1} \left( {2 + q\beta^{2} } \right) + x_{2} q\beta } \right]$, which is positive when the input production cost is large enough.¹³ When the input production cost is large enough, the positive effect from reducing input B’s price on consumer surplus of product 2 is significant, which dominates the negative effect from increasing input A’s cost on consumer surplus of product 1. Therefore, an increase in input production cost benefits the consumer surplus when the input production cost is large. From (9), we already show that the higher the input production cost is, the higher is the downstream firm’s profit. Therefore, it shows that an increase in input production cost benefits the consumer surplus and downstream firm’s profits when the input production cost is large. If we further assume the upstream firms are all foreign firms, then an increase in input production cost may enhance domestic social welfare. This result bears policy implication for both emerging and developing countries where foreign suppliers supply inputs. However, if the upstream firms are all domestic firms, then an increase in input production cost lowers the social welfare due to less profit from upstream market.

There is a similar analysis for an increase in bargaining power on consumer surplus, which is¹⁴:

$$\frac{{dCS_{1} }}{d\phi } = \underbrace {{\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A} }}\frac{{\partial w_{A} }}{\partial \phi }}}_{\left( - \right)} + \underbrace {{\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B} }}\frac{{\partial w_{B} }}{\partial \phi }}}_{( + )} = \frac{{ - x_{1} \left( {2 + q\beta^{2} } \right)\left[ {\left( {1 - c} \right)\left( {2 + q\beta^{2} } \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }} < 0,$$

(13a)

$$\frac{{dCS_{2} }}{d\phi } = \underbrace {{\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B} }}\frac{{\partial w_{B} }}{\partial \phi }}}_{\left( + \right)} = \frac{{x_{2} q\beta \left[ {\left( {1 - c} \right)\left( {2 + q\beta^{2} } \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }} > 0.$$

(13b)

From (13a) and (13b), we see there are two effects to determine the impacts of bargaining power on the consumer surplus. Here, $\frac{{d\left( {CS_{1} + CS_{2} } \right)}}{d\phi } = \frac{{\left[ {\left( {1 - c} \right)\left( {2 + q\beta^{2} } \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }}\left[ { - x_{1} \left( {2 + q\beta^{2} } \right) + x_{2} q\beta } \right]$, which is positive when the input production cost is large enough.¹⁵ The intuition behind the result is similar to that of the impacts of input production cost on the consumer surplus. We thus obtain the following proposition.

Proposition 2

When the products are sold to the separate markets, as long as the input production cost is high enough, an increase in the input production cost or the bargaining power of the specific upstream firm raises the consumer surplus.

The result interestingly shows that as long as the input production cost is high enough, the consumer surplus and downstream firm’s profit both improve as the input production cost or the bargaining power of the specific upstream firm increases. This result also relates to the strands of literature regarding cost asymmetric and profit. For example, Zhao (2001) investigates the effects of cost reduction on total industry profit and consumer surplus without considering the upstream market. That paper shows that an increase in an inefficient firm’s marginal cost increases the total industry profit while reducing consumer surplus. In our model, the multi-input-multi-product firm plays a key role, because a higher input production cost or bargaining power of a specific upstream firm shifts the demand of product 1 inward, decreasing the common input price. When the gain from a lower common input price dominates the loss from a higher specific input price, the consumer surplus and the downstream firm’s profit both improve.

In the next section we explore the model to the one market case and highlight the importance of the marginal product of common input if we further introduce competition between two products.

3 One market

We have so far assumed that there are two separate markets and the two products are independent. However, in reality these two products might compete in the same market. In this section we employ a common market to analyze the effects of cost disadvantages on the profit of the downstream firm and consumer surplus. The indirect utilities of consumer θ in this market are expressed as $U_{i} = \theta q_{i} - p_{i}$, $i = 1,2$. Accordingly, the index of this market’s marginal consumer who has the same utilities from purchasing product 1 (product 2) and product 2 (none) is respectively given by $\theta_{1} = \frac{{p_{1} - p_{2} }}{1 - q}$ and $\theta_{2} = \frac{{p_{2} }}{q}$. Therefore, we derive the inverse demand functions of product 1 and product 2 as $p_{1} = \left( {1 - x_{1} } \right) - qx_{2}$ and $p_{2} = q\left( {1 - x_{1} - x_{2} } \right)$.

The game structure in the one market model is the same as before. In the final stage, the multi-product firm determines its outputs in the market. The profit function of the multi-product firm is $\pi^{D} \equiv \pi_{1}^{D} + \pi_{2}^{D} = \left( {p_{1} - w_{A} - {\upbeta }w_{B} } \right)x_{1} + \left( {p_{2} - w_{B} } \right)x_{2}$, where $w_{i}$ denotes the input price for supplier i (i = A, B) when two products compete in the one market:

The first-order conditions are:

$$\frac{{\partial \pi^{D} }}{{\partial x_{1} }} = 1 - 2x_{1} - 2qx_{2} - w_{A} - \beta w_{B} = 0,$$

(14a)

$$\frac{{\partial \pi^{D} }}{{\partial x_{2} }} = q - 2qx_{1} - 2qx_{2} - w_{B} = 0.$$

(14b)

The equilibrium output levels are $x_{1} = \frac{{1 - q - w_{A} - w_{B} \left( {\beta - 1} \right)}}{{2\left( {1 - q} \right)}}$ and $x_{2} = \frac{{qw_{A} + w_{B} \left( {q\beta - 1} \right)}}{{2q\left( {1 - q} \right)}}$. From this expression, it is clear that the outputs of products 1 and 2 are a function of $w_{A}$ and $w_{B}$, which are different from those under two separate markets.

In the first stage, the upstream firm A bargains over its input price, $w_{A}$, with the downstream firm. At the same time, $w_{B}$ is determined by upstream firm B. From the above, the generalized Nash bargaining product goes as follows: $U_{A} = \left( {\pi^{A} - 0} \right)^{\phi } \left( {\pi^{D} - \pi_{2}^{M} } \right)^{1 - \phi }$, where $\pi_{2}^{M}$ is the outside option for the downstream firm when the bargain fails as product 2 is a monopolist. We write the first-order condition as:

$$\phi \left( {x_{1} + qx_{2} } \right)\left[ {\left( {w_{A} - c} \right) - 2\left( {1 - q} \right)x_{1} } \right] + \left( {1 - \phi } \right)\left( {w_{A} - c} \right)[q(x_{2} + qx_{1} ) + 2\left( {1 - q} \right) x_{1} ] = 0.$$

(15a)

Using (15a), we re-write the first-order condition of input A as a linear combination of bargaining power, $\phi$, which goes as follows:

$$w_{A} \left( {w_{B} } \right) = \left( {1 - \phi } \right)w_{A}^{P} \left( c \right) + \phi w_{A}^{M} \left( {w_{B} } \right),$$

(15b)

where $w_{A}^{P}$ represents the price of input A when the market of input A is perfect competition—that is, $\phi = 0$. Moreover, $w_{A}^{M}$ represents that the market of input A is a monopoly—that is, $\phi = 1$.

Supplier B’s objective function and the first-order condition are the same as those in (6) and (7). By substituting the equilibrium derived in the second stage into (7), we find the first-order condition for the profit maximization of supplier B as:

$$\frac{{\partial {\uppi }^{B} }}{{\partial w_{B} }} = w_{B} \left( { - \beta^{2} q + 2\beta q - 1} \right) + 2q\left( {1 - q} \right)\left( {\beta x_{1} + x_{2} } \right) = 0.$$

(16)

By solving (15b) and (16) simultaneously, we derive the equilibrium wholesale price of inputs A and B as the two products compete in the same market, $w_{i}^{I} , i = A,B$.

From the above equilibrium, we derive the following comparative static effects as:

$$\frac{{\partial w_{A}^{I} }}{\partial c} = \frac{{2\left( {2 - \phi } \right)\left[ {q\left( {\beta - 1} \right)^{2} + \left( {1 - q} \right)} \right]}}{{\Phi }} > 0,$$

(17a)

$$\frac{{\partial w_{B}^{I} }}{\partial c} = \frac{{q\left( {2 - \phi } \right)\left( {1 - \beta } \right)}}{{\Phi }},$$

(17b)

where $\Phi \equiv \left[ {\left( {\beta - 1} \right)^{2} q\left( {4 - \phi } \right) + 4\left( {1 - q} \right)} \right] > 0$ due to $0 \le \phi \le 1$ and $0 < q < 1$.

Lemma 2

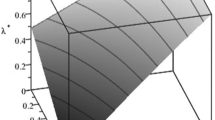
When products are sold to the one market, an increase in the specific input production cost c raises the equilibrium price of the specific input, but the equilibrium price of the common input might increase or decrease with the cost of the specific input, depending on the marginal product of common input, $\beta$.

The intuition behind the aforementioned result runs as follows. There are two effects arising from this result. When the two products compete in the one market, an increase in the cost of the specific input raises the specific input’s equilibrium price, which alleviates cannibalization. The multi-product downstream firm then reallocates the outputs by shifting the output of product 1 to the output of product 2. Therefore, the derived demand of common input and its price rise. However, as product 1 requires β units of common input, this also lowers the derived demand of common input due to the output shifting from product 1. Therefore, the degree of decrease in the derived demand and the equilibrium price of common input depend on β. When $\beta > 1$, a decrease in the output of product 1 lowers the derived demand of common input significantly, which dominates the greater derived demand of common input due to an increase in the output of product 2. Finally, the equilibrium price of the common input drops. Under this case, the input prices are strategically substituted, and thus we find the price of common input decreases with the cost of specific input—that is, $\frac{{\partial w_{B}^{I} }}{\partial c} < 0$.¹⁶

When $0 < \beta < 1$, since the manufacturing of product 1 requires less common input, the derived demand for common input falls slightly. On the other hand, the output shifting from product 1 to product 2 lifts the derived demand of the common input. Thus, the total derived demand of common input and the input price still increase, showing that the two input prices are strategic complementarity. Therefore, we have $\frac{{\partial w_{B}^{I} }}{\partial c} > 0$. It is also worth noting that when $\beta = 1$, an increase in the cost of the specific input lowers the derived demand of common input, which is exactly offset by the raising derived demand due to the output shifting from product 1 to product 2. Therefore, the total derived demand of common input and the input price do not change—that is, $\frac{{\partial w_{B}^{I} }}{\partial c} = 0$.¹⁷

It is intriguing to compare Lemma 2 to Lemma 1, as we find under two separated market cases that an increase in the specific input production cost raises the specific input’s equilibrium price, but lowers the common input’s price for any $\beta$. On the contrary, in the case of one market, the price of the common input falls with the specific input production cost that only occurs in the large marginal product of the common input of product 1—that is, $\beta > 1$.

We next move to analyze the impact of the input production cost to the downstream firm’s profit when two products compete in one market. From the above, we re-write the objective function of the downstream firm as: $\pi^{D} \left( {x_{1} \left( {w_{A}^{I} ,w_{B}^{I} } \right),x_{2} \left( {w_{A}^{I} ,w_{B}^{I} } \right),w_{A}^{I} ,w_{B}^{I} } \right)$. By differentiating $\pi^{D}$ with respect to c, we derive¹⁸:

$$\frac{{d{\uppi }^{D} }}{dc} = \underbrace {{\left( {\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A}^{I} }}\frac{{\partial w_{A}^{I} }}{\partial c}} \right)}}_{{{\text{input production cost effect}} \left( - \right)}} + \underbrace {{\left( {\frac{{\partial \pi_{1}^{D} }}{{\partial w_{B}^{I} }}\frac{{\partial w_{B}^{I} }}{\partial c}} \right)}}_{{{\text{complementary effect}}\left( ? \right)}} + \underbrace {{\left( {\frac{{\partial \pi_{2}^{D} }}{{\partial w_{B}^{I} }}\frac{{\partial w_{B}^{I} }}{\partial c}} \right)}}_{{{\text{multi}} - {\text{product effect}}\left( ? \right)}}.$$

(18)

It is easy to perceive the contrast between (9) and (18). Here, the complementary effect and the multi-product effect are no longer positive. The profit of the downstream firm may increase or decrease with the input production cost, depending on the marginal product of the common input. The intuition behind the result is similar to Lemma 2; when $0 < \beta < 1$, the complementary effect and multi-product effect turn negative, and thus the profit of the downstream firm decreases with the input production cost—that is, $\frac{{d{\uppi }^{D} }}{dc} < 0$. When $\beta = 1$, the complementary effect and multi-product effect vanish, only leaving the input production cost effect, which reduces the downstream firm’s profit. We further note that (18) is positive, or $\frac{{d{\uppi }^{D} }}{dc} > 0$, when $\beta > 1$, and the cost of a specific input is large enough—that is, $\overline{C} < c \le C_{1}$, where $C_{1}$ is the upper limit for the production cost of the specific input supplier to ensure positive outputs of products under the one market case.It shows that an increase in the input production cost results in both a positive complementary effect and a multi-product effect.

We now analyze the impacts of the bargaining power on input prices. By differentiating $\pi^{D}$ with respect to ϕ, we derive:

$$\frac{{\partial w_{A}^{I} }}{\partial \phi } = \frac{{ - 4\psi \left[ {q\left( {\beta - 1} \right)^{2} + \left( {1 - q} \right)} \right]}}{{\Phi^{2} }} > 0,$$

(19a)

$$\frac{{\partial w_{B}^{I} }}{\partial \phi } = \frac{{2q\left( {\beta - 1} \right)\psi }}{{\Phi^{2} }},$$

(19b)

where $\psi \equiv c\left[ {q\left( {\beta - 1} \right)^{2} + 2\left( {1 - q} \right)} \right] - \left( {1 - q} \right)\left[ {2\left( {1 - q} \right) + q\left( {\beta - 2} \right)\left( {\beta - 1} \right)} \right] < 0$ due to the positive output of product 1.¹⁹ Equation (19b) shows that $\frac{{\partial w_{B}^{I} }}{\partial \phi } \ge \left( < \right)0$ if $\beta \le ( > )1$. Again, the marginal product of the common input plays the main role of determining the effect of bargaining power on the downstream firm’s profit. By differentiating $\pi^{D}$ with respect to $\phi$, we derive:

$$\frac{{d{\uppi }^{D} }}{d\phi } = \underbrace {{\left( {\frac{{\partial \pi_{1}^{D} }}{{\partial w_{A}^{I} }}\frac{{\partial w_{A}^{I} }}{\partial \phi }} \right)}}_{ \left( - \right)} + \underbrace {{\left( {\frac{{\partial \pi_{1}^{D} }}{{\partial w_{B}^{I} }}\frac{{\partial w_{B}^{I} }}{\partial \phi }} \right)}}_{\left( ? \right)} + \underbrace {{\left( {\frac{{\partial \pi_{2}^{D} }}{{\partial w_{B}^{I} }}\frac{{\partial w_{B}^{I} }}{\partial \phi }} \right)}}_{\left( ? \right)}.$$

(20)

The results are similar to (18), in which the downstream firm’s profit may increase or decrease with the bargaining power of a specific input supplier, depending on the marginal product of the common input. Here, $\frac{{d{\uppi }^{D} }}{d\phi } < 0$ when $0 < \beta \le 1$ due to $\frac{{\partial w_{B}^{I} }}{\partial \phi } < 0$. However, when ${\upbeta } > 1$, we have $\frac{{d{\uppi }^{D} }}{d\phi } > 0$ when the production cost of a specific input supplier is large enough—that is, $\overline{C} < c \le C_{1}$. It implies that the downstream firm’s profit increases with bargaining power.²⁰ The intuition behind the result is similar to Lemma 2. From the above discussions, we establish the following proposition.

Proposition 3

When two products compete in the same market and $\beta > 1$, an increase in the production cost c or the bargaining power of the specific upstream firm raises the downstream firm’s profit as the production cost of a specific input supplier is large enough—that is, $\overline{C} < c \le C_{1}$.

When two products compete in the same market, an increase in the price of a specific input alleviates cannibalization between the two products. Thus, the price of the common input may rise through shifting the output of product 1 to the output of product 2 from the multi-product downstream firm. Therefore, the cannibalization spotlights the role of the marginal product of the common input of product 1 for improving the downstream firm’s profit, which is not discussed in Kopel et al. (2016). They assume that a multi-input-multi-product downstream firm produces two independent products, which is like two products are sold to separate markets in our model. Comparing to the two separate market case, it shows that the downstream firm’s profits improve with a cost disadvantage arising from the specific upstream sector and only hold when $\beta > 1$. This result is along the lines of the existing literature; see for example, Kimmel (1992) and Zhao (2001). The former assumes that all firms are in constant returns to scale with a Cournot oligopoly and shows that cost increases may benefit some or all firms. The latter assumes asymmetric costs for firms and finds that a firm’s cost increase is profitable for industry profit if and only if its market share is small.

We now consider the analysis to consumer surplus and provide industry policy implications as two products compete in the one market. Total consumer surplus is $CS \equiv CS_{1} + CS_{2}$, where $CS_{1} = \mathop \smallint \nolimits_{{\theta_{1} }}^{1} \left( {\theta - p_{1} } \right)d\theta = \frac{{x_{1}^{2} }}{2} + qx_{1} x_{2}$ and $CS_{2} = \mathop \smallint \nolimits_{{\theta_{2} }}^{{\theta_{1} }} \left( {\theta q - p_{2} } \right)d\theta = \frac{{qx_{2}^{2} }}{2}$, respectively. The effect of a rising input production cost on the consumer surplus is²¹:

$$\frac{{dCS_{1} }}{dc} = \underbrace {{\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right)} \right]}}_{\left( - \right)}\frac{{\partial w_{A}^{I} }}{\partial c} + \underbrace {{\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)} \right]}}_{\left( ? \right)}\frac{{\partial w_{B}^{I} }}{\partial c},$$

(21a)

$$\frac{{dCS_{2} }}{dc} = \underbrace {{\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right)}}_{\left( + \right)}\frac{{\partial w_{A}^{I} }}{\partial c} + \underbrace {{\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)}}_{\left( - \right)}\frac{{\partial w_{B}^{I} }}{\partial c}.$$

(21b)

It shows when $\beta \ge 1$ that we have $\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)} \right] = - \beta x_{1} \left( {1 - q} \right) - qx_{2} \left( {\beta - 1} \right) < 0$ and $\frac{{\partial w_{B}^{I} }}{\partial c} \le 0$ from (17b). Therefore, it implies that an increase in specific input production cost may raise total consumer surplus when ${\upbeta } \ge 1$, because $\frac{{dCS_{1} }}{dc}$ is ambiguous and $\frac{{dCS_{2} }}{dc} > 0$.

Using (21a) and (21b), we have $\frac{dCS}{{dc}} = \frac{ - 1}{2}\left[ {x_{1} \frac{{\partial w_{A} }}{\partial c} + \left( {\beta x_{1} + x_{2} } \right)\frac{{\partial w_{B} }}{\partial c}} \right]$. Interestingly, we have $\frac{dCS}{{dc}} > 0$ due to $\frac{{\partial w_{B} }}{\partial c} < 0$ when β > 1 as long as the production cost of the specific input is large enough—that is, $\overline{C} < c \le C_{1}$.

The effect of rising bargaining power of a specific input supplier on the consumer surplus is:

$$\frac{{dCS_{1} }}{d\phi } = \underbrace {{\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right)} \right]}}_{\left( - \right)}\frac{{\partial w_{A}^{I} }}{\partial \phi } + \underbrace {{\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)} \right]}}_{\left( ? \right)}\frac{{\partial w_{B}^{I} }}{\partial \phi },$$

(22a)

$$\frac{{dCS_{2} }}{d\phi } = \underbrace {{\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right)}}_{\left( + \right)}\frac{{\partial w_{A}^{I} }}{\partial \phi } + \underbrace {{\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)}}_{\left( - \right)}\frac{{\partial w_{B}^{I} }}{\partial \phi }.$$

(22b)

From (22a) and (22b), similar to the above results, we have $\frac{dCS}{{d\phi }} > 0$ when β > 1 as long as the production cost of the specific input is large enough—that is, $\overline{C} < c \le C_{1}$.

Using Lemma 2, the similar intuition is provided. A higher bargaining power of the specific upstream firm shifts the demand of product 1 to product 2, leading the common input price to drop only if the marginal product of the common input of product 1 is large. From the above discussions, we establish the following proposition.

Proposition 4

When two products compete in the same market and $\beta > 1$, an increase in the production cost c or the bargaining power of the specific upstream firm raises the consumer surplus as the production cost of a specific input supplier is large enough—that is, $\overline{C} < c \le C_{1}$.

We further find that ${ }\frac{{\partial \overline{C}}}{\partial \phi } = \frac{{ - 2q\left( {1 - q} \right)\left( {\beta - 1} \right)}}{{\left[ {q\left( {\beta - 1} \right)^{2} + 4\left( {1 - q} \right)} \right]\left( {2 - \phi } \right)^{2} }} < 0$ if $\beta > 1$. It implies that Proposition 3 and Proposition 4 are more likely to be supported when the bargaining power of the specific input supplier increases as $\beta > 1$. Interestingly, the higher bargaining power of the specific input supplier is more desirable for the downstream firm and the consumers as the marginal product of common input of product 1 is large. Our paper highlights that the marginal product of the common input of the high-quality product is crucial in the one market once again.

4 Extensions

4.1 Horizontally differentiated products

In this sub-section, we consider the case in which the two products are horizontally differentiated products instead of vertically differentiated products, and the remaining settings are the same. Under the model settings of one market, we have $\frac{{\partial w_{A} }}{\partial c} = \frac{{2\left[ {\left( {\beta - r} \right)^{2} + \left( {1 - r^{2} } \right)} \right]\left( {2 - \phi } \right)}}{{\left( {4 - \phi } \right)\left( {\beta - r} \right)^{2} + 4\left( {1 - r^{2} } \right)}} > 0$ and $\frac{{\partial w_{B} }}{\partial c} = \frac{{ - \left( {2 - \phi } \right)\left( {\beta - r} \right)}}{{\left( {4 - \phi } \right)\left( {\beta - r} \right)^{2} + 4\left( {1 - r^{2} } \right)}}$, where $r$ measures the degree of product differentiation and $r \in \left[ {0,{ }1} \right]$. It implies that the price of the specific input increases with its own cost, whereas the price of the common input might increase or decrease with the cost of the specific input, depending on the marginal product of common input β. We obtain qualitatively similar results when we consider horizontally differentiated products instead of vertical differentiation. As long as $\beta > r$, we have $\frac{{\partial w_{B} }}{\partial c} < 0$, which turns the complementary effect and multi-product effect to be positive in (19a, 19b). Therefore, the downstream firm’s profit may increase with the cost of the specific input supplier.

4.2 Price competition

In this sub-section, we consider the case in which the game is solved by price rather than quantity in both the benchmark and extension models. In the one market case, the inverse demand functions of the two products are $x_{1} = \frac{{1 - q + p_{2} - p_{1} }}{1 - q}$ and $x_{2} = \frac{{qp_{1} - p_{2} }}{{q\left( {1 - q} \right)}}$ respectively. The multi-product downstream firm maximizes its profit to determine the optimal prices of two products—that is, $\pi_{D} = \left( {p_{1} - w_{A} - w_{B} } \right)x_{1} + \left( {p_{2} - w_{B} } \right)x_{2}$. The equilibrium prices are $p_{1} = \frac{{1 + w_{A} + \beta w_{B} }}{2}$ and $p_{2} = \frac{{q + w_{B} }}{2}$. By substituting $p_{i}$ into $x_{i}$, we derive the equilibrium outputs in the price competition stage as $x_{1} = \frac{{1 - q - w_{A} - w_{B} \left( {\beta - 1} \right)}}{{2\left( {1 - q} \right)}}$ and $x_{2} = \frac{{qw_{A} + w_{B} \left( {q\beta - 1} \right)}}{{2q\left( {1 - q} \right)}}$. Note that the equilibrium outputs are the same as the equilibrium outputs when the strategic variable is the quantity, because the downstream firm is a monopolist. Therefore, the optimal input prices are the same in the first stage, because the game is solved by quantity and the corresponding propositions still hold.

4.3 Two products need the specific input

In this sub-section, we consider the case in which the firm producing product 1 (product 2) needs 1 unit of the specific input and $\beta_{1}$ ($\beta_{2}$) units of the common input. Moreover, we assume that the specific input supplier has full bargaining power to determine the input price. Other settings are the same as the basic model. The profit function of multi-product firms in the case of separate market is: $\pi_{D} = \left( {p_{1} - w_{A} - \beta_{1} w_{B} } \right)x_{1} + \left( {p_{2} - w_{A} - \beta_{2} w_{B} } \right)x_{2}$.

In the first stage, the profit function of the specific input supplier is $\pi_{A} = \left( {w_{A} - c} \right)\left( {x_{1} + x_{2} } \right)$ and the profit function of the common input supplier is $\pi_{B} = w_{B} \left( {\beta_{1} x_{1} + \beta_{2} x_{2} } \right)$. The input supplier maximizes its utility function to determine the optimal input prices simultaneously and separately. Next, we have the effect of marginal cost of the specific input supplier on the input prices as ${ }\frac{{\partial w_{A}^{*} }}{\partial c} > 0$ and $\frac{{\partial w_{B}^{*} }}{\partial c} < 0$.²² We find that an increase in the marginal cost of the specific input supplier increases the price of the specific input and decreases the price of the common input. The intuition is that an increase in the marginal cost of the specific input supplier decreases the derived demand of common inputs, leading the price of the common input to decrease. The impact of the input production cost to the downstream firm’s profit can then be derived as $\frac{{d\pi^{D} }}{dc} = \frac{{\partial \pi^{D} }}{{\partial w_{A} }}\frac{{\partial w_{A}^{*} }}{\partial c} + \frac{{\partial \pi^{D} }}{{\partial w_{B} }}\frac{{\partial w_{B}^{*} }}{\partial c}$. It shows that an increase in the marginal cost of the specific input supplier may increase the profit of the downstream firm as the latter effect dominates the former. Therefore, we obtain qualitatively similar results when we consider that producing product 1 (product 2) needs 1 unit of the specific input and $\beta_{1}$ ($\beta_{2}$) units of the common input.

4.4 Bilateral bargaining

Considering the bilateral bargaining in the one market case, in which each input supplier–downstream pair bargains the input price simultaneously and independently, we assume that each supplier’s bargaining powers can be generalized to $\phi_{i}$, $i = A,B$. The objective functions of the specific input supplier and the common input supplier are respectively:

$$\begin{array}{*{20}c} {{\text{Max}} U_{A} } \\ {w_{A} } \\ \end{array} = \left( {\pi_{A} \left( {w_{i} \left( {\phi_{i} } \right)} \right) - 0} \right)^{{\phi_{A} }} \left( {\pi_{D} \left( {w_{i} \left( {\phi_{i} } \right)} \right) - \pi_{D2} \left( {w_{B} \left( {\phi_{B} } \right)} \right)} \right)^{{1 - \phi_{A} }} ,$$

(23a)

$$\begin{array}{*{20}c} {{\text{Max }}U_{B} } \\ {w_{B} } \\ \end{array} = \left( {\pi_{B} \left( {w_{i} \left( {\phi_{i} } \right)} \right) - 0} \right)^{{\phi_{B} }} \left( {\pi_{D} \left( {w_{i} \left( {\phi_{i} } \right)} \right) - 0} \right)^{{1 - \phi_{B} }} .$$

(23b)

Here, $\phi_{i}$ (1$- \phi_{i}$) $i = A,B,$ is the bargaining power of the input supplier (downstream firm); $\pi_{i}$ is the profit of the input supplier i; $\pi_{D}$ is the total profit of the downstream firm; and $\pi_{D2}$ is the profit of the downstream firm from only producing the low-quality product.

By total differentiating (23a) and (23b), if we assume $\phi_{B} \ne 1$, then we still have $\frac{{\partial w_{A}^{*} }}{\partial c} > 0$ and $\frac{{\partial w_{B}^{*} }}{\partial c} < 0$ as long as $\phi_{B}$ is large.²³ Therefore, we conclude our findings still hold if $\phi_{B}$ is large enough and there is no quantitative change in the bilateral bargaining case.

5 Conclusion

This research challenges the conventional wisdom that a higher input production cost or stronger upstream firms always make downstream firms worse off. We identify a situation under the view that downstream firms’ profits are increasing with the input production cost or the bargaining power of upstream firms. In a market consisting of a vertically differentiated product firm, an increase in the cost or bargaining power of upstream firms may benefit not only the downstream firm, but also consumer surplus when the two inputs are complementary. Our results might occur in two separate markets and in one market.

We set up a vertically differentiated model in which there is one multi-input-multi-product firm to analyze the impacts of input production cost or the upstream firm’s bargaining power upon the downstream firm’s profit. We find that an increase in the cost or bargaining power of the upstream firm may raise the downstream firm’s profit and consumer surplus either in two separate markets or in the one market case. Specifically, in the one market case, we shed light on the importance of the marginal product of the common input of the high-quality product for the downstream firm’s profit and for improving consumer surplus, which have not been discussed in two separate market cases. We also provide key insights into the vital influence of the market power of the common input supplier on the downstream firm’s profit. The contrary intuitive result is provided, in which the downstream firm can benefit from the cost disadvantage from the input sector, as long as the common input supplier has the market power. On the contrary, if the common input market is perfect competition, then a high specific input price is always detrimental to the downstream firm’s profit. Moreover, we check the robustness of our findings for extension by considering horizontal product differentiation, price competition, using the specific input for two products, and bilateral bargaining. We demonstrate that our main findings still hold.

There is a number of ways in which this research work could be extended in future studies. For example, our model could be modified to examine the case in which the downstream market is duopolistic or oligopolistic. We believe this study sheds light on these lines of research. We also believe that this paper offers important insights, especially when examining the relationship between the input production cost and the downstream firm’s profit, or the bargaining power and a firm’s profits. Aside from that, cost reduction is generally believed to enhance consumer surplus. However, this belief may be false in the multi-input-multi-product firm case: an increase in cost has been shown to enhance consumer surplus if the input production cost is large.

6 Appendix A: The effect of increasing specific input cost on the downstream firm’s profit

By differentiating $\pi^{D}$ with respect to c and using the envelope theorem ($\partial \pi^{D} /\partial x_{1}$) = ($\partial \pi^{D} /\partial x_{2}$) = 0, we derive ($d\pi^{D} /dc$), which is (9). Making use of the results in the first stage, (9) can be rewritten as:

$$\frac{{d\pi^{D} }}{dc} = A_{1} \left\{ { - \left( {1 - c} \right)\left( {2 - \phi } \right)\left( {q\beta^{2} + 4} \right) + 2q\beta \left( {3 - \phi } \right)} \right\},$$

(24)

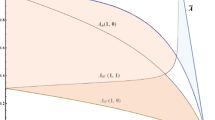
where $A_{1} \equiv \frac{{\left( {q\beta^{2} + 1} \right)\left( {2 - \phi } \right)}}{{2\left[ {4 + q\beta^{2} \left( {4 - \phi } \right)} \right]^{2} }} > 0{ }$ and ${ }\frac{{d^{2} \pi^{D} }}{{dc^{2} }} = A_{1} \left( {2 - \phi } \right)\left( {q\beta^{2} + 4} \right) > 0$. It implies that there is a U-shaped relationship between input production cost and the downstream firm’s profitability. We find that (24) is positive if $\overline{c} \equiv \frac{{\left( {2 - \phi } \right)\left[ {q\left( {\beta - 2} \right)^{2} + 4\left( {1 - q} \right)} \right] + 2q\beta \left( {1 - \phi } \right)}}{{\left( {q\beta^{2} + 4} \right)\left( {2 - \phi } \right)}} < c < c_{1}$. To ensure positive outputs, we assume that $c < c_{1}$, where $c_{1} = \frac{{q\left( {\beta - 1} \right)^{2} + \left( {2 - q} \right) + q\beta }}{{q\beta^{2} + 2}}$. By comparing $c_{1}$ and $\overline{c}$, we see that $c_{1} - \overline{c} = \frac{{\beta q\left[ {4 + q\beta^{2} \left( {4 - \phi } \right)} \right]}}{{\left( {q\beta^{2} + 2} \right)\left( {q\beta^{2} + 4} \right)\left( {2 - \phi } \right)}} > 0$. It implies for any β that the higher the input production cost is, the higher the downstream firm’s profit is, if the cost of input A is between $\overline{c}$ and $c_{1}$. We also have $\frac{{\partial \overline{c}}}{\partial q} = \frac{{ - 8\beta \left( {3 - \phi } \right)}}{{\left( {q\beta^{2} + 4} \right)\left( {2 - \phi } \right)}} < 0$ and $\frac{{\partial \overline{c}}}{\partial \phi } = \frac{ - 2q\beta }{{\left( {q\beta^{2} + 4} \right)\left( {2 - \phi } \right)}} < 0$. We see that $\overline{c}$ decreases with $q$ and $\phi$.

7 Appendix B: Proof of Proposition 1

By differentiating $\pi^{D}$ with respect to $\phi$, we derive (12) and re-write it as:

$${ }\frac{{d\pi^{D} }}{d\phi }{ } = \frac{{A_{2} \left( {1 + q\beta^{2} } \right)}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]}}\left\{ { - \left( {1 - c} \right)\left( {2 - \phi } \right)\left( {q\beta^{2} + 4} \right) + 2q\beta \left( {3 - \phi } \right)} \right\},$$

(25)

where $A_{2} \equiv \frac{{\left[ {\left( {1 - c} \right)\left( {q\beta^{2} + 2} \right) - q\beta } \right]}}{{\left[ {q\beta^{2} \left( {4 - \phi } \right) + 4} \right]^{2} }} > 0$ due to $c < c_{1}$.

From (25), we derive that $\frac{{d\pi^{D} }}{d\phi } > 0$ when $\phi > \overline{\phi } \equiv \frac{{2\left[ {\left( {1 - c} \right)\left( {q\beta^{2} + 4} \right) - 3q\beta } \right]}}{{\left[ {\left( {1 - c} \right)\left( {q\beta^{2} + 4} \right) - 2q\beta } \right]}}$. Using $\overline{\phi }$, $\overline{\phi }$ is positive if $c < c_{2} = \frac{{q\left( {\beta - 2} \right)^{2} + 4\left( {1 - q} \right) + q\beta }}{{4 + q\beta^{2} }}$. Due to $c_{2} > c_{1}$, it implies $\overline{\phi } > 0$ when $c < c_{1}$. To make sure that $\overline{\phi } \in \left[ {0, 1} \right]$, we derive $1 - \overline{\phi } = \frac{{ - \left( {1 - c} \right)\left( {4 + q\beta^{2} } \right) + 4q\beta }}{{\left( {1 - c} \right)\left( {4 + q\beta^{2} } \right) - 2q\beta }} > 0$, if $c > c_{\phi } \equiv \frac{{q\left( {\beta - 2} \right)^{2} + 4\left( {1 - q} \right)}}{{4 + q\beta^{2} }}$. Comparing $c_{1}$ with $c_{\phi }$, we have $c_{1} - c_{\phi } = \frac{{q\beta \left( {3q\beta^{2} + 4} \right)}}{{\left( {2 + q\beta^{2} } \right)\left( {4 + q\beta^{2} } \right)}} > 0$. Therefore, we find that $\overline{\phi } \ge ( < )1$ when $c \le ( > )c_{\phi }$.

In conclusion, we are able to demonstrate that $\frac{{d\pi^{D} }}{d\phi } \le 0$ for any $\phi$ if $0 \le c \le c_{\phi }$. However, we have $0 < \overline{\phi } < 1$ when $c > c_{\phi }$, and hence we present that $\frac{{d\pi^{D} }}{d\phi } > ( < )0$ when $\overline{\phi } < \phi \le 1 \left( {0 \le \phi \le \overline{\phi }} \right)$ if $c_{\phi } < c \le c_{1} .$

8 Appendix C: Proof of Proposition 3

To assure that the equilibrium outputs are positive, by substituting (17) into the equilibrium output of product 1 at the second stage, we derive:

$$x_{1} = \frac{{ - \left( {2 - \phi } \right)\psi }}{{2\left( {1 - q} \right)\Phi }},$$

(26)

where $\psi \equiv c\left[ {q\left( {\beta - 1} \right)^{2} + 2\left( {1 - q} \right)} \right] - \left( {1 - q} \right)\left[ {2\left( {1 - q} \right) + q\left( {\beta - 2} \right)\left( {\beta - 1} \right)} \right].$ To assure that $x_{1} > 0$ (that is, (26)), $\psi$ should be negative, and so we can derive the condition as:

$$c < C_{1} \equiv \frac{{\left( {1 - q} \right)\left[ {2\left( {1 - q} \right) + q\left( {2 - \beta } \right)\left( {1 - \beta } \right)} \right]}}{{\left[ {q\left( {\beta - 1} \right)^{2} + 2\left( {1 - q} \right)} \right]}}.$$

(27)

We next move to analyze the impact of the input production cost to the downstream firm’s profit when two products compete in the same market. By differentiating $\pi^{D}$ with respect to c, we re-write (18) as follows:

$$\frac{{d\pi^{D} }}{dc} = \frac{{\left( {2 - \phi } \right)}}{{\Phi }}\left\{ {x_{1} \left[ {q\left( {\beta - 1} \right)\left( {2 - \beta } \right) - 2\left( {1 - q} \right)} \right] + qx_{2} \left( {\beta - 1} \right)} \right\}.$$

(28)

By substituting equilibrium outputs in the first stage into (28), we derive the condition for $\frac{{d\pi^{D} }}{dc} > 0$ as:

$$c > \overline{C} \equiv \frac{{\left( {1 - q} \right)A_{3} }}{{\left( {2 - \phi } \right)\left[ {q\left( {\beta - 1} \right)^{2} + 4\left( {1 - q} \right)} \right]}},$$

(29)

where $A_{3} \equiv 4\beta \phi q + 2\beta^{2} q - \beta^{2} \phi q - 10\beta q + \phi q + 8 - 4\phi$.

By subtracting (27) from (29), we have:

$$C_{1} - \overline{C} = \frac{{q\left( {1 - q} \right)\left( {\beta - 1} \right)\Phi }}{{\left( {2 - \phi } \right)\left[ {q\left( {\beta - 1} \right)^{2} + 2\left( {1 - q} \right)} \right]\left[ {q\left( {\beta - 1} \right)^{2} + 4\left( {1 - q} \right)} \right]}}$$

(30)

and we are able to show that $\overline{C} \ge C_{1}$ if $0 < \beta \le 1$. In other words, $\frac{{d\pi^{D} }}{dc} \le 0$ when $0 \le c \le C_{1}$ if $0 < \beta \le 1$. However, when $\beta > 1,$ we derive

$\frac{{d\pi^{D} }}{dc} > \left( \le \right)0$ as $\overline{C} < c \le C_{1}$ $\left( {0 \le c \le \overline{C}} \right)$.

By differentiating $\pi^{D}$ with respect to $\phi$, we re-write (21) as follows:

$$\frac{{d\pi^{D} }}{d\phi } = \frac{ - 2\psi }{{{\Phi }\left( {2 - \phi } \right)}}\left\{ {x_{1} \left[ {q\left( {\beta - 1} \right)\left( {2 - \beta } \right) - 2\left( {1 - q} \right)} \right] + qx_{2} \left( {\beta - 1} \right))} \right\},$$

(31)

where $\psi < 0$. By substituting equilibrium outputs in the first stage into (31), we derive the condition for $\frac{{d\pi^{D} }}{d\phi } > 0$ as $c > \overline{C}$, which is the same condition as (29). Comparing $C_{1}$ with $\overline{C}$, we have (30).

According to the above, we show that $\overline{C} \ge C_{1}$ if $0 < \beta \le 1$, which implies that $\frac{{d\pi^{D} }}{dc} \le 0$ and $\frac{{d\pi^{D} }}{d\phi } \le 0$ when $0 \le c \le C_{1}$ if $0 < \beta \le 1$. When $\beta > 1,$ we derive $C_{1} > \overline{C}$. In other words, $\frac{{d\pi^{D} }}{dc} > 0$ and $\frac{{d\pi^{D} }}{d\phi } > 0$ when $\overline{C} < c \le C_{1}$ if $\beta > 1$. This completes the proof of Proposition 3.

9 Appendix D: Proof of Proposition 4

The total consumer surplus $CS = CS_{1} + CS_{2}$ from the one market case can be shown as $CS_{1} = CS_{1} \left( {x_{1} \left( {w_{A}^{I} \left( c \right),w_{B}^{I} \left( c \right)} \right),x_{2} \left( {w_{A}^{I} \left( c \right),w_{B}^{I} \left( c \right)} \right) } \right)$ and $CS_{2} = CS_{2} \left( {x_{2} \left( {w_{A}^{I} \left( c \right),w_{B}^{I} \left( c \right)} \right)} \right)$. By differentiating $CS_{i}$ with respect to c and $\phi$, we have (21a), (21b), (22a), and (22b).

We further use $\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{A}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right)} \right] = \frac{{ - x_{1} \left( {1 - q} \right) - qx_{2} }}{{2\left( {1 - q} \right)}} < 0$, $\left[ {\left( {\frac{{\partial CS_{1} }}{{\partial x_{1} }}\frac{{\partial x_{1} }}{{\partial w_{B}^{I} }}} \right) + \left( {\frac{{\partial CS_{1} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right)} \right] = \frac{{ - \beta x_{1} \left( {1 - q} \right) - qx_{2} \left( {\beta - 1} \right)}}{{2\left( {1 - q} \right)}}$, $\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{A}^{I} }}} \right) = \frac{{qx_{2} }}{{2\left( {1 - q} \right)}} > 0$, and $\left( {\frac{{\partial CS_{2} }}{{\partial x_{2} }}\frac{{\partial x_{2} }}{{\partial w_{B}^{I} }}} \right) = \frac{{x_{2} \left( {q\beta - 1} \right)}}{{2\left( {1 - q} \right)}}$. We now re-write (21a) and (21b) as follows:

$$\frac{{dCS_{1} }}{dc} = \frac{{\left( {2 - \phi } \right)}}{{2\left( {1 - q} \right){\Phi }}}\left\{ {x_{1} \left( {1 - q} \right)\left[ { - q\left( {\beta - 1} \right)\left( {\beta - 2} \right) - 2\left( {1 - q} \right)} \right] - qx_{2} \left[ {q\left( {\beta - 1} \right)^{2} + 2\left( {1 - q} \right)} \right]} \right\},$$

(32)

$$\frac{{dCS_{2} }}{dc} = \frac{{qx_{2} \left( {2 - \phi } \right)}}{{2\left( {1 - q} \right)\Phi }}\left\{ {2\left[ {q\left( {\beta - 1} \right)^{2} + \left( {1 - q} \right)} \right] + \left( {q\beta - 1} \right)\left( {1 - \beta } \right)} \right\}.$$

(33)

Using (32) and (33), we have $\frac{dCS}{{dc}} = \frac{ - 1}{2}\left\{ {x_{1} \frac{{\partial w_{A}^{I} }}{\partial c} + \left( {\beta x_{1} + x_{2} } \right)\frac{{\partial w_{B}^{I} }}{\partial c}} \right\}$ and re-write it as follows:

$$\frac{dCS}{{dc}} = \frac{{\left( {2 - \phi } \right)}}{2\Phi }\left\{ {x_{1} \left[ {q\left( {\beta - 1} \right)\left( {2 - \beta } \right) - 2\left( {1 - q} \right)} \right] + qx_{2} \left( {\beta - 1} \right)} \right\}.$$

(34)

By substituting equilibrium outputs in the first stage into (34), we can derive the condition for $\frac{dCS}{{dc}} > 0$ as $c > \overline{C}$ when ${\upbeta } > 1$, which is the same condition as (29). Comparing $C_{1}$ with $\overline{C}$ to ensure the consistency, we have (30).

Using (22a) and (22b), we have $\frac{dCS}{{d\phi }} = \frac{ - 1}{2}\left\{ {x_{1} \frac{{\partial w_{A}^{I} }}{\partial \phi } + \left( {\beta x_{1} + x_{2} } \right)\frac{{\partial w_{B}^{I} }}{\partial \phi }} \right\}$ and re-write it as follows:

$$\frac{dCS}{{d\phi }} = \frac{ - \psi }{{2\Phi^{2} }}\left\{ {x_{1} \left[ {q\left( {\beta - 1} \right)\left( {2 - \beta } \right) - 2\left( {1 - q} \right)} \right] + qx_{2} \left( {\beta - 1} \right)} \right\}.$$

(35)

By substituting equilibrium outputs in the first stage into (35), we can derive the condition for $\frac{dCS}{{d\phi }} > 0$ as $c > \overline{C}$ when $\beta > 1$—that is, the same condition as (29). Comparing $C_{1}$ with $\overline{C}$, we have (30).

According to the above, we show that $\overline{C} \ge C_{1}$ if $0 < \beta \le 1$, which implies that $\frac{dCS}{{dc}} \le 0$ and $\frac{dCS}{{d\phi }} \le 0$ when $0 \le c \le C_{1}$. When $\beta > 1,$ we can derive $C_{1} > \overline{C}$. It implies that $\frac{dCS}{{dc}} > 0$ and $\frac{dCS}{{d\phi }} > 0$ when $\overline{C} < c \le C_{1}$ if $\beta > 1$. This completes the proof of Proposition 4.