Characterizing existence of equilibrium for large extensive form games: a necessity result

Abstract

What is the minimal structure that is needed to perform equilibrium analysis in large extensive form games? To answer this question, this paper provides conditions that are simultaneously necessary and sufficient for the existence of a subgame perfect equilibrium in any well-behaved perfect information game defined on a large game tree. In particular, the set of plays needs to be endowed with a topology satisfying two conditions. (a) Nodes are closed as sets of plays; and (b) the immediate predecessor function is an open map.

1 Introduction

Extensive form games with large action spaces and/or an infinite horizon are pervasive in economics. Examples include oligopoly models à la Cournot (1838), Bertrand (1883), or von Stackelberg (1934), infinite bilateral bargaining (Rubinstein 1982), or stochastic games (Shapley 1953). By contrast, the theory of games is best understood when the representation of the game is finite. When it is not, because of large action spaces and/or an infinite horizon, then one is forced to add structure. For instance, in repeated games, one assumes identical action sets at each stage as well as utility functions that are additively separable across stages.

Suppose no particular class of games is given. What is a reasonable criterion to identify which structure needs to be added? The goal here is to provide necessary conditions that need to be imposed if one takes as a postulate the existence of subgame perfect equilibria in well-behaved perfect information games. This is in contrast to the more popular exercise of proving existence of equilibrium for certain classes of games. In fact, sufficient conditions for existence of subgame perfect equilibria in perfect information games (Kuhn 1953) have been provided for different classes of large extensive form games by Fudenberg and Levine (1983), by Harris (1985b), by Hellwig and Leininger (1987), and recently also by ourselves in a companion paper (Alós-Ferrer and Ritzberger 2016). Necessary conditions have not received attention so far.

Yet, for the purpose of deducing structure from an abstract postulate, a necessity result strikes us as more important. The analysis of sufficient conditions amounts to the development of existence theorems, which the applied analyst will ultimately rely on. Without a necessity result, however, it is unclear which conditions are crucial and which conditions have been added for analytical convenience and could eventually be dropped (leading to a more powerful result). A result on necessity identifies crucial assumptions, which the analyst simply cannot do without if existence is to obtain. To give just one analogy, suppose one wishes to study games where mixed and behavior strategies are equivalent. Assuming perfect information is sufficient to obtain this equivalence. But perfect information is unnecessarily restrictive, for, as Kuhn’s theorem (Kuhn 1953) shows, it can be weakened to perfect recall and the equivalence still obtains. The most important part of Kuhn’s theorem, however, states that if mixed and behavior strategies are equivalent for a given game, then the game needs to satisfy perfect recall. It is this necessity that leads the analyst to adopt the assumption of perfect recall in applications, because this condition has been identified as the weakest possible one.

Therefore, this paper aims at identifying the minimal topological conditions that guarantee equilibrium existence. The focus on topological conditions is natural. For, equilibrium has two aspects: individual optimization and pasting together individual decisions to obtain an outcome. The identification of individual maxima is of course an order-theoretic issue, but the topological approach to optimization has proven powerful, and it is routinely assumed if one focuses on continuity to ensure existence of maxima. It will be shown that pasting together individual optimization problems can also be reduced to a topological problem in a particularly relevant case, namely perfect information games. The reason is that under perfect information, every player holds the same views as an outside observer, and there are no simultaneous decisions. Hence, no issues regarding subjective beliefs arise.

Of course, care has to be taken in order not to trivialize the problem. It is easy to construct examples where no equilibrium exists, for instance, when preferences are not continuous. Hence, we will restrict the analysis to “well-behaved” perfect information games. Those are games where all players’ preferences are continuous and decision points are suitably assigned (see Definition 3 below) to ensure that local optimization problems are well posed. Yet, even for such well-behaved games, compactness and continuity of preferences are not enough. If the structure of the tree is irregular enough, existence may fail even if compactness holds and all preferences are continuous, as illustrated by the following example.

Example 1

Consider a two-player perfect information game, where player 1 picks at the root of the tree either a pair $(a, b)\in \left[ 0, 1\right] ^2$ with $a < 1$ or sets $a=1$ and gives the move to player 2. In the former case ($a < 1$), the game ends with payoffs $U_1\left( a, b\right) = ab$ and $U_2\left( a, b\right) = 1 - b$. In the latter case ($a = 1$), player 2 receives the opportunity to choose $b\in \left[ 0, 1\right]$ and, once b has been selected, the game ends with payoffs $U_1\left( 1, b\right) = b$ and $U_2\left( 1, b\right) = 1 - b$. The set W of possible outcomes (plays) can be identified with the unit square $W = \left[ 0, 1\right] ^2$ and endowed with the relative Euclidean topology of the plane. Then W is compact, and payoff functions are continuous. Since player 2, if called upon to move, will always choose $b = 0$, player 1’s “value” function has no maximum and the game no subgame perfect equilibrium.

In this example, preferences are continuous and the space of outcomes (or plays) is compact, yet existence of equilibrium fails. (The example also illustrates a few other points to which we will return below.) This means that asking for existence of subgame perfect equilibrium in perfect information games defined on a given tree does constrain the topological structure imposed on the domain of players’ preferences, i.e., on plays of the tree. Therefore, the task is to identify, for a given arbitrarily large game tree, the minimal added (topological) structure needed for existence of subgame perfect equilibria in all perfect information games defined on this tree. In other words, the objective is to provide topological conditions on the set of outcomes (plays) of the game which are necessary and sufficient for the existence of (subgame perfect) equilibria. Sufficiency is the familiar exercise. It means that, given a game tree and a topology satisfying certain conditions, every (well-behaved) game defined on that tree has an equilibrium. Necessity is the novel and arguably more important part of the analysis. It means that, given a game tree, if a topology on outcomes admits an equilibrium for every well-behaved game defined on that tree, then the topology fulfills our conditions. In other words, the existence theorem derived from the sufficiency part cannot be generalized any further in the topological dimension. This is the sense in which the conditions are minimal.

It will be shown that there are precisely two conditions that are necessary and sufficient, and both are in terms of how nodes and plays are related in the game tree. The first is simply that nodes in the tree are closed as sets of plays. The second demands that the function assigning to each (finite) node of the tree its immediate predecessor is an open map in the appropriate topology on nodes. Equivalently, as shown in Alós-Ferrer and Ritzberger (2016, Lemma 5), the correspondence, which assigns to each move its immediate successors, is lower hemi-continuous. Henceforth, topologies satisfying these two conditions are called “tree topologies.” The present results show that tree topologies provide a characterization of the statement that subgame perfect equilibria exist for every well-behaved perfect information game on a given tree. Hence, they capture precisely the structure that needs to be added in order to do equilibrium analysis in large (extensive form) games (of perfect information).

The virtue of a characterization is that it pins down precisely which conditions are needed and which are not. For example, the present result shows that no condition on upper hemi-continuity of the successor correspondence is needed to establish existence of subgame perfect equilibrium, neither are specific topological separation properties (as, e.g., the assumption of Hausdorff action spaces) on the “stages” of a game. Both of these properties have indeed been assumed in previous existence theorems (e.g., Harris 1985b).

Sufficiency has been established in a companion paper (Alós-Ferrer and Ritzberger 2016) in the form of an existence theorem. The present paper is devoted to the arguably more important task of identifying necessary conditions. That is, it will be shown that without a tree topology, there exists a (well-behaved) perfect information game that has no subgame perfect equilibrium, even though the game is well-behaved in the sense that preferences are continuous and the assignment of decision points ensures that local optimization problems are well posed.

Section 2 introduces the basic objects of analysis, discrete game trees, (well-behaved) perfect information games, and topologies that admit equilibrium analysis. Section 3 presents the result on the necessity of tree topologies (Theorem 1). An application of the existence result in Alós-Ferrer and Ritzberger (2016) yields the characterization (Theorem 2). Section 3.2 is devoted to the proof of Theorem 1. Section 4 discusses a few fine points, and Sect. 5 concludes.

2 Perfect information games

Many alternative definitions of extensive form games have been introduced in the literature. Since the goal is to consider topological properties of preferences, and preferences are defined on ultimate outcomes of the game, it is convenient to follow the original approach of von Neumann and Morgenstern (1944, Section 8). Although Kuhn (1953) later popularized the “graph approach” where trees are viewed as graphs on abstract nodes, in the original approach by von Neumann and Morgenstern (1944) extensive form games are defined on trees, but the latter are not seen as graphs. Rather, trees are viewed as collections of (nonempty) subsets of an underlying set of outcomes (also called plays). That is, a node is simply a collection of outcomes. The relation between both approaches is simple: A node should be seen as the set of outcomes which are still available when a player decides at that node. In that way, a node precedes another node if and only if the latter node is properly contained in the former. Intuitively, decisions discard possible outcomes and hence reduce the size of the nodes. Alós-Ferrer and Ritzberger (2005, 2013) provided “translations” between both approaches in the form of equivalence theorems.

Though Kuhn’s approach by graphs has become popular for textbook expositions (especially for the case of finite games), other models were used in the literature, in particular when large games were at stake. For example, Harris (1985b) proposed a sequence-approach that was later popularized by Osborne and Rubinstein (1994). The following subsection illustrates why the set-tree approach by von Neumann and Morgenstern (1944) is most convenient for the present purposes.

2.1 Nodes as sets versus plays as sequences

We begin with a simple example that illustrates the relations between different formalizations of extensive form games.

Example 2

Player 1 decides $a\in [0,1]$ at the root and, after observing a, player 2 decides $b\in [0,1]$. Following von Neumann and Morgenstern (1944), the root corresponds to a node encompassing the whole set of potential outcomes, $W=[0,1]^2$. At this node, player 1 decides, which amounts to picking a smaller subset, a node of the form $\{a\}\times [0,1]$ where a has been selected but b remains to be decided. At each of these intermediate nodes, player 2 decides, choosing a final node of the form $\left\{ (a,b)\right\}$, which contains only one outcome. The game then ends. Hence, the representation of the game in our approach relies on a set of nodes N which collects all the sets (nodes) described above,

$$\begin{aligned} N = \left\{ W,\left( \{a\}\times \left[ 0, 1\right] \right) _{a\in \left[ 0, 1\right] },\left( \{w\}\right) _{w\in W}\right\} \end{aligned}$$

and is ordered by set inclusion. For this example, the “graph approach” is merely a representation of the approach above, with the sets being interpreted as abstract nodes. But the cardinality of the example prevents a graphical illustration (see Alós-Ferrer and Ritzberger 2005 for details on the equivalence). The “sequence approach” would consider the root as a null sequence, the intermediate nodes as length-one sequences of the form (a), and the final nodes as length-two sequences (a, b). The correspondence to the approach above is straightforward.

The next example shows how distinct formal approaches can lead to substantial differences, not only when modeling games, but also when analyzing them. The example is a game that is easily captured by our approach and where subgame perfect equilibria always exist (for continuous preferences). However, if the game is modeled by other approaches, the result is a less natural construction that creates formal difficulties. Even worse, as a consequence of those, existence results from the literature fail to apply.

Example 3

Two players jointly decide a real number $a\in [0,1]$ and a natural number $n\in \{1,2,3,4\}$. The rules are as follows. Player 1 can either choose $a<1$ and let player 2 choose $b\in \{1,2,3,4\}$, or fix $a=1$ and simultaneously choose “Low” or “High.” In the latter case, if player 1 chooses Low, player 2 will be able to choose $b\in \{1,2\}$, while if player 1 chooses High, player 2 will be able to choose $b\in \{3,4\}$. The natural set of outcomes is $W=[0,1]\times \{1,2,3,4\}$, which can be endowed with the relative Euclidean topology (which coincides with the product of the Euclidean topology on [0, 1] and the discrete topology on $\{1,2,3,4\}$). The set of nodes is also easy to construct. The root is simply W itself. The “terminal” nodes are those of the form $\{(a,n)\}$ with $(a,n)\in W$. There is a continuum of intermediate nodes (where player 2 decides). Those are the nodes of the form $\left\{ \{a\}\times \{1,2,3,4\}\;\left| \; \; a<1\right. \right\}$, plus the two distinguished nodes $x_{L}=\{(1,1),(1,2)\}$ and $x_{H}=\{(1,3),(1,4)\}$. The set of nodes is

$$\begin{aligned} N = \left\{ W, x_{L}, x_{H},\left( \{a\}\times \{1,2,3,4\}\right) _{a\in [0,1)},\left( \{w\}\right) _{w\in W}\right\} \end{aligned}$$

once again ordered by set inclusion.

The sequence approach is cumbersome in this example. Following the pioneering work in this approach (Harris 1985b), one examines each stage of the game and endows each player with a fixed universal set of actions for that stage. In Harris’s (1985b) approach, this is without loss of generality, because a later restriction reduces the resulting product set to the subset of plays, incorporating all constraints given by the game. In the present example, the natural choice of the (compact) action set for player 1 is $A_1=[0,1]\times \{\hbox {Low}, \hbox {High}\}$, since this player may (but need not) choose both a and either High or Low. For player 2, the natural choice is $A_2 = \{1,2,3,4\}$. This results in the product space $A=A_1\times A_2=[0,1]\times \{\hbox {Low}, \hbox {High}\}\times \{1,2,3,4\}$, which is strictly larger than the actual set of outcomes W. Again following Harris (1985b), the structure of the game is recovered by restricting attention to the set H of plays, a subset of A. First, all plays must be included where player 1 sets $a<1$, which yields the subset $H_1=\left\{ ((a,\mathrm{Low}),n)\;\left| \; \; a<1\right. \right\}$. In this set, the coordinate Low is merely a marker which does not constrain the future choices of player 2. (We could instead use High as a marker, or a third marker which would complicate things even further, but some marker is needed because the sequence approach is based on a product construction.) Second, all plays must be included where player 2 sets $a=1$, which must then incorporate the appropriate constraint on player 2’s choice. This yields the set $H_2=\{((1,\mathrm{Low},1),(1,\mathrm{Low},2),(1,\mathrm{High},3),(1,\mathrm{High},4)\}$. The set of plays is the subset of $[0,1]\times \{\mathrm{Low},\mathrm{High}\}\times \{1,2,3,4\}$ given by $H = H_{1}\cup H_{2}$.

The fact that the sequence approach results in artificially enlarged product sets creates a conceptual difficulty in games which do not have a straightforward stage structure, as Example 3. In his existence theorem, Harris (1985b) assumes that the action sets $A_i$ are compact and separated, which is unproblematic with the construction given above and the (natural) Euclidean topologies on the sets $A_i$. Yet, a further, crucial assumption requires the set H to be a closed subset of A. This property is not guaranteed by the construction. Consider the sequence $w_{n} = \left( \left( a_{n}, \hbox {Low}\right) , 4\right)$ with $0\le a_{n} < 1$ for all $n =1 , 2,\ldots$ and $a_{n}\rightarrow _{n\rightarrow \infty } 1$. Then $w_{n}\in H$ for all $n = 1, 2, \ldots$, but $w_{n}\rightarrow _{n\rightarrow \infty }\left( \left( 1, \hbox {Low}\right) , 4\right) \not \in H$. Hence, the existence theorem in Harris (1985b) does not apply because its assumptions are not fulfilled: Compactness has been lost purely because of the construction. However, this game has a subgame perfect equilibrium for any assignment of continuous payoffs to players. This can be shown by applying the existence theorem in Alós-Ferrer and Ritzberger (2016), whose assumptions do cover this example. We show it here directly.

Let $U_1$ and $U_2$ be continuous payoff functions for players 1 and 2. For each $a\in [0,1]$ (including $a=1$), let F(a) be the number n that maximizes $U_2$ in the set $\{(a,1),(a,2),(a,3),(a,4)\}$. The correspondence $F:[0,1]\mapsto \{1,2,3,4\}$ is u.h.c. by the maximum theorem. Further, since both the domain and the codomain are metrizable and compact, the graph of F is a closed subset of W, hence compact. Let $(a^*,n^*)$ maximize the continuous function $U_1$ on the graph of F. Let f be a selection from F such that $f(a^*)=n^*$. Further, let $n^{\mathrm{Low}}\in \{1,2\}$ and $n^{\mathrm{High}}\in \{3,4\}$ maximize $U_2(1,n)$ on the sets $\{1,2\}$ and $\{3,4,\}$, respectively.

Note that $f(1)\in \{n^{\mathrm{Low}},n^{\mathrm{High}}\}$. Suppose $f(1)=n^{\mathrm{Low}}$ (the argument if $f(1)=n^{\mathrm{High}}$ is symmetric). Hence, $U_1(a^*,n^*)\ge U_1(1,n^{\mathrm{Low}})$. Suppose $U_1(a^*,n^*)\ge U_1(1,n^{\mathrm{High}})$. Then there is a subgame perfect equilibrium where player 1 chooses $a^*$ and player 2 chooses f(a) for each $a<1$, $n^{\mathrm{Low}}$ after $(1,\mathrm{Low})$, and $n^{\mathrm{High}}$ after $(1,\mathrm{High})$. Alternatively, suppose $U_1(a^*,n^*)< U_1(1,n^{\mathrm{High}})$. Then there is a subgame perfect equilibrium where player 1 chooses $(1,\mathrm{High})$ and player 2 chooses as above.

Example 3 illustrates that the sequence approach can artificially enlarge the relevant set in such a way that seemingly technical conditions are violated and the analysis of a game becomes unnecessarily complex. This may lead to a failure of existence theorems based on the sequence approach, even though existence holds and is readily obtained under our approach (this example is covered by the existence theorem in Alós-Ferrer and Ritzberger 2016). The next example revisits Example 1 and shows that the problems of the sequence approach can actually lead to the consideration of artificial product sets that are far larger than the relevant outcome sets.

Example 4

Recall Example 1. Player 1 can either decide on the whole pair (a, b) with $a<1$ or fix $a=1$, and let player choose b. Constructing the set of nodes is again simple. Let again $W = \left[ 0, 1\right] ^2$ be the set of plays. The root and the “terminal” nodes are as in the previous example, but this time there is only one intermediate node (player 2’s only decision point), namely the set $\{1\}\times \left[ 0, 1\right]$ where $a=1$ has been fixed but b remains to be decided. The set of nodes is hence

$$\begin{aligned} N = \left\{ W,\{1\}\times \left[ 0, 1\right] ,\left( \{w\}\right) _{w\in W}\right\} \end{aligned}$$

again ordered by set inclusion.

The sequence approach is again cumbersome in this example. Following Harris (1985b), the natural choice of the action set for player 1 is $A_1 = \left[ 0, 1\right] ^2$, since this player may (but need not) choose both a and b. For player 2, the action set is clearly $A_2 = \left[ 0, 1\right]$. This results in the product space $A = A_{1}\times A_{2} = \left[ 0, 1\right] ^3$. That is, the sequence approach turns a two-dimensional object into a three-dimensional one. To recover the structure of the game, we must consider the set H of plays (viewed as sequences) as a subset of A. In the present case, this must include all plays where player 1 has fixed both a and b, and player 2 does not get to choose. This requires the subset $H_1 = \left\{ \left( \left( a, b_{1}\right) , b_{2}\right) \;\left| \; \; b_1 = b_2,\ a < 1\right. \right\}$ to be one part of the set of plays. The fact that player 2 does not decide on b is incorporated in $H_1$ by the restriction that $b_2 = b_1$. The set $H\subseteq A$ must also include all plays where player 1 has chosen $a = 1$ and player 2 decides on $b\in \left[ 0, 1\right]$. This gives the set $H_2 = \left\{ \left( \left( a, 0\right) , b\right) \;\left| \; \; a = 1, b\in \left[ 0, 1\right] \right. \right\}$. The coordinate 0 in $\left( a, 0\right)$ is an arbitrary marker indicating that player 1 does not actually decide on b. Any other marker would also do, but it would be incorrect to write $\left( a, b\right)$, because if $a = 1$, player 2’s choice of b is unconstrained by player 1’s decision. The set of plays finally is the subset of $[0,1]^3$ given by $H = H_{1}\cup H_{2}$.

The point of this example is that the phenomenon illustrated in Example 3 is not peculiar to that example. The sequence approach unnecessarily blows up the relevant outcome space into a potentially large product set (even requiring additional dimensions). Ultimately, the reason for the difficulties above is that the sequence approach naturally leads to a Tychonoff construction, which first identifies the action sets at each stage, then imposes topological constraints on those, and finally takes the product set. The construction then needs to be “patched up” by adding additional assumptions which need not be guaranteed in well-behaved examples. In Example 3, existence of equilibria holds, but previous existence theorems do not apply, because the construction seems to destroy compactness (even though the set of plays is compact in the natural topology). In Example 4, an analogous argument shows that the set H is not a closed subset of A. Indeed, consider the sequence $w_{n} = \left( \left( a_{n}, 1\right) , 1/2\right)$ with $0\le a_{n} < 1$ for all $n =1, 2,\ldots$ and $a_{n}\rightarrow _{n\rightarrow \infty } 1$. Then $w_{n}\in H$ for all $n = 1, 2, \ldots$, but $w_{n}\rightarrow _{n\rightarrow \infty }\left( \left( 1, 1\right) , 1/2\right) \not \in H$. Hence, the approach of Harris (1985b) does not work. However, this obscures the fact that failure of compactness is not the reason for the failure of existence in Example 4. Compactness assumptions are immediately fulfilled under our approach, for the outcome space $W=[0,1]^2$ is compact under the natural topology, and this is the set of interest. As will be discussed below, the reason for the failure of existence in this example is the failure of a completely different condition that concerns the structure of the tree and not of the outcome space. In summary, what Example 4 shows is that the search for necessary topological conditions is better undertaken under our approach, for otherwise one needs to consider additional, extraneous conditions relating the product set of actions and the set of plays viewed as a subset thereof. An analysis of which conditions are necessary cannot be carried out under the sequence approach, because artificial conditions have been introduced there that obscure the analysis.

2.2 Extensive form games of perfect information

For the reasons pointed out above, we follow the original approach by von Neumann and Morgenstern. In its generalized form, this approach is already well established in the literature. We have used it in our previous work on large extensive form games, in particular Alós-Ferrer and Ritzberger (2005, 2008, 2013, henceforth AR1, AR2, and AR3, respectively). These papers develop the concept of a game tree, show that viewing nodes as sets of plays ordered by set inclusion is without loss of generality (AR1), characterize the class of game trees for which every pure strategy combination induces an outcome and does so uniquely (AR2; see also Alós-Ferrer et al. 2011), and characterize discrete game trees and the associated extensive forms (AR3). In this paper, however, a relatively small part of the formalism is needed, because only games of perfect information are considered, and those are relatively simple.

Formally, we work with discrete game trees as introduced in AR3, which are defined as follows (see also Ritzberger 2001, Definition 3.1).¹

Definition 1

A discrete (rooted and complete) game tree $\left( N,\supseteq \right)$ is a collection of nonempty subsets $x\in N$ (the nodes) of a given set W (of plays or outcomes) partially ordered by set inclusion such that $W\in N$, $\left\{ w\right\} \in N$ for all $w\in W$, and

(GT1) $h\subseteq N$ is a chain² if and only if there is $w\in W$ such that $w\in \cap _{x\in h}x$,

(GT2) every chain in the set $X=N{\setminus }\left\{ \left\{ w\right\} \right\} _{w\in W}$ (of moves) has a maximum, and it either has an infimum in the set $E=\left\{ \left\{ w\right\} \right\} _{w\in W}$ (of terminal nodes) or it has a minimum.³

Property (GT1) requires that if two nodes have a nonempty intersection, then one contains the other (“Trivial Intersection”), and that all chains have a nonempty intersection (“Boundedness”). Property (GT2) is discreteness. Its first part (the existence of maxima) essentially states that nodes have immediate successors, which are the maxima of maximal chains of successors (AR2, p. 235). This property is called “up-discreteness” and is necessary for every pure strategy combination to induce a unique play/outcome (AR2, Theorem 6 and Corollary 5; see also Alós-Ferrer et al. 2011). Its second part (the existence of minima or infima) implies that every move is reached after finitely many decisions (AR3, Theorem 1). This property, called “down-discreteness,” is satisfied in all standard applications and greatly simplifies the formalism, without excluding large action spaces or an infinite horizon. (Property (GT2) excludes games in continuous time, though.)

For each node $x\in N$ define the up-set (“the past”) $\uparrow \!\!x$ and the down-set (“the future”) $\downarrow \!\!x$ by

$$\begin{aligned} \uparrow \!\! x=\left\{ y\in N\left| y\supseteq x\right. \right\} \quad \text { and }\quad \downarrow \!\! x=\left\{ y\in N\left| x\supseteq y\right. \right\} \text {. } \end{aligned}$$

(1)

By the if-part of (GT1), $\uparrow \!\!x$ is a chain for all $x\in N$. A play is a chain of nodes $h\subseteq N$ that is maximal in N, i.e., there is no $x\in N{\setminus } h$ such that $h\cup \left\{ x\right\}$ is a chain. Intuitively, a play is a complete history of all events along the tree, from the beginning (the root $W\in N$) to the “end”—if there is an end: Since infinite histories are allowed, plays need not be finite.

The advantage of game trees is that the set of plays can be one-to-one identified with the underlying set W (AR1, Theorem 3(c)). That is, for every ultimate outcome $w\in W$, the set $\uparrow \!\!\{w\}$ is a play, and for every play h, there exists a unique outcome w such that $h=\uparrow \!\!\{w\}$, or, equivalently, $\cap _{x\in h}x=\left\{ w\right\}$. Therefore, one can identify outcomes and plays. That is, an element $w\in W$ can be seen either as a possible outcome (element of some node) or as a play (maximal chain of nodes). Henceforth, we will not distinguish between plays and outcomes. A node can then be identified with the set of plays passing through it, and the underlying set W represents all plays.

For a discrete game tree $\left( N,\supseteq \right)$, let (by a slight abuse of notation) $W:N\twoheadrightarrow W$ denote the correspondence⁴ that assigns to every node, viewed as an element of the tree, the set of its constituent plays, that is, the node itself viewed as a set of plays, i.e., $W\left( x\right) =x$ for all $x\in N$. For a set $Y\subseteq N$ of nodes, write $W\left( Y\right) =\cup _{x\in Y}x\subseteq W$ for the union, and refer to $W\left( Y\right)$ as the plays passing through Y.

In an extensive form game, every node which has proper successors corresponds to a decision point where some player is active. In contrast, nodes (if any) “at the end” of the tree do not capture decisions. Formally, for a discrete game tree, $\left( N,\supseteq \right)$ a node $x\in N$ is terminal if $\downarrow \!\!x = \{x\}$. A node is a move if it is not terminal. It can be shown (see AR2, Lemma 1, and AR3, Lemma 3(b)) that a node $x\in N$ in a discrete game tree is terminal if and only if there is $w\in W$ such that $x=\left\{ w\right\}$. Hence, the set $E=\left\{ \left\{ w\right\} \right\} _{w\in W}$ introduced in (GT2) coincides with the set of terminal nodes. Likewise, the set $X=N{\setminus } E$ is the set of moves.

In discrete game trees, no move is reached “in the limit” after infinitely many decisions. That is, if a node is at the end of an infinite chain of decisions (as, e.g., in the case of an infinite horizon), it is necessarily a terminal node. Yet, some terminal nodes can also be reached after finitely many decisions. These properties were demonstrated in AR3 using the concept of finite and infinite nodes. A node $x\in N{\setminus }\left\{ W\right\}$ is finite if $\uparrow \!\!x{\setminus }\left\{ x\right\}$ has a minimum and infinite if $x=\inf \uparrow \!\!x{\setminus }\left\{ x\right\}$. By Proposition 3 of AR3 in a discrete game tree, every node is either finite or infinite. By Theorem 1(c) of AR3, all moves are finite (equivalently, every infinite node is terminal).

Denote by $F\left( N\right)$ the set of finite nodes together with the root $W\in N$. On this set, a function $p:F\left( N\right) \rightarrow X$ can be defined that assigns to every finite node its immediate predecessor. Namely, for each $x\in F\left( N\right) {\setminus }\left\{ W\right\}$ let

$$\begin{aligned} p\left( x\right) =\min {\uparrow } x{\setminus }\left\{ x\right\} \end{aligned}$$

(2)

and $p\left( W\right) =W$ by convention. Hence, $x\subset p\left( x\right) =\cap \left\{ y\left| y\in \uparrow x{\setminus }\left\{ x\right\} \right. \right\}$ for all $x\in F\left( N\right) {\setminus }\left\{ W\right\}$.

Since every move is a finite node, the nodes of a discrete game tree $\left( N,\supseteq \right)$ with set W of plays can be partitioned as follows. Namely, let $Y_{0}=\left\{ W\right\}$ and $Y_{t}=\left\{ x\in N\left| p^{t-1}\left( x\right) \subset p^{t}\left( x\right) =W\right. \right\}$ for all $t=1,2,\ldots$ Nodes in the slice $Y_{t}$ are pairwise disjoint: For, if $x\cap y\ne \varnothing$, then by the if-part of (GT1) either $y\subset x$ or $x\subseteq y$, so that either $y\in Y_{t}$ implies $x\in Y_{t-k}$ for some $k>0$ or $x\in Y_{t}$ implies either $y=x$ or $y\in Y_{t-k}$ for some $k>0$.⁵ Infinite (terminal) nodes do not belong to any slice.

For instance, in Example 1, the slice $Y_1$ consists of terminal nodes $\left\{ \left( a, b\right) \right\} \in N$ with $a < 1$ plus the move $\{1\}\times \left[ 0, 1\right]$. The slice $Y_2$ consists of the terminal nodes $\left\{ \left( 1, b\right) \right\} \in E$ only. In Example 3, the slice $Y_1$ consists of moves of the form $\{a\}\times \{1,2,3,4\}$ with $a<1$ plus the two distinguished nodes $x_{L}=\{1\}\times \{1,2\}$ and $x_{H}=\{1\}\times \{3,4\}$.

In order to define general extensive form games, one needs the concept of choices and the derived concept of information sets. That framework has been developed in AR1 and AR2 and specialized to discrete trees in AR3. However, since this paper deals only with perfect information, it is sufficient to determine a game by the tree, the set of players, their decision points, and their preferences on W.

Definition 2

An extensive form game with perfect information (EFPI) is a tuple $\left( T,I,\mathcal {X},\precsim \right)$, where $T=\left( N,\supseteq \right)$ is a discrete game tree, I is the (possibly infinite) set of players, $\mathcal {X}=\left( X_{i}\right) _{i\in I}$ is a partition of the set of moves X of the tree T into the sets of decision points for players $i\in I$, and $\precsim \,=\left( \precsim _{i}\right) _{i\in I}$ is a profile of complete, reflexive, and transitive binary relations on the set of plays W of T, one preference relation $\precsim _i$ for each player $i\in I$.

In an EFPI at every move $x\in X$, the player, for whom $x\in X_i$, makes a decision and selects an immediate successor⁶ $y\in p^{-1}(x)$. Moves of nature are ruled out. For the present purpose, this is natural, because existence of subgame perfect equilibria may be destroyed by the presence of chance moves (Luttmer and Mariotti 2003).

A pure strategy for player $i\in I$ in an EFPI $\left( T,I,\mathcal {X},\precsim \right)$ is a function $s_{i}:X_{i}\rightarrow N$ such that $p(s_i(x))=x$ for all $x\in X_i$, i.e., a function that specifies which of the immediate successors of each $x\in X_i$ is chosen by player i. The set $S_{i}$ of all such functions is player i’s pure strategy space. A (pure) strategy combination is a tuple of pure strategies, one for each player.

A subgame of an EFPI is the perfect information game that starts at some move $x\in X$. Under perfect information, every move $x\in X$ is the root of a subgame. For every $x\in X$, there is a function $\phi _{x}:S\rightarrow x$ which assigns to the subgame starting at $x\in X$ the play $\phi _{x}\left( s\right) \in x$ that the strategy combination $s\in S$ (uniquely) induces in the subgame starting at x. Formally this follows from AR3, Theorem 3, and AR2, Theorems 2 and 6, and Corollary 5.

Since every strategy combination induces a unique outcome, preferences on plays induce preferences on strategy combinations. A (pure) Nash equilibrium is a pure strategy combination $s\in S$ such that no player has an incentive to deviate from it. A (pure) subgame perfect equilibrium (SPE; Selten 1965) is a pure strategy combination that induces a Nash equilibrium in every subgame.

2.3 Well-behaved perfect information games

The description of an extensive form game entails two levels. The tree provides an “objective” description of the potential events. Choices, the assignment of decision points, and preferences bring in the decision makers and make the tree into a game. Accordingly, an EFPI may fail to have an SPE for two sets of reasons. One has to do with the topology $\tau$ on the set W of plays of the tree (the first level), the other with the game (the second level). The former will be studied in detail in later sections. The latter is readily explained here.

For instance, the preference relations may not be continuous.⁷ If a single player chooses $a\in \left[ 0,1\right]$ from the unit interval (endowed with the relative Euclidean topology) such that $a\prec _{1}a^{\prime }\Leftrightarrow a<a^{\prime }$ for all $a,a^{\prime }\in \left[ 0,1\right)$, but $1\precsim _{1}\bar{a}$ for some $\bar{a}<1$, then there is no equilibrium. This existence failure is caused by the preferences $\precsim _{1}$.⁸

Alós-Ferrer and Ritzberger (2016) point out that a further problem, which potentially prevents equilibrium existence, may arise from the assignment $\mathcal {X}=\left( X_{i}\right) _{i\in I}$ of decision points. The associated example is as follows (Example 2 of Alós-Ferrer and Ritzberger 2016).

Example 5

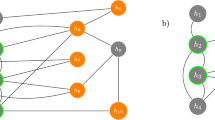
Let $W=\left[ 0,1\right] ^{2}$ and $N=\left\{ W,\left( \left\{ a\right\} \times \left[ 0,1\right] \right) _{a\in \left[ 0,1\right] },\left( \left\{ w\right\} \right) _{w\in W}\right\}$ be the set of plays and nodes, respectively, and for three players, $I=\left\{ 1,2,3\right\}$, let $X_{1}=\left\{ W\right\}$, $X_{2}=\left\{ \left( \left\{ a\right\} \times \left[ 0,1\right] \right) _{a\in \left[ 0,1/2\right) }\right\}$, and $X_{3}=\left\{ \left( \left\{ a\right\} \times \left[ 0,1\right] \right) _{a\in \left[ 1/2,1\right] }\right\}$ (see Fig. 1). Endow W with the relative Euclidean topology of the plane, making W compact and all nodes closed. Preferences are represented by the continuous payoff functions $U_{1}\left( a,b\right) =a\left( 1-b\right)$, $U_{2}\left( a,b\right) =-b$, and $U_{3}\left( a,b\right) =b$, where $w=\left( a,b\right) \in W$. Player 3 will optimally choose $b=1$, and player 2 will choose $b=0$. Thus, player 1’s value function yields a if $a<1/2$ and zero if $a\ge 1/2$ and has no maximum.

Fig. 1

Graphical representation of Example 5. Player 1 chooses a number a in [0, 1], then either player 2 (if $a<1/2)$ or player 3 (if $a\ge 1/2$) chooses another number in [0, 1]

In this example, the union of the decision points for player 2 in the slice $Y_{1}$ is not closed, even though all individual nodes are closed. And this is the reason for why there is no equilibrium.

In other words, the two objects $\mathcal {X}$ and $\precsim$ that make a tree into an EFPI need to satisfy conditions with respect to the topological space $\left( W,\tau \right)$ in order to admit existence of equilibrium. To isolate these conditions, they are summarized in the next definition of a “well-behaved” perfect information game.

Definition 3

An EFPI $\left( T,I,\mathcal {X},\precsim \right)$ is well behaved with respect to a topology $\tau$ on W if

• (WB1) for each $t=0,1,\ldots$ the nonterminal part $Y_{t}{\setminus } E$ of the slice $Y_{t}$ is partitioned into finitely many nonempty cells of the form $Y_{it}=X_{i}\cap Y_{t}$ with $i\in I$ such that $W\left( Y_{it}\right)$ is closed in $\tau$ for all $i\in I$;

• (WB2) for each player $i\in I$, the preference relation $\precsim _{i}$ is continuous with respect to the topology $\tau$.

For instance, Example 5 fails (WB1), while Example 1 fulfills it, as the only move other than the root, $\{1\}\times \left[ 0, 1\right] \in Y_1$, is a closed set of plays. Example 3 also fulfills (WB1), because player 2 decides at all nodes in the intermediate slice $Y_1$ and $W(Y_1)=W$.

The definition of well-behaved perfect information games restricts the analysis to preferences that are continuous with respect to the topology $\tau$, (WB2), and rules out ill-behaved assignments of decision points, (WB1). Hence, both problems that could surface when the tree is turned into a game, with the preference relations $\precsim$ and with the assignment of decision points $\mathcal {X}$, are taken care of.

The objective here is to characterize the class of topologies on the set of plays of a given tree such that all well-behaved perfect information games defined on that tree admit a subgame perfect equilibrium. This is reflected by the following definition.

Definition 4

The topology $\tau$ on the set W of plays of a discrete game tree $\left( N,\supseteq \right)$ admits equilibrium analysis if some well-behaved EFPI can be defined on it and every EFPI that is well behaved with respect to $\tau$ has an SPE.

If a topology $\tau$ does not admit equilibrium analysis, then there will be a perfect information game on this tree with this topology that does not have an equilibrium, even though preferences are continuous and decision points are suitably assigned. Thus, Definition 4 captures a minimal requirement on a topology. It is also natural to require that a topology only admits equilibrium analysis if some well-behaved EFPI can be defined on it. This is merely a nontriviality requirement. For, otherwise a topology would trivially admit equilibrium analysis when no well-behaved EFPI can be defined on it. This is illustrated in the following example.

Example 6

Let $W=\left[ 0,1\right] ^{2}$ and $\left( N,\supseteq \right)$ be given by

$$\begin{aligned} N=\left\{ W,\left( \left\{ a\right\} \times \left[ 0,1\right] \right) _{a\in \left[ 0,1/2\right) },\left( \left\{ w\right\} \right) _{w\in W}\right\} . \end{aligned}$$

Denote by $\tau \left| W\left( Y_{t}\right) \right.$ the topology $\tau$ relative to $W\left( Y_{t}\right)$ for all $t=0,1,\ldots$ ⁹ Here this is the Euclidean topology relative to $W\left( Y_{0}\right) = W\left( Y_{1}\right) =\left[ 0,1\right] ^{2}$ and $W\left( Y_{2}\right) =\left[ 0,1/2\right) \times \left[ 0,1\right]$. Then $W\left( Y_{1}\cap X\right) =\left[ 0,1/2\right) \times \left[ 0,1\right]$ is not closed relative to $W\left( Y_{1}\right)$. But by (WB1), the moves in this slice, $Y_{1}{\setminus } E=Y_{1}\cap X$, must be partitioned into finitely many cells $Y_{i1}$ with $i\in I$ such that each $W\left( Y_{i1}\right)$ is closed, so that $W\left( Y_{1}\cap X\right)$ must be closed as a finite union of closed sets—a contradiction.

3 Tree topology

There are precisely two conditions that a topology $\tau$ on the set W of plays has to respect in order to admit equilibrium analysis. They are neither about preferences $\precsim$ nor about the assignment $\mathcal {X}$ of decision points. Rather, they both reflect the relation between nodes and plays.

Theorem 1

For a discrete game tree $\left( N,\supseteq \right)$ with set W of plays, every perfectly normal¹⁰ topology $\tau$ on W that admits equilibrium analysis satisfies

• (CN) $W{\setminus } x\in \tau$ for all $x\in N$, and

• (OP) for all $t=0,1,\ldots$ and all sets $V\subseteq Y_{t+1}$ of nodes, if $W\left( V\right) \in \tau \left| W\left( Y_{t+1}\right) \right.$, then $W\left( p\left( V\right) \right) \in \tau \left| W\left( Y_{t}\right) \right.$.

Before proceeding to the proof (in the next subsection), the two properties (CN) and (OP) are briefly discussed. The “closed nodes” property (CN) requires that all nodes are closed as sets of plays. If it fails, simple counterexamples to existence of SPE can be constructed. For instance, if $W=\left[ 0,2\right]$ were endowed with the relative Euclidean topology and $N=\left\{ W, \left[ 0,1\right) , \left[ 1,2\right] , \left( \left\{ w\right\} \right) _{w\in W}\right\}$, then a single player maximizing the continuous payoff function $U_{1}\left( w\right) =w$ at the node $\left[ 0,1\right) \in N$ would not be able to do so.

The “open predecessors” condition (OP) requires that if the union of a set of nodes in a slice is open, then the union of its immediate predecessors is also open. Intuitively, if a node y in a slice $Y_{t+1}$ is slightly perturbed, then this translates into a slight perturbation of its predecessor $x = p\left( y\right)$. This is a “pasting condition” that can also be stated in a topology on nodes.

Specifically, because nodes in a slice $Y_t$ are pairwise disjoint, the projection $\text {proj}_{t}: W\left( Y_t\right) \rightarrow Y_t$ is uniquely defined by $w\in \text {proj}_{t}\left( w\right)$ for all $w\in W\left( Y_t\right)$. The quotient topology is the finest topology on $Y_t$ that makes the projection $\text {proj}_t$ continuous when $W\left( Y_t\right)$ is endowed with the relative topology induced by $\tau$. It is not difficult to show that a set of nodes in a slice $Y_t$ is open in the quotient topology if and only if its union is open as a set of plays (see Lemma 2 of Alós-Ferrer and Ritzberger 2016). Hence, the quotient topology is a perfectly natural choice. With this topology on nodes in a slice (OP) states that the function $p : Y_{t+1}\rightarrow Y_t$ from (2) restricted to slices maps open sets to open sets, i.e., it is an open map. Theorem 17.7 of Aliprantis and Border (1999, p. 560) shows that this is equivalent to lower hemi-continuity of the immediate successor correspondence.

Example 7

Recall Example 3. All nodes except the root are finite and, hence, (CN) follows immediately since we adopt the (relative) Euclidean topology on $W=[0,1]\times \{1,2,3,4\}$. Consider condition (OP). For $Y_1$ this condition is trivially fulfilled, since the predecessor of any node in this slice is the root. Hence, (OP) only needs to be verified for $Y_3$. In this slice, all nodes are terminal, and $W(Y_3)=W(Y_2)=W$. Let V be a set of nodes in $Y_3$ such that W(V) is open. Condition (OP) requires that the set W(p(V)) is also open. Let $(a,n)\in W(p(V))$ with $a<1$. This implies that $(a,n') \in W(V)$ for some $n'$. Since W(V) is open in W, the projection of V on [0, 1] is an open set and hence contains an open neighborhood B of $(a,n')$. Then $B\times \{1,2,3,4\}$ is an open neighborhood of (a, n) in W(p(V)). Let now $(1,n)\in W(p(V))$, and suppose $(1,n)\in x_{L}=\{(1,1),(1,2)\}$ (the case where it is in $x_{H}$ is analogous). Hence, there is $(1,n')\in W(V)\cap x_{L}$. By an analogous argument as above, the projection of V on [0, 1] is an open set, and hence it contains an open neighborhood $B'$ of $(a,n')$ in that open set. Then, $\left( B' \cap [0,1)\right) \times \{1,2,3,4\} \cup \{(1,1),(1,2)\}$ is an open set contained in W(p(V)) that contains (1, n). Therefore, W(p(V)) is open in $W(Y_2)=W$, completing the proof of (OP).

Example 8

Condition (OP) is what fails in Example 1 (recall also Example 4) when the unit square $W = \left[ 0, 1\right] ^2$ carries the relative Euclidean topology. Consider the set $V = \left\{ \{\left( 1, b\right) \}\vert \ 1/2 - \varepsilon < b < 1/2 + \varepsilon \right\} \subseteq Y_2$, for some $\varepsilon \in \left( 0, 1/2\right)$, of terminal nodes reached after player 2 has decided. The set $W\left( V\right) \subseteq W\left( Y_2\right)$ is clearly relatively open; hence, V is open in the quotient topology on $Y_2$. Its immediate predecessor set $p\left( V\right)$, though, consists of the singleton $\{1\}\times \left[ 0, 1\right] \in X$, which is not open. Hence, (OP) fails in this example. This shows that the ultimate reason for the failure of existence in this example is a violation of (OP), that is, a problem with the specification of the tree, and not a failure of compactness in a derived Tychonoff construction.

Some form of property (OP) has always been assumed, to the best of our knowledge, in previous proofs of existence of SPE for perfect information games without much ado, even though sometimes in disguised form. For instance, in the formalism of Harris (1985b, p. 618, Assumption 4), it shows up as lower hemi-continuity¹¹ of the “action correspondence.” Harris (1985b, p. 618) calls this property “curious.” Apparently it has not been recognized so far that (OP) is necessary for existence of SPE. Further, the assumptions of Harris (1985b) also imply upper hemi-continuity (and hence full continuity) of the action correspondence, which is not necessary in the present setting (as shown by Example 7 of Alós-Ferrer and Ritzberger 2016).

A topology $\tau$ on the set W of plays of a discrete game tree $\left( N,\supseteq \right)$ that satisfies (CN) and (OP) will henceforth be called a tree topology. With this terminology, Theorem 1 states that every perfectly normal topology that admits equilibrium analysis must be a tree topology.

3.1 A characterization

In a companion paper (Alós-Ferrer and Ritzberger 2016), sufficient conditions were established for the existence of SPE in well-behaved perfect information games. In that paper, for a given game tree $T =\left( N,\supseteq \right)$, a compact topology that fulfills (CN) is called T-admissible. The main result of the paper states that every separated¹² T-admissible topology that satisfies (OP) admits equilibrium analysis (Alós-Ferrer and Ritzberger 2016, Theorem 1).

Even though this is the most general existence theorem in the literature for SPE in perfect information games with continuous preferences, without Theorem 1 there would still be the possibility that the frontier can be pushed further. The main result of the present paper, though, makes sure that tree topologies are precisely what is needed for equilibrium analysis in large games. The two main hypotheses of the theorem in Alós-Ferrer and Ritzberger (2016), (CN) and (OP), are the conclusions in Theorem 1.

On the other hand, the sufficiency theorem uses one hypothesis that is neither a conclusion nor a hypothesis in Theorem 1: compactness. One may guess that this is actually also a necessary condition. Unfortunately, the underlying issue is undecidable, as will be discussed in more detail in Sect. 4.2. Furthermore, the sufficiency result uses a hypothesis that is implied by the hypothesis of Theorem 1, since every perfectly normal topology is separated. Adopting the stronger separation axiom plus compactness yields the following characterization.

Theorem 2

Let $T = \left( N,\supseteq \right)$ be a discrete game tree with set W of plays and $\tau$ a compact perfectly normal topology on W for which some well-behaved EFPI exists. Then, $\tau$ admits equilibrium analysis if and only if it is a tree topology.

Theorem 1 does not invoke compactness and hence is stronger than the only-if direction of Theorem 2. What is maintained is the separation axiom that $\tau$ is perfectly normal. This is a rather weak assumption, though. For, in practice, one may want to employ a topology that is, for instance, induced by a metric (as, e.g., in Hellwig and Leininger 1987) and, therefore, satisfies a much stronger separation axiom. In particular, every metric space is perfectly normal. Therefore, this hypothesis captures the relevant cases.

Of course, counterexamples to existence of SPE are not enough to establish the necessity of a tree topology, because the theorem says nothing about the tree nor about the particular topology (except for perfect normality). Therefore, the following subsection is devoted to the proof of Theorem 1.

3.2 Proof of Theorem 1

The proof proceeds by three lemmata and three propositions. The first step is to show that in a given slice $Y_t$, the sets of plays $W(Y_{t}\cap E)$ ending at $Y_t$ and those that do not, $W(Y_{t}\cap X)$, are closed. (This lemma is also needed in the companion paper on sufficiency, see Alós-Ferrer and Ritzberger 2016, Lemma 1.)

Lemma 1

Let $\tau$ be a topology on the set W of plays for a discrete game tree $T = \left( N,\supseteq \right)$ such that a well-behaved EFPI can be defined. Then, the sets $W(Y_t)$ and $W(Y_t\cap X)$ are closed in $\tau$, for all $t=1,2,\ldots$

Proof

Suppose that some well-behaved EFPI with respect to $\tau$ can be defined. Then the set $Y_t{\setminus } E=Y_t\cap X$ is partitioned into finitely many cells of the form $Y_{it}=X_i\cap Y_t$ for $i\in I$. Since nodes in a slice are disjoint, it follows that $W\left( Y_{t}\cap X\right)$ is partitioned into finitely many cells of the form $W\left( Y_{it}\right)$ for $i\in I$. Further, each $W\left( Y_{it}\right)$ is closed. Therefore, $W\left( Y_{t}\cap X\right)$ is closed as a finite union of closed sets. That also $W\left( Y_{t}\right)$ is closed in $\tau$ follows from $W\left( Y_{0}\right) =W$ and $W\left( Y_{t}\right) =W\left( Y_{t-1}\cap X\right)$ for $t=1,2,\ldots$

$\square$

Lemma 1 implies that if the topology admits equilibrium analysis—thus, a well-behaved EFPI can be defined—then, for a slice $Y_t$, the subsets $W\left( Y_{t}\right)$ of plays passing through nodes in $Y_t$ and $W\left( Y_{t}\cap X\right)$ of plays passing through moves in $Y_t$ are closed. The following is an immediate but important consequence of this fact.

Lemma 2

If a topology $\tau$ on the set W of plays for a discrete game tree $T = \left( N,\supseteq \right)$ admits equilibrium analysis, then any EFPI for which all moves in each slice are assigned to the same player, $Y_{t}\cap X=Y_{it}$ for some $i\in I$ for all $t=0,1,\ldots$, satisfies (WB1) from Definition 3.

If $\tau$ admits equilibrium analysis, by Lemma 1 the plays passing through moves in a slice $Y_t$ form a closed set in $\tau$. Therefore, the set $W\left( Y_t \cap E\right)$ of plays ending at the slice $Y_t$ must be relatively open in $\tau$. Yet, under the hypothesis of Theorem 1, that $\tau$ admits equilibrium analysis implies that this set is also closed.

Proposition 1

If a perfectly normal topology $\tau$ on the set W of plays for a discrete game tree $T = \left( N,\supseteq \right)$ admits equilibrium analysis, then the set $W\left( Y_t \cap E\right)$ of plays ending at slice $Y_t$ is closed, for all $t = 1,2,\ldots$

Proof

Suppose that for some $t=0,1,\ldots$ the set of plays $W\left( Y_{t}\cap E\right)$ passing through the terminal nodes in $Y_{t}$ is not closed. This implies that $Y_{t}\cap X\ne \varnothing$, because otherwise $W\left( Y_{t}\right) =W\left( Y_{t}\cap E\right)$ would be closed by Lemma 1. It follows that there is a cluster point $w_0$ of $W\left( Y_{t}\cap E\right)$ which does not belong to $W\left( Y_{t}\cap E\right)$. Since $W(Y_t\cap E)\subseteq W(Y_t)$ and the latter is closed by Lemma 1, it follows that $w_0\in W(Y_t)$, and hence $w_0\in W(Y_t\cap X)$. Since $w_{0}$ is a cluster point of $W\left( Y_{t}\cap E\right)$, for every neighborhood $u\in \tau$ of $w_{0}\in u$ there is $w\in u\cap W\left( Y_{t}\cap E\right)$. Fix such a neighborhood $u_{0}\in \tau$ of $w_{0}\in u_{0}$. Because $\left( W,\tau \right)$ is perfectly normal, Urysohn’s lemma (Aliprantis and Border 1999, p. 45) implies that there is a continuous function $f:W\rightarrow \left[ 0,1\right]$ such that $f^{-1}\left( 0\right) =W{\setminus } u_{0}$ and $f^{-1}\left( 1\right) =\left\{ w_{0}\right\}$, because singletons are closed in a perfectly normal (hence, in particular, T$_1$) space.

Assign all moves before $Y_{t}$ to player 1, $X_{1}=\cup _{k=0}^{t-1}\left( Y_{k}\cap X\right)$, and all moves from $Y_{t}$ onward to player 2, $X_{2}=\cup _{k\ge t}\left( Y_{k}\cap X\right)$. Preferences are represented by the continuous functions

$$\begin{aligned} U_{1}\left( w\right) =f\left( w\right) \quad \,{\text {and}}\,\quad U_{2}\left( w\right) =-f\left( w\right) \quad \,{\text {for all}}\, w\in W. \end{aligned}$$

By continuity of $U_{1}$ and $U_{2}$ and Lemma 2, this is a well-behaved EFPI.

For every $\lambda \in \left[ 0,1\right)$, player 1 can guarantee herself a payoff that is strictly larger than $\lambda$. For, the strict upper contour set $u_{\lambda }=\left\{ w\in W\left| U_{1}\left( w\right) >\lambda \right. \right\}$ is an open neighborhood of $w_{0}$ by continuity and, hence, there is $w'\in u_{\lambda }\cap W\left( Y_{t}\cap E\right)$, that is, there is $\left\{ w'\right\} \in Y_{t}\cap E$ such that $U_{1}\left( w'\right) >\lambda$. If player 1 picks $w'\in u_{\lambda }\cap W\left( Y_{t}\cap E\right)$, she obtains more than $\lambda$, since player 2 does not get to choose. Therefore, player 1 must obtain payoff $U_{1}\left( w\right) =1$ in any Nash equilibrium. $U_{1}\left( w\right) =1$ implies $w=w_{0}$, yet $\left\{ w_{0}\right\} \notin Y_{t}\cap E$. Hence, $w_{0}\in x_{0}$ for some $x_{0}\in Y_{t}\cap X=Y_{t}\cap X_{2}$. Since $x_{0}\in X$ and $E= \left\{ \left\{ w\right\} \right\} _{w\in W}$, there is $w'\in x_{0}{\setminus }\left\{ w_{0}\right\}$ such that $U_{2}\left( w'\right) >-1=U_{2}\left( w_{0}\right)$. Because player 2 controls all moves from $Y_{t}$ onward, picking $w'\in x_{0}$ constitutes a profitable deviation for player 2. Therefore, there is no Nash equilibrium and in particular no SPE.$\square$

It follows that for each slice $Y_t$, the sets $W\left( Y_t \cap X\right)$ of plays passing through moves and $W\left( Y_t \cap E\right)$ of plays ending at $Y_t$ are both open and closed (“clopen”) in $\tau$ whenever $\tau$ admits equilibrium analysis. Hence, the set of plays $W\left( Y_t\right)$ passing through a slice $Y_t$ cannot be connected when it contains terminal nodes.¹³

The last lemma states the obvious. The existence of subgame perfect equilibria for one-player EFPIs boils down to existence of maxima at every move.

Lemma 3

If a topology $\tau$ on the set W of plays for a discrete game tree $T = \left( N,\supseteq \right)$ admits equilibrium analysis, then every continuous preference relation $\precsim$ on W has a maximum at every move.

Proof

By Lemma 2 assigning all moves to a single player, i.e., $X_{1}=X$, endowed with continuous preferences $\precsim$ yields a well-behaved EFPI. By hypothesis, an SPE $s^*$ exists. Fix a move $x\in X$, and let $w^*=\phi _x(s^*)$ be the play induced by $s^*$ in the subgame starting at x. If $w'\succ w^*$ for some $w'\in x$, there is a strategy that picks $w'\succ w^*$ (since every play can be reached by some strategy profile by Theorem 4 of AR2). Hence, $w^*$ is a maximum of $\succeq$ at x.$\square$

With this preparation out of the way, we are ready to prove the first part of Theorem 1, the necessity of (CN).

Proposition 2

For a discrete game tree $T= \left( N,\supseteq \right)$ with set W of plays, every perfectly normal topology $\tau$ on W that admits equilibrium analysis satisfies (CN).

Proof

Suppose that for some $t=0,1,\ldots$ there is $x\in Y_{t}$ that is not closed. Then there is $w_{0}\in W{\setminus } x$ (a cluster point of x) such that for every neighborhood $u\in \tau$ of $w_{0}\in u$ there is $w\in u\cap x$. Fix such a neighborhood $u_{0}\in \tau$ of $w_{0}\in u_{0}$. Because $\left( W,\tau \right)$ is perfectly normal by hypothesis, Urysohn’s Lemma again implies that there is a continuous function $f:W\rightarrow \left[ 0,1\right]$ such that $f^{-1}\left( 0\right) =W{\setminus } u_{0}$ and $f^{-1}\left( 1\right) =\left\{ w_{0}\right\}$, as singletons are closed in a perfectly normal space. We claim that the preferences on W represented by the continuous function $U_{1}\left( w\right) =f\left( w\right)$ for all $w\in W$ have no maximum at the node x, in contradiction to Lemma 3.

To see the claim, it is enough to observe that for every $\lambda \in \left[ 0,1\right)$, the player can guarantee herself a payoff that is strictly larger than $\lambda$. For, the strict upper contour set $u_{\lambda }=\left\{ w\in W\left| U_{1}\left( w\right) >\lambda \right. \right\}$ is an open neighborhood of $w_{0}$ by continuity and, therefore, has a nonempty intersection with x. Choosing a play $w\in u_{\lambda }\cap x$, the player obtains more than $\lambda$. But the maximal payoff 1 remains infeasible, because $U_{1}\left( w\right) =1$ implies $w=w_{0}\notin x$. Therefore, the payoff function has no maximum at x.$\square$

The last step is to establish the necessity of the open predecessor condition (OP). This will then complete the proof of Theorem 1.

Proposition 3

For a discrete game tree $T= \left( N,\supseteq \right)$ with set W of plays, every perfectly normal topology $\tau$ on W that admits equilibrium analysis satisfies (OP).

Proof

If (OP) fails, then for some $t=0,1,\ldots$ there is a set $V\subseteq Y_{t+1}$ of nodes such that $W\left( V\right) \in \tau \left| W\left( Y_{t+1}\right) \right.$, but $W\left( p\left( V\right) \right) \notin \tau \left| W\left( Y_{t}\right) \right.$, where $p\left( V\right) =\left\{ p\left( y\right) \left| y\in V\right. \right\}$. It follows that the set $W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \notin p\left( V\right) \right. \right\} \right)$ is not closed in $\tau \left| W\left( Y_{t+1}\right) \right.$. For, if it were, then its complement would be open in $\tau \left| W\left( Y_{t+1}\right) \right.$, i.e., there would be $v\in \tau$ with $W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \in p\left( V\right) \right. \right\} \right) =v\cap W\left( Y_{t+1}\right)$. Since $W\left( Y_{t}\cap E\right)$ is closed by Proposition 1, $v'=v{\setminus } W\left( Y_{t}\cap E\right) \in \tau$ as the complement of a closed set, hence,

$$\begin{aligned} W\left( p\left( V\right) \right) =W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \in p\left( V\right) \right. \right\} \right) =v\cap W\left( Y_{t+1}\right) =v'\cap W\left( Y_{t}\right) \end{aligned}$$

would be open in $\tau \left| W\left( Y_{t}\right) \right.$, in contradiction to the hypothesis that $W\left( p\left( V\right) \right) \notin \tau \left| W\left( Y_{t}\right) \right.$.

That $W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \notin p\left( V\right) \right. \right\} \right)$ is not closed implies that there exists some $w_{0}\in W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \in p\left( V\right) \right. \right\} \right)$ such that for every neighborhood $\hat{v}\in \tau$ of $w_{0}\in \hat{v}$, there is some $w\in \hat{v}{\setminus }\left\{ w_{0}\right\}$ with $w\in W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \notin p\left( V\right) \right. \right\} \right)$. Let $y_{0}={{\text {proj}}}_{t+1}\left( w_{0}\right) \in Y_{t+1}$ be the unique node in $Y_{t+1}$ such that $w_{0}\in y_{0}$. Then $y_{0}$ does not belong to V, i.e., $y_{0}\notin V$. For, if it did, then, with $\hat{v}\in \tau$ such that $\hat{v}\cap W\left( Y_{t+1}\right) =W\left( V\right)$, that $w_{0}\in y_{0}\subseteq \hat{v}$ would imply that there is some $w'\in \hat{v}{\setminus }\left\{ w_{0}\right\}$ with $p\left( {\text {proj}}_{t+1}\left( w'\right) \right) \notin p\left( V\right)$ even though $w'\in \hat{v}$ implies ${\text {proj}}_{t+1}\left( w'\right) \in V$, a contradiction. On the other hand, $w_{0}\in W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \in p\left( V\right) \right. \right\} \right)$ implies that $p\left( y_{0}\right) \in p\left( V\right)$, and the latter implies that there is some $y_{1}\in V$, $y_1\ne y_0$, such that $p\left( y_{1}\right) =p\left( y_{0}\right)$. Let $\bar{x}=p\left( y_{0}\right) =p\left( y_{1}\right) \in Y_{t}$.

Choose $w_{1}\in y_{1}\in p^{-1}\left( \bar{x}\right) \cap V$, and recall that $w_{0}\in y_{0}\in p^{-1}\left( \bar{x}\right) {\setminus } V$. Because $\left( W,\tau \right)$ is separated, there are $u_{0},\hat{u}_{1}\in \tau$ such that $w_{0}\in u_{0}$, $w_{1}\in \hat{u}_{1}$, and $u_{0}\cap \hat{u}_{1}=\varnothing$, and the singletons $\left\{ w_{0}\right\}$ and $\left\{ w_{1}\right\}$ are closed. Setting $u_{1}=\hat{u}_{1}\cap v\in \tau$, it follows that $u_{1}\cap W\left( Y_{t+1}\right) \subseteq W\left( p\left( V\right) \right)$. Since $W{\setminus } u_{0}$ and $W{\setminus } u_{1}$ are closed as complements of open sets, again by Urysohn’s lemma there are continuous functions $f_{1}:W\rightarrow \left[ 0,1\right]$ and $f_{2}:W\rightarrow \left[ 0,1\right]$ such that $f_{1}^{-1}\left( 1\right) =\left\{ w_{0}\right\}$, $f_{1}^{-1}\left( 0\right) =W{\setminus } u_{0}$, $f_{2}^{-1}\left( 1\right) =\left\{ w_{1}\right\}$, and $f_{2}^{-1}\left( 0\right) =W{\setminus } u_{1}$, as $\left( W,\tau \right)$ is perfectly normal by hypothesis.

Assign all moves before $Y_{t}$ to player 1, $X_{1}=\cup _{k=0}^{t-1}\left( Y_{k}\cap X\right)$, and all moves from $Y_{t}$ onward to player 2, $X_{2}=\cup _{k\ge t}\left( Y_{k}\cap X\right)$, so that $Y_{t}{\setminus } E\subseteq X_{2}$ but $Y_{t-1}{\setminus } E\subseteq X_{1}$. Preferences for the two players $i=1,2$ are represented by the continuous functions

$$\begin{aligned} U_{1}\left( w\right) =f_{1}\left( w\right) \quad \,{\text {and}}\,\quad U_{2}\left( w\right) =\frac{1}{2}f_{1}\left( w\right) +f_{2}\left( w\right) \quad \,\text {for all}\, w\in W. \end{aligned}$$

By Lemma 2 and continuity of $U_{i}$ ($i=1,2$) this yields a well-behaved EFPI.

In an SPE, player 1 can guarantee herself a payoff that strictly exceeds $\lambda$ for any $\lambda \in \left[ 0,1\right)$. For, the strict upper contour set $u_{\lambda }=\left\{ w\in W\left| U_{1}\left( w\right) >\lambda \right. \right\}$ is open in $\tau$ by continuity of $U_{1}$ and a neighborhood of $w_{0}\in u_{\lambda }$. Thus, there is $w_{\lambda }\in u_{\lambda }{\setminus }\left\{ w_{0}\right\}$ such that $w_{\lambda }\in W\left( \left\{ y\in Y_{t+1}\left| p\left( y\right) \notin p\left( V\right) \right. \right\} \right)$. Hence, there is $y_{\lambda }={\text {proj}}_{t+1}\left( w_{\lambda }\right) \in Y_{t+1}$ such that $p\left( y_{\lambda }\right) \equiv x_{\lambda }\in Y_{t}{\setminus } p\left( V\right)$. Since $u_{1}\cap W\left( Y_{t+1}\right) \subseteq W\left( p\left( V\right) \right)$ implies $W\left( Y_{t}{\setminus } p\left( V\right) \right) =W\left( Y_{t}\right) {\setminus } W\left( p\left( V\right) \right) \subseteq W{\setminus } u_{1}$ and $U_{1}\left( w\right) =2U_{2}\left( w\right)$ for all $w\notin u_{1}$, if player 1 chooses $x_{\lambda }$, then (by subgame perfection) player 2 will choose $w\in \arg \max _{w'\in x_{\lambda }}U_{2}\left( w'\right) =\arg \max _{w'\in x_{\lambda }}U_{1}\left( w'\right)$, which yields player 1 strictly more than $\lambda$, because $w_{\lambda }\in y_{\lambda }\subset x_{\lambda }\Rightarrow w_{\lambda }\in x_{\lambda }\cap u_{\lambda }$.

Therefore, player 1 must obtain payoff $U_{1}\left( w\right) =1$ in each SPE. But $U_{1}\left( w\right) =1$ implies $w=w_{0}\in \bar{x}\in Y_{2t}$. Consider the subgame starting at $\bar{x}\in Y_{2t}$. Since player 2 controls all moves from $Y_{t}$ onward, she can in particular choose $w_{1}\in y_{1}\in V$. This gives her a payoff of at least 1 which is strictly more than what she can obtain outside of $u_{1}$, that is, $\arg \max _{w'\in \bar{x}}U_{2}\left( w'\right) \subseteq u_{1}\cap W\left( Y_{t+1}\right)$. But then player 1’s best payoff from choosing $\bar{x}\in Y_{t}$ is zero. Hence, player 1’s value function has no maximum and no SPE exists.$\square$

4 Discussion

This section discusses a few fine points about the previous arguments. The first concerns separation properties, specifically the assumption of a perfectly normal topology. Without this assumption, there exist very weak (coarse) topologies that may admit equilibrium analysis without satisfying (OP). The example below illustrates that such topologies are of purely theoretic interest, because only very few preference relations will be continuous with respect to them. The second point is the discussion about the role of compactness that has been touched upon before. And the third concerns topologies on the space of pure strategies.

4.1 The Fort example

Theorem 1 states that any topology $\tau$ on the set W of plays that admits equilibrium analysis must be a tree topology. The result employs the hypothesis that $\left( W,\tau \right)$ is perfectly normal, though. Therefore, there could be very coarse topologies that admit equilibrium analysis which are not tree topologies. Yet, if that is the case, it may severely constrain the set of preferences that are still continuous with respect to such a coarse topology. The following example is constructed to fail perfect normality in such a way that (OP) fails, but the topology still admits equilibrium analysis. The price paid for this is that the only functions that are continuous with respect to this topology are those with countably many values.

Example 9

Let $W=\left[ -2,-1\right] \cup \left[ 1,2\right]$ and $N=\{W,\left( \left\{ -w,w\right\} \right) _{w\in W}, \left( \left\{ w\right\} \right) _{w\in W}\}$. For any set of players I, let $1\in I$ denote the player who chooses at the root. The topology is the Fort topology, i.e., the open sets are those whose complements are either finite or contain the point $1\in W$. (That is, a closed set is either a finite set or contains $1\in W$.) This is a compact Hausdorff space that is not perfectly normal (see Steen and Seebach 1978, p. 52).

To see (CN), note that all nodes except the root are finite sets, hence closed, and the root contains $1\in W$. The Fort topology fails (OP), though. For, consider the terminal node (singleton set) $x=\left\{ -1\right\}$, which is open by $1\notin x$. Its immediate predecessor is $p\left( x\right) =\left\{ -1,1\right\}$, which contains $1\in W$ but is not cofinite, and thereby not open.¹⁴ That is, while $W\left( \left\{ x\right\} \right)$ is open, $W\left( p\left( \left\{ x\right\} \right) \right)$ is not, and (OP) fails.

Any continuous preference relation $\precsim _{i}$ on W satisfies the following. First, for every $w\in W$ with $1\prec _{i}w$, the upper contour set $\left\{ w^{\prime }\in W\left| w\precsim _{i}w^{\prime }\right. \right\}$ is finite, because it must be closed, but cannot contain 1. Analogously, for every $w\in W$ with $w\prec _{i}1$, the lower contour set $\left\{ w^{\prime }\in W\left| w^{\prime }\precsim _{i}w\right. \right\}$ is finite. Hence, the indifference sets $\left\{ w^{\prime }\in W\left| w^{\prime }\sim _{i}w\right. \right\}$ are also finite for any $w\in W$ with $w\prec _{i}1$ or $1\prec _{i}w$. This implies that the strict upper contour set $\left\{ w^{\prime }\in W\left| 1\prec _{i}w^{\prime }\right. \right\}$ is countable. To see this, consider the quotient space

$$\begin{aligned} \varPhi _{1}\equiv \left\{ w\in W\left| 1\prec _{i}w\right. \right\} /\sim _{i}{.} \end{aligned}$$

This set can be enumerated (mapped one-to-one to a subset of the natural numbers) by assigning to each class $V\in \varPhi _{1}$ the (finite) number of elements of W which are weakly preferred to the elements of V. Hence, $\varPhi _{1}$ is countable. The strict upper contour set $\left\{ w^{\prime }\in W\left| 1\prec _{i}w^{\prime }\right. \right\}$ is the union of all elements of $\varPhi _{1}$, hence a countable union of finite sets and, therefore, countable. Analogously, the strict lower contour set $\left\{ w^{\prime }\in W\left| w^{\prime }\prec _{i}1\right. \right\}$ is countable.

Let continuous preference relations $\precsim _{i}$ for the players $i\in I$ be given. At each move $\left\{ -w,w\right\}$, there is a best element for player $i\in J\left( \left\{ -w,w\right\} \right)$, who controls it, say $m\left( w\right)$, by finiteness. We claim that $\precsim _{1}$ is maximized on the set $M=\left\{ m\left( w\right) \left| w\ne 1\right. \right\}$. Proceeding indirectly, suppose that there is no best element with respect to $\precsim _{1}$ on M. It follows that $w\precsim _{1}1$ for all $w\in M$, for otherwise taking any $w\in M$ with $1\prec _{1}w$ that $\left\{ w^{\prime }\in W\left| w\precsim _{1}w^{\prime }\right. \right\}$ is finite would imply the existence of a best element. If further $w\prec _{1}1$ would hold for all $w\in M$, then the uncountable set M were a subset of the countable set $\left\{ w^{\prime }\in W\left| w^{\prime }\prec _{1}1\right. \right\}$. Therefore, there must be $w\in M$ with $w\sim _{1}1$, but then $w\in M$ is a best element with respect to $\precsim _{1}$, a contradiction.

Let $w^{*}$ be a best element with respect to $\precsim _{1}$ in M. Then $\precsim _{1}$ is also maximized on $M\cup \left\{ m\left( 1\right) \right\}$, either at $m\left( 1\right)$ or at $w^{*}=m\left( w^{*}\right)$. There is an SPE where each player at $\left\{ -w,w\right\}$ chooses $m\left( w\right)$ and player 1 chooses $\left\{ -1,1\right\}$ if $w^{*}\prec _{1}m\left( 1\right)$ or $\left\{ -w^{*},w^{*}\right\}$ otherwise. It follows that the Fort topology admits equilibrium analysis, but violates (OP).

If the set $W=\left[ -2,-1\right] \cup \left[ 1,2\right]$ of plays from this example were endowed with the more natural relative Euclidean topology, then (OP) would hold. That is, the failure of (OP) is due to the choice of a coarse topology. (The coarseness of the Fort topology is also responsible for the fact that so few functions are continuous with respect to this topology.) This illustrates why the necessity conditions in Theorem 1 are indeed stronger than the necessity conditions in analogous results would be if those only assumed T$_{1}$ or T$_{2}$.

4.2 Is compactness necessary?

In Theorem 2, compactness is an added hypothesis for the characterization. Of course, compactness is a mild assumption which is usually included in existence theorems involving continuity of preferences without much ado. For, a priori existence of maxima for continuous preferences may fail in noncompact spaces. Hence, it is natural to ask whether compactness can also be obtained as a necessary condition in Theorem 1.

The answer to this question is surprising. It is closely related to a class of topological spaces called “pseudocompact.” A pseudocompact topological space is one where each real-valued continuous function is bounded. It is easy to show that this is equivalent to the statement that every real-valued continuous function has maxima and minima. It is known that every countably compact topological space is pseudocompact. Further, for normal spaces (i.e., for spaces such that disjoint closed sets can be separated by disjoint open neighborhoods), the converse is true. Since perfect normality implies normality, it follows that every pseudocompact perfectly normal space is countably compact.

By Lemma 3, if a topological space admits equilibrium analysis, then it must be pseudocompact. If pseudocompactness would imply compactness, then we would conclude that compactness is necessary for equilibrium analysis.

Fedorchuck (1976) and Ostaszewski (1976) constructed (in the set-theoretic sense) examples of countably compact (hence pseudocompact) and perfectly normal spaces that are not compact. Hence, not every pseudocompact space is compact. Further, for this space, every real-valued continuous function has maxima. Consider a tree defined on this space (as set of plays) which includes only the root and the singletons of plays. The only possible assignment of players to nodes is a single player, who directly chooses a final outcome. It follows that for any continuous payoff function, this game has an SPE, even though the topology is not compact.¹⁵ Hence, compactness is not a necessary condition for equilibrium analysis.

Alas, the constructions in Fedorchuck (1976) and Ostaszewski (1976) rely on more than just the standard Zermelo–Fraenkel-Choice (ZFC) axioms, on which standard set theory is based. They make use of an additional axiom known as Jensen’s Combinatorial Principle $\Diamond$, which is a consequence of Gödel’s Axiom of Constructibility ($V=F$) and is stronger than the Continuum Hypothesis. This axiom is independent of ZFC. Hence, what the result actually means is that there exists an extension of ZFC such that compactness is not a necessary condition for equilibrium analysis.

Weiss (1978) showed that if one assumes that the Continuum Hypothesis is false (which is perfectly justified, as the Continuum Hypothesis is independent of ZFC) and adds a further axiom to ZFC, known as Martin’s Axiom, we obtain an alternative extension of the standard mathematical system where a remarkable result (known as Weiss’ Theorem) can be shown: Every countably compact perfectly normal space is compact. Since under perfect normality countably compact is equivalent to pseudocompact, this can be restated as follows: Every pseudocompact perfectly normal topological space is actually compact. Martin’s Axiom is known to be implied by the Continuum Hypothesis, but it is also consistent with its negation. Hence, we obtain a new extension of ZFC in which, as argued above, whenever a topological space admits equilibrium analysis, it must be compact.

In short, there exist extensions of the standard ZFC axiom system where compactness is necessary for equilibrium analysis—and extensions where it is not. That is, the question of whether compactness can be added as a necessary condition to our set of properties has neither a negative nor a positive answer under ZFC. It is undecidable (neither provable nor refutable) in the sense of Gödel (1931). Given this state of affairs, we are content with adding compactness as a hypothesis for Theorem 2.

4.3 Topologies on strategies

In the above approach, the topological structure is imposed on the set W of plays for a discrete game tree $\left( N,\supseteq \right)$. There is a way, of course, to translate this into a topology on the strategy space S. In particular, the weak (or initial) topology on S is the weakest (or coarsest) topology on S that makes the function $\phi :S\rightarrow W$, as identified in AR2 (Theorems 2 and 6, and Corollary 5), continuous when W is endowed with a tree topology $\tau$. This is the topology generated by the collection of sets $\left\{ \phi ^{-1}\left( u\right) \left| u\in \tau \right. \right\}$ as a subbasis. A basis for this topology is the collection of finite intersections of the form $\cap _{k=1}^{n}\phi ^{-1}\left( u^{k}\right)$ with $u^{k}\in \tau$ for all $k=1,\ldots ,n\in \mathbb {N}$. Interestingly, topologies on strategies as generated by topologies on the set of plays have been productively used in the previous literature, e.g., by Fudenberg and Levine (1983) and Harris (1985a).

5 Conclusions

This paper provides necessary conditions on the topology on the set of plays of a potentially large discrete game tree such that every well-behaved perfect information game defined on this tree has a subgame perfect equilibrium. A full characterization is obtained for the class of compact and perfectly normal topologies: Such topologies admit equilibrium analysis if and only if they are tree topologies. This characterization rests on two stronger results. The conditions (CN) and (OP) are necessary under perfect normality, but compactness is not required. The same conditions are sufficient for compact topologies, even if those are only separated (Hausdorff).

Since the result is a characterization, the conclusion is that a tree topology is the minimal structure that needs to be added when studying infinite games. As pointed out in Alós-Ferrer and Ritzberger (2016), the two conditions are weaker than those used in other existence results in the literature. For instance, (OP) is equivalent to lower hemi-continuity of the “action correspondence” (the assignment of immediate successors in the present setting), but upper hemi-continuity is not necessary. Further, even if the game has a stage structure, Example 7 in Alós-Ferrer and Ritzberger (2016) shows that (OP) and (CN) do not necessarily imply that the topologies on the slices fulfill separation axioms, as, e.g., Hausdorff, which is frequently assumed in the literature. Conceptually, a characterization has become possible only because the present approach focuses on topologies on the set of plays (as a natural consequence of the work started in Alós-Ferrer and Ritzberger 2005, 2008, 2013), rather than deriving such topologies from assumptions on “stages” or local action sets.

In summary, the result goes beyond the existing literature, because we identify conditions for equilibrium existence which turn out to be also necessary. That is, they provide an answer to the question “How general can a topological existence theorem for large extensive form games become?”