Shear-layer instability in the Mach reflection of shock waves

Abstract

The Kelvin–Helmholtz instability (KHI) is an instability that takes the form of repeating wave-like structures which forms on a shear layer where two adjacent fluids are moving at a relative velocity to one another. Such a shear layer forms in the Mach reflection of shock waves. This work focuses on experimentally visualising the presence of the KHI in Mach reflection as well as its evolution. Experimentation was performed at shock Mach numbers of 1.34, 1.46 and 1.61. Plane test pieces and parabolic profiled pieces followed by a plane section having wedge angles of 30$^\circ$ and 38$^\circ$ were tested. Flow field visualisation was performed with a schlieren optical system. The KHI was best visualised with the camera-side knife edge perpendicular to the shear layer (i.e. the axis of sensitivity along the length of the shear layer). The structure and growth of the instability were readily identified. The KHI forms more readily with increasing Mach number and wedge angle. Second-order Euler, and Navier–Stokes numerical simulations of the flow field were also conducted. It was found that the Euler and laminar Navier–Stokes solvers achieved very similar results, both producing the KHI, but at a much less developed state than the experimental cases. The k$-\epsilon$ solver, however, did not produce the instability.

1 Introduction

1.1 Background

A shear layer is the interface between two flows of differing properties, most notably velocity. Theoretically a shear layer, or slipstream, in Mach reflection analysis is usually treated as a discontinuity, but in practice the shear layer has a thickness as a velocity gradient due to shear forms on both sides of the layer and mixing between the layers occur, thus a shear layer is often referred to as a mixing layer [1]. It has been found that the shear layer thickness, and thus the magnitude of mixing, decreases with increasing velocity difference, this pattern is exaggerated as the shear layer flow becomes compressible [2]. If the relative velocity across the shear layer is greater than a critical velocity (dependent on various factors including the surface tension between the layers and the densities of the fluids), small perturbations on this layer evolve into wave-like structures, which develop into vortices, often referred to as “cat’s eye” type structures [3]. Ultimately the whole system breaks down into turbulence, the understanding of which makes the study of the Kelvin–Helmholtz instability (KHI) important. The effects on the formation of the KHI in a compressible flow, as opposed to in an incompressible flow, are: a lower critical relative velocity across the shear layer before the onset of the instability, and reduced growth rate.

In the context of Mach reflection, there have been some studies on the shear layer behaviour, by assuming the flows on either side of the layer are not parallel. However, there is little comment on the void that would be created if the flows are diverging. Only one publication could be found which analyses the spread. The most pertinent study is that of Rikanati et al. [4]. They compared the experimental growth rate of the Mach reflection shear layer to that of the theoretical large-scale KHI turbulent mixing zone, by comparing the spread angles. The experimental spread angles were measured off holographic interferometry and the theoretical spread angle was obtained from the work of Brown and Roshko [5]. The majority of results they present, and all of the interferograms, are for an initial pressure in the shock tube driven section of 10 kPa and low Reynolds number. They estimate the spread of the shear layer from the spread of the fringes in the interferograms.

Clear imaging of the instability structure was obtained in a study of the transition point from initial Mach Reflection to a Transitioned Mach Reflection on a curved surface at an initial Mach number of 1.5 as shown in Fig. 1 [6]. Pieces of tape were stuck to the surface to create perturbation waves. It appears that these waves are in contact with the larger loops of the KHI; thus it was presumed that they were triggered by the waves.

Fig. 1

Experimental images of the Kelvin–Helmholtz instability in a Mach reflection off a curved surface M = 1.5 [6]

A study by Gvozdeva [7] investigated the magnitude of mixing across shear layers (caused by both Mach reflection and shock wave diffraction) relative to the ratio of specific heats $\gamma$ of the working fluid. The specific heat ratios tested ranged from 1.18 to 1.66 and were achieved with the use of different gases namely: argon, air, nitrogen, carbon dioxide and freon. It was found that the magnitude of the mixing across the shear increased with decreasing specific heat ratio.

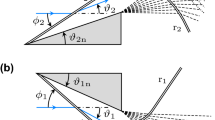
1.2 Three-shock theory

Three-shock theory [8] considers the flow across three plane shock waves separating four regions as shown in the inset of Fig. 2. The incident wave, I, reflected wave, R, and Mach stem, M, meet at the triple point T, with the Mach stem terminating perpendicular to the wall. The boundary conditions imposed are that the flows in regions (2) and (3) must be parallel and have the same pressure. The usual independent variables taken for the shear layer are the velocity and density differences across it, but there is also a temperature difference which may have an effect in practice. The theoretical values for $\gamma =1.4$ are given in Figs. 2 and 3, both of which increase with increasing wedge angles and incident shock wave Mach number.

Fig. 2

Theoretical velocity difference across the shear layer as a function of initial Mach number for various wedge angles

Fig. 3

Theoretical density difference across the shear layer as a function of initial Mach number for various wedge angles

2 Method

Physical experiments were conducted in a conventional shock tube with good reproducible characteristics and standard schlieren visualisation techniques. A variety of test pieces were employed over a range of Mach numbers and the results were supported by numerical simulation runs.

2.1 Shock tube facility

The shock tube test section is 180 mm high and 75 mm wide and is fitted with 300 mm diameter windows. The driven section is 6 m long and the tube uses a double diaphragm technique with a small intermediate chamber which when vented suddenly causes the diaphragms to burst. This technique results in highly repeatable shock strengths. For M = 1.33, the maximum and minimum deviations from the nominal Mach number were $-$0.137 and $-$0.006, respectively; for M = 1.45, the deviations were $-$0.015 and $-$0.010; and for M = 1.6, the deviations were $-$0.013 and $-$0.004. All images presented are from different tests. A maximum Mach number of approximately 1.84 can be attained with ambient conditions of nominally 83.3 kPa and 293 K with air ($\gamma \,=\,1.4$) in the driven section. A grid of vertical and horizontal threads at 25 mm spacing is positioned just outside the one window.

2.2 Test pieces

The test pieces employed are identified in Table 1. The first four, A to D, consist of an initial parabolic section, with the length measured in the direction of shock motion, and with a zero entrance angle, followed by a plane surface at a fixed angle. Earlier work [6] had shown that this resulted in the Mach reflection and associated shear layer being initiated away from the surface thereby reducing the influence of the wall boundary layer. The other two test pieces were plane wedges having wall angles of 30$^\circ$ and 38$^\circ$. Tests were conducted at incident shock Mach numbers of 1.34, 1.46, and 1.61.

Table 1 Critical test piece dimensions

2.3 Simulation

A commercial CDF package, Fluent 13, was used to obtain numerical results for the experimentally tested Mach numbers. The domain was setup to mimic that of the experimental cases, with an upstream section of length 1.5 times that of the flow field height to allow the formation of a steady normal shock wave. An initial 2-mm mesh was used across the entire flow field. Five levels of mesh refinement were used to refine the mesh in regions of high gradients. Further refinement gave no improvement. A typical refined case in the region of the triple point is given in Fig. 4. Inviscid, laminar and $k-\epsilon$ solvers were used. Three simulations of each geometry and boundary condition configuration were run. All simulation results presented are from the inviscid solver.

Fig. 4

Mesh refinement for the Mach reflection

The main effect of the leading curved section on some models is illustrated in the simulations shown in Fig. 5. As the incident shock propagates up the curved section, the Mach reflection does not immediately initiate but curves forward with increasing strength with a steepening compression wave behind it. This results in a shear gradient behind the curved wave. Eventually, the compressions will coalesce into a reflected shock wave and the shear gradient will become the slipstream of a Mach reflection.

Fig. 5

Numerical contours of density showing flow patterns on models E (top) and C (bottom), $M_0 = 1.46$

2.4 Camera-side knife-edge position

The axis of sensitivity of a schlieren system is perpendicular to the alignment of the camera-side knife edge. The effect of changing the sensitivity direction on the visualisation of the KHI is apparent in the images in Fig. 6 which were taken with: the camera-side knife edge orientated perpendicular to the shear layer, parallel to the shear layer, vertical, and completely removed, respectively. The Model D test piece was used with an incident shock Mach number of $M_0 = 1.46$. Note the 25 mm grid overlay. Since this test piece has a curved initial section, the Mach reflection starts away from the inlet and forms from the steepening compression wave, also resulting in an increasing shear gradient behind it before the fully developed shear layer forms behind the triple point.

Fig. 6

Effect of knife-edge orientation, M = 1.46. Images rotated parallel to wedge surface of test piece D. a Perpendicular to the shear layer, b parallel to the shear layer, c vertical camera-side knife edge, d Shadowgraph (no knife edge)

In the case of the knife edge being perpendicular to the shear layer, Fig. 6a, the KHI can be easily discerned highlighting the repeating pattern of the braided structure. The adverse case to this is the knife edge parallel to the shear layer, Fig. 6b, resulting in the shear layer appearing as a thick black line, with no indication of the structure. It is interesting to note how wide it is, thereby indicating the existence of strong density gradients adjacent to the braids. This will be considered further later. The shear gradient resulting from the initial compression wave before the development of the Mach reflection is also very evident.

For the case of a vertical knife edge, Fig. 6c, the blurring of the shear layer is less pronounced and if viewed closely perturbations can be seen along it, which indicate the presence of the instability. Figure 6d is a shadowgraph image (no camera-side knife edge) of this case. The less pronounced definition of the shock waves reveal the lack of sensitivity of this optical system compared to its schlieren counterparts. The KHI on the shear layer, however, is clearly visible. The contrast between the individual KHI loops is less than that of the perpendicular knife-edge case, but internal features of the instability are better discerned.

The differences shown above between the different knife-edge orientations could have contributed to many images in the literature not showing well-defined instabilities.

3 Observations

Many tests were done on each model at three Mach numbers, gradually increasing the time delay to examine the evolution of the wave in time. A typical series is given in Fig. 7. Only selected frames are included for the other cases. Again the images are rotated and cropped to show the shear layer.

Fig. 7

KHI evolution for a 30$^\circ$ plane wedge (Model E), $M_0 = 1.61$. 20 ${\upmu \mathrm{s}}$ between frames

It is difficult to determine the point where the instability initiates, but inspection of the images clearly shows the presence of a repeating braided pattern along the shear layer typical of the Kelvin–Helmholtz instability. As expected, the shock wave pattern and trajectory of the shear layer is self-similar for plane walls, there being no characteristic length in the flow. Whether this applies to the growth of the shear layer itself will be discussed later. The shear layer grows in width with some very marked loops developing close to the surface. At later times a series of perturbations arise from the surface close behind the Mach stem, and will be considered later.

3.1 Model A

Figures 8, 9 and 10 detail the KHI evolution on Model A with incident shock wave strengths of $M_0 = 1.34$, $M_0 = 1.46$ and $M_0 = 1.61$, respectively. They show that as the Mach reflection develops the length of the shear layer increases, the instability initiates along the shear layer and grows in both length and width ultimately forming well-defined KHI loops. KHI is present at all tested Mach numbers, and it starts earlier the greater the Mach number. It is also apparent that the greater the Mach number the longer the respective Mach stem and steeper the angle of the shear layer to the wedge surface, resulting in it being shorter. The braided section increases in width until it merges with the shear region developed from the initial curved region of the model profile.

Fig. 8

KHI evolution for Model A, $M_0 = 1.34$. 75 ${\upmu \mathrm{s}}$ between images

Fig. 9

KHI evolution for Model A, $M_0 = 1.46$. 75 ${\upmu \mathrm{s}}$ between images

Fig. 10

KHI evolution for Model A, $M_0 = 1.61$. 80 ${\upmu \mathrm{s}}$ between images

In nearly all cases there is strong evidence of a regular repeating flow structure at the surface itself.The boundary layer is clearly visible, throughout the Model A progressions, as a white line along the test piece surface behind the Mach stem. A magnified portion (approximately the first quarter) of the boundary layer of Fig. 8 is shown in Fig. 11. On close inspection this indicates the possible presence of similar instability to that in the shear layer. The coupling between these warrants further attention.

Fig. 11

Magnification of the boundary layer, Model A, $M_0 = 1.34$. Image length covers a physical length of 27.5 mm

3.2 Model C

Figures 12, 13 and 14 detail the KHI evolution on Model C. The progression is very similar to that of Model A with some exceptions. The length of the Mach stem is greater and the angle of the shear layer less steep,relative to that formed on Model A, thus allowing for the formation of a longer shear layer. There is no formation of the KHI along the shear layer for the $M_0 = 1.34$ case due to the lower relative velocity because of the gentler wedge angle. There is also the presence of a perturbation on the shear layer in all cases although the relative size of the perturbation to the shear layer is greater in the $M_0 = 1.34$ case. Later on, after the formation of the first perturbation, multiple perturbations form on the shear layers of the $M_0 = 1.46$ and $M_0 = 1.61$ cases. The position of these perturbations is consistent throughout the progression, and is repeatable, as each image was from a different test. The KHI abruptly constricts and ceases near the end of the shear layer due to the junction between the shear gradient, before the formation of the Mach reflection, and the shear layer of the Mach reflection. There is no clear indication of the boundary layer instability as there was on Model A.

Fig. 12

KHI evolution for Model C, $M_0 = 1.34$. 50 and 75 ${\upmu \mathrm{s}}$ between images

Fig. 13

KHI evolution for Model C, $M_0 = 1.46$. 75 ${\upmu \mathrm{s}}$ between images

Fig. 14

KHI evolution for Model C, $M_0 = 1.61$. 60 ${\upmu \mathrm{s}}$ between images

3.3 Model E

Figures 15, 16 and 17 detail the KHI evolution on Model E with incident shock wave strengths of $M_0 = 1.34$, $M_0 = 1.46$ and $M_0 = 1.61$, respectively. Unlike Models A and C, Model E does not have a parabolic entrance, but is a plane wedge. The progression of Model E is very similar to that of Models A and C with some exceptions (it should be noted that Models C and E both have a 30$^\circ$ wedge angle). The shear layer is longer and extends to the test piece surface rather than terminating above it. The shear layer appears to have a more noticeable curve when compared to any of the parabolic entrance test pieces. This would be because the flow field behind the Mach stem is different to that of a test piece with a parabolic entrance. There are well defined and large KHI loops close to the surface. These large loops, unlike those that developed from small perturbations along the shear layer as mentioned for the Model A and C cases, are not consistent between images, thus indicating that their formation is random. These loops are in contact with the surface, and thus the boundary layer.

Fig. 15

KHI evolution for Model E, $M_0 = 1.34$. 100 and 75 ${\upmu \mathrm{s}}$ between images

Fig. 16

KHI evolution for Model E, $M_0 = 1.46$. 100 and 75 ${\upmu \mathrm{s}}$ between images

Fig. 17

KHI evolution for Model E, $M_0 = 1.61$. 80 ${\upmu \mathrm{s}}$ between images

4 Results

4.1 CFD comparison

Simulations using Euler, laminar Navier–Stokes and k$-\epsilon$ solvers were run at the same time step and with the same boundary conditions and meshes. The results produced by the Euler and Navier–Stokes solvers are almost identical. The general Mach reflection geometry is clearly visible. The shear gradient, caused by the incident shock wave interacting with the parabolic section of the wedge, is clear as shown in Fig. 18. In most cases, the instability is evident. The k$-\epsilon$ solution, however, dampens out vorticity and the KHI does not form. The shear layer also is much wider than in the other two cases. Simulations for Model C did not show instabilities although there was some indication of them starting to develop in the Mach 1.61 case.

Fig. 18

Numerical simulations for Model A compared to experiment. $M_0 = 1.46$

Figure 19 shows that the numerical simulations for the plain wedge (Model E) case show a more accurate development of the KHI but it is still notably less developed than the experimental cases. However, the most developed section of the KHI in the numerical simulation of the $M_0 = 1.61$ case is of similar width to the experimental case, but the length of the numerical instability is shorter than its experimental counterpart, thus the length of stable shear layer between the KHI and the triple point is greater. The less developed braided structure was found throughout the numerical part of this study. In an associated study [9], on a different geometry, it was found that higher order calculations may be necessary to get better agreement in predicting these instabilities.

Fig. 19

Numerical simulations for Model E compared to experiment. Top: $M_0 = 1.34$, Middle: $M_0 = 1.46$, Bottom: $M_0 = 1.61$

Of particular note in these numerical results is the significant density gradients adjacent to the shear layer. This is probably the reason for the wider width recorded in some cases, such as shown in Fig. 6b, resulting from schlieren knife-edge orientation.

4.2 Quantitative data

A computer program, DigXY, was used to extract dimensional data from the experimental images.

The co-ordinates of 16 points were obtained from each image and then read into a MATLAB code for processing. Many of the points were taken from small regions of the image resulting in variability. Thus, although the data have a lot of scatter the trends and comparisons are clear. The main co-ordinates extracted were:

• Position point This is a specific intersection of the wire grid whose position within the test section is known.

• Scaling point This is a specific intersection of the wire grid, used for scale as the dimensions of the grid were known.

• Incident shock The point where the incident shock wave intersects a specific horizontal wire, used to calculate its position within the test section.

• Triple point The point where the Mach stem, incident and reflected shock waves meet.

• Mach stem and wedge surface contact point This was used to calculate the length of the Mach stem.

• End of shear layer The point after which the shear layer can no longer be identified. It was used to calculate the length of the shear layer. This was calculated by taking the length of a spline through points on the shear layer from the earliest point where the KHI can be discerned on the shear layer to the last point it could be discerned.

• KHI edge points Five pairs of points (immediately above and below the shear layer) were taken at equal intervals along the entire length of the KHI. These were used to calculate the average width of the KHI.

Basic geometry was used to calculate the distances. The images were magnified for a more accurate extraction of the width, but due to the lack of definition of the flow features at this magnification the accuracy was $\pm 0.3$ mm. Thus, the percentage errors are larger closer to the triple point and at early times. Because of the self-similar nature of the overall flow field for shock reflection off a plane wedge it would be expected that the shear layer length would grow uniformly with time, for the equivalent shock position up the wedge. The length also increases with the increase in wedge angle. Figure 20 indicates that the average width of the KHI also appears to increase linearly, as the flow field progresses. Whilst the scatter is quite high due to the limited accuracy of measurement the trends are clear. This is time-averaged data due to the shock propagation up the wedge. It indicates the overall growth in time and that higher Mach numbers give larger average widths. Higher resolution experiments would be needed in order to distinguish better between flow cases. The KHI is also wider the greater the Mach number, due to the greater relative velocity across the shear layer. The increase of the KHI thickness from $M_0 = 1.34$ to $M_0 = 1.46$ is noticeably greater than the increase from $M_0 = 1.46$ to $M_0 = 1.61$ even though the relative increase in Mach number is smaller. This would be expected as results usually become less sensitive to Mach number as it increases.

Fig. 20

Shear layer average width

4.3 Slipstream spread

From the measurements of slipstream length and width, and the fact that the width grows linearly, [4], an effective slipstream spread angle may be determined to compare with the other available data. At a position along the length of the shear layer, from a test at late times when the flow is well developed, a measurement of the layer width and distance to the triple point is made. The ratio of these two dimensions allows an effective spread angle to be determined. The results are given in Fig. 21. The angles are small and subject to error due to measurement accuracy of the shear layer width. Errors could be as large as 25 % for low Mach numbers and up to 10 % for the higher Mach numbers.

Fig. 21

Variation of shear layer spread with Mach number

There have been some studies of the shear layer behaviour, by assuming the flows in regions 2 and 3 diverging without considering the flow, and void, between them. However, one publication has been found which analyses the spread. This work, by Rikanati et al. [4], is done in the context of turbulent mixing, and develops a theory which is successful in comparison with experiments done using holographic interferometry. The majority of results they present, and all of the interferograms, are for an initial pressure of 10 kPa and low Reynolds number. Fortunately they give data for reflection off a 30$^\circ$ wall and an initial pressure of 100 kPa giving a similar Reynolds number to those in the current tests. They estimate the spread of the shear layer from the spread of the fringes in the interferograms. However, there are very few of these in the region surrounding the shear layer; insufficient to resolve the braided structure of the instability, and particularly its edge. The spread determined is thus influenced by the fringe spacing. Only one of their tests was at similar Reynolds number to the current tests. This is a test at Mach 1.55 into air initially at 100 kPa on a 30$^\circ$ ramp. The comparison with the current data is shown in Fig. 21, and gives a shear layer spread about half that of [4]. The reason for this may lie in the measurement technique using interferometry where fringe spacing depends on the width of the test section optical path and light frequency. It is noted that in some cases reported on there are only three fringes delineating the shear region in the interferograms.

4.4 Test piece scaling

Models A and B have the same geometry but Model B is twice the size of A. Tests were conducted to examine the similarity in the shear layer profiles. The overall wave pattern and shear layer length are found to scale according to the model size.

A comparison of the shear layer structure when the incident shock has just passed the meeting point between the curved and straight section of the model is given with zoomed images in Fig. 22. They are for the incident shock in the same relative position to this meeting point, i.e. the image for model A is zoomed to twice that of model B. There are noticeable differences in structure with that of model B showing an apparent greater width and larger loops in the instability than model A. This is probably because it has been in existence twice as long. Similar issues were noted for previous work on curved walls, as shown in Fig. 1. The nature of shear layer behaviour generated by Mach reflection on curved walls of different curvature would thus appear to warrant further attention. It is also interesting to note the similarity in the perturbations arising on the wall. Since the surfaces are polished this can be related to boundary layer effects as discussed below.

Fig. 22

Comparison between Model A (top) and Model B (bottom), with a parabolic entrance of twice the scale, with the incident shock wave at the same scaled position, with half the magnification. $M_0 = 1.61$

The average width of the KHI as the incident shock wave moves much further up the wedge for both test pieces is shown in Fig. 23 with the values for Model B halved so that they can be easily compared with those of Model A. The data collapse for the $M_0 =1.43$ case but the average width appears slightly less for Model B for the highest Mach number of $M_0 = 1.61$. This result is not conclusive since the error bounds on the data ($\pm 0.3$ mm) overlap. However, as noted, the average width for model A grows quite rapidly in a linear fashion. Similar data could not be obtained for model B because the curved portion of the model covered most of the test window area, limiting tests on the plane section.

Fig. 23

Comparison of average KHI widths vs incident shock wave position for Models A and B. Note: The results for Model B are at half scale

4.5 Effect of wedge angle

The effect of wall angle is shown in Fig. 24. This compares the flow patterns for a Mach 1.34 incident shock at the same position on the 30$^\circ$ and 38$^\circ$ plane walls.On the shallower wall no instability loops are apparent. The Mach stem and shear layer length are much longer than for the steeper wall as is to be expected. For the steeper wall both the density and velocity difference across the layer are significantly greater as shown in Figs. 2 and 3 and the braided structure of the instability develops.

Fig. 24

Effect of wall angle on shear layer. Top and middle images: Flow pattern for incident shock in the same position, for reflection off plane wedges of 30$^\circ$ and 38$^\circ$, respectively. $M_0 = 1.34$. Bottom image is an enlarged view of a section of the middle image

In the upper image the boundary layer on the wall can be seen thickening toward the tail of the shear layer as it gets closer to the wall. Its structure is not clear under magnification but may be becoming turbulent. For the larger angle wedge, however, there is very clear coupling between the braided structure of the shear layer and the underlying boundary layer. This exhibits a structure of wavelets at similar spacing to that of the loops in the shear layer.

5 Conclusion

A series of experiments has been conducted to visualise the overall characteristics of the KHI that occur on the shear layer developed in the Mach reflection of shock waves. The instability develops and grows more substantially the stronger the shock and greater the test piece wedge angle. The orientation of the schlieren camera-side knife edge plays a large role in resolving the braided structure, which is best defined when the camera-side knife edge is perpendicular to the shear layer.

A plane wedge allows prompt formation causing the instability to grow from the test piece surface and be most developed at this point. A parabolic entrance to the test piece causes the Mach reflection to form later on, with a shear gradient forming before the shear layer, this causing an abrupt termination of the instability above the test piece surface. Evidence of coupling between the loops of the shear layer and the boundary layer on the model surface is identified.