Abstract
In real-time precise point positioning (RT-PPP), PPP one-way timing is used to steer local oscillators, but the timing performance could be significantly affected by the datum stability of the satellite clock product. To measure the stability of a satellite clock datum relative to the hydrogen maser (H-MASER) clock, a new GNSS satellite clock datum stability assessing model based on the overlapping Allan variance (AVAR) is proposed for both PPP one-way timing and time synchronization. Experiments were carried out with nine Global Navigation Satellite System (GNSS) stations at time laboratories with an external H-MASER clock to analyze the datum stability performance. In the experiments, RT satellite products from five RT Analysis Centers (ACs): CNES, ESA, GFZ, GMV, WHU, and the final satellite product from IGS were used in the comparison. Results show that the datum stability of all RT products tended to be similar, i.e., 6 to 8E−15/day, where WHU and GMV outperformed other RT ACs. Moreover, these datum stability results indicate that RT-PPP for steering local oscillators improves stability to 6 to 8E−15/day when selected with an appropriate RT product. The estimation noise in all RT ACs was at about the same level, i.e., 1 to 2E−15/day, but WHU delivered the most stable performance. Thus, datum stability is an effective guide for setting parameters and making long-term stability predictions when steering local oscillators, and satellite clock datum stability can be measured conveniently and quickly using the GNSS satellite clock datum stability assessing model proposed in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Precise point positioning (PPP) technology is widely used in positioning, navigation, and timing (Lou et al. 2015; Zumberge et al. 1997). Based on PPP, sub-nanosecond time transfer and centimeter or millimeter positioning can be realized by using GNSS carrier phase and high-precision satellite ephemeris. Though the International GNSS Service (IGS) releases the final, rapid and ultra-fast products via FTP, these high-precision products were only available for post-processing since even the ultra-fast products have a latency of several hours. The Real-Time Working Group (RTWG) of IGS, since April 1, 2013, has made real-time (RT) high-precision products publicly available through RT Analysis Centers (ACs): CNES, ESA, GFZ, GMV, and WHU. More details about the IGS RTWG can be found at https://igs.org/rts. Significant efforts have been made toward the applications of PPP with IGS RT products in positioning and navigation, and a wide range of literature has been published. Liu et al. (2020) evaluated multi-system ambiguity resolution (AR) in RT-PPP and proposed a triple-frequency PPP AR solution with a better ambiguity fixing percentage. Ge et al. (2020) studied Galileo's RT-PPP performance of the CNES AC. This AC delivered short-term frequency stability performance was similar to PPP time transfer in the final satellite products, but the long-term frequency was less stable. Ouyang et al. (2021) assessed the performance of the RT-PPP products from the CNES, DLR, WHU, and GFZ ACs, finding that CNES had the highest precision orbit and clock estimations.
In the time–frequency transfer, Orgiazzi et al. (2005) evaluated the short-term noise in GPS PPP based on the observation of nine timing laboratories distributed worldwide. Petit and Jiang (2007) confirmed that the PPP technique could be used for International Atomic Time (TAI) time–frequency transfers by comparing the PTBB and USNO time laboratories. PPP has been used for TAI time transfer ever since. Li et al. (2018) used IGS RT products to analyze the time transfer results from four international time laboratories and demonstrated that a root mean square (RMS) error less than 0.3 ns can be achieved in the reference time with a daily time transfer stability of about 2E−15. The PPP technique only eliminates first-order ionospheric delay; thus, Pireaux et al. (2010) analyzed the influence of the higher-order ionospheric delay on PPP time transfer. Their results showed that the influence of the higher-order ionosphere was about 10 ps during the magnetic storms. Qin et al. (2020) performed different clock estimation strategies of BeiDou-2 navigation systems (BDS-2) and BDS-3 to explore the time delay bias effect on RT PPP time transfer, and deem it necessary to correct time delay bias at BDS PPP time transfer. This research indicates that the PPP time transfer has emerged as a research hotspot; however, most of these studies focus on the time synchronization of separated GNSS receivers rather than PPP one-way timing.
Receiver clock estimates with PPP are biased by jumps in the satellite clock product, but this bias can be canceled out in the time synchronization between stations. Thus, PPP time synchronization is insensitive to the satellite clock datum stability in different products. Guo et al. (2019) designed a system that used the RT-PPP to steer the local oscillator for one-way timing, which could reproduce a frequency output stability matching the RT-PPP product datum. This result confirms that multi-GNSS RT-PPP can achieve sub-nanosecond one-way timing precision and 2E-14/day frequency output stability. Rønningen and Danielson (2019) have used RT product, open-source software, standard hardware, and dual-frequency GPS receivers to discipline local oscillators, yielding stability that surpasses the specifications of high-performance Cesium clocks. Mishagin et al. (2020) have shown that long-term frequency stability of local oscillators steering is determined and limited by RT-PPP satellite clock datum stability. The stability of the satellite clock datum is an essential parameter for steering the local oscillator, which illustrates the importance of a steering reference datum.
To sum up, the performance of RT-PPP in time transfer has begun to receive increasing attention in the GNSS community, and PPP one-way timing is still understudied, especially considering the effect of the clock datum. Thus, more studies are needed to understand the PPP timing with different RT AC products in-depth. Aiming to explore the temporal stability of clock datum and its impact on PPP one-way timing and time synchronization, we took the hydrogen maser (H-MASER) as maintained by time laboratories and PPP as a means to measure the reference datum stability relative to the H-MASER. For the experiments, we selected nine time laboratory GNSS observation stations and RT products from five ACs: CNES, ESA, GFZ, GMV, and WHU. A PPP one-way timing and time synchronization experiment were carried out. The clock datum stability was evaluated by combining one-way timing and time synchronization's overlapping Allan variance (AVAR). The article's structure is arranged as follows: Sect. 2 introduces the methodology of PPP time transfer, and a statistic is suggested for the clock datum stability evaluation. Section 3 describes the data processing strategies and presents PPP one-way timing and time synchronization results. Section 4 summarizes this article and draws conclusions.
2 Methodology
A new GNSS satellite clock datum stability assessing model was established based on the overlapping Allan variance. A dual-frequency (DF) ionospheric-free (IF) PPP process was derived for PPP one-way timing and time synchronization. The effect of the satellite clock datum on PPP time transfer was analyzed, and the proposed satellite datum stability assessing model implemented using RT ACs satellite orbit and clock products.
2.1 Effect of GNSS reference clock in PPP
Defining the IF transformation matrix \({J}_{ij}\) on frequency \(i, j \left(i\ne j\right)\) as:
Then, the DF IF combination observation with the ionosphere effect removed can be derived as:
where \({P}_{LC}^{{s}_{i}}\) and \({\Phi }_{{LC}}^{{s}_{i}}\) are the IF pseudorange and carrier phase in meters; \({\rho }_{r}^{{s}_{i}}\) is the true geometric range, i.e., \({\rho }_{r}^{{s}_{i}}=\left|{r}^{{s}_{i}}-{r}_{r}\right|\); \({t}^{{s}_{i}}\) and \({t}_{r}\) are the clock difference for satellite and receiver; \({T}^{{s}_{i}}\) is the slant tropospheric delay; \({b}_{LC}^{{s}_{i}}={{\varvec{J}}}_{12}\cdot {\left(\begin{array}{cc}{b}_{1}^{{s}_{i}}& {b}_{2}^{{s}_{i}}\end{array}\right)}^{T}\) and \({b}_{r,LC}={{\varvec{J}}}_{12}\cdot {\left(\begin{array}{cc}{b}_{r,1}& {b}_{r,2}\end{array}\right)}^{T}\) are the IF code bias for satellite \({s}_{i}\) and receiver \(r\), respectively; \({N}_{r,LC}^{{s}_{i}}\) is the IF phase ambiguity in unit of cycle, i.e., \({N}_{r,LC}^{{s}_{i}}={{\varvec{J}}}_{12}\cdot {\left(\begin{array}{cc}{N}_{r,1}^{{s}_{i}}& {N}_{r,2}^{{s}_{i}}\end{array}\right)}^{T}\); \(\lambda \) is the wave length; \({\varepsilon }_{p,LC}\) and \({\varepsilon }_{\Phi ,LC}\) are the corresponding measurement noise, including the multipath effect. Therefore, the phase center corrections, relative effect, earth rotation error, phase-windup, and loading effects are assumed to be corrected.
Linear dependence of code bias and clock difference is usually lumped together in the IF data processing (Yang et al. 2019):
the symbol \({:}=\) here means “is replaced by.” Similarly, denote
Then, Eq. (2) can be simplified to:
Equation (5) is the observation model utilized in PPP. In time transfer applications, \({t}^{{s}_{i}}\) must be refined. As all signals transmitted by a GNSS satellite are directly derived from the “reading” clock of the satellite (Wübbena 1988), thus \({t}^{{s}_{i}}\) stands for bias between the “reading” clock and the chosen time reference. However, the satellite clock deviates from the “true” so we may choose to define the reference clock more abstractly (Allan 1987). Thus, the estimate of \({t}^{{s}_{i}}\), i.e., \({\widehat{t}}^{{s}_{i}}\), is biased by the chosen reference clock.
In the satellite clock solution, extra conditions should be applied to separate the satellite clock and receiver clock. The most widely used constraint can be expressed as (Yang et al. 2019):
thus in which \({{\varvec{u}}}_{sys}={\left(\begin{array}{cc}\begin{array}{cc}1& 1\end{array}& \begin{array}{cc}\cdots & 1\end{array}\end{array}\right)}^{T}\) is a vector with one entry, with a length equal to the number of satellites in one system; so the superscript \(sys\in \left(\begin{array}{cc}\begin{array}{cc}G& R\end{array}& \begin{array}{cc}C& E\end{array}\end{array}\right)\) denotes different GNSS systems; and \({{\varvec{t}}}^{{\varvec{s}}{\varvec{y}}{\varvec{s}}}={\left(\begin{array}{cc}\begin{array}{cc}{t}^{{s}_{1}}& {t}^{{s}_{2}}\end{array}& \begin{array}{cc}\cdots & {t}^{{s}_{n}}\end{array}\end{array}\right)}^{T}\) stands for the satellite clock vector for this one system. The chosen reference clock is defined with Eq. (6), clock datum constraints in GNSS satellite clock estimation, which can cause a reference clock offset \({t}^{0}\). In addition, due to the linear dependence of the satellite clock and the carrier phase ambiguity, an additional bias \({t}_{0}^{{s}_{i}}\) could also emerge after the convergence of the ambiguity for each satellite \({s}_{i}\). Thus, a detailed expression of the satellite clock estimate \({\widehat{t}}^{{s}_{i}}\) can be written as
where \({t}^{0}\) is the reference clock offset due to the linear dependence of satellite clock and receiver clock, which is identical for different satellites of the same system; \({t}_{0}^{{s}_{i}}\) is the reference clock offset due to the linear dependence of satellite clock and ambiguity, which is different for different satellites as presented in Appendix A; \({\varepsilon }^{{s}_{i}}\) is the estimation noise.
By substituting Eq. (7) into Eq. (5), we have:
where the operator \(\Delta \) presents the between epoch difference; \({\Delta \Phi }_{{LC}}^{{s}_{i}}\) is involved since, that the carrier phase is only sensitive to the receiver clock time-varying, and the initial receiver clock is determined by pseudorange. From this point of view, the receiver clock estimate can be expressed as:
where \({\widehat{t}}_{r}\left(0\right)\)=\({t}_{r}\left(0\right)-{t}^{0}\left(0\right)-\overline{{t }_{0}^{s}}\left(0\right)\) is the initial receiver clock; \({\varepsilon }_{r,P}\) and \({\varepsilon }_{r,\Delta \Phi }\) is the corresponding estimation noise for pseudorange and epoch difference carrier phase; \({\Delta \widehat{t}}_{P,LC}=\Delta {t}_{r}-\Delta {t}^{0}-\Delta \overline{{t }_{0}^{s}}\) and \({\Delta \widehat{t}}_{\Phi ,LC}=\Delta {t}_{r}-\Delta {t}^{0}\) is the receiver clock time-varying estimated by pseudorange and carrier phase, respectively;\(\overline{{t }_{0}^{s}}\) is the weighted mean of the \({t}_{0}^{{s}_{i}}\) of the involved satellite, and the term \(\Delta \overline{{t }_{0}^{s}}\) emerges as a different satellite involved in the pseudorange solution, while it is eliminated by between epoch difference in the carrier phase solution. Then without loss of generality, the receiver clock estimates with both pseudorange and carrier phase can be expressed as:
where \({w}_{P}\) and \({w}_{\Phi }\) present the weight of pseudorange and carrier phase, respectively, and \({w}_{P}:{w}_{\Phi }=1:100\) generally due to the observation accuracy of pseudorange and carrier phase; \({\varepsilon }_{r}\) is the joint effect of \({\varepsilon }_{r,P}\) and \({\varepsilon }_{r,\Delta \Phi }\). Thus, the receiver clock time-varying is dominated by carrier phase:
from which it is suggested that the time-varying of receiver clock, the effect of \(\overline{{t }_{0}^{s}}\) is almost can be ignored after convergence. When performing time synchronization of two receivers \({r}_{a}\) and \({r}_{b}\) with PPP, their time difference is derived as:
so the term \({t}^{0}\) is canceled out once all the receivers use the same AC product; although \(\Delta {\overline{{t }_{0}^{s}}}_{{a},{b}}\) cannot be canceled out for long baselines as different satellites may be involved in PPP time transfer for receivers \({r}_{a}\) and \({r}_{b}\), its effect can be neglected for the stability of \({\Delta t}_{{r}_{a}{r}_{b}}\) after PPP convergence. Equation (11) and Eq. (12) are regarded as the solution for PPP one-way timing and time synchronization; but the terms \({t}^{0}\) and \({t}_{0}^{{s}_{i}}\) are usually not explicitly defined in the PPP model as the receiver coordinate is unaffected by these clock datum terms.
2.2 Assessment of clock stability with PPP
Based on the series of the receiver clock \({\widehat{t}}_{r}\) generated with Eqs. (11) and (12), its stability can be evaluated with the overlapping Allan variance (AVAR) (Allan 1987; Lei et al. 2019):
where \(\tau =m{\tau }_{0}\) represents the average time, \(m\) and \({\tau }_{0}\) represent the averaging factor and the basic measurement interval, respectively; \(N\) represents the number of measured values; \(x\) represents the \(N\) phase values spaced by the measurement interval \({\tau }_{0}\). By substituting Eq. (11) into Eq. (13), be aware that \(\overline{{t }_{0}^{s}}\) could be ignored after convergence, thus we have:
In Eq. (15), the first term denotes the AVAR of the receiver clock itself. The second term is the AVAR of the satellite clock datum \({t}^{0}\), which is dominated by the algorithm in the satellite clock solution of each AC. The third term is the AVAR introduced by the PPP clock estimation noise. The fourth term is their cross-term.
Thus, the direct assessment of PPP derived receiver clock \({\widehat{t}}_{r}\) represents a joint effect, and the evaluation of the reference clock stability for different ACs is not a trivial task since the reference clock \({t}^{0}\) is only implicitly defined in the receiver clock estimate \({\widehat{t}}_{r}\). Fortunately, once an ideal clock, e.g., the time laboratories’ GNSS receiver with the external H-MASER equipped, the effect of \({t}_{r}\) in Eq. (15) is relatively neglectable as its stability can reach about 5 to 7E−15/100 s and 5 to 7E−16/day. We can find the model of clock used in time laboratories from (https://webtai.bipm.org/database/clocklab.html). In this case, \({\delta }_{y}^{2}\left(\tau ,{\widehat{t}}_{r}\right)\) can be simplified as:
Similarly, for the PPP time synchronization, substituting Eq. (12) into Eq. (13) and being aware that the effect of \({t}_{r}\) and \(\Delta {\overline{{t }_{0}^{s}}}_{\mathrm{a},\mathrm{b}}\) may be ignored then we have:
As for IGS reference stations with the precise products of the same AC, their PPP performance can be safely regarded as identical. Thus, the subscript of \(r\) can be omitted in Eqs. (17) and (18), e.g., \({\delta }_{y}^{2}\left(\tau ,{\upvarepsilon }_{r}\right)={\delta }_{y}^{2}\left(\tau ,\upvarepsilon \right) (r=a,b,\cdots )\). In addition, as evidenced in the Appendix B experiment 1 with simulated data, for two independent power law clock noises with a similar noise parameter, their cross-term will be one order lower than the Allan deviation of each term, i.e., \(\frac{1}{2\left(N-2m\right){\tau }^{2}}{\sum }_{i=1}^{N-2m}2S\left({\varepsilon }_{{r}_{a}}\right)S\left({\varepsilon }_{{r}_{b}}\right)\ll {\delta }_{y}^{2}\left(\tau ,{\upvarepsilon }_{r}\right)={\delta }_{y}^{2}\left(\tau ,\upvarepsilon \right) (r=a,b,\cdots )\). Then, Eq. (18) can be further simplified to
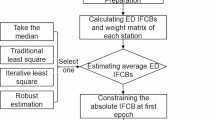
Once there are \({\delta }_{y}^{2}\left(\tau ,{\widehat{t}}_{r}\right)\) as Eq. (17) from \(k\) receivers, and \(k-1\) time synchronization AVAR \({\delta }_{y}^{2}\left(\tau ,{\Delta t}_{{r}_{a}{r}_{b}}\right)\) with respect to the first receiver as Eq. (19), we can solve the terms \({\delta }_{y}^{2}\left(\tau ,\varepsilon \right)\) and \({\delta }_{y}^{2}\left(\tau ,{t}^{0}\right){:}={\delta }_{y}^{2}\left(\tau ,{t}^{0}\right)-\frac{1}{2\left(N-2m\right){\tau }^{2}}{\sum }_{i=1}^{N-2m}2S\left({t}^{0}\right)S\left(\varepsilon \right)\) with the GNSS satellite clock datum stability assessing model:
in which \({{\varvec{u}}}_{{\varvec{k}}}\) is defined as that in Eq. (6); \({{\varvec{z}}}_{{\varvec{k}}}={\left(\mathrm{0,0}\dots 0\right)}^{T}\) is a \(k\times 1\) vector with zero entries. Note that the AVAR \({\delta }_{y}^{2}\left(\tau ,{t}^{0}\right)\) derived from Eq. (20) is actually biased by \(-\frac{1}{2\left(N-2m\right){\tau }^{2}}{\sum }_{i=1}^{N-2m}2S\left({t}^{0}\right)S\left(\varepsilon \right)\). Simulation in Appendix B experiment 2 illustrates the effect of the cross-term could be neglected safely on the datum stability. Thus, \({\delta }_{y}^{2}\left(\tau ,{t}^{0}\right)\) in this study presented an appropriate estimation of the clock datum stability in PPP.
3 Experiment
This section further analyzes the stability of the IGS RT satellite clock of different ACs and their performance in PPP one-way timing and time synchronization using the proposed satellite datum stability assessing model. RT satellite products from five IGS ACs and observing data from stations at nine time laboratories over DOY (day of the year) 011 to 046, 2022 were collected for the experiments.
3.1 Dataset and processing strategy
Shown in Table 1 is the summary of RT products from five ACs used in this study, including CNES (Centre National d’Etudes Spatiales), ESA (European Space Agency’s Space Operations Centre), GFZ (Helmholtz Centre Potsdam - German Research Centre for Geosciences), GMV (GMV innovating solutions), and WHU (Wuhan University). Both products of APC (Antenna Phase Centre) and CoM (Centre of Mass) were available from these ACs, while the CoM products were selected in this study. Moreover, most ACs provide satellite products of Global Positioning System (GPS), BeiDou Navigation Satellite System (BDS), GLONASS (GLO), and Galileo satellite navigation system (GAL).
For PPP one-way timing, the RT IGS products from Table 1 and broadcast ephemeris are matched by Issue of Data Ephemeris (IODE) to generate a precise satellite orbit and clock. For more details on the RT IGS products and the precise satellite orbit and clock recovery algorithm, please refer to the BKG Ntrip Client software (BNC, https://igs.BKG.bund.de/) provided by BKG and Li et al. (2018). The release interval of the products in Table 1 is 5 s. To get a measure of the availability of the RT products from these ACs, we calculated the product integrity rate according to the interval for different ACs. The results are presented in Fig. 1.
As shown, although the loss of RT products is unavoidable due to network problems (Shi et al. 2019), almost all these ACs had an integrity rate of over 90% for our experimental period. In addition, the IGS final product of the experimental period was also collected in this study for comparative purposes. PPP processing, however, uses not only ephemeris data from RT ACs, but also observation data released by observing stations.
A summary of the external clock, distance, and locational data for the nine observing stations is presented in Table 2. All nine stations at time laboratories are equipped with a high stability active H-MASER maintained by the time laboratory.
Recalling Eq. (17), in the case of these nine stations, the clock estimates vary with PPP, i.e., so \(\widehat{t}_{r}\), is subject to stability of the satellite clock datum and the receiver clock estimation noise. In addition, as we take OP71 as the central node for time synchronization, thus the distance from other stations varies from 262.3 to 8892.4 km. We can analyze the residual effect of the satellite clock datum in PPP time synchronization for different baselines, but this depends on the processing strategy.
The PPP data processing strategy is shown in Table 3. As shown, the GPS dual-frequency IF combination is involved with SRIF (Square Root Information Filter) in the simulated RT mode. Although the receivers were all equipped with high accuracy H-MASER, the receiver clock difference parameters were treated as white noise in PPP for this study.
After formulating the PPP processing strategy, we selected software for PPP processing. The experiments were performed with the FUSING (FUSing IN GNSS) software (Gu et al. 2021, 2020; Zhao et al. 2019). The FUSING software was developed for high-precision real-time GNSS data processing, multi-sensor navigation, and atmospheric modeling (Luo et al. 2020, 2021). RT satellite orbit and clock from SSRC00WHU0 in Table 1 were also generated with FUSING software, and the nine stations analyzed in this study were not included in the RT products processing. After PPP processing with FUSING, we get the result of PPP one-way timing.
3.2 PPP one-way timing
Shown in Fig. 2 is the receiver clock series for PPP one-way timing, i.e., \({\widehat{t}}_{r}\), from DOY 011 to 046, 2022 with products of five RT ACs and IGS for nine stations. Since the selected external clock of these stations was the high stability active H-MASER, the variation of the one-way timing series in Fig. 2 was subjected to the effect of the GNSS reference clocks of each ACs.
A comparison of these sequences shows that clock differences behave similarly for all stations. This confirms that the selected H-MASER has a very slight frequency deviation. The result of GFZ AC however contained more noise than other RT ACs, which may be due to different satellite clock generation strategy. Moreover, the IGS series was shifted by 13 ns for convenience in plotting.
Furthermore, a systematic trend was found in all these solutions, which is reflected in the offset between each product's start and end epoch compared in Fig. 2. This trend was most likely due to the divergence in the time scales of the H-MASER at the time laboratory stations and the GPS satellite atomic clock, but the long-term trend does not affect short-term stability.
To obtain the stability of PPP one-way timing, we further calculate its overlapping Allan deviations (ADEV) based on the results shown in Fig. 2. Figure 3 further presents the ADEV of the PPP one-way timing receiver clock series, i.e., \({\widehat{t}}_{r}\), from DOY 011 to 046, 2022 with products of five RT ACs and IGS. As shown, the performance of ADEVs at all stations was similar, which means that two to three stations are sufficient for a rough assessment of the datum stability differences among the products. The GFZ reference clock, however, was unstable due volume of noise in its clock difference. GMV and WHU were slightly more stable for most stations than IGS before 1000 s, and IGS was the most stable after 1000 s. The stability of all RT products tended to be similar, i.e., 7 to 9E−15/day for most of the RT ACs.
The stability of the H-MASER clocks equipped by the GNSS receiver from time laboratories can reach about 5 to 7E−15/100 s and 5 to 7E−16/day. This again confirms that the clock oscillator noise as Eqs. (17) and (19) indicate theoretically. So far, only the effect of the satellite clock datum on one-way timing has been analyzed, but its effect on time synchronization must also be explored in time synchronization experiments.
3.3 PPP time synchronization
Time synchronization experiments between stations were conducted based on the nine IGS stations shown in Table 2. These experiments established eight different time links with OP71 as the reference station. Shown in Fig. 4 is the PPP time synchronization from DOY 011 to 046, 2022 with products of different ACs. The long-term trends of short baseline time synchronization appearing in Fig. 4 may be due to the time laboratory steering of the local H-MASER. These do not affect the stability of the time synchronization for intervals of a day or less. The ESA, WHU, and GFZ ACs show the same trend as IGS. The effect of satellite-specific biases on the long baseline time synchronization between different products does not seem significant, which means the effect can be safely ignored.
To further illustrate the stability of time synchronization between stations in Fig. 4, the ADEV of the time synchronization series is shown in Fig. 5. The IGS AC is slightly more unstable in the short term than RT ACs. Moreover, all products have similar time synchronization day stability, i.e., 1 to 3E−15, and the effect of baseline length is not immediately apparent. The ESA, WHU, and GFZ ACs delivered consistent short-term stability for most time links during the experimental period.
After getting the results of PPP one-way timing and time synchronization based on the PPP time transfer model, we used the proposed satellite datum stability assessing model to measure the stability of the satellite clock datum and PPP estimation noise.
3.4 Stability of PPP time transfer
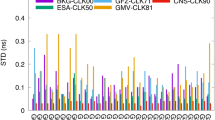
We can assess the stability of the satellite clock reference of the five RT ACs as well as the PPP noise by solving Eq. (20) using the ADEV in PPP one-way timing and time synchronization. The results are drawn in Fig. 6.
Shown in Fig. 6 are the ADEVs of the satellite clock datum \({t}^{0}\) (top panel) and PPP clock estimation noise \({\varepsilon }_{r}\) (bottom panel) with the five RT AC products collected from DOY 011 to 046, 2022. All RT ACs showed similar stability in the satellite clock datum over a one day period, i.e., 6 to 8E−15. The GMV and WHU ACs were more stable and kept pace with IGS over the short term before the 1000 s. For PPP estimation noise, IGS, however, was slightly unstable before 1000 s during the experiment for unknown reasons, which might be explored in future research. Overall the estimation noise of all RT ACs stayed at almost the same level, i.e., 1 to 2E−5/day.
Overall the slopes of the ADEVs in the PPP estimation noise shown in Fig. 6 were between − 1 and − 1/2, i.e., corresponding to the flicker phase modulation noise, white phase modulation noise, and white frequency modulation noise. Since only white frequency modulation noise produces random walks in phase, i.e., a colored noise that accumulates over time, which may lead to the protracted time scale drift in time synchronization but was invisible over the experimental period.
In addition, we summarized the ADEVs of the satellite clock datum and PPP estimation noise for 120 s, 10,020 s, and 86,400 s from Fig. 6, shown in Table 4.
As shown in Table 4, the datum stability of WHU as 3.05E−13/120s and GMV as 6.56E−15/day perform more stable than other RT ACs. IGS is more stable than five RT ACs by half a magnitude. The datum stability results suggested that RT-PPP for local oscillator steering can improve its stability to 6 to 8E−15/day by selecting an appropriate RT product. Moreover, there is little difference in estimation noise stability between five RT ACs, of which WHU has the more stable performance of 8.46E−14/120s and 1.50E−15/day, even lower than IGS. The PPP estimation noise results showed little difference in the time synchronization stability between RT and IGS final products.
4 Conclusions
This paper introduces a new GNSS satellite clock datum stability assessing model derived from the overlapping Allan variance expression for receiver clocks in PPP one-way timing and time synchronization. A theoretical analysis showed that the overlapping Allan variance of one-way timing reflects the joint effect of the variance of the receiver clock, the satellite clock datum, the PPP estimation noise, and their cross-term. By combining the overlapping Allan variance of both one-way timing and time synchronization, we developed a new datum stability measure for the clock datum stability evaluation based on the time laboratory GNSS receivers equipped with external H-MASER clocks.
PPP one-way timing and time synchronization experiments using RT products from CNES, ESA, GFZ, GMV, and WHU from DOY 011 to 046, 2022 demonstrate the effectiveness of the proposed satellite datum stability assessing model. The datum effect of the satellite clock products was analyzed in detail with nine observing stations at time laboratories equipped with H-MASER; the results indicate the PPP one-way timing stability of all RT products tended to be similar, i.e., 7 to 9E−15/day for most of the RT ACs. GMV and WHU were slightly more stable for most stations than IGS before 1000 s. All products have similar time synchronization day stability, i.e., 1 to 3E−15. In addition, the result with IGS final satellite products was also included as a reference in the experiment, and its satellite clock datum stability is most stable after 1000 s.
The satellite clock datum stability suggests that GMV and WHU are slightly more stable than IGS before 1000 s, and IGS is most stable after 1000 s. The datum stability of all RT products will tend to be similar, i.e., 6 to 8E−15/day for most RT ACs. The datum stability of WHU as 3.05E−13/120 s and GMV as 6.56E−15/day performs more stable than other RT ACs. The datum stability results suggested that RT-PPP for local oscillator steering can improve its stability to 6 to 8E−15/day by selecting an appropriate RT product. Moreover, five RT ACs reached the same level for PPP estimation noise, i.e., 1 to 2E−15/day, which indicated little difference in the time synchronization stability between RT and IGS final products
Satellite clock datum stability can be measured conveniently and quickly using the GNSS satellite clock datum stability assessing model proposed in this paper. The experimental datum stability results indicate that RT-PPP for steering the local oscillator can improve the stability to 6 to 8E−15/day when an appropriate RT product is selected. So the datum stability as measured by the proposed model is an effective guide for setting parameters and making long-term stability predictions when steering local oscillators.
Data availability
GNSS data are released by the IGS data center CDDIS at https://cddis.nasa.gov/archive/. The RT product files used in the experiment can be accessed from ftp://120.27.221.11/RT_011_046_2022/, username: share, password: 123456.
References
Allan DW (1987) Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators. IEEE Trans Ultrason Ferroelectr Freq Control 34(6):647. https://doi.org/10.1109/t-uffc.1987.26997
Ge Y, Ding S, Qin W, Zhou F, Yang X (2020) Carrier phase time transfer with Galileo observations. Measurement. https://doi.org/10.1016/J.MEASUREMENT.2020.107799
Gu S, Dai C, Fang W, Zheng F, Wang Y, Zhang Q, Lou Y, Niu X (2021) Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation. J Geodesy. https://doi.org/10.1007/S00190-021-01514-8
Gu S, Wang Y, Zhao Q, Zheng F, Gong X (2020) BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation. J Geodesy: Contin Bull Géodésique Manuscripta Geodaetica. https://doi.org/10.1007/s00190-020-01364-w
Guo W, Song W, Niu X, Lou Y, Gu S, Zhang S, Shi C (2019) Foundation and performance evaluation of real-time GNSS high-precision one-way timing system. GPS Solut. https://doi.org/10.1007/s10291-018-0811-1
Lei Y, Tan J, Guo W, Cui J, Liu J (2019) Time-domain evaluation method for clock frequency stability based on precise point positioning. IEEE Access 7:132413–132422. https://doi.org/10.1109/ACCESS.2019.2940515
Li G, Lin Y, Shi F, Liu J, Yang Y, Shi J (2018) Using IGS RTS products for real-time subnanosecond level time transfer. In: 9th China Satellite Navigation Conference (CSNC) - Location, Time of Augmentation, Harbin, Peoples Republic of China. https://doi.org/10.1007/978-981-13-0005-9_40
Liu T, Jiang W, Laurichesse D, Chen H, Liu X, Wang J (2020) Assessing GPS/Galileo real-time precise point positioning with ambiguity resolution based on phase biases from CNES. Adv Space Res 66(4):810. https://doi.org/10.1016/j.asr.2020.04.054
Lou Y, Zheng F, Gu S, Liu Y (2015) The impact of non-nominal yaw attitudes of GPS satellites on kinematic PPP solutions and their mitigation strategies. J Navig 68(4):718. https://doi.org/10.1017/S0373463315000041
Luo X, Gu S, Lou Y, Cai L, Liu Z (2020) Amplitude scintillation index derived from C/N0 measurements released by common geodetic GNSS receivers operating at 1 Hz. J Geodesy: Contin Bull Géodésique Manuscripta Geodaetica. https://doi.org/10.1007/s00190-020-01359-7
Luo X, Lou Y, Gu S, Li G, Xiong C, Song W, Zhao Z (2021) Local ionospheric plasma bubble revealed by BDS Geostationary Earth Orbit satellite observations. GPS Solut. https://doi.org/10.1007/S10291-021-01155-6
Mishagin KG, Lysenko VA, Medvedev SY (2020) A practical approach to optimal control problem for atomic clocks. IEEE Trans Ultrason Ferroelectr Freq Control 67(5):1080–1087. https://doi.org/10.1109/TUFFC.2019.2957650
Orgiazzi D, Tavella P, Lahaye FBI (2005) Experimental assessment of the time transfer capability of Precise Point Positioning (PPP). In: IEEE International Frequency Control Symposium, 345 E 47TH ST, New York, NY 10017 USA. https://doi.org/10.1109/FREQ.2005.1573955
Ouyang C, Shi J, Huang Y, Guo J, Xu C (2021) Evaluation of BDS-2 real-time orbit and clock corrections from four IGS analysis centers. Measurement. https://doi.org/10.1016/j.measurement.2020.108441
Petit G, Jiang ZBI (2007) Precise point positioning for TAI computation, 345 E 47TH ST, New York, NY 10017 USA. https://doi.org/10.1109/FREQ.2007.4319104
Pireaux S, Defraigne P, Wauters L, Bergeot N, Baire Q, Bruyninx C (2010) Higher-order ionospheric effects in GPS time and frequency transfer. GPS Solut 14(3):267–277. https://doi.org/10.1007/s10291-009-0152-1
Qin W, Ge Y, Zhang Z, Su H, Wei P, Yang X (2020) Accounting BDS3–BDS2 inter-system biases for precise time transfer. Measurement. https://doi.org/10.1016/j.measurement.2020.107566
Rønningen OP, Danielson M (2019) A novel PPP Disciplined Oscillator. In: 2019 Joint conference of the IEEE international frequency control symposium and European frequency and time forum (EFTF/IFC). https://doi.org/10.1109/FCS.2019.8856034
Shi C, Guo S, Gu S, Yang X, Gong X, Deng Z, Ge M, Schuh H (2019) Multi-GNSS satellite clock estimation constrained with oscillator noise model in the existence of data discontinuity. Springer, Berlin, Heidelberg 93(4):515. https://doi.org/10.1007/s00190-018-1178-3
Wu JT, Wu SC, Hajj GA, Bertiger WI, Lichten SM (1993) Effects of antenna orientation on GPS carrier phase. Manuscripta Geodaetica (No.2), 91–98
Wübbena G (1988) GPS carrier phases and clock modeling. GPS-Tech Appl Geodesy Surv. https://doi.org/10.1007/BFb0011350
Yang X, Gu S, Gong X, Song W, Lou Y, Liu J (2019) Regional BDS satellite clock estimation with triple-frequency ambiguity resolution based on undifferenced observation. GPS Solut. https://doi.org/10.1007/s10291-019-0828-0
Yao Y, He Y, Yi W, Song W, Cao C, Chen M (2017) Method for evaluating real-time GNSS satellite clock offset products. GPS Solut 21(4):1417–1425. https://doi.org/10.1007/s10291-017-0619-4
Zhao Q, Wang Y, Gu S, Zheng F, Shi C, Ge M, Schuh H (2019) Refining ionospheric delay modeling for undifferenced and uncombined GNSS data processing, vol 93(4). Springer, Berlin, Heidelberg. https://doi.org/10.1007/s00190-018-1180-9
Zumberge JF, Heflin MB, Jefferson DC, Watkins MM, Webb FH (1997) Precise point positioning for the efficient and robust analysis of GPS data from large networks, vol 102(B3). Wiley, Hoboken. https://doi.org/10.1029/96JB03860
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant 41974038 and 42174029. The authors show great gratitude to IGS for providing data and products.
Author information
Authors and Affiliations
Contributions
Author WG and SG designed the research; WG, HZ, FM, and SG performed the research; XG, CX, and SG provided the region products; WG, HZ and SG analyzed the result; WG, HZ, and SG drafted the paper. All authors discussed, commented on, and reviewed the manuscript.
Corresponding author
Appendices
Appendix A
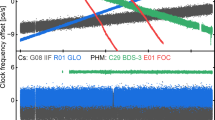
The satellite clock double difference, i.e., the difference between WHU RT product and IGS final product, and further between satellites, from DOY (day of the year) 016, 2022 is presented in Fig. 7 to show the existence of \({t}_{0}^{{s}_{i}}\) (Yao et al. 2017). As shown in Fig. 7, \({t}_{0}^{{s}_{i}}\) is rather stable.
Appendix B
To confirm that the cross-term of two independent power law clock noise with a similar noise parameter is one or two orders lower than the Allan deviation of each term, we used Stable32 software (http://www.wriley.com/) to generate a noise sequence n1 and n2 with the strategy of Table
5.
Where \(\tau \) represents the average time, \(N\) is the number of points, WPM is White Phase Modulation Noise, FPM is Flicker Phase Modulation Noise, WFM is White Frequency Modulation Noise, FFM is Flicker Frequency Modulation Noise, and RWFM is Random Walk Frequency Modulation Noise. The power law noises mentioned have a specific power spectral density of their fractional frequency fluctuations of the form \({\mathrm{S}}_{\mathrm{y}}\left({f}\right)\propto {{f}}^{\mathrm{a}}\), where \(f\) is the Fourier or sideband frequency in hertz; and \(a\) is the power law exponent. The \(a\, {\text {of}}\, \mathrm{WPM},\mathrm{ FPM},\mathrm{ WFM},\mathrm{ FFM},\mathrm{ and\, RWFM\, are }\,2, 1, 0, -1,\mathrm{ and }-2.\)
The Overlapping Allan deviation graph of n1, n2, and cross-term of n1 and n2 was as follows:
As shown in Fig. 8, the cross-term was about one order lower than that of the two origin random noises, i.e., n1 and n2. Note that the cross-term is not always positive, and the log–log diagram only presented the positive sequence.
In order to explain the effect of the cross-term between the reference and the noise on the reference, we simulate the similar overlapping Allan deviation curve by our experiment result and give the simulation parameters in Table
6.
We generate a noise sequence r and n as reference and noise. The Overlapping Allan variance graph of r, n, and the cross-term of r and n was as follows (Fig. 9).
The effect of the cross-term on reference needs to be discussed here because the noise has been detached from the reference. From the simulation results, the cross-term on the impact of the reference is minimal.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Guo, W., Zuo, H., Mao, F. et al. On the satellite clock datum stability of RT-PPP product and its application in one-way timing and time synchronization. J Geod 96, 52 (2022). https://doi.org/10.1007/s00190-022-01638-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-022-01638-5