Introduction

The development of global navigation satellite systems (GNSS) and the improvement of precise orbit and clock products promote real-time precise applications of GNSS, such as real-time precise point positioning (PPP) (Elsobeiey and Al-Harbi 2016), real-time meteorology and ionospheric modeling (Lee et al. 2013; Abdelazeem et al. 2016), and tsunami and earthquake early warning (Li et al. 2013; Hoechner et al. 2013). To support these applications, real-time precise orbit and clock products for navigation satellites are essential. Unlike precise orbit that can be determined based on observations in the recent past and predicted to real-time with high precision, the precise clock should be estimated and updated in real-time (Kouba and Héroux 2001). Actually, the real-time precise clocks of navigation satellites are usually estimated from real-time observations from reference stations of a ground network (Zhang et al. 2011; Ge et al. 2012a), and need to be broadcast along with predicted satellite orbits to the real-time users via communication satellites or Internet (El-Mowafy et al. 2017).

For real-time clock estimation, it is usual to process the ionospheric-free (IF) combinations of dual-frequency code and phase observations in a Kalman filter (Hauschild and Montenbruck 2008, 2009; Laurichesse et al. 2013) or sequential least squares (Fu et al. 2018). Real-time clock estimation methods fall into three classes according to the observation models they adopt, i.e., the undifferenced (UD) method, epoch-differenced (ED) method, and mixed-differenced (MD) method. The ED method eliminates all ambiguity parameters and preserves only the differential satellite clock, receiver clock, and tropospheric delay by differencing observations between consecutive epochs. Because of fewer unknowns, the ED method is characterized by simplicity and high-computation efficiency, which has been used in the early days (Mervart et al. 2008; Zhang et al. 2011). The UD method estimates real-time clock together with ambiguity and tropospheric delay based on the UD IF code and phase observations, which is more rigorous and results into more precise clock solutions. With the advent of multi-GNSS, the UD method is not efficient enough to estimate multi-GNSS clocks in real-time. As a tradeoff, the MD method, which employs both UD code observations and ED phase observations, is developed to balance computation efficiency and solution precision (Ge et al. 2012a; Zhang et al. 2015). Alternatively, a parallel algorithm that runs the UD or ED methods with different updating rate in two independent processes has been studied in recent years for high-computation efficiency (Zhang et al. 2011; Dai et al. 2018).

The aforementioned methods have been applied successfully by many international GNSS service (IGS) analysis centers (ACs) and organizations (Mervart et al. 2008; Hauschild and Montenbruck 2009), which have contributed to the generation of real-time clock products. These methods, however, have a common defect that the phase ambiguity parameters are estimated as float numbers or eliminated by epoch differencing, without being fixed to integer numbers. It has been demonstrated that ambiguity fixing will bring significant improvement to parameter estimation in GNSS data processing (Dong and Bock 1989; Ge et al. 2005). Thus, there is room for precision improvements in current real-time clock products. In fact, of all the IGS ACs, the Centre National d’Etudes Spatiales (CNES) of France is providing a much more precise clock product by fixing phase ambiguity (Laurichesse and Mercier 2007; Laurichesse et al. 2008, 2009). Figure 1 presents the standard deviations (STD) with respect to the IGS 30 s final products for five IGS real-time clock products of the global positioning system (GPS) on the day of year (DOY) 182, 2017 (https://igs.bkg.bund.de/ntrip/orbits). As shown in the figure, the clock precision varies not only between different products, but also between satellites for the same product. Overall, the real-time clock products of the IGS ACs will achieve a normal precision of around 0.15 ns without fixing phase ambiguities. With ambiguity parameters fixed to integer numbers, the CNES real-time clock product exhibits extremely high precision which is better than 0.05 ns. Obviously, ambiguity-fixing in real-time clock estimation significantly improves the clock precision and real-time service performance.

Fig. 1
figure 1

STDs of the real-time clock products from five IGS ACs with respect to the IGS 30 s final products on DOY 182, 2017. CLKxx, are the product IDs in IGS context; BKG, Bundesamt für Kartographie und Geodäsie (Federal Agency for Cartography and Geodesy); ESA, European Space Agency; GFZ, Deutsches GeoForschungsZentrum (German Research Centre for Geosciences); GMV, the GMV Innovation Solutions Corp; CNS, the Centre National d’Etudes Spatiales (France Space Agency)

Full size image

The ambiguity of a GNSS phase observation consists of an integer number of cycles and a fractional bias due to uncalibrated phase delays (UPDs) in satellite and receiver. Consequently, the ambiguity parameters cannot be fixed directly and are usually estimated as float numbers. In the early stages of GNSS precise positioning, the float ambiguities were differenced between-satellite and between-receiver to eliminate the receiver and satellite UPDs, resulting in the fixable double-differenced (DD) ambiguities. The DD ambiguity-fixing method has been studied extensively and widely (Blewitt 1989; Teunissen 1995; Ge et al. 2006). However, the DD ambiguity-fixing method is not a good choice in real-time clock estimation because this method has to loop over all the available undifferenced ambiguities to form the set of independent DD ambiguities and search the most-easy-to-fix ones.

Gabor and Nerem (1999, 2002) have demonstrated that the satellite wide-lane (WL) UPDs are stable enough to be estimated from a ground reference network with high precision and reliability. The stability of satellite narrow-lane (NL) UPDs has been further demonstrated by Laurichesse and Mercier (2007) and Ge et al. (2008). If a correction for the UPD is applied, the undifferenced or between-satellite single-differenced ambiguities of an independent receiver can be fixed to integers. Several methods or variants have been proposed and formulated to estimate UPDs and support the single-receiver ambiguity-fixing, which differ in how the satellite UPDs are estimated by network processing and corrected for in PPP. Geng et al. (2010) and Shi and Gao (2013) compared the methods and demonstrated their equivalence. Teunissen and Khodabandeh (2014) have also compared these methods in detail, proving that all the methods are equivalent and transformable between each other. Furthermore, their research has shown that these methods are equivalent to the traditional DD ambiguity-fixing method in the frame of S-system theory.

The single-receiver ambiguity-fixing strategies not only free the end-users from selecting reference stations by correcting the ambiguities for UPDs, but can also simplify ambiguity-fixing in network data processing by estimating the common and stable UPDs. To decompose the satellite and receiver UPDs, Laurichesse and Mercier (2007) proposed the integer recovery clock (IRC) model and Collins et al. (2008) developed the similar decoupled clock (DC) model, in which the undifferenced ambiguities are fixed to integers with the NL UPDs being assimilated into the respective satellite and receiver clock offsets. The newly defined satellite clock, which is known as phase clock, exhibits much higher precision because the ambiguities have been fixed. However, the standard IGS clock product has to be provided alternatively to support the usage of code observations. Unlike the IRC/DC models, the UPD model estimates UPDs independently from the ambiguity estimates without modifications to the current data processing strategy and clock definition. Thus, the UPD model is compatible with the classical clock estimation method and suitable for ambiguity-fixing in real-time clock estimation. To improve the standard real-time clock product, we extend the traditional real-time clock estimation method by employing the UPD model to estimate satellite and receiver UPDs and fix the undifferenced ambiguities in real-time.

We start with a review of real-time clock estimation, UPD estimation and ambiguity-fixing. Next, the necessary mathematical basics for real-time clock estimation, UPD estimation and ambiguity fixing, and generation of ambiguity-fixed clock solution are introduced. Based on this introduction, the actual data processing flow of the proposed method is demonstrated. We then test and evaluate the proposed algorithm in clock estimation and kinematic PPP based on real data. The resulting UPD estimates, clock solutions and PPP solutions are analyzed to demonstrate the performance of the proposed method. Finally, a summary and conclusions are presented.

Method

The mathematical basics for real-time clock estimation, UPD estimation and ambiguity fixing, and generation of the ambiguity-fixed clock is presented in detail in this section. Then, the actual epoch processing flow of the proposed method is summarized and introduced.

Real-time precise clock estimation

The real-time satellite clock offsets are usually estimated from the IF combinations of dual-frequency phase and code observations. Thus, the observation equations used in clock estimation can be expressed as:

$$\begin{aligned} L_{{{\text{r,IF}}}}^{{\text{s}}} & =\;\rho _{{\text{r}}}^{{\text{s}}}+c \cdot (\delta {t_{\text{r}}} - \delta {t^{\text{s}}})+{T_{\text{r}}}+{\lambda _n} \cdot a_{{{\text{r,IF}}}}^{{\text{s}}}+{\varepsilon _{{\text{L,IF}}}} \\ P_{{{\text{r,IF}}}}^{{\text{s}}} & =\rho _{{\text{r}}}^{{\text{s}}}+c \cdot (\delta {t_{\text{r}}} - \delta {t^{\text{s}}})+{T_{\text{r}}}+{\varepsilon _{{\text{P,IF}}}} \\ a_{{{\text{r,IF}}}}^{{\text{s}}} & =N_{{{\text{r,IF}}}}^{{\text{s}}}+{b_{{\text{r,IF}}}}+b_{{{\text{,IF}}}}^{{\text{s}}} \\ \delta {t_{\text{r}}} & =\delta {{\tilde {t}}_{\text{r}}}+{d_{{\text{r,IF}}}} \\ \delta {t^{\text{s}}} & =\delta {{\tilde {t}}^{\text{s}}}+d_{{{\text{,IF}}}}^{{\text{s}}} \\ \end{aligned}$$
(1)

where \(r\) and \(s\) are the index of receiver and satellite, respectively, \(L_{{{\text{r,IF}}}}^{{\text{s}}}\) and \(P_{{{\text{r,IF}}}}^{{\text{s}}}\) represent the ionospheric-free phase and code combinations in meters, \({\varepsilon _{{\text{L,IF}}}}\) and \({\varepsilon _{{\text{P,IF}}}}\) are the corresponding measurement noise, \(\rho _{{\text{r}}}^{{\text{s}}}\) is the geometric distance from receiver \(r\) to satellite \(s\), which can be computed from the high precision coordinates of reference station and predicted satellite orbit, \({T_{\text{r}}}\) is the signal path delay due to the troposphere, \(c\) is the speed of light in vacuum, \({\lambda _n}\) and \({f_n}\) represent the wavelength and frequency of the IF phase combination, \(\delta {\tilde {t}_{\text{r}}}\) and \(\delta {\tilde {t}^{\text{s}}}\) denote the true receiver and satellite clock offsets, \({d_{{\text{r,IF}}}}\) and \(d_{{{\text{,IF}}}}^{{\text{s}}}\) are the code hardware delay of receiver and satellite respectively, \({b_{{\text{r,IF}}}}\) and \(b_{{{\text{,IF}}}}^{{\text{s}}}\) are the phase hardware delay of receiver and satellite, \(N_{{{\text{r,IF}}}}^{{\text{s}}}\) is the ionospheric-free phase ambiguity, \(a_{{{\text{r,IF}}}}^{{\text{s}}}\) is the estimated ionospheric-free phase ambiguity in clock estimation. To eliminate the rank defects, it is usual to combine code hardware delays of satellite and receiver with the corresponding clock offset parameters and phase hardware delays with phase ambiguities. \(\delta {t_{\text{r}}}\), \(\delta {t^{\text{s}}}\) and \(a_{{{\text{r,IF}}}}^{{\text{s}}}\) represent the corresponding unknown parameters that absorb hardware delays in the clock estimation filter. Thus, the estimated clock offsets depend on the combined code observations. Different code combinations lead to different clock estimates. In fact, the IGS clock products are by convention relative to the ionospheric-free combination of the P1 and P2 codes.

For a network consisting of several reference stations, there will be large amounts of observations at each epoch \(k\) which can be expressed as:

$${{\mathbf{z}}_k}={{\mathbf{A}}_k}{{\mathbf{x}}_k}+{{\mathbf{v}}_k}$$
(2)

where \({{\mathbf{z}}_k}\) is the observation vector including all IF phase and code observations at epoch \(k\), \({{\mathbf{v}}_k}\) is the corresponding measurement noise vector, \({{\mathbf{x}}_k}\) is the unknown parameter vector including satellite and receiver clock offsets, tropospheric delays and the IF ambiguities, and \({{\mathbf{A}}_k}\) is the design matrix. Adding these observations into the filter as a measurement update will result in the following estimates of unknowns:

$${{\mathbf{\hat {x}}}_k}={\left[ {\begin{array}{*{20}{c}} {{\mathbf{\hat {x}}}} \\ {{\mathbf{\hat {a}}}} \end{array}} \right]_k}={\left[ {\begin{array}{*{20}{c}} {{{\mathbf{Q}}_{{\mathbf{xx}}}}}&{{{\mathbf{Q}}_{{\mathbf{xa}}}}} \\ {{{\mathbf{Q}}_{{\mathbf{ax}}}}}&{{{\mathbf{Q}}_{{\mathbf{aa}}}}} \end{array}} \right]_k}{\left[ {\begin{array}{*{20}{c}} {{{\mathbf{v}}_{\mathbf{x}}}} \\ {{{\mathbf{v}}_{\mathbf{a}}}} \end{array}} \right]_k}$$
(3)

in which \({\mathbf{\hat {a}}}\) is the vector of estimated IF ambiguities and \({\mathbf{\hat {x}}}\) is the estimates of the other unknowns, and \({{\mathbf{Q}}_{{\mathbf{xx}}}}\), \({{\mathbf{Q}}_{{\mathbf{aa}}}}\) and \({{\mathbf{Q}}_{{\mathbf{xa}}}}\) are the variance and covariance matrices corresponding to the estimated vectors.

UPD estimation and ambiguity fixing

The IF ambiguity is real-valued because of the real-valued combination coefficients, and are usually expressed as combination of WL and NL ambiguities:

$$a_{{{\text{r,IF}}}}^{{\text{s}}}=\frac{{{f_1}{f_2}}}{{f_{1}^{2} - f_{2}^{2}}}a_{{{\text{r,w}}}}^{{\text{s}}}+\frac{{{f_1}}}{{{f_1}+{f_2}}}a_{{{\text{r,}}n}}^{{\text{s}}}$$
(4)

where \({f_i}\) \(\left( {i=1,2} \right)\) denotes the signal frequency and \(a_{{r,w}}^{s}\) and \(a_{{{\text{r,n}}}}^{{\text{w}}}\) are the corresponding WL and NL ambiguities.

The WL and NL ambiguities cannot be estimated simultaneously in clock estimation due to the rank defects. It is usual to compute the WL ambiguity first by averaging the Hatch-Melbourne-Wübbena (HMW) combinations over several epochs (Hatch 1983; Melbourne 1985; Wübbena 1985):

$$\hat {a}_{{{\text{r,w}}}}^{{\text{s}}}=\left\langle {{{\left( {\frac{{{f_1}}}{{{f_1} - {f_2}}}{L_1} - \frac{{{f_2}}}{{{f_1} - {f_2}}}{L_2} - \frac{{{f_1}}}{{{f_1}+{f_2}}}{P_1}+\frac{{{f_2}}}{{{f_1}+{f_2}}}{P_1}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{f_1}}}{{{f_1} - {f_2}}}{L_1} - \frac{{{f_2}}}{{{f_1} - {f_2}}}{L_2} - \frac{{{f_1}}}{{{f_1}+{f_2}}}{P_1}+\frac{{{f_2}}}{{{f_1}+{f_2}}}{P_1}} \right)} {{\lambda _{\text{w}}}}}} \right. \kern-0pt} {{\lambda _{\text{w}}}}}} \right\rangle =N_{{{\text{r,w}}}}^{{\text{s}}}+{b_{{\text{r,w}}}}+b_{{{\text{,w}}}}^{{\text{s}}}+{\varepsilon _{{\text{a,w}}}}$$
(5)

in which \(\langle\)\(\rangle\) denotes the average over epochs, \({L_i}\) and \({P_i}\) \(\left( {i=1,2} \right)\) are the original phase and code observations on each carrier, \({\lambda _{\text{w}}}\) denotes the wavelength of the WL combination, \({\varepsilon _{a,w}}\) is the WL noise.

Assuming the WL ambiguity is successfully fixed to the correct integer \(N_{{{\text{r,w}}}}^{{\text{s}}}\), the NL ambiguity can be derived from (4) as:

$$\hat {a}_{{r,n}}^{s}=\frac{{{f_1}+{f_2}}}{{{f_1}}}\hat {a}_{{{\text{r,IF}}}}^{{\text{s}}} - \frac{{{f_2}}}{{{f_1} - {f_2}}}N_{{{\text{r,w}}}}^{{\text{s}}}=N_{{{\text{r,n}}}}^{{\text{s}}}+{b_{{\text{r,n}}}}+b_{{{\text{,n}}}}^{{\text{s}}}+{\varepsilon _{{\text{a,n}}}}$$
(6)

where \(\hat {a}_{{{\text{r,IF}}}}^{{\text{s}}}\) is the output of clock estimation, \({\varepsilon _{{\text{a,n}}}}\) is the NL estimate noise.

Obviously, both the WL and NL ambiguities in (5) and (6) are biased by the satellite and receiver UPDs, which are real-valued and unfixable in nature. To perform ambiguity fixing, the UPDs should be removed from these ambiguity estimates. Considering that both the WL and NL ambiguity estimates are fixed in the same procedure and have similar forms, we ignore the WL and NL specifiers in the following discussion if not necessary. Given that the estimated ambiguity \(\hat {a}_{{\text{r}}}^{{\text{s}}}\) is precise enough and the a priori UPD \({b_{{\text{0,r}}}}\) and \(b_{{\text{0}}}^{{\text{s}}}\) are available and rather precise, we can determine the corresponding integer ambiguity \(\hat {N}_{{\text{r}}}^{{\text{s}}}\) and the pre-fit ambiguity residual \(\hat {\varphi }_{{\text{r}}}^{{\text{s}}}\) as:

$$\begin{aligned} \hat {N}_{{\text{r}}}^{{\text{s}}}= & {\text{int}}\left( {\hat {a}_{{\text{r}}}^{{\text{s}}} - {b_{{\text{0,r}}}} - b_{{\text{0}}}^{{\text{s}}}} \right) \\ \hat {\varphi }_{{\text{r}}}^{{\text{s}}}= & \hat {a}_{{\text{r}}}^{{\text{s}}} - {b_{{\text{0,r}}}} - b_{{\text{0}}}^{{\text{s}}} - \hat {N}_{{\text{r}}}^{{\text{s}}} \\ \end{aligned}$$
(7)

where \({\text{int}}()\) rounds a float number to the nearest integer number. The fixing decision is made according to the fixation probability \({P_0}\), which is calculated with the following formula (Dong and Bock 1989):

$${P_0}=1 - \sum\limits_{{i=1}}^{\infty } {\left[ {{\text{erfc}}\left( {\tfrac{{i - |a - n|}}{{\sqrt 2 \sigma }}} \right) - {\text{erfc}}\left( {\tfrac{{i+|a - n|}}{{\sqrt 2 \sigma }}} \right)} \right]}$$
(8)

with

$${\text{erfc}}(x)=\frac{2}{{\sqrt \pi }}\int\limits_{x}^{\infty } {{{\text{e}}^{ - {t^2}}}{\text{d}}t} ,$$
(9)

where \(a\) is the ambiguity estimate with UPDs corrected and \(\sigma\) its STD, and \(n\) the nearest integer.

For a given confidence level \(\alpha\), e.g., 0.1% as usual, the ambiguity can be fixed to the nearest integer if \({P_0}>1 - \alpha\), otherwise not.

Assuming there are \(r\) stations and \(s\) available satellites and each station observes \({s_i}\begin{array}{*{20}{c}} {} \end{array}({s_i} \leq s,\begin{array}{*{20}{c}} {} \end{array}i=1,2, \ldots ,r)\) satellites, we can get \({n_a}=\sum\nolimits_{{i=1}}^{r} {{s_i}}\) available WL/NL ambiguity estimates at each epoch. All the WL/NL ambiguity estimates can be expressed as (Ge et al. 2012b; Li and Zhang 2012):

$$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{\hat {a}}}}_{{s_1} \times 1}}} \\ {{{{\mathbf{\hat {a}}}}_{{s_2} \times 1}}} \\ \vdots \\ {{{{\mathbf{\hat {a}}}}_{{s_r} \times 1}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{I}}_{{s_1} \times {s_1}}}}&{\mathbf{0}}& \cdots &{\mathbf{0}}&{{{\mathbf{R}}_{{s_1} \times r}}}&{{{\mathbf{S}}_{{s_1} \times s}}} \\ {\mathbf{0}}&{{{\mathbf{I}}_{{s_2} \times {s_2}}}}& \cdots &{\mathbf{0}}&{{{\mathbf{R}}_{{s_2} \times r}}}&{{{\mathbf{S}}_{{s_2} \times s}}} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\mathbf{0}}&{\mathbf{0}}& \cdots &{{{\mathbf{I}}_{{s_r} \times {s_r}}}}&{{{\mathbf{R}}_{{s_r} \times r}}}&{{{\mathbf{S}}_{{s_r} \times s}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathbf{N}}_{{s_1} \times 1}}} \\ {{{\mathbf{N}}_{{s_2} \times 1}}} \\ \vdots \\ {{{\mathbf{N}}_{{s_r} \times 1}}} \\ {{{\mathbf{b}}_r}} \\ {{{\mathbf{b}}^s}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} {{{\mathbf{v}}_{{s_1} \times 1}}} \\ {{{\mathbf{v}}_{{s_2} \times 1}}} \\ \vdots \\ {{{\mathbf{v}}_{{s_r} \times 1}}} \end{array}} \right]$$
(10)

in which \({{\mathbf{\hat {a}}}_{{s_i} \times 1}}\) and \({{\mathbf{N}}_{{s_i} \times 1}}\) are vectors of the estimated float ambiguities and integer ambiguities of station \(i\), \({{\mathbf{v}}_{{s_i} \times 1}}\) is the corresponding error vector, \({{\mathbf{b}}_r}\) and \({{\mathbf{b}}^s}\) are the respective unknown vectors of receiver and satellite UPDs, \({{\mathbf{I}}_{{s_i} \times {s_i}}}\) is the \({s_i} \times {s_i}\) unit matrix corresponding to \({{\mathbf{N}}_{{s_i} \times 1}}\), \({{\mathbf{R}}_{{s_i} \times r}}\) denotes the design matrix corresponding to \({{\mathbf{b}}_r}\), in which the elements of the \(i\)-th column are 1, \({{\mathbf{S}}_{{s_i} \times s}}\) is the design matrix corresponding to \({{\mathbf{b}}^s}\), in which the elements of each row are 1 if the corresponding satellite is observed, otherwise 0.

To eliminate the rank defects of (10), the integer parts \({{\mathbf{\hat {N}}}_{{s_i} \times 1}}\) of the real-valued ambiguity estimates are determined and subtracted in advance, resulting in the ambiguity residuals:

$$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{\hat {\varphi }}}}_{{s_1} \times 1}}} \\ {{{{\mathbf{\hat {\varphi }}}}_{{s_2} \times 1}}} \\ \vdots \\ {{{{\mathbf{\hat {\varphi }}}}_{{s_r} \times 1}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{\hat {a}}}}_{{s_1} \times 1}} - {{{\mathbf{\hat {N}}}}_{{s_1} \times 1}}} \\ {{{{\mathbf{\hat {a}}}}_{{s_2} \times 1}} - {{{\mathbf{\hat {N}}}}_{{s_2} \times 1}}} \\ \vdots \\ {{{{\mathbf{\hat {a}}}}_{{s_r} \times 1}} - {{{\mathbf{\hat {N}}}}_{{s_r} \times 1}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{{\mathbf{R}}_{{s_1} \times r}}}&{{{\mathbf{S}}_{{s_1} \times s}}} \\ {{{\mathbf{R}}_{{s_2} \times r}}}&{{{\mathbf{S}}_{{s_2} \times s}}} \\ \vdots & \vdots \\ {{{\mathbf{R}}_{{s_r} \times r}}}&{{{\mathbf{S}}_{{s_r} \times s}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathbf{b}}_r}} \\ {{{\mathbf{b}}^s}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} {{{\mathbf{v}}_{{s_1} \times 1}}} \\ {{{\mathbf{v}}_{{s_2} \times 1}}} \\ \vdots \\ {{{\mathbf{v}}_{{s_r} \times 1}}} \end{array}} \right]$$
(11)

where \({{\mathbf{\hat {\varphi }}}_{{s_i} \times 1}}\) can be treated as the pseudo-observation vector of satellite and receiver UPDs. The rank defect of (11) is 1, which can be eliminated by selecting a reference satellite and fixing its UPD as an arbitrary constant. Then, the UPD estimates \({{\mathbf{\hat {b}}}_r}\) and \({{\mathbf{\hat {b}}}^s}\) at the current epoch can be solved from (11) using the least-square adjustment. It is important to note that, the ambiguity estimates that have low elevation angle, a short observation period, or cannot be fixed according to the fixation decision, are discarded and excluded from (11).

Generation of the ambiguity-fixed clock solution

After fixing all fixable ambiguities, the integer ambiguities and the corresponding UPD estimates can be used to impose constraints on the float-ambiguity clock solution to generate the ambiguity-fixed clock solution. Substituting the fixed WL and NL ambiguities and the WL and NL UPD estimates into (4), the fixed IF ambiguities can be expressed as:

$$\tilde {a}_{{{\text{r,IF}}}}^{{\text{s}}}=\frac{{{f_1}{f_2}}}{{f_{1}^{2} - f_{2}^{2}}}\left( {\hat {N}_{{{\text{r,w}}}}^{{\text{s}}}+{{\hat {b}}_{{\text{r,w}}}}+\hat {b}_{{{\text{,w}}}}^{{\text{s}}}} \right)+\frac{{{f_1}}}{{{f_1}+{f_2}}}\left( {\hat {N}_{{{\text{r,n}}}}^{{\text{s}}}+{{\hat {b}}_{{\text{r,n}}}}+\hat {b}_{{{\text{,n}}}}^{{\text{s}}}} \right)$$
(12)

and the ambiguity-fixed clock solution can be read as (Dong and Bock 1989; Geng et al. 2012):

$${\mathbf{\tilde {x}}}={\mathbf{\hat {x}}}+{{\mathbf{Q}}_{{\mathbf{xa}}}} \cdot {\mathbf{Q}}_{{{\mathbf{aa}}}}^{{ - 1}} \cdot \left( {{\mathbf{\hat {a}}} - {\mathbf{\tilde {a}}}} \right),$$
(13)

where \({\mathbf{\tilde {x}}}\) is the refined estimate vector after ambiguity fixing.

Ambiguity-fixing algorithm in real-time clock estimation

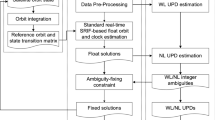
Based on the above mathematical formulation, we summarize the epoch processing flow of real-time clock estimation with ambiguity-fixing in Fig. 2. As shown in the figure, the left process performs real-time clock estimation and the right one is in charge of ambiguity fixing. At the beginning of epoch \(k\), the real-time observations from the reference stations are first screened in a preprocessing module that checks data completeness, finds gross errors in code observations and detects and marks cycle slips in phase observations. Next is the orbit update module that checks if the current orbit product is expired and updates the latest one. Then, the clean observations and orbits are fed into the real-time clock estimation module which is an implementation of the square root information filter (SRIF) in our software (Bierman 1982). This module estimates the real-time clock offsets and other parameters without fixing ambiguities, generating the float-ambiguity clock solutions.

Fig. 2
figure 2

Epoch processing flow of real-time clock estimation with ambiguity-fixing

Full size image

To recover the integer nature of the phase ambiguity, another independent process is developed based on the aforementioned strategy to successively fix WL and NL ambiguities. In this process, the clean observations are first fed into a WL ambiguity estimation module in which the float WL ambiguities are computed and averaged over epochs. After a period, the WL ambiguity estimates are precise enough to be fixed and used in UPD estimation. According to (7), the fixable WL ambiguity estimates are calibrated with the a priori WL UPDs and rounded off to the nearest integers, from which the ambiguity residuals are decomposed. The ambiguity residuals are pseudo-observations of the satellite and receiver UPD unknowns, which are far more than the UPD unknowns. Then they are adjusted in a WL UPD adjustment module to derive the adjusted satellite and receiver WL UPD estimates. Based on the fixed WL ambiguities, the ambiguity decomposition module transforms the IF ambiguity estimates fed from clock estimation process to the NL ambiguities. Similarly, the float NL ambiguity estimates are corrected with the a priori NL UPDs and fixed to integers in the NL ambiguity fixing module and the ambiguity residuals are adjusted in the NL UPD adjustment module to resolve the NL UPD estimates. If the number of fixed ambiguities is greater than 0, the fixed IF ambiguities are recovered from the WL/NL integer ambiguities and UPDs and then used to impose constraints on the float-ambiguity clock solution, resulting in the ambiguity-fixed clock solution as output. Otherwise, the program only outputs the float-ambiguity clock solution. After outputting the current clock solution, the program enters into the next epoch processing cycle.

In the ambiguity fixing process, the float ambiguity estimates and a priori UPDs should be precise enough so that the corrected ambiguities are much closer to integers with low errors, which guarantees that the float ambiguities are fixed to the correct integers with high probability (Dong and Bock 1989). Since the SRIF needs a few hours to converge to a stable state, the ambiguity-fixing process will only start after attaining a certain convergence level. In our processing, the ambiguity-fixing function is turned on 12 h after starting the program. When a satellite rises above the cutoff elevation angle and is re-observed by a station or a cycle slip occurs, the corresponding ambiguity parameter will be reset and excluded from ambiguity-fixing until for the next 600 s. Considering the stability in short time, the UPD estimates from the previous epoch are used as the a priori UPDs to correct the ambiguity estimates at the current epoch. For the special situation at the first epoch of ambiguity fixing, the a priori UPDs should be derived from the WL/NL ambiguities. We first fix the UPD of a reference satellite to an arbitrary value between − 0.5 and 0.5, which is subtracted from the ambiguities associated with this satellite. The corrected ambiguities are rounded to the closest integers and the fractional remainders are adopted as the a priori UPDs of receivers associated with these corrected ambiguities. Similarly, the unfixed ambiguities associated with these receivers are corrected with the a priori receiver UPDs and rounded to integers, resulting in the integer ambiguities and a priori satellite UPDs. This procedure will repeat until all the satellite and receiver a priori UPDs are determined. When there are multiple receivers (or satellites) UPD-corrected ambiguities associated with a satellite (or receiver), we will get more than one a priori UPD for the satellite (or receiver) which can be averaged to generate more precise a priori UPD. Finally, these a priori UPDs are subtracted from the rest of unfixed ambiguities to get the integer ambiguities and UPD residuals for adjustment.

Algorithm test and results analysis

The proposed algorithm has been implemented based on the Position And Navigation Data Analyst (PANDA) software for data processing in our experiments (Jing-nan and Mao-rong 2003). First, we generated the ambiguity-fixed GPS clock solutions based on globally distributed reference stations in a pseudo-real-time mode. For comparison, the float-ambiguity clock solutions were generated using the same program with the ambiguity-fixing function turned off. Both the ambiguity-fixed and float-ambiguity clock solutions are compared with the IGS 30 s final products to exhibit their precision. Then, the two clock solutions are used in a float-ambiguity kinematic PPP test to further demonstrate their real-time positioning performance.

Data collection and experiment configurations

The clock estimation experiment is based on 85 global reference stations that are primarily selected from the IGS network. For good distribution, a few stations of the multi-GNSS experiment (MGEX) network are selected as a supplement though we only use the GPS data. Another 12 independent stations are selected to perform PPP verification. All the selected stations used in clock estimation and PPP test are illustrated in Fig. 3.

Fig. 3
figure 3

Distribution of reference stations used in the clock estimation (red) and PPP test (green)

Full size image

The experiment period is from DOY 180–209, 2017 and the observation interval is 30 s. All data is processed epoch by epoch to simulate the real-time situation in a post-processing mode. To represent the true real-time situation, the predicted part of IGS ultra-rapid orbit is employed to calculate satellite positions, which is updated every 6 h with the delay of 3 h. Table 1 lists the general and specific configurations in our experiments. The common configurations are presented together for brevity and the specific configurations for clock estimation, ambiguity fixing and PPP are listed separately.

Table 1 General and specific configurations in the experiments
Full size table

UPD estimation and ambiguity fixing

Ambiguity fixing and constraining in clock estimation directly depends on the precision of UPD estimates. To demonstrate the performance of UPD estimation, we investigate the post-fit ambiguity residual, which is defined as the float ambiguity estimate minus the integer ambiguity and receiver and satellite UPD estimates. Thus, the post-fit ambiguity \(\Delta _{{\text{r}}}^{{\text{s}}}\) can be expressed as:

$$\Delta _{{\text{r}}}^{{\text{s}}}=\hat {a}_{{\text{r}}}^{{\text{s}}} - \hat {N}_{{\text{r}}}^{{\text{s}}} - {\hat {b}_{\text{r}}} - {\hat {b}^{\text{s}}}$$
(14)

in which \(\hat {a}_{{\text{r}}}^{{\text{s}}}\) is the float ambiguity estimate, \(\hat {N}_{{\text{r}}}^{{\text{s}}}\) is the fixed integer ambiguity and \({\hat {b}_{\text{r}}}\) and \({\hat {b}^{\text{s}}}\) denote the receiver and satellite UPD estimates. Obviously, the absolute values of post-fit ambiguity residuals will be less than 0.5 cycles. High precision ambiguity and UPD estimates will result in the small absolute values of the post-fit ambiguity residuals. Thus, the post-fit ambiguity residuals will reflect the consistency and precision of UPD and ambiguity estimates.

During the whole experiment, the post-fit ambiguity residuals are computed at each epoch after the float ambiguities are fixed and UPDs are estimated successfully; their statistical distribution is presented in Fig. 4 showing the normalized frequency and cumulative frequency of the post-fit WL and NL ambiguity residuals, respectively. As shown in the figure, 99.96% of the WL ambiguity residuals fall in the range of (− 0.3, 0.3), with the standard deviation (STD) of 0.045 cycles, and 99.31% NL ambiguity residuals are in the range of (− 0.3, 0.3), with the STD of 0.074 cycles. Both the WL and NL ambiguity residuals are rather small, which illustrates the high precision and consistency of UPD and ambiguity estimates.

Fig. 4
figure 4

Normalized frequency (histogram) and cumulative frequency (green line) of post-fit ambiguity residuals

Full size image

Clock solutions comparison

The ambiguity-fixed and float-ambiguity clock solutions are now compared with the IGS 30 s final clock product to derive the clock differences for all available satellites. To remove the clock reference difference, the average clock difference of all available satellites is subtracted from each satellite clock difference at each epoch (Yao et al. 2017). Then, we compute the daily STD from the unbiased clock difference for each satellite. Figure 5 shows the clock STD of all available satellites for each solution on DOY 182, 2017. As shown in the figure, the ambiguity-fixed clock solution exhibits much higher precision than the float-ambiguity solution, with the STD less than 0.04 ns for most satellites. Specifically, the clock precision of the float-ambiguity solution varies dramatically, within the range of 0.03–0.14 ns, while that of the ambiguity-fixed solution is more stable, varying in the range of 0.02–0.08 ns. Ambiguity-fixing in real-time clock estimation brings significant improvement to the clock solution, especially for the satellites with rather low float-ambiguity precision.

Fig. 5
figure 5

STD of the ambiguity-fixed and float-ambiguity clock solutions with respect to the IGS final clock products

Full size image

For further illustration, Fig. 6 shows the clock differences of the ambiguity-fixed and float-ambiguity solutions with respect to the IGS final clock product for G03, G13, G21 and G30 satellites. As shown in this figure, the clock differences of the ambiguity-fixed solution are less variable over the full day, while that of the float-ambiguity solution exhibit noticeable variations and spikes at a few epochs.

Fig. 6
figure 6

Clock differences of the ambiguity-fixed (red line) and ambiguity-float (green line) solutions with respect to the IGS final clock product

Full size image

Based on the 30 days of results, the contribution of ambiguity-fixing in real-time clock estimation is investigated. Figure 7 presents the mean and maximum daily precision improvement of the ambiguity-fixed solution over the float-ambiguity solution for each satellite. As shown in the fiugre, the maximum clock precision improvement brought by ambiguity-fixing is as much as 50–87%, with an average daily improvement over the 30 days of 24–50% for each satellite. Over all satellites, an average daily precision improvement of around 30% can be expected in the ambiguity-fixed clock solution.

Fig. 7
figure 7

Mean (red) and max (green) improvement of ambiguity-fixed clock solution over ambiguity-float clock solution

Full size image

PPP verification

To demonstrate the positioning performance of different clock solutions, the ambiguity-fixed and float-ambiguity clock solutions are tested on another 12 stations in a float-ambiguity kinematic PPP experiment. As listed in Table 1, most configurations are the same in the PPP test as in the clock estimation experiment, except that the satellite clocks are corrected using the clock solutions and the station coordinates are estimated in a float-ambiguity kinematic mode. The test period is from DOY 180-209, 2017 and the PPP software is restarted in the beginning of each day. The two PPP solutions of the test stations are compared to the station true coordinates, resulting in the coordinate differences in the north, east and vertical components for analysis.

Figure 8 demonstrates the coordinate differences of the two PPP solutions in the north, east and vertical components for the respective stations GRAC on 180, 2017 and PDEL on 187, 2017. As shown in this figure, compared to the PPP solutions using the float-ambiguity clocks, the PPP solutions using the ambiguity-fixed clocks exhibit shorter convergence time and more stable and precise coordinate series in all components.

Fig. 8
figure 8

PPP coordinate differences of different clock solutions in north, east and vertical components

Full size image

Based on the two kinds of daily PPP solutions, we assessed the average improvement and RMS of coordinate components of each test station. As shown in Fig. 9, all the PPP solutions using the ambiguity-fixed clocks exhibit smaller average RMS than the solutions using the float-ambiguity clocks in all components. The average improvements of the test stations show that the ambiguity-fixed clocks can bring 5–30%, 10–50% and 10–30% improvement to the respective north, east and vertical coordinate components, with respect to the float-ambiguity clocks.

Fig. 9
figure 9

Average improvement (top) and RMS (bottom) of coordinate components of each test station computed from the two kinds of daily PPP solutions

Full size image

Summary and conclusions

GNSS real-time precise point positioning is heavily dependent on the real-time clock products that should be estimated from real-time observations of reference stations of a ground network. The recent real-time clock estimation strategy that is widely used by IGS and most of its ACs estimates the phase ambiguities as float parameters, ignoring their integer nature. For further improvement in the precision of real-time clock products, an undifferenced ambiguity fixing strategy is proposed for the real-time clock estimation method, which only processes the ambiguity estimates without changing the existing data processing strategy and product consistency. A real-time ambiguity fixing process independent of the clock estimation process is implemented. The IF ambiguity estimates generated by the clock estimation module, along with the WL ambiguity estimates, are fed to this ambiguity fixing process to estimate the WL/NL UPDs and fix the WL/NL undifferenced ambiguities at each epoch. Fixed IF ambiguities are then computed from these WL/NL UPDs and integer ambiguities and used as constraints to refine the float-ambiguity clock solution.

The proposed ambiguity fixing and clock estimation strategies are tested in a pseudo-real-time mode based on the 30 s GPS observations that are collected from 85 globally distributed reference stations of the IGS and MGEX networks during DOY 180-209, 2017. For comparison, the float-ambiguity clock solution is generated in a pseudo-real-time mode using the same software with the ambiguity-fixing function turned off. Analysis of the fixed ambiguities shows that 99.96% of the post-fit residuals of WL ambiguities and 99.31% of the post-fit residuals of NL ambiguities fall in the range of (− 0.3, 0.3), with the STD of 0.045 and 0.074 cycles, respectively. The rather small and concentrated post-fit ambiguity residuals demonstrate the high precision and consistency of UPDs and fixed ambiguities. Using these fixed ambiguities and associated UPDs as constraints, the float-ambiguity clock solution is further refined, resulting in the ambiguity-fixed clock solution. Comparison to the IGS 30 s final clock product shows that ambiguity-fixing brings up to 50–87% precision improvement over the float-ambiguity clock solution for different satellites, and the average daily improvement over the 30 days is 24–50% for each satellite. When used in the float-ambiguity kinematic PPP test, the ambiguity-fixed clock solution brings at least 5% improvement to the north component and at least 10% improvement to the east and vertical components.