Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation

Abstract

Precise point positioning (PPP) is receiving increasing interest due to its cost-effectiveness, global coverage and high accuracy. However, its application in the urban environment is still full of challenges due to the satellite tracking sky-view. Thus, we presented a comprehensive positioning model by fusing the multi-GNSS (global navigation satellite system) combination, GNSS/INS (inertial navigation system) tightly coupled integration as well as the ionospheric and tropospheric augmentation in the undifferenced and uncombined PPP. The performance of this model in dual-frequency and single-frequency positioning was assessed with two experiments that denoted as T019 and T023, respectively, and both the experiments were carried out in a real urban environment. Particularly, the experiment T023 was carried out in the Second Ring Road of Wuhan city, which can be regarded as a typical downtown environment. Concerning the regional atmospheric augmentation, observations from 5 reference stations with an inter-station distance of about 40 km were also collected during the experimental time. The comparison between reference stations suggested that the regional tropospheric model had a precision of better than 0.6 cm in terms of zenith tropospheric delay, while the regional ionospheric model had a precision of around 0.5 total electron content unit in terms of Vertical Total Electron Content. It can be concluded that the GPS-only PPP can be improved significantly for urban vehicle navigation with these techniques, i.e., the multi-GNSS, INS tightly coupled integration and the atmospheric augmentation, through the positioning analysis, while INS tightly coupled integration makes the most contributions under the downtown environment, and the improvement of the regional atmospheric augmentation in single-frequency PPP is more significant since that single frequency is more sensitive to the ionospheric delay. In addition, it is proved that the regional atmospheric augmentation accelerates positioning convergence. The 3D positioning root-mean-square (RMS) with the comprehensive positioning model for dual frequency are 0.22 m and 0.77 m for T019 and T023, respectively. Concerning single-frequency PPP, the 3D RMS is 0.45 m and 1.17 m for T019 and T023, respectively. Moreover, taking the lane-level navigation under the downtown environment of T023 into consideration, we further presented the cumulative frequency of the horizontal positioning error less than 1 m, i.e., $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$, and the best solution can be found with PPP by fusing all the techniques, in which $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$ is 99.0% and 93.2% for dual frequency and single frequency, respectively.

1 Introduction

The potential of global navigation satellite systems (GNSS) as an efficient tool in providing precise positioning has been widely recognized. Specifically, the precise point positioning (PPP) technique proposed by Zumberge et al. (1997) is receiving increasing interest due to its cost-effectiveness, global coverage and high accuracy (Kouba and Héroux 2001; Shi et al. 2018; Elmezayen and El-Rabbany 2019). Recognizing the enormous potential benefits of PPP in positioning, navigation and timing (PNT), GNSS meteorology, as well as earthquake and tsunami early warning, etc., nowadays, PPP is experiencing rapid development attribute to the efforts of GNSS community (Li et al. 2014; Wright et al. 2012; Luo et al. 2018; Handoko et al. 2020). However, the application of PPP is still full of challenges. For example, the reliable and continuous kinematic positioning under the urban environment is a crucial issue due to limited satellite tracking sky-view for PPP (Angrisano et al. 2013), as well as other GNSS positioning techniques such as SPP (standard point positioning) and RTK (real-time kinematic).

Along with the development of multi-GNSS, i.e., GPS, GLONASS, BDS, Galileo, extensive efforts have been made to improve the PPP performance by multi-GNSS observation (Cai et al. 2015; Li et al. 2015). Limited by the satellite number of GLONASS during its initial stage, Cai and Gao (2007) had failed to improve the PPP solution with combined GPS and GLONASS satellites. It was not until 2011 when the full GLONASS constellation recovered, the benefit of additional satellites was proved with an accuracy improvement of 50% and a shorter time for initialization (Cai and Gao 2007, 2013). Furthermore, attributed to BDS and Galileo, Lou et al. (2016) presented a comprehensive analysis of quad-constellations’ PPP for both single- and dual-frequency receivers in simulated real-time mode. Compared with GPS-only solution, the results suggested that in kinematic mode the four-system combined PPP can accelerate the convergence by more than 60% on average, and the positioning RMS was improved by about 25% and 40% for single- and dual-frequency PPP, respectively (Lou et al. 2016). Later, Jiao et al. (2019) added BDS-3 and Galileo new satellites into quad-constellations’ dual-frequency PPP and obtained similar conclusion.

In an urban or canyon area, the GNSS receiver may easily fail in satellite tracking, and PPP would be very flimsy due to the frequent re-convergence even with multi-constellation. On the other hand, the inertial navigation system (INS) outputs the navigation states, i.e., position, velocity and attitude, continuously without external information, and is thus regarded as a promising approach to provide continuous positioning and navigation service in the case that GNSS signal is blocked (Cox 1978). A wide range of valuable studies in the coupled GNSS/INS positioning were published, and developed the loosely coupled model and tightly coupled model for GNSS PPP/INS integration according to the observation processing strategy (Rabbou and El-Rabbany 2015a; Gao et al. 2017) while, compared to the loosely coupled model, tightly coupled model is more efficient, especially under the poor GNSS signal environment (Weiss and Kee 1995). More recently, with the development of MEMS (micro-electro-mechanical system)-IMU, Rabbou and El-Rabbany (2015b) carried out the study of integrated PPP with GPS and MEMS-based inertial system. The results suggested that in the existence of 30 s outages of GPS signal, the positioning accuracy of decimeter level can still be achieved.

Besides the additional measurements from multi-GNSS and INS, another efficient approach to improve the positioning performance is to augment PPP with precise atmosphere corrections, i.e., ionospheric delay and tropospheric delay. Concerning the ionospheric delay, the so-called ionosphere-free (IF) combination is typically utilized. For dual-frequency users, the IF combination is derived from observation on different frequencies, while, for single-frequency users, the IF combination is derived by the linear combination of pseudo-range and carrier-phase (Zumberge et al. 1997; Kouba and Héroux 2001; Gao and Shen 2002; Shi et al. 2012). However, the undifferenced and uncombined data processing strategy to avoid any combination has begun to receive increasing interests within the GNSS community (Schönemann et al. 2011; Zhang et al. 2011, 2019; Gu et al. 2013, 2015a, b), for it can make full use of single- and multi-frequency observations, and easily utilize the a priori information of ionosphere delay. Among which, Shi et al. (2012) proposed an elaborated ionospheric parameterization method, i.e., DESIGN (deterministic plus stochastic ionosphere model for GNSS), for the undifferenced and uncombined data processing. The DESIGN has taken the spatial and temporal correlation of ionospheric delay into consideration and further constrained the ionospheric delay with a prior correction model, e.g., the global ionosphere map (GIM). More recently, Zhao et al. (2018) went one step further by modeling the daily variation of the deterministic part of DESIGN with Fourier series and updating the stochastic part correspondingly. The efficiency of the undifferenced and uncombined observation model constrained with DESIGN has already been demonstrated with both single- and dual-frequency observations, in which GIM was utilized as a prior ionospheric delay correction (Shi et al. 2012; Lou et al. 2016; Zhao et al. 2018). It should be noted that in all these studies, the GNSS observations were collected by IGS stations with an open sky-view. Gao et al. (2015) presented the result of PPP/INS tightly coupled integration with GIM as a prior ionospheric model. However, only the dual-frequency PPP was studied in an urban area. Thus, the performance of both single- and dual-frequency PPP/INS with regional high-precision atmospheric delay is still left for further analysis for the downtown vehicle navigation.

Unlike the ionospheric delay, the non-dispersive tropospheric delay cannot be removed by linear combination in PPP. Typically, the performance of empirical tropospheric delay models, e.g., Hopfield, Saastamoinen, relies on the meteorological elements. Therefore, Böhm et al. (2007) have tried to express the spatial and temporal variation of pressure and temperature with spherical harmonic parameters and proposed the global pressure temperature (GPT) model in 2007. Then, the GPT model is further refined by Lagler et al. (2013) and Böhm et al. (2015), each adding their own contributions. However, even with these elaborate empirical models, the residual tropospheric delay effect may still reach up to several centimeters. Thus, a straightforward method based on real-time GNSS observation derived tropospheric delay model is promoted (Yao et al. 2014; Lu et al. 2015). Specifically, Zheng et al. (2018) established a high-accuracy high-resolution ZTD model of China by using the GNSS data of the National BDS Augmentation Service System (NBASS). The results with BDS PPP indicated that the improvement is significant, and the convergence time of vertical component for BDS PPP is reduced by 20–50% (Zheng et al. 2018). Constrained with the ionospheric and tropospheric model, Han and Wang (2017) demonstrated the efficiency of atmospheric delay in GNSS/INS tightly coupled integration. However, only RTK was analyzed in this study.

To sum up, multi-GNSS combination and GNSS/INS integration can improve the positioning accuracy and continuity of PPP. Ionospheric and tropospheric augmentation can reduce the convergence time and improve the positioning accuracy of PPP. Moreover, regional ionospheric maps fit better than global ionospheric maps (Banville et al. 2014; Zhou et al. 2020). Fusing these methods is expected to improve the positioning performance in urban vehicle navigation. Towards the reliable high-precision urban navigation, this study tries to fuse all these techniques in a single comprehensive positioning model to further excavate the potential of both single- and dual-frequency PPP. This paper is organized as follows: First, with the undifferenced and uncombined PPP model and state equation of INS, we derive the PPP/INS tightly coupled integration model. Then the accuracy of the regional tropospheric delay and ionospheric delay model is evaluated. Afterward, the efficiency of different techniques, i.e., multi-GNSS, INS and regional atmospheric augmentation in urban vehicle navigation, is analyzed. Finally, we present the conclusions.

2 Mathematical models

To derive the multi-GNSS PPP/INS tightly coupled integration model augmented with high-precision atmospheric delay, the undifferenced and uncombined PPP, INS model, as well as the PPP/INS tightly integration model are presented in this section. In addition, the systems GPS and GLONASS are denoted as G and R, respectively, as suggested in RINEX 3.02.

2.1 Undifferenced and uncombined PPP model

The undifferenced and uncombined observations of the GNSS pseudo-range and carrier phase are described as follows (Zhao et al. 2018):

$$ \left. {\begin{array}{*{20}c} {P_{r,f}^{s} = \rho_{r}^{s} + t_{r,sys} + \alpha_{r}^{s} T_{z} + \frac{40.3}{{f^{2} }}\gamma_{r}^{s} I_{r}^{s} - b^{s,f} + b_{r,f} + \varepsilon_{p} } \\ {\Phi_{r,f}^{s} = \rho_{r}^{s} + t_{r,sys} + \alpha_{r}^{s} T_{z} - \frac{40.3}{{f^{2} }}\gamma_{r}^{s} I_{r}^{s} + \lambda N_{r,f}^{s} + \varepsilon_{\Phi } } \\ \end{array} } \right\} $$

(1)

where $P_{r,f}^{s}$ and ${\Phi }_{r,f}^{s}$ are the pseudo-range and carrier phase on frequency f from receiver r to satellite s in metric units;$\rho_{r}^{s}$ is the geometric distance for specific satellite s and receiver r pair;$t_{{r,{\text{sys}}}}$ denotes the receiver clock offset corresponding to the system ${\text{sys}} \in \left( {\begin{array}{*{20}c} G & R \\ \end{array} } \right)$;$\alpha_{r}^{s}$ and $T_{z}$ stand for the mapping function and the zenith tropospheric delay, respectively; $\gamma_{r}^{s}$ and $I_{r}^{s}$ are the mapping function and the zenith total electron content, respectively; $b^{s,f}$ and $b_{r,f }$ are the frequency-dependent code bias delay for satellite and receiver, respectively; $N_{r,f}^{s}$ denotes the float ambiguity in the cycle unit, and $\lambda$ is the corresponding wavelength;$\varepsilon_{p}$, $\varepsilon_{\Phi }$ denote the measurement noise together with the un-model multipath error for pseudo-range and carrier phase, respectively. Meanwhile, satellite orbit and clock errors, the phase center corrections, relative effect, earth rotation error, phase-windup as well as the loading effects are assumed to be corrected in Eq. (1). Furthermore, for $b^{s,1}$ and $b^{s,2}$, and $b_{r,1}$ and $b_{r,2 }$ are linear dependent, it is assumed that

$$ \left. {\begin{array}{*{20}c} {b^{s,1} = 0} \\ {b_{r,1 } = 0} \\ \end{array} } \right\} $$

(2)

to make it uniquely solvable (Gu et al. 2015a).

By correcting the satellite code bias and the a priori tropospheric delay, the linearized error equation of model (1) can be expressed as:

$$ \left. {\begin{array}{*{20}l} {{\Delta }P_{r,f}^{s} = {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} \delta {\varvec{x}}_{{\varvec{r}}}^{{\varvec{e}}} + t_{{r,{\text{sys}}}} + \alpha_{r}^{s} {\updelta }T_{w} + \frac{40.3}{{f^{2} }}\gamma_{r}^{s} I_{r}^{s} + b_{r,f} + \varepsilon_{p} } \hfill \\ {{\Delta }\Phi_{r,f}^{s} = {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} \delta {\varvec{x}}_{{\varvec{r}}}^{{\varvec{e}}} + t_{{r,{\text{sys}}}} + \alpha_{r}^{s} {\updelta }T_{w} - \frac{40.3}{{f^{2} }}\gamma_{r}^{s} I_{r}^{s} + \lambda N_{r,f}^{s} + \varepsilon_{\Phi } } \hfill \\ \end{array} } \right\} $$

(3)

where ${\Delta }P_{r,f}^{s}$ and $\Delta \Phi_{r,f}^{s}$ are the OMC (observed-minus-computed) of pseudo-range and carrier phase, respectively; ${\varvec{h}}_{r}^{s}$ is the partial derivatives of geometry distance $\rho_{r}^{s}$ with respect to the receiver coordinate; ${{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}}^{{\varvec{e}}}$ is the correction vector of the approximate receiver coordinate, and the superscript $\cdot^{e}$ stands for e-frame (earth-centered earth-fixed frame); ${\Delta }T_{w}$ denotes the residual of tropospheric delay. Concerning the ionospheric delay parameterization in Eqs. (1) and (3), the DESIGN model is adopted in this study which can be expressed as:

$$ \left. {\begin{array}{*{20}l} {I_{r}^{s} = a_{0} + a_{1} {\text{d}}L + a_{2} {\text{d}}B + a_{3} {\text{d}}L^{2} + a_{4} {\text{d}}B^{2} + r_{r}^{s} } \hfill \\ {\tilde{I}_{r}^{s} = a_{0} + a_{1} {\text{d}}L + a_{2} {\text{d}}B + a_{3} {\text{d}}L^{2} + a_{4} {\text{d}}B^{2} + r_{r}^{s} + \varepsilon_{{\tilde{I}_{r}^{s} }} } \hfill \\ \end{array} } \right\} $$

(4)

where $a_{i}$ (i = 0, 1, 2, 3, 4) are the coefficients that describe the deterministic behavior of ionospheric delay; $r_{r}^{s}$ is the residual of ionospheric effect for each satellite that describes the stochastic behavior of ionospheric delay; dL, dB are the longitude and latitude differences between the ionospheric pierce point (IPP) and the approximate location of station, respectively.$\tilde{I}_{r}^{s}$ is the vertical ionospheric delay pseudo-observation with the corresponding noise $\varepsilon_{{\tilde{I}_{r}^{s} }}$, and it is typically derived from the global ionosphere map (GIM) or regional ionosphere model. For more details of Eq. (4) and the DESIGN model, the readers are suggested to refer to Shi et al. (2012) and Zhao et al. (2018). Note that the DESIGN-5 algorithm is adopted in this study.

Supposing $j$ satellites are tracked by a dual-frequency receiver $r$ for a given epoch, the corresponding observation model in matrix form thus can be expressed as:

$$ {\varvec{z}} = {\varvec{H}}_{{{\varvec{PPP}}}} {\varvec{x}}_{{{\varvec{ppp}}}} + {\varvec{\varepsilon}} $$

(5)

$$ \left. {\begin{array}{*{20}l} {z = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\varvec{P}}_{{{\varvec{r}},1}} } & {{\varvec{P}}_{{{\varvec{r}},2}} } & {{{\varvec{\Phi}}}_{{{\varvec{r}},1}} } \\ \end{array} } & {{{\varvec{\Phi}}}_{{{\varvec{r}},2}} } & {\tilde{\varvec{I}}_{{\varvec{r}}} } \\ \end{array} } \right)^{{\text{T}}} } \hfill \\ {{\varvec{x}}_{{{\varvec{ppp}}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}} } & {t_{r} } & {{\updelta }T_{w} } \\ \end{array} } & {\begin{array}{*{20}c} {b_{r} } & {{\varvec{N}}_{{\varvec{r}}} } & {\begin{array}{*{20}c} {{\varvec{a}}_{{\varvec{r}}} } & {{\varvec{r}}_{{\varvec{r}}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}} } \hfill \\ {{\varvec{H}}_{{{\varvec{PPP}}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{\varvec{t}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{T}}_{{\varvec{w}}} }} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{H}}_{{{\varvec{b}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{\varvec{N}}_{{\varvec{r}}} }} } & {\begin{array}{*{20}c} {{\varvec{H}}_{{{\varvec{a}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{\varvec{r}}_{{\varvec{r}}} }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right)} \hfill \\ \end{array} } \right\} $$

(6)

where $\varvec{z },\,{\varvec{H}}_{{{\varvec{PPP}}}} \varvec{ }\,{\text{and}}\varvec{ x}_{{{\varvec{ppp}}}} \varvec{ }$ are the measurement vector, the design matrix and the error state vector, respectively; ${\varvec{P}}_{{{\varvec{r}},{\varvec{f}}}}$, ${{\varvec{\Phi}}}_{{{\varvec{r}},{\varvec{f}}}}$ are the observation vector of pseudo-range and carrier phase on frequency $f \in \left( {\begin{array}{*{20}c} 1 & 2 \\ \end{array} } \right)$, respectively; $\tilde{\varvec{I}}_{{\varvec{r}}} = \left( {\begin{array}{*{20}c} {\tilde{\varvec{I}}_{{\varvec{r}}}^{1} } & \cdots & {\tilde{\varvec{I}}_{{\varvec{r}}}^{{\varvec{j}}} } \\ \end{array} } \right)^{{\text{T}}}$ is the pseudo-observation vector of the vertical ionospheric delay derived from a prior ionospheric delay model; ${\varvec{N}}_{{\varvec{r}}} = \left( {\begin{array}{*{20}c} {{\varvec{N}}_{{{\varvec{r}},1}} } & {{\varvec{N}}_{{{\varvec{r}},2}} } \\ \end{array} } \right)^{{\text{T}}}$ is the ambiguity vector on both frequency; ${\varvec{a}}_{{\varvec{r}}} = \left( {\begin{array}{*{20}c} {a_{0} } & {a_{1} } & {\begin{array}{*{20}c} {a_{2} } & {a_{3} } & {a_{4} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}}$ and ${\varvec{r}}_{{\varvec{r}}} = \left( {\begin{array}{*{20}c} {r_{{\varvec{r}}}^{1} } & \ldots & {r_{{\varvec{r}}}^{j} } \\ \end{array} } \right)^{{\text{T}}}$ are the deterministic and stochastic ionospheric parameter vector, respectively,$\varvec{ \varepsilon }$ is the measurement noise vector. In “Appendix,” we further present the details of the design matrix ${\varvec{H}}_{{{\varvec{PPP}}}}$.

2.2 INS model

Based on the dead reckoning algorithm, INS provides the navigation status through the integration with the initial position, velocity and attitude, and the dynamic equation of INS in the e-frame can be described as:

$$ \left( {\begin{array}{*{20}c} {\dot{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ {\dot{\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ {\dot{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{f}}^{{\varvec{b}}} - 2{\varvec{\omega}}_{{{\varvec{ie}}}}^{{\varvec{e}}} \times {\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} + {\varvec{g}}^{{\varvec{e}}} } \\ {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {{\varvec{\Omega}}}_{{{\varvec{eb}}}}^{{\varvec{b}}} } \\ \end{array} } \right) $$

(7)

where ${\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}}$,${\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}}$ denote the position and velocity vectors of IMU in the e-frame, respectively; ${\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}}$ is the rotation matrix from body frame (b-frame) to e-frame; ${\varvec{f}}^{{\varvec{b}}}$ is the specific force vector in the b-frame; ${\varvec{\omega}}_{{{\varvec{ie}}}}^{{\varvec{e}}}$ is the earth rotation vector of e-frame against inertial frame (i-frame) in the e-frame;${\varvec{g}}^{e}$ is the gravity vector in the e-frame; ${{\varvec{\Omega}}}_{{{\varvec{eb}}}}^{{\varvec{b}}}$ is the skew-symmetric matrix of ${{\varvec{\upomega}}}_{{{\varvec{eb}}}}^{{\varvec{b}}} = {{\varvec{\upomega}}}_{{{\varvec{ib}}}}^{{\varvec{b}}} - {\mathbf{C}}_{{\varvec{e}}}^{{\varvec{b}}} {{\varvec{\upomega}}}_{{{\varvec{ie}}}}^{{\varvec{e}}}$, while ${{\varvec{\upomega}}}_{{{\varvec{ib}}}}^{{\varvec{b}}}$ is the rotation angular rate of gyroscopes output and ${\mathbf{C}}_{{\varvec{e}}}^{{\varvec{b}}}$ is the inverse matrix of ${\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}}$.

Based on model (7), the error state model of INS can be described by Phi-angle error model through perturbation method (Shin 2005):

$$ \left( {\begin{array}{*{20}c} {\delta \dot{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ {\delta \dot{\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ {\dot{\phi }} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\delta {\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ { - 2{\varvec{\omega}}_{ie}^{e} \times \delta {\varvec{v}}_{{{\varvec{INS}}}}^{{\varvec{e}}} + {\varvec{C}}_{b}^{e} {\varvec{f}}^{{\varvec{b}}} \times \phi + {\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} \delta {\varvec{f}}^{{\varvec{b}}} + {\varvec{N}}^{{\varvec{e}}} \delta {\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ { - {\varvec{\omega}}_{ie}^{e} \times \phi - {\varvec{C}}_{b}^{e} \delta {\varvec{\omega}}_{{{\varvec{ib}}}}^{{\varvec{b}}} } \\ \end{array} } \right) $$

(8)

where $\phi$ is the correction vector of attitude; ${\varvec{N}}^{{\varvec{e}}} \varvec{\delta x}_{{{\varvec{INS}}}}^{{\varvec{e}}}$ is part of the gravity that derived from positioning error, and the detail of ${\varvec{N}}^{{\varvec{e}}}$ is presented in Appendix; $\varvec{\delta f}^{{\varvec{b}}}$ and $\varvec{\delta \omega }_{{{\varvec{ib}}}}^{{\varvec{b}}}$ is the uncertainty of the sensor, that can be modeled as bias error, scale factor error and white noise (Shin 2005):

$$ \left\{ {\begin{array}{*{20}c} {\delta {\varvec{f}}^{{\varvec{b}}} = {\varvec{B}}_{{\varvec{a}}} + {\text{diag}}\left( {{\varvec{f}}^{{\varvec{b}}} } \right){\varvec{S}}_{{\varvec{a}}} + {\varvec{w}}_{{\varvec{v}}} } \\ {\delta {\varvec{\omega}}_{{{\varvec{ib}}}}^{{\varvec{b}}} = {\varvec{B}}_{{\varvec{g}}} + {\text{diag}}\left( {{\varvec{\omega}}_{{{\varvec{ib}}}}^{{\varvec{b}}} } \right){\varvec{S}}_{{\varvec{g}}} + {\varvec{w}}_{\phi } } \\ \end{array} } \right. $$

(9)

${\varvec{B}}_{{\varvec{a}}}$ and ${\varvec{B}}_{{\varvec{g}}}$ denote the bias errors of accelerometer and gyroscope, respectively; ${\varvec{S}}_{{\varvec{a}}}$ and ${\varvec{S}}_{{\varvec{g}}}$ denote the scale factor errors of accelerometer and gyroscope, respectively; ${\varvec{w}}_{{\varvec{v}}}$ and ${\varvec{w}}_{\phi }$ are the processing noise of velocity and angular rate, respectively. And the errors of accelerometer and gyroscope are typically modeled as first-order Gauss–Markov processes (Shin 2005):

$$ \left\{ {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\dot{\varvec{B}}_{{\varvec{a}}} } \\ {\dot{\varvec{B}}_{{\varvec{g}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{ - 1}{{\tau_{ba} }}{\varvec{B}}_{{\varvec{a}}} } \\ {\frac{ - 1}{{\tau_{bg} }}{\varvec{B}}_{{\varvec{g}}} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{\varvec{w}}_{{{\varvec{ba}}}} } \\ {{\varvec{w}}_{{{\varvec{bg}}}} } \\ \end{array} } \right)} \\ {\left( {\begin{array}{*{20}c} {\dot{\varvec{S}}_{{\varvec{a}}} } \\ {\dot{\varvec{S}}_{{\varvec{g}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{ - 1}{{\tau_{sa} }}{\varvec{S}}_{{\varvec{a}}} } \\ {\frac{ - 1}{{\tau_{sg} }}{\varvec{S}}_{{\varvec{g}}} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{\varvec{w}}_{{{\varvec{sa}}}} } \\ {{\varvec{w}}_{{{\varvec{sg}}}} } \\ \end{array} } \right)} \\ \end{array} } \right. $$

(10)

where $\tau_{ \cdot }$ and ${\varvec{w}}_{ \cdot }$ are the corresponding correlation time and driving white noise, respectively. Then, by setting ${\varvec{x}}_{{{\varvec{INS}}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{\varvec{\updelta}}}{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } & {\varvec{\delta v}_{{{\varvec{INS}}}}^{{\varvec{e}}} } & \phi \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{B}}_{{\varvec{a}}} } & {{\varvec{B}}_{{\varvec{g}}} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{S}}_{{\varvec{a}}} } & {{\varvec{S}}_{{\varvec{g}}} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}}$, the state equation of INS derived from Eq. (8) to Eq. (10) can be written as:

$$ \dot{\varvec{x}}_{{{\varvec{INS}}}} = {\varvec{F}} \cdot {\varvec{x}}_{{{\varvec{INS}}}} + {\varvec{G}} \cdot \varvec{w } $$

(11)

where for the details of F, G and ${\varvec{w}}$, we refer to Appendix.

2.3 PPP/INS tightly coupled integration model

Typically, the IMU central position ${\varvec{x}}_{INS}^{e}$ and the GNSS receiver antenna reference point (ARP) ${\varvec{x}}_{GNSS}^{e}$ do not overlap with each other, and their relation is described with the lever-arm correction vector ${\varvec{l}}^{b}$ as (Shin 2005):

$$ {\varvec{x}}_{{{\varvec{GNSS}}}}^{{\varvec{e}}} = {\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} + {\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{l}}^{{\varvec{b}}} $$

(12)

similarly, we have the relation for the approximate coordinates $\tilde{\varvec{x}}_{GNSS}^{e}$ and $\tilde{\varvec{x}}_{INS}^{e}$

$$ \tilde{\varvec{x}}_{{{\varvec{GNSS}}}}^{{\varvec{e}}} = \tilde{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} + \tilde{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{l}}^{{\varvec{b}}} $$

(13)

where $\tilde{\varvec{C}}_{b}^{e}$ is the approximate rotation matrix from b-frame to e-frame, and satisfies

$$ \tilde{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} = \left( {{\varvec{I}} - \phi \times } \right){\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} $$

(14)

Substituting (14) in (13), the following equation of $\varvec{ \delta x}_{GNSS}^{e}$ and ${\updelta }{\varvec{x}}_{INS}^{e}$ can be derived by (12) minus (13):

$$ \delta {\varvec{x}}_{GNSS}^{e} = {\updelta }{\varvec{x}}_{INS}^{e} + {\varvec{C}}_{b}^{e} {\varvec{l}}^{b} \times \phi $$

(15)

Considering the error state is differently defined in PPP and PPP/INS, the sign of $\delta {\varvec{x}}_{GNSS}^{e}$ and ${{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}}^{{\varvec{e}}}$ is opposite. Substituting (15) and (4) in (3), the augmented measurement model of PPP/INS tightly coupled integration model can be derived as follows:

$$ \left. {\begin{array}{*{20}l} {{\Delta }P_{r,f}^{s} = - {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} {{\varvec{\updelta}}}{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} - {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} {\varvec{C}}_{b}^{e} {\varvec{l}}^{b} \times \phi + t_{{r,{\text{sys}}}} + \alpha_{r}^{s} {\updelta }T_{w} + b_{r,f} + \varepsilon_{p} } \hfill \\ {\quad \quad + \frac{40.3}{{f^{2} }}\gamma_{r}^{s} \left( {a_{0} + a_{1} {\text{d}}L + a_{2} {\text{d}}B + a_{3} {\text{d}}L^{2} + a_{4} {\text{d}}B^{2} + r_{r}^{s} + \varepsilon_{{\tilde{I}_{r}^{s} }} } \right)} \hfill \\ {{\Delta }\Phi_{r,f}^{s} = - {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} {{\varvec{\updelta}}}{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} - {\varvec{h}}_{{\varvec{r}}}^{{\varvec{s}}} {\varvec{C}}_{b}^{e} {\varvec{l}}^{b} \times \phi + t_{{r,{\text{sys}}}} + \alpha_{r}^{s} {\updelta }T_{w} + \lambda N_{r,f}^{s} + \varepsilon_{\Phi } } \hfill \\ {\quad \quad - \frac{40.3}{{f^{2} }}\gamma_{r}^{s} \left( {a_{0} + a_{1} {\text{d}}L + a_{2} {\text{d}}B + a_{3} {\text{d}}L^{2} + a_{4} {\text{d}}B^{2} + r_{r}^{s} + \varepsilon_{{\tilde{I}_{r}^{s} }} } \right)} \hfill \\ {\tilde{I}_{r}^{s} = a_{0} + a_{1} {\text{d}}L + a_{2} {\text{d}}B + a_{3} {\text{d}}L^{2} + a_{4} {\text{d}}B^{2} + r_{r}^{s} + \varepsilon_{{\tilde{I}_{r}^{s} }} } \hfill \\ \end{array} } \right\} $$

(16)

Combining state vector ${\varvec{x}}_{{{\varvec{ppp}}}}$ in Eqs. (6) and (11), we have the augmented state vector of the system:

$$ {\varvec{x}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{\varvec{\updelta}}}{\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} } & {\varvec{\delta v}_{{{\varvec{INS}}}}^{{\varvec{e}}} } \\ \end{array} } & {\begin{array}{*{20}c} \phi & {\varvec{B}} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{S}} & {t_{r} } \\ \end{array} } & {\begin{array}{*{20}c} {{\updelta }T_{w} } & {b_{r} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{N}}_{{\varvec{r}}} } & {{\varvec{a}}_{{\varvec{r}}} } & {{\varvec{r}}_{{\varvec{r}}} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}} $$

(17)

with ${\varvec{B}} = \left( {\begin{array}{*{20}c} {{\varvec{B}}_{{\varvec{a}}} } & {{\varvec{B}}_{{\varvec{g}}} } \\ \end{array} } \right)$ and ${\varvec{S}} = \left( {\begin{array}{*{20}c} {{\varvec{S}}_{{\varvec{a}}} } & {{\varvec{S}}_{{\varvec{g}}} } \\ \end{array} } \right)$, thus the design matrix in Eq. (6) should be extended to:

$$ {\varvec{H}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{v}}_{{\varvec{r}}} }} } \\ \end{array} } & {\begin{array}{*{20}c} {\varvec{ H}_{\phi } } & {\varvec{ H}_{{\varvec{B}}} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{ H}_{{\varvec{S}}} } & {{\varvec{H}}_{{{\varvec{t}}_{{\varvec{r}}} }} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{T}}_{{\varvec{w}}} }} } & {{\varvec{H}}_{{{\varvec{b}}_{{\varvec{r}}} }} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{H}}_{{{\varvec{N}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{\varvec{a}}_{{\varvec{r}}} }} } & {{\varvec{H}}_{{{\varvec{r}}_{{\varvec{r}}} }} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}} $$

(18)

the new introduced symbols, i.e., ${\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{v}}_{{\varvec{r}}} }}$, $\varvec{ H}_{\phi }$, $\varvec{ H}_{{\varvec{B}}}$ and $\varvec{ H}_{{\varvec{S}}}$ are design matrixes corresponding to the INS state parameters, and their details are presented in Appendix. Then the measurement model of the PPP/INS tight integration is ready.

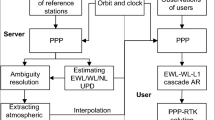
Shown in Fig. 1 is the structure of PPP/INS tight integration with atmospheric augmentation. This algorithm is developed based on the FUSING (FUSing IN Gnss) software (Shi et al. 2018; Zhao et al. 2018; Gu et al. 2020). At present, the FUSING software is capable for the real-time multi-GNSS precise orbit determination, satellite clock estimation, ionospheric and atmospheric modeling as well as multi-frequency precise positioning, using either IF combination or undifferenced and uncombined observation. Note that, since tightly coupled technique was used in this study, the specific force and angular velocity of IMU were processed directly in FUSING software.

Fig. 1

PPP/INS tight integration algorithm structure

3 Experiment

To evaluate the performance of PPP under the urban environment, and assess the contribution of Multi-GNSS, IMU tightly coupled integration and the high-precision atmospheric delay augmentation to real-time dynamic positioning, three datasets were collected around Wuhan City of China on January 19 and 23, 2018, respectively. For simplicity in the following discussion, the experiments corresponding to these datasets were denoted as T019 and T023, respectively, according to their DOY (day of year). In these experiments, both single- and dual-frequency positioning are carried out in simulated real-time mode based on the FUSING software, including the UPD estimation and atmospheric delay modeling. Compared with the true real-time applications, the main differences lay in two factors: First, the final orbit and clock were used in the experiment; second, the accuracy of the products may decrease slightly due to the coding and broadcasting. Thus, the accuracy of the following results may not be obtainable in true real-time.

3.1 Overview of the experiment

Shown in Fig. 2 are the trajectories of the experiments, and Fig. 3 further presents the number of satellites and the corresponding PDOP (precision dilution of positioning) values with a cutoff angle of 10°. As we can see, since all these experiments were carried out in a real urban environment, there were obvious fluctuations in the series of satellite number. Among these experiments, T019 was under a relatively open sky environment with an average tracking satellite number of 14.95. Compared with T019, T023 suffered more frequent interruptions in the satellite tracking since that it was carried out in the Second Ring Road of Wuhan city. There were many high-rise buildings, viaducts and tunnels, which can cause great interference to the signal and influence the positioning continuity and accuracy. The red color lines of number of satellites and PDOP are cut off by the horizontal axis in the right panel of Fig. 3. So, it seems that red color line overlaps between number of satellites and PDOP. Figure 4 shows the real scene in the Second Ring Road of Wuhan city. INS can improve the positioning continuity and accuracy of GNSS in this scenario. So, the performance of T023 can be regarded as a typical result of PPP/INS tightly coupled integration under the downtown environment.

Fig. 2

The trajectories of the two experiments T019 (left panel) T023 (right panel), respectively

Fig. 3

PDOP and satellite number of GPS and GPS + GLONASS for the experiments T019 (left panel) and T023 (right panel), respectively

Fig. 4

The real scene in the Second Ring Road of Wuhan city, where the dataset T023 was collected

A PPOI-D09 IMU and a Trimble NetR9 receiver are carried on the experimental vehicle in Fig. 5. The yellow rectangles denote the GNSS antenna and the IMU for these experiments. The parameters of IMU are listed in Table 1. The PPOI-D09 collected the IMU data with a sampling rate of 200 Hz, while the Trimble NetR9 receiver was used for the GNSS data collection with a sampling rate of 1 Hz.

Fig. 5

Equipment setup of experimental vehicle

Table 1 Parameters of the PPOI-D09

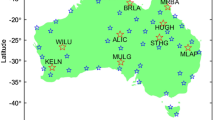
Besides the multi-GNSS and IMU-aided algorithm, the high-precision atmosphere models, i.e., ionospheric and tropospheric delay corrections, present another potential method to improve the performance of PPP. Thus, five reference stations distributed in Fig. 6 were further utilized to generate the high-precision atmospheric products. The green lines in Fig. 6 denote the experimental trajectories of Fig. 2 and the inter-station distance of the reference stations is around 40 km. All these stations collect GPS and GLONASS data with an interval of 30 s.

Fig. 6

Distribution of reference stations for atmospheric products estimation

Presented in Table 2 is the detail of the data processing strategy. For simplicity, the characters ‘G’, ‘R’, ‘I’ and ‘A’ denote the solution with GPS, GLONASS, INS and Atmosphere augmentation, respectively. For instance, GRI stands for the positioning with GPS/GLONASS PPP/INS integration, while GRIA stands for the positioning of GRI further constrained with the high-precision regional atmospheric model. Note that the most basic solution, i.e., G, presented in this study was also undifferenced and uncombined model augmented with the GIM model. Thus, the comparison of GRI and GRIA mainly presented the advantage of regional ionospheric map over the global ionospheric map. To assess the performance of the different methods, the positioning accuracy was evaluated by RMS, with respect to the reference trajectories that calculated by the RTK/INS loosely coupled solution with bi-directional smoothing algorithm while the same GNSS receiver and IMU were involved in the reference trajectories. In addition, the reference trajectories were generated with the commercial software, i.e., GINS (http://www.whmpst.com/cn/). And the RTK/INS loosely coupled solution was the only high-precision solution supported by GINS. The nominal accuracy of the RTK/INS loosely coupled solution provided by GINS is at the level of 2 cm for horizontal position and 3 cm for vertical position.

Table 2 The strategies of PPP experiments

3.2 Performance analysis

In this section, we begin with the generation and evaluation of the regional atmospheric delay model. Then, the performance of dynamic PPP under the urban environment is analyzed with different strategies as summarized in Table 2.

3.2.1 Atmospheric delay modeling

As presented in Table 2, except that the coordinates of the reference stations are fixed, the algorithm of GNSS atmospheric delay estimation is identical with that of PPP, i.e., GR solution. And it should be noted that since the undifferenced and uncombined observation model is utilized, the tropospheric and ionospheric delay can be derived simultaneously in a single filter, which is expected to give the most consistent result theoretically.

Concerning the accuracy of the tropospheric and ionospheric products, the atmospheric delay generated from station WH11 is regarded as the reference value and used to evaluate the interpolated tropospheric and ionospheric delay of the left four reference stations. It is noted that the “true value” of atmospheric delay is unavailable, and thus the results in the following evaluation mainly presented the correction precision of the atmospheric products for GNSS users. Figure 7 illustrates the series of the reference ZTD (zenith tropospheric delay) and the interpolated ZTD, and the RMS is 0.59 cm and 0.48 cm for T019 and T023, respectively.

Fig. 7

Series of the reference ZTD from WH11 and the interpolated ZTD from the left four reference stations in Fig. 6 for the experiments T019 (black) and T023 (red), respectively

In addition, by the comparison of the reference VTEC and the interpolated VTEC, Fig. 8 presents the distribution of the differenced ionospheric delay for GPS and GLONASS, respectively. The results suggest that the ionospheric delay generated from GPS performs slightly better than that of GLONASS. The ionospheric delay generated from GPS is 0.04 total electron content unit (TECU) and 0.13TECU smaller than that of GLONASS for T019 and T023, respectively. As we can see, the overall precision of the experiments is around 0.5 TECU, which performs much better than that of IGS GIM product with a precision of 2–8 TECU (http://www.igs.org/products).

Fig. 8

The distribution of the differenced ionospheric delay for GPS (black) and GLONASS for the experiments T019 (upper panel) and T023 (bottom panel), respectively

3.2.2 Positioning comparison

In Tables 3 and 4, we present the horizontal and three-dimensional (3D) RMS of the experiments T019 and T023 with the dual- and single-frequency PPP, respectively. Note that the results of the first 15 min were excluded in the statistics here, for it takes about 15-min for PPP to converge. To illustrate the improvement of each solution with respect to the GPS-only PPP, and the contribution of additional technique with respect to the former solution, we derived the statistics I and II and listed them in these tables. For example, the horizontal improvement of GRIA with respect to G and GRI is 43.3% and 22.7%, respectively.

Table 3 RMS of PPP for T019

Table 4 RMS of PPP for T023

The main conclusions that can be drawn from these statistics are, that concerning the urban vehicle navigation, the GPS-only PPP can be improved significantly with these techniques, i.e., the multi-GNSS, INS tightly coupled integration and the atmospheric augmentation. Compared with the GR solution, though the improvement of GRI is rather limited as presented in Table 3, significant improvement can be found in Table 3, i.e., Table 4. The results suggest that INS tightly coupled integration makes the most contributions under the downtown environment, while the improvement of the regional atmospheric augmentation in single-frequency PPP is more significant since that single frequency is more sensitive to the ionospheric delay. The 3D positioning RMS with GRIA solution for dual frequency is 0.22 m and 0.77 m for T019 and T023, respectively. Concerning single-frequency PPP, the 3D RMS is 0.45 m and 1.17 m for T019 and T023, respectively.

The corresponding positioning difference series are given in Figs. 9, 10, 11 and 12. As we can see, the positioning accuracy is degraded due to the frequency loss of satellite tracking in GNSS PPP solution, i.e., G and GR, especially for the experiment T023. The results tightly coupled with INS are more resistance to the failure of satellite tracking. Concerning the positioning performance during the first 15 min, i.e., initialization period, the corresponding series with background painted gray of Figs. 9, 10, 11 and 12 are further enlarged in the right panels. Obviously, the GRIA solution converges faster than GRI in all these cases, which implies that the high-precision atmospheric augmentation plays an important role in reducing the convergence time.

Fig. 9

Position difference series of T019 with dual-frequency observations for N (north, upper panel), E (east, middle panel) and U (up, bottom panel), respectively

Fig. 10

Position difference series of T019 with single-frequency observations for N (north, upper panel), E (east, middle panel) and U (up, bottom panel), respectively

Fig. 11

Position difference series of T023 with dual-frequency observations for N (north, upper panel), E (east, middle panel) and U (up, bottom panel), respectively

Fig. 12

Position difference series of T023 with single-frequency observations for N (north, upper panel), E (east, middle panel) and U (up, bottom panel), respectively

The horizontal positioning error distribution of T023 for both dual-frequency and single-frequency PPP is presented in Fig. 13, and the cumulative frequency of the horizontal positioning error less than 1 m, i.e., $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$, is also plotted in detail for different solutions. This statistic of T023 is selected since that the experiment was carried out in the Second Ring Road of Wuhan city, which can be regarded as a typical downtown environment, and the lane-level (sub-meter level) navigation is of special interest to the automatic drive. Using RTK/INS loosely coupled with bi-directional smoothing to derive the reference trajectory, the best solution can be found with GRIA among these four solutions, and $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$ is 99.0% and 93.2% for dual frequency and single frequency, respectively. GR is close to G for $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$. Taking the performance for the interval $\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}$ into consideration, the contribution of INS is rather limited as implied by Fig. 13 for single frequency. As presented in Table 4, the horizontal RMS of T023 with GRI is 0.86 m and 1.47 m, respectively, while horizontal positioning error of GRI solution is distributed mainly within the interval of $\left[ {\left. {\begin{array}{*{20}c} {0.5} & {1.0} \\ \end{array} } \right)} \right.$ and $\left[ {\left. {\begin{array}{*{20}c} {1.0} & {1.5} \\ \end{array} } \right)} \right.$ for dual and single frequency, respectively. So, we conclude that INS contributes to keeping the positioning accuracy at a mean level.

Fig. 13

Horizontal positioning error distribution of T023 for the dual-frequency PPP (upper panel) and single-frequency PPP (bottom panel), respectively, while the cumulative frequency of the horizontal positioning error less than 1 m, i.e., $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$ is also plotted

As an example, Figs. 14 and 15 further present the details of the GRIA solution for T019. As shown in Fig. 14, the RMS of residual of pseudo-range is about 0.66 m and 0.87 m for C1 and P2, respectively, while the RMS of residual on L1 and L2 is 0.29 cm and 0.19 cm, respectively. Shown in Fig. 15 are the series of receiver DCB, gyroscope bias and accelerometer bias. As we can see, the receiver DCB is rather stable and has a value of about − 10 ns. The gyroscope bias stability is 0.027°/h. The standard deviations of the series of gyroscope bias in three direction are 0.019°/h, 0.018°/h and 0.027°/h, respectively, which are consistent with the parameter presented in Table 1. Concerning the accelerometer bias, it is almost zero for the X and Y components for the first 20 min since that the vehicle was parked during this period.

Fig. 14

Residual series of the pseudo-range (upper panel) and carrier phase (bottom panel) on each frequency for the experiment T019 with the GRIA solution

Fig. 15

Series of the receiver DCB (upper panel), gyroscope bias (middle panel) and accelerometer bias (bottom panel) for the experiment T019 with the GRIA solution

4 Conclusion

With the intention to improve the performance of PPP and get a reliable and continuous kinematic positioning under the urban environment, we presented a comprehensive positioning model by fusing the techniques of multi-GNSS combination, GNSS/INS tight integration as well as the regional ionospheric and tropospheric augmentation in the undifferenced and uncombined PPP. To evaluate the performance of this positioning model, two experiments denoted as T019 and T023 were carried out in a real urban environment with single- and dual-frequency PPP. Specially, the experiment T023 was carried out in the Second Ring Road of Wuhan city, and its performance thus can be regarded as a typical PPP/INS tightly coupled integration result under the downtown environment. Concerning the regional atmospheric augmentation, observations from 5 reference stations with an inter-station distance of about 40 km were also collected during the experimental period.

Before the positioning evaluation, the tropospheric delay and ionospheric delay of the reference stations were generated with the undifferenced and uncombined PPP. The comparison between reference stations suggested that the regional tropospheric model had a precision of better than 0.6 cm in terms of ZTD, while concerning the regional ionospheric model, the overall precision was around 0.5 TECU in term of VTEC.

By denoting the technique of GPS, GLONASS, INS and atmosphere augmentation with character ‘G’, ‘R’, ‘I’ and ‘A’, respectively, the solutions with different combination of techniques are then denoted as G, GR, GRI and GRIA, respectively. As illustrated by the vehicle navigation experiments under urban environment, the GPS-only PPP can be improved significantly with these techniques, i.e., multi-GNSS, INS tightly coupled integration and atmospheric augmentation, while INS tightly coupled integration makes the most contributions under the downtown environment, and the improvement of the regional atmospheric augmentation in single-frequency PPP is more significant since that single frequency is more sensitive to the ionospheric delay. The 3D positioning RMS with GRIA solution for dual frequency are 0.22 m and 0.77 m for T019 and T023, respectively. Concerning single-frequency PPP, the 3D RMS is 0.45 m and 1.17 m for T019 and T023, respectively. By analyzing the positioning performance during the first 15 min, it is proved that the regional atmospheric augmentation accelerates positioning convergence. Moreover, taking the lane-level navigation under the downtown environment into consideration, we further presented the cumulative frequency of the T023 horizontal positioning error less than 1 m, i.e., $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$, and the best solution can be found with GRIA PPP, in which $P\left( {\sqrt {{\text{d}}N^{2} + {\text{d}}E^{2} } < 1\;{\text{m}}} \right)$ is 99.0% and 93.2% for dual frequency and single frequency, respectively. Concerning the contribution of INS, our results suggest that INS is limited in improving the positioning accuracy at the level of better than 1 m, while INS helps keeping the positioning accuracy in a stable level.

By fusing the techniques of multi-GNSS/INS tightly integration and the regional atmospheric augmentation, the technique presented in this study is promising in urban navigation. However, the performance of this technique in true real-time applications with low-cost single-frequency GNSS and MEMS-based INS is still left for further study. In addition, it is expected that the performance would be further improved by GNSS PPP ambiguity resolution.

5 Data availability statement

The GNSS observation and INS measurement and the region atmosphere augmentation products can be accessed from ftp://59.172.176.192; The precise clock, orbit and GIM products are released from by IGS data center CDDIS and can be accessed from ftp://cddis.gsfc.nasa.gov/.

Appendix

Here, we presented the details concerning the PPP/INS observation model. First, a few symbols and notions are defined for future reference: $\otimes$ and $\circ$ are the Kronecker product and Schur product, respectively (Rao 1973; Davis et al. 1962); $\times$ demotes the skew-symmetric matrix of the vector (Shin 2005); and the notions are defined as:

$$ {\varvec{z}}_{{\varvec{s}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} \ldots & 0 \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}} $$

(19)

$$ {\varvec{u}}_{{\varvec{s}}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 1 \\ \end{array} } & {\begin{array}{*{20}c} \ldots & 1 \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}} $$

(20)

$$ {\varvec{Z}}_{{\varvec{s}}} = \left( {\begin{array}{*{20}c} 0 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0 \\ \end{array} } \right) $$

(21)

$$ {\varvec{U}}_{{\varvec{s}}} = \left( {\begin{array}{*{20}c} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \\ \end{array} } \right) $$

(22)

$$ {\text{diag}}\left( {\varvec{a}} \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {a_{1} } \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {a_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } \\ {\begin{array}{*{20}c} \ddots \\ \cdots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {a_{n} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right) $$

(23)

thus, ${\varvec{z}}_{{\varvec{s}}}$ is a $s$ by $1$ vector with zero entries and ${\varvec{u}}_{{\varvec{s}}}$ is a $s$ by $1$ vector with one entries, while ${\varvec{Z}}_{{\varvec{s}}}$ is a $s$ by $s$ matrix with zero entries and ${\varvec{U}}_{{\varvec{s}}}$ is a $s$ by $s$ identity matrix, and ${\text{diag}}\left( {\varvec{a}} \right)$ denotes the diagonal matrix with the elements of vector ${\varvec{a}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {a_{1} } & {a_{2} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {a_{n} } \\ \end{array} } \\ \end{array} } \right)^{{\text{T}}}$ on the main diagonal. The dimensions and lengths of such vectors will generally be obvious from context, and the symbols are exactly the same as that of Sect. 2.

According to Eqs. (19)–(23), and denotes the frequency number as $k$, then the design matrix ${\varvec{H}}_{{{\varvec{PPP}}}}$ is expressed as:

$$ {\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{x}}_{{\varvec{r}}} }} = \left( {\begin{array}{*{20}c} {{\varvec{u}}_{{2 \cdot {\varvec{k}}}} } \\ 0 \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {h_{r}^{1} } \\ \vdots \\ {h_{r}^{j} } \\ \end{array} } \right) $$

(24)

$$ {\varvec{H}}_{{t_{r} }} = \left( {\begin{array}{*{20}c} {{\varvec{u}}_{{2 \cdot {\varvec{j}} \cdot {\varvec{k}}}} } \\ {{\varvec{z}}_{{\varvec{j}}} } \\ \end{array} } \right) $$

(25)

$$ {\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{T}}_{{\varvec{w}}} }} = \left( {\begin{array}{*{20}c} {{\varvec{u}}_{{2 \cdot {\varvec{k}}}} } \\ 0 \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {\alpha_{r}^{1} } \\ \vdots \\ {\alpha_{r}^{j} } \\ \end{array} } \right) $$

(26)

$$ {\varvec{H}}_{{{\varvec{b}}_{{\varvec{r}}} }} = \left( {\begin{array}{*{20}c} {{\varvec{z}}_{{\varvec{j}}}^{{\mathbf{T}}} } & {{\varvec{u}}_{{\varvec{j}}}^{{\mathbf{T}}} } & {\begin{array}{*{20}c} {{\varvec{z}}_{{\varvec{j}}}^{{\mathbf{T}}} } & {{\varvec{z}}_{{\varvec{j}}}^{{\mathbf{T}}} } & {{\varvec{z}}_{{\varvec{j}}}^{{\mathbf{T}}} } \\ \end{array} } \\ \end{array} } \right)^{{\mathbf{T}}} $$

(27)

$$ {\varvec{H}}_{{{\varvec{N}}_{{\varvec{r}}} }} = \left( {\begin{array}{*{20}c} {{\varvec{Z}}_{j \cdot k} } \\ {{\varvec{U}}_{j \cdot k} } \\ {{\varvec{z}}_{{\varvec{k}}}^{{\varvec{T}}} \otimes {\varvec{Z}}_{{\varvec{j}}} } \\ \end{array} } \right) $$

(28)

$$ {\varvec{H}}_{{{\varvec{a}}_{{\varvec{r}}} }} = \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} 1 \\ { - 1} \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {\frac{40.3}{{f_{1}^{2} }}} \\ {\frac{40.3}{{f_{2}^{2} }}} \\ \end{array} } \right)} \\ 0 \\ \end{array} } \right) \otimes \left( {{\varvec{u}}_{5}^{{\varvec{T}}} \otimes \left( {\begin{array}{*{20}c} {{\varvec{\gamma}}_{r}^{1} } \\ \vdots \\ {{\varvec{\gamma}}_{r}^{j} } \\ \end{array} } \right) \circ \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} {\hbox{d}L_{r}^{1} } \\ \vdots \\ {\hbox{d}L_{r}^{j} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hbox{d}B_{r}^{1} } \\ \vdots \\ {\hbox{d}B_{r}^{j} } \\ \end{array} } & {\begin{array}{*{20}c} {\hbox{d}L_{r}^{12} } \\ \vdots \\ {\hbox{d}L_{r}^{j2} } \\ \end{array} } & {\begin{array}{*{20}c} {\hbox{d}B_{r}^{12} } \\ \vdots \\ {\hbox{d}B_{r}^{j2} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right)} \right) $$

(29)

$$ {\varvec{H}}_{{{\varvec{r}}_{{\varvec{r}}} }} = \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} 1 \\ { - 1} \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {\frac{40.3}{{f_{1}^{2} }}} \\ {\frac{40.3}{{f_{1}^{2} }}} \\ \end{array} } \right)} \\ 0 \\ \end{array} } \right) \otimes \left( {{\varvec{u}}_{5}^{{\varvec{T}}} \otimes \left( {\begin{array}{*{20}c} {{\varvec{\gamma}}_{r}^{1} } \\ \vdots \\ {{\varvec{\gamma}}_{r}^{j} } \\ \end{array} } \right) \otimes {\varvec{U}}_{{\varvec{j}}} } \right) $$

(30)

By the way, the Eq. (15) in our previous study Gu et al. (2015a) should be corrected to Eqs. (29) and (30) of this study.

Concerning ${\varvec{N}}^{{\varvec{e}}}$ in Eq. (12) we have:

$$ {\varvec{N}}^{{\varvec{e}}} = \frac{kM}{{r^{3} }}\left( {\begin{array}{*{20}c} { - 1 + \frac{{3x^{2} }}{{r^{2} }}} & {\frac{3xy}{{r^{2} }}} & {\frac{3xz}{{r^{2} }}} \\ {\frac{3xy}{{r^{2} }}} & { - 1 + \frac{{3y^{2} }}{{r^{2} }}} & {\frac{3yz}{{r^{2} }}} \\ {\frac{3xz}{{r^{2} }}} & {\frac{3yz}{{r^{2} }}} & { - 1 + \frac{{3z^{2} }}{{r^{2} }}} \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\omega_{e} } & 0 & 0 \\ 0 & {\omega_{e} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right) $$

(31)

where $kM$ is the product of the gravitational constant and the mass of the earth; ${\varvec{x}}_{{{\varvec{INS}}}}^{{\varvec{e}}} = \left( {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right)^{{\text{T}}}$; $r = \sqrt {x^{2} + y^{2} + z^{2} }$; and $\omega_{e}$ is the earth rotation rate.

Derived from Eqs. (8) to (10), the matrixes in the state Eq. (11) are presented as:

$$ {\mathbf{F}}\varvec{ = }\left( {\begin{array}{*{20}l} 0 \hfill & {\varvec{U}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{\varvec{N}}^{{\varvec{e}}} } \hfill & { - 2{\varvec{\omega}}_{{{\varvec{ie}}}}^{{\varvec{e}}} \times } \hfill & {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{f}}_{{\varvec{b}}} \times } \hfill & {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} } \hfill & 0 \hfill & {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{diag}}\left( {{\varvec{f}}^{{\varvec{b}}} } \right)} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - {\varvec{\omega}}_{{{\varvec{ie}}}}^{{\varvec{e}}} \times } \hfill & 0 \hfill & { - {\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} } \hfill & 0 \hfill & { - {\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{diag}}\left( {{\varvec{\omega}}_{{{\varvec{ib}}}}^{{\varvec{b}}} } \right)} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - 1/{\varvec{\tau}}_{{{\varvec{ba}}}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 1/{\varvec{\tau}}_{{{\varvec{bg}}}} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 1/{\varvec{\tau}}_{{{\varvec{sa}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 1/{\varvec{\tau}}_{{{\varvec{sg}}}} } \hfill \\ \end{array} } \right) $$

(32)

$$ {\varvec{G}} = {\text{diag}}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{U}} & {{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} } & { - {\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} } \\ \end{array} } & {\begin{array}{*{20}c} {\varvec{U}} & {\varvec{U}} \\ \end{array} } & {\begin{array}{*{20}c} {\varvec{U}} & {\varvec{U}} \\ \end{array} } \\ \end{array} } \right) $$

(33)

$$ {\varvec{w}} = {\text{diag}}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{Z}} & {{\varvec{w}}_{{\varvec{v}}} } & {{\varvec{w}}_{\phi } } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{w}}_{{{\varvec{ba}}}} } & {{\varvec{w}}_{{{\varvec{bg}}}} } \\ \end{array} } & {\begin{array}{*{20}c} {{\varvec{w}}_{{{\varvec{sa}}}} } & {{\varvec{w}}_{{{\varvec{sg}}}} } \\ \end{array} } \\ \end{array} } \right) $$

(34)

The design matrixes corresponding to the INS state parameters in Eq. (18) can be expressed as

$$ \varvec{ H}_{\phi } = \left( {\begin{array}{*{20}c} {{\varvec{u}}_{{2 \cdot {\varvec{k}}}} } \\ 0 \\ \end{array} } \right) \otimes \left( {\begin{array}{*{20}c} {h_{r}^{1} } \\ \vdots \\ {h_{r}^{j} } \\ \end{array} } \right) \otimes \left( {\tilde{\varvec{C}}_{{\varvec{b}}}^{{\varvec{e}}} {\varvec{l}}^{{\varvec{b}}} \times } \right) $$

(35)

$$ {\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{v}}_{{\varvec{r}}} }} = {\varvec{z}}_{3}^{{\text{T}}} \otimes {\varvec{z}}_{{2 \cdot {\varvec{j}} \cdot {\varvec{k}} + {\varvec{j}}}} $$

(36)

$$ \varvec{ H}_{{\varvec{B}}} = \varvec{ H}_{{\varvec{S}}} = {\varvec{z}}_{6}^{{\text{T}}} \otimes {\varvec{z}}_{{2 \cdot {\varvec{j}} \cdot {\varvec{k}} + {\varvec{j}}}} $$

(37)

$\varvec{ H}_{\phi }$ indicates that the GNSS observations are sensitive to the attitude through the lever-arm correction vector in Eq. (15), while the zero entries in ${\varvec{H}}_{{{{\varvec{\updelta}}}{\varvec{v}}_{{\varvec{r}}} }}$, ${ }{\varvec{H}}_{{\varvec{B}}}$ and $\varvec{ H}_{{\varvec{S}}}$ indicate that the GNSS observations have no direct relation with the velocity and sensor errors of INS.