On the spherical and spheroidal harmonic expansion of the gravitational potential of the topographic masses

Abstract

This paper is devoted to the spherical and spheroidal harmonic expansion of the gravitational potential of the topographic masses in the most rigorous way. Such an expansion can be used to compute gravimetric topographic effects for geodetic and geophysical applications. It can also be used to augment a global gravity model to a much higher resolution of the gravitational potential of the topography. A formulation for a spherical harmonic expansion is developed without the spherical approximation. Then, formulas for the spheroidal harmonic expansion are derived. For the latter, Legendre’s functions of the first and second kinds with imaginary variable are expanded in Laurent series. They are then scaled into two real power series of the second eccentricity of the reference ellipsoid. Using these series, formulas for computing the spheroidal harmonic coefficients are reduced to surface harmonic analysis. Two numerical examples are presented. The first is a spherical harmonic expansion to degree and order 2700 by taking advantage of existing software. It demonstrates that rigorous spherical harmonic expansion is possible, but the computed potential on the geoid shows noticeable error pattern at Polar Regions due to the downward continuation from the bounding sphere to the geoid. The second numerical example is the spheroidal expansion to degree and order 180 for the exterior space. The power series of the second eccentricity of the reference ellipsoid is truncated at the eighth order leading to omission errors of 25 nm (RMS) for land areas, with extreme values around 0.5 mm to geoid height. The results show that the ellipsoidal correction is 1.65 m (RMS) over land areas, with maximum value of 13.19 m in the Andes. It shows also that the correction resembles the topography closely, implying that the ellipsoidal correction is rich in all frequencies of the gravity field and not only long wavelength as it is commonly assumed.

1 Introduction

The topographic effects on functionals of the gravity field, such as the direct and indirect effects, geoid–quasigeoid separation and gravity gradients, have been traditionally computed using numerical integration. This employed the planar approximation in earlier days (e.g., Forsberg 1984; Sideris and Forsberg 1990; Wang and Rapp 1990) and later replaced it by a more accurate spherical approximation (Martinec 1998; Kuhn 2000; Heck and Seitz 2007; Wild-Pfeiffer 2008). Numerical integrations of the topographic effects are performed primarily in a limited area, either to achieve computational efficiency or because the user’s data extent is limited to their local area. Another drawback of numerical integration is in the linear approximation used in the computation of the topographic effects (Moritz 1968), and the difficulty to account for the contribution of ignored higher order terms.

Alternatively, the topographic effects can be computed from a high-degree harmonic expansion of the gravitatio-nal potential of topographic masses (e.g., Novák 2010; Wang et al. 2010; Balmino et al. 2012). In addition, such an expansion can be used to augment to a global gravity model a much higher resolution of the gravitational potential of topographic masses. The ultra-high frequencies of the gravity field are difficult to get from gravity observations alone due to data coverage and sampling rates. Consequently, the accuracy of gravity modeling could benefit from such an augmentation. An example of such a useful augmentation is the “Helmertization” of EGM2008, which is necessary when the full power of EGM2008 is used as a reference model in the Helmert’s second condensation method for geoid computation (Wang et al. 2012). A unique advantage of the harmonic analysis over numerical integration is the fact that it could be done globally, once and for all, using a widely accepted digital elevation model (DEM) such as the Shuttle Radar Topography Mission (SRTM) (Slater et al. 2006). What remains for the user to do for his/her own local area and application is to synthesize the required quantity using the coefficients of the harmonic expansion and a synthesis program disseminated with those coefficients.

Recent topographic expansions were developed using various approximations, namely the spherical approximation and a Taylor expansion that retains only a few terms (cf., Novák 2010; Wang et al. 2012; Balmino et al. 2012). The goal of this paper is to expand the gravitational potential of the topographic masses in the most accurate way, avoiding all approximations.

It is well known that several numerical difficulties arise in the computation of high-degree spherical harmonic expansions (Holmes and Featherstone 2002; Jekeli et al. 2007; Fukushima 2012). An additional difficulty, which is often ignored in these studies, is the downward continuation effect on ultra-high-degree spherical harmonic series in regions of high latitude. More specifically, the popular expression of spherical harmonic series, such as Eq. (1) in Pavlis et al. (2012) represents a spherical harmonic series expanded around a bounding sphere of radius $a$, usually taken as the semi-major axis of the reference ellipsoid. Because high-latitude areas, including the Polar Regions, can reach 21 km below the surface of this sphere, evaluation of the series in those areas implicitly uses downward continuation. Since the downward continuation effect increases exponentially with increasing frequency, errors in the coefficients are amplified exponentially with the downward continuation. In order to avoid the upward/downward continuation between the bounding sphere and the reference ellipsoid, we explore the spheroidal harmonic expansion of the topography later in this paper.

Since the gravitational potential of the topographic masses is needed on the geoid, which is partially inside the topography, for computing the indirect effect and the geoid–quasigeoid separation (e.g., Flury and Rummel 2009), formulas for the interior space are also given in this paper.

Formulation of the spherical harmonic expansion is given in Sect. 2 and a numerical realization of such an expansion to degree and order 2700 is presented in Sect. 4. The topographic effect on geoid heights is computed at sea level to demonstrate the numerical problem caused by downward continuation from the bounding sphere to the ellipsoid. To expand the gravitational potential of the topographic masses rigorously avoiding the above-mentioned downward continuation, the spheroidal harmonic expansion is introduced in Sect. 3. To facilitate the efficient numerical computation of spheroidal coefficients, the computation formulas for spheroidal harmonic expansion are reduced from solid to surface harmonic analysis using Laurent’s series of the Legendre functions. Detailed equations for expanding Legendre’s functions of the first and second kinds in Laurent series are given in the Appendix. Subsequently, the series are scaled in two real functions that have the radial component of the spherical harmonic expansion as their principal term. Higher order terms (which represent the ellipsoidal correction to the topographic potential) contain powers of the second eccentricity of the reference ellipsoid. Section 5 shows a numerical example of the spheroidal harmonic expansion to degree and order 180. A discussion and conclusions are given in Sect. 6.

2 The spherical harmonic expansion

The Earth’s surface is defined as the outermost level of the land and sea. The topography is defined as the land masses above a reference surface, such as the geoid or the reference ellipsoid. We use the latter in this paper. The height of the ocean surface is defined as zero, although the oceans are considered as mass deficiency areas in isostatic studies. Since the mass deficiency and isostatic masses can be treated in the same way as the topographic masses, they can be added separately (e.g., Novák 2010). In this paper, we only focus on the topographic masses.

Formulas of the spherical harmonic expansion of the gravitational potential of the topographic masses under the spherical approximation and Taylor expansion are abundant in the literature (e.g. Sjöberg 1977; Rummel et al. 1988; Wang 1997; Novák 2010; Wang et al. 2012). In this section, we derive formulas for spherical harmonic expansion without the spherical approximation and the use of a Taylor expansion.

The gravitational potential of the topography, $V_t$, at any given point, $P$, can be expressed in spherical coordinates by Newton’s integral

$$\begin{aligned} V_t (r_P ,\mathbf{x}_P )=G\int \int \limits _\sigma {\int _{r_E }^{r_S } {\frac{\rho }{l}} r^{2}}\,\mathrm{d}r\,\mathrm{d}\sigma , \end{aligned}$$

(1)

where $G$ is Newton’s gravitational constant; $r_P$ is the radial distance to the point $P, \mathbf{x}_P$ denotes the surface coordinate pair ($\theta , \lambda$), where $\theta$ is the polar distance, and $\lambda$ is the geocentric longitude, $r_S$ and $r_E$ are the radial distances to points on the Earth’s surface $S$ and the reference ellipsoid $E$, respectively; $l$ is the distance between the computation point $P$ and the integration element:

$$\begin{aligned} l=\sqrt{r^{2}-2rr_P \cos \psi +r_P^2} \end{aligned}$$

(2)

where $\psi$ is the angular distance between the radius vectors $r$ and $r_P ; \rho$ is the density of the topographic masses and assumed to be independent of the radial variable $r$.

Using the spherical harmonic expansion of the reciprocal distance (Heiskanen and Moritz 1967, p 33), Eq. (1) can be written separately as

$$\begin{aligned} V_t^e&= \frac{G}{r_P }\sum _{n=0}^\infty {\int \int \limits _\sigma {\rho P_n (\psi )\int _{r_E }^{r_S } {\left( \frac{r}{r_P }\right) ^{n}r^{2}\,\mathrm{d}r} \,\mathrm{d}\sigma }}\end{aligned}$$

(3)

$$\begin{aligned} V_t^i&= \frac{G}{r_P }\sum _{n=0}^\infty {\int \int \limits _\sigma {\rho P_n (\psi )\int _{r_E }^{r_S } {\left( \frac{r_P }{r}\right) ^{n+1}r^{2}\,\mathrm{d}r} \,\mathrm{d}\sigma }} \end{aligned}$$

(4)

where $P_n$ is the Legendre polynomials and the subscripts “$e$” and “$i$” denote the potentials of the exterior and interior spaces. In this paper, we simply define the exterior and interior spaces as the points just above and just inside the Earth’s physical surface, respectively. It is well known that the series in Eq. (3) is convergent at points with radial distance $r_p \ge R_B$, where $R_B =\max (r_S )$, the radius of the Brillouin sphere (Moritz 1980). The convergence of the spherical harmonic series (3) on the Earth’s surface has been the subject of an extensive discussion (Moritz 1961; Cook 1967; Morrison 1969; Levallois 1973; Arnold 1978; Arnorld 1980; Sjöberg 1977, 1980; Jekeli 1981; Wang 1997). The use of this series for computations on the Earth’s surface or geoid is supported by Runge’s theorem (Moritz 1980; Wang 1997). But, we should keep in mind that the harmonic downward continuation is an ill-posed problem. The use of Eq. (3) on the Earth’s surface or sea level is highly unstable at ultra-high degrees. As mentioned before, the high-frequency errors are amplified exponentially in this process.

We assume that the density of the topography is a function of the latitude and longitude only in this study. Thus, the integrals in (3) and (4) can be evaluated with respect to $r$ (e.g., Sjöberg 1977). We denote

$$\begin{aligned} I_n^e (\mathbf{x})&= \int _{r_E }^{r_S } {r^{n+2}\,\mathrm{d}r} =\frac{1}{n+3}(r_S^{n+3} -r_E^{n+3})\end{aligned}$$

(5)

$$\begin{aligned} I_n^i (\mathbf{x})&= \int _{r_E }^{r_S } {r^{-(n-1)}\,\mathrm{d}r}\nonumber \\&= \left\{ {{\begin{array}{ll} {\frac{1}{n-2}\left( \frac{1}{r_E^{n-2} }-\frac{1}{r_S^{n-2} }\right) }&{} {n\ne 2}\\ {\ln (r_S /r_E )}&{} {n=2} \\ \end{array}}}\right. \end{aligned}$$

(6)

The integrands (5) and (6) are functions of the radial distance of the reference ellipsoid and the Earth’s surface; both can be computed rigorously by (Torge 1980, p. 52):

$$\begin{aligned} r_E&= N\sqrt{\cos ^{2}\phi +(1-e^{2})^{2}\sin ^{2}\phi }\nonumber \\ r_S&= \sqrt{(N+h)^{2}\cos ^{2}\phi +[(1-e^{2})N+h]^{2}\sin ^{2}\phi }\nonumber \\ N&= \frac{a}{\sqrt{1-e^{2}\sin ^{2}\phi }} \end{aligned}$$

(7)

where $a$ is the semi major axis of the reference ellipsoid, $N$ is the radius of curvature of the reference ellipsoid, $e$ is the first eccentricity of the reference ellipsoid, $h$ is the ellipsoidal height of the topography, and $\phi$ is the geographic (geodetic) latitude.

Replacing the radial integrals in (3) and (4) by (5) and (6) leads to

$$\begin{aligned} V_t^e (r_P ,\mathbf{x}_P )&= G\sum _{n=0}^\infty {\frac{1}{r_P^{n+1}}\int \int \limits _\sigma {\rho I_n^e P_n (\cos \psi )\,\mathrm{d}\sigma }}\end{aligned}$$

(8)

$$\begin{aligned} V_t^i (r_P ,\mathbf{x}_P )&= G\sum _{n=0}^\infty {r_P^{n+1} \int \int \limits _\sigma {\rho I_n^i P_n (\cos \psi )\,\mathrm{d}\sigma }} \end{aligned}$$

(9)

Using the decomposition formula (Heiskanen and Moritz 1967, p. 33), the potentials represented by (8) and (9) can be written in a form for easy use of existing software:

$$\begin{aligned} V_t^e (r_P ,\mathbf{x}_P )&= \frac{GM}{r_P }\sum _{n=0}^\infty {\left( \frac{a}{r_P }\right) ^{n}}\nonumber \\&\times {\sum _{m=0}^{n}{[a_{nm}\,\overline{R}_{nm} (\mathbf{x}_P )+}}b_{nm}\,\overline{S}_{nm} (\mathbf{x}_P)]\end{aligned}$$

(10)

$$\begin{aligned} V_t^i (r_P ,\mathbf{x}_P )&= \frac{GM}{r_P }\sum _{n=0}^\infty {\left( \frac{r_P }{a}\right) ^{n+1}}\nonumber \\&\times {\sum _{m=0}^n {[c_{nm}\, \overline{R}_{nm} (\mathbf{x}_P )+} } d_{nm}\, \overline{S}_{nm} (\mathbf{x}_P )] \end{aligned}$$

(11)

where $\overline{R}_{nm}$ and $\overline{S}_{nm}$ are the fully normalized surface spherical harmonic functions, $M$ is the total mass of the Earth, and the coefficients $a_{nm}$ and $b_{nm}$ can be computed by the following equation:

$$\begin{aligned} \left( {{\begin{array}{l} {a_{nm} } \\ {b_{nm} } \\ \end{array}}}\right)&= \frac{1}{(2n+1)M}\int \int \limits _\sigma {\rho \frac{I_n^e (\mathbf{x})}{a^{n}}} \left( {{\begin{array}{l} {\overline{R}_{nm} (\mathbf{x})} \\ {\overline{S}_{nm} (\mathbf{x})} \\ \end{array} }} \right) \,\mathrm{d}\sigma \nonumber \\&= \frac{a^{3}}{(2n+1)(n+3)M}\int \int \limits _\sigma {\rho \left( \frac{r_E }{a}\right) ^{n+3}}\nonumber \\&\times {\left[ \left( \frac{r_S }{r_E }\right) ^{n+3}-1\right] } \left( {{\begin{array}{l} {\overline{R}_{nm} } \\ {\overline{S}_{nm} } \\ \end{array} }} \right) \,\mathrm{d}\sigma \end{aligned}$$

(12)

The coefficients $c_{nm}$ and $d_{nm}$ ($n\ne 2)$ are computed by:

$$\begin{aligned} \left( {{\begin{array}{l} {c_{nm} } \\ {d_{nm} } \\ \end{array}}}\right)&= \frac{1}{(2n+1)M}\int \int \limits _\sigma {\rho a^{n+1}I_n^i } (\mathbf{x})\left( {{\begin{array}{l} {\overline{R}_{nm} (\mathbf{x})}\\ {\overline{S}_{nm} (\mathbf{x})}\\ \end{array} }} \right) \,\mathrm{d}\sigma \nonumber \\&= \frac{a^{3}}{(2n+1)(n-2)M}\int \int \limits _\sigma {\rho \left( \frac{a}{r_E }\right) ^{n-2}}\nonumber \\&\times {\left[ 1-\left( \frac{r_E }{r_S }\right) ^{n-2}\right] } \left( {{\begin{array}{l} {\overline{R}_{nm} } \\ {\overline{S}_{nm} } \\ \end{array} }} \right) \,\mathrm{d}\sigma \end{aligned}$$

(13)

For $n=2$, the coefficients are computed by

$$\begin{aligned} \left( {{\begin{array}{l} {c_{2m}} \\ {d_{2m}} \\ \end{array}}} \right) = \frac{a^{3}}{5M}\int \int \limits _\sigma {\rho \ln \frac{r_S }{r_E }} \left( {{\begin{array}{l} {\overline{R}_{nm} (\mathbf{x})} \\ {\overline{S}_{nm} (\mathbf{x})} \\ \end{array} }} \right) \,\mathrm{d}\sigma \end{aligned}$$

(14)

The coefficients $a_{nm} , b_{nm} , c_{nm}$ and $d_{nm}$, defined by (12—14), can be computed using numerical quadrature to the desired degrees and orders.

3 The spheroidal harmonic expansion

The reference ellipsoid is closer to the Earth’s shape than the sphere of the mean Earth. Thus, it is useful to expand the gravitational potential of the topographic masses in spheroidal harmonics which are eigenfunctions of the Laplace operator in space bordered by an ellipsoid of revolution (or spheroid). The spheroidal coordinates $u, \vartheta ,\lambda$ are related to the rectangular coordinates $x, y, z$ by (Heiskanen and Moritz 1967, p. 40):

$$\begin{aligned} x&= \sqrt{u^{2}+E^{2}}\sin \vartheta \cos \lambda \nonumber \\ y&= \sqrt{u^{2}+E^{2}}\sin \vartheta \sin \lambda \nonumber \\ z&= u\cos \vartheta \end{aligned}$$

(15)

where $E^{2}=a^{2}-b^{2}$ is the linear eccentricity, $b$ is the semi-minor axis of the reference ellipsoid and $\vartheta$ is the complement of the reduced latitude $\beta$. In spheroidal coordinates, Newton’s integral reads

$$\begin{aligned} V_t =G\int \int \limits _\sigma {\int _b^{b+h} {\frac{\rho }{l}\,\mathrm{d}\upsilon }}, \end{aligned}$$

(16)

where $h$ is the increment of the variable $u$ relative to the reference ellipsoid, which can be approximated by the ellipsoidal height in numerical computations, $\mathrm{d}\upsilon$ is the volume element given by (ibid., p.41)

$$\begin{aligned} \mathrm{d}\upsilon&= h_1 h_2 h_3 \,\mathrm{d}u\,\mathrm{d}\vartheta \,\mathrm{d}\lambda \nonumber \\&= (u^{2}+E^{2}\cos ^{2}\vartheta )\sin \vartheta \,\mathrm{d}u\,\mathrm{d}\vartheta \,\mathrm{d}\lambda \end{aligned}$$

(17)

The spheroidal harmonic expansion of the reciprocal distance can be found in Hobson (1931), Baranov (2004) and Pohanka (1999, 2011). For $u_P >u$, it reads

$$\begin{aligned} \frac{1}{l}&= \frac{i}{E}\sum _{n=0}^\infty {\sum _{m=-n}^n {(-1)^{m}\frac{(n-| m |)!}{(n+| m |)!}} } P_{n| m |} \left( i\frac{u}{E}\right) \nonumber \\&\times Q_{n| m |} \left( i\frac{u_P}{E}\right) Y_{nm} (\mathbf{x})Y_{nm}^*(\mathbf{x}_P ), \end{aligned}$$

(18)

and for $u_P <u$ it is

$$\begin{aligned} \frac{1}{l}&= \frac{i}{E}\sum _{n=0}^\infty {\sum _{m=-n}^n {(-1)^{m}\frac{(n-| m)!}{(n+| m |)!}}} P_{n| m |} \left( i\frac{u_P }{E}\right) \nonumber \\&\times Q_{n|m|} \left( i\frac{u}{E}\right) Y_{nm} (\mathbf{x})Y_{nm}^{*} (\mathbf{x}_P), \end{aligned}$$

(19)

where

$$\begin{aligned} Y_{nm} (\mathbf{x})=\sqrt{(2n+1)\frac{(n-| m |)!}{(n+| m |)!}}P_{n| m |} (\cos \vartheta )e^{im\lambda }, \end{aligned}$$

(20)

and $Y_{nm}^*$ is its conjugate, x denotes the surface variable pair $(\vartheta , \lambda ),i=\sqrt{-1}$, and $Q_{nm}$ is Legendre’s function of the second kind.

Our applications require only real-valued spherical harmonics. The real basis of the surface harmonics is related to the complex one by

$$\begin{aligned} Y_{nm} (\mathbf{x})=\left\{ {{\begin{array}{l@{\qquad }l} {\frac{1}{\sqrt{2}}(Y_{nm} +Y_{nm}^*)=\overline{R}_{nm} }&{} {m>0} \\ {Y_{n0} =\overline{R}_{n0} }&{} {m=0} \\ {\frac{1}{\sqrt{2}}(Y_{nm} -Y_{nm}^*)=\overline{S}_{n| m |} }&{} {m<0} \\ \end{array}}} \right. \end{aligned}$$

(21)

Notice that we have used the same notation for the surface harmonics in the complex and real form. In the rest of this paper, we only use the real form.

Substituting the complex surface harmonics in (18) and (19) with the real basis (21) gives

$$\begin{aligned} \frac{1}{l}&= \frac{i}{E}\sum _{n=0}^\infty {\sum _{m=0}^n {(-1)^{m}\frac{(n-m)!}{(n+m)!}} } P_{nm} \left( i\frac{u}{E}\right) \nonumber \\&\times Q_{nm} \left( i\frac{u_P }{E}\right) \overline{Y}_{nm} (\mathbf{x},\mathbf{x}_P )\quad u_P>u\end{aligned}$$

(22)

$$\begin{aligned} \frac{1}{l}&= \frac{i}{E}\sum _{n=0}^\infty {\sum _{m=0}^n {(-1)^{m}\frac{(n-m)!}{(n+m)!}} } P_{nm} \left( i\frac{u_P }{E}\right) \nonumber \\&\times Q_{nm} \left( i\frac{u}{E}\right) \overline{Y}_{nm} (\mathbf{x},\mathbf{x}_P ) \quad u_P <u \end{aligned}$$

(23)

where

$$\begin{aligned} \overline{Y}_{nm} (\mathbf{x},\mathbf{x}_P )=\overline{R}_{nm} (\mathbf{x})\overline{R}_{nm} (\mathbf{x}_P )+\overline{S}_{nm} (\mathbf{x})\overline{S}_{nm} (\mathbf{x}_P ) \end{aligned}$$

(24)

To avoid unnecessary imaginary operations, Legendre’s functions with imaginary variables in the above equations can be replaced by two real functions $p_{nm}$ and $q_{nm}$ defined by (65) and (66) in the Appendix. Equations (22) and (23) are then simplified to

$$\begin{aligned} \frac{1}{l}&= \frac{1}{b}\sum _{n=0}^\infty {\frac{1}{2n+1}\sum _{m=0}^n {p_{nm} } } (u)q_{nm} (u_P )\overline{Y}_{nm} (\mathbf{x},\mathbf{x}_P ) \quad u_P >u\end{aligned}$$

(25)

$$\begin{aligned} \frac{1}{l}&= \frac{1}{b}\sum _{n=0}^\infty {\frac{1}{2n+1}\sum _{m=0}^n {p_{nm} } } (u_P )q_{nm} (u)\overline{Y}_{nm} (\mathbf{x},\mathbf{x}_P ) \quad u_P <u \end{aligned}$$

(26)

The function $p_{nm}$ and $q_{nm}$ represent the radial components of the spheroidal expansion and therefore will hereafter be called “the radial functions”.

Equations (25) and (26) look quite different than their spherical harmonic counterparts (Heiskanen and Moritz 1967, p 33), but they should be very closely related to them. The difference is characterized by the eccentricity, $\varepsilon$, of the reference ellipsoid. From the definition of the radial functions (65) and (66), one can see that the principal term of the radial component in (25) is $(u/b)^{n}(b/u_P )^{n+1}/b=u^{n}/u_P^{n+1}$, which is exactly the radial component of the spherical harmonic expansion. It is easy to show that the radial component in (26) reduces to the spherical harmonic expansion for $u_P <u$, or $r_P <r$ when $\varepsilon \rightarrow 0$.

Inserting (25) and (26) into (16), the gravitational potential of the topographic masses is expanded in spheroidal harmonic series as follows:

$$\begin{aligned} V^{e}(u_P,\mathbf{x}_P)&= \sum _{n=0}^\infty {\sum _{m=0}^n {\frac{q_{nm} (u_P )}{q_{nm} (b)}} }\nonumber \\&\times [\alpha _{nm}\, \overline{R}_{nm} (\mathbf{x}_P )+\beta _{nm}\,\overline{S}_{nm} (\mathbf{x}_P )]\end{aligned}$$

(27)

$$\begin{aligned} V^{i}(u_P,\mathbf{x}_P )&= \sum _{n=0}^\infty {\sum _{m=0}^n {\frac{p_{nm} (u_P )}{p_{nm} (b)}} }\nonumber \\&\times [\mu _{nm}\, \overline{R}_{nm} (\mathbf{x}_P )+\nu _{nm}\,\overline{S}_{nm} (\mathbf{x}_P )] \end{aligned}$$

(28)

The division by the constant factors $q_{nm} (b)$ and $p_{nm} (b)$ in (27) and (28) ensures that, on the ellipsoid, these equations reduce to

$$\begin{aligned} \begin{aligned} V^{e}(\mathbf{x}_P )&= \sum _{n=0}^\infty {\sum _{m=0}^n [\alpha _{nm}}\, \overline{R}_{nm} (\mathbf{x}_P )+\beta _{nm}\,\overline{S}_{nm} (\mathbf{x}_P )]\\ V^{i}(\mathbf{x}_P )&= \sum _{n=0}^\infty {\sum _{m=0}^n {[\mu _{nm}}}\, \overline{R}_{nm} (\mathbf{x}_P )+\nu _{nm}\,\overline{S}_{nm} (\mathbf{x}_P )] \end{aligned} \end{aligned}$$

(29)

The spheroidal harmonic coefficients are computed by

$$\begin{aligned} \left( {{\begin{array}{l} {\alpha _{nm} } \\ {\beta _{nm} } \\ \end{array}}}\right)&= \frac{p_{nm} (b)}{2n+1}G\int \int \limits _\sigma {\rho I_{nm}^e (\mathbf{x})\left( {{\begin{array}{l} {\overline{R}_{nm} (\mathbf{x})} \\ {\overline{S}_{nm} (\mathbf{x})} \\ \end{array} }} \right) \,\mathrm{d}\sigma }\end{aligned}$$

(30)

$$\begin{aligned} \left( {{\begin{array}{l} {\mu _{nm} } \\ {v_{nm} } \\ \end{array}}} \right)&= \frac{q_{nm} (b)}{2n+1}G\int \int \limits _\sigma {\rho I_{nm}^i (\mathbf{x})\left( {{\begin{array}{l} {\overline{R}_{nm} (\mathbf{x})} \\ {\overline{S}_{nm} (\mathbf{x})} \\ \end{array} }} \right) \,\mathrm{d}\sigma } \end{aligned}$$

(31)

where

$$\begin{aligned} I_{nm}^e (\mathbf{x})&= \frac{1}{b}\int _b^{b+h} {p_{nm} (u)} (u^{2}+E^{2}\cos ^{2}\vartheta )\,\mathrm{d}u\nonumber \\ I_{nm}^i (\mathbf{x})&= \frac{1}{b}\int _b^{b+h} {q_{nm} (u)} (u^{2}+E^{2}\cos ^{2}\vartheta )\,\mathrm{d}u\end{aligned}$$

(32)

$$\begin{aligned} \mathrm{d}\sigma&= \sin \vartheta \,\mathrm{d}\vartheta \,\mathrm{d}\lambda \end{aligned}$$

(33)

Now let us analytically integrate the right side of (32). We introduce a general integral function for all positive and negative integers $n$ as

$$\begin{aligned} I(n,x)\!=\!\frac{1}{b}\int _b^{b+h} {\left( \frac{u}{b}\right) ^{n}\,\mathrm{d}u\!=\!} \left\{ {{\begin{array}{ll} {\frac{1}{n+1}(x^{n+1}-1)}&{} {n\ne -1} \\ {\ln x}&{} {n=-1} \\ \end{array} }} \right. \quad \end{aligned}$$

(34)

where

$$\begin{aligned} x(\mathbf{x})=1+\frac{h}{b} \end{aligned}$$

(35)

Using Eqs. (65), (66) and (34), the integrals in (32) can be expressed in terms of the integral function $I$ as

$$\begin{aligned} I_{nm}^e (\mathbf{x})&= b^{2}\sum _{k=0}^\infty {\varepsilon ^{2k}c_k^{nm}}[I(n-2k+2,x)\nonumber \\&+\,\,\varepsilon ^{2}I(n-2k,x)\cos ^{2}\vartheta ]\nonumber \\&= b^{2}I(n+2,x)+b^{2}\sum _{k=1}^\infty \varepsilon ^{2k}(c_k^{nm}\nonumber \\&+\,\,c_{k-1}^{nm} \cos ^{2}\vartheta ) I(n-2k+2,x)\end{aligned}$$

(36)

$$\begin{aligned} I_{nm}^i (\mathbf{x})&= b^{2}\sum _{k=0}^\infty {(-1)^{k}\varepsilon ^{2k}d_k^{nm} } [I(-n-2k+1,x)\nonumber \\&+\,\,\varepsilon ^{2}I(-n-2k-1,x)\cos ^{2}\vartheta ]\nonumber \\&= b^{2}I(-n+1,x)+b^{2}\sum _{k=1}^\infty {(-1)^{k}}\nonumber \\&\times \varepsilon ^{2k}(d_k^{nm} -d_{k-1}^{nm} \cos ^{2}\vartheta )I(-n-2k+1,x) \end{aligned}$$

(37)

The zero order terms in (36) and (37) are the same as the expressions of the spherical harmonic expansion under the spherical approximation. The rest of the series is purely due to the eccentricity of the reference ellipsoid, and could be viewed as the ellipsoidal correction to the topographic potential. They decrease by the order of $\varepsilon ^{2}$ from one term to the next. This feature provides a significant numerical advantage: the evaluation of the series in (36) and (37) can be truncated at a certain order, $k$, at which the contribution of ignored terms becomes insignificant or below a specified accuracy requirement.

To evaluate the spheroidal harmonics in (27) and (28), accurate and efficient methods for computing the radial functions are sought. The recurrence relation between the radial functions for different degrees or orders is given in the Appendix and can be used for such computations. The radial function can also be computed using the power series (65) and (66) to a certain power of the second eccentricity of the reference ellipsoid.

Note that the radial functions are scaled Legendre’s functions; thus its computation is directly related to the computation of Legendre’s functions of the first and second kinds. Computation of Legendre’s function of the second kind has been studied extensively (e.g., Thong 1989; Sona 1995; Gil and Segura 1998; Sebera et al. 2012; Fukushima 2013). The same computation mechanism may be extended to the radial functions $p_{nm}$ and $q_{nm}$. In addition, the Laurent series (65) and (66) provide an alternative computation method.

4 Numerical realization of spherical harmonic expansion to degree and order 2700

In this section, we expand the gravitational potential of the topographic masses in spherical harmonics to degree and order 2700, using formulas developed in Sect. 2. The expansion takes advantage of existing software for spherical harmonic analysis.

For this practical exercise, a $1'\times 1'$ mean orthometric elevation grid was created by averaging the SRTM$30''$ Digital Elevation Model (DEM) (Slater et al. 2006). The spheroidal height was obtained by adding EGM96 geoid undulation (Lemoine et al. 1998) to the orthometric height. All $1'\times 1'$ oceanic cells are set to zero elevation. The global mean, RMS and maximum values of the $1'\times 1'$ DEM are 376, 933 and 8,550  m, respectively. For each degree, the integrand (5) and (6) are computed at all nodes of the $1'\times 1'$ grid using Eq. (7), producing a total of 2700 such grids, each for the exterior and interior expansions. The coefficients of the spherical harmonic expansion were obtained by a harmonic analysis of each grid using numerical quadrature. The derived spherical harmonic spectrum extended from $N_\mathrm{min} = 0$ to $N_\mathrm{max} = 2700$. For this calculation, the $1'\times 1'$ DEM was assumed to be equi-angular in geodetic latitude and longitude, where the geodetic coordinates of each $1'\times 1'$ cell are referenced to the surface of an ellipsoid of dimensions:

• Semi-major axis (a) = 6,378,136.3 m

• Semi-minor axis (b) = 6,356,751.55863 m

For the spherical harmonic analysis, each $1'\times 1'$ cell was mapped onto the unit sphere by first taking the geodetic coordinates of each $1'\times 1'$ cell [geodetic latitude, longitude and geodetic height ($H = 0 m$)] and transforming these to geocentric latitude, longitude, and radial distance. The geocentric latitudes and longitudes, so computed, are adopted for the harmonic analysis as the geocentric coordinates on the unit sphere.

The topographic effect on geoid height is computed by

$$\begin{aligned} N_t^e (\mathbf{x}_P)&= \frac{GM}{\gamma r_E }\sum _{n=0}^{2700} {\left( \frac{a}{r_E }\right) ^{n}}\nonumber \\&\times {\sum _{m=0}^n {[a_{nm}\, \overline{R}_{nm} (\mathbf{x}_P )+} } b_{nm}\,\overline{S}_{nm} (\mathbf{x}_P )]\end{aligned}$$

(38)

$$\begin{aligned} N_t^i (\mathbf{x}_P )&= \frac{GM}{\gamma r_E }\sum _{n=0}^{2700} {\left( \frac{r_E }{a}\right) ^{n+1}}\nonumber \\&{\times \sum _{m=0}^n {[c_{nm}\, \overline{R}_{nm} (\mathbf{x}_P )+} } d_{nm}\,\overline{S}_{nm} (\mathbf{x}_P )] \end{aligned}$$

(39)

where $\gamma$ is the normal gravity on the ellipsoid, $N_t^e$ and $N_t^i$ are the contributions of the topographic potential for the exterior and interior spaces, respectively. The radial distance of the reference ellipsoid $r_E$ is computed using Eq. (7).

The topographic effect of Eq. (39) is computed and plotted in Fig. 1.

Fig. 1

Topographic effect on geoid height (max. degree 2700)

Figure 1 shows that the topographic effect on the geoid is directly related to the topographic height. Even if the topography is set to zero over the oceans, the topographic effect is non-zero because the gravity is a long-range force. The minimum occurs in the Pacific Ocean at the furthest point from topographic masses. The topographic effect is roughly one order of magnitude smaller than the topographic elevations, which agrees with the rule of thumb about the relationship between the topographic height and its effect on geoid height.

The topographic effect of Eq. (38) represents the effect of the topography on the geoid height due to the downward continued topographic potential. This effect is similar to Fig. 1 and it is not plotted here. Instead, the difference between the topographic effects represented by (38) and (39) is plotted in Fig. 2.

Fig. 2

Difference between topographic effects on geoid height (downward continued potential–true potential)

The difference is of the order of $h^{2}$ and is the so-called analytical downward continuation error by Sjöberg (1977) and Wang (1997). Figure 2 shows unpleasant track patterns at high latitudes which reach decimeters. It is believed that this is caused by errors in coefficients at high degree and orders which are amplified by the downward continuation of the exterior potential from the bounding sphere to the ellipsoid. Notice that the downward continuation is represented by the factor $(a/r_E )^{n}$ in Eq. (38). The factor changes from 1 at the equator $(r_E =a)$ to $10^{4}$ at the poles $(r_E =b)$ at degree 2700. In other words, the coefficients of degree 2700 are multiplied by 1 at the equator, but by several thousand at high-latitude areas. This numerical feature affects computations in two ways: first, it affects the computations of the coefficients. The factor $(r_E /a)^{n+3}$ in Eq. (12) decreases rapidly from one to zero from the equator to the poles when $n$ is large. This implies that the high-degree coefficients are dominated by the contribution from lower latitude regions and that high-latitude areas have little input. Secondly, this effect is reversed in the use of a coefficients model to compute the gravity field on the Earth’s surface or the ellipsoid: the factor $(a/r_E)^{n}$ increases very fast at higher latitudes for large $n$. The larger the degree $n$, the less stable the computation becomes.

Notice that under the spherical approximation, the height attenuation factor,$(a/r_E )^{n}$, becomes one. Thus, high-degree spherical harmonic models under the spherical approximation (e.g., Novák 2010; Wang et al. 2010) do not suffer from the presence of this height attenuation term. Because of this approximation, the resulting coefficients cannot be directly augmented to global gravity models such as EGM2008. To avoid the spherical approximation, and the upward/downward continuation between the bounding sphere and the ellipsoid, the spheroidal harmonic expansion provides a better alternative.

5 Numerical example of spheroidal expansion to degree and order 180

To demonstrate the feasibility of the spheroidal expansion of the topographic potential, we expand the potential of the topographic masses for the exterior space to degree and order 180. The zero order term is identical to the spherical harmonic expansion under the spherical approximation. The higher order terms are caused by the eccentricity of the reference ellipsoid. Therefore, we hereafter refer to their sum as “the ellipsoidal correction”.

To compute spheroidal harmonic coefficients, the integrand $I_{nm}^e$ needs to be computed globally for each degree $n$ and order $m$; it involves computations of the coefficients $c_k^{nm}$ and the infinite power series of $\varepsilon ^{2}$. The coefficients $c_k^{nm}$ are computed using the recurrence relations (54–56).

To verify the correctness of the formulation of the radial function, $p_{nm} (b)$ is computed using the first 20 terms of (65) and the recurrence relation (71) and (72). The results show that both methods agree almost perfectly up to degree 30. Then the recursion starts diverging afterwards. We find that the recursive computation of $p_{nm}$ over $n$ is stable. The divergence happens in the recursion over large $m$ due to accumulation of the round-off errors. The latter are multiplied by a factor of $2n$ in each iteration in the computation of $p_{nn}$. We solve this problem using a backward recursion instead. In other words, we start the recursion from the initial values of $p_{nn} (b)$ and $p_{n,n-1} (b)$, and compute $p_{nm}$ with decreasing $n$ and $m$.

Using the definitions of $P_{nm} (z)$ in Eqs. (43) and (65), it is easy to show that

$$\begin{aligned} p_{nn} (u)&= \left( \frac{u^{2}}{b^{2}}+\varepsilon ^{2}\right) ^{n/2}\end{aligned}$$

(40)

$$\begin{aligned} p_{n,n-1} (u)&= \frac{u}{\sqrt{u^{2}+E^{2}}}p_{nn} (u) \end{aligned}$$

(41)

On the ellipsoid, we obtain the initial values

$$\begin{aligned} p_{nn} (b)\!=\!(1\!+\!\varepsilon ^{2})^{n/2}\!=\!(a/b)^{n},\quad p_{n,n\!-\!1} (b)\!=\!(a/b)^{n-1}\quad \end{aligned}$$

(42)

Using (42) as initial values, the backward recursion computation of $p_{nm} (b)$ is stable. Figure 3 shows the degree variances computed using the backward recursion and a truncated Laurent series at order 20.

Fig. 3

$p_{nm} (b)$ computed using the backward recursion and the first 20 terms of the Laurent series. Both curves lay on top of each other

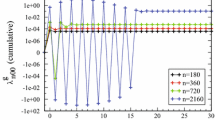
Figure 3 shows very good agreement of the computation methods using the backward recursion and the first 20 terms of the Laurent series. However, some differences do exist. By limiting the upper bound of $k$ in (65), the truncation error is introduced. We use the value computed from the recursion as the true value, the truncation error is then the difference between the true value and the one computed from the truncated Laurent series. The truncation errors are plotted in Fig. 4. In order to get the most significant digits, quadruple-precision floating-point is used in the computations.

Fig. 4

The truncation error in computation of the Laurent series at $k = 4, 8, 20, 50$ and $100$

Figure 4 shows that the errors increase monotonically with degree. If only 4 terms are taken into account, the error reaches $10^{5}$, an order of magnitude smaller than the value of the function. For some unknown reason, the error increases suddenly at degree 600, if only 20 terms are taken in the account. If the first 50–100 terms of the Laurent series are considered, the errors are below $10^{{-}20}$ even at degree 2700, which is sufficient for all practical applications. Notice that the Laurent series have infinite terms when $m$ is an odd number. Figure 4 shows that only the lower-order terms have meaningful value, and it is safe to truncate the series (36) at the eighth order, which contains $\varepsilon ^{16}$, for an expansion to degree and order 180.

Figure 5 shows the ellipsoidal correction to geoid heights. It shows clearly that the ellipsoidal correction is larger in rough mountains, such as the Himalayas and Andes. The maximum correction reaches 13.19 m in Andes (latitude $-27.25^{\circ }$ and longitude $291.5^{\circ }$); the minimum value of $-2.1$ m is located at latitude $6.75^{\circ }$ and longitude $285.75^{\circ }$. Overall, the RMS value of the ellipsoidal correction is 1.65 m for land areas, which is significant for gravity field determination.

Fig. 5

Ellipsoidal correction (to $\varepsilon ^{16}$) to geoid height (max. degree = 180)

The ellipsoidal correction (Fig. 5) resembles the topography closely, implying that it is rich in all wavelengths, not only in the long wavelengths. This fact does not agree with the common assumption that the ellipsoidal correction is only associated with long wavelengths.

Since the series in Eq. (36) is truncated at $k = 8$, we also compute the omission errors (Fig. 6), which are caused by omitting higher terms. Note that the unit is in $10^{{-}9 }$ m, or nm.

Fig. 6

Omission error (contribution of terms above $\varepsilon ^{16}$, max. degree = 180)

This figure shows that the omission errors occur mostly at lower latitudes. The extreme values of the omission error are of the order of 0.5 mm, and the RMS value is merely 25 nm for land areas only. These negligible omission errors imply that the first eight terms of (36) are sufficient for any practical accuracy requirement.

6 Conclusions and discussion

This paper is devoted to the rigorous spherical and spheroidal harmonic expansion of the gravitational potential of the topographic masses. The spherical harmonic expansion is well documented in the literature. It continues to undergo various approximations, e.g., the approximation of the geoid by a sphere of the mean Earth (the spherical approximation), and a truncated Taylor expansion is used for the Earth’s topography. We show that the rigorous spherical harmonic expansion can be accomplished by modifying existing surface harmonic analysis software. The bounding sphere is the surface on which the spherical harmonic analysis is computed. This sphere was also used in the conversion of EGM2008 spheroidal harmonic coefficients to spherical harmonic coefficients (Pavlis et al. 2012). Since areas of high latitudes are far below this sphere, the downward continuation is implicitly used in evaluating the coefficients of the expansion. The higher the latitude and the harmonic degree, the more are existing high-frequency errors magnified in the evaluation of the harmonic coefficients. Consequently, it is difficult to compute the high frequencies of the gravity field accurately. A spherical harmonic expansion to degree and order 2700 shows this problem clearly.

Theoretically, spherical and spheroidal harmonic expressions of the gravitational potential of the topographic masses are equivalent. The transformation between the coefficients of these two kinds of expansions for the exterior space is given by Hotine (1969) and Jekeli (1988). Notice that the up/downward continuation from the bounding sphere to the reference ellipsoid is used in these transformations. On the other hand, spheroidal harmonic expansion avoids the upward/downward continuation between the bounding sphere and the reference ellipsoid. Without those continuations, numerical evaluations should not be prone to errors in high-degree coefficients. This is very important for harmonic expansions of ultra-high degrees and orders. Favoring the spheroidal over spherical harmonic expansion is merely due to numerical computation stability at ultra-high degrees and orders.

The difficulty in the use of the spheroidal harmonic series in practice is due to the computation of Legendre’s functions of the first and second kinds. Efforts on computation methods and software have been made, e.g., Thong (1989), Sona (1995), Gil and Segura (1998), Sebera et al. (2012) and Fukushima (2013). To expand the topographic potential into spheroidal harmonics, not only the computation of Legendre’s functions, but also their integration over the vertical variable, are required. Thus, Legendre’s functions are scaled into two Laurent series $p_{nm}$ and $q_{nm}$. The Laurent series are power series of the second eccentricity of the reference ellipsoid, and have the principal terms $(u/b)^{n}$ and $(b/u)^{n+1}$, similar to its spherical counterparts. Using the Laurent series and under the assumption of only lateral change in density, computations of spheroidal coefficients are reduced to surface harmonic analysis.

To demonstrate the feasibility of the spheroidal expansion, the potential of the topography for the exterior space is expanded to degree and order 180. Since the zero-order term is identical to the spherical harmonic expansion under the spherical approximation, only the ellipsoidal correction to the topographic potential is shown. In the computations, the series (36) is truncated at the eighth order and the omission error is negligible (RMS value of 25 nm with the extreme value of 0.5 mm). The ellipsoidal correction reaches 13.19 m in the Andes, and the RMS value is 1.65 m for land areas. The results show that the ellipsoidal correction resembles the topography closely. This suggests that the correction is rich in all frequencies of the gravity field, not only at long wavelengths as it is commonly assumed.

In the numerical examples we used a constant density of the topography. The formulas developed in this paper were derived under the assumption that the density is independent of the height and changes only laterally. In practical applications, the topography has been categorized in various terrain types, such as sediments, ice cap/snow coverage, lakes and oceans (Lemoine et al. 1998; Pavlis et al. 2012). Each terrain type has its own density specification, generally a constant. Thus they can be expanded into spherical/spheroidal harmonics separately, and added together. Another way to treat the different terrain type is to compute the average density for every vertical column, so that the density of the topography is reduced to a laterally changing function. The formulation in this paper can then be applied.

This paper serves as the first step in the application of spheroidal harmonic expansion to the Earth’s topographic potential. Spheroidal expansions to ultra-high degrees and orders are under development and software for the spheroidal harmonic synthesis, similar to the spherical harmonic synthesis, will become publicly available after those models are completed and tested.

Appendix

Integrating Legendre’s functions of the first and second kinds, $P_{nm}$ and $Q_{nm}$, over variable $u$ can reduce the spheroidal harmonic expansion into two-dimensional surface harmonic analysis. To accomplish this, Legendre’s functions are expanded in Laurent series and then scaled into two real functions as follows.

The Legendre function $P_{nm}$ of the complex variable $z=i\frac{u}{E}$ is defined as (Hobson 1931, p. 91)

$$\begin{aligned} P_{nm} (z)=\frac{1}{2^{n}n!}(z^{2}-1)^{m/2}\frac{\mathrm{d}^{n+m}}{\mathrm{d}z^{n+m}}(z^{2}-1)^{n} \end{aligned}$$

(43)

Expanding $(z^{2}-1)^{n}$ into a binominal series, then differentiating it $n +m$ times, we obtain

$$\begin{aligned} P_{nm} (z)&= \frac{1}{2^{n}n!}(z^{2}\!-\!1)^{m/2}\frac{\mathrm{d}^{n+m}}{\mathrm{d}z^{n+m}}(z^{2}-1)^{n}\nonumber \\&= \frac{1}{2^{n}n!}(z^{2}\!-\!1)^{m/2}\sum _{l=0}^r {(-1)^{l}C_n^l \frac{(2n-2l)!}{(n-m-2l)!}} z^{n-m-2l}\nonumber \\ \end{aligned}$$

(44)

where $r=(n-m)/2$ or $r=(n-m-1)/2$ whichever is an integer, and $C_n^l$ is the binominal coefficient given by

$$\begin{aligned} C_n^l =\frac{n!}{l!(n-l)!} \end{aligned}$$

(45)

Using the binominal expansion

$$\begin{aligned} (z^{2}-1)^{m/2}=z^{m}\left( 1-\frac{1}{z^{2}}\right) ^{m/2}=z^{m}\sum _{k=0}^\infty {(-1)^{k}C_{m/2}^k } z^{-2k}\nonumber \\ \end{aligned}$$

(46)

where

$$\begin{aligned} C_{m/2}^k=\frac{\frac{m}{2}\left( \frac{m}{2}-1\right) \left( \frac{m}{2}-2\right) \cdots \left( \frac{m}{2}-k+1\right) }{k!}, \end{aligned}$$

(47)

gives

$$\begin{aligned} P_{nm} (z)&= \frac{1}{2^{n}n!}\sum _{k=0}^\infty {(-1)^{k}C_{m/2}^k } z^{m-2k}\sum _{l=0}^r {(-1)^{l}C_n^l \frac{(2n-2l)!}{(n-m-2l)!}} z^{n-m-2l}\nonumber \\&= \frac{1}{2^{n}n!}\sum _{k=0}^\infty {\sum _{l=0}^r {(-1)^{l+k}C_{m/2}^k C_n^l \frac{(2n-2l)!}{(n-m-2l)!}} } \frac{(n-m)!}{(2n)!}z^{n-2k-2l}\nonumber \\ \end{aligned}$$

(48)

Note that the power of $z$ is independent of $m$. This reflects the fact that the reference ellipsoid is a spheroid and the function $P_{nm} (z)$ is independent of the longitude. The summation over $k$ is infinite when $m$ is odd. For even values of $m$, the binominal coefficient $C_{m/2}^k$ becomes zero after $k=m/2$, thus the summation over $k$ is only to $k=m/2$.

In order to apply the Cauchy theorem for multiplication of two infinite series, we can define the coefficients above $r$ as zeros and extend the upper limit of the summation over $l$ to infinity. Then Eq. (48) can be abbreviated as

$$\begin{aligned} P_{nm} (z)=k_{nm} \sum _{k=0}^\infty {(-1)^{k}c_k^{nm}\,z^{n-2k}} \end{aligned}$$

(49)

where

$$\begin{aligned} k_{nm} =\frac{(2n)!}{2^{n}n!(n-m)!}, \end{aligned}$$

(50)

and $c_k^{nm}$ is the Cauchy product defined as

$$\begin{aligned} c_k^{nm}&= \sum _{l=t}^k {c_{k,l}^{nm}}\end{aligned}$$

(51)

$$\begin{aligned} c_{k,l}^{nm}&= C_{m/2}^l C_n^{k-l} \frac{(n-m)!}{(2n)!}\frac{[2n-2(k-l)]!}{[n-m-2(k-l)]!} \end{aligned}$$

(52)

The summation of the Cauchy product generally starts from zero while the summation in (51) starts from $t$ defined as

$$\begin{aligned} t=k-r\ge 0 \end{aligned}$$

(53)

since the coefficients below $t$ in (51) are zeros.

As mentioned above, the binominal coefficient $C_{m/2}^l$ is zero for $l\ge t>m/2$ and even values of $m$. In this situation the coefficient $c_{k,l}^{nm}$ becomes zero and the infinite series in (49) is reduced to finite.

The coefficient $c_{k,l}^{nm}$ satisfies the following recurrence relationship:

$$\begin{aligned}&c_{k,l+1}^{nm} \nonumber \\&=\frac{(m-2l)(k-l)(2n-2k+2l+1)}{(l+1)(n-m-2k+2l+1) (n-m-2k+2l+2)}c_{k,l}^{nm}\nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned}&c_{k+1,l}^{nm} =\frac{(n-m-2k+2l-1)(n-m-2k+2l)}{2(k-l+1)(2n-2k+2l-1)}c_{k,l}^{nm}\nonumber \\ \end{aligned}$$

(55)

The initial value (54) can be computed using the following recurrence relation:

$$\begin{aligned} \begin{aligned} c_{0,0}^{nm}&=1 \\ c_{k,0}^{nm}&=\frac{n!(n-m)!}{(2n)!}\frac{(2n-2k)!}{k!(n-k)!(n-m-2k)!}\\ c_{k+1,0}^{nm}&=\frac{(n-m-2k-1)(n-m-2k)}{2(k+1)(2n-2k-1)}c_{k,0}^{nm} \end{aligned} \end{aligned}$$

(56)

The Legendre function $Q_{nm}$ can be expressed in a hypergeometric series as (Hobson 1931, p. 108):

$$\begin{aligned} Q_{nm} (z)&= j_{nm} (z^{2}-1)^{m/2}\frac{1}{z^{n+m+1}}\nonumber \\&\times F\left( \frac{n+m+2}{2}, \frac{n+m+1}{2};n+\frac{3}{2};\frac{1}{z^{2}}\right) \nonumber \\&= j_{nm} (z^{2}-1)^{m/2}\frac{1}{z^{n+m+1}}\sum _{l=0}^\infty {f_l \frac{1}{z^{2l}}}\nonumber \\&= j_{nm} \frac{1}{z^{n+1}}\sum _{k=0}^\infty {\sum _{l=0}^\infty {(-1)^{k}} } C_{m/2}^k f_l \frac{1}{z^{2k+2l}} \end{aligned}$$

(57)

where

$$\begin{aligned} j_{nm}&= (-1)^{m}\frac{2^{n}n!(n+m)!}{(2n+1)!}\end{aligned}$$

(58)

$$\begin{aligned} f_l&= \frac{\left( \frac{n+m+2}{2}\right) _l \left( \frac{n+m+3}{2}\right) _l }{(\frac{2n+3}{2})_l l!} \end{aligned}$$

(59)

The Pochhammer symbol $(n)_l$ in (59) is defined as

$$\begin{aligned} (n)_l =\left\{ \begin{array}{ll} 1&{}\quad {l=0} \\ n(n+1)\cdots (n+l-1)&{}\quad l>0 \\ \end{array}\right. \end{aligned}$$

(60)

It is easy to show that the coefficient $f_l$ satisfies the following recurrence relation:

$$\begin{aligned} f_0&= 1 \nonumber \\ f_{l+1}&= \frac{(n+m+2l+2)(n+m+2l+1)}{2(l+1)(2n+2l+3)}f_l \end{aligned}$$

(61)

Equation (61) is useful for computing the coefficient $f_l$ to $l$th term of the hypergeometric series.

Using the Cauchy product, (57) can be written as

$$\begin{aligned} Q_{nm} (z)=j_{nm} \frac{1}{z^{n+1}}\sum _{k=0}^\infty {d_k^{nm} } \frac{1}{z^{2k}} \end{aligned}$$

(62)

where

$$\begin{aligned} d_k^{nm} =\sum _{l=0}^k {(-1)^{l}C_{m/2}^l\,f_{k-l} } =\sum _{l=0}^k {d_{k,l}^{nm}} \end{aligned}$$

(63)

The coefficient $d_{k,l}^{nm}$ satisfies the following recurrence relation:

$$\begin{aligned}&d_{k,0}^{nm} = f_k \nonumber \\&d_{k,l+1}^{nm}\nonumber \\&= -\frac{(m\!-\!2l)(k-l)(2n\!+\!2k\!-\!2l+1)}{(l\!+\!1) (n\!+\!m\!+\!2k-2l)(n+m+2k-2l-1)}d_{k,l}^{nm}\nonumber \\ \end{aligned}$$

(64)

The coefficient $f_k$ can be computed using the recurrence relation (61). Since $d_{k,0}^{nm}$ never becomes zero for every $k$, the series in (63) is an infinite series.

Now we substitute $z=i\frac{u}{E}$ in (49) and (62), and introduce two real functions by scaling the Legendre functions $P_{nm}$ and $Q_{nm}$ in such a way that the series are power series of $\varepsilon ^{2}$:

$$\begin{aligned} p_{nm} (u)&= \frac{1}{i^{n}k_{nm} }\varepsilon ^{n}P_{nm} \left( i\frac{u}{E}\right) =\sum _{k=0}^\infty {\varepsilon ^{2k}c_k^{nm} } \left( \frac{u}{b}\right) ^{n-2k}\end{aligned}$$

(65)

$$\begin{aligned} q_{nm} (u)&= \frac{i^{n+1}}{j_{nm} \varepsilon ^{n+1}}Q_{nm} \left( i\frac{u}{E}\right) \nonumber \\&= \sum _{k=0}^\infty {(-1)^{k}\varepsilon ^{2k}d_k^{nm}}\times \left( \frac{b}{u}\right) ^{n+2k+1} \end{aligned}$$

(66)

where $\varepsilon =E/b$, the second eccentricity of the reference ellipsoid.

On the ellipsoid, the radial functions are reduced to

$$\begin{aligned} p_{nm} (b)&= \sum _{k=0}^\infty {\varepsilon ^{2k}c_k^{nm} } =1+O(\varepsilon ^{2})\end{aligned}$$

(67)

$$\begin{aligned} q_{nm} (b)&= \sum _{k=0}^\infty {(-1)^{k}\varepsilon ^{2k}d_k^{nm} } =1+O(\varepsilon ^{2}) \end{aligned}$$

(68)

where $O(\varepsilon ^{2})$ denotes terms with powers of $\varepsilon ^{2}$.

The radial functions are scaled Legendre’s functions, thus they should satisfy the recurrence relations of Legendre’s functions. For different $n$, the recurrence relations of Legendre’s functions are (Hobson 1931, p. 290)

$$\begin{aligned} \left\{ \begin{array}{l} (2n+1)zP_{nm} (z)-(n-m+1)P_{n+1,m}(z)\\ \,\,\,-(n+m)P_{n-1,m} (z)=0 \\ (2n+1)zQ_{nm} (u)-(n-m+1)Q_{n+1,m} (u)\\ \,\,\,-(n+m)Q_{n-1,m} (u)=0 \\ \end{array}\right. \end{aligned}$$

(69)

For different $m$:

$$\begin{aligned} \left\{ \begin{array}{l} P_{n,m+2} (z)+2(m+1)\frac{z}{\sqrt{z^{2}-1}}P_{n,m+1} (z)\\ \,\,\,-(n-m)(n+m+1)P_{nm} (z)=0 \\ Q_{n,m+2} (z)+2(m+1)\frac{z}{\sqrt{z^{2}-1}}Q_{n,m+1} (z)\\ \,\,\,-(n-m)(n+m+1)Q_{nm} (z)=0 \\ \end{array}\right. \end{aligned}$$

(70)

Using the relationship between the Legendre functions $P_{nm}$ and $Q_{nm}$, we obtain the recurrence relation of the radial functions for different $n$:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{u}{b}p_{nm} (u)-p_{n+1,m} (u)+\varepsilon ^{2}\frac{n^{2}-m^{2}}{4n^{2}-1}p_{n-1,m} (u)=0 \\ \frac{u}{b}q_{nm} (u)+\frac{(n+m+1)(n-m+1)}{(2n+1)(2n+3)}\varepsilon ^{2}q_{n+1,m} (u)\\ \,\,\,-q_{n-1,m} (u)=0 \\ \end{array}\right. \end{aligned}$$

(71)

For different $m$, the recurrence relation is given by

$$\begin{aligned} \left\{ \begin{array}{l} {p_{n,m+2}(u)+\frac{2(m+1)}{n-m-1}\frac{u}{\sqrt{u^{2}+E^{2}}}p_{n,m+1}(u)}\\ \,\,\,{-\frac{n+m+1}{n-m-1}p_{nm} (u)=0} \\ {q_{n,m+2}(u)-\frac{2(m+1)}{n+m+2}\frac{u}{\sqrt{u^{2}+E^{2}}}q_{n,m+1}(u)}\\ \,\,\,{-\frac{n-m}{n+m+2}q_{nm} (u)=0} \\ \end{array}\right. \end{aligned}$$

(72)

Based on (71), one can see that the function $p_{nm}$ can be computed in forward recurrence. However, it is difficult to do the same for $q_{n+1,m}$ since the computation of the latter involves the difference of similar quantities ($q_{n-1,m} -(u/b)q_{nm} )$ divided by the small number $\varepsilon ^{2}$, which is unstable numerically. This agrees with Gil and Segura’s (1998) assessment, and they use backward recurrence relation to compute $Q_{nm}$. The quantity $q_{n+1,m}$ can be computed in the same way.

The initial values of $p_{nm}$ and $q_{nm}$ to degree and order 1 are needed for the above recurrence computation and are shown in the rest of this Appendix. Degree and order 2 are included also and can be used for the verification of the recurrence relations.

Using the definition of $P_{nm}$ (44) and $p_{nm}$ (67), we get

$$\begin{aligned} \begin{aligned} P_{00} (u)&=1, \quad \qquad \qquad \qquad P_{10} (u)=\frac{u}{b},\\ P_{11} (u)&=\frac{1}{b}\sqrt{u^{2}+E^{2}}, \quad P_{20} (u)=\left( \frac{u}{b}\right) ^{2}+\frac{\varepsilon ^{2}}{3},\\ P_{21} (u)&=\frac{u}{b^{2}}\sqrt{u^{2}+E^{2}}, \quad P_{22} (u)=\frac{1}{b^{2}}(u^{2}+E^{2}). \end{aligned} \end{aligned}$$

(73)

The close form of $Q_{nm}$ to degree and order 4 can be found in (Suschowk 1959). Using the definition of $q_{nm}$ in (66), we list the function to degree and order 2 as follows:

$$\begin{aligned} q_{00} (u)&= \frac{1}{\varepsilon }\tau _R , \quad \qquad \qquad \qquad \qquad q_{10} (u)=-\frac{3}{\varepsilon ^{2}}\left( \frac{u}{E}\tau _R -1\right) ,\nonumber \\ q_{11} (u)&= \frac{3}{2\kappa \varepsilon ^{2}}\left( \kappa ^{2}\tau _R -\frac{u}{E}\right) , \quad q_{20} (u)\!=\!\frac{15}{4\varepsilon ^{3}}\left[ \left( 1\!+\!3\frac{u^{2}}{E^{2}}\right) \tau _R \!-\!3\frac{u}{E}\right] ,\nonumber \\ q_{21} (u)&= -\frac{5}{2\kappa \varepsilon ^{3}}\left( 3\frac{u}{E}\kappa ^{2}\tau _R -3\frac{u^{2}}{E^{2}}-2\right) ,\nonumber \\ q_{22} (u)&= \frac{5}{8\kappa ^{2}\varepsilon ^{3}}\left( 3\kappa ^{4}\tau _R -3\frac{u^{3}}{E^{3}}-5\frac{u}{E}\right) . \end{aligned}$$

(74)

where

$$\begin{aligned} \kappa =\frac{\sqrt{u^{2}+E^{2}}}{E}, \tau _R =\tan ^{-1}\frac{E}{u} \end{aligned}$$

(75)