Reverse selective obnoxious center location problems on tree graphs

Abstract

In this paper, we investigate a variant of the reverse obnoxious center location problem on a tree graph $T=(V,E)$ in which a selective subset of the vertex set V is considered as locations of the existing customers. The aim is to augment or reduce the edge lengths within a given budget with respect to modification bounds until a predetermined undesirable facility location becomes as far as possible from the customer points under the new edge lengths. An ${\mathcal {O}}(|E|^2)$ time combinatorial algorithm is developed for the problem with arbitrary modification costs. For the uniform-cost case, one obtains the improved ${\mathcal {O}}(|E|)$ time complexity. Moreover, optimal solution algorithms with ${\mathcal {O}}(|E|^2)$ and ${\mathcal {O}}(|E|)$ time complexities are proposed for the integer version of the problem with arbitrary and uniform cost coefficients, respectively.

1 Introduction

Location problems have always attracted considerable attention in operations research due to their wide range of applications in the real world. In a location problem, one is interested in locating one or more facilities on a system (graph or d-dimensional real space) in order to serve a given set of customers in an optimal way. For a detailed survey on classical location problems, the interested reader is referred to Mirchandani and Francis (1990), Zanjirani and Hekmatfar (2009), Cappanera et al. (2003), and Eiselt (2011). Two well-known models in location theory are the center problem and the obnoxious center problem. Whereas the goal of the center problem is to determine the best locations for facilities to minimize the maximum distance from the customers to the nearest facility, the obnoxious center problem asks to obtain the best locations of some (undesirable) facilities such that the minimum distance between customers and the closest facility is maximized. Center location problems arise in locating the desirable facilities such as fire stations, hospitals, police offices and etc. However, examples of obnoxious center problems include locating military installations, garbage dump sites, mega-airports, oil plants and chemical plants.

In contrast to the classical location problems, there may exist some situations in practice such that the facilities have already been established and cannot serve the existing customers in the best way at the present. Furthermore, the replacement of them is not possible for the sake of some limitations. In this case, the decision maker may wish to formulate and to solve one of the following improvement problems:

• (a) Inverse location problem Modify some certain input parameters of the underlying system in the cheapest possible way until the prespecified facility locations become optimal.

• (b) Reverse location problem Modify some specific input parameters of the underlying system within a given modification budget so that the predetermined facility locations are improved as much as possible.

In the literature, several published papers on the issue of the reverse center location models can be found. In Berman et al. (1994) presented a ${\mathcal {NP}}$-hardness proof for the reverse 1-center location problem on unweighted graphs. Hence, polynomial time exact approaches have been developed only for solvable special cases, e.g. Zhang et al. (2000) considered the reverse 1-center problem with edge length reductions on an unweighted tree network and proposed a combinatorial algorithm with running time ${\mathcal {O}}(|V|^2 \log |V|)$. In Nguyen (2015) considered the uniform-cost reverse 1-center problem with edge length variations on weighted trees and developed an ${\mathcal {O}}(|V|^2)$ time method. In the context of the inverse center location problems, we refer the interested reader to the papers (Alizadeh and Burkard 2011a, b; Alizadeh et al. 2009; Cai et al. 1999; Nguyen and Sepasian 2016; Yang and Zhang 2008).

To the best of our knowledge, there have been appeared only two papers on the subject of inverse/reverse ‘obnoxious’ center problems up to now. In 2012, the inverse obnoxious center location problem with edge length modifications on general graphs was treated by Alizadeh and Burkard (2012) and a linear time combinatorial algorithm was developed for it. Recently, Alizadeh and Etemad (2016) investigated the reverse obnoxious center problem on general networks under different norms in which all of the vertices on the underlying network are considered as existing customer points. They proposed a linear time approach for determining an optimal solution of the problem.

While all the previous works in the context of inverse and reverse location problems consider the vertex set of the underlying graph as locations of the existing customers, this paper is concerned with a general variant of the reverse obnoxious center location model in which a “selective” subset of the vertex set of a given graph is considered as existing customer points. We develop novel combinatorial algorithms with polynomial running times for solving the problem on trees with continuous and integer decision variables.

The paper is organized as follows: In the next section, we formally state the reverse selective obnoxious center location problem on trees and give some basic properties. Exact combinatorial algorithms are proposed for the problem with continuous variables in Sect. 3. Section 4 is dedicated to combinatorial solution methods for the integer version of the problem. Finally, some concluding remarks are presented in Sect. 5.

2 Problem statement and preliminaries

Let an undirected tree graph (tree network) $T=(V,E)$ with vertex set V and edge set E be given so that $|V|=|E|+1$. Every edge $e\in E$ has a positive length $\ell _e$. Let $S_c\subseteq V$ be the set of existing customer points and $S_f\subseteq T$ stand for the set of candidate facility locations. The task of the classical selective obnoxious center location problem on T is to find a point $x\in S_f$ which maximizes

$$\begin{aligned} \min _{v\in S_c} d_\ell (x, v), \end{aligned}$$

where $d_\ell (x,v)$ denotes the length of the unique path between x and v on the tree T with respect to the edge lengths $\ell =\left( \ell _e\right) _{e\in E}$.

Now, let us state the reverse selective obnoxious center location problem (RSOCP for short) as follows: Let the underlying tree T with associated edge lengths $\ell$ and customer sites $S_c\subseteq V$ be given. Furthermore, let $s\in S_f$ be a predetermined vertex of T which denotes the location of an established facility. We assume without loss of generality that s does not coincide with any customer point because otherwise, the problem is trivial. We want to modify the edge lengths of T within a given budget ${\mathcal {B}}$ such that the minimum of the distances between s and the customer locations $v\in S_c$ becomes maximum under the new edge lengths. According to the specific structure of the RSOCP model, we can immediately observe that any reduction of the edge lengths imposes us an additional cost. Therefore, in order to solve the RSOCP model on the given tree T, it suffices to augment the edge lengths $\ell$ in the cheapest possible way. The edge lengths $\ell _e, e\in E$, are not allowed to be modified arbitrarily. Then, let $\overline{p}_e$ denote the bound for augmenting $\ell _e$. Moreover, let $c_e$ be the corresponding cost for augmenting each length $\ell _e$ by one unit. Using the notations introduced above, the RSOCP model on the underlying tree T can formally be stated as follows:

Augment the original edge lengths $\ell _e, e\in E$, by the continous (or integer) amounts $p_e\in \mathbb R$ (or $p_e\in \mathbb Z$) to the new lengths $\tilde{\ell }_e=\ell _e+p_e$ such that the following three statements hold:

• (i) The objective value

  $$\begin{aligned} \min \big \{ d_{\tilde{\ell }}(s,v): v\in S_c \big \} \end{aligned}$$

  becomes maximum.

• (ii) The budget constraint

  $$\begin{aligned} \sum _{e\in E} c_e p_e\leqslant {\mathcal {B}} \end{aligned}$$

  (1)

  is satisfied.

• (iii) The modifications $p_e$ fulfill the bound

  $$\begin{aligned} 0\leqslant p_e \leqslant \overline{p}_e, \quad \forall e\in E. \end{aligned}$$

A special case of the RSOCP model is the case in which all vertices of the network are considered as existing customer locations, namely $S_c=V$. This special problem has already been studied in Alizadeh and Etemad (2016).

Assume that ${\mathcal {L}}(T)=\left\{ z_1, \ldots ,z_n\right\}$ indicates the set of leaves of the tree T rooted at s. The unique path between s and any leaf $z_i, i=1,\ldots ,n$, is denoted by $P(s, z_i)$. Suppose that $v_{c_i}$ is the closest customer to s on the path $P(s, z_i)$. If there does not exist any customer on $P(s,z_i)$, then set $v_{c_i}=s$. Now, let us define the “critical subtree” $T_{\text {cri}}\subseteq T$ by

$$\begin{aligned} T_{\text {cri}}=\bigcup _{i=1}^n P(s, v_{c_i}). \end{aligned}$$

We need the following standard terminology:

Definition 1

Let T be a tree with associated edge lengths $\ell$ which is rooted at a vertex s. The critical distance of T is defined as

$$\begin{aligned} \rho (T,\ell )=\min \left\{ d_{\ell }(s, z) :\; z \in {\mathcal {L}}(T) \right\} . \end{aligned}$$

(2)

We can obviously conclude the following essential lemma.

Lemma 1

In order to solve the RSOCP model on a tree T, it is sufficient to augment the lengths $\ell$ of the subtree $T_{\text {cri}}$ into $\tilde{\ell }$ subject to the budget and bound constraints until $\rho (T_{\text {cri}},\tilde{\ell })$ becomes maximum.

The specific structure of the continuous (and integer) RSOCP models on the given tree T supports us to derive purely combinatorial solution algorithms with polynomial running times in the following.

3 Optimal algorithms for the continuous RSOCP models

In this section, we first develop a combinatorial solution algorithm for the continuous RSOCP model with arbitrary cost coefficients on the given tree T. Then, we show that the problem can be solved in linear time by applying a novel different solution approach, if the cost coefficients are assumed to be uniform.

3.1 The arbitrary cost model

Our proposed solution method for the continuous RSOCP model with arbitrary cost coefficients relies on a finite sequence of min-cuts in an auxiliary network $N(T_{\text {cri}})=(\widehat{V},\widehat{E})$ corresponding to the critical subtree $T_{\text {cri}}$. A survey on the Zhang’s approach (Zhang et al. 2000), supported us to derive this key idea. The network $N(T_{\text {cri}})$ is constructed in the following way. Given the tree T rooted at the predetermined facility location s, we add an additional vertex t to the corresponding critical subtree $T_{\text {cri}}$ and set

$$\begin{aligned} \widehat{V}=V_{\text {cri}} \cup \{t\} \quad \text {and}\quad \widehat{E}=E_{\text {cri}} \cup \left\{ (z,t)\ :\ z\in {\mathcal {L}}(T_{\text {cri}}) \right\} . \end{aligned}$$

Let ${\mathrm {hgt}}$ denote the height of the tree $T_{\text {cri}}$ which is defined by

$$\begin{aligned} {\mathrm {hgt}}=\max \big \{ d_{\ell }(s,z)\ :\ z\in {\mathcal {L}}(T_{\text {cri}}) \big \}. \end{aligned}$$

(3)

We define the edge length vector $\widehat{\ell }=(\widehat{\ell }_e)_{e\in \widehat{E}}$, upper bound vector $\widehat{p}=\left( \widehat{p}_e\right) _{e\in \widehat{E}}$ and cost vector $\widehat{c}=\left( \widehat{c}_e\right) _{e\in \widehat{E}}$ for the network $N(T_{\text {cri}})$ by

$$\begin{aligned} \widehat{\ell }_e&={\left\{ \begin{array}{ll} \ell _e &{}\quad \text {if}\;\ e\in E_{\text {cri}},\\ {\mathrm {hgt}} -d_\ell (s,z) &{} \quad \text {if}\;\ e=(z,t),\ z\in {\mathcal {L}}(T_{\text {cri}}), \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} \widehat{p}_e&={\left\{ \begin{array}{ll} \overline{p}_e&{}\quad \text {if}\;\ e\in E_{\text {cri}},\\ d_\ell (s,z)-\rho (T_{\text {cri}},\ell ) &{}\quad \text {if}\;\ e=(z,t),\ z\in {\mathcal {L}}(T_{\text {cri}}), \end{array}\right. } \end{aligned}$$

(5)

$$\begin{aligned} \widehat{c}_e&={\left\{ \begin{array}{ll} c_e&{}\quad \text {if}\;\ e\in E_{\text {cri}},\ \widehat{p}_e>0, \\ 0 &{}\quad \text {if}\;\ e=(z,t),\ z\in {\mathcal {L}}(T_{\text {cri}}),\ \widehat{p}_e>0,\\ M &{}\quad \text {else}, \end{array}\right. } \end{aligned}$$

(6)

where M is a very big value. We assume that all edges of the network $N(T_{\text {cri}})$ are directed from s to t. Observe that for any leaf $z\in {\mathcal {L}}(T_{\text {cri}})$, there exists a path $P_z=P(s,z)\cup \{(z,t)\}$ from s to t on the auxiliary network $N(T_{\text {cri}})$. Moreover, all the paths $P_z$, $z\in {\mathcal {L}}(T_{\text {cri}})$, have equal lengths ${\mathrm {hgt}}$. From the specific structure of the auxiliary network $N(T_{\text {cri}})$, we conclude that there exists a one to one correspondence between the problem of augmenting the critical distance $\rho (T_{\text {cri}}, \ell )$ and the problem of augmenting the lengths of all paths $P_z$, $z\in {\mathcal {L}}(T_{\text {cri}})$.

On the other hand, note that we have to satisfy the budget constraint. Hence, the critical distance $\rho (T_{\text {cri}}, \ell )$ can be augmented as much as possible, if we take the edges with smallest corresponding cost coefficients on each path $P_z$, $z\in {\mathcal {L}}(T_{\text {cri}})$, for our modifications. Observe that by augmenting the lengths of the edges contained in a minimum $s-t$ cut in the network $N(T_{\text {cri}})$ with capacities $\hat{c}$, one can augment the lengths of all paths $P_z$, $z\in {\mathcal {L}}(T_{\text {cri}})$, at the minimum total cost. Let ${\mathcal {K}}$ be a minimum $s-t$ cut in $N(T_{\text {cri}})$ and $E\left( {\mathcal {K}}\right)$ be the set of the edges contained in the cut ${\mathcal {K}}$. The capacity of ${\mathcal {K}}$ is given by

$$\begin{aligned} C({\mathcal {K}})=~\sum _{e\in E\left( {\mathcal {K}}\right) } \widehat{c}_e. \end{aligned}$$

(7)

It is easy to see that if $C({\mathcal {K}}) \geqslant M$, then there exists at least one path $P_z$, $z\in {\mathcal {L}}(T_{\text {cri}})$, with $d_\ell (s,z)=\rho (T_{\text {cri}},\ell )$ that cannot be augmented anymore. Consequently, the critical distance $\rho (T_{\text {cri}},\ell )$ cannot be augmented anymore and its current value is optimal in this case. For the case $C({\mathcal {K}})<M$, one can simultaneously augment the lengths of all $s-t$ paths on $N(T_{\text {cri}})$ at the minimum total cost by augmenting the lengths of all edges in $E({\mathcal {K}})$. Observe that

$$\begin{aligned} \gamma ({\mathcal {K}}) =\min \big \{\min \left\{ \widehat{p}_e :\ e\in E\left( {\mathcal {K}}\right) \right\} , \xi ({\mathcal {K}}) \big \} \end{aligned}$$

(8)

where

$$\begin{aligned} \xi ({\mathcal {K}})= \frac{{\mathcal {B}}}{C({\mathcal {K}})} \end{aligned}$$

is the maximum amount by which the lengths of all edges in $E({\mathcal {K}})$ can be augmented with respect to the budget and bound constraints. Then, in order to solve the problem under investigation, we first determine a minimum $s-t$ cut ${\mathcal {K}}$ in $N(T_{\text {cri}})$ and augment the edge lengths of ${\mathcal {K}}$ by $\gamma ({\mathcal {K}})$, namely we set

$$\begin{aligned} \widehat{\ell }_e&={\left\{ \begin{array}{ll} \widehat{\ell }_e+\gamma ({\mathcal {K}}) &{}\quad \text {if}\;\ e\in E\left( {\mathcal {K}}\right) ,\\ \widehat{\ell }_e &{}\quad \text {else}. \end{array}\right. } \end{aligned}$$

(9)

This implies that the critical distance of $T_{\text {cri}}$ is augmented by $\gamma ({\mathcal {K}})$ incurring the cost $C({\mathcal {K}})\gamma ({\mathcal {K}})$. If the budget and bound constraints permit further improvement, we repeat the above procedure on the network $N(T_{\text {cri}})$ with the updated costs $\widehat{c}$ and bounds $\widehat{p}$ as

$$\begin{aligned} \widehat{c}_e&={\left\{ \begin{array}{ll} M&{} \quad \text {if}\; \ e\in E\left( {\mathcal {K}}\right) ,\ \widehat{p}_e=\gamma ({\mathcal {K}}), \\ \widehat{c}_e &{}\quad \text {else}, \end{array}\right. } \end{aligned}$$

(10)

$$\begin{aligned} \widehat{p}_e&={\left\{ \begin{array}{ll} \widehat{p}_e-\gamma ({\mathcal {K}}) &{}\quad \text {if}\;\ e\in E\left( {\mathcal {K}}\right) ,\\ \widehat{p}_e &{}\quad \text {else} \end{array}\right. } \end{aligned}$$

(11)

under the remaining budget

$$\begin{aligned} {\mathcal {B}}:={\mathcal {B}}-C({\mathcal {K}})\gamma ({\mathcal {K}}). \end{aligned}$$

(12)

When this process is iterated, it leads to a finite sequence of minimum $s-t$ cuts ${\mathcal {K}}_i$, $i = 1,\ldots , q$, that augment successively the critical distance of $T_{\text {cri}}$ by the amounts $\gamma ({\mathcal {K}}_i)$, $i = 1,\ldots , q$, respectively. Finally, the optimal objective value

$$\begin{aligned} \rho (T_{\text {cri}},\ell ^*)=\rho (T_{\text {cri}},\ell )+\sum _{i=1}^q \gamma ({\mathcal {K}}) \end{aligned}$$

is given, where $\ell ^*$ denotes the optimal edge length vector. Algorithm 1 states the preceding considerations in more details.

Algorithm 1

(solves the continuous RSOCP model on a tree T )

Step 1 :

Specify the critical subtree $T_{\text {cri}}$.

Step 2 :

Construct the auxiliary network $N(T_{\text {cri}})=(\widehat{V}, \widehat{E})$ of $T_{\text {cri}}$.

Step 3 :

Find a minimum $s-t$ cut $\mathcal {K}$ in $N(T_{\text {cri}})$ and compute its capacity $C(\mathcal {K})$ according to (7).

Step 4 :

If $C(\mathcal {K})\geqslant M$, then stop; otherwise, obtain $\gamma (\mathcal {K})$ by (8).

Step 5 :

Update the lengths $\widehat{\ell }$, the costs $\widehat{c}$ and the bounds $\widehat{p}$ according to (9), (10) and (11), respectively.

Step 6 :

If $\gamma (\mathcal {K})=\xi (\mathcal {K})$, then stop; otherwise, update the budget $\mathcal {B}$ by (12) and go to Step 3.

According to the above discussions, we can conclude that Algorithm 1 works correctly. We are now going to determine the time complexity of Algorithm 1. Step 1 and Step 2 are performed in linear time. In each iteration of the algorithm, the cost of at least one edge e of the minimum $s-t$ cut ${\mathcal {K}}$ in $N(T_{\text {cri}})$ is updated to $\widehat{c}_e=M$. Since an edge e with $\widehat{c}_e=M$ is not contained anymore in any minimum $s-t$ cut except in the last iteration, the total number of iterations of the algorithm is bounded by ${\mathcal {O}}(|E|)$. The task of finding a minimum $s-t$ cut in $N(T_{\text {cri}})$ in each iteration can be done in ${\mathcal {O}}(|E|)$ time, since $N(T_{\text {cri}})-\{t\}$ is an arborescence [see e.g., Vygen (2002)]. Moreover, the time required for updating the data of the network $N(T_{\text {cri}})$ in each iteration is bounded by ${\mathcal {O}}(|E|)$. Hence, the overall running time of Algorithm 1 is ${\mathcal {O}}(|E|^2)$. Altogether, we get

Theorem 1

The continuous reverse selective obnoxious center location problem with arbitrary modification costs can be solved in ${\mathcal {O}}(|E|^2)$ time on a tree T.

To illustrate Algorithm 1, let us consider an example.

Example

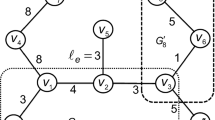
Consider the tree T given in Fig. 1 with the prespecified facility location s and the associated edge lengths $\ell _e$, augmentation bounds $\overline{p}_e$ and cost coefficients $c_e$. Assume that the set of existing customer points is $S_c=\left\{ v_3, v_5, v_6, v_{12}, v_{13}, v_{15}\right\}$ and the total budget given for modifying the edge lengths is ${\mathcal {B}}=7.8$. We aim to obtain an optimal solution of the continuous RSOCP model on T by applying Algorithm 1. First, the critical subtree $T_{\text {cri}}$ is constructed by deleting the edges $(v_3,v_4), (v_4,v_5), (v_6,v_7), (v_6,v_8)$ and $(v_{12},v_{13})$ on T.

Fig. 1

Illustration of the tree T with the corresponding input data

The computational results of the execution of Algorithm 1 on the subtree $T_{\text {cri}}$ are summarized in Table 1. We observe that the optimal critical distance of $T_{\text {cri}}$ is obtained as $\rho (T_{\text {cri}},{\ell }^*)=9.82$. Hence, an optimal solution of the problem contains

$$\begin{aligned} p^*_{(s,v_1)}=2,\quad p^*_{(v_1,v_2)}=1,\quad p^*_{(v_2,v_3)}=0.62,\quad p^*_{(v_9,v_{10})}=0.32, \end{aligned}$$

while the other decision variables are chosen to be 0.

Table 1 The results obtained by applying Algorithm 1 on the tree T of Fig. 1

3.2 The uniform cost model

This subsection is concerned with developing a novel linear time solution algorithm for the continuous RSOCP model on the underlying tree network T with associated cost coefficients C. We can assume that $C=1$. Since otherwise, we can immediately replace the budget constraint by $\sum _{e\in E_{\text {cri}}} p_e\leqslant {\mathcal {B}}/C,$ where $E_{\text {cri}}$ is the edge set of the critical subtree $T_{\text {cri}}$.

Observe that the critical distance $\rho (T_{\text {cri}},\ell )$ cannot exceed the bound

$$\begin{aligned} \rho _{\max } = \min _{z \in {\mathcal {L}}(T_{\text {cri}})} \left\{ d_\ell (s,z) + \sum _{e\in E\left( P(s,z)\right) } \overline{p}_e \right\} \end{aligned}$$

(13)

after any modification with respect to the given bounds $\overline{p}_e$, $e\in E_{\text {cri}}$. Hence, the critical distance $\rho (T_{\text {cri}},\ell )$ can be augmented by at most

$$\begin{aligned} \delta _{\max } =\rho _{\max } -\rho (T_{\text {cri}},\ell ) \end{aligned}$$

subject to the modification bounds $\overline{p}_e, e\in E_{\text {cri}}$. In the following, we first try to derive a procedure for augmenting $\rho (T_{\text {cri}},\ell )$ by any amount $0<\delta \leqslant \delta _{\max }$ at the minimum total cost $\sum _{e\in E_{\text {cri}}} p_e$ with respect to the given modification bounds $\overline{p}_e, e\in E_{\text {cri}}$. This procedure will be applied as a subroutine in our solution algorithm, where it determines an optimal solution for the problem after the optimal objective modification $\delta ^*$ is computed.

Let all edges on the critical subtree $T_{\text {cri}}$ be directed from the root s to the leaves. For any edge $e=(u,v)\in E_{\text {cri}}$, let $T_{\text {cri}}(e)$ denote the unique subtree of $T_{\text {cri}}$ starting with the edge e which is rooted at u. First, we compute the critical distance $\rho (T_{\text {cri}}(e), \ell )$ for every edge $e\in E_{\text {cri}}$. Next, we scan the edges of the subtree $T_{\text {cri}}$ in a depth-first-search way starting with the edges $e=(s,v)\in E_{\text {cri}}$. Every edge $e=(u,v)$ gets two label $\delta _e$ and $\lambda _u$ during the execution of the algorithm. The label $\delta _e$ denotes the amount by which the critical distance of $T_{\text {cri}}(e)$ has to be augmented in order that $\rho (T_{\text {cri}},\ell )$ is augmented by $\delta$. Moreover, the label $\lambda _u$ is the length of the unique path from s to the vertex u with respect to the edge lengths obtained from augmenting $\rho (T_{\text {cri}},\ell )$ by $\delta$.

We are now ready to outline our novel approach for augmenting $\rho (T_{\text {cri}},\ell )$ by any feasible amount $\delta$ as Procedure ACD.

Procedure ACD (augments $\rho (T_{\text {cri}},\ell )$ by the amount $\delta$)

• 1. Direct all edges of $T_{\text {cri}}$ from the root s to the leaves ${\mathcal {L}}(T_{\text {cri}})$.

• 2. Compute the critical distance $\rho (T_{\text {cri}}(e), \ell )$, for all edges $e\in E_{\text {cri}}$.

• 3. Set $\lambda _s=0$.

• 4. For every edge $e=(s,v)\in E_{\text {cri}}$, call Subprocedure ${\mathcal {P}}(e)$.

Subprocedure ${\mathcal {P}}(e)$] /* assume $e=(u,v)$ */

• 1. Calculate $\delta _e=\big (\rho (T_{\text {cri}},\ell )+\delta \big ) -\big (\lambda _u+\rho \left( T_{\text {cri}}(e), \ell \right) \big )$.

• 2. If $\delta _e\leqslant 0$, then stop; otherwise, set

  $$\begin{aligned} \tilde{\ell }_e=\ell _e+\min \left\{ \delta _e, \overline{p}_e\right\} ,\quad \lambda _v=\lambda _u+\tilde{\ell }_e. \end{aligned}$$

• 3. If $\delta _e\leqslant \overline{p}_e$, then stop; otherwise, for every edge $e^\prime =(v, w)\in E_{\text {cri}}$, call Subprocedure ${\mathcal {P}}(e^\prime )$.

Now, we analyze the time complexity of the procedure. Beginning from the leaves to the root, the values $\rho (T_{\text {cri}}(e), \ell )$ for all $e\in E_{\text {cri}}$ can be computed in ${\mathcal {O}}(|E|)$ time. The algorithm calls Subprocedure ${\mathcal {P}}(e)$ for at most |E| times and each ${\mathcal {P}}(e)$ takes a constant time. Altogether, we get

Theorem 2

Procedure ACD augments the critical distance $\rho (T_{\text {cri}},\ell )$ by an amount $\delta$ at the minimum total cost on a tree T in linear time.

For solving the continuous RSOCP model with uniform cost coefficients on the tree T, we need the cost for augmenting the critical distance $\rho (T_{\text {cri}},\ell )$ by any feasible amount $\delta$. This cost is given by the “critical-distance cost function” $f(\delta )$. Observe that the cost function $f(\delta )$ is a piecewise linear function which can be presented by the start point $\delta _0=0$, the endpoint $\delta _k=\delta _{\max }$ and $k-1$ break points $\delta _i$, where the slopes of $f(\delta )$ vary. The slopes $m_i$, $i=1,\ldots , k$, of the function $f(\delta )$ on any interval $[\delta _{i-1}, \delta _i]$ are given as

$$\begin{aligned} m_1=\alpha , \quad m_i=m_{i-1}+1,\ \quad i=2, \ldots , k, \end{aligned}$$

where $\alpha$ equals the number of the vertex disjoint paths form s to the leaves of the critical subtree $T_{\text {cri}}$ having the length $\rho (T_{\text {cri}}, \ell )$. It is clear that

$$\begin{aligned} 0=\delta _0\leqslant \delta _1 \leqslant \delta _2 \leqslant \cdots \leqslant \delta _k=\delta _{\max } \end{aligned}$$

and then according to the above statements, the critical-distance cost function $f(\delta )$ is given by

$$\begin{aligned} f(\delta )=\left\{ \begin{array}{ll} \alpha \delta &{}\quad \text{ if }\; 0\leqslant \delta \leqslant \delta _1,\\ (\alpha +1)\delta -\delta _1 &{}\quad \text{ if }\; \delta _1\leqslant \delta \leqslant \delta _2,\\ \vdots &{} \\ (\alpha +k-1)\delta -\sum _{i=1}^{k-1}\delta _i &{}\quad \text{ if }\; \delta _{k-1}\leqslant \delta \leqslant \delta _{k}\\ \end{array} \right. \end{aligned}$$

(14)

which is piecewise linear and increasing on the interval $[0, \delta _{\max }]$. In the following, we present a procedure for determining the break points of $f(\delta )$:

Procedure BPCF (determines the break points of $f(\delta )$)

• (i) Let $p_e$ be the amount by which the length of any edge $e\in E_{\text {cri}}$ is augmented, when we modify the critical distance $\rho (T_{\text {cri}}, \ell )$ to $\rho (T_{\text {cri}}, \ell )+\delta _{\max }$ by Procedure ACD.

• (ii) Construct an auxiliary tree $T^\text {a}$ with the same vertices and edges as the subtree $T_{\text {cri}}$, where the edge lengths are given by $\ell ^\text {a}_e=p_e$ for all $e\in E(T^\text {a})$. Scan the auxiliary tree $T^\text {a}$ in a breadth-first approach starting from the leaves to the root s and associate with every edge $e=(u,v)\in E(T^\text {a})$ two labels $({\mathrm {hgt}}_e, \omega _e)$. The label ${\mathrm {hgt}}_e$ stands for the height of the subtree $T^\text {a}(e)$ beginning with edge $e=(u,v)$ and the label $\omega _e$ is a leaf of $T^\text {a}(e)$ which is the farthest vertex from u.

• (iii) Using the labels $({\mathrm {hgt}}_e, \omega _e)$ of the edges incident with the root vertex, find a longest path on $T^\text {a}$. Remove all edges of this longest path on $T^\text {a}$ to get a forest of directed subtrees of $T^\text {a}$ with root set R.

• (iv) For every edge $e=(u,v)$ with $u\in R$, a new subtree $T^\text {a}(e)$ is derived. We number these edges by $e_1, \ldots , e_\theta$ and get the corresponding subtrees $T^\text {a}(e_1), \ldots , T^\text {a}(e_\theta )$. For any $i=1, \ldots , \theta$, a new break point $\delta =\delta _{\max }-{\mathrm {hgt}}_{e_i}$ is computed.

• (v) For any $i=1, \ldots , \theta$, perform the steps (iii) and (iv) on the subtree $T^\text {a}(e_i)$ provided that $T^\text {a}(e_i)$ is not a single vertex. The above process is iterated until all subtrees become single vertices.

Considering the steps of Procedure BPCF, we can get

Lemma 2

The break points of the critical-distance cost function $f(\delta )$ can be computed in linear time by Procedure BPCF.

Proof

Every leaf $z\in {\mathcal {L}}(T_{\text {cri}})$ contributes the term

$$\begin{aligned} \zeta (z)= \max \left\{ \rho (T_{\text {cri}},\ell )+\delta _{\max }-d_{\ell }(s,z),0\right\} \end{aligned}$$

to $f(\delta _{\max })$. Let $T^\text {a}(e)$ be a subtree identified in Step (iv) such that $z \in {\mathcal {L}}(T^\text {a}(e))$. The amount $\zeta (z)-{\mathrm {hgt}}_{e}$ is the augmentation value related to the intersection of P(s, z) and the longest path of $T^\text {a}$. In the augmenting process, when the critical distance $\rho (T_{\text {cri}},\ell )$ reaches to the value

$$\begin{aligned} \rho (T_{\text {cri}},\ell )+\delta _{\max }-{\mathrm {hgt}}_{e} \end{aligned}$$

an edge of $T^\text {a}(e)$ is added to the set of augmenting edges. As a result, the slope of the cost function is augmented by one unit. Then, $\delta =\delta _{\max }-{\mathrm {hgt}}_{e}$ is a break point of $f(\delta )$.

The time complexity follows from the fact that the computation of all labels $({\mathrm {hgt}}_e, \omega _e)$ takes linear time. Furthermore, the decomposition of $T^\text {a}$ into subtrees and hence the determination of the values $\delta _i$ are done in linear time. $\square$

In order to find an optimal solution for the uniform-cost continuous RSOCP model on the underlying tree T, we have to find an interval $[\delta _i, \delta _{i+1}] , 0\leqslant i\leqslant k-1$, which contains the optimal objective modification $\delta ^*$, where $f(\delta ^*)= {\mathcal {B}}$. A straightforward approach for finding such an interval is to construct the function $f(\delta )$ directly and then find an interval $[f(\delta _i), f(\delta _{i+1})]$ that contains ${\mathcal {B}}$. To this end, we should first sort the obtained break points $\delta _i$ in an increasing order. In this case, an optimal solution can be found in ${\mathcal {O}}(|E|\log |E|)$ time. But, we attempt to develop a linear time algorithm for which the construction of the function $f(\delta )$ is not required and we only have to determine the break points $\delta _i$ of $f(\delta )$ by Procedure BPCF.

Let ${\mathcal {S}}$ denote the set of all break points $\delta _i, i=1,\ldots , k$, and $\sim$ be any of the relations $<,=,>, \leqslant , \geqslant$. For any arbitrary amount $\mu$ with $0<\mu \leqslant \delta _{\max }$, we use the notation ${\mathcal {S}}^\mu _\sim = \big \{\delta \in {\mathcal {S}}\ :\ \delta \sim \mu \big \}.$ Obviously, we have

$$\begin{aligned} f(\mu )=(\alpha +| {\mathcal {S}}^\mu _< |)\mu - \sum _{\delta \in {\mathcal {S}}^\mu _< } \delta . \end{aligned}$$

In our solution approach, we first find the median $\mu$ of the set ${\mathcal {S}}$ and compute $f(\mu )$. If ${\mathcal {B}}<f(\mu )$, then it means that $\delta ^*< \mu$. In this case, we delete all break points $\delta \in {\mathcal {S}}^\mu _\geqslant$ from ${\mathcal {S}}$. In an analogous way, if ${\mathcal {B}}>f(\mu )$, then all break points $\delta \in {\mathcal {S}}^\mu _\leqslant$ will be deleted. We again find the median of the new set ${\mathcal {S}}$ and continue this process until ${\mathcal {S}}=\emptyset$. Our new solution method for the uniform-cost model is summarized in Algorithm 2.

Algorithm 2

(solves the uniform-cost continuous RSOCP model on a tree)

Step 1 :

Construct the critical subtree $T_{\text {cri}}$.

Step 2 :

Set $a=0$, $b=0$ and find the set $\mathcal {S}$ of the break points by applying Procedure BPCF.

Step 3 :

If $\mathcal {S}\ne \emptyset$, then find the median $\mu$ of the set $\mathcal {S}$; otherwise, go to Step 8.

Step 4 :

Compute

$$\begin{aligned} f(\mu ) =(\alpha +|\mathcal {S}^\mu _<|+a)\mu -\sum \limits _{\delta \in \mathcal {S}^\mu _<} \delta -b. \end{aligned}$$

Step 5 :

If $\mathcal {B}>f(\mu )$, then update a, b as

$$\begin{aligned} a=a+|\mathcal {S}^\mu _\leqslant |,\quad b=b+\sum \limits _{\delta \in \mathcal {S}^\mu _\leqslant } \delta , \end{aligned}$$

set $\mathcal {S}=\mathcal {S}^\mu _>$ and go to Step 3.

Step 6 :

If $\mathcal {B}<f(\mu )$, then set $\mathcal {S}=\mathcal {S}^\mu _<$ and go to Step 3.

Step 7 :

If $f(\mu )=\mathcal {B}$, then let $\delta ^{*} =\mu$ and stop.

Step 8 :

Set $\varDelta =({\mathcal {B}+b})/({\alpha +a})$.

Step 9 :

If $\varDelta \leqslant \delta _{\max }$, then set $\delta ^*=\varDelta$; otherwise, set $\delta ^*=\delta _{\max }$.

Step 10 :

Apply Procedure ACD to augment $\rho (T_{\text {cri}}, \ell )$ by $\delta ^*$ and derive an optimal solution.

Recall that the critical subtree $T_{\text {cri}}$ is constructed in ${\mathcal {O}}(|E|)$ time. Let T(k) denote the worst-case running time for k elements. The median of a set of k elements can be determined in ${\mathcal {O}}(k)$ time [see e.g., Cormen et al. (2001)]. Moreover, in each iteration of the algorithm, we drop ${\mathcal {O}}\left( \left\lceil \dfrac{|{\mathcal {S}}|}{2}\right\rceil \right)$ elements of the current set ${\mathcal {S}}$ at Step 5 or Step 6. Therefore, Step 3 up to Step 7 of the algorithm require the total running time $T(k)=T\left( \left\lceil \dfrac{k}{2} \right\rceil \right) +{\mathcal {O}}(k)$ which implies $T(k)={\mathcal {O}}(k)$. Since we have $k\leqslant |E|$ and also the execution of Procedure ACD in Step 10 takes ${\mathcal {O}}(|E|)$ time, we finally conclude.

Theorem 3

The continuous reverse selective obnoxious center location problem with uniform modification costs is solvable in ${\mathcal {O}}(|E|)$ time on a given tree.

Example

(Cont’d). Consider the tree T of Fig. 1 with uniform cost coefficient $c_e=1$ for all $e\in E$. By applying Procedure BPCF, the set of break points is found as ${\mathcal {S}}=\{3.3, 4.2, 5.2\}.$ The computational results of the execution of Algorithm 2 are given in Table 2. Then, an optimal modification value $\delta ^*=5.1$ and consequently the optimal objective value $\rho (T_{\text {cri}}, {\ell }^*)=11.3$ is derived. Moreover, an optimal solution of the problem consists of

$$\begin{aligned}&p^*_{(s,v_1)}=2, \quad p^*_{(v_1,v_2)}=1,\quad p^*_{(v_2,v_3)}=2.1,\quad p^*_{(v_2,v_6)}=0.9,\\&p^*_{(s,v_9)}=1, \quad p^*_{(v_9,v_{10})}=0.8,\quad \end{aligned}$$

while all other decision variables are chosen to be 0.

Table 2 The results obtained by applying Algorithm 2 to the uniform-cost instance

4 Optimal algorithms for the integer RSOCP models

As mentioned in Sect. 2, the integer RSOCP model on a tree T can be formulated as an integer linear programming problem. The specific structure of our problem allows the design of exact solution algorithms with polynomial running times. In the following, we will always deal with the integer part of the augmentation bounds $\overline{p}_e, e\in E$, and then we set $\overline{p}_e=\left\lfloor \overline{p}_e \right\rfloor$, without loss of generality, where $\lfloor . \rfloor$ stands for the floor function.

4.1 The arbitrary cost model

Since the modification amounts of the edge lengths are provided to be integers, the fractional part of any distance $d_{\ell }(s,z)$, $z \in {\mathcal {L}}(T_{\text {cri}})$, remains unchanged in any feasible augmentation of edge lengths. Then, in order to solve the integer RSOCP model with arbitrary cost coefficients on T, we first define the auxiliary distances

$$\begin{aligned} d^{\text {a}}_{\ell }(s,z)=\left\lfloor d_{\ell }(s,z)\right\rfloor \quad \forall \, z\in {\mathcal {L}}(T_{\text {cri}}), \end{aligned}$$

which by putting them in (2) and (3), we get the auxiliary critical distance $\rho ^{\text {a}}(T_{\text {cri}},\ell )$ and the auxiliary height ${\mathrm {hgt}}^{\text {a}}$, respectively. Next, we construct a network $N(T_{\text {cri}})$ with same vertices $\widehat{V}$ and edges $\widehat{E}$ as the network of Sect. 3.1. We define the edge lengths $\widehat{\ell }$, the upper bounds $\widehat{p}$ and the cost coefficients $\widehat{c}$ of the network $N(T_{\text {cri}})$ by (4), (5) and (6), respectively, with respect to the values $d^{\text {a}}_{\ell }$, $\rho ^{\text {a}}(T_{\text {cri}},\ell ), {\mathrm {hgt}}^{\text {a}}$. In order to determine the integer part of the optimal critical distance $\rho (T_{\text {cri}}, \ell ^*)$, we are required to apply Algorithm 1 with the parameter

$$\begin{aligned} \xi ({\mathcal {K}})=\left\lfloor \frac{{\mathcal {B}}}{C({\mathcal {K}})} \right\rfloor \end{aligned}$$

to the network $N(T_{\text {cri}})$ introduced above which yields the temporary length $\ell ^{\text {t}}_e$ and bound $p^{\text {t}}_e=\overline{p}_e-(\ell ^{\text {t}}_e-\ell _e)$ for any edge $e\in \widehat{E}$. Note that the parameter $\gamma ({\mathcal {K}})$ is an integer value for every minimum cut ${\mathcal {K}}$ generated in each iteration of Algorithm 1. Hence, we have $\ell ^{\text {t}}_e-\ell _e\in \mathbb Z$ for all $e\in \widehat{E}$. Define

$$\begin{aligned} {\mathcal {A}}=\big \{z\in {\mathcal {L}}(T_{\text {cri}}) : \left\lfloor d_{\ell ^{\text {t}}}(s,z)\right\rfloor = \left\lfloor \rho (T_{\text {cri}},\ell ^{\text {t}})\right\rfloor \big \}. \end{aligned}$$

(15)

The following lemma describes the connection between the optimal objective value $\rho (T_{\text {cri}}, \ell ^*)$ and the temporary edge lengths $\ell ^{\text {t}}$.

Lemma 3

There exists a $z^*\in {\mathcal {A}}$, the so-called critical leaf $z^*$, such that $\rho (T_{\text {cri}}, \ell ^*)=d_{\ell ^{\text {t}}}(s,z^*)$ and

$$\begin{aligned} d_{\ell ^*}(s,z)={\left\{ \begin{array}{ll} d_{\ell ^{\text {t}}}(s,z)+1 &{}\quad \text {if}\; z\in {\mathcal {A}},\ d_{\ell ^{\text {t}}}(s,z)<d_{\ell ^{\text {t}}}(s,z^*),\\ d_{\ell ^{\text {t}}}(s,z) &{}\quad \text {else} \end{array}\right. } \end{aligned}$$

(16)

for any leaf $z\in {\mathcal {L}}(T_{\text {cri}})$, where $\ell ^*$ is the optimal modified edge length.

Proof

Suppose that $\rho (T_{\text {cri}}, \ell ^*)\ne d_{\ell ^{\text {t}}}(s,z)$, for all $z\in {\mathcal {A}}$. Therefore, we get $d_{\ell ^{\text {t}}}(s,z)< \rho (T_{\text {cri}}, \ell ^*)$, for every $z\in {\mathcal {A}}$. Based on the definition of $\rho (T_{\text {cri}}, \ell ^*)$, we can state $d_{\ell ^{\text {t}}}(s,z)< d_{{\ell }^*}(s,z)$, for all $z\in {\mathcal {A}}$. This means that the budget and bound constraints let all distances $d_{\ell ^{\text {t}}}(s,z)$, $z\in {\mathcal {A}}$, be augmented at least by one unit. Recall that the lengths $\ell ^{\text {t}}$ are obtained after the execution of Algorithm 1 with new parameter $\xi ({\mathcal {K}})=\left\lfloor \frac{{\mathcal {B}}}{C({\mathcal {K}})} \right\rfloor$. This algorithm terminates if the upper bounds do not let further improvement or $\gamma ({\mathcal {K}})=\xi ({\mathcal {K}})$. The equality $\gamma ({\mathcal {K}})=\xi ({\mathcal {K}})$ means that there is not enough budget to augment all distances $d_{\ell ^{\text {t}}}(s,z)$, $z\in {\mathcal {A}}$ by one unit. This is a contradiction. Considering the above arguments, we can immediately conclude the correctness of (16). $\square$

Lemma 3 implies that the integer part of the optimal critical distance $\rho (T_{\text {cri}}, \ell ^*)$ is equal to $\left\lfloor \rho (T_{\text {cri}},\ell ^{\text {t}})\right\rfloor$. For obtaining the exact value of $\rho (T_{\text {cri}}, \ell ^*)$, we need to determine the critical leaf $z^*\in {\mathcal {A}}$. To this end, we first sort all the values

$$\begin{aligned} d_{\ell ^{\text {t}}}(s,z)\in \left[ \rho (T_{\text {cri}},\ell ^{\text {t}}), \rho _{\max }\right] , \end{aligned}$$

$z\in {\mathcal {A}}$, in a strictly decreasing order

$$\begin{aligned} d_{\ell ^{\text {t}}}(s,z_1)> d_{\ell ^{\text {t}}}(s,z_2)>\cdots >d_{\ell ^{\text {t}}}(s,z_r)=\rho (T_{\text {cri}},\ell ^{\text {t}}), \end{aligned}$$

(17)

where $r\leqslant |{\mathcal {A}}|$. In the next step, we start with $z_{1}$ and try to determine whether $z^*=z_{1}$ or not. Let ${\mathcal {B}}^\prime$ be the remaining budget at the end of Algorithm 1, namely

$$\begin{aligned} {\mathcal {B}}^\prime ={\mathcal {B}}-\sum _{e\in E_{\text {cri}}}c_e\left( \ell ^{\text {t}}_e-\ell _e\right) . \end{aligned}$$

Considering Lemma 3, we should check the possibility of augmenting all distances $d_{\ell ^{\text {t}}}(s,z_j)$, $j=2,3, \ldots , r$, by one under the condition that the incurred cost for this modification does not exceed the remaining budget ${\mathcal {B}}^\prime$. To this end, we define the network $\overline{N}=(\widehat{V}, \widehat{E})$ with the cost vector $\overline{c}=\left( \overline{c}_e\right) _{e\in \widehat{E}}$, where

$$\begin{aligned} \overline{c}_e={\left\{ \begin{array}{ll} c_e&{} \quad \text {if}\;\ e\in E_{\text {cri}},\ p^{\text {t}}_e>0,\\ 0 &{}\quad \text {if}\;\ e=(z,t),\ d_{\ell ^{\text {t}}}(s,z)\geqslant d_{\ell ^{\text {t}}}(s,z_1),\\ M &{}\quad \text {else}. \end{array}\right. } \end{aligned}$$

(18)

$\widehat{V}$ and $\widehat{E}$ are the same vertex set and edge set of $N(T_{\text {cri}})$ and M is a very big value. Let $\overline{{\mathcal {K}}}$ be a minimum $s-t$ cut in $\overline{N}$ with the corresponding capacity $C(\overline{{\mathcal {K}}}).$ We can observe that an edge of every path $P(s,z_j)$, $j=2,3, \ldots , r,$ is contained in $\overline{{\mathcal {K}}}$. Now, if $C(\overline{{\mathcal {K}}})\leqslant {\mathcal {B}}^\prime$, then $z^*=z_1$ and consequently $\rho (T_{\text {cri}}, \ell ^*)= d_{\ell ^{\text {t}}}(s,z_1).$ If $C(\overline{{\mathcal {K}}})> {\mathcal {B}}^\prime$, then it is implied that the remaining budget ${\mathcal {B}}^\prime$ does not allow us to increase the critical distance $\rho (T_{\text {cri}}, \ell )$ to $d_{\ell ^{\text {t}}}(s,z_1)$ and we should check the leaf $z_2$. Repeating the above procedure on the leaves $z_i$, $2\leqslant i\leqslant r$, together with the following edge cost update

$$\begin{aligned} \overline{c}_e={\left\{ \begin{array}{ll} 0&{}\quad \text {if}\;\ e=(z,t), z\in {\mathcal {L}}(T_{\text {cri}}), d_{\ell ^{\text {t}}}(s,z)\geqslant d_{\ell ^{\text {t}}}(s,z_i)\\ \overline{c}_e &{}\quad \text {else} \end{array}\right. } \end{aligned}$$

(19)

in each shift from $z_{i-1}$ to $z_i$, we finally determine the critical leaf $z^*=z_{i^*}$, $1\leqslant i^*\leqslant r$, with corresponding minimum cut $\overline{{\mathcal {K}}}^*$. Altogether, we summarize our procedure for determining $z^*$ on $T_{\text {cri}}$ as follows:

Procedure CL (finds the critical leaf $z^*$ and the cut $\overline{{\mathcal {K}}}^*$)

• 1. Specify ${\mathcal {A}}$ according to (15).

• 2. Sort the values $d_{\ell ^{\text {t}}}(s,z)\in \left[ \rho (T_{\text {cri}},\ell ^{\text {t}}), \rho _{\max }\right]$, $z\in {\mathcal {A}}$, in a strictly decreasing order as (17).

• 3. Set $i=1$ and construct $\overline{N}=(\widehat{V}, \widehat{E})$ with edge costs (18).

• 4. If $i=r$, then let $z^*=z_r$, $\overline{{\mathcal {K}}}^*=\emptyset$ and stop; otherwise, find a minimum cut $\overline{{\mathcal {K}}}$ in $\overline{N}$.

• 5. If $C(\overline{{\mathcal {K}}})\leqslant {\mathcal {B}}^\prime$, then set $z^*=z_i$, $\overline{{\mathcal {K}}}^*=\overline{{\mathcal {K}}}$ and stop; else update the costs $\overline{c}$ as in (19), let $i=i+1$ and return to Step 4.

Observe that the set ${\mathcal {A}}$ is determined in ${\mathcal {O}}(|E|)$ time in a depth-first way. The ordering of the distances $d_{\ell ^{\text {t}}}(s,z)$ is performed in ${\mathcal {O}}(|E|\log |E|)$ time. The number of the iterations of Procedure CL is bounded by ${\mathcal {O}}(|E|)$. On the other hand, in any iteration, a cut $\overline{{\mathcal {K}}}$ is determined in ${\mathcal {O}}(|E|)$ time, since $\overline{N}$ is a tree-like network [see e.g., Vygen (2002)]. Altogether, we get

Lemma 4

Procedure CL finds a critical leaf $z^*$ of the subtree $T_{\text {cri}}$ in ${\mathcal {O}}(|E|^2)$ time.

As soon as the leaf $z^*$ and the cut $\overline{{\mathcal {K}}}^*$ are determined by Procedure CL, the optimal edge lengths of the integer RSOCP model on the given tree T can be obtained by

$$\begin{aligned} \ell ^*_e={\left\{ \begin{array}{ll} \ell ^{\text {t}}_e+1&{}\quad \text {if}\; \ e\in E_{\text {cri}}\cap E\left( \overline{{\mathcal {K}}}^*\right) ,\\ \ell ^{\text {t}}_e&{}\quad \text {if}\; \ e\in E_{\text {cri}}{\setminus } E\left( \overline{{\mathcal {K}}}^*\right) ,\\ \ell _e&{}\quad \text {else}. \end{array}\right. } \end{aligned}$$

(20)

Finally, our purely combinatorial approach for solving the integer RSOCP model with arbitrary cost coefficients on the underlying tree graph T is outlined in Algorithm 3.

Algorithm 3

(solves the integer RSOCP model on a tree T )

Step 1 :

Specify the critical subtree $T_{\text {cri}}$.

Step 2 :

For every leaf $z\in \mathcal {L}(T_{\text {cri}})$, define the auxiliary distance

$$\begin{aligned} d^{\text {a}}_{\ell }(s,z)=\left\lfloor d_{\ell }(s,z)\right\rfloor . \end{aligned}$$

Step 3 :

Construct the auxiliary network $N(T_{\text {cri}})$ with respect to the auxiliary values $d^{\text {a}}_{\ell }$, $\rho ^{\text {a}}(T_{\text {cri}},\ell )$ and $\mathrm {hgt}^{\text {a}}$.

Step 4 :

Apply Algorithm 1 with the parameter $\xi (\mathcal {K})=\left\lfloor \frac{\mathcal {B}}{C(\mathcal {K})} \right\rfloor$ to determine the temporary lengths $\ell ^{\text {t}}$.

Step 5 :

Determine the critical leaf $z^*$ and the corresponding cut $\overline{\mathcal {K}}^*$ by executing Procedure CL.

Step 6 :

Derive the optimal edge lengths $\ell ^*$ according to (20).

We are now going to determine the time complexity of the algorithm: the critical subtree $T_{\text {cri}}$ and the auxiliary network $N(T_{\text {cri}})$ are constructed in linear time. Algorithm 1 is executed in ${\mathcal {O}}(|E|^2)$ time. The time complexity of Procedure CL is ${\mathcal {O}}(|E|^2)$ and the optimal lengths $\ell ^*$ are computed in ${\mathcal {O}}(|E|)$ time. Hence, we get

Theorem 4

The integer reverse selective obnoxious center location problem with arbitrary modification costs can be solved in ${\mathcal {O}}(|E|^2)$ time on a given tree.

Example

(Cont’d). Consider the integer RSOCP model on the tree T of Fig. 1 with associated budget ${\mathcal {B}}=14.3$. Applying Algorithm 1 on the auxiliary network $N(T_{\text {cri}})$, yields the results presented in Table 3. Algorithm 1 terminates in four iterations while the temporary edge lengths

$$\begin{aligned} \ell ^{\text {t}}_{(s,v_1)}=4.1,\quad \ell ^{\text {t}}_{(v_1,v_2)}=2.1,\quad \ell ^{\text {t}}_{(v_2,v_3)}=4,\quad \ell ^{\text {t}}_{(v_9,v_{10})}=4 \end{aligned}$$

and $\ell ^{\text {t}}_e=\ell _e$ for all other edges with corresponding $\rho (T_{\text {cri}},\ell ^{\text {t}})=10.2$ are obtained. For the next step, the remaining budget is ${\mathcal {B}}^\prime =4.3$. We get ${\mathcal {A}}=\left\{ v_3, v_6, v_{12}\right\}$ with $z_1=v_{12}$, $z_2=v_6$ and $z_3=v_3$. The computational results of the execution of Procedure CL are given in Table 4. Then, the critical leaf $z^*=v_6$ is determined with the corresponding cut

$$\begin{aligned} \overline{{\mathcal {K}}}^*=\left\{ (v_2,v_3), (v_6,t), (v_{12},t), (v_{15},t) \right\} . \end{aligned}$$

Finally, the optimal objective value $\rho (T_{\text {cri}},\ell ^*)=10.4$ is given, where an optimal length modification leads to

$$\begin{aligned} \ell ^*_{(s,v_1)}=4.1,\quad \ell ^*_{(v_1,v_2)}=2.1,\quad \ell ^*_{(v_2,v_3)}=5,\quad \ell ^*_{(v_9,v_{10})}=4, \end{aligned}$$

and $\ell ^*_e=\ell _e$ for all other edges.

Table 3 The results obtained by applying Algorithm 1 on $N(T_{\text {cri}})$

Table 4 The results obtained by executing Procedure CL on $\overline{N}$

4.2 The uniform cost model

Assume that in the integer RSOCP model on the underlying tree T, the associated cost coefficients for modification of edge lengths are uniform. Without loss of generality, suppose $c_e=1$ for all $e\in E$. In the following, we aim to develop a combinatorial algorithm with lower time complexity for this uniform cost model. Our method contains two phases, where the integer part of the optimal objective value $\rho (T_{\text {cri}},\ell ^*)$ is determined in the first phase and then the exact optimal objective value $\rho (T_{\text {cri}},\ell ^*)$ and the optimal modified edge lengths $\ell ^*$ are achieved in the second phase through deriving the fractional part of $\rho (T_{\text {cri}},\ell ^*)$.

In order to acquire the integer part of the optimal objective value $\rho (T_{\text {cri}},\ell ^*)$, it is equivalently required to find the maximum integer value $\delta ^*\in \mathbb Z$ so that the incurred cost for augmenting $\left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor$ by $\delta ^*$ does not exceed the total budget ${\mathcal {B}}$. For this matter, we should first find a way for augmenting $\left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor$ by any integer amount $\delta \in \mathbb Z^+$ with $\delta \leqslant \left\lfloor \rho _{\text {max}}\right\rfloor - \left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor$ at the minimum total cost with respect to the given modification bounds where $\rho _{\max }$ is defined by (13). As a subroutine, this can be done by executing Procedure ACD with the parameter

$$\begin{aligned} \delta _e= \left\lfloor \rho (T_{\text {cri}}, \tilde{\ell }) \right\rfloor -\Big \lfloor \lambda _u+\rho \left( T_{\text {cri}}(e), \ell \right) \Big \rfloor \end{aligned}$$

in Subprocedure ${\mathcal {P}}(e)$.

Let $f(\delta )$ be a function which returns the cost for augmenting $\left\lfloor \rho (T_{\text {cri}}, {\ell }) \right\rfloor$ by any amount $\delta \in \mathbb Z^+.$ It is observed that $f(\delta )$ is piecewise linear and has a representation as (14), where $\alpha$ is the number of the vertex disjoint paths P(s, z), $z\in {\mathcal {L}}(T_{\text {cri}})$, with $\left\lfloor d_{\ell }(s,z)\right\rfloor = \left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor .$ Moreover, the break points $\delta _1, \ldots , \delta _k$ can be computed applying Procedure BPCF, where in Step (i), $\left\lfloor \rho (T_{\text {cri}},\ell )\right\rfloor$ is augmented to $\left\lfloor \rho (T_{\text {cri}}, \ell )+\delta _{\max }\right\rfloor$ in an optimal way and in Step (iv), a new break point is computed by $\delta =\left\lfloor \delta _{\max }-{\mathrm {hgt}}_{e_i}\right\rfloor .$ Note that we have $\delta _i\in \mathbb Z$, for $i=1,\ldots , k$. By applying Algorithm 2 with the redefined parameters

$$\begin{aligned} \varDelta =\left\lfloor \dfrac{{\mathcal {B}}+b}{\alpha +a}\right\rfloor \end{aligned}$$

and

$$\begin{aligned} \delta _{\max } =\left\lfloor \rho _{\max }\right\rfloor - \left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor , \end{aligned}$$

the integer value $\delta ^*$ and the temporary lengths $\ell ^{\text {t}}_e$, $e\in E_{\text {cri}}$, are attained. Define the temporary bounds $p^{\text {t}}_e$, $e\in E_{\text {cri}}$, by

$$\begin{aligned} p^{\text {t}}_e=\overline{p}_e-(\ell ^{\text {t}}_e-\ell _e)\in \mathbb Z. \end{aligned}$$

Let ${\mathcal {B}}^\prime$ be the remaining budget after augmenting the original lengths $\ell$ to the temporary length $\ell ^{\text {t}}$ at the end of Algorithm 2. We can immediately conclude the following result.

Lemma 5

There exists a leaf $z^*\in {\mathcal {L}}(T_{\text {cri}})$ with $\left\lfloor d_{\ell ^{\text {t}}}(s,z^*) \right\rfloor = \left\lfloor \rho (T_{\text {cri}},\ell ^{\text {t}})\right\rfloor$ such that $\rho (T_{\text {cri}},\ell ^*)=d_{\ell ^{\text {t}}}(s,z^*).$

According to Lemma 5, the integer part of the optimal objective value $\rho (T_{\text {cri}},\ell ^*)$ is equal to $\left\lfloor \rho (T_{\text {cri}}, \ell ) \right\rfloor +\delta ^*$. Moreover, the above lemma implies that the equality $d_{\ell ^*}(s,z)=d_{\ell ^{\text {t}}}(s,z)+1.$ is satisfied for every $z\in {\mathcal {L}}(T_{\text {cri}})$ with $d_{\ell ^{\text {t}}}(s,z)<\rho (T_{\text {cri}},\ell ^*).$ Therefore, the exact value of $\rho (T_{\text {cri}},\ell ^*)$ can be determined, if we find the maximum value $d_{\ell ^{\text {t}}}(s,z^*)$ such that the remaining budget ${\mathcal {B}}^\prime$ could augment all distances $d_{\ell ^{\text {t}}}(s,z)<d_{\ell ^{\text {t}}}(s,z^*)$ by one unit. For determining $d_{\ell ^{\text {t}}}(s,z^*)$, we proceed as follows: We first construct a new tree $T^\prime$ from $T_{\text {cri}}$ containing only the edges of $T_{\text {cri}}$ that can be augmented by at least one unit. The tree $T^\prime =(V^{\prime }, E^{\prime })$ is constructed in the following way. Direct all edges of $T_{\text {cri}}$ from the root s to the leaves ${\mathcal {L}}(T_{\text {cri}})$. Then, scan all edges of $T_{\text {cri}}$ in a breadth-first way starting with the edges $(s,v)\in E_{\text {cri}}$ and contract all edges that cannot be augmented anymore. For any edge $e = (u,v)$, we do:

If $p^{\text {t}}_e=0$, do:

• For all descendant edges $e^\prime = (v,w)\in E_{\text {cri}}$, set $\ell ^{\text {t}}_{e^\prime }=\ell ^{\text {t}}_{e^\prime } +\ell ^{\text {t}}_e$.

• contract e.

Let $\ell ^{\prime }_e$ be the length of the edge $e\in E^{\prime }$ obtained by the above procedure. We compute for all edges $e=(s,v)\in E^{\prime }$ outgoing from s, the critical distance of the subtrees $T^\prime (e)$ with respect to the edge lengths $\ell ^{\prime }$ in linear time.

Define

$$\begin{aligned} {\mathcal {I}}=\left\{ e=(s,v)\in E^{\prime }\ :\ \rho (T^\prime (e), {\ell }^{\prime })< \rho _{\text {max}},\ \left\lfloor \rho (T^\prime (e), {\ell }^{\prime }) \right\rfloor = \left\lfloor \rho (T_{\text {cri}}, \ell ^{\text {t}}) \right\rfloor \right\} . \end{aligned}$$

Observe that the remaining budget ${\mathcal {B}}^\prime$ can improve the lengths of $\left\lfloor {\mathcal {B}}^\prime \right\rfloor$ edges in ${\mathcal {I}}$ by one unit. Therefore, we get

Lemma 6

Let $\rho ^*$ be the $(\left\lfloor {\mathcal {B}}^\prime \right\rfloor +1)$-th largest value in the set $\left\{ \rho (T^\prime (e), {\ell }^{\prime })\ :\, e\in {\mathcal {I}}\right\} .$ Then, we have $\rho (T_{\text {cri}},\ell ^*)=\rho ^*$.

It should be noted that if $\left| {\mathcal {I}}\right| =0$, we have $\rho (T_{\text {cri}},\ell ^*)=\rho (T_{\text {cri}},\ell ^{\text {t}})$. But, if $0<\left| {\mathcal {I}}\right| <\left\lfloor {\mathcal {B}}^\prime \right\rfloor +1,$ the equation $\rho (T_{\text {cri}},\ell ^*)=\rho _{\text {max}}$ is satisfied.

As soon as the optimal value $\rho ^*$ is determined, we augment the length of the corresponding original edge $e\in E_{\text {cri}}$ of any edge $e^{\prime }\in {\mathcal {I}}$ with $\rho (T^\prime (e^\prime ), {\ell }^{\prime }) <\rho ^*$ to the optimal value $\ell ^*_e=\ell ^{\text {t}}_e+1$ and let all other temporary edge lengths remain unchanged. Now, according to the above results and observations, we can summarize our novel solution method in Algorithm 4.

Algorithm 4

(solves the uniform-cost integer RSOCP model on a tree T)

Step 1 :

Construct the critical subtree $T_{\text {cri}}$.

Step 2 :

Apply Algorithm 2 to obtain $\delta ^*$ and $\ell ^{\text {t}}$.

Step 3 :

Construct the tree $T^\prime$ and then specify the set $\mathcal {I}$.

Step 4 :

Determine the optimal objective value $\rho (T_{\text {cri}},\ell ^*)$ according to Lemma 6. The optimal edge lengths $\ell ^*$ are obtained immediately.

Note that the subtree $T_{\text {cri}}$ is constructed in ${\mathcal {O}}(|E|)$ time. Since Algorithm 2 runs in linear time, the temporary lengths $\ell ^{\text {t}}$ and $\delta ^*$ are computed in ${\mathcal {O}}(|E|)$ time. The required time for constructing $T^\prime$ and determining the set ${\mathcal {I}}$ is bounded by ${\mathcal {O}}(|E|)$. Furthermore, the $(\left\lfloor {\mathcal {B}}^\prime \right\rfloor +1)$-th largest element of a set is found in linear time [see e.g., Cormen et al. (2001)]. Altogether, we conclude

Theorem 5

The integer reverse selective obnoxious center location problem with uniform modification costs is solvable in ${\mathcal {O}}(|E|)$ time on a tree T.

Example

(Cont’d). Consider the uniform-cost version of the RSOCP model on the tree T of Fig. 1 with the associated budget ${\mathcal {B}}=7.8$. By applying Algorithm 2, we obtain $\delta ^*=4$ with the temporary edge lengths including

$$\begin{aligned} \ell ^{\text {t}}_{(s,v_1)}=4.1,\quad \ell ^{\text {t}}_{(v_1,v_2)}=2.1,\quad \ell ^{\text {t}}_{(v_2,v_3)}=4,\quad \ell ^{\text {t}}_{(s,v_9)}=4.1 \end{aligned}$$

while all other edge lengths of T remain unchanged. We get $\rho (T_{\text {cri}}, \ell ^{\text {t}})=10.2$ and ${\mathcal {B}}^\prime =2.8$. The corresponding tree $T^\prime$ of $T_{\text {cri}}$ is constructed as shown in Fig. 2. We derive the set ${\mathcal {I}}=\left\{ (s,v_3), (s,v_6), (s,v_{10})\right\}$ and then according to Lemma 6, the optimal critical distance $\rho (T_{\text {cri}}, \ell ^*)=10.5$ is achieved with

$$\begin{aligned} {\ell }^*_{(s,v_1)}=4.1,\quad {\ell }^*_{(v_1,v_2)}=2.1,\quad {\ell }^*_{(v_2,v_3)}=5,\quad {\ell }^*_{(v_2,v_6)}=5.2,\quad {\ell }^*_{(s,v_9)}=4.1 \end{aligned}$$

while the other original edge lengths remain unchanged.

Fig. 2

Illustration of the tree $T^\prime$ with edge lengths $\ell ^{\prime }$

5 Concluding remarks

If the incurred cost for changing the lengths of the tree T is measured by the bottleneck-type Hamming distance, the problem can efficiently be solved by setting

$$\begin{aligned} p^*_e={\left\{ \begin{array}{ll} \overline{p}_e &{}\quad \text {if}\;\ c_e\leqslant {\mathcal {B}},\\ 0&{}\quad \text {else},\\ \end{array}\right. } \end{aligned}$$

for all $e\in E$. Also, the optimal solution of the problem under the Chebyshev distance is simply given by $p^*_e=\min \{\overline{p}_e, {\mathcal {B}}/c_e\},$ for all $e\in E$. Moreover, in case of the sum-type Hamming distance, we can easily conclude that the problem is ${\mathcal {NP}}$-hard.

For further research, developing combinatorial solution algorithms for the problem on other special networks like cycles, sun graphs and etc. is promising.