The reverse selective balance center location problem on trees

Abstract

The classically balanced facility location problems aim to find the location of one or several new facilities such that some balanced function is optimized. This paper concerns the problem of improving the balanced objective at a prespecified vertex of a tree as much as possible within a given budget. We call such a problem the reverse selective balance center location problem on trees. All vertices are partitioned into two disjoint sets, in which one set consists of selective vertices. The balanced function is considered to be the difference in distance between the furthest demand point in the selective set and the nearest one in the remaining set. We first formulate the problem as linear programming. Then we propose a strategy to reduce the objective value in the case of variable edge lengths. An algorithm is developed to solve the reverse selective balance center location problem on trees in quadratic time.

1 Introduction

Over the past decade, location theory has experienced significant and powerful growth within the field of operational research, driven by its intriguing outcomes and real-world applications [2, 8]. Various real-world contexts can be framed as location problems, encompassing subjects ranging from human settlement and industrial site selection to understanding consumer behavior. The fundamental objective of classical location problems is to determine the optimal location of one or multiple new facilities, considering various environmental factors such as time, cost, and distances between customers and servers. Notably, the p-center and p-median problems stand out as the most widely recognized models in location science. In the context of the p-median problem, [1] introduced a modified firefly algorithm for solving this problem under different distance norms like rectilinear, Chebyshev, and Euclidean. Nevertheless, certain real-life situations restrict the relocation of servers, and the challenge becomes adjusting specific parameters with minimal cost to enhance the structure of the perturbed location problem. This concept has given rise to two new models in location theory. The first model involves altering edge lengths or vertex weights within a network to optimize predetermined locations in a modified environment while minimizing the overall modification cost. This problem is referred to as the inverse location problem and has been extensively explored [3, 7, 22]. The second model entails adjusting parameters to maximize the objective function at a fixed location within the constraints of a given budget. This is known as the reverse location problem. Early contributions by [5, 6] investigated enhancing the reverse 1-median and 1-center objectives through edge length reductions. [15] presented an $O(n\log n)$ algorithm for the inverse and reverse 2-facility location problems with equality measures.

The reverse center problem improves the efficiency and effectiveness of existing facility networks while considering practical constraints. As cities and urban areas evolve, the distribution of demand and resources may change. The reverse center problem addresses the need to reconfigure facility locations to better align with current demand patterns and resource availability. Furthermore, adapting existing facility networks can lead to cost savings related to transportation, operational efficiency, and other factors. [16] introduced a $O(n^2)$ algorithm for the reverse 1-center problem on weighted trees based on a greedy method. Furthermore, [9] explored a general variant of the reverse undesirable center location problem on cycle graphs, presenting a combinatorial $O(n \log n)$ algorithm for continuous modifications. They improved the algorithm for the uniform cost problem, achieving linear time complexity. [10] extended their research to reverse obnoxious center problems on tree graphs, delivering an $O(n^2)$ algorithm. [21] tackled the reverse 1-maxian problem while maintaining the 1-median, devising an algorithm with $O(n \log n)$ complexity. [23] studied two variants of reverse 1-center problems with a uniform linear cost function involving edge length reductions. An algorithm rooted in dynamic programming was introduced for the first problem, while the same algorithm was adapted to address the second problem in $O(n \log (nK))$ time, with K dependent on problem parameters. In 2021, [17] investigated the reverse total weighted distance problem on networks with variable edge lengths, demonstrating its NP-hardness and presenting a linear algorithm for trees. [24] considered the reverse 1-center problem on trees with vertex weights under a convex piecewise-linear cost function.

The balanced facility location problem arises from the practical need to ensure fairness and equitable distribution in facility placement while considering cost-effective solutions. In various applications such as public services, healthcare, and education, it’s crucial to ensure that facilities are located in a way that provides relatively equal access to all individuals or regions. Balancing the allocation of facilities helps avoid situations where certain groups or areas are disproportionately underserved. In philanthropic or humanitarian contexts, organizations strive to maximize the impact of their efforts by strategically placing facilities where they can benefit the largest number of people. In urban planning and infrastructure development, balanced facility placement can contribute to more evenly distributed traffic flow and infrastructure usage, promoting sustainable growth. The balanced facility location problem has been studied by many authors. [12] focused on maximizing the distance disparity between the nearest and farthest demand points. [4] considered the problem of finding p locations for p facilities such that the weights attracted to each facility are as close as possible to one another. [14] considered discrete facility locations with balanced customer allocations to plants. Nguyen et al. [20] explored balanced vertices in general trees and introduced a linear time algorithm to identify them. [25] introduced balancing the Efficiency and Effectiveness of the k-Facility Relocation Problem. [11] studied the balanced 2-median and 2-maxian problems on a tree.

The reverse balanced facility location problem is motivated by the desire to reconfigure existing facility networks in a way that not only optimizes operational efficiency and cost but also ensures a fair and equitable distribution of services. Over time, demand patterns can shift due to population changes, urban development, or economic fluctuations. In imbalanced networks, certain facilities may be overutilized while others remain underutilized. The reverse balanced facility location problem addresses the need to adjust existing facility networks to accommodate these changing demands. Although the problem has many practical applications, there are only a few results relevant to this topic. Omidi et al. [19] introduced algorithms with $O(n \log n)$ time complexity for inverse and reverse balanced facility location problems on trees, accounting for variable edge lengths. Omidi and Fathali [18] addressed an inverse single facility location problem on a tree with minimal edge length adjustments. They offered algorithms with $O(n \log n)$ and $O(n^2)$ complexities for cases of unbounded and bounded edge lengths, respectively. Previous studies have motivated us to further investigate the reverse balanced facility location problems.

In this paper, we delve deeper into the topic of reverse selective balance center location problems on trees. The organization of the paper is as follows. In section 2, we introduce the model for the reverse selective balance center location problems on trees. Section 3 focuses on presenting key properties related to the problem. Building upon these properties, section 4 proposes an algorithm designed to solve the reverse selective balance center location problems on trees. To illustrate the efficacy of the algorithm, we provide a numerical example that demonstrates its application and results. In Sect. 5, we summarize the findings and contributions of the paper.

2 Preliminaries

Given an undirected tree $T=(V, E)$ where V is the vertex set and E is the edge set. Each edge $e\in E$ has a length $l_e>0$. A point $s \in T$ is either a vertex or lies on the interior of an edge. The distance between a point s and a vertex v is defined as the length of the path connecting s and v, denoted by d(s, v).

In the context of a classical 1-center problem on an unweighted tree, the objective is to locate a point s within the tree T in such a way that the objective $F(s) = \mathop {\max }\limits _{v \in V} d\left( {s,{v}} \right)$ is minimized. In the scope of this paper, we consider the extension of the 1-center problem that incorporates the balancing function.

Let $V_1$ be the set of desirable vertices selected from set V and ${V_2} = V \backslash {V_1}$ be the set of obnoxious vertices. The selective balance distance function at a point s is defined as follows.

$$\begin{aligned} \mathcal {B}(s):=\max _{v\in V_1} d(s,v)-\min _{v\in V_2} d(s,v). \end{aligned}$$

It is remarkable that if either $V_2 = \emptyset$ or $V_1 =\emptyset$, then the function ${{\mathcal {B}}}(s)$ operates as a 1-center or an obnoxious 1-center function.

For a prespecified point $v^*$ in T, we can assume that it is a vertex. Otherwise, the edge $e=(u,v)$ that contains vertex $v^*$ is split into two sub-edges $e_1$ and $e_2$ such that $e_1\cap e_2=\{ v^* \}$ with $l_{e_1}=d(v^*, u)$ and $l_{e_2}=d(v^*, v)$. The setting of the reverse selective balance center location problem on trees is given as follows. The length of an edge can be increased (or decreased) by an amount of $p_e$ (or $q_e$). These amounts are bounded by $0 \le p_e \le \bar{p}_e$ and $0 \le q_e \le \overline{q}_e \le l_e$ to ensure that the modified edge lengths are always positive. Each unit of modification will have a cost of c(e) in both increasing and decreasing edge lengths. The goal is to modify the edge lengths such that the modified objective function at a vertex $v^* \in T$ is minimized and the total cost of modification is limited within a given budget B.

We may assume that there always exists a vertex $u \in V_2$ such that $u \in P(v^*,v)$ for some vertex $v \in V_1$. Otherwise, all vertices except $v^*$ belong to set $V_1$. If $V_1=V {\setminus } \{ v^* \}$, then the selective balance distance function at $v^*$ is $\mathcal {B}(v^*) = \max _{v \in V_1}d(v^*,v)$. The latter one is indeed the objective function of the reverse 1-center location problem. By this assumption, the modified objective value is always positive, i.e.,

$$\begin{aligned} \mathcal {B}(v^*) = \max _{v\in V_1} d(v^*,v) -\min _{v\in V_2} d(v^*,v)>0. \end{aligned}$$

Let $\hat{V}_1 \subseteq V_1$ be the set of vertices satisfying that if $v \in {\hat{V}}_1$, then $v \notin P(v^*,u)$ for any $u \in V_1$. Let ${\hat{V}}_2 \subseteq V_2$ be the set vertices such that if $v'\in {\hat{V}}_2$, then there is no $u' \in V_2$ satisfying $u' \in P(v^*,v')$. As $\max _{v\in V_1} d(v^*,v)=\max _{v\in \hat{V}_1}d(v^*,v)$ and $\min _{v\in V_2} d(v^*,v)=\min _{v\in \hat{V}_2}d(v^*,v)$, the selective balance distance function can be simplified as follows.

$$\begin{aligned} \mathcal {B}(v^*):=\max _{v\in \hat{V}_1}d(v^*,v)-\min _{v\in \hat{V}_2} d(v^*,v). \end{aligned}$$

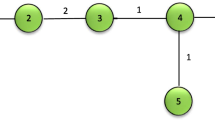
We consider Example 1 to show the computation of the objective function at a vertex.

Example 1

Given a tree with vertices and edge lengths depicted as in Fig. 1. We select $V_1= \{ v_3, v_5, v_6 \}$ and deduce $V_2 = \{ v_1, v_2, v_4 \}$. The objective function is $\mathcal {B}(v^*)=\max _{v\in {V}_1}d(v^*,v)-\min _{v\in {V}_2} d(v^*,v) = d(v^*,v_5)-d(v^*,v_2)=4$. Furthermore, we can determine two sets $\hat{V}_1 =\{v_3, v_5, v_6 \}$, $\hat{V}_2 = \{ v_1, v_2 \}$ and calculate $d(v^*,v_5) =\max _{v\in \hat{V}_1}d(v^*,v)$, $d(v^*,v_2)= \min _{v\in \hat{V}_2} d(v^*,v)$. Therefore, $\mathcal {B}(v^*)=\max _{v\in \hat{V}_1}d(v^*,v)-\min _{v\in \hat{V}_2}d(v^*,v) = 4$.

Fig. 1

A tree in Example 1

We denote by $\tilde{l}_e$ for all $e \in E$ and $\tilde{d}(u,v)$ the edge lengths and the distance from u to v after modification, respectively. Then $\tilde{l}_e=l_e+p_e-q_e$ and the modified objective function is

$$\begin{aligned} \tilde{\mathcal {B}} ({v^*}) = {\max _{v \in {\hat{V}_1}}}\tilde{d}({v^*},v) - {\min _{v \in {{\hat{V}}_2} }}{\tilde{d}}({v^*},v). \end{aligned}$$

Moreover, the total cost is limited to the budget of B. Applying the mentioned notation, the reverse selective balance center location problem on trees can be modeled as a linear program (LP) as follows.

$$\begin{aligned} \begin{aligned} {\min }\hspace{1.5cm}&\tilde{\mathcal {B}} (v^*) \\ \text { s.t. } \hspace{1.4cm}&\tilde{d}(v^*,v):=\sum _{e\in P(v^*,v)} (l_e+p_e-q_e), \quad v \in \hat{V}_1\cup \hat{V}_2 ,\\&\sum _{e\in E} c(e)(p_e+q_e)\leqslant B,\\&0\leqslant p_e\leqslant \overline{p}_e, \qquad \forall e\in E, \\&0\leqslant q_e\leqslant \overline{q}_e, \qquad \forall e\in E . \end{aligned} \end{aligned}$$

3 Solution method

Let $A_1=\{v\in \hat{V}_1: d(v^*,v)=\max _{v'\in \hat{V}_1} d(v^*,v')\}$ be the set of furthest vertices in $V_1$ and $A_2=\{v\in \hat{V}_2: d(v^*,v)=\min _{v'\in \hat{V}_2} d(v^*,v')\}$ be the set of nearest vertices in $V_2$. We get the following property on the modification of edge lengths.

Proposition 1

Let $v_1$ and $v_2$ be two vertices in $A_1$ and $A_2$, respectively. Then $p_e=0$ for $e\in P(v^*,v_1)$ and $q_e=0$ for $e\in P(v^*,v_2)$.

Proof

The balanced distance function at vertex $v^*$ is given by

$$\begin{aligned} \mathcal {B}(v^*):=\max _{v\in \hat{V}_1}d(v^*,v)-\min _{v\in \hat{V}_2} d(v^*,v). \end{aligned}$$

Since $v_1 \in A_1$ and $v_2 \in A_2$, we obtain that $\max _{v \in \hat{V}_1} d(v^*,v) = d({v^*},{v_1})$ and $\min _{v \in \hat{V}_2} d(v^*,v) = d({v^*},{v_2})$. Thus, $\mathcal {B}(v^*):= d(v^*,v_1) - d(v^*,v_2)$. Hence, if we increase the length of any edge $e \in P\left( {{v^*},{v_1}} \right)$ or reduce the length of any edge $e \in P\left( {{v^*},{v_2}} \right)$, then the balanced value distance increases. $\square$

According to Proposition 1, we set $\overline{p}_e=0$ for all $e\in \cup _{v_1 \in A_1} P(v^*,v_1)$ and $\overline{q}_e=0$ for $e \in \cup _{v_2\in A_2} P(v^*,v_2)$.

Corollary 1

If $e\in P(v^*,v_1)\cap P(v^*,v_2)$ for $v_1\in A_1$ and $v_2\in A_2$, then the length of edge e is fixed.

Example 2

Consider the tree given in Fig. 1. We can determine two sets $A_1=\{v_5\}$, $A_2=\{v_2\}$ and the balanced distance value at $v^*$ is $B(v^*)=4$. Suppose that we increase the length of edge $(v_2,v_5)$ by 1 unit. We calculate $B(v^*) =7-2=5$. Therefore, $B(v^*)$ also increases by 1 unit. This contradicts the assumption that we want to modify the edge length to reduce the objective value at the vertex $v^*$. Hence, for edges $e \in P(v^*, v_5)$ we set $p_e=0$. Similarly, we set $q_e=0$ with edges $e \in P(v^*,v_2)$. Furthermore, the edge $(v^*,v_2) \in P(v^*,v_5) \cap P(v^*,v_2)$ satisfies $p_e =0$ and $q_e=0$, so its length is fixed.

Corollary 2

If there exists a vertex $v_2 \in A_2$ such that $v_2 \in P(v^*,v_1)$ for $v_1 \in A_1$, then $\min _{v\in \hat{V}_2} \tilde{d}(v^*,v)=d(v^*,v_2)$.

We recall the concept of minimum cut applied to solve the problem. An s-t cut C in a graph $G=(V, E)$ refers to a set of edges such that removing them from the graph will result in the absence of a path connecting two vertices s and t. Suppose that R, S are two disjoint subsets of V satisfying $s \in R$ and $t \in S$, then the set C is represented as $C =\{(u,v) \in E \mid u \in R, v \in S \}$. A minimum s-t cut is an s-t cut with the smallest weighted sum among all other s-t cuts. The following example illustrates an s-t cut.

Example 3

Consider a simple graph with four vertices and edge weights as given in Fig. 2. All s-t cuts are $C_1 = \{(s, v_1), (s, v_2)\}$, $C_2= \{(s, v_1), (v_1, v_2), (v_2, t)\}$, $C_3 = \{(s, v_2), (v_1, v_2), (v_1, t)\}$, $C_4 = \{(v_1, t), (v_2, t)\}$. The minimum s-t cut of the graph in Fig. 2 is $C_3$ with a minimum weight of 6.

Fig. 2

A min s-t cut C

We now show the procedure of edge length modification by generating two graphs. One graph is used to increase the value of $\min _{v\in \hat{V}_2} d(v^*,v)$, while the other one is to reduce the $\max _{v \in \hat{V}_1} d(v^*,v)$ value. Based on the original graph $T=(V, E)$ and the sets $A_1, A_2$, we determine the auxiliary graphs $G_1, G_2$ to use for the calculation results later. Let $G_1=(V'_1,E'_1)$ be a graph with

$$\begin{aligned} V'_1=\{ v \in \cup _{v \in \hat{V}_1} P(v^*,v) \} \cup \{z\} \end{aligned}$$

and

$$\begin{aligned} E'_1=E_1^1\cup E_1^2 \end{aligned}$$

with $E_1^1 = \{e: e \in \cup _{v\in \hat{V}_1} P(v^*,v) \}$ and $E_1^2=\{(v,z):v\in \hat{V}_1\}$.

The weights of edges in $E'_1$ are defined as follows. If $e\in E_1^1$, then

$$\begin{aligned} w_1(e)={\left\{ \begin{array}{ll} c(e),\text { if } \overline{q}_e>0, \\ \infty ,\text { if } \overline{q}_e=0. \end{array}\right. } \end{aligned}$$

If $e \in E_1^2$, then

$$\begin{aligned} w_1(e)={\left\{ \begin{array}{ll} \infty ,\text { if } e = (v,z) \text { for } v\in A_1, \\ 0 ,\text { if } e = (v,z) \text { for } v \notin A_1. \end{array}\right. } \end{aligned}$$

Consider the minimum cut problem of graph $G_1$ with a source $v^*$, a sink z. [13] presented a polynomial algorithm for finding a minimum cut of a network in near-linear time. Denote $\mathcal {S}_1$ the cut set of minimum $v^*$-z cut problem in the graph $G_1$. If $\mathcal {S}_1 \ne \emptyset$, then the total cost for reducing the value of $\max _{v\in V_1} d(v^*,v)$ by $\delta$ is

$$\begin{aligned} \left( \sum _{e\in \mathcal {S}_1\cap E_1^1} c(e) \right) \delta , \end{aligned}$$

(1)

where the cut set $\mathcal {S}_1$ contains some edges in $e \in E_1^1$ satisfying $e\in \cup _{v\in A_1} P(v^*,v)$ or edges $e = (v,t) \in E^2_1$ with $v \in \hat{V}_1 {\setminus } {A_1}$. Note that reducing the length of an edge e by an amount $\delta$ leads to the reduction of the length of path $P(v^*,v)$ by $\delta$ for $v\in A_1$.

Let ${G_2} = ({V'_2},{E'_2})$ be a graph where

$$\begin{aligned} V'_2= \{v: v\in \cup _{v\in \hat{V}_2} P(v^*,v) \} \cup \{t\} \end{aligned}$$

and

$$\begin{aligned} E'_2=E_2^1\cup E_2^2 \end{aligned}$$

with $E_2^1 = \{e: e \in \cup _{v\in \hat{V}_2} P(v^*,v) \}$ and $E_2^2 = \left\{ (v,t): v\in \hat{V}_2 \right\}$.

Each edge $e \in E'_2$ is assigned by the weight. If $e \in E^1_2$, then

$$\begin{aligned} w_2(e)={\left\{ \begin{array}{ll}c(e), \text { if } \overline{p}_e >0, \\ \infty ,\text { if } \overline{p}_e =0. \end{array}\right. } \end{aligned}$$

If $e \in E^2_2$, then

$$\begin{aligned} w_2(e)={\left\{ \begin{array}{ll}\infty , \text { if } e = (v,t) \text { for } v\in A_2,\\ 0,\text { if } e = (v,t) \text { for } v \notin A_2. \end{array}\right. } \end{aligned}$$

We denote the set of minimum cutting edges by $\mathcal {S}_2$, and it contains some edges in $E_2^1$ with $e \in \cup _{v\in A_2} P(v^*,v)$ or edges $e=(v,t) \in E^2_2$ with $v \in {{\hat{V}}_2}\backslash {A_2}$. For any $e\in E_2^1$ with $\overline{p}_e>0$, we set $p_e=\delta$ for all $e\in \mathcal {S}_2\cap E_2^1$ in order to increase the value of $\min _{v \in \hat{V}_2} d(v^*,v)$ by a small amount of $\delta$. If $\mathcal {S}_2 \ne \emptyset$, the total cost after modification is

$$\begin{aligned} \left( \sum _{e\in \mathcal {S}_2\cap E_2^1} c(e) \right) \delta , \end{aligned}$$

(2)

and the objective value is also reduced by $\delta$. We set

$$\begin{aligned} \begin{aligned} \Delta _1=\sum _{e\in \mathcal {S}_1\cap E_1^1} c(e),\\ \Delta _2=\sum _{e\in \mathcal {S}_2\cap E_2^1} c(e),\\ \text { and } \Delta =\min \{\Delta _1,\Delta _2\}. \end{aligned} \end{aligned}$$

The efficiency of the cuts $\mathcal {S}_1, \mathcal {S}_2$ and the minimization base on the costs given in (1) and (2).

Proposition 2

To reduce the selective balance distance function value at $v^*$, we decrease the lengths of all edges $e\in \mathcal {S}_1\cap E_1^1$ by $\delta$ if $\Delta _1<\Delta _2$ or increase the lengths of all edges $e\in \mathcal {S}_2\cap E_2^1$ by $\delta$ if $\Delta _2\leqslant \Delta _1$. The cost of modification is $\Delta \delta$.

Proof

Suppose we want to reduce the distance function by an amount of $\delta$. According to the above arguments, to reduce the balanced distance function value by an amount of $\delta$, we either decrease the lengths of the edges $e \in \mathcal {S}_1 \cap E_1^1$ by $\delta$ or increase the lengths of the edges $e\in \mathcal {S}_2\cap E_2^1$ by $\delta$. The objective value $B(v^*)$ is reduced by $\delta$. The total cost of modification is $\Delta _1 \delta$ or $\Delta _2 \delta$. If $\Delta _1<\Delta _2$, then $\Delta _1 \delta < \Delta _2 \delta$. Note that reducing the edge length $e\in \mathcal {S}_1\cap E_1^1$ is less costly than increasing edge lengths of $e\in \mathcal {S}_2\cap E_2^1$. Thus, if $\Delta _1<\Delta _2$, then we reduce the lengths of edges $e\in \mathcal {S}_1\cap E_1^1$. Otherwise, we increase the edge lengths of $e\in \mathcal {S}_2\cap E_2^1$. $\square$

During the edge length modification, the objective value is reduced. Moreover, the structure of the graph $G_1$ or $G_2$ also changes. We need to take into account the point where this change occurs. Let $m=d(v^*,v)$, for $v \in A_2$ and ${{\mathcal {M}}} = d(v^*,v)$, for $v \in A_1$. We set

$$\begin{aligned} {\alpha } = \min \left\{ {{{\mathcal {M}}} - d({v^*},v):v \in {{{\hat{V}}}_1}\backslash {A_1}} \right\} \end{aligned}$$

and

$$\begin{aligned} {\beta } = \min \left\{ {d({v^*},v) - m:v \in {{{\hat{V}}}_2}\mathrm{{\backslash }}{\mathrm{{A}}_2}} \right\} . \end{aligned}$$

For edges $e\in \mathcal {S}_1\cap E_1^1$, we reduce all edge lengths by $\delta = \min \{ \overline{q}_e, \alpha \}$. If ${q_e} = \alpha$, then we can set $A_1=A_1\cup \{v\}$ where $e\in P(v^*,v)$. For edges $e\in \mathcal {S}_2\cap E_2^1$, we increase all edge lengths by $\delta = \min \{ \overline{p}_e, \beta \}$. Then the weight of edge e may be changed or we set $A_2=A_2\cup \{v\}$ with $e\in P(v^*,v)$.

4 Algorithm and numerical example

We propose Algorithm 1 to solve the problem.

Theorem 1

Algorithm 1 solves the reverse balance center location problem on trees in $O(n^2)$ time.

Proof

In each iteration, we can set $\overline{p}_e$ or $\overline{q}_e$ to 0. Hence, there are at most linearly many iterations. In each iteration, we find the min-cut set $\mathcal {S}_1$ and $\mathcal {S}_2$ in linear time. Moreover, we find $\alpha$ and $\beta$ in linear time by a breadth-first search algorithm in linear time. Therefore, the algorithm runs in $O(n^2)$ time. $\square$

To illustrate Algorithm 1, we consider the following example.

Example 4

An instance of the tree network is given as in Fig. 3, where the vertex $v^*$ is prespecified as the location of the facility, and each edge $e=(v_i,v_j)$ has a weight of a triple $\left( {l_e, \bar{z}_e, c(e)} \right)$ with $\bar{z}_e =\bar{p}_e =\bar{q}_e$. For example, edge $e'=\left( {{v^*},{v_1}} \right)$ has length $l_{e'}=4$, the upper bound of modification for both increasing and decreasing edge length $\bar{z}_{e'}=2$ and the cost of modifying one unit $c(e')= 3$. The total budget is given by $B =50$.

Fig. 3

A tree network in Example 4

Let ${V_1} = \left\{ {v_1},{v_2},{v_6}, {v_8},{v_9},{v_{10}},{v_{11}},{v_{12}},{v_{13}},{v_{14}} \right\}$ and ${V_2} = \left\{ {{v_3},{v_4},{v_5}, {v_7}} \right\}$. Then $\hat{V}_1=\{ v_8, v_9, v_{10}, v_{11}, v_{12}, v_{13}, v_{14} \}$ and $\hat{V}_2=\{v_3,v_4,v_5\}$. Moreover,

$$\begin{aligned} \max _{v\in \hat{V}_1} d(v^*,v)=16, \; \min _{v\in \hat{V}_2} d(v^*,v)=8. \end{aligned}$$

Hence $\mathcal {B}(v^*) = 16 -8 =8$. We solve the problem in the following iterations.

In the first iteration, we can find ${A_1} = \left\{ {{v_{10}}} \right\}$, ${A_2} = \left\{ {{v_3}} \right\}$ and construct two graphs $G_1, G_2$ as in Fig. 4 and 5.

Fig. 4

Graph $G_1$ constructed in Example 4

Fig. 5

Graph $G_2$ constructed in Example 4

The minimum $v^*$-z cut of $G_1$ is

$$\begin{aligned} \mathcal {S}_1 = \{(v_8,z), (v_1,v_4), (v_{11},z), (v_{12},z), (v_{13},z), (v_{14},z)\}, \end{aligned}$$

and $\Delta _1 = \sum _{e\in \mathcal {S}_1\cap E} c(e) =2$. In $G_2$, the minimum $v^*$-t cut is

$$\begin{aligned} \mathcal {S}_2 =\{ (v_1,v_3), (v_4,t), (v_5,t) \}, \end{aligned}$$

and $\Delta _2=\sum _{e\in \mathcal {S}_2\cap E} c(e) =2$. Hence, we can determine $\Delta = \min \{\Delta _1, \Delta _2\} =2$. Since $\Delta _2 \le \Delta _1$, we increase the length of edge $(v_1,v_3)= \mathcal {S}_2 \cap E$ by an amount of $\delta =\min \{{\bar{p}} _e, \beta , \frac{B}{\Delta } \}=1$. We update $B=48$, $\mathcal {B}(v^*)=7$, and edge $(v_1,v_3)$ has a weight of (5, 2, 2). Similarly, iterations 2, 3, 4, 5 and 6 can be executed in the same way as iteration 1. The algorithm stops after iteration 6 since the budget $B=0$. The modified objective value at vertex $v^*$ is minimized. Thus, the edge lengths after modification can be repeated as in Fig. 6.

Table 1 shows a summary of the results of the calculations over the six iterations in Example 4.

Table 1 Summary of the computational results in Example 4

Fig. 6

The optimal edge lengths in Example 4

5 Conclusions

In this paper, we have considered the reverse 1-center location problem on a tree under the selective balance cost function. Our problem generalizes the results from the reverse 1-center location problem on trees with variable edge lengths. We proposed a quadratic time algorithm to solve the problem based on a minimum cut approach on a series–parallel graph. Moreover, it is noted that the developed algorithm can be applied to solve the problem to which our problem generalizes in the same running time.

The principles of balance and the reverse approach have been independently incorporated into a wide array of prominent optimization models, including assignment problems, network flows, and location analysis. These integrated models have played a pivotal role in driving forward both theoretical understanding and practical application. As a result, the arena of future research focused on reverse balance optimization problems appears exceedingly promising. For instance, this encompasses the reverse balance single/multiple median problems on trees or general networks, as well as reverse balance assignment problems, among others.