Performance analysis of a reflected fluid production/inventory model

Abstract

We study the performance of a reflected fluid production/inventory model operating in a stochastic environment that is modulated by a finite state continuous time Markov chain. The process alternates between ON and OFF periods. The ON period is switched to OFF when the content level reaches a predetermined level q and returns to ON when it drops to 0. The ON/OFF periods generate an alternative renewal process. Applying a matrix analytic approach, fluid flow techniques and martingales, we develop methods to obtain explicit formulas for the cost functionals (setup, holding, production and lost demand costs) in the discounted case and under the long-run average criterion. Numerical examples present the trade-off between the holding cost and the loss cost and show that the total cost appears to be a convex function of q.

1 Introduction

Inventory control has long focused on managing certain specific types and sources of uncertainty in the production and demand process. Manufacturing systems, operating in random environment, are implemented by a variety of manufacturing firms in the food-processing industry, such as sugar (Grunow et al. 2007), electronic computer industries and the pharmaceutical industry (see also Mohebbi 2006). In practice, the average production rate of these facilities is higher than the average demand. As a consequence, the production facility has to be switched off once in a while to prevent inventory from growing without bound. In the special case of constant demand and production, the production–inventory system reduces to the classical economic production quantity (EPQ) model of Taft (1918). In the classic EPQ model every production cycle is composed of ON and OFF deterministic periods. There exists a predetermined level q such that the system is ON and the inventory level increases from level 0 up to level q. When level q is reached, the production is stopped and the inventory decreases down to 0. The time it takes from q to 0 is the OFF period.

In contrast with the assumption that production facilities can be switched off, many industries are characterized by high setup times and high setup costs where switching off the production is financially or operationally prohibitive. Thus, for both financial and operational reasons, it is critical to establish a proper production process early in the planning process; an overly high production rate results in high holding costs due to excess inventory, while a low production rate results in high penalty costs due to frequent stockouts and subsequent lost-sales.

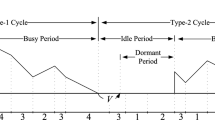
In this paper we aim at filling some of this category. Specifically, we consider the heavy traffic version of a EPQ system in which neither production nor demand never stop (another interpretation to the latter assumption could be the case in which customers are allowed to return items to the system). Here, too, we assume two periods, ON and OFF; however, the production and demand rates differ during ON/OFF periods and are modulated by a continuous-time Markov chain (CTMC) which represents the environment. For example, the rates can change due to weather, economy, competition, seasonal promotion, customer status, forecasting, etc. We further assume that the average growth rate (which is the production rate minus the demand rate) is positive during ON periods and negative during OFF periods. Thus, each cycle is composed of two parts; the first part is the ON period which ends when the content level reaches a predetermined level q and the second part, the OFF period, is the time it takes from q until the content level reaches level 0; we assume that switching from one period to the other takes no time. Finally, we assume that backlogging is not allowed (i.e., demands that cannot be satisfied directly from the inventory are lost); hence, the content level is generated by reflection on the total production minus the total demand (satisfied or unsatisfied), with 0 acting as the reflecting barrier.

For background on stochastic EPQ models, Vickson (1986) studied a continuous review, single product stochastic cycling problem with demand modelled as a Brownian motion process. Recently, Wu and Chao (2013) extend this result to include a two-dimensional Brownian motion process. Berman and Perry (2001) present an ON/OFF model with a reflected Brownian motion. Boxma et al. (2001) consider a fluid system in which during the OFF times the buffer content increases as a piecewise linear process according to some semi-Markov process, and during the ON times, it decreases with a state-dependent rate. They derive the stationary distribution, steady state Laplace–Stieltjes transform and moments of the buffer content. Berman et al. (2007) study the long-run average performance of a fluid production/inventory model which alternates between ON periods and OFF periods and derive the pertinent reward functionals in a closed form.

Further examples on the ON/OFF process come from queueing literature (e.g., Kella and Whitt 1992; Boxma et al. 2005; Zhang and Zwart 2012), limited-capacity industries (e.g., Perry and Posner 2002), service systems, seasonal food products (i.e., ice cream, soup powder) and epidemics in which the quantity of interest is the number of susceptibles and the OFF period corresponds to mass preventive actions whenever the number of susceptibles exceed a specific number (Taylor 1968).

An example that the authors are familiar with comes from EL-AL, Israel Airline Ltd., (www.elal.com). EL-AL has internal workshops that are responsible for the maintenance of the aircraft. Their activity is to repair the damaged aircraft spare parts. Huge cost and time associated with switching assembly lines off cause the workshops to operate continuously in a 24/7 manner. Due to the stochastic nature of the production (damaged components) and the demand (repaired items) processes, inventories (items waiting to be repaired) may reach undesirably high levels and can cause a shortage of repaired items essential for the airlines operations. Thus, each time a predetermined inventory level is reached, the workshop reduces the inventory level by increasing the rate of repair.

Another potential application of our study arises from customers which are allowed to return items to the buffer and negative inventory is not allowed. Inventory management with returning items have received a lot of attention in the literature; for example, Beltran and Krass (2002) experience with a major Canadian catalogue retailer that 30–40 % of inventory for many fashion items was due to returns, which made this source of “re-supply” very important. Recently, Shaharudin et al. (2015) study product returns and recovery management among six manufacturing firms in Malaysia. More examples of this line of research are Fleischmann et al. (2002) and Pinçe et al. (2008).

Our paper is also related to the literature encompasses a compound Poisson demand (e.g., Shi et al. 2014; Barron et al. 2014) or demand process that is a mixture of continuous demand and compound Poisson demand (e.g., Kok et al. 1984; Germs and Foreest 2014). For models based on Markovian decision process see e.g., Song and Zipkin (1993).

The underlying inventory process studied in this paper can also describe a variety of interpretations drawn from the contexts of perishable models. There are two types of perishable inventory models. The first family of models assumes that the quality of the items is slowly decreases over time; for example, a plant that produces ice-cream (see Boxma et al. 2014, 2015). The second family is models with obsolescences. Here, the items might perish at each period with some probability which is typically increasing over time. Examples of obsolescence models range from avionics and military sectors, high tech products, communications, construction equipment, medical devices, transportations and supply chain networks [we refer the readers to Tyler (2004), Song and Lau (2004), Shen and Willems (2014) for more examples].

In this paper we study four types of costs: (i) fixed setup cost; (ii) holding cost for the inventory; (iii) production cost and (iv) lost demand cost due to the reflection at level zero. Our objective is to obtain tractable formulas for the appropriate cost functionals. We focus on the discounted cost criterion using a discount factor $\beta >0;$ however, we also deal with the long run average cost criterion. To the best of our knowledge, although the related literature is voluminous, our model seems to be more general and new and has been never investigated in the inventory literature; thus our research differs. Furthermore, while the afore-mentioned papers involve analytic derivations of the quantities of interest, we emphasize our study using a more probabilistic approach via exit-time results and regenerative theory. this enables a simple derivation of quantities of interest and obtains easy-to-implement explicit formulas.

Our analysis is based on a combination of a certain martingale technique and an application of fluid flow theory. The martingale approach was introduced by Asmussen and Kella (2000) and was frequently used in the study of inventory models, see e.g., Kella et al. (2003), Barron (2015), Barron et al. (2014) and Shi et al. (2013) and the references given therein. Markov-modulated fluid flow models have been an active area of research in recent years; one of their main applications is to the modeling the traffic evolution in communication channels. Silva and Latouche (2005) consider fluid queue with a buffer of a finite capacity where the behavior of the background Markov process is allowed to change whenever the buffer is empty or when it is full. We use results of Ramaswami (1999) who initiated an unified matrix-analytic algorithmic approach to fluid flows, and this was followed by a series of papers by him, Ahn and others (see Ramaswami 2006; Ahn et al. 2007).

Our analysis enables a simple derivation of quantities of interest and obtains easy-to-implement explicit formulas. These explicit formulas can then be used for an analysis of the dependence of the cost functionals on the system parameters, or for optimization purposes when some of these parameters (e.g., the costs, production rates and the storage capacity) are taken as decision variables. Through numerical examples we display the behavior of the costs and present the trade-off between the holding cost and the lost demand cost as a function of q. We show that the set up and holding costs are similar to those associated with the classical EPQ model. Finally, our observations show that the expected discounted total cost appears to be a convex function of q; thus it is worthwhile for the controller to determine the optimal q in order to minimize the total cost.

The remainder of the paper is organized as follows. In Sect. 2 we present the mathematical description of the model and the cost functionals. The crucial tools of our analysis are introduced in Sect. 3. In Sect. 4 all the cost functionals for the discounted case derived in closed form. Finally, the long-run average analysis is given in Sect. 5. We also provide some numerical examples and insights.

2 Mathematical description of the model

We apply similar notations and definitions presented by Barron (2015). Let I(t) be the fluid level in the buffer at time t. The rate of change of the fluid level is modulated by a CTMC $\{\mathcal {J}(t):t\ge 0\}$ on a finite state space $S=\{1,2,\ldots ,n\}$ with a generator matrix $Q=[Q_{ij}]$. Let $\pi =[\pi _{1},\ldots ,\pi _{n}]$ be the limiting distribution of the $\mathcal {J}(t)$ process, i.e., $\pi$ is the unique solution to $\pi Q=0,\pi e=1$ (where 0 is a row vector with all 0’s and e is a column vector with all 1’s). Let $\upsilon =[\upsilon _{1},\upsilon _{2},\ldots ,\nu _{n}]$ be the initial probability vector of $\mathcal {J}(t)$. We assume $I(0)=0.$ The process I(t) can be partitioned into two parts, $I^{+}(t)$ and $I^{-}(t).$ The first part of the cycle is the ON period $\tau$ and this period ends whenever the content level reaches a predetermined level q. The second part of the cycle, the OFF period T,  is the time it takes from $\tau$ until the content level reaches level 0. Each period is characterized by stochastic inputs (production) and outputs (demand). However, we assume two sets of production rates $\{p_{1} ^{1},\ldots ,p_{n}^{1}\}\subset (0,\infty )$ and $\{p_{1}^{2},\ldots ,p_{n} ^{2}\}\subset (0,\infty )$ and two sets of demand rates $\{d_{1}^{1} ,\ldots ,d_{n}^{1}\}\subset (0,\infty )$ and $\{d_{1}^{2},\ldots ,d_{n} ^{2}\}\subset (0,\infty ).$ The rate at which the inventory is filled at time t is determined by the current environmental state $\mathcal {J}(t)$ and the period. During the ON period (OFF period) and as long as $\mathcal {J}(t)$ is in state i,  the production occurs continuously at rate $p_{i}^{1}$ ($p_{i}^{2}$),  and there is a demand at rate $d_{i}^{1}$ ($d_{i}^{2}$). The growth rate is the difference of the production rate and the demand rate, $r_{i}^{1}=p_{i}^{1}-d_{i}^{1}$ ($r_{i}^{2}=p_{i}^{2}-d_{i}^{2}$). Note that $r_{i}^{1},r_{i}^{2}$ $i=1,\ldots ,n$ may be either negative or positive. Let $R_{1}=\{r_{1}^{1},\ldots ,r_{n}^{1}\}$ and $R_{2}=\{r_{1}^{2},\ldots ,r_{n}^{2}\}.$ In our model we do not allow backlog; thus when the content level drops to level 0 (notice that this event can occurs only during ON periods), it stays there as long as the environmental growth rate is negative and until the environmental state changes to some positive growth rate. Furthermore, the behavior of the process during each period is different; during the OFF period $R_{2}$ satisfies

$$\begin{aligned} \sum _{i=1}^{n}\pi _{i}r_{i}^{2}<0, \end{aligned}$$

(1)

and during the ON period, $R_{1}$ satisfies

$$\begin{aligned} \sum _{i=1}^{n}\pi _{i}r_{i}^{1}>0. \end{aligned}$$

(2)

A typical sample path of the inventory process is given in Fig. 1.

Fig. 1

A sample path of the inventory process I(t)

Note that, (1) is a necessary and sufficient condition for the stability of the OFF process (see Kulkarni and Yan 2007), while the ON process, with the absence of (2), is stable due to the reflection at level 0; however, (2) is assumed in order to avoid high lost demand. We assume that conditions (1) and (2) hold for the rest of this paper. Note that, due to the stochastic behavior of the process, the content level can exceeds q during the OFF period.

Remark 1

The model described above can be easily generalized by assuming arbitrary initial content level $\gamma >0$ (see e.g., Berman et al. 2007). Obviously, the long-run average cost is not affected; however, it affects the discounted cost. For simplicity, and since the case of $\gamma >0$ can be easily derived from our analysis, we assume $\gamma =0.$

Clearly, the content level process is a semi-regenerative process which alternates between ON periods and OFF periods. Define the following stopping times:

$$\begin{aligned} T_{0}&=0 \\ T_{n}&=\inf \left\{ t>\tau _{n}:I(t)=0\right\} \quad n=1,2,\ldots \\ \tau _{n}&=\inf \left\{ t\ge T_{n-1}:I(t)=q\right\} \quad n=1,2,\ldots \end{aligned}$$

$T_{n},n=1,2,\ldots$ are the times of switchings from OFF to ON and $\tau _{n},n=1,2,\ldots$ are the time instants of switchings from ON to OFF. Thus, the content level process is a semi-regenerative process with $T_{n}^{\prime }s$ are semi-regenerative points. Define the nth cycle as the time elapsed between $T_{n-1}$ and $T_{n},n=1,2,\ldots$ and let $C_{n}=T_{n}-T_{n-1} ,n=1,2\ldots$ be the nth cycle length. Note that, if the ON periods are deleted from the sample path and the OFF periods are glued together we obtain a fluid EOQ model with refillings every time level 0 is reached.

For the rest of the paper, we use P (E) to denote the underlying probability measure (expectation), and $P_{i}$ $(E_{i})$ denotes conditional probability (expectation) given initial state $i\in S.$ $\mathbf {E}$ and $\mathbf {E}_{i}$ are the corresponding vector expectation and conditional vector expectation operators. $\mathbb {E},\mathbb {P}$ represent a matrix-valued expectation and probability operators, respectively. We denote by $e_{i}$ a vector with the ith component equal to 1 and all the other components 0,  by I the identity matrix (all of the appropriate sizes) and by $\mathbf {1}_{\{A\}}$ the indicator of an event A.

2.1 The cost functionals

Let us now introduce the functionals representing the various expected discounted costs in our model, using the discount factor $\beta >0$. We will use the fact that the inventory process is a semi renewal Markov process with $T_{n}^{\prime }s$ points as semi-regenerative points. For the rest of the paper let $\tau =\tau _{1},T=T_{1},T^{\prime }=T-\tau$ and $C=C_{1}$ (so $C=\tau +T^{\prime }$). Note that I(t) is partitioned into two parts, $I^{+}(t)$ (the ON period, the time until $\tau$) and $I^{-}(t)$ (the OFF period, the time that elapses from $\tau$ until T); furthermore, conditioning on the state at time $\tau$ and the common background environmental process,  the two process $I^{+}(t)_{0\le t\le \tau }$ and $I^{-}(t)_{\tau \le t\le T}$ are independent.

In this paper we consider four costs: (a) the setup cost, (b) the holding cost of the inventory, (c) the production cost and (d) the unsatisfied demand cost. Our main objective is to develop techniques enabling us to determine all these costs in closed form under the discounted as well as under the long run average cost criterion. In the course of our derivations we will determine not only the cost functionals themselves but also various other transforms and probabilities describing the inventory level process that may be of independent interest.

• (a) Set up cost Let $k_{1}$ be the setup cost to switch from OFF to ON (at time T) and $k_{2}$ be the setup cost to switch from ON to OFF (at time $\tau )$. The expected discounted set-up cost $SC_{\infty }(\beta )$ is given by

  $$\begin{aligned} \textit{SC}_{\infty }(\beta )=\upsilon E \sum \limits _{n=1}^{\infty } \left( k_{1}\exp \left( -\beta T_{n}\right) +k_{2}\exp \left( -\beta \tau _{n}\right) \right) . \end{aligned}$$

  (3)

  where $\upsilon$ is the initial probability vector. Since I(t) is a semi-regenerative process, $\textit{SC}_{\infty }(\beta )$ can be expressed in terms of one cycle:

  $$\begin{aligned} \textit{SC}_{\infty }(\beta )=\upsilon \left( I-\mathbb {E}\left( e^{-\beta C}\right) \right) ^{-1}\left( k_{1}\mathbb {E}\left( e^{-\beta C}\right) +k_{2}\mathbb {E}\left( e^{-\beta \tau }\right) \right) e. \end{aligned}$$

  (4)

  We use $\mathbb {E}( e^{-\beta C})$ as a shorthand notations for the $(n\times n)$ matrix whose ijth component is given by

  $$\begin{aligned} \left[ \mathbb {E}\left( e^{-\beta C}\right) \right] _{ij}=E\left( e^{-\beta C}\mathbf {1}_{\left\{ \text {level}\,0\,\text {hit at time}\,C\,\text {in phase}\,j\right\} }\mid \mathcal {J}(0)=i\right) . \end{aligned}$$

  (5)

  Similarly, the ijth component of the $(n\times n)$ matrix $\mathbb {E}(e^{-\beta \tau })$ is given by

  $$\begin{aligned} \left[ \mathbb {E}\left( e^{-\beta \tau }\right) \right] _{ij}=E\left( e^{-\beta \tau }\mathbf {1}_{\left\{ \text {level}\,q\,\text {hit at time}\,\tau \,\text {in phase}\,j\right\} }\mid \mathcal {J}(0)=i\right) . \end{aligned}$$

  (6)

• (b) Holding cost The total expected discounted holding cost can be expressed by the functional

  $$\begin{aligned} \textit{HC}_{\infty }(\beta )=\textit{hE}\left( {\displaystyle \int \limits _{0}^{\infty }} e^{-\beta t}I(t)dt\right) , \end{aligned}$$

  where hdt is the holding cost for a unit of stock during the time interval dt. Revoking the ergodic theorem for regenerative process, we can write $HC_{\infty }(\beta )$ in terms of the first cycle and have

  $$\begin{aligned} \textit{HC}_{\infty }(\beta )=h\upsilon \left( I-\mathbb {E}\left( e^{-\beta C}\right) \right) ^{-1}\left( \widehat{\mathbf {h}}_{1}(\beta )+\mathbb {E} \left( e^{-\beta \tau }\right) \widehat{\mathbf {h}}_{2}(\beta )\right) , \end{aligned}$$

  where $(n\times 1)$ vectors $\widehat{\mathbf {h}}_{1}(\beta )$ and $\widehat{\mathbf {h}}_{2}(\beta )$ are given by

  $$\begin{aligned} \widehat{\mathbf {h}}_{1}(\beta )=\mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta t}I^{+}(t)dt\right) ,\quad \widehat{\mathbf {h}}_{2} (\beta )=\mathbf {E}\left( {\int \limits _{0}^{T^{\prime }}} e^{-\beta t}I^{-}(t+\tau )dt\right) . \end{aligned}$$

• (c) Production cost Let c be the production cost for one unit. Similarly, the expected discounted production cost $\textit{PC}_{\infty }(\beta )$ is given by

  $$\begin{aligned} \textit{PC}_{\infty }(\beta )= & {} \textit{cE}\left( {\int \limits _{0}^{\infty }} p_{_{\mathcal {J}(t)}}e^{-\beta t}dt\right) \\= & {} c\upsilon \left( I-\mathbb {E}\left( e^{-\beta C}\right) \right) ^{-1}\left( \widehat{\mathbf {p}}_{1}(\beta )+\mathbb {E}\left( e^{-\beta \tau }\right) \widehat{\mathbf {p} }_{2}(\beta )\right) , \end{aligned}$$

  where $\widehat{\mathbf {p}}_{1}(\beta )$ and $\widehat{\mathbf {p}}_{2}(\beta )$ are $(n \times 1)$ vectors represent the expected discounted production amount during ON and OFF periods, respectively.

  $$\begin{aligned} \widehat{\mathbf {p}}_{1}(\beta )=\mathbf {E}\left( {\int \limits _{0}^{\tau }} p_{_{\mathcal {J}(t)}}^{1}e^{-\beta t}dt\right) ,\quad \widehat{\mathbf {p}}_{2}(\beta )=\mathbf {E}\left( {\int \limits _{0}^{T^{\prime }}} p_{_{\mathcal {J}(t+\tau )}}^{2}e^{-\beta t}dt\right) . \end{aligned}$$

• (d) Lost demand cost In our mode, backlog is not allowed; any demand which cannot be satisfied immediately is lost. Clearly, there is no unsatisfied demand during the OFF period. During ON period, once level 0 is reached the process stays there until the environment changes to state with a positive growth rate. Assume the process hits 0 at state i (for some $r_{i}^{1}<0),$ the demand is lost with rate $(-r_{i} ^{1})$ until the environmental state changes. Let wdt be the cost for a lost unit during a time interval of length dt ($w>0$). As a measure for the expected discounted lost demand cost one can use the functional

  $$\begin{aligned} \textit{UC}_{\infty }(\beta )&=-\textit{wE}\left( {\int \limits _{0}^{\infty }} e^{-\beta t}r_{\mathcal {J}(t)}^{1}\mathbf {1}_{\{I^{+}(t)=0\}}dt\right) \nonumber \\&=-w\upsilon \left( I-\mathbb {E}\left( e^{-\beta C}\right) \right) ^{-1} \mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta t}r_{\mathcal {J}(t)}^{1}\mathbf {1}_{\{I^{+}(t)=0\}}dt\right) \nonumber \\&=w\upsilon \left( I-\mathbb {E}\left( e^{-\beta C}\right) \right) ^{-1} \widehat{\mathbf {u}}(\beta ). \end{aligned}$$

  (7)

  The $(n\times 1)$ vector $\widehat{\mathbf {u}}(\beta )$ is the expected discounted production loss during the first cycle. Notice that the lost demand can be written in terms of the local time process. Consider the process $X(t)=\int \nolimits _{0}^{t}r_{\mathcal {J}(u)}^{1}du$ and let $L(t)=-\min _{0\le u\le t}X(u).$ The process X(t) represents the inventory level at time t of the unrestricted process (the process without a barrier at level 0). The process L(t) is known as the local time and is a non-decreasing process that increases only whenever $I^{+}(t)=0.$ Therefore, an appropriate functional for the unsatisfied demand is

  $$\begin{aligned} \widehat{\mathbf {u}}(\beta )=\mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta t}dL(t)\right) . \end{aligned}$$

  (8)

  A simple cost function for the entire system would be the sum, say $\textit{TC}(\beta )$, of these four expected discounted costs:

  $$\begin{aligned} \textit{TC}_{\infty }(\beta )=\textit{SC}_{\infty }(\beta )+\textit{PC}_{\infty }(\beta )+\textit{HC}_{\infty } (\beta )+\textit{UC}_{\infty }(\beta ). \end{aligned}$$

  (9)

  The cost functionals $\mathbb {E}(e^{-\beta C}),$ $\mathbb {E} (e^{-\beta \tau }),$ $\widehat{\mathbf {p}}_{1}(\beta )$, $\widehat{\mathbf {p}}_{2}(\beta )$, $\widehat{\mathbf {h}}_{1}(\beta )$, $\widehat{\mathbf {h}}_{2}(\beta )$ and $\widehat{\mathbf {u}}(\beta )$ will be derived in Sect. 4. The crucial tools of our analysis are introduced in the next section.

3 Preliminaries

For the determination of the cost functionals we use two tools: (a) an application of optional sampling theorem to a multi-dimensional martingale first presented by Asmussen and Kella (2000) and (b) the matrix-analytic approach and the theory of Markov-modulated fluid flows initiated by Ramaswami (2006). We summarize them shortly in order to make this paper self-contained.

3.1 The multi-dimensional martingale

Let $\{\mathsf {X}(t),t\ge 0\}$ be a right continuous Markov modulated Lévy process with modulating process $\{\mathcal {J}(t),t\ge 0\}$ which is a right continuous irreducible finite state space continuous time Markov chain. Let $\{ Y(t),t\ge 0\}$ be an adapted continuous process with a finite expected variation on finite intervals and let $Z(t)=\mathsf {X} (t)+Y(t)$. Asmussen and Kella (2000) have shown, that for such a process, the matrix with elements $E_{i}[ e^{\alpha \mathsf {X} (t)};\mathcal {J}(t)=j]$ has the form of $e^{tK(\alpha )}$ for some matrix $K(\alpha )$. Theorem 2.1 in Asmussen and Kella (2000) yields that under certain mild conditions on $\{ Z(t),t\ge 0\} ,$ the multi-dimensional process

$$\begin{aligned} M(\alpha ,t)= & {} \int _{0}^{t}e^{aZ(s)}\mathbf {1}_{\mathcal {J}(s)}ds K(\alpha )+e^{aZ(0)}\mathbf {1}_{\mathcal {J}(0)}-e^{aZ(t)}\mathbf {1}_{\mathcal {J} (t)}\nonumber \\&+\,\alpha \int _{0}^{t}e^{aZ(s)}\mathbf {1}_{\mathcal {J}(s)}dY(s) \end{aligned}$$

(10)

is a (row) vector valued zero mean martingale.

In our model, the inventory content level I(t) is a special case of $\mathsf {X}(t)$ and has piecewise linear sample paths with slope $r_{j}^{1}$ during ON period and $r_{j}^{2}$ during OFF period on intervals where $\mathcal {J(}t\mathcal {)}$ $=j\in S;$ Thus, some of the relevant functionals in this paper will be obtained by applying the optional stopping theorem (OST) (or Doob’s optional sampling theorem) to appropriate special cases of (10).

3.2 The fluid inventory model

The conventional Markov-modulated fluid flow (MMFF) process is a fluid input-output process in which the rates of changes of fluid level are all linear and are governed by underlying Markov chain with infinitesimal generator Q and state space S $(\vert S\vert =n)$. Let us partition the Markov chain phases as two sets $\{ S_{1},S_{2}\}$ where $S_{1}$ is the set of phases with increasing rates and $S_{2}$ is the set of phases with decreasing rates $(S=S_{1}\cup S_{2},\vert S_{1}\vert =n_{1},\vert S_{2}\vert =n_{2}).$ Comfortingly to $S_{1}$ and $S_{2}$, the infinitesimal generator can be expressed as $Q=\left( \begin{array} [c]{cc} Q_{11} &{}\quad Q_{12}\\ Q_{21} &{}\quad Q_{22} \end{array} \right)$. During the sojourn time when the Markov phase is in $i\in S_{1},$ the fluid level increases with rate (slope) $r_{i}>0$ and decreases with slope $\vert r_{i}\vert$ (for $r_{i}<0)$ during $i\in S_{2}$ (provided the fluid level is positive). We construct diagonal matrices $U_{j} =diag\{\vert r_{i}\vert$, $i\in S_{j}\},j=1,2$ and $U=diag(U_{1} ,U_{2})$ from these rates.

Table 1 LST of first passage times

Let $\mathcal {F}(t)$ be the fluid level at time t and $\mathcal {J}(t)$ the phase of the Markov chain at time t; the two dimensional stochastic process $\{\mathcal {F}(t),\mathcal {J}(t),t\ge 0\}$ is called the MMFF process. In the analysis of MMFF-related process, first passage times play important roles. Let $\sigma (x)=\inf \{t>0,\mathcal {F}(t)=x\}$ be the first passage time to level x and define the following Laplace–Stieltjes transforms (LST)

$$\begin{aligned} \left[ \Psi (\beta )\right] _{ij}=E\left( e^{-\beta \sigma (0)},\mathcal {J} (\sigma (0))=j\mid \mathcal {F}(0)=0,\mathcal {J}(0)=i\right) \quad i\in S_{1},\quad j\in S_{2}. \end{aligned}$$

(11)

$[\Psi (\beta )]_{ij}$ represents the LST of $\sigma (0)$ restricted to the event that the fluid process hits level 0 at state $j\in S_{2},$ given $\mathcal {F}(0)=0$ and $J(0)=i\in S_{1}.$ Ramaswami (2006, Appendix 1, p. 512) shows how to compute the matrix $\Psi (\beta )$ and provides a good algorithm for this. Let $_{a}^{b}\tau (x,y)$ (for $x\ge 0,y\ge 0$) be the first passage time of $\mathcal {F}$ from level x to level y avoiding a visit to the levels in $[0,a]\cup [b,\infty )$ enroute (note that in the case of unlimited visit, a and b are omitted). We use the notation $_{a}^{b}\widehat{f}(x,y,\beta )$ to denote the matrix of Laplace–Stieltjes transform of the joint distribution of the first passage time $_{a}^{b}\tau (x,y)$ and the state of the phase process at each first passage time. Once we have computed $\Psi (\beta )$, the LST matrix $_{a}^{b}\widehat{f}(x,y,\beta )$ is straightforward to evaluate. In the “Appendix”, we present the detailed algorithm to compute $\Psi (\beta )$ and the formulas for other LST matrices. For more details, we refer the readers to Ramaswami (2006).

Regarding our model, each ON/OFF period has one type of rates $(R_{1}$ or $R_{2})$; hence, given the state at switching epoch and the common environment, the ON/OFF periods are independent. Thus, we can analyze the inventory content level within each period independently using MMFF process. Specifically, we consider two fluid processes $\mathcal {F}^{+}$ (with $Q^{+}$) and $\mathcal {F}^{-}$ (with $Q^{-}$) corresponding to the ON and OFF periods, respectively; we also have the matrices $U^{+}=diag(U_{1}^{+},U_{2}^{+})$ and $\Psi ^{+}(\beta )$ $(U^{-}=diag(U_{1}^{-},U_{2}^{-}),\Psi ^{-} (\beta ))$ corresponding to the ON (OFF) process. We list in Table 1 LST matrices for hitting times, that we will use throughout our derivation. As mentioned before, these matrices are straightforward to evaluate once we have computed $\Psi (\beta )$ and are given in Ramaswami (2006). Note that, for our model, each LST matrix should be derived for ON (marked as +) and OFF (marked as $-$) processes. For the rest of the paper we do not insert the marks + or $-$ corresponding to ON/OFF processes; it should be clear from the context which of the marks applies.

Remark 2

In the course of our derivations, we will apply the phase type distribution. A phase-type distribution with representation $(\mathcal {E},\alpha _{0},\mathbf {\alpha ,T})$ is the distribution of the time to absorption for a CTMC with a finite state space $\mathcal {E}$ and one absorbing state. $\alpha _{0}\in [0,1)$ is the probability of immediate absorption or the atom at 0; it is omitted if the distribution has no atom at 0. $\mathbf {\alpha }$ is the initial probability vector on the set of transient states and $\mathbf {T}$ is the matrix of transition rates among the transient states. Let X be a phase type distributed, then

$$\begin{aligned} E(X)&=\alpha \left( -\mathbf {T}^{-1}\right) e\\ M_{X}(\beta )&=\alpha _{0}+\alpha \left( \beta I-\mathbf {T}\right) ^{-1}T^{o} \end{aligned}$$

where $M_{X}(\beta )$ is the Laplace–Stieltjes transform of X and $T^{o}=-\mathbf {T}e$.

In this paper, for any matrix B, we shall denote its elements by $(B)_{ij}$ or by $[B] _{ij}$ and reserve the notation $B_{ij}$ for the sub-matrix of B with row indices in $S_{i}$ and column indices in $S_{j}$. Furthermore, for matrices A and B we use the shorthand notation (A, B) to denote the matrix obtained by stringing the matrix B after the matrix A (obviously, A and B have the same number of rows).

4 The discounted model

Let us now derive the seven functionals indicating the expected discounted costs in our model using a discount factor $\beta >0$.

4.1 Setup cost functionals

In order to obtain the setup costs we have to derive the $(n\times n)$ matrices $\mathbb {E}(e^{-\beta \tau })$ and $\mathbb {E}(e^{-\beta C})$ [see (5), 6)].

4.1.1 The matrix $\mathbb {E}(e^{-\beta \tau })$

Let $\widehat{\mathbb {E}}(e^{-\beta \tau })$ be an $(n\times n_{1})$ matrix whose ijth component is the LST of the time to reach level q in phase $j\in S_{1},$ given initial phase $i\in S$. Since time $\tau$ occurs only for states in $S_{1}$, $\mathbb {E}(e^{-\beta \tau })$ has the form of

$$\begin{aligned} \mathbb {E}\left( e^{-\beta \tau }\right) =\left( \widehat{\mathbb {E}}\left( e^{-\beta \tau }\right) , \mathbf {0}_{(n\times n_{2})}\right) \end{aligned}$$

(12)

where $\mathbf {0}_{a\times b}$ is a shorthand notation for an $(a\times b)$ matrix with all entries equal to 0. For convenience, we will drop the size $(a\times b)$ and apply $\mathbf {0}$ in the cases that were previously mentioned (instead of $\mathbf {0}_{a\times b}$).

Now, for the derivation of $\widehat{\mathbb {E}}(e^{-\beta \tau })$ we introduce two similar LST matrices which differ only with their initial environment: (i) an $(n_{1}\times n_{1})$ matrix $\widehat{f}_{11}(0,q,\mathfrak {\beta })$ whose ijth component $(\widehat{f}_{11}(0,q,\mathfrak {\beta })) _{ij}$ represents the LST of the time until the content level hits q in state $j\in S_{1}$, given $I(0)=0$ and $\mathcal {J}(0)=i\in S_{1}$ and (ii) an $(n_{2}\times n_{1})$ matrix $\widehat{f}_{21}(0,q,\mathfrak {\beta })$ whose ijth component $(\widehat{f}_{21}(0,q,\mathfrak {\beta })) _{ij}$ represents the LST of the time until the content level hits q in state $j\in S_{1}$, given $I(0)=0$ and $\mathcal {J}(0)=i\in S_{2}$.

Proposition 4.1

The matrix $\widehat{f}_{11}(0,q,\mathfrak {\beta })$ and $\widehat{f} _{21}(0,q,\mathfrak {\beta })$ are given by

$$\begin{aligned} \widehat{f}_{11}(0,q,\mathfrak {\beta })&=\, _{0}\widehat{f}_{11} (0,q,\mathfrak {\beta })+\,^{q}\!\Psi (\mathfrak {\beta }) \left( \beta I-Q_{22}\right) ^{-1}Q_{21} \widehat{f}_{11}(0,q,\mathfrak {\beta })\end{aligned}$$

(13)

$$\begin{aligned} \widehat{f}_{21}(0,q,\beta )&= \left( \beta I-Q_{22}\right) ^{-1} Q_{21} \widehat{f}_{11}(0,q,\mathfrak {\beta }). \end{aligned}$$

(14)

Proof

Assume $I(0)=0,\mathcal {J}(0)\in S_{1}.$ There are two scenarios to reach level $q>0$. In the first scenario, I(t) hits level q avoiding 0. Applying the fluid parameters and Table 1, the LST matrix of that time is $_{0}\widehat{f}_{11}(0,q,\mathfrak {\beta }).$ In the second scenario, I(t) drops to level 0 before reaching level q (with LST matrix $^{q} \Psi (\mathfrak {\beta })$). Once the process hits level 0, it stays there for a phase-type distributed time with transition matrix $Q_{22}.$ Thus, $( \beta I-Q_{22})^{-1}Q_{21}$ is the expected discounted time until exiting from level 0 with environmental in $S_{1}$. From that point, the process starts again from level 0. The proof of (14) is similar. $\square$

The matrix $\widehat{\mathbb {E}}(e^{-\beta \tau })$ is given by

$$\begin{aligned} \widehat{\mathbb {E}}\left( e^{-\beta \tau }\right) =\left( \begin{array} [c]{c} \widehat{f}_{11}(0,q,\mathfrak {\beta })\\ \widehat{f}_{21}(0,q,\beta ) \end{array} \right) . \end{aligned}$$

(15)

Substituting (15) in (12) returns $\mathbb {E}(e^{-\beta \tau }).$

Notice that substituting $\beta =0$ in (12) and (15) returns the $(n\times n)$ probability matrix

$$\begin{aligned} \mathbb {E}\left( \mathbf {1}_{\mathcal {J}(\tau )}\right) =\left( \left( \begin{array} [c]{c} \widehat{f}_{11}(0,q,0)\\ \widehat{f}_{21}(0,q,0) \end{array} \right) ,\mathbf {0}\right) . \end{aligned}$$

(16)

The ijth component of $\mathbb {E}(\mathbf {1}_{\mathcal {J}(\tau )})$ is the probability that the ON process hits level q at state j given $\mathcal {J}(0)=i\in S$.

4.1.2 The matrix $\mathbb {E}(e^{-\beta C})$

Given the state at time $\tau ,$ the ON period and the OFF period are independent. Thus, regarding $C=\tau +T^{\prime }$ we obtain

$$\begin{aligned} \mathbb {E}\left( e^{-\beta C}\right) =\mathbb {E}\left( e^{-\beta \tau }\right) \mathbb {E}\left( e^{-\beta T^{\prime }}\right) . \end{aligned}$$

$\mathbb {E}(e^{-\beta \tau })$ is given by (12). Let $\widehat{\mathbb {E}}(e^{-\beta T^{\prime }})$ be an $(n\times n_{2})$ matrix whose ijth components is the LST of the time to reach level 0 in phase $j\in S_{2},$ given $\mathcal {J}(0)=i\in S,I(0)=q.$ Since time $T^{\prime }$ occurs only for states in $S_{2}$, $\mathbb {E}(e^{-\beta T^{\prime }})$ has the form of

$$\begin{aligned} \mathbb {E}\left( e^{-\beta T^{\prime }}\right) =\left( \mathbf {0}_{(n\times n_{1})}, \widehat{\mathbb {E}}\left( e^{-\beta T^{\prime }}\right) \right) . \end{aligned}$$

(17)

It is easy to see that the matrix $\widehat{\mathbb {E}}(e^{-\beta T^{\prime }})$ is given by

$$\begin{aligned} \widehat{\mathbb {E}}\left( e^{-\beta T^{\prime }}\right) =\left( \begin{array} [c]{c} _{0}\widehat{f}_{12}(q,0,\beta )\\ _{0}\widehat{f}_{22}(q,0,\beta ) \end{array} \right) . \end{aligned}$$

(18)

where $_{0}\widehat{f}_{12}(q,0,\beta )$ and $_{0}\widehat{f}_{22}(q,0,\beta )$ are given in Table 1, with q replacing x. Notice that substituting $\beta =0$ in (17) and (18) returns the $(n\times n)$ matrix

$$\begin{aligned} \mathbb {E}(\mathbf {1}_{J(T^{\prime })})=\left( \mathbf {0},\left( \begin{array} [c]{c} \widehat{f}_{12}(q,0,0)\\ \widehat{f}_{22}(q,0,0) \end{array} \right) \right) . \end{aligned}$$

(19)

The ijth component of $\mathbb {E}(\mathbf {1}_{J(T^{\prime })})$ is the probability that the OFF process hits level 0 at state j given $\mathcal {J}(\tau )=i$.

Substituting (12) and 17) in (4) leads to the expected discounted set-up cost.

4.2 Holding cost

We start with the derivation of the $(n\times 1)$ vector $\widehat{\mathbf {h} }_{1}(\beta )$, the expected discounted inventory level during the ON period. Recall that since we are now dealing with the ON period, for all the matrices in Table 1 we have to add the index + and use the corresponding matrices associated to $\mathcal {F}^{+}(t)$.

4.2.1 $\widehat{\mathbf {h}}_{1}(\beta )$ Functional

The basic tool we use to derive $\mathbf {E}( {\int \limits _{0}^{\tau }} e^{-\beta t}I^{+}(t)dt)$ (and all other the required integrals, here and in the following sections) is optional sampling theory (OST) to the Asmussen–Kella multi-dimensional martingale, as introduced in Sect. 3.1. Consider the process

$$\begin{aligned} X(t)&=\int _{0}^{t}r_{\mathcal {J}(u)}du\quad 0\le t\le \tau \nonumber \\ X(0)&=0 \end{aligned}$$

(20)

as defined in Sect. 2.1(d). Chapter XI, p. 311 of Asmussen (2003) yields that

$$\begin{aligned} E_{i}\left[ e^{\alpha X(t)};\mathcal {J}(t)=j\right] =\left( e^{tK(\alpha )}\right) _{ij} \end{aligned}$$

where

$$\begin{aligned} K(\alpha )=Q+\alpha U. \end{aligned}$$

(21)

(specifically, $K^{+}(\alpha )=Q^{+}+\alpha U^{+}$ and $Q^{+}$, $U^{+}$ are given in Sect. 3.2).

Recall that $L(t)=-\min \nolimits _{0\le u\le t}X(u)$ is the local time and let $Z(t)=X(t)+L(t)$. It is not difficult to see that the latter process up to time $\tau ,$ i.e., $(Z(t)) _{0\le t<\tau },$ has the same distribution as $(I(t))_{0\le t<\tau }.$ Finally, define $Y(t)=L(t)-(\beta /\alpha ) t,$ for arbitrary $\beta \ge 0$ and $\alpha <0,$ and $W(t)=X(t)+Y(t)=Z(t)-(\beta /\alpha )t$. Since Y is adapted and has paths of finite expected total variation on bounded intervals, Theorem 2.1 of Asmussen and Kella (2000) yields that the process

$$\begin{aligned} M(\alpha ,t)= & {} \left( M^{1}(\alpha ,t),M^{2}(\alpha ,t),\ldots ,M^{n} (\alpha ,t)\right) ^{\intercal }\nonumber \\= & {} {\int \limits _{0}^{t}} e^{\alpha W(u)}\mathbf {1}_{\mathcal {J}(u)}du K(\alpha ) +e^{\alpha W(0)}\mathbf {1}_{\mathcal {J}(0)}-e^{\alpha W(t)}\mathbf {1}_{\mathcal {J} (t)}\nonumber \\&+\,\alpha \left( {\int \limits _{0}^{t}} e^{\alpha W(u)}\mathbf {1}_{\mathcal {J}(u)}dY(u)\right) \nonumber \\= & {} {\int \limits _{0}^{t}} e^{\alpha Z(u)-\beta u}\mathbf {1}_{\mathcal {J}(u)}du\left( K\left( \alpha \right) -\beta I\right) +e^{\alpha Z(0)}\mathbf {1}_{\mathcal {J} (0)}-e^{\alpha Z(t)-\beta t}\mathbf {1}_{\mathcal {J}(t)}\nonumber \\&+\,\alpha \left( {\int \limits _{0}^{t}} e^{-\beta u}\mathbf {1}_{\mathcal {J}(u)}dL(u)\right) \end{aligned}$$

(22)

is an n-row vector-valued zero mean martingale. Here $\mathbf {1} _{\mathcal {J}(t)}$ denotes the $(1\times n)$ vector $\mathbf {1}_{\mathcal {J} (t)}=(\mathbf {1}_{\{\mathcal {J}(t)=1\}},\ldots ,\mathbf {1}_{\{\mathcal {J} (t)=n\}})$.

Recall that $\mathbb {E}$ is the matrix-valued expectation operating on n-row vector random variables like $M(\alpha ,t)$ whose (i, j) component is the conditional expectation of the jth $(j\in S\mathcal {)}$ entry given $\mathcal {J}(0)=i\in S$. For example, $[\mathbb {E}(M(\alpha ,t))] _{i,j}=[ E(M^{i}(\alpha ,t))]_{j}.$

The OST yields $\mathbb {E}(M(\alpha ,\tau )) =\mathbb {E}(M(\alpha ,0)) =0$,

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{\tau }} e^{\alpha Z(u)-\beta u}\mathbf {1}_{\mathcal {J}(u)}du\right)&=\left[ \mathbb {E}\left( e^{\alpha Z(\tau )-\beta \tau }\mathbf {1} _{\mathcal {J}(\tau )}\right) -\mathbb {E}\left( e^{\alpha Z(0)} \mathbf {1}_{\mathcal {J}(0)}\right) \right. \\&\left. \quad -\,\alpha \mathbb {E}\left( {\textstyle \int \limits _{0}^{\tau }} e^{-\beta u}\mathbf {1}_{\mathcal {J}(u)}dL(u)\right) \right] \left( K(\alpha ) -\beta I\right) ^{-1}.\nonumber \end{aligned}$$

(23)

Since $\mathcal {J}(0)=i\in S$ and $Z(0)=0$ we obtain $\mathbb {E}(e^{\alpha Z(0)}\mathbf {1}_{\mathcal {J}(0)}) =I$. Applying $Z(\tau )=q$ and the fluid method yields

$$\begin{aligned} \mathbb {E}\left( e^{\alpha Z(\tau )-\beta \tau }\mathbf {1}_{\mathcal {J}(\tau )}\right) =e^{\alpha q}\mathbb {E}\left( e^{-\beta \tau }\right) \end{aligned}$$

(24)

where $\mathbb {E}(e^{-\beta \tau })$ is given by (12).

To finish the computation of (23), we have to derive the $(n\times n)$ matrix $\mathbb {E}( {\int \limits _{0}^{\tau }} e^{-\beta u}\mathbf {1}_{\mathcal {J}(u)}dL(u))$, which is the expected discounted lost demand until time $\tau$. First, we assume that the process starts at level 0 with environment in $S_{2}$ and derive the expected lost demand until first exiting from 0. Notice that a loss occurs only during states in $S_{2}.$ For that, we introduce the $(n_{2}\times n_{2})$ matrix $\mathbf {\Upsilon }(\beta )$ whose ijth component, $\Upsilon _{ij}(\beta ),$ is the expected discounted loss in state $j\in S_{2}$ until exiting level 0, given that the process starts at level 0 with state $i\in S_{2}.$ $\mathbf {\Upsilon }(\beta )$ is given by

$$\begin{aligned} \mathbf {\Upsilon }(\beta )=-\mathbb {E}\left( \,\, {\int \limits _{t=0}^{\mathbf {\xi }}} \mathbf {r}e^{-\beta t}dt\right) +\mathbb {E}\left( e^{-\beta \mathbf {\xi } }\right) \mathbb {P}_{\Upsilon }\mathbf {\Upsilon }(\beta ). \end{aligned}$$

(25)

Note that once the inventory process hits 0 in state $i\in S_{2},$ it stays there for an exponential random time $\xi _{i}$ with parameter $-Q_{22}(i,i).$ The matrix $-\mathbb {E}( {\int \limits _{t=0}^{\mathbf {\xi }}} \mathbf {r}e^{-\beta t}dt)$ is an $(n_{2}\times n_{2})$ diagonal matrix represents the expected discounted loss during time $\xi _{i};$ its (ii)th component is given by $-\frac{r_{i}}{\beta }\left( 1+\frac{Q_{22}(i,i)}{\beta -Q_{22}(i,i)}\right) .$ From that point, with probability $\frac{Q_{22}(i,j)}{-Q_{22}(i,i)},$ the state changes to $j\in S_{2}$, and the expected discounted loss from state j is $\Upsilon _{ji}(\beta ).$ Thus, $\mathbb {E}( e^{-\beta \mathbf {\xi }})$ is an $(n_{2}\times n_{2})$ diagonal matrix whose (ii)th component is given by $\frac{-Q_{22}(i,i)}{\beta -Q_{22}(i,i)}$ and $\mathbb {P}_{\Upsilon }$ is an $(n_{2}\times n_{2})$ probability matrix with $( \mathbb {P}_{\Upsilon }) _{ij}=\frac{Q_{22}(i,j)}{-Q_{22}(i,i)}$ for $i\ne j$ and 0 otherwise.

Now, we apply $\mathbf {\Upsilon }(\beta )$ to the derivation of the loss until time $\tau .$ Since the lost demand occurs only for states in $S_{2},$ the matrix $\mathbb {E}( {\int \limits _{0}^{\tau }} e^{-\beta u}\mathbf {1}_{\mathcal {J}(u)}dL(u))$ has the form

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta u}\mathbf {1}_{\mathcal {J}(u)}dL(u)\right) =\left( \mathbf {0} , \widehat{\mathbf {L}}(\beta )\right) \end{aligned}$$

(26)

where $\widehat{\mathbf {L}}(\beta )$ is an $( n\times n_{2})$ matrix whose ijth component is the expected discounted loss in state $j\in S_{2}$ until $\tau ,$ given $\mathcal {J}(0)=i\in S$. Let $\widehat{\mathbf {L} }_{1}(\beta )$ be an $(n_{1}\times n_{2})$ sub-matrix of $\widehat{\mathbf {L} }(\beta )$ includes all rows corresponding to states in $S_{1}$ and $\widehat{\mathbf {L}}_{2}(\beta )$ be an $(n_{2}\times n_{2})$ sub-matrix of $\widehat{\mathbf {L}}(\beta )$ includes all rows corresponding to states in $S_{2}$ such that

$$\begin{aligned} \widehat{\mathbf {L}}(\beta )=\left( \begin{array} [c]{c} \widehat{\mathbf {L}}_{1}(\beta )\\ \widehat{\mathbf {L}}_{2}(\beta ) \end{array} \right) . \end{aligned}$$

(27)

Proposition 4.2

$$\begin{aligned} \widehat{\mathbf {L}}_{1}(\beta )&=\left( I-\,^{q}\Psi (\beta )\left( \beta I-Q_{22}\right) ^{-1}Q_{21}\right) ^{-1}\,^{q}\Psi (\beta )\mathbf {\Upsilon }(\beta )\nonumber \\ \widehat{\mathbf {L}}_{2}(\beta )&=\mathbf {\Upsilon }(\beta ) +\left( \beta I-Q_{22}\right) ^{-1}Q_{21} \widehat{\mathbf {L}}_{1} (\beta ) \end{aligned}$$

(28)

Proof

Assume $\mathcal {J}(0)\in S_{1}.$ $\widehat{\mathbf {L}}_{1}(\beta )$ satisfies the following equation

$$\begin{aligned} \widehat{\mathbf {L}}_{1}(\beta )=\,^{q}\!\Psi (\beta )\left( \mathbf {\Upsilon }(\beta )+\left( \beta I-Q_{22}\right) ^{-1}Q_{21} \widehat{\mathbf {L}}_{1}(\beta )\right) . \end{aligned}$$

(29)

Lost demand occurs when the process drops to level 0 avoiding q. The LST of that event is $^{q}\Psi (\beta )$. From that point, by the proof of (25), $\mathbf {\Upsilon }(\beta )$ is the discounted lost demand. The term $(\beta I-Q_{22}) ^{-1}Q_{21}$ is the discounted time until exiting level 0 with environmental state in $S_{1}$ and starting again with LST $\widehat{\mathbf {L}}_{1}(\beta ).$ Solving (29) for $\widehat{\mathbf {L}}_{1}(\beta )$ yields (28). The matrix $\widehat{\mathbf {L}}_{2}(\beta )$ has a similar proof. $\square$

Substitute (26) and (24) in (23), multiply by e returns

$$\begin{aligned} \mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{\alpha Z(u)-\beta u}du\right) =\left( e^{\alpha q}\mathbb {E} \left( e^{-\beta \tau }\right) -I-\alpha \left( 0_{n\times n_{1}},\widehat{\mathbf {L}} (\beta )\right) \right) \left( K(\alpha ) -\beta I\right) ^{-1}e. \end{aligned}$$

(30)

Taking the derivation of (30) with respect to $\alpha$ and setting $\alpha =0$ leads to

$$\begin{aligned} \widehat{\mathbf {h}}_{1}(\beta )&=\mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta u}I^{+}(u)du\right) =\mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta u}Z(u)du\right) \nonumber \\&\left. = \frac{\partial }{\partial \alpha }\left[ \left( e^{\alpha q}\mathbb {E} \left( e^{-\beta \tau }\right) -I-\alpha \left( 0_{n\times n_{1}},\widehat{\mathbf {L}} (\beta )\right) \right) \left( K(\alpha ) -\beta I\right) ^{-1}e\right] \right| _{\alpha =0}\nonumber \\&= \left( q\mathbb {E}\left( e^{-\beta \tau }\right) -I-\left( 0_{n\times n_{1} },\widehat{\mathbf {L}}(\beta )\right) \right) \left( Q-\beta I\right) ^{-1}e-\left( \mathbb {E}\left( e^{-\beta \tau }\right) -I\right) \nonumber \\&\quad \left( Q-\beta I\right) ^{-2}Ue. \end{aligned}$$

(31)

which is the expected discounted inventory level during the ON period.

4.2.2 $\widehat{\mathbf {h}}_{2}(\beta )$ Functional

In order to finish the holding cost we have to find the $( n\times 1)$ vector $\widehat{\mathbf {h}}_{2}(\beta )=\mathbf {E}( {\int \limits _{0}^{T^{\prime }}} e^{-\beta t}I^{-}(t)dt)$. Recall that since we are now dealing with the OFF period, for all the matrices in Table 1 we have to add the index ($-$) and use the corresponding matrices associated to $\mathcal {F}^{-}(t).$ The OFF period stars at time $\tau$. We shift the time origin to $\tau$ so that the OFF period starts at time 0. Consider $\widetilde{X}(t)$ similar to (20) but with $Q^{-}$ and $U^{-}$ and $\widetilde{X}(0)=q.$ Clearly, the latter process up to time $T^{\prime },$ i.e., $(\widetilde{X}(t)) _{0\le t<T^{\prime }},$ has the same distribution as $(I(t)) _{0\le t<T^{\prime }}.$ Let $\widetilde{W} (t)=\widetilde{X}(t)+\widetilde{Y}(t)$ with $\widetilde{Y}(t)=-(\beta /\alpha )t$, for arbitrary $\beta \ge 0$ and $\alpha <0$. Applying the optional sampling theory to the multi-dimensional martingale (22) with $T^{\prime }$ replacing $\tau$ we obtain

$$\begin{aligned} \mathbf {E}\left( {\int \limits _{0}^{T^{\prime }}} e^{\alpha \widetilde{X}(s)-\beta s}ds\right)= & {} \left[ \mathbb {E}\left( e^{\alpha \widetilde{X}\left( T^{\prime }\right) -\beta T^{\prime }}\mathbf {1}_{\mathcal {J} \left( T^{\prime }\right) }\right) -\mathbb {E}\left( e^{\alpha \widetilde{X}(0)} \mathbf {1}_{\mathcal {J}(0)}\right) \right] \nonumber \\&\times \left( K(\alpha ) -\beta I\right) ^{-1}e. \end{aligned}$$

(32)

Substituting $\widetilde{X}(0)=q$ and $\widetilde{X}(T^{\prime })=0$ returns

$$\begin{aligned} \mathbb {E}\left( e^{\alpha \widetilde{X}(0)}\mathbf {1}_{\mathcal {J} (0)}\right)&=e^{\alpha q}I\nonumber \\ \mathbb {E}\left( e^{\alpha \widetilde{X}\left( T^{\prime }\right) -\beta T^{\prime } }\mathbf {1}_{\mathcal {J}(T^{\prime })}\right)&=\mathbb {E}\left( e^{-\beta T^{\prime }}\right) \end{aligned}$$

(33)

where $\mathbb {E}(e^{-\beta T^{\prime }})$ is given by (17). Substituting (33) in (32), take the derivative with respect to $\alpha$ and let $\alpha =0$ leads to

(34)

4.3 Production cost

The expected discounted production vector costs $\widehat{\mathbf {p}} _{1}(\beta )=\mathbf {E}(\int \nolimits _{0}^{\tau }e^{-\beta s} p_{\mathcal {J}(s)}^{1}ds)$ and $\widehat{\mathbf {p}}_{2} (\beta )=\mathbf {E}(\int \nolimits _{0}^{T^{\prime }}e^{-\beta s}p_{\mathcal {J}(s)}^{2}ds)$ (of order $(n\times 1)$) can be easily derived as follows. For the derivation of $\widehat{\mathbf {p}}_{1}(\beta )$ (ON period), let $\mathbf {C}_{1}^{+},\mathbf {C}_{2}^{+}$ and $\mathbf {C}^{+}$ be diagonal matrices as follows:

$$\begin{aligned} \mathbf {C}_{j}^{+}&=diag\left\{ p_{i}^{1},i\in S_{j}\right\} ,\quad j=1,2.\nonumber \\ \mathbf {C}^{+}&=diag\left( \mathbf {C}_{1}^{+},\mathbf {C}_{2}^{+}\right) . \end{aligned}$$

(35)

Let $\mathbb {E}(\int \nolimits _{0}^{\tau }e^{-\beta s}\mathbf {1} _{\mathcal {J}(s)}ds)$ be an $( n\times n)$ matrix whose (i, j) component represents the expected discounted time in phase $j\in S$ given $I(0)=i\in S$. Clearly, $\widehat{\mathbf {p}}_{1}(\beta )$ is given by

$$\begin{aligned} \widehat{\mathbf {p}}_{1}(\beta )=\mathbb {E}\left( \int \nolimits _{0}^{\tau }e^{-\beta s}\mathbf {1}_{\mathcal {J}(s)}ds\right) \mathbf {C}^{+}e, \end{aligned}$$

Applying (23) to get

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{\tau }} e^{\alpha Z(s)-\beta s}\mathbf {1}_{\mathcal {J}(s)}ds\right) =\left( e^{\alpha q}\mathbb {E}\left( e^{-\beta \tau }\right) -I-\alpha \left( \mathbf {0}, \widehat{\mathbf {L}}(\beta )\right) \right) \left( K\left( \alpha \right) -\beta I\right) ^{-1}. \end{aligned}$$

(36)

Substituting $\alpha =0$ yields

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{\tau }} e^{-\beta s}\mathbf {1}_{\mathcal {J}(s)}ds\right) =\left( \mathbb {E} \left( e^{-\beta \tau }\right) -I\right) \left( (0) -\beta I\right) ^{-1}. \end{aligned}$$

(37)

Now multiplying (37) by the vector $\mathbf {C}^{+}e$ returns the expected discounted production cost, $\widehat{\mathbf {p}} _{1}(\beta )$, for the ON process.

Regarding $\widehat{\mathbf {p}}_{2}(\beta )$ and similar to above, we apply (32) to get the $( n\times n)$ matrix

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{T^{\prime }}} e^{\alpha \widetilde{X}(s)-\beta s}\mathbf {1}_{\mathcal {J}(s)}ds\right)&=\left[ \mathbb {E}\left( e^{\alpha \widetilde{X}\left( T^{\prime }\right) -\beta T^{\prime }}\mathbf {1}_{\mathcal {J}\left( T^{\prime }\right) }\right) -\mathbb {E}\left( e^{\alpha \widetilde{X}(0)}\mathbf {1}_{\mathcal {J}(0)}\right) \right] \nonumber \\&\quad \left( K(\alpha )-\beta I\right) ^{-1}\nonumber \\&=\left( \mathbb {E}\left( e^{-\beta T^{\prime }}\right) -e^{\alpha q}I\right) \left( K(\alpha ) -\beta I\right) ^{-1}. \end{aligned}$$

(38)

Now, define $\mathbf {C}^{-},\mathbf {C}_{j}^{-},j=1,2$ as in (35) with $p_{i}^{2}$ replacing $p_{i}^{1}$. Substitute $\alpha =0$ in (38) and multiply by the matrix $\mathbf {C}^{-}$ we obtain the expected discounted production rate for the OFF process

$$\begin{aligned} \widehat{\mathbf {p}}_{2}(\beta )=\mathbb {E}\left( {\int \limits _{0}^{T^{\prime }}} e^{-\beta s}\mathbf {1}_{\mathcal {J}(s)}ds\right) \mathbf {C}^{-}e=\left( \mathbb {E}\left( e^{-\beta T^{\prime }}\right) -I\right) \left( K(0) -\beta I\right) ^{-1}\mathbf {C}^{-}e. \end{aligned}$$

4.4 Loss cost

To end our discounted analysis, we need to derive the $(n \times 1)$ expected discounted production loss vector $\widehat{\mathbf {u}}(\beta )=\mathbf {E} ( {\int \limits _{0}^{\tau }} e^{-\beta t}dL(t)).$

Corollary 4.1

It is easy to see that $\widehat{\mathbf {u}}(\beta )=\widehat{\mathbf {L}}(\beta )e$.

We summarize the main computation steps of the performance measures for the discounted case:

• 1. Compute $\Psi (\beta )$ and the LST matrices (see Table 1).

• 2. Obtain $\widehat{f}_{11}(0,q,\mathfrak {\beta })$ and $\widehat{f}_{21}(0,q,\mathfrak {\beta })$ using (13) and (14).

• 3. Compute $\mathbb {E} (e^{-\beta \tau }),\widehat{\mathbb {E}}(e^{-\beta \tau })$ and $\mathbb {E} (e^{-\beta C})$ [Eqs. (12)–(18)] which leads to $SC_{\infty }(\beta )$.

• 4. Applying (31) and (34) returns $\widehat{\mathbf {h}}_{1}(\beta )$ and $\widehat{\mathbf {h}}_{2}(\beta )$ which leads to $\textit{HC}_{\infty }(\beta )$.

• 5. Applying (37) and (38) to obtain $\widehat{\mathbf {p}}_{1} (\beta )$ and $\widehat{\mathbf {p}}_{2}(\beta ),$ and thus $\textit{PC}_{\infty }(\beta )$.

• 6. Finally, Corollary 4.1 returns $\widehat{\mathbf {u} }(\beta )$ which leads to $\textit{UC}_{\infty }(\beta )$.

Example 1

We consider a Markov chain with $n=4$ states with the following generator matrix

$$\begin{aligned} Q=\left( \begin{array} [c]{cccc} -7 &{}\quad 1.5 &{}\quad 2.5 &{}\quad 3\\ 3 &{}\quad -9 &{}\quad 2 &{}\quad 4\\ 2 &{}\quad 4 &{}\quad -9 &{}\quad 3\\ 4 &{}\quad 3 &{}\quad 2 &{}\quad -9 \end{array} \right) . \end{aligned}$$

As initial probability vector we take $\upsilon =(0.2,0.3,0.35,0.15).$ We take the following basic values for the parameters:

$$\begin{aligned} \beta =0.01,\quad k_{1}=5,\quad k_{2}=5,\quad c=3,\quad h=1,\quad w=1. \end{aligned}$$

Let $\gamma _{1}$ and $\gamma _{2}$ be the average growth rates (in short, drifts) of the ON and OFF periods, respectively, i.e.,

$$\begin{aligned} \gamma _{1}=\sum _{i=1}^{n}\pi _{i}r_{i}^{1}>0,\quad \gamma _{2}=\sum _{i=1} ^{n}\pi _{i}r_{i}^{2}<0 \end{aligned}$$

Fig. 2

The expected discounted setup cost, $\textit{SC}_{\infty }(\beta )$

Fig. 3

The expected discounted holding cost, $\textit{HC}_{\infty }(\beta )$

Fig. 4

The expected discounted loss cost, $\textit{UC}_{\infty }(\beta )$

We assume $\gamma _{2}=-0.214.$ Let $\gamma _{1}$ vary in $\{0.207,0.48,0.69,0.96\}$ (by changing the production rates during the ON period) and q vary in $\{1,2,3,4,5\}.$ We determine the expected discounted setup, holding, loss and total cost. We do not reproduce lengthy tables of calculated values (which could be easily done, but is not very illuminating); instead we present our results in terms of graphical displays. Figures 2, 3 and  4 shows $\textit{SC}_{\infty }(\beta )$, $\textit{HC}_{\infty }(\beta )$, $\textit{UC}_{\infty }(\beta )$ and $\textit{TC}_{\infty }(\beta )$ as functions of $\gamma _{1}$ and q, respectively. We see that $SC_{\infty }(\beta )$ decreases as a function of q and almost unaffected by $\gamma _{1}.$ Figure 3 shows that $\textit{HC}_{\infty }(\beta )$ increases as a function of both $\gamma _{1}$ and q;  however, $\textit{UC}_{\infty }(\beta )$ has an opposite behavior, since increasing production rates or increasing q decrease the number of drops to level 0 and cause less loss. In Fig. 5 we see that the total cost increases as a function of $\gamma _{1}$ and appears to be a convex function of q; thus we can conclude that for each $\gamma _{1}$ there is an optimal q which minimize the total cost. Notice that, the behavior of $\textit{SC}_{\infty }(\beta )$, $\textit{HC}_{\infty }(\beta )$ and $\textit{TC}_{\infty }(\beta )$ as a function of q is similar to those associated with the classical EPQ model.

Furthermore, since we see that the expected discounted total cost appears to be a convex function of q, we have been carried out additional numerical checkings and present in Table 2 the optimal value $q^{*}$ and $\textit{TC}_{\infty }^{*}(\beta )$ for $\gamma _{1}$ vary in $\{0.207,0.48,0.69,0.96\}.$ We can see that the optimal value $q^{*}$ and the optimal discounted total cost $TC_{\infty }^{*}(\beta )$ increase in $\gamma _{1}$.

Fig. 5

The expected discounted total cost, $\textit{TC}_{\infty }(\beta )$

5 Long run average analysis

Let $\textit{TC}(t)$ be the total cost until time t. We are interested in the long run average total cost per time unit:

$$\begin{aligned} \overline{\textit{TC}}=\underset{t\rightarrow \infty }{\lim }\frac{\textit{TC}(t)}{t}. \end{aligned}$$

Regarding $T_{n},$ let $\mathcal {J}_{n}=\mathcal {J}(T_{n}),n=0,1,\ldots$ be the environmental state at $T_{n}$ (at the beginning of each cycle). Notice that $(\mathcal {J}_{n},T_{n})$ is a Markov renewal process, and the content level process I(t) is a semi-regenerative process with respect to $(\mathcal {J}_{n},T_{n}).$ $T_{n}^{^{\prime }}s$ are semi-regenerative points of the process. Thus, the process $\mathcal {J} _{n},n=0,1,2,\ldots$ is an irreducible positive recurrent Markov chain; we denote its transition probability matrix by $\mathbb {P}^{*}.$ Let $\pi ^{*}$ be the corresponding stationary probability vector. $\pi ^{*}$ is determined by the following equations:

$$\begin{aligned} \pi ^{*}&=\pi ^{*} \mathbb {E}\left( \mathbf {1}_{\mathcal {J}(\tau )}\right) \mathbb {E}\left( \mathbf {1}_{\mathcal {J}(T^{\prime })}\right) \nonumber \\ \pi ^{*}e&=1, \end{aligned}$$

(39)

where $\mathbb {E}(\mathbf {1}_{\mathcal {J}(\tau )})$ and $\mathbb {E} (\mathbf {1}_{\mathcal {J}(T^{\prime })})$ are given in (16) and (19), respectively.

Table 2 ${q}^{*}$ and ${\textit{TC}_{\infty }^{*}(\beta )}$ for $\gamma _{1}$ vary in ${\{0.207,0.48,0.69,0.96\}}$

The long run average cost $\overline{\textit{TC}}$ can be derived from $\textit{TC}_{\infty }(\beta )$ by a well-known procedure

$$\begin{aligned} \overline{\textit{TC}}=\underset{\beta \longrightarrow 0}{\lim }\beta \textit{TC}(\beta )=\overline{\textit{SC}}+\overline{\textit{HC}}+\overline{\textit{PC}}+\overline{\textit{UC}} \end{aligned}$$

where on the right side we have the long-run average costs of the set-up, holding stock, production and unsatisfied demand, respectively.

Let N(t) be the number of cycles until time t, i.e., $N(t)=\sup \{n\ge 0\mid T_{0}+\cdots +T_{n}\le t\},t\ge 0$. Following Asmussen (2003), Chapter VI, Theorem 3.1 and Chapter VII, Proposition 5.2, the four long-run quantities can be given in terms of the first-cycle functionals as follows:

Note that E(C) denotes the steady-state expected value of C. Clearly, $E(C)=\pi ^{*}\mathbf {E}(C)$ where $\mathbf {E}(C)$ is an $( n \times 1)$ vector whose ith component is $E_{i}(C)=E(C\mid \mathcal {J}_{0}=i\in S].$

To apply the above equations we have to compute $\widehat{\mathbf {h}}_{1}(0),\widehat{\mathbf {h}}_{2} (0),\widehat{\mathbf {p}}_{1}(0),\widehat{\mathbf {p}}_{2}(0),\mathbf {E}\left( L(\tau )\right) ,\mathbf {E}(C)$ and $\pi ^{*}$.

5.1 Long-run average inventory level

In order to derive $\widehat{\mathbf {h}}_{1}(0)$ set $\beta =0$ in (23) leads to

$$\begin{aligned} \mathbf {E}\left( {\int \limits _{0}^{\tau }} e^{\alpha Z(u)}du\right)= & {} \left[ \mathbb {E}\left( e^{\alpha Z(\tau )}\mathbf {1}_{\mathcal {J}(\tau )}\right) -\mathbb {E}\left( e^{\alpha Z(0)}\mathbf {1}_{\mathcal {J}(0)}\right) \right. \nonumber \\&\left. -\,\alpha \mathbb {E}\left( {\int \limits _{0}^{\tau }} \mathbf {1}_{\mathcal {J}(u)}dL(u)\right) \right] K(\alpha ) ^{-1}e. \end{aligned}$$

(40)

Applying $Z(\tau )=q$ leads to the $(n\times n)$ matrix

$$\begin{aligned} \mathbb {E}\left( e^{\alpha Z(\tau )}\mathbf {1}_{J(\tau )}\right) =e^{\alpha q}\mathbb {E}\left( \mathbf {1}_{J(\tau )}\right) . \end{aligned}$$

Clearly $\mathbb {E}(e^{\alpha Z(0)}\mathbf {1}_{J(0)})=I.$ For the final term, set $\beta =0$ in (26)–(28). Notice that once the process drops to level 0, it stays there for a phase type distributed random variable with transition rate matrix $Q_{22}.$ Thus

$$\begin{aligned} \mathbf {\Upsilon }(0)=\left( -Q_{22}\right) ^{-1}. \end{aligned}$$

(for a proof, see Latouche and Ramaswami 1999, Theorem 2.4.3). Now take the derivation of (40) with respect to $\alpha$ and set $\alpha =0.$ However this is not possible as $K(\alpha )$ is singular at $\alpha =0.$ Instead we have to use (23) to conclude that

$$\begin{aligned} \frac{\partial }{\partial \alpha }\left[ \left( e^{\alpha q}\mathbb {E} \left( \mathbf {1}_{\mathcal {J}(\tau )}\right) -I-\alpha \left( 0,\widehat{\mathbf {L} }(0)\right) \right) K(\alpha ) ^{-1}e\right] \longrightarrow \mathbf {E}\left( {\int \limits _{0}^{\tau }} Z(u)du\right) \end{aligned}$$

(41)

as $\alpha \longrightarrow 0$ through values for which $K(\alpha )$ is non-singular. Relation (41) amounts to applying L’Hôpital’s rule in order to determine the $(n \times 1)$ vector $\widehat{\mathbf {h}}_{1}(0)=\mathbf {E}( {\int \limits _{0}^{\tau }} Z(u)du) =\mathbf {E}( {\textstyle \int \limits _{0}^{\tau }} I^{+}(u)du).$

For the derivation of $\widehat{\mathbf {h}} _{2}(0)$ and similar as above, substituting $\beta =0$ in (32) leads to

$$\begin{aligned} \frac{\partial }{\partial \alpha }\left[ \left( \mathbb {E}\left( \mathbf {1} _{\mathcal {J}\left( T^{\prime }\right) }\right) -e^{\alpha q}I\right) K(\alpha ) ^{-1}e\right] \rightarrow \mathbb {E}\left( {\int \limits _{0}^{T^{\prime }}} \widetilde{X}(s)ds\right) \end{aligned}$$

(42)

as $\alpha \rightarrow 0$ through values for which $K(\alpha )$ is non-singular. Applying L’Hôpital’s rule determines the $( n \times 1)$ vector $\widehat{\mathbf {h}}_{2}(0)=\mathbf {E}( {\int \limits _{0}^{T^{\prime }}} \widetilde{X}(s)ds) =\mathbf {E}({\int \limits _{0}^{T^{\prime }}} I^{-}(s)ds)$.

5.2 Long-run average production rate

To compute $\widehat{\mathbf {p}}_{1}(0)$ set $\beta =0$ in (36). Then, we would like to set $\alpha =0$; however, this is not viable, as $\det K(0)=0$. Instead we have to use (36) to conclude that

$$\begin{aligned} \left( e^{\alpha q}\mathbb {E}\left( \mathbf {1}_{\mathcal {J}(\tau )}\right) -I-\alpha \left( 0,\widehat{\mathbf {L}}(0)\right) \right) K(\alpha ) ^{-1}\mathbf {C}^{+}e\longrightarrow \mathbf {E}\left( {\int \limits _{0}^{\tau }} \mathbf {1}_{\mathcal {J}(s)}ds\right) \end{aligned}$$

(43)

as $\alpha \longrightarrow 0$ through values for which $\det K(0)\ne 0$. Relation (43) amounts to applying L’Hôpital’s rule in order to determine the vector $\widehat{\mathbf {p}}_{1}(0)=\mathbf {E} ( {\int \limits _{0}^{\tau }} \mathbf {1}_{\mathcal {J}(s)}ds).$

Similarly as above, set $\beta =0$ in (38) returns

$$\begin{aligned} \mathbb {E}\left( {\int \limits _{0}^{T^{\prime }}} e^{\alpha \widetilde{X}(s)}\mathbf {1}_{\mathcal {J}(s)}ds\right) =\left( \mathbb {E}\left( \mathbf {1}_{\mathcal {J}\left( T^{\prime }\right) }\right) -e^{\alpha q}I\right) K(\alpha )^{-1}. \end{aligned}$$

(44)

By setting $\alpha \longrightarrow 0$ and applying L’Hôpital’s rule we obtain $\widehat{\mathbf {p}}_{2}(0).$

5.3 Long-run average lost demand

$\widehat{\mathbf {u}}(0)$ has been defined as the $(n \times 1)$ vector whose ith component, $( \widehat{\mathbf {u}}(0)) _{i},$ represents the expected total demand loss until time $\tau$ given $\mathcal {J}_{0}=i\in S,$ i.e.,

$$\begin{aligned} \widehat{\mathbf {u}}(0)=\mathbf {E}\left( \int \limits _{0}^{\tau }dL(t)\right) =\mathbf {E}\left( L(\tau )\right) . \end{aligned}$$

(45)

Corollary 5.1

It is easy to see that $\widehat{\mathbf {u}} (0)=\widehat{\mathbf {L}}(0)e.$

Remark 3

Notice that $L_{i}(\tau ),$ the total demand loss until time $\tau$ given $\mathcal {J}_{0}=i\in S,$ has a phase type distribution with representation

$$\begin{aligned} \left\{ \begin{array} [c]{ll} \textit{PH} \left( S_{2},\,e_{i}\,_{0}\widehat{f}_{11}(0,q,0)e, e_{i} \,^{q}\Psi (0), Q_{22}+Q_{21}\,^{q}\Psi (0)\right) &{}\quad i\in S_{1}\\ \textit{PH}\left( S_{2},\,0, e_{i},\,Q_{22}+Q_{21}\,^{q} \Psi (0)\right) &{}\quad i\in S_{2} \end{array} \right\} . \end{aligned}$$

The proof is as follows. We distinguish between two cases: (i) $i\in S_{1}$ and (ii) $i\in S_{2}$. In the first case $e_{i}\,_{0}\widehat{f}_{11}(0,q,0)e$ is the probability of no loss. According to Table 1, $e_{i}\,^{q}\Psi (0)$ is the probability vector to hit level 0 avoiding q. From that point on, there is a demand loss for a time period that has the same distribution as the time to absorption in a CTMC with transition rate matrix $Q_{22}+Q_{21}\,^{q}\Psi (0).$ (The rate matrix $Q_{22}$ refers to internal rate changes; the matrix $Q_{21}$ is the rate matrix to exit level 0 and with probability $^{q}\Psi (0)$ the process returns to 0 avoiding q.) For the second case, the inventory process starts with lost demand; thus the probability of no loss is 0. The rest of the proof is similar.

5.4 The expected cycle length

Regarding $E(C)=E(\tau )+E(T^{\prime }),$ let $\mathbf {E}(\tau )$ be the $(n\times 1)$ vector whose ith component is $E_{i}(\tau )=E(\tau \mid \mathcal {J}_{0}=i)$ and, similarly, let $\mathbf {E}(T^{\prime })$ be the $(n \times 1)$ vector whose ith component is $E_{i}(T^{\prime })=E(T^{\prime }\mid \mathcal {J}(\tau )=i)$. Obviously,

$$\begin{aligned} E(\tau )&=\pi ^{*}\mathbf {E}(\tau )\nonumber \\ E\left( T^{\prime }\right)&=\pi ^{*}\mathbb {E}\left( \mathbf {1}_{\mathcal {J}\left( \tau \right) }\right) \mathbf {E}\left( T^{\prime }\right) . \end{aligned}$$

(46)

Finally, we will determine $\mathbf {E}(\tau )$ and $\mathbf {E}(T^{\prime }).$

5.4.1 The expected ON period length

In order to obtain $E_{i}(\tau )$ (hence, we apply the quantities associated with $\mathcal {F}^{+}(t)$), we use the notation of (20) and (21) and apply the method introduced in Asmussen (2003), Sect. XI, pp. 312–313. The matrix $K( \alpha )$ [see (21)] has a real eigenvalue $k(\alpha )$ with maximal real part (c.f. Asmussen 2003, Chapter XI, p. 312). The corresponding left and right eigenvectors $\mathbf {\upsilon }^{\alpha }$ and $\mathbf {h}^{\alpha }$ may be chosen with strictly positive components. Moreover, without loss of generality, it can be assumed that $\mathbf {\upsilon }^{\alpha }\mathbf {h}^{\alpha }=1,$ and that $\pi \mathbf {h}^{\alpha }=1$ where $\pi =\mathbf {\upsilon }^{0 }$is the stationary distribution of $\mathcal {J}(t)$ and $\mathbf {h}^{0}$ is a column vector of 1’s. Let $\mathbf {h}^{\prime }$ be the derivative of $\mathbf {h}^{\alpha }$ at $\alpha =0.$ Corollary 2.6, Chapter XI, p. 313 of Asmussen (2003) implies that for any stopping time $\tau$ with $E_{i}(\tau )<\infty$,

$$\begin{aligned} E_{i}(X(\tau ))=k^{\prime }(0)E_{i}(\tau )+h_{i}^{\prime } -E_{i}\left( h_{\mathcal {J}(\tau )}^{\prime }\right) . \end{aligned}$$

(47)

By Corollaries 2.7 and 2.8, Chapter XI, p. 313 of Asmussen (2003):

$$\begin{aligned} k^{\prime }(0)= {\sum \limits _{i\in S}} \pi _{i}r_{i}^{1}. \end{aligned}$$

(48)

To find the vector $\mathbf {h}^{\prime }$ we apply the same technique as in Asmussen and Kella (2000, p. 385). We start from

$$\begin{aligned} k(\alpha )\mathbf {h}^{\alpha }=K(\alpha )\mathbf {h}^{\alpha }. \end{aligned}$$

(49)

Take the derivative of (49) with respect to $\alpha ,$ let $\alpha =0$. Furthermore, use $k(0)=0,\mathbf {h}^{0}=e,$ $K^{\prime }(0)=U$ and $K(0)=Q$. This yields

$$\begin{aligned} k^{\prime }(0)e=Q\mathbf {h}^{\prime }+Ue. \end{aligned}$$

(50)

Note that $\pi \mathbf {h}^{\alpha }=1,$ so that $\pi \mathbf {h}^{\prime }=0$. Subtracting $e\pi \mathbf {h}^{\prime }=0$ from the two sides of (50) shows that

$$\begin{aligned} \mathbf {h}^{\prime }=(Q-e\pi )^{-1}\left[ k^{\prime }(0)I-U\right] e. \end{aligned}$$

(51)

Now notice that $Z(t)=X(t) +L(t)$ where L(t) represents the lost demand until time t. Thus, applying (47) we obtain

$$\begin{aligned} E_{i}(X(\tau ))=E_{i}(Z(\tau ) )-E_{i}(L(\tau ))=k^{\prime }(0)E_{i}(\tau ) +h_{i}^{\prime } -E_{i}\left( h_{\mathcal {J}(\tau )}^{\prime }\right) , \end{aligned}$$

(52)

where

$$\begin{aligned} E_{i}(Z(\tau ))&=q\nonumber \\ E_{i}(h_{\mathcal {J}(\tau )}^{\prime })&=e_{i}\mathbb {E}\left( \mathbf {1} _{\mathcal {J}(\tau )}\right) \mathbf {h}^{\prime }. \end{aligned}$$

(53)

For the derivation of $E_{i}(L(\tau ))$ see (45). Substituting (53) in (52) , we obtain the $(n \times 1)$ vector of expectations

$$\begin{aligned} \mathbf {E}(\tau ) =\frac{qe-\widehat{\mathbf {u}}(0)-\mathbf {h} ^{\prime }+\mathbb {E}(\mathbf {1}_{\mathcal {J}(\tau )})\,\mathbf {h}^{\prime } }{k^{\prime }(0)}. \end{aligned}$$

(54)

5.4.2 The expected OFF period length

We shift the origin time to $\tau$ and assume $\mathcal {J}(\tau )=i\in S$. Consider $\widetilde{X}(t)_{0\le t\le T^{\prime }}$ as defined in Sect. 4.2.2 but with $X(0)=0$ (clearly with the quantities associated with $\mathcal {F}^{-}(t)).$ It is easy to see that $\{\widetilde{X}(t)\}_{0\le t\le T^{\prime }}$ has the same distribution as $\{I(t)-q\}_{0\le t\le T^{\prime }}$. Applying again the method of Sect.  5.4.1 to derive $E_{i}(T^{\prime })$ leads to

$$\begin{aligned} E_{i}\left( \widetilde{X}\left( T^{\prime }\right) \right) =k^{\prime }(0)E_{i}\left( T^{\prime }\right) +h_{i}^{\prime }-E_{i}\left( h_{\mathcal {J}\left( T^{\prime }\right) }^{\prime }\right) , \end{aligned}$$

(55)

with

$$\begin{aligned} k^{\prime }(0)&= {\sum \limits _{i\in S}} \pi _{i}r_{i}^{2}.\\ \mathbf {h}^{\prime }&=(Q-e\pi )^{-1}\left[ k^{\prime }(0)I-U\right] e. \end{aligned}$$

In a similar way we obtain

$$\begin{aligned} E_{i}\left( \widetilde{X}\left( T^{\prime }\right) \right)&=-q\nonumber \\ E_{i}\left( h_{\mathcal {J}\left( T^{\prime }\right) }^{\prime }\right)&=e_{i} \mathbb {E}\left( \mathbf {1}_{\mathcal {J}(T^{\prime })}\right) \,\mathbf {h}^{\prime }. \end{aligned}$$

(56)

Substituting (56) in (55) leads to the $( n \times 1)$ vector of expectations

$$\begin{aligned} \mathbf {E}\left( T^{\prime }\right) =\frac{-qe-\mathbf {h}^{\prime } -\mathbb {E}\left( \mathbf {1}_{\mathcal {J}(T^{\prime })}\right) \mathbf {h}^{\prime }}{k^{\prime }(0)}. \end{aligned}$$

(57)

Substituting (57) and (54) in (46) returns the average cycle length.

We summarize the main computation steps of the performance measures for the average case:

• 1. Applying (39), (54) and (57) to obtain $\pi ^{*},\mathbf {E}(\tau )$ and $\mathbf {E}(T^{\prime })$; then derive E(C) and $\overline{\textit{SC}}$.

• 2. Using (41) and (42) to obtain $\widehat{\mathbf {h}}_{1}(0)$ and $\widehat{\mathbf {h}}_{2}(0)$; then compute $\overline{\textit{HC}}.$

• 3. Similarly, use (43) and (44) to obtain $\widehat{\mathbf {p}}_{1}(0)$ and $\widehat{\mathbf {p}}_{2}(0)$ which leads to $\overline{\textit{PC}}.$

• 4. Finally, Corollary 5.1 and (27) leads to $\widehat{\mathbf {u}}(0)$ and $\overline{\textit{UC}}.$

Fig. 6

The average production cost, $\overline{\textit{PC}}$

Fig. 7

The average ON period length, $E(\tau )$

Fig. 8

The average OFF period length, $E(T^{\prime })$

Example 2

We consider the same data as in Example 1. This time we vary q in $\{5,7,10,12,15\}$. Figures 6, 7 and 8 presents the average production cost $\overline{\textit{PC}}$, the average ON period length $E(\tau )$ and the average OFF period length $E(T^{\prime })$. As expected, $\overline{\textit{PC}}$ increases as a function of both $\gamma _{1}$ and q. Figures 6 and 7 shows that both $E(\tau )$ and $E(T^{\prime })$ increases as a function of q;  however $E(\tau )$ decreases as a function of $\gamma _{1}$ and $E(T^{\prime })$ almost unaffected by $\gamma _{1}$ since increasing $\gamma _{1}$ does not affect on the OFF functionals.

Appendix

In this “Appendix” we introduce the algorithm developed in Ramaswami (2006) for the computation of the matrix $\Psi (\beta )$ associated with the MMFF process $(\mathcal {F}(t),\mathcal {J}(t),t\ge 0)$, as described in Sect. 3.2. Let $\sigma (x)=\inf \{t>0,\mathcal {F}(t)=x\}$ be the first passage time to level x and define the following LST

$$\begin{aligned}{}[\Psi (\beta )] _{ij}=E\left( e^{-\beta \sigma (0)},\mathcal {J} (\sigma (0))=j\mid \mathcal {F}(0)=0,\mathcal {J}(0)=i\right) \quad i\in S_{1},\quad j\in S_{2}. \end{aligned}$$

(58)

$[\Psi (\beta )] _{ij}$ represents the LST of $\sigma (0)$ restricted to the event that the fluid process hits level 0 at state $j\in S_{2},$ given $\mathcal {F}(0)=0$ and $J(0)=i\in S_{1}.$ Ramaswami (2006, Appendix 1, p. 512) shows how to compute the matrix $\Psi (\beta )$ and provides a good algorithm for this. The algorithm for $\Psi (\mathfrak {\beta })$ is given as follows.

For $\lambda >0,$ let

$$\begin{aligned} P_{\lambda }=\frac{1}{\lambda }U^{-1}Q+I \end{aligned}$$

where U and Q define in Sect. 3.2. Choose (fixed) positive numbers $\lambda$ and $\delta$ such that

$$\begin{aligned}&\lambda \ge \max _{i\in s}\left\{ -[U^{-1}Q]_{ii}\right\} \\&\max _{i\in S}\left[ \frac{{\text {Re}}(\mathfrak {\beta })}{\lambda } U^{-1}\right] _{ii}\le \delta <1,\quad \hbox {and}\\&\max _{i\in S}\left[ P_{\lambda }-\frac{{\text {Re}}(\mathfrak {\beta } )}{\lambda }U^{-1}\right] _{ii}>0 \end{aligned}$$

Define the matrices

$$\begin{aligned} A_{2}(\mathfrak {\beta },\lambda )= & {} \left( \begin{array} [c]{cc} 0 &{}\quad 0\\ 0 &{}\quad \lambda U_{2}\left( \mathfrak {\beta }I+2\lambda U_{2}\right) ^{-1} \end{array} \right) \\ A_{1}(\mathfrak {\beta },\lambda )= & {} \Lambda U(\mathfrak {\beta }I+\Lambda U)^{-1}\left( \begin{array} [c]{cc} 0 &{}\quad 0\\ \frac{1}{2}P_{21} &{}\quad \frac{1}{2}P_{22} \end{array} \right) \\ A_{0}(\mathfrak {\beta },\lambda )= & {} \left( \begin{array} [c]{cc} P_{11}-\frac{\beta }{\lambda }U_{1}^{-1} &{}\quad P_{12}\\ 0 &{}\quad 0 \end{array} \right) \end{aligned}$$

where $\Lambda =diag(\lambda I_{\vert S_{1}\vert },2\lambda I_{\vert S_{2}\vert })$ and $P=P_{\lambda }.$ Consider now the following algorithm.

1.1 Algorithm

Fix $\epsilon >0$ and set $diff=100$;

$$\begin{aligned}&H^{**}(1,\mathfrak {\beta },\lambda )=\left( I-A_{1}(\mathfrak {\beta } ,\lambda )\right) ^{-1}A_{0}(\mathfrak {\beta },\lambda );\\&L^{**}(1,\mathfrak {\beta },\lambda )=\left( I-A_{1}(\mathfrak {\beta } ,\lambda )\right) ^{-1}A_{2}(\mathfrak {\beta },\lambda );\\&G^{**}(1,\mathfrak {\beta },\lambda )=L^{**}(1,\mathfrak {\beta },\lambda );\\&T(1)=H^{**}(1,\mathfrak {\beta },\lambda );\\&Dowhile (diff>\epsilon )\\&\begin{array} [c]{cl} &{} k=k+1;\\ &{} U^{**}(k,\mathfrak {\beta },\lambda )=H^{**}(k-1,\mathfrak {\beta },\lambda )L^{**}(k-1,\mathfrak {\beta },\lambda )\\ &{} \quad \quad \quad \quad \quad \quad \qquad +\,L^{**}(k-1,\mathfrak {\beta },\lambda )H^{**}(k-1,\mathfrak {\beta },\lambda );\\ &{} M=(H^{**}(k-1,\mathfrak {\beta },\lambda ))^{2};\\ &{} H^{**}(k,\mathfrak {\beta },\lambda )=(I-U^{**}(k,\mathfrak {\beta },\lambda ))^{-1}M;\\ &{} M=(L^{**}(k-1,\mathfrak {\beta },\lambda ))^{2};\\ &{} L^{**}(k,\mathfrak {\beta },\lambda )=(I-U^{**}(k,\mathfrak {\beta },\lambda ))^{-1}M;\\ &{} G^{**}(k,\mathfrak {\beta },\lambda )=G^{**}(k-1,\mathfrak {\beta },\lambda )+T(k-1)L^{**}(k,\mathfrak {\beta },\lambda );\\ &{} T(k)=T(k-1)H^{**}(k,\mathfrak {\beta },\lambda );\\ &{} diff=\mathop {max}\limits _{j,k\in S}\left\{ [G^{**}(k,\mathfrak {\beta },\lambda )]_{j,k}-[G^{**}(k-1,\mathfrak {\beta },\lambda )]_{j,k}\right\} ; \end{array} \\&end\\&\Psi (\mathfrak {\beta })\cong G_{12}^{**}(k,\mathfrak {\beta } ,\lambda )G_{22}^{**}(k,\mathfrak {\beta },\lambda )^{-1}. \end{aligned}$$

Table 3 Transform matrices

Table 4 LST of first-passage times

Once we have computed $\Psi (\beta )$, the LST matrix of other hitting times are straightforward to evaluate; we list these matrices and their sizes in Tables 3 and 4. All matrices have nice probabilistic interpretations. For more details see Ahn et al. (2007).

The following LSTs of first-passage times are needed in our analysis: