Martingale methods for pricing inventory penalties under continuous replenishment and compound renewal demands

Abstract

This paper addresses the problem of inventory penalty pricing under the risk-neutral valuation principle. The underlying production-inventory system has a constant replenishment rate and a compound renewal demand stream (i.e., iid demand interarrival times are independent of iid demand sizes), and is subject to underage and overage penalties. Our pricing approach treats the penalties as a series of perpetual American options, and constructs auxiliary martingale processes in term of the inventory process. We provide a necessary and sufficient martingale condition for general compound renewal demands. Explicit expressions of penalty functions for underage and overage are obtained for the case where demand arrivals follow a Poisson process.

1 Introduction

Consider a production-inventory system with a constant replenishment rate. Demands arrive according to a compound renewal process, that is, both inter-arrival times and demand sizes are mutually independent random sequences, each being independent and identically distributed (iid). The system is subject to overage and/or underage penalties, both assessed against the firm (owner of the system). An underage penalty is assessed whenever a demand arrival encounters a stockout, whereby all or a portion of the demand cannot be satisfied from on-hand inventory, while an overage penalty is assessed whenever the inventory level hits a prescribed target level (e.g., the base stock level in a make-to-stock production-inventory system).

We define the perpetual inventory penalty as the discounted total penalty over an infinite time horizon. The standard penalty valuation problem in production-inventory context is the computation of the expected perpetual inventory penalty. In contrast, the problem we address in this paper is the inverse penalty valuation problem of devising proper dynamic penalty functions for assessing underage and/or overage penalties, such that the expected perpetual inventory penalty equals a prescribed value; the latter is interpreted as the penalty budget given to an inventory manager at time 0 to defray the cost of future underage and overage penalties. Throughout this paper, we assume that interest is compounded continuously at a given constant rate r≥0; accordingly, the present value of one unit of cash at time t is e ^−rt.

Both underage and overage are detrimental to the economics of production-inventory systems. Underage causes tangible and intangible losses that impact both the firm (e.g., lost sales, lost goodwill) and the customer (e.g., reduced service levels with potential business losses incurred by customers). In a similar vein, overage increases holding costs, and empirical evidence shows that even in well-managed businesses, a significant proportion of the inventory constitutes overage at any given time (Relph and Barrar 2003). While it is reasonable to assess overage penalties in terms of inventory holding costs, it is much more challenging to assess the firm’s loss of (intangible) goodwill and the costs of business losses sustained by a customer encountering stockouts. Similarly, it is also hard to evaluate the full extent of overage penalty because the supplier may sustain additional losses stemming from the enforcement of supply contracts (e.g., returned items). The latter are often ignored in supply chain studies (Zipkin 2000).

Most inventory optimization models capture overage and underage penalties as important cost components, but rarely address the practical problem of valuating them using real-life metrics. The traditional approach is to assume a prescribed fixed stockout cost that is incurred as a tangible loss by each stockout occurrence (Ernst and Powell 1995). However, intangible losses such as goodwill are not explicitly captured (Walter and Grabner 1975). The literature on the valuation of inventory penalties is relatively sparse. Schwartz (1966, 1970) point out that the effect of goodwill loss is characterized by the fact that disappointed customers react by changing their future purchasing habits. Thus some lingering stockout effects tend to adversely perturb future demand, a phenomenon quite different from the instantaneous imposition of a penalty at its time of occurrence. Early studies of the properties of perturbed demand appear in Schwartz (1966, 1970).

Several statistical studies have recently addressed the evaluation problem of lost sales. For example, in order to estimate the value of lost sales opportunities, Ofenbakh (2008) analyzes historical sales data to assess the underlying lost demand. Other studies meld finance methods and inventory management in a framework that treats inventory as a financial asset, and an inventory policy (or strategy) as a contingent claim. Accordingly, some well-known financial models have been applied to inventory management problems. For example, Stowe and Su (1997) view inventory as an option on future sales and show how some basic inventory problems can be solved using pricing models. The reader is referred to Stowe and Su (1997) for a literature survey of applications of financial theory to inventory decisions.

Our approach to the inverse penalty valuation problem is motivated by the risk-neutral valuation framework for contingent claims, and specifically by the special case of perpetual American options. A perpetual American call (put) option is a legal contract giving the holder of the option the right to buy (sell) a particular stock at a particular price at any time in the future (there is no option expiry date). The principle of risk-neutral valuation states that the option is risk-neutral if its expected value, discounted to the present time, equals its present value. It is known that if a contingent claim is risk neutral, then the stochastic process of its discounted version over time forms an exponential martingale process over a modified probability space (Hull 2002); this fact motivates us to apply a martingale approach to the penalty valuation problem and the inverse problem.

In this paper, we shall treat the imposition of an inventory underage or overage penalty as an exercise action of a perpetual American option; accordingly, the inventory penalty values are derived by using the risk-neutral principle. More specifically, the main idea is that inventory penalties are incurred stochastically at stopping times of the inventory process, which are analogous to the exercise times in a series of perpetual American options. To this end, we shall use techniques similar to those employed in financial valuation models to construct auxiliary exponential martingale processes, and derive functional equations for the requisite expected discounted penalties. The aforementioned auxiliary martingale processes will then be further used to derive the Laplace transform of the probability density function (pdf) of the stopping times at which penalties are incurred. To this end, we use techniques similar to those in the insurance model of Gerber and Shiu (1998), and obtain a penalty function by solving an equation with a prescribed present value of the respective penalties over an infinite time horizon. For the case of compound Poisson demands, explicit expressions for the underage penalty and overage penalty are obtained in Theorem 3 and Theorem 5, respectively.

The main contributions of this paper are listed below:

• (1) For an underlying production-inventory system with a general compound renewal demand process and constant replenishment, we construct an exponential process and provide a necessary and sufficient condition for this process to be a martingale. This result extends a known result for the special case of compound Poisson demand arrivals, known as Lundberg’s fundamental equation (Gerber and Shiu 1998).

• (2) For the same underlying system with lost sales, we derive explicit expressions for the underage penalty sequence.

• (3) For the same underlying system with backorders, we derive explicit expressions for the overage penalty sequence.

Throughout the rest of this paper, we use the following notation. The set of real numbers is denoted by ℝ. For any real number x∈ℝ, x ⁺=max{x,0}. The indicator function of a set A is denoted by 1 _A . For a random variable X, the functions f _X (x), F _X (x) and $\bar{F}_{X}(x) = 1 - F_{X}(x)$ denote respectively its probability density function (pdf), its cumulative distribution function (cdf) and its complementary cdf. The Laplace transform of a real function f(x) is defined by $\tilde{f}(z) = \int_{0}^{\infty} e^{ - z x} f(x) \,dx$.

The rest of this paper is organized as follows. Section 2 introduces assessment functions and a concise relevant background of the martingale methodology. Section 3 formulates the inventory model with compound-renewal demand arrivals. Sections 4, 5 and 6 treat the special case of compound Poisson demands, with Section 5 addressing underage penalties and Section 6 addressing overage penalties. Finally, Section 7 concludes this paper.

2 Assessment functions

In this section we provide a brief description of a typical assessment problem. Let {Y(t):t≥0} be a real-valued right-continuous stochastic process which models the time evolution of a stock price, inventory level, etc. Let further $\{ \tau_{i}^{(L)}: i \ge 1\}$ be the sequence of successive hitting times of a level L by the process {Y(t)}, (i.e., $Y(\tau_{i}^{(L)} - ) = L$) at which times certain assessments (e.g., penalties), $W_{i}^{(L)} =W_{i}^{(L)}(Y(\tau_{i}^{(L)}),L)$, are computed as a function of the level L and the state, $Y(\tau_{i}^{(L)} + ) = Y(\tau_{i}^{(L)})$. The assessment $W_{i}^{(L)}$ may be a random variable with a distribution that depends on $Y(\tau_{i}^{(L)})$ or a deterministic function. One typical example is the exercise of a perpetual American option [cf. Gerber and Shiu 1994, 1996], where the owner should exercise the option as soon as the value of the stock price reaches a particular level L. Following our notational conventions, we denote the pdf of $\tau_{i}^{(L)}$ conditioned on Y(0) by $f_{\tau _{i}^{(L)}|Y(0)}(t|y)$, and its Laplace transform by $\tilde{f}_{\tau _{i}^{(L)}|Y(0)}(s|y)$.

Following the standard finance methodology, the risk-neutral value of the assessments conditional on the initial state at time 0 is the total expected discounted value of all the assessments, given by

(2.1)

Of special interest is the expected discounted value of the assessment at the first level hitting time $\tau_{1}^{(L)}$, namely,

(2.2)

Using a renewal argument, the risk-neutral value of Eq. (2.1) can be obtained recursively by conditioning on the value of the state, $Y(\tau_{1}^{(L)})$, at $\tau_{1}^{(L)}$.

A classic example of the general standard valuation problem above is the expected discounted deficit at ruin time in an insurance setting (Gerber and Shiu 1998). Specifically, let Y(t) be the surplus of an insurance firm at time t, with Y(0)=y denoting the initial surplus. The firm will encounter bankruptcy at the ruin time $\tau_{1}^{(0)}$ when its surplus hits zero for the first time.

In the special case of $W_{i}^{(L)} = w_{i}(L)$ (deterministic level-dependent assessments), Eq. (2.2) reduces to

(2.3)

A case in point is the valuation of a perpetual American call option. Here, Y(t) is the underlying stock price at time t, L is the exercise level and K is the exercise (strike) price. Without loss of generality, we assume that the option is out of the money at time 0, that is, Y(0)<K, so that exercising the option at time t=0 can be excluded. Then the payoff of the corresponding perpetual American option is given by w(L)=[L−K]⁺=L−K.

Recall that the standard valuation problem under the risk-neutral principle is to price the action of “exercising the option” by using Eq. (2.1) with a given payoff function w(L), while the inverse valuation problem is to deduce w(L), given a present valuation, C(L,y). In an inventory budget-planning context, the inverse valuation problem can be interpreted as follows: An inventory manager is given a prescribed perpetual inventory penalty budget to defray the cost of future underage and overage penalties; such a budget can be viewed as a performance metric of the system (e.g., cost component, service-level, etc.). A risk-neutral inventory manager is then faced with the (inverse valuation) problem of deriving the appropriate penalty values to assess per underage/overage event occurrence under the principle of risk-neutral valuation, that is, subject to the constraint that the total expected discounted value of perpetual inventory penalties equals the prescribed budget.

It follows from Eq. (2.1) that the functional relationship between C(L,y) and w(L) is specified in terms of $\tilde{f}_{\tau _{1}^{(L)}|Y(0)}(r|y)$, and consequently, this Laplace transform needs to be derived first. To this end, we shall construct in Section 4, an auxiliary martingale sequence {M(t):t≥0} to define the requisite sequence of penalty functions. Recall that a martingale process {M(t):t≥0} satisfies the regularity condition

(2.4)

and the martingale property

(2.5)

We shall further make use of the Optional Stopping Theorem (also called the Optional Sampling Theorem). One version of the theorem is given below [cf. Karr 1993].

Theorem 1

Let {M(t):t≥0} be a martingale process and let τ be a stopping time of {M(t):t≥0}, such that

• (a) $\mathbb{E}[ \tau] < \infty$,

• (b) {M(t)} is bounded or uniformly integrable.

Then,

Finally, we shall need the following definition

Definition 1

Let {X(t),t≥0} be a stochastic process and let {τ _i ,i≥0} be a sequence of increasing hitting times measurable on the sigma-algebra generated by {X(t),t≥0}. Then {X(t)} has an embedded martingale {X(τ _i ):i≥0}, if it satisfies for any 0≤i≤j,

(2.6)

The motivation for defining auxiliary martingale processes as a tool for solving for $\tilde{f}_{\tau _{1}^{(L)}|Y(0)}(r|y)$ draws on classic martingale methodology as applied in the context of financial derivatives valuation. In particular, the time evolution of an underlying security price process, {S(t)}, is often modeled as a geometric Brownian motion, that is, X(t)=logS(t) is a shifted Brownian motion. The reason this model is routinely used in the analysis of financial derivatives (e.g., American options), is its continuity and independent-increment property. In a risk-neutral setting, the discounted-price process of financial derivatives over time is a martingale {M(t)} of the form [cf. Luenberger 1998],

(2.7)

where g(x) is a real-valued function, and e ^g(X(t)) is the price of the financial derivatives at time t. By the martingale property, $\mathbb{E}[ M(t)|M(0) ] = M(0)$. If {M(t)} is a bounded process, then

(2.8)

where the second equality is due to the Optional Stopping Theorem applied to the stopping time τ ^(L), and the third equality follows since the definition of τ ^(L) implies that S(τ ^(L))=L. Equation (2.8) readily implies

(2.9)

Equation (2.9) exhibits the relation between the Laplace transform of τ ^(L) and the martingale process of Eq. (2.7), and will be used to solve for the former [cf. Eq. (5.7) in Gerber and Shiu 1998].

The general martingale methodology outlined above will be employed in this paper to assess overage and underage penalties, under the principle of risk-neutral valuation. To this end, the inventory-level process {I(t):t≥0} will play a role analogous to X(t)=logS(t), and the hitting time τ ^(L) will map to hitting times of prescribed inventory levels that incur underage and overage penalties. Furthermore, the function g(x) will be chosen as the linear function g(x)=cx, where c is a real constant, such that the auxiliary process {M(t),t≥0}, defined by

(2.10)

is a martingale. The requisite value of such a constant c is specified in Lemma 1.

3 Inventory model formulation

We consider a general continuous-review production-inventory system. Replenishment occurs at a constant (deterministic) rate ρ>0. The demand stream is a compound renewal process denoted by {(A _i ,D _i ):i≥0}, where the demand arrival-time process {A _i } and the corresponding demand-size process {D _i } are mutually independent. The process {A _i :i≥0} is a renewal process with arrival rate λ and the convention A ₀=0. Let {T _i :i≥1} be the corresponding sequence of demand interarrival times, where T _i =A _i −A _i−1 are iid with common pdf f _T (t) satisfying f _T (0)=0. Let further {N _A (t):t≥0} be the counting process of demand arrivals, where N _A (t)=sup{n≥0:A _n ≤t} is the number of demand arrivals in the interval (0,t]. The corresponding demand sizes {D _i :i≥0}, where D ₀=0 by convention, are iid random variables with common pdf f _D (x) and cdf F _D (x). Under constant replenishment at rate ρ>0, the inventory process {I(t):t≥0} is given by

(3.1)

where a negative inventory level means that backordering is in effect.

Next, define the auxiliary process

(3.2)

where the value of the constant c is chosen so as to ensure that {M(A _i )} is an embedded martingale process.

Lemma 1

The process {M(t)} of Eq. (3.2) has an embedded martingale {M(A _i )} if and only if c satisfies

(3.3)

Proof

See Appendix. □

We next investigate the roots of Eq. (3.3). To this end, define

(3.4)

and

(3.5)

and note that Eq. (3.3) is equivalent to

(3.6)

The following result provides key properties of these functions.

Lemma 2

• (a) l _T (c) is strictly decreasing and strictly concave in c.

• (b) l _D (c) is strictly decreasing and strictly convex in c.

Proof

See Appendix. □

The following Proposition establishes a key property for the roots of Eq. (3.3).

Proposition 1

Equation (3.3) has two real roots, c ₁≤0 and c ₂≥0.

Proof

This follows immediately from Lemma 2 and the fact that l _D (0)=0<l _T (0) by Eqs. (3.4) and (3.5). □

Figure 1 depicts the functional form of l _T (c) and l _D (c), as well as the relative location of the roots, c ₁ and c ₂.

Fig. 1

The two roots of the equation l _T (c)=l _D (c)

Using the two roots c ₁ and c ₂, we define the two auxiliary processes

(3.7)

and

(3.8)

Recall that by Lemma 1, each of these auxiliary processes has an associated embedded martingale at demand arrival times, {A _i }.

4 Compound Poisson demand arrivals

In this section and the rest of this paper, we consider the case where the demand size is general, but demand arrivals follow a Poisson process with arrival rate λ>0, that is, the interarrival times are iid with pdf f _T (t)=λe ^−λt and Laplace transform $\tilde{f}_{T}(c) = \frac{\lambda}{\lambda + c}$. Then Eq. (3.3) becomes

(4.1)

Equation (4.1) is well known in the context of insurance models, where it is referred to as Lundberg’s fundamental equation (Gerber and Shiu 1998). Accordingly, we shall refer to Eq. (3.3) as the renewal extension of Lundberg’s fundamental equation.

The following example provides the two roots for the case of Poisson demand arrivals and exponentially distributed demand sizes.

Example 1

Consider the case of exponential demand sizes with parameter β>0, that is, f _D (x)=βe ^−βx. Hence, $\tilde{f}_{D}(c)= \frac{\beta}{\beta + c}$, and Eq. (4.1) can be rewritten as

or equivalently,

Finally, this equation has two roots, given by

(4.2)

(4.3)

For Poisson demand arrivals, we can prove the following stronger result for the auxiliary processes of Section 3.

Proposition 2

If the demand arrivals follow a Poisson process and c ₁≤0 and c ₂≥0 satisfy Eq. (4.1), then the processes {M ₁(t)} of Eq. (3.7) and {M ₂(t)} of Eq. (3.8) are both continuous martingales.

Proof

The proof readily follows from that of Lemma 1 by using the memorylessness property of Poisson processes and by replacing A _i and A _j with deterministic t and s, respectively. □

By Proposition 2, both {M ₁(t)} and {M ₂(t)} are martingales if c ₁ and c ₂ satisfy Eq. (3.3), which in our case becomes Eq. (4.1). We mention that the martingale property does not always hold for processes embedded at stopping times (e.g., underage or overage stopping times). However, the martingale property does hold for {M ₁(t)} and {M ₂(t)} when we associate {M ₁(t)} with underage and {M ₂(t)} with overage. This is demonstrated in Section 5 and 6 respectively.

5 Underage penalty functions

In this section, we study production-inventory systems with infinite capacity, subject to the lost-sales policy, that is, the unmet portion of a demand size is lost. The system is subject to an underage (or lost-sale) penalty which is assessed whenever the inventory level hits 0 due to a shortage. In Theorem 3 below we derive explicit expressions for underage penalties in the special case of Poisson demand arrivals and exponential demand sizes. To this end, we shall employ the process {M ₁(t)}, through which we derive some cost properties pertaining to the system.

Let L(A _i ) denote the lost-sales size at demand arrival time A _i , given by

(5.1)

Here the inventory process {I(t):t≥0} satisfies the following equation:

(5.2)

where the summation term represents the cumulative amount of demands that have been satisfied. Let the stopping times of shortages (underage times) associated with the inventory process of Eq. (5.2) be defined by

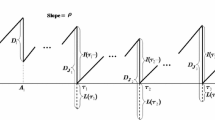
Here and in the sequel we use the superscript “0” to denote the hitting of inventory level 0 at lost-sales occurrences. Accordingly, let $D_{i}^{(0)}$ denote the size of the demand that arrived at the i-th loss occurrence time, $\tau_{i}^{(0)}$. In a similar vein, let $L_{i}^{(0)} =L(\tau_{i}^{(0)})$ denote the lost-sales size at $\tau_{i}^{(0)}$. Figure 2 illustrates a sample path of the inventory level process.

Fig. 2

A sample path of the inventory level subject to lost sales

The following simple lemma will be needed in the sequel.

Lemma 3

Let the demand size process be iid with a general distribution. Then, for any x≥0 and y>0,

(5.3)

Proof

The first equality follows directly from the identity $D_{i}^{(0)} =I(\tau_{i}^{(0)} - ) + L_{i}^{(0)}$.

The second equality readily follows from the equality

in view of the fact that $\mathbb{P}\{D_{i}^{(0)} > I(\tau_{i}^{(0)} - )\} = 1$. □

The next theorem establishes an embedded martingale property of {M ₁(t)}.

Theorem 2

Suppose that demands arrive according to a compound Poisson process. Then the process {M ₁(t)} in Eq. (3.7) has the martingale property at $\tau_{1}^{(0)}$.

Proof

By Proposition 2, {M ₁(t)} is a martingale. Furthermore, on $\{ \tau_{1}^{(0)} < \infty\}$, we have 0≤M ₁(t)≤1 by Eq. (3.7), since c ₁≤0 by Proposition 1, implying −rA _i +c ₁ I(A _i )≤0. The proof is completed by applying the Optional Sampling Theorem. □

Let $w_{k}^{(0)}( I(\tau_{k}^{(0)} - ), L(\tau_{k}^{(0)}) )$ denote the underage penalty for the k-th shortage occurrence. Our goal is to derive explicit expressions for the underage penalties. To this end, we shall first derive the expected discounted penalty for the first underage in Section 5.1; we then proceed to derive the corresponding subsequent underage sequence over an infinite time horizon in Section 5.2; and finally, we derive the requisite penalty expressions.

5.1 The first underage

In this section, we derive the conditional expected discounted penalty for the first underage. To this end, we revisit the inventory process given by Eq. (5.2). Figure 3 illustrates a sample path of the inventory process.

Fig. 3

A sample path of the inventory level process until the first underage

In view of Theorem 2, we can write

which in turn can be rewritten as

(5.4)

For the remainder of Section 5.1, we consider the special case where demand arrivals follow a Poisson process and the demand size has an exponential distribution with pdf f _D (x)=βe ^−βx, β>0. Recall that for this case, the two roots of Eq. (3.3) are given by Eqs. (4.2) and (4.3) in Example 1. We then have the following result.

Proposition 3

Suppose that demand arrivals form a Poisson process and demand sizes are exponentially distributed with rate parameter β>0. Then for any u≥0,

(5.5)

Proof

See Appendix. □

In particular, for u=0 in Eq. (5.5), one has

(5.6)

More specifically, let the penalty function be a function $w^{(0)}(L(\tau_{1}^{(0)}) )$ of the underage size only, and let D denote the demand size at time $\tau_{1}^{(0)}$. Then,

(5.7)

Here, conditioning on the event $\{ D > I(\tau_{1}^{(0)} - )\}$ in the first equality is justified by the fact that a loss occurred at $\tau_{1}^{(0)}$ by definition. The second equality is a consequence of the extended memorylessness property of the exponential distribution, namely, if X is exponential and Y is any random variable independent of X, then ℙ{X−Y>z|X>Y}=ℙ{X>z} [cf. Ross 1996]; accordingly, we note that each demand size is independent of the history of the inventory process prior to the demand arrival, and therefore D is independent of $I(\tau_{1}^{(0)} - )$. The expected discounted penalty for the first lost sale can be computed as

(5.8)

Here, the second equality follows from Eq. (5.7) and the last equality follows from Eq. (5.5).

5.2 The subsequent underage sequence

In this section, we continue to investigate the special case where demand arrivals follow a Poisson process and the demand size has an exponential distribution with pdf function f _D (x)=βe ^−βx, β>0. Specifically, we shall study the subsequent underage cost sequence at the hitting times $\{ \tau_{k}^{(0)}:k > 1\}$, and obtain an expression for the conditional expected total discounted underage penalties over an infinite horizon.

For k>1, we have

(5.9)

where the last equality holds by Eq. (5.6). Applying Eq. (5.9) recursively to the second term on the rightmost side above with the aid of Eq. (5.5) yields

(5.10)

Denoting the prescribed perpetual underage penalty budget by p _U , we have the following result.

Theorem 3

Suppose that demand arrivals form a Poisson process and demand sizes are exponentially distributed with rate parameter β>0. Suppose further that the underage penalty functions $w_{k}^{(0)}(y) =w^{(0)}(y)$ are functions of the underage size only and independent of k. Then, for I(0)=u, one form of w ⁽⁰⁾(y) is given by

(5.11)

Proof

By Eqs. (5.8) and (5.10), one has

(5.12)

By the principle of risk-neutral valuation, the right hand side of Eq. (5.12) equals p _U , which is the amount a risk-neutral manager would budget at time 0 to defray the future expected cost of discounted underage penalties. It follows that

Noting that exponential demand implies $\mathbb{E}[ w^{(0)}(D) ] =\beta\tilde{w}^{(0)}(\beta)$, the equation above yields

(5.13)

Finally, taking the inverse Laplace transform of Eq. (5.13) completes the proof. □

We point out that Eq. (5.13) does not determine $\tilde{w}^{(0)}$ since it holds only at the prescribed β. Consequently, other solutions for $\tilde{w}^{(0)}$ cannot be excluded.

6 Overage penalty functions

In this section, we study make-to-stock production-inventory systems with a base stock level S>0, that is, replenishment is governed by the base-stock policy as follows: while the inventory level is below S, continuous replenishment restocks the inventory at a constant rate ρ>0; otherwise, replenishment is suspended. All demand shortages are backordered. The system is subject to an overage penalty whenever the inventory level hits level S from below. In Theorem 5 below we derive explicit expressions for overage penalties in the case of Poisson demand arrivals and general demand-size distributions.

To this end, we consider the inventory process {I(t):t≥0}, which in this case has the representation

(6.1)

For u<S, we define a sequence of stopping times $\{ \tau_{k}^{(S)}:k \ge 1\}$ when the inventory level hits S, namely,

(6.2)

where $\tau_{0}^{(S)} = 0$ by convention. Note that {I(t)} can only decrease by jumps and only increase continuously, whence with probability 1,

(6.3)

Figure 4 depicts the behavior of a sample path of the inventory process.

Fig. 4

A sample path of the inventory level process with base stock level S

We next proceed to derive the penalty functions for overages. Let $\alpha_{k}^{(S)} = A_{N_{A}(\tau _{k}^{(S)}) + 1}$ denote the time of the first demand arrival after the occurrence of the k-th overage. Then the corresponding replenishment idle time, $T_{k}^{(S)}$, is given by

(6.4)

By the memorylessness property of the exponential distribution, the random sequence $\{ T_{k}^{(S)}\}$ is iid, and each $T_{k}^{(S)}$ is exponentially distributed with rate parameter λ, whence

(6.5)

Let the k-th overage penalty be denoted by $w_{k}^{(S)}$. Then the conditional expected total discounted penalty for the overage sequence is

(6.6)

Our goal is to derive explicit expressions for the overage penalties. To this end, we first derive the conditional expected discounted penalty for the first overage in Section 6.1; we then proceed to derive the corresponding subsequent overage sequence over an infinite time horizon in Section 6.2; and finally, we derive the requisite penalty expressions.

6.1 The first overage

In this section, we study the first overage penalty, assuming that the demand arrival process is Poisson. Figure 5 depicts a sample path of the inventory level process.

Fig. 5

A sample path of the inventory process until the occurrence of the first overage

The next theorem establishes an embedded martingale property of {M ₂(t)}.

Theorem 4

Suppose that demands arrive according to a compound Poisson process. Then the process {M ₂(t)} in Eq. (3.8) has the martingale property at $\tau_{1}^{(S)}$.

Proof

By Proposition 2, {M ₂(t)} is a martingale. Furthermore, on $\{\tau_{1}^{(S)} < \infty\}$, we have the inequalities $0 \le M_{2}(t) \le e^{c_{ 2}u}$ uniformly in t by Eq. (3.8). The proof is completed by applying the Optional Sampling Theorem. □

From Theorem 4 we have $M_{2}(0) = \mathbb{E}[ M_{2}(t)|I(0) =u ]$. It readily follows that at $t = \tau_{1}^{(S)}$,

(6.7)

where the second equality follows from Eq. (6.3). It follows that

(6.8)

so the expected conditional discounted penalty for the first overage is

(6.9)

where the second equality holds by Eq. (6.8).

We mention that Eqs. (6.7)–(6.9) are also valid for u≤0 and u=S. Accordingly, we shall assume that the initial inventory level satisfies u≤S.

6.2 The subsequent overage sequence

In this section, we study the sequence of subsequent overage penalties, assuming that the demand arrival process is Poisson but the demand size is generally distributed.

For k>1, the hitting times $\{ \tau_{k}^{(S)}\}$ constitute renewal times of the inventory process. Therefore, the time increment $\tau_{k}^{(S)} - \tau_{k - 1}^{(S)}$ is independent of both $\tau_{k}^{(S)}$ and I(0). Consequently, we can write

(6.10)

Next, write $\tau_{k}^{(S)} - \tau_{k - 1}^{(S)} = T_{k - 1}^{(S)} +(\tau_{k}^{(S)} - \tau_{k - 1}^{(S)} - T_{k - 1}^{(S)})$, and note that the (k−1)-th replenishment idle time, $T_{k - 1}^{(S)}$, is independent of the residual time to hit S, namely, $\tau_{k}^{(S)} -\tau_{k - 1}^{(S)} - T_{k - 1}^{(S)}$; furthermore, by a renewal argument the latter is distributed as $\tau_{1}^{(S)}$, given I(0)=S. Using these observations, we can write

Next, observe that on the right-hand side above, the first term is given by Eq. (6.5) and the second term follows from Eq. (6.8), yielding for all k≥1,

(6.11)

Note that 0<γ<1 since $0 < \frac{\lambda}{\lambda + r} < 1,0 < e^{ - c_{ 2} S} < 1$ and $0 < \tilde{f}_{D}( - c_{ 2}) < 1$. Substituting Eq. (6.11) into Eq. (6.10), we obtain the recursive relation

(6.12)

and applying Eq. (6.12) k−1 times, we obtain in view of Eq. (6.8)

(6.13)

Finally, utilizing Eq. (6.13), we have

(6.14)

Denoting the prescribed perpetual overage penalty budget by p _O , we have the following result.

Theorem 5

If the overage penalty functions $w_{k}^{(S)} = w^{(S)}$ for level S are constant, independent of k, then the overage penalty is given by

(6.15)

where $\gamma = \frac{\lambda}{\lambda + r}e^{ - c_{2}S}\tilde{f}_{D}( - c_{ 2})$.

Proof

Substituting $w_{k}^{(S)} = w^{(S)}$ into Eq. (6.14), one has

(6.16)

By the principle of risk-neutral valuation, Eq. (6.16) equals p _O , which is the amount a risk-neutral manager would budget at time 0 to defray the future cost of discounted overage penalties. Therefore,

(6.17)

The result readily follows via simple algebra. □

Theorem 5 shows that in the special case, I(0)=u=S, the overage penalty becomes $w^{(S)} = p_{O}( 1 - \frac{\lambda}{\lambda + r}e^{ -c_{ 2}S}\tilde{f}_{D}( - c_{ 2}) )$.

7 Concluding remarks

The main goal of this investigation was to formulate the inventory penalty function problem and derive explicit expressions for overage and underage penalties under the principle of risk-neutral valuation for production-inventory systems with constant replenishment and compound renewal demand stream, with special emphasis on Poisson demand arrivals and exponential demand sizes.

The problem we addressed in this paper was the inverse valuation problem, namely, devising proper dynamic penalty functions for assessing overage and underage penalties, given a prescribed penalty budget. Our solution approach treated inventory overage and underage penalties as a series of perpetual American options. To price such options, we first constructed auxiliary exponential martingale processes in terms of the underlying inventory process. Each auxiliary martingale process was then used to establish some intermediate results which were further used to derive the expected discounted perpetual inventory penalties, conditioned on the initial inventory level. Under the risk-neutral valuation principle, the obtained conditional expected total discounted perpetual inventory penalty equals a prescribed value of the penalty budget that a risk-neutral inventory manager would set aside at time zero to defray the cost of future penalties. Accordingly, we derived the requisite penalty functions for both overage and underage penalties, subject to a prescribed penalty budget.

For general compound renewal demands, we obtained the requisite necessary and sufficient martingale condition. We proceeded to prove that this equation has two roots: one negative and one positive. We then used the negative root to construct a martingale process, associated with underage penalties, while the positive root was used to construct a martingale process, associated with overage penalties. Finally, we obtained explicit expressions for underage and overage penalty functions for some special cases of compound Poisson demand arrivals and exponential demand sizes.

Appendix

Proof of Lemma 1

Substituting Eq. (3.1) into Eq. (2.10) and noting that I(t) and M(t) determine each other for each t, we rewrite the left hand side of Eq. (2.6) for any 0≤i≤j as

(8.1)

For the embedded martingale condition to hold, it is necessary and sufficient that the right-most side of Eq. (8.1) be equal to M(A _i ), which is equivalent to the condition

Equation (3.3) now readily follows, since $\tilde{f}_{T}(r - c \rho)\tilde{f}_{D}(c)$ is non-negative. □

Proof of Lemma 2

To prove part (a), we show that the derivatives of l _T (c) satisfy

(8.2)

(8.3)

Equation (8.2) follows from the facts

(8.4)

(8.5)

where Eq. (8.4) is an immediate consequence of the Laplace transform, and Eq. (8.5) follows by the Leibniz integral rule.

To prove (8.3), note that the denominator is positive, so it remains to show that the numerator is positive too. Differentiating Eq. (8.5) with the aid of the Leibniz integral rule yields

(8.6)

Substituting (8.4), (8.5) and (8.6) into the numerator of Eq. (8.3), the latter becomes

(8.7)

Finally, applying the Cauchy-Schwarz inequality (Karr 1993) to the product of expectations in the first term of Eq. (8.7) results in the inequality,

(8.8)

where the strict inequality follows from the fact that the random variables on the left-hand side above are not proportional to each other. Equation (8.8) establishes that the numerator of Eq. (8.3) is positive, thereby completing the proof of part (a).

To prove part (b), we apply an argument similar to that for part (a). Accordingly, we show that the derivatives of l _D (c) satisfy

(8.9)

(8.10)

Equation (8.9) follows from the facts

(8.11)

(8.12)

where Eq. (8.11) is an immediate consequence of the Laplace transform, and Eq. (8.12) follows by the Leibniz integral rule.

To prove Eq. (8.10), note that the denominator is positive, so it remains to show that the numerator is positive too. Differentiating Eq. (8.12) with the aid of the Leibniz integral rule yields,

(8.13)

Substituting Eqs. (8.11), (8.12) and (8.13) into the numerator of Eq. (8.10), the latter becomes

(8.14)

Finally, applying the Cauchy-Schwarz inequality to the first term of Eq. (8.14) results in the inequality,

(8.15)

where the strict inequality follows from the fact that the random variables on the left-hand side above are not proportional to each other. Equation (8.15) establishes that the numerator of Eq. (8.10) is positive, thereby completing the proof of part (b). □

Proof of Proposition 3

Let D denote a generic exponential demand size with pdf f _D (x)=βe ^−βx,β>0. By Lemma 3 we can write

(8.16)

where the second equality follows from the memorylessness of the exponential distribution.

Define the functions

(8.17)

and

(8.18)

Next, we rewrite Eq. (8.17) as

(8.19)

where the first equality holds by the chain rule of conditional probabilities,

and the second equality follows from Eq. (8.16) combined with the fact that $f_{L(\tau _{1}^{(0)})| I(\tau _{1}^{(0)} - ),\tau _{1}^{(0)}, I(0)} = f_{L(\tau _{1}^{(0)})| I(\tau _{1}^{(0)} - )}$. In view of Eqs. (8.18) and (8.19), we now have

(8.20)

Furthermore, integrating both sides of Eq. (8.18) with respect to x from zero to infinity, we get

(8.21)

Next, we write

(8.22)

Here, the first equality follows from the fact that $L(\tau_{1}^{(0)}) =- I(\tau_{1}^{(0)})$, the second and third equality hold by definition, the fourth equality holds by Eq. (8.20), the fifth equality follows from (8.21), and the sixth equality is a consequence of exponentially distributed demand sizes. Finally, the above equation equals $e^{c_{1}u}$ by Eq. (5.4), which completes the proof. □