Integrated data depth for smooth functions and its application in supervised classification

Abstract

This paper concerns depth functions suitable for smooth functional data. We suggest a modification of the integrated data depth that takes into account the shape properties of the functions. This is achieved by including a derivative(s) into the definition of the suggested depth measures. We then further investigate the use of integrated data depths in supervised classification problems. The performances of classification rules based on different data depths are investigated, both in simulated and real data sets. As the proposed depth function provides a natural alternative to the depth function based on random projections, the difference in the performances of these two methods are discussed in more detail.

1 Introduction

Data depth or depth functions became a very popular tool of nonparametric multivariate methods in the last two decades. A depth function is a map $D:\mathbb S \times \mathcal P(\mathbb S) \rightarrow \mathbb R^+$ or $\rightarrow [0,1]$, where $\mathbb S$ is a sample space and $\mathcal P(\mathbb S)$ the space of all probability distributions on $\mathbb S$. Hence, a depth function defines a linear ordering (semi-ordering) on the sample space with respect to a given probability distribution. A depth function is usually defined such that it satisfies some properties; these were summarized by Zuo and Serfling (2000). A depth should define ordering in an central-outward sense reflecting a “position” of a point with respect to a probability distribution. In particular if a distribution has a point of symmetry this should be the deepest point of the distribution and a depth should decrease when the distance from the point of symmetry increases. The most popular depths include the halfspace depth (Tukey 1975), the simplicial depth (Liu 1990) or the zonoid depth (Mosler 2002). Each depth function has its advantages and disadvantages concerning their performance on data sets, statistical properties and computational issues.

There are many applications of the multivariate ordering induced by the data depth. One of the most popular applications of data depth is its use to the classification problem. Since the data are ordered in the central-outward sense the classification rule may be based on this univariate variable. In this sense a data depth serves as a dimension reduction of the multivariate data setting to a univariate setting. Different depth functions may then be compared with respect to their classification performance.

Recently, data depth functions for functional (infinite dimensional) data have attracted considerable attention. While our paper is motivated by the integrated data depth introduced in Fraiman and Muniz (2001), the other approaches include ‘random projection depths’ (Cuevas et al. 2007), and ‘band depths’ (López-Pintado and Romo 2007), among others. It has been proved that the basic desirable properties of depth functions as listed in Zuo and Serfling (2000) hold also for the integrated depth and for the band depth for functional data (López-Pintado and Romo 2009; Claeskens et al. 2014).

Often one can assume that the observed curves, in this infinite dimensional setting, are smooth. Then it can be of interest to make use of the information contained in the derivatives of the curves. Within the framework of ‘random projection depths’ (Cuevas et al. 2007 suggested a depth function suitable for smooth functions that involves the information in derivatives. Inspired by this work we propose an alternative depth function that is based on the integrated depth and that utilizes the information about the derivatives of the observed curves. Thus our approach generalizes the definition of the integrated data depth (Fraiman and Muniz 2001) and complements the results in Cuevas et al. (2007). Further, analogously as in Cuevas et al. (2007) we illustrate the performance of the suggested data depth on supervised classification.

The aim of this paper is threefold: (i) to introduce a new integrated data depth function for functional data; (ii) to investigate the performances of integrated data depth functions (including the proposed one) in supervised classification; (iii) to compare this performance with other supervised classification methods.

The paper is organized as follows. The newly-proposed integrated data depth for smooth functional data is presented in Sect. 2, where it is also related to other recent data depth functions involving derivatives. In Sect. 3 the problem of supervised classification is discussed, together with some available classification methods. In Sect. 4 the introduced integrated data depth functions are used for classification of both simulated and real functional data.

2 Integrated data depth for smooth functions

Suppose the observations are independent and identically distributed smooth stochastic processes $X_{1}(t),\cdots ,X_{n}(t)$. More precisely, $X_{i}$ is a random variable with values in the space of continuously $K$-times differentiable functions on the interval $[a,b]$. We denote this space by $C^{(K)}([a,b])$. Without loss of generality in the following we assume that $[a,b] = [0,1]$.

As mentioned in the introduction there are several concepts of depth measures for functional data. In this paper we concentrate on the integrated data depth function suggested by Fraiman and Muniz (2001). In the next section we briefly discuss how to build integrated data depths that incorporate information on the original observed curves as well as information on derivative curves.

2.1 Integrated data depth functions

Denote by $P_n$ the empirical distribution of the observed random functions $X_{1},\cdots ,X_{n}$ and let $P_{t,n}$ be the marginal distribution of $P_{n}$ at the point $t$, i.e. $P_{t,n}$ is the empirical distribution of the sample $X_{1}(t),\cdots ,X_{n}(t)$. Further, let $D_{k}$ be a depth function on $\mathbb {R}^{k}$, for instance Tukey’s halfspace depth (Tukey 1975) or the simplicial depth (Liu 1990). The integrated depth function is now defined as

$$\begin{aligned} ID(x;P_{n},D_1) = \int _{0}^{1} D_{1}\big (x(t);P_{t,n}\big )\,\text {d}t, \end{aligned}$$

(1)

where $D_{1}(x(t);P_{t,n})$ is a univariate depth of the point $x(t)$ with respect to the distribution $P_{t,n}$.

In this paper the interest goes to integrated data depths for smooth functions. Therefore, next to the observed random functions $X_{1},\cdots ,X_{n}$, we can also consider the $k$th derivatives of the observed functions, i.e. $X_{1}^{(k)},\cdots ,X_{n}^{(k)}$, up to order $K$. Let $P_{n}^{(k)}$ be the empirical distribution of $X_{1}^{(k)},\cdots ,X_{n}^{(k)}$ and note that $P_{n}^{(0)}$ coincides with the standard empirical measure $P_{n}$. Let $w_{0},\cdots ,w_{K}$ be non-negative weights that sum up to one. Then a straightforward modification of the integral depth function defined by (1) is given by

$$\begin{aligned} FD(x;P_{n},D_1) = \sum _{k=0}^{K} w_{k}\,ID^{(k)}\big (x;P_{n},D_1 \big ), \end{aligned}$$

(2)

where

$$\begin{aligned} ID^{(k)}(x;P_{n},D_1) = \int _{0}^{1} D_{1}\big (x^{(k)}(t);P_{t,n}^{(k)}\big )\,\text {d}t \end{aligned}$$

stands for the integrated depth calculated for the $k$th derivative of the function $x$ with respect to the distribution $P_{n}^{(k)}$. Note that for $w_{k}=1$ (implying that all the other weights are zero), the definition of $FD(x;P_{n},D_1)$ given by (2) coincides with the integrated data depth of Fraiman and Muniz (2001) calculated from the $k\hbox {th}$ order derivatives of the observed functions.

Note that in (2) each of the derivatives is considered separately and then the final depth is calculated as a weighted average of depths of derivatives. Sometimes however it is advantageous to consider the function and its derivatives jointly. See for example Sect. 4.3. This brings us to the following definition of a depth function for smooth functions. For $0 \le j_{1} < j_{2} < \cdots < j_{k} \le K$ let $X_{i}^{(j_{1},\cdots ,j_k)}$ stand for the vector $(X_{i}^{(j_{1})},\cdots ,X_{i}^{(j_{k})})$ of the $j_{1}$th, ..., $j_{k}\hbox {th}$ derivative of the function $X_{i}$. Further, let $P_{n}^{(j_{1},\cdots ,j_k)}$ be the empirical distribution based on $X_{1}^{(j_{1},\cdots ,j_k)},\cdots ,X_{n}^{(j_{1},\cdots ,j_k)}$. Now, we suggest that the depth of $x \in C^{(K)}([a,b])$ is measured as

$$\begin{aligned} FD(x;P_{n}) = \mathop {\mathop {\mathop {\sum }\limits _{\left\{ j_1,\cdots ,j_k\right\} \subset \{0,1,\cdots ,K\}}}\limits _{j_{1} < j_{2} < \cdots < j_{k}}}\limits _{k=1,\cdots ,K+1 } w_{j_1,\cdots ,j_k}\,ID^{(j_{1},\cdots ,j_k)}\bigl (x;P_{n},D_k\bigr ), \end{aligned}$$

(3)

where the summation runs over all non-empty subsets of $\{0,1,\cdots ,K\}$; further $\{w_{j_1,\cdots ,j_k}\}$ are some non-negative weights that sum up to one and

$$\begin{aligned} ID^{(j_{1},\cdots ,j_k)}\bigl (x;P_{n},D_k\bigr ) = \int _{0}^{1} D_{k}\bigl (x^{(j_{1},\cdots ,j_k)};P_{t,n}^{(j_{1},\cdots ,j_k)} \bigr )\,\text {d}t \end{aligned}$$

(4)

stands for the integrated depth calculated for the vector function $x^{(j_{1},\cdots ,j_k)}$ with respect to the empirical distribution of vector functions $P_{n}^{(j_{1},\cdots ,j_k)}$.

Since in (3) several multivariate depth functions (univariate, bivariate, ..., $(K+1)$-variate) may be used, we dropped the notation “D”, and simply use the notation $FD(x;P_{n})$.

It is instructive to look into some examples.

Example 1

We first discuss the situation $K=1$ in detail. In this case (3) becomes

$$\begin{aligned} FD(x;P_{n})&= w_{0}\,ID^{(0)}\bigl (x;P_{n},D_1\bigr ) + w_{1}\,ID^{(1)}\bigl (x;P_{n},D_1\bigr ) \nonumber \\&+\, w_{0,1}\,ID^{(0,1)}\bigl (x;P_{n},D_2\bigr ). \end{aligned}$$

(5)

Thus, when using data depth for instance for classification one can tune the weights $w_{0}, w_{1}, w_{0,1}$ in order to focus on differences in the curves and/or their derivatives. While $ID^{(0)}$ (respectively $ID^{(1)}$) concentrate on classification based on the differences in the original (respectively first derivative) values of the curves, $ID^{(0,1)}$ pays attention to both their original values as well as the values of the first derivative. Moreover, $ID^{(0,1)}$ has the potential to detect differences between curves that can be discovered from the joint distribution of original curves and their derivatives, but that cannot be discovered by considering original curves and their derivatives separately (see for example Sect. 4.3.1). Some interesting special cases of (5) are:

• 1. The three cases: (i) $w_0=1, w_1=0, w_{0,1}=0$; (ii) $w_0=0, w_1=1, w_{0,1}=0$; (iii) $w_0=0, w_1=0, w_{0,1}=1$; in which one focuses entirely on either: (i) the observed curves themselves; (ii) the derivative curves; (iii) the joint distribution of the observed curves and their derivatives.

• 2. The case $w_0=w_1= w/2$ and $w_{0,1}=1-w$, with $w \in [0,1]$. In this case, looking separately at the observed curves or their derivatives gets an equal weight.

• 3. The cases $w_0=w_1=w_{0,1}=1/3$.

• 4. The cases: $w_0=w,\, w_1=0$ and $w_{0,1}=1-w$, and $w_0=0,\, w_1=w$ and $w_{0,1}=1-w$, where the curves themselves and the joint distribution, respectively the first derivatives of the curves, and the joint distribution come into play, in a balanced way.

In Sect. 4.3 we investigate some of these scenarios in a simulation study regarding supervised classification.

Example 2

We now look at the case $K=2$. In this case (3) becomes

$$\begin{aligned} FD(x;P_{n})&= w_{0}\,ID^{(0)}\bigl (x;P_{n},D_1\bigr ) + w_{1}\,ID^{(1)}\bigl (x;P_{n},D_1\bigr ) + w_{2}\,ID^{(2)}\bigl (x;P_{n},D_1\bigr )\\&+\, w_{0,1}\,ID^{(0,1)}\bigl (x;P_{n},D_2\bigr ) + w_{0,2}\,ID^{(0,2)}\bigl (x;P_{n},D_2\bigr )\\&+\, w_{1,2}\,ID^{(1,2)}\bigl (x;P_{n},D_2\bigr ) + w_{0,1,2}\,ID^{(0,1,2)} \bigl (x;P_{n},D_3\bigr ). \end{aligned}$$

The suggested depth in (3) is thus very versatile, and allows a lot of flexibility in the actual choice of the depth measure considered. In Sect. 4.3 the advantages of such a versatile rule will be seen.

Note that the computational cost for calculating the depth $FD(x;P_n)$ is similar to that for calculating integrated depths, for a given (maximal) order of derivatives $K$ to be included. In real data applications, the random functions are not observed on the whole domain, but only at a discrete (dense) grid of points in the domain. From the observed function values at the discrete points, one computes via for example (linear) interpolation, approximate values for all points in the domain. See for example (Claeskens et al. 2014), as well as Sect. 4.

Remark 1

So far we have discussed the empirical depth calculated using the empirical measure $P_{n}$ based on the observed curves. The population analogue of the suggested data depth is defined simply by replacing $P_{n}$ with the population distribution $P$ in the definition of $FD$.

2.2 Other data depth functions involving derivatives

As discussed in the introduction several depth functions for function-valued random variables have been suggested recently in the literature and the integrated data depth is only one of the possible approaches. While it is quite straightforward to use the depth measures with the derivatives instead of the original curve (as in $ID^{(k)}$), the idea of considering the joint distribution of the original curves and their derivatives has not attracted, to the best of our knowledge, much attention yet.

A first approach we are aware of is the double random projection methods suggested in Cuevas et al. (2007). This method runs as follows. Let $a$ be a random process on $[0,1]$ (called random direction in Cuevas et al. 2007). The data are first reduced to a bi-dimensional sample by taking inner products between the random direction and the observed process on the one hand and between the random direction and the derivatives of the observed curves on the other hand, i.e. $\big (\langle a,X_{1} \rangle , \langle a,X^{(1)}_{1} \rangle \big ), \cdots , \big (\langle a,X_{n} \rangle , \langle a,X^{(1)}_{n} \rangle \big )$. Now, one can use one of the many available methods to calculate the depth from bivariate observations. As the resulting depths depend on $a$, in the last step these depths are averaged with respect to the distribution of the process $a$.

Another approach that was proposed in the recent literature is in Claeskens et al. (2014). They start from a multivariate set of observed curves, all observed in the same time points $t_{\ell }$, with $\ell =1, \dots , T$, and then consider a $k$-variate depth function $D_k$ to define

$$\begin{aligned} \displaystyle \sum _{\ell =1}^T D_k\left( x^{(j_1, \dots , j_k)}; P_{t_{\ell },n}^{(j_1, \dots , j_k)} \right) W\left( t_{\ell } \right) \,. \end{aligned}$$

So, in contrast to (4), the role of the weights $W\left( t_{\ell } \right)$ is to give possibly different importance to different regions of the domains of the curves involved. The proposed depth measure, defined in (3), does not differentiate in importance of regions, but combines different depth measures instead.

In Sect. 4 we compare, among others, the performances of the (double) random projection methods with the proposed depth function in (3), when used in a supervised classification problem.

3 Supervised classification and data depth

In Sect. 4 we illustrate the properties of the suggested data depth function (3) by applying it to the problem of supervised classification. This problem can be described as follows. Suppose we have $G$ populations $P_{1},\cdots ,P_{G}$. For each population $P_{g}$ we have a ‘training sample’ of independent $n_{g}$ observations $X_{1}^{(g)},\cdots ,X_{n_{g}}^{(g)}$ that comes from $P_{g}$. The aim is to classify a new observation $X$ into one of the $G$ populations.

The classification of functional data is a challenging problem that attracts considerable attention since the last years. For a recent survey of existing methods see Ferraty and Romain (2011) and the references therein. Among the available classification methods there are various generalizations of linear discrimination rules (see e.g. James and Hastie 2001), distance-based and kernel rules (see e.g. Ferraty and Vieu 2006), partial least squares method (see e.g. Liu and Rayens 2007), reproducing kernel methods (see e.g. Berlinet and Thomas-Agnan 2004) and methods based on depth measures. Another classification and clustering method based on projection of the functional data to a relatively small number of chosen coordinates has appeared recently in Delaigle et al. (2012). Analogously as Cuevas et al. (2007) we concentrate in the following on comparison of several standard distance-based methods with several methods based on integrated and random projection data depth.

3.1 Methods based on the distances of the functions

Probably the most widely used method for classification is the $m\hbox {th}$-nearest neighbours method (with $m$ a given positive integer). Note that in the context of functional data, the method can be based either on the original curves or their $j\hbox {th}$ order derivatives. Further one has to choose a distance function that measures the proximity of the curves.

Among other available methods we mention the $h$-mode method described in Sect. 2 of Cuevas et al. (2007). This method assigns the curve $x$ to the distribution with the largest value of the function

$$\begin{aligned} \widehat{f}_{h}^{(g)}(x) = \frac{1}{n_{g}} \sum _{i=1}^{n_{g}} L\Big (\tfrac{\Vert x-X_{i}^{(g)}\Vert }{h}\Big ), \end{aligned}$$

where $L$ is a kernel function, $\Vert \cdot \Vert$ is a suitable norm and $h>0$ is a bandwidth. Note that in case of equal sizes of the groups in the training sample this method coincides with the method described in Chapter 8.2 of Ferraty and Vieu (2006) with the bandwidth $h$ fixed (and equal for all groups). Note that in principle different bandwidths $h_{1},\cdots ,h_{g}$ for the different groups could be allowed.

3.2 Data depth based methods

When speaking about data depth based classification methods, it should be noted that there are many ways how a given depth function can be converted into a classification rule (see e.g. López-Pintado and Romo 2006; Li et al. 2012; Lange et al. 2014).

The most straightforward method is to use the maximum depth rule (Ghosh and Chaudhuri 2005) which can be described as follows. Let $P_{g,n_{g}}$ stand for the empirical distribution of the training sample from $P_{g}$ and $D(X; P_{g,n_{g}})$ measures the considered depth of the observation $X$ with respect to $P_{g,n_{g}}$, based on the given depth function. Then $X$ is assigned to the distribution $P_g$ if $D(X;P_{g,n_{g}}) > D(X;P_{j,n_{j}})$ for all $j \ne g$, $j\in \{1,\ldots ,G\}$. Among the more sophisticated methods are these that use the DD-plot (depth-versus-depth plot) suggested in Li et al. (2012). In fact the maximum depth rule is a special case of the DD-classifier that uses the axis of the first quadrant as the separation line in the DD-plot.

In our comparative simulation study in Sect. 4 we restrict to the maximum depth rule.

4 Simulation study: applying data depth in supervised classification

To investigate the properties of classification methods described in Sect. 3 we conducted a simulation study incorporating two distance-based methods and several (integrated) data depth based methods. The simulation study involves five different models, which allows us to compare the performances of the different classification rules in quite different settings. A first setting illustrates a situation where we find the suggested data depth (3) in particular useful. The second and the third model are inspired by Model 1 from the simulation study of Cuevas et al. (2007). The fourth model is inspired by the Berkeley growth data (see e.g. Chapter 6.8.2 Ramsay and Silverman 2002). Finally the last model complements the simulation study of Chapter 8.4.2 of Ferraty and Vieu (2006) based on the well-known spectrometric data (‘Tecator dataset’).

4.1 Methods involved in the simulation study

From the distance-based methods we used the $m\hbox {th}$-nearest neighbours method and the $h$-mode method both based on the $L_{2}$ distance to measure the proximity of the curves. Similarly as in Cuevas et al. (2007) we took $m=5$ for the $m$th-nearest neighbours method and $h$ as the $20$th percentile of the $L_{2}$ distances between the functions in the training sample. Both methods can be based either on the original curves $(\mathtt {mNN^{(0)}},\, \mathtt {mode^{(0)}})$ or their $j\hbox {th}$ order derivatives $(\mathtt {mNN^{(j)}},\, \mathtt {mode^{(j)}})$.

The depth based classification methods in the simulation study were based on the maximum depth rule described in Sect. 3.2. From the depth functions we apply the integrated depth $(ID)$ and the random projection depth $(RD)$. Following the convention used in Sect. 2, put $\mathtt {ID^{(j)}}\, (\mathtt {RP^{(j)}})$ for the classification rule based on the integral (random projection) depth of the $j\hbox {th}$ order derivative of the curve. Further, put $\mathtt {ID^{(j,k)}}$ for the classification rule based on $ID^{(j,k)}$ defined in (4). Finally, let $\mathtt {RP2}$ and $\mathtt {RPD}$ stand for the rules based on the corresponding double random projection methods as described in Cuevas et al. (2007). Roughly speaking, these methods differ in a way how they treat a bi-dimensional sample obtained by projecting the original curves and their derivatives (see Sect. 2.2). While $\mathtt {RP2}$ is based on (another) random projecting of this bivariate sample, the method $\mathtt {RPD}$ uses an $h$-mode method.

Table 1 summarizes the methods used in the main part of the simulation study, and lists the abbreviations used for them in the plots and tables later on.

Table 1 Main methods in the simulation study, and the abbreviations used

For the sake of simplicity, if the highest value of the depth (with respect to the training samples) is reached for more than one group, then we randomly assign $X$ to one of the groups exposing this highest depth value.

4.2 Simulation settings

The quality of the classification rule is measured by the misclassification rate that is estimated as the ratio of incorrectly classified functions to the number of all functions that were to be classified.

Unless stated otherwise, we used two probability distributions, i.e. $G=2$. In each of the $1\,000$ independent runs, a training sample of size $100$ observations was generated, obtained by a sample of size 50 from each of the distributions $P_1$ and $P_2$. Further, a test sample of size $50$ observations from each distribution was generated independently of the training samples, resulting into a test sample of $100$ observations. The functions were observed on a grid of $51$ equispaced points in the $[0,1]$ interval. The derivatives of the functions were calculated as follows. First, the function was approximated by fitting a cubic spline function with knots located at each grid point of the generated functions. The least squares method was used for the fitting here. Then the fitted function is differentiated and the derivative is discretized back to the grid points. We used the implementation of this method in the functions $\mathtt {D1ss}$ and $\mathtt {D2ss}$ of the package sfsmisc (Maechler 2013).

The R-computing environment (R Core Team 2013) was used to perform the simulations.

4.3 Simulation study

4.3.1 Model 1: randomly shifted exponentials with random slopes

Let $(A_{1},B_{1})$ be a random vector with a bivariate normal distribution with mean $\varvec{\mu }_{1} = (0,1)$ and the variance-covariance matrix determined by unit variances and correlation coefficient $0.9$. Similarly, let $(A_{2},B_{2})$ be a random vector with a bivariate normal distribution with mean $\varvec{\mu }_{2} = (0,-1)$ and the same variance-covariance matrix. The probability model $P_{i}\, (i=1,2)$ for the functional data on $[0,1]$ is now given by the distribution of the process $X$

$$\begin{aligned} X(t) = A_{i} + B_{i}\,\mathrm {e}^{t} + \tfrac{1}{6}\,\epsilon (t), \quad t\in [0,1],\quad i=1,2, \end{aligned}$$

(6)

where $\epsilon$ is a noise function defined as

$$\begin{aligned} \epsilon (t) = U_{1}\,\sin (2\pi t) + U_{2}\,\cos (2\pi t) + U_{3}, \end{aligned}$$

(7)

with $U_{1}$, $U_{2}$ and $U_{3}$ independent random variables, uniformly distributed on $[-\tfrac{1}{2},\tfrac{1}{2}]$. Note that in Models 1 and 2 of Cuevas et al. (2007) the authors use as a noise function a Gaussian process which implies that $X$ is also a Gaussian process. However, this brings a methodological difficulty in the considered context, since it is known that a non-degenerate Gaussian process is not differentiable almost everywhere (see e.g. Chapter 2 Theorem 9.18 and Problem 9.17 of Karatzas and Shreve 1991). To prevent from this difficulty we use the noise process given by (7). While in this model the impact of the noise is pretty limited, due to the coefficient $\tfrac{1}{6}$ in front of $\epsilon (t)$ in (6), the noise will have a more substantial impact in the models presented in Sects. 4.3.2 and 4.3.3.

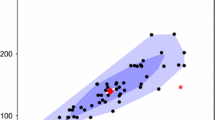
One training sample of size 50 generated from (6) is plotted in Fig. 1 and the simulation results for the methods in Table 1 are summarized as boxplots in Fig. 2. From Fig. 1 it can be seen that there is evidently some difference in the horizontal shift among the groups of the curves (as well as their derivatives). It is may be surprising though that the classification rule $\mathtt {ID^{(0,1)}}$, that looks at the original curves and their derivatives simultaneously, achieves the highest median correct classification rate, which is close to $0.95$. To explain this it is instructive to have a look at the empirical marginal joint distributions of the two groups of curves at a given $t$. This is done in Fig. 3 for three different values of $t$, where different symbols (crosses and circles) were used to distinguish the observations from different groups. Note that thanks to the high correlation of the random coefficients $A_{i}$ and $B_{i}$ one can pretty well distinguish the two clouds of points that correspond to the two groups. As for the other values of $t$ one can see very similar scatterplots as in Fig. 3, this explains why the $\mathtt {ID^{(0,1)}}$ works so well in this situation. Figure 3 also nicely illustrates why considering only the (marginal) distributions of the original curves or its derivatives cannot distinguish the groups so well as the joint distribution.

Fig. 1

One training sample generated from Model 1: a original curves; b first derivatives. Red curves represent the observations with highest depth value in both groups. These are obtained using depth (5) with weights $(w/2, w/2, 1-w)$, for $w\in [0,1]$ chosen by twofold cross-validation (colour figure online)

Fig. 2

Box plots for the proportions of correct classification in Model 1

Fig. 3

Plots of the empirical joint distributions of curves and their derivatives for three values of $t$

To investigate this example further, we summarize in Table 2 the simulation results obtained when using different values for the correlation coefficient $\rho$. For convenience we also include the previous results for the case $\rho =0.9$ (see the last column). As expected it is, in general, for several methods harder to distinguish between the groups when the correlation coefficient is smaller. The method $\mathtt {ID^{(0,1)}}$ is still among the best performing methods for smaller values of $\rho$.

Table 2 Median correct classification proportions for Model 1 for several values of $\rho$

In a practical setting one mostly does not know whether a classification rule should be based on the original curve, its derivative curves or should look at these jointly. In other words, one does not know whether a preference should be given to the methods $\mathtt {ID^{(0)}},\, \mathtt {ID^{(1)}}$ or $\mathtt {ID^{(0,1)}}$. This then brings us to investigate the more generally defined integrated depth in (3), or in the context of this example, to investigate the depth function given in (5). Of course, one could try to find an optimal weighting scheme $(w_0, w_1, w_{0,1})$ for which a ‘best’ classification rule would be obtained. For illustration purpose, we only investigate the weighting scenarios as described in items 2 and 4 of Example 1 in Sect. 2.1. In Fig. 4 we plot, as a solid curve, for each of the three weighting scenarios, the average proportion of correct classification, as a function of $w$, calculated on the basis of $1\,000$ independent runs. Note the impact of the value of the weight $w$ in each of the scenarios. We indicate, with horizontal lines, the results obtained for the special cases when using the data depths $\mathtt {ID^{(0)}},\, \mathtt {ID^{(1)}}$ or $\mathtt {ID^{(0,1)}}$. These can for example be compared with the value obtained when using the data-driven choice of $w$ under the specific weighting scenario.

Fig. 4

Model 1: approximate proportions of correct classification as a function of the weight $w$, according to the three scenarios

We implemented two procedures for obtaining a data-driven choice of $w$. In a first naive approach we build, for each fixed value of $w$ on a considered grid, the classification rule based on the training sample. We then apply the classification rule to classify each element in the training sample. This results into a missclassification rate. We repeat the same for all values of $w$ on the considered grid. The data-driven value of $w$, denoted by say $\widehat{w}_{\text{ N }}$, is then the value that led to the smallest missclassification rate. We repeated this for $1\,000$ independent runs, and depict in Fig. 4 (as a horizontal “$\times \!\!\times \!\!\times \!\!\times \!\!\times$” line) the average correct classification rate obtained when using this data-driven choice of $w$.

We also implemented a 2-fold cross-validation approach for obtaining a data-driven choice for $w$. For one run, the data-driven choice of $w$ is made as follows. For each value of $w$ in the considered grid of values, we split the pooled training sample into two disjoint sets of the same cardinality, preserving the ratio of functions from both distributions in both sets. Then, we proceed as if the group labels of the curves from the first set were known and the labels from the second set unknown, and classify the functions from the second set with respect to the curves from the first set. Finally, the same procedure is applied with reversed roles of the new sets. For a given value of $w$ the performance measure is then the mean of the missclassification rates of the two classifications performed. This is repeated for each value in the considered grid of $w$-values. The selected data-driven value of $w$, denoted by $\widehat{w}_{\text{ CV }}$, is then the one with the smallest mean missclassification rate. We repeated this for $1\,000$ independent runs, and present in Fig. 4 the average correct classification rate obtained when using this data-driven choice of $w$. See the horizontal “$\diamond \! \diamond \! \diamond \! \diamond \! \diamond$” line. This cross-validation procedure is computationally more intensive, but it can lead to better results than the naive approach.

As can be seen from Fig. 4, both the naive data-driven $\widehat{w}_{\text{ N }}$ choice as well as the cross-validated data-driven choice $\widehat{w}_{\text{ CV }}$ perform very well. Note that for all scenarios, the two horizontal lines for flexible integrated data depth classification rule with the data-driven choices of $w$, namely $\widehat{w}_{\text{ N }}$ and $\widehat{w}_{\text{ CV }}$, fall on top of each other. Both on average lead to the best possible choice among the three (individual) integrated data depth classification rules, namely $\mathtt {ID^{(0,1)}}$, and this in all scenarios considered.

4.3.2 Model 2: location shift with goniometric noise

In this simulation model, the probability model $P_{i}\, (i=1,2)$ for the functional data on $[0,1]$ is described as

$$\begin{aligned} X(t)=m_i(t) + \sigma \,\epsilon (t),\,t\in [0,1],\ i=1,2 \end{aligned}$$

(8)

where

$$\begin{aligned} m_1(t)=30\,(1-t)\,t^{1.2}, \quad m_2(t)=30\,t\,(1-t)^{1.2}, \quad \sigma = \sqrt{\tfrac{6}{5}}, \end{aligned}$$

and $\epsilon (t)$ is the noise function defined in (7) and $\sigma$ is a parameter controlling the amount of noise. In what follows we choose $\sigma = \sqrt{6/5}$ in (8) so that $\mathsf {var}\big (\sigma \,\epsilon (t)\big ) = 0.2$ for each $t \in [0,1]$ which mimics the marginal variance of the Gaussian noise used in Cuevas et al. (2007).

One training sample generated from Model 2 is plotted in Fig. 5. Note that although there is already a clear difference in the groups when looking at the original curves, the difference becomes even more obvious when considering the first derivatives of the curves.

The observation that derivatives are more informative when distinguishing between the curves is for most of the methods confirmed by the proportions of correct classifications in $1\,000$ independent runs presented in Fig. 6 in the forms of box plots. Note that all methods used in the simulation results do a very good job with a median correct classification rate better than 94 %. But in particular the $\mathtt {mNN^{(1)}}$ and the $\mathtt {mode^{(1)}}$ methods perform excellently classifying all the curves in all the runs correctly. This can be explained by the fact that both methods are based on the $L_{2}$-distance which is very suitable to detect the local differences in the derivatives of the curves that occur near the points $0$ and $1$. Similarly one can explain why the methods based on random projections $(\mathtt {RP^{(0)}},\, \mathtt {RP^{(1)}},\, \mathtt {RP2},\, \hbox {and}\, \mathtt {RPD})$ perform better than the corresponding methods based on the integrated data depth $(\mathtt {ID^{(0)}},\, \mathtt {ID^{(1)}},\, \hbox {and}\, \mathtt {ID^{(0,1)}})$. The reason is that projections are better suited to preserve local features of functions. On the other hand the integrated data depth is constructed to be a robust measure that is less sensitive to local violations of the trends (see also Sect. 4.3.3). Note that the random projection method $\mathtt {RPD}$ is doing almost as well as $\mathtt {mNN^{(1)}}$ and $\mathtt {mode^{(1)}}$.

Fig. 5

One training sample generated from Model 2: a original curves; b first derivatives. Red curves represent the observations with highest depth value in both groups (colour figure online)

Fig. 6

Box plots for the proportions of correct classification in Model 2

The classification problem becomes harder when the noise level increases. This can be seen from Table 3 which summarizes simulation results obtained for some different values of $\sigma$ in (8). For convenience we include again the median values of the proportion of correct classifications for the value of $\sigma$ considered before (i.e. $\sigma =\sqrt{6/5}$, see column 2 in Table 3). Note that in general all methods perform worse in case of larger values of $\sigma$.

Table 3 Median correct classification proportions for Model 2 for several values of $\sigma$

Finally, we investigate again the three weight scenarios for the integrated data depth in (3), as described in (5) in Sect. 2.1. Figure 7 depicts the approximate proportion of correct classifications in function of the weight $w$. Also here we present, for each scenario, the result obtained with the data-driven choices of the weight $w$ ($\widehat{w}_{\text{ N }}$, via the naive procedure, and $\widehat{w}_{\text{ CV }}$ via the cross-validation procedure). Note that in scenario 1 and 2 (left and middle panels) there is a substantial gain made by using the combined rule with data-driven weight $w$, instead of using one of the individual ID-based classification rules.

Fig. 7

Model 2: approximate proportions of correct classification as a function of the weight $w$, according to the three scenarios

4.3.3 Model 3: location shift with a randomly placed jump

The model considered here is the same as in Sect. 4.3.1 except for the noise term that now equals $\epsilon (t)$ with

$$\begin{aligned} \epsilon (t) = \tfrac{1+U_{0}}{a} \arctan \big (100\,(t+\tfrac{1}{2}-V)\big ) + \tfrac{U_{1}}{3}\,\sin (2 t \pi ) + \tfrac{U_{2}}{3}\,\cos (2 t \pi ) + U_{3}, \end{aligned}$$

(9)

where $a=2$, and $U_{0},\, U_{1},\, U_{2},\, U_{3}$ and $V$ are independent random variables with uniform distribution on $[-\tfrac{1}{2},\tfrac{1}{2}]$.

Note that now the first term in the noise function, on the right-hand side of (9), plays the main role in that noise function. This term represents a ‘smooth jump’ (or ‘bump’) randomly placed somewhere in the unit interval $(0,1)$. This is illustrated in Fig. 8, where one testing sample is plotted.

Fig. 8

One training sample generated from Model 3: a original curves; b first derivatives. Red curves represent the observations with highest depth value in both groups (colour figure online)

The simulation results for this model are summarized in Fig. 9. Note that in this situation the methods based on the integrated data depth outperform the methods based on random projections with $\mathtt {ID^{(1)}}$ being the best from the considered methods, followed closely by $\mathtt {ID^{(0,1)}}$. Note that although $\mathtt {mode^{(0)}},\, \mathtt {mode^{(1)}}$ and $\mathtt {mNN^{(0)}}$ still perform very well, they are not as excellent as in Model 2. Moreover, as these methods are based on the $L_{2}$ distance, one could suspect them to perform even worse when considering a model in which the jump is made larger (sharper) or in which another steep jump is added.

Fig. 9

Box plots for the proportions of correct classification in Model 3

The size of the ‘smooth jump’ in Model 3, is determined by the factor $1/a$ in (9). In Table 4 we summarize the simulation results for a few other values of $a$. The last column lists the results obtained before $(\hbox {where}\,\, a=2)$. Note that for larger values of $a$ all methods tend to perform better, but that the general comparison between the performances of the methods is as discussed before. Note in particular the extremely good performance of the $\mathtt {ID^{(1)}}$ method, for all values of $a$.

Table 4 Median correct classification proportions for Model 3 for several values of the factor $a$ in (9)

Finally, we illustrate the performance of a classification rule using the more flexible integrated data depth of (3). In this example, one could expect that Scenarios 1 and 3 are most appropriate. Note again that in all scenarios the flexible integrated data depth classification rule with data-driven choice of the weight performs very well (Fig. 10).

Fig. 10

Model 3: approximate proportions of correct classification as a function of the weight $w$, according to the three scenarios

4.3.4 Example 4: the Berkeley growth data

Following Cuevas et al. (2007) and López-Pintado and Romo (2006) the next study is motivated by the well known data of children’s growth curves (see e.g. Chapter 6.8.2 Ramsay and Silverman 2002). The observations represent the heights of $54$ girls and $39$ boys measured at $31$ time points between the age 1 and 18 years. The data can be found as a data set called growth in the R-package fda (Ramsay et al. 2013).

As the final height at $18$ is a very simple and powerful predictor of the gender, we only use in this study the age interval from 1 to 15 years. The original curves and their derivatives are plotted in Fig. 11. Note that the curves are already smoothed using a local cubic spline smoothing technique in order to achieve monotonicity of the original curves.

Fig. 11

One training sample generated from Model 4: a original observations; b first derivatives. Red curves represent the observations with highest depth value in both groups (colour figure online)

In the same way as in Cuevas et al. (2007) we chose, in each run, a random subsample with $30$ observations of boys’ and $30$ observations of girls’ curves as the training groups and the remaining $33$ observations were used as the curves to be classified. As in the other simulation examples, $1\,000$ independent runs were carried out.

The simulation results based on these runs are summarized in Fig. 12. Note that similarly as in Model 1 in Sect. 4.3.1 the methods based on the $L_{2}$-distance of the first derivatives do the best job. The reason is that both $\mathtt {mode^{(1)}}$ and $\mathtt {mNN^{(1)}}$ can capture the difference between the first derivatives of the heights of boys and girls between 10 and 15 years. This difference corresponds to a different timing of the growth spurt that starts (as well as ends) sooner for girls. Finally, the random projection methods are performing better than the integrated depth methods. This can be explained by the fact that random projections are better suited to uncover this kind of (local) differences.

Fig. 12

Box plots for the proportions of correct classification in Model 4

4.3.5 Example 5: the tecator data

The tecator dataset contains 215 spectra of light absorbance as functions of the wavelength, observed on finely chopped pieces of meat. For a more detailed description of the data see Chapter 2.1 of Ferraty and Vieu (2006) or Chapter 10.4.1 of Ferraty and Romain (2011) and the references therein. The data are available as a data set called tecator in the R-package fda.usc (Febrero-Bande and Oviedo de la Fuente 2012).

To each spectral curve there corresponds a three-dimensional vector – percentage of (fat, protein, water) in each piece of meat. In this study we used only the fat content and in the same way as in Chapter 8.4.2 of Ferraty and Vieu (2006) we created two groups simply by distinguishing the pieces of meat with fat content either lower or greater than 20 per cent. A random sample of 50 curves from each of the groups is plotted in Fig. 13. As it is common to use the second derivatives in the analysis of this dataset, we plot only the first and the second derivatives of the original curves. Also the classification methods were used on the first and/or the second derivatives of the original curves.

Fig. 13

One training sample generated from Model 5: a first derivatives; b second derivatives. Red curves represent the observations with highest depth value in both groups (colour figure online)

Following the simulation study in Ferraty and Vieu (2006) we have chosen, in each run, a random subsample of $43$ and $77$ observations so that the proportion of groups in the training sample and in the whole sample is preserved. The remaining curves were used as the testing sample. We conducted in this way $1\,000$ independent runs.

The results of the ‘simulation’ study are summarized in Fig. 14. Note that all depth based methods that include the second derivatives do very well and are comparable with $\mathtt {mode^{(1)}}$ and $\mathtt {mNN^{(1)}}$. Among the depth based methods, the method $\mathtt {ID^{(1,2)}}$ performs the best with a slightly better performance than the other depth based methods.

Fig. 14

Box plots for the proportions of correct classification in Model 5

5 Further discussion and conclusions

In this paper we studied supervised classification using (integrated) data depths. More specifically, we introduce a general data depth function suitable for studying smooth functions. Our approach is based on the integrated data depth and thus complements the recent proposal of Cuevas et al. (2007) based on random projections. We illustrate in the simulation study that considering the joint distribution of the original curves and their derivatives can reveal structures that are hidden when considering only marginal distributions of either the original curves and/or their derivatives. In addition, we show the performance of the more general integrated data depth with a data-driven choice of weight function.

When comparing the methods based on the integrated data depth with the data depth based on random projections as suggested by Cuevas et al. (2007), our simulation study shows the following. If the curves stay close together on most of the domain and local behaviour of the curves is important, then depth based on random projections are preferable. On the other hand if one is interested how the curves are ordered for most of the domain and wants to prevent the local behaviour to blur this ordering, then the integrated data depth presents a better choice.