Multivariate and functional classification using depth and distance

Abstract

We construct classifiers for multivariate and functional data. Our approach is based on a kind of distance between data points and classes. The distance measure needs to be robust to outliers and invariant to linear transformations of the data. For this purpose we can use the bagdistance which is based on halfspace depth. It satisfies most of the properties of a norm but is able to reflect asymmetry when the class is skewed. Alternatively we can compute a measure of outlyingness based on the skew-adjusted projection depth. In either case we propose the DistSpace transform which maps each data point to the vector of its distances to all classes, followed by k-nearest neighbor (kNN) classification of the transformed data points. This combines invariance and robustness with the simplicity and wide applicability of kNN. The proposal is compared with other methods in experiments with real and simulated data.

1 Introduction

Supervised classification of multivariate data is a common statistical problem. One is given a training set of observations and their membership to certain groups (classes). Based on this information, one must assign new observations to these groups. Examples of classification rules include, but are not limited to, linear and quadratic discriminant analysis, k-nearest neighbors (kNN), support vector machines, and decision trees. For an overview see e.g. Hastie et al. (2009).

However, real data often contain outlying observations. Outliers can be caused by recording errors or typing mistakes, but they may also be valid observations that were sampled from a different population. Moreover, in supervised classification some observations in the training set may have been mislabeled, i.e. attributed to the wrong group. To reduce the potential effect of outliers on the data analysis and to detect them, many robust methods have been developed, see e.g. Rousseeuw and Leroy (1987) and Maronna et al. (2006).

Many of the classical and robust classification methods rely on distributional assumptions such as multivariate normality or elliptical symmetry (Hubert and Van Driessen 2004). Most robust approaches that can deal with more general data make use of the concept of depth, which measures the centrality of a point relative to a multivariate sample. The first type of depth was the halfspace depth of Tukey (1975), followed by other depth functions such as simplicial depth (Liu 1990) and projection depth (Zuo and Serfling 2000).

Several authors have used depth in the context of classification. Christmann and Rousseeuw (2001) and Christmann et al. (2002) applied regression depth (Rousseeuw and Hubert 1999). Jörnsten (2004) used $L^1$ depth for classification and clustering, whereas Müller and Sawitzki (1991) employed the notion of excess mass. The maximum depth classification rule of Liu (1990) was studied by Ghosh and Chaudhuri (2005) and extended by Li et al. (2012). Dutta and Ghosh (2011) used projection depth.

In this paper we present a novel technique called classification in distance space. It aims to provide a fully non-parametric tool for the robust supervised classification of possibly skewed multivariate data. In Sects. 2 and 3 we describe the key concepts needed for our construction. Section 4 discusses some existing multivariate classifiers and introduces our approach. A thorough simulation study for multivariate data is performed in Sect. 5. From Sect. 6 onwards we focus our attention on the increasingly important framework of functional data, the analysis of which is a rapidly growing field. We start by a general description, and then extend our work on multivariate classifiers to functional classifiers.

2 Multivariate depth and distance measures

2.1 Halfspace depth

If Y is a random variable on $\mathbb {R}^p$ with distribution $P_{Y}$, then the halfspace depth of any point $\varvec{x}\in \mathbb {R}^p$ relative to $P_{Y}$ is defined as the minimal probability mass contained in a closed halfspace with boundary through $\varvec{x}$:

$$\begin{aligned} \text{ HD }(\varvec{x};P_{\,Y})= \inf _{||\varvec{v}||=1} \; P_{\,Y} \left\{ \varvec{v}'Y \geqslant \varvec{v}'\varvec{x}\right\} . \end{aligned}$$

Halfspace depth satisfies the requirements of a statistical depth function as formulated by Zuo and Serfling (2000): it is affine invariant (i.e. invariant to translations and nonsingular linear transformations), it attains its maximum value at the center of symmetry if there is one, it is monotone decreasing along rays emanating from the center, and it vanishes at infinity.

For any statistical depth function D and for any $\alpha \in [0,1]$ the $\alpha$-depth region $D_\alpha$ is the set of points whose depth is at least $\alpha$:

$$\begin{aligned} D_\alpha = \{ \varvec{x}\in \mathbb {R}^p \; ; \; \text{ D }(\varvec{x};P_{\,Y}) \geqslant \alpha \} \; . \end{aligned}$$

(1)

The boundary of $D_\alpha$ is known as the $\alpha$-depth contour. The halfspace depth regions are closed, convex, and nested for increasing $\alpha$. Several properties of the halfspace depth function and its contours were studied in Massé and Theodorescu (1994) and Rousseeuw and Ruts (1999). The halfspace median (or Tukey median) is defined as the center of gravity of the smallest non-empty depth region, i.e. the region containing the points with maximal halfspace depth.

The finite-sample definitions of the halfspace depth, the Tukey median and the depth regions are obtained by replacing $P_{Y}$ by the empirical probability distribution $P_n$. Many finite-sample properties, including the breakdown value of the Tukey median, were derived in Donoho and Gasko (1992).

To compute the halfspace depth, several affine invariant algorithms have been developed. Rousseeuw and Ruts (1996) and Rousseeuw and Struyf (1998) provided exact algorithms in two and three dimensions and an approximate algorithm in higher dimensions. Recently Dyckerhoff and Mozharovskyi (2016) developed exact algorithms in higher dimensions. Algorithms to compute the halfspace median have been developed by Rousseeuw and Ruts (1998) and Struyf and Rousseeuw (2000). To compute the depth contours the algorithm of Ruts and Rousseeuw (1996) can be used in the bivariate setting, whereas the algorithms constructed by Hallin et al. (2010) and Paindaveine and Šiman (2012) are applicable to at least $p=5$.

2.2 The bagplot

The bagplot of Rousseeuw et al. (1999) generalizes the univariate boxplot to bivariate data, as illustrated in Fig. 1. The dark-colored bag is the smallest depth region with at least 50 % probability mass, i.e. $B = D_{\tilde{\alpha }}$ such that $P_{\,Y}(B) \geqslant 0.5$ and $P_{\,Y}(D_\alpha ) < 0.5$ for all $\alpha > \tilde{\alpha }$. The white region inside the bag is the smallest depth region, which contains the halfspace median (plotted as a red diamond). The fence, which itself is rarely drawn, is obtained by inflating the bag by a factor 3 relative to the median, and the data points outside of it are flagged as outliers and plotted as stars. The light-colored loop is the convex hull of the data points inside the fence.

Fig. 1

Bagplot of a bivariate dataset

The bagplot exposes several features of the bivariate data distribution: its center (by the Tukey median), its dispersion and shape (through the sizes and shape of the bag and the loop) and the presence or absence of outliers. In Fig. 1 we see a moderate deviation from symmetry as well as several observations that lie outside the fence. One could extend the notion of bagplot to higher dimensions as well, but a graphical representation then becomes harder or impossible.

2.3 The bagdistance

Although the halfspace depth is small in outliers, it does not tell us how distant they are from the center of the data. Also note that any point outside the convex hull of the data has zero halfspace depth, which is not so informative. Based on the concept of halfspace depth, we can however derive a statistical distance of a multivariate point $\varvec{x}\in \mathbb {R}^p$ to $P_{Y}$ as in Hubert et al. (2015). This distance uses both the center and the dispersion of $P_{Y}$. To account for the dispersion it uses the bag B defined above. Next, $\varvec{c}(\varvec{x}):=\varvec{c}_{\varvec{x}}$ is defined as the intersection of the boundary of B and the ray from the halfspace median $\varvec{\theta }$ through $\varvec{x}$. The bagdistance of $\varvec{x}$ to Y is then given by the ratio of the Euclidean distance of $\varvec{x}$ to $\varvec{\theta }$ and the Euclidean distance of $\varvec{c}_{\varvec{x}}$ to $\varvec{\theta }$:

$$\begin{aligned} bd(\varvec{x};P_{\,Y}) = \left\{ \begin{array}{ll} 0 &{} \quad \text{ if } \varvec{x}= \varvec{\theta }\\ \left||\varvec{x}-\varvec{\theta }\right||/\left||\varvec{c}_{\varvec{x}}-\varvec{\theta }\right|| &{} \quad \text{ elsewhere }. \end{array} \right. \end{aligned}$$

(2)

The denominator in (2) accounts for the dispersion of $P_Y$ in the direction of $\varvec{x}$. Note that the bagdistance does not assume symmetry and is affine invariant. In $p=2$ dimensions it is similar to the distance proposed by Riani and Zani (2000).

Fig. 2

Illustration of the bagdistance between an arbitrary point and a sample

The finite-sample version of the bagdistance is illustrated in Fig. 2 for the data set in Fig. 1. Now the bag is shown in gray. For two new points $\varvec{x}_1$ and $\varvec{x}_2$ their Euclidean distance to the halfspace median is marked by dark blue lines, whereas the orange lines correspond to the denominator of (2) and reflect how these distances will be scaled. Here the lengths of the blue lines are the same (although they look different as the scales of the coordinates axes are quite distinct). On the other hand the bagdistance of $\varvec{x}_1$ is 7.43 and that of $\varvec{x}_2$ is only 0.62. These values reflect the position of the points relative to the sample, one lying quite far from the most central half of the data and the other one lying well within the central half.

Similarly we can compute the bagdistance of the outliers. For the uppermost right outlier with coordinates (3855, 305) we obtain 4.21, whereas the bagdistance of the lower outlier (3690, 146) is 3.18. Both distances are larger than 3, the bagdistance of all points on the fence, but the bagdistance now reflects the fact that the lower outlier is merely a boundary case. The upper outlier is more distant, but still not as remote as $\varvec{x}_1$.

We will now provide some properties of the bagdistance. We define a generalized norm as a function $g:\mathbb {R}^p \rightarrow [0, \infty [$ such that $g(\varvec{0})=0$ and $g(\varvec{x}) \ne 0$ for $\varvec{x}\ne \varvec{0}$, which satisfies $g(\gamma \varvec{x})=\gamma g(\varvec{x})$ for all $\varvec{x}$ and all $\gamma >0$. In particular, for a positive definite $p \times p$ matrix $\varvec{\Sigma }$ it holds that

$$\begin{aligned} g(\varvec{x}) = \sqrt{\varvec{x}'\varvec{\Sigma }^{-1}\varvec{x}} \end{aligned}$$

(3)

is a generalized norm (and even a norm).

Now suppose we have a compact set B which is star-shaped about zero, i.e. for all $\varvec{x}\in B$ and $0 \leqslant \gamma \leqslant 1$ it holds that $\gamma \varvec{x}\in B$. For every $\varvec{x}\ne \varvec{0}$ we then construct the point $\varvec{c}_{\varvec{x}}$ as the intersection between the boundary of B and the ray emanating from $\varvec{0}$ in the direction of $\varvec{x}$. Let us assume that $\varvec{0}$ is in the interior of B, that is, there exists $\varepsilon >0$ such that the ball $B(\varvec{0},\varepsilon ) \subset B$. Then $\left||\varvec{c}_{\varvec{x}}\right||>0$ whenever $\varvec{x}\ne \varvec{0}$. Now define

$$\begin{aligned} g(\varvec{x}) = {\left\{ \begin{array}{ll} 0&{} \quad \text {if} \,\, \varvec{x}=\varvec{0}\\ \frac{\left||\varvec{x}\right||}{\left||\varvec{c}_{\varvec{x}}\right||} &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(4)

Note that we do not really need the Euclidean norm, as we can equivalently define $g(\varvec{x})$ as $\;\inf \{\gamma > 0;\;\gamma ^{-1} \varvec{x}\in B\}$. We can verify that $g(\cdot )$ is a generalized norm, which need not be a continuous function. The following result shows more.

Theorem 1

If the set B is convex and compact and $\varvec{0}\in \text{ int }{(B)}$ then the function g defined in (4) is a convex function and hence continuous.

Proof

We need to show that

$$\begin{aligned} g(\lambda \varvec{x}+ (1-\lambda )\varvec{y}) \leqslant \lambda g(\varvec{x}) + (1-\lambda )g(\varvec{y}) \end{aligned}$$

(5)

for any $\varvec{x},\varvec{y}\in \mathbb {R}^p$ and $0 \leqslant \lambda \leqslant 1$. In case $\left\{ \varvec{0},\varvec{x},\varvec{y}\right\}$ are collinear the function g restricted to this line is 0 in the origin and goes up linearly in both directions (possibly with different slopes) so (5) is satisfied for those $\varvec{x}$ and $\varvec{y}$. If $\left\{ \varvec{0},\varvec{x},\varvec{y}\right\}$ are not collinear they form a triangle. Note that we can write $\varvec{x}= g(\varvec{x})\varvec{c}_{\varvec{x}}$ and $\varvec{y}= g(\varvec{y})\varvec{c}_{\varvec{y}}$ and we will denote $\varvec{z}:= \lambda \varvec{x}+ (1-\lambda )\varvec{y}$. We can verify that $\widetilde{\varvec{z}} := (\lambda g(\varvec{x}) + (1-\lambda )g(\varvec{y}))^{-1} \varvec{z}$ is a convex combination of $\varvec{c}_{\varvec{x}}$ and $\varvec{c}_{\varvec{y}}$. By compactness of B we know that $\varvec{c}_{\varvec{x}},\varvec{c}_{\varvec{y}} \in B$, and from convexity of B it then follows that $\widetilde{\varvec{z}} \in B$. Therefore

$$\begin{aligned} \left||\varvec{c}_{\varvec{z}}\right|| = \left||\varvec{c}_{\widetilde{\varvec{z}}}\right|| \geqslant \left||\widetilde{\varvec{z}}\right|| \end{aligned}$$

so that finally

$$\begin{aligned} g(\varvec{z}) = \frac{\left||\varvec{z}\right||}{\left||\varvec{c}_{\varvec{z}}\right||} \leqslant \frac{\left||\varvec{z}\right||}{\left||\widetilde{\varvec{z}}\right||} = \lambda g(\varvec{x}) + (1-\lambda )g(\varvec{y}).\quad \end{aligned}$$

$\square$

Note that this result generalizes Theorem 2 of Hubert et al. (2015) from halfspace depth to general convex sets. It follows that g satisfies the triangle inequality since

$$\begin{aligned} g(\varvec{x}+\varvec{y}) = 2 g\left( \frac{1}{2} \varvec{x}+\frac{1}{2} \varvec{y}\right) \leqslant 2\frac{1}{2} g(\varvec{x}) + 2\frac{1}{2} g(\varvec{y}) = g(\varvec{x})+g(\varvec{y}). \end{aligned}$$

Therefore g (and thus the bagdistance) satisfies the conditions

• (1) $g(\varvec{x}) \geqslant 0$ for all $\varvec{x}\in \mathbb {R}^p$

• (2) $g(\varvec{x}) = 0$ implies $\varvec{x}= \varvec{0}$

• (3) $g(\gamma \varvec{x}) = \gamma g(\varvec{x})$ for all $\varvec{x}\in \mathbb {R}^p$ and $\gamma \geqslant 0$

• (4) $g(\varvec{x}+\varvec{y}) \leqslant g(\varvec{x}) + g(\varvec{y})$ for all $\varvec{x},\varvec{y}\in \mathbb {R}^p$.

This is almost a norm, in fact, it would become a norm if we were to add

$$\begin{aligned} g(-\varvec{x}) = g(\varvec{x}) \quad \text{ for } \text{ all } \varvec{x}\in \mathbb {R}^p. \end{aligned}$$

The generalization makes it possible for g to reflect asymmetric dispersion. (We could easily turn it into a norm by computing $h(\varvec{x}) = (g(\varvec{x}) + g(-\varvec{x}))/2$ but then we would lose that ability.)

Also note that the function g defined in (4) does generalize the Mahalanobis distance in (3), as can be seen by taking $B = \left\{ \varvec{x}; \,\, \varvec{x}'\varvec{\Sigma }^{-1}\varvec{x}\leqslant 1 \right\}$ which implies $\varvec{c}_{\varvec{x}} = (\varvec{x}'\varvec{\Sigma }^{-1}\varvec{x})^{-1/2} \varvec{x}$ for all $\varvec{x}\ne \varvec{0}$ so $g(\varvec{x}) = \left||\varvec{x}\right||/((\varvec{x}'\varvec{\Sigma }^{-1}\varvec{x})^{-1/2}\left||\varvec{x}\right||) = \sqrt{ \varvec{x}'\varvec{\Sigma }^{-1}\varvec{x}}.$

Finally note that Theorem 1 holds whenever B is a convex set. Instead of halfspace depth we could also use regions of projection depth or the depth function in Sect. 3. On the other hand, if we wanted to describe nonconvex data regions we would have to switch to a different star-shaped set B in (4).

In the univariate case, the compact convex set B in Theorem 1 becomes a closed interval which we can denote by $B=[-\frac{1}{b},\frac{1}{a}]$ with $a, b > 0$, so that

$$\begin{aligned} g(x) = ax^+ + bx^-. \end{aligned}$$

In linear regression the minimization of $\sum _{i=1}^{n} g(r_i)$ yields the $a/(a+b)$ regression quantile of Koenker and Bassett (1978).

It is straightforward to extend Theorem 1 to a nonzero center by subtracting the center first.

To compute the bagdistance of a point $\varvec{x}$ with respect to a p-variate sample we can first compute the bag and then the intersection point $\varvec{c}_{\varvec{x}}$. In low dimensions computing the bag is feasible, and it is worth the effort if the bagdistance needs to be computed for many points. In higher dimensions computing the bag is harder, and then a simpler and faster algorithm is to search for the multivariate point $\varvec{c}^*$ on the ray from $\varvec{\theta }$ through $\varvec{x}$ such that

$$\begin{aligned} \text {HD}(\varvec{c}^*;P_n) = \mathop {{\text {med}}}\limits _i \; \{ \text {HD}(\varvec{y}_i;P_n)\} \end{aligned}$$

(6)

where $\varvec{y}_i$ are the data points. Since HD is monotone decreasing on the ray this can be done fairly fast, e.g. by means of the bisection algorithm.

Table 1 lists the computation time needed to calculate the bagdistance of $m \in \left\{ 1, 50, 100, 1000\right\}$ points with respect to a sample of $n=100$ points in dimensions $p \in \left\{ 2, 3, 4, 5\right\}$. For $p=2$ the algorithm of Ruts and Rousseeuw (1996) is used and (6) otherwise. The times are averages over 1000 randomly generated data sets. In each of the 1000 runs the points were generated from a centered multivariate normal distribution with a randomly generated covariance matrix. Note that the time for $m=1$ is essentially that of the right hand side of (6).

Table 1 Computation times for the bagdistance ($n=100$), in units of 0.001 seconds

3 Skew-adjusted projection depth

Since the introduction of halfspace depth various other affine invariant depth functions have been defined [for an overview see e.g. Mosler (2013)], among which projection depth (Zuo 2003) which is essentially the inverse of the Stahel-Donoho outlyingness (SDO). The population SDO (Stahel 1981; Donoho 1982) of an arbitrary point $\varvec{x}$ with respect to a random variable Y with distribution $P_{\,Y}$ is defined as

$$\begin{aligned} \text{ SDO }(\varvec{x};P_{Y})=\sup _{||\varvec{v}||=1} \, \frac{| \; \varvec{v}' \varvec{x}- {{\mathrm{med}}}(\varvec{v}'Y) \; |}{\text {MAD}(\varvec{v}'Y)} \end{aligned}$$

from which the projection depth is derived:

$$\begin{aligned} \text{ PD }(\varvec{x};P_{Y})=\frac{1}{1+\text{ SDO }(\varvec{x};P_{Y})}. \end{aligned}$$

Since the SDO has an absolute deviation in the numerator and uses the MAD in its denominator it is best suited for symmetric distributions. For asymmetric distributions Brys et al. (2005) proposed the adjusted outlyingness (AO) in the context of robust independent component analysis. It is defined as

$$\begin{aligned} \text{ AO }(\varvec{x};P_{Y})= \sup _{||\varvec{v}||=1} \; \text {AO}_1(\varvec{v}'\varvec{x};P_{\,\varvec{v}'Y}) \end{aligned}$$

where the univariate adjusted outlyingness $\text {AO}_1$ is given by

$$\begin{aligned} \text {AO}_1(z;P_Z) = \left\{ \begin{array}{ll} \frac{z-{{\mathrm{med}}}(Z)}{w_2(Z) - {{\mathrm{med}}}(Z)} &{} \quad \text{ if } z > {{\mathrm{med}}}(Z) \\ \frac{{{\mathrm{med}}}(Z) - z}{{{\mathrm{med}}}(Z) - w_1(z)} &{} \quad \text{ if } z \leqslant {{\mathrm{med}}}(Z). \\ \end{array} \right. \end{aligned}$$

(7)

Here

$$\begin{aligned} w_1(Z)&= Q_1(Z)-1.5 \, e^{-4\text {MC}(Z)} \, \text{ IQR }(Z)\\ w_2(Z)&= Q_3(Z)+1.5 \, e^{+3\text {MC}(Z)} \, \text{ IQR }(Z) \end{aligned}$$

if $\text {MC}(Z) \geqslant 0$, where $Q_1(Z)$ and $Q_3(Z)$ denote the first and third quartile of Z, $\text {IQR}(Z) = Q_3(Z)-Q_1(Z)$ and $\text {MC}(Z)$ is robust measure of skewness (Brys et al. 2004). If $\text {MC}(Z) < 0$ we replace (z, Z) by $(-z,-Z)$. The denominator of (7) corresponds to the fence of the univariate adjusted boxplot proposed by Hubert and Vandervieren (2008).

The skew-adjusted projection depth (SPD) is then given by (Hubert et al. 2015):

$$\begin{aligned} \text{ SPD }(\varvec{x};P_{\,Y})=\frac{1}{1+\text{ AO }(\varvec{x};P_{\,Y})} . \end{aligned}$$

To compute the finite-sample SPD we have to rely on approximate algorithms, as it is infeasible to consider all directions $\varvec{v}$. A convenient affine invariant procedure is obtained by considering directions $\varvec{v}$ which are orthogonal to an affine hyperplane through p randomly drawn data points. In our implementation we use 250p directions. Table 2 shows the time needed to compute the AO (or SPD) of $m \in \left\{ 1, 50, 100, 1000\right\}$ points with respect to a sample of $n=100$ points in dimensions $p \in \left\{ 2, 3, 4, 5\right\}$, as in Table 1. Here the time for $m=1$ is the fixed cost of computing those 250p directions and projecting the original data on them.

Table 2 Computation times for the AO ($n=100$), in units of 0.001 s

We see that computing AO is much faster than computing the bagdistance (Table 1), and that this difference becomes more pronounced at larger p and m. This is mainly due to the fact that AO does not require to compute the deepest point in multivariate space, unlike the bagdistance (2) which requires $\varvec{\theta }$.

4 Multivariate classifiers

4.1 Existing methods

One of the oldest nonparametric classifiers is the k-nearest neighbor (kNN) method introduced by Fix and Hodges (1951). For each new observation the method looks up the k training data points closest to it (typically in Euclidean distance), and then assigns it to the most prevalent group among those neighbors. The value of k is typically chosen by cross-validation to minimize the misclassification rate.

Liu (1990) proposed to assign a new observation to the group in which it has the highest depth. This MaxDepth rule is simple and can be applied to more than two groups. On the other hand it often yields ties when the depth function is identically zero on large domains, as is the case with halfspace depth and simplicial depth. Dutta and Ghosh (2011) avoided this problem by using projection depth instead, whereas Hubert and Van der Veeken (2010) employed the skew-adjusted projection depth.

To improve on the MaxDepth rule, Li et al. (2012) introduced the DepthDepth classifier as follows. Assume that there are two groups, and denote the empirical distributions of the training groups as $P_1$ and $P_2$. Then transform any data point $\varvec{x}\in \mathbb {R}^p$ to the bivariate point

$$\begin{aligned} (\text{ depth }(\varvec{x}; P_1),\text{ depth }(\varvec{x}; P_2)) \end{aligned}$$

(8)

where depth is a statistical depth function. These bivariate points form the so-called depth-depth plot, in which the two groups of training points are colored differently. The classification is then performed on this plot. The MaxDepth rule corresponds to separating according to the 45 degree line through the origin, but in general Li et al. (2012) calculate the best separating polynomial. Next, they assign a new observation to group 1 if it lands above the polynomial, and to group 2 otherwise. Some disadvantages of the depth-depth rule are the computational complexity of finding the best separating polynomial and the need for majority voting when there are more than two groups. Other authors carry out a depth transform followed by linear classification (Lange et al. 2014) or kNN (Cuesta-Albertos et al. 2015) instead.

4.2 Classification in distance space

It has been our experience that distances can be very useful in classification, but we prefer not to give up the affine invariance that depth enjoys. Therefore, we propose to use the bagdistance of Sect. 2.3 for this purpose, or alternatively the adjusted outlyingness of Sect. 3. Both are affine invariant, robust against outliers in the training data, and suitable also for skewed data.

Suppose that G groups (classes) are given, where $G \geqslant 2$. Let $P_g$ represent the empirical distribution of the training data from group $g=1,\ldots ,G$. Instead of the depth transform (8) we now carry out a distance transform by mapping each point $\varvec{x}\in \mathbb {R}^p$ to the G-variate point

$$\begin{aligned} (\text{ dist }(\varvec{x}; P_1),\ldots ,\text{ dist }(\varvec{x}; P_G)) \end{aligned}$$

(9)

where $\text{ dist }(\varvec{x}; P_g)$ is a generalized distance or an outlyingness measure of the point $\varvec{x}$ to the g-th training sample. This G-variate point will be called a representation of $\varvec{x}\in \mathbb {R}^p$ in distance space. Note that the dimension G of the distance space may be lower, equal, or higher than the original dimension p. After the distance transform any multivariate classifier may be applied, such as linear or quadratic discriminant analysis. The simplest version is of course MinDist, which just assigns $\varvec{x}$ to the group with smallest coordinate in (9). When using the Stahel-Donoho or the adjusted outlyingness, this is equivalent to the MaxDepth rule based on projection depth or skew-adjusted projection depth. However, we prefer to apply kNN to the transformed points. This combines the simplicity and robustness of kNN with the affine invariance offered by the transformation. Also note that we never need to resort to majority voting. In the simulations in Sect. 5 we will see that the proposed DistSpace method (i.e. the distance transform (9) followed by kNN) works quite well.

Fig. 3

Scatterplot matrix of the 4-dimensional banknote authentication data. The authentic banknotes are shown in orange, the forged ones in blue

We now illustrate the distance transform on a real world example, available from the UCI Machine Learning Repository (Bache and Lichman 2013). The data originated from an authentication procedure of banknotes. Photographs of 762 genuine and 610 forged banknotes were processed using wavelet transformations, and four features were extracted. These are the four coordinates shown in the scatterplot matrix in Fig. 3.

Fig. 4

Distance-distance plot of the banknote authentication data

Note that $G=2$. Using the bagdistance, the distance space of this data is Fig. 4. It shows that forged and authentic banknotes are well-separated and that the authentic banknotes form a tight cluster compared to that of the forged ones. Any new banknote would yield a new point in this plot, allowing kNN to classify it.

5 Computational results

To evaluate the various classifiers we apply them to simulated and real data. Their performance is measured by their average misclassification percentage $\sum _{g=1}^{G} e_g n_g / N$ with $e_g$ the percentage of misclassified observations of group g in the test set, $n_g$ the number of observations of group g in the training set, and N the total size of the training set. This weights the misclassification percentages in the test set according to the prior probabilities. In each scenario the test set consists of 500 observations per group. This procedure is repeated 2000 times for each setting.

Setting 1: Trivariate normals ($G=3,p=3$). We generate data from three different normal distributions. The first group $C_1$ has parameters

$$\begin{aligned} \varvec{\mu }_1= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \qquad \text {and} \qquad \varvec{\Sigma }_1 = \begin{pmatrix} 5 &{} 3 &{} 1 \\ 3 &{} 2 &{} 1 \\ 1 &{} 1 &{} 3 \end{pmatrix}. \end{aligned}$$

The second group is generated like $C_1$ but we flip the sign of the second coordinate. The third group is again generated like $C_1$ but then shifted by the vector $\left( 1,-2,-4\right)$. The training data consist of 50 observations in each group.

Setting 2: Multivariate normal and skewed ($G=2, p=6$). We consider two 6-variate distributions. The first group $C_1$ is drawn from the standard normal distribution. The coordinates in the second group are independent draws from the exponential distribution with rate parameter 1:

$$\begin{aligned} C_1 \sim \text{ N }\left( \varvec{0}, \varvec{I}_6 \right) \quad \text { and } \quad C_2 \sim (\text{ Exp }(1),\text{ Exp }(1),\text{ Exp }(1), \text{ Exp }(1),\text{ Exp }(1),\text{ Exp }(1))'. \end{aligned}$$

The training data has 150 observations drawn from group $C_1$ and 100 from $C_2$.

Setting 3: Concentric distributions ($G=2, p=7$). This consists of two groups of data. The first group is drawn from the standard normal distribution. The second group is obtained by generating points on the unit sphere in $\mathbb {R}^p$ and multiplying them by lengths which are generated uniformly on [12, 13]. The training data has 150 observations from group $C_1$ and 250 from $C_2$.

Setting 4: Banknote authentication data ($G=2,\;p=4$). We first standardize the data by the columnwise median and $\text{ MAD }$. The training sets are random subsets of 500 points from the original data set, with the test sets each time consisting of the remaining 872 observations.

Among the depth-based classification rules, halfspace depth (HD) is compared to projection depth (PD) and skew-adjusted projection depth (SPD). We run the MaxDepth rule, DepthDepth followed by the best separating polynomial and DepthDepth followed by kNN. The degree of the polynomial and the number of neighbors k are selected based on leave-one-out cross-validation.

Among the distance-based classifiers, the bagdistance based on halfspace depth (bd ) is compared to the Stahel-Donoho outlyingness (SDO) and the adjusted outlyingness (AO). Here the MinDist and DistSpace classifiers are considered.

We evaluate all classifiers on the uncontaminated data, and on data where 5 and 10 % of the observations in each group are mislabeled by assigning them randomly to another group. Figures 5, 6, 7, 8 summarize the results with boxplots of the misclassification percentages.

Fig. 5

Misclassification percentages in 2000 runs of setting 1 (trivariate normals). The results for clean data are shown in gray, for 5 % mislabeled data in orange, and for 10 % mislabeled data in blue

In setting 1, most of the depth- and distance-based methods did better than kNN. The halfspace depth HD did not perform well in MaxDepth and DepthDepth + kNN, and in fact mislabeling improved the classification because it yielded fewer points with depth zero in both groups. Halfspace depth appeared to work better in DepthDepth + polynomial but this is due to the fact that whenever a point has depth zero in both groups, Li et al. (2012) fall back on kNN in the original data space. Also note that DepthDepth + polynomial by construction improves the MaxDepth rule on training data, but it does not always perform better on test data.

Fig. 6

Misclassification percentages in 2000 runs of setting 2 (6-variate normal and skewed) using the same color code

In setting 2 we note the same things about HD in the depth-based methods. The best results are obtained by DepthDepth + poly and DistSpace, where we note that the methods that are able to reflect skewness (HD, SPD, bd, AO) did a lot better than those that aren’t (PD, SDO). This is because the data contains a skewed group.

Fig. 7

Misclassification percentages in 2000 runs of setting 3 (concentric groups)

In the third setting one of the groups is not convex at all, and the MaxDepth and MinDist boxplots lie entirely above the figure. On the other hand the DepthDepth and DistSpace methods still see structure in the data, and yield better results than kNN on the original data.

Fig. 8

Misclassification percentages in 2000 runs of setting 4 (banknote data)

In the banknote authentication example (setting 4), all methods except HD work well. For clean data, the two methods using the bagdistance outperform all others.

6 Functional data

The analysis of functional data is a booming research area of statistics, see e.g. the books of Ramsay and Silverman (2005) and Ferraty and Vieu (2006). A functional data set typically consists of n curves observed at time points $t_1, \ldots , t_T$. The value of a curve at a given time point is a p-variate vector of measurements. We call the functional dataset univariate or multivariate depending on p. For instance, the multi-lead ECG data set analyzed by Pigoli and Sangalli (2012) is multivariate with $p=8$.

When faced with classification of functional data, one approach is to consider it as multivariate data in which the measurement(s) at different time points are separate variables. This yields high-dimensional data with typically many highly correlated variables, which can be dealt with by penalization (Hastie et al. 1995). Another approach is to project such data onto a lower-dimensional subspace and to continue with the projected data, e.g. by means of support vector machines (Rossi and Villa 2006; Martin-Barragan et al. 2014). Li and Yu (2008) proposed to use F-statistics to select small subintervals in the domain and to restrict the analysis to those. Other techniques include the weighted distance method of Alonso et al. (2012) and the componentwise approach of Delaigle et al. (2012).

To reflect the dynamic behavior of functional data one can add their derivatives or integrals to the analysis, and/or add some preprocessing functions (warping functions, baseline corrections,...) as illustrated in Claeskens et al. (2014). This augments the data dimension and may add valuable information that can be beneficial in obtaining a better classification. We will illustrate this on a real data set in Sect. 7.3.

The study of robust methods for functional data started only recently. So far, efforts to construct robust classification rules for functional data have mainly used the concept of depth: López-Pintado and Romo (2006) used the modified band depth, Cuesta-Albertos and Nieto-Reyes (2010) made use of random Tukey depth, and Hlubinka et al. (2015) compared several depth functions in this context.

6.1 Functional depths and distances

Claeskens et al. (2014) proposed a type of multivariate functional depth (MFD) as follows. Consider a p-variate stochastic process $Y=\left\{ Y(t), t \in U \right\}$, a statistical depth function $D(\cdot ,\cdot )$ on $\mathbb {R}^p$, and a weight function w on U integrating to 1. Then the MFD of a curve X on U with respect to the distribution $P_{Y}$ is defined as

$$\begin{aligned} \text{ MFD }(X;P_{Y}) = \int _{U}{D(X(t); P_{Y(t )}) \, w(t) \, dt} \end{aligned}$$

(10)

where $P_{Y(t)}$ is the distribution of Y at time t. The weight function w(t) allows to emphasize or downweight certain time regions, but in this paper will be assumed constant. The functional median $\Theta (t)$ is defined as the curve with maximal MFD. Properties of the MFD may be found in (Claeskens et al. 2014), with emphasis on the case where $D(\cdot ,\cdot )$ is the halfspace depth. Several consistency results are derived in Nagy et al. (2016).

For ease of notation and to draw quick parallels to the multivariate non-functional case, we will denote the MFD based on halfspace depth by fHD, and the MFD based on projection depth and skew-adjusted projection depth by fPD and fSPD.

Analogously, we can define the functional bagdistance (fbd) of a curve X to (the distribution of) a stochastic process Y as

$$\begin{aligned} \text{ fbd }(X;P_{Y}) = \int _{U}{bd(X(t); P_{Y}(t)) \, dt}. \end{aligned}$$

(11)

Similar extensions of the Stahel-Donoho outlyingness SDO and the adjusted outlyingness AO to the functional context are given by

$$\begin{aligned} \text{ fSDO }(X; P_{Y}) = \int _U {\text{ SDO } (X(t); P_{Y}(t)) \; dt} \; \end{aligned}$$

(12)

$$\begin{aligned} \text{ fAO }(X; P_{Y}) = \int _U {\text{ AO }(X(t); P_{Y}(t)) \; dt} \; . \end{aligned}$$

(13)

6.2 Functional classifiers

The classifiers discussed in Sect. 4 are readily adapted to functional data. By simply plugging in the functional versions of the distances and depths all procedures can be carried over. For the k-nearest neighbor method one typically uses the $L^2$-distance:

$$\begin{aligned} d_2(X_1,X_2) = \left( \int _{U}{\left||X_1(t)-X_2(t)\right||^2 \, dt} \right) ^{1/2}\;\; . \end{aligned}$$

The functional kNN method will be denoted as fkNN. It is simple but not affine invariant. Analogously we use the MaxDepth and DepthDepth rules based on fHD, fPD, and fSPD, as well as the MinDist and DistSpace rules based on fbd, fSDO, and fAO. Note that Mosler and Mozharovskyi (2016) already studied DepthDepth on functional data after applying a dimension reduction technique.

7 Functional data examples

7.1 Fighter plane dataset

The fighter plane dataset of Thakoor and Gao (2005) describes seven shapes: of the Mirage, Eurofighter, F-14 with wings closed, F-14 with wings opened, Harrier, F-22 and F-15. Each class contains 30 shape samples obtained from digital pictures, which Thakoor and Gao (2005) then reduced to the univariate functions in Fig. 9. We obtained the data from the UCR Time Series Classification Archive (Chen et al. 2015).

Fig. 9

Functions describing the shapes of fighter planes

In all, the plane data set consists of 210 observations divided among seven groups. For the training data we randomly drew 15 observations from each group, and the test data were the remaining 105 observations. Repeating this 200 times yielded the misclassification percentages in Fig. 10.

Fig. 10

Misclassification percentages in 200 runs of the fighter plane data

In this data set the DistSpace method performed best, followed by kNN which however suffered under 10 % of mislabeling. Figure 10 contains no panel for DepthDepth + poly because the computation time of this method was infeasible due to the computation of the separating polynomials combined with majority voting for $G=7$.

7.2 MRI dataset

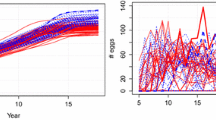
Felipe et al. (2005) obtained intensities of MRI images of 9 different parts of the human body (plus a group consisting of all remaining body regions, which was of course very heterogeneous). They then transformed their data to curves. This data set was also downloaded from (Chen et al. 2015). The $G=9$ classes together contain 547 observations and are of unequal size. For example $n_1=112, n_2=65, n_3=75,...$. The curves for 4 of these classes are shown in Fig. 11 (if we plot all nine groups together, some become invisible).

Fig. 11

Curves computed from MRI intensities

For the training data we drew unequally sized random subsets from these groups. The misclassification rates of 200 experiments of this type are shown in Fig. 12.

Fig. 12

Misclassification percentages in 200 runs of the MRI data

Here DistSpace performs a bit better than fkNN under contamination, and much better than MaxDepth and MinDist. Also in this example the DepthDepth + poly method took too long to compute.

7.3 Writing dataset

The writing dataset consists of 2858 character samples corresponding to the speed profile of the tip of a pen writing different letters, as captured on a WACOM tablet. The data came from the UCI Machine Learning Repository (Bache and Lichman 2013). We added the x- and y-coordinates of the pen tip (obtained by integration) to the data, yielding $p=4$ overall unlike both previous examples which had $p=1$. We further processed the data by removing the first and last time points and by interpolating to give all curves the same time domain. Samples corresponding to the letters ‘a’, ‘c’, ‘e’, ‘h’ and ‘m’ were retained. This yields a five-group supervised classification problem of four-dimensional functional data. Figure 13 plots the curves, with the 5 groups shown in different colors.

Fig. 13

Coordinates (upper) and speed (lower) of the writing data. Each group has a different color

For each letter the training set was a random subset of 80 multivariate curves. The outcome is in Fig. 14. There is no panel for the DepthDepth + poly classifier with separating polynomials and majority voting as its computation time was infeasible. MaxDepth and DepthDepth combined with kNN perform well except for fHD, again due to the fact that HD is zero outside the convex hull. DistSpace outperforms MinDist, and works well with all three distances. The best result was obtained by DistSpace with fbd.

Finally we applied fkNN and DistSpace to the original two-dimensional velocity data only. This resulted in larger median misclassification errors for all methods and all 3 data settings (0, 5 and 10 % mislabeling). For example, DistSpace with fbd on the two-dimensional data yielded a median misclassification error of 0.35 %, whereas the median error was zero on the 4-dimensional augmented data. This shows that adding appropriate data-based functional information can be very useful to better separate groups.

Fig. 14

Misclassification percentages in 200 runs of the writing data

8 Conclusions

Existing classification rules for multivariate or functional data, like kNN, often work well but can fail when the dispersion of the data depends strongly on the direction in which it is measured. The MaxDepth rule of Liu (1990) and its DepthDepth extension (Li et al. 2012) resolve this by their affine invariance, but perform poorly in combination with depth functions that become zero outside the convex hull of the data, like halfspace depth (HD).

This is why we prefer to use the bagdistance bd, which is based on HD and has properties very close to those of a norm but is able to reflect skewness (while still assuming some convexity). Rather than transforming the data to their depths we propose the distance transform, based on bd or a measure of outlyingness such as SDO or AO.

After applying the depth or distance transforms there are many possible ways to classify the transformed data. We found that the original separating polynomial method did not perform the best. Therefore we prefer to apply kNN to the transformed data.

In our experiments with real and simulated data we found that the best performing methods overall were DepthDepth + kNN (except with halfspace depth) and DistSpace + kNN. The latter approach combines affine invariance with the computation of a distance and the simplicity, lack of assumptions, and robustness of kNN, and works well for both multivariate and functional data.

In the multivariate classification setting the depth and distance transforms perform about equally well, and in particular MinDist on SDO and AO is equivalent to MaxDepth on the corresponding depths PD and SPD. But the bagdistance bd beats the halfspace depth HD in this respect because the latter is zero outside the convex hull of a group.

One of the most interesting results of our simulations is that the approaches based on the depth and distance transforms behave more differently in the functional setting. Indeed, throughout Sect. 7 classification based on the distance transform outperformed classification using the depth transform. This is because distances are more additive than depths, which matters because of the integrals in the definitions of functional depth MFD (10) to functional AO (13). For the sake of simplicity, let us focus on the empirical versions where the integrals in (10)–(13) become sums over a finite number of observed time points. These sums are $L^1$ norms (we could also use $L^2$ norms by taking the square root of the sum of squares). In the context of classification, we are measuring how different a new curve X is from a process Y or a finite sample from it. When X differs strongly from Y in a few time points, the integrated depth (10) will have a few terms equal to zero or close to zero, which will not lead to an extremely small sum, so X would appear quite similar to Y. On the other hand, a functional distance measure like (11)–(13) will contain a few very large terms, which will have a large effect on the sum, thereby revealing that X is quite far from Y. In other words, functional distance adds up information about how distinct X is from Y. The main difference between the two approaches is that the depth terms are bounded from below (by zero), whereas distance terms are unbounded from above and thus better able to reflect discrepancies.