A new generalization of lifetime distributions

Abstract

In the current study, we set out to extend the three-parameter Modified Weibull (MW) distribution in an attempt to propose a four-parameter distribution named the Modified Weibull Poisson (MWP) distribution including such noticeable submodels as Exponential Poisson, Weibull Poisson, and Rayleigh Poisson known as the distributions subsumed under the umbrella term MWP. Depending on its parameter values, this overarching distribution was demonstrated by this work to exhibit some hazard rates like decreasing, increasing, bathtub, and upside-down bathtub ones. In addition to the hazard rates of the MWP, the mathematical properties as well as the properties of maximum likelihood estimations were brought to the forefront, and the very capability of the quantile measures to be explicitly expressed in terms of the Lambert W function was vigorously discussed. To shed light on the functioning of the maximum likelihood estimators and their asymptomatic results for the finite sample sizes, some numerical experiments were carried out leading to two data sets intended chiefly to illustrate or explicate the higher levels of importance and flexibility of the MWP in comparison with its standard counterparts, namely the Weibull, Gamma, and MW distributions.

1 Introduction

In many, if not all, applied sciences such as medicine, engineering and finance modeling and analyzing lifetime data are crucial. Several lifetime distributions like the exponential, Weibull, Gamma or their generalizations have been used to model such kinds of data. Each distribution has its own characteristics due specifically to the shape of the hazard function which may be monotonically decreasing, increasing, or constant in its behavior, on the one hand, or non-monotonically bathtub-shaped or even upside-down bathtub-shaped, on the other hand.

Here we consider the Modified Weibull (MW) distribution, introduced by Lai et al. (2003). The MW distribution characterized best by the density and distribution functions $g\left( x \right) =\alpha x^{\gamma -1}(\gamma +\beta x)e^{\beta x-\alpha x^{\gamma }e^{\beta x}}$ and $G\left( x \right) =1-e^{-\alpha x^{\gamma }e^{\beta x}}$, where $\alpha >0, \beta \ge 0, \gamma >0$, respectively. It has recently received considerably high attention. For example, Carrasco et al. (2008) extended the MW distribution by adding another shape parameter in order to introduce a four-parameter Generalized Modified Weibull (GMW). Also, Silva et al. (2010) introduced the beta modified Weibull by combining the beta and MW distributions. In similar vein, the aim of this paper is to introduce a generalization of the MW distribution which offers a more flexible distribution for modelling lifetime data. As for the procedure through which the authors went to achieve the extension goal, the MW distribution was combined with the Poisson distribution using the concept of minimum order statistics distribution. Needless to say, the genuine motives behind the introducing of this new distribution were both its quantile formula, which can be written in terms of the Lambert W function, and flexibility in accommodating different types of density and hazard functions. Judiciously used, the two data sets were intended to show that the proposed distribution represents a good alternative to the most popular Gamma and Weibull lifetime distributions that fail to exhibit bathtub and upside-down bathtub-shaped hazards. Another striking feature of the new distribution is that it has closed-form expressions for its cumulative distribution function (cdf) and hazard function, which is not the case, for instance, for the Gamma distribution. Moreover, it has several particular cases. Hence, the new distribution is expected to provide a flexible framework which could have a wider range of applications in the lifetime studies.

After the MW distribution is explicated, the Modified Weibull Poisson (MWP) distribution along with some of its basic properties such as shapes, moments and quantiles are dealt with in the second section followed by a discussion about the survival and hazard functions made in Sect. 3. Afterwards, the maximum likelihood estimations and a simulation study of the MWP distribution are presented. Prior to drawing a conclusion in the last, but not the least, part of the current paper, much importance and emphasis is attached to and placed upon the new distribution proposed by the authors in Sect. 5. Interestingly enough, this distribution is fit to two real data sets with the aim of conducting a comparative investigation.

2 The Modified Weibull Poisson distribution

Let $Z_1 ,Z_2 ,\ldots ,Z_n$ be a random sample from distribution with the probability density function (pdf) $\alpha z^{\gamma -1} (\gamma +\beta z)e^{\beta z-\alpha z^{\gamma }e^{\beta z}}$. Also, let $n$ be a random variable with the zero-truncated Poisson probability mass function (pmf) $\lambda e^{-\lambda }/\left[ {n!\left( {1-e^{-\lambda }} \right) } \right] , \lambda >0$ for $n\in {\mathbb {N}}$ where $Z$ and $n$ are independent. Let us define $X=\min \left\{ {Z_i } \right\} _{i=1}^n$. Then $f\left( {x\hbox {|}n} \right) =\alpha n e^{-\alpha nx^{\gamma }e^{\beta x}}x^{\gamma -1} (\gamma +\beta x)e^{\beta x},$ and the marginal pdf of $X$ can be obtained as

$$\begin{aligned} f\left( {x;\varvec{\theta } } \right) =\alpha \lambda x^{\gamma -1} \left( {1-e^{-\lambda }} \right) ^{-1}\left( {\gamma +\beta x} \right) \hbox { }e^{\beta x- \alpha x^{\gamma }e^{\beta x} -\lambda \left( {1-e^{-\alpha x^{\gamma }e^{\beta x}}} \right) }, x>0 \end{aligned}$$

(1)

where $\varvec{\theta } =(\alpha , \beta ,\gamma ,\lambda )$. The pdf of (1) is termed the Modified Weibull Poisson (MWP) density function. The cdf corresponding to (1) can be derived as follow:

$$\begin{aligned} F\left( {x; \varvec{\theta } } \right) =1-e^{-\lambda \left( {1-e^{-\alpha x^{\gamma }e^{\beta x}}} \right) },\hbox { }\alpha , \lambda >0, \beta ,\gamma \ge 0 \end{aligned}$$

(2)

The MWP distribution contains some noticeable, compounded distributions. The Weibull-Poisson (WP) arises as a special sub-distribution for $\beta =0$ and its special cases are also special sub-distributions of the MWP distribution. In addition, the exponential-Poisson (EP) introduced by Kus (2007) and Raleigh-Poisson (RP) distributions are interesting particular cases from the MWP distribution arise for $\beta =0$, when $\gamma =1$ and $\gamma =2$, respectively. The MW distribution is the limiting case of the MWP distribution for $\lambda \downarrow 0$.

Now, let us study the shape of the MWP density function. Since the behavior of $f\left( {x;\varvec{\theta } } \right)$ is completely similar to that of $\log f\left( {x;\varvec{\theta } } \right)$, for simplicity we consider the behavior of $\log f\left( {x;\varvec{\theta } } \right) \!.$ The first derivative of $\log f\left( {x;\varvec{\theta } } \right)$ is:

$$\begin{aligned} \gamma -1+\beta x\left( {\gamma +\beta x} \right) ^{-1}+\beta x=\alpha \left( {\gamma +\beta x} \right) x^{\gamma }e^{\beta x}\left( {1-\lambda e^{-\alpha x^{\gamma }e^{\beta x}}} \right) \end{aligned}$$

(3)

There may be more than one root to equation (3). To study the shapes of the MWP density function with respect to its parameters, suppose $f_1 \left( x \right) =\gamma -1+\beta x \left( {\gamma +\beta x} \right) ^{-1}+\beta x$, and $f_2 \left( x \right) =\alpha \left( {\gamma +\beta x} \right) x^{\gamma }e^{\beta x}( {1-\lambda e^{-\alpha x^{\gamma }e^{\beta x}}} )$ be two parts of relation (3). Clearly, $f_1 \left( x \right)$ is an increasing function of $x$ and $f_2 \left( x \right)$ is an increasing function of $x$ when $0<\lambda \le 1$, and $f_2 \left( x \right) <0$ when $\lambda >1$. Thus, from (3), it can be seen that:

• 1. For $\lambda >1$, $\gamma >1$, $\alpha \downarrow 0$ and $\beta \downarrow 0$, $f_1 \left( x \right) -f_2 \left( x \right) >0$ and hence $dlog f\left( {x;\varvec{\theta } } \right) \!/dx>0$ which implies the increasing behavior of $f(x)$.

• 2. For $\lambda \downarrow 0$ and $x<e^{-\{ {\ln ( \alpha )+\gamma \hbox {LambertW}[ {\beta e^{-\frac{\ln \alpha }{\gamma }}/\gamma }]} \}/\gamma }$, $f_1 \left( x \right) -f_2 \left( x \right) <0$ and hence $dlog f\left( {x;\varvec{\theta } } \right) /dx<0$ which implies the decreasing behavior of $f(x)$. [For more information on the Lambert W function see Corless et al. (1996)]

• 3. For $0<\gamma <1$ and $\alpha \downarrow 0$, there exists a change point $\tau _1 =\beta ^{-1}\left( {-\gamma +\sqrt{\gamma }} \right)$, when $0<x<\tau _1$, $f\left( {x;\varvec{\theta } } \right)$ is decreasing and when $x>\tau _1$, $f\left( {x;\varvec{\theta } } \right)$ is increasing. Hence, the density function exhibits a uniantimodal shape.

• 4. For $\gamma \downarrow 0, \lambda \downarrow 0$ and $0<\alpha <1$, there is a change point $\tau _2 =-\beta ^{-1}\log \alpha$, when $0<x<\tau _2$, $f\left( {x;\varvec{\theta } } \right)$ is decreasing and when $x>\tau _2$, $f\left( {x;\varvec{\theta } } \right)$ is increasing. As a result, the density function shows a uniantimodal shape.

Using the expansion of $e^{\lambda e^{-\alpha x^{\gamma }e^{\beta x}}}\!$ in Eq. (1) results in

$$\begin{aligned} f\left( {x;\varvec{\theta } } \right) =\sum \limits _{j=0}^\infty w_j g(\alpha \left( {j+1} \right) , \beta , \gamma ) \end{aligned}$$

(4)

where $w_j =\lambda ^{j+1}e^{-\lambda }\left[ {\left( {1-e^{-\lambda }} \right) \left( {j+1} \right) !} \right] ^{-1}$ are constants such that $\sum \nolimits _{j=0}^\infty w_j =1$ and $g(\alpha \left( {j+1} \right) , \beta ,\gamma )$ is the pdf of the MW distribution. Expression (4) indicates that the MWP distribution can be expressed as an infinite weighted sum of the MW distribution with common shape and accelerated parameters, and a different scale parameter. From (4) we can obtain an elementary expression for the $r$th moment of the MWP distribution $\mathop {\mathop {\mu }\limits ^{\prime }}\nolimits _r =\sum \nolimits _{j=0}^\infty w_j \eta _r^{\prime } (j)$ where $\eta _r^{\prime } \left( j \right)$ denotes the $r$th moment of the MW$(\alpha \left( {j+1} \right) , \beta , \gamma )$ distribution. Using the general representation for the $r$th moment of the MW distribution offered by Carrasco et al. (2008), we obtain

$$\begin{aligned} \mathop {\mathop {\mu }\limits ^{\prime }}\nolimits _r = \sum \limits _{j=0}^\infty \sum \limits _{i_1 ,\ldots , i_r =1}^\infty w_j \frac{A_{i_1 ,\ldots , i_r } { \Gamma }(s_r /\gamma +1)}{\left[ {\alpha \left( {j+1} \right) } \right] ^{s_r /\gamma }} \end{aligned}$$

(5)

where $A_{i_1 ,\ldots , i_r } =a_{i_1 } \ldots a_{i_r }$, $s_r =i_1 +\ldots + i_r$ and $a_i =\frac{(-1)^{i+1}i^{i-2}}{\left( {i-1} \right) !} \left( {\frac{\beta }{\gamma }} \right) ^{i-1}$.

We can simulate the MWP distribution and derive the quantile measures in terms of the Lambert W function by solving the nonlinear equation $F\left( x \right) =u$, $0<u<1$ with respect to $x$. Using MAPLE to solve the equation $\gamma \log x+\beta x=C$ where $C=\log \left[ {-\left( {\log \left\{ {1+ \log \left[ {1-u (1- e^{-\lambda })} \right] /\lambda } \right\} } \right) /\alpha } \right]$ leads to the following expression:

$$\begin{aligned} x_u =e^{-\gamma \left\{ {\left[ {\hbox {Lambert W}\left( {\frac{\beta e^{\frac{C}{\gamma }}}{\gamma }} \right) } \right] \gamma -C} \right\} } \end{aligned}$$

(6)

3 Survival and hazard functions

Let $X$ be distributed according to the MWP $(\alpha ,\beta , \gamma , \lambda )$, the corresponding survival and hazard functions can be written, respectively, as $S\left( x \right) =e^{-\lambda }\left( {1-e^{-\lambda }} \right) ^{-1}\big ( {e^{\lambda e^{-\alpha x^{\gamma }e^{\beta x}}}-1}\big )$, and

$$\begin{aligned} h\left( x \right) =\alpha \lambda e^{\lambda }x^{\gamma -1}\left( {\gamma +\beta x} \right) \left( {e^{\lambda e^{-\alpha x^{\gamma } e^{\beta x}}}-1} \right) ^{-1}e^{\beta x-\alpha x^{\gamma }e^{\beta x}-\lambda \left( {1-e^{-\alpha x^{\gamma }e^{\beta x}}} \right) } \end{aligned}$$

(7)

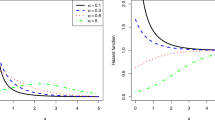
Here, we show that the hazard function of the MWP distribution can be increasing, decreasing, bathtub-shaped or upside-down bathtub-shaped, depending on its parameter values. Mathematically, the study of the hazard function involves the analysis of the $d\log h(x) /dx$, i.e,

$$\begin{aligned} \gamma -1+\beta x\left( {\gamma +\beta x} \right) ^{-1}+\beta x-\alpha v\left( {\gamma +\beta x} \right) \left[ {1-\lambda e^{-\lambda e^{-\alpha v}}\left( {1-e^{-\lambda e^{-\alpha v}}} \right) ^{-1}} \right] \nonumber \\ \end{aligned}$$

(8)

where $v=x^{\gamma }e^{\beta x}$ and $0<e^{-\lambda e^{-\alpha v}}<1$. To characterize (8) with respect to its parameters, let us define $h_1 \left( x \right) =\gamma -1+\beta x\left( {\gamma +\beta x} \right) ^{-1}+\beta x$, and $h_2 \left( x \right) =\alpha v\left( {\gamma +\beta x} \right) \big [ {1-\lambda e^{-\lambda e^{-\alpha v}}\big ( {1-e^{-\lambda e^{-\alpha v}}} \big )^{-1}}\big ]$. Clearly, $h_1 \left( x \right)$ is an increasing function of $x$, but $h_2 \left( x \right)$ exhibits different behaviors of $x$ due to its functional form and parameter values. It is not difficult to observe that some items discussed before are common between density and hazard functions. Therefore, we summarize them as follows:

• 1. For $\alpha \downarrow 0$ and $\gamma >1$, $h(x)$ is increasing.

• 2. For $\lambda >1$, $0<\gamma <1$ and$\beta \downarrow 0$, $h(x)$ is decreasing.

• 3. For $0<\gamma <1$and $\alpha \downarrow 0$, hazard function exhibits a bathtub shape.

• 4. If $\lambda \downarrow 0$, $\beta \downarrow 0$ and $\gamma >1$ hazard function exhibits an upside-down bathtub shape.

• 5. For $\gamma \downarrow 0, \lambda \downarrow 0$ and $0<\alpha <1$, the hazard function exhibits an upside-down bathtub shape. Fig. 1 represents two types of shapes of the MWP hazard function.

Fig. 1

The hazard function of the MWP distribution for some values of the parameters

4 Maximum likelihood estimation

4.1 Inference

Let $x_1 , x_2 ,\ldots , x_n$ be an independent random sample of size $n$ from the MWP distribution with an unknown parameter vector $\varvec{\theta } =\left( {\alpha , \beta , \gamma ,\lambda } \right) ^{T}$. The MLEs of the parameters can be obtained by solving a system of equations by setting the following partial derivatives equal to zero (provided they fall within the feasible region).

$$\begin{aligned} U_\alpha&= \frac{\partial \ell \left( \varvec{\theta } \right) }{\partial \alpha }=n\alpha ^{-1}-\sum \limits _{i=1}^n x_i^\gamma e^{\beta x_i } (1+\lambda e^{-u_i }),\\ U_\beta&= \frac{\partial \ell \left( \varvec{\theta } \right) }{\partial \beta }=\sum \limits _{i=1}^n \frac{x_i }{\gamma +\beta x_i }+\sum \limits _{i=1}^n x_i -\sum \limits _{i=1}^n x_i u_i (1+\lambda e^{-u_i }),\\ U_\gamma&= \frac{\partial \ell \left( \varvec{\theta } \right) }{\partial \gamma }=\sum \limits _{i=1}^n \log x_i +\sum \limits _{i=1}^n \frac{1}{\gamma +\beta x_i }-\sum \limits _{i=1}^n u_i \left( {1+\lambda e^{-u_i }} \right) \log x_i ,\\ U_\lambda&= \frac{\partial \ell \left( \varvec{\theta } \right) }{\partial \lambda }=n\lambda ^{-1}-\frac{ne^{-\lambda }}{1-e^{-\lambda }}-\sum \limits _{i=1}^n \left( {1-e^{-u_i }} \right) , \end{aligned}$$

where $u_i =\alpha x_i^\gamma e^{\beta x_i }$ is a transformed observation.

Applying the usual large sample approximation, the MLE of $\varvec{\theta }$ can be treated as being approximately 4-variate and normal with the mean $\varvec{\theta }$ and variance-covariance matrix, which is the inverse of the information matrix ${\varvec{J}}_{\varvec{\theta }}$. The elements of the information matrix, ${\varvec{J}}_{\varvec{\theta }}$, are calculated by taking the expectations of the elements of the observed Fisher information matrix, $I_F \left( \varvec{\theta } \right) =-\partial ^{2}\ell \left( \varvec{\theta } \right) \!/\!\partial \varvec{\theta } \partial {\varvec{\theta }}^{T}$. The elements of the observed Fisher information and information matrices are given in the Appendix. The inverse of ${\varvec{J}}_{\varvec{\theta }}$ evaluated at $\hat{\varvec{\theta }}$ provides the asymptotic variance-covariance matrix of the MLEs. Hence, the 4-variate normal distribution can be used to construct approximate confidence intervals for the parameters when the sample size is sufficiently large. We examine the effect of the small sample size on the confidence intervals through a simulation study presented in the following subsection.

4.2 Simulation study

Here, we present some numerical experiments to see how the MLEs and their asymptotic results work for finite samples. All numerical computations have been performed using the following random generator algorithm. This method is checked out by the following steps

Step 1: Sample the random variable $n$ from the zero-truncated Poisson $(\lambda )$ pmf.

Step 2: For each value of $n$ generate $Z_1 , Z_2 , \ldots , Z_n$ from the MW pdf, say:

$$\begin{aligned} Z=e^{- \gamma ^{-1}\left\{ {\left[ {\hbox {Lambert W}\left( {\frac{\beta e^{\frac{I}{\gamma }}}{\gamma }} \right) } \right] \gamma -I} \right\} } \end{aligned}$$

where, $I=\log \left[ {-\log \left( {1-u} \right) /\alpha } \right]$ and $u$ is a random variable with the uniform $U(0,1)$ distribution. Note that the MW random variable formula is attained using the MAPLE.

Step 3: Set the minimum of $Z_i$’s, say $X=\min (Z_1 , Z_2 , \ldots , Z_n )$ as a realization of the MWP distribution.

The numerical study (based on 1,000 iterations) has been performed for the MWP distribution with R package. One thousand samples of the sizes 25, 50, 100, 200 and 400 have been randomly sampled for each value of $\varvec{\theta }$. For each iteration the MLE of $\varvec{\theta }$ is obtained by solving a system of nonlinear equations using the iterative technique. The averages of the 1,000 MLEs $av(\hat{\varvec{\theta }})$ together with the standard error $s.e(\hat{\varvec{\theta }})$ are computed. The results are given in Table 1. Moreover, to study the asymptotic behaviors of the MLEs, we approximated the variance-covariance matrix of the MLEs from the information matrix. The results based on the 1,000 random samples of the sizes 50, 100, 500, 1,000 and 10,000 are presented. The approximated values determined by averaging the corresponding values obtained from the information matrix and the observed information matrix are separately displayed in Tables 2 and 3.

Table 1 The mean and standard error of the simulated MWP

Some of the points are very clear from the numerical experiments. It is observed that for all the parametric values the bias and standard error of the parameters decrease when the sample size increases. It verifies the large sample properties of the MLEs as mentioned in Sect. 4.1. For fixed $\beta$ as $\lambda$ increases, the bias of $\lambda$ increases, whereas the corresponding standard errors and biases of $\beta$ decrease for all sample sizes. Therefore, estimation of $\lambda$ becomes better as $\lambda$ decreases. On the other hand, for fixed $\beta$, as $\lambda$ increases, the biases of both $\beta$ and $\lambda$ increase. Note that the $\hat{\gamma }/\gamma$ remains constant for all parameter values when the sample size increases. It can also be observed that the MLEs of $\beta$ and $\gamma$ are positively and negatively biased, respectively, although the biases go to zero as the sample size increases. Interestingly, it can be seen that the variances and covariances of the MLEs obtained from the observed information matrix are quite close to those of the information matrix for large values of $n$ (Tables 2 and 3). This is also followed by the asymptotic behaviors of the MLEs.

Table 2 The approximated variances and covariances obtained from the observed information matrix

Table 3 The approximated variances and covariances obtained from the information matrix

Note that similar results were obtained when we generated the MWP random variable based on the expression (6) or inverse transform sampling method (The results are not shown here).

As part of the numerical experiments, we also investigated the confidence intervals of the MLEs via bootstrap sampling in small samples. To this end, we generated a data set from the MWP$(x;\alpha , \beta , \gamma , \lambda )$ distribution of size $n$. Two thousand samples of the sizes 10, 15, 20 and 25 have been sampled using sampling with replacement. Then, the vector $\varvec{\theta }$ is estimated 2,000 times. For each parameter of $\varvec{\theta }$ the 5 and 95% quantiles are found. The results of desired confidence intervals are illustrated in Table 4. It is observed that confidence intervals become more precise as the sample size increases. It is also detected that most of the approximated confidence intervals maintain the true and estimated values for the small sample sizes. Therefore, the MLEs and their asymptotic results can be used for estimation and construction of confidence intervals even for the small sample sizes.

Table 4 Simulated 95% confidence intervals of the MLEs of $\varvec{\theta }$ based on 2000 bootstrapping

5 Applications

In this section we illustrate the applicability of the MWP distribution to lifetime data by drawing on two data sets. The first was a widely used data on lifetime of 50 components from Aarset (1987). The second data set representing the failure times (in minutes) for a sample of 15 electronic components in an accelerated life test was adopted from Lawless (2003).

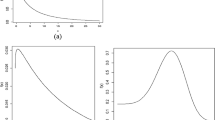
In order to identify the hazard shape of the two data sets, we used a graphical method based on the TTT transform introduced by Barlow and Campo (1975). The empirical TTT transform for Aarset’s data possess a bathtub-shaped failure rate property as shown in the left panel of Fig. 2. Since it is initially convex, but becomes subsequently concave, this leads to the bathtub hazard. The right panel of Fig. 2 also shows that the TTT plot of the second data set leads to an increasing hazard. Hence, fitting the MWP distribution to these data sets seems to be a good choice.

Fig. 2

The TTT plot for the first (left panel) and second data (right panel)

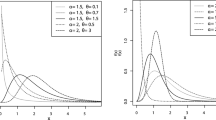
We fit the MWP distribution to the two data sets and compare its fitting with some usual lifetime distributions. Table 5 shows the fitting of the MWP along with the Weibull, Gamma and MW distributions. The MLEs of the parameters and values of the log-likelihood function are calculated. We also provide formal goodness-of-fit tests in order to compare the fitting of the mentioned distributions to these data sets. We apply the Cramér-von Mises ($W^{*})$ and Anderson-Darling ($A^{*})$ test statistics described in detail by Chen and Balakrishnan (1995). Generally, the smaller the values of the statistics $W^{*}$ and $A^{*}$, the better they fit the data. The computations are made with R package. The lower values of the log-likelihood and goodness-of-fit tests for the MWP and MW distributions indicate that these distributions could be chosen the best distributions to fit the two data sets. In any case, since the differences between the statistics are quite small for the Weibull and Gamma distributions, the proposed distribution seems to be a very competitive distribution for lifetime data analysis. Figure 3 shows the goodness-of-fitting for the distributions that are depicted by Table 5 for both data sets.

Table 5 Estimates of the parameters along with comparison criteria

Fig. 3

Estimated densities of distributions fitted to the two data sets presented in Table 5

6 Conclusion

In this paper we proposed a new four-parameter distribution called the MWP distribution by combining the modified Weibull and Poisson distributions using the concept of minimum order statistics distribution. It was observed that the MWP exhibits various forms of density and hazard functions which are desirable for lifetime data analysis purposes. We provided expansions for the density function and moments. Also, the quantile measures were derived in an explicit form in terms of the Lambert W function. Maximum likelihood estimates of the parameters were discussed. The results of the numerical study carried out for the finite sample confirmed the asymptotic behavior of the MLEs. These two real data sets we showed that the proposed distribution is a very competitive distribution compared with its standard counterpart’s distributions.

Appendix

The Fisher observed information matrix for the parameter vector $\varvec{\theta }$ whose elements are given by:

$$\begin{aligned} U_{\alpha \alpha }&= -n\alpha ^{-2}+\lambda \sum \limits _{i=1}^n \left( {x_i^\gamma e^{\beta x_i }} \right) ^{2}e^{-u_i },\\ U_{\alpha \beta }&= U_{\beta \alpha } =-\alpha ^{-1}\sum \limits _{i=1}^n x_i u_i \left[ {1+\lambda \left( {1-u_i } \right) e^{-u_i }} \right] ,\\ U_{\alpha \gamma }&= U_{\gamma \alpha } =-\alpha ^{-1}\sum \limits _{i=1}^n u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \log x_i , U_{\alpha \lambda } =U_{\lambda \alpha } \\&= -\alpha ^{-1}\sum \limits _{i=1}^n u_i e^{-u_i }\\ U_{\beta \beta }&= -\sum \limits _{i=1}^n x_i^2 \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n x_i^2 u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] ,\\ U_{\gamma \beta }&= U_{\beta \gamma } =-\sum \limits _{i=1}^n x_i \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n x_i u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \log x_i ,\\ U_{\beta \lambda }&= U_{\lambda \beta } =-\sum \limits _{i=1}^n x_i u_i e^{-u_i },\\ U_{\gamma \gamma }&= -\sum \limits _{i=1}^n \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \left( {\log x_i } \right) ^{2}\\ U_{\gamma \lambda }&= U_{\lambda \gamma } =-\sum \limits _{i=1}^n u_i e^{-u_i }\log x_i \hbox { and } U_{\lambda \lambda } =-n\lambda ^{-2}+ne^{-\lambda }\left( {1-e^{-\lambda }} \right) ^{-2}\\ \end{aligned}$$

Using the $X^{\gamma }e^{\beta X}\sim EP(\alpha ,\lambda )$, the Fisher information matrix can be obtained as:

$$\begin{aligned} E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha ^{2}}} \right)&= n\alpha ^{-2}-0.25 n\lambda e^{-\lambda }\alpha ^{-2}\left( {1-e^{-\lambda }} \right) ^{-1} F_{3,3} \left( {\left[ {2,2,2} \right] , \left[ {3,3,3} \right] ,\lambda } \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \beta }} \right)&= n I\left( {\gamma +1,0,1,0} \right) +n\lambda I\left( {\gamma +1,0,1,1} \right) -n\lambda I\left( {2\gamma +1,0,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \gamma }} \right)&= nI\left( {\gamma ,1,1,0} \right) +n\lambda I\left( {\gamma ,1,1,1} \right) -n\alpha \lambda I\left( {2\gamma ,1,2,0} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \lambda }} \right)&= 0.25 n\lambda e^{-\lambda } \left[ {\alpha \left( {1-e^{-\lambda }} \right) } \right] ^{-1}F_{2,2} \left( {\left[ {2,2} \right] , \left[ {3,3} \right] ,\lambda } \right) ,\\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta \partial \lambda }} \right)&= nI(\left( {\gamma +1,0,1,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta ^{2}}} \right)&= nJ\left( {2,2} \right) +n\alpha I\left( {\gamma +2,0,1,0} \right) +n\alpha \lambda I\left( {\gamma +2,0,1,1} \right) \\&-n\alpha \lambda I\left( {2\gamma +2,0,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta \partial \gamma }} \right)&= n J\left( {1,2} \right) +n\alpha I\left( {\gamma +1,1,1,0} \right) +n\alpha \lambda I\left( {\gamma +1,1,1,1} \right) \\&+n\alpha \lambda I\left( {2\gamma +1,1,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \gamma ^{2}}} \right)&= n J\left( {0,2} \right) +n\alpha I\left( {\gamma ,2,1,0} \right) +n\alpha \lambda I\left( {\gamma ,2,1,1} \right) \\&-n\alpha ^{2}\lambda I\left( {2\gamma ,2,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \gamma \partial \lambda }} \right)&= n\alpha I(\left( {\gamma ,1,1,1} \right) , E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \lambda ^{2}}} \right) =n\lambda ^{-2}-ne^{-\lambda }\left( {1-e^{-\lambda }} \right) ^{-1}, \end{aligned}$$

where $F_{v,w} \left( {\left[ {a_1 ,\ldots ,a_v } \right] , \left[ {b_1 ,\ldots ,b_w } \right] ,\gamma } \right)$ is the generalized hypergeometric function with the following definition provided by Gradshteyn and Ryzhik (2000).

$$\begin{aligned} F_{v,w} \left( {\left[ {a_1 ,\ldots ,a_v } \right] , \left[ {b_1 ,\ldots ,b_w } \right] ,\gamma } \right) =\sum \limits _{k=0}^\infty \frac{\gamma ^{k}\mathop \prod \nolimits _{i=1}^v {\Gamma }\left( {a_i +k} \right) {\Gamma }^{-1}(a_i )}{{\Gamma }\left( {k+1} \right) \mathop \prod \nolimits _{i=1}^w {\Gamma }\left( {b_i +k} \right) {\Gamma }^{-1}(b_i )}, \end{aligned}$$

and $I\left( {i,j,k,l} \right) =E\left[ {X^{i}\left( {\log X} \right) ^{j} e^{k\beta X-l\alpha X^{\gamma }e^{\beta X}}} \right]$, $J\left( {i,j} \right) =E\left[ {X^{i}\left( {\gamma +\beta X} \right) ^{-j}} \right]$ are expectations which can be computed numerically.