Bootstrap prediction intervals in beta regressions

Abstract

We address the issue of constructing prediction intervals for responses that assume values in the standard unit interval, $(0,1)$. The response is modeled using the class of beta regression models and we introduce percentile and $\hbox {BC}_a$ (bias-corrected and accelerated) bootstrap prediction intervals. We present Monte Carlo evidence on the finite sample behavior of such intervals. An empirical application is presented and discussed.

1 Introduction

The beta distribution is commonly used to model random variables that assume values in $(0,1)$, such as rates, percentages and proportions. The beta density can display quite different shapes depending on the parameter values. Oftentimes the variable of interest is related to a set of independent (explanatory) variables. Ferrari and Cribari-Neto (2004) introduced a regression model in which the response is beta-distributed, its mean being related to a linear predictor through a link function. The linear predictor includes independent variables and regression parameters. Their model also includes a precision parameter whose reciprocal can be viewed as a dispersion measure. In the standard formulation of the beta regression model it is assumed that the precision is constant across observations. However, in many practical situations this assumption does not hold. Smithson and Verkuilen (2005), among others, consider a beta regression specification in which dispersion is not constant, but is a function of covariates and unknown parameters. Such models are known as varying dispersion beta regression models. Parameter estimation is carried out by maximum likelihood (ML) and standard asymptotic hypothesis testing can be easily performed. Practitioners can use the betareg package, which is available for the R statistical software (http://www.r-project.org), for fiting beta regressions. Cribari-Neto and Zeileis (2010) provide an overview of varying dispersion beta regression modeling using the betareg package.

An empirical application we shall address in this paper relates to the distribution of natural gas for home usage (e.g., in stoves, ovens and water heaters) in São Paulo, Brazil. Such a distribution is based on a simultaneity factor that assumes values in the standard unit interval, $(0,1)$. It relates to the nominal power and to the number of appliances that use natural gas. Given these factors, the company that supplies the gas tries to forecast the probability of simultaneous appliances usage in order to decide how much gas to supply to a given residential unit. According to Zerbinatti (2008), in 2005 the Instituto de Pesquisas Tecnológicas (IPT) e a Companhia de Gás de São Paulo (COMGÁS) computed the simultaneity factor for a number of residences. Zerbinatti (2008) modeled such data using different regression models and concluded that the best performing model was the logit model that used the natural logarithm of the computed power indicator as a covariate. It is noteworthy that one has to be careful not to underestimate the simultaneity factor when making projections using an estimated regression model since that could cause a shortage of natural gas supply. The author shows that the beta regression model can underpredict the response; see Zerbinatti (2008, Figure 4.11.b). It is thus important to have at disposal prediction intervals that can be used with beta regressions. This is the motivation for our paper.

Our main goal is to propose and numerically evaluate bootstrap prediction intervals that can be used with the beta regression model. That is, we construct intervals for unobserved response values corresponding to a given set of covariate values. At the outset, we consider the percentile method as described by Davison and Hinkley (1997) for generalized linear models. We also consider a more refined prediction interval, namely: the $\hbox {BC}_a$ (bias-corrected accelerated). We obtain the $\hbox {BC}_a$ prediction interval for new response values. (Notice that we construct prediction intervals, not confidence intervals.) The finite sample performances of the bootstrap intervals are evaluated using Monte Carlo simulations. Finally, the empirical application briefly described above is addressed.

2 The bootstrap method

Let $x = (x_1, \ldots ,x_n)$ be a random sample from the random variable $X$ whose distribution function is $\mathbb {F}$. Let $\theta = t(\mathbb {F})$ be the parameter that indexes the population and let $\,{\widehat{\! \theta }} = S(x)$ be an estimator of $\theta$. In the bootstrap method, one obtains, from the original sample $x$, a large number of pseudo-samples (bootstrap samples) $x^* = (x^*_1, \ldots ,x^*_n)$, computes the quantity of interest for each pseudo sample (i.e., $\,{\widehat{\! \theta }}\,^* = S (x^*)$), and then one uses the empirical distribution of $\,{\widehat{\! \theta }}\,^* = S (x^*)$ as an estimate of the distribution of $\,{\widehat{\! \theta }}$. Bootstrap sampling can be performed from the empirical distribution function of $x$, given by $\widehat{\mathbb {F}\,}(\iota ) ={{\#\{x_i\le \iota \}}/ n},\,\,\iota \in \mathbb {R}$, or from $\mathbb {F}$ after replacing $\theta$ by $\,{\widehat{\! \theta }}$, a consistent parameter estimator. The former is known as the nonparametric bootstrap whereas the latter is known as the parametric bootstrap.

3 Beta regression prediction intervals

Let $y_1, \ldots , y_n$ be independent random variables such that each $y_t$, for $t=1,\ldots ,n$, is beta distributed, i.e., each $y_t$ has density function given by

$$\begin{aligned} f(y; \mu , \phi ) = {\Gamma (\phi ) \over \Gamma (\mu \phi ) \Gamma ((1-\mu )\phi )} y^{\mu \phi -1}(1-y)^{(1-\mu )\phi -1},\quad 0 < y < 1, \end{aligned}$$

(1)

where $0 < \mu < 1$ and $\phi > 0$. Here, $\mathrm{E}(y) = \mu$ and $\mathrm{var}(y) = {V(\mu ) / (1+\phi )}$, where $V(\mu ) = \mu (1-\mu )$. In the beta regression model introduced by Ferrari and Cribari-Neto (2004) the mean of $y_t$ can be written as

$$\begin{aligned} g(\mu _t) =x_t^{\!\top }\beta = \eta _t. \end{aligned}$$

(2)

In addition to the relation given in (2), it is possible to assume that the precision parameter is not constant and write

$$\begin{aligned} h(\phi _t) = z_t^{\!\top }\gamma = \vartheta _t. \end{aligned}$$

(3)

In (2) and (3), $\eta _t$ and $\vartheta _t$ are linear predictors, $\beta = (\beta _1, \ldots , \beta _k)^{\!\top }$ and $\gamma = (\gamma _1, \ldots , \gamma _q)^{\!\top }$ are unknown parameter vectors ($\beta \in \mathbb {R}^k$; $\gamma \in \mathbb {R}^q$), $x_{t1}, \ldots , x_{tk}$ and $z_{t1}, \ldots , z_{tq}$ are fixed covariates ($k+q < n$) and $g(\cdot )$ and $h(\cdot )$ are link functions, which are strictly increasing and twice-differentiable.

Fitted regression models are oftentimes used to predict out-of-sample response values. In the regression model described by (1)–(3), $x_t^{\!\top } = (x_{t1}, \ldots , x_{tk})$ is a set of observed covariate values and $y_t$ is the $t$th observed response. Let $x_+^{\!\top } = (x_{+1},\ldots , x_{+k})$ denote a new set of covariate values and let $y_{+}$ be the corresponding unobserved response value. The latter can be predicted by $\widehat{\mu }_{+}\! = {g}^{-1}(\sum _{i=1}^k x_{+i}\hat{\beta }_i)$, where $\hat{\beta }_i$ is the maximum likelihood estimate of $\beta _i$ computed using the original sample. It is useful to obtain a prediction interval, which is given by lower and upper limits that are statistics associated with a given desired coverage level. In what follows, we shall construct such an interval using estimates of the prediction error distribution.

3.1 Percentile prediction intervals for beta regressions

Let $\mathcal{R}(y,\mu )$ denote a monotonic function of $y$ that has constant variance for all observations. Assume that the mean $\mu _{+}$ and the distribution of $\mathcal{R}(y,\mu )$ are known, and denote the $\alpha$th quantile of such a distribution by $\delta _{\alpha }$ ($0 < \alpha < 1/2$). The limits of the $1-\alpha$ prediction interval has lower and upper limits given by $y_{+,\alpha /2}$ and $y_{+,1-\alpha /2}$, respectively, which satisfy $\mathcal{R}(y_{+,\alpha /2},\mu _+) =\delta _{\alpha /2}$ and $\mathcal{R}(y_{+,1-\alpha /2},\mu _+) =\delta _{(1-\alpha /2)}$, where $\mathcal{R}(y,\mu _+)$ is the prediction error. If $\widehat{\mu }$, the estimate of $\mu$, is computed independently from $y_+$ and the quantiles of $\mathcal{R} (y_+,\widehat{\mu })$ are known, the prediction interval can be easily computed. The distribution of $\mathcal{R}(y_+,\widehat{\mu })$, however, is typically unknown. In what follows, we shall use data resampling to estimate it and then obtain the desired quantiles from such an estimated distribution, which are used to construct the prediction interval. In the data resampling mechanism we shall work with a normalized version of $\mathcal{R}(y,\widehat{\mu })$ whose distribution has constant variance.

For the beta regression model, we consider

$$\begin{aligned} \mathcal{R}(y,\mu ) = {y^*_t - \mu ^*_t \over \sqrt{v_t}}, \end{aligned}$$

(4)

where $\mathrm{E}(y^*_t) = \mu _t^*$ and $\mathrm{var}(y^*_t) = v_t$, with $v_t = \psi '(\mu _t\phi _t) + \psi '((1-\mu _t)\phi _t)$. Here,

$$\begin{aligned} y_t^* = \log \{ y_t / (1-y_t)\} \quad \mathrm{and} \quad \mu _t^* = \psi (\mu _t\phi _t)- \psi ((1-\mu _t)\phi _t). \end{aligned}$$

(5)

Hence, $\mathcal{R}(y,\mu )$ is a monotonic function of $y$ with zero mean and unit variance [see Ferrari et al. 2008, Eq. (8)]. In the data resampling mechanism we shall use the standardized version of $\mathcal{R}(y,\widehat{\mu })$ given by

$$\begin{aligned} r_t = {y^*_t - {\widehat{{\mu }}^*}_t \over \sqrt{\widehat{v}_t(1 - h_{tt}^*)}}, \end{aligned}$$

(6)

which was proposed in Espinheira et al. (2011) and is known as standardized weighted residual 2. It is a standardized residual obtained using Fisher’s scoring iterative algorithm for $\beta$ under varying dispersion. Here, $h_{tt}^*$ is the $t$th diagonal element of

$$\begin{aligned} H^* = (\widehat{W}\widehat{\mathcal{V}})^{1/2}X(X^{\!\top }\widehat{\mathcal{V}} \widehat{W} X)^{-1}X^{\!\top }(\widehat{\mathcal{V}} \widehat{W})^{1/2}, \end{aligned}$$

where $X$ is the $n\times k$ matrix of covariates ($k < n$), $W = \mathrm{diag}\{ w_1, \ldots , w_n\}$ with $w_t = \phi _t v_t /\{g'(\mu _t)\}^2$ and

$$\begin{aligned} \mathcal{V} = \mathrm{diag}\{\phi _1,\ldots ,\phi _n\}. \end{aligned}$$

(7)

Using the approach outlined by Davison and Hinkley (1997, p. 340) for generalized linear models we can construct the $1-\alpha$ percentile prediction interval using the $\alpha /2$ and $1 - \alpha /2$ quantiles of $\widehat{G}$, the bootstrap approximation to $\mathcal{R}(y_+,\widehat{\mu })$.

It is well known that percentile confidence interval for $\theta$, the parameter that indexes a given population, can display poor behavior in small samples when based on a highly biased estimator of that parameter (DiCiccio and Tibshirani 1987). A more refined approach is known as $\hbox {BC}_a$ (bias-corrected and accelerated). It accounts for bias and for the fact that the estimator standard error may vary with $\theta$.

3.2 $\hbox {BC}_a$ confidence intervals

Assume that there exists a function $h(\theta )= \rho$, which is monotic decreasing, and constants $a$ and $v_0$ such that $\widehat{\rho }- \rho \sim \mathcal{N}(-v_0(1 + a\rho ), (1 + a\rho )^2)$. The exact upper limit of the $1 - \alpha$ confidence interval for $\rho$ is $\rho [\alpha ] = \widehat{\rho }+ \mathrm{se}{_{\widehat{\rho }}}\{{v_0 + z_{\alpha }\}/ \{1 - a(v_0 + z_{\alpha })}\}$, where $z_{\alpha }$ is the $\alpha$ standard normal quantile. Let $P$ denote the distribution function of $\widehat{\theta }$. Using the inverse transformation $h^{-1}(\cdot )$, we obtain an estimate of $\alpha$:

$$\begin{aligned} \,\widetilde{\alpha }= \Phi \bigg (\widehat{v}_0 + {{\widehat{v}_0 + z_{\alpha }}\over {1 - \widehat{a}(\widehat{v}_0 + z_{\alpha })}}\bigg ), \end{aligned}$$

(8)

where $\Phi$ is the standard normal distribution function. The $1 - \alpha$ BC$_a$ confidence interval is given by the $\,\widetilde{\alpha }/2$ and $1 - \,\widetilde{\alpha }/2$ quantiles of $\widehat{G}$ when $z_{\alpha }$ in (8) is replaced by $z_{\alpha /2}$ and $z_{1-\alpha /2}$, respectively.

The constant $v_0$ accounts for any bias of the plug-in estimator. According to Efron (1987) it can be estimated as

$$\begin{aligned} \widehat{v}_0 = \Phi ^{-1}\Bigg ({\#{\widehat{\theta }_b<\widehat{\theta }}\over {B}}\Bigg ), \end{aligned}$$

(9)

where $\widehat{\theta }_b$ is the $b$th bootstrap estimate of $\theta$ and $B$ is the number of bootstrap replications. Roughly speaking, $\widehat{v}_0$ measures the discrepancy between the median of $\widehat{\theta }^*$ and $\widehat{\theta }$, in normal units. If $\widehat{v}_0 = 0$, then $\widehat{\theta }= \mathrm{median} (\widehat{\theta }^*)$ and the bias correction is not needed.

The acceleration constant $a$ accounts for the rate of change in the standard error of $\widehat{\theta }$ with respect to $\theta$. According to Efron (1987), in one parameter models a good approximation to $a$ is

$$\begin{aligned} a \approx {1\over 6}\mathrm{skew}_{\theta = \widehat{\theta }}( \dot{\ell \,}_{\theta }), \end{aligned}$$

(10)

where $\dot{\ell }_{\theta } = \dot{\ell \,} = d \log f(y; \theta )/d\theta$. Note that the skewness of $\dot{\ell \,}$, $\mathrm{E} [(\dot{\ell \,} - \mathrm{E}[\dot{\ell \,}])^3]/ \{\mathrm{E}[ (\dot{\ell \,} - \mathrm{E}[\dot{\ell \,}])^2]\}^{3/2}$, is evaluated at $\widehat{\theta }$. According to Davison and Hinkley (1997) the expression in (10) is equivalent to

$$\begin{aligned} a\approx {1\over 6}{{\mathrm{E}[ \dot{\ell \,}(\widehat{\theta })^3]}\over {\mathrm{var}[ \dot{\ell \,}(\widehat{\theta })]^{3/2}}}, \end{aligned}$$

(11)

which can be estimated using data resampling.

3.3 $\hbox {BC}{_a}$ prediction intervals for the realization of a random variable

Our goal in this paper, however, is not to construct confidence intervals for a parameter, but to construct prediction intervals for the realization of a random variable. In that sense, we shall now consider the proposal made in Mojirsheibani and Tibshirani (1996). The authors develop prediction intervals for $\widehat{\theta }_+$, an efficient estimator of a scalar parameter $\theta$, based on a new sample of size $n^+$.

Based on expressions (8)–(10), the authors suggest the following choice of value for $v_0$:

$$\begin{aligned} \widehat{v}_0 = \Phi ^{-1}\Bigg ({\#{\widehat{\theta }_{+,b}<\widehat{\theta }_n}\over {B}}\Bigg ), \end{aligned}$$

(12)

where $\widehat{\theta }_n$ and $\widehat{\theta }_+$ are the MLEs of $\theta$ obtained using $y_n$ and $y_+$, respectively, $y_n= (y_{1},\ldots ,y_{n})^{\top }$ being the original sample and $y_+ = (y_{1^+},\ldots ,y_{n^+} )^{\top }$ being the new sample values. Additionally, they suggest using

$$\begin{aligned} a = {1\over 6}\mathrm{skew}_{\theta = \widehat{\theta }_n}( \dot{\ell \,}_{\theta }(\widehat{\theta }_+)) \end{aligned}$$

(13)

with a multiplicative correction of $(n/n^+)^{-1/2}$.

3.4 $\hbox {BC}_{a}$ prediction intervals for new and unobserved response values

The $\hbox {BC}_{a}$ scheme presented Sect. 3.3 can be used to construct prediction intervals for $\widehat{\theta }_+$ under new response values. Our goal, nonetheless, is to construct prediction intervals for new, unobserved response values given a set of covariates values. The BC$_a$ method we propose is a modification of the existing BC$_a$ methods (Sects. 3.2 and 3.3). In particular, we obtain expressions for $a$ and $v_0$ when the interest lies in predicting a given observation. This is the main difference between our result and the existing results and is also our main contribution to the literature.

Based on (10), we propose using

$$\begin{aligned} a = {1\over 6}\mathrm{skew}_{\theta = \widehat{\theta }_n}( \dot{\ell \,} (\,\widehat{\!\mu }_{+})) \approx {1\over 6}{{\mathrm{E} [\dot{\ell \,}_+^3]}\over {\mathrm{var}[\dot{\ell \,}_+]^{3/2}}}, \end{aligned}$$

(14)

which is to be corrected by the multiplicative factor given by $(n/n^+)^{-1/2}$. It can be shown that, in the class of beta regressions, $\dot{\ell }_t = d \log f(y; \mu , \phi )/d\mu = \phi _t(y_t^* - {\!\mu }_t^*)$. Thus, $\dot{\ell }_+ = \phi _+(y_+^* - {\!\mu }_+^*)$, which becomes $\dot{\ell }_+ = \phi (y_+^* - {\!\mu }_+^*)$ under constant dispersion.

Estimation of $a$ can be performed using data resampling, e.g., bootstrap. We used that approach in a numerical experiment, i.e., we used the bootstrap to obtain estimates of ${\mathrm{E}[ \dot{\ell \,}_t^3]}$ and ${\mathrm{var}[ \dot{\ell \,}_t]}$, which in turn allowed us to obtain an estimate for $a$. Our numerical results showed, however, that this approach did not display good small sample performance. A better performing approach proved to be the one in which $a$ is calculated analytically. For the varying dispersion beta regression model we obtain, after some algebra, ${\mathrm{E}[ \dot{\ell \,}_t^3]} = \varphi _t = \phi _t^3 \{\psi ''({\!\mu }_{t}\phi _t) - \psi ''((1-{\!\mu }_{t})\phi _t)\}$ and ${\mathrm{var}[ \dot{\ell \,}_t]} = v_t =\phi _t^2 \{\psi '({\!\mu }_{t}\phi _t) + \psi '((1-{\!\mu }_{t})\phi _t)\}$. It then follows that ${\mathrm{E}[ \dot{\ell \,}_+^3]} = \varphi _+$, ${\mathrm{var}[\dot{\ell \,}_+]} = v_+$ and $\widehat{a}={ (1/ 6)} {\widehat{\varphi }_{+} / \widehat{v}_{+}^{ 3 / 2}}$, with $\widehat{\varphi }_{+} = \widehat{\phi }_+^3 \{\psi ''({\widehat{\mu }}_{+}\widehat{\phi }_+) - \psi ''((1-{\widehat{\mu }}_{+})\widehat{\phi }_+)\}$ and $\widehat{v}_{+} =\widehat{\phi }_+^2 \{\psi '({\widehat{\mu }}_{+}\widehat{\phi }_+) + \psi '((1-{\widehat{\mu }}_{+})\,\widehat{\phi }_{+})\}$. Here,

$$\begin{aligned} \,\widehat{\!\phi }_{+}= {h}^{-1}\left( \sum _{j=1}^q z_{+,j}\widehat{\gamma }_{j}\right) . \end{aligned}$$

(15)

In (15), $\widehat{\gamma }_{j}$ is the MLE of ${\gamma }_{j}$ and $z_{+,j}$ is the $j$th component of $z_+^{\!\top } = (z_{+1},\ldots , z_{+q})$, i.e., it is the $j$th component of the set of dispersion regressors associated with the unobserved response $y_{+}$.

Next, we shall propose an estimator for ${v}_0$. Since our interest lies in the estimation of the distribution of $\mathcal{R}(y_+,\widehat{\mu })$ we shall use an estimate which is based on such quantity. Our proposal is to use

$$\begin{aligned} \widehat{v}_0 = \Phi ^{-1}\Bigg ({\#{\mathcal{R}_{a_+,b}<\mathcal{R}_{m}}\over {B}}\Bigg ), \end{aligned}$$

(16)

where $\mathcal{R}_{m}$ is the median of $\mathcal{R}_{1},\ldots ,\mathcal{R}_{n}$, which is computed using the original data and (4), and $\mathcal{R}_{a_+,b}$ is defined in algorithm given below; see Eq. (17).

3.5 Algorithm

Our algorithm can be outlined as follows. It is intended for $n_1$ predictions and uses $B$ bootstrap replications. The bootstrap replications are indexed as $b=1,\ldots , B$.

• 1. For $t=1,\ldots ,n$, randomly draw $r_{t,b}$ from $r_1,\ldots ,r_n$ (with replacement).

• 2. Construct a bootstrap sample $(y_{b},X,Z)$, where $y_{b} = (y_{1,b}, \ldots , y_{n,b})^{\!\top }$, such that

  $$\begin{aligned} y_{t,b} = {\mathrm{exp}({\widehat{{\mu }}^*}_t + r_{t,b}\sqrt{\widehat{v}_t }) \over {1+{\mathrm{exp}({\widehat{{\mu }}^*}_t + r_{t,b}\sqrt{\widehat{v}_t })} }} \end{aligned}$$

  is obtained as the solution to $\mathcal{R}(y_t,\widehat{\mu }_t)= r_{t,b}$.

• 3. Using $(y_{b},X,Z)$ compute $\,\widehat{\!\beta }_b$ and $\widehat{\gamma }_b$, the bootstrap estimates of $\beta$ and $\gamma$, respectively. Here, $Z$ is the $n\times q$ matrix of covariates used in the dispersion submodel. Using the matrices of new observations on the regressors, $X_+$ ($n_1\times k$) and $Z_+$ ($n_1\times q$), together with $\,\widehat{\!\beta }_b$ and $\widehat{\gamma }_b$, obtain $\,\widehat{\!\mu }_{+,b}$, $\,\widehat{\!\phi }_{+,b}$, ${\widehat{{\mu }}^*}_{+,b}$ $\widehat{v}_{+,b}$, which are $n_1$-vectors.

• 4. For each new observation $a_+=1,\ldots ,n_1$:

• (a) Randomly draw $r_{a_+,b}$ from $r_1,\ldots ,r_n$.

• (b) Compute

  $$\begin{aligned} y_{a_+,b} = {\mathrm{exp}({\widehat{{\mu }}^*}_{a_+,b} + r_{a_+,b} \sqrt{\widehat{v}_{a_+,b} }) \over {1+{\mathrm{exp}({\widehat{{\mu }}^*}_{a_+,b} + r_{a_+,b}}\sqrt{\widehat{v}_{a_+,b})} }}. \end{aligned}$$

• (c) Compute the prediction error

  $$\begin{aligned} \mathcal{R}_{a_+,b} (y_{a_+,b},{\widehat{{\mu }}^*}_{a_+,b}) = {y_{a_+,b}^*- \widehat{{\mu }}^*_{a_+,b}\over \sqrt{\widehat{v}_{a_+,b}}}, \end{aligned}$$

  (17)

  where $y_{a_+,b}^* =\log \left\{ {y_{a_+,b}/(1-y_{a_+,b})}\right\}$. For each new observation, sort the $B$ values $\mathcal{R}_{a_+}$, such that ${\mathcal{R}_{a_+}}_{(1)}\le \cdots \le {\mathcal{R}_{a_+}}_{(B)}$. Compute the percentile quantiles

  $$\begin{aligned} {\delta ^{\star }_{\mathrm{{P}}^{a_+}_a}}_{(\alpha /2)}={\mathcal{R}_{a_+}}_{(B(\alpha /2))} \hbox { and } {\delta ^{\star }_{\mathrm{{P}}^{a_+}_a}}_{(1-\alpha /2)}={\mathcal{R}_{a_+}}_{(B(1-\alpha /2))}, \end{aligned}$$

  and the BC$_a$ quantiles

  $$\begin{aligned} {\delta ^{\star }_{\mathrm{{BC}}^{a_+}_a}}_{(\alpha /2)}={\mathcal{R}_{a_+}}_{(B(\,\widetilde{\alpha }/2))}\hbox { and } {\delta ^{\star }_{\mathrm{{BC}}^{a_+}_a}}_{(1-\alpha /2)}={\mathcal{R}_{a_+}}_{(B(1-\,\widetilde{\alpha }/2))}, \end{aligned}$$

  with $\,\widetilde{\alpha }/2$ given in (8). Finally, obtain the prediction interval limits, percentile (${\delta ^{\star }_{a_+}} = {\delta ^{\star }_{\mathrm{{P}}^{a_+}_a}}$) or $\hbox {BC}_a$ (${\delta ^{\star }_{a_+}} = {\delta ^{\star }_{\mathrm{{BC}}^{a_+}_a}}$), using

  $$\begin{aligned} y_{{a_+},I}&= {\mathrm{exp}({\widehat{{\mu }}^*}_{a_+} + {\delta ^{\star }_{a_+}}_{(\alpha /2)} \sqrt{\widehat{v}_{a_+} }) \over {1+{\mathrm{exp}({\widehat{{\mu }}^*}_{a_+} + {\delta ^{\star }_{a_+}}_{(\alpha /2)}}\sqrt{\widehat{v}_{a_+})} }}\\ y_{{a_+},S}&= {\mathrm{exp}({\widehat{{\mu }}^*}_{a_+} + {\delta ^{\star }_{a_+}}_{(1-\alpha /2)} \sqrt{\widehat{v}_{a_+} }) \over {1+{\mathrm{exp}({\widehat{{\mu }}^*}_{a_+} + {\delta ^{\star }_{a_+}}_{(1-\alpha /2)} }\sqrt{\widehat{v}_{a_+})} }}. \end{aligned}$$

  Here, ${\widehat{{\mu }}^*}_{a_+}$ and $\widehat{v}_{a_+}$ are the quantities $\mu ^*$ and $v$ evaluated at ${\widehat{{\mu }}}_{a_+}= g^{-1}(x^{\top }_{a_+}\,\widehat{\!\beta })$ and ${\widehat{{\phi }}}_{a_+}= {h}^{-1}(z^{\top }_{a_+}\,\widehat{\!\gamma })$, $x^{\top }_{a_+}$ and $z^{\top }_{a_+}$ being the $a_+$-th rows of $X_+$ and $Z_+$ relative to the new observations, respectively, $a_+=1,\ldots ,n_1$. The values $y_{{a_+},I}$ and $y_{{a_+},S}$ are obtained, respectively, as the solutions to $\mathcal{R}(y_{a_+},{\widehat{\mu }}_{a_+})= {\delta ^{\star }_{a_+}}_{(\alpha /2)}$ and $\mathcal{R}(y_{a_+},{\widehat{\mu }}_{a_+})= {\delta ^{\star }_{a_+}}_{(1-\alpha /2)}$.

4 Simulation results

The simulation results presented in this section were obtained using both fixed and varying dispersion beta regressions as data generating processes. Table 1 contains numerical results for the fixed dispersion beta regression model given by

$$\begin{aligned} \log \left( \frac{\mu _t}{1-\mu _t}\right) = \beta _1 + \beta _2 x_{t2}. \end{aligned}$$

The sample sizes are $n=40,80,120$ and the precisions are $\phi = 50, 150, 400$. There are five different scenarios. In the first three scenarios, $\mu \in (0.15,0.80)$, $\mu \in (0.95,0.98)$ and $\mu \in (0.02,0.07)$; the covariate values were generated from the standard normal distribution. In the remaining two scenarios we generated the covariate values from the $t_3$ and unit mean exponential distributions in order to introduce leverage points in the data. The number of Monte Carlo replications is 5,000 and for each replication we perform $B=500$ bootstrap replications. The nominal coverage of all intervals is 95 %. The figures in Table 1 are empirical coverages ($\%$).

Table 1 Empirical coverages ($\%$). The model is $\log ( {\mu _t}/{(1-\mu _t)}) = \beta _1 + \beta _2 x_{t2}$, $B=500$ and the nominal coverage is $95\,\%$

The numerical results presented in Table 1 show that the $\hbox {BC}_{a}$ and percentile intervals perform similarly, the $\hbox {BC}_{a}$ outperforming the percentile method in some situations. For instance, when $\mu \in (0.02,0.07)$, $\phi = 50$ and $n=40$, the percentile coverage equals $87.3\,\%$ whereas the $\hbox {BC}_{a}$ coverage is $97.5\,\%$. We also note that when the covariate values are generated from the exponential distribution, the $\hbox {BC}_{a}$ is consistently superior to the percentile method. For example, when $\phi = 50$ and $n=80$, the $\hbox {BC}_{a}$ and percentile coverages are 96.3 and $90.1\,\%$, respectively. There are some situations, however, in which the percentile outperforms the $\hbox {BC}_{a}$, such as when $\phi = 150$ and $n=80$; their respective coverages are 93 and $90\,\%$. It is also noteworthy that the finite sample performances of both interval estimators improve when the sample size increases and also when the value of the precision parameter increases.

We have also carried out Monte Carlo simulations using a varying dispersion beta regression model. The data generating process is

$$\begin{aligned} \log \left( \frac{\mu _t}{1-\mu _t}\right) = \beta _1 + \beta _2 x_{t2} \hbox { and } \log (\phi _t) = \gamma _1 + \gamma _2 x_{t2}. \end{aligned}$$

We measure the intensity of nonconstant dispersion as $\lambda = \phi _{\max }/\phi _{\min }$ and report results for $\lambda = 20, 50, 100$. The empirical coverages are given in Table 2. The results show that the empirical coverages are sensitive to the intensity of nonconstant dispersion. Overall, the two methods are competitive. The percentile method outperforms the $\hbox {BC}_{a}$ when the data include leverage points (covariate values obtained as random draws from the $t_3$ distribution). For instance, when $\lambda = 20$ and $n=40$, their coverages are 94.2 and $91.6\,\%$, respectively. On the other hand, the $\hbox {BC}_{a}$ outperforms the percentile method when $\mu \in (0.02,0.07)$. For example, when $\lambda = 50$ and $n=80$, the respective coverages are 94.8 and 90.7 %.

Table 2 Empirical coverages ($\%$)

We performed additional simulations in which we increased the number of covariates, used different covariates in the mean and precision submodels and incorrectly estimated a fixed dispersion beta regression when the true data generating process had varying dispersion. The new numerical results are presented in Tables 3, 4 and 5. We considered the following beta regression model:

$$\begin{aligned} \log \left( \frac{\mu _t}{1-\mu _t}\right)&= \beta _1 + \beta _2 x_{t2} + \beta _3 x_{t3}+ \beta _4 x_{t4} + \beta _5 x_{t5},\end{aligned}$$

(18)

$$\begin{aligned} \log (\phi _t)&= \gamma _1 + \gamma _2 z_{t2}+ \gamma _3 z_{t3}+ \gamma _4z_{t4} + \gamma _5z_{t5}. \end{aligned}$$

(19)

The covariate values in the mean submodel were obtained as random draws from the standard uniform distribution whereas those in the precision submodel were obtained as random draws from the ${\mathcal U}(-0.5,0.5)$ distribution. Thus, the covariate values in the two submodels are not the same. The results in Table 3 were obtained using $\log (\phi _t) = \gamma _1$ (constant dispersion). The results in Table 4 were obtained using different values for the $\beta$’s and $\gamma$’s which lead to models with different number of covariates. Additionally, $\lambda = 20, 50, 100$. Finally, we considered the case in which the true data generating process has varying dispersion but a fixed dispersion beta regression is estimated; see Table 5. The results in Table 3 show that the intervals do not become considerably less accurate when the number of covariates increases, especially when the precision parameter equals $150$ or $400$. When $\phi =50$ and $n=40$ the percentile interval displays smaller coverage. The $\hbox {BC}_{a}$ finite sample performance is not altered. The average interval lengths are also not substantially affected. The simultaneous increase in the number of covariates in the two submodels also does not noticeably affect the intervals finite sample performances; see Table 4.

Table 3 Empirical coverages ($\%$)

Table 4 Empirical coverages ($\%$)

Table 5 Empirical coverages ($\%$)

The intervals finite sample behavior slightly change when the true data generating process has varying dispersion, but a fixed dispersion beta regression model is estimated. The results are presented in Table 5. The most extreme change takes place when $\lambda = 50$ and $n=40$. For the correctly specified one-covariate model the percentile and BC$_a$ coverage rates (average lengths) are $95.3$ and $92.6\,\%$ ($0.16$ e $0.15$), respectively. When the fixed dispersion model is estimated, these coverage rates (average lengths) become $100.0\,\%$ and $100.0\,\%$ ($0.36$ e $0.20$). Overall, the BC$_a$ average lengths are smaller than the percentile average lengths. Here, the coverage rates tend to decrease when the number of covariates increases. For instance, when there are three covariates, $\lambda = 20$ and $n=80$ the percentile coverage (average length) becomes $88.4\%$ ($0.33$).

5 Empirical application

We shall now return to the application briefly described in the Introduction. Recall that it relates to the distribution of natural gas for home usage in São Paulo, Brazil. The distribution of natural gas is based on a simultaneity factor that assumes values in the standard unit interval, $(0,1)$.

Using the simultaneity factor one obtains the release indicator, i.e., an indicator of gas release in a given tubulation section: $Q_p = F \times Q_{max}$, where $Q_p$ is the release, $F$ is the simultaneity factor and $Q_\mathrm{max}$ is the maximum possible release. $F$ assumes values in $(0,1)$, and can be interpreted as the ratio between effective and maximal intensities. We note that overpredictions of the simultaneity factor leads to excess supply of gas and, as consequence, inefficient allocation and higher costs.

According to Zerbinatti (2008), the Instituto de Pesquisas Tecnológicas (IPT) and the Companhia de Gás de São Paulo (COMGÁS) performed an extensive study in which data were collected in order to build a database on simultaneity factors and the corresponding maximal releases (computed power). The sampled households were visited in the second semester of 2004. They all had stoves and gas-based water heating. One hundred visits were made and they yielded 42 valid measurements. The response values range from 0.02 to 0.46, its median being 0.07. The data can be found in Zerbinatti (2008, p. 67). At the outset, we shall select the beta regression model that yields the best fit. The response is the simultaneity factor and the covariate is the release. We considered different link functions for the two submodels (mean and precision). Model selection was based on the PRESS (prediction sum of squares) criterion; see Allen (1974). For each estimated model we computed $PRESS ={ {\sum _{t=1}^{42}(y_t - \widehat{y}_{(t)})^2} / { 42 }}$, where $\widehat{y}_{(t)}$ denotes the estimate of $y_t$ obtained after excluding such an observation from the data. The best model is the one that minimizes the criterion. The following constant dispersion model was selected: logit link and log of release used as covariate. The maximum likelihood parameter estimates are $\widehat{\beta }_1 = -1.76$, $\widehat{\beta }_2 = -0.76$ and $\widehat{\phi }= 88.79$.

5.1 Bootstrap inference

In what follows we shall build and evaluate bootstrap-based prediction intervals for the response. To that end, we shall use the selected model, build each interval and compute its coverage rate using 42 different samples. Each sample is obtained by removing an observation from the data, which is done sequentially. For each sample, we construct the prediction interval and determine whether it contains the omitted response. The coverage rate is computed as the ratio between the number of prediction intervals that covered (included) the omitted response and the total number os intervals. The number of bootstrap replications was $B=500$ and all intervals correspond to the 95 % nominal level.

The empirical coverage of the percentile prediction interval was $90.4\,\%$. The intervals did not include observations 11, 16, 33 and 35. The $\hbox {BC}_{a}$ intervals covered all omitted responses but those corresponding to observations 16 and 35, its coverage rate being $95.2\,\%$. For instance, $y_{41} = 0.041$ and the 95 % $\hbox {BC}_{a}$ interval is $(0.036,0.180)$. The prediction interval thus covers the response. That does not hold true for the percentile interval, which is $(0.042,0.177)$. Additionally, $y_{33} = 0.147$ and the $\hbox {BC}_{a}$ and percentiles intervals are $(0.023,0.152)$ and $(0.026,0.147)$, respectively. Again, unlike the percentile interval, the $\hbox {BC}_{a}$ covers the omitted response. We note that the empirical coverage rates remained constant when we increased the number of bootstrap replications to $B=2000$. The intervals lengths slightly decreased.

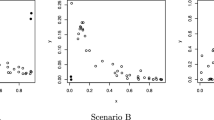
In Fig. 1 we plot the data (simultaneity factor vs. computed power) together with the curves created connecting the upper limits of all prediction intervals and also their lower limits. The upper panel, (a), corresponds to the $\hbox {BC}_{a}$ interval whereas the lower panel, (b), is for percentile intervals. Figure 1 shows that the percentile prediction interval fails when it comes to observation 16; the upper interval limit bends below the observed value. The same behavior takes place when the focus lies in the prediction of $y_{33}$ (observation 33). We also note that both intervals have similar lengths.

Fig. 1

Dispersion plots and prediction intervals; $\hbox {BC}_{a}$ (a) and percentile (b)