A novel method to minimize the five-axis CNC machining error around singular points based on closed-loop inverse kinematics

Abstract

Singularities in five-axis machining are a series of positions where the exact motion of the rotary axis becomes unpredictable or incalculable. In the neighborhood of a singular point, machining may cause unstable movements of drive axes and deteriorative dynamic performance of machine tools. In this paper, we proposed a closed-loop inverse kinematics method to solve accurately the five-axis joints’ parameters around singular points. To achieve this purpose, the damped Jacobian pseudoinverse algorithm is introduced and the machine joints’ velocities are calculated directly by the velocities of the five-axis cut points. The joints are then obtained by integrating the corresponding velocities. Furthermore, a feedback control method is applied to reduce the integrating error. In the end, simulations and experiments’ results demonstrated the effectiveness of the closed-loop inverse kinematics method.

1 Introduction

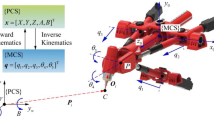
Five-axis machining tools have the ability to combine position and orientation and complete machining without the repositioning process and have been widely used in machining dies, molds, and impellers. Some workpieces with a complex surface, such as a turbine blade, can only be manufactured by five-axis machining tools. The primary function of any five-axis CNC program is to transform cutter location data into machine commands (G-code), and the essential function is the inverse kinematics function (Fig. 1). Compared with three-axis machining tools, five-axis machining tools have two rotation axis, and the inverse kinematics of five-axis machining tools is a nonlinear function, which transforms the CL data $(x,y,z,o_i,o_j,o_k)^T$ into the machine commands of five-axis as $(P_x,P_y,P_z,\theta _A,\theta _C)$ or $(P_x,P_y,P_z,\theta _A,\theta _B)$ or $(P_x,P_y,P_z,\theta _B,\theta _C)$. The notation of the rotation axes is either $(\theta _A, \theta _C)$ or $(\theta _A,\theta _B)$ or $(\theta _B,\theta _C)$ that depends on the structure of the five-axis machine.

While the orientation of the rotation axis is parallel to the tool direction, the exact solution of the inverse kinematics equation does not exist. Then the rotary axis will be unpredictable and may rotate $180^{\circ }$ abruptly. These deadly positions are called singularities. Machining near such singularities may cause unstable movements of the drive axis and deteriorate the dynamic performance of machine tools. Furthermore, an abrupt change of the rotary axis will bring shock to the servo motor, lower the machining precision and even damage the machined quality. Therefore, the detection and avoidance of singularity should be conducted in five-axis machining.

To avoid singularities, there are currently four categories of methods, the locally deforming method [1,2,3,4,5,6] the forbidden region and acceptable region-based method [7,8,9], the workpiece position reorientation method [10,11,12,13] and the kinematics-based method [14,15,16].

The locally deforming method is based on the deforming of the tool path to devoid of the singularity. Affouard et al. [1] presented the concept of “singular cone” and use B-spline curves to describe tool trajectory. Singularity was detected and avoided in the studies of Yang and Altintas [2] based on the general kinematic model with screw theory and singularity was eliminated by modifying the B-spline control points. Wang et al. [3] projected the three dimension “singular cone” into two-dimension space, and the singularity phenomenon is avoided by changing the B-spline control points with an optimal method. The same method was also used for singularity avoidance of a 5-axis hybrid robot [4]. In this study, the sudden change of C-type rotation was eliminated and the tracking error could also be limited. Sun et al. [5] proposed a local gouge-free tool path modification method for singularity avoidance with consideration of compliant axes kinematics, and they also considered the singular phenomena in robotic machining [6].

Fig. 1

Forward and inverse kinematics of five-axis machines

The forbidden region method is mainly based on translating orientation polyline to avoid the singularity. Lin et al. [7] projected the orientation vector into the C-space, and the singularities are detected by contact checking between the orientation polyline and the tapper circle. Lin et al. [8, 9] also considered the surface texture in avoiding singularity, and the acceptable-texture orientation region concept (ATOR) was proposed.

The workpiece position reorientation method is based on resetting the workpiece orientation to make no orientation vertical and thus avoids the singularity. Cripps et al. [10] firstly analyzed the cause of singularity, and they proposed a position reorientation method to avoid the singularity. By analyzing the forces transmitted to the rotary drives as torque disturbances, Yang et al. [11] identified the workpiece location on the rotary to minimize tracking errors in five-axis machining. With the analysis of the machine’s kinematic behavior, Pessoles et al. [12] designed the workpiece reorientation method to minimize the overall distance traveled by the rotary axes and avoided singularity. Recently, Gao et al. [13] developed a workpiece setup optimization method, which not only considered the singularity avoidance requirement but also considered the five-axis kinematic stability.

Kinematic based method is different from the previous method and avoids singularity by the optimization of inverse kinematics. Munlin et al. [14] considered the kinematic error near singular points, by the optimization of the required rotations on the inverse kinematics equation, the singularity was avoided. Shen et al. [15] proposed a double solutions-based optimisation method. The singularity was determined during inverse kinematics, which chooses the appropriate solution set within rotary ranges and avoided the disturbance of the rotary axis near singular points. My and Bohez [16] developed the five-axis inverse kinematic method near singular points, with the feedback control method, the rotary axis was directly evaluated.

There are also some other methods to avoid singularity. Sørby [17] proposed the kinematics of a five-axis machine with non-orthogonal rotary axes. Gray [18] proposed a $3\frac{1}{2}\frac{1}{2}$ axis machining method. In $3\frac{1}{2}\frac{1}{2}$ axis machining, only its three linear axes were moved and the two rotary axes were locked, and had the ability to pass the singular region. Grandguillaume et al. [19] proposed a tool path patching strategy method, which avoids the singular by modifying the tool axes orientation while respecting maximum velocity, acceleration, and jerk of the machine tools.

However, most of the mentioned solutions are based on the geometric approximation and regeneration of the tool path near the singular points. In this paper, a robust algorithm is designated for computing the tool path across singular points, and the singularity problems are changed to a matrix ill-conditioned problem. While the Jacobian matrix of five-axis kinematics is ill-conditioned, a small disturbance of the orientation vector may cause a huge change in the rotary axes in a five-axis machine, which means a small cutter point’s velocity may cause a huge rotary velocity. To overcome the ill-conditioned problem of the Jacobian matrix, the damping least-square Jacobian method is used in this paper. Then the five-axis joints’ positions (three linear joints and two rotary joints) can be calculated directly by integrating the joints’ velocities numerically. When integrating the joints’ velocities, a feedback control system is applied to limit the integration error.

The remainder of this paper is organized as follows. In Sect. 2, kinematic singularity and inverse kinematics of the five-axis CNC machine are presented. In Sect. 3, damping least-square Jacobian and feedback control methods are described detailed. Simulation and experimental results are given in Sect. 4. Section 5 provides some concluding remarks and future works.

2 Kinematic singularity of 5-axis CNC machine

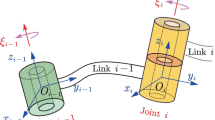
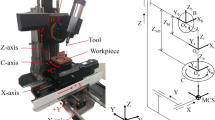
The tool paths generated by CAM software are calculated basing the input on the part surface models, the surface quality required, the cutter definition, the tool path pattern, etc. [16] The output tool paths are defined in a workpiece coordinate system. However, the machine tool is controlled by the motor in each axes, which is based on the machine tool coordinate. The two coordinates are connected via a kinematic chain of transformation. In this paper, an A-C rotary type five-axis machine tool is used to illustrate the five-axis kinematics. The A-C type five-axis has a rotary table that rotates about the vertical Z-axes (C-rotation) and a tilting table that turns about the X-axis (A-rotation). Usually, the workpiece is mounted on the rotary table.

The tool path is defined as a piecewise curve passing CL points (cutter location points), which are generated by CAM system, and defined in standardised format (x, y, z, i, j, k), where (x, y, z) is tool tip position and (i, j, k) is the orientation vector. The transform function between axes parameters and CL points coordinates can be found

$$\begin{aligned} \begin{bmatrix} x\\ y\\ z\\ i\\ j\\ k \end{bmatrix} = \begin{bmatrix} C_CP_x+S_CC_AP_y+S_CS_AP_z+L_x \\ -S_CP_x+C_CC_AP_y+C_CS_AP_z+L_y\\ -S_AP_y+C_AP_z+L_z\\ S_CS_A\\ C_CS_A\\ C_A \end{bmatrix} \end{aligned}$$

(1)

In the above equation, $(L_x, L_y, L_z)$ defines the offsets of the pivot point of the two rotary axes A and C relative to the workpiece coordinate system origin and it is a constant vector. $(P_x,P_y,P_z)$ represents the five-axis joint coordinates. A, C are the two rotary coordinates and $S_A, S_C, C_C, C_A$ represent sin(A), sin(C), cos(C), cos(A) respectively.

According to equation Eq. 1, the rotary axis parameters A and C can be calculated directly:

$$\begin{aligned} \begin{aligned} A&=cos^{-1}(k) \quad (0\le A\le \pi )\\ C&=atan2(i,j) \quad (-\pi <C\le \pi ) \end{aligned} \end{aligned}$$

(2)

Combine equation Eq. 2 and Eq. 1, the prismatic axis parameters $(P_x,P_y,P_z)$ can be calculated as follows:

$$\begin{aligned} \begin{aligned} P_x&= C_C(x-L_x)-S_C(y-L_y)\\ P_y&= S_C C_A(x-L_x) + C_C C_A (y-L_y) -S_A(z - L_z)\\ P_z&=S_C S_A(x-L_x) + C_C S_A (y- L_y) + C_A (z - L_z) \end{aligned} \end{aligned}$$

(3)

As $k=\pm \sqrt{1-i^2-j^2}$, the tool path can be represented by $\varvec{r}=(x,y,z,i,j)\in W^5\subset \mathbb {R}^5$ in work space. We denote $\varvec{q}=[q_1,q_2,q_3,q_4,q_5]^{T}\in Q^5 \subset \mathbb {R}^5$ as an axis variable in joint (axes) space, where $q_1,q_2,q_3,q_4,q_5$ represent $P_x,P_y,P_z,A,C$ respectively. The forward kinematic function of five-axis tool machine can be written as follows:

$$\begin{aligned} \varvec{r}= f(\varvec{q})= \begin{bmatrix} C_{q_5}{q_1}+S_{q_5}C_{q_4}q_2+S_{q_5}S_{q_4}q_3+L_x \\ -S_{q_5}q_1+C_{q_5}C_{q_4}q_2+C_{q_5}S_{q_4}q_3+L_y\\ -S_{q_4}q_2+C_{q_4}q_3+L_z\\ S_{q_5}S_{q_4}\\ C_{q_5}S_{q_4} \end{bmatrix}, \end{aligned}$$

(4)

where $f: Q^5 \rightarrow W^5$ is a nonlinear map. The kinematic differential equation can be obtained as follows:

$$\begin{aligned} \dot{\varvec{r}} = J(\varvec{q})\dot{\varvec{q}}, \end{aligned}$$

(5)

where $J(\varvec{q})=\frac{\partial f(\varvec{q})}{\partial \varvec{q}}\in \mathbb {R}^{5\times 5}$ is the Jacobian matrix. Equation 5 represents the relationship between the joint velocities and the cutter point’s velocities.

According to the equation Eq. 4 and Eq. 5, we can also calculate the joint variable $\varvec{q}$ from $\varvec{r}$ and joint velocity $\dot{\varvec{q}}$ from cutter point velocity $\dot{\varvec{r}}$.

$$\begin{aligned} \begin{aligned} \varvec{q}&= f^{-1}(\varvec{r})\\ \dot{\varvec{q}}&= J^{-1}(q)\dot{\varvec{r}} \end{aligned} \end{aligned}$$

(6)

For both equation Eq. 4 and equation Eq. 5, the condition of inverse function consistence is as follows:

$$\begin{aligned} Det(J(\varvec{q}))\ne 0,\nonumber \end{aligned}$$

therefore, the singularity position can be determined by solving the equation $Det(J(\varvec{q}))=0$. The Jacobian matrix in equation Eq. 5 can be calculated directly from equation Eq. 4:

$$\begin{aligned} J(\varvec{q})= \left[ {\begin{array}{ccccc} C_{q_5} &{} S_{q_5}C_{q_4}&{} S_{q_5}S_{q_4}&{}q_3C_{q_4}S_{q_5}-q_2S_{q_4}S_{q_5}&{}q_2C_{q_4}C_{q_5}-q_1S_{q_5}+q_3C_{q_5}S_{q_4} \\ -S_{q_5} &{} C_{q_4}C_{q_5} &{} C_{q_5}S_{q_4} &{} q_3C_{q_4}C_{q_5}-q_2C_{q_5}S_{q_4}&{}-q_1C_{q_5}-q_2C_{q_4}S_{q_5}-q_3S_{q_4}S_{q_5}\\ 0&{} -S_{q_4} &{}C_{q_4}&{} -q_2C_{q_4}-q_3S_{q_4}&{}0\\ 0&{}0&{}0&{}C_{q_4}S_{q_5}&{}C_{q_5}S_{q_4}\\ 0&{}0&{}0&{}C_{q_4}C_{q_5}&{}-S_{q_4}S_{q_5} \end{array} } \right] \end{aligned}$$

(7)

According to the above equation Eq. 7, we get the determinate of $J(\varvec{q})$:

$$\begin{aligned} Det(J(\varvec{q}))=-C_{q_4}S_{q_4}. \end{aligned}$$

(8)

Usually the angle range of $q_4,q_5$ is: $q_4\in [0,\pi ]$, $q_5\in (-\pi ,\pi )$, and the singular points are the points which corresponding to $q_4=0$. In those points $\varvec{r}=(r_1,r_2,r_3,0,0)$, which corresponds to the CL points $(r_1,r_2,r_3,0,0,1)$ in CAM system.

3 Singularity avoidance method

3.1 Inverse kinematics at singularity

Consider curve $\varvec{r}(t)$ that passes through all of the CL points, this curve is called the desired trajectory when cutting across the singular points. While the $Det(J(\varvec{q}))=0$, the analytic solution for $\varvec{q}=f^{-1}(\varvec{r})$ is not defined, and joint variable $\varvec{q}$ cannot be computed according to the given CL points.

It should be noticed that if the joint velocity $\dot{\varvec{q}}$ can be calculated, the joint variable $\varvec{q}$ can be calculated by integrating numerically. If the $\dot{\varvec{q}}$ can be determined more conveniently than $\varvec{q}(t)$, then the inverse kinematics could consider $\dot{\varvec{q}}(t)$ as known, instead of $\varvec{q}(t)$.

To solve the equation Eq. 6, an appropriate inverse of the Jacobian matrix must be applied. The Jacobian Pseudoinverse (JP) algorithm [20] is widely used and a generalized inverse for the Jacobian matrix can be defined as follows:

$$\begin{aligned} J^{+} = J^{T}{(JJ^{T})}^{-1}. \nonumber \end{aligned}$$

Then the joint velocity vector can be calculated by

$$\begin{aligned} \dot{\varvec{q}} = J^{+}(\varvec{q})\dot{\varvec{r}} \end{aligned}$$

(9)

However, when a five-axis machine tool reaches a singularity, the pseudoinverse matrix may have too large condition values. By computing the Singular Value Composition (SVD) of Jacobian matrix J:

$$\begin{aligned} J=U\Sigma V^{T}=\sum _{i=1}^{n}\sigma _i\varvec{u}_i\varvec{v}^{T}_i, \end{aligned}$$

(10)

where $\sigma _i$ is the singular value of $J^{+}$, $\sigma _1\ge \sigma _2\ge \dots \ge \sigma _n\ge 0$, $\varvec{u}_i, \varvec{v}_i$ is the ith column of the matrix U and V. By the equation Eq. 10, the condition number of J is $\kappa (J)=\frac{\sigma _1}{\sigma _n}$. As U and V are orthogonal matrices, then the pseudoinverse of J is

$$\begin{aligned} J^{+}=V\Sigma ^{+}U^{T}=\sum _{i=1}^{n}\frac{1}{\sigma _i}\varvec{v}_i\varvec{u}^{T}_i, \end{aligned}$$

(11)

And then we can find out that the condition number of the pseudoinverse matrix $J^{+}$ is $\kappa (J^{+})=\frac{\sigma _1}{\sigma _n}$, which tends to be infinity at singularity points.

To avoid the big condition number near singular points, the Jacobian Damping (JD) pseudoinverse was proposed in [21,22,23]:

$$\begin{aligned} J^{+}_D ={(J^{T}J+{\lambda }^2I)}^{-1}J^{T}=\sum _{i=1}^{n}\frac{\sigma _i}{{\sigma _i}^2+\lambda ^2}\varvec{v}_i{\varvec{u}^{T}_i}, \end{aligned}$$

(12)

where $\lambda \ge 0$ is the damping factor, I is the identity matrix. Then the solution corresponds to the JD is

$$\begin{aligned} \dot{\varvec{q}}=J^{+}_D\dot{\varvec{r}}={(J^{T}J+{\lambda }^2I)}^{-1}J^{T}\dot{\varvec{r}}. \end{aligned}$$

(13)

Notice that, if $\lambda =0$, then $J^{+}_D=J^{+}$ and it is ill-conditioned near the singularity. It is important to point out that Eq. equationJD satisfies the following equation:

$$\begin{aligned} \min _{\dot{\varvec{q}}} \left\{ {\Vert \dot{\varvec{r}}-J\dot{\varvec{q}}\Vert }^2+\lambda ^2{\Vert \dot{\varvec{q}}\Vert }^2 \right\} \end{aligned}$$

(14)

Since the sum in equation Eq. optimal can be written as follows:

$$\begin{aligned} \left\| \begin{pmatrix} J\\ \lambda I \end{pmatrix} \dot{\varvec{q}} - \begin{pmatrix} \dot{\varvec{r}}\\ 0 \end{pmatrix} \right\| ^2 \end{aligned}$$

(15)

The unique minimizer $\dot{\varvec{q}}$ is given by the solution of normal equation:

$$\begin{aligned} {(J^{T}J+{\lambda }^2I)}\dot{\varvec{q}}=J^{T}\dot{\varvec{r}} \end{aligned}$$

(16)

It can be easily shown that the solution to equation Eq. 16 can be formally written as follows:

$$\begin{aligned} \dot{\varvec{q}}={(J^{T}J+{\lambda }^2I)}^{-1}J^{T}\dot{\varvec{r}}. \end{aligned}$$

(17)

For a five-axis machine tool, the velocity of the C-axes may become very large. In Eq. 14, $\lambda$ is a tradeoff between least-square condition and the least norm condition. In Eq. 14, small values of $\lambda$ will cause a high accuracy solution but low robustness in the neighbor of singularity, while high values of $\lambda$ will result in low accuracy. It is essential to choose a suitable value for $\lambda$.

It is noticed that while the CL point is not in the singular region, the normal inverse can be used directly. A singular region can be defined and the DJ is applied only to the CL point entering the region. To this purpose, an adapted factor damped Jacobian method is proposed in [23]:

$$\begin{aligned} {\lambda }^{2}=\left\{ \begin{array}{ll}0&{} {\sigma }_{n}\ge \epsilon \\ \left( 1-{\left( \frac{{\sigma }_{n}}{\epsilon }\right) }^{2}\right) {\lambda }_{max}^{2}&{} {\sigma }_{n}<\epsilon \end{array}\right. \end{aligned}$$

(18)

where $\sigma _n$ is the minimum singular value of the Jacobian matrix, $\epsilon$ is the width of the singular region, and $\lambda _{max}$ is the maximum allowed damping factor.

Fig. 2

Procedure of the proposed singularity avoidance method and the block scheme corresponding to the feedback control system

3.2 Integrator method

If the initial joint value $\varvec{q}(0)$ is known, the joint position could be computed by integrating velocity over time:

$$\begin{aligned} \varvec{q}(t)=\varvec{q}(0)+\int _{0}^{t}\dot{\varvec{q}}(t)dt \end{aligned}$$

(19)

The integration can be calculated in discrete time by resorting to numerical techniques. The simplest method is based on the Euler integrator method. If the joint positions and velocities at time $t_k$ are known, the joint position at time $t_{k+1}=t_k+\Delta t$ can be computed as follows:

$$\begin{aligned} \varvec{q}_{k+1} = \varvec{q}_k+\dot{\varvec{q}}(t_k)\Delta t. \end{aligned}$$

(20)

However, the $\varvec{q}(t)$ obtained by equation Eq. 20 could not satisfy equation Eq. 4 due to the accumulated error and the integrator error may exceed the preset tolerance. To overcome the drawback, a feedback correction term [24] can be introduced by replacing the end-effector velocity by

$$\begin{aligned} \dot{\varvec{r}}_d+\varvec{Ke}, \end{aligned}$$

(21)

where $\dot{\varvec{r}}_d$ denotes the desired velocity, $\varvec{K}$ is a positive definite matrix, usually a diagonal $5\times 5$ matrix, and $\varvec{e}$ represents the error between the desired and the evaluated CL point: $\varvec{e}(t) = \varvec{r}_d(t)-f(\varvec{q}(t))$. According to the above analysis, the inverse kinematics of the Five-axis machine tools can be written by the equation:

$$\begin{aligned} \left\{ \begin{array}{l}{\varvec{q}}\left( t\right) ={\varvec{q}}\left( 0\right) +{\int }_{0}^{t}\dot{{\varvec{q}}}\left( t\right) dt\\ \dot{{\varvec{q}}}\left( t\right) ={\left( {J}^{T}J+{\lambda }^{2}I\right) }^{-1}{J}^{T}\left( {\dot{{\varvec{r}}}}_{d}+{\varvec{K}}{\varvec{e}}\right) \end{array}\right. \end{aligned}$$

(22)

The equation Eq. 22 can be converted to discrete form:

$$\begin{aligned} \left\{ \begin{aligned} \varvec{e}(t_i)&= \varvec{r}_d(t_i)-f(\varvec{q}(t_i))\\ \dot{\varvec{q}}(t_i)&= {[{J^{T}(\varvec{q}(t_i)) J(\varvec{q}(t_i))+{\lambda ^2(\varvec{q}(t_i))}I]}^{-1}{J^{T}(\varvec{q}(t_i))}[\dot{\varvec{r}}_d(t_i)+\varvec{K}\varvec{e}(t_i)] }\\ \varvec{q}(t_{i+1})&= \varvec{q}(t_{i}) + \Delta t\cdot \dot{\varvec{q}}(t_{i}) \\ (t_i&= \frac{i}{N},\Delta t = \frac{1}{N}, t_0=0, i = 0,1,2,\cdots ,N) \end{aligned} \right. \end{aligned}$$

(23)

The flowchart of the proposed method is shown in Fig. 2

In the equation Eq. 23, $\varvec{e}(t) = \varvec{r}_d(t)-f(\varvec{q}(t))$, which includes both tool tip position error and tool orientation error. $\varvec{r}_d(t)$ is the desired tool position. Slerp is shorthand for spherical linear interpolation. Let $p_0$ and $p_1$ be the first and last points of the arc, and let t be the parameter, $0 \le t \le 1$. Let $\Omega$ is the angle of the arc, and $cos(\Omega )=p_0\cdot p_1$, then the geometric Slerp of the two vectors is as follows:

$$\begin{aligned} Slerp(p_0,p_1;t) = \frac{sin[(1-t)\Omega ]}{sin(\Omega )}p_0+\frac{sin[t\Omega ]}{sin(\Omega )}p_1 \end{aligned}$$

(24)

In fact, a Slerp path is a spherical geodesic. A Quaternion can be used to represent a vector. If we transform normal vectors $p_0, p_1$ to quaternion $q_0,q_1$, then the quaternion Slerp of the two quaternions is as follows:

$$\begin{aligned} Slerp(q_0,q_1;t) = q_0({q^{-1}_0}q_1)^t = ({q^{-1}_1}q_0)^{t}q_0 \end{aligned}$$

(25)

In Fig. 2, the quaternion is used to represent tool orientation. After quaternion Slerp, we use b-spline to interpolate those discrete quaternions, and evaluates the desired velocities $\dot{\varvec{r}}_d(t_i)$.

Fig. 3

Inverse kinematic algorithm with Jacobian Damping (JD) pseudoinverse

Fig. 4

Machining surface in Siemens NX

On the assumption that $J^{+}_D ={(J^{T}J+{\lambda }^2I)}^{-1}J^{T}$, so $J^{+}_D$ is square and nonsingular, while equation

$$\begin{aligned} \dot{\varvec{q}}(t)= J^{+}_D(\dot{\varvec{r}}_d+\varvec{Ke}) \end{aligned}$$

(26)

leads to the equivalent linear system

$$\begin{aligned} \dot{\varvec{e}}+\varvec{Ke} = 0 \end{aligned}$$

(27)

If $\varvec{K}$ is a positive definite (usually diagonal) matrix, the system Eq. 27 is asymptotically stable. The error trends to zero with a convergence rate that depends on the eigenvalues of $\varvec{K}$. The larger eigenvalues, the faster convergence. However, since the system is discrete-time system, there will be a limit for the maximum eigenvalue of $\varvec{K}$ under which asymptotic stability of the error system is guaranteed. The block scheme corresponding to the inverse kinematics algorithm in Eq. 27 is illustrated in Fig. 3, where block $\varvec{K}$ represents the diagonal matrix. The block $J^{+}_D$ represents the JD matrix. The block scheme shows the presence of a string of integrators on the forward loop, which depends on the discrete Euler integration method. Further, the feed forward action provided by $\dot{\varvec{r}}_d$ for a time-varying reference ensures that the error is kept to zero along the whole trajectory. The discrete form of the feed back control system is the equation Eq. 23. For more details, please refer to [25].

Fig. 5

a CL points file generated by Siemens NX CAM systems; b tool paths created by the CL points file, the red tool path corresponds to the circled CL points in (a) and the blue points are the singular points, whose orientation is (0, 0, 1)

Fig. 6

The simulation and real cut result of the NX CAM generated G-codes

4 Simulation and experimental results

In the following examples, the workpiece models are constructed by Siemens NX 12.0 software, and the CL points and the G-codes are generated by the CAM module in the Siemens NX system. Before real cutting, VERICUT software is used to simulate CNC machining. Finally, the whole machining process is verified by an A-C type five-axis machine tool.

The proposed method in this paper is a kinematics-based method. We compared our method with My and Bohez [16] theoretically. And the inverse kinematics system in [16] is as follows:

$$\begin{aligned} \left\{ \begin{aligned} \varvec{q}(t)&= \varvec{q}(0) + \int _{0}^{t}\dot{\varvec{q}}(t) dt \\ \dot{\varvec{q}}(t)&= J^{+}(\dot{\varvec{r}}_d+\varvec{Ke}), \end{aligned} \right. \end{aligned}$$

(28)

where $J^{+}={(J^{T}J)}^{-1}J$. As it is discussed in Sect. 3.1, the condition number of the pseudoinverse matrix $J^{+}$ is $\kappa (J)=\frac{\sigma _1}{\sigma _n}$, which tends to be infinity at singular points, and it not suit for our experiments. According to the conclusion in [26], $\lambda$ should have a high value to avoid the maximum $\frac{1}{2\sigma }$ of the condition number at $\sigma _n=\lambda$, but on the other hand, $\lambda$ must also have a very small value to avoid conditioning tends to infinity as $\sigma _n$ decreases. By those reasons, we choose the adapted factor damped Jacobian method. The maximum damped factor $\lambda _max = 0.001$, and it’s an empirical numbers.

4.1 Experiment 1

The workpiece is a cylinder with a height of 80 mm and a diameter of 40 mm and the origin of the workpiece coordinate system is the center of the upper circle of the cylinder, which is shown in Fig. 4(a). The model is generated by boolean operation of two cylinders and it is shown in Fig. 4(b).

In this example, the coordinate of the rotary center of the A-C axis in a 5-axis tool machine is $(0,0,-108)$. A ball nose end cutter R2 (radius 2 mm) is selected. The feed rate is constant and it is 250mm/min.

In the Siemens NX CAM systems, the zigzag tool path pattern is applied and the tool direction parallels the surface normal. The singular points can be found in the neighbor of the middle points in each tool path. The CL points are outputted by the Siemens NX CAM systems, and the CL points including singular points are detailed in Fig. 5.

Based on the CL points, the tool tip can be computed using the inverse kinematic method as usual.

The CL points are used to evaluate the 5-axis joint parameters, and G-code is created by the result of the postprocessor. We find that the postprocessor in Siemens NX CAM systems is based on the inverse kinematic equation (2) and (3).

In the NX CAM generated G-codes, the C rotary axis changes from $180^{\circ }$ to $0^{\circ }$ and then changes to $180^{\circ }$ from $0^{\circ }$ and repeat this process. In the actual machine process, the sudden changes of C-axes cause the machine error, which is shown in Fig. 6.

Fig. 7

The deviation between the proposed method and the original 25 CL points when each adjacent point is divided into 50 segments. a The maximum tool tip error is $8.8446\times 10^{-4}mm$, the average tool tip error is $2.0449\times 10^{-4}mm$; b the maximum tool orientation error is $6.2862\times 10^{-5}rad$, the average tool orientation error is $9.6662\times 10^{-6}rad$

Fig. 8

The red line is the angle of the C rotary axis and the blue line is the angle of the A rotary axis. The horizontal coordinate represents the order of CL points and the vertical coordinate represents the degree of the rotary axis

Fig. 9

The blue line is the initial velocity of the A-C axis, and the red line is the velocity of the A-C axis with the proposed method. The horizontal coordinate represents the order of CL points and the vertical coordinate represents the angular velocity

Fig. 10

The simulation and real cut results of the proposed method

Fig. 11

Machining surface in Siemens NX

Fig. 12

a CL points file generated by Siemens NX CAM systems; b tool paths created by the CL points file, the red tool path corresponds to the circled CL points in (a) and the blue points are the singular points, whose orientation is (0, 0, 1)

Fig. 13

The deviation between the proposed method and the original 21 CL points when each adjacent point is divided into 50 segments. a The maximum tool tip error is $4.8516\times 10^{-4}mm$, the average tool tip error is $1.9456\times 10^{-4}mm$; b the maximum tool orientation error is $1.0908\times 10^{-5}rad$, the average tool orientation error is $1.9214\times 10^{-6}rad$

Fig. 14

The deviation between the proposed method and the original 21 CL points when each adjacent point is divided into 100 segments. a The maximum tool tip error is $1.8669\times 10^{-4}mm$, the average tool tip error is $9.4322\times 10^{-5}mm$; b the maximum tool orientation error is $6.5500\times 10^{-5}rad$, the average tool orientation error is$1.1011\times 10^{-6}rad$

Fig. 15

The red line is the C axis and the blue line is the A axis. The horizontal coordinate represents the order of CL points and the vertical coordinate represents the degree of the rotary axis. The number of the CL points is 841, and the number of the CL points is 21

The VERICUT software is used to simulate the G-code, and we find the cut path includes some circles in Fig. 6. The five-axis machine tool used in this example doesn’t have the RTCP (Rotation Tool Center Point) function, those circles are the overcut part, which is caused by the sudden changes in the C-axis. In Fig. 5(b), there are 25 points on the selected tool path. B-spline is used to interpolate the positions coordinate of the tool path and quaternion is used to represent the orientations, then quaternion slerp (spherical linear interpolation) is used to interpolate two adjacent orientations.

In equation Eq. 23, the damping factor $\lambda$ is evaluated directly by the equation Eq. 18. In this equation, $\epsilon$ and $\lambda _{max}$ represent the width of the singular region and maximum allowed damping factor respectively. Based on the paper [26], we set $\epsilon = \lambda _{max}=0.001$.

In this example, the diagonal matrix K is set to be $200*diag[1,1,1,4,4]$. The $\varvec{r}_d(t_i)$ and $\dot{\varvec{r}}_d(t_i)$ are evaluated by B-spline interpolation and quaternion Slerp.

The tool tip error and tool orientation error compared with the original 25 CL points is shown in Fig. 7. In Fig. 7, horizontal ordinate t is the parameter of B-spline. In this experiment, each adjacent point is divided into 50 segments. In Eq. 23, $N = 24\times 50=1200$, $\Delta t = \frac{1}{N}=\frac{1}{1200}$ and $t\in [0,1]$. The maximum tool tip error is $8.8446\times 10^{-4}mm$ and the maximum tool orientation error is $6.2862\times 10^{-5}rad$, which is small enough for the real five-axis machine tool.

In this example, each tool path has one singular point. The proposed method can also be used for all tool paths, and the A-C values can be optimized globally.

In Fig. 8(a), the C axis changes suddenly in each singular point, while in Fig. 8(c), the C axis almost keeps constant. By comparing Fig. 8(b) and Fig. 8(d), it is easy to find that function A-C axis changes smoothly when crossing the singular point.

The velocity of the A-C axis after optimization is shown in Fig. 9. In original G-codes, the C axis changes abruptly in singular points. While with the proposed method, the angular velocity of the C axis has decreased significantly.

In Fig. 10(b), there is the real cut result of the proposed method. Compared with Fig. 6, the real cut result with the proposed method is better.

Fig. 16

The blue line is the initial velocity of the A-C axis, and the red line is the velocity of the A-C axis with the proposed method. The horizontal coordinate represents the order of CL points and the vertical coordinate represents the angular velocity

Fig. 17

The simulation and real cut results

4.2 Experiment 2

The machining surface is designed in Siemens NX software and it is presented in Fig. 11. The model is generated by Boolean operation between a ball and a cylinder, which is shown in Fig. 11(b).

The CL points including singular points are shown in Fig. 12.

In this example, there is only one singular point, however, the C rotary axis still changes abruptly in each tool path, which is shown in Fig. 15(a). In this example, we also set $\epsilon = \lambda _{max}=0.001$, $\varvec{K}$=100*diag[1,1,1,4,4]. There are 21 points on the selected tool path and each adjacent point is divided into 50 segments. The tool tip error and tool orientation error compared with the original 21 CL points is shown in Fig. 13. In Fig. 13, the horizontal ordinate is the parameter of B-spline, and $t\in [0,1]$. In this experimental, $N=20\times 50=1000$, $\Delta t=\frac{1}{N}=\frac{1}{1000}$. The maximum tool tip error is $4.8516\times 10^{-4}mm$ and the maximum tool orientation error is $1.0908\times 10^{-5}rad$, which is small enough for the real five-axis machine tool.

The accuracy can also be improved by dividing the adjacent points into more segments. In Fig. 14, the adjacent points are divided into 100 segments, the maximum tool tip error decreases to $1.8669\times 10^{-4}mm$ and the maximum tool orientation error decreases to $6.5500\times 10^{-5}rad$.

The proposed method can also be used for all of the 841 CL points, and the A-C axis values are optimized. In Fig. 15(a), the C axis changes abruptly in each tool path, while in Fig. 15(c), the C axis almost keep constant. By comparing Fig. 15(b) and Fig. 15(d), it is easy to find that C axis changes smoothly when crossing the singular point. The feed rate is set to be 250mm/min, and the velocity of A-C axis with the proposed method is shown in Fig. 16.

In Fig. 17(a), the part circled by the red rectangular is the region with singular points. In Fig. 17(b), there are the simulation and real cut results of the proposed method. The result with the proposed method is smoother than the original result, which verifies the effect of the proposed method.

5 Conclusion

The whole machining process is verified by an A-C type five-axis machine tool. While the orientation of the rotation axis is parallel to the tool direction, the exact solution of the inverse kinematics equation does not exist. Then B-C and A-B type machines also have the singular phenomenon. In the singular points, the Jacobi matrix will be singular or ill-conditioned. This paper proposed a kinematic-based method to avoid singularity for five-axis machine tools by using Jacobian Damping (JD) pseudoinverse, which is suit for all kinds of ill-conditioned problems. And it is natural that the proposed method can be extended to A-B and B-C type machines. The main contributions are as follows:

• (1) Jacobian Damping pseudoinverse technology is first used to overcome the ill-condition problem in the five-axis machine tool.

• (2) The method optimizes the joint velocities, which means it not only avoids singularity but also makes the rotary axis smoother, and it is shown in the previous two experiments.

• (3) Experimental results confirm that the tool tip error and tool orientation error are small enough and the real cut results prove the effectiveness of the proposed method.

This paper provides a general inverse kinematics method for CL points near singular region and the rotary axis can be optimized by a discrete integrator. However, the kinematics method in this paper considers only pose errors. Further improvement can be achieved by taking the acceleration limit into consideration, and the feedback integrator method will be extended to a second-order integrator. In the future, we will extend our kinematics method by considering above aspects to develop better machining strategy.