Piecewise modeling and compensation of geometric errors in five-axis machine tools by local product of exponentials formula

Abstract

Until now, most integrated geometric error models of five-axis machine tools ignore the influence of the backlash, which does affect the machining accuracy for complex curved workpieces. This paper proposes a piecewise geometric error modeling and compensation method to reduce the influence from the backlash and other error sources in five-axis machine tools, only based on the measurement of distance variation in the tool end. By utilizing the local product of exponentials (POE) formula, kinematic errors are lumped into initial poses’ deviations, and joint twists retain their nominal values. In this way, extra orthogonalization and normalization of joint twists are not required throughout the identification process, thus promoting the model’s accuracy. In addition, the damping factor is introduced in the identification process to cater for the kinematic error model with redundant parameters, which guarantees the robustness of the least square method in the presence of noisy data. To improve the accuracy of bidirectional motion of the tilting table, the kinematic error model is further revised to be piecewise, where the gear backlash is naturally integrated into deviations of initial poses, depending on the rotational direction. The simulation and experimental results demonstrate the effectiveness and superiority of the proposed method.

1 Introduction

The five-axis machine tool, which includes two rotational axes on top of its three-axis counterpart [1], has become core equipment for processing parts with complex curved surface [2]. However, due to the existence of geometric errors, the machining accuracy is greatly reduced [3, 4]. In general, geometric errors can be classified as position independent geometric errors (PIGEs) and position dependent geometric errors (PDGEs) [5]. PIGEs are caused by inaccurate assembly of machine parts, such as joint misalignments and angular offset, which can be approximately treated as constants. PDGEs are mainly from imperfect manufacturing of machine parts, such as bending of guideways and backlash of gears [6]. PIGEs are the main factors affecting the quality of machining parts [7], while PDGEs caused by gear backlash degrade the accuracy of reciprocating motion of machine tools significantly [8]. Hence, modeling and compensating geometric errors are essential to improve machining accuracy of five-axis machine tools [9,10,11].

Until now, various methods have been developed to model the geometric error, which include homogeneous transformation matrix (HTM) method [12, 13], Denavit-Hartenberg (D-H) convention [14] and screw theory [15]. Though HTM method is widely used in the calibration of machine tools, kinematic error terms need to be measured by the laser interferometry system [16], which is time-consuming. Meanwhile, the geometric error model obtained by D-H convention is not continuous when axes of consecutive joints are nearly parallel. In recent decades, the global product of exponentials (POE) formula based on the screw theory is used to model geometric errors of five-axis machine tools [17, 18]. It describes the coordinates of joint twists in a global frame. However, additional errors are induced during the orthogonalization and normalization of joint twists throughout the identification process. Such errors may be reduced by utilizing the global POE based on the common perpendicular line transformation [19], which, however, complicates the identification procedures [20].

Unlike global POE formula, the local POE formula is to express the coordinates of joint twists in the local frames [21, 22]. As the kinematics errors are lumped into deviations of initial poses of local frames, the joint twists are set at their nominal values throughout identification process. This not only greatly simplifies the calibration model, but also avoids above orthogonalization and normalization process [23, 24]. As it is difficult to obtain the tool pose for five-axis machine tool, the geometric error model based on the pose information as in [21] is not directly applicable. In contrast, the distance variation is easy to be measured by the double ballbar [18, 19, 25]. Hence, it is worthy to deduce the error model based on local POE formula related to the distance information. General methods include Extended Kalman Filter (EKF) algorithm [26] and the Gauss-Newton iteration method [18, 19, 27] are proposed to identify the geometric error parameters [20]. However, complex identification process limits the application of EKF method. If Gauss-Newton iteration method is used for parameter identification, they may not converge in the presence of large noise due to the existence of redundant parameters in the kinematic error model. Therefore, it is still a challenge to propose a concise and robust identification method for the geometric error.

The geometric error can be effectively compensated by utilizing the inverse kinematics of the calibrated model. Analytical models are deduced for compensating PIGEs [18] or both PIGEs and PDGEs [28] based on global POE formula. Such approaches may bring calculation error, as the geometric premise of Paden-Kahan subproblems may not be applicable for actual machine tools. Hence, linearized models that regard geometric errors and joint displacement increments as linear are developed for compensating PIGEs [29, 30]. Besides PIGEs, PDGEs have also been taken into consideration [31]. One typical PDGE is the error caused by gear backlash [32]. The gear backlash may lead to the steady-state offset, affecting the machining accuracy of complex curved surface in reciprocating motion [33]. Such error can be effectively reduced by using high-precision transmission parts, which, however, rises the cost sharply [34]. The mathematical model of the backlash has been built to reveal its nonlinear behavior [35]. However, it is time-consuming to measure such error existing in every axis of the machine tools by laser interferometers [36], and the fitting process for such a data-driven model is tedious too [37]. Thus, it is desirable to compensate the PDGEs induced by backlash without prior modeling process.

In this paper, a geometric error model of five-axis machine tools is established based on the local POE formula, where only the distance measurement from the workpiece to the tool is utilized. Compared with the recent modeling methods based on the global POE formula [17, 18], orthogonalization and normalization of joint twists are avoided throughout the identification process by assuming joint twists retain their nominal values. This gives a more accurate model. To prevent the divergence of redundant kinematic error parameters in the presence of large measurement noise as mentioned in [22], an iterative least squares method with damping factor is proposed. In addition, to compensate the error caused by gear backlash without tedious nonlinear modeling process as in [35], a piecewise kinematic error compensation method is proposed accordingly to the motion directions of rotational axes. This also improves the efficiency of backlash-induced error compensation compared with such error is compensated by using the laser interferometer in [36]. The simulation and experiments prove the effectiveness and superiority of the proposed method.

The description of various symbols used in this work is shown in Table 1.

Table 1 Nomenclature

2 Kinematics model based on the local POE formula

As the prerequisite of subsequent model-based compensation of kinematic error, the kinematics model of serial five-axis machine tools based on the local POE formula is introduced in this section.

2.1 Introduction of the local POE formula

Consider an n-link series chain system, two adjacent links $i-1$ and i are connected by joint i as shown in Fig. 1, such a combination is called dyad. After the joint i rotates the angle $\theta _i$, the position and orientation of the local frame $\{i\}$ with respect to (w.r.t.) the local frame $\{i-1\}$ is expressed as

$$\begin{aligned} {T_{i - 1,i}}({\theta _i}) = {T_{i - 1,i}}(0)e^{ {\hat{\xi }}_i \theta _i }, \end{aligned}$$

(1)

where ${T_{i - 1,i}(0)}$ describes the initial pose of frame $\{i\}$ w.r.t. frame $\{i-1\}$, $\hat{\xi }_i$ represents the twist of joint i expressed in frame $\{i\}$, and $\theta _i$ is the ith joint displacement.

Fig. 1

Pose relationship between any two adjacent joints

According to the definition of matrix logarithm, there exists at least an element of $\hat{h}\in se(3)$ for a given $T\in SE(3)$ such that $T_{i - 1,i}(0)=e^{\hat{h}_i}$, where SE(3) is a special Euclidean group, and se(3) is the Lie algebra of SE(3). Hence, ${T_{i - 1,i}}(0)$ is written as

$$\begin{aligned} T_{i - 1,i}(0) =\begin{bmatrix} R_{i - 1,i}\left( 0 \right) &{} p_{i - 1,i}\left( 0 \right) \\ 0&{}1 \end{bmatrix}=e^{\hat{h}_i}, \end{aligned}$$

(2)

where $R_{i-1,i}(0)$ and $p_{i - 1,i}(0)$ are the initial orientation and position of frame $\{i\}$ w.r.t frame $\{i-1\}$, $e^{\hat{h}_i}$ is the initial pose of frame $\{i\}$ w.r.t frame $\{i-1\}$. Remarkably, the initial pose of frame $\{i-1\}$ w.r.t. frame $\{i\}$ is written as $T_{i,i-1}(0)=e^{\hat{h}_{i-1}}$.

The element of se(3) is represented by a general matrix as

$$\begin{aligned} \hat{\xi }= \begin{bmatrix} \hat{\omega }&{} v\\ 0 &{} 0 \end{bmatrix}\in \mathrm {R}^{4 \times 4}, \end{aligned}$$

(3)

where the axis of rotation is $\omega = {[\omega _x, \omega _y,\omega _z]}^T \in {R ^{3 \times 1}}$, $\hat{\omega }\in se(3)$ is denoted as the skew-symmetric matrix of $\omega$, $v = {[v_x,v_y,v_z]}^T=-\omega \times q \in R^{3 \times 1}$ demonstrates the spatial position of the axis, $q\in R^{3\times 1}$ is an arbitrary point on the axis. $\hat{\xi }$ can be transformed into $\xi$ by the operator $\vee$, and the inverse operator $\wedge$ can change $\xi$ into $\hat{\xi }$, as given in Appendix Joint twist. For the twist $\xi =(v;\omega )$ of a revolute joint, $\left\| \omega \right\| \mathrm{{ = }}1, \omega ^{T}v=0$. For the twist $\xi =(v;0)$ of a prismatic joint, $\omega = 0, \left\| v \right\| = 1$.

2.2 Nominal forward kinematics model

The nominal forward kinematics model is utilized to obtain the tool pose $\chi$ in workpiece frame $\{w\}$ when the joint displacements $\theta$ in the base frame $\{b\}$ are given. As shown in Fig. 2, the AC table-tilting five-axis machine tool is selected as the example to demonstrate the modeling process based on the local POE formula. Remarkably, the following modeling method is also applicable to other types of machine tools.

Fig. 2

3D model of AC table-tilting five-axis machine tool

For our 5-axis machine tool, there are 2 joints in the workpiece side and 3 joints in the tool side. By setting the machine frame $\{m\}$ as the base frame $\{b\}$, two open kinematic chains are formed as shown in Fig. 3. The prerequisite of using the local POE formula is to define the local frames. One of the advantages of the local POE formula is that local frames can be arbitrarily defined in their respective links. Therefore, to make the initial poses of adjacent local frames as simple as possible, the conventions that set the local frames of the AC table-tilting five-axis machine tools are given as

• The origin of frame $\{b\}$ is fixed at the tool tip, and the origins of frame $\{w\}$, the tool frame $\{t\}$ and frames $\{x\}$, $\{y\}$ and $\{z\}$ are set to coincide with the origin of frame $\{b\}$. The origins of local frames $\{a\}$ and $\{c\}$ in two rotational axes are set to coincide with their intersection. This gives initial positions of adjacent local frames.

• The orientations of other local frames are set to be the same as that of frame $\{b\}$. This gives initial orientations of adjacent local frames.

Fig. 3

Kinematics chain of AC table-tilting five-axis machine tool

To match the theory in Sect. 2.1, the index of frame $\{b\}$ is denoted as 0. The indexes of frames in the open chain that is from frame $\{b\}$ to frame $\{t\}$ are positive, otherwise, the indexes of frames are negative. Therefore, as shown in Fig. 3, we can denote $i\in \{-3,-2,-1,0,1,2,3,4\}\triangleq \{w,c,a,b,y,x,z,t\}$. In this way, the kinematics model of frame $\{t\}$ w.r.t. frame $\{b\}$ is given as

$$\begin{aligned} \begin{aligned} T_{b,t}&=T_{0,1}(0) e^{\hat{\xi }_y \theta _y} T_{1,2}(0) e^{\hat{\xi }_x \theta _x} T_{2,3}(0) e^{\hat{\xi }_z \theta _z} T_{3,4}(0)\\ &=e^{\hat{h}_y} e^{\hat{\xi }_y \theta _y} e^{\hat{h}_x} e^{\hat{\xi }_x \theta _x} e^{\hat{h}_z} e^{\hat{\xi }_z \theta _z} e^{\hat{h}_t}, \end{aligned} \end{aligned}$$

(4)

Similarly, the kinematics model of frame $\{w\}$ w.r.t. frame $\{b\}$ is given by

$$\begin{aligned} \begin{aligned} T_{b,w}&=T_{0,-1}(0) e^{\hat{\xi }_a \theta _a} T_{-1,-2}(0) e^{\hat{\xi }_c \theta _c} T_{-2,-3}(0) \\ &=e^{\hat{h}_a} e^{\hat{\xi }_a \theta _a} e^{\hat{h}_c} e^{\hat{\xi }_c \theta _c} e^{\hat{h}_w}. \end{aligned} \end{aligned}$$

(5)

Combining (4) and (5), the nominal forward kinematics model of AC table-tilting five-axis machine tool is expressed as

$$\begin{aligned} \begin{aligned} T_{w,t}(\theta )&=e^{-\hat{h}_w} e^{ - \hat{\xi }_c \theta _c} e^{-\hat{h}_c} e^{ - \hat{\xi }_a \theta _a} e^{ -\hat{h}_a} e^{\hat{h}_y} e^{\hat{\xi }_y\theta _y} e^{\hat{h}_x} e^{\hat{\xi }_x \theta _x} e^{\hat{h}_z} e^{\hat{\xi }_z \theta _z} e^{\hat{h}_t}, \end{aligned} \end{aligned}$$

(6)

where $\theta = (\theta _x,\theta _y,\theta _z,\theta _a,\theta _c)$ are denoted as the joint displacements in frame $\{b\}$. The twist coordinates $\xi$ and the vectors of the initial pose $h_j$ are given by

$$\begin{aligned} \xi _x &=(1, 0, 0, 0, 0, 0)^T, \xi _y =(0, 1, 0, 0, 0, 0)^T,\\ \xi _z &=(0, 0, 1, 0, 0, 0)^T, \xi _a =(0, 0, 0, 1, 0, 0)^T,\\ \xi _c &=(0, 0, 0, 0, 0, 1)^T, h_{j} =(x_{j}, y_{j}, z_{j}, 0, 0, 0)^T, \end{aligned}$$

where $j\in \{w,c,a,y,x,z,t\}$.

Hence, the tool pose $\chi =[p_w;r_w]$ in frame $\{w\}$ is

$$\begin{aligned} \begin{bmatrix} p_w &{} r_w\\ 1 &{} 0 \end{bmatrix}= T_{w,t} (\theta ) \begin{bmatrix} p_t &{} r_t\\ 1 &{} 0 \end{bmatrix}, \end{aligned}$$

(7)

where $p_w\in R^{3\times 1}$, $r_w\in R^{3\times 1}$ are denoted as the position and the orientation of the tool in frame $\{w\}$, respectively. $p_t=[0,0,0]^T$ is the position of the tool in frame $\{t\}$, and $r_t=[0,0,1]^T$ is the orientation of the tool in frame $\{t\}$.

2.3 Actual kinematics for the five-axis machine tool

Due to the existence of kinematic errors, the tool poses cannot be accurately obtained by the nominal kinematics model with the nominal joint displacements. The errors may due to the deviations of joint twists, initial poses and joint displacements [21], such deviations are denoted as $\delta \xi$, $\delta h$, and $\delta \theta$, respectively. The actual kinematics of AC table-tilting five-axis machine tool is expressed as $T_{w,t}^\mathrm {a}=f(\xi ^\mathrm {a},h^\mathrm {a},\theta ^\mathrm {a})$, where $(\bullet )^\mathrm {a}$ denotes the actual value of the respective variable $(\bullet )$.

2.3.1 Actual joint twists $\xi ^\mathrm {a}$

To analyze factors of PIGEs in joint twists, the following procedures are proposed in [38] to construct five actual axes $\rho ^\mathrm {a}$, where $\rho \in \{x,y,z,a,c\}$.

Firstly, as the direction of $x^\mathrm {a}$-axis is set to be coincided with the direction of the x-axis, there is no error in $x^\mathrm {a}$-axis. Whereas the $y^\mathrm {a}$-axis is not perpendicularity to the x-axis, there is an angular error $\varepsilon _{zy}$ around z in the plane determined by x- and y-axes. For $z^\mathrm {a}$-axis, there are two angular errors include $\varepsilon _{xz}$ around x-axis and $\varepsilon _{yz}$ around y-axis.

Additionally, $a^{\mathrm {a}}$- or $c^\mathrm {a}$-axes has two angular error components. As the $a^\mathrm {a}$-axis can rotate $\varepsilon _{ya}$ around y-axis and rotate $\varepsilon _{za}$ around z-axis, the angular errors exists for the $c^\mathrm {a}$-axis including $\varepsilon _{xc}$ around x-axis and $\varepsilon _{yc}$ around y-axis. Nominally, the a-axis and the c-axis intersect perpendicularly. However, the $a^\mathrm {a}$-axis and the $c^\mathrm {a}$-axis may not intersect due to the installation error. Taking the $a^\mathrm {a}$-axis as the reference, the $c^\mathrm {a}$-axis has a distance deviation $\delta _{yc}$ along the direction of y-axis.

Remarkably, $\Vert \omega _\rho + \delta \omega _\rho \Vert = 1$, and $( \omega _\rho + \delta \omega _\rho )^T ( v_\rho + \delta v_\rho ) = 0$ for revolute joints. $\Vert v_\rho + \delta v_\rho \Vert = 1$ for the prismatic joints [19]. Therefore, the actual twists of revolute and prismatic joints $\xi _\rho ^\mathrm {a}=(v_\rho ^\mathrm {a};\omega _\rho ^\mathrm {a})$ are constructed as

$$\begin{aligned} \begin{aligned} \xi _x^\mathrm {a} =& \ (1,0,0,0,0,0)^T,\\ \xi _y^\mathrm {a} =& \ (- \sin \varepsilon _{zy}, \cos \varepsilon _{zy},0,0,0,0)^T,\\ \xi _z^\mathrm {a} =& \ (\sin \varepsilon _{yz}, - \sin \varepsilon _{xz} \cos \varepsilon _{yz}, \cos \varepsilon _{xz} \cos \varepsilon _{yz},0,0,0)^T,\\ \xi _a^\mathrm {a} =& \ (0,0,0,\cos \varepsilon _{ya} \cos \varepsilon _{za},\sin \varepsilon _{za}, - \sin \varepsilon _{ya} \cos \varepsilon _{za})^T, \\ \xi _c^\mathrm {a} =& \ (\delta _{yc} \cos \varepsilon _{xc} \cos \varepsilon _{yc}, 0, -\delta _{yc}\sin \varepsilon _{yc}, \sin \varepsilon _{yc}, \\&- \sin \varepsilon _{xc} \cos \varepsilon _{yc}, \cos \varepsilon _{xc} \cos \varepsilon _{yc})^T. \end{aligned} \end{aligned}$$

2.3.2 Actual initial poses $h^\mathrm {a}$ and joint displacements $\theta ^\mathrm {a}$

The initial pose matrix in the entire kinematic chain as shown in Fig. 3 is $e^{\hat{h}_j}$. Denote $\delta {h_j} \triangleq (\delta {x_j}, \delta {y_j}, \delta {z_j},\delta {\alpha _j},\delta {\beta _j}, \delta {\gamma _j})^T$ to be the deviations of the initial pose, so the actual initial pose matrix is expressed as $e^{\hat{h}_j^\mathrm {a}}=e^{\hat{h}_j}e^{\hat{\delta {h_j}}}$. In addition, denote $\delta {\theta } \triangleq (\Delta {\theta _x},\Delta {\theta _y},\Delta {\theta _z},\Delta {\theta _a},\Delta {\theta _c})$ to be the deviation between the nominal and actual joint displacements, so the actual joint displacements are given as $\theta ^\mathrm {a}=\theta +\delta \theta$.

3 Modeling and parameter identification of kinematic errors

3.1 Basic ideas

By differentiating the forward kinematic model $T=f(\xi , h, \theta )$, and right-multiplying $T^{-1}$, the model of kinematic errors is obtained as

$$\begin{aligned} \delta T \cdot T^{-1} = \left( \frac{\partial f}{\partial \xi }\delta \xi + \frac{\partial f}{\partial h} \delta h + \frac{\partial f}{\partial \theta } \delta \theta \right) T^{-1}. \end{aligned}$$

(8)

For such an error model, there are 13 error parameters in the ith dyad, that is, 6 in $\xi _i$, 6 in $h_i$, and 1 in $\theta _i$. That makes the parameters in the kinematic error model be highly redundant, which increases the complexity of the error model in the identification process. Since the error of a screw can be expressed as the error in terms of its initial pose by the adjoint transformation [39], as given in Appendix Adjoint transformation. Hence, to simplify (8), kinematic error terms in the ith dyad are assumed to be lumped into $h_i$, while $\xi _i$ and $\theta _i$ retain their nominal values during the entire calibration process [21]. This yields,

$$\begin{aligned} \delta T \cdot T^{-1} = \frac{\partial f}{\partial h}\delta h\cdot T^{-1}, \end{aligned}$$

(9)

The purpose of parameter identification is to find a set of suitable parameters $\delta h$ to minimize the difference between the estimated end pose from the calibrated model and the actual end pose by measurement, i.e.

$$\begin{aligned} \min {\left\| {\delta T \cdot T^{-1}-\frac{\partial f}{\partial h}\delta h \cdot T^{-1}}\right\| }^2. \end{aligned}$$

(10)

3.2 Modeling of kinematic errors

The kinematic error model is derived based on the forward kinematics model of the AC table-tilting five-axis machine tool in (6).

3.2.1 Kinematic error model based on pose error

As the propose of error modeling is to identify parameters of kinematic errors that are lumped into the initial pose $h_j$, we can take the partial derivative of (6) w.r.t. $\hat{h}_j$, $\forall j\in \{w,c,a,y,x,z,t\}$, yielding

$$\begin{aligned} \begin{aligned} \delta T_{w,t} =&-e^{-\hat{h}_w}\delta \hat{h}_w e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a} e^{\hat{h}_y}e^{\hat{\xi }_y\theta _y}\\&e^{\hat{h}_x}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z}e^{\hat{\xi }_z\theta _z}e^{\hat{h}_t}-e^{ -\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c}\delta \hat{h}_c \\&e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a}e^{\hat{h}_y}e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z}e^{\hat{\xi }_z\theta _z}e^{\hat{h}_t}+\\&\cdots + e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a}e^{\hat{h}_y}e^{\hat{\xi }_y\theta _y} \\&e^{\hat{h}_x}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z}e^{\hat{\xi }_z\theta _z}e^{\hat{h}_t} \delta \hat{h}_t, \end{aligned} \end{aligned}$$

(11)

By multiplying of both sides of (11) by $T_{w,t}^{-1}$, the kinematic error model of the five-axis machine tool is obtained as

$$\begin{aligned} \begin{aligned} \left( \delta T_{w,t}T_{w,t}^{-1}\right) ^\vee =& \ [-e^{-\hat{h}_w}\delta \hat{h}_w e^{\hat{h}_w}]^\vee - [e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}\\& \ e^{-\hat{h}_c} \delta \hat{h}_c e^{\hat{h}_c}e^{\hat{\xi }_c\theta _c}e^{\hat{h}_w}]^\vee +\cdots +\\&[e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c} e^{-\hat{h}_c}\cdots e^{\hat{h}_t}\delta \hat{h}_t e^{-\hat{h}_t} \\&\cdots e^{\hat{h}_c}e^{\hat{\xi }_c\theta _c}e^{\hat{h}_w}]^\vee \\ =&-\mathrm{Ad}_{e^{-\hat{h}_w}}\delta h_w -\mathrm{Ad}_{e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c}}\\&\delta h_c + \cdots +\mathrm{Ad}_{e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c} \cdots e^{\hat{h}_t}}\\&\delta h_t. \end{aligned} \end{aligned}$$

(12)

Meanwhile, according to the matrix logarithm formula defined on SE(3),

$$\begin{aligned} \left( \delta T_{w,t}T_{w,t}^{-1}\right) ^\vee =\log \left( T_{w,t}^\mathrm{a}T_{w,t}^{-1} \right) ^ \vee , \end{aligned}$$

(13)

where $T_{w,t}$ is the nominal kinematics model, and $T_{w,t}^\mathrm{a}$ is the actual kinematics model of the five-axis machine tool. In this way, (12) is given in the form of matrix multiplication as

$$\begin{aligned} \begin{aligned} \log \left( T_{w,t}^\mathrm{a}T_{w,t}^{-1} \right) ^\vee =& \ [-\mathrm{Ad}_{g_w}, -\mathrm{Ad}_{g_c}, \cdots ,\mathrm{Ad}_{g_t} ]\\&\cdot \begin{bmatrix} \delta h_w^T, \delta h_c^T, \cdots , \delta h_t^T \end{bmatrix}^T, \end{aligned} \end{aligned}$$

(14)

where $g_w=e^{-\hat{h}_w}; g_c=e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c}; g_t=e^{-\hat{h}_w}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c} \cdots e^{\hat{h}_t}$. (14) is indeed a linear equation as

$$\begin{aligned} y=J \cdot \phi , \end{aligned}$$

(15)

where $y = \log \left( T_{w,t}^\mathrm{a}T_{w,t}^{-1}\right) ^\vee \in R^{6 \times 1}$ is the pose error vector of the tool, $J = [- \mathrm{{Ad}}_{g_w},-\mathrm{{Ad}}_{g_c}, \cdots , \mathrm{{Ad}}_{g_t}]\in R^{6 \times 42}$ is the Jacobian matrix in terms of initial poses related to y, $\phi = \left[ \delta h_w^T,\delta h_c^T, \cdots , \delta h_t^T \right] ^T \in R^{42 \times 1}$ is the parameter vector of PIGEs.

3.2.2 Kinematic error model based on position error

Due to the insufficient resolution and limited range of orientation measurement, it is difficult to obtain the actual pose of the tool by the laser tracker. By contrast, the double ballbar is frequently used to obtain the dynamic accuracy of machine tools, and it measures the distance variation along its axial direction. Therefore, the error model in (15) can be converted to its counterpart solely based on the distance variation. In the following part, the kinematic error model based on the position information is firstly derived, and it is further converted to the model solely based on distance variation.

According to (7), the transformation from $p_w$ to $p_t$ is given by

$$\begin{aligned} \bar{p}_w=T_{w,t}\bar{p}_t, \end{aligned}$$

(16)

where $(\bar{\bullet })=[(\bullet );1]$. In addition, by differentiating both sides of (16),

$$\begin{aligned} \delta \bar{p}_w = \delta T_{w,t}\bar{p}_t + T_{w,t} \delta \bar{p}_t, \end{aligned}$$

(17)

where $\delta (\bar{\bullet })=[\delta (\bullet ); 0 ]$.

Since the tool frame is fixed at the tool tip, $p_t$ is the position of the tool tip in frame $\{t\}$, i.e. $p_t=[0, 0, 0]^T$, $\delta {p_t}=[0, 0, 0]^T$, and (17) is obtained as

$$\begin{aligned} \delta \bar{p}_w&= \delta T_{w,t} \bar{p}_t =\left( \delta T_{w,t}T_{w,t}^{-1}\right) T_{w,t} \bar{p}_t \nonumber \\&= \left( \delta T_{w,t}T_{w,t}^{ -1} \right) \bar{p}_w. \end{aligned}$$

(18)

As $\left( \delta T_{w,t}T_{w,t}^{-1}\right) \in se(3)$, it can be written as a twist $\hat{\xi }= \begin{bmatrix} \hat{\omega }&v;&0&0 \end{bmatrix}$. Remarkably, $\left( \delta T_{w,t}T_{w,t}^{-1}\right) ^\vee = \xi = [\omega ; v]$. So (18) is rewritten as

$$\begin{aligned} \delta \bar{p}_w = \hat{\xi }\bar{p}_w = \begin{bmatrix} \begin{bmatrix} I_3 &{} - \hat{p}_w \end{bmatrix} \xi \\ 0 \end{bmatrix}. \end{aligned}$$

(19)

Combining (13)~(19), the position-based error model is given as

$$\begin{aligned} y_p=J_p \cdot \phi , \end{aligned}$$

(20)

where $y_p =\delta p_w= p_w^\mathrm{a} - p_w \in {R ^{3 \times 1}}$ is the position error of the tool, $p^\mathrm{a}_w$ and ${p_w}$ are the actual and nominal positions of the tool in frame $\{w\}$, $J_p = \begin{bmatrix} I_3&-\hat{p}_w \end{bmatrix} \cdot J \in R ^{3 \times 42}$ is the Jacobian matrix in terms of initial poses related to $y_p$.

3.2.3 Kinematic error model based on distance variation

To accommodate the distance measurement, the position error of the tool should finally be projected along the axial direction of the double ballbar. Therefore, the kinematic error model based on the distance variation is given by

$$\begin{aligned} y_d=J_d\cdot \phi . \end{aligned}$$

(21)

where $y_d = r_d \cdot y_p \in R ^{1}$ is the distance variation measured by the double balllbar at one point, $J_d = r_d \cdot J_p \in R ^{1 \times 42}$ is the gradient in terms of initial poses related to $y_d$, $r_d=[\begin{matrix} r_{di}&r_{dj}&r_{dk} \end{matrix}]$ is the unit vector of axial direction of the ballbar in frame $\{w\}$.

3.3 Identification of parameters in the kinematic error model

For any type of five-axis machine tools, there are $(m+1)$ links from the machine frame to the workpiece, while there are $(n+1)$ links from the machine frame to the tool, where $m+n=5$. Therefore, to identify the parameters in the kinematic error model, the total number of measurement points M should satisfy

$$\begin{aligned} M > 6\left( {m + 1} \right) + 6\left( {n + 1} \right) . \end{aligned}$$

(22)

And (21) is expanded as

$$\begin{aligned} \mathcal {Y}_d = \mathcal {J}_d\cdot \phi , \end{aligned}$$

(23)

where

$$\begin{aligned} \mathcal {Y}_d&= [y_{d1},y_{d2}, \cdots ,y_{dM}]^T \in R^{M \times 1},\\ \mathcal {J}_d&= [J_{d1}^T,J_{d2}^T \cdots J_{dM}^T]^T \in R^{M \times 42}. \end{aligned}$$

To obtain the parameter vector of kinematic errors $\phi$, the Gauss-Newton iteration algorithm is used. However, due to the existence of redundant error parameters in the kinematic error model, singularity problems of the Jacobian matrix may be encountered in the identification process [22]. This degrades the robustness of the conventional algorithm, especially when the measurement data are corrupted by large noisy data. To solve this problem, an iterative least square method with damping factor is proposed. So $\phi$ is identified by

$$\begin{aligned} \phi =(\mathcal {J}_d^T \mathcal {J}_d+\mu I)^{-1} \mathcal {J}_d^T\mathcal {Y}_d, \end{aligned}$$

(24)

where $\mu$ denotes the damping factor, which is in the range of $0.0001 \sim 1$. $\mu$ can be selected as $\mu =\tau \cdot \max\{\mathrm{diag}(\mathcal {J}_d^T \mathcal {J}_d)\}$, where $\tau$ is depended on the order of magnitude of the error data [40]. The initial parameter vector $\phi$ is set to be zero. And the initial pose $e^{\hat{h}_j}$ is updated by

$$\begin{aligned} e^{\hat{h}_j^\mathrm{new}}=e^{\hat{h}_j^\mathrm{old}}e^{s\delta \hat{h}_j}, \forall j\in \{w,c,a,y,x,z,t\}, \end{aligned}$$

(25)

where $s=-1$ if the motion axis is on the kinematic chain from the machine frame to the workpiece, otherwise, $s=1$. $\delta {h_j} \triangleq (\delta {x_j}, \delta {y_j}, \delta {z_j},\delta {\alpha _j},\delta {\beta _j}, \delta {\gamma _j})^T$ is the parameter vector of PIGEs.

Fig. 4

Procedure for kinematic errors identification

The above steps are repeated iteratively until the norm of the distance variation $\Vert \mathcal {Y}_d \Vert$ is less than the threshold $\varepsilon$. Ultimately, the calibrated initial pose $e^{\hat{h}^\mathrm{c}}$ is given by

$$\begin{aligned} e^{\hat{h}^\mathrm{c}}=\left[ e^{\hat{h}_w^\mathrm{c}},e^{\hat{h}_c^\mathrm{c}},e^{\hat{h}_a^\mathrm{c}}, e^{\hat{h}_y^\mathrm{c}}, e^{\hat{h}_x^\mathrm{c}}, e^{\hat{h}_z^\mathrm{c}}, e^{\hat{h}_t^\mathrm{c}}\right] . \end{aligned}$$

(26)

Therefore, the calibrated kinematics model $T_{w,t}^\mathrm{c}$ is also updated as

$$\begin{aligned} \begin{aligned} T_{w,t}^\mathrm{c}(\theta )=& \ e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x^\mathrm{c}}\\&e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z^\mathrm{c}}e^{\hat{\xi }_z\theta _z}e^{\hat{h}_t^\mathrm{c}}, \end{aligned} \end{aligned}$$

(27)

The calibrated tool pose $\chi ^\mathrm {c}=[p^\mathrm {c}_w;r^\mathrm {c}_w]$ in frame $\{w\}$ is

$$\begin{aligned} \begin{bmatrix} p^\mathrm {c}_w &{} r^\mathrm {c}_w\\ 1 &{} 0 \end{bmatrix}= T_{w,t}^\mathrm {c} \begin{bmatrix} p_t &{} r_t\\ 1 &{} 0 \end{bmatrix}, \end{aligned}$$

(28)

where $p^\mathrm {c}_w$ and $r^\mathrm {c}_w$ are the calibrated position and orientation of the tool, respectively. The identification process is summarized in Fig. 4.

3.4 Piecewise model for backlash compensation

It is noteworthy that the earlier kinematic error model can effectively cover the PIGEs, which, however, neglect the PDGEs. The backlash-induced error is one of major PDGEs. Due to the existence of the gear backlash, the contouring accuracy will degrade when the tool tip performs reciprocating motion for milling complex curved surface. In general, 80% geometric errors are from rotational axes [29]. Hence, to simplify the follow-up compensation process, only the backlash-induced error in rotational axes is considered, such error in translational axes is ignored. Remarkably, the backlash takes place when the motion directions change, and it can be considered as a form of initial pose deviation of the joints. Hence, a piecewise calibrated kinematics model is proposed according to the directions of rotation of A and C axes to additionally compensate the backlash-induced error.

For the AC table-tilting five-axis machine tools in Fig. 2, the rotation range of A and C axes are $\theta _a\in [-90^{\circ }, 90^{\circ }]$ and $\theta _c\in [0^{\circ }, 360^{\circ }]$. Denote $\tilde{\theta }_{(*)}(k)=\theta _{(*)}{(k+1)}-\theta _{(*)}{(k)}$, where $(*)\in \{a,c\}$, $\theta _{(*)}(k)$ and $\theta _{(*)}(k+1)$ are the kth and $(k+1)$th joint displacements of $(*)$-axes. Therefore, the forward and reverse motions of $(*)$-axes is represented by $\tilde{\theta }_{(*)}(k)>0$ and $\tilde{\theta }_{(*)}(k)<0$, respectively. According to the knowledge of permutations and combinations, 4 subdomains named ARCF, AFCF, ARCR and AFCR in the domain are obtained, where “A” and “C” stand for axes’ names, “R” and “F” stand for reverse and forward motions. In each subdomain, we can obtain a vector of distance variation $\mathcal {Y}_d$ when the measurements are taken in M points. By utilizing (24), 4 sets of $\phi$ are identified in 4 subdomains. Ultimately, following (25)~(27), the piecewise calibrated kinematics model $T_{w,t}^\mathrm {c}$ in its domain is given by

$$\begin{aligned} T_{w,t}^\mathrm {c}={\left\{ \begin{array}{ll} T_{w,t}^\mathrm {c1} &{} \tilde{\theta }_a(k)<0, \tilde{\theta }_c(k)>0, \quad (29\mathrm{a}) \\ T_{w,t}^\mathrm {c2} &{} \tilde{\theta }_a(k)>0, \tilde{\theta }_c(k)>0, \quad (29\mathrm{b})\\ T_{w,t}^\mathrm {c3} &{} \tilde{\theta }_a(k)<0, \tilde{\theta }_c(k)<0, \quad (29\mathrm{c})\\ T_{w,t}^\mathrm {c4} &{} \tilde{\theta }_a(k)>0, \tilde{\theta }_c(k)<0. \quad (29\mathrm{d})\end{array}\right. } \end{aligned}$$

(29)

where $T_{w,t}^\mathrm {c1}$, $T_{w,t}^\mathrm {c2}$, $T_{w,t}^\mathrm {c3}$ and $T_{w,t}^\mathrm {c4}$ are 4 calibrated kinematics models in ARCF, AFCF, ARCR and AFCR, respectively.

To evaluate the calibration results of the machine tools, the mean position error dp and mean orientation error dr in each subdomain are defined as

$$\begin{aligned} dp=\frac{1}{M}\sum \limits _{k = 1}^M \left\| p_{w}^\mathrm{a}(k) - p_{w}^\mathrm{c}(k) \right\| , \end{aligned}$$

(30)

$$\begin{aligned} dr=\frac{1}{M}\sum \limits _{k = 1}^M \left\| r_{w}^\mathrm{a}(k) - r_{w}^\mathrm{c}(k) \right\| . \end{aligned}$$

(31)

where M represents the total number of measured points, $p_{w}^\mathrm{a}$ and $r_{w}^\mathrm{a}$ are the actual position and orientation of the tool in frame $\{w\}$.

4 Kinematic error compensation

The calibrated model can be used for the compensation of the kinematic errors. However, as the numerical control (NC) system of the five-axis machine tool is not opened for user, its kinematic parameters cannot be directly modified. Instead, we firstly solve the inverse kinematics of the calibrated model, so that the calibrated joint displacements are obtained. Ultimately, the kinematic error compensation is achieved by inputting the calibrated joint displacement to the NC system.

4.1 Inverse kinematics of the calibrated model

Due to the existence of manufacturing and assembly errors, the condition of perpendicularity or intersection between translation or rotational axes of the five-axis machine tool may be violated. In this case, solving the inverse kinematic problem by decomposing it into Paden-Kahan subproblems as in [18] will bring the calculation error. Instead, the numerical method based on screw theory is developed [41].

Similar to (13), the deviations between the nominal kinematics model $T_{w,t}$ and the calibrated kinematics model $T_{w,t}^\mathrm{c}$ can be expressed in a first-order approximation as

$$\begin{aligned} y^\mathrm{c} =\left[ \delta T_{w,t}^\mathrm{c}\cdot (T_{w,t}^\mathrm{c})^{-1}\right] ^\vee = \log \left( T_{w,t} (T_{w,t}^\mathrm{c})^{-1} \right) ^\vee , \end{aligned}$$

(32)

where $y^\mathrm{c}=[y_p^\mathrm{c}; y_r^\mathrm{c}]\in R^{6 \times 1}$ denotes the pose error of the tool between the calibrated and nominal models, $y_p^\mathrm{c}$ and $y_r^\mathrm{c}$ denote the position and orientation error of the tool, respectively.

To make the tool reach the desired pose, the calibrated joint displacements $\theta ^{\mathrm {c}}$ needs to be obtained. Take the derivative of $T_{w,t}^c$ w.r.t. $\theta _\rho$, $\forall \rho \in \{x,y,z,a,c\}$, as

$$\begin{aligned} \begin{aligned} \delta T_{w,t}^\mathrm{c} =&-e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}\hat{\xi }_c\delta \theta _c e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}e^{\hat{\xi }_y\theta _y}\\&e^{\hat{h}_x^\mathrm{c}}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z^\mathrm{c}}e^{\hat{\xi }_z\theta _z} e^{\hat{h}_t^\mathrm{c}}-e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}\\&e^{-\hat{\xi }_a\theta _a}\hat{\xi }_a\delta \theta _a e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^c\mathrm{c}}e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x^\mathrm{c}}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z^\mathrm{c}}e^{\hat{\xi }_z\theta _z}\\&e^{\hat{h}_t^\mathrm{c}}+\cdots +e^{-\hat{h}_{w}^c}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}\\&e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x^\mathrm{c}}e^{\hat{\xi }_x\theta _x}e^{\hat{h}_z^\mathrm{c}}e^{\hat{\xi }_z\theta _z}\hat{\xi }_z\delta \theta _z e^{\hat{h}_t^\mathrm{c}}. \end{aligned} \end{aligned}$$

(33)

Multiply both sides of (33) by $(T_{w,t}^\mathrm{c})^{-1}$, we have

$$\begin{aligned} \begin{aligned} \left[ \delta T_{w,t}^\mathrm{c}(T_{w,t}^\mathrm{c})^{-1}\right] ^\vee =& -\mathrm{Ad}_{f_c}\xi _c\delta \theta _c - \mathrm{Ad}_{f_a}\xi _a\delta \theta _a \\ &+ \mathrm{Ad}_{f_y}\xi _y\delta {\theta _y}+ \mathrm{Ad}_{f_x}\xi _x\delta {\theta _x}+ \mathrm{Ad}_{f_z}\xi _z\delta {\theta _z}, \end{aligned} \end{aligned}$$

(34)

where

$$\begin{aligned} \begin{aligned} f_c&=e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c},\\ f_a&=e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a},\\ f_y&=e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}e^{\hat{\xi }_y\theta _y},\\ f_x&=e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x^\mathrm{c}}e^{\hat{\xi }_x\theta _x},\\ f_z&=e^{-\hat{h}_w^\mathrm{c}}e^{-\hat{\xi }_c\theta _c}e^{-\hat{h}_c^\mathrm{c}}e^{-\hat{\xi }_a\theta _a}e^{-\hat{h}_a^\mathrm{c}}e^{\hat{h}_y^\mathrm{c}}e^{\hat{\xi }_y\theta _y}e^{\hat{h}_x^\mathrm{c}}e^{\hat{\xi }_x\theta _x} e^{\hat{h}_z^\mathrm{c}}e^{\hat{\xi }_z\theta _z}. \end{aligned} \end{aligned}$$

Combining (32)~(34), a linear matrix equation is given as

$$\begin{aligned} y^\mathrm{c}=J^\mathrm{c}\cdot \psi , \end{aligned}$$

(35)

where $J^\mathrm{c}$ is the Jacobian matrix in terms of joint displacements related to $y^\mathrm {c}$, $\psi$ is the increment of the joint displacements $\theta$, and

$$\begin{aligned} J^\mathrm{c}&=\left[ -\mathrm{Ad}_{f_c}\xi _c, -\mathrm{Ad}_{f_a}\xi _a, \mathrm{Ad}_{f_y}\xi _y, \mathrm{Ad}_{f_x}{\xi _x},\mathrm{Ad}_{f_z}\xi _z \right] \\&\in {R^{6 \times 5}},\\ \psi &=\left[ {\delta \theta _c},\delta \theta _a,\delta \theta _y,\delta \theta _x,\delta \theta _z\right] ^T\in R ^{5 \times 1}. \end{aligned}$$

However, (35) is overdetermined, so there is no analytical solutions in general. This problem is addressed by utilizing the error model based on pure position information as in [41]. Similar to (16)~(20), the position error of the tool $y_p^\mathrm{c}$ between the calibrated and nominal models is given by

$$\begin{aligned} y_p^\mathrm{c}=J_p^\mathrm{c} \cdot \psi , \end{aligned}$$

(36)

where $y_p^\mathrm{c}= p_w^\mathrm{c}-p_w \in R^{3 \times 1}$, $p_w^\mathrm{c}$ is the position of the tool calculated from the calibrated kinematics model, $J_p^\mathrm{c}=\begin{bmatrix}I_{3}&- \hat{p}_w^\mathrm{c}\end{bmatrix}\cdot J^\mathrm{c} \in R ^{3 \times 5}$ is Jacobian matrix in terms of joint displacements related to $y^\mathrm {c}_p$.

The increment $\psi$ of joint displacements is obtained by the iterative least square method as follows

$$\begin{aligned} \psi =\left( (J_p^\mathrm{c})^T J_p^\mathrm{c}\right) ^{-1} (J_p^\mathrm{c})^T \cdot y_p^\mathrm{c}, \end{aligned}$$

(37)

The calibrated joint displacements of five axes are updated by $\theta ^\mathrm{c}_\mathrm{new}=\theta ^\mathrm{c}_\mathrm{old}+\psi$. Next, $\theta ^\mathrm{c}_\mathrm{new}$ are substituted into the calibrated kinematics model in (27). In this way, $y_p^\mathrm{c}$ and $J_p^\mathrm {c}$ can be recalculated. The final calibrated joint displacement $\theta ^\mathrm {c}$ is obtained when $\Vert y_p^\mathrm{c} \Vert$ is less than the threshold $\eta$.

4.2 Procedure of piecewise kinematic error compensation

To further deal with the kinematic error caused by gear backlash to enhance the machining accuracy, the model-based piecewise error compensation is performed by utilizing the piecewise model in (29). First, we design a tool path, which is composed of a series of tool pose data $\chi (\kappa )$ in frame $\{w\}$, where $\kappa \in \{1,2,\cdots N\}$ is the index of points on the contour. Based on these data, the nominal joint displacements $\theta (\kappa )$ are obtained by solving inverse kinematics of nominal model from the reference [18].

To utilize the piecewise calibrated model to compensate the backlash-induced error, the signs of $\tilde{\theta }_a(\kappa )$ and $\tilde{\theta }_c(\kappa )$ are used to determine the corresponding subdomain. In this way, the calibrated sub-model is selected from the piecewise model $T_{w,t}^\mathrm {c}$ in (29). Subsequently, the calibrated joint displacement $\theta ^\mathrm{c}(\kappa )$ in each subdomain is numerically solved by the procedures in Sect. 4.1, with $\theta (\kappa )$ as the initial value. Ultimately, $\theta ^\mathrm{c}(\kappa )$ is used as the input of the NC system, and the geometric error compensation is achieved. By lumping the error caused by backlash into the initial poses in dyads, we can compensate the kinematic error due to gear backlash without directly modeling it.

To evaluate the effectiveness of the piecewise kinematic error compensation, the mean position error $dp^\mathrm{c}$ is defined as

$$\begin{aligned} dp^\mathrm{c} = \frac{1}{N}\sum \limits _{\kappa = 1}^N \left\| p_{w}^\mathrm{c}(\kappa )-p_{w}(\kappa ) \right\| , \end{aligned}$$

(38)

where N is the total number of the points on the contour.

The procedure of the piecewise kinematic error compensation is summarized in Fig. 5.

Fig. 5

Procedure for piecewise kinematic error compensation

5 Simulation

To show the effectiveness and robustness of the calibration method based on the error model derived from local POE formula, the simulation verification is conducted. In this section, only the compensation of PIGEs is performed, while the compensation of hybrid PIGEs and PDGEs is given in the coming experiments.

5.1 Preset values of kinematic errors

In the kinematic model point of view, kinematic errors may due to the deviations of initial poses h, joint twists $\xi$ and joint displacements $\theta$. They need to be preset for simulating the actual kinematics. The values of deviations of twists of the revolute and prismatic joints are set as in Table 2, while the preset deviations on the initial poses and joint displacements of five axes are given in Table 3.

Table 2 The deviations of twists of the revolute and prismatic joints

Table 3 The deviations of initial poses and joint displacements

5.2 Parameter identification and kinematic error compensation

To observe the convergence of kinematic error model’s parameters in identification process, a test trajectory is designed firstly by referring to NC codes of QC20-W ballbar from Renishaw official website. Subsequently, 100 sets of joint displacements in NC codes are selected, and they are substituted into the nominal kinematics model and the actual kinematics model with the preset $\delta {\xi }$, $\delta {h}$ and $\delta {\theta }$. In this way, the distance variation data in simulation are obtained by (13) and (21). In addition, uniformly distributed noise within $[0,10^{-5}]$ m is added to the above data, and then they are used for parameter identification by the procedures in Fig. 4. To evaluate the complexity of this algorithm, the time complexity index is utilized, and the algorithm takes about 2.2 seconds to run once on a computer with the brand of ThinkPad E480. The mean position error dp is used as the evaluation index of algorithm convergence. As shown in Fig. 6, the parameter identification based on the Gauss-Newton method fails to converge. When the least square method with a damping factor $\mu$ is used, dp converges to a stable value which is in the same order of magnitude as that of the injected noise. The identified parameter vector $\phi$ is shown in Table 4. This shows the robustness of the proposed identification method.

Fig. 6

Comparison about mean position errors when the conventional and proposed methods are used

Table 4 Identified 42 components of $\phi$ based on the preset kinematic errors in simulation

The calibrated kinematic model in the form of (27) is obtained after the parameter identification is conducted. To compare it with the simulated actual kinematics model, another 100 sets of joint displacements are selected. As shown in Fig. 7a–c, the x-, y-, and z-coordinates of the tool tip in frame $\{w\}$ predicted by the calibrated kinematics model are basically consistent with those from the actual kinematics model, and the prediction errors are in the same order of magnitude as the injected noise as shown in Fig. 7d–f. Therefore, we can conclude that the calibrated kinematics model based on the local POE formula is accurate.

Fig. 7

Actual and predicted values for (a) x-, (b) y-, (c) z-coordinates of the tool tip; Prediction error for (d) x-, (e) y-, (f) z-coordinates of the tool tip

Remarkably, when the PDGEs are absent, the unified kinematic error model is sufficient. As described in Sect. 4.1, using the iterative least squares method based on the position information, the increment $\psi$ of joint displacements is solved. As shown in Fig. 8, the mean position error $dp^{c}$ is reduced to zero when the final calibrated joint displacement $\theta ^c$ is taken as the updated input in Sect. 4.1. This validates the effectiveness of model-based error compensation.

Fig. 8

Mean position error during performing model-based error compensation

5.3 Calibration results based on local and global POE formulas

To compare the calibration results based on the global POE formula, the initial conditions of two calibration models based on the local and the global POE formulas should be set to the same. $\delta \xi$ are set to be consistent with that in [18], while $\delta h$ and $\delta \theta$ are set as zero. After injecting the uniformly distributed noise within $[0,10^{-6}]$ m, the results of convergence of the performance index by two models are compared. As shown in Figs. 9 and 10, the kinematic error model derived by the local POE formula gives better identification results compared with the model derived by the global POE formula, in terms of both the mean position error dp and the mean orientation error dr. The main reason is that the orthogonalization and normalization of joint twists are not required throughout the identification process, as they always keep their nominal values throughout entire calibration process by assuming geometric errors are lumped into the deviations of initial poses. Thereby, no extra quantization error is introduced.

Fig. 9

Mean position error using local and global POE formulas

Fig. 10

Mean orientation error using local and global POE formulas

6 Experimental validation

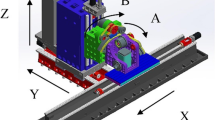
In order to further verify the effectiveness of the proposed method, the experiments are conducted on an AC table-tilting five-axis machine tool prototype, as shown in Fig. 11. Remarkably, low machining accuracy may be encountered due to the lack of pre-calibration on such a prototype.

Fig. 11

The experimental setup for the calibration of five-axis machine tool

6.1 Data acquisition

In this experiment, QC20-W ballbar is used to measure the distance variation between the ball of the tool end and the ball of the workpiece end during the operation of the machine tool. The sensor resolution of the ballbar is 0.1 µm, the measuring range of the ballbar is $\pm 1.0$ mm, and its maximum sampling rate is 1000 Hz. The distance variation data are transmitted via Bluetooth in real time. Ultimately, they are recorded to the Ballbar Trace software installed on the computer.

Following the conventions described in Sect. 2.2, the initial local frames are assigned in Fig. 12. Operate the control handle to make the workbench be perpendicular to the z-axis, and make the ball in the tool end coincide with the ball in the workpiece end. Set such configuration as the home position of five-axis machine tool. Subsequently, the initial positions of adjacent local frames are measured by a dial indicator. For detailed information, please refer to the explanation of $Pr3031 \sim Pr3033$ in SYNTEC CNC Parameters Manual. Finally, the measured initial positions can be used to replace the nominal initial positions that are not given in the operating manual of the machine tool. In this way, the initial poses are given as

$$\begin{aligned} h_w&=\left[ 0.1585,-0.0029,0.073858,0,0,0\right] ^T \\ h_c&=\left[ 0,-0.00003,0.000495,0,0,0\right] ^T \\ h_a&=\left[ -0.1585,0.00293, - 0.073363,0,0,0\right] ^T \\ h_y&=h_x=h_z=h_t=\left[ 0,0,0,0,0,0\right] ^T \end{aligned}$$

where all units are SI.

Fig. 12

The layout of local frames when the five-axis machine tool is in home position

Rewrite the NC codes used in simulation by utilizing the above initial poses. If the Rotated Tool Center Point (RTCP) function were turned on, the distance between the tool ball and the workpiece ball could be guaranteed as a constant. However, the RTCP function of the NC system of the experimental prototype is not given for cost saving purpose. Hence, to equivalently achieve the RTCP function, we need to correct the displacements of the origin of frame $\{w\}$ caused by the motions of the rotational axes during post data processing phase. The corrections along x, y, and z axes are given by

$$\begin{aligned} \left[ d\theta _x, d\theta _y, d\theta _z, 1 \right] ^T&= T_{b,w}(\theta _a,\theta _c) \cdot \left[ 0,0,0,1\right] ^T \end{aligned}$$

(39)

where $d\theta _x, d\theta _y$ and $d\theta _z$ are the corresponding corrections of translational axes in the NC codes, $T_{b,w}(\theta _a,\theta _c)=e^{\hat{h}_a} e^{\hat{\xi }\theta _a} e^{\hat{h}_c} e^{\hat{\xi }\theta _c} e^{\hat{h}_w}$.

The NC codes are composed of 7204 groups of joint displacements, and the test method is in accordance with BK4 of ISO 10791-6 [42]. According to the nominal forward kinematics model in (6), we can get the coordinates of 7204 tool tip points in frame $\{w\}$. Figure 13 shows the trajectory of the tool tip with a constant distance L = 100 mm. The sensitive direction of the ballbar is parallel to its telescope bar. To set the QC20-W ballbar correctly, we can refer to the procedures in Renishaw official website. After inputting the NC codes to the machine tool, the distance variation is measured by the ballbar, as shown in Fig. 13. Remarkably, the profile errors of the ballbar can be integrated into deviations of initial poses.

Fig. 13

The trajectory with $L=100$ mm and associated distance variation

6.2 Parameter identification and compensation of piecewise model

For ease of references, the proposed method in this paper is named as AC-FR method. As shown in Table 5, the entire trajectory is divided into 4 segments according to the directions of rotation of A and C axes, which corresponds to 4 associated subdomains ARCF, AFCF, ARCR, and AFCR in (29) respectively. To obtain the piecewise calibrated kinematic models, 100 sample points are selected in each subdomain to identify the corresponding error parameters $\phi$ in (24) by following the procedures in Fig. 4. Table 6 shows 42 components of $\phi$ including 21 position errors and 21 orientation errors. These errors are sufficient to describe the kinematic model of five-axis machine tool. Ultimately, the piecewise calibrated kinematics model in (29) is used to perform the piecewise kinematic error compensation.

Fig. 14

Predicted distance variation versus actual distance variation, (a) from AC-FR, (b) from C-FR, (c) from No-FR; the corresponding prediction error, (d) from AC-FR, (e) from C-FR, (f) from No-FR

Table 5 Partitions of trajectories according to the rotational directions of A and C axes

Table 6 Identified 42 components of $\phi$ based on the experimental data with AC-FR method

To show the superiority of the proposed method, two methods named C-FR method and No-FR method are used as the comparisons. C-FR method refers to the kinematic error modeling method that only the forward and reverse motions of the C axis are considered. So that a piecewise calibrated kinematics model with 2 subdomains is built for compensation. No-FR method is the method without considering the influence of the directions of rotation, so that a unified kinematic error model is built within the workspace.

Subsequently, 200 sample points are selected to evaluate the predicted results using above three methods. As shown in Fig. 14a–c, by using AC-FR method, the predicted distance variation is more consistent with the actual distance variation, compared with the results from C-FR and No-FR methods. In addition, from Fig. 14d–f, the mean prediction errors using AC-FR, C-FR and No-FR methods are given as 6.20$\times 10^{-6}$ m, 1.25$\times 10^{-5}$ m and 1.75$\times 10^{-5}$ m, respectively. Hence, we can conclude that a more accurate calibrated kinematics model is obtained for compensation with the proposed AC-FR method.

Fig. 15

Compensation results in 4 segments of the trajectory. (a) from ARCF; (b) from AFCF; (c) from ARCR; (d) from AFCR

Following the procedures in Fig. 5, the piecewise kinematic error compensation is conducted. Table 7 shows the part of NC codes before compensation, while Table 8 is modified NC codes obtained with AC-FR method respectively. Input the entire modified NC codes to the five-axis machine tool, the distance variation after compensation is measured by the double ballbar. The method that drives the tool tip without kinematic error compensation is named as uncompensated method. We can see that the distance variation data are closer to zero with the AC-FR method from Fig. 15. As shown in Fig. 16, the maximum and the median of the distance variation data with AC-FR method are smaller; this shows that the proposed method can perform more accurate and consistent contouring. Compared with uncompensated method, the maximum of the distance variation by AC-FR method is decreased by 64.4%, while its counterparts by C-FR and No-FR methods are reduced by 48.9% and 44.2% respectively. Such results demonstrate that the proposed piecewise kinematic error compensation method can improve the accuracy of bidirectional contouring in the presence of gear backlash on the rotational axes.

Table 7 Part of NC codes before compensation. (unit for X, Y, Z: mm, unit for A, C:$^\circ$)

Fig. 16

Boxplot for compensation results from three methods in auto-validation with $L=100$ mm

Table 8 Part of NC codes after compensation. (unit for X, Y, Z: mm, unit for A, C: $^\circ$)

To validate the generality of the piecewise kinematic error compensation based on local POE formula, a compensation experiment is performed along another trajectory. First, Table 9 shows part of NC codes composed of five axes motion commands. Input entire NC codes to the machine tool, we can obtain the trajectory of the tool tip that tends to maintain a constant distance $L=150$ mm between the ball in the tool end and the ball in the workpiece end, as shown in Fig. 17. Subsequently, data of the distance variation measured from the trajectory with $L=100$ mm are used to obtain the piecewise calibrated kinematics model with AC-FR method. Finally, this piecewise calibrated kinematics model is used to compensate the trajectory with $L=150$ mm. From Fig. 18, it is found that the maximum of the distance variation is reduced by 69.5% after compensation. This verifies the effectiveness of the piecewise kinematic error compensation method within a large workspace.

Table 9 Part of NC codes for the trajectory of the tool tip with a constant distance $L=$150 mm. (unit for X, Y, Z: mm, unit for A, C: $^\circ$)

Fig. 17

Two different trajectories of the tool tip in the workpiece frame for the cross validation experiment

Fig. 18

Boxplot for compensation results with AC-FR method

7 Conclusion

In this paper, by utilizing the local POE formula, we develop a geometric error modeling method for AC table-tilting five-axis machine tool based on distance variation of the ballbar. It strictly fits the kinematic constraints of joint twists by retaining their nominal values throughout the calibration process, thus improving modeling accuracy compared with that based on the global POE formula. To cater for calibration model with redundant parameters, an iterative least squares method with a damping factor is utilized to identify the parameters of kinematic errors. This ensures the convergence of the algorithm in the presence of large noisy data. To further reduce the error caused by the backlash during bidirectional motions of the tilting table, the above kinematic error model is further revised to be piecewise. The gear backlash is naturally integrated into the deviations of initial poses in kinematic error model, so that compensation of the gear backlash is eventually achieved without directly modeling it. Simulation and experimental results show the effectiveness and generality of the proposed method.

Appendix

1.1 Joint twist

Define $\xi =\begin{bmatrix} v\\ \omega \end{bmatrix}\in \mathrm{{R}^{6 \times 1}}$ to be the twist coordinates of the twist $\hat{\xi }$, the operator $\vee$ can extract the 6-dimensional vector from a twist $\hat{\xi }$, and the inverse operator $\wedge$ can form a twist $\hat{\xi }$ from a 6-dimensional vector $\xi$. They are represented as follows

$$\begin{aligned} \left[ \hat{\xi }\right] ^\vee = \begin{bmatrix} \hat{\omega }&{}v\\ 0&{}0 \end{bmatrix}^{\vee }=\xi = \begin{bmatrix} v\\ \omega \end{bmatrix},\quad \left[ \xi \right] ^{\wedge }=\hat{\xi }. \end{aligned}$$

1.2 Adjoint transformation

The adjoint transformation of $g=(p,R)\in SE(3)$ on $\xi \in se(3)$ is

$$\begin{aligned} \mathrm{Ad}_g(\hat{\xi })=g\cdot \hat{\xi }\cdot g^{-1}= \begin{bmatrix}R&{}p\\ 0&{}1\end{bmatrix}\begin{bmatrix}\hat{\omega }&{}v\\ 0&{}0\end{bmatrix} \begin{bmatrix}R&{}p\\ 0&{}1\end{bmatrix}^{-1}. \end{aligned}$$

When the twist $\hat{\xi }$ is represented by a 6-dimensional vector $\xi =\begin{bmatrix} v\\ \omega \end{bmatrix}$, the adjoint transformation of g on $\xi$ is

$$\begin{aligned} \mathrm{Ad}_g\xi = \begin{bmatrix} R&{}\hat{p}R\\ 0&{}R \end{bmatrix} \begin{bmatrix} v\\ \omega \end{bmatrix}. \end{aligned}$$