Keywords

1 Introduction

Gear skiving is a highly productive rough-cutting gear machining method for both external and internal gear types due to its advantages compared with traditional gear machining, including increased productivity, decreased manufacturing costs [1,2,3]. The power skiving technology is the interesting and focusing topic for the researchers based on the performance enhancement of the machine tool and cutter materials. However, a design method of skiving cutter that considers grinding allowance is lacking in previous studies.

Following advancements in gear skiving technology, several researchers have explored methods to design and improve skiving technology. Guo et al. [4] use the modification coefficient and tapered teeth based on helix angle of work gear to design the skiving cutter profile for machining involute part of internal gear. These same authors further presented the correction method for both skived tooth flanks of involute part by optimizing the machine setting of skiving motion [5] or the cutter profile [6] to improve the accuracy of skived gear. Employing a different approach, Moriwaki et al. [7] calculated the cutting edges of rake face based on the barrel-shaped pinion surface conjugated with an internal gear to reduce profile errors. Shih and Li [8] established a mathematical model to generate the cutting edges of a conical skiving tool by using the intersection curve of the rake face and a set of generating gears that is the result of decreasing profile shifted coefficients with the work gears. However, all these works have failed to investigate the skiving cutter considering the grinding allowance of work gear.

In this paper, the rack modification method is firstly proposed to generating the skiving tool with pre-defined grinding allowance of work gear. The segment on the normal rack corresponding with the involute part of the work gear is defined by linear equation based on the grinding allowance. The effects of coefficients of rack equation on normal errors in the gear tooth profile are calculated to construct sensitivity matrix. This matrix is used along with Levenberg–Marquardt (L-M) algorithm to obtain the modified rack which is used to design the skiving cutter for manufacturing both internal and external gear with required grinding allowance. The validity of the proposed method for power skiving is demonstrated by numerical example.

2 Mathematical Model for Skived Gear

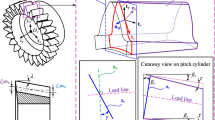
To generate the skiving cutter, several coordinate systems shown in Fig. 1 are defined to present the design method for skiving cutter. The coordinate systems \(S_{r} (x_{r} ,y_{r} ,z_{r} )\) and \(S_{s} (x_{s} ,y_{s} ,z_{s} )\) are rigidly connected to the transverse section i of the skiving cutter and the transverse rack, respectively; \(S_{r1} (x_{r1} ,y_{r1} ,z_{r1} )\), \(S_{s1} (x_{s1} ,y_{s1} ,z_{s1} )\) and \(S_{s2} (x_{s2} ,y_{s2} ,z_{s2} )\) are auxiliary coordinate systems.

According to the gear theory, the equation of normal rack segments corresponding to the involute segments of the work gear can be described as:

$$ y_{n} = a_{i} x_{n} + b_{i} ,\quad i = 1\quad {\text{for external gear}},\quad i = 2\quad {\text{for internal gear}} $$
(1)

where \(a_{i}\), \(b_{i}\) are the polynomial coefficients of rack equation.

The position vector \({\mathbf{r}}_{r}\) and unit normal vector \({\mathbf{n}}_{r}\) of transverse rack can be expressed through the position vector of normal rack \({\mathbf{r}}_{n} = \left[ {x_{n} ,y_{n} ,0,1} \right]\) as follows:

$$ {\mathbf{r}}_{r} \left( u \right) = \left[ {x_{r} \left( u \right),y_{r} \left( u \right),0,1} \right]^{T} = \left[ {x_{n} \left( u \right)/\cos \beta_{c} ,y_{n} \left( u \right),0,1} \right]^{T} $$
(2)
$$ {\mathbf{n}}_{r} \left( u \right) = \frac{{{\mathbf{k}} \times \partial_{u} {\mathbf{r}}_{r}^{\prime } }}{{\left| {{\mathbf{k}} \times \partial_{u} {\mathbf{r}}_{r}^{\prime } } \right|}} $$
(3)

where \({\mathbf{r}}_{r}^{\prime }\) is a vector of the first three elements of \({\mathbf{r}}_{r}\), and \(\beta_{c}\) is a helix angle of skiving cutter.

Fig. 1.
figure 1

Calculation process of generating cutting edge of skiving tool

Full size image

Using the motional relationships between the rack and the cutter profile, the locus equations \({\mathbf{r}}_{c}^{(i)}\) and the unit normal vectors \({\mathbf{n}}_{c}^{(i)}\) for each section of skiving body can be determined in the coordinate system \(S_{s}\), as follows:

$$ {\mathbf{r}}_{c}^{(i)} \left( {u,\varphi ,l_{i} } \right) = {\mathbf{M}}_{sr} \left( {\varphi ,l_{i} } \right) \cdot {\mathbf{r}}_{r} \left( u \right),i = 1\sim cs_{n} $$
(4)
$$ {\mathbf{n}}_{c}^{(i)} \left( {u,\varphi ,l_{i} } \right) = {\mathbf{L}}_{sr} \left( {\varphi ,l_{i} } \right) \cdot {\mathbf{n}}_{r} \left( u \right) $$
(5)

where \({\mathbf{L}}_{sr}\) is an upper-left submatrix of the first \(3 \times 3\) elements of the transformation matrix \({\mathbf{M}}_{sr}\).

To apply the enveloping method [9], the meshing condition between the transverse rack and each section of skiving cutter can be determined by:

$$ f_{0} = {\mathbf{n}}_{c}^{(i)} \cdot {{\partial {\mathbf{r}}_{c}^{\prime (i)} \left( {u,\varphi ,l_{i} } \right)} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{c}^{\prime (i)} \left( {u,\varphi ,l_{i} } \right)} {\partial \varphi }}} \right. \kern-\nulldelimiterspace} {\partial \varphi }} = 0,i = 1\sim cs_{n} $$
(6)

where \({\mathbf{r}}_{c}^{\prime (i)}\) is a vector of the first three elements of \({\mathbf{r}}_{c}^{(i)}\).

The meshing angle \(\varphi\) can be obtained by solving the Eq. (6) after substituting the parameter of normal rack u and the position of transverse section of cutter profile \(l_{i}\). The section profile of cutter is defined by substituting the set of parameters \(\left( {u,\varphi ,l_{i} } \right)\) into Eq. (4).

Subsequently, the cutter body of skiving are generated by positioning the transverse section as follows:

$$ {\mathbf{r}}_{c} \left( {u,\varphi ,l_{i} } \right) = {\mathbf{M}}_{cs} \left( {\varphi ,l_{i} } \right) \cdot {\mathbf{r}}_{c}^{(j)} ,i = 1\sim cs_{n} $$
(7)
$$ {\mathbf{n}}_{c} \left( {u,\varphi ,l_{i} } \right) = {\mathbf{L}}_{cs} \left( {\varphi ,l_{i} } \right) \cdot {\mathbf{n}}_{c}^{(j)} $$
(8)

The cutting edge is determined as the intersecting between the cutter body and the rake plane. The tangent vector for each point of cutting edge \({\mathbf{t}}_{c}\) can be obtained as follows:

$$ {\mathbf{t}}_{c} = \left( {{{\partial {\mathbf{r}}_{c}^{\prime } \left( {u,\varphi ,l_{i} } \right)} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{c}^{\prime } \left( {u,\varphi ,l_{i} } \right)} {\partial \varphi }}} \right. \kern-\nulldelimiterspace} {\partial \varphi }} \times {{\partial {\mathbf{r}}_{c}^{\prime } \left( {u,\varphi ,l_{i} } \right)} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{c}^{\prime } \left( {u,\varphi ,l_{i} } \right)} {\partial l_{i} }}} \right. \kern-\nulldelimiterspace} {\partial l_{i} }}} \right) \times {\mathbf{n}}_{rp} $$
(9)

Figure 2 shows the applied coordinate systems for simulating the skived gear. The position vector \({\mathbf{r}}_{w}\) and tangent vector \({\mathbf{t}}_{w}\) of gear skiving can be derived by transforming \({\mathbf{r}}_{c}\) and \({\mathbf{t}}_{c}\) in coordinate system \(S_{c}\) to coordinate system \(S_{w}\) as follows:

$$ {\mathbf{r}}_{w} (\varphi_{c} ,v) = \left( {x_{w} ,y_{w} ,z_{w} ,1} \right)^{T} = {\mathbf{M}}_{wc} (\varphi_{c} ,v) \cdot {\mathbf{r}}_{c} $$
(10)
$$ {\mathbf{t}}_{w} (\varphi_{c} ,v) = {\mathbf{L}}_{wc} (\varphi_{c} ,v) \cdot {\mathbf{t}}_{c} $$
(11)
Fig. 2.
figure 2

General coordinate system for gear skiving

Full size image

where \({\mathbf{L}}_{wc}\) is an upper-left submatrix of the first \(3 \times 3\) elements of the transformation matrix \({\mathbf{M}}_{wc}\).

The meshing condition between the skiving tool and work gear can be expressed as follows:

$$ f_{1} = {\mathbf{t}}_{w} \cdot ({{\partial {\mathbf{r}}_{w}^{\prime } } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{w}^{\prime } } {\partial v}}} \right. \kern-\nulldelimiterspace} {\partial v}} \times {{\partial {\mathbf{r}}_{w}^{\prime } } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{w}^{\prime } } {\partial \varphi_{c} }}} \right. \kern-\nulldelimiterspace} {\partial \varphi_{c} }}) = 0 $$
(12)

To simulate the gear with skiving cutter on the multi-axis CNC machine, the position of different section in z-axis direction, \(l_{i}\), is firstly defined as \(z_{w} = l_{i}\) (\(i = 1\sim cs_{n}\)), and then the corresponding parameters, \(\nu\) and \(\varphi_{c}\), are solved together with Eq. (12). The simulated gear skiving tooth surface at section \(l_{i}\) can be obtained by substituting the set of parameters \(\left( {\nu ,\varphi_{c} } \right)\) into Eq. (10).

According to the mathematical model for skived gear, the polynomial coefficients of equations of normal rack segments corresponding to the involute segments of the work gear is only determined for the standard rack. However, the method for calculating these coefficients of the normal rack with grinding allowance of work gear has yet been presented in previous studies. Therefore, this section presents a rack modification method to evaluate the polynomial coefficients of rack equations by using the sensitivity matrix, L-M algorithm, and the required grinding allowance. These variables can be solved after several closed-loop iterations.

To simplify the closed-loop procedure, a sensitivity matrix \({\mathbf{M}}_{s}\) is firstly constructed from the influences of polynomial coefficients of normal rack, \(\delta \lambda_{j}\), on the normal deviation of the skived gear. The values of variables \(\left\{ {\delta \lambda_{j} } \right\}\) can be specified by using the grinding allowance design \(\left\{ {\delta \varsigma_{j} } \right\}\):

$$ \left\{ {\delta \varsigma_{j} } \right\} = {\mathbf{M}}_{s} \cdot \left\{ {\delta \lambda_{i} } \right\} = \left[ {{{\partial \varsigma_{j} } \mathord{\left/ {\vphantom {{\partial \varsigma_{j} } {\partial \lambda_{i} }}} \right. \kern-\nulldelimiterspace} {\partial \lambda_{i} }}} \right]\left\{ {\delta \lambda_{i} } \right\},i = 1\sim 4,j = 1\sim 10 $$
(13)

The variables \(\delta \lambda_{j}\) in the system can be solved by using the L–M algorithm [10, 11] with the grinding allowance at all points of gear tooth surface, like so:

$$ \left\{ {\delta \lambda_{i} } \right\} = \left( {{\mathbf{M}}_{s}^{T} {\mathbf{M}}_{s} + \mu {\mathbf{I}}} \right)^{ - 1} {\mathbf{M}}_{s}^{T} \cdot \left\{ {\delta \varsigma_{j} } \right\} $$
(14)

where the damping parameter \(\mu\) is adjusted at each iteration and calculated as an element of matrix \({\mathbf{M}}_{s}\) with the minimum absolute value and I is the identity matrix.

3 Numerical Example

The numerical examples are used to verify the correctness of design method for conical skiving cutter through the modified rack with both of skived internal and external helical gear with pre-defined grinding allowance. The basic, calculated, and assembly parameters of the work gears and skiving cutters used in this example are shown in Table 1.

Table 1. Parameters of work gear and skiving tool
Full size table

The correction rack is used to generate the skiving cutter and cutting edge by applying the proposed method for simulating the cutting process. The results are shown in Figs. 3.

Fig. 3.
figure 3

Topography of the skived gear tooth: (a) external gear and (b) internal gear

Full size image

In skived external gear, the maximum and minimum normal error of involute part of tooth profile generated by correction rack are 3.399 µm and 0.979 µm, respectively. In skived internal gear, the maximum and minimum normal error of involute part of tooth profile generated by correction rack are 4.319 µm and 0.541 µm, respectively. The normal errors are large for the internal gear. The maximum normal deviations of left and right sides for external gear are 2.263 µm and 3.399 µm, respectively. The maximum normal deviations of left and right sides for internal gear are 4.319 µm and 2.044 µm, respectively. The accuracy of gear tooth profile on the right side is better than it’s on the left side for internal gear, while the accuracy of gear tooth profile on the right side is lower than it’s on the left side for external gear. The reason of these issues is the same helical direction, right side, of the skiving cutter and workpiece. This example proves that the proposed method is substantially applied for designing the skiving cutter with pre-defined grinding allowance.

4 Conclusion

In this study, a general coordinate system for gear skiving was established to design and simulate the skiving process of a helical gear with a conical skiving cutter considering grinding allowance. The proposed skiving cutter is generated by correcting the normal rack, in which the normal rack segments corresponding to the involute segments of the work gear are defined by linear equation based on the grinding allowance. In the illustrated example, the normal deviations of the topologies of the skived gear tooth profiles were no greater than 4.319 µm, demonstrating that the mathematical model for simulating the skiving process and designing the skiving cutter considering grinding allowance is both accurate and feasible.