1 Introduction

As a key functional component of CNC machine tools, CNC machine tool manufacturers have focused on motorized spindle for its advantages of compact structure, low noise and fast response [1]. The performance degradation of motorized spindle seriously affects the machining accuracy and efficiency of CNC machine tools and causes serious economic losses [2]. Using the monitoring information collected by sensors to infer the health condition of the motorized spindle and further develop maintenance strategies is an effective means of preventing motorized spindle failure [3, 4]. When the motorized spindle fails, the vibration signal at the bearings shows nonlinear and non-stationary characteristics. For such signals, the commonly used signal pre-processing methods include wavelet packet transform (WPT), empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), and local mean decomposition (LMD) [5,6,7,8]. The combination of the above methods with machine learning to obtain accurate results has aroused the research interest of scholars. Fei proposed the combination of WPT and SVM to realise the fault evaluation of rolling bearings [9]. Sun et al. proposed that EEMD to decompose vibration signals and used PSO-SVM to identify the faults of bevel gears [10]. Tian et al. proposed to use of LMD and SVD to process vibration signals and then ELM to identify rolling bearing faults [11]. Although the above methods have been applied, some shortcomings remain; for example, WPT requires the artificial selection of parameters [12]. EMD has some problems, such as modal aliasing and the endpoint effect. Although LMD can reduce the mode aliasing to a certain extent, it is greatly affected by noise [13]. EEMD is limited by its large amount of computation and requires human experience to determine the added white noise amplitude and the number of iterations [14]. VMD is an adaptive, non-recursive modal variational signal processing method that can overcome the shortcomings of the above methods to a certain extent [15, 16]. An and Zhang proposed to use of VMD to decompose the vibration signals of bearing loosening and gear faults and carry out the envelope demodulation analysis of sensitive modal components [17].

However, the traditional VMD is susceptible to the influence of penalty factor α and decomposition layers K, and the setting of these two key parameters is a problem that must be urgently solved. Kumar et al. used kernel mutual information as a fitness function, genetic algorithm to optimise two parameters, and the optimised VMD to extract the early fault features of bearings [18]. Zhong et al. proposed to use the whale algorithm to optimize two parameters, and proposed a millimeter-wave radar FOD detection method based on the optimised VMD [19]. To sum up, on the basis of a reasonable fitness function, the penalty factor α and decomposition layers K in the VMD can be optimised by using a heuristic algorithm. In addition, the performance of the heuristic algorithm can determine the computational efficiency of this process. Therefore, the STOA is proposed to optimise two parameters in the VMD. In terms of convergence and computational complexity, the STOA is highly competitive with nine other heuristic algorithms [20].

The essence of data-driven health condition evaluation is to establish the mapping relationship between the feature space and the health condition. Compared with some intelligent algorithms such as artificial neural networks (ANN), decision tree (DT), support vector machine (SVM), hidden Markov model (HMM) has the advantages of simple structural expression and strong physical interpretation, which can be better applied to the health condition evaluation of motorized spindle [21,22,23]. However, the signal measured by a sensor is a continuous signal. Although this signal can be discretised, the use of limited discrete symbols to represent continuous observation variables will inevitably lead to information loss. Aiming at the above problems, the continuously fault features can be represented by introducing a probability density function. Theoretically, the Gaussian mixture model (GMM) can use several weighted Gaussian distributions to approximate the probability density function of the observation matrix in each condition. GMM-HMM has better modelling and analysis abilities than HMM. Liu et al. proposed to use of GMM-HMM for bearing fault diagnosis, input the test data into the trained GMM-HMM, and output the bearing state [24]. Zheng and Gao proposed to use GMM-HMM to create classifiers for diagnosing the down-dole operating conditions of sucker rod pumping [25].

This paper uses the optimised VMD to remove the noise component in the original signal and combines the dynamic modelling ability of GMM-HMM to construct the health condition evaluation model of the motorized spindle. The rest of this paper is arranged as follows. In Sect. 2, the related methods of this paper are briefly introduced. In Sect. 3, the steps of the proposed method are described in detail. In Sect. 4, the hybrid simulation signal is analysed by using the optimised VMD to verify the superiority of this method. In Sect. 5, the rotor unbalance fault experiment is carried out on a motorized spindle, and the proposed method is used to diagnose the health condition to verify the effectiveness and superiority of the proposed method. The paper is summarised in Sect. 6.

2 Methodology

2.1 Optimised VMD

VMD has a complete mathematical theoretical basis and can decompose the original signal (f) into a series of intrinsic mode functions (IMFs) nonlinearly and determine the frequency centre and bandwidth of the IMFs. The constrained variational model can be expressed as follows:

$$\left\{\begin{array}{l}\begin{array}{cl} {\mathop {\min }\limits_{{\left\{ {u_{k} } \right\},\left\{ {\omega_{k} } \right\}}} } & {\left\{ {\sum\limits_{k} {\left\| {\partial_{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{\pi t}} \right) * u_{k} \left( t \right)} \right] \cdot e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } } \right\}} \\ {s.t} & {\sum\limits_{k} {u_{k} = f} } \end{array}\end{array}\right.$$
(1)

where uk(t) is the intrinsic modal function, ωk is the centre frequency, ∂t is the gradient relative to the time series, and δ(t) is the unit pulse function.

Equation (1) is transformed into an unconstrained variational problem using penalty factor α and Lagrange multiplier λ(t) as follows:

$$\begin{aligned} L\left( {u_{k} ,\omega_{k} ,\lambda } \right) & = \alpha \sum\limits_{k} {\left\| {\partial_{t} [(\delta (t) + \frac{j}{\pi t}) * u_{k} (t)] \cdot e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } \\ & \quad + \left\| {f - \sum\limits_{k} {u_{k} (t)} } \right\|_{2}^{2} + \left\langle {\lambda (t),f - \sum\limits_{k} {u_{k} (t)} } \right\rangle \end{aligned}$$
(2)

An alternating direction multiplier algorithm is used to update relevant parameters as follows:

$$\hat{u}_{k}^{n + 1} (\omega ) = \frac{{\hat{f}(\omega ) - \sum\limits_{i \ne k} {\hat{u}_{i} (\omega )} + \hat{\lambda }(\omega )/2}}{{1 + 2\alpha (\omega - \omega_{k} )^{2} }}$$
(3)
$$\omega_{k}^{n + 1} = \frac{{\int_{0}^{\infty } {\omega \left| {\hat{u}_{k} (\omega )} \right|^{2} d\omega } }}{{\int_{0}^{\infty } {\left| {\hat{u}_{k} (\omega )} \right|^{2} d\omega } }}$$
(4)
$$\hat{\lambda }^{{n{ + }1}} (\omega ){ = }\hat{\lambda }^{n} (\omega ){ + }\tau {[}\hat{f}(\omega ){ - }\sum\limits_{k} {\hat{u}_{k}^{n + 1} (\omega )]}$$
(5)

where τ is the fidelity coefficient, ^ represents the Fourier transform, and n is the number of iterations Given discrimination accuracy ε, i.e. ε > 0, if Eq. (6) is satisfied, then the iteration is stopped.

$$\sum\limits_{k} {{{\left\| {u_{k}^{n + 1} - u_{k}^{n} } \right\|_{2}^{2} } \mathord{\left/ {\vphantom {{\left\| {u_{k}^{n + 1} - u_{k}^{n} } \right\|_{2}^{2} } {\left\| {u_{k}^{n} } \right\|_{2}^{2} }}} \right. \kern-\nulldelimiterspace} {\left\| {u_{k}^{n} } \right\|_{2}^{2} }}} < \varepsilon$$
(6)

However, the traditional VMD is susceptible to the influence of penalty factor α and decomposition layers K. When penalty factor α is improperly selected, VMD cannot obtain the optimal bandwidth IMF. When decomposition layers K is set improperly, over-decomposition or under-decomposition will occur. To solve this problem, this paper proposes to optimise the two parameters of the VMD by using the STOA and takes composite index KEI as the fitness function. Sooty terns are marine gregarious birds that mainly feed on fish, earthworms and insects. The racial characteristics of sooty terns include migratory and aggressive behaviours, and the mathematical model is as follows:

Migration behaviour: During migration, sooty terns should meet three conditions, namely, avoiding conflict, gathering and updating. The relevant descriptions are shown in Eqs. (7)–(9).

$$\left\{ \begin{array}{l} \overline{C}_{st} = S_{A} \times \overline{P}_{st} (z) \hfill \\ S_{A} = C_{f} - [z \times (C_{f} /Max_{iterations} )] \hfill \\ z = 1,2,3 \cdots ,Max_{iterations} \hfill \\ \end{array} \right.$$
(7)

where \(\overline{C}_{st}\) represents the position of an individual that does not collide with other individuals, \(\overline{P}_{st} (z)\) represents the current location of the individual, SA is a variable used to avoid conflicts between adjacent individuals, Cf is the control variable used to adjust SA, and z represents the iteration times.

$$\left\{ \begin{array}{l} \overline{M}_{st} = C_{B} \times [\overline{P}_{bst} (z) - \overline{P}_{st} (z)] \hfill \\ C_{B} = 0.5 \times R_{and} \hfill \\ \end{array} \right.$$
(8)

where \(\overline{M}_{st}\) represents the different locations of individual \(\overline{P}_{st}\) towards best fit individual \(\overline{P}_{bst} (z)\), CB is the random variable responsible for improved exploration, and Rand is a random number between 0 and 1.

$$\overline{D}_{st} = \overline{C}_{st} + \overline{M}_{st}$$
(9)

where \(\overline{D}_{st}\) represents the gap between the individual and best fit individual.

Aggressive behaviour: When sooty terns attack their prey, their spiral behaviour in the air can be described as follows:

$$\left\{ \begin{array}{l} x^{\prime} = R_{adius} \times \sin (i) \hfill \\ y^{\prime} = R_{adius} \times \cos (i) \hfill \\ z^{\prime} = R_{adius} \times i \hfill \\ r = u \times e^{kv} \hfill \\ \end{array} \right.$$
(10)

where Radius represents the radius of each spiral, i is a variable between 0 and 2π, and u and v are constants for defining the spiral shape.

According to Eq. (10), the position of the updated individual is as follows:

$$\overline{P}_{st} (z) = \left[ {\overline{D}_{st} \times \left( {x^{\prime} + y^{\prime} + z^{\prime}} \right)} \right] \times \overline{P}_{bst} (z)$$
(11)

where \(\overline{P}_{st} (z)\) represents updating the positions of other search individuals and saving the best optimal solution.

Another key problem of the optimised VMD is the construction of a fitness function. In the field of mechanical fault diagnosis, envelope entropy and kurtosis indexes are mainly used to measure the degree of fault. However, envelope entropy can only reflect the periodicity of the signal but not the impact characteristics of the signal. The kurtosis index only considers the distribution density of the impact signal and ignores the highly dispersed components. In this paper, the characteristics of the two indexes are comprehensively considered, the envelope entropy is modified by the kurtosis index, and fitness function KEI is constructed. The relevant definitions are as follows:

$$KEI = \frac{{K_{v}^{k} }}{{H_{e}^{k} }}, \, k = 1,2, \cdots K$$
(12)

where Kvk is the kurtosis index of the kth IMF, and Hek is the envelope entropy of the kth IMF. The relevant definitions are as follows:

$$\left\{ \begin{array}{l} p_{k} (t_{i} ) = \frac{{h_{k} (t_{i} )}}{{\sum\limits_{i = 1}^{N} {h_{k} (t_{i} )} }} \hfill \\ H_{e} = \frac{{ - \sum\limits_{i = 1}^{N} {p_{k} (t_{i} )\ln p_{k} (t_{i} )} }}{{{\text{l}}n\,N}} \hfill \\ \end{array} \right.$$
(13)

where N is the number of data points, and hk(ti) is the envelope signal after Hilbert demodulation. He is the corresponding envelope entropy.

$$\left\{ \begin{array}{l} K_{v} = \frac{{\frac{1}{N - 1}\sum\limits_{i = 1}^{N} {\left[ {u_{k} (t_{i} ) - \overline{u}_{k} (t)} \right]^{4} } }}{{\sigma_{k}^{4} }} \hfill \\ \overline{u}_{k} (t) = \frac{1}{N}\sum\limits_{i = 1}^{N} {u_{k} (t_{i} )} \hfill \\ \sigma_{k} = \sqrt {\frac{1}{N - 1}\sum\limits_{i = 1}^{N} {\left[ {u_{k} (t_{i} ) - \overline{u}_{k} (t)} \right]^{2} } } \hfill \\ \end{array} \right.$$
(14)

where \(\overline{u}_{k} (t)\) is the mean value of the IMFs, and σk is the standard deviation of the IMFs.

Considering that the optimised VMD takes the minimum fitness value as the optimisation objective, the optimisation objective is expressed as follows:

$$\left\{ \begin{array}{l} fit = \min \left\{ { - KEI} \right\} \hfill \\ s.t. \, k_{\min } \le k \le k_{\max } , \, \alpha_{\min } \le \alpha \le \alpha_{\max } \hfill \\ \end{array} \right.$$
(15)

2.2 GMM-HMM

The HMM is a double stochastic process, including a Markov process that describes the transition between conditions and a stochastic process that describes the observed sequence in each condition. The relationship between these processes is shown in Fig. 1. Generally, the HMM consists of the following five elements:

  1. 1.

    Q is the number of hidden states. If the state at time t is denoted as qt, then \(q_{t} \in \{ S_{1} ,S_{2} ,....,S_{Q} \}\).

  2. 2.

    M is the number of the observation symbols. If the observations at t time is ot, then \(o_{t} \in \{ v_{1} ,v_{2} ,....,v_{M} \}\).

  3. 3.

    A is the state transition probability matrix. \(A = \{ a_{ij} \}_{Q \times Q}\), and aij represents the probability of transition from state Si at time t to state Sj at time t + 1.

    $$a_{ij} = P(q_{t + 1} = S_{j} |q_{t} = S_{i} ), \, i \ge 1, \, j \le Q$$
    (16)
  4. 4.

    B is the observation probability matrix. \(B = \{ b_{i} (v_{m} )\}_{Q \times M}\), and bi(vm) represents the probability that the observation symbol is vk when the state is Si at time t.

    $$b_{i} (v_{k} ) = P(v_{k} |q_{t} = S_{i} ), \, 1 \le k \le M$$
    (17)
  5. 5.

    π is the initial state distribution. πi represents the probability of being in state Si at the initial time.

    $$\pi_{i} = P(q_{1} = S_{i} ),1 \le i \le Q,\sum\limits_{i = 1}^{Q} {\pi_{i} = 1}$$
    (18)
Fig. 1
figure 1

Schematic of the structure of the HMM

Full size image

A complete HMM can be represented by λ = (π, A, B). However, in the actual process of condition monitoring, the observation symbols of the signal are usually continuous variations. Although the continuous signal can be discretised, the use of discrete symbols to represent continuous observation variables will inevitably cause information loss. To solve the above problems, the GMM can be used to approximate the probability density function of the observation matrix in each state. The observations at time t is assumed to be a D-dimensional vector. For state Si, the continuous probability distribution function bi(ot) can be expressed as follows:

$$\left\{ \begin{array}{l} b_{i} (o_{t} ) = \sum\limits_{m = 1}^{{M_{i} }} {w_{im} b_{im} (o_{t} ) = } \sum\limits_{m = 1}^{{M_{i} }} {w_{im} N(o_{t} ,\mu_{im} ,Cov_{im} )} \hfill \\ \sum\limits_{m = 1}^{{M_{i} }} {w_{im} = 1, \, w_{im} \ge 0} \hfill \\ \end{array} \right.$$
(19)

where Mi is the number of Gaussian components, bim(ot) is the probability density function of the mth component, wim is the weight of the mth Gaussian component, μim is the mean vector, Covim is the covariance matrix, and \(N(o_{t} ,\mu_{im} ,Cov_{im} )\) is the Gaussian probability density function:

$$\begin{array}{l} N(o_{t} ,\mu_{im} ,Cov_{im} ) \hfill \\ = \frac{1}{{\sqrt {(2\pi )^{D} \left| {Cov_{im} } \right|} }}\exp [ - \frac{1}{2}(o_{t} - \mu_{im} )^{{\text{T}}} Cov_{im}^{ - 1} (O_{t} - \mu_{im} )] \hfill \\ \end{array}$$
(20)

In this part, the algorithms used are the Forward–Backward and Baum–Welch algorithms.

3 Proposed method

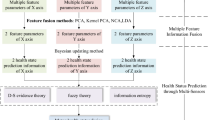
In this study, a health condition evaluation method for motorized spindle on the basis of optimised VMD and GMM-HMM is proposed. The flow of the proposed method is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed method

Full size image

Step 1

According to the historical information, divide the health condition into L levels and collect the original signals of each level.

Step 2

Initialise the parameters of the STOA.

Step 3

Randomly initialise the search individuals and calculate the fitness value of each search individual. Update the individual location and record the global optimal fitness value. If the iteration condition is reached, then the optimal parameter combination [α, K] is produced. Otherwise, the iteration continues.

Step 4

The original signal is decomposed by the optimised VMD, and the KEI of the IMFs is calculated. The IMFs are sorted by the KEI, and the former ⌈K/2⌉ IMFs are reconstructed. ⌈K/2⌉ indicates that K/2 is rounded up.

Step 5

Extract the 10-dimensional time (P1–P10), 5-dimensional frequency (P11–P15) and 10-dimensional scale (P16–P25) domain features of the reconstructed signals to construct and normalise the multi-domain high-dimensional feature matrix F.

The mathematical expressions of time domain and frequency domain features are shown in Table 1. The main parameters of multi-scale weighted permutation entropy include embedding dimension l = 5, delay time τ = 1 and scale factor s = 10 [26, 27].

Table 1 Mathematical expressions of time domain and frequency domain features
Full size table

In Table 1, P1-P10 are time-domain features, and P11-P15 are frequency domain features. x(t) is the reconstructed signal, and N is the number of data points. s(y) is the frequency spectrum of x(t), Y is the number of spectral lines, and fy is the frequency value of the y-th spectral line. The intermediate parameter σ is defined as follows:

$$\sigma { = }\sqrt {{{\sum\limits_{i = 1}^{N} {[x(t) - \overline{x}(t)]^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N} {[x(t) - \overline{x}(t)]^{2} } } {N - 1}}} \right. \kern-\nulldelimiterspace} {N - 1}}}$$
(21)

Step 6

Use the supervised L-Isomap (SL-Isomap) for the secondary feature extraction of multi-domain high-dimensional feature matrix F to obtain low-dimensional feature matrix F′ [28, 29].

Step 7

Divide the training and test data according to a certain proportion. Train the GMM-HMM of each health condition using the Baum–Welch algorithm and establish the GMM-HMM library.

Step 8

Substitute the test data into the GMM-HMM library and calculate the log-likelihood probability (LLP) of each model using the Forward–Backward algorithm. Meanwhile, the Softmax function is used to map LLP into [0, 1] to obtain intuitive results, namely:

$${\text{SLLP}}_{i} { = } = \frac{{{\text{exp}}({\text{LLP}}_{i} )}}{{\sum\limits_{i = 1}^{N} {{\text{exp}}({\text{LLP}}_{i} )} }}{,}\;1 \le i \le L$$
(22)

The SLLP can reflect the degree of membership between the test data and each model, so the condition corresponding to the maximum SLLP is the most probable health condition, that is,

$$Label(O) = {\text{arg max}}\{ {\text{SLLP}}_{i} )\} , \, 1 \le i \le L$$
(23)

4 Simulation signal analysis

In this section, the hybrid simulation signal y(t) is analysed by using the optimised VMD. The purpose of the analysis is to determine the sensitive IMF with the most fault information and further extract the fault frequency. The hybrid simulation signal y(t) consists of 4 parts, including fault impact signal x(t), the rotation signal r(t) of other components, random impact signal h(t) and random noise n(t). Among them, fault impact signal x(t) is based on the partial fault of the sun gear in the planetary gearbox, and its mathematical model can be expressed as follows [30]:

$$\left\{ \begin{array}{l} x(t) = s(t)\sum\limits_{k = 1}^{K} {a_{k} (t)\cos } [2\pi kf_{m} t + b_{k} (t) + \varphi_{k} ] \hfill \\ s(t) = 1 - \cos (2\pi nf_{sr} t) \hfill \\ a_{k} (t) = \sum\limits_{n = 1}^{N} {A_{kn} \cos (2\pi nf_{s} t + \alpha_{kn} )} \hfill \\ b_{k} (t) = \sum\limits_{n = 1}^{N} {B_{kn} \cos (2\pi nf_{s} t + \beta_{kn} )} \hfill \\ \end{array} \right.$$
(24)

where ak(t) and bk(t) are amplitude and frequency modulations, respectively; s(t) is amplitude modulation caused by the rotation of the sun gear; fm is the gear meshing frequency; fs is fault frequency; and fsr is the absolute rotation frequency of the sun gear.

The rotation signal r(t) of the other components can be represented by multiple harmonic components as follows:

$$r(t) = \sum\limits_{i} {C_{i} } \sin (2\pi f_{i} t + \theta_{i} )$$
(25)

where Ci, fi and θi represent the amplitude, frequency and phase of each harmonic component, respectively.

The random impact signal h(t) is shown as follows:

$$\left\{ \begin{array}{l} h(t) = \sum\limits_{i} {R_{j} H(t - Tr_{j} )} \hfill \\ H(t) = e^{ - \beta t} \sin (2\pi f_{RE} t) \hfill \\ \end{array} \right.$$
(26)

where Rj is a random variable, H(t) is the unit pulse component, β is the damping coefficient, and fRE is the pulse resonance frequency.

Random noise n(t) is an AWGN with SNR =  − 8db. The sampling frequency is set to 5120 Hz and the sampling time to 2 s. The main parameter values of hybrid simulation signal y(t) are shown in Table 2.

Table 2 Main parameter value of hybrid simulation signal
Full size table

The time domain waveform of the hybrid simulation signal y(t) is shown in Fig. 3, and the FFT spectrum and the envelope spectrum is shown in Fig. 4. Figure 3 shows that fault impact signal x(t) has been completely covered by strong background noise, and the periodic impact caused by the fault cannot be observed in the time-domain waveform. In the FFT spectrum of hybrid simulation signal y(t), only the frequencies (f1 and f2) of the two harmonic components can be observed, and fault frequency fs cannot be observed. In the envelope spectrum of hybrid simulation signal y(t), although the fault frequency fs can be observed, its amplitude is not prominent, and there are many interference components around. During calculation, the search range of penalty factor α is set as [1000, 8000], the search range of decomposition layers K is set to [3, 7], the number of searched individuals is 15, and the maximum iteration number is 25. The optimal parameter combination calculated by the STOA is [5, 4100], and the iteration process is shown in Fig. 5. Convergence can be achieved after 10 iterations.

Fig. 3
figure 3

Hybrid simulation signal

Full size image
Fig. 4
figure 4

FFT spectrum and envelope spectrum of hybrid simulation signal

Full size image
Fig. 5
figure 5

Iterative process

Full size image

The decomposition result of the optimised VMD is shown in Fig. 6. In Fig. 6a, the IMF corresponding to the maximum value of KEI is IMF3, so IMF3 is selected as the sensitive component and envelope spectrum analysis is carried out. The analysis results are shown in Fig. 6b. The fault frequency and its frequency multiplier (fs = 50 Hz, 2 fs = 1000 Hz, 3 fs = 150 Hz, 4 fs = 200 Hz), the absolute rotation frequency of the sun gear (fsr = 30 Hz) and related frequency (fs-fsr = 20 Hz) can be clearly extracted. The above results verify the effectiveness of the optimised VMD.

Fig. 6
figure 6

Decomposition results of optimised VMD

Full size image

To further verify the superiority of the optimised VMD, this method is compared with EMD and EEMD. Among them, 9 IMFs were obtained by EMD, and 13 IMFs are obtained by EEMD. Figure 7 shows the envelope spectra of the first 4 IMFs by EMD and EEMD.

Fig. 7
figure 7

Decomposition results of EMD and EEMD

Full size image

In Fig. 7a, EMD can extract absolute rotation frequency fsr, fault frequency fs and its 2 times frequency, but many interference components exist within the range of 100 Hz to 200 Hz. In Fig. 7b, EEMD can extract absolute rotation frequency fsr and fault frequency fs, but many interference components also exist within the range of 50 Hz to 200 Hz. The above results further verify the superiority of the optimised VMD.

5 Case analysis

5.1 Rotor unbalance fault experiment of motorized spindles

In this paper, the rotor unbalance fault simulation experiment of a certain type of motorized spindle was carried out by using the motorized spindle performance monitoring test platform. The structure of the test platform is shown in Fig. 8. The test platform is controlled by the control cabinet and the computer, which can simulate the actual working conditions of the motorized spindle. The tested motorized spindle is fixed by the clamping device, and the auxiliary devices such as oil–gas lubrication device, water cooler and frequency converter can ensure the operation of the tested electric spindle.

Fig. 8
figure 8

Motorized spindle performance monitoring test platform

Full size image

Rotor unbalance fault is simulated by adding different numbers of bolts at the output end of the tested motorized spindle without applying force and torque. The health condition is divided into five levels. During the experiment, the vibration signal of the front bearing of the tested motorized spindle was monitored. The model of the acquisition device was NI-cDAQ9184, the spindle speed was 5000r/min, the sampling frequency was 1.28 kHz, the sampling time of the sample signal was 0.1 s, and 50 groups of sample signals were collected at each level.

According to Steps 2 to 4 in Sect. 3, the sample signal is decomposed by the optimised VMD, the KEI of the IMFs is calculated, and the selected IMFs is reconstructed. According to Step 5, the multi domain features of the reconstructed signal are extracted, and the normalised high-dimensional feature matrix is constructed. The mean value feature curves of all levels are shown in Fig. 9.

Fig. 9
figure 9

Mean feature curves of all levels

Full size image

In Fig. 9, time domain features P1, P2, P3, P5 and frequency feature P11 can effectively identify each health condition. Although the entropy features (P17 to P22) in the scale domain can accurately identify levels 4 and 5, the recognition effect for levels 1 to 3 is poor. To sum up, if all 25-dimensional features are used to represent the health condition of the motorized spindle, redundant information will be inevitably produced. According to Step 6, SL-Isomap was used to carry out secondary feature extraction to construct low-dimensional feature matrix F′. In SL-Isomap, the nearest neighbour parameter is set to 50 and regulating factor a to 0.5. The visualisation result of a low-dimensional feature matrix is shown in Fig. 10. In Fig. 10, intrinsic dimension d = 3, the samples of each health condition can be basically stripped, and the spacing between the samples is clear.

Fig. 10
figure 10

Visualisation of low-dimensional feature matrix

Full size image

The training and test samples were randomly divided in 2:3. Ready, the number of hidden states of the GMM-HMM was set to four, the number of Gaussian components to two, and the maximum number of iterations to 50. The iteration process is shown in Fig. 11. The curves of all the levels converge after the 24th, 11th, 16th, 22nd, and 8th iterations. The library is constructed based on GMM-HMM, and then the test samples are respectively input into the library to calculate LLP. The health condition corresponding to the maximum LLP is the most likely condition of the motorized spindle.

Fig. 11
figure 11

Training curves of GMM-HMM

Full size image

The evaluation results of five health condition levels are shown in Fig. 12 in which solid points represent the real labels of the test samples. The label corresponding to the highest point in each sample is the evaluation result. In Fig. 12, the evaluation accuracy of level 1 is 90%, level 2 is 90%, level 3 is 86.67%, level 4 is 90%, level 5 is 86.67%, and the average evaluation accuracy of the five levels is 88.67%. When the evaluation result is wrong, the evaluation label and the real label are always adjacent, which also conforms to the degradation law of motorized spindle. The above results verify the effectiveness of the proposed method.

Fig. 12
figure 12

Evaluation results of five health condition levels

Full size image

5.2 Comparison and analysis

The ‘SL-ISOMAP + GMM-HMM’ was compared with several combination methods to further verify the superiority of the method. Various combination methods are composed of three manifold learning methods and two classical classifiers [31, 32]. The three manifold learning methods include Isomap, t-Distributed Stochastic Neighbour Embedding (t-SNE), and Laplacian eigenmaps (LE). The two classical classifiers include PSO–SVM and genetic algorithm optimisation-ELM (GA-ELM).

The nearest neighbour parameter of the Isomap, the LLE and the LE is set to 50, and the perplexity of the t-SNE to 30. In PSO–SVM, the population size is 20, the learning factor is 1.5, the inertia weight is 0.6, the maximum number of iterations is 50, and the radial basis function is selected as the kernel function. In GA–ELM, the population size is 20, the generation gap is 0.95, the crossover probability is 0.7, the mutation probability is 0.01, the maximum genetic generation number is 50 and the number of neurons in the hidden layer is 30. Taking the average accuracy as the performance index, the calculation results of various combination methods are shown in Table 3.

Table 3 Evaluation accuracy of combined methods
Full size table

In Table 3, the average accuracy of ‘SL-Isomap + GMM-HMM’ ranks first among the combination methods. Compared with ‘SL-Isomap + PSO-SVM’ and ‘SL-Isomap + GA-ELM’, the average accuracy of the proposed method improved by 4% and 5.33%, respectively. For the same manifold learning method, the average accuracy of GMM-HMM is the highest, and that of GA-ELM is the worst. For the same classifier, SL-Isomap has the best dimension reduction performance, while LE has the worst. For levels 3, 4 and 5, the accuracy of ‘SL-Isomap + GMM-HMM’ is higher than the other combined methods. For level 1, the accuracy of ‘SL-Isomap + GMM-HMM’ and ‘SL-Isomap + GA-ELM’ is 90%. For level 2, the accuracy of ‘SL-Isomap + GMM-HMM’ and ‘SL-Isomap + PSO-SVM’ is 90%. The above results further verify the superiority of ‘SL-Isomap + GMM-HMM’.

6 Conclusion

Extracting and using the useful information of vibration signals in the industrial environment with a strong noise are the key problem of the health condition evaluation of motorized spindle. In this paper, a health condition evaluation method for motorized spindles on the basis of the optimised VMD and the GMM-HMM is proposed. This paper is summarised as follows:

  1. 1.

    The optimised VMD is used to decompose the hybrid simulation signal, and the fault frequency and its frequency doubling part can be clearly extracted from the envelope spectrum of the sensitive IMF. The results show that the optimised VMD can effectively extract the fault information hidden in strong background noise.

  2. 2.

    To verify the proposed method, rotor unbalance experiment was carried out on a certain type of motorized spindle. The evaluation results show that the accuracy of levels 1 to 5 is 90%, 90%, 86.67%, 90%, and 86.67%, respectively, and the average accuracy is 88.67%, indicating that the proposed method can effectively evaluate the health condition of motorized spindle.

  3. 3.

    The average accuracy of ‘SL-Isomap + GMM-HMM’ ranks first among the combination methods. The result further verifies the superiority of the proposed method.