1 Introduction

In general, the high-quality machining of a complex curve consists of two aspects, i.e., high speed and high accuracy.

In terms of high speed machining, it means that a machine tool can processing a complex curve in the shortest cycle time. An appropriate feedrate scheduling method guarantees short cycle time. For example, in view of a long tool path, an interval adaptive feedrate scheduling method based on a dynamic moving look-ahead window is proposed [1]. This method divides a long spline into several intervals, and generates the smooth s-shape feedrate profile for each interval successively based on limited jerks. The finite impulse response filter (FIR) is another efficient smooth feedrate scheduling method. Based on FIR-chain techniques, the smooth and accurate reference motion profile can be generated, as well as the acceleration and jerk continuous motion profiles [2]. For a blend path, it is of significance with an efficient feedrate scheduling method. A typical blend path consists of small line segments and small parametric curves. And the sharp corners formed by the intersection of two line segments are smoothed with parametric curves which have C2 [3] or C3 continuity [4]. The feedrate of this kind of blend curve can be planned with the bidirectional scan algorithm [5].

More recently, for pursuing short cycle time, the optimization method is introduced to feedrate scheduling. For example, a heuristic trajectory planning algorithm is proposed [6]. It can provide a near-optimal minimum time trajectory for problems with higher order dynamic states. To suppress the unwanted vibration in the processing of parts, motion commands are generated based on optimal frequency spectra of each axial acceleration [7]. In this method, kinematic limits are considered to constrain the frequency spectra, and the Quadratic programming is used to obtain the optimal solution. In addition, optimization methods also play an important role in the corner blending problems. Especially, mixing linear path with polynomial curves can be formulated as a convex optimization problem [8].

Since the optimal control has inherent advantages in path planning [9, 10] and trajectory generation [11, 12], it has attracted more and more attentions. A Bang-Bang control is adopted to plan the feedrate for a multi-axis system in Frenet-Serret frame [13]. Afterwards, linear programming is used to solve the optimal control problem restrained by kinematic constraints. And a feedback interpolation method is developed for real-time interpolation. Meanwhile, a parallel windowing (PWin) algorithm is also integrated into the process of feedrate optimization [14]. Considering dynamics constraints, the path tracking task of a manipulator is formulated as an optimal control problem [15]. In this literature, to reduce the solution difficulty, the optimal control problem is transformed into a convex optimization problem. Since the feedrate profile of a machine tool is optimized, the cycle time is significantly reduced with these methods. However, to improve optimization efficiency, appropriate solving techniques should be adopted during applying optimization-based methods.

In terms of the high-precision machining, there are many ways to realize this objective. For example, through restraining some indexes, high accuracy machining results can be gained. Tracking errors of a multi-axis machine tool are usually considered as constraints of an optimal control problem except kinematic ones, such as jerks, accelerations, and feedrate [16]. Then machining accuracy can be improved by restraining tracking errors below permissible value. However, the tracking error reduction is an indirect way to improve accuracy, whereas the contour error is a direct manner. Here is a simple explanation. In general, a machining task is implemented in cartesian space. Taking a 3-axis machine tool for example, a processed curve is the synthesis of displacement of the tool tip on three axes. Three independent servo systems work in coordination to drive the tool tip to the reference position. Even if tracking errors on all axes are small, the contour error is not necessarily small, and vice versa. Therefore, an appropriate controller can be designed to control the contour error directly, such as cross coupling controller (CCC). For example, a single-input fuzzy-logic controller is taken as the CCC to improve the contouring accuracy [17]. Except CCC strategy, the model predictive control (MPC)-based scheme is also used for contour error suppression. In each receding optimization, both contour error components and tracking errors are taken into performance index, with assigning the former greater weight than the latter [18]. For a dual 5-dof manipulator, a MPC-based controller is adopted to reduce the equivalent contour error [19], and the integral sliding mode control [20] is integrated to improve robustness.

From above, contour error reduction and feedrate optimization are generally implemented alone. Actually, we can perform both at the same time. For instance, through introducing contour error constraints, servo error pre-compensation and time optimal feed optimization are performed synchronously [21]. Under the optimal control framework, this kind of synchronous optimization is more easily to be realized.

The real-time interpolation is another significant factor which affects the machining accuracy. For parameter tool paths, there are many mature interpolation methods, such as Taylor expansion-based interpolator [22], predictor–corrector-based interpolator [23], and Adams–Bashforth methods [24]. However, there are some drawbacks needed to be overcome for these methods. For instance, some methods may lead to the fluctuation of feedrate. Some other methods may take longer time than interpolation period to obtain a next interpolation point. Hence, some scholars proposed minimal fluctuation methods to suppress feedrate fluctuation. A polynomial equation-based interpolation method for Nurbs tool paths is proposed [25]. According to sample step size, this method formulates the polynomial equation with respect to the curve parameter. Afterwards, the Newton’s method is used to obtain numerical solution of the next interpolation point. Nurbs curves can be also used to construct the relationship between curve parameter and arc length of a tool path [26]. It is a key point of the minimal fluctuation methods that the exact functional relationship should be determined in advance.

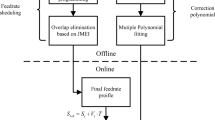
In this paper, we propose an integrated jerk-limited method of minimal time trajectory planning with confined contour error (IJLMTPC). Firstly, considering the OCP of feed planning, we adopt the CVP technique to solve the convex optimization problems. To improve solving efficiency, the jerk constraints are replaced with contour error ones, because they are included in the contour error deduced based on high-order transfer function. Secondly, since the feedrate profile obtained from the first stage is the function of curve parameter, it is mapped into time domain to adapting with six types of forward planning profiles. The limited tangent jerk is also used to further smooth the feed. The distance constraints are introduced into the backward planning to ensure that the deceleration can be forecast. Finally, a minimal fluctuation methods is used in the real-time interpolation. In order to accurately describe the functional relationship between arc length and curve parameter, we propose parameter correction b-spline and corresponding refining algorithm. The outline of the proposed scheme is elaborated with following diagram in Fig. 1.

Fig. 1
figure 1

The architecture of proposed IJLMTPC

Full size image

The remainder of this paper is arranged as follows. For convenience, Section 2 introduces the parameter correction b-spline, as well as the refining algorithm. The basic optimal control formulation known as nominal problem of smooth trajectory generation (NPSTG) is investigated in Section 3. And the simplification of NPSTG is also described. Our proposed scheme, i.e., the integrated jerk-limited method of minimal time trajectory planning with confined contour error, is addressed in Section 4. The scheme is also named IJLMTPC for short. Section 5 illustrates the proposed method with two benchmark tool paths. Finally, conclusions are given in Section 6.

2 Parameter correction b-spline

Since most free curves are of non-arc-length parameterization, researchers proposed many available methods for obtaining the relationship between parameters and arc lengths [27]. Herein, a quintic b-spline is adopted to realize the mapping between the arc length and the parameter of a free curve.

Given a free parameter curve C(q) = [x(q),y(q)]T,q ∈ [0,1], the approximation arc length Λ(qa,qb) on the interval [qa,qb] can be calculated with the Simpson rule, i.e.,

$$ {\varLambda}(q_{a},q_{b})=\frac{\bar{h}}{3}(l(q_{a})+4l(q_{c})+l(q_{b})), $$
(1)

where qc = (qa + qb), \(\bar {h}=(q_{b}-q_{a})/2\), and \(l=\|\mathbf {C}^{\prime }(q)\|_{2}\) denotes the 2-norm. Given predefined arc length tolerance error ε1, Λ(qa,qb) is considered as the arc length, if it satisfies the following condition [28],

$$ |{\varLambda}(q_{a},q_{c})+{\varLambda}(q_{c},q_{b})-{\varLambda}(q_{a},q_{b})|<10*\varepsilon_{1}. $$
(2)

If (2) is not satisfied, the interval [qa,qb] is split into two equal parts, i.e., [qa,qc] and [qc,qb]. Then, (1) and (2) are applying to the two intervals, respectively.

By applying above operations iteratively, the whole interval [0,1] is split into many subintervals, and (2) holds on each subinterval. All the endpoints of these subintervals form a set Ξ1 = {q0,q1,⋯ ,qN− 1,qN}, where 0 = q0 < q1 < ⋯ < qN− 1 < qN = 1. Accordingly, at each qi(i = 0,1,⋯ ,N), the corresponding arc length Λi is obtained. Note that Λi is arc length on the interval [q0,qi], which can be easily computed through simple addition. If the interpolation technology was used to gain the relationship between qi and Λi at this time, the interpolation accuracy would not be guaranteed.

To guarantee the accuracy, although (2) has been satisfied on each subinterval, we still construct another set Ξ2 = {q(0,1),⋯ ,q(N− 1,N)} as a test data set, where q(i,i+ 1)(i = 0,⋯ ,N − 1) is the midpoint of interval [qi,qi+ 1]. Define Ξ = Ξ1 ∪Ξ2, and arrange the elements in ascending order in set Ξ. Equation (1) is adopted to compute the arc length of C(q) on each interval defined by any two adjacent elements of Ξ. As a result, a series of value pair (Λj,qj) are obtained, where qj(j = 0,⋯ ,2N) ∈Ξ, and Λj is the arc length on the interval [q0,qj]. To avoid ill-conditioning, Λj is normalized through

$$ {\tau_{j}^{f}} =({\varLambda}_{j}-{\varLambda}_{0})/({\varLambda}_{2N}-{\varLambda}_{0}). $$
(3)

A 5th-degree b-spline is interpolated to value pairs \(({\tau ^{f}_{j}},q_{j}), q_{j} \in {\varXi }_{1}\), which is expressed as

$$ q_{j}=Q\left( {\tau^{f}_{j}}\right)={\sum}_{l=0}^{L} F_{l,5}\left( {\tau^{f}_{j}}\right)P_{l}, $$
(4)

where Pl denotes the control point sequence, and \(F_{l,5}\left ({\tau ^{f}_{j}}\right )\) is the basis function.

The knots vector \(\mathbf {SX}=[\underbrace {0,\cdots ,0}_{5+1},sx_{6},sx_{7},\cdots \), sxM−p− 1, \(\underbrace {1,\cdots ,1}_{5+1}]\) is calculated through average method according to qj ∈Ξ1, and M = N + p + 1. Define \(\mathrm {\Phi }=[q_{0},\cdots ,q_{j},\cdots ]^{T}, q_{j} \in {\varXi }_{1}\). From (4), the following linear equations are obtained,

$$ \mathbf{TP}=\mathrm{\Phi}, $$
(5)

where

$$ \begin{array}{@{}rcl@{}} &&\mathbf{T}_{(N+1)\times (N+1)}=\\ &&\begin{bmatrix} 1&0&\cdots&0&0\\ F_{0,5}(q_{1})&F_{1,5}(q_{1})&\cdots&\cdots&0\\ \vdots&\vdots&{\vdots} &\vdots&\vdots\\ 0&0&{\cdots} &F_{L-1,5}(q_{N-1})&F_{L,5}(q_{N-1})\\ 0&0&\cdots&0&1 \end{bmatrix}, \end{array} $$
$$ \mathbf{P}_{(N+1)\times 1}= \begin{bmatrix} P_{0}& P_{1}& \cdots& P_{N-1}& P_{N} \end{bmatrix}^{T}, $$

and

$$ \mathrm{\Phi}_{(N+1)\times 1}= \begin{bmatrix} {\Phi}_{0}& {\Phi}_{1}& \cdots& {\Phi}_{L-1}& {\Phi}_{L}& \end{bmatrix}^{T}. $$

Equation (5) can be solved efficiently with some methods, such as least square and LU decomposition. In this paper, the Bragman iteration algorithm is utilized to solve (5), in order to avoid possible ill-condition and to gain sparse solution. Once control points vector is obtained, the quintic b-spline is expressed. However, the initial interpolation curve Q0(τ) is not necessarily satisfactory. We propose Algorithm 1 to refine the interpolation curve with test value pairs\([{\tau ^{t}_{j}},q_{j}],q_{j} \in {\varXi }_{2}\). The final output \(q_{j}=Q^{f}\left ({\tau ^{f}_{j}}\right )\) is the parameter correction b-spline, which is used to obtain precise parameter values during the interpolation stage of CNC machining.

figure a

Likewise, the mapping function from parameter to normalized arc length can also be interpolated to value pairs

$$ {\tau^{f}_{j}}=Q^{-1}(q_{j})={\sum}_{l=0}^{L} F_{l,5}(q_{j})\overline{P}_{l}. $$
(6)

This quintic b-spline function, i.e., \({\tau ^{f}_{j}}=Q^{-1}(q_{j})\), is known as the inverse function of parameter correction b-spline, which can be used to calculate the arc lengths.

3 Problem of smooth time optimal feedrate scheduling

The problem of smooth time optimal feedrate scheduling (PSTOF) is usually formulated as an optimization problem. To realize high speed machining, the time optimal objective function is given as

$$ OBJ=\min_{V} {\int}_{0}^{t_{f}} 1dt, $$
(7)

where V is the optimal feedrate profile. When machining a planar curve C(q), the motion of a machine tool is restrained by its kinematic abilities, such as command feedrate, axial accelerations, and axial jerks, which are written as

$$ {V^{2}(t)\leq {F_{B}^{2}},\quad |A_{h}(t)| \leq A_{Bh}, \quad |J_{h}(t)|\leq J_{Bh},} $$
(8)

where FB is the command feedrate bound, ABh are axial acceleration bounds, JBh are axial jerk bounds, and h ∈{x,y}. Nevertheless, the final time is free, which makes the PSTOF difficult to be solved.

The tool path C(q) = [x(q),y(q)]T is a free parametric curve. Assume that C(q) has a third-order continuous derivative at least. Let the symbol “⋅” be a derivative with respect to time. And Define that “′” denotes a derivative with respect to parameter q. After introducing parameter q into velocity, acceleration, and jerk, they can be written as [29]

$$ \left \{ \begin{aligned} &{\mathbf{v}=\dot{\mathbf{C}}=\mathbf{C}^{\prime}\dot{q},} \\ &{\mathbf{A}=\dot{\mathbf{v}}=\mathbf{C}^{\prime}\ddot{q}+\mathbf{C}^{\prime\prime}\dot{q}^{2},} \\ &{\mathbf{J}=\dot{\mathbf{A}}=\mathbf{C}^{\prime}\dddot{q}+3\mathbf{C}^{\prime\prime}\ddot{q}\dot{q}+\mathbf{C}^{\prime\prime\prime}\dot{q}^{3},} \end{aligned} \right. $$
(9)

where

$$ \mathbf{C}^{\prime}=\frac{d\mathbf{C}}{dq},\mathbf{C}^{\prime\prime}=\frac{d^{2}\mathbf{C}}{dq^{2}},\mathbf{C}^{\prime\prime\prime}=\frac{d^{3}\mathbf{C}}{dq^{3}}, $$

with parameter being neglected for simplification.

Define state variables as \(b=\dot {q}^{2}\) and \(\alpha =\ddot {q}\). Let the control variable be \(\beta =\frac {\dddot {q}}{\dot {q}}\) [30]. The PSTOF is transformed into an optimal control problem. Obviously, the system dynamics are expressed as

$$ \left \{ \begin{array}{cc} & b^{\prime}(q)=2\alpha(q),b(0)=\dot{q}^{2}_{0},\\ & \alpha^{\prime}(q)=\beta(q),\alpha(0)=\ddot{q}_{0}, \end{array} \right. $$
(10)

with a path constraint and final time constraints,

$$ \begin{array}{cc} & b(q)>0,q\in[0,1],\\ & b(1)=\dot{q}^{2}_{f},\alpha(1)=\ddot{q}_{f}. \end{array} $$
(11)

Since \(\dot {q}=\frac {dq}{dt}\), we have \(dt=\frac {dq}{\dot {q}}\) [31]. Through replacing variable t with q, (7) can be transformed into following cost function

$$ { OBJ=\min_{b,\alpha, \beta} {{\int}_{0}^{1}} \frac{1}{\dot{q}}dq=\min_{b,\alpha, \beta}{{\int}_{0}^{1}} \frac{1}{\sqrt{b}}dq,} $$
(12)

where \(\dot {q}\) is known as the parameter velocity. Likewise, after introducing state variables and control variable, the constraints (8) are rewritten as

$$ { V^{2}=\|\mathbf{v}\|^{2}=\|\mathbf{C^{\prime}}\|^{2}b\leq {F_{B}^{2}}, } $$
(13a)
$$ { |A_{h}|=|C^{\prime\prime}_{h}b+C^{\prime}_{h}\alpha|\leq A_{Bh},} $$
(13b)
$$ \left \{ \begin{array}{ll} &{|J_{h}|=|\sqrt{b}{\varGamma}|\leq J_{Bh},}\\ &{{\varGamma}=C^{\prime\prime\prime}_{h}b+3C^{\prime\prime}_{h}\alpha+C^{\prime}_{h}\beta,} \end{array} \right. $$
(13c)

where h ∈{x,y}. Consequently, the optimal problem consisting of (12), (10), (11), and (3) is known as the nominal problem of smooth trajectory generation (NPSTG) [32].

To improve solution efficiency, the NPSTG is further reformulated into two convex subproblems. One of them is the following problem of minimal time trajectory planning (PMTTP),

$$ \begin{array}{@{}rcl@{}} && OBJ=\min_{b,\alpha}{{\int}_{0}^{1}}\frac{1}{\sqrt{b}} dq \\ &&s.t. \left \{ \begin{array}{ll} & b^{\prime}(q)=2\alpha(q),b(0)=\dot{q}^{2}_{0},\\ & \|\mathbf{C^{\prime}}(q)\|b(q)\leq {F_{B}^{2}},\\ & |C^{\prime\prime}_{h}(q)_{h}b(q)+C^{\prime}_{h}(q)_{h}u(q)|\leq A_{Bh},\\ & b(q)>0,q\in[0,1],\\ &b(1)=\dot{q}^{2}_{f},\alpha(1)=\ddot{q}_{f},\\ &h \in \{x,y\}. \end{array} \right. \end{array} $$
(14)

Consequently, the optimal solution b∗(q) of (14) is adopted to relax (13c) as [29]

$$ |J(t)| \leq |\sqrt{b^{*}(q)}{\varGamma}(q)|\leq J_{Bh}. $$
(15)

Replace (13c) with (15) in the NPSTG, and pseudo problem of smooth trajectory generation (PPSTG) is obtained. As a result, the nonlinearity of the NPSTG is significantly alleviated, and a smooth feedrate profile is generated. Furthermore, because of convexity of two subproblems, the unique solution is obtained, which guarantees that the same part is gained in each machining. However, the feedrate profile is a function of parameter q, other than that of time. This kind of feedrate profile is inconvenient for time-based interpolation method. In addition, the contour error constraint is not considered in problems above. To settle these drawbacks, we propose an integrated jerk-limited method of minimal time trajectory planning with confined contour error (IJLMTPC).

4 The proposed method

The contour error is defined as the shortest distance from the current actual position to the desired machined tool path. It is of significance for machining accuracy. In our opinion, limited jerks should be taken into consideration at last. In that case, the coarse feedrate profile gained with optimal control can be smoothed further. Hence, the contour error constraint is added into the NPSTG, instead of axial jerk constraints.

4.1 Tracking error development

For a typical servo system of a single axis, its dynamic model is shown in Fig. 2 [33]. Taking x-axis for example, the closed-loop transfer function of the model is derived as

$$ { G_{tx}(s)=\frac{G_{c}(s)G_{o}(s)}{1+G_{c}(s)G_{o}(s)}=\frac{R(s)}{X(s)},} $$
(16)

where R(s) and X(s) denote the output signal and reference signal, respectively. Accordingly, the tracking error transfer function is described as

$$ { G_{ex}(s)=\frac{X(s)-R(s)}{X(s)}=\frac{1}{1+G_{c}(s)G_{o}(s)}=\frac{E_{x}(s)}{X(s)}.} $$
(17)

Through Taylor series expansion of Gex at s = 0, we have

$$ \begin{array}{@{}rcl@{}} E_{x}(s)&=&G_{ex}(0)X(s)+G^{(1)}_{ex}(0)sX(s)+\frac{1}{2!}G^{(2)}_{ex}(0)s^{2}X(s)\\ &&+\frac{1}{3!}G^{(3)}_{ex}(0)s^{3}X(s)+\cdots. \end{array} $$
(18)

For the servo system of a CNC machine tool, the instantaneous part of tracking error is very small. In terms of final theorem of Laplace transform, the tracking error is approximated with its steady part, i.e.,

$$ e_{x} \approx \lim_{s\rightarrow 0}(sG_{ex}(s)X(s)). $$
(19)

The inverse Laplace transform of (18) is written as

$$ e_{x} \approx {\sum}_{i=0}^{\infty}{W_{i}^{x}}x^{(i)}(t). $$
(20)

where \({W_{i}^{x}}=\frac {1}{i!}G_{ex}^{(i)}(0)\), indicates the dynamic error coefficient. Since the open loop model of a position servo system is I-type at least, the coefficient \({W_{0}^{x}}\) is always zero [33]. Ignoring the high-order term, ex is further approximated as

$$ e_{x} \approx {W_{1}^{x}}x^{(1)}(t)+{W_{2}^{x}}x^{(2)}(t)+{W_{3}^{x}}x^{(3)}(t), $$
(21)

where x(i)(t) is the i th-order derivative with respect to time. According to the derivative relationship, we have

$$ \begin{array}{@{}rcl@{}} & & x^{(1)}(t)=C_{x}^{\prime}(q)\sqrt{b(q)},\\ & & x^{(2)}(t)=C_{x}^{\prime\prime}(q)b(q)+C_{x}^{\prime}(q)\alpha(q),\\ & & x^{(3)}(t)=\sqrt{b(q)}(C_{x}^{\prime\prime\prime}(q)b(q)+C_{x}^{\prime\prime}(q)\alpha(q)+C_{x}^{\prime}(q)\beta(q)). \end{array} $$
(22)

Actually, it is clear that each axial jerk is included in the tracking error. In the next subsection, the tracking errors of two axes are used to estimate the contour error. That is another reason why we replace (13c) with the contour error constraint.

Fig. 2
figure 2

A typical diagram of closed-loop servo model

Full size image

4.2 Contour error estimation

Generally, to improve real-time performance, the contour error is estimated according to some information of real-time machining, such as desired positions, actual positions, and the tracking errors.

The contour error can be estimated by many methods. For a planer tool path shown in Fig. 3, the contour error is estimated as [34]

$$ E_{c}=-\sin\theta e_{x}+\cos\theta e_{y}, $$
(23)

where ex and ey denote the tracking errors of x-axis and y-axis, respectively. 𝜃 is the angle between tangent of tool path and X-axis of the machine tool coordinate system, which can be calculated with

$$ \theta =\cos^{-1} \frac{C^{\prime}_{x}(q)}{\sqrt{C^{\prime2}_{x}(q)+C^{\prime2}_{y}(q)}}. $$
(24)

From (21), (22), and (23), the contour error is rewritten as

$$ \begin{array}{@{}rcl@{}} E_{c}&=&w_{1}b(q)+w_{2}\alpha(q)+w_{3}\sqrt{b(q)}\\ &&+(w_{4}b(q)+w_{5}\alpha(q)+w_{6}\beta(q))\sqrt{b(q)}. \end{array} $$
(25)

where wi(i = 1,⋯ ,6) are real value functions of q.

Fig. 3
figure 3

Contour error for a 2D curve

Full size image

4.3 trajectory planning with confined contour error

To clarify the problem of minimal time trajectory planning with confined error (MTPC), it is formulated as following form,

$$ \begin{array}{@{}rcl@{}} & & OBJ=\min_{b,\alpha,\beta}{{\int}_{0}^{1}}\frac{1}{\sqrt{b(q)}} dq \\ &&s.t. \left \{ \begin{array}{ll} & b^{\prime}(q)=2\alpha(q),b(0)=\dot{q}^{2}_{0},\\ & \alpha^{\prime}(q)=\beta(q),\alpha(0)=\ddot{q}_{0},\\ & \|\mathbf{C^{\prime}}(q)\|b(q)\leq {F^{2}_{B}},\\ & |C^{\prime\prime}_{h}(q)b(q)+C^{\prime}_{h}(q)\alpha(q)|\leq A_{Bh},\\ & |E_{c}|\leq E_{B},\\ & b(q)>0,q\in[0,1],\\ &b(1)=\dot{q}^{2}_{f},\alpha(1)=\ddot{q}_{f},\\ &h \in \{x,y\}. \end{array} \right. \end{array} $$
(26)

To efficiently solve problem (26), it is also divided into two convex subproblems. One is exactly the (14). Referring to the (15), the contour error constraint is relaxed as

$$ \begin{array}{@{}rcl@{}} |E_{c}|&\leq& |\hat{E}_{c}|\\ &=&|w_{1}b(q)+w_{2}\alpha(q)+(w_{3}+w_{4}b(q)\\ &&+w_{5}\alpha(q)+w_{6}\beta(q))|\sqrt{b^{*}(q)}. \end{array} $$
(27)

After replacing |Ec| with \(|\hat {E}_{c}|\) in (26), we have the other convex subproblem, which is

$$ \begin{aligned} & OBJ=\min_{b,\alpha,\beta}{{\int}_{0}^{1}}\frac{1}{\sqrt{b(q)}} dq \\ &s.t. \left \{ \begin{array}{ll} & other \quad constraints,\\ & |\hat{E}_{c}|\leq E_{B}. \end{array} \right. \end{aligned} $$
(28)

In order to obtain the optimal solution of problem (14) and (28), the control vector parameterization (CVP) is adopted to discretize them. Taking (28) for example, divide parameter domain into K + 1 grids, i.e., 0 = p0 < p1 < ⋯ < pK− 1 < pK = 1. The corresponding control action is defined as

$$ \beta={\sum}_{k=1}^{K}\bar{\beta}_{k}\varpi_{k}(p), $$
(29)

where \(\bar {\mathbf {\beta }}=[\bar {\beta }_{1},\cdots ,\bar {\beta }_{K}]^{T}\) denotes the decision vector, and ϖk(p) is the k th basis function. For piecewise constant approximation, ϖk(p) is defined as

$$ \varpi_{k}(p)= \left \{ \begin{array}{ll} &1 \quad p \in[p_{k-1},p_{k}),\\ &0 \quad otherwise. \end{array} \right. $$
(30)

Hence, in this paper, the control action and the decision vector is the same.

Substitute the control vector into system dynamics, and through solving derivative equations, corresponding state vectors are obtained, i.e.,

$$ \begin{array}{ll} & \bar{\mathrm{\alpha}}(\bar{\beta})=[\bar{\alpha}_{1},\cdots,\bar{\alpha}_{K}]^{T},\\ & \bar{\mathbf{b}}(\bar{\beta})=[\bar{b}_{1},\cdots,\bar{b}_{K}]^{T}. \end{array} $$
(31)

Define Δp = pk − pk− 1, the objective function is discretized as

$$ OBJ={\sum}_{k=1}^{K}\frac{1}{\bar{b}_{k}}{{\varDelta}} p. $$
(32)

Consequently, problem (28) is transformed into a nonlinear programming problem as following,

$$ \begin{aligned} & OBJ=\min_{\bar{\beta}_{k}}{\sum}_{k=1}^{K}\frac{1}{\bar{b}_{k}}{{\varDelta}} p \\ &s.t. \left \{ \begin{array}{ll} & \|\mathbf{C^{\prime}}(q_{k})\|\bar{b}_{k}\leq {F^{2}_{B}},\\ & |C^{\prime\prime}_{h}(q_{k})\bar{b}_{k}+C^{\prime}_{h}(q_{k})\bar{\alpha}_{k}|\leq A_{Bh},\\ & |\hat{E}_{c}(\bar{\beta}_{k})|\leq E_{B},\\ & \bar{b}_{k}>0,k=1,\cdots,K,\\ & \bar{b}_{K}=\dot{q}^{2}_{f},\bar{\alpha}_{K}=\ddot{q}_{f}. \end{array} \right. \end{aligned} $$
(33)

Problem (33) can be solved with mature method, such as SQP. Likewise, problem (14) is also discretized and solved in the same way. Please note that problem (14) must be solved firstly.

4.4 Feedrate re-planning

Although the feedrate profile has been planned in the last subsection, it is a function of parameter p. In this subsection, the feedrate profile is re-planned, considering the limited jerk. Consequently, the feedrate profile becomes a function of time, which is convenient for interpolation.

Before re-scheduling feed, sharp corner points are searched firstly. Sharp corner points consist of minimum speed points, maximum speed points, the starting point, and the terminal point on the initial feedrate profile. The arc length between each two adjacent sharp corner points, i.e., \(L^{i}_{ble}(i=0,\cdots ,D)\), is easily computed by (6). Note that inverse normalization needs to be performed. For any two adjacent points, the feed at each point and the arc length between them are known. Given tangent jerk bound Jtb, the jerk-limited feedrate can be re-planned. However, these sharp corner points may be involved in “ripple effect” [24, 35]. It means that the arc length between two adjacent sharp points can not match the speeds at the two points based on bell shape feedrate profile. We deal with the “ripple effect” with following backward planning algorithm.

figure b

After finishing backward algorithm, the “ripple effect” is overcome. Then the forward planning can be implemented. In terms of different distance between sharp corner points, there are six types of feedrate profiles. For any two adjacent sharp corner points, the distance between them has been obtained, i.e., \(L^{i}_{ble}\). Given planned feedrates vi and vi+ 1, tangent acceleration Atb, and command feedrate FB, the forward planning types are determined according to Fig. 4.

Fig. 4
figure 4

The flowchart of types of forward planning determination

Full size image

Each arc whose length equals to \(L^{i}_{ble}\) is considered as a single acceleration or deceleration (Acc/Dec) unit. However, there are D + 1 Acc/Dec units. Which type is chosen for each Acc/Dec unit depends on three critical distances. Lc1 is used to determine whether the arc length is long enough to allow the cutter to reach the command feedrate. It is defined as

$$ L_{c1}=(v_{i}+F_{B})\left( T_{c1}+\frac{T_{c2}}{2}\right)+(v_{i+1}+F_{B})\left( T_{c5}+\frac{T_{c6}}{2}\right), $$
(34)

where Tc1 and Tc2 are calculated with

$$ \left \{ \begin{array}{ll} &if \quad F_{B}-v_{i}>J_{tb}T^{2}, \\ &T_{c1}=T, T_{c2}=\frac{F_{B}-v_{i}}{J_{tb}T}-T; \\ &otherwise,\\ &T_{c1}=\sqrt{\frac{F_{B}-v_{i}}{J_{tb}}}, T_{c2}=0. \end{array} \right. $$
(35)

Likewise, Tc5 and Tc6 are calculated with

$$ \left \{ \begin{array}{ll} &if \quad F_{B}-v_{i+1}>J_{tb}T^{2},\\ &T_{c5}=T, T_{c6}=\frac{F_{B}-v_{i+1}}{J_{tb}T}-T; \\ &otherwise,\\ &T_{c5}=\sqrt{\frac{F_{B}-v_{i+1}}{J_{tb}}}, T_{c6}=0; \end{array} \right. $$
(36)

where \(T=\frac {A_{tb}}{J_{tb}}\). Lc2 is used to determine whether a peak speed is needed to be searched or not. Define \(v_{high}=\max \limits (v_{i},v_{i+1})\), \(v_{low}=\min \limits (v_{i},v_{i+1})\), and Δv = vhigh − vlow.Then, Lc2 is written as

$$ \begin{aligned} &L_{c2}=\\ &\left \{ \begin{array}{ll} &(v_{i}+v_{i+1})(T+{{\varDelta}} v/A_{tb})/2, \quad {{\varDelta}} v>J_{tb}T^{2};\\ &(v_{i}+v_{i+1})\sqrt{{{\varDelta}} v/A_{tb}}, \quad {{\varDelta}} v \leq J_{tb}T^{2}. \end{array} \right. \end{aligned} $$
(37)

Lc3 can distinguish whether the acceleration profile is trapezoidal or triangular, and it is written as

$$ L_{c3}=2v_{low}T+J_{tb}T^{3}. $$
(38)

When one type of feedrate profile is selected, it will be used for real-time interpolation. Hence, the time parameters of jerk-limited feed profile should be computed. This kind of feed is also known as bell shape profile. A complete profile includes seven phases, and its time parameters are shown in Fig. 5. Some other profile may contain fewer than seven phases. For example, type 3 only has four phases whose parameters satisfy T5 = T6 = T7 = 0. The detail solutions of these parameters of each type are listed in Table 1. It is worth mentioning that the peak speed vp in type 2 is obtained with following equation,

$$ v_{p}=\max(v^{j}_{pm}). $$
(39)

where \(v^{j}_{pm}=v_{high}+j\cdot \frac {v_{b}-v_{high}}{\xi }, j=1,2,\cdots ,\xi , \xi \in N^{+}\), satisfying \(L_{c2}<L_{acc}+L_{dec}<L^{ble}_{i}\). The maximal value of \(v^{j}_{pm}\) is selected with bisection search method. To avoid vp being too close to vhigh, ξ can be chosen as a large integer. That is why vp may not exist.

Fig. 5
figure 5

Time parameters of type 2

Full size image
Table 1 Time parameters for types 1 − 6
Full size table

4.5 Interpolation based on parameter correction B-spline

The first-order approximation interpolation based on Taylor expansion is expressed as

$$ q_{i+1} =q_{i}+\frac{v_{i}T_{s}}{\|\mathbf{C}^{\prime}(q)\|}+H.O.T, $$
(40)

where Ts is the sample period, and H.O.T is the truncation error which is neglected in practice. Since viTs is very small, it is considered as the arc length increment in i th sample period. Then (40) is rewritten as

$$ {\varDelta} q=q_{i+1} -q_{i} \approx \frac{v_{i}T_{s}}{\|\mathbf{C}^{\prime}(q)\|}=f(v_{i}T_{s}), $$
(41)

From (41), the more accurate the relationship between arc length and parameter, and the smaller the feedrate fluctuation and contour error are [36].

Theoretically, parameter correction b-spline can guarantee high accuracy relationship between normalized arc length and parameter. Define Li be the whole displacement of tool tip before i th sample period. Then, Li+ 1 = Li + viTs. After normalization of Li+ 1, substitute it into (4), and the corresponding parameter is obtained.

5 Numerical examples

To verify effectiveness of the proposed method, two benchmark tool paths [30, 33] are adopted to validate it. In the two cases, the constraint bounds and some parameters adopted are listed in Table 2. In addition, the servo models of x-axis and y-axis come from literature [38].

Table 2 The values of constraint bounds, predefined errors, and constants
Full size table

5.1 Example 1: A fan tool path

The test case in example 1 is a fan curve shown in Fig. 6a. The blue circles on the curve indicate all the sharp corner points (SCP) including the start point.

Fig. 6
figure 6

The IJLMTPC results for a fan tool path: a the fan pattern; b the functional curve of the parameter correction b-spline; c the tangent feedrate profiles; d the profiles of tangent acceleration and tangent jerk; e the estimated contour error; d partial enlarged view of interpolation result of the fan path

Full size image

Apparently, some of sharp corner points are so close to each other. Therefore, the arc lengths between them are not long enough for the jerk-limited Acc/Dec process. By performing the backward planning (BPL), this kind of problems is alleviated. To clearly illustrate the effort of the backward planning, feedrate profiles are shown in Fig. 6c. The upper half of Fig. 6c is the feedrate before backward planing, i.e., the planning result of Section 4.3. The circled positions represent the speeds at sharp corner points before BPL. The bottom half demonstrates the feedrate profile after backward planning and forward planning. Note that the tangent jerk constraint has been imposed on the re-planned feedrate, and the profile has been smoothed. The sharp corner points are marked by inverted triangles, which have different tangent feedrate from those in the upper half figure.

During forward planning, the arc lengths between sharp corner points are needed to be computed. Different with the method based on Simpson’s rule [35], (6) is used to obtain the arc length corresponding to given parameter. It is the inverse function of (4). The top sub-graph of Fig. 6b exhibits the mapping function curve after implementing refining Algorithm 1. The bottom sub-graph shows that the relative error has been reduced bellow predefined value. The middle sub-graph indicates the interpolation relative error before refining. As stated in Algorithm 1, the relaitve error can be calculated with following formula,

$$ RSE=|{\tau^{0}_{g}}-{\tau^{t}_{g}}|/{\tau^{t}_{g}}. $$
(42)

The upper half of Fig. 6d shows the profile of acceleration, whereas the jerk profile is drawn in the bottom half. With limited jerk, the feedrate become smoother, as shown in Fig. 6c. When motion between two adjacent sharp corner points, the displacement of a tool tip must fall within the arc length range. To satisfy this requirement, the backward planning makes the feedrate at sharp corner points not too fast or too slow, but close to a certain intermediate value. To some extent, the cycle time is reduced. On the other hand, the contour error may become large at some sharp corners. The locations marked with diamonds on the profile in Fig. 6e are just such cases. But the overall contour error profile is not affected, because the contour errors at most interpolation points are very small. The partial enlarged view shown in Fig. 6f also proves this.

5.2 Example 2: A butterfly tool path

Another tested tool path is a butterfly pattern as shown in Fig. 7. The coordinates of reference points from interpolation methods are sent to servo systems in this example. And the actual coordinates generated by servo system are used to estimate the actual contour errors. The Newton Raphson iteration method [39] is utilized to calculate the actual contour errors offline.

Fig. 7
figure 7

The butterfly pattern

Full size image

For comparison, two other methods are adopted, except our proposed algorithm. One method plans the feedrate with NPSTG, and generates the reference coordinates with the first-order approximation interpolation based on Taylor series expansion. Since NPSTG is solved based on pseudo jerk, this method is named PJNPSTG for short. The other method also adopts the first order approximation interpolation, but plans the feedrate with the same way as the proposed, i.e., the IJLMTPC-based method. To distinguish it with the proposed scheme, this method is named FTMTPC. Detail explanations are listed in Table 3.

Table 3 Three methods for machining the butterfly pattern
Full size table

As shown in Fig. 8, the proposed method has the shortest cycle time, i.e., 6.426 s. The other two methods both finish machining the tool path with longer time, i.e., 7.123 s for FCMTPC and 7.912 s for PJNPSTG. In terms of cycle time, our proposed scheme has great advantages, comparing to the other two methods. Nevertheless, our proposed method leads to larger contour errors than the PJNPSTG, but smaller than the FTMTPC (Fig. 9). In terms of contour errors, detail performances of three methods are listed in Table 4. Actually, the contour error based on our proposed method can be further reduced by imposing smaller EB on (28). As a result, the cycle time will become longer. Therefore, one should make a trade-off between efficiency and accuracy, depending on actual situation.

Fig. 8
figure 8

The feed profiles of three interpolation methods for the butterfly tool path

Full size image
Fig. 9
figure 9

The estimated contour error profiles of three interpolation methods for the butterfly pattern

Full size image
Table 4 Performance comparison of three methods in terms of contour errors
Full size table

6 Conclusion

To merge the contour error reduction and feedrate optimization into one procedure, we propose an integrated jerk-limited method of minimal time trajectory planning with confined contour error (IJLMTPC). Compared to the NPSTG problem, our method reduce the solution difficulty by excluding axial jerk constraints. Through adding contour error constraint, servo errors are pre-compensated. Furthermore, the feedrate profile on the parameter domain solved by the optimal control, is transformed to that on time domain. Our method not only utilizes the advantage of the optimal control, but also makes the resulting time optimal feedrate convenient for real-time interpolation. This will make optimal control-based trajectory planning method for CNC machining more practical than ever. Meanwhile, for realizing real-time interpolation, parameter correction b-spline is introduced. It reduces the fluctuation of feedrate and facilitates re-planning.