1 Introduction

Coordinate Measuring Machines (CMMs) are used by automotive, aerospace, and defense industries to measure geometrical features of parts. They are commonly controlled by a computer for inspection of parts. CMMs can be utilized for efficient inspection and rapid feedback for correction of processing parameters in a production line. A CMM has a probe to collect the data. The probe selection is the key factor in CMMs. The speed and accuracy of a CMM are mainly determined by its probe. The measurement speed for CMMs with mechanical probes is limited as it takes time to position the probe and follow the measurement path. The measurement speed limitation can be overcome by replacing a mechanical probe with a laser probe to collect the data without a physical movement. The accuracy of the data collected by a CMM affects the measurement outcome. It is clear that an accurate measurement cannot be achieved with a distorted set of sampled data. To meet the measurement accuracy of a few micrometers for parts, the undesired effects of environmental factors have to be taken into consideration. Industrial environments are prone to the vibration that can compromise the accuracy and repeatability of CMMs [1,2,3].

There are several methods to reduce the effects of vibration on CMM measurement in a manufacturing facility. Depending on the vibration source, it may be simply possible to increase the distance between the vibration source and the measurement equipment. Vibration isolation materials, such as foams and pads, can be used for the purpose of vibration isolation. In practice, the vibration isolation materials do not provide enough isolation to properly measure geometrical features of auto-parts. Vibration isolation tables are commonly used by auto-industry to satisfy the measurement requirements for auto-parts. These tables are designed to significantly damp vibration to ensure a working environment supporting accurate measurement. As electric vehicles move into the mainstream, the margin of tolerance for parts becomes narrower requiring costly and complex isolation tables. The active vibration damping method is used for noise reduction in space telescopes [4]. In this method, the vibration profile is extracted by sensors and used to eliminate the noise added by vibration. To further reduce the impact of environmental factors on measurement results, CMMs can be installed in temperature-controlled rooms. Another efficient and cost-effective solution to reduce the effects of vibration effects on CMM measurements is the sampling method. Different sampling methods to minimize measurement error have been proposed [5,6,7,8,9]. Cross-secti on line sampling[10] and point sampling [11] methods have also been implemented with promising results. Depending on the physical and environmental conditions of the manufacturing facility, vibration can be modeled by noise on the sampled data, which can be minimized by known noise reduction techniques. Moreover, in [12], the effects of temperature on CMM arms, and the measurement results are taken into consideration for accurate measurement. A technique to calibrate and compensate for the error caused by CMM arms is proposed in [13]. The model is focused on the compensation for the deformations due to the bending and torsion affecting the arms. In [14], a kinematic model of a CMM arm is developed and its parameters are determined. Taking the proposed techniques in [11,12,13], since CMMs are not rigorously calibrated the same as other instruments against standards and only maximum permissible errors are evaluated, verification of CMMs (as mentioned in ISO 10360) is a proper scheme to deal with error of their arms.

Many techniques are reported in the literature to reduce the effects of noise on the measurement data. The maximum distance method, chordal deviation method, curve-fitting method, and angular method are reported as methods to filter vibration noise [15, 16]. Among the mentioned methods, the maximum distance method is capable of removing isolated points or outliers and is suitable for uniformly distributed datasets. The chordal deviation method uses three adjacent points and specifies whether the deviation is greater or less than a threshold. The curve-fitting method determines the distance between sample points and a fitted curve [17]. The angular method considers three points and two segments formed by the points. The angle of the segments is then compared with a predefined threshold to reduce the noise [18]. In [15], a modified Self-Estimated Angular Threshold (SAT) method is presented for the data generated by a laser scanner. The above-mentioned methods present different solutions to remove noise from the collected data, considerably. However, measurement accuracy in accordance to ISO 10360-2 demands further improvement in this area. Environmental noise, either systematic or random, varies dimensions of manufactured parts around mean values. Therefore, a statistical model can be developed to validate the measurement results. In this paper, a method based on data integration for multi-sample CMM data is investigated.

Technically, when the number of sensors in a system is more than one, the data should be integrated, and all datasets should be combined together. Increasing the number of sensors can improve measurement accuracy, but the dataset may grow considerably and become complicated to process [19]. Conventional approaches, such as Algebraic functions [20], Kalman filter [21], weighted average [22], Bayesian estimator, and nonlinear system fusion [23,24,25], are used for data fusion where the data collected by multiple sensors are integrated to produce more accurate and consistent information.

Implementation details of CMM modeling and probe error modeling are presented in [26]. A curve network-based sampling method to enhance the efficiency of the measurement of the freeform surfaces on CMMs is proposed in [27]. A detailed explanation regarding the application of the machine vision method in 3-D coordinate measurement of feature points on the surface of a large-scale workpiece is given in [28] and a measuring method is proposed. In [29], a continuous motion model of a spinning ping-pong ball is derived and then, an optimal state estimation method using the gradient descent method based on the derived CMM is proposed.

The main concentration of this paper is on vibration filtering and a multi-sampling data fusion technique in CMMs. An improved Modified Multi-Class Support Vector Machines (iMMC-SVM) algorithm is developed in this paper to filter noise and determine the performance of manufacturing lines by comparing manufactured parts with a reference part. The proposed solution utilizes a vibration filtering method and a multi-sampling data fusion technique to process the sampled data by a CMM. In this paper, to the knowledge of the authors, for the first time, a new machine learning-based approach is presented to automatically determine the geometrical features of a new part by a CMM. The proposed solution reduces the time required to characterize and add a new part to the CMM library significantly. In other words, the focal points in this paper are the measurement accuracy, precision, and speed to reduce the costs. Experimental measurements conducted on various parts validate the performance of the proposed solution. It should be noted that the multi-sampling data fusion method has never been used to increase the measurement accuracy of CMMs.

The rest of the paper is organized as follows. Section 2 discusses the proposed methodology. The experimental results are presented in Sect. 3 and conclusions are drawn in Sect. 4.

2 Proposed methodology

The data collected by a CMM is affected by many factors including environmental conditions, such as temperature and vibration, operator’s error and inspection plan, quality, and accuracy of measuring device. In general, the measurement process in CMM is performed step by step to extract the geometrical features of a part. There are different uncertainty factors in the measurement process that have to be taken into consideration. The pseudocode presented in Table 1 shows the flowchart of the proposed methodology, which is developed to ensure measurement accuracy [30].

Table 1 The flowchart of the proposed methodology
Full size table

There are two important assumptions in the proposed methodology: (a) The geometrical features are extracted properly from data without additional error calculation. This means that measurement errors can be traced back to the collected data rather than the calculation error. (b) There is no correlated motion between the CMM and the manufactured part. Therefore, vibrations can be attributed to the environmental conditions and not the motion correlation between the part and the CMM. The proposed algorithm is divided into three main parts, which are described as follows:

2.1 Preprocessing

In this stage, the part is loaded and properly secured on the CMM. Then, the sampling probe is configured and aligned either manually or automatically. A point on the part is selected as the initial point where the CMM starts capturing the data samples. Finally, the data is collected and then, used to extract geometrical features. The key factor in the algorithm development to measure geometrical features is to properly filter the collected data.

2.2 Noise calculation

The collected data is compared with the reference data, provided by the manufacturer as a reference part. The measurement error is calculated as follows:

Step 1: Assume that the measurement process starts from point “A” and a dataset of \(A=\left\{{A}_{i}\right\}\) is collected where \(i=1, 2, \dots , n\) and \(n\) indicates the total number of collected samples. The sampling process is repeated to collect data for all sections of the part. For each section in only two dimensions, the corresponding \(X\) and \(Y\) can be stored in a matrix, as follows:

$$\left[{S}_{j}\right]=\left[\begin{array}{cc}{X}_{1}& {Y}_{1}\\ \vdots & \vdots \\ {X}_{i}& {Y}_{i}\end{array}\right] \mathrm{for}\left\{\begin{array}{c}\left(i=1, \dots , n\right)\\ (j=1, \dots , k)\end{array}\right.$$
(1)

where \({S}_{j}\), \({X}_{i}\), and \({Y}_{i}\) represent the \(j^{\mathrm{th}}\) section, the corresponding value on the \(X\) axis, and the corresponding value on the \(Y\) axis, respectively. In addition, \(k\) represents the total number of sections of the shape.

As the measurement domain for each section is the same, the corresponding values on the \(X\)-axis for all sections are the same.

Step 2: Integrating all sections together, a new dataset is generated as follows:

$$\lbrack T\rbrack=\left[\begin{array}{c}X_1\\\vdots\\X_i\end{array}\left|\begin{array}{ccc}Y_{(1,1)}&\cdots&Y_{(1,k)}\\\vdots&\ddots&\vdots\\Y_{(i,1)}&\cdots&Y_{(i,k)}\end{array}\right.\right]$$
(2)

Step 3: When the dataset is completed, it can be compared with the reference dataset, as shown below:

$$\lbrack T-R\rbrack=\left[\begin{array}{c}X_1\\\vdots\\X_i\end{array}\left|\begin{array}{ccc}Y_{(1,1)}-R_{(1,1)}&\cdots&Y_{(1,k)}-R_{(1,k)}\\\vdots&\ddots&\vdots\\Y_{(i,1)}-R_{(i,1)}&\cdots&Y_{(i,k)}-R_{(i,k)}\end{array}\right.\right]$$
(3)

and

$$\lbrack E\rbrack=\left[\begin{array}{c}X_1\\\vdots\\X_i\end{array}\left|\begin{array}{ccc}E_{(1,1)}&\cdots&E_{(1,k)}\\\vdots&\ddots&\vdots\\E_{(i,1)}&\cdots&E_{(i,k)}\end{array}\right.\right]$$
(4)

where \([R]\) and \([E]\) represent the reference and error matrices, respectively, in which \(i\) represents the collected sample index and \(k\) shows the section index.

Step 4: The sampled data in each column present a minor variation from nominal values making error detection quite challenging. To deal with this issue, instead of point-by-point comparison, the sum of the corresponding coordinates in each section is calculated and then, the variance or standard deviation of each column is determined as follows:

$$\left\{\begin{array}{c}{V}^{j}=\frac{1}{n}\sum {({Y}_{i}^{j}-\overline{Y })}^{2} \\ {SD}^{j}=\sqrt{\frac{1}{n}\sum {\left({Y}_{i}^{j}-\overline{Y }\right)}^{2}}\end{array}\right.$$
(5)

where \(V\), \(\overline{Y }\), and \(SD\) are the variance, mean value, and standard deviation of the \(j\) th section, respectively.

If the standard deviation falls below an acceptable level specified by the part manufacturer, then, the data is used for feature extraction using the iMMC-SVM algorithm explained below.

2.3 iMMC-SVM algorithm evaluation

Each column in the preprocessed dataset represents a certain feature. To improve the overall accuracy, the redundant data are removed from the total dataset. Thereafter, the feature set is normalized to generate training and test datasets. In the next step, the iMMC-SVM model is trained using the Radial Basis Function (RBF) kernel function with the best feature set [31]. In order to classify the data that is not linearly separable, the RBF kernel function is used for the iMMC-SVM model. The RBF kernel equation can be written as:

$$K\left({x}^{\left({t}_{1}\right)},{x}^{\left({t}_{2}\right)}\right)=\mathrm{exp}\left(-{\lambda |\left|{x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right||}^{2}\right),\lambda >0$$
(6)

where \(K\) indicates the kernel function and shows the similarity of the two vectors, \({x}^{\left({t}_{1}\right)} (m\times n)\) and \({x}^{\left({t}_{2}\right)} (r\times s)\), and in fact, \({x}^{\left({t}_{2}\right)}\) represents the point of reference vector; \(m\), \(n\), \(r\), and \(s\) show the dimensions on the two vectors, respectively; and \(\lambda\) is a function of standard deviation.

\(\left|{x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right|\) shows the Euclidean distance between \({x}^{\left({t}_{1}\right)}\) and \({x}^{\left({t}_{2}\right)}\). Considering \({x}^{\left({t}_{1}\right)}\approx {x}^{\left({t}_{2}\right)}\), the difference between these two vectors becomes zero. Hence, \(\mathrm{exp}\left(0\right)\approx 1\). This indicator shows that the two vectors are the same for both \({t}_{1}\) and \({t}_{2}\). Assuming that \({x}^{\left({t}_{1}\right)}\) is far from \({x}^{\left({t}_{2}\right)}\), the difference between the two vectors becomes a large number, and according to Eq. (6), \(\mathrm{exp}\left(-\infty \right)\approx 0\), and it can be concluded that the two vectors cannot be similar and they have less influence on each other.

Considering a large positive value for \(\lambda\), the iMMC-SVM attempt to avoid misclassifying the training dataset, which causes overfitting. As a result, the iMMC-SVM decision boundary depends on the points that are closest to the hyperplane and ignores the points that are far away. In other words, either the two vectors can be the same (close to each other) or different (far from each other). \(\lambda\) defines how far the influence of a single training data reaches and as stated before, and \(\lambda\) depends on the standard deviation, as follows:

$$\lambda =\frac{1}{2{\sigma }^{2}}$$
(7)

where \(\sigma\) indicates the variance.

Considering \(\sigma =1\),

$${e}^{(-\frac{{\left({x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right)}^{2}}{2})}={e}^{(-\frac{{({{x}^{\left({t}_{1}\right)})}^{2}+({x}^{\left({t}_{2}\right)})}^{2}-2{x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)}}{2})}={e}^{(-\frac{1}{2}({({{x}^{\left({t}_{1}\right)})}^{2}+({x}^{\left({t}_{2}\right)})}^{2})}{e}^{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}$$
(8)

Using the Taylor series expansion:

$${e}^{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}=1+\frac{1}{1!}\left({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)}\right)+\frac{1}{2!}{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}^{2}+\frac{1}{3!}{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}^{3}+\dots +\frac{1}{n!}{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}^{n}$$
(9)

Using the dot product, Eq. (9) also be written as Eq. (10). Taking Eq. (6) into consideration, Eq. (11) can be derived. Assuming \(M=\sqrt{{e}^{(-\frac{1}{2}\left({({{x}^{\left({t}_{1}\right)})}^{2}+({x}^{\left({t}_{2}\right)})}^{2}\right))}}\), Eq. (11) can be rewritten as Eq. (12).

According to Eq. (12), the value of \({e}^{(-\frac{{\left({x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right)}^{2}}{2})}\) is the relationship between the two corresponding values of the points in two vectors in infinite dimensions.

After training the iMMC-SVM model, it is tested under different conditions and the corresponding labels for evaluation are predicted. Lastly, the accuracy of the iMMC-SVM technique is checked separately, as follows:

$$Accuracy=\frac{\mathrm{Accurate\;fault\;classification}}{\mathrm{No.\;of\;test\;samples}}\times 100$$
(10)

3 Experimental results

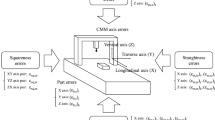
The experimental measurement setup in Fig. 1 includes a CMM [32], which is designed by the research team. The CMM includes a laser scanner to allow non-contact measurement, which reduces the measurement error. It is also implemented on a vibration isolation table to reduce the effects of vibration on measurement results. To further suppress the vibration effects, the collected data is processed using the proposed iMMC-SVM algorithm as explained earlier.

Fig. 1
figure 1

a Implemented CMM by the research team, b Keyence laser scanner used to sample data points, and c screenshot of the user interface developed

Full size image

3.1 Settings

Figures 2 and 3 illustrate a bevel gear used as a part under test to conduct the measurements. The blue line on the part shows the laser beam used to scan the part and collect data.

Fig. 2
figure 2

Bevel gear (from the side)

Full size image
Fig. 3
figure 3

Bevel gear (from the top)

Full size image

According to Eqs. (1) and (2), and for better illustration, \(X\) and \(Y\) coordinates for one section of the manufactured part are shown in Fig. 4.

Fig. 4
figure 4

\(X\) and \(Y\) coordinates for one section of the manufactured part (from the top)

Full size image

The setup to measure \(X\) and \(Y\) coordinates of the part to extract the features is shown in Fig. 5. In the coordinate measuring stage, the manufactured part is rotated about its vertical axis to scan the part and collect the measurement data.

Fig. 5
figure 5

The bevel gear and CMM

Full size image

3.2 Data acquisition

The collected data (raw data) from the CMM includes the coordinates of the bevel gear in 599 rows (\(i\)) and 3600 columns (\(j\)). When the laser beam is reflected, the collected data varies from −15 mm and +15 mm. When there is no reflection, −90 mm is returned. This is a method to impute missing data in the dataset [33].

$${e}^{({x}^{\left({t}_{1}\right)}{x}^{\left({t}_{2}\right)})}=\left(1,\sqrt{\frac{1}{1!}}{x}^{\left({t}_{1}\right)},\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{1}\right)})}^{2},\dots ,\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{1}\right)})}^{n}\right).\left(1,\sqrt{\frac{1}{1!}}{x}^{\left({t}_{2}\right)},\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{2}\right)})}^{2},\dots ,\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{2}\right)})}^{n}\right)$$
(11)
$${e}^{(-\frac{{\left({x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right)}^{2}}{2})}={e}^{(-\frac{1}{2}({({{x}^{\left({t}_{1}\right)})}^{2}+({x}^{\left({t}_{2}\right)})}^{2})}[\left(1,\sqrt{\frac{1}{1!}}{x}^{\left({t}_{1}\right)},\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{1}\right)})}^{2},\dots ,\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{1}\right)})}^{n}\right).\left(1,\sqrt{\frac{1}{1!}}{x}^{\left({t}_{2}\right)},\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{2}\right)})}^{2},\dots ,\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{2}\right)})}^{n}\right)]$$
(12)
$${e}^{(-\frac{{\left({x}^{\left({t}_{1}\right)}-{x}^{\left({t}_{2}\right)}\right)}^{2}}{2})}=\left(M,M\sqrt{\frac{1}{1!}}{x}^{\left({t}_{1}\right)},M\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{1}\right)})}^{2},\dots ,M\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{1}\right)})}^{n}\right).\left(M,M\sqrt{\frac{1}{1!}}{x}^{\left({t}_{2}\right)},M\sqrt{\frac{1}{2!}}{{(x}^{\left({t}_{2}\right)})}^{2},\dots ,M\sqrt{\frac{1}{n!}}{{(x}^{\left({t}_{2}\right)})}^{n}\right)$$
(13)

3.3 Results and discussions

3.3.1 Measurements

In this section, the proposed algorithm is evaluated to examine its validity. The profile of a section of the bevel gear is shown in Fig. 6. It can be observed that there are two dents where \(-90\) mm is returned as the collected data indicates that the laser beam is not reflected. The collected data has \(599\) rows and \(3600\) columns (a matrix of \(599\times 3600\)). There are \(90\) sections and each section is stored in a matrix of \(599\times (40+1)\), in which \(1\) shows that the label corresponds to the section. The label matrix is a matrix of \(23960\times 1.\) In order to train the algorithm, \(75\%\) of the collected data is used, which is a matrix of \(599\times 2700\). In addition, \(15\%\) of the collected data is used for validation, which is a matrix of \(599\times 540\). Lastly, \(10\%\) of the collected data is used for the test, which is a matrix of \(599\times 360\). The reference dataset is a matrix \(599\times (40+1)\), in which \(1\) shows the label (REFERENCE label). According to Eq. (6) and its explanations, \(m=599\), \(n=2700\), \(r=599\), and \(s=40\).

Fig. 6
figure 6

The profile of the second column of the first section of the reference data

Full size image

In order to check the impact of noise and vibration on the measured data, profiles of the reference data and the measured data are compared with each other. Figure 7 shows the comparison result indicating a close agreement between the data collected through measurement with the reference data. It can also be observed that the noise on the dataset leads to additional false dents (shadow) between \(-12.75\) mm and \(-11.8\) mm and also \(-3.0\) mm and \(-1.80\) mm on the \(X\)-axis.

Fig. 7
figure 7

Comparison between the measured data for the part-under-test and the reference part

Full size image

The sampled data varies from value of about \(-13.7\) to \(+10.2\) mm. The collected data experiences a few sharp transitions from higher than \(-10\) to about \(-90\) mm. This is due to the fake dents where the laser beam is not reflected resulting in a minimum measurement value of \(-90\) mm.

3.3.2 Error calculations

The difference between the measured data and the reference can readily be calculated. Figure 8 shows the calculated error, which represents the error due to vibration. The \(3600\) samples in Fig. 7 represent the data obtained through one full rotation of the bevel gear. As noted, the vibration error becomes visible.

Fig. 8
figure 8

The calculated error after measurement

Full size image

To evaluate the statistical nature of the measured data, the variance of the collected dataset is calculated. Figure 9 shows the variance of the measured data. While the data in Fig. 8 shows that the error rises for samples between \(2000\)th and \(3250\)th, the measured data indicates that the data variance becomes higher for sampled data from 1250th to 1750th. Therefore, for the tested gear, it can be concluded that the vibration has the highest impacts on the collected samples for 30th and 44th sections.

Fig. 9
figure 9

The variance of the measured data

Full size image

Based on the provided explanations for Algorithm 1, Figs. 10 and 11 show the results of the noise reduction process. As shown in those figures, the proposed algorithm not only has successfully reduced the noise due to the vibration but also has detected the two dents correctly. It should be noted that only a few samples are not well-detected during the noise-reduction process. It should be noted that the positive and negative errors in Fig. 11 indicate the overestimation and underestimation of the predicated samples by the proposed method, respectively.

Fig. 10
figure 10

Comparison between the results obtained by applying the proposed noise reduction method and the measured data

Full size image
Fig. 11
figure 11

The error in the noise reduction process

Full size image

3.4 iMMC-SVM algorithm evaluation

The noise due to the vibration can be reduced by repeating the measurement and applying proper CMM settings. The best features can be extracted from the measured data by trial and error method, and they can be fed into the iMMC-SVM algorithm for evaluation. The proposed iMMC-SVM algorithm is a supervised learning algorithm with an adaptive computational learning solution, which classifies the dataset based on a nonlinear classification hyperplane. The capability of the iMMC-SVM algorithm can be improved by optimizing the distance between the two separation hyperplanes [29]. As mentioned in Sect. 2.3, using a kernel function that can convert the experimental dataset from its original dimension space into a higher dimension space by constructing a nonlinear hyperplane is the essential characteristic of the proposed iMMC-SVM algorithm. The accuracy of the iMMC-SVM algorithm depends on how accurately the hyperplane can be chosen. This process is completed by changing the number of classes.

In order to check the quality of the manufactured part, the bevel gear is tested several times, and its internal 2-D dimensions are determined based on the algorithm presented in Table 1. The measured dataset is added to the reference data with its corresponding label.

In the proposed iMMC-SVM algorithm, the dataset is classified into two classes of the test dataset and the training dataset. The test dataset is then compared with the training dataset to evaluate/predict the label of the test data. In order to train the proposed iMMC-SVM algorithm, the following parameters are considered:

  • Kernel function

  • Scaling factor

  • Convergence criterion

The kernel function, scaling factor, and convergence criterion in the proposed iMMC-SVM algorithm are “RBF,” “1000000,” and “kkt-violation-level,” respectively. During the iMMC-SVM evaluation, it is preferred to maximize the margin between classes. This is achieved by choosing a large value as the scaling factor (RBF sigma). Due to the fact that the values in the training dataset and the test datasets are closed to each other, the proposed iMMC-SVM algorithm may not converge. Hence, the “kkt-violation-level” convergence criterion is selected, in which a fraction of data is allowed to violate the KKT conditions for the Sequential Minimal Optimization (SMO). Faster convergence can be achieved by choosing a large positive value for the “kkt-violation-level.” It should be noted that the “kkt-violation-level” is a value between the range \([0 1]\).

The structural parameters of the proposed iMMC-SVM algorithm vary based on the type of application, the sampling rate, and the number of tests. These parameters are (1) \(SV\), which is basically a matrix of the data point with each row corresponding to a support vector; (2) \(\alpha\), which is the vector of the Lagrange multiplier; (3) \(B\), which is the intercept of the hyperplane that separates the two groups; (4) \(L\), which represents the label of each group; and (5) \(SD\), which shows the information of the scaling factor.

Table 2 shows the accuracy of the predicted label by the proposed iMMC-SVM algorithm based on the number of classes. Upon the iMMC-SVM evaluation, it is observed that increasing the number of classes (\(C\)), where \(C\in {\mathbb{Z}}^{+}, 1\le C\le 90\), significantly adversely affects the accuracy. As the difference between the coordinates is in the micrometer range, some points cannot be predicted by increasing the number of classes, and therefore, the overall accuracy of the process decreases.

Table 2 Accuracy of the predicted labels by the proposed algorithm based on the number of classes
Full size table

The training time also has a direct relationship with the number of classes. The more the number of classes, the higher the training time. However, the accuracy can be evaluated instantly using the test dataset. As shown in Table 2, if the number of classes is limited to two classes of perfect or imperfect, the proposed algorithm can effectively determine the quality of the manufactured part with the maximum accuracy.

3.4.1 Comparison

The collected data has been used for comparison purposes and as shown in Table 3, K-Nearest Neighbors (KNN) algorithm, Multi-Class SVM (MC-SVM) method with linear kernel function, and Neural Networks (NN) method have been evaluated. In this table, the computation time and accuracy have been considered for comparison between different algorithms for a two-class classification evaluation. Neglecting the complexity of the implementation, the proposed iMMC-SVM is faster than the NN method, and more accurate than the KNN algorithm and MC-SVM algorithm with linear kernel function algorithm. When the number of classes increases, overlap among the classes can be observed, and still, the other algorithms have less accuracy.

Table 3 Comparison between different algorithms for a two-class classification evaluation
Full size table

The proposed method is very effective in high dimensional spaces, and also it has a reasonable performance when there is no clear margin of separation between classes. Compared to the other SVM-based algorithms, the risk of overfitting is less in the proposed method. The proposed kernel function is appropriate to solve complex problems, mainly for industrial applications.

4 Conclusions

In this paper, an auto-learning algorithm to reduce the time required to add a new part to a Coordinate Measuring Machines (CMMs) library is presented. The measured data with errors due to vibration is stored in a dataset and the aggregated dataset containing errors is evaluated by an improved Modified Multi-Class Support Vector Machines (iMMC-SVM) algorithm to measure the geometrical features of a part. Practical tests are performed using a laser-based CMM to check the performance and robustness of the proposed algorithm. The measurement results demonstrate that the features of the parts can be accurately determined even in the presence of vibration noise if two classes of perfect and imperfect are defined. Moreover, the proposed method supports fast training and it is easy to implement in practice.