Theoretical Analysis of Measuring Accuracy of Three Linear Axis CMMs from Position Errors

Abstract

The measuring accuracy of coordinate measuring machines (CMMs) depends on different factors such as the errors associated to the CMM axis movement, the working table and other CMM elements. In order to estimate the measuring errors that can be present during the dimensional evaluation of mechanical components, the nature and relevance of the distinct factors involved in the inspection process should be properly identified, such as the position errors, straightness errors, part errors and other geometrical and dynamic deviations. The knowledge about the influence of the main errors related to the elements integrated in the CMM, can serve to estimate the expected accuracy during the geometrical evaluation of manufactured products or machinery components. In this work, the effect of position errors will be evaluated by separate in order to deduce the contribution of this factor to the resultant measuring accuracy. This study is oriented to the analysis of three-axis coordinate measuring machines, and distinct types of CMM axis errors will be discussed. The results shown in this work are focused on CMMs type FXYZ, although similar studies could be developed for other structural configurations.

1 Introduction

During the last years, there are different studies that were developed with the purpose of improving the performance of coordinate measuring machines (CMMs). Among the topics covered in these works, the definition of new devices to enhance the measuring process, new methodologies to characterize the geometrical errors associated to this equipment and numerical models to estimate the measuring accuracy can be found.

Some authors proposed different models that could serve to carry out the analysis of the CMM performance and the influence of some errors of machine axis and probes. In order to estimate the uncertainty associated to the coordinate measuring systems (CMS), the virtual machine model of Sładek and Gąska could be applied [1]. This model implements the errors related to the probe head and CMS kinematics, and employs the Monte Carlo method to evaluate the effect of these error sources.

Zhang proposed a model to evaluate the thermal deformation of the elements integrated in CMMs [2]. This work was focused on coordinate measuring machines with a rotary working table, and considered distinct CMM configurations during the analysis of the main machine errors. The most typical errors of CMMs can be studied by the model of Huang and Ni. This numerical model can be applied for on-time compensation of these geometrical errors [3].

The correction of errors in five-axis multi-sensor CMMs can be made by the parametric model of Ramu et al. [4]. These authors provided a virtual machine for this type of coordinate measuring machines, as well as a parametric model that can be helpful to obtain guidelines for reducing the influence of these errors. In the case of coordinate measuring arms (CMA), the machine errors can be analysed by the kinematic model of Sładek et al. This model serves to improve the resultant accuracy of CMAs, by using a correction matrix that allows the error compensation [5].

The method developed by Thompson and Cogdell [6] could be assumed to increase the accuracy of precision cylindrical CMMs. This method makes possible to deduce the intersection error that describes the normal distance between the rotation axis and probe tip, and to minimize the errors related to the probe alignment.

The expected accuracy of six-freedom-degree parallel mechanism CMMs can be enhanced by the method provided by Meng et al. [7]. It consists of a direct-error-compensation method that can be used to evaluate the probe position errors, process errors associated to the force, heat and control system, and other different machine errors. The multi-probe calibration method of Yang et al. can be applied to kinematic errors of micro-coordinate measuring machines. The method proposed by these authors serves to identify the yaw and straightness errors related to the machine stage displacement, which is carried out by using an autocollimator and two laser interferometers [8].

A recent review about technical advances on coordinate measuring machines was developed by Swornowski. This work remarked some of the main limitations of this equipment, such as the selection of high testing speeds, the selection of optimum measurement points, the deflection errors on the stylus and the evaluation of ball tip radius [9]. The relationship between the dynamic errors and the CMM performance was analysed by Echerfaoui et al. [10]. From the experimental results obtained in this work, the effect of some parameters such as the positioning speed, positioning distance, approaching speed and approaching distance was discussed.

The optimum sampling conditions for the inspection of mechanical products was studied by Raghunandan and Venkateswara Rao. These authors analyzed the effect of sample size and sample points during the measuring of flatness error, and applied a computational method to choose the sampling conditions as a function of the surface finish [11]. Among the different factors to be considered, González-Madruga et al. analysed the effect of operators during the application of Articulated Arm Coordinate Measuring Machines (AACMMs). With this purpose, these authors developed a new methodology that serves to determine the contribution of AACMM, operator and measuring technique to the measurement uncertainty [12].

In order to characterize the performance of coordinate measuring machines (CMMs), the quick check method deduced by Curran and Phelan can be employed [13]. This method is based on using a telescoping ball-bar instead of laser interferometry, and provides a simplified procedure for verification of this equipment. A device based on implementing a fiber-type interferometer was proposed for CMM’s axis verification by Chanthawong et al. The multi-Fabry-Pérot etalon (multi-FPE) developed by these authors, can be recommended before the conventional techniques for CMM verification [14].

Jinwen and Yanling presented a model to enhance the measuring accuracy of CMMs during fast scanning-probing by means of error compensation [15]. The proposed model includes the influence of CMM geometric and dynamic errors such as the position and straightness errors associated to the probe tip, and the angular errors in the linear axes Y and Z. The dimensional measuring of curve surfaces by coordinate measuring machines was studied by Ahn et al. This work describes a transformation algorithm that compensates the probe tip radius and pre-travel errors, and then can be applied to enhance the CMM accuracy [16].

The device conceived by Krajewski and Wozniak can be also valid to compensate the dynamic errors of coordinate measuring machines. These authors discussed the effect of scanning speed on the measuring process, and developed a simple master artefact that serves to improve the CMM resultant accuracy [17]. In order to increase the CMM performance during the dimensional inspection of freeform surfaces, the artifact of Savio and De Chiffre can be helpful. It can be applied when a CAD model is adopted as geometrical reference for the freeform measurements, and then the measuring traceability can be enhanced [18].

Besides the different works that were carried out during the last years in relation with of the optimization of coordinate measuring machines (CMMs), more research studies are required with the purpose of improving the expected accuracy of this type of equipment during the dimensional inspection of mechanical components. For this reason, a new analysis about the influence of some of the main errors associated to the CMM axis displacement was developed in this work, which is specially focused on the discussion about the contribution of position errors among the rest of geometric and dynamic deviations of these devices.

In the present study, a simplified mathematical model is considered to evaluate the influence of position errors that can be originated during the CMM axis movement, as well as the straightness errors related to the distinct CMM linear axes and the dimensional deviations that are found on the part surface. An adequate random algorithm was implemented in this model in order to describe the unexpected variations in positions not covered during the periodical calibration of CMM linear axes, such as all the positions that correspond to the intermediate range between consecutive calibration points. A parameter named as the maximum local deviation for each error source will be assumed to represent the random deviations in the different axes and the part to be tested.

2 Modelling of CMM Dimensional Accuracy from Position Errors

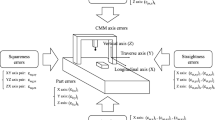
The errors associated to the CMM axis movement can be remarked as one of the main factors that affect the dimensional accuracy of coordinate measuring machines (CMM). These CMM axis errors represent a totality of 21 error sources, and they can be divided in 3 position errors, 6 straightness errors, 3 squareness errors and 9 angular errors in the case of a three-axis coordinate measuring machine [2]. During the numerical modelling of the CMM accuracy, the totality of these errors could be assumed.

The performance of CMM will be also affected by other dimensional and geometrical errors such as the deviations associated to the working table and the part to be tested, as well as other different factors involved in the measuring process. These error factors could be included in the numerical modelling in order to increase the validity of the results.

The 21 error sources related to the CMM axis displacement are illustrated in Fig. 1, including the position, straightness, squareness and angular errors for the different linear axes. The geometrical errors of the part to be measured are also depicted. The symbols employed in this study to identify each CMM axis error are contained in this figure, and the ijk subscripts denote the coordinates (x, y, z) of the CMM probe inside the overall working volume.

Fig. 1

Schematic representation of errors associated to CMM axis displacement

Since the aim of this work consists of analyzing the effect of position and straightness errors on the expected accuracy of CMM during the dimensional inspection of mechanical components, the influence of these axis errors will be specially discussed. For this purpose, only the position, straightness and part errors will be considered, and the rest of error sources of coordinate measuring machines will not be introduced in the numerical modelling.

In the following subsections, a brief definition about the main types of error sources of Fig. 1 can be found, mostly about the geometrical errors that will be analyzed in this work. A graphical explanation about the position and straightness errors will be provided as follows, as well as the mathematical expressions that will be employed to estimate the position, straightness and part errors in this study.

Among the models employed in the works of other authors, there are basically theoretical models that consider the 21 typical errors sources of CMMs, that also integrate the errors associated to the rotary working table of some CMM models, that are specially focused on the probe alignment errors, or that were developed for the analysis of coordinate measuring arms (CMAs) instead of coordinate measuring machines (CMMs). Nevertheless, the simplified model of the present work is limited to some specific errors with a great influence on the CMM measuring accuracy, such as the position errors and straightness errors, in order to facilitate a more detailed analysis of these geometrical errors.

The error sources assumed in this model are the 3 forms of position errors, the 9 forms of straightness errors and the deviations originated in the part geometry, which imply a reduced number of 13 geometrical errors to be evaluated. It allows to optimize the mathematical modelling, and to achieve almost a half of the computational times needed for the analysis of the CMM measuring accuracy.

In addition, this new numerical model include a mathematical algorithm for estimating the random variation of CMM geometrical errors in the interval between calibration points, to facilitate the analysis of the expected accuracy that would result when using different models of coordinate measuring machine. As will be explained in the following subsection, this random algorithm is based on the Marsaglia and Bray’s method, and will be applied to the totality of geometrical errors that are assumed in this work.

The implementation of this random error generation algorithm, allows the analysis of different possible conditions with a similar calculation time, saving the computation time that would be required to repeat the theoretical modelling with different error distributions in the distinct linear axes of CMM.

As will be explained in Sect. 2.7, the model employed in this work is oriented to coordinate measuring machines of the most typical structural configuration, such as the configuration type FXYZ, which corresponds to moving bridge CMMs. It also helped to simplify the numerical model that is applied in this study, although the proposed model can be easily redefined for other machine configurations.

2.1 Modelling of Random Errors Generation by Marsaglia and Bray’s Method

The random variations that occur in the errors associated to CMM axis displacement and the errors detected on part surface, can be estimated by a mathematical algorithm for random error generation. Among the different well-known algorithms that exist for this purpose, in this work the Marsaglia and Bray’s method was applied, which consists of a random algorithm based on the Montecarlo method.

This mathematical algorithm can be used to deduce the possible variations in each axis error between the consecutive calibration points, as well as the possible deviations on the surface of the mechanical part to be measured. This algorithm is divided in two distinct stages, such as the generation and validation of each pair of uniform variables, and the deduction of each value according to the resultant normal variable.

In the first stage of Marsaglia and Bray’s method, a pair of variables u_1i and u_2i that correspond to a uniform distribution U(− 1,1) should be generated, and the following mathematical restriction must be satisfied by each pair of values for these uniform variables:

$$u_{1i}^{2} + u_{2i}^{2} < 1$$

(1)

In the case that this condition was not achieved, a new pair of values should be generated for variables u_1i and u_2i, and the previous restriction should be checked again. On the contrary, if this condition is satisfied, a variable δ_i that corresponds to a normal distribution N(0,1) can be deduced by using the following mathematical expression:

$$\updelta_{i} = u_{1i} \sqrt { - 2 \ln \left( {u_{1i}^{2} + u_{2i}^{2} } \right)/\left( {u_{1i}^{2} + u_{2i}^{2} } \right)}$$

(2)

From this equation, a resultant variable δ_i of normal distribution N(0,1) with random values between 0 and 1 can be determined for each value of subscript i = 0, 1, 2,…n. In this work, this normal variable will be employed to deduce the random values of position, straightness and part errors during the modelling of CMM performance.

2.2 Modelling of Position Errors during Dimensional Verification by CMMs

The deviations that correspond to the position errors associated to each CMM linear axis, are illustrated in Fig. 2. As an example, this figure represents the position errors related to axis X, while a similar schematic representation could be assumed for axes Y and Z. These errors represent the discrepancies that can be registered between the theoretical and real position adopted by the CMM probe during its displacement in the direction of the different CMM linear axes, as depicted in this figure.

Fig. 2

Schematic representation of position errors in coordinate measuring machines

The position errors in the longitudinal, traverse and vertical axes of CMM can be identified as (ε_ps,x)_i, (ε_ps,y)_j and (ε_ps,z)_k, and the following mathematical expression can be applied for instance to deduce the CMM axis errors in longitudinal axis from the random values provided by the Marsaglia and Bray’s method:

$$(\varepsilon_{ps,x} )_{i} = (\delta_{ps,x} )_{i} \, {(\varepsilon_{ps,x})}_{\text{max}}$$

(3)

where the i subscript corresponds to the position x_i in the longitudinal axis (in which this geometrical error is evaluated), (δ_ps,x)_i is a random value between 0 and 1 that was previously generated for position x_i, and (ε_ps,x)_max represents the maximum local deviation for position errors associated to the longitudinal axis, which is expressed in terms of the standard deviation deduced from the fluctuations evidenced in this CMM axis error.

This equation serves to estimate the position error in the direction of longitudinal axis (axis X) for the different points to be considered along this linear axis, while a similar expression could be also applied for the traverse and vertical axes (axes Y and Z) of coordinate measuring machine (CMM).

2.3 Modelling of Straightness Errors during Dimensional Verification by CMMs

Figure 3 provides a schematic representation of CMM axis errors that are identified as straightness errors. This figure depicts the straightness errors that can be registered in vertical axis (axis Y) during the CMM probe displacement along the direction of longitudinal axis (axis X), while a similar illustration could be assumed for the straightness errors in other CMM linear axes. These errors describe the variations that can be evidenced in each specific normal axis during the CMM movement along a certain linear axis.

Fig. 3

Schematic representation of straightness errors in coordinate measuring machines

In this work, a random algorithm based on the Marsaglia and Bray’s method will be also adopted to estimate the straightness errors, and so a mathematical expression similar to that previously established for position errors can be applied. In this sense, the straightness errors during the displacement in the axis X that are observed on normal axis Y can be calculated by the following expression:

$$(\varepsilon_{st,xy} )_{i} = (\delta_{st,xy} )_{i} \, {(\varepsilon_{st,xy})}_{\text{max}}$$

(4)

where the i subscript represents the position x_i in the displacement axis (which in this case corresponds to the axis X), (δ_st,xy)_i is a random value between 0 and 1 that must be previously generated for this position in the displacement axis, and (ε_st,xy)_max consists of the maximum local deviation for straightness errors during the displacement of axis X that is registered on normal axis Y.

2.4 Modelling of Squareness Errors during Dimensional Verification by CMMs

During the characterization of geometrical errors of coordinate measuring machines (CMMs), each pair of orthogonal linear axes (such as the axis pairs XY, YZ, and ZX) can experience a certain deviation with regards to their expected orthogonal orientation. These geometrical deviations are named as squareness errors, and could influence the resultant measuring accuracy of CMM.

In three linear axis CMMs, a total number of 3 squareness errors are involved, and in the present work are identified as ε_sq,xy, ε_sq,yz and ε_sq,zx (Fig. 1). These machine errors will be neglected in this work, in order to analyse by separate the effect of position, straightness and part errors on the CMM performance.

2.5 Modelling of Angular Errors during Dimensional Verification by CMMs

Each linear axis of a coordinate measuring machine, can experience a certain angular deviation in three distinct directions, such as rotation around this linear axis during probe displacement in the axis direction, inclination in the plane constituted by this linear axis and one of the normal axes, and inclination in the plane formed by this linear axis and the other normal axis. These geometrical deviations are known as angular errors, and could present a certain influence on the CMM performance.

The angular errors of each CMM linear axis are named as the roll, pitch and yaw errors. The roll errors describe the rotation around the direction of this linear axis, while the pitch and yaw errors correspond to the inclination in each one of the planes formed with both normal axes. Since 3 angular errors can be defined in each linear axis of a coordinate measuring machine, a total number of 9 angular errors must be considered in three linear axis CMMs.

As an example, the roll, pitch and yaw errors originated during the CMM probe displacement along the axis X can be denoted by (ε_ar,x)_i, (ε_ap,xz)_i and (ε_ay,xy)_i, respectively (Fig. 1). Similar symbols can be employed for the angular errors related to the movement along the other two linear axes of coordinate measuring machines. The angular errors are also neglected in this work, in order to analyze by separate the influence of position, straightness and part errors.

2.6 Modelling of Part Errors during Dimensional Verification by CMMs

Not only the geometrical errors of coordinate measuring machines, but also the deviations observed in the surface of part to be measured can affect the results of the measuring process. For this reason, the deviations of part geometry should be also considered for an adequate modelling of the CMM performance.

The Marsaglia and Bray’s method is also assumed in this work to describe the possible variations in the part geometry, and then these errors are estimated by using a mathematical expression similar to that applied for position and straightness errors, as can be observed in the following equation:

$$(\varepsilon_{0,x} )_{i} = (\delta_{0,x} )_{i} \, {(\varepsilon_{0,x})}_{\text{max}}$$

(5)

where the i subscript refers to the position x_i in the displacement axis (in this case axis X), (δ_0,x)_i corresponds to a random value between 0 and 1 that was previously generated for position x_i, and (ε_0,x)_max is the maximum local deviation for part errors in the direction of displacement axis. This equation corresponds to the case of probe displacement in longitudinal axis (axis X), and similar expressions should be assumed for the rest of CMM linear axes.

In this work, a total number of 3 part errors are implemented, which represent the deviations originated in the normal direction to the part surface according to the different linear axes of coordinate measuring machine. The part errors registered on the direction of axes X, Y and Z, can be denoted by (ε_0,x)_i, (ε_0,y)_j and (ε_0,z)_k, respectively.

2.7 Modelling of Expected Accuracy of Coordinate Measuring Machine

From the different typical configurations of coordinate measuring machines, the FXYZ, XFYZ, YXFZ and ZYXF configurations can be remarked, and additional cases could also be considered when a rotary table is contained. This work is focused on the coordinate measuring machines that are most commonly employed in the industry, which correspond to the configuration type FXYZ (or moving bridge CMMs). The mathematical expressions applied to evaluate the CMM measuring accuracy will be affected by the machine configuration. The equations for a configuration type FXYZ will be described as follows, and some modifications would be needed in the other cases.

In order to evaluate the overall error in the position of the measuring probe in three linear axis CMMs, the reference systems O₁X₁Y₁Z_1, O₂X₂Y₂Z₂ and O₃X₃Y₃Z₃ associated to the linear axes X, Y and Z must be considered, and a transformation matrix can be used to deduce the coordinates that correspond to the stationary coordinate system OXYZ within the CMM working volume [2]. The measuring accuracy of the CMM can be expressed by the following equation:

$$\Delta {\text{S = P}} - ( {\text{S}} + {\text{P}}_{ 3} )$$

(6)

where P₃ = O₃ P₃ is the position of CMM probe according to the coordinate system O₃X₃Y₃Z₃, S = O O₃ is the position of the origin of coordinate system O₃X₃Y₃Z₃ expressed in the CMM stationary coordinate system OXYZ, P = O P is the position of the measuring probe in the stationary coordinate system, and ΔS = ΔO O₃ represents the errors in the CMM probe position in the stationary coordinate system.

The expected accuracy of CMM can be also expressed in matrix format as indicated in the following equation, which contains the geometrical errors that were previously described:

$$\left[ {\begin{array}{*{20}c} \begin{aligned} \Delta x_{ijk} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{aligned} \\ \begin{aligned} \Delta y_{ijk} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{aligned} \\ {\Delta z_{ijk} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \begin{aligned} (\varepsilon_{ps,x} )_{i} +\, (\varepsilon_{st,yx} )_{j} + (\varepsilon_{st,zx} )_{k} - y\varepsilon_{sq,xy} - z\varepsilon_{sq,zx} - y(\varepsilon_{ap,xz} )_{i} \\ +\,z[(\varepsilon_{ar,y} )_{j} + (\varepsilon_{ay,xy} )_{i} ] - y_{p3} [(\varepsilon_{ar,z} )_{k} + (\varepsilon_{ap,xz} )_{i} + (\varepsilon_{ay,yz} )_{j} ] \\ + z_{p3} [(\varepsilon_{ar,y} )_{j} + (\varepsilon_{ay,xy} )_{i} + (\varepsilon_{ap,zy} )_{k} ] + (\varepsilon_{0,x} )_{i} \\ \\ \end{aligned} \\ \begin{aligned} (\varepsilon_{ps,y} )_{j} + (\varepsilon_{st,xy} )_{i} + (\varepsilon_{st,zy} )_{k} - z\varepsilon_{sq,yz} - z[(\varepsilon_{ar,x} )_{i} + (\varepsilon_{ap,yx} )_{j} ] \\ +\, x_{p3} [(\varepsilon_{ar,z} )_{k} + (\varepsilon_{ap,xz} )_{i} + (\varepsilon_{ay,yz} )_{j} ] \\ - \,z_{p3} [(\varepsilon_{ar,x} )_{i} + (\varepsilon_{ap,yx} )_{j} + (\varepsilon_{ay,zx} )_{k} ] + (\varepsilon_{0,y} )_{j} \\ \\ \end{aligned} \\ \begin{aligned} (\varepsilon_{ps,z} )_{k} + (\varepsilon_{st,xz} )_{i} + (\varepsilon_{st,yz} )_{j} + y(\varepsilon_{ar,x} )_{i} \\ -\, x_{p3} [(\varepsilon_{ar,y} )_{j} + (\varepsilon_{ay,xy} )_{i} + (\varepsilon_{ap,zy} )_{k} ] \\ +\, y_{p3} [(\varepsilon_{ar,x} )_{i} + (\varepsilon_{ap,yx} )_{j} + (\varepsilon_{ay,zx} )_{k} ] + (\varepsilon_{0,z} )_{k} \\ \end{aligned} \\ \end{array} } \right]$$

(7)

This study is focused on the analysis of the effect of position errors on the expected accuracy of CMM, and then only the position errors associated to the axis displacement will be assumed, as well as the straightness errors in this linear axis and the deviations detected on the part to be tested. For this reason, the rest of CMM geometric errors will be neglected during the numerical modelling applied in this work.

3 Analysis Procedure

The present work is focused on the analysis of the influence of position errors on the CMM performance, in order to evaluate the measuring accuracy that could be achieved during the dimensional verification of mechanical parts. The applied methodology can be used to study the expected accuracy of three linear axis CMMs, and the results contained in this work correspond to the dimensional inspection in the direction of the main axis of this equipment. A three linear axis DEA PIONEER 6.10.6 CMM with a working volume of 600 × 1000 × 600 mm, maximum measuring error of 6.8 μm and maximum probing error of 3.0 μm was considered.

The CMM measuring accuracy is estimated by means of the distance between two opposite plane faces on the evaluated part. According to the procedure established in this work, the results are registered by the distance between the planes constructed from the points measured on both part faces, and the totality of results correspond to the dimensional verification of a 50 mm length prismatic part.

During the numerical analysis of CMM measuring accuracy that was carried out in this work, a range of maximum local deviation for position errors between 0 and 2 μm was assumed. In general terms, part errors of 1 μm and straightness errors of 0.2 and 0.5 μm were considered in these numerical simulations. In order to identify the behavior that could present two CMMs with distinct axis errors, the results that correspond to two series of simulations with different sets of random errors will be illustrated. In addition, some series of simulations without part errors and straightness errors were also executed to identify the effect of position errors by separate.

In this work, during the discussion of the effect of the different error sources, the measuring accuracy obtained in terms of the real resolution of 1 μm that corresponds to three-axis coordinate measuring machines are compared to the results expressed according to a computing resolution of 0.1 μm that can be considered during the numerical analysis. The numerical predictions for a CMM computing resolution of 0.1 μm will allow to better understand the tendency followed by the measuring accuracy, which usually can not be clearly identified from the rounded results provided by the CMM real resolution of 1 μm.

4 Results and Discussions

4.1 Characterization of CMM Axis Errors

The geometrical deviations associated to the CMM axis displacement, can be evidenced during the periodical calibration of this equipment. Figure 4 represents the position errors that correspond to the distinct linear axes of the machine considered in this study, from the results obtained during the CMM calibration.

Fig. 4

Measured position errors during the calibration of CMM displacement along the longitudinal axis

The curves of this figure illustrate the deviations registered at the coordinates assumed as calibration points along each linear axis of the coordinate measuring machine. These deviations could be compensated by the control system of this equipment, but the possible fluctuations inside the intervals between consecutive calibration points should be estimated for the numerical modelling of CMM performance.

The magnitude of the possible fluctuation in the positions belonging the intermediate range between consecutive calibration points, can be deduced from the dispersion in the results obtained for the total length of each CMM linear axis. According to the results shown in Fig. 4, a fluctuation of about 0.38 μm can be assumed in terms of standard deviation inside these intervals for the position errors associated to this three linear axis coordinate measuring machine.

In this study, the numerical analysis of CMM performance will be carried out from different levels of possible fluctuations for the geometrical errors in the CMM axis displacement, in order to discuss about the expected accuracy for coordinate measuring machines with distinct error levels. These fluctuations will be described by the maximum local deviation that was previously defined for each axis error.

4.2 Effect of Position Errors on Measuring Error

The results shown in this section, correspond to the modelling of CMM performance considering uniquely the influence of position errors associated to the linear axes of this equipment. A series of numerical simulations without other error sources was developed in this section, in order to identify by separate the effect of position errors.

Figures 5, 6, 7 and 8 depict the measuring accuracy that can be achieved during the application of three-axis CMM for dimensional verification of prismatic parts. These curves show the maximum and minimum limits that represent the expected variation range of measuring results during the inspection process. The Marsaglia and Bray’s method was used to estimate the random deviations that can be originated in the distinct position errors within the working volume of CMM.

Fig. 5

Expected CMM measuring errors from position errors with real resolution and first set of random errors (for null part errors and straightness errors)

Fig. 6

Expected CMM measuring errors from position errors with real resolution and second set of random errors (for null part errors and straightness errors)

Fig. 7

Expected CMM measuring errors from position errors with computing resolution and first set of random errors (for null part errors and straightness errors)

Fig. 8

Expected CMM measuring errors from position errors with computing resolution and second set of random errors (for null part errors and straightness errors)

These figures illustrate the measuring results that can be expected for different levels of machine errors in terms of the maximum local deviation for position errors. The represented results correspond to different values of maximum local deviation for position errors inside the range from 0 up to 2 μm.

The numerical predictions for an extended range of maximum local deviation for position errors between 0 and 2 μm are shown in the illustrations a) of these figures, while the illustrations b) reflect the results that correspond to a closer range of position errors between 0 and 1 μm.

Figures 5 and 6 represent the numerical predictions for a CMM real resolution of 1 μm, and CMM computing resolution of 0.1 μm was considered for Figs. 7 and 8, as previously indicated in the section dedicated to the description of the analysis procedure. The results shown in Figs. 5 and 6 were obtained after rounding to the 3 digits that correspond to the measuring resolution of coordinate measuring machine (real resolution), while a higher resolution of 4 digits provided by numerical computing was assumed in Figs. 7 and 8 (computing resolution).

Two distinct sets of random errors were considered, in order to evaluate the expected results for different zones inside the working volume of coordinate measuring machine. Figures 5 and 7 depict the results for a first set of random values for the position deviations along the CMM longitudinal axis, while Figs. 6 and 8 correspond to a second set of random errors.

Experimental results are also contained in these figures, in order to validate the simulations provided by the numerical model. Two different zones 1 and 2 along the direction of axis X of coordinate measuring machine were considered. The experimental results for both zones will serve to carry out the validation of numerical simulations that correspond to the first and second sets of random errors.

Figures 5 and 7 illustrate the results of dimensional verification of a prismatic part at a certain location identified as zone 1 inside the axis X, while the experimental results of Figs. 6 and 8 correspond to the inspection of this part at the zone 2 along the direction of this linear axis.

The totality of curves contained in Figs. 5 and 6 reveal a linear increase in the expected measuring error as a function of the fluctuation level in the position errors associated to the CMM linear axes, which is expressed in terms of the maximum local deviation for these machine errors. This linear tendency can be easily evidenced in the curves registered with a maximum local deviation between 0 and 2 μm (Figs. 5a, 6a). A linear increase can also be observed in the curves for position errors between 0 and 1 μm (Figs. 5b, 6b). The deviation observed at the first points of these curves can be attributed to the rounding of measuring results according to the CMM measuring resolution.

The numerical modelling provides a increasing tendency in the CMM measuring accuracy for both sets of random errors, as can be seen in Figs. 5 and 6 respectively. Nevertheless, higher measuring deviations are obtained from the second set of random errors (Fig. 6) if compared to the results provided by numerical simulations under the first set of random errors (Fig. 5).

If a CMM computing resolution of 0.1 μm is considered (Figs. 7 and 8), the influence of maximum local deviation for position errors on the expected measuring accuracy can be analyzed with a greater detail. From this higher resolution, smoother curves are registered during the numerical modelling of CMM performance.

According to the results shown in Figs. 5, 6, 7 and 8, the expected fluctuations during the measuring process for different values of position errors are about 6 times lower when a computing resolution of 0.1 μm is assumed (Figs. 7, 8), with regards to the curves showing the measuring error for a real resolution of 1 μm (Figs. 5, 6).

The experimental results registered during the dimensional verification of a prismatic part exceed the maximum and minimum limits represented in Figs. 5, 6, 7 and 8, specially in the figures that depict the results obtained for CMM real resolution. This can be attributed to the fact that in this section only the position errors are considered during the numerical simulation of CMM performance. Nevertheless, these experimental results will satisfy the limits provided by the numerical modelling when other error sources are also assumed, as will be discussed in the next sections of this work.

4.3 Effect of Part Errors on Measuring Error

After the analysis of CMM measuring accuracy as a function of position errors by separate, in this section the effect of other error sources such as the part errors and straightness errors will be also considered, and so the CMM performance could be discussed in a more realistic form. In this series of numerical simulations, a maximum local deviation for part errors of 1 μm was assumed in order to describe the possible deviations on the part surface. The numerical results of this section were carried out from two different values of maximum local deviation for straightness errors, such as 0.2 and 0.5 μm. Only the first set of random errors was assumed in the totality of simulations of the present section.

Figures 9 and 10 illustrate the expected measuring accuracy for a three-axis coordinate measuring machine according to a CMM real resolution of 1 μm, and CMM computing resolution of 0.1 μm was adopted for Figs. 11 and 12.

Fig. 9

Expected CMM measuring errors from position errors with real resolution and first set of random errors (for part errors of 1 μm and straightness errors of 0.2 μm)

Fig. 10

Expected CMM measuring errors from position errors with real resolution and first set of random errors (for part errors of 1 μm and straightness errors of 0.5 μm)

Fig. 11

Expected CMM measuring errors from position errors with computing resolution and first set of random errors (for part errors of 1 μm and straightness errors of 0.2 μm)

Fig. 12

Expected CMM measuring errors from position errors with computing resolution and first set of random errors (for part errors of 1 μm and straightness errors of 0.5 μm)

From the curves of Figs. 9 and 10, a clear tendency cannot be evidenced in the CMM accuracy as a function of position errors when the maximum local deviation for these errors is between zero and 0.5 μm (Figs. 9b, 10b). On the contrary, an increasing linear tendency can be observed when the maximum local deviation for position errors is higher than 0.5 μm.

If a CMM computing resolution of 0.1 μm is adopted (Figs. 11, 12), smoother curves are provided by the numerical model. These curves show a gradual increase in the CMM measuring accuracy for the complete range of maximum local deviations for position errors, and help to understand the effect of position errors when part errors and straightness errors are also considered. Again, an increasing linear tendency is only evidenced for position errors greater than 0.5 μm.

Lower differences in the curve tendency were evidenced between the numerical predictions for both real or computing resolution of Figs. 9, 10, 11 and 12, if compared to the results represented in Figs. 5, 6, 7 and 8. It can be explained by the effect of the part errors and straightness errors, since these error sources were not assumed during the numerical modelling of CMM performance in Sect. 4.2 and so higher fluctuations as a function of position errors were provided in those numerical predictions.

The curves of Figs. 9 and 11 represent the CMM measuring accuracy that can be achieved for a maximum local deviation for straightness errors of 0.2 μm, while Figs. 10 and 12 correspond to straightness deviations of 0.5 μm. The discrepancies between these results for both straightness deviations are about 34% when the real resolution and position errors up to 1 μm are considered, but it can be negligible in the rest of cases.

When not only the position errors but also the part errors and straightness errors are considered (as occurs in Figs. 9, 10, 11 and 12), a lower slope is registered in the curves showing the variation of CMM measuring accuracy as a function of the maximum local deviation for position errors. This can be explained by the influence of part errors and straightness errors, since they present a greater weight on the overall machine errors when the lowest values of maximum local deviation for position errors are adopted. In fact, an almost constant CMM measuring accuracy about 1 μm is found in the range of position errors between zero and 0.5 μm when these error sources are also considered (Figs. 9b, 10b), while an increasing variation from zero to about 1 μm is depicted in this interval when only the position errors are analyzed (Fig. 5b).

The experimental results registered during the dimensional inspection of a prismatic part in two different zones 1 and 2 along the axis X of coordinate measuring machine, are comprised inside the variation ranges defined by the maximum and minimum limits of Figs. 9, 10, 11 and 12. It serves to validate the predictions provided by the numerical model proposed in this work.

4.4 Effect of Random Errors on Measuring Error

The measuring accuracy of three-axis CMMs can be strongly affected by the deviations originated at the different positions covered by the CMM probe along the axis displacement and by the geometrical deviations that occur at the different points of the part surface. The influence of these unexpected deviations can be evaluated by adopting distinct sets of random errors during the numerical modelling of CMM performance.

A few results from different random errors were facilitated in Sect. 4.2, but the present section is specially dedicated to discuss the influence of the random errors by separate. For this purpose, the totality of numerical simulations of this section were developed from a second set of random errors, and their effect on the CMM measuring accuracy will be discussed in comparison with the results of the previous sections of this work.

The results shown in the following figures correspond to the numerical modelling with a maximum local deviation for position errors in the range from zero up to 2 μm, straightness errors of 0.2 and 0.5 μm and part errors of 1 μm, in all the cases with a second set of random errors. Figures 13 and 14 illustrate the results provided by the numerical modelling for CMM real resolution, while CMM computing resolution was assumed for Figs. 15 and 16.

Fig. 13

Expected CMM measuring errors from position errors with real resolution and second set of random errors (for part errors of 1 μm and straightness errors of 0.2 μm)

Fig. 14

Expected CMM measuring errors from position errors with real resolution and second set of random errors (for part errors of 1 μm and straightness errors of 0.5 μm)

Fig. 15

Expected CMM measuring errors from position errors with computing resolution and second set of random errors (for part errors of 1 μm and straightness errors of 0.2 μm)

Fig. 16

Expected CMM measuring errors from position errors with computing resolution and second set of random errors (for part errors of 1 μm and straightness errors of 0.5 μm)

A certain increasing tendency is probed in both sets of random errors in the complete range of position errors between zero and 2 μm, when a computing resolution of 0.1 μm is considered (Figs. 11, 12, 15, 16). Nevertheless, a higher slope is evidenced in the curves that represent the results obtained from the second set of random errors, and the measuring errors that correspond to this set of random errors are a 12% greater.

The discrepancies in the curve tendency between both sets of random errors are specially remarked in the range of position errors up to 0.5 μm. An almost constant CMM measuring accuracy was obtained for position errors between zero and 0.5 μm when the first set of random errors is considered (Figs. 11b, 12b), while a higher slope was registered in this interval in the case of the second set of random errors (Figs. 15b, 16b).

The expected measuring accuracy of coordinate measuring machine could be estimated by the overall maximum and minimum limits that would result as the average between the maximum and minimum limits provided by the numerical model for each one of both sets of random errors considered in this section.

According to the results presented in this section, it can be concluded that the numerical model of this work can be applied to estimate the measuring accuracy of a certain CMM from the possible deviations that can occur in the intermediate positions between successive calibration points. For this purpose, the numerical simulation of CMM performance should be executed with different sets of random errors, and finally the expected CMM measuring accuracy could be determined by the overall maximum and minimum limits to be deduced as the average between the maximum and minimum limits for the distinct sets of random errors.

4.5 Effect of Position Error on Measuring Dispersion During Dimensional Inspection

In order to understand the influence of the axis displacement errors on the CMM performance, the measuring dispersion associated to the successive measures to be executed during the dimensional verification of mechanical parts should be also discussed, since it can contribute to explain the gradual increment evidenced in the variation range that is defined between the maximum and minimum limits illustrated in previous sections of this work for the different analysis conditions.

The following figures represent the measuring dispersion that results from the different dimensional measures to be made with the CMM during the inspection process, according to the predictions provided by the numerical modelling. Figures 17 and 18 show the results obtained for a real resolution of 1 μm and computing resolution of 0.1 μm, respectively.

Fig. 17

Expected CMM measuring errors from position errors with real resolution and two sets of random errors (for part errors of 1 μm and straightness errors of 0–2 μm)

Fig. 18

Expected CMM measuring errors from position errors with computing resolution and two sets of random errors (for part errors of 1 μm and straightness errors of 0–2 μm)

Figures 17 and 18 represent the measuring dispersion to characterize the achievable CMM measuring accuracy, instead of using the maximum and minimum limits that were discussed in the previous sections. These figures depict the measuring dispersion as a function of the maximum local deviation for position errors, and comprise a series of curves that exhibits the results obtained for different values of straightness errors between zero and 2 μm. A maximum local deviation for part errors of 1 μm and two different sets of random errors are assumed in this section.

The differences among the successive curves of these figures can be more easily identified in Fig. 18, since it illustrates the results for a computing resolution of 0.1 μm. Figures 18a and b show a similar increasing tendency, although a distinct slope is obtained for each set of random errors.

The curves of Fig. 18 that correspond to the lowest values of straightness errors are closer to consecutive curves, and a greater distance between them is observed as the maximum local deviation for straightness errors is incremented. A gradual increase in the distance between consecutive curves can be more easily identified in the range of position errors from 1 to 2 μm.

The experimental results obtained from the dimensional verification of a prismatic part, are comprised inside the variation range defined by the measuring dispersion that correspond to the conditions assumed during the numerical modelling of CMM performance. It serves to check the validity of the numerical model that was proposed in this work.

5 Conclusions

The variation of the CMM measuring accuracy as a function of certain error sources such as the position errors related to the CMM axis displacement was evaluated in this work. Different conditions were analyzed with the purpose if deducing the specific influence of position errors, from the numerous factors that affect the CMM performance. A simplified numerical model limited to the contribution of position errors, straightness errors and part errors was applied, in order to minimize the computing time required for studying the expected measuring accuracy when a three-axis CMM is employed. This work was focused on the analysis of three-axis coordinate measuring machines (CMMs) type FXYZ, although similar studies could be also carried out for other machine structural configurations. According to the results obtained in this work, a increasing linear tendency is identified in the CMM measuring accuracy as a function of the maximum local deviation for position errors, when only these error sources are examined and when the part errors and straightness errors are also assumed. From the results obtained with all these error sources, an almost constant measuring accuracy is found for position errors up to 0.5 μm, while it is gradually incremented for higher values of maximum local deviation for position errors. If the measuring dispersion associated to the successive dimensional measures is represented as a function of position errors for different values of straightness errors, a lower slope and a higher distance between consecutive curves can be observed as greater values of maximum local deviation for straightness error are adopted. The proposed model was proved to be valid to estimate the CMM measuring accuracy, by identifying the measuring range that would comprise the expected results from the dimensional inspection of mechanical parts.