1 Introduction

There is a surging demanding for precisely manufactured parts and precision machine tools. The accuracy of precision machine tools is affected by many errors including geometric errors, force-induced errors, and thermally induced errors which is usually named as thermal errors. When in operation, the heat generated by rotating spindle, moving liner axes, machining processes, and ambient temperature results in thermal gradients on the machine tool. These thermal gradients lead to the thermal deformation of the machine tool components which in combination extremely deteriorate the machine tool accuracy [1, 2]. Many studies suggest that 40~70% of the overall profile errors of the machined workpiece is caused by the thermal errors of machine tools [3,4,5]. Usually, the higher the precision of the machine tools, the greater the proportion of the thermal errors. Therefore, the thermal errors should be reduced. In general, the there are three methods to reduce thermal errors: (1) cooling the machine tool or the environment to control the temperature or using aerostatic/hydrostatic spindle, screws, or slides to reduce heat generation; (2) thermal-symmetrical design of the machine tool structure or using thermal insensitive materials to reduce thermal deformation; and (3) compensation or correction the thermal errors through CNC controller. However, it is challenging to realize the first two methods because of the special cooling and assembly equipment and the designing and manufacturing expertise needed, which eventually be costly. Hence, the easier, cheaper, and more flexible compensation method which readjusts the moving axes to the desired position through the CNC controller is widely used.

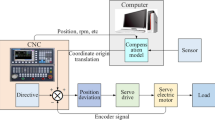
The thermal error compensation can be realized by direct compensation and indirect (model-based) compensation. In direct compensation, the thermal errors at the tool center point (TCP) are intermittently measured by the touch-trigger probe and are intermittently used to readjust the moving axes [6]. The drawbacks of direct compensation are the need to interrupt the machining process to measure the thermal errors and the non-continuous compensation [7]. In contrast, in indirect (model-based) compensation, the thermal errors used to readjust the moving axes are calculated by a thermal error model in real time [8]. It is flexible, cost-effective, and easy to implement and becomes one of the most widely used compensation methods. Hence, in this study, when it comes to thermal error compensation, it refers to indirect (model-based) compensation.

Various thermal error models have been proposed for compensation. Generally, they include the numerical simulation model and the statistical model [3]. With regard to numerical simulation model, partial differential equation (PDE) [9], finite difference method (FDM) [10], and finite element method (FEM) [11, 12] are proposed to simulate the thermal deformation process. However, it is complicated and time-consuming to create an accurate numerical simulation model of the machine tool to precisely predict the thermal errors due to the factors as needing the 3D model of the machine tool, needing the accurate material properties and needing to determine the complex thermal boundary conditions [13,14,15,16,17]. As a result, the statistical model has received more attention [18]. Taking the advantage of the mapping relationship between the thermal error data and the temperature data from experiment, the proper machine learning algorithms can be used to build the statistical thermal error model which can represent and reveal the thermal-mechanical characteristics and the thermal deformation process of the machine tool. Then, input the real-time measured temperature data to the built thermal error model, the thermal error values can be predicted and used to compensate on-the-fly.

There are two key issues to be addressed in statistical thermal error modeling: (1) selecting the key temperature points/critical temperature points/temperature-sensitive points as the model input, and (2) adopting suitable modeling method to build the thermal error model [19]. The measured temperature data and thermal error data from thermal error experiment are the base of thermal error modeling. In thermal error experiment, it is impossible and not necessary to measure the temperatures of the whole machine tool. Usually, a certain number of temperature sensors are initially installed on the machine tool structure based on experience to capture the time-varying temperature states as comprehensive as possible. However, it is unsuitable to build the thermal error model with so many temperature points as the input due to the redundancy and multicollinearity between some temperature points and the additional cost of using too many temperature sensors. Thus, based on the measured data, some key temperature points should be selected, whose temperatures can best infer the thermal error. Basically, the key temperature points selection involves the use or combination use of the clustering technique [20], the correlation analysis [21], the grey correlation analysis [22], the principal component analysis [23], the decomposition technique [17], or the model-related technique [24]. Finally, suitable statistical learning algorithms, such as the multiple linear regression (MLR) [25], the least squares support vector machine (LSSVM) [26], the neural networks (NN) [27], or the hybrid methods [28] can be applied to establish the thermal error model by regarding the temperatures of the key temperature points as input and the thermal errors as output. Nevertheless, some studies revealed that the key temperature points may not be constant but changeable [29, 30]. Thus, the prediction performance of the thermal error model which is based on the group of selected key temperature points may remain unguaranteed.

In the present study, the changeable characteristics of the key temperature points are further revealed and a more robust thermal error modeling method is proposed to predict the spindle thermal error of a machine tool. The time-varying characteristics of the key temperature points are revealed based on the temperature data and thermal error data from experiment with the combination use of the popular fuzzy c means (FCM) clustering and correlation analysis (CA) method. Considering the time-varying characteristics of the key temperature points, the segment fusion LSSVM (SF-LSSVM) thermal error modeling method is proposed. Firstly, the temperature data and thermal error data are divided into different segments according to time. Then, using the LSSVM with excellent nonlinear mapping capabilities as the basic model, the sub-LSSVM thermal error model building and the corresponding key temperature points selection in each segment are fulfilled with genetic algorithm (GA) in a wrapper manner to preserve the corresponding local prediction characteristics. Finally, pick some of or all the sub LSSVM thermal error models to fuse together as one final thermal error model, which is expected to achieve better prediction performance. The rest of this paper is as follows. In Section 2, the thermal deformation of a horizontal machining center under the spindle rotation is briefly introduced and the spindle thermal error experiment of the horizontal machining center is conducted. In Section 3, the time-varying characteristics of the key temperature points are revealed with the combination use of FCM and CA. In Section 4, the SF-LSSVM thermal error modeling method is introduced in detail and the corresponding SF-LSSVM thermal error model is built. In Section 5, the reasonability and effectiveness the proposed model are verified with the comparison with another two traditional thermal error models. In Section 6, the conclusions are summarized.

2 Thermal error experiment of machine tool spindle system

2.1 Thermal deformation

The schematic diagram of the thermal deformation of a horizontal machining center induced by the generated heat of the spindle rotation is illustrated in Fig. 1. The relative thermal deformation reflected between the spindle and the worktable is named as the spindle thermal error of the horizontal machining center. The present study investigates the thermal error modeling and prediction of this spindle thermal error.

Fig. 1
figure 1

Thermal deformation diagram of a horizontal machining center

Full size image

2.2 Thermal error experiment

2.2.1 Experiment procedure

The temperature data and thermal error data from thermal error experiment are the foundation of thermal error modeling. Thus, the spindle thermal error experiment of the horizontal machining center is firstly carried out per international standard ISO 230–3 “Test code for machine tools - Part 3: determination of thermal effects” [31] to obtain the temperature data and thermal error data.

The experimental setup is illustrated in Figs. 2 and 3. As shown in Fig. 2, a total of 20 PT100 temperature sensors are initially mounted on the horizontal machining center based on experience. The arrangement details are listed in Table 1. The spindle is the dominant heat source of the horizontal machining center. Hence, its temperatures are thoroughly measured by 7 temperature sensors T1–T7 mounted on the front part along the shaft axis and 3 temperature sensors T8–T10 mounted on the rear part along the shaft axis, respectively. Moreover, T11–T13 are mounted on the side of the spindle box, T14-T16 are mounted on the side of the column, T17–T18 are mounted on the bed, and T19 is mounted on the worktable, respectively. The ambient temperature is measured by T20. As shown in Fig. 3, three capacitive displacement sensors are mutually perpendicularly fixed on the worktable to measure their relative displacements with respect to the mandrel clamped in the tool holder. The measured relative displacements between the sensors and the mandrel are regarded as the thermal errors of the spindle in three directions, including the thermal elongation in axial direction (Z direction) and the thermal drift in radial directions (X and Y direction). In addition, an infrared thermal imager is used to capture the temperature field of the front part of the spindle.

Fig. 2
figure 2

Temperature sensors arrangement. (a) Isometric view, (b) Oblique rear view

Full size image
Fig. 3
figure 3

Capacitive displacement sensors arrangement and the experimental setup. 1. Temperature sensors, 2. Temperature data acquisition device, 3. Capacitive displacement sensors (X, Y, Z), 4. Displacement data acquisition device, 5. Infrared thermal imager

Full size image
Table 1 Temperature sensors arrangement locations
Full size table

To stimulate the horizontal machining center to generate thermal errors like actual operation state, the thermal error experiment is carried out when the spindle is running at a speed spectrum, named as S1=speed spectrum 1 as shown in Fig. 4. During the experiment, the horizontal machining center starts from the cold state and operates according to the preset speed spectrum continuously for about 6 h without air conditioning and then stop to cool down. At the same time, the temperature data and thermal error data are synchronously recorded from the respective sensors in real-time with a 1-min interval.

Fig. 4
figure 4

Spindle speed S1=speed spectrum 1

Full size image

2.2.2 Experiment data

The measured temperature data and thermal error data at the same time interval is regarded as a sample and a total of t=360 samples are collected form the 6h experiment, as shown in Fig. 5. For the ease of use in thermal error modeling and prediction, the temperature data are presented as the temperature rise data relative to the initial temperatures. As shown in Fig. 5(a), the temperatures near the spindle system fluctuate with the speed spectrum, while the temperatures far away from the spindle system gradually rise slowly. As expected, the temperature rise of the spindle is the largest and fastest, the spindle box comes next, and the temperature rise of the column and bed which are far away from the heat source is the smallest and slowest. In addition, the rear part temperatures measured by T8–T10 differ a lot, while the front part temperatures measured by T1–T7 are relatively uniform. The similar difference and closeness pattern can also be observed from the temperatures of the spindle box measured by T11–T13 and the temperatures of the column and bed measured by T14–T19, respectively.

Fig. 5
figure 5

Temperature data and thermal error data in S1. (a) Temperature data, (b) Thermal error data

Full size image

As shown in Fig. 5(b), the thermal errors in the axial direction (Z direction) are the most obvious and dominant, while the thermal errors in the two radial directions (X and Y direction) are minor and almost negligible. Therefore, in the present study, only the thermal errors in the axial direction (Z direction) are considered in thermal error modeling and prediction. Basically, the thermal errors have similar variation trends with the temperatures and fluctuate almost following the temperatures. Thus, the thermal errors can be considered as dynamic errors which change with the temperatures, and the temperatures are almost dynamic which change with the spindle rotation speeds and running time. This dynamic relationship gives the foundation to build the thermal error model between temperatures and thermal errors.

The infrared thermal images of the front part of the spindle at 4 typical moments are shown in Fig. 6. As we can see, the similar temperature distribution changing process can be observed. Moreover, the temperature is uniform along the circumference of the spindle, which proves the rationality of only arranging the temperature sensors along the axial direction.

Fig. 6
figure 6

Temperature field changes of the spindle system on S1

Full size image

The relationships between the temperatures of two typical temperature points of T1 and T8 and the thermal errors are shown in Fig. 7. It is clearly seen that the thermal errors generally increase with the temperatures. However, from the relationship between the temperatures of T8 and the thermal errors, when temperature decreases, the thermal error still increases for a while. From the relationship between the temperatures of T1 and the thermal errors, when temperature decreases, the thermal error decreases as well but following a path different from the increasing path. These relationships indicate that there exists thermal hysteresis effect between the temperatures and the thermal errors and different parts have different thermal hysteresis effects. These thermal hysteresis effects indicate that the thermal errors are highly nonlinearly correlated with the temperatures and pose the difficulty of thermal error prediction.

Fig. 7
figure 7

Relationships between the temperatures and the thermal errors

Full size image

3 Key temperature points

3.1 Key temperature points selection

Because of the redundancy and multicollinearity among the n initial temperature points specified on the machine tool based on experience, taking too many, too few, and improper temperature points as the model input are all harmful to the robust thermal error prediction. Therefore, the key temperature points should be properly selected.

The combining use of FCM and CA is one of the commonly used key temperature points selection method, which clusters the temperature points into different clusters and then picks out one temperature point from each cluster as the key temperature point. The details are presented as follows.

In FCM, the degree of membership is defined and calculated to quantify the degree to which each temperature point belongs to a specific cluster. Clustering the n initial temperature points T j (j=1, 2, …, n) into c fuzzy clusters are realized by minimizing the objective function value J according to Eqs. (1)–(3).

$$ J=\sum \limits_{j=1}^n\sum \limits_{k=1}^c{u}_{jk}^m{\left\Vert {T}^j-{\overline{T}}^k\right\Vert}^2 $$
(1)
$$ {u}_{jk}=\frac{1}{\sum \limits_{l=1}^c{\left(\frac{\left\Vert {T}^j-{\overline{T}}^k\right\Vert }{\left\Vert {T}^j-{\overline{T}}^l\right\Vert}\right)}^{\frac{2}{w-1}}} $$
(2)
$$ {\overline{T}}^k=\frac{\sum \limits_{j=1}^n{u}_{jk}^w{T}^j}{\sum \limits_{j=1}^n{u}_{jk}^w} $$
(3)

where ujk (j=1, 2, …, n; k=1, 2, …, c) represents the degree of membership of the jth temperature point T j belonging to the kth cluster, \( {\overline{T}}^k \) and \( {\overline{T}}^l \) represent and the center of the kth cluster and lth cluster, respectively, and w∈[1.5, 2.5] is the fuzzy weight index. Once setting the clustering number c, i.e., the number of key temperature points, the clustering results are accordingly obtained.

At the same time, the Pearson correlation coefficients ρ between temperatures of each temperature point and thermal errors are calculated according to Eq. (4). Then, select the temperature point with the largest Pearson correlation coefficient in each cluster to compose as the final key temperature points subset.

$$ {\rho}_{T^j,e}=\frac{\sum \limits_{i=1}^t\left({T}_i^j-{\overline{T}}^j\right)\left({e}_i-\overline{e}\right)}{\sqrt{\sum \limits_{i=1}^t{\left({T}_i^j-{\overline{T}}^j\right)}^2}\sqrt{\sum \limits_{i=1}^t{\left({e}_i-\overline{e}\right)}^2}}\left(j=1,2,\dots, n\right) $$
(4)

where t is the number of temperature and thermal error data samples, \( {T}_i^j \) and \( {\overline{T}}^j \) are the ith and average temperature data of the jth temperature point, respectively, and ei and ē are the ith and average thermal error data, respectively.

3.2 Time-varying characteristics of key temperature points

Provided the temperature data and thermal error from the thermal error experiment, the FCM and CA can be applied to select the key temperature points. Usually, all the temperature data and thermal error data from the 6-h experiment are used in FCM and CA. The selection results are listed in the last column of Table 2. As we can see, different combinations of key temperature points are selected corresponding to different clustering number c. For example, the selected 5 key temperature points are (T1, T6, T8, T13, T19) when c=5. The corresponding Pearson correlation coefficients are listed in the last column of Table 3. As shown, most of the temperature points are highly correlated with the thermal errors with the Pearson correlation coefficients more than 0.95, which justifies the necessity to conduct key temperature points selection to reduce the redundancy and collinearity.

Table 2 Key temperature points in different spindle speeds and different clustering numbers
Full size table
Table 3 The Pearson correlation coefficients between temperatures and thermal errors
Full size table

The above selection is conducted on the all 6h temperature data and thermal error data corresponding to the 6h experiment. However, it is also desirable to know the key temperature points selection results when the selection is conducted on the first 2 h or the first 4h temperature data and thermal error data. Applying the same selection procedure combining FCM and CA, the corresponding selection results are listed in the first two columns of Table 2. As we can see, the selected key temperature points have changed. For example, the selected 5 key temperature points have changed to (T3, T4, T5, T19, T20) when c=5 for the first 2h temperature data and thermal error data. Moreover, the corresponding Pearson correlation coefficients are listed in the first two columns of Table 3. As shown, the Pearson correlation coefficients for different temperature points have also changed. The obvious one is T11 which measures the temperatures of the side of the spindle box. Its Pearson correlation coefficient is only 0.8534 in the first 2 h which indicates a relative low correlation with the thermal errors. While in the first 4h and 6h, its Pearson correlation coefficients have reached to 0.9520 and 0.9569 respectively which indicate a high correlation with the thermal errors. The another obvious one is T20 which measures the ambient temperatures. Its Pearson correlation coefficients are 0.9945, 0.5197, and 0.7777 for the first 2 h, the first 4 h, and 6 h respectively. The Pearson correlation coefficient of 0.9945 in the first 2 h indicating a very high correlation with thermal errors is greatly reduced to 0.5197 in the first 4 h indicating a very low correlation with thermal errors. These findings indicate that the so-called key temperature points are time-varying. So, it may be inadequate to select just one group of key temperature points from all temperature data and thermal error data to build the thermal error model to predict the thermal errors.

4 Thermal error modeling using segment fusion LSSVM

To incorporate the time-varying characteristics of the key temperature points, the thermal error model is built with segmented modeling and fusion strategy using LSSVM in this paper.

4.1 Least squares support vector machine

The LSSVM introduced by J.A.K. Suykens [32] is one of the extensively used and powerful thermal error modeling methods, which can accurately reflect the nonlinear dependency of thermal errors on temperatures using kernel trick. The basic regression formula of the LSSVM is as follows:

$$ f\left({T}^c\right)={w}^T\varphi \left({T}^c\right)+b $$
(5)

where f (Tc) is the predicted thermal error value, φ(Tc) is the nonlinear mapping function from primitive low dimensional space to high dimensional space, w is a vector of regression coefficients, and b is a constant intercept.

Through the Lagrangian function, the following linear system can be obtained:

$$ \left[\begin{array}{cccc}0& 1& \cdots & 1\\ {}1& K\left({T}_1^c,{T}_1^c\right)+1/\gamma & \cdots & K\left({T}_1^c,{T}_t^c\right)\\ {}\vdots & \vdots & \ddots & \vdots \\ {}1& K\left({T}_1^c,{T}_1^c\right)& \cdots & K\left({T}_t^c,{T}_t^c\right)+1/\gamma \end{array}\right]\left[\begin{array}{c}b\\ {}{a}_1\\ {}\vdots \\ {}{a}_t\end{array}\right]=\left[\begin{array}{c}0\\ {}{e}_1\\ {}\vdots \\ {}{e}_t\end{array}\right] $$
(6)

where ai (i=1, 2, …, t) are the Lagrangian multipliers, γ is a tradeoff parameter balancing solving scale and training errors, and \( K\left({T}_i^c,{T}_j^c\right)=\varphi {\left({T}_i^c\right)}^T\varphi \left({T}_j^c\right) \) is the kernel function. And the popular Gaussian kernel function is as follows:

$$ K\left({T}_i^c,{T}_j^c\right)=\exp \left(\frac{{\left\Vert {T}_i^c-{T}_j^c\right\Vert}^2}{2{\sigma}^2}\right) $$
(7)

where σ2 characterizes the kernel width.

Once the hyperparameters γ and σ2 are identified, the parameters ai (i=1, 2, …, t) and b can be directly calculated by solving Eq. (6) with least squares method. And the final LSSVM thermal error model can be obtained as follows:

$$ f\left({T}^c\right)=\sum \limits_{i=1}^t{a}_iK\left({T}^c,{T}_i^c\right)+b $$
(8)

4.2 Segment fusion LSSVM

4.2.1 Segmented modeling and collaborative training

Using the LSSVM as the basic model, the segmented modeling and collaborative training can be conducted. Specifically, the all 6h temperature data and thermal error data are segmented into three segments firstly: the first 2h data, the first 4h data and the all 6h data. And then, three sub LSSVM models are collaboratively trained based on the temperature data and thermal error data of the three segments, respectively. Subsequently, pick two of or all the three sub LSSVM models to fuse together as one final SF-LSSVM model by taking the average of their prediction results. Each sub LSSVM model training involves selecting its corresponding key temperature points and identifying its corresponding two hyperparameters. The collaborative training of the three sub LSSVM models is concurrently selecting the corresponding three groups key temperature points and identifying the corresponding three groups hyperparameters using genetic algorithm (GA) in a wrapper manner, because it is essentially an optimization problem with the goal to ensure the minimum prediction error. This method can ensure selecting the best suitable key temperature points for the corresponding sub LSSVM model and ensure identifying the best hyperparameters for the corresponding key temperature points. The procedure of the segmented modeling and collaborative training of the SF-LSSVM thermal error model using GA is illustrated in Fig. 8. The sub LSSVM model built with different segment data can well preserve the nonlinear relationship in that segment time. By fusing the sub LSSVM models together to form the SF-LSSVM model, the whole nonlinear relationship can be well reflected.

Fig. 8
figure 8

Segmented modeling and collaborative training of the SF-LSSVM thermal error model using GA

Full size image

4.2.2 Hyperparameters and key temperature points as optimization variables

The SF-LSSVM thermal error model with three sub LSSVM models has 6 hyperparameters. The 6 hyperparameters and the three groups key temperature points for the three sub LSSVM models are represented as the chromosome of binary GA as shown in Fig. 9. The binary vector \( {T}_{{\left[0,1\right]}_{20}} \) directly represents the selection status of temperature points with “0” and “1”. The real values of the 6 hyperparameters are represented in binary form using Eq. (9).

$$ h={h}_{\mathrm{min}}+\frac{h_{\mathrm{max}}-{h}_{\mathrm{min}}}{2^r-1}{h}_{{\left[0,1\right]}_r}{d}_r $$
(9)

where hmin and hmax stand for the minimum value and maximum value of the searching scope of the hyperparameters respectively, \( {h}_{{\left[0,1\right]}_r} \) is the binary form of the hyperparameters, dr = [20, 21, …, 2r − 1]T is the resolution vector.

Fig. 9
figure 9

The 6 hyperparameters and the three groups key temperature points represented as chromosome

Full size image

4.2.3 Fitness function designing

The fitness function F is designed to concurrently minimize the validation error and the number of key temperature points, as shown in Eq. (12). The validation error VSF-LSSVM is the mean validation error of the three sub LSSVM models, as shown in Eq. (11). To ensure the prediction performance and avoid overfitting, the training, validation, and key temperature points selection for each sub LSSVM model are conducted in 3-fold cross-validation mode. That is the segment data for each sub LSSVM model are equally divided into three parts and take turns to use two parts to train the model and the left one part to validate the model. The validation error Vsub of each sub LSSVM model is the mean validation error of the corresponding three folds, as shown in Eq. (10). The validation error Vfold of each fold is the root-mean-square error (RMSE) between the predicted thermal errors and the measured thermal errors on that fold.

$$ {V}_{sub}=\frac{V_{fold1}+{V}_{fold2}+{V}_{fold3}}{3} $$
(10)
$$ {V}_{SF- LSSVM}=\frac{V_{sub1}+{V}_{sub2}+{V}_{sub3}}{3} $$
(11)
$$ F={V}_{SF- LSSVM}+\frac{c_1+{c}_2+{c}_3}{20} $$
(12)

where Vfoldi (i=1,2,3) is the RMSE between the predicted thermal errors and the measured thermal errors on the ith fold; Vsubi (i=1,2,3) is the mean validation error of the three folds for the ith sub LSSVM model; VSF-LSSVM is the mean validation error of the three sub LSSVM models; c1, c2, and c3 are the number of selected key temperature points for the three sub LSSVM models respectively. Through these designing, the fitness function can well guide the GA to search the optimal results preserving a small prediction error and a small number of key temperature points simultaneously.

4.2.4 Modeling result

The data samples with a size of t=360 from the thermal error experiment are used to establish the SF-LSSVM thermal error model. By setting the searching scope of the hyperparameters as [0.1, 2000] and the parameter settings of GA as listed in Table 4, the identified hyperparameters and key temperature points for each of the three sub LSSVM models are listed in Table 5. Putting the identified three groups of key temperature points (T1, T15, T20), (T1, T13), and (T1, T2, T13, T16) together, there are only 6 different temperature points (T1, T2, TT13, T15, T16, T20) in total. Then, the parameters asi(s=1, 2, 3; i=1, 2, …, t) and bs(s=1, 2, 3) for each sub LSSVM model can be calculated by solving Eqs. (6)–(8) and they are not listed due to space limitation.

Table 4 Parameter settings of GA
Full size table
Table 5 The identified hyperparameters and key temperature points for each of the three sub LSSVM models
Full size table
Table 6 Prediction accuracy of different thermal error models on different spindle speeds
Full size table

5 Thermal error prediction validation

5.1 Traditional thermal error models

To validate the effectiveness and superiority of the proposed SF-LSSVM thermal error modeling method, two traditional thermal error models are built for comparison. In traditional thermal error modeling, the key temperature points are selected through applying FCM and CA on the all 6h temperature data and thermal error data. The selected key temperature points vary with the clustering number c as shown in Section 3.2. Usually, the clustering number c corresponding to the not obvious reduction of the minimum objective function value in FCM is chosen as the optimal clustering number c. The minimum objective function value curve for the clustering number c=2~7 is plotted in Fig. 10. Thus, the 5 temperature points (T1, T6, T8, T13, T19) corresponding to c=5 are chosen as the key temperature points in traditional thermal error modeling.

Fig. 10
figure 10

Minimum objective function values for c=2~7

Full size image
Table 7 Mean generalization accuracy of different thermal error models on different spindle speeds
Full size table

Then, the traditional LSSVM thermal error model and the traditional MLR thermal error model are built with the selected 5 key temperature points as input. For fair comparison, the hyperparameters γ and σ2 of LSSVM thermal error model are also identified in the scope of [0.1, 2000] and in 3-fold cross-validation mode using GA to ensure the best prediction performance. The identified hyperparameters are (γ=2000.00, σ2=257.72). The MLR thermal error model built with least squares method is shown in Eq. (13).

$$ {e}_{\mathrm{MLR}}=3.5195+5.6912{T}_1+2.3456{T}_6+0.0571{T}_8+9.2685{T}_{13}-46.2047{T}_{19} $$
(13)

5.2 Prediction performance comparison

The prediction performance comparison is investigated both on the fitting performance on the spindle speed S1 and the generalization performance on other spindle speeds. The evaluation indicators are the RMSE between the predicted thermal errors and the actual thermal errors. In order to evaluate the generalization performance, another 4 thermal error experiments are conducted in another 4 spindle speeds. They include three constant spindle speeds S2=2000r/min, S3=4000r/min, and S4=6000r/min, and another speed spectrum S5=speed spectrum 2 as shown in Fig. 11 which is almost the reverse version of S1=speed spectrum 1 in Section 2.2. The experiments follow the same procedure as in Section 2.2.

Fig. 11
figure 11

Spindle speed S5=speed spectrum 2

Full size image

The obtained temperature data and thermal error data of the 4 spindle speeds are shown in Figs. 12 and 13 respectively. For the spindle speeds S2, S3, and S5, the same total of t=360 samples are collected for each of them. While for the spindle speed S4, a total of t=270 samples are collected because the machine tool only ran about 4.5 h in that speed for fear of excessive temperature rise which could harm the spindle. The up and down pattern of the rear part temperatures measured by T8–T10 in S4 is due to the internal active cooling effect to protect the spindle from suffering the excessive high temperatures.

Fig. 12
figure 12

Temperature data in S2, S3, S4, and S5. (a) Temperature data in S2=2000 r/min, (b) Temperature data in S3=4000 r/min, (c) Temperature data in S4=6000 r/min, (d) Temperature data in S5=speed spectrum 2

Full size image
Fig. 13
figure 13

Thermal error data in S2, S3, S4, and S5

Full size image

The thermal error prediction on S1 with the three sub LSSVM models and the SF-LSSVM model are shown in Fig. 14. As shown, the sub LSSVM 2 model and sub LSSVM 3 model can well predict the thermal errors, thus SF-LSSVM model is preferred to be fused by these two sub LSSVM models for all the spindle speeds of speed spectrum. For all other constant spindle speeds, the SF-LSSVM model is preferred to be fused by all the three sub LSSVM models as expected.

Fig. 14
figure 14

Thermal error prediction on S1 with the three sub LSSVM models and the SF-LSSVM model

Full size image
Fig. 15
figure 15

Thermal error prediction on S2, S3, S4, and S5

Full size image
Fig. 16
figure 16figure 16

Thermal error prediction on S2, S3, S4, and S5 with the three sub LSSVM models and the SF-LSSVM model, respectively. (a) Thermal error prediction on S2 with the three sub LSSVM models and the SF-LSSVM model. (b) Thermal error prediction on S3 with the three sub LSSVM models and the SF-LSSVM model. (c) Thermal error prediction on S4 with the three sub LSSVM models and the SF-LSSVM model. (d) Thermal error prediction on S5 with the three sub LSSVM models and the SF-LSSVM model

Full size image

Table 6 lists the fitting accuracy of the SF-LSSVM thermal error model and the two traditional thermal error models on the spindle speed S1. As shown, all the RMSE values are less than 1.5 μm. The LSSVM thermal error model is slightly better than the other two models with the RMSE value being 0.9 μm. The SF-LSSVM thermal error model and the MLR thermal error model are similar with each other with the RMSE value being about 1.3 μm. The small fitting RMSE values indicate that all the models can fit on the training data quite well. However, the fitting performance is just one aspect of the prediction performance, and the more important aspect is the generalization performance on other spindle speeds, which is the actual use situation.

Therefore, Table 6 also lists the generalization accuracy of different thermal error models on the 4 spindle speeds S2, S3, S4, and S5. The comparison results demonstrate that the SF-LSSVM thermal error model significantly outperforms the compared traditional thermal error models on the spindle speeds S3, S4, and S5 with the RSME values being only 3.1 μm, 2.2 μm, and 2.4 μm, respectively. On the spindle speed S2, the MLR thermal error model is better and the SF-LSSVM thermal error model and the LSSVM thermal error model are quite similar with each other with the RMSE value being about 6.2 μm. Furthermore, the comparison of residual thermal errors after compensation listed in Table 6 also indicates that the SF-LSSVM thermal error model has better prediction performance on most of the spindle speeds with residual thermal errors being no more than 10μm.

The thermal error prediction graphical results on the 4 spindle speeds S2, S3, S4, and S5 are shown in Fig. 15. In each graph, the upper curves denote the comparison between the measured thermal errors and the predicted thermal errors by different models, and the lower curves denote the residual thermal errors after compensation by different models. The comparison results in Fig. 13 also demonstrate that the proposed SF-LSSVM thermal error model has better prediction performance than the traditional MLR and LSSVM thermal error models on most of the spindle speeds especially on S3 and S4. On the spindle speed S2, the SF-LSSVM thermal error model is still competitive.

The thermal error prediction on S2, S3, S4, and S5 with the three sub LSSVM models and the SF-LSSVM model are shown in Fig. 16. As shown, different sub LSSVM models can preserve different local prediction characteristics. By fusing them together, the SF-LSSVM model can well incorporate both the local and global prediction characteristics. Moreover, it also verifies the reasonability of fusing the sub LSSVM 2 model and sub LSSVM 3 model to compose the SF-LSSVM model for all the speed spectrums and fusing all the three sub LSSVM models to compose the SF-LSSVM model for all the constant spindle speeds.

Table 7 lists the mean prediction accuracy of different thermal error models on the 5 spindle speeds. The SF-LSSVM thermal error model is the best with the mean RMSE value being only 3.1μm. Compared with the MLR and LSSVM thermal error models, the relative reduction of the mean RMSE of the SF-LSSVM thermal error model is about 51% and 33%, respectively. The results further demonstrate that the SF-LSSVM thermal error model has better prediction performance. The results also indicate that the LSSVM thermal error model is generally better than the MLR thermal error model due to the stronger nonlinear mapping capability of the LSSVM and is suitable to be used as the basic model in SF-LSSVM. Thus, the reasonability and effectiveness of the proposed segmented modeling and fusing using LSSVM to build SF-LSSVM thermal error model are verified.

6 Conclusions

The main objective of this paper is proposing a SF-LSSVM thermal error modeling method to predict the spindle thermal errors of machine tools more accurately. The thermal error experiments were carried out on the studied horizontal machining center to acquire the temperature data and thermal error data as the modeling foundation. The comparative study with two traditional models was conducted to verify the reasonability and effectiveness of the proposed modeling method. The following conclusions are summarized:

  1. (1)

    The spindle thermal errors of the horizontal machining center overwhelmingly take place in the axial (Z) direction. The selection results of key temperature points using FCM and CA reveals that the key temperature points are time-varying. The relationships between the temperatures and the thermal errors are nonlinear because there exist thermal hysteresis effects between them.

  2. (2)

    The temperature data and thermal error data from the spindle speed of S1=speed spectrum 1 is suitable to be used to establish the thermal error model. The LSSVM model is suitable to be used as the basic model of the SF-LSSVM thermal error model. The 6 hyperparameters and the three groups of key temperature points of the SF-LSSVM thermal error model can be concurrently identified using GA.

  3. (3)

    The SF-LSSVM thermal error model has the best prediction performance on most of the spindle speeds among the compared traditional MLR thermal error model and LSSVM thermal error model, with the mean RMSE being only 3.1μm. Compared with the two traditional models, the relative reduction of the mean RMSE of the SF-LSSVM thermal error model is about 51% and 33%, respectively.

  4. (4)

    This research confirms that segmented modeling and fusion using LSSVM is an alternative approach for thermal error modeling and prediction and can lead to promising results.