1 Introduction

Assembly process planning (APP) is a delicate process in automotive industry and border between product design and manufacturing. It contains assembly sequence planning (ASP) and assembly tool and fixture planning. An ASP is expressed in terms of a series of assembly operation for constituent parts of final product from one station to another station in the MSA systems which is influenced by assembly line configuration, equipment, and fixtures. In addition, ASP drastically affects dimensional quality, cycle time, cost, and the assembly process efficiency [1, 2].

An automotive body-in-white (BIW) is made up to 150 to 250 deformable parts assembled in a hierarchical MSA system [3]. The parts (subassemblies) are held by 1700–2100 locators and joined with different fastening techniques at more than 100 stations based on a preplanned sequence [4]. In such a complex system, process-planning engineers are interested in understanding how a BIW is assembled out of the given sheet metal parts to meet several objectives generally expressed through various performance indicators. Significant efforts have been made over the past decades with respect to ASP, which can be classified into two streams:

  • Generation of feasible assembly sequences

  • Evaluation or optimization of ASP

Generating assembly sequences is a difficult combinatorial problem. Most existing methodologies are based on the graph or tree search theory along with constraint analysis. That way, all feasible assembly sequences must satisfy both product geometrical and manufacturing process constraints [5]. Bourjault first proposed an answering-question algorithm for automatic assembly sequence generation by presenting a product with a liaisons graph [6]. The method was developed later by De Fazio and Whitney through a symbolic knowledge of assembly and using net graph to represent the assembly sequences [7]. De Mello and Sanderson introduced the cut-set-based ASP method and used AND/OR graph to represent the assembly sequences [8, 9]. Mantripragada and Whitney presented a product with a directed graph, called Datum Flow Chains (DFC), wherein part-to-part joining precedence relationships constrained by assembly process are represented as a directed line [10]. Zhang et al. described a procedure to derive all feasible assembly sequences automatically for automotive body assembly [11]. Xing et al. employed an adjacency matrix and utilized three different mathematical patterns of subassemblies (serial, parallel, and loop) to generate all feasible assembly sequences [12]. Wang and Ceglarek [13] expands current approaches in sequence generation applicable for binary assembly process (k = 2) to a k-ary assembly process (k > 2) by including: (i) non-binary state between two parts, i.e., multiple joints between two parts or subassemblies, is taken into consideration, and (ii) simultaneous assembly of Y > 3 parts or subassemblies.

Optimization of assembly sequence in MSA system has been a challenging task so far, because only few parts in a mechanical assembly can lead to numerous assembly sequences. Moreover, this is a many-sided problem that relies on both, quality and non-quality criteria [14]. Hence, among the feasible assembly sequence set, there are only some options which optimize the MSA system with respect to certain criteria. In this stream, various methods have been proposed in the literature to evaluate or optimize ASPs. Almost all of them are generally limited to non-quality aspects such as design for assembly (DFA) criteria. The most popular DFA objectives include minimizing the number of re-orientations, tool change, and assembly type change. Other factors such as cost optimization, assembly cycle time, and tool traveling path have not been taken into account in most cases [15].

Although extensive research has been carried out on ASP with DFA criteria, however, the quality element especially related to dimensional quality has been investigated by few studies. Wang and Ceglarek described a quality-based methodology for BIW assembly planning, considering geometrical integrity [16]. The generated sequences were assessed through a beam-based quality model for variation propagation [17, 18]. In addition, Chen et al. developed a case-based reasoning methodology which could automatically generate the optimal assembly sequences and joint types for the best final product quality [19]. They performed variation analysis based on the homogeneous transformation matrixes. Hu and Stecke showed the existence of the trade-offs between geometrical quality and system performance for various assembly line configurations [20] through productivity formula and the application of method of influence coefficient (MIC) which was introduced by Liu and Hu [21]. An assembly sequence optimization approach was presented by Lai et al. using genetic algorithm (GA) and liaison graph. The Jacobian matrix was employed by authors to model the relation between Key Control Characteristic (KCC) and Key Product Characteristic (KPC) [22]. Similarly Xing and Wang investigated ASP through a more effective and efficient optimization method by combining GA and particle swarm optimization algorithm [23]. Mounaud et al. studied the influence of assembly sequence on geometric deviations (manufacturing and assembly process defects) through MIC [24]. Based on a linear methodology called statistical variation analysis and finite element analysis (SVA-FEA), Franciosa et al. demonstrated the effect of several assembly scenarios and fastened joints on product quality in the preliminary designing phase [25]. Ni et al. developed an ASP optimization method that simultaneously minimizes the length of riveting path and the dimensional errors caused by riveting deviations [26]. The optimal result showed an improvement in both operational efficiency and dimensional accuracy. Ghandi and Masehian presented the scatter search algorithm to produce high-quality solutions by optimizing both the number of assembly direction changes and the maximum applied stress exerted for performing assembly operations [27]. Masoumi and Jandaghi Shahi approached optimizing assembly sequence and fixture layout simultaneously in order to minimize in-plane KPC variations in MSA systems. They used GA along with the self-adaptive penalty function to find feasible and optimal solution [28].

The conducted quality-driven studies have assessed ASP under the assumption that individual parts are manufactured accurately at their nominal dimensions or their shapes do not change during the assembly process. Whereas in the real-world of assembled products such as BIW, final dimensional quality is affected by both part fabrication errors (non-ideal parts) as well as their deformability throughout the MSA system. Therefore, the main purpose of the present paper is robust optimization of ASP based on product dimensional quality through the development of quantitative criteria which is less sensitive to part deviations, and also an analytical tool that is capable of simulating variation propagation in MSA system with consideration to a batch of compliant and non-ideal parts in the form of stochastic simulations. Table 1 positions the current work in relation to the extant literature.

Table 1 Summary of literature review and the current work position
Full size table

This paper is organized as follows: Section 2 describes the problem formulation and dimensional quality indices. Section 3 discusses and establishes the proposed methodology. Lastly, an industrial case study and paper conclusions are presented in Sections 4 and 5, respectively.

2 Problem description

The BIW assembly process can be designed in various assembly sequences and line configurations which produce different dimensional quality, cycle time, reliability, and cost. To measure the efficiency of assembly process, it is essential to develop an analytical tool which is capable of modeling or simulating the process according to a given evaluation criteria. The key idea proposed in this paper is to develop an indicator that allows quantifying the effect of ASP on dimensional variation propagation in MSA system for given deviation associated with a batch of compliant non-ideal parts.

The dimensional accuracy of BIW assembly (subassembly) is evaluated through its KPCs defined by part features (holes, slots), edge features, etc. The KPCs must be controlled within lower and upper specification limits (as allocated by product designer) in order to ensure that design requirements meet product functions. KCCs refer to stochastic and deterministic assembly process variables. For instance, stochastic variables represent manufacturing errors (i.e., batch of non-ideal parts or tooling variations); whereas, deterministic variables express assembly sequence and assembly line configuration. Moreover, design constraints (DCs) in terms of allowed range (as allocated by process designer) are defined for each KCC.

2.1 MSA system for compliant non-ideal parts

An assembly process consists of sequential operations where dimensional defects at each station affect downstream stations. Inherent variations in MSA are heavily affected by inevitable manufacturing errors such as part geometrical defects (GD&T), fixture, and tool deviations [29, 30]. Moreover, station-to-station interactions introduced by repositioning of parts (subassemblies) and also releasing of fixtures are recognized among the most important factors which can affect final product quality [31].

A real single-station in BIW assembly process includes four operations: placing, clamping, fastening, and releasing, which are known as single-PCFR cycle [32]. In an assembly station, parts (subassemblies) are placed first on fixture, and then, are clamped. Next, they are fastened by a joining technique. Finally, the subassembly is released from the fixtures, leading to the occurrence of spring-back phenomenon. In order to complete the assembly process, the subassembly is transferred to the downstream station. Hence, several single-PCFR cycles are usually required to assemble the product, referred to as multiple-PCFR cycles (Fig. 1).

Fig. 1
figure 1

Multiple-PCFR cycles in MSA considering three non-ideal parts

Full size image

A typical MSA system with NS stations is depicted in Fig. 2. Assembled operation at each station is modeled by performing a single-PCFR cycle. Therefore, at the i th station (∀i = 1,...,NS − 1), the PCFR cycle is required to assemble individual parts. At the measurement station (i = NS), the final assembly is only placed and clamped by checking fixture; then, KPCs variations are measured by coordinate measuring machine (CMM) or 3D scanner [33, 34].

Fig. 2
figure 2

Representation of MSA system with NS stations and station inputs

Full size image

In the compliant part assembly process, an N-2-1 locating scheme N > 3 is generally used to perform physical support for a part (subassembly) at each station. A fixture layout (N= 4) including two pins (L1,L2), three NC-blocks (L3,L4,L5), and one clamp (L6) is illustrated in Fig. 3. Therefore, fixture location points (FLP), joining location points (JLP), and assembled parts should be defined for all stations. Accordingly, any station in the assembly line can be presented by a ternary set in Eq. 1. For measurement station, only FLP(NS) as a checking fixture is required, and no part is added to the prior subassembly.

$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} {\mathbf{S}}\left( i \right)\text{=}\left[ \text{FLP}\left( i \right), \text{JLP} \left( i \right), {\varDelta}\mathbf{P} \left( i \right) \right] \end{array} \end{array} $$
(1)
Fig. 3
figure 3

A 4-2-1 fixture layout for compliant part

Full size image

FLP and JLP are extracted directly from CAD data, and shape variations of compliant parts (non-ideal parts) are generated practically by Morphing Mesh Producers (MMP) [35]

2.2 Variation response methodology

Batch of non-ideal parts is defined as parts with the same shape pattern or mode errors which presumably represents the production population. In compliant parts assembly process, one leading challenge is identification of the relationship mapping between non-ideal parts (as input KCCs) and dimensional variations (as output KPCs). For this purpose, a FEM-based method is generally utilized in order to simulate of the PCFR cycle during the assembly process. Two common approaches in this area are MIC and Variation Response Methodology (VRM). The traditional MIC considers the ideal parts and ignores the non-linear effects, such as contact and interaction between parts [36]. Hence, it does not fit perfectly with the real assembly process. On the other hand, VRM is only developed to simulate the single-station assembly process considering non-ideal parts and their contacts [37,38,39,40]. Hence, to fill the research gaps, in the proposed methodology, VRM is upgraded for variation propagation modeling in MSA through the simulation of station-to-station repositioning errors and spring-back phenomenon. Equation 2 indicates stochastic variation of KPCs can be obtained by developed variation response methodology for given an ASP option and assembly station inputs.

$$ {\mathbf{X}_{m}}={\text{VRM}}\left( {\varGamma}_{n},{\mathbf{S}}\left( i \right) \right) \forall i=1, ... , {{N}_{\text{S}}} $$
(2)

2.3 Stochastic dimensional quality criteria

Part deviations (KCCs) in batch of non-ideal parts are inherently stochastic; hence, KPC variations should be presented through the probability distributions. The quality criteria (Ω) in this paper are defined by combining two indicators which are called quality conformity rate (Ψ) and quality target index (Υ). These indicators are able to examine MSA system performance in terms of dimensional quality due to variety of ASPs and line configurations.

Since several KPCs are considered to evaluate dimensional quality of final product, it is necessary to keep them simultaneously within their different tolerance intervals (Im). Therefore, the first indicator, as shown in Fig. 4, is determined through the multivariate integration of the KPC probability density function over the given tolerance domains, as presented in Eq. 3.

$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} {{{\varPsi} }_{{{{\varGamma} }_{n}}}}={\int}_{{I}_{1}}\cdots{\int}_{{I}_{m}}\mathbf{PDF}({\mathbf{X}_{1}}\cdots{\mathbf{X}_{m}}) d{\mathbf{X}_{1}} {\cdots} d{\mathbf{X}_{m}}\\ \\ \forall m=1, ... , {{N}_{\text{KPC}}} \end{array} \end{array} $$
(3)

Here \({{{{\varPsi } }_{{{{\varGamma } }_{n}}}}\in \left [0,1\right ]}\), shows the probability of success for a given ASP option, which is capable of meeting the design requirements. In other words, the conformity rate represents the percentage of KPC variations falling within the allowable limits. For a given batch of non-ideal parts, e.g., \({{\varPsi } }_{{\varGamma }_{n}}=0.5\) means that the related ASP option (Γn) has 50% chances to control all KPC variations within their tolerance intervals.

The second indicator is derived from Taguchi’s loss function [41]. The loss associated with a stochastic value of KPC variation is a powerful measure for showing loss caused by deviation from the KPC target. The quality target index is formulated in Eq. 4 by summation of loss density integration for each KPC over its allowable tolerance interval. As illustrated in Fig. 4, while KPC dimension deviates or moves further away from its target value, an increasing loss will be incurred. Hence, to reduce the loss, quality target index must be decreased through aligning the mean of variation distribution with the target, and by variation reduction, i.e., making probability curve narrower.

$$ {{{\varUpsilon} }_{{{{\varGamma} }_{n}}}}=\sum\limits_{m=1}^{{{N}_{\text{KPC}}}}{\int}_{{{I}_{m}}}{\mathbf{PDF}({\mathbf{X}_{m}})} . {\mathbf{L}_{m}\left( {\mathbf{X}_{m}} \right)} $$
(4)
Fig. 4
figure 4

KPC variation distribution and the quality indicators concept

Full size image

Therefore, the objective of ASP optimization is to maximize quality conformity rate and minimize quality target index simultaneously taking into consideration presence of stochastic manufacturing errors both at product and process levels, and formulated in Eq. 5.

$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} {{{\varGamma} }_{\text{optimal} }}=\text{Min}\left\{{{\varOmega}_{{{{\varGamma} }_{n}}}}={{\varUpsilon}_{{{{\varGamma} }_{n}}}}/{{{\varPsi} }_{{{{\varGamma} }_{n}}}}\right\}\\ \forall n=1, ... , {{N}_{\text{ASP}}} \\ \text{s.t.}\rightarrow\text{KCCs}\subseteq \text{DCs} \end{array} \end{array} $$
(5)

3 The proposed methodology

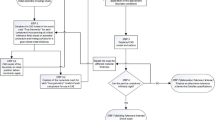
This methodology focuses on properly selecting ASP and assembly line configuration in order to maximize dimensional accuracy of final product. As shown in Fig. 5, the methodology consists of three main steps: (i) Generation of assembly sequence and line configuration; (ii) Simulation of multi-PCFR cycles with capability to model batch of non-ideal compliant parts, station-to-station repositioning error, and spring-back phenomenon; and, (iii) Stochastic robust optimization of ASP based on the both quality indicators.

Fig. 5
figure 5

The overall workflow of the proposed methodology

Full size image

3.1 Assembly sequence generation

MSA systems can be designed in several assembly line configurations depending product architecture which includes number of parts and subassemblies of a given product, cycle time, permitted number of stations which determine length of assembly line and floor space, and maximum number of assembly operations at each single station. An initial suboptimal line configuration can be determined by equipment selection and task assignment methods [42]. Then, in the next step, all feasible sequences can be generated.

By taking a predetermined assembly line configuration, feasible ASP generation consists of two steps: representing mechanical assembly and identifying part or joint orders; in this respect, both geometric and process constraints should be taken into consideration. Assembly representation includes CAD model, the relations between connected parts, or functional-precedence constraints between the connections. Frequently assembly representations use graph based data structure with capabilities to integrate with graph search algorithms or iterative procedures for identification feasible sequences. This paper utilizes the methodology of k-ary assembly to represent and generate part assembly sequences for a MSA line configuration [13].

Figure 6 shows a MSA system with \(\left \{ {{k}_{1}},{{k}_{2}},\text { }\ldots ,{{k}_{{{N}_{S}}-1}} \right \}\)-ary operation which is able to assembly ki-parts (subassemblies) (ki ≥ 3) as inputs at i th station. Compared with the currently used liaisons graph (or datum flow chain) representation which shows part-to-part assembly relations, the k-ary representation (k-piece graph or k-piece mixed graph) shows that not only binary (2-hand assembly) but also non-binary states between two parts, i.e., (i) multiple joints between two parts or subassemblies; and, (ii) assembly of more than two parts at any station are taken into consideration. Thus, all feasible subassemblies for a predetermined assembly line configuration can be identified, and all of the sequences for a k-ary assembly process can be generated [13]. The sequence generation method includes four steps for any predetermined assembly line configuration:

  • Step (1): Represent part (joint) relations (DFC) for assembly (Fig. 7a) through a mixed graph M = (V,E,A), in which V, E, and A represent a set of part, set of unordered pairs of distinct parts, and a set of ordered pairs of parts, respectively (Fig. 7b).

  • Step (2): Generate ki-piece mixed graph \({{C}_{{{k}_{i}}}}(M)\) for assemblies with precedence constraints at station i from M, where a source vertex implies a feasible k-ary subassembly. The k-piece mixed graph is generated as follows: vertex set consists of all induced connected k-vertex subgraphs of M; besides, two vertices of \({{C}_{{{k}_{i}}}}(M)\) are adjacent to \({{C}_{{{k}_{i}}}}(M)\) if subgraph intersection is a connected (k-1)-vertex subgraph. The k-piece mixed graph generalizes representation of the datum flow chain to include all feasible k-ary assemblies. Figure 7 c–e show the iterative process of generating (k= 2, 3, 4)-piece mixed graph of an automotive side frame assembly with four parts.

  • Step (3): Select one of the feasible subassemblies among the vertices set in \({{C}_{{{k}_{i}}}}(M)\) for a given ki. All vertices for a given ki represent all feasible sequences of k-ary assemblies at station i. For instance, (v1v4), (v1v2), (v1v3), and (v2v3) for k1= 2 are shown in Fig. 8.

  • Step (4): Repeat steps (1), (2), and (3) for downstream station (i=i + 1).

Fig. 6
figure 6

Representation of k-ary operation at each station

Full size image
Fig. 7
figure 7

a Automotive side frame assembly with four parts (v1 − v4), and iterative process of generating k-piece mixed graph for side frame, b Part-joint mixed-graph C1(M), c binary C2(M), d ternary C3(M), e quaternary C4(M) subassemblies [13]

Full size image
Fig. 8
figure 8

Subassembly selection for MSA based on k-piece mixed graph [13]

Full size image

The precedence (geometrical) constraints of any ASP are comprehended by adjacency matrix associated with ki-piece mixed graph. In addition, it is assumed that all sequences are feasible considering process constraints such as tools accessibility. ASP options for predetermined assembly line configuration are presented through an ordered list of assembly operations, which is a language-based assembly sequence representation. For instance, an assembly sequence consists of four serial stations in Fig. 7c can be presented in the format of Eq. 6.

$$ {\varGamma} \text{=}\underbrace{\text{(}\overbrace{{ {v}_{1}} {{v}_{4} }}^{\text{parts}}\text{)}}_{\text{Station (1)}}- \underbrace{\text{(}\overbrace{{ {v}_{1,4}} }^{\text{subassembly}}, \overbrace{{ {v}_{2} }}^{\text{parts}}\text{)}}_{\text{Station (2)}}- \underbrace{\text{(}\overbrace{{ {v}_{1,4,2}} }^{\text{subassembly}}, \overbrace{{ {v}_{3} }}^{\text{parts}}\text{)}}_{\text{Station (3)}}- \underbrace{\text{(}\overbrace{{ {v}_{1,4,2,3}} }^{\text{side frame}}\text{)}}_{\text{Station (4)}} $$
(6)

3.2 Variation propagation modeling in MSA system

The compliant parts in BIW have inherent geometric variations caused by stamping, handling, or upstream assembly processes. In this subsection, variation propagation simulation for MSA, considering a batch of non-ideal parts, is developed to examine final assembly quality produced by a variety of ASPs and assembly line configurations. Non-ideal parts extremely affect the dimensional accuracy of product and can be described by stochastic KCCs. Part deviation patterns are assumed independent, meaning that the interactions between KCCs are not considered. In addition, stochastic distribution of each KCC is assumed to be Gaussian. Deviations are generated using MMP and a set of KCC parameters [36, 39, 40]. The mathematical relationship between stochastic KCCs and part deviations is expressed in Eq. 7. Stochastic samples can be produced by Monte-Carlo sampling or polynomial chaos [43]. This paper implemented Monte-Carlo sampling approach.

$$ {\varDelta}\mathbf{P}^{j}\left( i \right)=\mathbf{f}_{{k}_{i}}\left( {\text{KCCs}^{j}} \right) \forall j=1, ..., {{N}_{\text{MC}}} $$
(7)

In MSA processes, KPC variation caused by part variation is accumulated gradually so that variation propagation mechanism is formally introduced by the discrete state-space representation [31] in Eq. 8.

$$ {\mathbf{X}^{j}}\left( i \right)={\mathbf{X}^{j}}\left( i-1 \right)+{\mathbf{U}^{j}}\left( i \right) \forall i=1, ... , {{N}_{\text{S}}} $$
(8)

where Xj (0) is equal to part deviation exactly after manufacturing process and Uj (i) is displacement field associated with the i th PCFR cycle finite element simulation and is obtained by “transfer function” in Eq. 9.

$$ {\mathbf{U}^{j}}\left( i \right)={\mathbf{F}^{j}}\left( \mathbf{S} \left( i\right) \right) $$
(9)

As presented in Figs. 1 and 5, four consecutive FE runs are required for PCFR simulation and extraction of displacement field vector. The FE simulations are executed using VRM which is a MATLAB-based finite element modeling software toolkit with capabilities of fast modeling specific features required by assembly process. Three FE simulations are related to the positioning (r=1), gap closing between parts at each JLP (r=2), and releasing process of fastening tool (r=3). The fourth simulation (r=4) is relevant to the clamps releasing and the setting up of a new fixture layout for the subassembly at the next station. In this study, the placing and clamping phases are performed simultaneously, and the effect of joining sequence has not been considered. During the fastening phase, the joining points on the parts should be coupled (depending on fastening technique type) together using multi-point constraints. For instance, the rigid elements can be defined to constrain the nodes in spot welding technique. To simulate the spring-back phenomenon, residual stresses were applied to each part of final assembly within two steps: (i) fastening tools releasing; (ii) clamps releasing. Thereafter, the subassembly was transferred to the downstream station and was repositioned by the next fixture layout; subsequently, they will be assembled to the other parts (subassemblies). For the i th station, KPC variation is derived by “transfer function” which is formulated based on the displacement field for r th FE simulation in Eq. 10.

$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} {\mathbf{F}^{j}}=\left\{\begin{array}{llll}\mathbf{Q}^{j}\left( i, r \right) \text{for subassembly from station}\left( i-1 \right) &\\ {\varDelta}\mathbf{P}^{j}\left( i \right)+\mathbf{Q}^{j}\left( i, r \right) \text{for} {{k}^{th}} \text{part at station} \left( i \right) & \end{array}\right.\\ \\ \forall r=1 \text{to} 4 \end{array} \end{array} $$
(10)

At measurement station, the difference between the actual value of KPC dimension and its nominal is obtained by deviation operator. Hence, the variation of m th KPC is presented by Euclidean distance between nominal and actual coordinate of KPC in the global coordinate system, as shown in Eq. 11.

$$ \begin{array}{@{}rcl@{}} \begin{array}{llll} \mathbf{X}_{m}^{j}=\sqrt {\left( {\varDelta}{x}_{m}^{j} \right)^{2}+\left( {\varDelta}{y}_{m}^{j} \right)^{2}+\left( {\varDelta}{z}_{m}^{j} \right)^{2}}\\ \\ \forall m=1, ... , {{N}_{\text{KPC}}} \end{array} \end{array} $$
(11)

3.3 Probability density and loss functions

MSA systems are generally a non-linear and complex process, hence probability density function can not be fitted out through the parametric model such as normal distribution, in addition, number of KPCs is often more than one. Hence, as shown in Fig. 4, multivariate Kernel Density Estimation (KDE) is used as a non-parametric PDF estimator method [44]. Let \({{\lambda }_{1}}, ...,{{\lambda }_{j}},...,{{\lambda }_{{{N}_{\text {MC}}}}}\) be a sample of mth variate KPC variation vectors drawn from a general distribution, based on KDE method, the PDF can be obtained by Eq. 12.

$$ \mathbf{PDF}(\lambda )=\frac{1}{{{N}_{\text{MC}}}}\sum\limits_{j=1}^{{{N}_{\text{MC}}}}{{{{K}_{H}}}(\lambda -{{\lambda }_{j}})} $$
(12)

Here λ = (X1...,Xm)T and λj = (X1j,...,Xmj)T. The kernel smoothing function choosing (KH) is not crucial to the accuracy of PDF estimators. In general, any positive functions with symmetry about the origin and finite second moment can be used as a kernel [44]. In this study, the Gaussian basis with zero mean and unit variance is assumed as kernel function. In contrast, the choice of bandwidth matrix is important which exhibits a strong effect on the performance of PDF. This free parameter is a diagonal and positive-definite matrix, and the optimal value can be expressed based on Silverman’s rule of thumb that minimizes the mean integrated squared error [44].

The quadratic loss function assigns a loss proportional to the square of the difference between KPC variation and its target. The general form of the loss function used in this study is expressed in Eq. 13.

$$ {\mathbf{L}({\lambda})}={{{K}_{L}}}{{\left( {\lambda}-{{T}} \right)}^{2}} $$
(13)

Coefficient KL is an arbitrary constant which is related to product replacing or repairing cost, etc. [41]. Taguchi divided loss functions into three types which are called nominal, smaller, and larger -the-better characteristics. The classification is depending on KPC variation target value. In this study, KPCs variations are always positive according to Eq. 11, thus a smaller-the-better output response is used where it is desired to minimize the result, with the ideal target being zero (T = 0).

4 Case study and results

In this section, the proposed methodology is applied to an automotive front-rail assembly process. As shown in Fig. 9, the front-rail consists of four sheet metal parts which are welded to each other by the resistance spot welding (RSW) technique. The parts thickness, fixture elements such as locators and clamps (FLPs), RSW weld location (JLPs), and key product characteristics (KPCs) coordinates are listed in Tables 2 and 3. Material characteristics such as Young’s module and Poisson’s ratio are assumed 210 GPa and 0.30 in FE model, respectively.

Fig. 9
figure 9

The automotive front-rail parts (A, B, C, D), KPCs, and JLPs

Full size image
Table 2 The part thickness, fixture elements, and KPCs coordinates (unit: mm)
Full size table
Table 3 Joining location points coordinates between the front-rail parts (unit: mm)
Full size table

First, five assembly line configurations in three categories (Fig. 10 a–c) are considered to generate the feasible assembly sequences. Using k-piece graphs in Fig. 11 and k-ary assembly sequence generation method, nine different ASP options are produced and listed in Table 4.

Fig. 10
figure 10

Five predetermined assembly line configurations with k-ary operations in three categories. a Three-stations. b Two-stations. c Single-station

Full size image
Fig. 11
figure 11

a Part-joint mixed-graph C1(M) for automotive front-rail, and iterative process of generating k-piece mixed graph: b binary C2(M), c ternary C3(M), d quaternary C4(M) subassemblies

Full size image
Table 4 The ASP options for each assembly line configuration
Full size table

The fixture layout and RSW points for each station are determined based on both FLPs and JLPs coordinates in Tables 2 and 3, respectively. For instance, assembly process information associated with Γ1 is depicted in Table 5.

Table 5 Assembly station inputs S (i) for Γ1
Full size table

ASP evaluation procedure for the front-rail subassembly is continued with variation propagation simulation throughout the MSA process. Hence, at the first step, the FE models are made of about 11,300 quadrilateral shell elements (Fig. 12a), and four contact pairs are defined as the part-to-part interfaces. MMP (\(\mathbf {f}_{{k}_{i}}\)) is employed for non-ideal part generation (Fig. 12b). Table 6 shows the KCC parameters (control points and influence radius) and their statistical values. The fixture elements are applied to the parts (subassemblies) as boundary conditions based on the FLPs layout (Fig. 12c). The initial gaps between non-ideal parts are closed in the fastening phase by RSW gun with a radius of 8 mm. For any spot weld, five rigid elements are used to couple the nodes. The final assembly is measured at the measurement station (Fig. 12d), and the KPC variations are calculated by Eqs. 8–11. The simulation of multi-PCFR cycle is iterated for each Monte-Carlo sample and 500 iterations are used to generate part deviations. The probability density functions of KPCs variations are obtained through multivariate KDE method (Fig. 13). The allowable tolerance interval (Im), KPC target (T), and loss function coefficient (KL) for the all KPCs are assumed [0, 2] mm, 0, and 1, respectively. The quality conformity rate and target index are calculated by Eqs. 3 and 4. Then the above steps have been repeated to attain the quality indicators for nine ASP options (Γ1–Γ9) which are listed in Table 7.

Fig. 12
figure 12

a FEM mesh. b Non-ideal parts. c Setup fixtures and RSW gun. d Multi-PCFR cycles simulation

Full size image
Table 6 MMP statistical parameters (KCCs) assigned to the pars (unit: mm)
Full size table
Fig. 13
figure 13

The KPC variation distributions. a Optimum ASP (\({{\Omega }_{{{\Gamma }_{7}}}}=3.70\)). b Worst ASP (\({{\Omega }_{{{\Gamma }_{3}}}}=9.12\))

Full size image
Table 7 Evaluation results of the ASP options based on the quality indicators
Full size table

The results imply that different assembly sequences and line configurations affect significantly on product dimensional accuracy. It can be seen in Table 7 that Γ7 is the optimum ASP (\({\varOmega }_{{\varGamma }_{7}} = 3.70\)) based on the Eq. 5 in terms of falling the KPCs variations in the tolerance range (\({\varPsi }_{{\varGamma }_{7}} = 0.82\)), and also proximity to the KPC target (\({\varUpsilon }_{{\varGamma }_{7}} = 3.04\)), while Γ3 is the worst quality-driven scenario (\({\varOmega }_{{\varGamma }_{3}} = 9.12\)) for assembling of automotive front-rail. Although, the difference between the quality conformity rates for Γ7 and Γ3 is not too much, but the target index for the worst case has been more than doubled (\({\varUpsilon }_{{\varGamma }_{3}} = 6.84\)). In addition, the quality conformity rate for Γ9 has the best situation (\({\varPsi }_{{\varGamma }_{7}} = 0.94\)), however the KPCs variations take a wider dispersion (\({\varUpsilon }_{{\varGamma }_{9}} = 4.17\)) than the optimum case. Moreover, even though the quality target index for Γ6 equals to 6.93 (the highest value), but it is capable to fall 79% of all KPCs variations in the tolerance interval. Therefore, it is understandable that both quality indicators should be considered simultaneously.

The results show that by decreasing the number of stations, the dimensional accuracy has been improved. For instance, the optimum case has one station less than the worst case. Generally, for any extra station which is added to the assembly line, an additional repositioning error source is introduced; hence, the error budget should be consider. On the other hand, less assembly stations cause longer cycle time due to more operations that must be done in a single station. Moreover, in the assembly line with the same number of stations, it can be concluded that the quality indicators are heavily dependent on both part deviations (non-ideal) and their mechanical stiffness. Consequently, for a given batch of non-ideal parts, ASP and assembly line configuration are two major contributors that must be taken into account in order for quality-driven evaluation or optimization of MSA system.

5 Conclusions

This paper presented a methodology for dimensional quality-driven optimization of ASP considering batch of compliant non-ideal parts. The key results are listed as follows:

  • Modeling of station-to-station repositioning errors and spring-back phenomenon was used for upgrading physics-driven assembly simulation for variation modeling in MSA, in which an analytical tool was developed to evaluate ASP based on the dimensional quality criteria.

  • The case study showed different ASP and line configuration can establish different ways of variation propagation. However, the proposed algorithm is very effective in improving either the combined or individual criteria by proper selection of ASP.

  • Results from the case study also showed that the design requirements could be met within a wide range of quality conformity rate (61–94%) and target index (2.73–6.93). Additionally, for each line configuration, there exists some sequences which can produce the best dimensional accuracy.

  • Although increasing the number of stations can lead to high assembly productivity and less cycle time, however, quality indicators drop dramatically due to increasing station-to-station repositioning errors.

  • In the MSA system with the same ASP, the quality indices are dependent on the non-ideal part (subassembly) stiffness, number of stations, and their configurations in MSA system. Therefore, it is necessary to evaluate the ASP through the proposed methodology.

Future research will be devoted to the integration of this methodology with other criteria, such as DFA metrics (cost, cycle time, etc.) to achieve both quality and non-quality criteria improvement. In addition, the effect of batch part varieties, and MMP statistical parameters (KCCs) on the objective function will be further explored by a sensitivity analysis.