1 Introduction

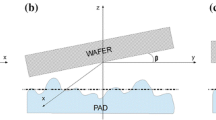
The chemical-mechanical polishing (CMP) mechanism consists of the wafer carrier, the carrier film, the pad and the platen as shown in Fig. 1. The carrier is attached to the wafer back by means of a vacuum. The wafer surface, i.e., the IC part to be planarised, is placed on the platen with one or more layers of pads. Slurry is sprayed continuously through a tube and uniformly scattered on the pad. The wafer is placed between the carrier and pad. The relative motion generated by the carrier and platen brings the wafer in contact with particles in the slurry, which generates multiple actions including the mechanical friction, the chemical reaction and the removal of the chemical solvent to accomplish the highly efficient material removal.

Fig. 1
figure 1

An illustration of CMP

Full size image

The CMP mechanism in Fig. 1 is intrinsically very complicated and not yet understood very clearly, and the polishing mechanism is extremely difficult to analyse. Therefore, it is necessary to simplify the CMP model. Runnels and Renteln [1] assumed no force transmission between the pad and wafer and an elastic pad, and ignored the effect of slurry on establishing an axisymmetric model. They simulated the stress distribution on the wafer surface and rewrote Preston's equation to infer the correlation between the stress and material removal rate. The result indicated that the normal stress had a significant effect on the removal rate. Runnels and Eyman [2] described the action of the chemical solvent by applying fluid dynamics. The model is satisfied simultaneously with the slurry transport model and the physical erosion model, but the latter is much closer to the experimental result. Kaanta and Landis [3] designed a wafer carrier composed of two different materials. The result showed that the upward deflection of the carrier caused by the two different expansion coefficients compensates the polishing effect produced by the irregular abrasive distributions, but it seems difficult to precisely control the deflection of the carrier. Warnock [4] presented a phenomenological erosion model. The pad compressibility was used to predict the polishing rate for different patterns. However, the behaviour of the wafer edge was unpredictable. Sivaram et al. [5] tried to use the deflection of the pad to predict the polishing rate and planarisation. The model became a more complex mathematical problem if predicting the global planarisation because the model only considered the local wafer surface. Wang et al. [6] established a two-dimensional axisymmetric elastic model for CMP by using an I-DEAS package ignoring the effect of slurry and assuming that the shear stress of the wafer surface was uniformly distributed on the surface. The von Mises stress distribution on the wafer surface was used to explore the wafer nonuniformity. The results confirmed that the von Mises stress distribution did have an effect on the surface nonuniformity. Srinivasa-Murthy et al. [7] developed a three-dimensional elastic model by using an ANSYS package to study the stress variation on the wafer surface when sustaining force during the CMP process. The result showed that the von Mises stress peaks at the edge. The profile of the stress distribution is similar to that described by Wang et al. [6], but the site of the peak stress is somewhat different. Lin and Lo [8] established a two-dimensional axisymmetric quasic-static model for CMP and developed a two-dimensional axisymmetric quasic-static finite element model for CMP. They found that the profile of the simulated von Mises stress distributions is similar to that of the experimental removal rate. The axial stress and the strain are the dominant factors of the von Mises stress distributions on the wafer surface and the wafer deformation, respectively. Baker [9] presented a pressure profile model and derived the deformation and the pressure distributions between the wafer and the pad while regarding the pad as an elastic plane. The result was that the pressure variation in the edge region matched the pressure variation in the nonuniform material removal.

2 Theoretical foundations

2.1 A two-dimensional axisymmetric quasi-static model

CMP is used mainly for the material removal of the wafer surface. The material removal rate (MRR) during the CMP process can be considered as a function of the applied normal pressure and the relative velocity. It is usually expressed by Preston's equation [10], i.e.:

$$ {MRR = C_{p} *P*V} $$
(1)

where P is the normal pressure, V is the relative velocity and C p is the Preston's constant.

The normal pressure can be controlled during the polishing process and the relative velocity can be deduced from the relationship between the wafer revolution and the pad revolution in Eq. 1. Fig. 2 illustrates the relative motion between the wafer and the pad. For point A on the wafer, its relative velocity to the pad can be expressed as:

Fig. 2
figure 2

An illustration of the relative motion between the wafer and pad

Full size image
$${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} } = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{w} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{p} }$$
(2)

where \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }}\) is the relative velocity of point A on the wafer to the pad, \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{w} }\) is the absolute velocity of point A on the wafer and \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{p} }\) is the absolute velocity of point A on the pad.

The absolute velocity quantities in Eq. 2 are given by:

$${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{w} = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{w} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{w} }$$
$${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }_{p} = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{p} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} }$$
(3)

where \({\vec{R}_{w} }\) is the distance from point A to the wafer centre, O'; \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{w} }\) is the revolution of the wafer, \({\vec{R}_{p} }\)is the distance from point A to the pad centre and O; \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} }\) is the revolution of the pad.

By incorporating Eq. 3 into Eq. 2, we get:

$${\matrix{ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} } = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{w} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{w} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{p} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} } \cr { = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{w} *{\left( {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{w} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} } \right)} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{{wp}} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} } \cr } }$$
(4)

where \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{{wp}} }\) is the distance between the pad centre and the wafer centre, OO'.

Yu et al. [11] showed that stresses on the wafer surface arise mainly from two sources, namely the pressure exerted by the carrier and the shear stress due to the relative motion between the wafer and the pad. If both the wafer revolution and pad revolution are assumed to be the same, i.e., \({\vec{\omega }_{w} = \vec{\omega }_{P} }\), the relative velocity of point A on the wafer to the pad, \({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over V} }}\) in Eq. 4 can be simplified as \({ - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} }_{{wp}} *{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over \omega } }_{p} }\). It is obviously a constant value, and it results in a constant shear stress uniformly distributed on the wafer surface-pad interface; therefore, the effect of the shear stress can be neglected and a quasi-static model is established. Furthermore, since the force is axisymmetrically distributed and the axisymmetric geometry of the pad can be achieved by assuming that it possesses a huge smooth surface, the CMP model in this paper can be simplified into a two-dimensional axisymmetric quasi-static model, as shown in Fig. 3.

Fig. 3
figure 3

A two-dimensional axisymmetric quasic-static model for CMP

Full size image

2.2 Two-dimensional axisymmetric finite element formulations

While an elastic body is exerted by a body force and a surface force, its total potential energy can be defined as:

$${\Pi = U_{P} - V_{P} }$$
(5)

where Π is the total potential energy, U p is the strain energy and V p is the work done on the body by the applied load.

The strain energy and the work done by the applied load in Eq. 5 can be expressed, respectively, as:

$${U_{P} = {1 \over 2}\mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ \varepsilon \right\}}^{T} {\left\{ \sigma \right\}}} dV}$$
(6)

where {ε} is the strain row vector, {σ} is the stress row vector and V is the volume.

$${V_{P} = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ d \right\}}^{T} {\left\{ {F_{b} } \right\}}} dV + \int\!\!\!\int\limits_S {{\left\{ d \right\}}^{T} {\left\{ {T_{d} } \right\}}} dS}$$
(7)

where d is the displacement, {F b } is the body force, {T d } is the surface tractions and S is the surface of the body on which the surface tractions are prescribed.

The principle of minimum potential energy can be stated as that of all possible displacement states (u and v for a two-dimensional case); it assumes that a body satisfies a compatibility and a given kinematic or displacement boundary condition, and in the meanwhile, the state which satisfies the equilibrium equations makes the potential energy be a minimum value. [12]

If the potential energy, Π is expressed in terms of the displacements u and v, the principle of minimum potential energy gives, at the equilibrium state:

$${\delta \Pi {\left( {u,v} \right)} = \delta U_{p} {\left( {u,v} \right)} - \delta V_{p} {\left( {u,v} \right)} = 0}$$
(8)

A displacement function of an arbitrary point in an element is defined as:

$${{\left\{ d \right\}} = {\left[ N \right]}{\left\{ \delta \right\}}}$$
(9)

where {d} is the displacement function, [N] is the shape function matrix and σ is the nodal displacement vector.

By substituting Hooke's law, \({{\left\{ \sigma \right\}} = {\left[ {D^{e} } \right]}{\left\{ \varepsilon \right\}}}\) and strain-displacement relations \({{\left\{ \varepsilon \right\}} = {\left[ B \right]}{\left\{ \delta \right\}}}\) into Eq. 9, we get:

$${{\left\{ \sigma \right\}} = {\left[ {D^{e} } \right]}{\left[ B \right]}{\left\{ \delta \right\}}}$$
(10)

where \({{\left[ {D^{e} } \right]}}\) is the elastic stress-strain relation matrix and [B] is the strain-displacement matrix.

By incorporating Eq. 10 into Eq. 6 and Eq. 9 into Eq. 7, the strain energy and the work done by the applied load become, respectively:

$${U_{P} {\left( {u,v} \right)} = {1 \over 2}\mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ \delta \right\}}^{T} {\left[ B \right]}^{T} {\left[ {D^{e} } \right]}{\left[ B \right]}{\left\{ \delta \right\}}} dV}$$
(11)
$${V_{P} {\left( {u,v} \right)} = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ \delta \right\}}^{T} {\left[ N \right]}^{T} {\left\{ {F_{b} } \right\}}} dV + \int\!\!\!\int\limits_S {{\left\{ \delta \right\}}^{T} {\left[ N \right]}^{T} {\left\{ {T_{d} } \right\}}} dS}$$
(12)

By substituting Eqs. 11 and 12 into Eq. 5, the total potential energy of an elastic body becomes:

$${\matrix{ {{\Pi {\left( {u,v} \right)} = {1 \over 2}\mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ \delta \right\}}^{T} {\left[ B \right]}^{T} {\left[ {D^{e} } \right]}{\left[ B \right]}{\left\{ \delta \right\}}} dV - \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left\{ \delta \right\}}^{T} {\left[ N \right]}^{T} {\left\{ {F_{b} } \right\}}} dV} \hfill} \cr {{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int\!\!\!\int\limits_S {{\left\{ \delta \right\}}^{T} {\left[ N \right]}^{T} {\left\{ {T_{d} } \right\}}} dS} \hfill} \cr } }$$
(13)

By incorporating Eq. 13 into Eq. 8 and by taking a first variation with respect to the displacement, we get:

$${{\left[ K \right]}_{e} {\left\{ \delta \right\}} = {\left\{ F \right\}}_{e} }$$
(14)

where

$$ {{\left[ {\rm{k}} \right]}_{{\rm{e}}} = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left[ B \right]}^{T} {\left[ {D^{e} } \right]}{\left[ B \right]}} dV} $$
$${{\left\{ F \right\}}_{e} = \mathop{\int\!\!\!\int\!\!\!\int}\limits_{\kern-5.5pt V} {{\left[ N \right]}^{T} {\left\{ {F_{b} } \right\}}} dV + \int\!\!\!\int\limits_S {{\left[ N \right]}^{T} {\left\{ {T_{d} } \right\}}} dS}$$

By expressing this step by step in terms of the whole domain, a governing equation for a two-dimensional finite element model is given by:

$${{\left[ K \right]}{\left\{ \delta \right\}} = {\left\{ F \right\}}}$$
(15)

where [K] is the elastic stiffness matrix, i.e., \({{\left[ K \right]} = {\sum\limits_1^n {{\left[ K \right]}_{e} } }}\) and {F} is the nodal force, i.e., \({{\left\{ F \right\}} = {\sum\limits_1^n {{\left\{ F \right\}}_{e} } }}\).

3 A finite element model

The CMP model in Fig. 3 is divided into a total of 6800 triangular elements and 3661 nodes. The basic assumptions are: (1) The surfaces of the carrier, the carrier film, the wafer and the pad are smooth. (2) The materials, including the carrier, the carrier film, the wafer and the pad are all isotropic. (3) All materials are tightly stacked. In addition, the boundary conditions are: (1) Only a uniformly distributed down pressure is considered, and it is applied on the top surface of the carrier (2) The bottom surface of the pad sustains a fixed support, while the nodes at the bottom are subject to a complete limitation in all directions (3) The left side is a symmetric boundary condition and enjoys a roller support, while the nodes on this side have an r direction limitation and are able to move freely in the z direction.

4 A verification of the model

Von Mises proposed in 1913 that yielding occurs when a combination of stresses, i.e., the von Mises stress, exceeds the yield strength of the material. The von Mises stress applied in a two-dimensional axisymmetric quasi-static CMP model can be simplified as:

$${\bar{\sigma } = {1 \over {{\sqrt 2 }}}{\left[ {{\left( {\sigma _{{rr}} - \sigma _{{zz}} } \right)}^{2} + {\left( {\sigma _{{zz}} - \sigma _{{\theta \theta }} } \right)}^{2} + {\left( {\sigma _{{rr}} - \sigma _{{\theta \theta }} } \right)}^{2} + 6\tau _{{rz}} ^{2} } \right]}^{{{1 \over 2}}} }$$
(16)

where σ̄ is the von Mises stress, and σ rr , σ θθ , σ zz and τ rz are the radial, hoop, axial and shear stresses, respectively.

With the condition that the effect of the slurry was ignored and the initial material properties and geometries for the carrier, the carrier film, the wafer and the pad listed in Table 1 [7] were used, a 0.0689655 MPa down pressure was applied on the top surface of the carrier and the von Mises stress distributions on the wafer surface were simulated by using the developed finite element model. Fig. 4a shows the correlation between the calculated von Mises stress distributions and the distance from the wafer centre. [8] To understand much more about the variations of the lower and flatter parts of the von Mises stress distributions in Fig.4a, the scale in the y axis of this part is magnified and plotted in Fig.4b. Figs. 4a, b show that near the wafer centre, the von Mises stress distribution was almost uniform, and then increased a small amount gradually. However, near the wafer edge, it decreased in a large range. Finally, it increased dramatically and peaked significantly at the edge. This result was similar to that of Srinivasa-Murthy et al. [7].

Table 1. Initial material properties and geometries [7]
Full size table
figure 4

Figure 4 von Mises distribution on the wafer surface is an experimental diagram for material removal rate variations by using two different carrier films. [6] The curves in Fig. 5 are oxide-polishing results obtained with two carrier films, R200T3 and DF200, which have an elastic modulus of 0.69 MPa and 0.407 MPa, respectively. It shows that there is an obvious variation in the material removal rate from the average values at the edges, for the two films. In comparing Figs. 4a,b and Fig. 5, although the simulated conditions in this paper are different from that of Fig. 5, the profile of the von Mises stress distributions in Figs. 4a,b is similar to the removal rate profile, i.e., the characteristics of the curves in Figs. 4a,b and Fig. 5 match qualitatively. It verifies that the proposed CMP model is acceptable.

Fig. 5
figure 5

The experimental material removal rates on the wafer surface [6]

Full size image

5 Results and discussion

5.1 The effect of compressibility for the pad and carrier film on wafer surface stress and nonuniformity

The different elastic modulus for both the pad and carrier film were then used to simulate the von Mises stress distribution and nonuniformity on the wafer surface. Four types of elastic modulus for the pad and carrier film are listed in Table 2. The 'standard' elastic modulus of the pad and carrier film in Table 2 means the initial elastic modulus in Table 1.

Table 2. The elastic modulus of the pad and the carrier film
Full size table

Fig. 6 shows the von Mises stress distribution on the wafer surface for a different compressibility of the pad. From the simulated results, it can be seen that the larger the elastic modulus of the pad, i.e., the smaller the compressibility, the wafer which was in contact with a harder pad would result in a larger von Mises stress.

Fig. 6
figure 6

The von Mises stress distributions on the wafer surface for a different pad compressibility

Full size image

Fig. 7 shows the von Mises stress distribution on the wafer surface for a different compressibility of the carrier film. According to Fig. 7, when the elastic modulus of the carrier film was larger (which meant that the compressibility was smaller) the von Mises stress would also be larger. However, the changes of the elastic modulus of the carrier film did not affect the von Mises stress distribution much, because the carrier film only came into contact with the wafer back, and its elastic modulus was significantly smaller than that of the pad.

Fig. 7
figure 7

The von Mises stress distributions on the wafer surface for a different carrier film compressibility

Full size image

Fig. 8 shows the relationship between the compressibility of both pad and carrier films and nonuniformity. In this study, according to the definition of nonuniformity of the wafer surface by Wang et al. [6], the relationship can be defined as follows:

Fig. 8
figure 8

The relationship between the pad and the carrier film compressibility and nonuniformity

Full size image
$${R = {{\sigma _{{\max }} } \over {\sigma _{c} }}}$$
(17)

where R is the nonuniformity of the wafer surface, σ max is the maximum von Mises stress on the wafer surface and σ c is the von Mises stress on the wafer centre.

In Fig. 8, when a down pressure is applied on the top surface of the wafer carrier, the larger the elastic modulus of the pad, the harder the material of the pad, and this would result in the smaller axial deformation on the wafer surface to decrease the nonuniformity of the wafer surface. Furthermore, since the carrier film only came into contact with the wafer back and its elastic modulus was significantly smaller than that of the pad, its elastic modulus variations did not affect the deformation very much, and the nonuniformity of wafer surface did not change much as well.

5.2 The effect of thickness for the pad and carrier film on wafer surface stress and nonuniformity

The different thicknesses of both the pad and the carrier film were then used to simulate the von Mises stress distribution and nonuniformity on the wafer surface. 4 kinds of thicknesses for the pad and the carrier films are listed in Table 3. The 'standard' thickness of the pad and carrier film in Table 3 means the initial thickness in Table 1.

Table 3. Thicknesses of the pad and the carrier film
Full size table

Fig. 9 shows the von Mises stress distributions on the wafer surface for different pad thicknesses. Since the elastic modulus of the pad was far less than that of the wafer, its elastic modulus effect on the wafer was more obvious when its thickness was increasing. It made the von Mises stress on the wafer surface reduce, but it made the axial deformation increase to result in a gradual increasing of the nonuniformity of the wafer surface, as shown in Fig. 10.

Fig. 9
figure 9

The von Mises stress distributions on the wafer surface for a different pad thickness

Full size image
Fig. 10
figure 10

The von Mises stress distributions on the wafer surface for a different carrier film thickness

Full size image

Fig. 11 shows the von Mises stress distributions on the wafer surface for different carrier film thicknesses. Although the elastic modulus of the carrier film was also far less than that of the wafer, its thickness change did not affect either the von Mises stress distribution or the deformation on the wafer surface very much, because the carrier film only came into contact with the wafer back, and its thickness and the thickness change were smaller than those of the pad. As a result, the nonuniformity of the wafer surface seldom changed with different thicknesses for the wafer film as shown in Fig. 11.

Fig. 11
figure 11

The relationship between the pad and the carrier film thickness and nonuniformity

Full size image

5.3 The effect of carrier loads on the wafer surface stress and nonuniformity

The different carrier loads were then used to simulate the von Mises stress distribution and nonuniformity on wafer surface. 5 kinds of carrier loads are listed in Table 4. The 'standard' carrier load in Table 4 indicates the initial pressure exerted on the top surface of the wafer, discussed in the previous section.

Table 4. The carrier loads
Full size table

Fig. 12 shows the von Mises stress distributions on the wafer surface for different carrier loads. As seen in Fig. 12, the von Mises stress on the wafer surface became larger when the load of the carrier was increasing. Meanwhile, the axial deformation of the wafer surface became larger to result in a gradual increasing of nonuniformity on the wafer surface as shown in Fig. 13. In other words, the magnitude of the load is proportional to the load of the von Mises stress and the nonuniformity on wafer surface.

Fig. 12
figure 12

The von Mises stress distributions on the wafer surface for different carrier loads

Full size image
Fig. 13
figure 13

The relationship between the carrier loads and nonuniformity

Full size image

In order to investigate more about the effect of carrier loads, the von Mises stress on the wafer centre, σ c and the maximum von Mises stress, σ max, for each curve in Fig. 12 and the nonuniformity, R, in Fig. 13 were extracted and are listed in Table 5. However, since the units of σ c and σ max are different from that of R, there is no way to compare them. Therefore, we defined four dimensionless quantities, that is, the load ratio, the σ c ratio, the σ max ratio and the R ratio as the the 'standard' load condition exerted on the top surface of the carrier as a basis. These four ratios mean that the values of the load σ c, σ max and R are divided by those under the the condition of 'standard' load. All of them are listed in Table 6 and plotted in Fig. 14. Three dimensionless curves including the σ c ratio, the σ max ratio and the R ratio under the condition of different load ratios are depicted in Fig. 14. Finally, we used the least square method [13] to search for a regressive linear equation for each curve which goes through one of the three simulated ratios, namely, the σ c ratio, the σ max ratio or R ratio, and found that the square summation of distance from each simulated ratio to its average value is minimum. The slopes can be acquired from all of these ratios, and they can be used to determine and compare how much the load affects the von Mises stress and nonuniformity.

Table 5. σ c , σmax and R for different carrier loads
Full size table
Table 6. Dimensionless quantities for the load ratio, the σ c ratio, the σmax ratio and the R ratio
Full size table
Fig. 14
figure 14

The relationships for the load ratio-stress ratio and the load ratio-nonuniformity ratio

Full size image

The mathematical form for a regressive linear equation can be expressed as:

$${y = a*x + b}$$
(18)

where x denotes the load ratio, y is the σ c ratio, σ max ratio or R ratio and a and b are the parameters.

In Eq. 18, a and b can be derived as:

$${a = {{{\sum {{\left( {x - \bar{x}} \right)}{\left( {y - \bar{y}} \right)}} }} \over {{\sum {{\left( {x - \bar{x}} \right)}} }^{2} }} = {{n{\sum {{\left( {xy} \right)} - {\left( {{\sum x }} \right)}{\left( {{\sum y }} \right)}} }} \over {n{\sum {x^{2} - {\left( {{\sum x }} \right)}^{2} } }}}}$$
$${b = \bar{y} - a\bar{x}}$$
(19)

where x̄ is the average load ratio and ȳ is the average σ c ratio, average σ max ratio or average R ratio.

By incorporating the data in Table 6 into Eq. 19, the quantities of a and b can be acquired. Then, by incorporating these into Eq. 18, a specified linear regressive equation for each curve and its slope can be obtained and listed in Table 7. Fig. 14 and Table 7 showed that the two curves of σ c ratio and σ max ratio approach each other and their slopes from the linear regressive equations are steeper and greater than that of the R ratio curve. The result indicated that the effect of the carrier load on the von Mises stress was more significant and obvious than that of the effect of the carrier load on the nonuniformity.

Table 7. Regressive equations for the σ c ratio, the σmax ratio and the R ratio and their slopes under the different load ratios by the least square method
Full size table

6 Conclusions

From the simulation and analysis of the CMP model developed in this paper for the different elastic modulus of the the pad and carrier film, the different thicknesses of the pad and carrier film and the different carrier loads, the following conclusions can be drawn:

(1).:

A two-dimensional axisymmetric quasi-static finite element model for CMP can be developed.

(2).:

The calculated von Mises stress distributions near the wafer centre are almost uniform, and then increase gradually with a small amount. However, the stress distributions decreased by a great deal near the wafer edge. Finally, the stress distributions increased dramatically and peaked significantly at the edge.

(3).:

The larger the elastic modulus of the pad, i.e., the smaller the compressibility, the larger the von Mises stress and the smaller the axial deformation on the wafer surface to reduce the nonuniformity of the wafer surface. Because the carrier film only came into contact with the wafer back and its elastic modulus was significantly smaller than that of the pad, its elastic modulus changes did not have much of an affect on either the von Mises stress distribution or the nonuniformity of the wafer surface.

(4).:

When the thickness of the pad increased gradually, the von Mises stress on wafer surface was reduced, but the deformation increased to make the nonuniformity of the wafer surface larger. However, the thickness changes of the wafer film did not affect the von Mises stress distribution very much and seldom changed the nonuniformity of the wafer surface because it only came into contact with the wafer back and its thickness and thickness change were smaller than those of the pad.

(5).:

The magnitude of the carrier load is proportional to the magnitude of the von Mises stress and the nonuniformity on the wafer surface, but the effect of the carrier load on the von Mises stress was more significant and obvious than that on the nonuniformity, when using the least square method with a dimensionless form.